Diffusion Patterns in Convergence among High-Technology Industries: A Co-Occurrence-Based Analysis of Newspaper Article Data
Abstract
:1. Introduction
2. Literature Review
3. Methodology
3.1. Data Collection and Processing
3.2. Degree of Industry Convergence
3.3. Estimation of a Diffusion Model of Industry Convergence
4. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ASCII | American Standard Code for Information Interchange |
| DIC | Degree of Industry Convergence |
| IPC | International Patent Classification |
| M&A | Merger and Acquisition |
| NE | Named Entity |
| NLP | Natural Language Processing |
| OECD | Organization for Economic Cooperation and Development |
| OLS | Ordinary Least Squares |
| PMI | Pointwise Mutual Information |
| RegEx | Regular Expression |
| R&D | Research and Development |
| SIC | Standard Industrial Classification |
Appendix A
| SIC Code Pair | Convergent-Industry Pair |
|---|---|
| 282–281 | Plastics materials and synthetic resins, synthetic—Industrial inorganic chemicals |
| 282–282 | Plastics materials and synthetic resins, synthetic—Plastics materials and synthetic resins, synthetic |
| 283–283 | Drugs—Drugs |
| 284–282 | Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations—Plastics materials and synthetic resins, synthetic |
| 285–283 | Paints, varnishes, lacquers, enamels, and allied—Drugs |
| 285–284 | Paints, varnishes, lacquers, enamels, and allied—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations |
| 285–285 | Paints, varnishes, lacquers, enamels, and allied—Paints, varnishes, lacquers, enamels, and allied |
| 286–282 | Industrial organic chemicals—Plastics materials and synthetic resins, synthetic |
| 286–283 | Industrial organic chemicals—Drugs |
| 287–281 | Agricultural chemicals—Industrial inorganic chemicals |
| 287–284 | Agricultural chemicals—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations |
| 289–281 | Miscellaneous chemical products—Industrial inorganic chemicals |
| 289–285 | Miscellaneous chemical products—Paints, varnishes, lacquers, enamels, and allied |
| 289–286 | Miscellaneous chemical products—Industrial organic chemicals |
| 289–287 | Miscellaneous chemical products—Agricultural chemicals |
| 356–281 | General industrial machinery and equipment—Industrial inorganic chemicals |
| 356–282 | General industrial machinery and equipment—Plastics materials and synthetic resins, synthetic |
| 356–284 | General industrial machinery and equipment—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations |
| 356–287 | General industrial machinery and equipment—Agricultural chemicals |
| 357–281 | Computer and office equipment—Industrial inorganic chemicals |
| 357–285 | Computer and office equipment—Paints, varnishes, lacquers, enamels, and allied |
| 357–286 | Computer and office equipment—Industrial organic chemicals |
| 357–287 | Computer and office equipment—Agricultural chemicals |
| 371–281 | Motor vehicles and motor vehicle equipment—Industrial inorganic chemicals |
| 371–285 | Motor vehicles and motor vehicle equipment—Paints, varnishes, lacquers, enamels, and allied |
| 372–281 | Aircraft and parts—Industrial inorganic chemicals |
| 372–285 | Aircraft and parts—Paints, varnishes, lacquers, enamels, and allied |
| 372–356 | Aircraft and parts—General industrial machinery and equipment |
| 382–284 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations |
| 382–285 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—Paints, varnishes, lacquers, enamels, and allied |
| 382–287 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—Agricultural chemicals |
| 382–356 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—General industrial machinery and equipment |
| 386–281 | Photographic equipment and supplies—Industrial inorganic chemicals |
| 386–284 | Photographic equipment and supplies—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations |
| 386–287 | Photographic equipment and supplies—Agricultural chemicals |
| 386–356 | Photographic equipment and supplies—General industrial machinery and equipment |
| 873–281 | Research, development, and testing services—Industrial inorganic chemicals |
| 873–282 | Research, development, and testing services—Plastics materials and synthetic resins, synthetic |
| 873–285 | Research, development, and testing services—Paints, varnishes, lacquers, enamels, and allied |
| 873–289 | Research, development, and testing services—Miscellaneous chemical products |
| 873–356 | Research, development, and testing services—General industrial machinery and equipment |
| 873–372 | Research, development, and testing services—Aircraft and parts |
| 873–382 | Research, development, and testing services—Laboratory apparatus and analytical, optical, measuring, and controlling instruments |
| 873–386 | Research, development, and testing services—Photographic equipment and supplies |
| 873–873 | Research, development, and testing services—Research, development, and testing services |
References
- Curran, C.-S.; Leker, J. Patent indicators for monitoring convergence-examples from NFF and ICT. Technol. Forecast. Soc. Chang. 2011, 78, 256–273. [Google Scholar] [CrossRef]
- Wang, C.H.; Lu, Y.H.; Huang, C.W.; Lee, J.Y. R&D, productivity, and market value: An empirical study from high-technology firms. Omega 2013, 41, 143–155. [Google Scholar]
- Hills, S.B.; Sarin, S. From market driven to market driving: An alternate paradigm for marketing in high technology industries. J. Mark. Theory Pract. 2003, 11, 13–24. [Google Scholar] [CrossRef]
- Benner, M.J.; Ranganathan, R. Divergent reactions to convergent strategies: Investor beliefs and analyst reactions during technological change. Organ. Sci. 2013, 24, 378–394. [Google Scholar] [CrossRef]
- Choi, D.; Valikangas, L. Patterns of strategy innovation. Eur. Manag. J. 2001, 19, 424–429. [Google Scholar] [CrossRef]
- Curran, C.-S. The Anticipation of Converging Industries; Springer: London, UK, 2013. [Google Scholar]
- Curran, C.-S.; Bröring, S.; Leker, J. Anticipating converging industries using publicly available data. Technol. Forecast. Soc. Chang. 2010, 77, 385–395. [Google Scholar] [CrossRef]
- Hacklin, F. Management of Convergence in Innovation: Strategies and Capabilities for Value Creation beyond Blurring Industry Boundaries; Springer: Berlin, Germany, 2008. [Google Scholar]
- Hacklin, F.; Marxt, C.; Fahrni, F. Coevolutionary cycles of convergence: An extrapolation from the ICT industry. Technol. Forecast. Soc. Chang. 2009, 76, 723–736. [Google Scholar] [CrossRef]
- Kim, N.; Lee, H.; Kim, W.; Lee, H.; Suh, J.H. Dynamic patterns of industry convergence: Evidence from a large amount of unstructured data. Res. Policy 2015, 44, 1734–1748. [Google Scholar] [CrossRef]
- Lee, G.K. The significance of network resources in the race to enter emerging product markets: The convergence of telephony communications and computer networking, 1989–2001. Strateg. Manag. J. 2007, 28, 17–37. [Google Scholar] [CrossRef]
- Srinivasan, R.; Haunschild, P.; Grewal, R. Vicarious learning in new product introductions in the early years of a converging market. Manag. Sci. 2007, 53, 16–28. [Google Scholar] [CrossRef]
- Bröring, S.; Leker, J. Industry convergence and its implications for the front end of innovation: A problem of absorptive capacity. Creat. Innov. Manag. 2007, 16, 165–175. [Google Scholar] [CrossRef]
- Preschitschek, N.; Niemann, H.; Leker, J.; Moehrle, M.G. Anticipating industry convergence: Semantic analyses vs. IPC co-classification analyses of patents. Foresight 2013, 15, 446–464. [Google Scholar] [CrossRef]
- Weenen, T.C.; Ramezanpour, B.; Pronker, E.S.; Commandeur, H.; Claassen, E. Food-pharma convergence in medical nutrition—Best of both worlds? PLoS ONE 2013, 8, e82609. [Google Scholar] [CrossRef] [PubMed]
- Hacklin, F.; Wallin, M.W. Convergence and interdisciplinarity in innovation management: A review, critique, and future directions. Serv. Ind. J. 2013, 33, 774–788. [Google Scholar] [CrossRef]
- Kim, W.; Kim, M. Reference quality-based competitive market structure for innovation driven markets. Int. J. Res. Market. 2015, 32, 284–296. [Google Scholar] [CrossRef]
- Lee, S.; Kim, W. Identifying the structure of knowledge networks in the U.S. mobile ecosystems: Patent citation analysis. Technol. Anal. Strateg. Manag. 2015, 28, 411–434. [Google Scholar] [CrossRef]
- Roco, M.C.; Bainbridge, W.S. Converging Technologies for Improving Human Performance: Nanotechnology, Biotechnology, Information Technology and Cognitive Science; Kluwer Academic Publishers: Norwell, MA, USA, 2003. [Google Scholar]
- Nordmann, A. Converging Technologies–Shaping the Future of European Societies; European Commission: Brussels, Belgium, 2004. [Google Scholar]
- Kim, W. Current transition in management of technology (MOT) education: The case of Korea. Technol. Forecast. Soc. Chang. 2015, 100, 5–20. [Google Scholar] [CrossRef]
- Lei, D.T. Industry evolution and competence development: The imperatives of technological convergence. Int. J. Technol. Manag. 2000, 19, 699–738. [Google Scholar] [CrossRef]
- Pennings, J.M.; Puranam, P. Market Convergence & Firm Strategy: New Directions for Theory and Research; ECIS Conference, The Future of Innovation Studies: Eindhoven, The Netherlands, 2001. [Google Scholar]
- Hamel, G. Strategy as revolution. Harv. Bus. Rev. 1996, 74, 69–82. [Google Scholar] [PubMed]
- Jaworski, B.; Kohli, A.K.; Sahay, A. Market-driven versus driving markets. J. Acad. Mark. Sci. 2000, 28, 45–54. [Google Scholar] [CrossRef]
- Cho, Y.; Kim, E.; Kim, W. Strategy transformation under technological convergence: Evidence from the printed electronics industry. Int. J. Technol. Manag. 2015, 67, 106–131. [Google Scholar] [CrossRef]
- Fai, F.; Von Tunzelmann, N. Industry-specific competencies and converging technological systems: Evidence from patents. Struct. Chang. Econ. Dyn. 2001, 12, 141–170. [Google Scholar] [CrossRef]
- Andergassen, R.; Nardini, F.; Ricottilli, M. Innovation waves, self-organized criticality and technological convergence. J. Econ. Behav. Organ. 2006, 61, 710–728. [Google Scholar] [CrossRef]
- D’Aveni, R.A.; Dagnino, G.B.; Smith, K.G. The age of temporary advantage. Strateg. Manag. J. 2010, 31, 1371–1385. [Google Scholar] [CrossRef]
- Hacklin, F.; Marxt, C.; Fahrni, F. An evolutionary perspective on convergence: Inducing a stage model of inter-industry innovation. Int. J. Technol. Manag. 2010, 49, 220–249. [Google Scholar] [CrossRef]
- Kim, E.; Cho, Y.; Kim, W. Dynamic patterns of technological convergence in printed electronics technologies: patent citation network. Scientometrics 2014, 98, 975–998. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, H. Innovation search of new ventures in a technology cluster: The role of ties with service intermediaries. Strateg. Manag. J. 2010, 31, 88–109. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.-D. Measuring the role of technology-push and demand-pull in the dynamic development of the semiconductor industry: The case of the global DRAM market. J. Appl. Econ. 2009, 12, 83–108. [Google Scholar] [CrossRef]
- Christensen, C. The Innovator’s Dilemma: When New Technologies Cause Great Firms to Fail; Harvard Business Press: Boston, MA, USA, 1997. [Google Scholar]
- Kwak, K.; Kim, W. Effect of service integration strategy on industrial firm performance. J. Serv. Manag. 2016, 27, 391–430. [Google Scholar] [CrossRef]
- Bierly, P.; Chakrabarti, A.K. Managing through industry fusion. In The Dynamics Innovation: Strategic and Managerial Implications; Brockhoff, K., Chakrabarti, A.K., Hauschildt, J., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1999; pp. 7–26. [Google Scholar]
- Mowery, D.C.; Oxley, J.E.; Silverman, B.S. Strategic alliances and interfirm knowledge transfer. Strateg. Manag. J. 1996, 17, 77–91. [Google Scholar] [CrossRef]
- Yun, J.J.; Won, D.; Park, K. Dynamics from open innovation to evolutionary change. J. Open Innov. Technol. Market Complex. 2016, 2, 1–22. [Google Scholar] [CrossRef]
- Kim, S.-J.; Kim, E.-M.; Suh, Y.; Zheng, Z. The effect of service innovation on R&D activities and government support systems: The moderating role of government support systems in Korea. J. Open Innov. Technol. Market Complex. 2016, 2, 1–13. [Google Scholar]
- Kodama, F.; Shibata, T. Demand articulation in the open-innovation paradigm. J. Open Innov. Technol. Market Complex. 2015, 1, 1–21. [Google Scholar] [CrossRef]
- Duysters, G.; Hagedoorn, J. Core competences and company performance in the world-wide computer industry. J. High Technol. Manag. Res. 2000, 11, 75–91. [Google Scholar] [CrossRef]
- Nelson, R.R.; Winter, S. An Evolutionary Theory of Economic Change; Harvard University Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Nill, J.; Kemp, R. Evolutionary approaches for sustainable innovation policies: From niche to paradigm? Res. Policy 2009, 38, 668–680. [Google Scholar] [CrossRef]
- Karvonen, M.; Kässi, T. Patent citations as a tool for analysing the early stages of convergence. Technol. Forecast. Soc. Chang. 2013, 80, 1094–1107. [Google Scholar] [CrossRef]
- Hsu, S.T.; Prescott, J.E. The alliance experience transfer effect: The case of industry convergence in the telecommunications equipment industry. Br. J. Manag. 2016. [Google Scholar] [CrossRef]
- Manning, C.D.; Surdeanu, M.; Bauer, J.; Finkel, J.R.; Bethard, S.; McClosky, D. The Stanford CoreNLP Natural Language Processing Toolkit. In Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics: System Demonstrations, Baltimore, MD, USA, 23–24 June 2014.
- Finkel, J.R.; Grenager, T.; Manning, C. Incorporating Non-Local Information into Information Extraction Systems by Gibbs Sampling. In Proceedings of the 43rd Annual Meeting on Association for Computational Linguistics, Ann Arbor, MI, USA, 25–30 June 2005.
- Hecker, D. High-technology employment: A broader view. Mon. Labor Rev. 1999, 122, 18–28. [Google Scholar]
- Engelberg, J.; Ozoguz, A.; Wang, S. Know thy neighbor: Industry clusters, information spillovers and market efficiency. Soc. Sci. Res. Netw. 2013. [Google Scholar] [CrossRef]
- Organisation for Economic Co-Operation and Development. ISIC REV. 3 Technology Intensity Definition. 2011. Available online: www.oecd.org/dataoecd/43/41/48350231.pdf (accessed on 12 October 2016).
- Bouma, G. Normalized (pointwise) mutual information in collocation extraction. In Proceedings of the International Conference of the German Society for Computational Linguistics and Language Technology, Potsdam, Germany, 30 September–2 October 2009.
- Church, K.W.; Hanks, P. Word association norms, mutual information, and lexicography. Comput. Linguist. 1990, 16, 22–29. [Google Scholar]
- Bass, F.M. A new product growth for model consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Mahajan, V.; Muller, E.; Bass, F.M. New product diffusion models in marketing: A review and directions for research. J. Mark. 1990, 54, 1–26. [Google Scholar] [CrossRef]
- Choi, J.Y.; Jeong, S.; Kim, K. A study on diffusion pattern of technology convergence: Patent analysis for Korea. Sustainability 2015, 7, 11546–11569. [Google Scholar] [CrossRef]
- Leeflang, P.; Wittink, D.R.; Wedel, M.; Naert, P.A. Building Models for Marketing Decisions; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Mahajan, V.; Peterson, R.A. Models for Innovation Diffusion; Sage: Beverly Hills, CA, USA, 1985. [Google Scholar]
- Oh, C.; Cho, Y.; Kim, W. The effect of firm’s strategic innovation decisions on its market performance. Technol. Anal. Strateg. Manag. 2014, 27, 39–53. [Google Scholar] [CrossRef]
| Information Source | Methodology | Literature |
|---|---|---|
| Patents | IPC co-classification analysis | Curran and Leker [1] |
| Preschitschek et al. [14] | ||
| Patent citation analysis | Karvonen and Kässi [44] | |
| Industry-technology concordance analysis | Curran et al. [7] | |
| Fai and Von Tunzelmann [27] | ||
| Pennings and Puranam [23] | ||
| Product-market entry | Interindustry product-market entry analysis | Hsu and Prescott [45] |
| Newspaper articles | Co-occurrence-based analysis | Kim et al. [10] |
| SIC Code | Industry |
|---|---|
| 281 | Industrial inorganic chemicals |
| 282 | Plastics materials and synthetic resins, synthetic |
| 283 | Drugs |
| 284 | Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations |
| 285 | Paints, varnishes, lacquers, enamels, and allied |
| 286 | Industrial organic chemicals |
| 287 | Agricultural chemicals |
| 289 | Miscellaneous chemical products |
| 351 | Engines and turbines |
| 356 | General industrial machinery and equipment |
| 357 | Computer and office equipment |
| 361 | Electric transmission and distribution equipment |
| 366 | Communications equipment |
| 371 | Motor vehicles and motor vehicle equipment |
| 372 | Aircraft and parts |
| 382 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments |
| 384 | Surgical, medical, and dental instruments and supplies |
| 386 | Photographic equipment and supplies |
| 737 | Computer programming, data processing, and other computer related services |
| 871 | Engineering, architectural, and surveying services |
| 873 | Research, development, and testing services |
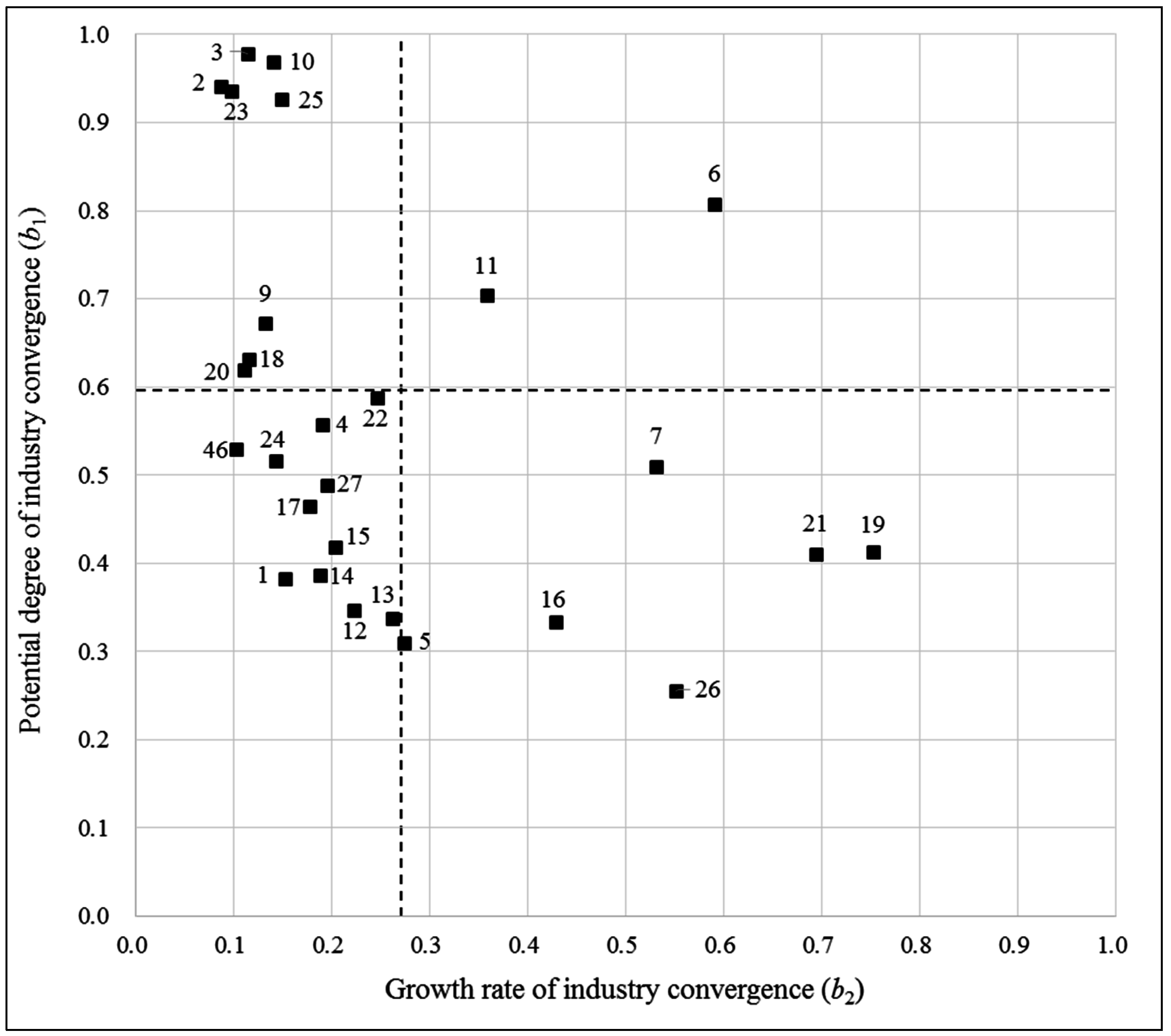
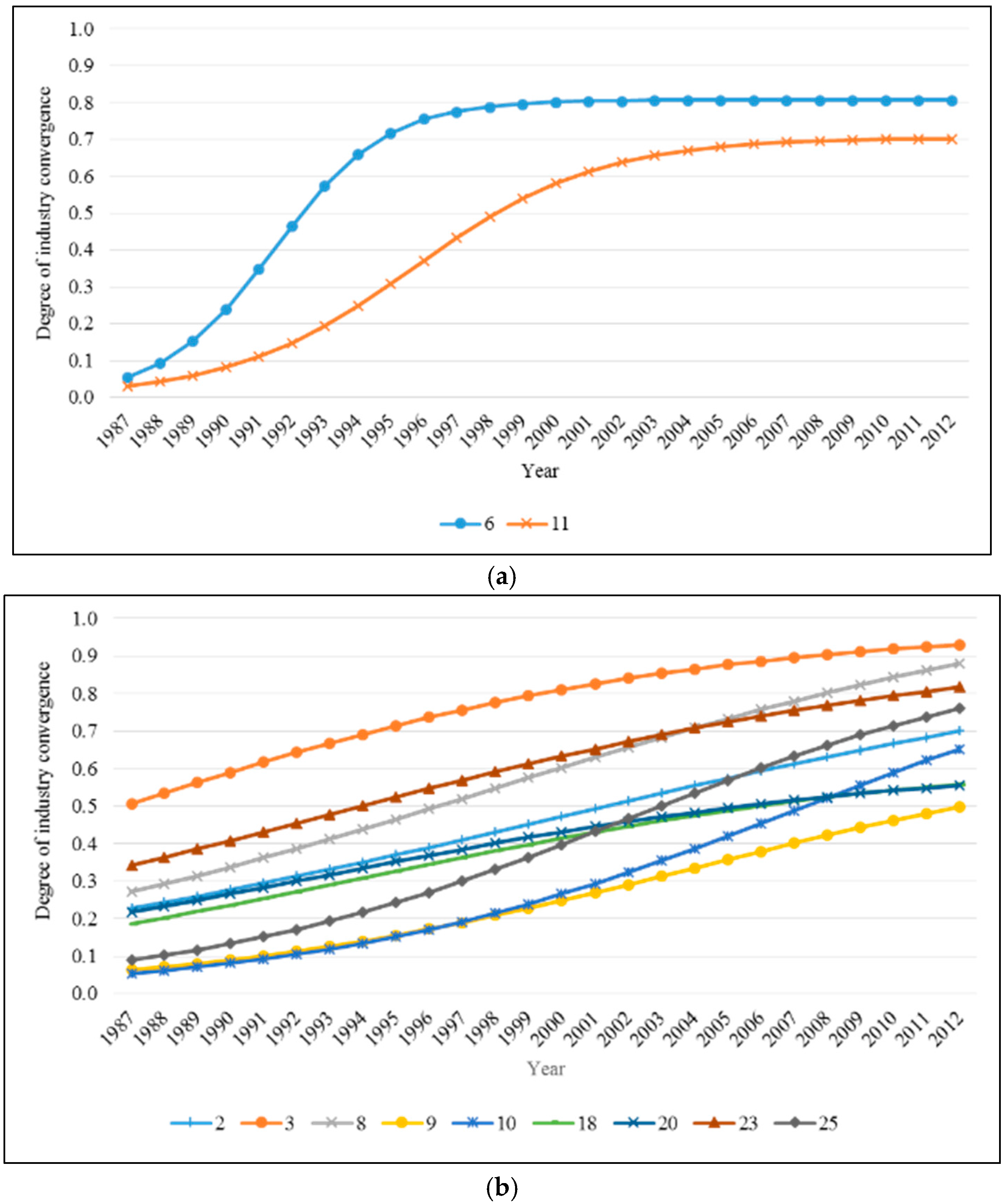
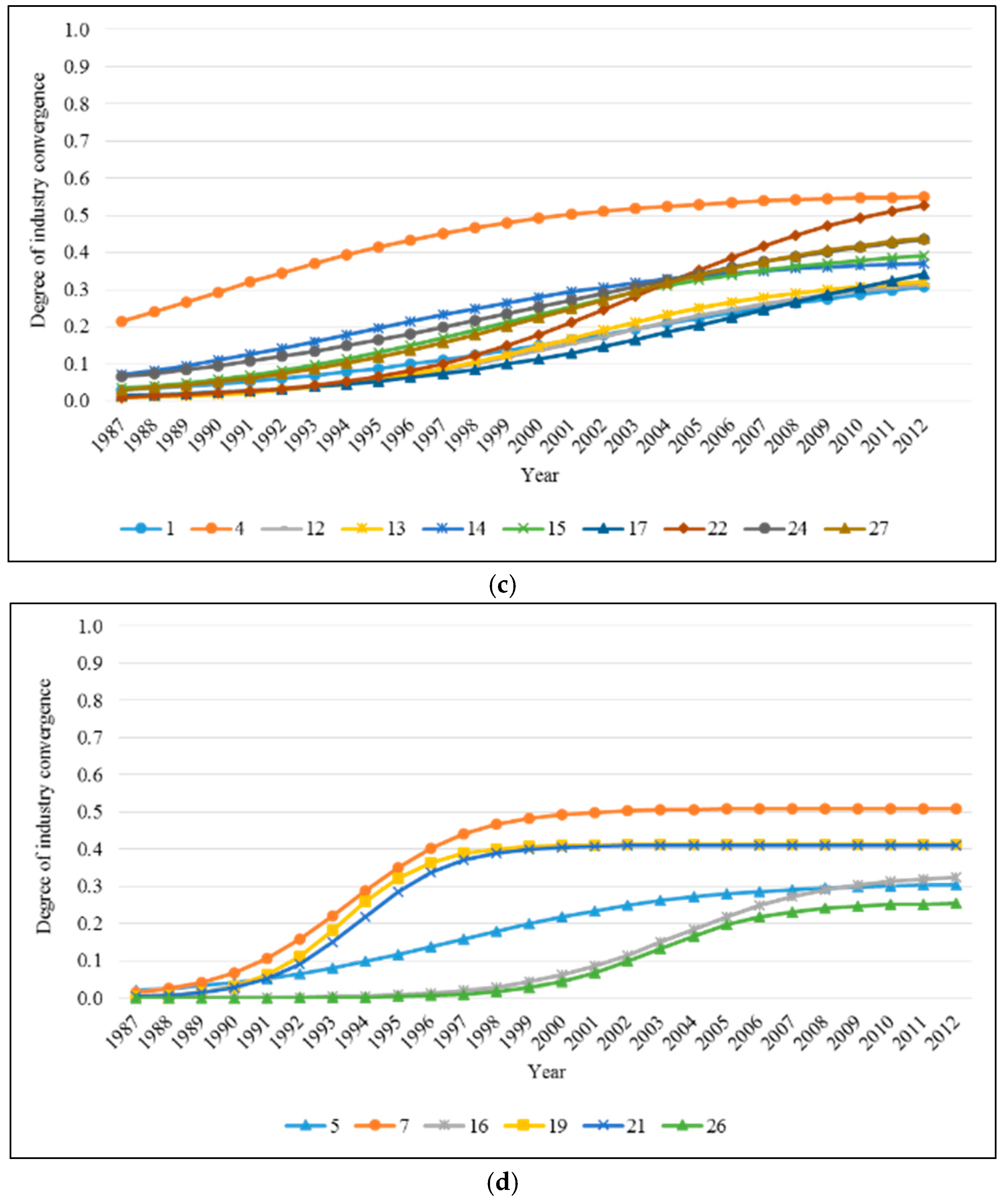
| No. | SIC Code Pair | Convergent-Industry Pair | Initial DIC (b0) | Potential DIC (b1) | Growth Rate (b2) |
|---|---|---|---|---|---|
| 1 | 284–282 | Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations—Plastics materials and synthetic resins, synthetic | 0.031 | 0.382 ** | 0.154 ** |
| 2 | 285–284 | Paints, varnishes, lacquers, enamels, and allied—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations | 0.228 *** | 0.941 ** | 0.088 ** |
| 3 | 285–285 | Paints, varnishes, lacquers, enamels, and allied—Paints, varnishes, lacquers, enamels, and allied | 0.506 *** | 0.978 *** | 0.115 * |
| 4 | 286–282 | Industrial organic chemicals—Plastics materials and synthetic resins, synthetic | 0.214 *** | 0.556 *** | 0.192 ** |
| 5 | 286–283 | Industrial organic chemicals—Drugs | 0.019 | 0.309 *** | 0.275 *** |
| 6 | 287–281 | Agricultural chemicals—Industrial inorganic chemicals | 0.053 * | 0.807 *** | 0.591 *** |
| 7 | 287–284 | Agricultural chemicals—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations | 0.015 | 0.509 *** | 0.532 *** |
| 8 | 356–281 | General industrial machinery and equipment—Industrial inorganic chemicals | 0.271 *** | 1.095 *** | 0.101 *** |
| 9 | 356–282 | General industrial machinery and equipment—Plastics materials and synthetic resins, synthetic | 0.064 * | 0.671 * | 0.133 * |
| 10 | 356–284 | General industrial machinery and equipment—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations | 0.055 * | 0.968 * | 0.142 ** |
| 11 | 356–287 | General industrial machinery and equipment—Agricultural chemicals | 0.030 | 0.703 *** | 0.359 *** |
| 12 | 357–285 | Computer and office equipment—Paints, varnishes, lacquers, enamels, and allied | 0.012 | 0.346 *** | 0.224 ** |
| 13 | 357–286 | Computer and office equipment—Industrial organic chemicals | 0.008 | 0.337 *** | 0.263 *** |
| 14 | 372–281 | Aircraft and parts—Industrial inorganic chemicals | 0.071 ** | 0.386 *** | 0.189 *** |
| 15 | 372–285 | Aircraft and parts—Paints, varnishes, lacquers, enamels, and allied | 0.034 | 0.418 *** | 0.205 *** |
| 16 | 372–356 | Aircraft and parts—General industrial machinery and equipment | 0.000 | 0.332 *** | 0.430 ** |
| 17 | 382–284 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations | 0.014 | 0.464 ** | 0.179 *** |
| 18 | 382–285 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—Paints, varnishes, lacquers, enamels, and allied | 0.187 *** | 0.630 *** | 0.117 ** |
| 19 | 382–287 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—Agricultural chemicals | 0.004 | 0.412 *** | 0.753 * |
| 20 | 386–281 | Photographic equipment and supplies—Industrial inorganic chemicals | 0.217 *** | 0.618 *** | 0.112 ** |
| 21 | 386–287 | Photographic equipment and supplies—Agricultural chemicals | 0.004 | 0.410 *** | 0.695 ** |
| 22 | 386–356 | Photographic equipment and supplies—General industrial machinery and equipment | 0.010 | 0.587 *** | 0.247 *** |
| 23 | 873–281 | Research, development, and testing services—Industrial inorganic chemicals | 0.341 *** | 0.935 *** | 0.099 *** |
| 24 | 873–282 | Research, development, and testing services—Plastics materials and synthetic resins, synthetic | 0.066 ** | 0.516 *** | 0.144 ** |
| 25 | 873–356 | Research, development, and testing services—General industrial machinery and equipment | 0.089 * | 0.926 *** | 0.150 ** |
| 26 | 873–372 | Research, development, and testing services—Aircraft and parts | 0.000 | 0.255 *** | 0.552 * |
| 27 | 873–386 | Research, development, and testing services—Photographic equipment and supplies | 0.031 | 0.488 *** | 0.196 ** |
| 28 | 282–281 | Plastics materials and synthetic resins, synthetic—Industrial inorganic chemicals | 0.279 *** | 0.579 *** | 0.115 |
| 29 | 285–283 | Paints, varnishes, lacquers, enamels, and allied—Drugs | 0.118 *** | 0.562 | 0.060 |
| 30 | 289–281 | Miscellaneous chemical products—Industrial inorganic chemicals | 0.336 *** | 0.570 *** | 0.126 |
| 31 | 289–285 | Miscellaneous chemical products—Paints, varnishes, lacquers, enamels, and allied | 0.289 *** | 0.526 *** | 0.160 |
| 32 | 289–286 | Miscellaneous chemical products—Industrial organic chemicals | 0.290 *** | 0.551 *** | 0.124 |
| 33 | 289–287 | Miscellaneous chemical products—Agricultural chemicals | 0.000 | 0.421 *** | 1.431 |
| 34 | 357–281 | Computer and office equipment—Industrial inorganic chemicals | 0.061 * | 1.343 | 0.079 |
| 35 | 357–287 | Computer and office equipment—Agricultural chemicals | 0.002 | 0.170 *** | 0.444 |
| 36 | 371–281 | Motor vehicles and motor vehicle equipment—Industrial inorganic chemicals | 0.000 | 0.151 *** | 1.287 |
| 37 | 371–285 | Motor vehicles and motor vehicle equipment—Paints, varnishes, lacquers, enamels, and allied | 0.022 | 0.197 * | 0.152 |
| 38 | 382–356 | Laboratory apparatus and analytical, optical, measuring, and controlling instruments—General industrial machinery and equipment | 0.081 ** | 1.251 | 0.092 * |
| 39 | 386–284 | Photographic equipment and supplies—Soap, detergents, and cleaning preparations; perfumes, cosmetics, and other toilet preparations | 0.036 * | 0.687 | 0.113 * |
| 40 | 873–285 | Research, development, and testing services—Paints, varnishes, lacquers, enamels, and allied | 0.323 *** | 1.132 * | 0.078 |
| 41 | 873–289 | Research, development, and testing services—Miscellaneous chemical products | 0.182 *** | 1.488 | 0.038 |
| 42 | 873–382 | Research, development, and testing services—Laboratory apparatus and analytical, optical, measuring, and controlling instruments | 0.089 ** | 0.820 | 0.093 |
| 43 | 282–282 | Plastics materials and synthetic resins, synthetic—Plastics materials and synthetic resins, synthetic | 0.106 ** | 0.306 *** | 0.132 |
| 44 | 283–283 | Drugs—Drugs | 0.335 *** | 0.667 ** | 0.069 |
| 45 | 873–873 | Research, development, and testing services—Research, development, and testing services | 0.212 *** | 1.429 | 0.072 |
| 46 | Total | 0.112 *** | 0.529 *** | 0.103 *** |
| Variable | Coeff. | 95% Confidence Interval |
|---|---|---|
| Growth rate | −0.538 ** (0.230) | [−1.012, −0.064] |
| Constant | 0.736 *** (0.076) | [0.580, 0.892] |
| R2 | 0.179 | |
| F | 5.46 ** |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Kim, N.; Kwak, K.; Kim, W.; Soh, H.; Park, K. Diffusion Patterns in Convergence among High-Technology Industries: A Co-Occurrence-Based Analysis of Newspaper Article Data. Sustainability 2016, 8, 1029. https://doi.org/10.3390/su8101029
Lee H, Kim N, Kwak K, Kim W, Soh H, Park K. Diffusion Patterns in Convergence among High-Technology Industries: A Co-Occurrence-Based Analysis of Newspaper Article Data. Sustainability. 2016; 8(10):1029. https://doi.org/10.3390/su8101029
Chicago/Turabian StyleLee, Hyeokseong, Namil Kim, Kiho Kwak, Wonjoon Kim, Hyungjoon Soh, and Kyungbae Park. 2016. "Diffusion Patterns in Convergence among High-Technology Industries: A Co-Occurrence-Based Analysis of Newspaper Article Data" Sustainability 8, no. 10: 1029. https://doi.org/10.3390/su8101029
APA StyleLee, H., Kim, N., Kwak, K., Kim, W., Soh, H., & Park, K. (2016). Diffusion Patterns in Convergence among High-Technology Industries: A Co-Occurrence-Based Analysis of Newspaper Article Data. Sustainability, 8(10), 1029. https://doi.org/10.3390/su8101029






