Monocentric or Polycentric? The Urban Spatial Structure of Employment in Beijing
Abstract
:1. Introduction
2. Research Area, Data and Methods
2.1. Research Area
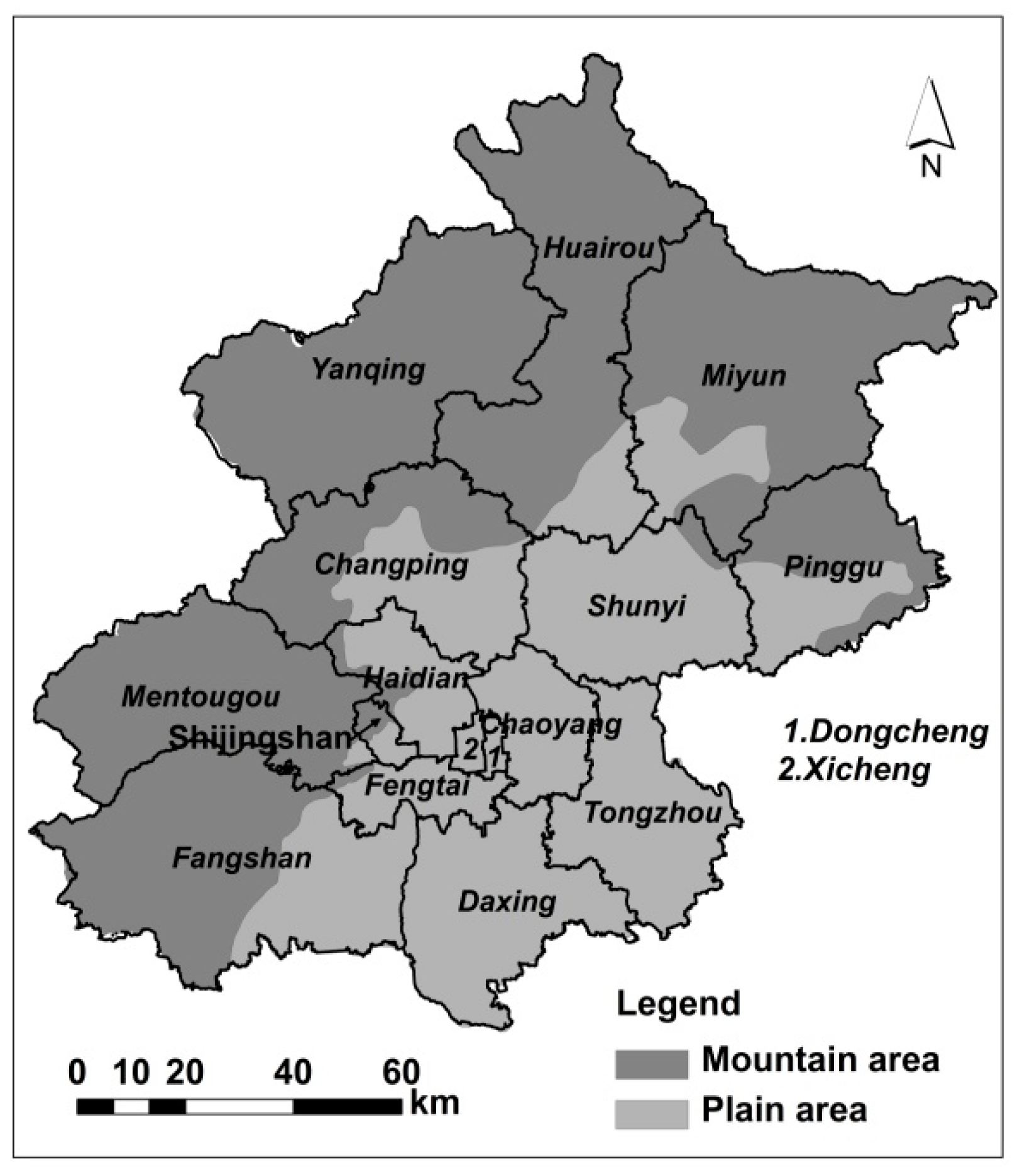
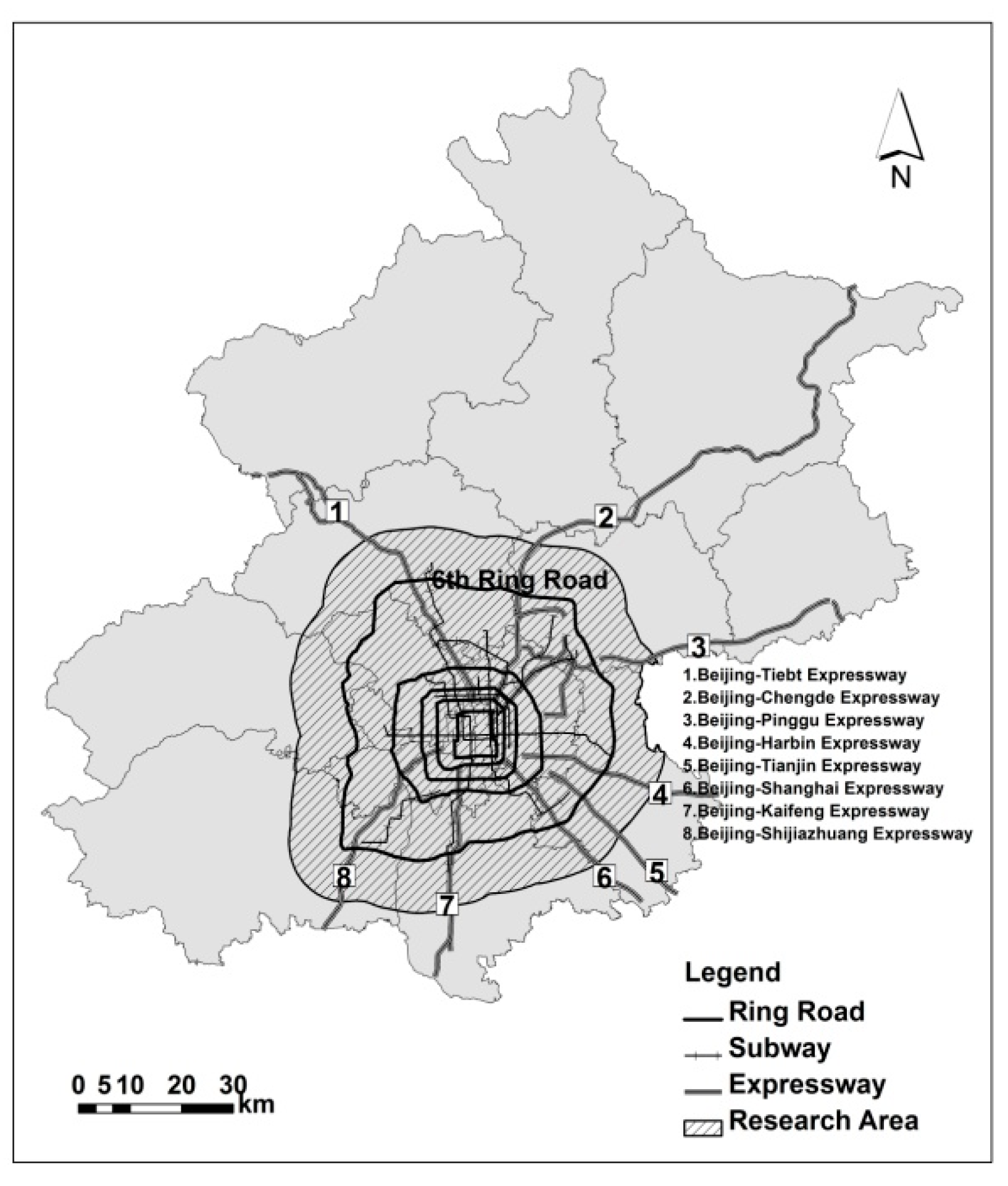
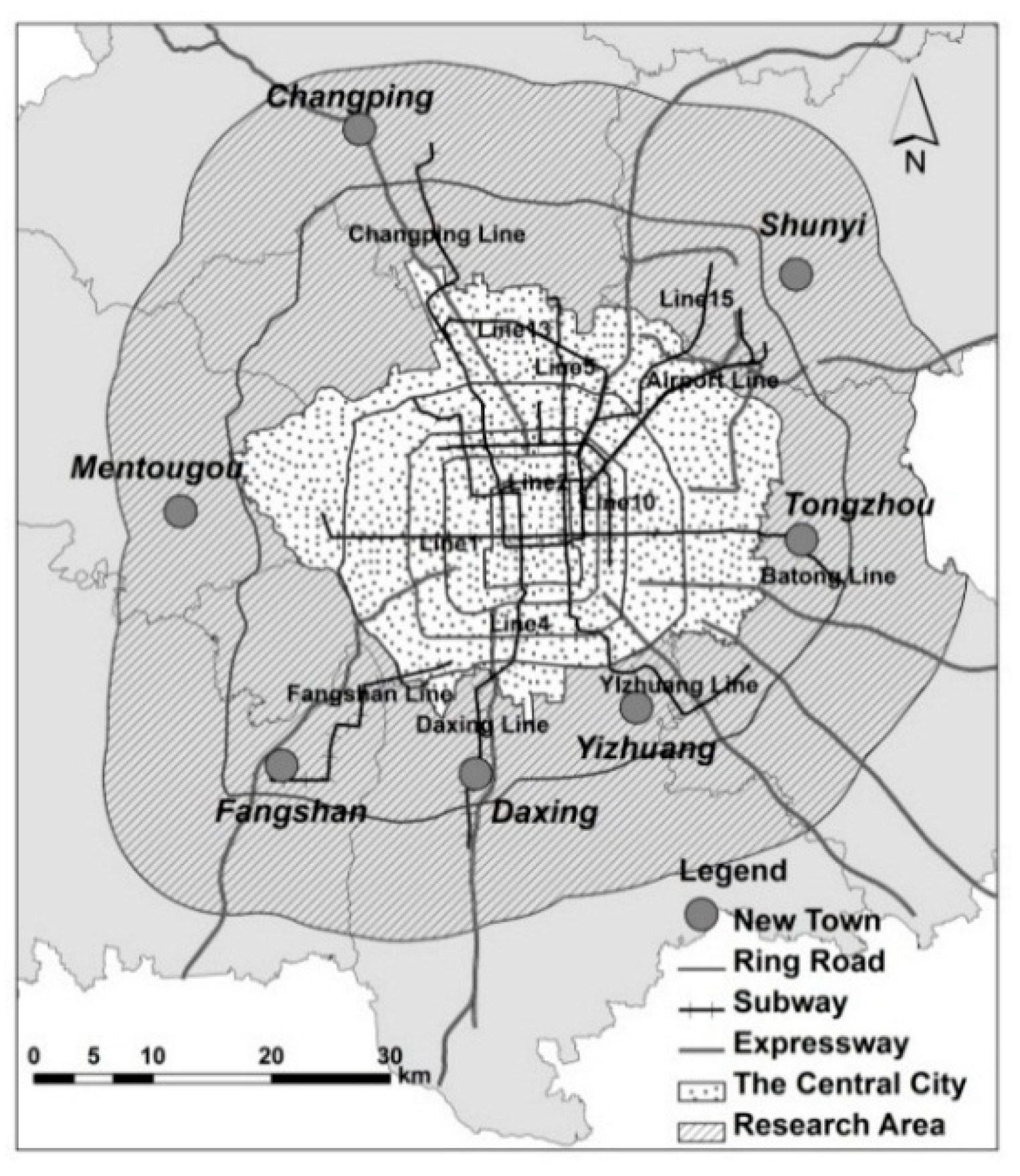
2.2. Data
| Data Source | Primary Industry | Secondary Industry | Tertiary Industry |
|---|---|---|---|
| Beijing Statistical Yearbook | 6.0% | 19.5% | 74.4% |
| Beijing Industry and Commerce Bureau | 1.6% | 22.3% | 76.1% |
| Top Ten Industries | Employment | Percentage of Total Employment |
|---|---|---|
| Business services | 942,957 | 6.3% |
| Technological exchange and promotion services | 878,809 | 5.9% |
| Wholesale trade | 857,681 | 5.8% |
| Education | 575,360 | 3.9% |
| Construction | 545,589 | 3.7% |
| Retail Trade | 527,912 | 3.5% |
| Real estate | 458,434 | 3.1% |
| Computer service industry | 348,745 | 2.3% |
| Catering trade | 340,799 | 2.3% |
| Health | 315,535 | 2.1% |
| Top ten total | 5,791,821 | 38.8% |
2.3. Methods
2.3.1. Defining the Research Unit
| Grid Cell Size | Study Unit Number | Null Value Unit | Employment Density (Person/km2) | |||
|---|---|---|---|---|---|---|
| Number | Percentage | Max | Min | Mean | ||
| 1 km × 1 km | 4266 | 1062 | 24.9% | 114,850 | 2 | 4767 |
| 1.5 km × 1.5 km | 1883 | 173 | 9.2% | 98,746 | 2 | 3822 |
| 2 km × 2 km | 1030 | 67 | 6.5% | 93,538 | 2 | 3670 |
2.3.2. Identifying Subcenters
2.3.3. Effect of the Potential Subcenter on Local Employment Density
3. Employment Density in Beijing
3.1. Density Declines from the Center to the Suburb
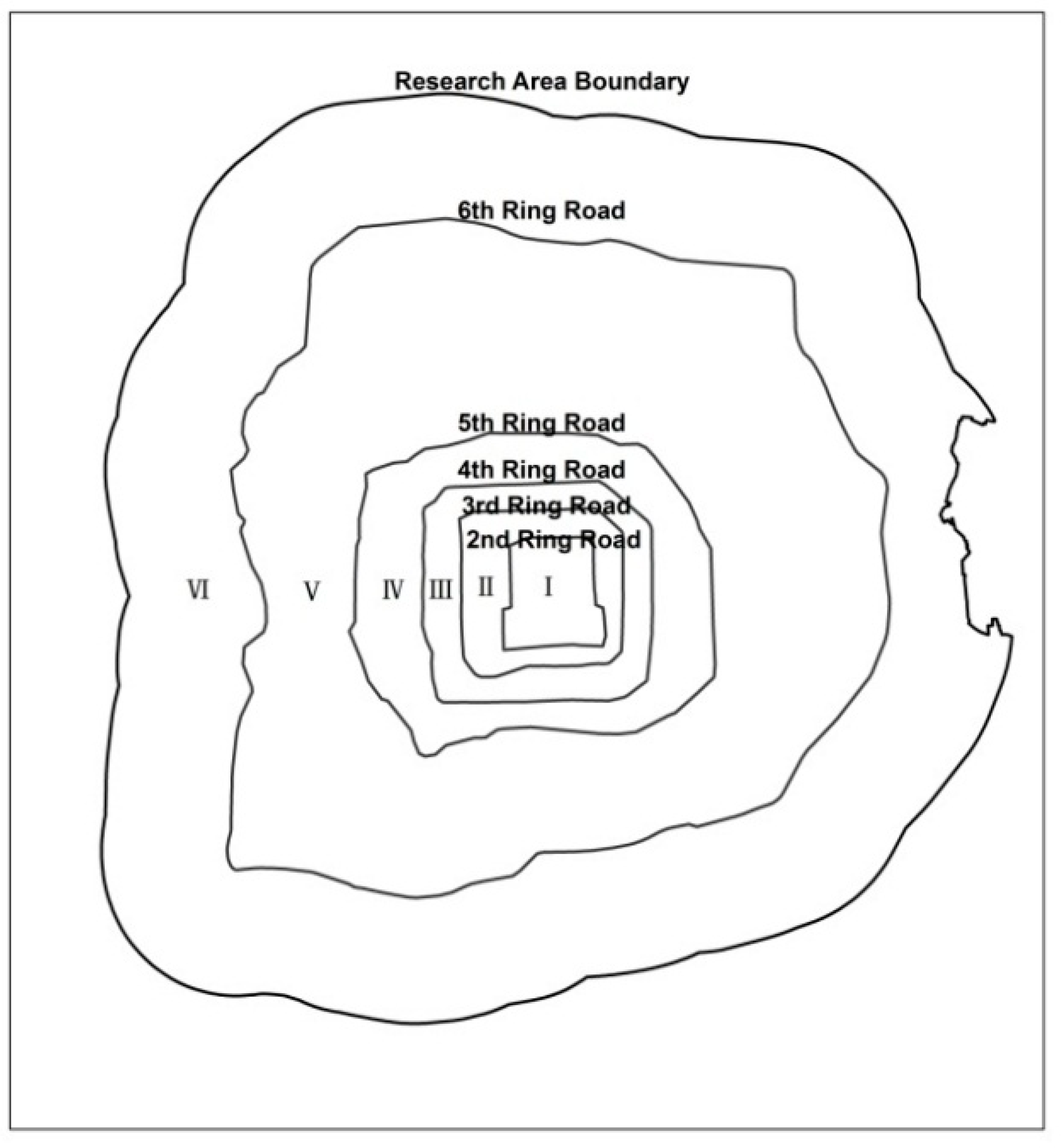
| Ring Zones | Area (km2) | Area Share (Percentage) | Enterprise Number Share (Percentage) | Enterprise Density (Per km2) | Employment Share (Percentage) | Employment Density (Per km2) |
|---|---|---|---|---|---|---|
| I (within 2nd Ring Road) | 62.0 | 1.4% | 11.7% | 775 | 13.1% | 29,248 |
| II (between 2nd and 3rd Ring Roads) | 97.1 | 2.2% | 20.8% | 878 | 22.1% | 31,547 |
| III (between 3rd and 4th Ring Roads) | 141.6 | 3.2% | 23.8% | 691 | 23.1% | 22,571 |
| IV (between 4th and 5th Ring Roads) | 311.7 | 7.0% | 15.6% | 206 | 15.5% | 6897 |
| V (between 5th and 6th Ring Roads) | 1664.6 | 37.6% | 18.3% | 45 | 17.4% | 1447 |
| VI (outside the 6th Ring Road) | 2152.5 | 48.6% | 9.8% | 19 | 8.8% | 563 |
| Zones | Area (km2) | Area Share (Percentage) | Enterprise Share (Percentage) | Enterprise Density (Per km2) | Employment Share (Percentage) | Employment Density (Per km2) |
|---|---|---|---|---|---|---|
| I (within 2nd Ring) | 62.0 | 1.4% | 11.7% | 775 | 13.1% | 29,248 |
| I + II (within 3rd Ring) | 159.1 | 3.6% | 32.5% | 838 | 35.2% | 30,651 |
| I + II + III (within 4th Ring) | 300.7 | 6.8% | 56.3% | 769 | 58.3% | 26,847 |
| I + II + III + IV (within 5th Ring) | 612.5 | 13.8% | 71.9% | 482 | 73.8% | 16,693 |
| I + II + III + IV + V (within 6th Ring) | 2269.0 | 51.2% | 90.2% | 163 | 91.2% | 5567 |
| Research area | 4429.6 | 100.0% | 100.0% | 93 | 100.0% | 3125 |
3.2. A Vast Employment Center
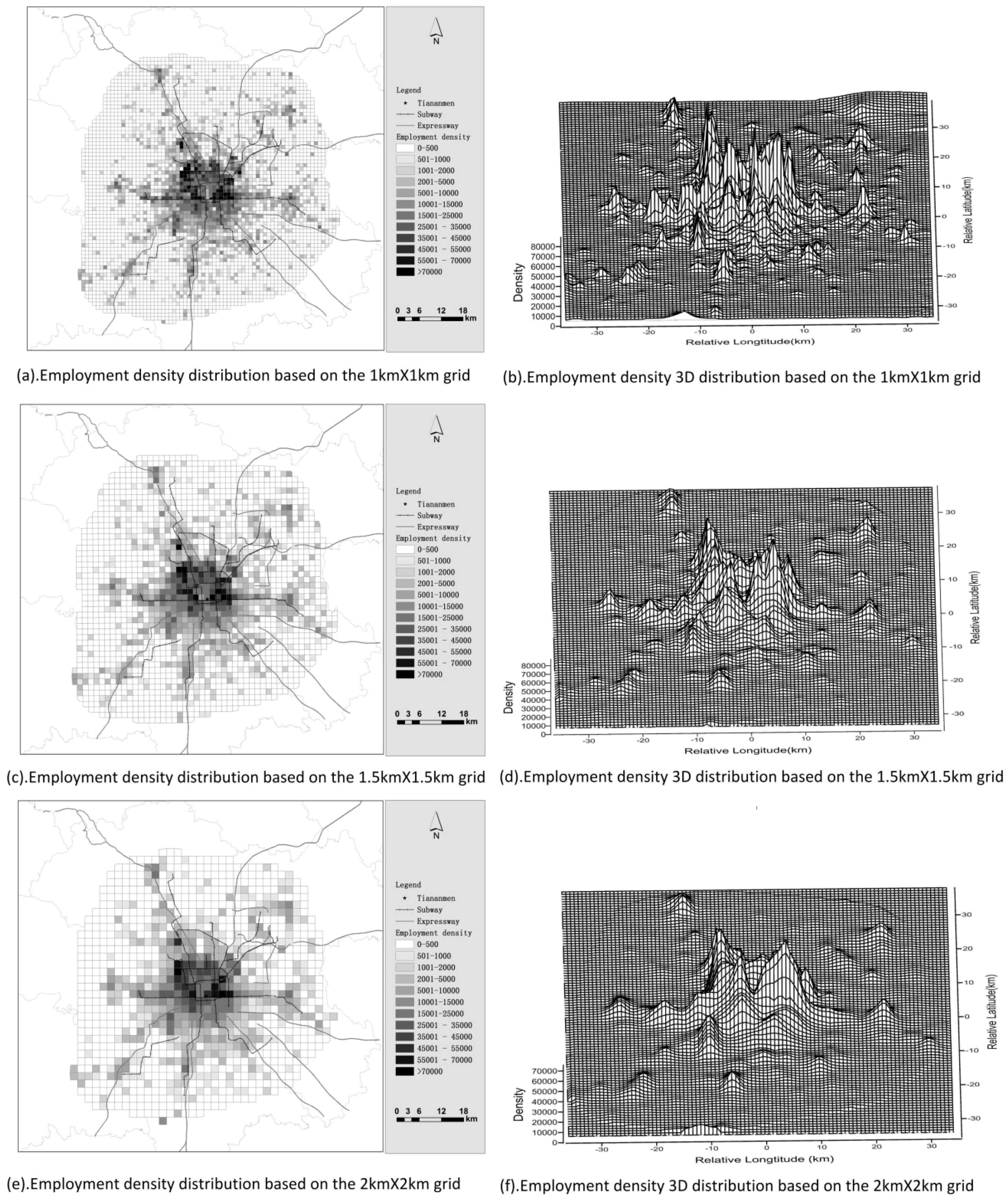
3.3. The Influence of Transportation
| Dependent Variables | ln (Employment Density) |
|---|---|
| constant | 9.361 *** |
| (78.71) | |
| s | −0.109 *** |
| (−15.91) | |
| shighway | −0.071 *** |
| (−2.61) | |
| ssubway | −0.099 *** |
| (−5.78) | |
| Adjusted R2 | 0.359 |
| F-test | 301.06 |
| Sample number | 1610 |
3.4. Employment Density Varies by Direction
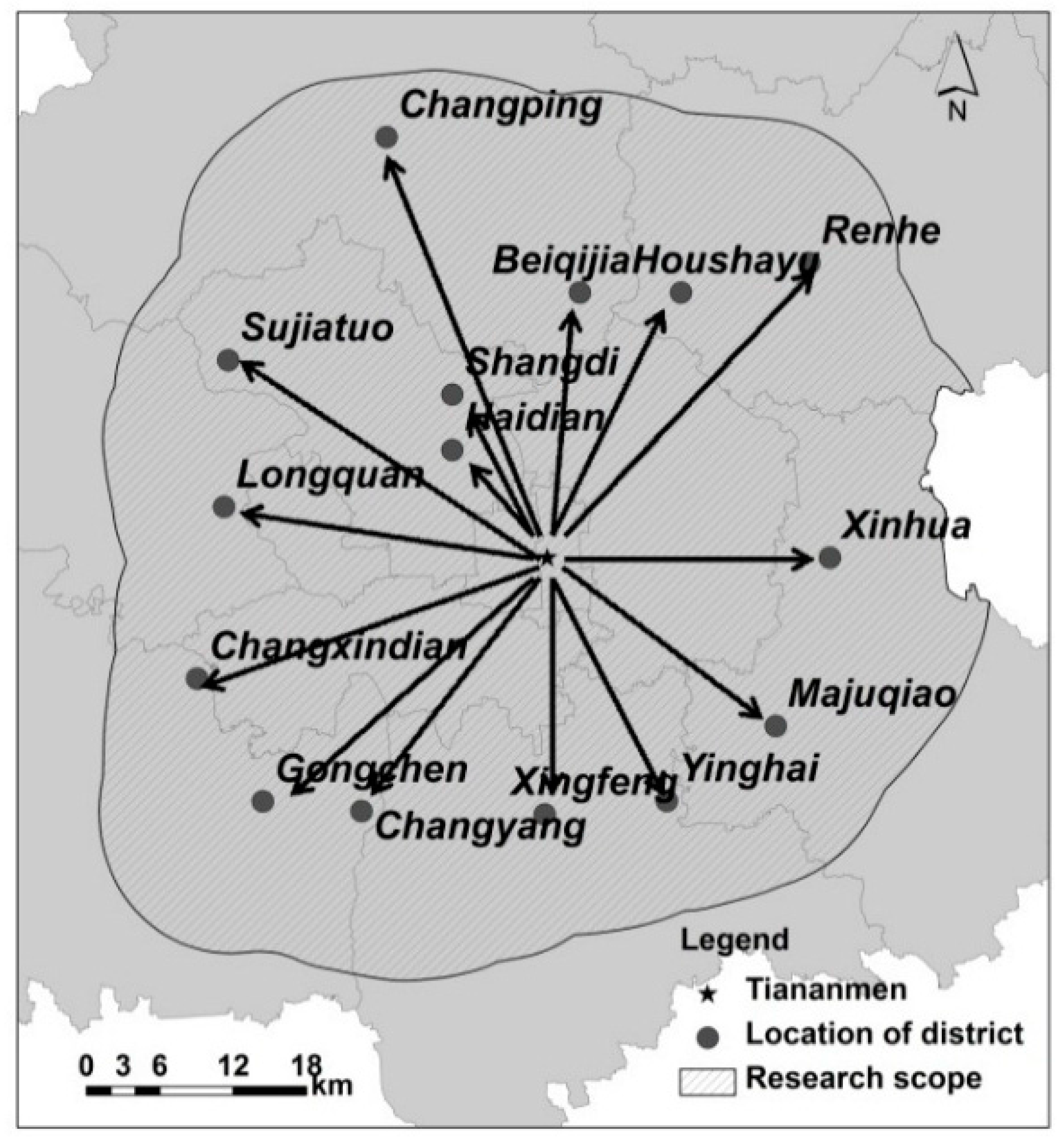
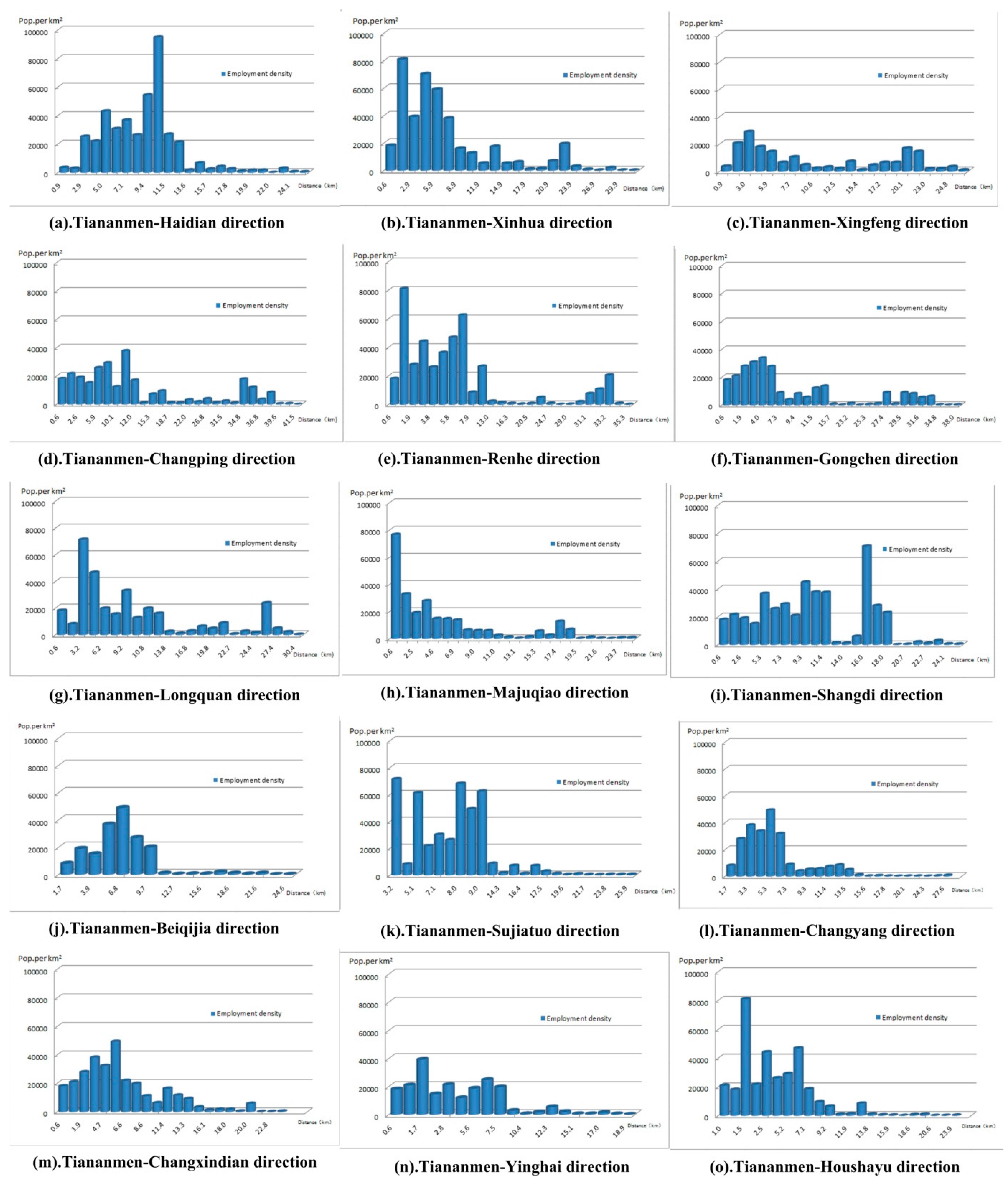
4. Identification of Employment Subcenters
4.1. Results from the Monocentric Model
| Dependent Variable: ln (Employment Density) | Research Area | Within the 6th Ring Road | Within the 5th Ring Road | Within the 4th Ring Road | Within the 3rd Ring Road |
|---|---|---|---|---|---|
| Constant | 9.552 *** | 10.391 *** | 11.486 *** | 10.695 *** | 10.392 *** |
| (83.04) | (60.05) | (61.45) | (66.87) | (49.60) | |
| s | −0.146 *** | −0.391 *** | −0.269 *** | −0.123 *** | −0.043 |
| (−29.83) | (20.87) | (−14.86) | (−4.91) | (−1.02) | |
| Adjusted R2 | 0.333 | 0.349 | 0.450 | 0.131 | 0.005 |
| F-test | 803.21 | 610.42 | 220.72 | 22.15 | 1.36 |
| Sample number | 1611 | 811 | 273 | 141 | 72 |
4.2. Subcenter Identification
4.2.1. Effects of Potential Employment Subcenters on Overall Employment Density
| Dependent Variable in (Employment Density) | Model Equation (4) (Distances to Subcenters) | Dependent Variable in (Employment Density) | Model Equation (5) (Inverse Distances to Subcenters) |
|---|---|---|---|
| Constant | 9.086 *** | Constant | 7.136 *** |
| (7.01) | (29.01) | ||
| s | −0.172 *** | S | −0.111 *** |
| (−7.45) | (−11.85) | ||
| s Haidian Street | −0.265 *** | 1/s Haidian Street | 3.469 *** |
| (−4.61) | (4.21) | ||
| s Shangdi Street | 0.302 *** | 1/s Shangdi Street | 0.568 |
| (4.32) | (0.65) | ||
| s Longquan Street | 0.089 *** | 1/s Longquan Street | 1.722 |
| (4.72) | (1.56) | ||
| s Xinhua Street | 0.065 ** | 1/s Xinhua Street | 1.716 *** |
| (2.15) | (2.86) | ||
| s Renhe Street | −0.101 *** | 1/s Renhe Street | 6.111 *** |
| (−5.89) | (5.63) | ||
| s Changping Urban District | −0.073 *** | 1/s Changping Urban District | 6.821 *** |
| (−3.24) | (7.42) | ||
| s Shahe Town | 0.019 | 1/s Shahe Town | −0.871 |
| (0.35) | (−0.95) | ||
| s Zhangjiawan Street | 0.019 | 1/s Zhangjiawan Street | 1.462 |
| (0.78) | (1.62) | ||
| s Gongchen Street | −0.063 *** | 1/s Gongchen Street | 4.735 *** |
| (−3.45) | (5.63) | ||
| x Airport | 0.088 *** | x Airport | 0.054 |
| 0–1 km from subway station | 1.389 *** | 0–1 km from subway station | 1.783 *** |
| (7.67) | (10.01) | ||
| 1–3 km from subway station | 0.835 *** | 1–3 km from subway station | 0.828 *** |
| (5.62) | (5.35) | ||
| 0–1 km from the highway | 0.362 *** | 0–1 km from the highway | 0.331 *** |
| (2.91) | (2.64) | ||
| 1–3 km from the highway | 0.134 | 1–3 km from the highway | 0.037 |
| (1.08) | (0.312) | ||
| Adjusted R2 | 0.441 | Adjusted R2 | 0.437 |
| F-test | 83.35 | F-test | 82.03 |
| Sample number | 1062 | Sample number | 1062 |
4.2.2. Effects of Potential Subcenters on Local Employment Density
| Dependent Variable | 5 km | 10 km | 15 km | 5 km | 10 km | 15 km | 5 km | 10 km | 15 km |
|---|---|---|---|---|---|---|---|---|---|
| Haidian Street | Changping Urban District | Renhe Street | |||||||
| Constant | 9.750 *** | 12.911 *** | 11.844 *** | 5.187 | 9.453 *** | 9.682 *** | 12.946 *** | 9.971 *** | 10.548 *** |
| (−71.49) | (30.12) | (40.83) | (1.67) | (7.72) | (10.29) | (3.52) | (9.03) | (9.39) | |
| S | −0.480 *** | −0.289 *** | −0.244 *** | 0.119 | −0.062 | −0.095 *** | −0.195 | −0.089 ** | −0.106 *** |
| (−17.63) | (−12.11) | (−18.3) | (1.36) | (−1.96) | (−4.13) | (−1.83) | (−2.04) | (−3.59) | |
| s subcenters | −0.301 ** | −0.124 ** | −0.038 | −0.206 *** | −0.300 *** | −0.146 *** | −0.026 | −0.215 *** | −0.213 *** |
| (−2.1) | (−2.54) | (−1.83) | (−4.30) | (−5.06) | (−4.21) | (−0.11) | (−2.90) | (−4.86) | |
| Adjusted R2 | 0.664 | 0.536 | 0.551 | 0.34 | 0.18 | 0.09 | 0.042 | 0.079 | 0.126 |
| F | 35.63 | 81.19 | 186.55 | 9.83 | 13.28 | 11.36 | 1.70 | 5.04 | 13.68 |
| Sample number | 37 | 141 | 355 | 34 | 116 | 203 | 34 | 96 | 177 |
| Gongchen Street | Xinhua Street | ||||||||
| Constant | 3.581 | 7.558 *** | 7.579 *** | 10.558 *** | 9.097 *** | 9.527 *** | 18.405 *** | 11.98 *** | 10.79 *** |
| (1.14) | (7.11) | (10.36) | (3.97) | (10.79) | (18.27) | (4.18) | (10.25) | (12.70) | |
| S | −0.157 | −0.022 | −0.072 *** | −0.051 | −0.062 ** | −0.127 *** | −0.335 | −0.209 *** | −0.204 *** |
| (−1.42) | (−0.65) | (−4.53) | (−0.46) | (−2.00) | (−7.90) | (−1.89) | (−4.52) | (−8.93) | |
| s subcenter | −0.559 ** | −0.231 *** | −0.016 | −0.730 *** | −0.238 *** | −0.074 ** | −1.097 *** | −0.256 *** | −0.038 |
| (−2.29) | (−3.18) | (−0.48) | (−2.71) | (−3.61) | (−2.38) | (−2.83) | (−2.72) | (−0.82) | |
| Adjusted R2 | 0.113 | 0.068 | 0.065 | 0.145 | 0.103 | 0.188 | 0.338 | 0.212 | 0.261 |
| F-test | 2.99 | 5.51 | 10.36 | 3.80 | 8.56 | 31.02 | 6.64 | 12.90 | 32.24 |
| Sample number | 33 | 125 | 270 | 35 | 132 | 260 | 30 | 99 | 184 |
| Shangdi Street | Shahe Town | Zhangjiawan Town | |||||||
| Constant | 12.650 *** | 12.346 *** | 11.490 *** | 9.945 *** | 8.854 *** | 8.10 *** | 7.240 | 8.862 *** | 10.599 *** |
| (8.28) | (21.13) | (35.16) | (3.63) | (11.49) | (18.74) | (1.78) | (3.77) | (7.71) | |
| S | −0.230 | −0.265 *** | −0.234 *** | −0.157 | −0.123 *** | −0.085 *** | −0.040 | −0.103 | −0.155 *** |
| (−1.41) | (−9.96) | (−18.73) | (−1.56) | (−4.79) | (−6.82) | (−0.32) | (−1.51) | (−3.89) | |
| s-subcenter | −0.295 ** | −0.069 | −0.018 | −0.044 | −0.036 | 0.006 | −0.086 | −0.066 | −0.102 |
| (−2.56) | (−1.23) | (−0.74) | (−0.02) | (−0.64) | (−0.82) | (−0.32) | (−0.66) | (−1.92) | |
| Adjusted R2 | 0.19 | 0.422 | 0.55 | 0.013 | 0.135 | 0.132 | 0.007 | 0.028 | 0.080 |
| F-test | 4.98 | 51.29 | 179.21 | 1.22 | 11.53 | 23.24 | 1.12 | 1.19 | 7.71 |
| Sample number | 37 | 140 | 293 | 35 | 136 | 292 | 29 | 61 | 156 |
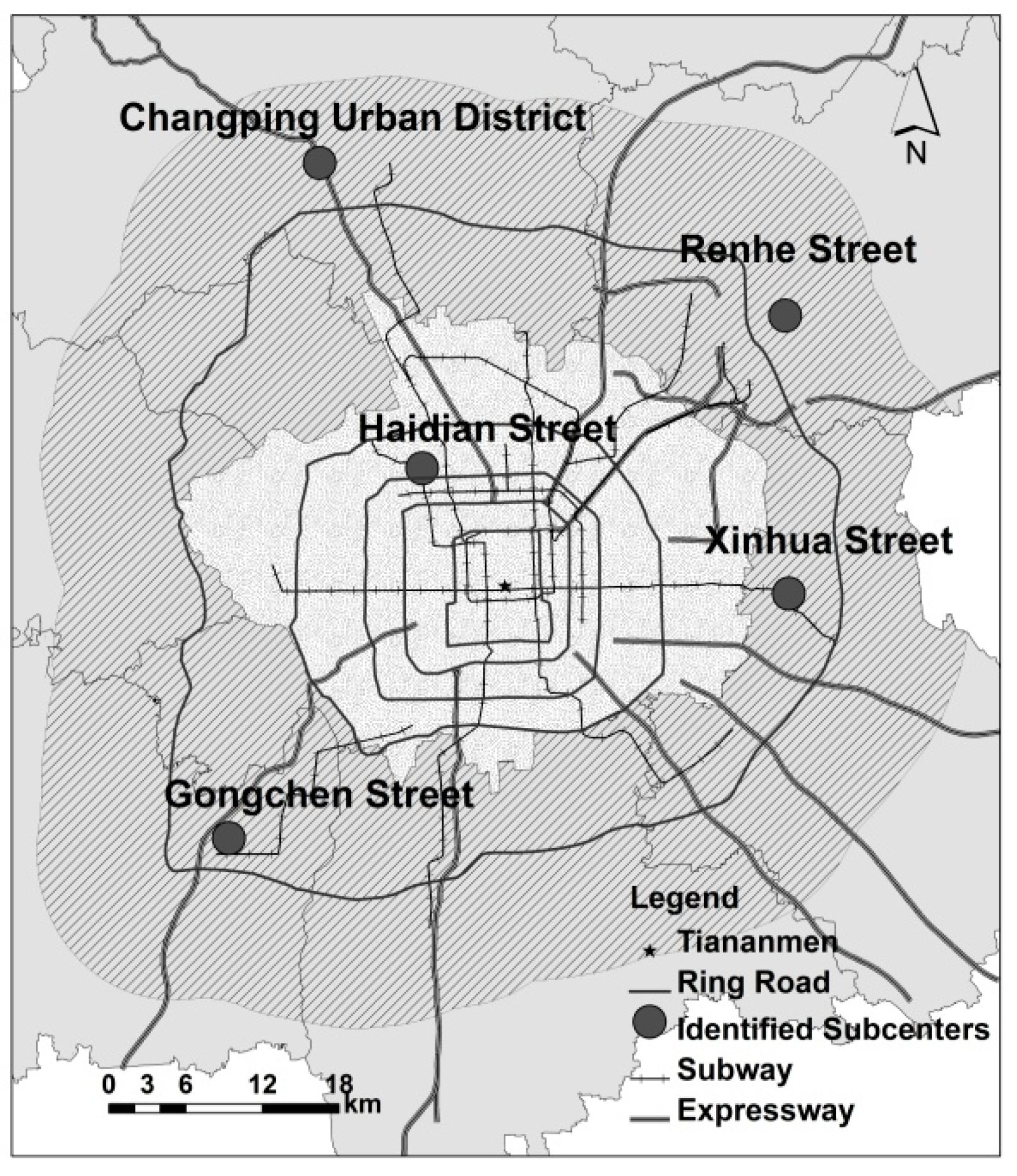
4.3. Polycentric Model
| Dependent Variable (Employment Density) | Monocentric Model (Add Control Variables) | Polycentric Model |
|---|---|---|
| Constant | 7.660 *** | 7.176 *** |
| (33.53) | (30.49) | |
| S | −0.096 *** | −0.112 *** |
| (−11.67) | (−12.46) | |
| 1/s Haidian Street | 2.953 *** | |
| (4.17) | ||
| 1/s Changping Urban District | 5.904 *** | |
| (7. 28) | ||
| 1/s Xinhua Street | 2.002 *** | |
| (2.71) | ||
| 1/s Renhe Street | 6.601 *** | |
| (5.82) | ||
| 1/s Gongchen street | 4.693 *** | |
| (5.68) | ||
| x Airport | 0.069 | 0.096 |
| (1.17) | (1.34) | |
| 0–1 km from subway station | 2.009 *** | 1.760 *** |
| (11.53) | (10.07) | |
| 1–3 km from subway station | 0.896 *** | 0.779 *** |
| (5.95) | (5.38) | |
| 0–1 km from the highway | 0.560 *** | 0.373 *** |
| (4.04) | (3.03) | |
| 1–3 km from the highway | 0.152 | 0.013 |
| (1.26) | (0.29) | |
| Adjusted R2 | 0.393 | 0.434 |
| F-test | 174.29 | 110.98 |
| Sample number | 1602 | 1602 |
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Bai, X.M.; Shi, P.J.; Liu, Y.S. Realizing China’s urban dream. Nature 2014, 509, 158–160. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z. Review and outlook of Population Scale in Beijing. Urban Stud. 2011, 18, 8–10. (In Chinese) [Google Scholar]
- Hu, Z. Review and Recognition on Urban Size of Beijing. J. Urban Reg. Plan. 2011, 2, 1–18. (In Chinese) [Google Scholar]
- Huang, D.; Jin, H.; Zhao, X.; Liu, S. Factors Influencing the Conversion of Arable Land to Urban Use and Policy Implications in Beijing, China. Sustainability 2015, 7, 180–194. [Google Scholar] [CrossRef]
- Sun, C.; Zheng, S.Q.; Wang, R. Restricting driving for better traffic and clearer skies: Did it work in Beijing? Transp. Policy 2014, 32, 34–41. [Google Scholar] [CrossRef]
- Wen, H.; Sun, J.; Zhang, X. Study on Traffic Congestion Patterns of Large City in China Taking Beijing as an Example. Procedia-Soc. Behav. Sci. 2014, 138, 482–491. [Google Scholar] [CrossRef]
- Cai, H.; Xie, S.D. Traffic-related air pollution modeling during the 2008 Beijing Olympic Games: The effects of an odd-even day traffic restriction scheme. Sci. Total Environ. 2011, 409, 1935–1948. [Google Scholar] [CrossRef] [PubMed]
- Hou, L.F.; Wang, S.; Dou, C.; Zhang, X.; Yu, Y.; Zheng, Y.N.; Avula, U.; Hoxha, M.; Diaz, A.; McCracken, J.; et al. Air pollution exposure and telomere length in highly exposed subjects in Beijing, China: A repeated-measure study. Environ. Int. 2012, 48, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Zhang, W.; Lin, Z.Q.; Zhang, H.S.; Xi, Z.G.; Chen, J.H.; Wang, W. Impact of Traffic Emissions on Local Air Quality and the Potential Toxicity of Traffic-related Particulates in Beijing, China. Biomed. Environ. Sci. 2012, 25, 663–671. [Google Scholar] [PubMed]
- Dang, Y.; Liu, Z.; Zhang, W. Land-based interests and the spatial distribution of affordable housing development: The case of Beijing, China. Habitat Int. 2014, 44, 137–145. [Google Scholar] [CrossRef]
- Yu, L.; Cai, H.P. Challenges for housing rural-to-urban migrants in Beijing. Habitat Int. 2013, 40, 268–277. [Google Scholar] [CrossRef]
- The urban planning aims to evacuate both the employment and population from the central city. For employment, the government, on one hand, encourages industries move to the suburb; on the other hand, it sets up many development zones in the suburb. For population, many residential communities have been built with the boom of the real estate in the suburb.
- Huang, D.Q.; Wan, W.; Dai, T.Q.; Liang, J.S. Assessment of industrial land use intensity: A case study of Beijing economic-technological development area. Chin. Geogr. Sci. 2011, 21, 222–229. [Google Scholar] [CrossRef]
- Dong, G. Sixty years and twenty years—Review and Prospect of the modernization development process in Beijing (2). Beijing Plan. Rev. 2010, 5, 168–171. (In Chinese) [Google Scholar]
- Dong, G. Sixty years and twenty years—Review and Prospect of the modernization development process in Beijing (1). Beijing Plan. Rev. 2010, 6, 177–180. (In Chinese) [Google Scholar]
- Kuang, W.; Liu, J.; Shao, Q.; Sun, C. Spatio-temporal patterns and driving forces of urban expansion in Beijing Central City since 1932. J. Geo-Inf. Sci. 2009, 4, 428–435. (In Chinese) [Google Scholar] [CrossRef]
- Beijing is composed of fourteen districts and two counties. The central city covers all of Xicheng District and Dongcheng District and part of Haidian District, Chaoyang District, Fengtai District, and Shijingshan District. Nine of the ten other suburban districts and counties have one new town each. Daxing district has two new towns: Huangcun new town, where Daxing district government is located, and Yizhuang new town, where Beijing Economic-Technological Development Area is located.
- Feng, J.; Zhou, Y. The Growth and Distribution of Population in Beijing Metropolitan Area (1982–2000). Acta Geogr. Sinica 2003, 58, 903–916. (In Chinese) [Google Scholar]
- Feng, J.; Zhou, Y. The social spatial structure of Beijing Metropolitan Area and its evolution: 1982–2000. Geogr. Res. 2003, 22, 465–483. (In Chinese) [Google Scholar]
- Feng, J.; Zhou, Y.; Wu, F. New trends of suburbanization in Beijing since 1990: From government-led to market-oriented. Reg. Stud. 2008, 42, 83–99. [Google Scholar] [CrossRef]
- Feng, J.; Wang, F.; Zhou, Y. The spatial restructuring of population in metropolitan Beijing: Toward polycentricity in the post-reform era. Urban Geogr. 2009, 30, 779–802. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, W. Characteristics and factors analyses of suburbanization in Beijing. Geogr. Res. 2006, 25, 121–130. (In Chinese) [Google Scholar]
- Wang, F.; Zhou, Y. Modelling urban population densities in Beijing 1982–1990: Suburbanisation and its causes. Urban Stud. 1999, 36, 271–287. [Google Scholar] [CrossRef]
- Alonso, W. Location and land use: Toward a general theory of land rent. Econ. Geogr. 1964, 42, 277–279. [Google Scholar]
- Brueckner, J.K. The structure of urban equilibria: A unified treatment of the Muth-Mills model. Handb. Reg. Urban Econ. 1987, 2, 821–845. [Google Scholar]
- Mills, E.S. An aggregative model of resource allocation in a metropolitan area. Am. Econ. Rev. 1967, 57, 197–210. [Google Scholar]
- Muth, R. Cities and Housing: The Spatial Patterns of Urban Residential Land Use; University of Chicago Press: Chicago, IL, USA, 1969. [Google Scholar]
- McMillen, D.P. Nonparametric employment subcenter identification. J. Urban Econ. 2001, 50, 448–473. [Google Scholar] [CrossRef]
- Tao, R.; Jin, Y. Improvement of Data Quality Assessment of Economic Census in China. Stat. Res. 2009, 26, 8–12. (In Chinese) [Google Scholar]
- Gu, Y.; Zheng, S.; Cao, Y. The Identification of Employment Centers in Beijing. Urban Stud. 2009, 9, 118–124. (In Chinese) [Google Scholar]
- Liu, X.; Sun, T.; Li, G. Research on the spatial structure of employment distribution in Beijing. Geogr. Res. 2011, 30, 1262–1270. (In Chinese) [Google Scholar]
- Sun, T.; Wang, L.; Li, G. Distributions of Population and Employment and Evolution of Spatial Structures in the Beijing Metropolitan Area. Acta Geogr. Sinica 2012, 67, 829–840. (In Chinese) [Google Scholar]
- Beijing has three levels of governments: The municipality, the district or county, and the town (township or street). The average area of towns (townships or streets) in Beijing is about 22 km2.
- The First Ring is actually the walls of the Forbidden City.
- Long, Y.; Zhang, Y.; Cui, C. Identifying Commuting Pattern of Beijing Using Bus Smart Card Data. Acta Geogr. Sin. 2012, 67, 1339–1352. (In Chinese) [Google Scholar]
- There are eleven new towns in all, but four of them are remote from the central city, averaging more than 65 km from the city center (Tiananmen)
- In matching the enterprise locations, “Exact matching” accounts for 79.3% and “Non-exact matching” accounts for 20.7%. It can be hard or impossible to match a company with a building exactly for two reasons. First, large companies can have multiple buildings, requiring us to use their geometrical center as the company’s geographic coordinate. Second, some company addresses—for example, No.19 XX Street—are not sufficiently detailed to allow us to specify an exact match. These cases lead to some errors, but these are acceptable given the size of the research unit (1.5 km × 1.5 km).
- Beijing Municipal Statistical Bureau. Beijing Statistical Yearbook 2011; China Statistics Press: Beijing, China, 2011.
- The 560 companies that were eliminated from our dataset were selected in two ways. First, some companies were identified as not limited to Beijing by their names, such as XX headquarters. Second, for companies with more than 3000 employees, we conducted internet searches on the distribution of their activities. If we found, for example, that the company has branches or factories in many locations, we eliminated it from our data.
- McMillen, D.P.; Lester, T.W. Evolving subcenters: Employment and population densities in Chicago, 1970–2020. J. Hous. Econ. 2003, 12, 60–81. [Google Scholar] [CrossRef]
- McDonald, J.F.; Prather, P.J. Suburban employment centres: The case of Chicago. Urban Stud. 1994, 31, 201–218. [Google Scholar] [CrossRef]
- Giuliano, G.; Small, K.A. Subcenters in the Los Angeles region. Reg. Sci. Urban Econ. 1991, 21, 163–182. [Google Scholar] [CrossRef]
- As more than a quarter of the towns (townships, streets) and other potential employment subcenters are smaller than 4 km2, the grid should be smaller than 4 km2.
- McMillen, D.P.; McDonald, J.F. Suburban subcenters and employment density in metropolitan Chicago. J. Urban Econ. 1998, 43, 157–180. [Google Scholar] [CrossRef]
- McDonald, J.F. The identification of urban employment subcenters. J. Urban Econ. 1987, 21, 242–258. [Google Scholar] [CrossRef]
- McDonald, J.F.; McMillen, D.P. Employment subcenters and land values in a polycentric urban area: The case of Chicago. Environ. Plan. A 1990, 22, 1561–1574. [Google Scholar] [CrossRef]
- Small, K.A.; Song, S.F. Population and employment densities—Structure and change. J. Urban Econ. 1994, 36, 292–313. [Google Scholar] [CrossRef]
- Employment density around Tiananmen is very low, but we still can regard it as the center. First, it is the city center in city planning. The Beijing government has always taken Tiananmen as the center to design the layout of the city. Second, its scope is so small that we can regard it as a point. Third, many studies have taken Tiananmen as the center to investigate the distribution of population and employment [21,31,32].
- Muñiz, I.; Garcia-López, M.À.; Galindo, A. The effect of employment sub-centres on population density in Barcelona. Urban Stud. 2008, 45, 627–649. [Google Scholar] [CrossRef]
- Heikkila, E.; Gordon, P.; Kim, J.I.; Peiser, R.B.; Richardson, H.W.; Dale-Johnson, D. What happened to the CBD-distance gradient? Land values in a policentric city. Environ. Plan. A 1989, 21, 221–232. [Google Scholar] [CrossRef]
- For example, the Xinhua Street which is the main part of Tongzhou new town specialized in comprehensive service, the Renhe Street which is the main part of Shunyi new town specialized in aviation logistics, the Gongchen Street which is the main part of Fangshan new town specialized in new materials industry, and the Changping urban district which is the main part of Changping new town specialized in research and development. Their developing directions have also different in the planning to undertake different functions of Beijing.
- The nine directions are Tianmen-Haidian, Tianmen-Xinhua, Tianmen-Xingfeng, Tianmen-Changping, Tianmen-Renhe, Tianmen-Gongchen, Tianmen-Longquan, Tianmen-Majuqiao and Tianmen-Shangdi.
- White, H. A heteroskedasticity-consistent covariance matrix estimator and a direct test for heteroskedasticity. Econometrica 1980, 48, 817–838. [Google Scholar] [CrossRef]
- McDonald [41] adopted seven forms of monocentric models to test the employment distribution of Chicago .The adjusted R2 is between 0.258 and 0.336 while the negative exponential model is 0.296. Small et al. [47] used the negative exponential model to examine the employment distribution in Los Angeles region. The adjusted R2 is 0.395 in 1970 and 0.388 in 1980.
- All seven of these are located in remote suburban districts, including four in Fangshan District and three in Shunyi District.
- The selection of a 3 km boundary is somewhat subjective. Related research has no strict definition of adjacency. McMillen et al. [40] defined it as within 1.5 miles. Giuliano et al. [42] defined it as at least 0.25 miles from a common border. Here we referred to the definition of McMillen et al. [40], and with an eye toward the size of our study unit, selected 3 km as constituting adjacency.
- The distance between Shangdi street and Haidian street is about 7 km and the correlation coefficient is 0.91. The distance between Shangdi street and Shahe street is about 8 km and the correlation coefficient is 0.93. The distance between Haidian street and Shahe street is about 13 km and the correlation coefficient is 0.76.
- Cervero, R.; Wu, K.L. Polycentrism, commuting, and residential location in the San Francisco Bay Area. Environ. Plan. A 1997, 29, 865–886. [Google Scholar] [CrossRef] [PubMed]
- Glaeser, E.L.; Kahn, M.E. Decentralized Employment and the Transformation of the American City. National Bureau of Economic Research, 2011. Availiable online: http://www.nber.org/papers/w8117 (accessed on 17 August 2015).
- Garcia-López, M.-À.; Muñiz, I. Employment decentralisation: Polycentricity or scatteration? The case of Barcelona. Urban Stud. 2010. [Google Scholar] [CrossRef]
- Hughes, H.L. Metropolitan structure and the suburban hierarchy. Am. Sociol. Rev. 1993, 58, 417–433. [Google Scholar] [CrossRef]
- Veneri, P. The identification of sub-centres in two Italian metropolitan areas: A functional approach. Cities 2013, 31, 177–185. [Google Scholar] [CrossRef]
- Compared with monocentric model, the explanatory power of the polycentric model has a significant improvement in the research of Small et al. [47] and Wang et al. [64].
- Wang, F.; Meng, Y. Analyzing urban population change patterns in Shenyang, China 1982–1990: Density function and spatial association approaches. Geogr. Inf. Sci. 1999, 5, 121–130. [Google Scholar]
- Ding, C.; Bethka, K. Employment Concentration and Urban Economic Growth. Urban Plan. Overseas 2005, 4, 11–18. (In Chinese) [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Liu, Z.; Zhao, X. Monocentric or Polycentric? The Urban Spatial Structure of Employment in Beijing. Sustainability 2015, 7, 11632-11656. https://doi.org/10.3390/su70911632
Huang D, Liu Z, Zhao X. Monocentric or Polycentric? The Urban Spatial Structure of Employment in Beijing. Sustainability. 2015; 7(9):11632-11656. https://doi.org/10.3390/su70911632
Chicago/Turabian StyleHuang, Daquan, Zhen Liu, and Xingshuo Zhao. 2015. "Monocentric or Polycentric? The Urban Spatial Structure of Employment in Beijing" Sustainability 7, no. 9: 11632-11656. https://doi.org/10.3390/su70911632
APA StyleHuang, D., Liu, Z., & Zhao, X. (2015). Monocentric or Polycentric? The Urban Spatial Structure of Employment in Beijing. Sustainability, 7(9), 11632-11656. https://doi.org/10.3390/su70911632





