Estimating Solar Irradiation Absorbed by Photovoltaic Panels with Low Concentration Located in Craiova, Romania
Abstract
:1. Introduction
2. Modeling and Simulation of Solar Irradiation
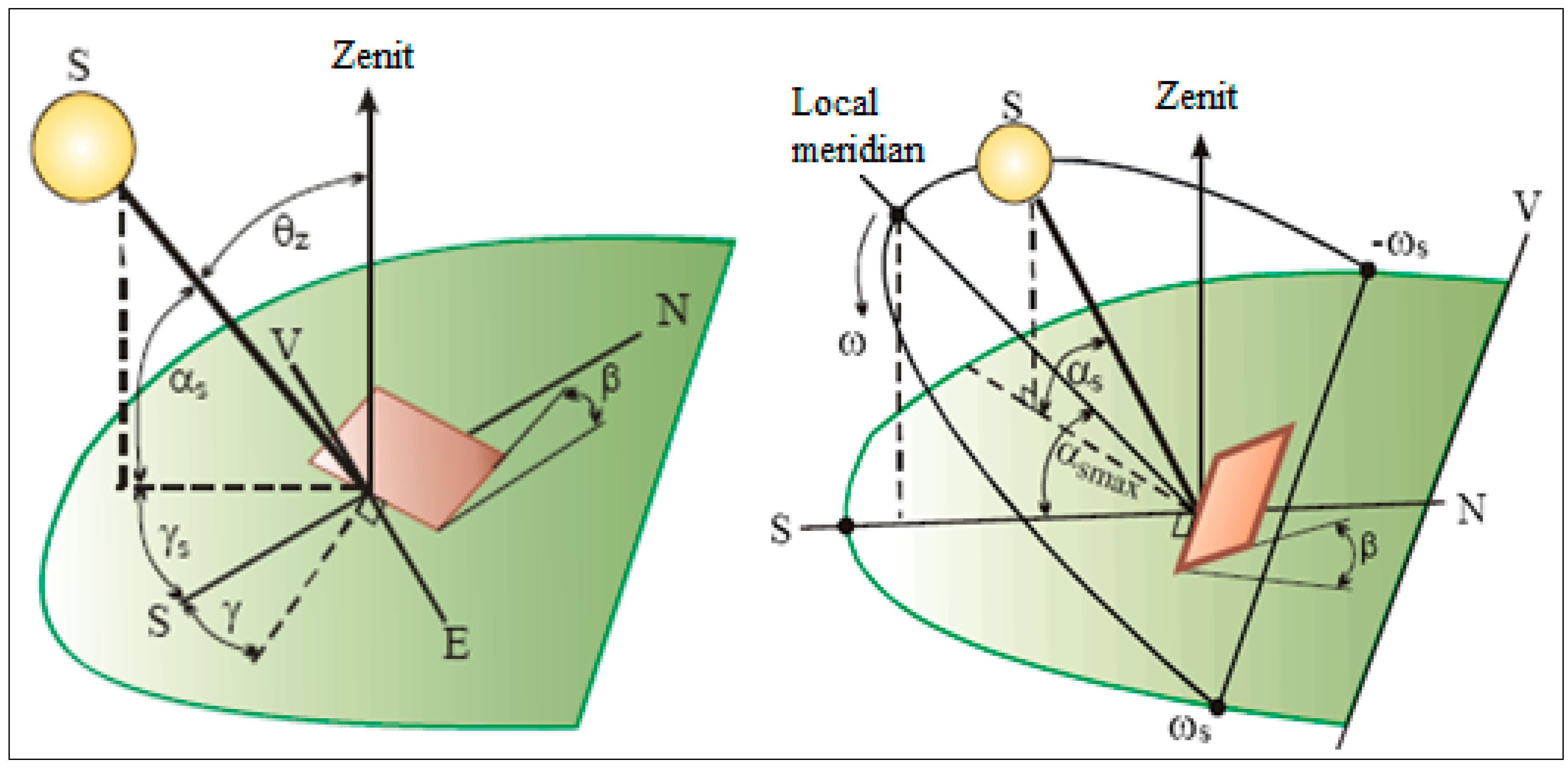
2.1. Extraterrestrial Irradiation
- S is the solar constant;
- n is the days’ number of the year;
- φ is the latitude of the considered location;
- δ represents the declination of the Earth;
- and ωs is the solar angle.

Influence of atmosphere
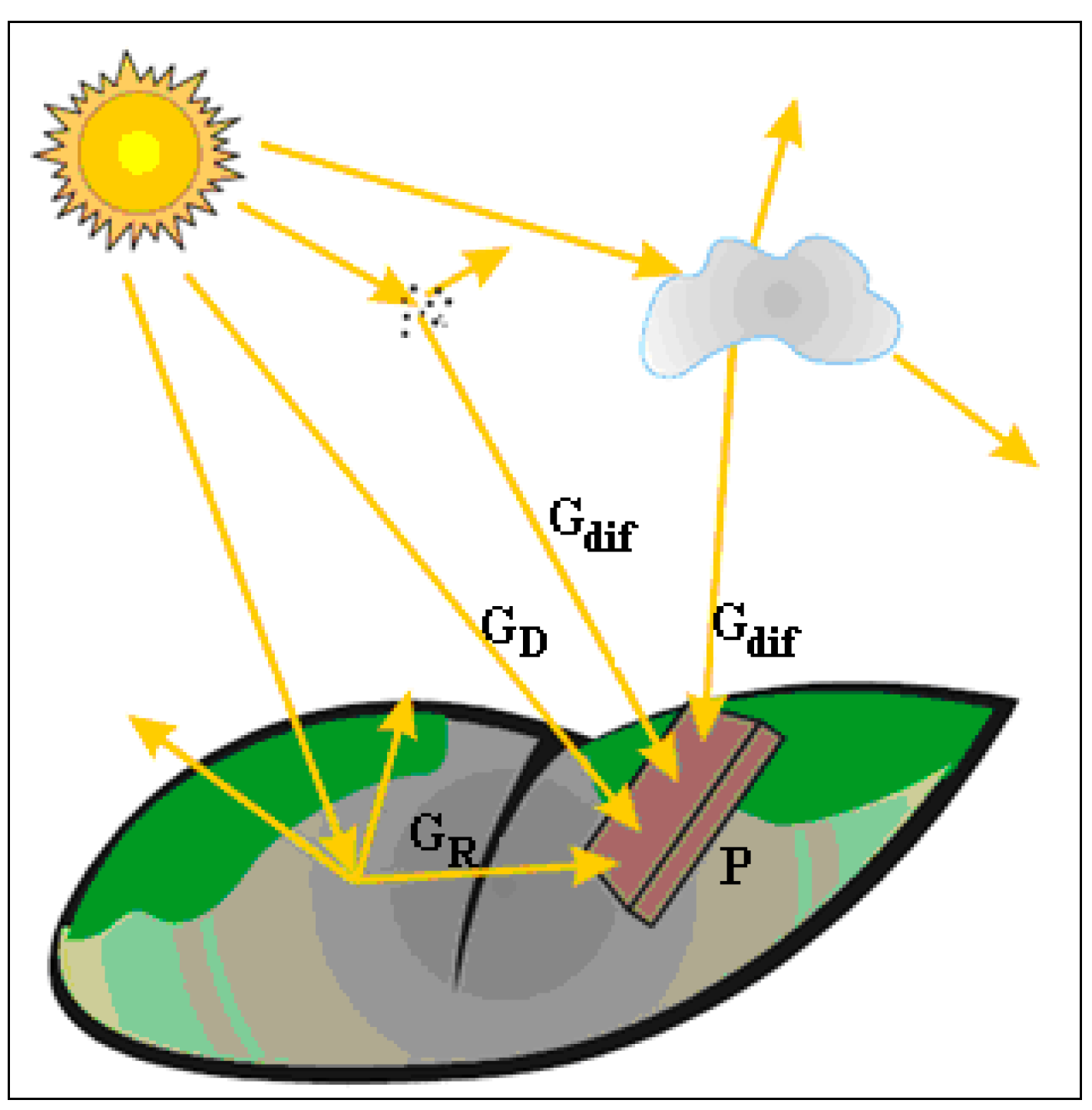
2.2. Terrestrial Irradiation
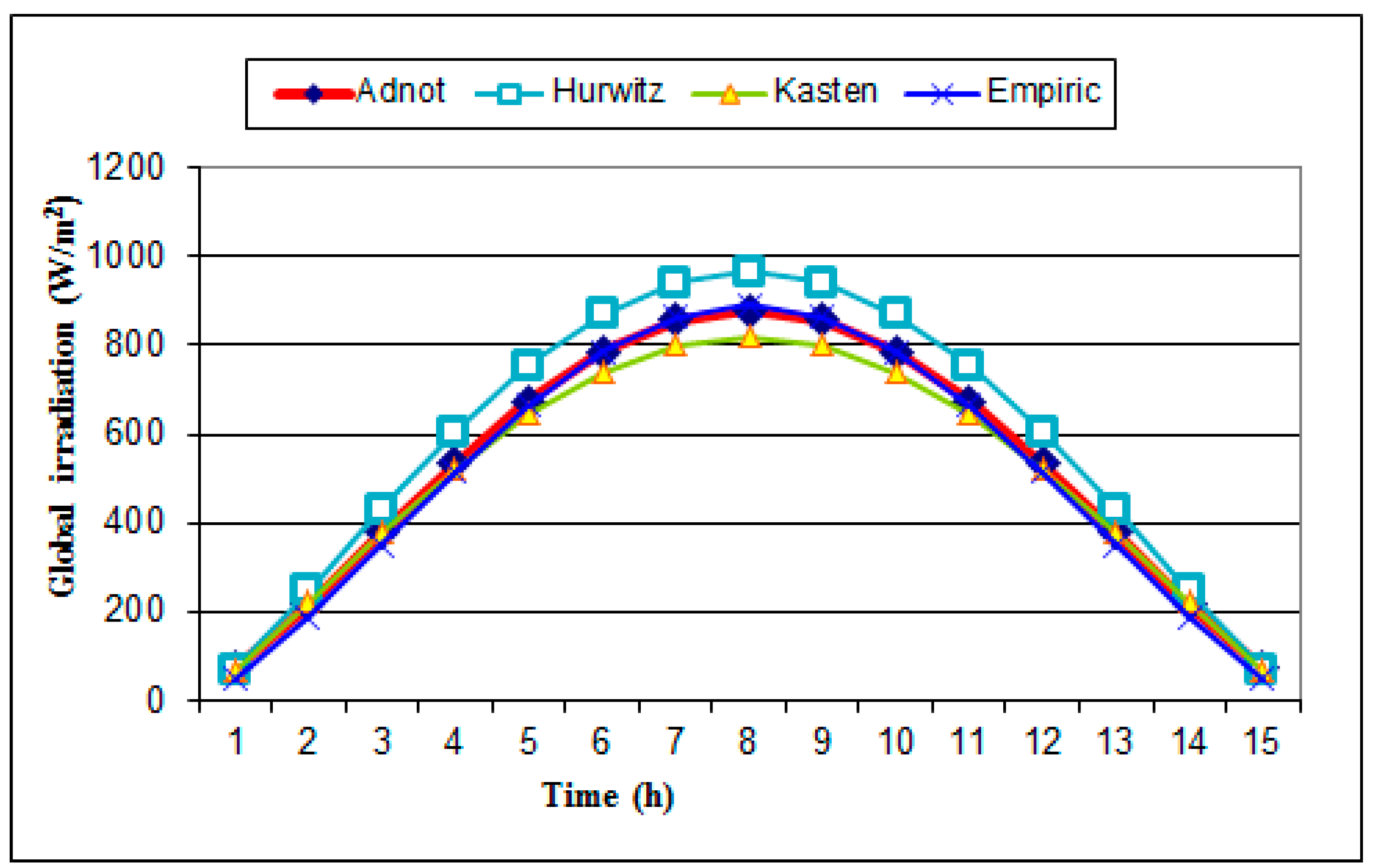
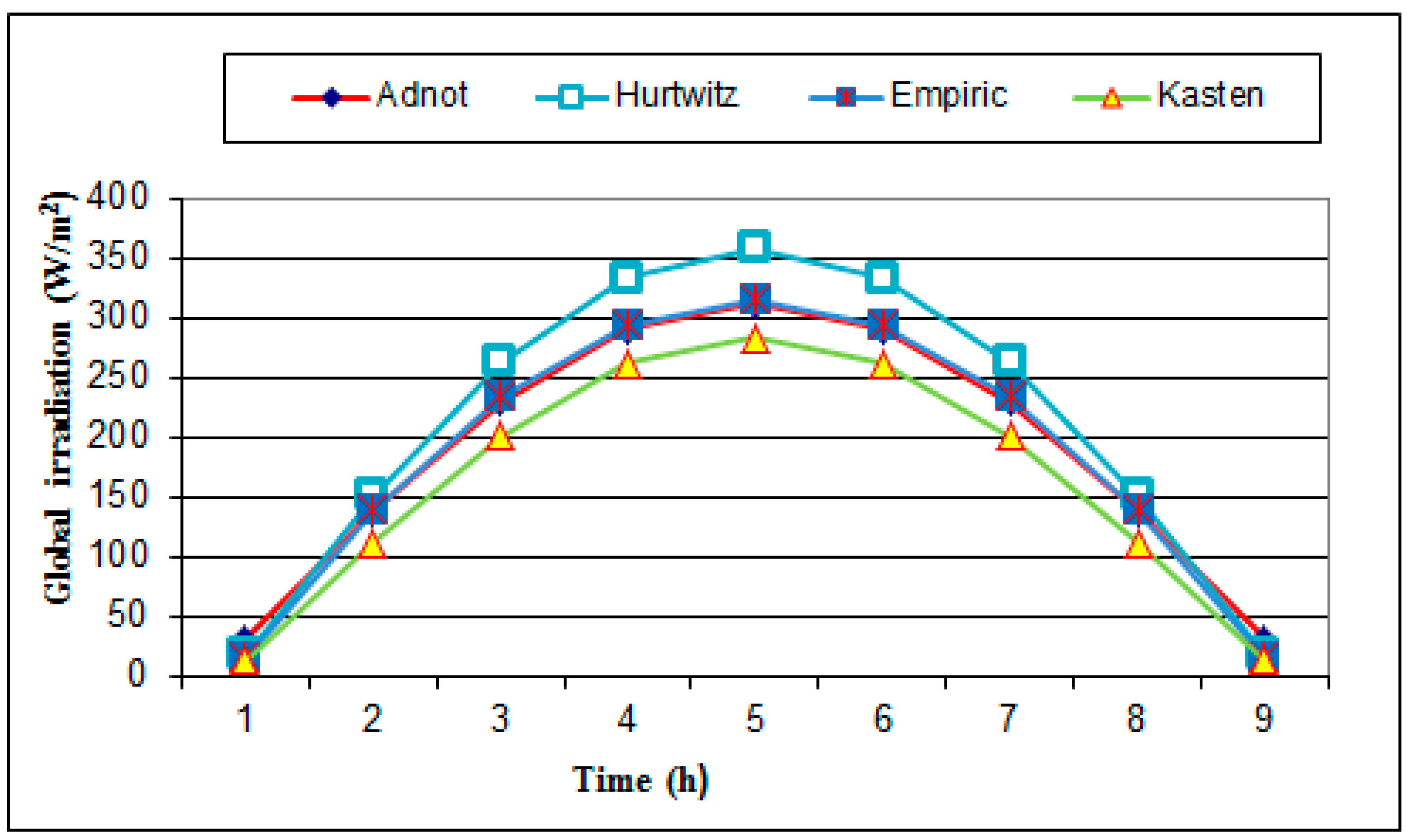
- Adnot model, which models global solar irradiation under conditions of a clear sky, by using the relationship [9]:
2.3. Solar Irradiation Absorbed by a Photovoltaic Panel without Concentration
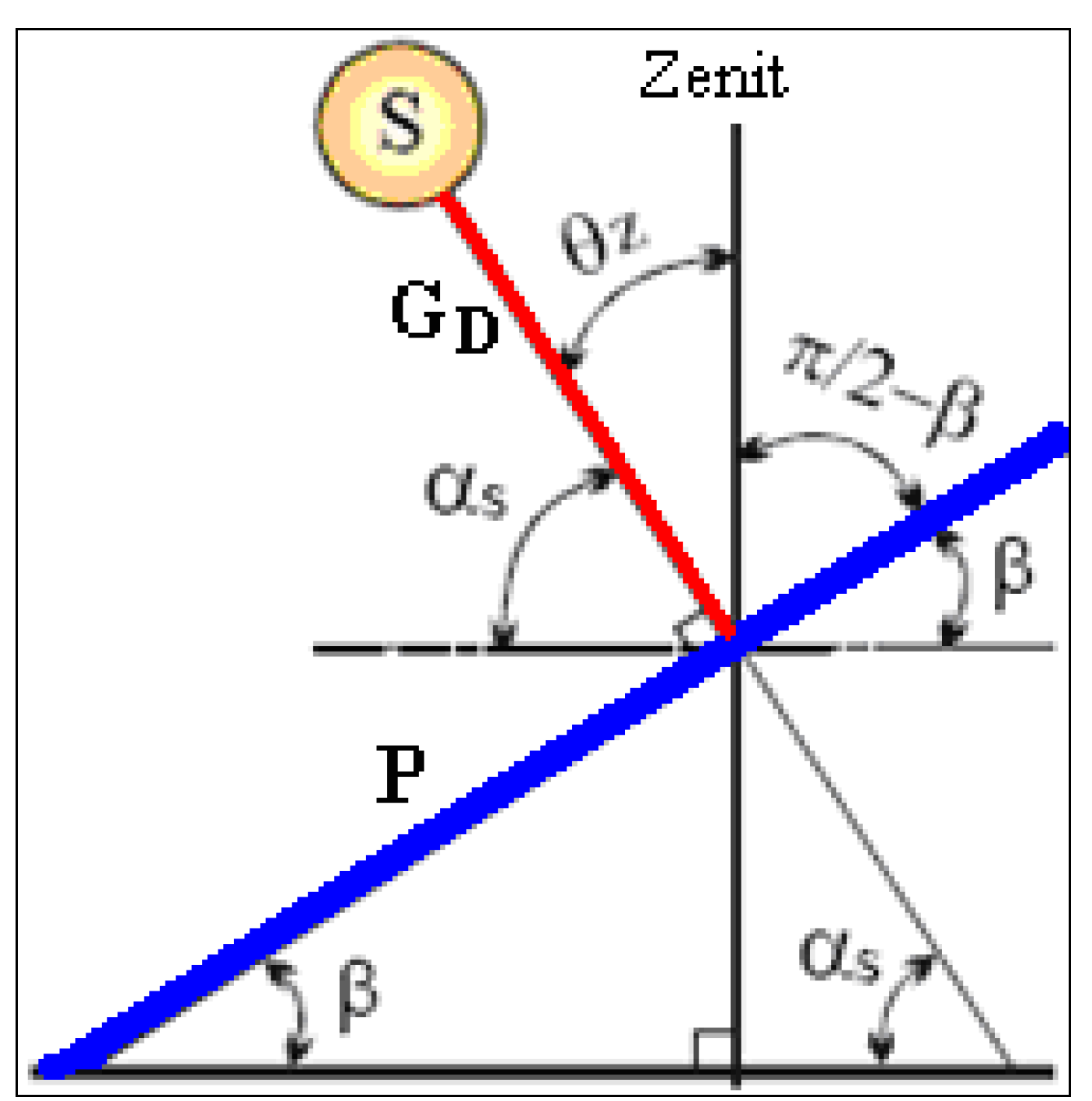
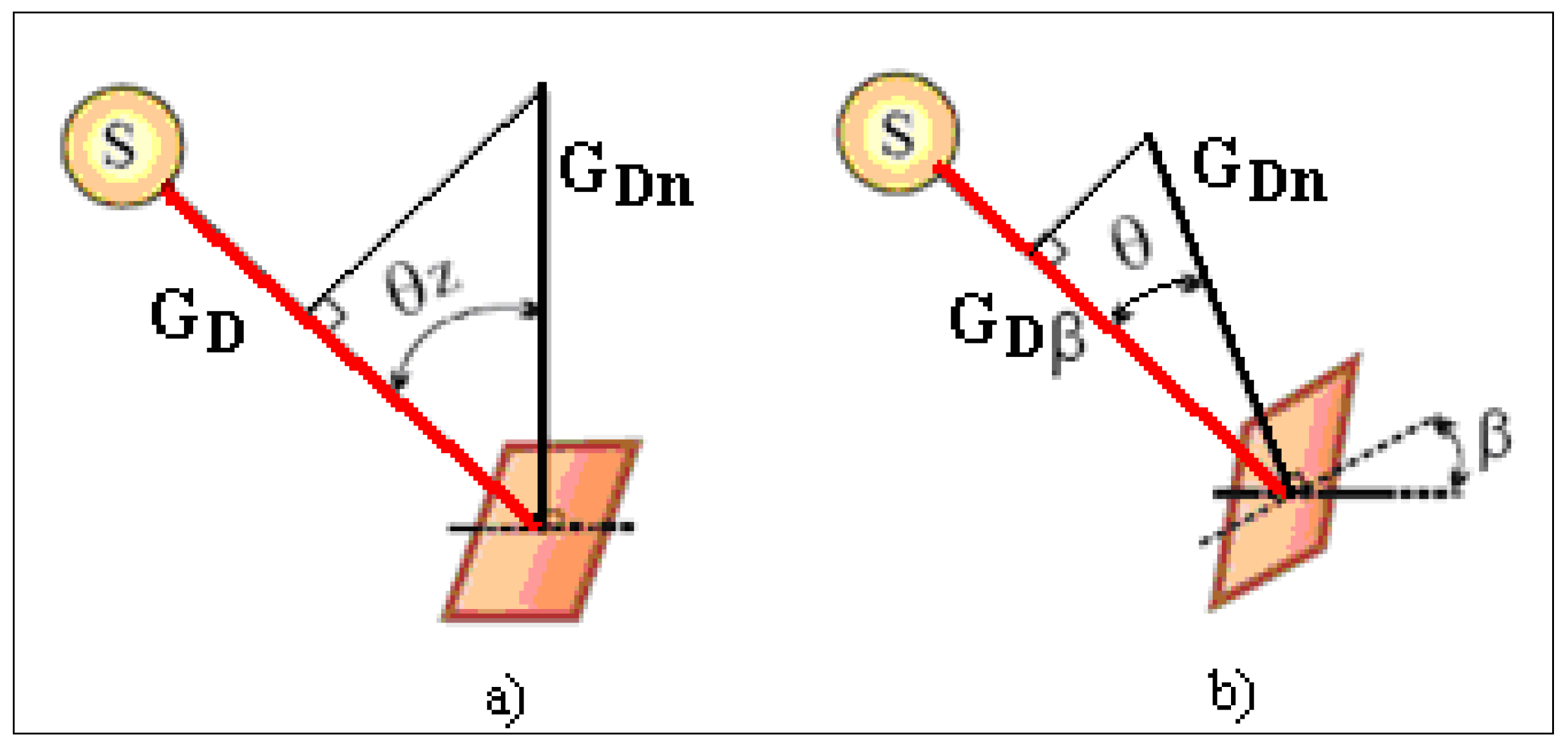
- ρ is the reflection coefficient of the Earth surface; and
- Gg is the global radiation on a horizontal surface.
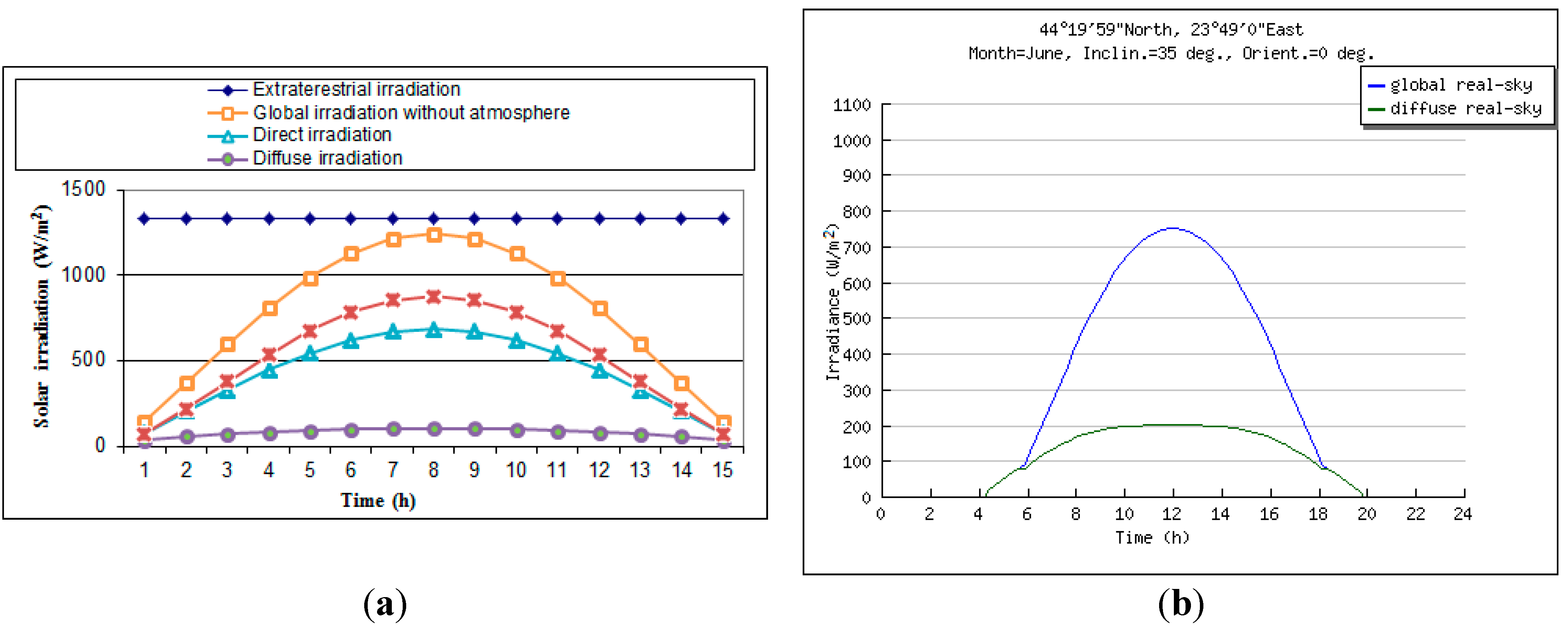
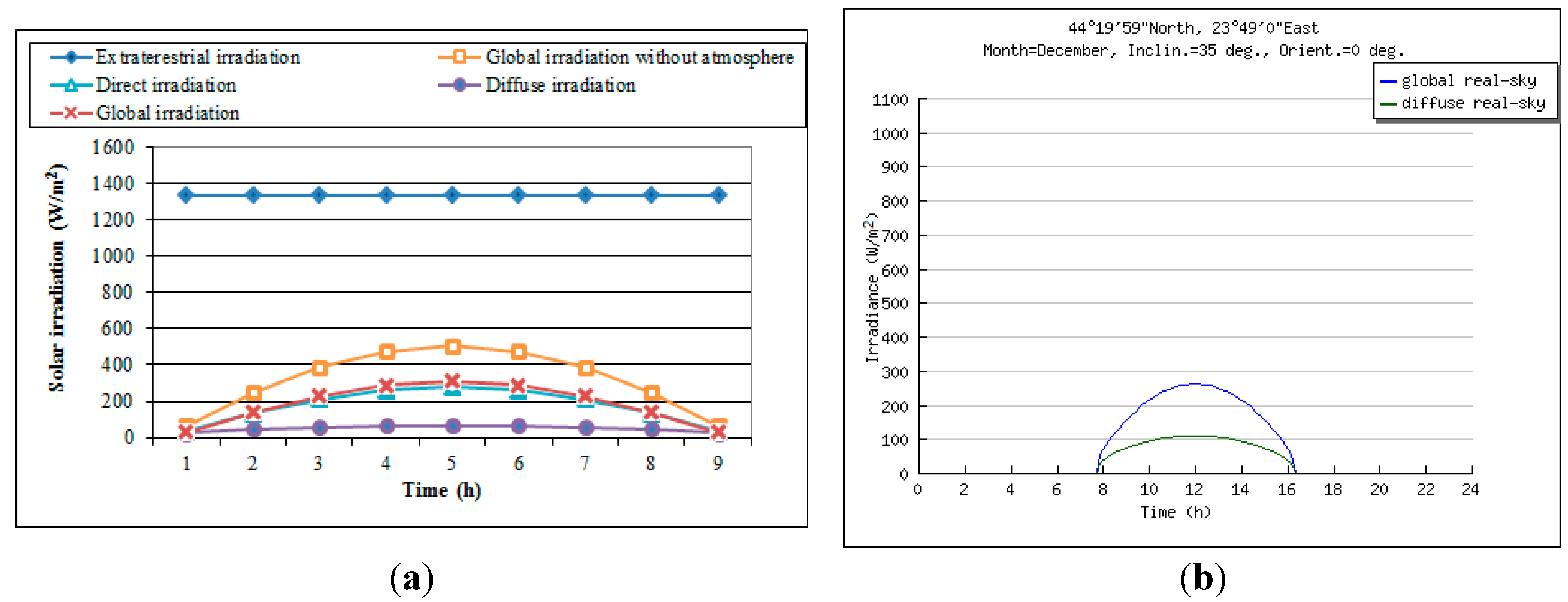
| Hour | June | December | ||||||
|---|---|---|---|---|---|---|---|---|
| Calculation (W/m2) | Literature (W/m2) | Relative Error (%) | Medium Error (%) | Calculation (W/m2) | Literature (W/m2) | Relative Error (%) | Medium Error (%) | |
| 5 | 0 | 0 | 0 | 3.84 | 0 | 0 | 0 | 3.16 |
| 6 | 73.5 | 100 | −26.5 | 0 | 0 | 0 | ||
| 7 | 218.2 | 250 | −12.72 | 0 | 0 | 0 | ||
| 8 | 377.5 | 400 | −5.625 | 40.5 | 55 | −26.3636 | ||
| 9 | 535 | 540 | −0.92593 | 138 | 158 | −12.6582 | ||
| 10 | 675 | 660 | 2.272727 | 230 | 220 | 4.545455 | ||
| 11 | 785.5 | 730 | 7.60274 | 290 | 260 | 11.53846 | ||
| 12 | 856 | 750 | 14.13333 | 311 | 280 | 11.07143 | ||
| 13 | 785.5 | 730 | 7.60274 | 290 | 260 | 11.53846 | ||
| 14 | 675 | 660 | 2.272727 | 230 | 220 | 4.545455 | ||
| 15 | 535 | 540 | −0.92593 | 138 | 158 | −12.6582 | ||
| 16 | 377.5 | 400 | −5.625 | 40.5 | 55 | −26.3636 | ||
| 17 | 218.2 | 250 | −12.72 | 0 | 0 | 0 | ||
| 18 | 73.5 | 100 | −26.5 | 0 | 0 | 0 | ||
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | ||
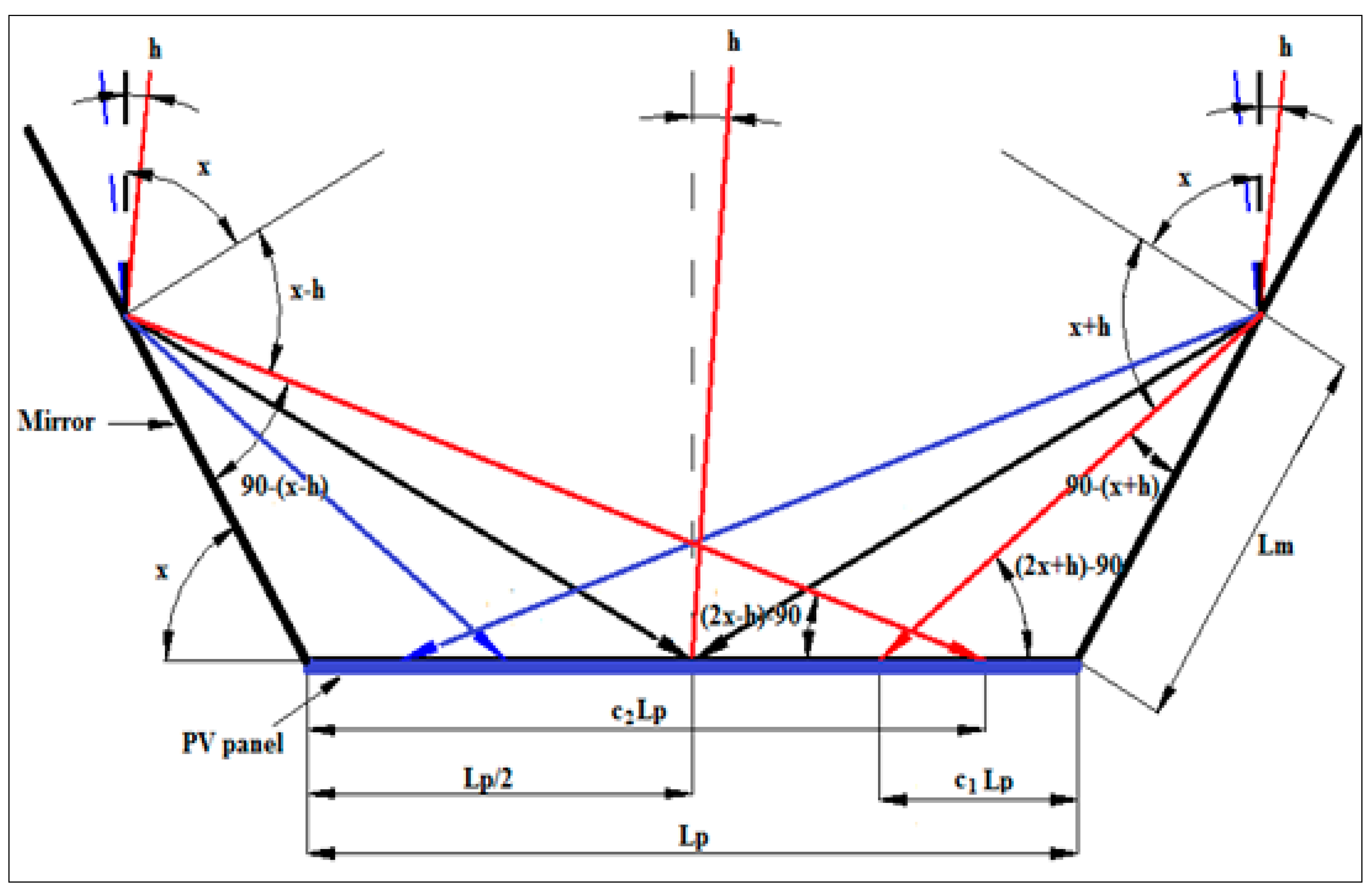
3. Mathematical Model of Solar Irradiation Absorbed by Photovoltaic Panel with Low Concentration

- -
- x is the angle between the mirror and the photovoltaic module, and is a constant parameter;
- -
- h is the maximum incidence angle created by the solar ray with the normal to the photovoltaic arrays;
- -
- k represents the ratio between the mirrors width (Lm) and the photovoltaic module width (Lp);
- -
- c1, c2 are the width coefficients of PV module brushed by the rays reflected by the mirror;
- -
- kl is the longitudinal deviation coefficient, defined as the ratio between the additional length of the mirror (necessary for the compensation of the deviation of solar rays reflected, caused by the elevation deviations of the PV module from the solar elevation) and the photovoltaic module width.
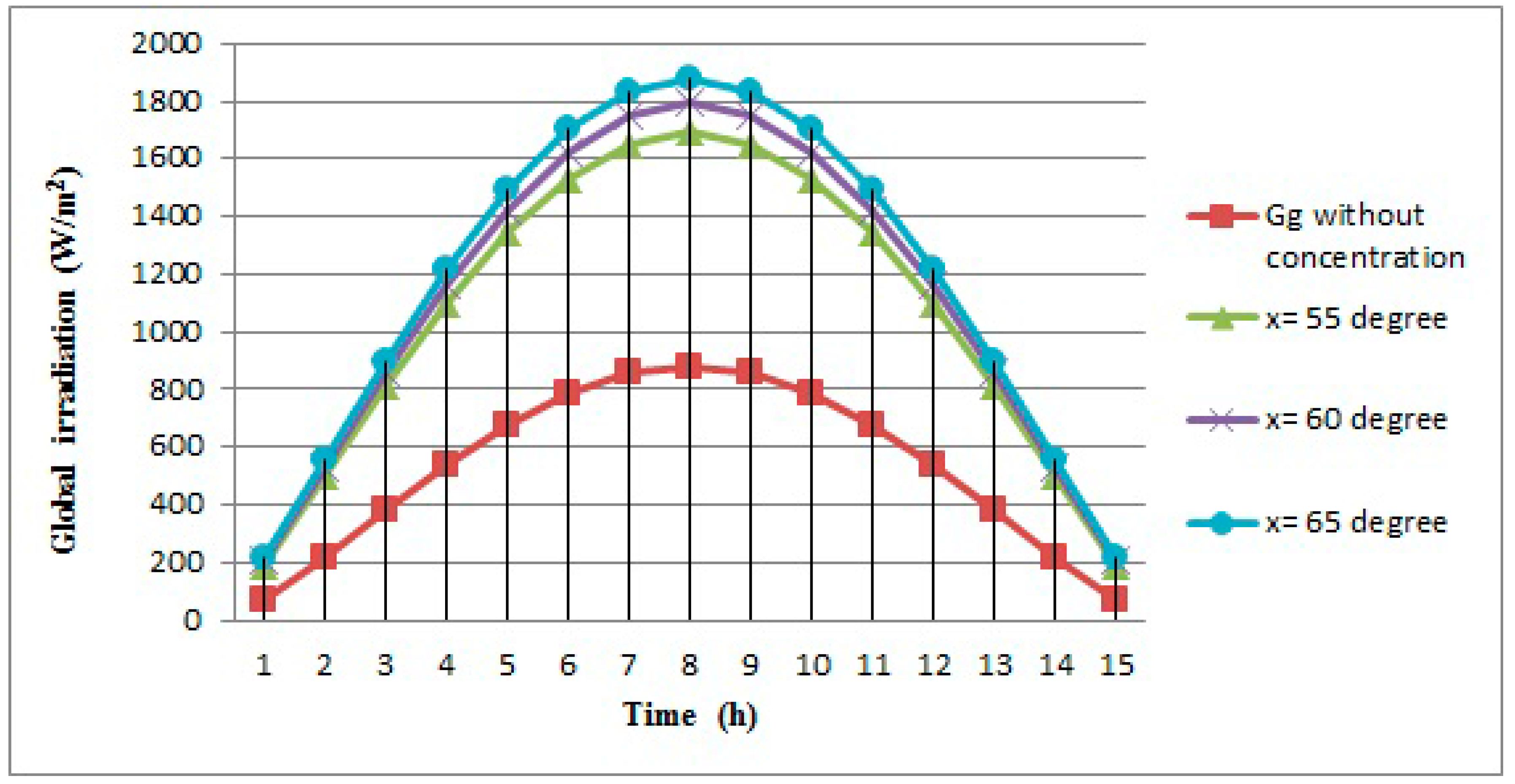
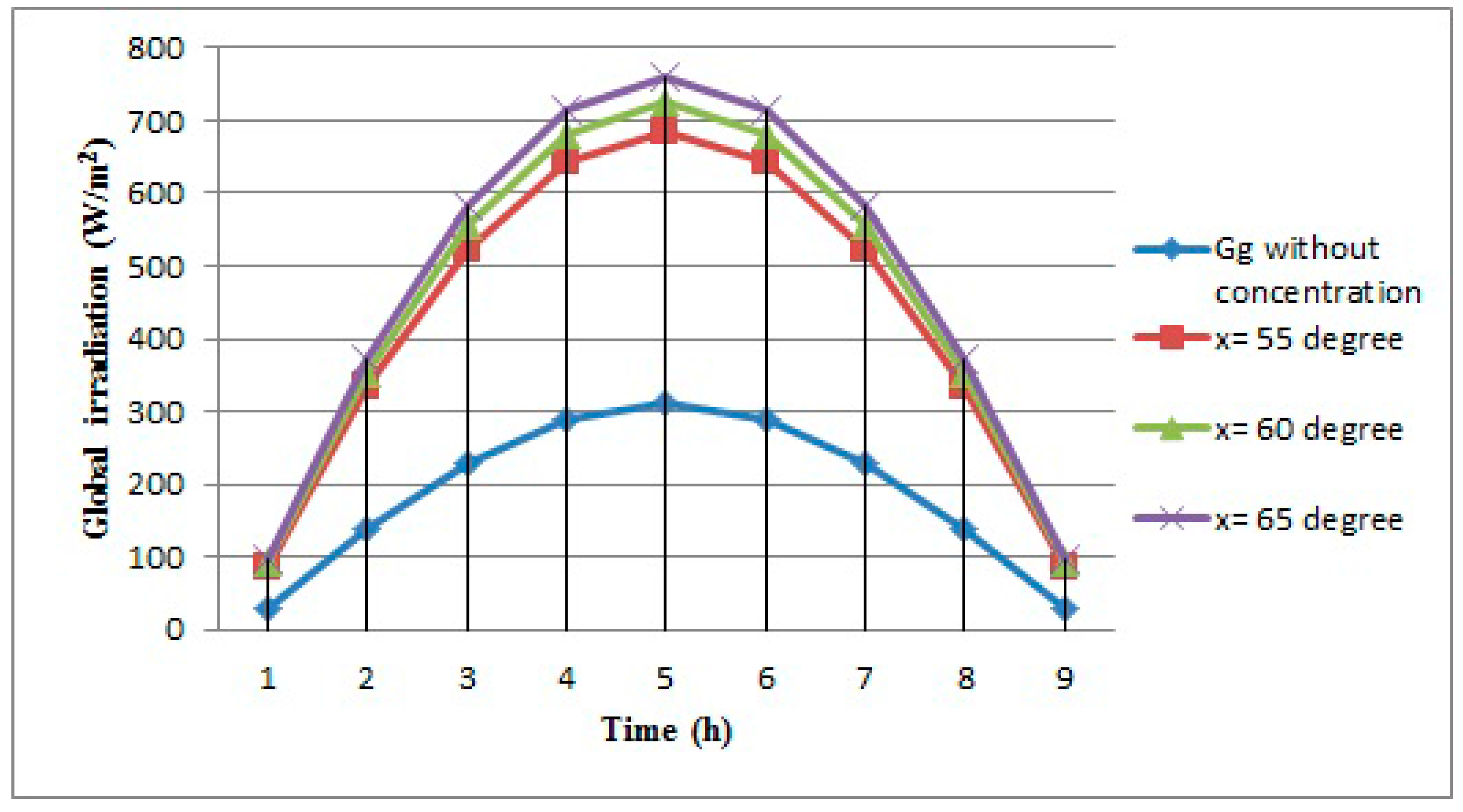
4. Experimental Results


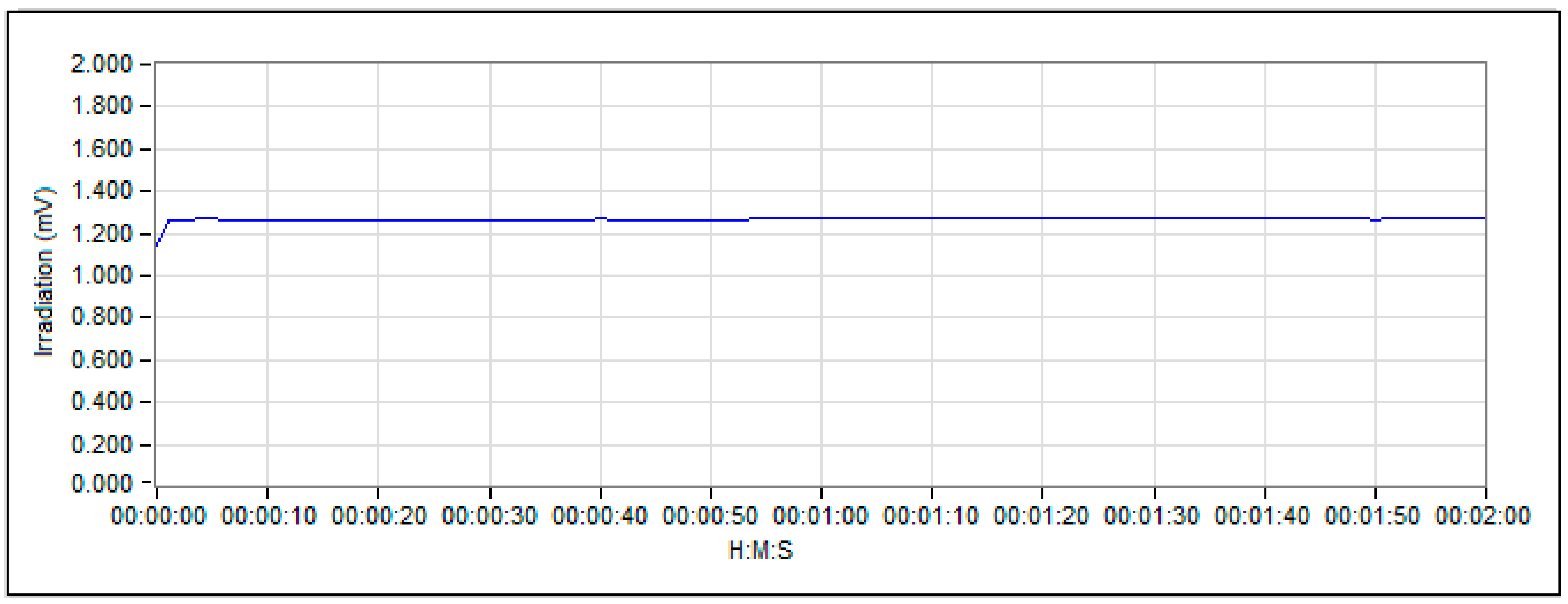
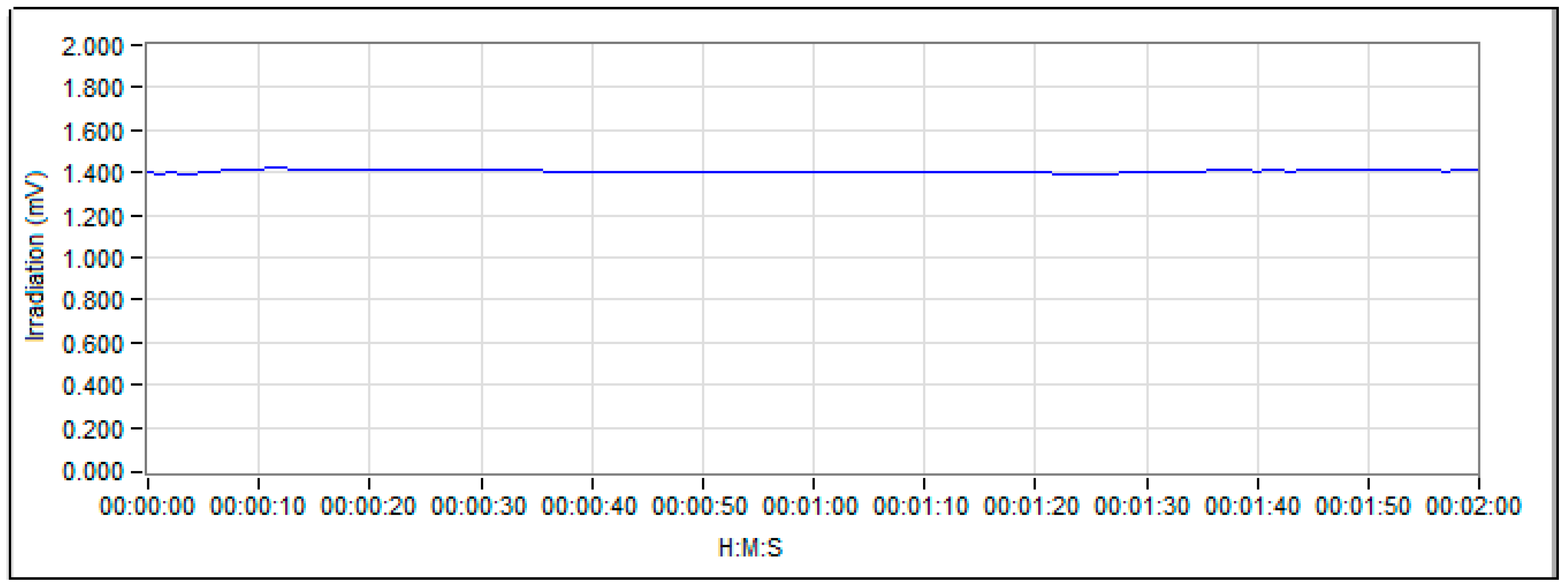
5. Conclusions
- -
- the models Adnot and Empiric for the global irradiation assessment can be adapted in the best way for the conditions of the location chosen for this study;
- -
- the main advantage of these models is their simplicity (these models have as input parameters only the location and time marks), which makes them easy to use in practice;
- -
- the values of solar irradiations obtained through the simulations are close enough to those indicated on the maps elaborated by professional institutes for the site took into study;
- -
- during travel through the atmosphere the solar rays decrease intensity as they are approaching the Earth;
- -
- the values of the solar irradiation on the PV panel plane are roughly two times higher than those on the PV panel plane without a concentration system.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Alboteanu, I.L.; Manolea, G.; Ravigan, F. Employement of photovoltaic energy for lighting vehicle railways. In Environmental Problems and Development, Proceedings of the 1st WSEAS International Conferences on Urban Rehabilitation and Sustainability (URES’08), Bucharest, Romania, 7–9 November 2008; pp. 104–110.
- Dazhia, Y.; Jirutitijaroena, P.; Walshb, W.M. The Estimation of Clear Sky Global Horizontal Irradiance at the Equator. Energy Procedia 2012, 25, 141–148. [Google Scholar]
- Alboteanu, I.L. Advanced Stand-Alone Photovoltaic System; “Universitaria” Publishing House: Craiova, Romania, 2013. [Google Scholar]
- Bratu, C. Evaluation of solar irradiance to a flat surface arbitrary oriented. Ann. Univ. Craiova Electr. Eng. Ser. 2008, 32, 310–314. [Google Scholar]
- Bădescu, V. Solar radiation availability in south-east of Romania. Renew. Energy Technol. Environ. 1992, 3, 2716–2720. [Google Scholar]
- Hermenean, I.; Vişa, I.; Dută, A.; Diaconescu, D. Modeling and Optimization of a CPV System with Equatorial Tracking. Bull. Transilv. Univ. Braşov. Ser. I Eng. Sci. 2010, 3, 79–86. [Google Scholar]
- Luque, A.; Andreev, L.V. Concentrator Photovoltaics; Springer-Verlag: Berlin, Germany, 2007. [Google Scholar]
- Grasso, G.; Morichetti, F.; Righetti, A.; Pietralunga, S.M. LCPV modules: A competitive solution. In Proceedings of the 38th IEEE Photovoltaic Specialists Conference (PVSC), Austin, TX, USA, 5–8 June 2012; IEEE: Washington, DC, USA, 2012; pp. 2048–2051. [Google Scholar]
- Paulescu, M.; Schlett, Z. Photovoltaic Conversion of Solar Energy; Mirton: Timişoara, Romania, 2001. [Google Scholar]
- Eftemie, E. Estimation of daily global and diffuse radiation for Brasov urban area, Romania. Available online: http://www.recentonline.ro/no_033.htm (accessed on 8 January 2015).
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering, 2nd ed.; Wiley-VCH: West Sussex, UK, 2011. [Google Scholar]
- Liu, B.Y.H.; Jordan, R.C. The inter-relationship and characteristic distribution of direct, diffuse and total solar radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar]
- Jurca, T.; Tulcan-Paulescu, E.; Dughira, C.; Lascua, M.; Gravila, P.; de Sabataa, A.; Luminosua, I.; de Sabataa, C.; Paulescu, M. Global Solar Irradiation Modeling and Measurements in Timisoara. Available online: http://dx.doi.org/10.1063/1.3647083 (accessed on 8 January 2015).
- Bostan, I.; Dulgheru, V.; Sobor, I.; Bostan, V.; Sochirean, A. Renewable Energy Conversion Systems; Tehnica-Info: Chisinau, Moldavia Republic, 2007. [Google Scholar]
- Messenger, R.; Ventre, J. Photovoltaic System Engineering, 2nd ed.; CRC Press: Boca Roton, FL, USA, 2004. [Google Scholar]
- Kasten, F.; Young, A. Revised optical air mass tables and approximation formula. Appl. Opt. 1989, 22, 4735–4738. [Google Scholar]
- Paulescu, M.; Schlett, Z. Performances assessment of global solar irradiation models under Romanian climate. Renew. Energy 2003, 5, 767–777. [Google Scholar]
- Photovoltaic Geographical Information System—Interactive Maps. Available online: http://re.jrc.ec.europa.eu/pvgis/apps4/pvest.php?lang=en&map=europe (accessed on 6 January 2015).
- Paulescu, M. Algorithms for Estimating Solar Energy; Matrix Rom: Bucharest, Romania, 2004. [Google Scholar]
- Alboteanu, I.L.; Ravigan, F.; Degeratu, S.; Sulea, C. Aspects of designing the tracking systems for photovoltaic panels with low concentration of solar radiation. In Computational Problems in Engineering II; Springer-Verlag: Cham, Switzerland, 2014. [Google Scholar]
- Alboteanu, I.L.; Bulucea, C.A.; Degeratu, S. Modeling of solar irradiation absorbed by a photovoltaic panel with low concentration. In Recent Advances in Environmental Sciences and Financial Development, Proceedings of the 2nd International Conferences on Environment, Energy, Ecosystems and Development—EEEAD 2014, Athens, Greece, 28–30 November 2014; pp. 16–21.
- WS Energia, Double Sun System. Available online: http://ws-energia.pt/np4PT/home.html (accessed on 9 January 2015).
- Hermenean, I.; Vişa, I.; Dută, A.; Diaconescu, D. Modelling and Optimization of a Concentrating PV-Mirror System. Renew. Energy Power Qual. J. 2010, 8, 480–486. [Google Scholar]
- LI-200 Pyranometer Light Sensors. Available online: http://www.licor.com/env/products/light/pyranometers/ (accessed on 6 January 2015).
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alboteanu, I.L.; Bulucea, C.A.; Degeratu, S. Estimating Solar Irradiation Absorbed by Photovoltaic Panels with Low Concentration Located in Craiova, Romania. Sustainability 2015, 7, 2644-2661. https://doi.org/10.3390/su7032644
Alboteanu IL, Bulucea CA, Degeratu S. Estimating Solar Irradiation Absorbed by Photovoltaic Panels with Low Concentration Located in Craiova, Romania. Sustainability. 2015; 7(3):2644-2661. https://doi.org/10.3390/su7032644
Chicago/Turabian StyleAlboteanu, Ionel L., Cornelia A. Bulucea, and Sonia Degeratu. 2015. "Estimating Solar Irradiation Absorbed by Photovoltaic Panels with Low Concentration Located in Craiova, Romania" Sustainability 7, no. 3: 2644-2661. https://doi.org/10.3390/su7032644
APA StyleAlboteanu, I. L., Bulucea, C. A., & Degeratu, S. (2015). Estimating Solar Irradiation Absorbed by Photovoltaic Panels with Low Concentration Located in Craiova, Romania. Sustainability, 7(3), 2644-2661. https://doi.org/10.3390/su7032644