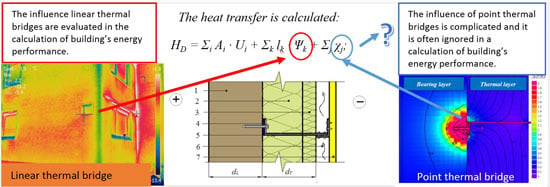
A Simplified Methodology for Evaluating the Impact of Point Thermal Bridges on the High-Energy Performance of a Passive House
Abstract
:1. Introduction
2. Methodology
2.1. Calculation of U-value of Building Element Assessing Thermal Bridges
2.2. Numerical Simulation
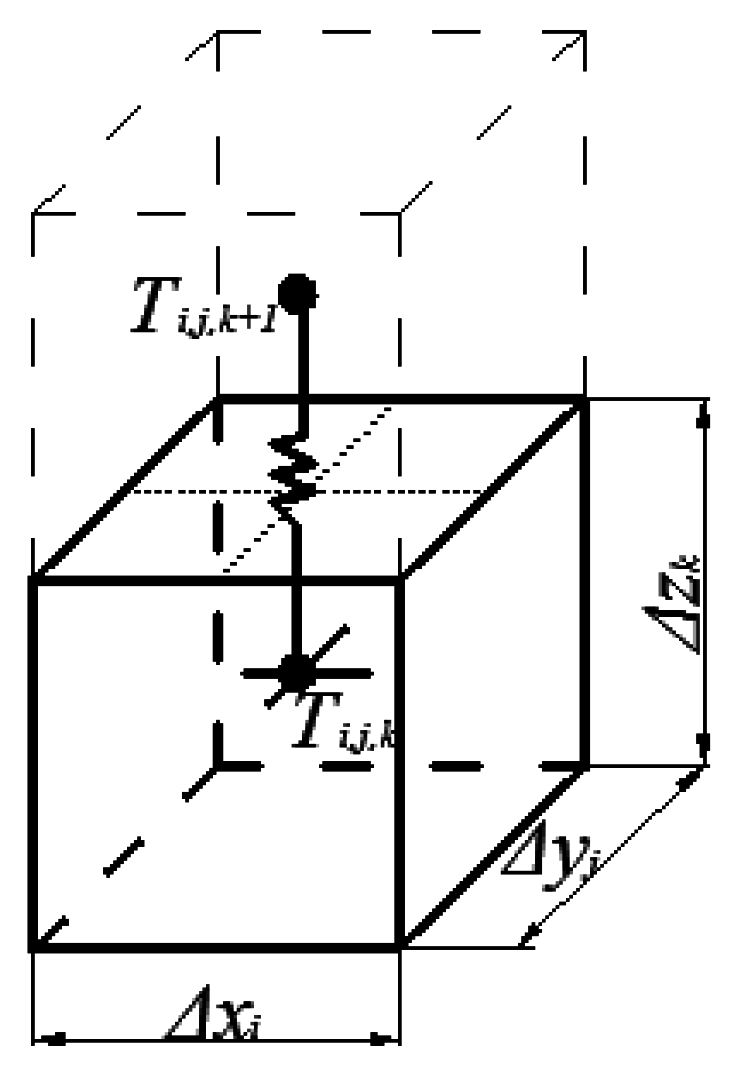
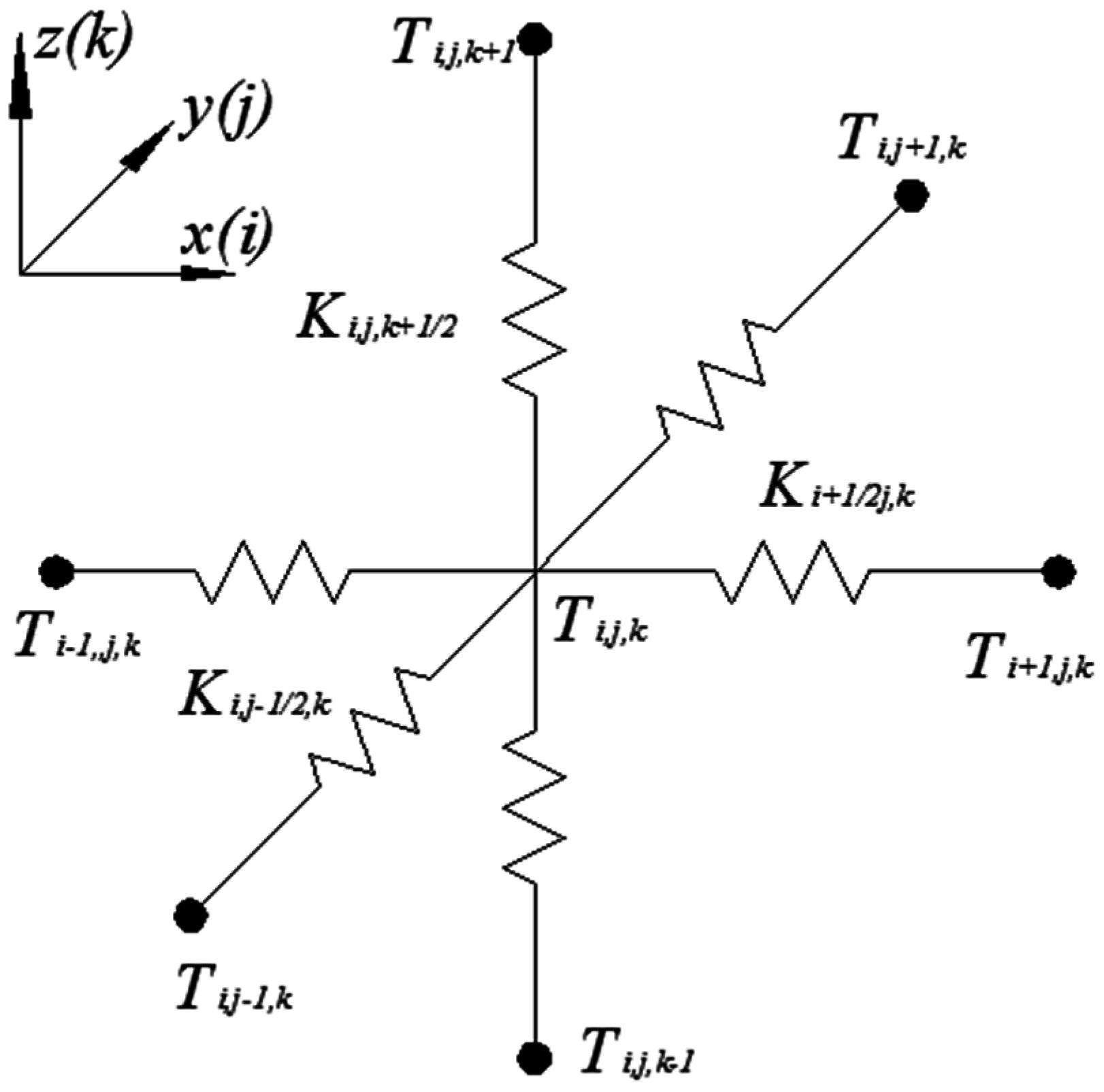
2.3. Simulation Parameters
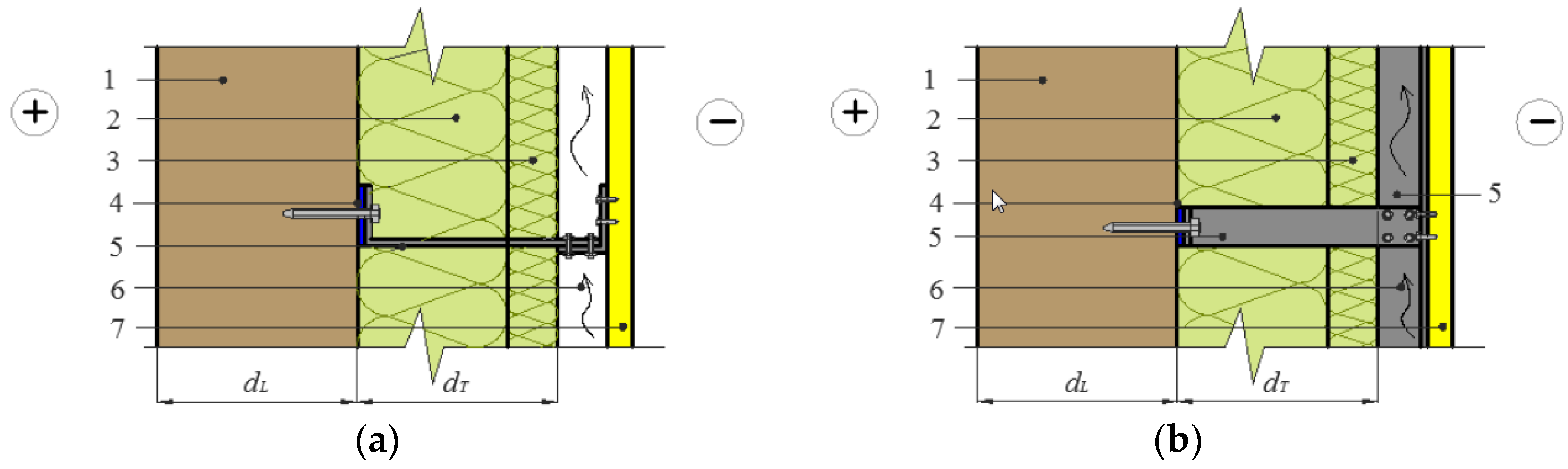
| Variants | dL (mm) | λL (W/ m∙K) | dT (mm) | λT (W/ m∙K) |
|---|---|---|---|---|
| Basic data | 200 | 0.5 | 150 | 0.034 |
| 1 | 200 | 0.1 ÷ 1 | 150 | 0.034 |
| 2 | 50 ÷ 500 | 0.5 | 150 | 0.034 |
| 3 | 200 | 0.5 | 150 | 0.030 ÷ 0.040 |
| 4 | 200 | 0.5 | 100 ÷ 200 | 0.034 |
2.4. Statistical Evaluation
3. Results
3.1. Heat Flow Behavior Through Point Thermal Bridge
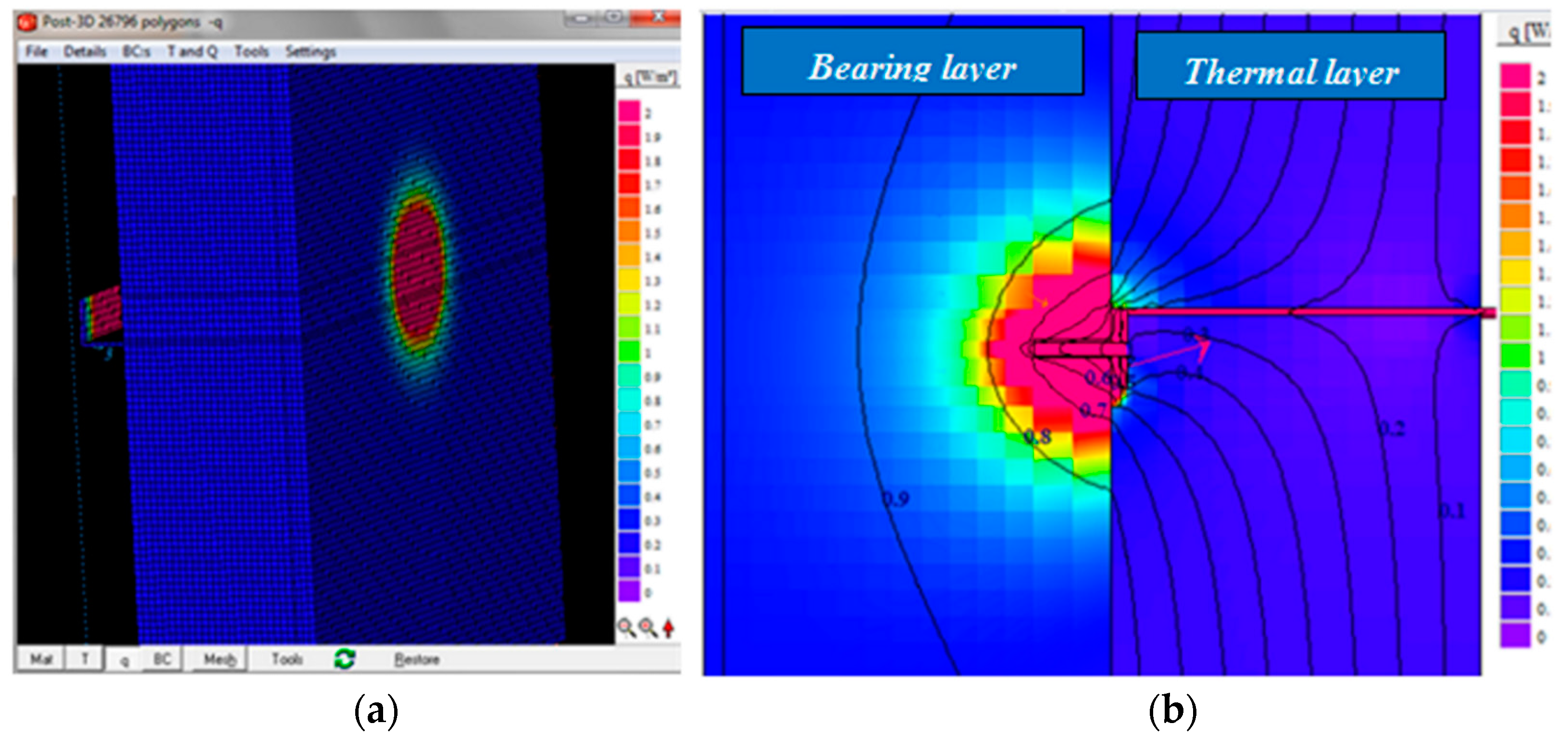
3.2. Evaluation of the Dependence of a Point Thermal Bridge

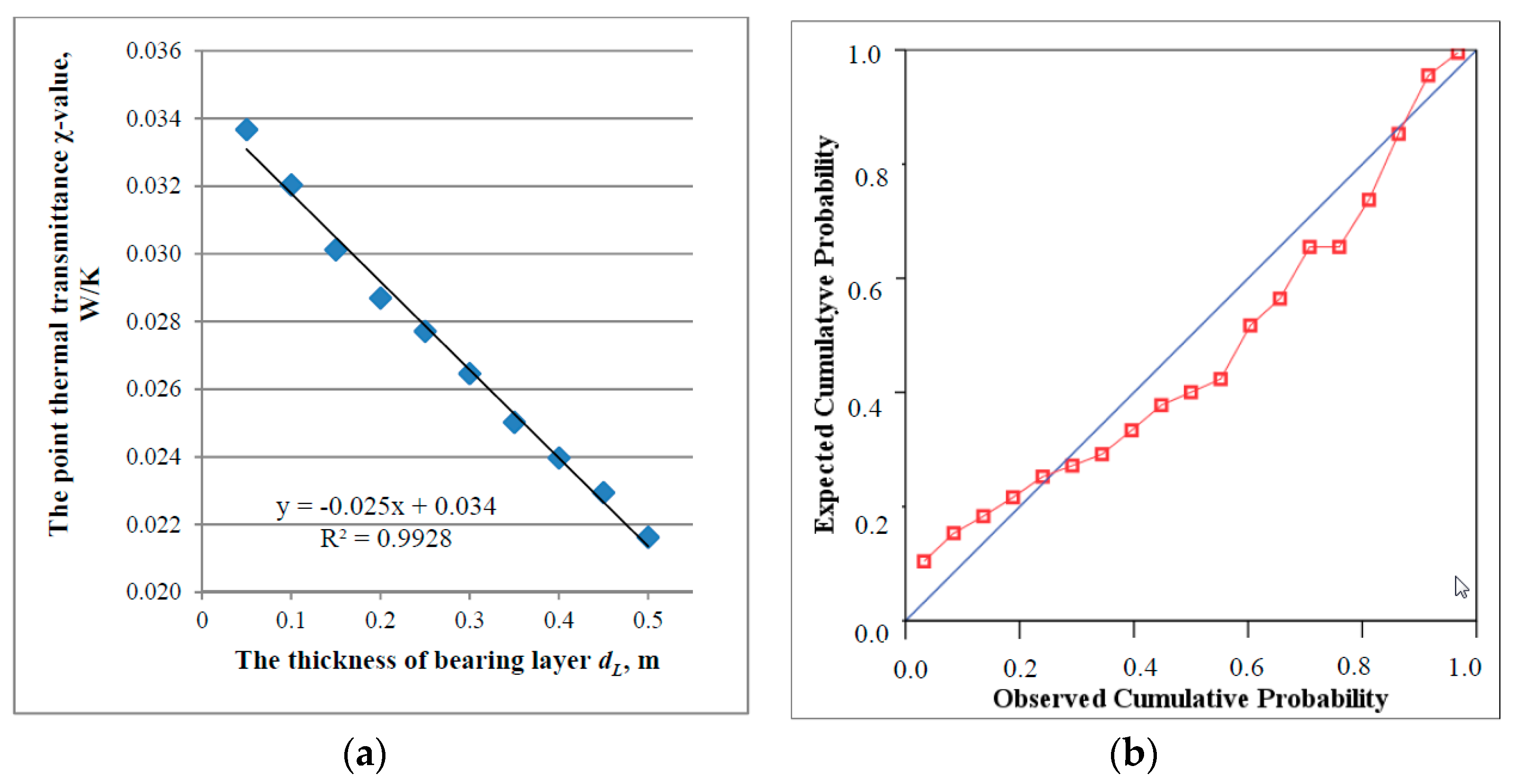
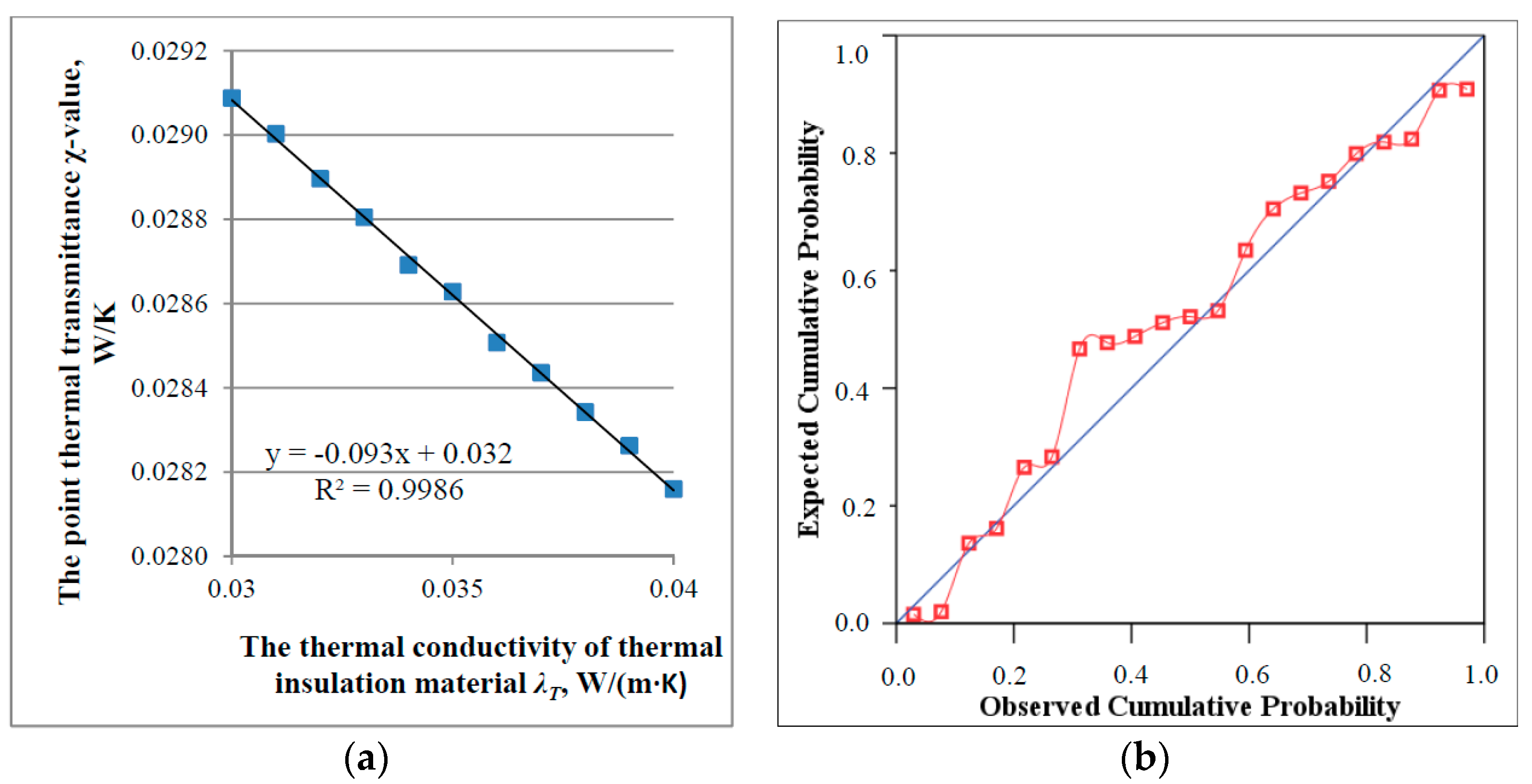
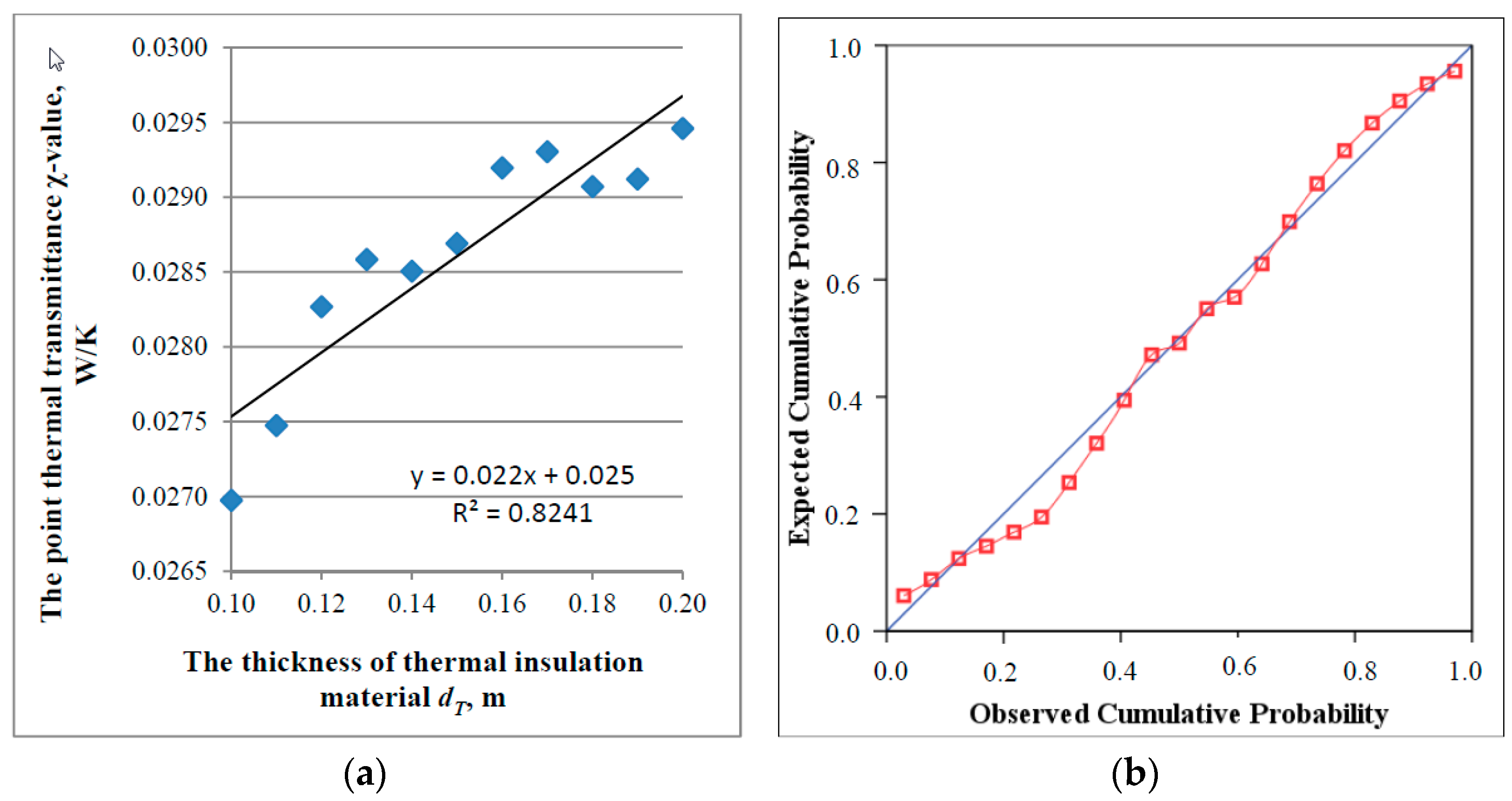
3.3. Simplified Methodology for the Evaluation of the Point Thermal Bridge
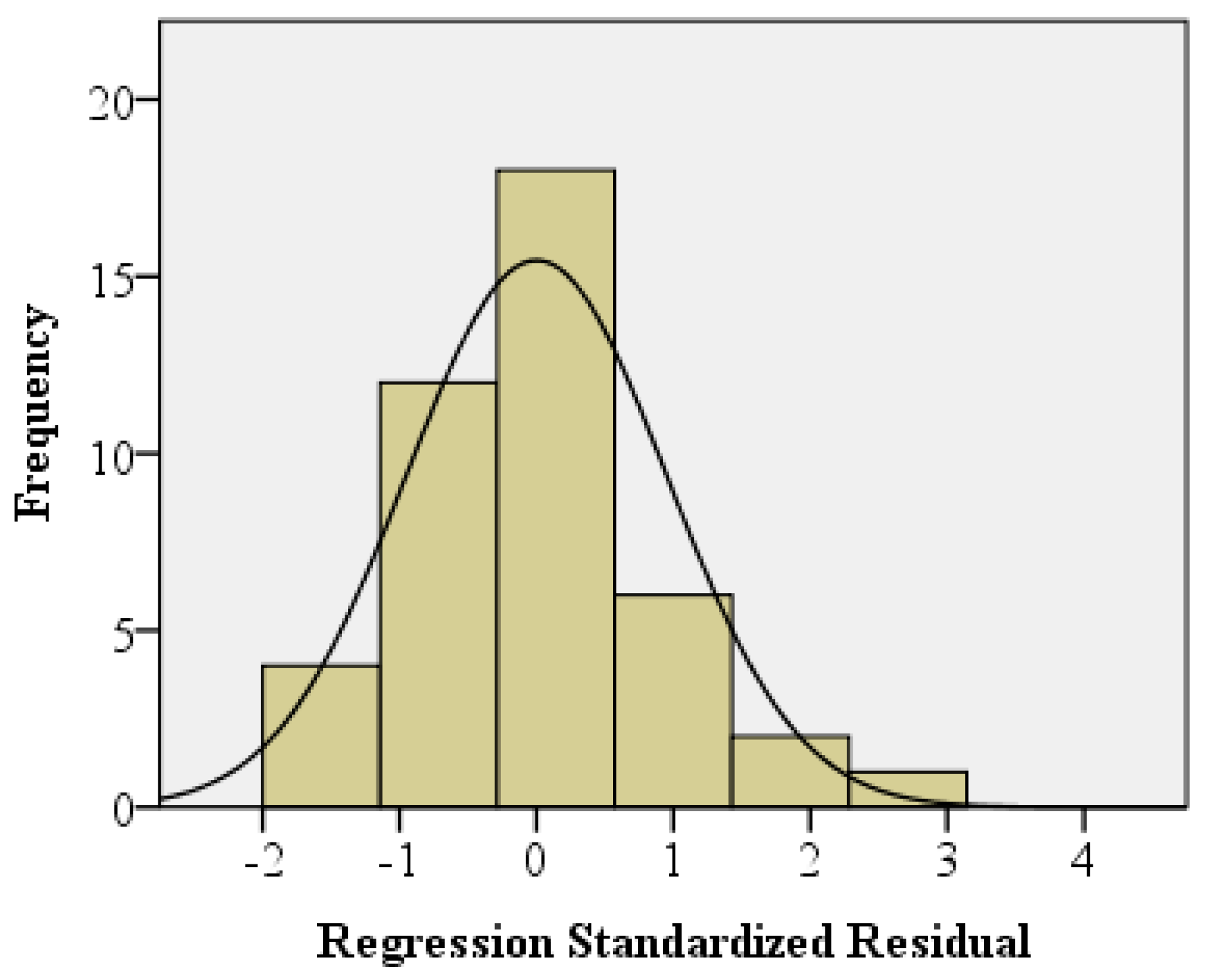

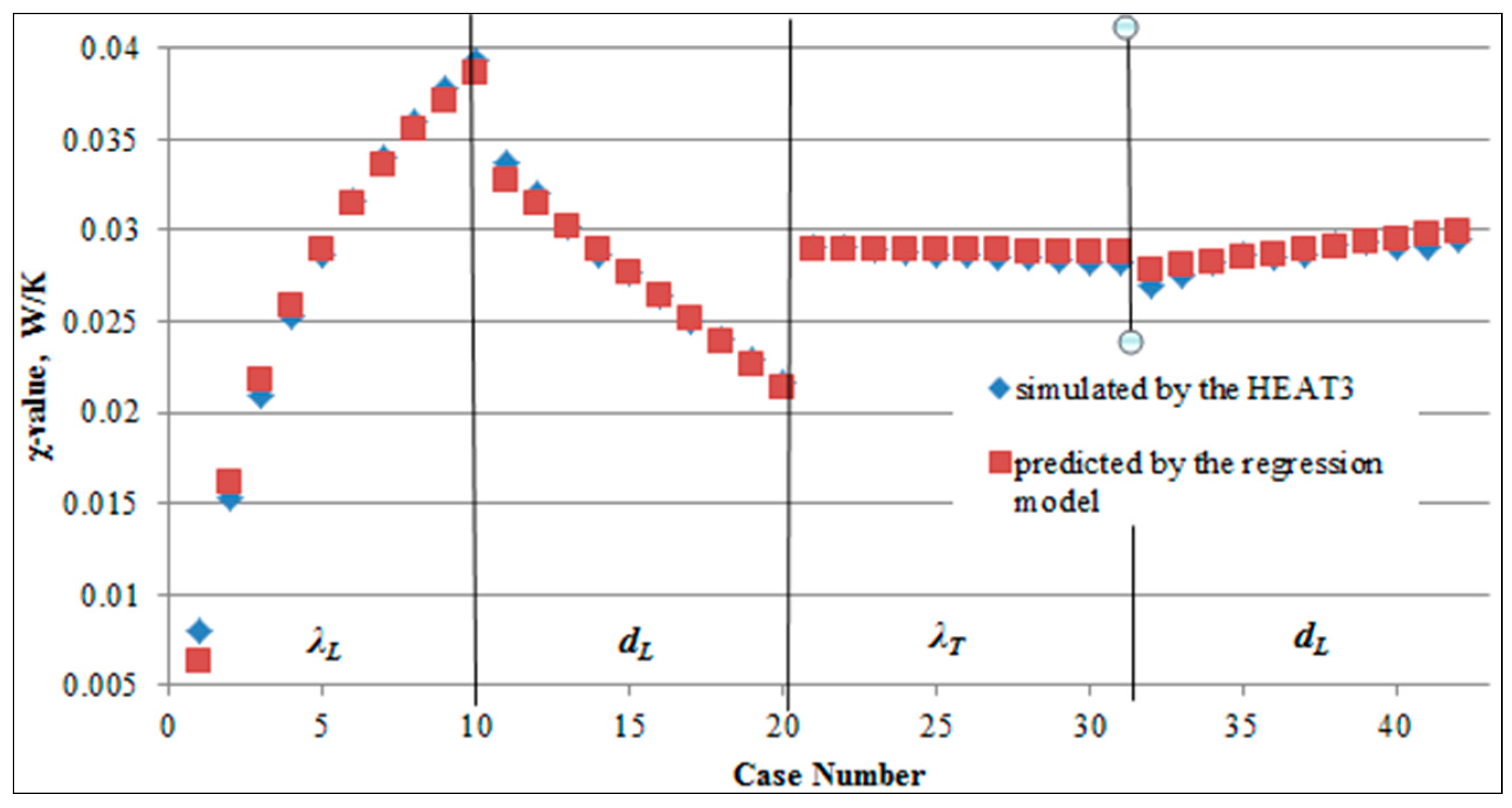
4. Discussion

5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| A | Area of element i of the building envelope [m2] |
| Ui | Thermal transmittance of element i of the building envelope [W/(m2∙K)] |
| Uj | Thermal transmittance of the 1-D component j separating the two environments being considered [W/(m2∙K)] |
| ΔU | Transmittance correction factor [W/(m2∙K)] |
| K | Thermal conductance [W/K] |
| lj | Length within the 2-D geometrical model over which the value of Uj applies [m] |
| lk | Length of linear thermal bridge k [m] |
| χj | Point thermal transmittance of the point thermal bridge j [W/K] |
| L2D | Linear thermal coupling coefficient obtained from a 2-D calculation of the component separating the two environments being considered [W/m∙K] |
| L3D | Thermal coupling coefficient obtained from a 3-D calculation of the component separating the two environments being considered [W/m∙K] |
| n | Number of fasteners per surface area [pcs./m2] |
| HS | Specific heat losses through repeated surface area without a fastener [W/K] |
| H | Specific heat losses through repeated surface area with a fastener [W/K] |
| H0 | Zero hypothesis [-] |
| Ha | Alternative hypothesis [-] |
| F | Fisher distribution [-] |
| hD | Direct heat transfer coefficient [W/K] |
| Qi,j,k, | Total heat flow to cell (i,j,k) from the six adjacent cells [W] |
| T | Temperature [K] |
| RT | Thermal resistance [(m2·K)/W] |
| R | Correlation coefficient [-] |
| d | Thickness of the layer [m] |
Regression sum of squares [-] | |
Residual sum of squares [-] | |
| Greek letters | |
| λ | Thermal conductivity coefficient [W/(m·K)] |
| Ψk | Linear thermal transmittance of linear thermal bridge k [W/(m∙K)] |
| Ψj | Linear thermal transmittance of linear thermal bridge j [W/(m∙K)] |
| Δxi·Δyj | Conductance referring to the total heat flow through the area [m] |
| Δzk | Z-direction for half of the cell (i,j,k) [m] |
| α | Significance level [-] |
| β | Coefficient of independent variables [-] |
| Subscripts | |
| L | Refers to the bearing layer of the external wall [-] |
| T | Refers to the insulation layer of the external wall [-] |
References
- The International Organization for Standardization (ISO). Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures--Detailed Calculations; The International Organization for Standardization (ISO): Geneva, Switzerland, 2007. [Google Scholar]
- Theodosiou, T.G.; Papadopoulos, A.M. The impact of thermal bridges on the energy demand of buildings with double brick wall constructions. Energy Build. 2008, 40, 2083–2089. [Google Scholar] [CrossRef]
- Evola, G.; Margani, G.; Marletta, L. Energy and cost evaluation of thermal bridge correction in Mediterranean climate. Energy Build. 2011, 43, 2385–2393. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; de Rossi, F.; Turni, G.; Vanoli, G.P. Different methods for the modelling of thermal bridges into energy simulation programs: Comparisons of accuracy for flat heterogeneous roofs in Italian climates. Appl. Energy 2012, 97, 405–418. [Google Scholar] [CrossRef]
- Theodosiou, T.; Tsikaloudaki, K.; Bikas, D.; Aravantinos, D.; Kontoleon, K.N. Assessing the Use of Simplilied and Analytical Methods for Approaching Thermal Bridges with Regard to Their Impact on the Thermal Performance of the Building Envelope. Available online: http://wsb14barcelona.org/programme/pdf_poster/P-059.pdf (accessed on 20 October 2015).
- Ascione, F.; Bianco, N.; de Masi, R.F.; Mauro, G.M.; Vanoli, G.P. Design of the building envelope: A novel multi-objective approach for the optimization of energy performance and thermal comfort. Sustainability 2015, 7, 10809–10836. [Google Scholar] [CrossRef]
- Capozzoli, A.; Gorrino, A.; Corrado, V. A building thermal bridges sensitivity analysis. Appl. Energy 2013, 107, 229–243. [Google Scholar] [CrossRef]
- Ge, H.; McClung, V.R.; Zhang, S. Impact of balcony thermal bridges on the overall thermal performance of multi-unit residential buildings: A case study. Energy Build. 2013, 60, 163–173. [Google Scholar] [CrossRef]
- Cappelletti, F.; Gasparella, A.; Romagnoni, P.; Baggio, P. Analysis of the influence of installation thermal bridges on windows performance: The case of clay block walls. Energy Build. 2011, 43, 1435–1442. [Google Scholar] [CrossRef]
- Citterio, M.; Cocco, M.; Erhorn-Klutting, H. Thermal Bridges in the EPBD Context: Overview on MS Approaches in Regulations. Available online: http://www.buildup.eu/sites/default/files/P064_EN_ASIEPI_WP4_IP1_p3073.pdf (accessed on 15 June 2015).
- Gao, Y.; Roux, J.J.; Zhao, L.H.; Jiang, Y. Dinamical building simulation: A low order model for thermal bridges losses. Energy Build. 2008, 40, 2236–2243. [Google Scholar] [CrossRef]
- Tadeu, A.; Simoes, I.; Simoes, N.; Prata, J. Simulation of dynamic liner thermal bridges using a boundary element method model in the frequency domain. Energy Build. 2011, 43, 3685–3695. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; de Masi, R.F.; Mauro, G.M.; Musto, M.; Vanoli, G.P. Experimental validation of a numerical code by thin film heat flux sensors for the resolution of thermal bridges in dynamic conditions. Appl. Energy 2014, 124, 213–222. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; De Masi, R.F.; de’Rossi, F.; Vanoli, G.P. Simplified state space representation for evaluating thermal bridges in building: Modelling, application and validation of a methodology. Appl. Therm. Eng. 2013, 61, 344–354. [Google Scholar] [CrossRef]
- Sierra, f.; Bai, J.; Maksoud, T. Impact of the simplification of the methodology used to assess the thermal bridge of the head of an opening. Energy Build. 2015, 87, 342–347. [Google Scholar] [CrossRef]
- Albatici, R.; Tonelli, A.M. Infrared thermovision technique for the assessment of thermal transmittance value of opaque building elements on site. Energy Build. 2010, 42, 2177–2183. [Google Scholar] [CrossRef]
- Desogus, G.; Mura, S.; Ricciu, R. Comparing different approaches to in situ measurement of building components thermal resistance. Energy Build. 2011, 43, 2613–2620. [Google Scholar] [CrossRef]
- Martin, K.; Escudero, C.; Erkoreka, A.; Flores, I.; Sala, J.M. Equivalent wall method for dynamic characterization of thermal bridges. Energy Build. 2012, 55, 704–714. [Google Scholar] [CrossRef]
- Bianchi, F.; Pisello, A.L.; Baldinelli, G.; Asdrubali, F. Infrared thermography assessment of thermal bridges in building envelope: Experimental validation in a test room setup. Sustainability 2014, 6, 7107–7120. [Google Scholar] [CrossRef]
- Berggren, B.; Wall, M. Calculation of thermal bridges in (Nordic) building envelopes—Risk of performance failure due to inconsistent use of methodology. Energy Build. 2013, 65, 331–339. [Google Scholar] [CrossRef]
- The International Organization for Standardization (ISO). Thermal Bridges in Building Construction—Linear Thermal Transmittance—Simplified Methods and Default Values; The International Organization for Standardization (ISO): Geneva, Switzerland, 2007. [Google Scholar]
- Petranek, V.; Subrit, R.; Plachy, J.; Nevrivova, L.; Petricek, T.; Kalousek, L.; Caha, Z. Thermal bridges in insulation system. Therm. Power Electr. Eng. 2013. [Google Scholar] [CrossRef]
- Qasass, R.; Gorgolewski, M.; Ge, H. Timber framing factor in Toronto residential house construction. Archit. Sci. Rev. 2014, 57, 159–168. [Google Scholar] [CrossRef]
- Gomes, A.P.; de Souza, H.A.; Tribess, A. Impact of thermal bridging on the performance of building using Light Steel Framing in Brazil. Appl. Therm. Eng. 2013, 52, 84–89. [Google Scholar] [CrossRef]
- Martin, K.; Erkoreka, A.; Flores, I.; Odriozola, M.; Sala, J.M. Problems in the calculation of thermal bridges in dynamic conditions. Energy Build. 2011, 43, 529–535. [Google Scholar] [CrossRef]
- De Andelis, E.; Serra, E. Light steel-frame walls: Thermal insulation performances and thermal bridges. Energy Procedia 2014, 45, 362–371. [Google Scholar] [CrossRef]
- The International Organization for Standardization (ISO). Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Method; The International Organization for Standardization (ISO): Geneva, Switzerland, 2007. [Google Scholar]
- Ministry of Environment of Republic of Lithuania. STR 2.05.01:2013. Energy performance of Buildings Design; Ministry of Environment of Republic of Lithuania: Vilnius, Lithuania, 2013. (In Lithuanian) [Google Scholar]
- Blomberg, T. Heat Conduction in two and three Dimensions Computer Modelling of Building Physics Applications; Report TVBH-1008; Byggnadsfysik LTH, Lunds Tekniska Högskola: Lund, Sweden, 1996. [Google Scholar]
- Claesson, J. Dynamic Thermal Networks: A Methodology to Account for Time-dependent Heat Conduction. Available online: http://www.irbnet.de/daten/iconda/CIB2503.pdf (accessed on 2 September 2015).
- Theodosiou, T.G.; Tsikaloudaki, A.G.; Kontoleon, K.J.; Bikas, D.K. Thermal bridging analysis on cladding systems for building facades. Energy Build. 2015, 109, 377–384. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šadauskienė, J.; Ramanauskas, J.; Šeduikytė, L.; Daukšys, M.; Vasylius, A. A Simplified Methodology for Evaluating the Impact of Point Thermal Bridges on the High-Energy Performance of a Passive House. Sustainability 2015, 7, 16687-16702. https://doi.org/10.3390/su71215840
Šadauskienė J, Ramanauskas J, Šeduikytė L, Daukšys M, Vasylius A. A Simplified Methodology for Evaluating the Impact of Point Thermal Bridges on the High-Energy Performance of a Passive House. Sustainability. 2015; 7(12):16687-16702. https://doi.org/10.3390/su71215840
Chicago/Turabian StyleŠadauskienė, Jolanta, Juozas Ramanauskas, Lina Šeduikytė, Mindaugas Daukšys, and Algimantas Vasylius. 2015. "A Simplified Methodology for Evaluating the Impact of Point Thermal Bridges on the High-Energy Performance of a Passive House" Sustainability 7, no. 12: 16687-16702. https://doi.org/10.3390/su71215840
APA StyleŠadauskienė, J., Ramanauskas, J., Šeduikytė, L., Daukšys, M., & Vasylius, A. (2015). A Simplified Methodology for Evaluating the Impact of Point Thermal Bridges on the High-Energy Performance of a Passive House. Sustainability, 7(12), 16687-16702. https://doi.org/10.3390/su71215840