Development of a High Performance PES Ultrafiltration Hollow Fiber Membrane for Oily Wastewater Treatment Using Response Surface Methodology
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Materials
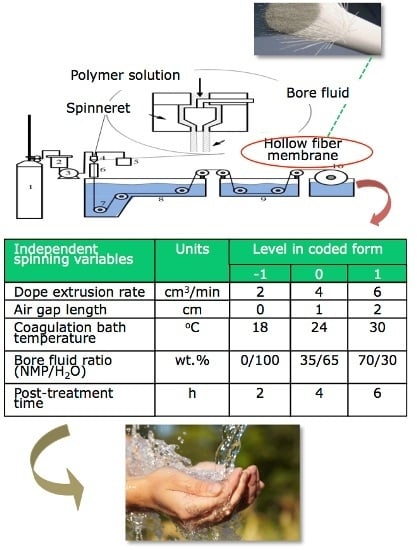
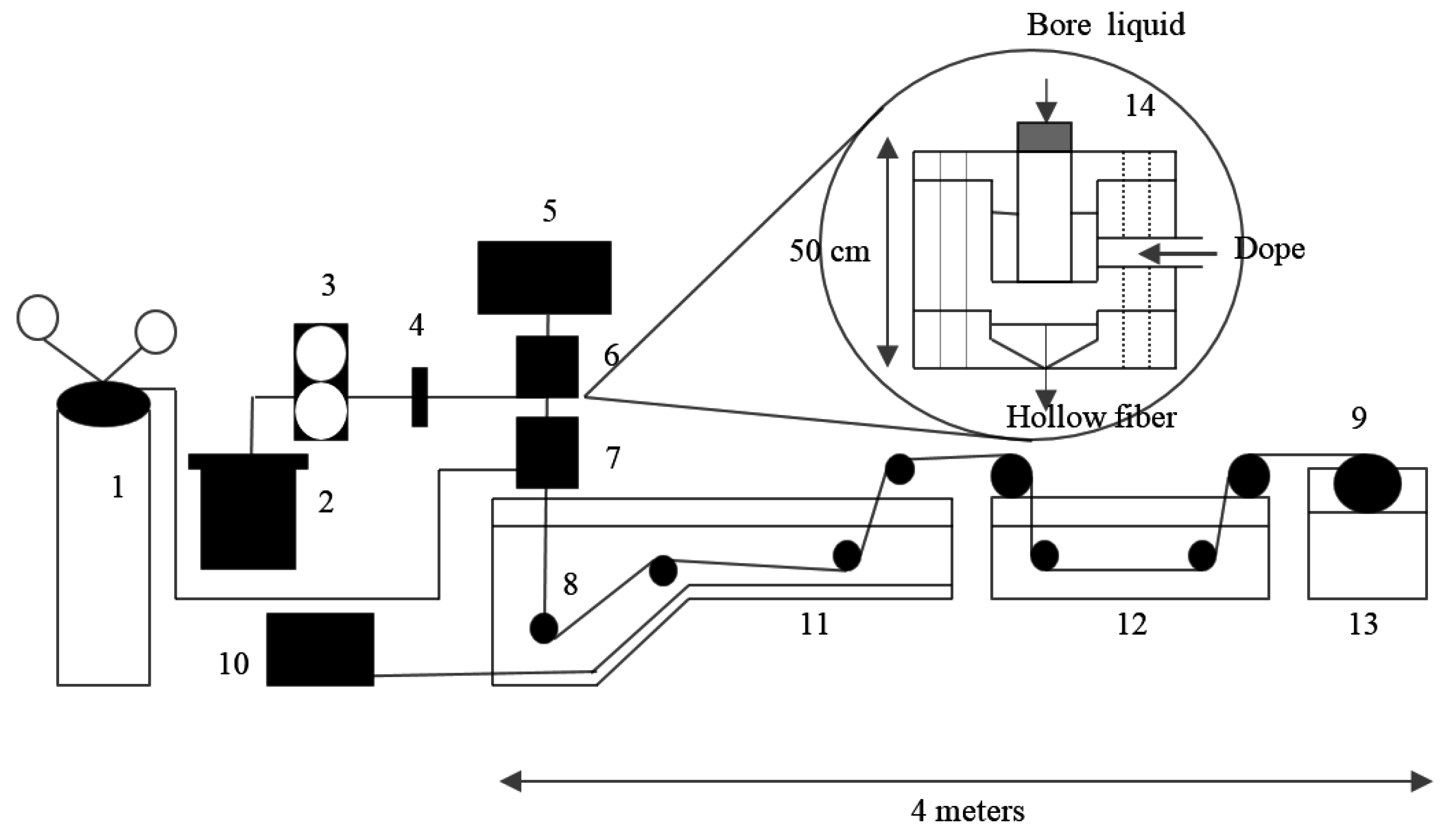
2.2. Procedures of the Dry/Wet Spinning Process
2.3. Oily Wastewater Treatment by Ultrafiltration Process

- Cp = the solute concentration of permeate;
- Cf = the solute concentration of feed.
2.4. Experimental Design
| Spinning Variables | Units | Level in Coded Form | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| DER, (A) | cm3/min | 2 | 4 | 6 |
| AGL, (B) | cm | 0 | 1 | 2 |
| CBT, (C) | °C | 18 | 24 | 30 |
| BFR, (D) | NMP/H2O, wt % | 0/100 | 35/65 | 70/30 |
| PT, (E) | h | 2 | 4 | 6 |
| Std. Order | Run Order | Values of Spinning Conditions | Response | ||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | Rejection (%) | ||
| 1 | 4 | 2 | 0 | 18 | 0/100 | 6 | 34.76 |
| 2 | 13 | 6 | 0 | 18 | 0/100 | 2 | 62.40 |
| 3 | 7 | 2 | 2 | 18 | 0/100 | 2 | 41.59 |
| 4 | 5 | 6 | 2 | 18 | 0/100 | 6 | 97.67 |
| 5 | 19 | 2 | 0 | 30 | 0/100 | 2 | 99.95 |
| 6 | 16 | 6 | 0 | 30 | 0/100 | 6 | 100 |
| 7 | 1 | 2 | 2 | 30 | 0/100 | 6 | 71 |
| 8 | 8 | 6 | 2 | 30 | 0/100 | 2 | 96.19 |
| 9 | 2 | 2 | 0 | 18 | 70/30 | 2 | 8.98 |
| 10 | 11 | 6 | 0 | 18 | 70/30 | 6 | 22 |
| 11 | 12 | 2 | 2 | 18 | 70/30 | 6 | 65.93 |
| 12 | 3 | 6 | 2 | 18 | 70/30 | 2 | 93 |
| 13 | 18 | 2 | 0 | 30 | 70/30 | 6 | 52.86 |
| 14 | 14 | 6 | 0 | 30 | 70/30 | 2 | 10.08 |
| 15 | 10 | 2 | 2 | 30 | 70/30 | 2 | 85.11 |
| 16 | 20 | 6 | 2 | 30 | 70/30 | 6 | 90 |
| 17 | 15 | 4 | 1 | 24 | 35/65 | 4 | 55 |
| 18 | 9 | 4 | 1 | 24 | 35/65 | 4 | 46.51 |
| 19 | 6 | 4 | 1 | 24 | 35/65 | 4 | 47.77 |
| 20 | 17 | 4 | 1 | 24 | 35/65 | 4 | 46.42 |
| 21 | 28 | 2 | 1 | 24 | 35/65 | 4 | 36.42 |
| 22 | 25 | 6 | 1 | 24 | 35/65 | 4 | 49 |
| 23 | 27 | 4 | 0 | 24 | 35/65 | 4 | 49.10 |
| 24 | 26 | 4 | 2 | 24 | 35/65 | 4 | 45.99 |
| 25 | 23 | 4 | 1 | 18 | 35/65 | 4 | 48.00 |
| 26 | 22 | 4 | 1 | 30 | 35/65 | 4 | 47.00 |
| 27 | 24 | 4 | 1 | 24 | 0/100 | 4 | 81.25 |
| 28 | 21 | 4 | 1 | 24 | 70/30 | 4 | 54.82 |
2.5. Response Surface Methodology
3. Results and Discussion
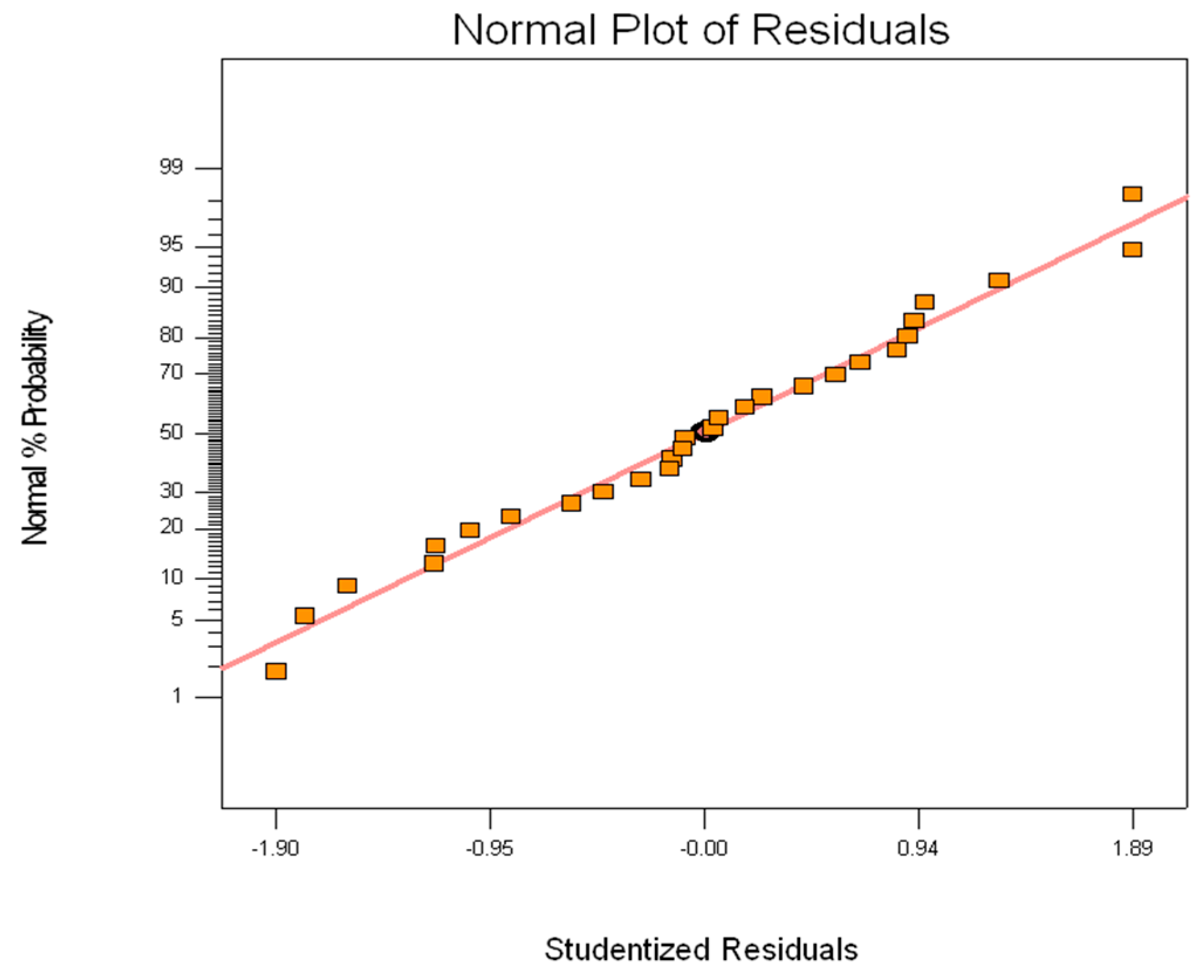
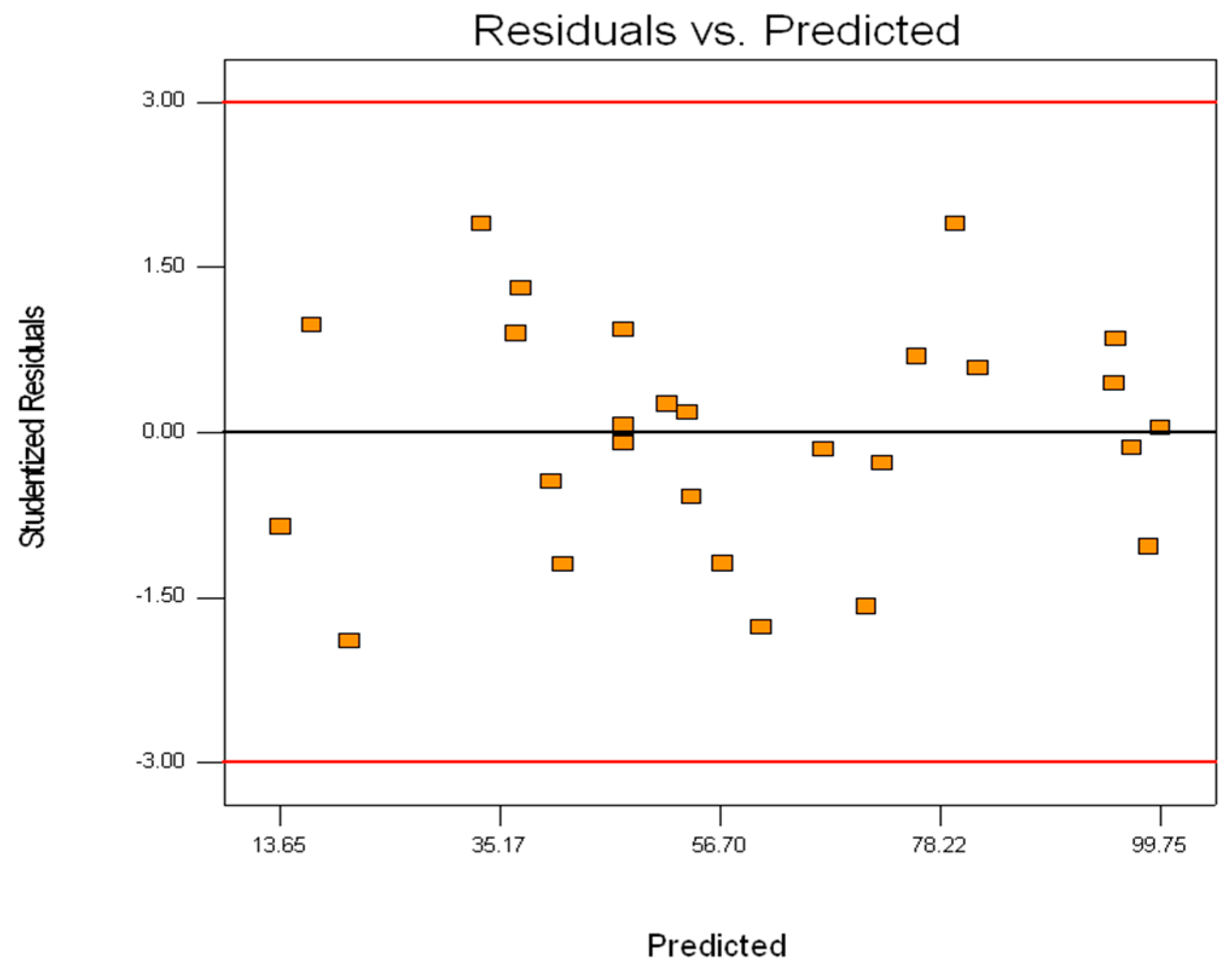
3.1. ANOVA Analysis
| Source | Sum of Squares | DF | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|---|
| Block | 561.59 | 1 | 561.59 | |||
| Model | 16,760.58 | 14 | 1197.18 | 11.83 | <0.0001 | sig. |
| A | 850.64 | 1 | 850.64 | 8.41 | 0.0133 | |
| B | 3371.57 | 1 | 3371.57 | 33.33 | <0.0001 | |
| C | 1757.45 | 1 | 1757.45 | 17.37 | 0.0013 | |
| D | 2267.56 | 1 | 2267.56 | 22.42 | 0.0005 | |
| A2 | 59.65 | 1 | 59.65 | 0.59 | 0.4574 | |
| B2 | 6.693 × 10−4 | 1 | 6.693 × 10−4 | 6.617 × 10−6 | 0.9980 | |
| C2 | 9.509 × 10−3 | 1 | 9.509 × 10−3 | 9.4 × 10−5 | 0.9924 | |
| D2 | 1062.46 | 1 | 1062.46 | 10.50 | 0.0071 | |
| AB | 830.88 | 1 | 830.88 | 8.21 | 0.0142 | |
| AC | 1163.83 | 1 | 1163.83 | 11.51 | 0.0053 | |
| AD | 712.36 | 1 | 712.36 | 7.04 | 0.0210 | |
| BC | 513.48 | 1 | 513.48 | 5.08 | 0.0438 | |
| BD | 3328.71 | 1 | 3328.71 | 32.91 | <0.0001 | |
| CD | 426.22 | 1 | 426.22 | 4.21 | 0.0626 | |
| Residual | 1213.88 | 12 | 101.16 | |||
| Lack of Fit | 1163.53 | 9 | 129.28 | 7.70 | 0.0601 | not sig |
| Pure Error | 50.35 | 3 | 16.78 | |||
| Cor Total | 18,534.04 | 27 | ||||
| Std. Dev. | 10.06 | R-Squared | 0.9325 | |||
| Mean | 58.53 | Adj R-Squared | 0.8537 | |||
| C.V. | 17.18 | Pred R-Squared | 0.5729 | |||
| PRESS | 7676.77 | Adeq Precision | 11.325 | |||
| Source | Sum of Squares | DF | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|---|
| Block | 561.59 | 1 | 561.59 | |||
| Model | 16,685.59 | 11 | 1516.87 | 17.65 | <0.0001 | sig. |
| A | 850.64 | 1 | 850.64 | 9.90 | 0.0067 | |
| B | 3371.57 | 1 | 3371.57 | 39.24 | <0.0001 | |
| C | 1757.45 | 1 | 1757.45 | 20.45 | 0.0004 | |
| D | 2267.56 | 1 | 2267.56 | 26.39 | 0.0001 | |
| D2 | 1462.89 | 1 | 1462.89 | 17.03 | 0.0009 | |
| AB | 830.88 | 1 | 830.88 | 9.67 | 0.0072 | |
| AC | 1163.83 | 1 | 1163.83 | 13.54 | 0.0022 | |
| AD | 712.36 | 1 | 712.36 | 8.29 | 0.0115 | |
| BC | 513.48 | 1 | 513.48 | 5.98 | 0.0273 | |
| BD | 3328.71 | 1 | 3328.71 | 38.74 | <0.0001 | |
| CD | 426.22 | 1 | 426.22 | 4.96 | 0.0417 | |
| Residual | 1288.87 | 15 | 85.92 | |||
| Lack of Fit | 1238.52 | 12 | 103.21 | 6.15 | 0.0805 | not sig |
| Pure Error | 50.35 | 3 | 16.78 | |||
| Cor Total | 18,536.04 | 27 | ||||
| Std. Dev. | 9.27 | R-Squared | 0.9283 | |||
| Mean | 58.53 | Adj R-Squared | 0.8757 | |||
| C.V. | 15.84 | Pred R-Squared | 0.7056 | |||
| PRESS | 5291.71 | Adeq Precision | 13.632 | |||
| Factors | Result |
|---|---|
| DER (A) | 2.13 |
| AGL (B) | 0 |
| CBT (C) | 30 |
| BFR (D) | 0.01/99.99 |
3.2. Effect of Spinning Variables on Rejection
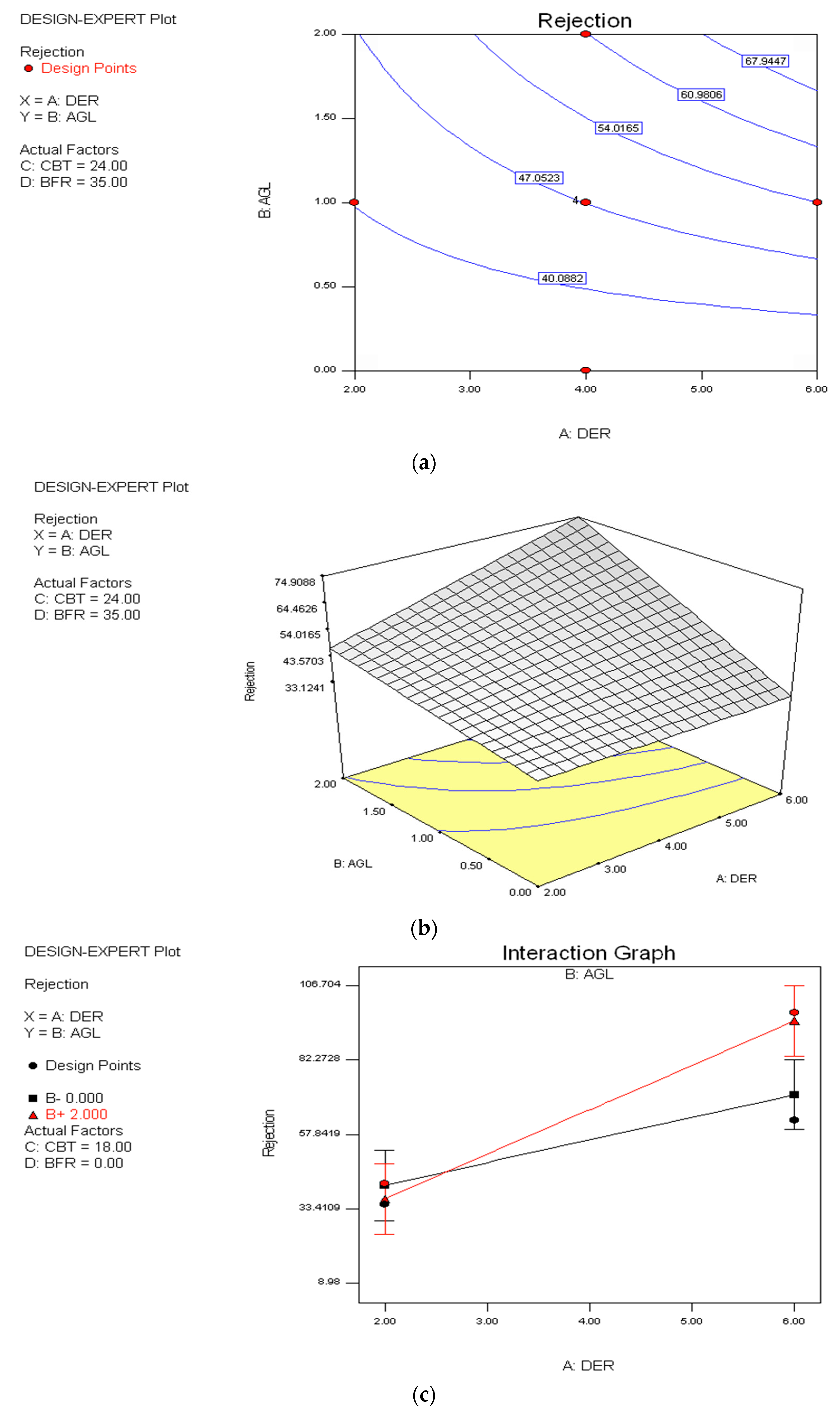
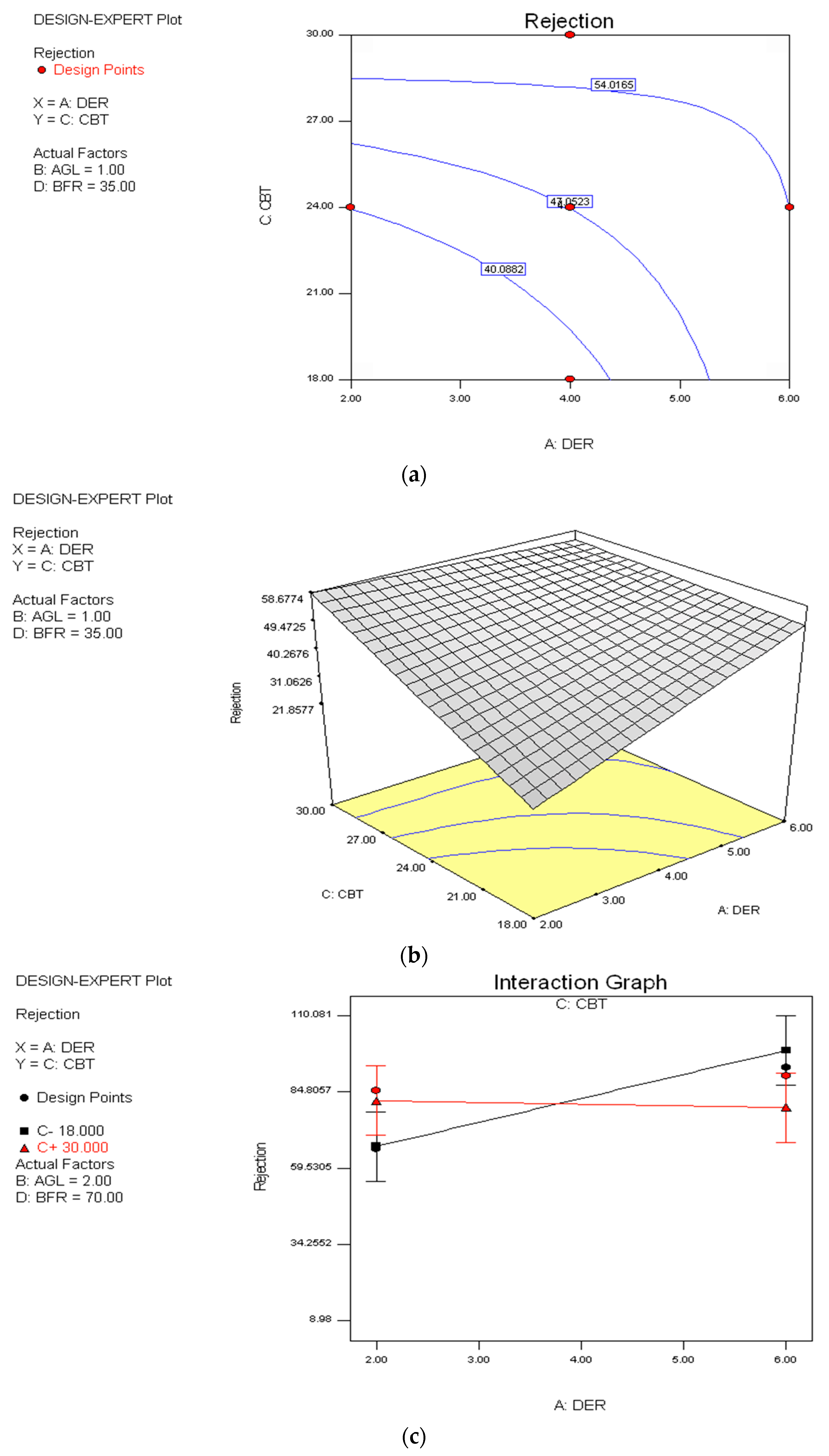
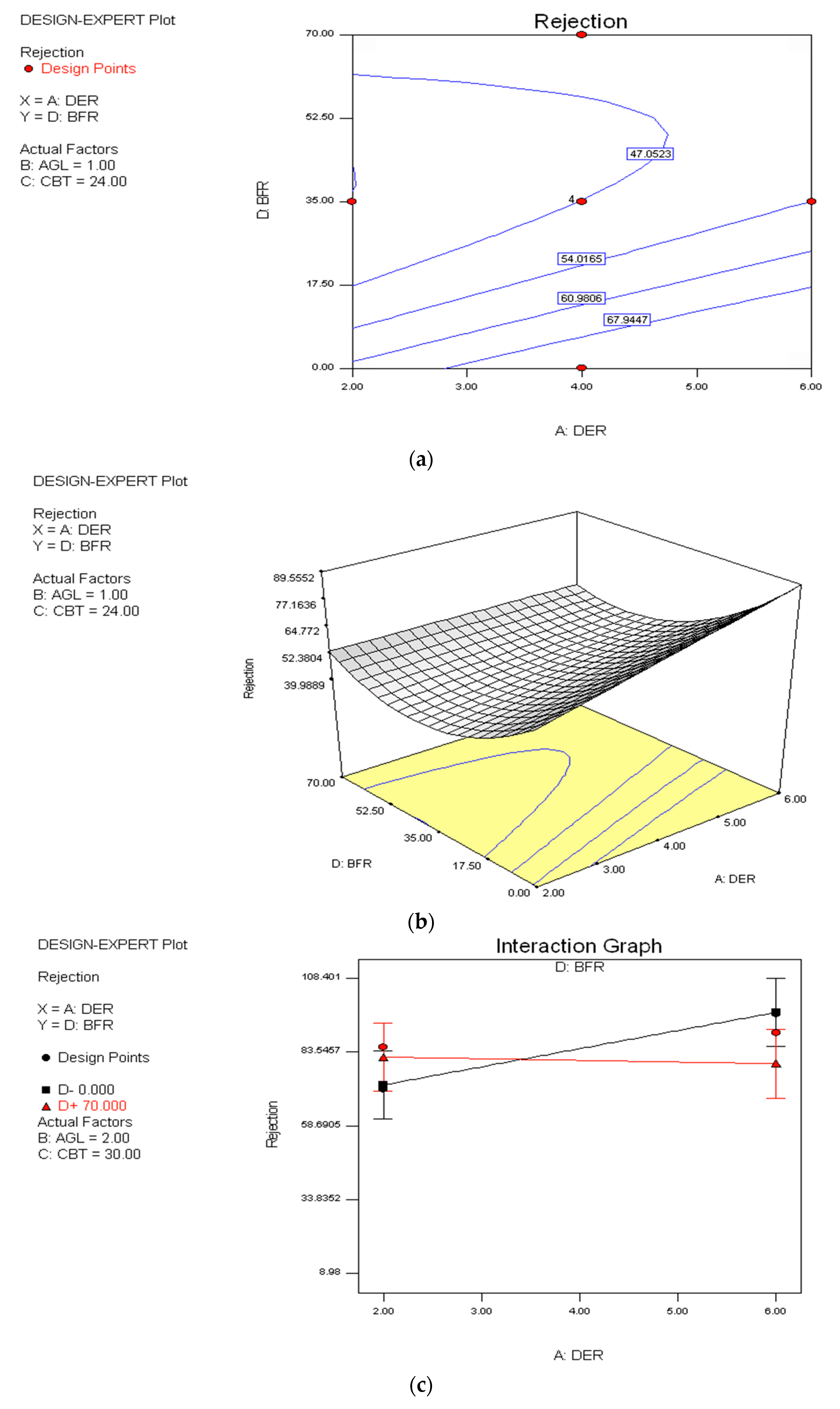

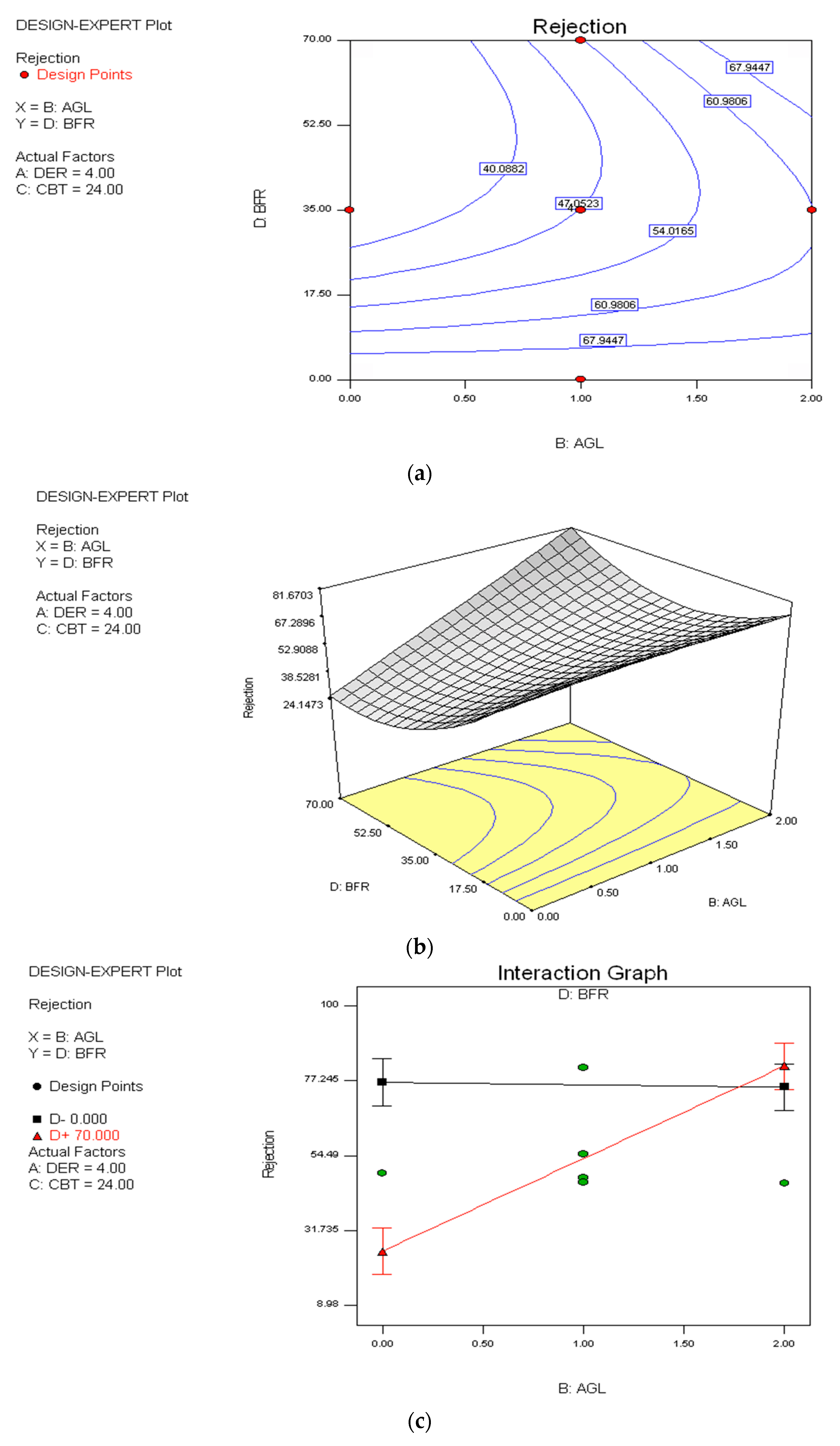
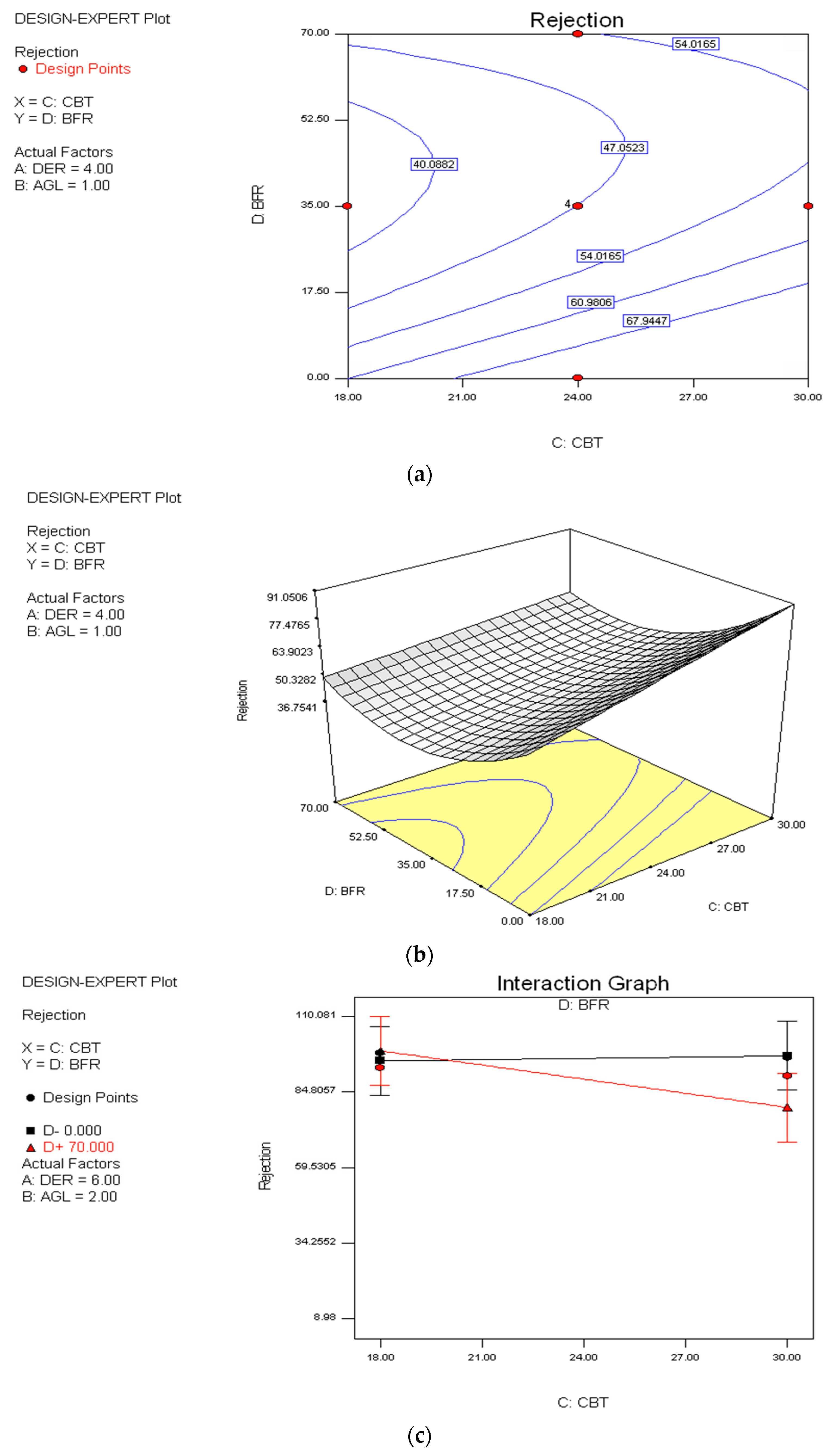
4. Model Validation and Confirmation Run
| No. | DER | AGL | CBT | BFR | PT | Actual | Predicted | Residual | Error |
|---|---|---|---|---|---|---|---|---|---|
| (cm3/min) | (cm) | (°C) | (NMP/H2O, wt %) | (h) | (%) | ||||
| 1 | 2.20 | 0 | 30 | 0/100 | 6 | 99.60 | 99.42 | 0.18 | 0.18 |
| 2 | 5 | 1.5 | 30 | 0/100 | 6 | 94.62 | 92.16 | 2.46 | 2.60 |
| 3 | 2.13 | 0 | 30 | 0.01/99.99 | 5 | 93.94 | 99.48 | −5.54 | −5.90 |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Howe, C.; Smith, J.B.; Henderson, J. Climate Change and Water: International Perspectives on Mitigation and Adaptation; American Water Works Association: Denver, CO, USA; IWA Publishing: London, UK, 2010. [Google Scholar]
- Mujeriego, R.; Asano, T. The role of advanced treatment in wastewater reclamation and reuse. Water Sci. Technol. 1999, 40, 1–9. [Google Scholar]
- Sójka-Ledakowicz, J.; Koprowski, T.; Machnowski, W.; Knudsen, H.H. Membrane filtration of textile dyehouse wastewater for technological water reuse. Desalination 1998, 119, 1–10. [Google Scholar] [CrossRef]
- Sadr Ghayeni, S.B.; Madaeni, S.S.; Fane, A.G.; Schneider, R.P. Aspects of microfiltration and reverse osmosis in municipal wastewater reuse. Desalination 1996, 106, 25–29. [Google Scholar] [CrossRef]
- Fähnrich, A.; Mavrov, V.; Chmiel, H. Membrane processes for water reuse in the food industry. Desalination 1998, 119, 213–216. [Google Scholar] [CrossRef]
- Fane, A.G. Membranes for water production and wastewater reuse. Desalination 1996, 106, 1–9. [Google Scholar] [CrossRef]
- Qin, J.J.; Chung, T.S.; Cao, C.; Vora, R.H. Effect of temperature on intrinsic permeation properties of 6FDA-Durene/1,3-phenylenediamine (mPDA) copolyimide and fabrication of its hollow fiber membranes for CO2/CH4 separation. J. Membr. Sci. 2005, 250, 95–103. [Google Scholar] [CrossRef]
- Khayet, M.; Feng, C.Y.; Khulbe, K.C.; Matsuura, T. Preparation and characterization of polyvinylidene fluoride hollow fiber membranes for ultrafiltration. Polymer 2002, 43, 3879–3890. [Google Scholar] [CrossRef]
- Chung, T.S.; Hu, X. Effect of air-gap distance on the morphology and thermal properties of polyethersulfone hollow fibers. J. Appl. Polym. Sci. 1997, 66, 1067–1077. [Google Scholar] [CrossRef]
- Chung, T.S.; Qin, J.J.; Gu, J. Effect of shear rate within the spinneret on morphology, separation performance and mechanical properties of ultrafiltration polyethersulfone hollow fiber membranes. Chem. Eng. Sci. 2000, 55, 1077–1091. [Google Scholar] [CrossRef]
- Chung, T.S.; Qin, J.J.; Huan, A.; Toh, K.C. Visualization of the effect of die shear rate on the outer surface morphology of ultrafiltration membranes by AFM. J. Membr. Sci. 2002, 196, 251–266. [Google Scholar] [CrossRef]
- Xu, Z.L.; Qusay, F.A. Polyethersulfone (PES) hollow fiber ultrafiltration membranes prepared by PES/non-solvent/NMP solution. J. Membr. Sci. 2004, 233, 101–111. [Google Scholar] [CrossRef]
- Chung, T.S.; Teoh, S.K.; Lau, W.W.Y.; Srinivasan, M.P. Effect of shear stress within the spinneret on hollow fiber membrane morphology and separation performance. Ind. Eng. Chem. Res. 1998, 37, 3930–3938. [Google Scholar] [CrossRef]
- Ismail, A.F.; Mustaffar, M.I.; Illias, R.M.; Abdullah, M.S. Effect of dope extrusion rate on morphology and performance of hollow fibers membrane for ultrafiltration. Sep. Purif. Technol. 2006, 49, 10–19. [Google Scholar] [CrossRef]
- Qin, J.J.; Wang, R.; Chung, T.S. Investigation of shear stress effect within a spinneret on flux, separation and thermomechanical properties of hollow fiber ultrafiltration membranes. J. Membr. Sci. 2000, 175, 197–213. [Google Scholar] [CrossRef]
- Kapantaidakis, G.C.; Koops, G.H.; Wessling, M. Effect of spinning conditions on the structure and the gas permeation properties of high flux polyethersulfone-polyimide blend hollow fibers. Desalination 2002, 144, 121–125. [Google Scholar] [CrossRef]
- Khayet, M. The effect of air gap length on the internal and external morphology of hollow fiber membranes. Chem. Eng. Sci. 2003, 58, 3091–3104. [Google Scholar] [CrossRef]
- Qin, J.J.; Gu, J.; Chung, T.S. Effect of wet and dry-jet wet spinning on the shear-induced orientation during the formation of ultrafiltration hollow fiber membranes. J. Membr. Sci. 2001, 182, 57–75. [Google Scholar] [CrossRef]
- Khayet, M.; Cojocaru, C.; Essalhi, M.; García-Payo, M.C.; Arribas, P.; García-Fernández, L. Hollow fiber spinning experimental design and analysis of defects for fabrication of optimized membranes for membrane distillation. Desalination 2012, 287, 146–158. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 4th ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Ismail, A.F. Novel Studies of Molecular Orientation in Synthetic Polymeric Membranes for Gas Separation. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 1997. [Google Scholar]
- Makki, H.F.; Al-Alawy, A.F.; Al-Hassani, M.H.; Rashad, Z.W. Membranes separation process for oily wastewater treatment. J. Eng. 2011, 17, 235–252. [Google Scholar]
- Ong, C.S.; Lau, W.J.; Goh, P.S.; Ng, B.C.; Ismail, A.F. Preparation and characterization of PVDF-PVP-TiO2 composite hollow fiber membranes for oily wastewater treatment using submerged membrane system. Desalin. Water Treat. 2015, 53, 1213–1223. [Google Scholar]
- Al-Alawy, A.F.; Al-Musawi, S.M. Microfiltration membranes for separating oil/water emulsion. Iraqi J. Chem. Petrol. Eng. 2013, 14, 53–70. [Google Scholar]
- Oliveira de Lima, L.M.; da Silva, J.H.; Ribeiro Patricio, A.A.; de Barros Neto, E.L.; Dantas Neto, A.A.; de Castro Dantas, T.N.; de Alencar Moura, M.C.P. Oily wastewater treatment through a separation process using bubbles without froth formation. Petrol. Sci. Technol. 2008, 26, 994–1004. [Google Scholar] [CrossRef]
- Sekman, E.; Top, S.; Uslu, E.; Varank, G.; Bilgili, M.S. Treatment of oily wastewater from port waste reception facilities by electrocoagulation. Int. J. Environ. Res. 2011, 5, 1079–1086. [Google Scholar]
- Agustin, M.B.; Sengpracha, W.P.; Phutdhawong, W. Electrocoagulation of palm oil mill effluent. Int. J. Environ. Res. Public Health 2008, 5, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Kurian, J.; Natarajan, K. Studies on wastewater from automobile service stations. Indian J. Environ. Health 1997, 39, 37–43. [Google Scholar]
- Patterson, J.W. Industrial Wastewater Treatment Technology, 2nd ed.; Butterworth: Stoneham, MA, USA, 1985. [Google Scholar]
- Kim, I.C.; Yun, H.G.; Lee, K.H. Preparation of asymmetric polyacrylonitrile membrane with small pore size by phase inversion and post-treatment process. J. Membr. Sci. 2002, 199, 75–84. [Google Scholar] [CrossRef]
- Wan, L.S.; Xu, Z.K.; Huang, X.J.; Che, A.F.; Wang, Z.G. A novel process for the post-treatment of polyacrylonitrile-based membranes: Performance improvement and possible mechanism. J. Membr. Sci. 2006, 277, 157–164. [Google Scholar] [CrossRef]
- Wang, D.; Li, K.; Teo, W.K. Porous PVDF asymmetric hollow fiber membranes prepared with the use of small molecular additives. J. Membr. Sci. 2000, 178, 13–23. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aluwi Shakir, N.A.; Wong, K.Y.; Noordin, M.Y.; Sudin, I. Development of a High Performance PES Ultrafiltration Hollow Fiber Membrane for Oily Wastewater Treatment Using Response Surface Methodology. Sustainability 2015, 7, 16465-16482. https://doi.org/10.3390/su71215826
Aluwi Shakir NA, Wong KY, Noordin MY, Sudin I. Development of a High Performance PES Ultrafiltration Hollow Fiber Membrane for Oily Wastewater Treatment Using Response Surface Methodology. Sustainability. 2015; 7(12):16465-16482. https://doi.org/10.3390/su71215826
Chicago/Turabian StyleAluwi Shakir, Noor Adila, Kuan Yew Wong, Mohd Yusof Noordin, and Izman Sudin. 2015. "Development of a High Performance PES Ultrafiltration Hollow Fiber Membrane for Oily Wastewater Treatment Using Response Surface Methodology" Sustainability 7, no. 12: 16465-16482. https://doi.org/10.3390/su71215826
APA StyleAluwi Shakir, N. A., Wong, K. Y., Noordin, M. Y., & Sudin, I. (2015). Development of a High Performance PES Ultrafiltration Hollow Fiber Membrane for Oily Wastewater Treatment Using Response Surface Methodology. Sustainability, 7(12), 16465-16482. https://doi.org/10.3390/su71215826