A Comparative Exergoeconomic Analysis of Waste Heat Recovery from a Gas Turbine-Modular Helium Reactor via Organic Rankine Cycles
Abstract
:1. Introduction
2. Configurations of GT-MHR/ORC Combined Cycles
- The combined cycles operate in a steady-state condition.
- Pressure drops through pipes are negligible.
- Isentropic efficiencies for the turbines and pumps in the ORCs are 80% and 85%, respectively.
- Changes in kinetic and potential energies are neglected.
- The effectiveness of the intercooler, the recuperator and the precooler is considered to be 90%.

3. Exergoeconomic Analysis
3.1. Application of SPECO Method to the System
3.1.1. Modeling
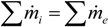
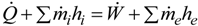
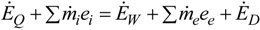
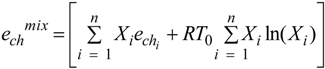

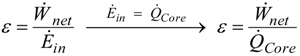
 is the produced energy in the reactor core.
is the produced energy in the reactor core.| Parameters | Value |
|---|---|
| P0 (kPa) | 100 |
| PRC | 1.5–5 |
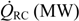 | 600 |
| T0 (°C) | 25 |
| T1 (°C) | 700–900 |
| TC (°C) | 40 |
| TE (°C) | 80–120 |
| ∆TE (°C) | 2–10 |
| ∆TSup (°C) | 0–15 |
| ηP (%) | 85 |
| ηT (%) | 80 |
| Effectiveness (for IC, R, PC) (%) | 90 |
| ∆PRC (kPa) | 100 |
| ∆PE, ∆PIC, ∆PPC (kPa) | 40 |
| ∆PR,HP (kPa) | 80 |
| ∆PR,LP (kPa) | 50 |
3.1.2. Defining the Fuel and Product for Each Component
3.1.3. Cost Balances
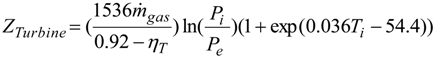
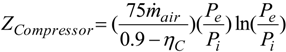
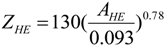

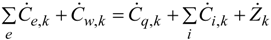
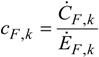
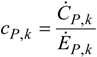
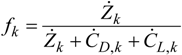
4. Results and Discussion
4.1. Exergoeconomic Analysis
| State No. | GT-MHR/SORC | GT-MHR/HORC | GT-MHR/RORC | |||
| Ċ ($/s) | c ($/GJ) | Ċ ($/s) | c ($/GJ) | Ċ ($/s) | c ($/GJ) | |
| 1 | 17.17 | 11.83 | 17.15 | 11.83 | 17.20 | 11.83 |
| 2 | 10.55 | 11.83 | 10.53 | 11.83 | 10.59 | 11.83 |
| 3 | 7.428 | 11.83 | 7.419 | 11.83 | 7.444 | 11.83 |
| 4 | 7.016 | 11.83 | 7.015 | 11.83 | 7.046 | 11.83 |
| 5 | 6.936 | 11.83 | 6.927 | 11.83 | 6.953 | 11.83 |
| 6 | 8.565 | 12.15 | 8.558 | 12.15 | 8.582 | 12.15 |
| 7 | 8.347 | 12.15 | 8.338 | 12.15 | 8.362 | 12.15 |
| 8 | 10.05 | 12.39 | 10.04 | 12.39 | 10.06 | 12.39 |
| 9 | 13.18 | 12.56 | 13.17 | 12.56 | 13.22 | 12.56 |
| 10 | 0.010 | 32.46 | 0.0009 | 18.5 | 0.0008 | 18.05 |
| 11 | 0.434 | 18.36 | 0.010 | 32.61 | 0.001 | 24.10 |
| 12 | 0.045 | 18.36 | 0.021 | 36.05 | 0.007 | 24.22 |
| 13 | 0.0009 | 18.36 | 0.438 | 18.50 | 0.016 | 28.98 |
| 14 | 0 | 0 | 0.046 | 18.50 | 0.427 | 18.05 |
| 15 | 0.085 | 72.86 | 0.039 | 18.50 | 0.006 | 18.05 |
| 16 | 0 | 0 | 0 | 0 | 0.042 | 18.05 |
| 17 | 0.222 | 59.80 | 0.093 | 66.88 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0.098 | 64.10 |
| 19 | 0.050 | 47.9 | 0.224 | 59.69 | 0 | 0 |
| 20 | - | - | 0 | 0 | 0.224 | 59.56 |
| 21 | - | - | 0.044 | 45.52 | 0 | 0 |
| 22 | - | - | - | - | 0.046 | 50.73 |
| Nuclear fuel | 2.424 | 4.040 | 2.422 | 4.036 | 2.422 | 4.036 |
| ẆT | 6.843 | 12.56 | 6.843 | 12.55 | 6.837 | 12.56 |
| ẆC,HP | 1.695 | 12.56 | 1.695 | 12.55 | 1.692 | 12.56 |
| ẆC,LP | 1.622 | 12.56 | 1.624 | 12.55 | 1.622 | 12.56 |
| ẆT,ORC | 0.458 | 26.68 | 0.461 | 26.89 | 0.449 | 26.21 |
| ẆP,ORC | 0.0085 | 26.68 | 0.0085 | 26.89 | 0.0006 | 26.21 |
| ẆP2,ORC | - | - | - | - | 0.008 | 26.21 |
| Component | GT-MHR/SORC | GT-MHR/HORC | GT-MHR/RORC | |||||||||
| ĖD | ε | ĊD | f | ĖD | ε | ĊD | f | ĖD | ε | ĊD | f | |
| (kW) | (%) | ($/s) | (%) | (kW) | (%) | ($/s) | (%) | (kW) | (%) | ($/s) | (%) | |
| Reactor core | 198,088 | 87.99 | 1.874 | 45.51 | 198,122 | 87.98 | 1.874 | 45.52 | 197,980 | 88.02 | 1.874 | 45.51 |
| Turbine | 14,868 | 97.34 | 0.176 | 55.40 | 14,878 | 97.34 | 0.176 | 55.37 | 14,837 | 97.35 | 0.176 | 55.54 |
| Recuperator | 25,397 | 90.37 | 0.301 | 4.262 | 25,315 | 90.38 | 0.299 | 4.275 | 25,605 | 90.36 | 0.303 | 4.238 |
| Evaporator | 11,436 | 67.10 | 0.153 | 8.339 | 11,035 | 67.64 | 0.131 | 9.154 | 10,591 | 68.57 | 0.125 | 8.997 |
| Precooler | 5599 | 17.22 | 0.066 | 6.760 | 6054 | 18.65 | 0.072 | 6.281 | 6324 | 19.41 | 0.075 | 6.048 |
| LP compressor | 10,536 | 91.84 | 0.132 | 5.180 | 10,541 | 91.85 | 0.132 | 5.181 | 10,520 | 91.86 | 0.132 | 5.186 |
| Intercooler | 14,226 | 20.68 | 0.173 | 2.180 | 14,368 | 20.71 | 0.175 | 2.158 | 14,354 | 20.76 | 0.174 | 2.166 |
| HP compressor | 10,830 | 91.98 | 0.136 | 5.119 | 10,835 | 91.98 | 0.136 | 5.120 | 10,815 | 91.98 | 0.136 | 5.125 |
| ORC turbine | 4014 | 81.05 | 0.074 | 48.56 | 4013 | 81.03 | 0.074 | 48.37 | 6221 | 81.41 | 0.112 | 38.07 |
| Condenser | 1369 | 43.29 | 0.025 | 18.59 | 1081 | 46.91 | 0.020 | 22.54 | 1352 | 40.25 | 0.024 | 17.98 |
| Pump | 320 | 85.43 | 0.009 | 10.36 | 45.85 | 85.43 | 0.001 | 44.19 | 3.084 | 85.46 | 0 | 64.02 |
| Pump 2 | - | - | - | - | - | - | - | - | 43.87 | 85.88 | 0.001 | 45.69 |
| IHE | - | - | - | - | 135 | 66.15 | 0.002 | 56.32 | - | - | - | - |
| OFOF | - | - | - | - | - | - | - | - | 78 | 78.73 | 0.002 | - |
| Overall | 296,683 | 49.61 | 3.101 | 38.1 | 296,425 | 49.58 | 3.092 | 38.22 | 298,724 | 49.56 | 3.134 | 37.85 |
4.2. Parametric Study
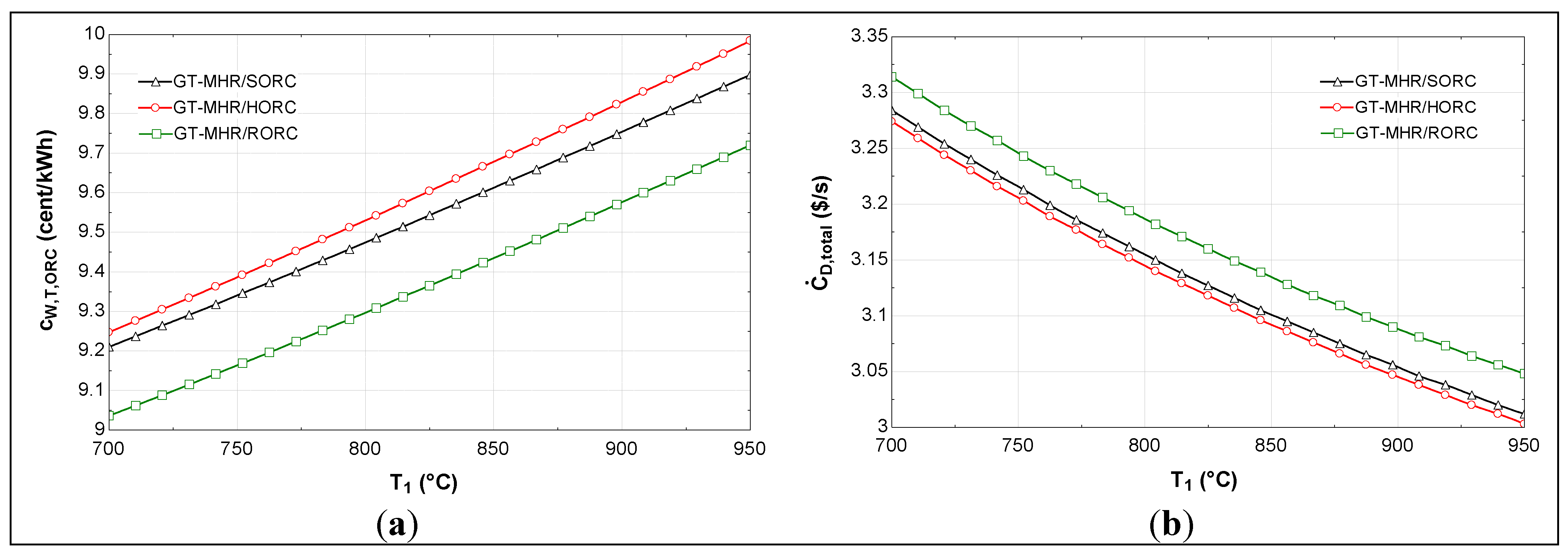

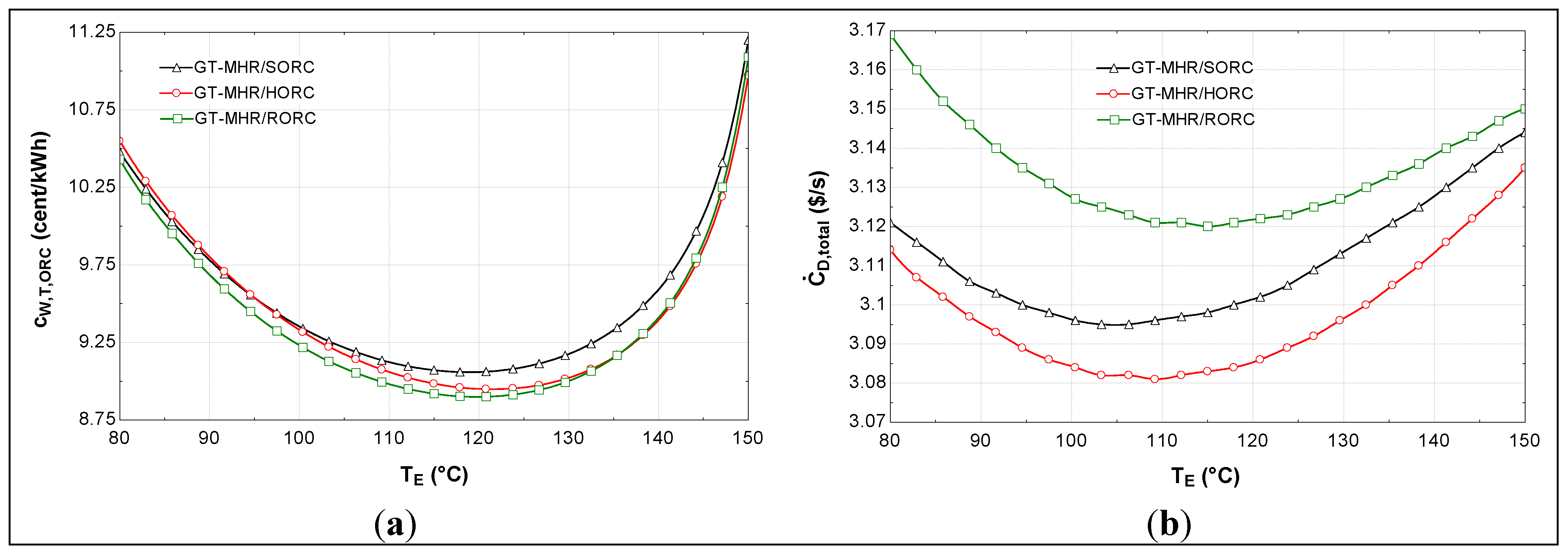
5. Conclusions
Nomenclature
| A | heat transfer area (m2) |
| c | cost per unit exergy ($/kJ) |
| Ċ | cost rate ($/s) |
| e | specific exergy (kJ/kg) |
| Ė | exergy rate (kW) |
| f | exergoeconomic factor |
| h | specific enthalpy (kJ/kg) |
| IHE | internal heat exchanger |
| ṁ | mass flow rate (kg/s) |
| OFOF | open feed organic fluid |
| P | pressure (bar, kPa) |
| PRC | compressor pressure Ratio |
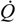 | heat transfer rate (kW) |
| R | gas constant (kJ/kg K) |
| s | specific entropy (kJ/kg K) |
| T | temperature (°C, K) |
| Ẇ | electrical power (kW) |
| X | mole fraction |
| Z | capital cost of a component ($) |
| Ż | capital cost rate ($/s) |
Greek letters
| η | isentropic efficiency |
| ε | exergy efficiency |
| ∆TE | pinch point temperature difference in the evaporator |
| ∆TSup | degree of superheat at the inlet to the ORC turbine |
Subscripts
| 0 | dead (environmental) state |
| 1, 2, 3, … | cycle locations |
| C | condenser |
| ch | chemical exergy |
| D | destruction |
| e | outlet |
| E | evaporator |
| F | fuel |
| HE | heat exchanger |
| HP | high pressure |
| IC | intercooler |
| i | inlet |
| j | j-th stream |
| k | k-th component |
| L | loss |
| LP | low pressure |
| P | pump, product |
| PC | precooler |
| ph | physical exergy |
| q | heat |
| R | recuperator |
| RC | reactor core |
| T | turbine |
| w | power |
Author Contributions
Conflicts of Interest
References
- Hemmes, K.; Kamp, L.M.; Vernay, A.B.H.; de Werk, G. A multi-source multi-product internal reforming fuel cell energy system as a stepping stone in the transition towards a more sustainable energy and transport sector. Int. J. Hydrogen Energ. 2011, 36, 10221–10227. [Google Scholar] [CrossRef]
- Cakir, U.; Comakli, K.; Yuksel, F. The role of cogeneration systems in sustainability of energy. Energ. Convers. Manag. 2012, 63, 196–202. [Google Scholar]
- Baldwin, D.; Campbell, M.; Ellis, C.; Richards, M.; Shenoy, A. MHR design, technology and applications. Energ. Convers. Manag. 2008, 49, 1898–1901. [Google Scholar] [CrossRef]
- Tournier, J.M.; El-Genk, M.S. Properties of noble gases and binary mixtures for closed Brayton Cycle applications. Energ. Convers. Manag. 2008, 49, 469–492. [Google Scholar] [CrossRef]
- Yari, M.; Mahmoudi, S.M.S. Utilization of waste heat from GT-MHR for power generation in organic Rankine cycles. Appl. Therm. Eng. 2010, 30, 366–375. [Google Scholar] [CrossRef]
- Schuster, A.; Karellas, S.; Kakaras, E.; Spliethoff, H. Energetic and economic investigation of organic Rankine cycle applications. Appl. Therm. Eng. 2009, 29, 1809–1817. [Google Scholar] [CrossRef]
- Drescher, U.; Bruggemann, D. Fluid selection for the organic Rankine cycle (ORC) in biomass power and heat plants. Appl. Therm. Eng. 2007, 27, 223–228. [Google Scholar] [CrossRef]
- Yari, M.; Mahmoudi, S.M.S. A thermodynamic study of waste heat recovery from GT-MHR using organic Rankine cycles. Heat Mass Transfer 2011, 47, 181–196. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I. Exergoenvironmental analysis and optimization of a cogeneration plant system using Multimodal Genetic Algorithm (MGA). Energy 2010, 35, 5161–5172. [Google Scholar] [CrossRef]
- Tsatsaronis, G. Definitions and nomenclature in exergy analysis and exergoeconomics. Energy 2007, 32, 249–253. [Google Scholar] [CrossRef]
- Sahoo, P.K. Exergoeconomic analysis and optimization of a cogeneration system using evolutionary programming. Appl. Therm. Eng. 2008, 28, 1580–1588. [Google Scholar] [CrossRef]
- Mohammadkhani, F.; Khalilarya, S.; Mirzaee, I. Exergy and exergoeconomic analysis and optimization of diesel engine based Combined Heat and Power (CHP) system using genetic algorithm. Int. J. Exergy 2013, 12, 139–161. [Google Scholar]
- Abusoglu, A.; Kanoglu, M. Exergoeconomic analysis and optimization of combined heat and power production: A review. Renew. Sust. Energ. Rev. 2009, 13, 2295–2308. [Google Scholar] [CrossRef]
- Yari, M. Performance analysis of the different organic Rankine cycles (ORCs) using dry fluids. Int. J. Exergy 2009, 6, 323–342. [Google Scholar] [CrossRef]
- Lazzaretto, A.; Tsatsaronis, G. SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 2006, 31, 1257–1289. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 5th ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- Dincer, I.; Rosen, M.A. Exergy: Energy, Environment and Sustainable Development, 2nd ed.; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- Klein, S.A.; Alvarda, S.F. Engineering Equation Solver (EES); F-chart Software: Madison, WI, USA, 2007. [Google Scholar]
- Bejan, A.; Tsatsaronis, G.; Moran, M. Thermal Design and Optimization; John Wiley and Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Baghernejad, A.; Yaghoubi, M. Exergoeconomic analysis and optimization of an Integrated Solar Combined Cycle System (ISCCS) using genetic algorithm. Energ. Convers. Manag. 2011, 52, 2193–2203. [Google Scholar] [CrossRef]
- Schultz, K.R.; Brown, L.C.; Besenbruch, G.E.; Hamilton, C.J. Large-scale production of hydrogen by nuclear energy for the hydrogen economy. In Proceedings of the National Hydrogen Association Annual Conference, Washington, DC, USA, 6–9 April 2003.
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Shokati, N.; Mohammadkhani, F.; Yari, M.; Mahmoudi, S.M.S.; Rosen, M.A. A Comparative Exergoeconomic Analysis of Waste Heat Recovery from a Gas Turbine-Modular Helium Reactor via Organic Rankine Cycles. Sustainability 2014, 6, 2474-2489. https://doi.org/10.3390/su6052474
Shokati N, Mohammadkhani F, Yari M, Mahmoudi SMS, Rosen MA. A Comparative Exergoeconomic Analysis of Waste Heat Recovery from a Gas Turbine-Modular Helium Reactor via Organic Rankine Cycles. Sustainability. 2014; 6(5):2474-2489. https://doi.org/10.3390/su6052474
Chicago/Turabian StyleShokati, Naser, Farzad Mohammadkhani, Mortaza Yari, Seyed M. S. Mahmoudi, and Marc A. Rosen. 2014. "A Comparative Exergoeconomic Analysis of Waste Heat Recovery from a Gas Turbine-Modular Helium Reactor via Organic Rankine Cycles" Sustainability 6, no. 5: 2474-2489. https://doi.org/10.3390/su6052474
APA StyleShokati, N., Mohammadkhani, F., Yari, M., Mahmoudi, S. M. S., & Rosen, M. A. (2014). A Comparative Exergoeconomic Analysis of Waste Heat Recovery from a Gas Turbine-Modular Helium Reactor via Organic Rankine Cycles. Sustainability, 6(5), 2474-2489. https://doi.org/10.3390/su6052474






