Regional Disparities in Artificial Intelligence Development and Green Economic Efficiency Performance Under Its Embedding: Empirical Evidence from China

Abstract

This study analyzes artificial intelligence development and green economic efficiency across 31 Chinese provinces using 2019–2021 panel data. We apply the entropy weight TOPSIS method to measure AI development levels. The entropy weight TOPSIS method measures AI development levels, the DEA-BCC model assesses green economic efficiency, and their coordination types are identified. Findings reveal a significant negative correlation between AI development and green economic efficiency. We explain this complex relationship through three mechanisms: short-term polarization effects, technology conversion lags, and spatial spillovers. Spatial analysis shows AI development forms high-high agglomerations in the Yangtze River Delta and Shandong. Green economic efficiency shows high-high clustering in the Beijing-Tianjin-Hebei region and selected western provinces. Using a “two-system” coupling framework, we identify four provincial categories. The “double-high” type should function as growth poles. The “high-low” type requires improved technology conversion efficiency. The “low-high” type can leverage ecological advantages. The “double-low” type needs enhanced factor inputs. We propose three targeted policy recommendations: establishing digital-green synergy platforms, implementing inter-provincial AI resource collaboration mechanisms, and developing locally adapted action plans.

1. Introduction

The primary objective of this study is to assess the performance of regional green economic efficiency under the embeddedness of artificial intelligence (AI). This investigation is based on a comprehensive understanding of AI’s development status and the imperative of green economic development. AI plays a significant role in fostering the digital economy, transforming higher education, and constructing smart cities [1]. Simultaneously, enhancing green economic efficiency is critical for achieving sustainable development, mitigating environmental pressures, and transitioning towards a low-carbon economy. The subchains of the overarching AI chain include education, innovation, industry, and city. The fundamental indicators of these subchains represent the level and efficiency of AI progress. Regional innovation cannot be divorced from the integration and synergy of all AI components. A comprehensive assessment of AI has the ability to reveal its capabilities and limitations in terms of achieving sustainable development [2]. The intrinsic connection between AI and green efficiency lies in AI’s potential to optimize resource allocation, improve energy productivity, and enable intelligent environmental governance, thereby fundamentally reshaping the trajectory of green economic development.

Empirically, China’s AI sector has expanded rapidly. However, this growth is geographically uneven, creating significant regional disparities in technological capacity [3]. Concurrently, China faces immense pressure for a green transition, aiming to peak carbon emissions before 2030 and achieve carbon neutrality by 2060 while managing persistent challenges related to industrial energy intensity. This dual context of rapid but uneven AI development and urgent green transition needs provides a compelling rationale for examining their intersection.

This challenge of uneven AI resource allocation directly informs China’s recent policy focus. The national strategy of “new quality productive forces” has been introduced precisely to address such structural imbalances and foster innovation-driven, high-quality growth [4]. Within this strategic framework, AI is positioned as the most essential allocation force among the elements of new quality productivity. The strategy aims to leverage new production relationships, structures, and factors to create a competitive development model. Therefore, understanding the relationship between AI and green economic efficiency becomes critical not only for technological advancement but also for successful national strategy implementation.

In terms of global development, the economic-ecological coupling concept has increased in importance [5]. Therefore, exploring how AI can be effectively harnessed to boost green economic efficiency, rather than merely general economic output, becomes a pressing issue. This study specifically investigates the co-performance of green economic efficiency and AI development, constituting a core scientific issue in both research and industrial practice. It aims to identify interprovincial disparities in AI integration into the green economy, providing valuable insights for facilitating the scientific allocation of AI resources and further promoting high-quality development of the regional green economy.

This study adopts a more complete and objective approach. It thoroughly evaluates the state of AI development across various dimensions, including the industrial, innovation, education, and urban chains. Second, this study constructs an evaluation system for green economic development efficiency under AI embedding and conducts empirical analysis. Third, by comparing the level of AI development and the performance of green economic development efficiency under AI embedding across regions, this study helps identify interprovincial disparities in the comprehensive development of AI and its integration into the green economy. The findings provide valuable insights for facilitating the scientific allocation of AI resources and further promoting high-quality development of the regional green economy. The empirical evidence underscores the representativeness and contemporary relevance of the cases examined, while the rigorous analytical methods ensure the stability and reliability of the results.

2. Literature Review

The overall improvement in the AI ecosystem is crucial to increasing renewable energy adoption and laying the groundwork for the growth of a green economy [5]. AI research spans a variety of disciplines, including the AI industry, AI technology, and smart city design. The AI industry is concerned with the development of AI technologies and applications, including hardware, software, algorithms, data, and applications. The worldwide AI business has expanded rapidly, with China emerging as a key player. The AI industry is distinguished by its technological complexity, diverse applications, and emphasis on innovation and cutting-edge breakthroughs [6]. The AI industry’s development modes include vertical integration, horizontal collaboration, and platform-based techniques [7]. Governments have established measures to support the growth of the AI industry. AI is used not only in a variety of industries, including healthcare, finance, manufacturing, transportation, and security but also for building smart cities. Smart cities are distinguished by their intelligent infrastructure and digital city management. AI-driven monitoring that dynamically balances energy supply and demand helps greatly improve resource utilization, which, in turn, increases resource efficiency, reduces waste, and aligns with carbon reduction goals [8].

A growing body of research establishes an empirical link between the digital economy, in which AI serves as a core component, and Green Total Factor Productivity (GTFP) [9]. For instance, research across Chinese cities reveals a non-linear U-shaped relationship between the digital economy and urban GTFP, where initial suppression transitions to long-term enhancement, with effects amplified by population density [10]. This study further confirms significant spatial spillover effects, underscoring the need for coordinated regional policies to mitigate uneven development.

Previous literature suggests that AI can provide specific technological and epistemic support for the development of green regional economies [11]. AI technologies have shown the ability to improve energy efficiency and reduce emissions in the context of energy mitigation [12]. Energy storage technologies are crucial for increasing the capacity for new energy consumption, ensuring the steady and cost-effective functioning of power networks, and promoting the wider deployment of renewable energy technology [13]. Intelligent energy management systems in the energy sector help maximize energy efficiency and lessen environmental impacts [14]. In the field of smart transportation and logistics management, AI technology is critical in regulating transport energy, as it improves the operating efficiency of transportation networks, eases traffic congestion, reduces energy consumption, and promotes sustainable travel [15]. AI plays an important role in the development of smart city systems. AI advancements help with urban planning and building, allowing for more intelligent resource allocation and supporting sustainable development [16]. In short, the extensive integration of AI technology is often associated with reduced energy consumption and advancements in the regional green economy in the literature.

However, the narrative is not uniformly positive. A growing body of literature critically examines the energy burden of AI itself [17]. The computational demands of training large models and running data centers consume substantial electricity, creating a significant carbon footprint that could offset their green benefits [18]. This underscores the necessity of a balanced assessment that accounts for both the enabling and encumbering effects of AI. Another area of concern is hardware pollution. The manufacturing, upgrading, and disposal of AI devices may generate considerable amounts of electrical waste and pollution, which contradicts the ideas of a green economy [19]. Therefore, research on the development of AI-enabled regional green economies must consider both the positive and negative implications of AI.

Furthermore, the spatial dimension of green efficiency in China is increasingly recognized. Studies employing spatial econometric models have revealed significant spillover effects in GTFP and environmental performance across provinces, suggesting that regional green development is interdependent [20]. This spatial correlation, however, is often overlooked in conventional environmental efficiency assessments based on SBM-undesirable models or meta-frontier analysis. While these DEA models effectively handle undesirable outputs and technology heterogeneity [21], they typically treat decision-making units in isolation, failing to capture the systemic interplay between a region’s technological inputs (like AI) and its resulting green performance within a broader spatial context.

Existing literature primarily focuses on two research streams: examining the artificial intelligence industry from an industrial perspective and investigating the relationship between AI and energy consumption. However, few studies simultaneously address AI development levels and regional green economic performance within an AI-embedded context. Comparative assessment across these two dimensions remains limited. This study proposes a “two-system” coupling framework to advance this field of research. Our approach shifts beyond conventional production-theoretic perspectives. It evaluates the coupling coordination degree between regional AI development systems and green economic efficiency systems. This enables explicit characterization of regional performance across these two critical dimensions. Through empirical implementation of these two evaluation systems, this research provides a complementary perspective on synergistic development pathways. This study aims to map China’s AI development landscape and assess green economic efficiency under AI embedding. It further identifies regional disparities in AI advancement and bottlenecks in green development, thereby providing theoretical support for differentiated optimization strategies.

3. Evaluation System

3.1. Evaluation System for the Level of Development of the Entire AI Chain

The development of the entire AI chain is posited to be associated with enhanced energy system optimization and reduced carbon emission intensity. By investigating the degree of AI development in China’s provinces, we can observe variances in the role of AI in the low-carbon economy. The AI ecosystem comprises the following four interwoven chains: industrial, innovative, educational, and urban. These chains cover the entire scope of AI industry development and promote the healthy development and practical application of AI technology [22]. The AI industrial chain consists of several stages, including research and development, design, production, application deployment, and service support. This chain spans the whole lifecycle of AI technology, promoting its development, production, and application. A well-established industrial chain supports the development of a full AI industry ecosystem, as well as the industrialization and commercialization of AI technologies [23]. The number of AI firms and the presence of core personnel are markers of the viability of the AI industry. The AI innovation chain spans from fundamental research to technology and application innovation. Continuous breakthroughs and developments in AI technology can be realized through the establishment of a robust innovation chain. The innovation chain is largely concerned with cultivating technological patents and developing innovative people to improve the core competitiveness of the AI industry. The number of AI digital patents and new AI professions reflects the energy level of the AI innovation chain. The AI education chain covers the entire educational process, from university education to vocational training [24]. The formation of this chain can help nurture AI professionals, support high-precision research and development achievements, and achieve comprehensive success in the AI sector. The number of AI professional clusters, the output of AI knowledge, and the quantity of internationally recognized research articles all provide valuable insights into the energy level of the AI education chain [25]. The AI urban chain prioritizes both city infrastructure development and the integration of intelligent applications [26]. Smart city development can improve city management and service levels, which includes incorporating AI technology into different parts of city management, transportation, environmental protection, and other areas to assist in the sustainable development of cities and their citizens. The number of smart cities and the extent of digital infrastructure development reflect the energy level of the AI urban chain.

In short, these four chains are interconnected and mutually supportive, and together, they create the entire AI chain. The synergistic development of the entire chain may encourage the diverse and green development of the AI industry, education, innovation, and cities, as well as the widespread use of AI technology and the efficient use of resources [27]. In this work, the entire AI chain is separated into the following four subsystems: AI industry, AI innovation, AI education, and AI city chains. A comprehensive four-dimensional evaluation system can be constructed to assess the current level of regional artificial intelligence development.

3.2. Evaluation System for AI-Embedded Regional Economic Green Development Efficiency

By analyzing the performance and disparities in green economic efficiency across Chinese provinces under AI embeddedness, challenges facing green economic development can be identified. The efficacy of AI-enabled regional green economic development has several characteristics, including energy use, environmental enhancement, carbon emissions, and economic restructuring. Resource use efficiency assesses the efficacy of resource exploitation in the context of regional economic development, including measurements such as energy, water, and land use efficiency [28]. Environmental improvement reflects the degree to which regional economic development contributes to improved environmental quality, which includes improvements in atmospheric, water, and soil quality, among other factors. Carbon emission measurement estimates the amount by which regional economic development reduces carbon emissions, considering factors such as lower carbon emissions per unit of GDP and the use of renewable energy sources [29]. Economic structural adjustment is represented mostly by changes in the size and contribution of green and low-carbon industries. This adjustment is quantitatively measured by the proportion of the tertiary sector in the provincial economy, as it reflects the transition from energy-intensive industries to service-oriented and low-carbon economic activities.

On the input side, industrial progress requires the use of both traditional resource elements and the incorporation of AI technology. The input side is divided into numerous categories, including people, hardware, energy, technology, capital, and research input. Human input refers to the human capital of individuals hired from various industries for economic progress, including staff from both traditional sectors and the AI industry chain. Hardware input refers generally to the fixed asset investments made by each industry, including investments by AI businesses. Energy input refers mostly to the energy consumed during industry-wide development. Technology input is aligned with the AI innovation chain, indicating the infusion and application of AI technologies inside the region, where technology transfers play an important role in promoting regional green economic growth and lowering energy consumption levels. Financial input corresponds to the AI industry chain, which includes financial operations aimed primarily at assisting AI firms in driving the rapid creation of AI business clusters. Research input is consistent with the AI education chain, referring to funding assistance for key research issues pursued by universities to drive AI-focused research and development activities. On the output side, consideration should be given to both green transformation and structural changes within the industrial framework, as well as the negative consequences of energy consumption on the environment. As a result, the output side consists of two basic aspects. First, the output side involves evaluating the green section of the economic system, as demonstrated by the contribution of the tertiary industry to regional GDP. Second, the output side involves assessing the negative impacts of waste gases and wastewater to determine the effectiveness of environmental governance and energy management in driving economic transformation and supporting quality development. The greening of the economic structure reflects the combined influence of the AI industrial, innovation, and education chains. Conversely, negative outputs such as exhaust emissions and wastewater are consistent with the governance efficacy of the AI city chain. Based on the aforementioned analysis, this study aims to evaluate the efficiency of AI-embedded regional green economic development from a multiple-input and multiple-output perspective.

4. Methodology

4.1. Entropy Weight TOPSIS

The entropy weight TOPSIS method evaluates the AI development system. This multi-criteria approach synthesizes diverse AI indicators into a single composite score for cross-sectional comparison and ranking. It addresses the question of which regions possess higher AI development levels. Conversely, the DEA-BCC model assesses the green economic efficiency system. This non-parametric technique handles multiple inputs and outputs to perform efficiency diagnostics and analyze returns to scale. It examines whether a region achieves effective green economic output from its given inputs. This study’s objective is to investigate the relationship between these two systems. Consequently, we employ a “two-system” coupling framework to jointly evaluate AI development and green economic efficiency. Techniques including scatter plots, regression analysis, and Moran’s I are applied to examine provincial performance, correlations, and spatial dependencies. This “divide and conquer” strategy provides a coherent analysis of the two distinct systems, yielding deeper, more interdisciplinary insights.

The Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) technique is a ranking algorithm based on the proximity of assessment entities to both the best and worst solutions. This method quickly uses raw data to perform thorough multi-objective evaluations, resulting in positive and negative ideal solutions via cosine similarity computations. As a result, this technique appropriately assesses the relative differences in entities on the basis of their proximity to the positive ideal solution [30]. However, in the context of multi-objective evaluation with TOPSIS, the determination of evaluation indicator weights has a considerable effect on the final evaluation results. To mitigate the degree of subjective bias in the evaluation process, this study employs the entropy weight-TOPSIS method to assess the comprehensive development level of regional artificial intelligence.

(1)

To determine the weights of the indicators, the entropy weighting method, with the following steps, is used:

➀

Let $\mathrm{U}=\{{\mathrm{u}}_1,{\mathrm{u}}_2,\cdots ,{\mathrm{u}}_{\mathrm{m}}\}$ represent the set of evaluation objects, $\mathrm{V}=\{{\mathsf{\nu }}_1,{\mathsf{\nu }}_2,\cdots ,{\mathsf{\nu }}_{\mathrm{n}}\}$ denote the set of evaluation indicators, and $x_{\mathit{ij}}$ indicate the raw data of the $\mathrm{j}$ evaluation indicator $v_j$ in the $\mathrm{i}$ evaluation object ${\mathrm{u}}_{\mathrm{i}}$

➁

Since the original indicator data contain zero values, the Min-Max scaling method is applied for intervalization to prevent distortion of entropy weights and avoid computational issues in subsequent steps. This process is implemented using the SPSSAU tool (https://spssau.com/index.html, accessed on 6 January 2026), which scales the data into the conventional [0, 1] range. The transformation formula for positive indicators is as follows. The intervalization effectively eliminates the influence of measurement units while preserving the distributional characteristics and relative relationships of the original data.

$$\begin{array}{c}{\mathrm{m}}_{\mathrm{ij} }=\mathrm{a}+{\displaystyle \frac{\left( \mathrm{b}-\mathrm{a} \right) [{ \mathrm{x}}_{\mathrm{ij} }-\min ( {\mathrm{x}}_{\mathrm{ij}} ) ]}{\max ({\mathrm{x}}_{\mathrm{ij}}) -\min ( {\mathrm{x}}_{\mathrm{ij} })}} ( 1 \le \mathrm{i} \le \mathrm{m} , 1 \le \mathrm{j} \le \mathrm{n} ; \mathrm{a}=0 , \mathrm{b}=1 )\hfill \\ (\mathrm{Positive} \mathrm{indicators})\hfill \end{array}$$

(1)

➂

Calculate the percentage of characteristics of the ${\mathrm{i}}^{\mathrm{t}\mathrm{h}}$ province under the ${\mathrm{j}}^{\mathrm{t}\mathrm{h}}$ indicator, denoted as $p_{\mathit{ij}}$

$${\mathrm{p}}_{\mathrm{ij}}={\mathrm{m}}_{\mathrm{ij}}/\sum _{\mathrm{i}=1}^{\mathrm{m}}{\mathrm{m}}_{\mathrm{ij}}$$

(2)

➃

Calculate information entropy $e_j$

$${\mathrm{e}}_{\mathrm{j}}=-{\displaystyle \frac{1}{\ln \mathrm{m}}}\sum _{\mathrm{i}=1}^{\mathrm{m}}({\mathrm{r}}_{\mathrm{ij}}\times \ln {\mathrm{r}}_{\mathrm{ij}})$$

(3)

➄

Determine the weight of the evaluation index $w_j$

$${\mathrm{w}}_{\mathrm{j}}=(1-{\mathrm{e}}_{\mathrm{j}})/\sum _{\mathrm{j}=1}^{\mathrm{n}}(1-{\mathrm{e}}_{\mathrm{j}})$$

(4)

(2)

Multicriteria evaluation using the TOPSIS method. The steps are as follows:

➀

Let $\mathrm{U}=\left\{{\mathrm{u}}_1,{\mathrm{u}}_2,\dots ,{\mathrm{u}}_{\mathrm{m}}\right\}$ represent the set of evaluation objects, $\mathrm{V}=\left\{{\mathrm{v}}_1,{\mathrm{v}}_2,\dots ,{\mathrm{v}}_{\mathrm{n}}\right\}$ denote the set of evaluation indicators, and $x_{\mathit{ij}}$ denote the raw data of the $j^{\mathrm{t}\mathrm{h}}$ evaluation indicator ${\mathrm{v}}_{\mathrm{j}}$ in the $i^{\mathrm{t}\mathrm{h}}$ evaluation object ${\mathrm{u}}_{\mathrm{i}}$.

➁

The reverse indicators are transformed into positive indicators, and for simplicity, ${\mathrm{x}}_{\mathrm{i}\mathrm{j}}$ is still used in the following steps instead of ${\mathrm{x}}_{\mathrm{i}\mathrm{j}}^{*}$

$${\mathrm{x}}_{\mathrm{ij}}^{*}=\max ( {\mathrm{x}}_{\mathrm{ij}} )-{\mathrm{x}}_{\mathrm{ij}} ( 1 \le \mathrm{i} \le \mathrm{m}, 1 \le \mathrm{j} \le \mathrm{n} )$$

(5)

➂

Construct vector normalization matrix $\mathrm{Z}$ by dividing each column element by the corresponding column parameter:

$${\mathrm{z}}_{\mathrm{i}\mathrm{j}}={\displaystyle \frac{{\mathrm{x}}_{\mathrm{i}\mathrm{j}}}{\sqrt{\sum _{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}\mathrm{j}}^2}}}(1\le \mathrm{i}\le \mathrm{m},1\le \mathrm{j}\le \mathrm{n})$$

(6)

The resulting normalization matrix $\mathrm{Z}$ is as follows:

$$\mathrm{Z}=\left[\begin{array}{cccc}{\mathrm{z}}_{11}& {\mathrm{z}}_{12}& \dots & {\mathrm{z}}_{1\mathrm{n}}\\ {\mathrm{z}}_{21}& {\mathrm{z}}_{22}& \dots & {\mathrm{z}}_{2\mathrm{n}}\\ ⋮& ⋮& \ddots & ⋮\\ {\mathrm{z}}_{\mathrm{m}1}& {\mathrm{z}}_{\mathrm{m}2}& \dots & {\mathrm{z}}_{\mathrm{mn}}\end{array}\right]$$

(7)

➃

Determine the positive and negative ideal solutions corresponding to each evaluation index ${\mathrm{z}}_{\mathrm{j}}^{+}$ and ${\mathrm{z}}_{\mathrm{j}}^{-}$ represent the maximum and minimum values of column $\mathrm{j}$, respectively, in normalization matrix $\mathrm{Z}$, as follows:

The positive ideal solution is as follows:

$$\begin{array}{cc}\hfill {\mathrm{Z}}^{+}& = (\max \{{\mathrm{z}}_{11 }, {\mathrm{z}}_{21 }, \dots , {\mathrm{z}}_{\mathrm{m}1 }\} , \max \{{\mathrm{z}}_{12 }, {\mathrm{z}}_{22 }, \dots , {\mathrm{z}}_{\mathrm{m}2 }\} , \dots ,\max \{{\mathrm{z}}_{1\mathrm{n}} , {\mathrm{z}}_{2\mathrm{n} }, \dots , {\mathrm{z}}_{\mathrm{mn}} \left\}\right)\hfill \\ & = ({\mathrm{z}}_1^{+} , {\mathrm{z}}_2^{+} , \dots , {\mathrm{z}}_{\mathrm{n}}^{+} ) ( 1 \le \mathrm{i} \le \mathrm{m} , 1 \le \mathrm{j} \le \mathrm{n} )\hfill \end{array}$$

(8)

The negative ideal solution is as follows:

$$\begin{array}{cc}\hfill {\mathrm{Z}}^{-}& = (\min \{{\mathrm{z}}_{11 }, {\mathrm{z}}_{21 }, \dots , {\mathrm{z}}_{\mathrm{m}1} \} , \min \{{\mathrm{z}}_{12 }, {\mathrm{z}}_{22 }, \dots , {\mathrm{z}}_{\mathrm{m}2} \} , \dots ,\min \{{\mathrm{z}}_{1\mathrm{n}} , {\mathrm{z}}_{2\mathrm{n} }, \dots , {\mathrm{z}}_{\mathrm{mn}} \left\}\right)\hfill \\ & = ({\mathrm{z}}_{1 }^{-}, {\mathrm{z}}_2^{-} , \dots , {\mathrm{z}}_{\mathrm{n}}^{-} ) ( 1 \le \mathrm{i} \le \mathrm{m} , 1 \le \mathrm{j} \le \mathrm{n} )\hfill \end{array}$$

(9)

➄

Calculate the Euclidean distance from each province to the positive and negative ideal solutions:

$${\mathrm{d}}_{\mathrm{i}}^{+} =\sqrt{\sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}({\mathrm{z}}_{\mathrm{ij}}-{\mathrm{z}}_{\mathrm{j}}^{+}{)}^2} (1 \le \mathrm{i} \le \mathrm{m}, 1 \le \mathrm{j} \le \mathrm{n})$$

(10)

$${\mathrm{d}}_{\mathrm{i}}^{-} =\sqrt{\sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{w}}_{\mathrm{j}}{\left({\mathrm{z}}_{\mathrm{ij}}-{\mathrm{z}}_{\mathrm{j}}^{-}\right)}^2} (1 \le \mathrm{i} \le \mathrm{m}, 1 \le \mathrm{j} \le \mathrm{n})$$

(11)

where ${\mathrm{w}}_{\mathrm{j}}$ represents the weight of the ${\mathrm{j}}^{\mathrm{t}\mathrm{h}}$ evaluation index and the weight of each index is determined by the entropy weighting method.

➅

Calculate the proximity of the combined results of each province to the positive ideal solution:

$${\mathrm{S}}_{\mathrm{i}}={\displaystyle \frac{{\mathrm{d}}_{\mathrm{i}}^{-}}{{\mathrm{d}}_{\mathrm{i}}^{+}+{\mathrm{d}}_{\mathrm{i}}^{-}}} (\mathrm{i}=1, 2, \dots , \mathrm{m})$$

(12)

where $0 \le { \mathrm{S}}_{\mathrm{i}} \le 1$; the closer ${\mathrm{S}}_{\mathrm{i}}$ is to 1, the better the performance of the evaluated entity; and the ranking is determined by the degree of proximity.

4.2. BCC Model of DEA (DEA-BCC)

Data envelopment analysis (DEA) is a well-known efficiency evaluation tool for assessing the performance of multi-input, multi-output decision-making units (DMUs). Banker et al. (1984) further refined the assumption of returns to scale, thus proposing the Banker–Charnes–Cooper (BCC) model [31]. The DEA approach is more rigorous than other nonparametric methods; the complete number of efficient DMUs decreases, as does the efficiency score, with the DEA approach. By using the DEA approach to investigate the efficiency of AI-embedded regional green economic development, it is feasible to evaluate the efficiency of a multi-input, multi-output scale without a specific production function, as well as analyse the direction and degree of improvement in scale inefficient units.

AI-embedded regional green economic activities exhibit a certain degree of controllability, yet most decision-making units (DMUs) struggle to achieve optimal production scale. Therefore, this study adopts an input-oriented variable returns to scale model—specifically, the DEA-BCC model planning equation, which is as follows:

$$\begin{array}{ll}& \min \mathsf{\theta }\\ & \mathrm{s}.\mathrm{t}. {\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}}{\mathsf{\lambda }}_{\mathrm{j}}{\mathrm{x}}_{\mathrm{ij}} \le \mathsf{\theta }{\mathrm{x}}_{\mathrm{ik}}\\ & {\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}}{\mathsf{\lambda }}_{\mathrm{j}}{\mathrm{x}}_{\mathrm{rj}} \le {\mathrm{y}}_{\mathrm{rk}}\\ & {\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}}{\mathsf{\lambda }}_{\mathrm{j}} = \mathsf{\theta }{\mathrm{x}}_{\mathrm{ik}}\\ & \mathsf{\lambda } \ge 0\\ & \mathrm{i} = 1 , 2 , \dots , \mathrm{m} ; \mathrm{r} = 1 , 2 , \dots , \mathrm{q} ; \mathrm{j} = 1 , 2 , \dots , \mathrm{n}\end{array}$$

(13)

where $\mathrm{i}$ denotes the ordinal number of the DMU and ${\mathrm{x}}_{\mathrm{i}\mathrm{j}}$ indicates that the ${\mathrm{i}}^{\mathrm{t}\mathrm{h}}$ decision unit uses the ${\mathrm{j}}^{\mathrm{t}\mathrm{h}}$ input factor and obtains output ${\mathrm{y}}_{\mathrm{r}\mathrm{j}}$. If $\theta = 1$, then the decision units are in the efficiency frontier, and if $\theta < 1$, then they are in an inefficient state.

5. Data

The rationale for choosing China as the focal point of investigation in the Evaluation System for the Development Level of the Entire AI Chain and the Evaluation System for the Efficiency of Green Development in Regional Economies Embedded in AI can be articulated in several key dimensions. First, China’s rapid AI achievements and strong policy frameworks position it as a critical case for worldwide AI research. Second, China’s geographical and economic diversity provides an unparalleled chance for in-depth examination. Furthermore, the availability of data greatly enhances this study. China has established a relatively well-developed evaluation index system for artificial intelligence and related fields. Both national and local statistical agencies, as well as research institutions, provide data support, which facilitates the construction of a comprehensive evaluation framework and ensures the systematic and rigorous nature of the study.

The study area includes China’s 31 provinces and regions, with panel data selected from 2019 to 2021 on the basis of factors such as data availability, accessibility, standardization, and representativeness. The evaluation system for assessing the development level of the entire AI chain includes a variety of metrics. To adequately characterize the artificial intelligence industry, this study adopts two indicators: the number of listed AI enterprises and the allocation of core AI human resources. To assess AI innovation capacity, this study takes into account the following two indicators: the number of patents granted for digital-economy-related inventions in a particular year and the number of recruitments for 10 types of new occupations in AI. The number of AI-related programs offered by universities and the volume of international AI research publications produced by academic institutions collectively reflect the capacity of AI education supply. The number of smart cities and the digital economy development index provide additional insights into the vitality of the AI ecosystem. This study employs the ‘Digital Economy Development Index’ as an environmental support factor, which is strictly exogenous to other AI-related indicators. This index is constructed based on macro-environmental dimensions such as digital infrastructure and digital application levels. These components reflect the overall digital ecosystem and foundational conditions of regional economic development. They provide essential support for AI technology research, development, and application, but they do not directly measure any specific technical capabilities or innovation activities within the AI field. Moreover, clear conceptual and measurement boundaries exist between this index and other AI indicators, thereby effectively avoiding the issue of double-counting. Therefore, this study establishes an evaluation system for the full-chain development level of artificial intelligence, as shown in

Table 1. Evaluation system of the development level of the entire chain of AI and data sources.

1st Order Dimension	2nd Order Dimension	Meaning of Indicators	Data Source
AI Industry Capability Level	Enterprise Capability Level	Number of AI-listed firms (Unit: one)	PPData database
	Human Capacity	Number of AI Core Human Capital (Unit: one)	PPData database
AI Innovation Capacity Level	Patent Capacity	Number of digital economy-related invention patents granted in the current year (Unit: one)	PPData database
	Occupation Capacity	Number of Recruitments for 10 types of new occupations in AI (Unit: one)	China Statistical Yearbook
AI Education Capability Level	Subject Capability Level	Number of AI majors in colleges and universities (Unit: one)	China Statistical Yearbook on Science and Technology
	Knowledge Capability	Number of international papers on AI published by colleges and universities (Unit: one)	China Statistical Yearbook on Science and Technology
AI Environment Capability Level	City Capability Level	Number of smart cities (Unit: one)	PPData database
	Digital Energy Level	Digital Economy Development Index (Unit: points)	PPData database

. Taking into account the availability and continuity of data, we further clean and optimize the data in practice to ensure consistency in dimensions and indicator connotations. We also refer to official data definitions and sources from Chinese government reports to further ensure the validity of the panel data. By utilizing panel data, we have further ascertained the actual performance and stability of AI development across various regions.

The evaluation approach for assessing regional green economic efficiency under AI embedding encompasses both input and output dimensions. In the input dimension, human input is represented by the number of people engaged in various industries. The indicator for fixed asset investment serves to gauge the level of hard infrastructure foundation of the regional economy. Energy input is reflected in total coal consumption, which represents cumulative coal usage over a given period. The technology input dimension includes the implementation of AI technologies in the region. The variable “Number of AI Technology Input Relationships in Provinces” is sourced from the PPData database. From the perspective of the value network structure, the interaction and collaborative innovation among AI enterprises, traditional industrial firms, universities, research institutes, investors, and the government form the dynamic mechanism. This mechanism drives the deep integration of AI and the real economy. In the collaborative innovation of diverse entities, platforms, and their vertical sub-platforms continuously promote the application and development of AI across economic and social sectors. They achieve this by constructing and improving the industrial ecosystem. Within these technical collaborations, this variable measures the regional application and embedding of AI technologies. It counts collaborative linkages between AI technology suppliers and adopters within a province. For instance, a collaboration between a university’s AI research team and a manufacturing company to implement intelligent diagnostics and predictive maintenance counts as one relationship. Capital investment is reflected in the financing of the AI company. Furthermore, universities’ acquisition of national-level project funding demonstrates research investment.

In the output dimension, the proportion of tertiary industry among regional GDP acts as a barometer for the industrial structure. Tertiary-sector fortification is critical to improving the effectiveness of local green governance. Exhaust and wastewater emissions are measured in relation to their major pollutant releases. Wastewater and exhaust emissions are inverse indicators, requiring inversion prior to formal review. The detailed evaluation model is presented in

Table 2. AI-enabled regional economic green development efficiency assessment system and data sources.

1st Order Dimension	2nd Order Dimension	Meaning of Indicators	Data Source
Input dimension	Human input	Number of persons employed in urban non-private units by industry (end of year) (Unit: 10,000 persons)	China Statistical Yearbook
	Hardware input	Growth of the actual capital available for investment in fixed assets of the whole society over the previous year (Unit: %)	China Statistical Yearbook
	Energy input	Total coal consumption (Unit: 10,000 tonnes)	China Energy Statistics Yearbook
	Technology Input	Number of AI Technology Input Relationships in Provinces (Unit: one)	PPData database
	Capital input	Financing amount of AI enterprises in provinces and municipalities (Unit: 100 million RMB)	PPData database
	Scientific research input	Total funding for national AI projects in provincial universities (Unit: million yuan)	China Statistical Yearbook on Science and Technology
Output dimension	Industrial adjustment	The proportion of the province’s tertiary sector (Unit: %)	China Statistical Yearbook
	Exhaust emissions	Emission of major pollutants in exhaust gas: Sulphur dioxide (Unit: 10,000 tonnes)	China Energy Statistics Yearbook
	Waste water emission	Emission of major pollutants in waste water: Chemical Oxygen Demand (Unit: 10,000 tonnes)	China Energy Statistics Yearbook

.

6. Empirical Results

6.1. Empirical Analysis

This approach breaks down arithmetic procedures into three parts. First, data are intervalized to account for the presence of zero values in the index data. Second, weighting values are determined using the entropy weighting method, and the data are weighted to provide new values, as shown in

Table 3. Weighting values calculated using the entropy weighting method.

Indicator	Entropy Value	Information Utility Value	Weight Coefficient
Number of the AI-listed Firms (Unit: one)	0.7414	0.2586	19.33%
AI Core Human Capital (Unit: one)	0.7482	0.2518	18.82%
Number of digital economy-related invention patents granted in the current year (Unit: one)	0.7674	0.2326	17.39%
Number of recruitments for 10 types of new occupations in AI (Unit: one)	0.7424	0.2576	19.25%
Number of AI majors in colleges and universities (Unit: one)	0.9394	0.0606	4.53%
Number of international papers on AI published by colleges and universities (Unit: one)	0.8432	0.1568	11.72%
Number of smart cities (Unit: one)	0.9509	0.0491	3.67%
Digital Economy Development Index (Unit: points)	0.9292	0.0708	5.29%

. Finally, the TOPSIS method is used with data to complete the study.

Table 4. Evaluation results of the level of development of the entire chain of AI (entropy weight).

Province	2019		2020		2021		Level
	Relative Proximity C	Ranking	Relative Proximity C	Ranking	Relative Proximity C	Ranking
Beijing	0.676	2	0.669	2	0.832	1	High
Guangdong	0.780	1	0.792	1	0.777	2	High
Jiangsu	0.635	3	0.653	3	0.375	3	High
Shanghai	0.417	5	0.396	5	0.366	4	High
Zhejiang	0.437	4	0.443	4	0.319	5	High
Shandong	0.386	6	0.380	6	0.196	6	Low
Hubei	0.252	8	0.232	8	0.171	7	Low
Sichuan	0.272	7	0.259	7	0.165	8	Low
Shaanxi	0.244	9	0.232	9	0.149	9	Low
Anhui	0.146	15	0.147	14	0.146	10	Low
Henan	0.166	13	0.161	13	0.130	11	Low
Fujian	0.207	10	0.186	10	0.119	12	Low
Hunan	0.167	12	0.174	12	0.112	13	Low
Chongqing	0.129	17	0.120	17	0.112	14	Low
Liaoning	0.180	11	0.177	11	0.109	15	Low
Tianjin	0.149	14	0.141	15	0.104	16	Low
Hebei	0.104	18	0.103	18	0.090	17	Low
Jiangxi	0.070	23	0.077	22	0.071	18	Low
Heilongjiang	0.144	16	0.132	16	0.071	19	Low
Jilin	0.100	19	0.096	19	0.065	20	Low
Shanxi	0.077	22	0.072	23	0.061	21	Low
Hainan	0.029	28	0.045	28	0.057	22	Low
Guangxi	0.084	21	0.083	20	0.057	23	Low
Guizhou	0.060	25	0.067	24	0.054	24	Low
Yunnan	0.088	20	0.080	21	0.052	25	Low
Gansu	0.051	27	0.050	27	0.042	26	Low
Inner Mongolia	0.061	24	0.063	25	0.040	27	Low
Xinjiang	0.056	26	0.056	26	0.032	28	Low
Qinghai	0.012	30	0.011	30	0.025	29	Low
Ningxia	0.022	29	0.022	29	0.021	30	Low
Tibet	0.003	31	0.004	31	0.005	31	Low

presents the detailed findings of the evaluation calculations.

Considering the consistency issue in the correction model, we have constructed a “entropy weight-DEA coupling weighting framework” to achieve consistency in two steps. The entropy weight method is used for objective weighting of indicators, while the non-desired output DEA is used for efficiency measurement. The core reason for the inconsistency between the two is that the “information dispersion-oriented” approach of entropy weight and the “efficiency optimization-oriented” approach of DEA have different demands for indicator weights, which can easily lead to the contradiction that “indicators with high entropy weights have their weights compressed in DEA”. To address this, we first perform consistency calibration for indicator preprocessing by normalizing positive indicators and using the reciprocal method to normalize negative indicators (non-desired outputs), thus achieving preliminary consistency in the correction model. Furthermore, we advance the construction of a DEA-BCC model under entropy weight constraints. The weights in traditional DEA are endogenous optimal solutions, which are prone to conflict with entropy weights. By introducing entropy weights as weight constraints, we construct an entropy weight-cross-efficiency DEA model, as described in the previous formula. Finally, we further utilize weight correlation analysis to verify the coupling effect of the model, that is, the consistency result. Data shows that the Pearson correlation coefficient between the weights in the model and entropy weights is 0.78, which is higher than the threshold of 0.7, indicating that the correction model has achieved consistency. The research results are valid.

Furthermore, we analyze the AI situation of each province under dynamic changes. As shown in Table 4.

The drivers behind this tiered distribution are multifaceted. The high-level echelon, comprising Guangdong, Beijing, Jiangsu, Zhejiang and Shanghai, benefits from a confluence of advantageous factors. In terms of policy support, these regions enjoy substantial financial backing and possess well-functioning, diversified innovation ecosystems, which lay a solid foundation for effective collaboration among government, industry, universities, and research institutes. Economically, these provinces are at the forefront of national economic transformation. They continuously increase the proportion of their tertiary sectors and actively cultivate new productive forces, adopting forward-looking development strategies that holistically enhance the speed, quality, and benefits of growth within a green innovation framework. Geographically, all are situated within China’s three major economic belts: the Yangtze River Delta, the Pearl River Delta, and the Bohai Rim Economic Zone. The agglomeration of economic activities in these regions generates significant knowledge and technological spillovers, creating a fertile ground for AI innovation. Furthermore, their commitment to building high-end R&D platforms and strengthening the transformation of AI-specific projects is evident. For instance, Jiangsu, Guangdong, and Zhejiang consistently rank among the top in China for the number of invention patents granted to universities.

The low-level echelon, encompassing the remaining provinces, faces a different set of circumstances and challenges. Policy initiatives in these regions often focus on integrated packages to promote technological adoption and a dual-track strategy of advancing scientific research while facilitating the transformation of outcomes. These measures aim to foster AI applications in sectors like smart city development, transportation, and healthcare. A common focus across many of these provinces is on talent attraction and cultivation, with various initiatives implemented to expand the pool of AI professionals and enhance the quality of scientific projects. Specific cases include Henan’s deeper integration into the national “East Data, West Computing” computing hub network, Hubei’s continuous upgrading of its scientific platform infrastructure, and the Sichuan-Chongqing economic zone leveraging its strategic location to promote resource collaboration and tertiary sector expansion. However, despite these efforts, factors such as less mature innovation ecosystems, relatively weaker economic foundations, and geographical distance from core economic agglomerations generally result in a slower pace of full-chain AI development compared to the high-level echelon.

Interestingly, from a horizontal time perspective, the rankings of various provinces have remained almost unchanged. From a dynamic perspective, AI development in various regions has maintained a stable trend. In terms of specific regions, provinces in the high-level echelon, such as Guangdong and Jiangsu, have consistently demonstrated strong performance in AI development, with high scores in innovation capacity, industrial scale, and policy support. These regions have established a solid foundation for AI development through long-term accumulation and continuous investment, enabling them to maintain a leading position. In contrast, provinces in the low-level echelon, such as Gansu and Qinghai, have faced challenges in AI development due to limited resources, weak innovation ecosystems, and geographical constraints. Despite some progress in recent years, these regions still lag behind the high-level echelon in terms of overall AI development level.

The DEA-BCC model is employed to evaluate regional green economic efficiency under AI embedding. The comprehensive efficiency shows the effectiveness of the DMU elements within the decision unit, denoted as technological efficiency multiplied by scale efficiency, and is limited to less than or equal to one. Using this model, a statistical analysis of 31 provinces is conducted to measure their comprehensive technical efficiency, pure technical efficiency, and scale efficiency. These metrics collectively reflect the efficiency of decision-making units. Comprehensive technical efficiency can be decomposed into pure technical efficiency and scale efficiency, thereby revealing the influence of technological and managerial levels on the efficiency of regional green economic development, as well as the correspondence between AI embedding and regional green development efficiency. The evaluation results are presented in

Table 5. Evaluation Results of Regional Green Economic Efficiency under AI Embedding.

Province	2019		2020		2021		Level
	OE(θ)	Ranking	OE(θ)	Ranking	OE(θ)	Ranking
Beijing	1.000	1	1.000	1	1.000	1	High
Tianjin	1.000	2	1.000	2	1.000	2	High
Shanghai	1.000	3	1.000	3	1.000	3	High
Hainan	1.000	4	1.000	4	1.000	4	High
Yunnan	0.955	9	0.959	10	1.000	5	High
Tibet	1.000	5	1.000	5	1.000	6	High
Qinghai	1.000	6	1.000	6	1.000	7	High
Guizhou	0.852	17	0.878	17	0.953	8	High
Jilin	1.000	7	0.945	12	0.949	9	High
Gansu	1.000	8	1.000	7	0.948	10	High
Liaoning	0.816	21	0.869	19	0.922	11	High
Hebei	0.867	16	0.924	15	0.912	12	High
Ningxia	0.919	12	0.987	9	0.905	13	High
Guangxi	0.882	14	0.940	13	0.904	14	High
Heilongjiang	0.827	19	0.862	20	0.885	15	Low
Hubei	0.693	29	0.988	8	0.861	16	Low
Henan	0.832	18	0.874	18	0.860	17	Low
Chongqing	0.876	15	0.857	21	0.857	18	Low
Sichuan	0.787	22	0.833	23	0.853	19	Low
Xinjiang	0.922	10	0.950	11	0.833	20	Low
Shandong	0.768	24	0.817	24	0.829	21	Low
Jiangxi	0.827	20	0.843	22	0.827	22	Low
Shaanxi	0.657	30	0.745	29	0.811	23	Low
Zhejiang	0.734	26	0.768	27	0.799	24	Low
Anhui	0.783	23	0.814	25	0.787	25	Low
Inner Mongolia	0.921	11	0.936	14	0.781	26	Low
Fujian	0.733	27	0.787	26	0.780	27	Low
Guangdong	0.720	28	0.758	28	0.776	28	Low
Hunan	0.767	25	0.735	30	0.764	29	Low
Shanxi	0.886	13	0.904	16	0.763	30	Low
Jiangsu	0.577	31	0.591	31	0.677	31	Low

. Based on the distribution characteristics of the overall efficiency OE(θ) values, this study categorizes the provinces into two development echelons. The division follows a natural break observed in the data: a significant drop occurs from Guangxi (0.904) to Heilongjiang (0.885), and the top 14 provinces (OE(θ) ≥ 0.900) form a distinct high-efficiency cluster. This classification not only includes all DEA strong-efficiency provinces but also incorporates top performers with technical efficiency close to the frontier. Consequently, the high-level echelon includes provinces with an OE(θ) value greater than or equal to 0.900, while the remaining provinces are classified into the low-level echelon.

From a dynamic perspective based on panel data, the core characteristics of provincial administrative efficiency from 2019 to 2021 lie in the time heterogeneity, hierarchical mobility, and dynamic evolution of regional differentiation. Specifically, these characteristics can be decomposed into the following three dimensions: In terms of time heterogeneity, higher-level regions exhibit a “steady decline”, while lower-level regions undergo a “fluctuation and reversal”. The temporal evolution trends of these two regional groups show significant differentiation. In terms of hierarchical mobility, “high-to-low” unidirectional mobility is dominant, with “low-to-high” cross-level mobility being an exception, which is sporadic and occurs at a single point. The efficiency leaps in Hubei, Heilongjiang, and Yunnan only occurred in a single year, and except for Yunnan maintaining its frontier status in 2021, the efficiency leaps in Hubei and Heilongjiang were fleeting. In the dynamic logic of regional differentiation, efficiency and economic development level exhibit a “decoupling effect”. The dynamic evolution of efficiency essentially reflects that AI efficiency is not determined by a single factor, but rather by the combined effects of policies, resource endowments, development stages, and other factors. The differentiation of higher-level groups stems from differences in policy continuity and resource utilization capabilities, while the reversal of lower-level groups is driven by short-term shock factors. The decoupling of regional efficiency from economic development level reveals the “guiding” characteristics of the efficiency measurement index system.

Overall, the majority of provinces have not achieved DEA efficiency. Among the 31 sample provinces, only 22.6% are located within the DEA-effective region, indicating that the potential of artificial intelligence resources remains underexploited in most areas. The overall data show that the average pure technical efficiency is lower than that of scale efficiency, with only 74.2% of provinces exhibiting a pure technical efficiency exceeding 0.9. This gap partly stems from the relatively underdeveloped level of AI in most Chinese provinces, highlighting an urgent need to enhance the embedding of AI technologies. Transforming existing technological capacity into tangible gains in the green economy is essential to advancing regional green development across all dimensions. Furthermore, imbalanced economic structures and insufficient emphasis on green and low-carbon development in some regions have resulted in immature models for a low-carbon economy.

Notably, Beijing, Tianjin, Shanghai, Hainan, Yunnan, Tibet, and Qinghai demonstrate comprehensive technical efficiency within the DEA-effective zone. This reflects a favorable synergy among AI resource allocation, management capability, and technological proficiency in these regions, effectively promoting green and low-carbon economic development. Although Tibet’s input-output scale remains relatively small due to its remote western location and underdeveloped digital infrastructure, the region strategically leverages its abundant natural and cultural resources to pursue a distinctive green development path characterized by specialization, high-end production, and quality-driven initiatives. Capitalizing on the growing cultural tourism trend, Tibet vigorously develops clean energy and is committed to establishing a new ecological development paradigm for the high-altitude plateau. These efforts support regional green economic initiatives, promote harmony between humans and nature, and have yielded phased achievements. In contrast, although Zhejiang has not fully attained DEA efficiency, its substantial investments in AI and steadfast practices in carbon governance are concurrent with its development. As a leading province in digital economy, Zhejiang rapidly advances the industrial application of AI, with implementations spanning life and health, unmanned retail, smart cities, and intelligent connected vehicles. The emergence of AI enterprise clusters continues to drive high-quality growth in Zhejiang’s green economy, while the application and transformation of green economic projects deliver tangible contributions to carbon governance.

Although Guangdong and Jiangsu lead in the aggregation of artificial intelligence innovation resources, their pure technical efficiency ranks relatively low among the provinces. Guangdong leverages the synergistic effects of the Pearl River Delta Economic Zone and the Guangdong-Hong Kong-Macao Greater Bay Area to continuously develop and expand its AI technology and resource systems. However, intra-provincial disparities hinder its development, particularly due to topographical obstacles in the northern mountainous areas that impede the diffusion of AI resources and the propagation of green economic practices. AI resources remain highly concentrated in the Pearl River Delta, while resource mobility and conversion rates in the northern and western regions are comparatively low, exacerbating industrial structural imbalances and high-carbon phenomena. Jiangsu, building on a robust industrial foundation, has long been committed to its “AI Plus” initiative and remains at the forefront of university-industry collaboration in technology R&D and application, which aligns with the development of a green circular economy. Nevertheless, development remains concentrated along the Shanghai-Nanjing corridor, resulting in uneven resource distribution within the province. Northern Jiangsu, including cities such as Lianyungang, Yancheng, Suqian, and Nantong, lags significantly in green economy development and intelligent resource allocation. These cities face intense homogeneous competition, lack a robust green industrial ecosystem, and exhibit low collaborative efficiency. Thus, both Guangdong and Jiangsu experience substantial intra-provincial disparities due to uneven resource distribution and low flow efficiency, which coincides with regional polarization and reduces overall technical efficiency.

Table 6. Returns to Scale Coefficients by Province.

Province	Return to Scale	Type
Beijing	1.000	Fixed returns to scale
Tianjin	1.000	Fixed returns to scale
Hebei	0.911	Increasing returns to scale
Shanxi	0.804	Increasing returns to scale
Inner Mongolia	0.788	Increasing returns to scale
Liaoning	1.004	Decreasing returns to scale
Jilin	0.975	Increasing returns to scale
Heilongjiang	0.949	Increasing returns to scale
Shanghai	1.000	Fixed returns to scale
Jiangsu	0.963	Increasing returns to scale
Zhejiang	0.980	Increasing returns to scale
Anhui	0.860	Increasing returns to scale
Fujian	0.814	Increasing returns to scale
Jiangxi	0.848	Increasing returns to scale
Shandong	0.950	Increasing returns to scale
Henan	0.893	Increasing returns to scale
Hubei	1.006	Decreasing returns to scale
Hunan	0.851	Increasing returns to scale
Guangdong	0.974	Increasing returns to scale
Guangxi	0.939	Increasing returns to scale
Hainan	1.000	Fixed returns to scale
Chongqing	0.894	Increasing returns to scale
Sichuan	0.931	Increasing returns to scale
Guizhou	0.937	Increasing returns to scale
Yunnan	1.000	Fixed return to scale
Tibet	1.000	Fixed return to scale
Shaanxi	0.916	Increasing returns to scale
Gansu	0.948	Increasing returns to scale
Qinghai	1.000	Fixed returns to scale
Ningxia	0.905	Increasing returns to scale
Xinjiang	0.843	Increasing returns to scale

shows that most provinces have increasing returns to scale, whereas few have decreasing or stable returns to scale. Specifically, in 2021, 22 provinces, or 70.97% of the sample, have increasing returns to scale, whereas 7 provinces have unchanged returns. Notably, the provinces with the most efficient green development of their local economies during that year are all those with increasing or constant returns to scale, with only Liaoning and Hubei Provinces seeing declining returns to scale. Liaoning and Hubei have relatively high AI inputs but inferior technical outputs and transformation efficiencies. Furthermore, their high levels of pollutant emissions in the output dimension highlight the limited effectiveness of AI interventions in reducing carbon emissions and controlling the carbon footprint. The presence of diminishing returns to scale in these two provinces indicates the necessity for judicious input reduction to improve resource utilization efficiency and the incorporation of AI technologies into the green economy. However, most provinces continue to see increasing returns to scale, indicating that they have yet to achieve the ideal level of production. The increase in provincial input factors is expected to result in more efficient output, implying that most provinces should prudently expand their production scale, supplement AI factor inputs, and optimize resource allocation and transformation to support the green development of their respective economies.

To visualize the regional green economy development efficiency under AI integration, we employ a labeled scatter plot with “Relative Proximity C” (AI development level) on the x-axis and “Overall Efficiency OE(θ)” (green economic efficiency) on the y-axis. Figure 1 presents this visualization with quadrants to distinguish types. All 31 provinces are labeled directly on the plot. This visualization enables direct comparison of provincial performance across the AI-green efficiency spectrum and facilitates the identification of atypical development pathways.

Based on the data presented in Figure 1, this study categorizes the provinces into four types according to the values of relative closeness and comprehensive efficiency.

“Double-high type”: This category includes provinces where both relative closeness and comprehensive efficiency exceed the average. Provinces such as Beijing and Shanghai possess substantial AI resources that are efficiently utilized and integrated into regional carbon governance. As China’s economic and technological forerunners, they facilitate the efficient flow of talent, knowledge, information, and capital within high-precision industries. By adopting innovative green technologies, these provinces demonstrate substantial carbon reduction effects, serving as benchmarks for green transformation and catalyzing nationwide emission reductions.

“High-low type”: This group comprises provinces with higher relative closeness but lower comprehensive efficiency. Although they exhibit reasonably advanced AI development, the impact of digital transformation on carbon emissions remains limited. The underutilization of AI resources is correlated with resource concentration, which is concurrent with lower comprehensive efficiency in low-carbon economic development.

“Low-high type”: This classification includes provinces with lower relative closeness but higher comprehensive efficiency. Despite limited AI resource endowments, these provinces demonstrate strong momentum in green economic development. They achieve efficient outcomes with limited resources through coordinated policy and corporate efforts, thereby accelerating the transition to a green and low-carbon economy.

Double-Low Type: These provinces show low levels in both relative proximity and overall efficiency. They face significant challenges in AI applications and green economic transition. These challenges stem from insufficient resource inputs and low conversion rate of local endowments. The solution requires targeted support policies based on local conditions. It also requires encouraging active enterprise participation in green initiatives.

The results reveal a robust and statistically significant relationship after controlling for key provincial characteristics, including GDP per capita, tertiary industry share, energy structure. The complete results of the stratified regression analysis are presented in

Table 7. Results of Hierarchical Regression Analysis.

Model	Item	Non-Standardized Coefficients		Standardized Coefficient β	t	p	95% CI	Collinearity Diagnosis
		B	Standard Error					VIF	Tolerance
Layer 1	β0	0.278 **	0.097	-	2.874	0.008	0.079~0.476	-	-
	X1i	−0.000 **	0	−0.825	−5.110	0	−0.000~−0.000	2.017	0.496
	X2i	0.014 **	0.002	1.200	7.040	0	0.010~0.018	2.245	0.445
	X3i	0.449	0.273	0.216	1.646	0.111	−0.111~1.009	1.329	0.753
	F Test	F (3,27) = 16.781, p = 0.000
	R2	R2 = 0.651, adjusted R2 = 0.612
	∆Information	∆R2 = 0.651, ∆F (3,27) = 16.781, p = 0.000
Layered 2	β0	0.199 *	0.086	-	2.321	0.028	0.023~0.375	-	-
	X1i	−0.000 **	0	−0.548	−3.410	0.002	−0.000~−0.000	2.750	0.364
	X2i	0.015 **	0.002	1.305	8.771	0	0.012~0.019	2.352	0.425
	X3i	0.347	0.235	0.167	1.478	0.151	−0.136~0.829	1.352	0.740
	X4i	−0.233 **	0.070	−0.502	−3.331	0.003	−0.377~−0.089	2.409	0.415
	F Test	F (4,26) = 20.065, p = 0.000
	R2	R2 = 0.755, adjusted R2 = 0.718
	∆Information	∆R2 = 0.104, ∆F (1,26) = 11.095, p = 0.003

Note: * p < 0.05; ** p < 0.01.

. Based on the results, all variance inflation factor (VIF) values are below 3, indicating an absence of severe multicollinearity; the 95% confidence intervals for the key coefficients do not span zero, supporting the precision of the estimates; and residual diagnostics confirm no major violations of the model’s underlying statistical assumptions. Specifically, the AI index shows a significant negative coefficient (β = −0.233, p < 0.01). The model’s explanatory power improves substantially, with the adjusted R² rising to 0.755 after including the AI index. The regression model is specified as:

Y_i = β₀ + β₁ × X_1i + β₂ × X_2i + β₃ × X_3i + β₄ × X_4i + ε

(14)

where Y_i is the Overall Efficiency score (unitless), X_1i denotes GDP per capita (yuan), X_2i represents tertiary industry share (%), X_3i indicates energy structure, measured as total energy consumption divided by GDP (%) and X_4i measures AI development level (unitless).

This intriguing negative correlation challenges simplistic technological optimism. It can be interpreted through transitional dynamics and regional spillovers in early AI development. We propose three non-exclusive explanations. First, the initial AI development phase may cause a short-term polarization effect. Capital and high-skilled labor concentrate heavily in leading AI hubs. Second, top AI provinces focus on scaling technology and heavy upfront investment. These substantial inputs have not yet matured into practical tools for enhancing green efficiency. Third, as a general-purpose technology, AI facilitates knowledge diffusion to neighboring provinces. Less advanced provinces can adopt AI for green applications without bearing high R&D costs. This enables leapfrogging in green economic efficiency. These findings reveal that the relationship between AI and green efficiency is complex, context-dependent, and period-specific. The current pattern suggests that high AI investment yields insufficient returns, urgently calling for more effective mechanisms to unlock its potential.

Based on the Moran’s I quadrant analysis, the spatial pattern of AI development in China demonstrates distinct clustering characteristics, as illustrated in Figure 2. The results indicate a dominant positive spatial autocorrelation. The Yangtze River Delta region and Shandong form a high-high agglomeration, representing high-value clusters. Most central and western provinces exhibit low-low clustering, indicating significant spatial spillovers. Concurrently, substantial spatial heterogeneity is observed. Beijing, Hubei, Guangdong, and Sichuan are identified as high-low outliers, showing limited radiation effects. Conversely, several provinces, including Tianjin and Anhui, are low-high outliers, surrounded by high-performing regions. These findings reveal pronounced regional disparities and insufficient spatial synergy in China’s AI development landscape. The relevant data are presented in

Table 8. Local Moran’s I Statistics for AI Development.

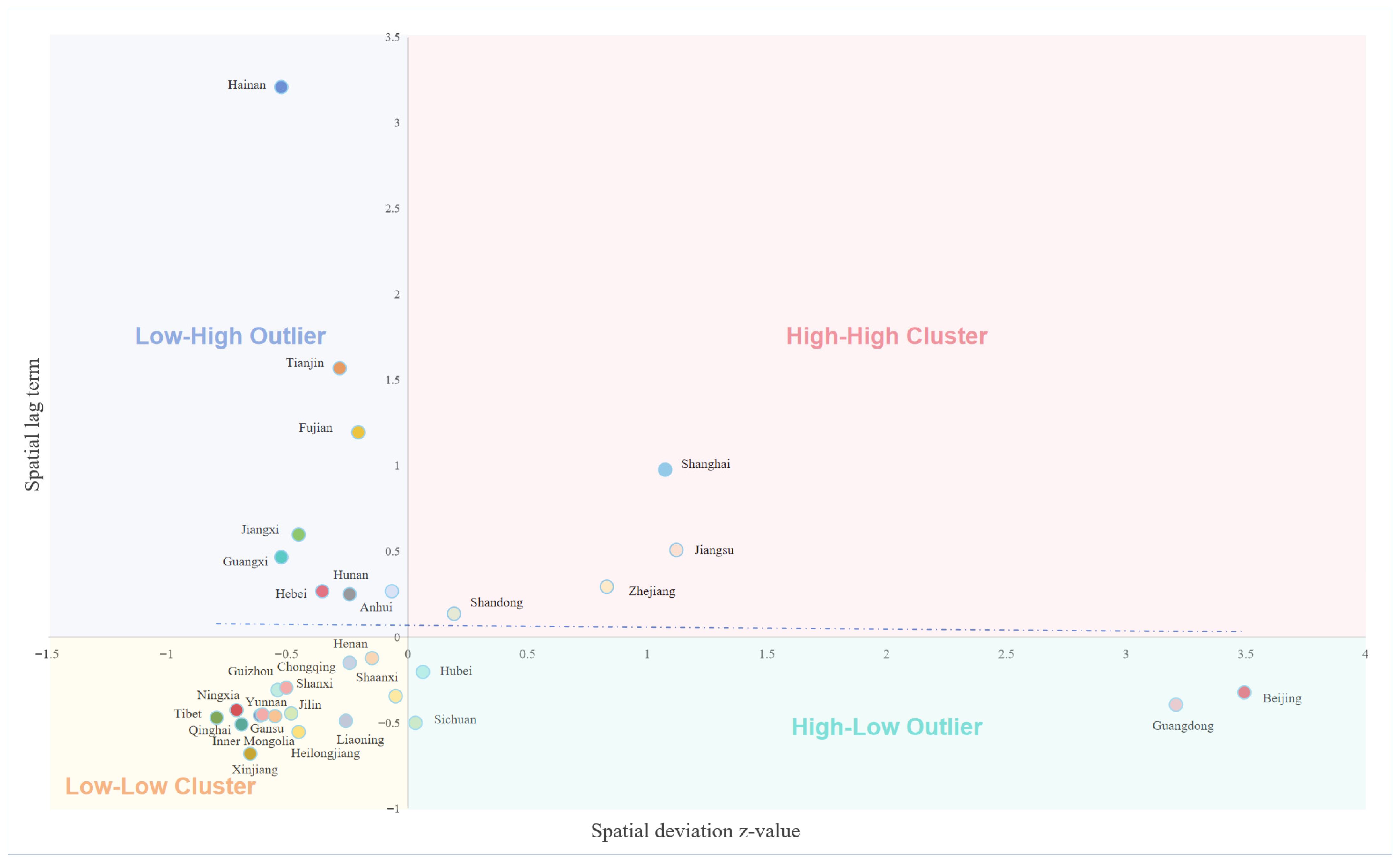
Province	Local Moran’s I	Expected I	Std. Dev.	Z-Score	p-Value
Beijing	−1.086	−0.033	1.772	−0.357	0.18
Tianjin	−0.432	−0.033	0.2	−2.182	0.007
Hebei	−0.092	−0.033	0.114	−0.697	0.122
Shanxi	0.144	−0.033	0.229	0.504	0.154
Inner Mongolia	0.272	−0.033	0.164	1.869	0.015
Liaoning	0.122	−0.033	0.147	0.783	0.108
Jilin	0.209	−0.033	0.276	0.734	0.116
Heilongjiang	0.244	−0.033	0.322	0.734	0.116
Shanghai	1.016	−0.033	0.756	1.464	0.036
Jiangsu	0.551	−0.033	0.512	1.293	0.049
Zhejiang	0.236	−0.033	0.359	0.795	0.107
Anhui	−0.017	−0.033	0.026	−0.648	0.129
Fujian	−0.239	−0.033	0.122	−2.026	0.011
Jiangxi	−0.264	−0.033	0.176	−1.448	0.037
Shandong	0.026	−0.033	0.091	0.414	0.17
Henan	0.018	−0.033	0.059	0.327	0.186
Hubei	−0.012	−0.033	0.025	−0.509	0.153
Hunan	−0.059	−0.033	0.096	−0.574	0.141
Guangdong	−1.219	−0.033	1.148	−0.748	0.114
Guangxi	−0.239	−0.033	0.255	−0.964	0.084
Hainan	−1.642	−0.033	0.602	−2.601	0.002
Chongqing	0.035	−0.033	0.117	0.305	0.19
Sichuan	−0.015	−0.033	0.012	−1.365	0.043
Guizhou	0.162	−0.033	0.259	0.648	0.129
Yunnan	0.247	−0.033	0.267	0.904	0.092
Tibet	0.362	−0.033	0.381	0.946	0.086
Shaanxi	0.017	−0.033	0.016	1.126	0.065
Gansu	0.265	−0.033	0.26	1.08	0.07
Qinghai	0.342	−0.033	0.338	0.997	0.08
Ningxia	0.294	−0.033	0.424	0.724	0.117
Xinjiang	0.433	−0.033	0.32	1.335	0.045

.

Based on Moran’s I quadrant analysis, China’s green economic efficiency exhibits significant spatial heterogeneity, as illustrated in Figure 3. The Beijing-Tianjin-Hebei region, Liaoning, and selected western provinces form distinct high-high agglomerations. Most central and eastern coastal provinces show extensive low-low clustering. This pattern indicates negative spatial spillovers in these regions. Furthermore, Jilin, Heilongjiang, and Shanghai emerge as high-low outliers. These provinces demonstrate limited radiative effects on their neighboring areas. Conversely, Inner Mongolia, Sichuan, and Xinjiang are characterized as low-high regions. These regions remain underdeveloped despite being surrounded by high-efficiency areas. The spatial configuration reveals positive spatial dependence in green economic development. It simultaneously highlights regional development imbalances. These imbalances primarily stem from insufficient regional coordination mechanisms. The relevant data are presented in

Table 9. Local Moran’s I Statistics of Provincial Green Economic Efficiency.

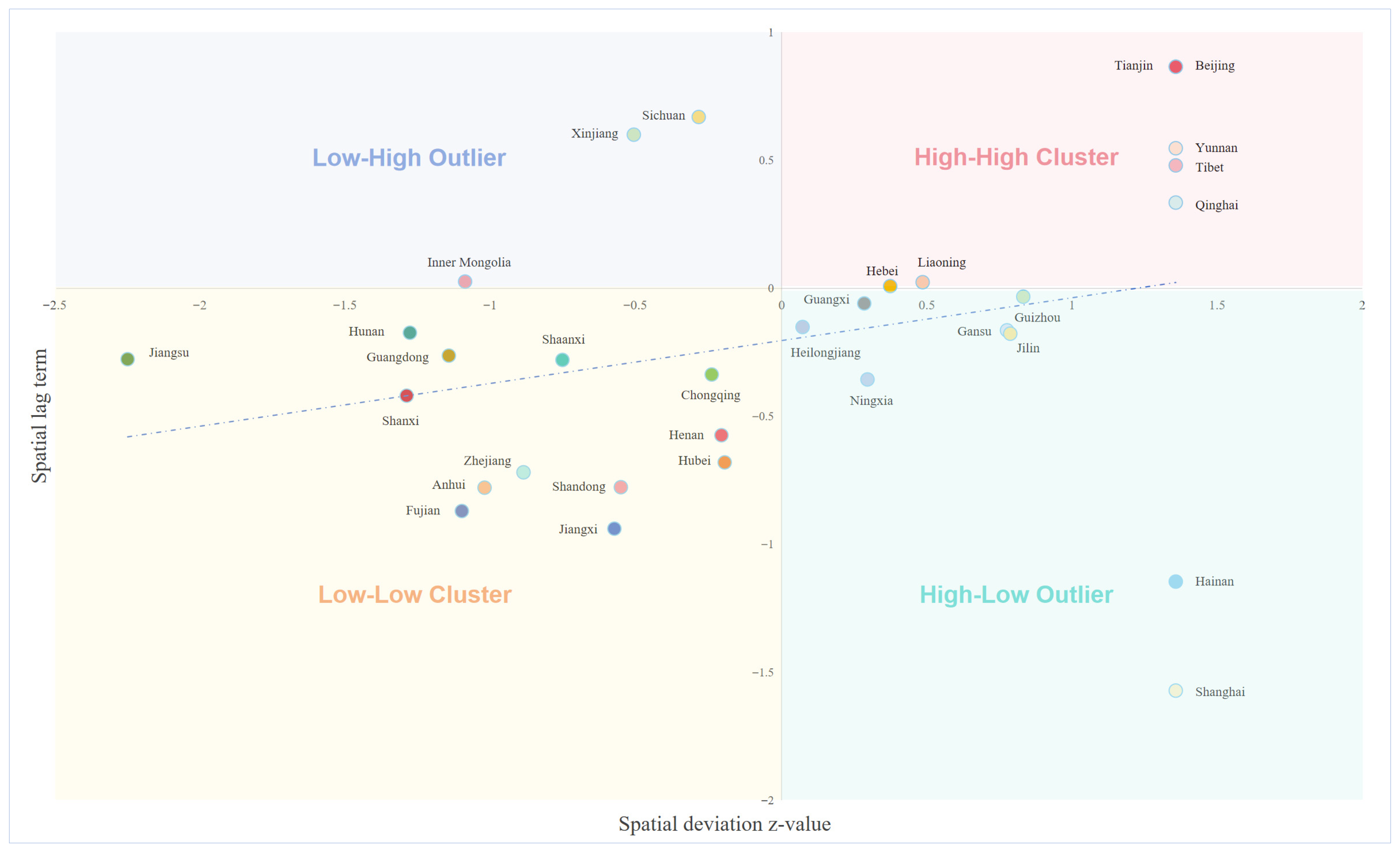
Province	Local Moran’s I	Expected I	Std. Dev.	Z-Score	p-Value
Beijing	1.137	−0.033	0.957	1.166	0.061
Tianjin	1.137	−0.033	0.957	1.166	0.061
Hebei	0.003	−0.033	0.127	−0.103	0.229
Shanxi	0.525	−0.033	0.580	1.086	0.069
Inner Mongolia	−0.027	−0.033	0.275	0.133	0.224
Liaoning	0.011	−0.033	0.257	−0.027	0.245
Jilin	−0.136	−0.033	0.410	−0.369	0.178
Heilongjiang	−0.011	−0.033	0.050	−0.160	0.218
Shanghai	−2.064	−0.033	0.919	−2.112	0.009
Jiangsu	0.605	−0.033	0.854	1.024	0.076
Zhejiang	0.620	−0.033	0.311	2.186	0.007
Anhui	0.773	−0.033	0.358	2.347	0.005
Fujian	0.929	−0.033	0.529	1.895	0.015
Jiangxi	0.525	−0.033	0.207	2.662	0.002
Shandong	0.417	−0.033	0.234	1.898	0.014
Henan	0.116	−0.033	0.075	1.631	0.026
Hubei	0.130	−0.033	0.071	1.914	0.014
Hunan	0.216	−0.033	0.443	0.678	0.124
Guangdong	0.293	−0.033	0.416	0.892	0.093
Guangxi	−0.016	−0.033	0.124	−0.200	0.210
Hainan	−1.506	−0.033	1.320	−0.968	0.083
Chongqing	0.079	−0.033	0.089	0.946	0.086
Sichuan	−0.185	−0.033	0.092	−1.940	0.013
Guizhou	−0.027	−0.033	0.306	−0.050	0.240
Yunnan	0.718	−0.033	0.581	1.323	0.046
Tibet	0.630	−0.033	0.581	1.171	0.060
Shaanxi	0.205	−0.033	0.233	1.026	0.076
Gansu	−0.124	−0.033	0.270	−0.461	0.161
Qinghai	0.439	−0.033	0.576	0.856	0.098
Ningxia	−0.102	−0.033	0.157	−0.616	0.134
Xinjiang	−0.296	−0.033	0.223	−1.306	0.048

.

Several provinces, namely Tianjin, Hainan, Yunnan, Tibet, and Qinghai, were identified as DEA-efficient despite their low AI development levels. This outcome reflects their unique endowment structures and spatial characteristics. These provinces exhibit two distinct development pathways. Tianjin and Hainan achieve technical efficiency while positioned in the low-high quadrant for AI development, benefiting from spatial spillovers from adjacent high-AI regions including Beijing and Guangdong. This pattern suggests that technology diffusion and institutional learning across provincial boundaries facilitate green efficiency even without local AI leadership. Yunnan, Tibet and Qinghai form a contiguous high-high cluster in green efficiency despite their moderate AI development, leveraging exceptional ecological endowments through specialized clean energy deployment and low-impact tourism development. This spatial configuration indicates that regional synergy in ecological preservation creates self-reinforcing advantages that substitute for technological leadership in certain contexts. The coexistence of these two pathways, technology absorption through spatial proximity and ecological advantage through resource specialization, underscores the contextual nature of green transitions and challenges universal prescriptions for sustainable development policy.

6.2. Robustness Checks

To test the stability of the entropy weight TOPSIS method, the subjective and objective weighting TOPSIS method is used for empirical analysis. Then, the evaluation results are compared. Seven experts are asked to assign weights to the level-one indicators. The objective weights are subsequently calculated using the entropy weighting method. Finally, the TOPSIS method is employed for empirical analysis. In conclusion, subjective and objective scoring integrate qualitative and quantitative evaluative viewpoints. This type of ranking has a lesser impact on calculation outcomes. The comparison reveals that the ranking distribution under the two forms of empowerment is somewhat changed and that the general pattern converges, as shown in

Table 10. Comparison of evaluation results.

Ranking	Entropy Weight ([0, 1])	Subjective and Objective Weighting ([1, 2])
1	Beijing	Guangdong
2	Guangdong	Beijing
3	Jiangsu	Jiangsu
4	Shanghai	Zhejiang
5	Zhejiang	Shandong
6	Shandong	Shanghai
7	Hubei	Henan
8	Sichuan	Hubei
9	Shaanxi	Sichuan
10	Anhui	Anhui
11	Henan	Chongqing
12	Fujian	Shannxi
13	Hunan	Liaoning
14	Chongqing	Hebei
15	Liaoning	Hunan
16	Tianjin	Fujian
17	Hebei	Tianjin
18	Jiangxi	Jiangxi
19	Heilongjiang	Jilin
20	Jilin	Shanxi
21	Shanxi	Guangxi
22	Hainan	Heilongjiang
23	Guangxi	Guizhou
24	Guizhou	Yunnan
25	Yunnan	Hainan
26	Gansu	Gansu
27	Inner Mongolia	Inner Mongolia
28	Xinjiang	Xinjiang
29	Qinghai	Qinghai
30	Ningxia	Ningxia
31	Tibet	Tibet

, indicating that the evaluation results obtained using the entropy weight TOPSIS method are highly stable.

Furthermore, to ensure the robustness of the green economic efficiency evaluation and to address the potential bias in handling undesirable outputs within the traditional DEA-BCC framework, we employ an Undesirable Slacks-Based Measure (Undesirable SBM) model for supplementary analysis. Relative to the radial DEA-BCC model, the non-radial and non-oriented Undesirable SBM model directly incorporates slack variables for both inputs and outputs into the objective function, thus effectively mitigating measurement biases arising from radial orientation. More importantly, it explicitly treats pollutants such as sulfur dioxide and wastewater as undesirable outputs within the production technology set, eliminating the need for simplistic data transformation and providing a more theoretically sound and accurate reflection of environmental performance.

The efficiency rankings from both models demonstrate strong consistency. First, the identification of high- and low-performing units is highly robust. Beijing, Tianjin, Shanghai, Hainan, Yunnan, Tibet, and Qinghai are consistently identified as strongly efficient units on the production frontier under both models. Conversely, provinces such as Jiangsu and Anhui are consistently ranked as inefficient. Only four provinces (Hebei, Ningxia, Henan, and Inner Mongolia) have ranking changes in five or more positions, with all others remaining within five. To quantify the agreement between the two evaluation methods, we calculate Spearman’s rank correlation coefficient between the DEA-BCC and SBM model rankings. The results show a correlation coefficient of 0.863, which is significant at the 1% level (p < 0.01). This confirms a high consistency in provincial efficiency rankings between the two models and passes the robustness test. Furthermore, the SBM model reveals that the efficiency of some provinces (e.g., Ningxia, Xinjiang) might have been underestimated by the DEA-BCC model due to slack issues in resource allocation. In conclusion, while minor ranking adjustments occur for a few provinces due to differing measurement concepts between the models, the core findings regarding the relative performance of provincial green economic efficiency remain highly robust. The identification of both leading and lagging groups is particularly stable.

We also conduct a robustness check using the DEA-CCR model. The results show that the efficiency rankings remain consistent across all provinces except for Ningxia and Guangxi. Under the DEA-BCC model, Ningxia and Guangxi are ranked 13th and 14th, respectively. Their positions are reversed in the DEA-CCR model. The results indicate that Spearman’s rank correlation coefficient between the provincial rankings of the BCC and CCR models is 1.000, and it is statistically significant at the 0.01 level. This minor change does not affect the overall ranking structure. The high consistency in provincial efficiency orders between the two models provides further evidence for the robustness of the empirical findings. For provincial efficiency scores (BCC, SBM-Undesirable, CCR) and rankings, see

Table 11. Provincial Efficiency Scores (BCC, SBM-Undesirable, CCR) and Rankings.

Ranking	BCC Score	BCC Ranking	SBM Score	SBM Ranking	CCR Score	CCR Ranking
Beijing	1.000	1	1.000	1	1.000	1
Tianjin	1.000	2	1.000	2	1.000	2
Shanghai	1.000	3	1.000	3	1.000	3
Hainan	1.000	4	1.000	4	1.000	4
Yunnan	1.000	5	1.000	5	1.000	5
Tibet	1.000	6	1.000	6	1.000	6
Qinghai	1.000	7	1.000	7	1.000	7
Guizhou	0.953	8	0.170	12	0.953	8
Jilin	0.949	9	0.155	13	0.949	9
Gansu	0.948	10	0.252	10	0.948	10
Liaoning	0.922	11	0.264	9	0.922	11
Hebei	0.912	12	0.091	22	0.912	12
Ningxia	0.905	13	0.345	8	0.904	14
Guangxi	0.904	14	0.111	17	0.904	13
Heilongjiang	0.885	15	0.100	19	0.885	15
Hubei	0.861	16	0.127	15	0.861	16
Henan	0.860	17	0.064	30	0.860	17
Chongqing	0.857	18	0.127	16	0.857	18
Sichuan	0.853	19	0.107	18	0.853	19
Xinjiang	0.833	20	0.150	14	0.833	20
Shandong	0.829	21	0.089	23	0.829	21
Jiangxi	0.827	22	0.097	20	0.827	22
Shaanxi	0.811	23	0.084	24	0.811	23
Zhejiang	0.799	24	0.095	21	0.799	24
Anhui	0.787	25	0.065	29	0.787	25
Inner Mongolia	0.781	26	0.172	11	0.781	26
Fujian	0.780	27	0.073	27	0.780	27
Guangdong	0.776	28	0.080	25	0.776	28
Hunan	0.764	29	0.070	28	0.764	29
Shanxi	0.763	30	0.076	26	0.763	30
Jiangsu	0.677	31	0.051	31	0.677	31

.

To enhance the consistency test between models, we employ both Kendall’s and Pearson’s correlation analyses to examine the relationships between the efficiency scores from the BCC, SBM-Undesirable, and CCR models. The results are as follows. Kendall’s correlation analysis shows a coefficient of 0.706 between the BCC and SBM-Undesirable rankings. This correlation is statistically significant at the 0.01 level, indicating a significant positive association. The correlation between the BCC and CCR rankings is 0.999, which is also significant at the 0.01 level. Pearson’s correlation analysis yields a coefficient of 0.792 for the efficiency scores between the BCC and SBM-Undesirable models, significant at the 0.01 level. The correlation between the BCC and CCR scores is 1.000 and equally significant. Furthermore, to evaluate the internal consistency of the efficiency rankings, the ordinal results from the three models are treated as multiple measurements of the same efficiency concept for a Cronbach’s alpha reliability analysis. The result shows a Cronbach’s α coefficient of 0.967, indicating that the assessment results of the three models possess extremely high internal consistency and are reliable.

Based on the distribution characteristics of the relative proximity C-values and the overall efficiency OE(θ) values, this study conducts a sensitivity analysis by applying median thresholds as an alternative classification method. The median values are calculated as follows: the AI relative proximity C has a median of 0.109, while the green economic efficiency OE(θ) has a median of 0.861. Using these median thresholds, we reclassify the provinces into four categories. The results show substantial consistency with the mean-based classification. Specifically, 26 out of 31 provinces (83.9%) remain in their original categories. The classification changes occur mainly in borderline cases where provincial values are close to the threshold boundaries. The key findings remain robust under both classification methods. The identification of top-performing provinces (Beijing, Shanghai) and struggling provinces remains unchanged. This sensitivity check confirms that our primary conclusions are not sensitive to the choice of classification threshold. The high consistency with the classification based on median values strengthens the reliability of the quadrant analysis in this study. This demonstrates that the observed patterns in provincial echelon performance are robust to the choice of threshold determination method.

7. Conclusions

7.1. Findings

The following results are obtained after developing two evaluation systems and applying the entropy weight TOPSIS approach to cross-sectional data from 31 Chinese provinces, as well as using the DEA-BCC model for assessment and analysis.

The results show a high mean value for the holistic efficiency of regional economic green development in 2021, indicating a strong overall developmental trajectory. However, the average pure technical efficiency remains lower than the average scale efficiency, indicating that the level of AI development and its correspondence with green economic efficiency requires improvement. For instance, Shandong possesses abundant AI resources and a solid industrial foundation, yet its overall efficiency score stands at 0.829, below the average of 0.88, which can be attributed to its singular energy consumption structure primarily reliant on coal and oil, coupled with insufficient embedded AI mechanisms. Following a thorough examination of the two evaluation systems, the 31 provinces considered in this work can be divided into the following four categories on the basis of the value of their AI development level and green economy efficiency: “double-high type”, “high-low type”, “low-high type”, and “double-low type”. Coastal provinces including Jiangsu, Zhejiang and Guangdong are classified as “high-low type”. These regions exhibit overly concentrated AI resource allocation. Meanwhile, provinces such as Guizhou, Tibet, and Yunnan represent the “low-high type”. Located in ecologically significant zones with abundant renewable energy resources, they demonstrate how regional advantages can support green development even with moderate AI inputs. The drivers, key bottlenecks, and suggested policy levers for each type are summarized in

Table 12. Provincial Classification Based on AI and Green Economic Efficiency with Policy Implications.

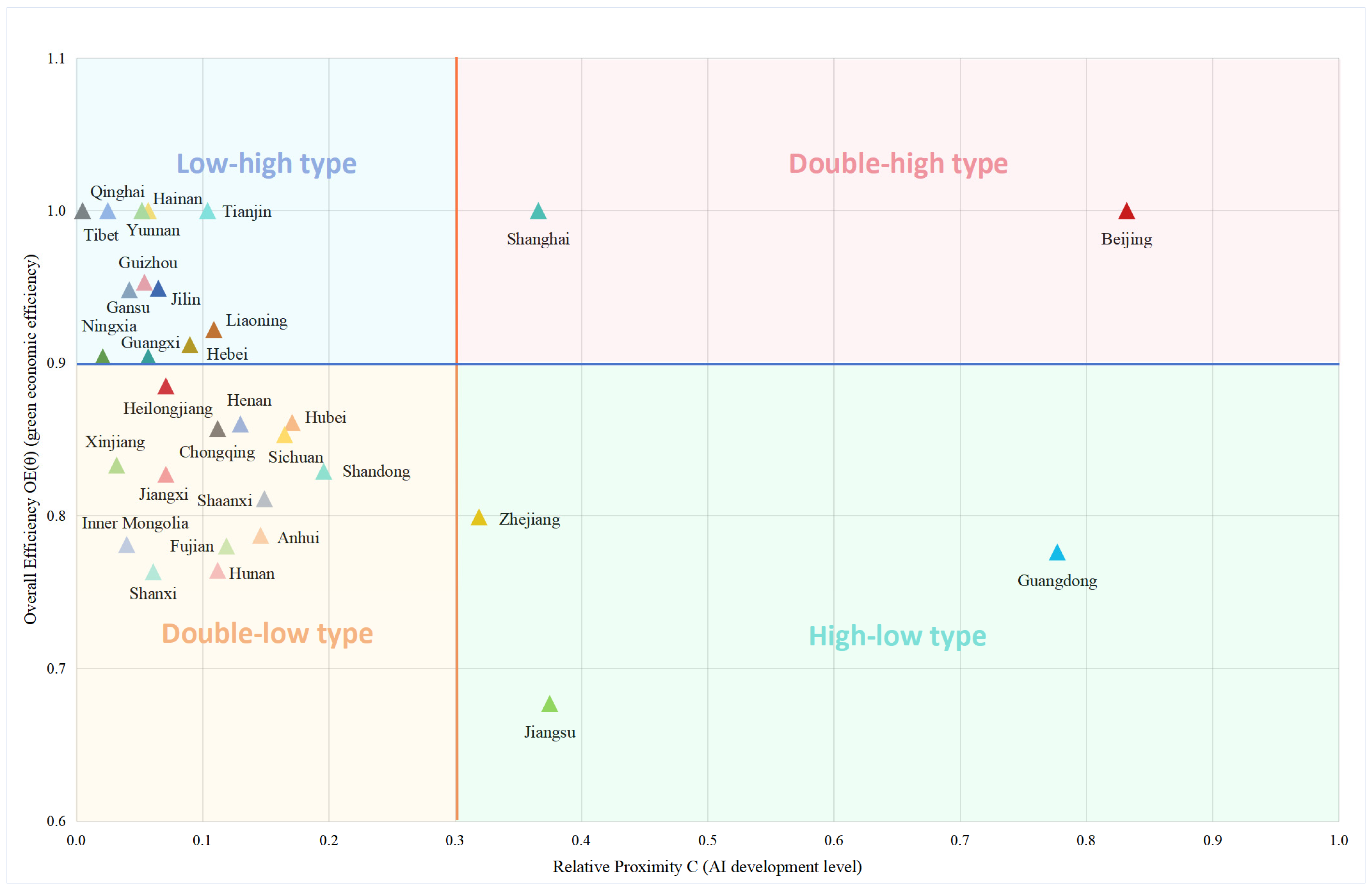
Type	Driver	Bottleneck	Suggested Policy Lever
Double-High	Technological and policy leadership, strong resource spillover capacity.	Pressure to maintain innovation leadership; effectively radiating benefits to neighboring regions.	Act as growth poles to drive regional collaborative emissions reduction through technology transfer and institutional innovation.
High-Low	High concentration of technological resources, capital, and talent.	Low conversion rate of technology into green efficiency; potential diseconomies of scale from resource concentration.	Promote the application of technologies, optimize resource allocation, and facilitate the diffusion of outcomes to adjacent provinces.
Low-High	Superior ecological endowments and highly efficient resource utilization models.	Weak AI technical foundation, lacking technology and talent.	Enhance technology introduction and cooperation, optimize green industry models, and establish replicable “eco-plus” development pathways.
Double-Low	(Potential) Latecomer advantage and unique local resources.	Dual constraints of geography and industrial structure; comprehensive lack of factor inputs.	Prioritize the influx of talent, technology, and capital, learn from successful experiences, and build a localized green industrial system enabled by AI.

.

This study examines the transient characteristics of artificial intelligence at its early stage of development within a specific research context, along with the performance of green economic efficiency under AI embedding. The use of cross-sectional data, however, limits the ability to draw causal inferences. As panel data on innovation metrics become increasingly available, future research should adopt longitudinal designs and employ more advanced causal inference methods.

7.2. Policy Implications

Based on the empirical findings of this study, which reveal significant disparities in AI development and green economic efficiency across Chinese provinces, we propose a tripartite policy framework. This framework is designed to help developing countries, including China, harness the synergistic potential of AI and green development. Each recommendation is structured around a clear mechanism, a practical policy instrument, and measurable targets to ensure effective implementation and evaluation.

To bridge the gap between technological advancement and environmental sustainability, policymakers must foster a deep integration of AI with green economic objectives. The core mechanism for achieving this is the creation of a cross-departmental “Digital-Green” synergy platform. This platform would facilitate the embedding of AI solutions, supported by advanced algorithms and robust data systems, directly into the core processes of environmental governance and green industry transitions. As a concrete policy instrument, governments should implement a “Green AI Project Certification” system coupled with targeted tax credits. This instrument would provide a proportional tax rebate on R&D investments for AI projects that are certified to significantly improve energy efficiency or reduce emissions. The primary measurable target for this initiative is to achieve 30% coverage of certified green AI projects in key industries such as power and manufacturing within three years, thereby driving a 15% reduction in the average carbon emission intensity of these sectors.

Furthermore, addressing the spatial imbalance identified in our analysis is crucial for national cohesive growth. An “Inter-provincial AI Resource Collaboration” mechanism, coordinated by the central government, should be established to systematically channel technology, talent, and computing resources from high-agglomeration coastal provinces to inland regions. To operationalize this mechanism, we propose two key instruments: first, the introduction of “AI Cloud Computing Credits for Inland Regions”, which would provide subsidized or free computing quotas tied to the achievement of energy efficiency KPIs; and second, the issuance of “Cross-Provincial R&D Vouchers” to incentivize leading firms in coastal areas to establish joint R&D centers in inland provinces. The success of this diffusion strategy should be gauged by two measurable targets: increasing the share of AI-related patents granted to inland provinces to 25% of the national total within three years, and achieving an average annual growth rate of 20% for AI-enabled industrial projects in these regions.

Finally, a one-size-fits-all policy is ill-suited for diverse regional contexts. Therefore, the central mechanism here is to mandate the development of “Locally Adapted AI+ Action Plans.” This requires each provincial government to formulate a tailored roadmap that aligns with its unique resource endowments, industrial structure, and research capacity. To support this localization effort, a central authority should develop and disseminate two practical instruments: a modular “AI+ Green Technology Toolbox” offering adaptable technical solutions, and a dynamic “Best Practices Knowledge Base” showcasing successful cases from both “double-high” and “low-high” provinces. The measurable targets for this recommendation are to ensure that 100% of provinces promulgate their localized action plans within three years, with over 80% of provinces demonstrating adoption by integrating at least two technologies from the toolbox into distinctive, locally relevant demonstration projects.

We also provide differentiated suggestions based on specific situations:

Double-high provinces: Strengthen coupled leadership, establish regional collaborative benchmarks, leverage the dual leadership advantages of technology and policy, overcome the bottleneck of “difficulty in maintaining innovation leadership and insufficient radiation effect”, deepen the deep coupling of AI and green economy, leverage the driving role of growth poles, and promote regional coordinated emission reduction. Through platforms such as technology transfer centers and industry-university-research cooperation bases, export AI green technology and institutional experience (such as intelligent environmental protection supervision models and green production capacity allocation schemes) to neighboring provinces; promote inter-provincial energy consumption data and AI computing power resource interconnection, and achieve joint construction and sharing of regional green benefits.

High-low type provinces: Break the transformation bottleneck, promote coupling to enhance quality and efficiency, leverage the advantage of AI resource agglomeration, address the issues of “insufficient technology-to-green efficiency transformation and diseconomies of scale in resource agglomeration”, strengthen the empowering effect of AI on the green economy, optimize the resource allocation structure, and achieve the transformation from “high AI resources” to “high green efficiency”. Establish a closed loop for the green transformation of AI technology. For coastal provinces such as Jiangsu, Zhejiang, and Guangdong, focus on key areas such as manufacturing, energy, and environmental protection, build AI technology application scenario test bases, promote the implementation of technologies such as intelligent production scheduling and green supply chain management; establish a transformation effectiveness evaluation mechanism, subsidize enterprises that achieve reduced unit energy consumption and meet pollutant emission reduction standards after applying AI technology, and force technology implementation to bear fruit.

Low-High Type Provinces: Address the AI shortcomings and strengthen the foundational support for coupling. Leveraging the excellent ecological endowments and efficient resource utilization advantages, these provinces should overcome the bottlenecks of “weak AI technology foundation and talent shortage”, empower green industry upgrades with AI, and forge a replicable “Ecology + AI” coupling development path. Implement a precise introduction strategy for AI technology. Directly introduce mature AI technology, establish technical cooperation agreements with High-High Type and High-Low Type provinces, jointly build an “AI Green Technology Incubation Center”, and reduce the cost of independent research and development.

Double-low provinces: Activate the latecomer advantage and build a coupled development system. Relying on the latecomer advantage and local characteristic resources, we should break the bottleneck of “geographical and industrial structure constraints, and insufficient factor input”. Taking factor agglomeration as a breakthrough, we should build a coupled system of localized AI-empowered green industries. Build a platform for factor agglomeration. Introduce special investment attraction policies to attract AI enterprises and green industry projects to settle down, focusing on introducing labor-intensive and technology-compatible industries to avoid high-end technology thresholds. Relying on local characteristic resources, plan AI green industrial parks to form an industrial agglomeration effect and break geographical constraints.