Measuring Real Energy Price Gaps: The Real PLI Framework for Competitiveness Monitoring

Abstract

Global energy markets have experienced persistent dispersion in real energy prices, creating structural competitiveness pressures that standard indicators often fail to capture in real time. These pressures have intensified as energy-intensive sectors face asymmetric exposure across advanced and emerging economies. This study addresses two critical gaps in international energy cost competitiveness. The first is a frequency gap: conventional indicators such as the Real Unit Energy Cost (RUEC) are typically published with delays of 2–5 years, limiting their usefulness for timely policy evaluation. Here, both RUEC and the Real Price Level Index for energy (Real PLI)—the ratio of the Purchasing Power Parity (PPP) for energy to that for GDP—are measured with only a 2–3-month lag for nine countries—four in Asia, four in Europe, and the U.S. The second is a competitiveness gap that calls for policy responses. Real PLIs indicate that the energy price disadvantages of Japan, Korea, France, Germany, Italy, and the UK have widened from 1.76–2.91 times the U.S. level before the pandemic to 2.14–3.28 times by Q3 2025, with the gaps relative to China and India also widening. Once country-specific thresholds are exceeded, output in energy-intensive and trade-exposed (EITE) industries tends to contract disproportionately. These findings highlight that sustainable transitions require not only internationally differentiated burden-sharing but also structural reforms to avoid persistent widening of energy price gaps. The Real PLI framework provides a timely indicator of competitiveness and an early-warning tool, signaling when growing asymmetries may undermine policy feasibility. Policy implications include the need to monitor real energy price dispersion as a core source of competitiveness risk, to strengthen structural measures that stabilize marginal energy costs, and to design transition pathways that account for heterogeneous adjustment pressures across countries.

1. Introduction

The Stern–Stiglitz framework emphasizes the importance of efficient and equitable carbon pricing as a central policy instrument [1,2] and argues that the green energy transition is coming at a time when the macroeconomic opportunity costs may be especially low and the benefits particularly high [3]. This framing—of low costs and high benefits—has provided a powerful rationale for governments to accelerate energy transitions and green investment worldwide, particularly since the late 2010s.

The sustainability transitions literature had earlier emerged as an academic field for analyzing socio-technical change more broadly (Geels [4], Markard et al. [5]). While conceptually distinct from the Stern–Stiglitz framework, parts of this field have become increasingly aligned with policy agendas as decarbonization has accelerated, contributing both to the theoretical articulation of ambitious transitions and to their critical analysis (Köhler et al. [6]). While this view has dominated policy narratives, its empirical validation has remained complex.

Empirical evidence on the relationship between energy prices and industrial competitiveness has shifted over time. Earlier work—largely covering data up to the early or mid-2010s—typically found limited or heterogeneous competitiveness effects of environmental regulation and the EU ETS on regulated firms (Dechezleprêtre and Sato [7], Löschel et al. [8]).

Since 2021, however, global energy prices have surged as economies recovered from the pandemic, exposing advanced economies to sharply higher costs. As these increases persisted, energy costs in advanced economies remained elevated relative to international competitors. At the same time, industrial performance weakened, and growing evidence emerged of relocation pressures in energy-intensive and trade-exposed (EITE) industries associated with persistent energy price gaps (Chiacchio et al. [9], Jäger [10], Vogel et al. [11], Saussay and Sato [12]). In 2024, the Draghi Report emphasizes that high energy costs pose a serious threat to European competitiveness. It advocates structural reforms—including energy market integration and revised cost-sharing mechanisms—to safeguard EITE sectors [13].

Most recently, in September 2025, DIHK [14] estimated that under current policies, the energy transition could impose cumulative costs of up to €5.4 trillion between 2025 and 2049, and called for a ‘Plan B’. These recent developments suggest predominantly adverse impacts in advanced economies and raise questions about whether current policies can ensure truly sustainable energy transitions. They also underscore the need for robust metrics that can capture how energy cost dynamics translate into competitiveness risks.

A key analytical challenge is to identify and measure vulnerabilities in the economic implications of energy transitions. Much of the existing literature relies on the Real Unit Energy Cost (RUEC), which expresses energy costs as a share of value added and has been widely used as an indicator of energy cost competitiveness. However, because RUEC reflects structural shifts, such as the relocation of EITE industries, cross-country RUEC gaps may understate energy cost disadvantages. Real energy price differentials, by contrast, offer a more direct gauge of international competitiveness. In this context, this paper introduces the Real Price Level Index for energy (hereafter, Real PLI)—a Purchasing Power Parity (PPP)-based indicator of energy prices relative to output prices—as a robust, exchange-rate-independent measure that provides a clearer basis for monitoring competitiveness risks.

Against this backdrop, the study’s contribution is twofold. First, it offers a real-time measure of international energy price competitiveness—addressing a critical gap in the existing literature, where indicators such as RUEC are published with multi-year delays and confound structural industry shifts with true price conditions. Second, it links these timely real price measures to nonlinear adjustments in EITE output, identifying country-specific thresholds beyond which competitiveness pressures intensify. This combination of high-frequency PPP-based measurement and threshold-type industrial responses represents a novel analytical direction within the energy competitiveness literature. These contributions are guided by three core research questions: how real energy price differentials evolve at high frequency across countries; whether nonlinear thresholds exist beyond which EITE output contracts; and how PPP-based indicators improve competitiveness monitoring relative to conventional measures.

In this context, national energy strategies have diverged since the mid-2020s, underscoring heterogeneity in policy responses and the risk of hollowing out EITE industries—an essentially irreversible process once large-scale facilities contract or relocate. These developments highlight the urgency of timely indicators to track emerging competitiveness pressures. However, existing measures are typically derived from annual national accounts or input–output tables and are published with substantial time lags. The Real PLI is therefore positioned as a timely tool for cross-country comparison and early warning, enabling closer monitoring of shifts in real energy price conditions shaped by policy and institutional responses.

The objectives of this study are fourfold. First, it advances the concept of the Real PLI by correcting the distortions that arise when market exchange rates are used to evaluate energy prices. Second, it applies this framework to nine countries—four in Asia (China, India, Japan, and Korea), four in Europe (France, Germany, Italy, and the UK), and the U.S.—contrasting the Real PLI with the RUEC gap and examining their implications for competitiveness. Third, it relates Real PLI dynamics to EITE output, assessing whether competitiveness pressures emerge nonlinearly once country-specific thresholds are crossed. Fourth, it draws implications for measurement and policy in monitoring the sustainability of the energy transition. The remainder of the paper reviews the literature (Section 2), sets out the measurement framework (Section 3), presents empirical evidence (Section 4), and concludes with a policy discussion (Section 5) and an overall conclusion (Section 6).

2. Literature Review

2.1. Social Dimensions of Energy Costs

The sustainability literature has long framed transitions around three pillars—environmental protection, economic growth, and social welfare (WCED [15], Elkington [16]). While environmental and economic dimensions have historically received greater analytical attention, the social pillar has increasingly become central to understanding heterogeneous exposure to energy costs. Research on energy poverty and distributional impacts (Schulte et al. [17], Bouzarovski [18]) highlights how energy price shocks disproportionately burden vulnerable households, while debates under the banners of energy justice and just transition emphasize procedural fairness and equitable burden-sharing. Wood and Roelich [19] have further deepened the conceptual foundations of energy justice by examining how different normative frameworks shape assessments of fairness and responsibility in energy systems.

Recent studies have extended these distributional perspectives to the global scale by assessing fairness in the energy transition, combining historical responsibility, financial capacity, and climate-related damages into composite indicators of equity in climate action (As-sya’bani et al. [20]). While such work highlights the broader social and ethical dimensions of energy costs, these indicators remain conceptually distinct from competitiveness-oriented metrics. They are not designed for harmonized cross-country price comparisons.

2.2. RUEC and Industrial Competitiveness

The economic pillar of transitions has relied more heavily on aggregate competitiveness indicators, most notably the RUEC, which measures energy costs as a share of value added and features prominently in European Commission assessments (European Commission [21,22]). Empirical studies find that higher energy costs weaken export performance, especially in EITE sectors (Faiella and Mistretta [23]), and that accounting for indirect energy embodied in intermediate inputs improves sectoral competitiveness metrics (Kaltenegger et al. [24], Kaltenegger [25]).

However, RUEC is strongly affected by compositional changes. In Japan, much of the decline in aggregate RUEC reflected contraction in the steel and chemical industries rather than efficiency gains (Nomura [26]), a pattern also observed during fossil-fuel phaseouts in Europe (UNIDO [27], Lynch et al. [28]). These patterns indicate that structural adjustment can mask underlying price pressures, making RUEC an unreliable indicator of international price competitiveness when the industrial composition is itself responding to energy cost shocks. As a result, cross-country RUEC gaps may understate true energy price disadvantages because they conflate structural change with genuine price effects. Recent work documenting relocation pressures in EITE industries (Chiacchio et al. [9], Jäger [10], Vogel et al. [11], Saussay and Sato [12]) underscores the need for timely indicators that can track emerging competitiveness risks as they unfold.

2.3. PPP-Based Energy Price Comparison

PPP-based price comparisons provide a more direct anchor for international cost competitiveness. The International Comparison Program (ICP) [29] focuses primarily on GDP-level PPPs; because energy is largely an intermediate input, it falls outside ICP’s main scope. In response, bilateral industry-level PPPs—including PPPs for intermediate inputs such as energy—were developed for Japan and the U.S. (Nomura et al. [30], Jorgenson et al. [31]). These studies show that Japan’s energy PPP has persistently exceeded its PPPs for output and non-energy inputs, indicating a long-standing structural cost disadvantage.

Despite these advances, existing PPP-based applications remain limited: (i) they are typically bilateral rather than multilateral; (ii) they rely on benchmark input–output tables, yielding low-frequency estimates; and (iii) they do not link PPP-based competitiveness metrics to industrial adjustment or nonlinear responses.

Conventional international price comparisons (e.g., IEA end-use prices [32]) rely on heat-unit adjustments that ignore large inter-fuel price differentials, including the several-fold gap between electricity and major fossil fuels, and lack a PPP-consistent aggregation framework. This constrains their usefulness as competitiveness indicators, since they do not isolate the real price component that matters for international cost comparisons.

2.4. Gaps and Study Positioning

Overall, prior research offers valuable insights but leaves three challenges unresolved: (i) no high-frequency, internationally comparable indicators of real energy price dispersion; (ii) limited ability of existing competitiveness measures (e.g., RUEC) to separate structural adjustment from true price effects; and (iii) absence of empirical evidence on nonlinear industrial responses to real energy price conditions across countries. These gaps are central because they limit policymakers’ and researchers’ ability to assess emerging competitiveness risks in real time.

This study addresses these gaps by constructing monthly PPP-consistent Real PLIs for nine countries and identifying country-specific nonlinear thresholds at which competitiveness pressures intensify. This approach yields a high-frequency measure of energy price disparities and identifies the ranges at which such disparities begin to generate measurable industrial adjustment.

3. Measurement Framework

The construction of PPP-consistent price level indices follows the standard index number theory used in international price comparisons and productivity accounting. Since energy products differ substantially in quality and economic value, a PPP-based aggregation across fuels provides a theoretically coherent means of measuring real cross-country price dispersion. This approach isolates the real price component relevant for competitiveness analysis, in contrast to heat-unit comparisons that mix price and composition effects.

This section outlines the measurement framework used in this study, which is based on the Energy Cost Monitoring (ECM) Database. The database was initially reported in preliminary Discussion Papers (Nomura and Inaba [33,34,35]) but has since been substantially revised and refined. Launched in 2022 with Japan as the initial focus, the ECM project has since broadened. It now enables the construction of nominal and real sectoral energy accounts with only a few months’ lag. The EITE output indices used in Section 4 are constructed as a monthly translog aggregate of five major energy-intensive manufacturing sectors—pulp and paper, chemicals excluding pharmaceuticals, non-metallic minerals, iron and steel, and non-ferrous metals. The underlying production and output series are taken from official national statistics and subsequently harmonized within the ECM to ensure the highest feasible degree of consistency with the SNA industry accounts. The harmonization procedure yields the most internally consistent and internationally comparable high-frequency measure available for monitoring industrial responses to real energy price conditions. Key definitions relevant to this study are summarized below; further details are provided in Appendix A and on the ECM website.

3.1. RUEC

The elementary level is defined by the cross-classification of products ($i$) and energy-consuming sectors ($j$). At the elementary level, the quantity of final energy consumption is denoted as $E_{ij}$, and its unit price as $P_{ij}^E$, measured in local currency units (LCU). The nominal value is then obtained as $V_{ij}^E=P_{ij}^E{E}_{ij}$. The total national consumption value ($V^E$) is given by ${\sum }_{ij}{V}_{ij}^E$.

At the national aggregate level, the quality-adjusted energy input can, in principle, be defined as the weighted sum of the growth rates of individual energy quantities. In this study, however, the emphasis is on cross-country comparisons. Accordingly, the detailed translog formulation is omitted, and the aggregate quality-adjusted energy input is denoted as $E$, with the corresponding quality-adjusted energy price ($P^E$) implicitly defined by $V^E/E$.

As the aggregate output, $V^X$ and $X$ represent nominal and real GDP, respectively, and the output (value added) price ($P^X$) is implicitly defined. The nominal unit energy cost (NUEC) is defined as the energy cost per unit of output:

$$\mathrm{N}\mathrm{U}\mathrm{E}\mathrm{C}=V^E/X.$$

(1)

The RUEC is determined by deflating the NUEC by the aggregate output price as:

$$\mathrm{R}\mathrm{U}\mathrm{E}\mathrm{C}=\mathrm{N}\mathrm{U}\mathrm{E}\mathrm{C}/P^X=V^E/V^X=\left(P^E/P^X\right)/\left(X/E\right).$$

(2)

The RUEC is the nominal share of energy cost in the nominal output value. It can be interpreted as the real energy price, $P^E/P^X$, divided by the inverse of gross energy productivity (GEP), $X/E$, highlighting the distinction between price and productivity effects.

3.2. Energy PPP

To clarify the overall structure before turning to formal definitions, Figure 1 illustrates the relationships among elementary-level energy prices in reference and comparison countries, PPPs for each product, aggregate PPPs and PLIs for both energy and output, and the Real PLI. This schematic provides an overview of the measurement framework developed in this section.

For a given reference country $c_1$ and comparison country $c_2$, the bilateral PPP for energy at the elementary level is defined as the ratio of energy unit prices expressed in LCU:

$${\mathrm{P}\mathrm{P}\mathrm{P}}_{ij, c_1{c}_2}^{\mathrm{E}}=P_{ij,c_2}^E/P_{ij,c_1}^E.$$

(3)

At the aggregate level, differences in the structure of energy consumption across products and sectors are accounted for by weighting quantities with their relative expenditure shares. This weighting scheme ensures that aggregation is quality-adjusted, since the relative economic value of energy types—such as electricity versus gas—is reflected in their prices rather than in purely physical units of heat. The Laspeyres PPP for energy is evaluated at the consumption structure of the reference country as:

$${\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}\left(\mathrm{L}\right)}={\sum }_{ij}{\displaystyle \frac{P_{ij,c_2}^E{E}_{ij,c_1}}{P_{ij,c_1}^E{E}_{ij,c_1}}}={\sum }_{ij}{w}_{ij,c_1}^E{\mathrm{P}\mathrm{P}\mathrm{P}}_{ij, c_1{c}_2}^{\mathrm{E}}, \mathrm{where} w_{ij,c_1}^E=V_{ij,c_1}^E/{\sum }_{ij}{V}_{ij,c_1}^E.$$

(4)

Similarly, the Paasche PPP for energy is evaluated at the consumption structure of the comparison country as:

$${\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}\left(\mathrm{P}\right)}={\sum }_{ij}{\displaystyle \frac{P_{ij,c_2}^E{E}_{ij,c_2}}{P_{ij,c_1}^E{E}_{ij,c_2}}}={\displaystyle \frac{1}{{\sum }_{ij}{w}_{ij,c_2}^E\left(1/{\mathrm{P}\mathrm{P}\mathrm{P}}_{ij, c_1{c}_2}^{\mathrm{E}}\right)}}, \mathrm{where} w_{ij,c_2}^E=V_{ij,c_2}^E/{\sum }_{ij}{V}_{ij,c_2}^E.$$

(5)

The Fisher PPP for energy is then obtained as the geometric mean of the Laspeyres and Paasche measures:

$${\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}\left(\mathrm{F}\right)}=\sqrt{{\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}\left(\mathrm{L}\right)}{\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}\left(\mathrm{P}\right)}}.$$

(6)

The Fisher index is preferred because it mitigates the upward bias of the Laspeyres and the downward bias of the Paasche, providing a more reliable measure of cross-country energy price disparities.

The bilateral Fisher PPP in Equation (6) by construction satisfies the country reversal test, which requires that the PPP between two countries equals the reciprocal of the PPP when the order is reversed. However, it does not satisfy the transitivity test, which requires consistency in multilateral comparisons. To address this limitation, the Éltető–Köves–Szulc (EKS) method is applied as follows:

$${\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}}={\prod }_{c_3}{\left({\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_3}^{\mathrm{E}\left(\mathrm{F}\right)}{\mathrm{P}\mathrm{P}\mathrm{P}}_{c_3{c}_2}^{\mathrm{E}\left(\mathrm{F}\right)}\right)}^{1/\mathrm{N}},$$

(7)

where $\mathrm{N}$ denotes the eight countries covered in the present measurement. Intuitively, the EKS method adjusts bilateral Fisher PPPs by taking the geometric average of all possible indirect comparison paths, thereby ensuring transitivity across countries. In what follows, the EKS-adjusted PPP is simply referred to as PPP.

3.3. Energy PLI

The Price Level Index (PLI) for energy is defined by combining the PPP for energy with the bilateral market exchange rate, expressed as the comparison country’s currency per unit of the reference country’s currency:

$${\mathrm{P}\mathrm{L}\mathrm{I}}_{c_1{c}_2}^{\mathrm{E}}={\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}}/{\mathrm{e}}_{c_1{c}_2}.$$

(8)

Intuitively, the PLI measures the relative cost of energy in one country relative to another, after accounting for exchange-rate differences. For example, suppose the electricity price is 30 yen per kWh in Japan and 0.10 USD per kWh in the U.S. The PPP for electricity in this case is 300 yen per USD, meaning that if the exchange rate were exactly 300 yen/USD, the purchasing power of the two currencies would be equal for electricity. If, however, the actual market exchange rate is 150 yen/USD, the resulting PLI for electricity is 2.0, indicating that Japanese electricity is twice as expensive as in the U.S. In other words, just as a time-series price index tracks changes in prices over time, a cross-sectional PLI captures price differentials between two countries at a point in time.

In international energy analyses, cross-country price differentials are typically reported in USD terms using market exchange rates, which effectively corresponds to a nominal PLI for energy as defined in Equation (8). However, because PLI is prone to an exchange-rate illusion, the tendency for exchange rate fluctuations to alter international price comparisons even when underlying cost structures remain unchanged, three caveats merit attention.

First, energy PLIs illustrate this illusion by exhibiting pronounced sensitivity to exchange-rate movements. In fuel-importing economies, depreciation raises the local-currency price of imported fossil fuels. In contrast, other cost components—such as capital and labor in power generation or the costs of domestically generated electricity (e.g., from nuclear or renewables)—remain relatively stable. As a result, under currency depreciation, the electricity PLI may paradoxically fall despite higher import costs, while under appreciation, it may rise despite lower import costs. In economies with substantial exchange rate volatility, the measured disparities in PLIs depend heavily on the specific exchange rate used, creating significant uncertainty in cross-country comparisons. Further complications arise for developing economies, where currencies tend to remain persistently undervalued relative to the PPP for GDP. This pattern is not accidental. It reflects both structural factors, such as the Balassa–Samuelson effect—where productivity gaps between tradable and non-tradable sectors translate into systematically lower overall price levels—and financial factors, including risk premia reflecting macroeconomic and policy uncertainty, which tend to keep developing-country currencies persistently undervalued. When combined, these forces systematically bias output PLIs downward, making energy appear less expensive in developing countries than it truly is in terms of economic burden. Moreover, widespread energy subsidies further depress domestic energy prices. Taken together, these mechanisms can lead to an overstatement of cost competitiveness and, in turn, foster overly optimistic assessments of the feasibility of energy transitions in such economies.

Second, this exchange-rate illusion arises in part because the energy PLI is not evaluated relative to the output PLI. Even when currency depreciation raises import fuel costs, the pass-through to domestic output prices may be limited if energy accounts for only a small share of production costs. In such cases, the output PLI may be lower than the energy PLI, implying that the real energy price has in fact increased. In this context, the problem is not illusory: without explicitly linking energy costs to output prices, PLIs risk conveying a distorted view of the effective economic burden.

Third, beyond these considerations of exchange rates and cost pass-through, the energy PLI also fails to capture how competitiveness conditions mediate the impact of energy prices. In advanced economies that produce differentiated products and services, high energy prices can be offset by raising output prices, thereby mitigating the effective impact of high energy costs. By contrast, in developing economies producing largely undifferentiated products, output prices are constrained by competitive markets. In these economies, even if the nominal energy price differential remains unchanged, intensified price competition compresses output prices, increasing the effective burden of energy costs. Taken together, these observations underscore the need for an indicator that directly links energy prices to output performance and competitiveness.

Such limitations highlight the need for the Real PLI, defined as the ratio of the energy PLI to the output PLI:

$$\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l} {\mathrm{P}\mathrm{L}\mathrm{I}}_{c_1{c}_2}^{\mathrm{E}}={\mathrm{P}\mathrm{L}\mathrm{I}}_{c_1{c}_2}^{\mathrm{E}}/{\mathrm{P}\mathrm{L}\mathrm{I}}_{c_1{c}_2}^{\mathrm{X}}={\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{E}}/{\mathrm{P}\mathrm{P}\mathrm{P}}_{c_1{c}_2}^{\mathrm{X}}.$$

(9)

A key property of the Real PLI is its immunity to exchange-rate movements, as it is defined solely as the ratio of two PPPs estimated independently of market exchange rates.

The Real PLI can also be linked to the RUEC gap. Since the RUEC is defined as the share of energy costs in value added in Equation (2), its bilateral ratio can be decomposed into the Real PLI and the inverse of the GEP gap—reflecting both within-industry energy productivity and differences in industrial structure.

$${\mathrm{R}\mathrm{U}\mathrm{E}\mathrm{C} \mathrm{g}\mathrm{a}\mathrm{p}}_{c_1{c}_2}={\mathrm{R}\mathrm{U}\mathrm{E}\mathrm{C}}_{c_2}/{\mathrm{R}\mathrm{U}\mathrm{E}\mathrm{C}}_{c_1}=\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l} {\mathrm{P}\mathrm{L}\mathrm{I}}_{c_1{c}_2}^{\mathrm{E}}/{\mathrm{G}\mathrm{E}\mathrm{P} \mathrm{g}\mathrm{a}\mathrm{p}}_{c_1{c}_2}.$$

(10)

As discussed in Section 2, the RUEC gap alone does not necessarily provide a reliable assessment of energy cost competitiveness since it conflates pure energy cost differences with broader structural effects. Overall, these properties establish the Real PLI as a particularly relevant indicator for monitoring international competitiveness.

4. Results

Cross-country evidence has long shown that rising energy costs place disproportionate pressure on energy-intensive industries. Yet existing indicators—such as RUEC or low-frequency PPP benchmarks—cannot reveal when such pressures become binding or how they evolve at higher frequencies. The results in this section extend this literature by providing PPP-consistent measures of real energy price disparities and identifying nonlinear thresholds at which competitiveness risks intensify. This paper first documents how the RUEC gap combines price and composition effects, and then analyzes the evolution of the Real PLI together with its implications for threshold-based competitiveness pressures across countries.

While a decline in the RUEC may appear to indicate progress in an energy transition, such changes can also reflect structural adjustments—such as deindustrialization—that reduce energy demand without improving cost competitiveness. The Real PLI therefore provides a clearer measure of cross-country disparities in energy price conditions and represents a necessary economic condition for a sustainable transition. Section 4.1 examines the RUEC gap, which combines the Real PLI with the GEP gap, as shown in Equation (10). Section 4.2 and Section 4.3 analyze the evolution of the Real PLI and its implications for competitiveness thresholds in EITE industries.

Before turning to the empirical results, it is important to note that although nominal PLIs for energy can be measured at a monthly frequency in the ECM Database, all indicators in this paper are reported at a quarterly frequency to ensure comparability with national accounts, as the Real PLI relies on GDP deflators that are available only quarterly. In addition, the analysis focuses on the aggregate economy because consistent industry-level output PPPs are not available across countries, either quarterly or annually. Further details are provided in Appendix A.1. The empirical coverage spans Q1 2015–Q3 2025.

4.1. RUEC Gaps

Figure 2 provides: (a) the RUEC level for each country, expressed as a percentage share (left panel), (b) the RUEC gap, measured relative to the U.S. (center panel), and (c) the GEP gap, also measured relative to the U.S. (right panel). Bilateral comparisons of Figure 2b,c using alternative reference countries are reported in

Table 1. Bilateral RUEC and GEP gaps: Q3 2025 and pre-pandemic average (2015–2019).

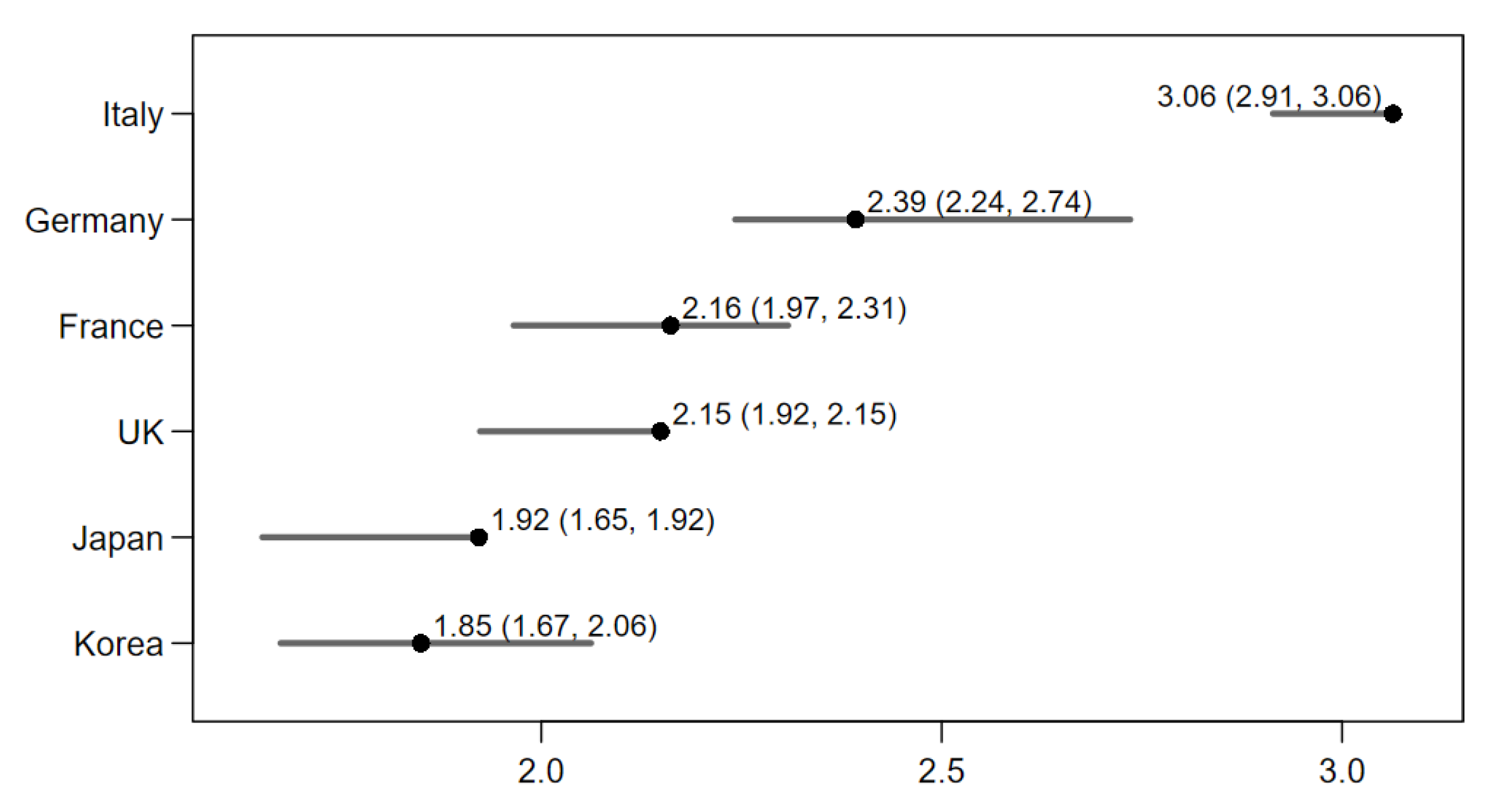
(a) RUEC gaps
		Comparison country
		CHN	IND	JPN	KOR	FRA	DEU	ITA	GBR	USA
Reference country	China (CHN)	1.00	1.05	0.74	0.87	0.66	0.74	0.84	0.47	0.50
		1.00	1.24	0.73	0.90	0.73	0.73	0.89	0.57	0.63
		(0%)	(−17%)	(2%)	(−3%)	(−10%)	(1%)	(−6%)	(−20%)	(−22%)
	India (IND)	0.95	1.00	0.71	0.83	0.63	0.70	0.80	0.45	0.48
		0.81	1.00	0.59	0.73	0.59	0.59	0.72	0.46	0.51
		(16%)	(0%)	(18%)	(13%)	(7%)	(18%)	(10%)	(−3%)	(−6%)
	Japan (JPN)	1.34	1.41	1.00	1.17	0.89	1.00	1.13	0.63	0.68
		1.37	1.70	1.00	1.23	0.99	1.00	1.22	0.78	0.86
		(−2%)	(−19%)	(0%)	(−5%)	(−11%)	(−0%)	(−8%)	(−21%)	(−24%)
	Korea (KOR)	1.14	1.20	0.85	1.00	0.75	0.85	0.96	0.54	0.58
		1.11	1.38	0.81	1.00	0.81	0.81	0.99	0.64	0.70
		(3%)	(−14%)	(5%)	(0%)	(−7%)	(4%)	(−3%)	(−17%)	(−19%)
	France (FRA)	1.52	1.60	1.13	1.33	1.00	1.12	1.28	0.71	0.77
		1.38	1.71	1.01	1.24	1.00	1.01	1.23	0.79	0.87
		(9%)	(−7%)	(11%)	(6%)	(0%)	(11%)	(3%)	(−10%)	(−13%)
	Germany (DEU)	1.35	1.42	1.00	1.18	0.89	1.00	1.14	0.64	0.68
		1.37	1.70	1.00	1.24	0.99	1.00	1.23	0.78	0.86
		(−2%)	(−18%)	(0%)	(−5%)	(−11%)	(0%)	(−8%)	(−21%)	(−24%)
	Italy (ITA)	1.19	1.25	0.88	1.04	0.78	0.88	1.00	0.56	0.60
		1.12	1.39	0.82	1.01	0.81	0.82	1.00	0.64	0.70
		(6%)	(−10%)	(8%)	(3%)	(−3%)	(8%)	(0%)	(−13%)	(−16%)
	UK (GBR)	2.13	2.24	1.58	1.86	1.40	1.57	1.79	1.00	1.07
		1.75	2.17	1.28	1.58	1.27	1.28	1.56	1.00	1.10
		(19%)	(3%)	(21%)	(16%)	(10%)	(21%)	(13%)	(0%)	(−3%)
	U.S. (USA)	1.98	2.08	1.47	1.73	1.31	1.47	1.67	0.93	1.00
		1.59	1.97	1.16	1.43	1.15	1.16	1.42	0.91	1.00
		(22%)	(5%)	(24%)	(19%)	(13%)	(23%)	(16%)	(3%)	(0%)
(b) GEP gaps
		Comparison country
		CHN	IND	JPN	KOR	FRA	DEU	ITA	GBR	USA
Reference country	China (CHN)	1.00	1.61	1.43	1.21	1.92	1.84	1.93	2.34	0.98
		1.00	1.46	1.29	1.04	1.51	1.64	1.74	1.85	0.85
		(0%)	(10%)	(10%)	(15%)	(24%)	(11%)	(10%)	(23%)	(14%)
	India (IND)	0.62	1.00	0.89	0.75	1.19	1.14	1.19	1.45	0.61
		0.69	1.00	0.88	0.71	1.03	1.12	1.19	1.27	0.58
		(−10%)	(0%)	(0%)	(5%)	(14%)	(1%)	(0%)	(13%)	(4%)
	Japan (JPN)	0.70	1.13	1.00	0.85	1.34	1.28	1.35	1.64	0.68
		0.78	1.13	1.00	0.81	1.17	1.27	1.35	1.44	0.66
		(−10%)	(−0%)	(0%)	(5%)	(13%)	(1%)	(−0%)	(13%)	(4%)
	Korea (KOR)	0.83	1.33	1.18	1.00	1.58	1.51	1.59	1.93	0.81
		0.96	1.40	1.24	1.00	1.45	1.57	1.67	1.78	0.82
		(−15%)	(−5%)	(−5%)	(0%)	(9%)	(−4%)	(−5%)	(8%)	(−1%)
	France (FRA)	0.52	0.84	0.75	0.63	1.00	0.96	1.01	1.22	0.51
		0.66	0.97	0.85	0.69	1.00	1.09	1.15	1.23	0.56
		(−24%)	(−14%)	(−13%)	(−9%)	(0%)	(−12%)	(−14%)	(−0%)	(−10%)
	Germany (DEU)	0.54	0.88	0.78	0.66	1.04	1.00	1.05	1.27	0.53
		0.61	0.89	0.79	0.64	0.92	1.00	1.06	1.13	0.52
		(−11%)	(−1%)	(−1%)	(4%)	(12%)	(0%)	(−1%)	(12%)	(3%)
	Italy (ITA)	0.52	0.84	0.74	0.63	0.99	0.95	1.00	1.21	0.51
		0.58	0.84	0.74	0.60	0.87	0.94	1.00	1.06	0.49
		(−10%)	(−0%)	(0%)	(5%)	(14%)	(1%)	(0%)	(13%)	(4%)
	UK (GBR)	0.43	0.69	0.61	0.52	0.82	0.79	0.82	1.00	0.42
		0.54	0.79	0.70	0.56	0.82	0.89	0.94	1.00	0.46
		(−23%)	(−13%)	(−13%)	(−8%)	(0%)	(−12%)	(−13%)	(0%)	(−9%)
	U.S. (USA)	1.02	1.65	1.46	1.24	1.96	1.88	1.97	2.39	1.00
		1.18	1.72	1.52	1.23	1.78	1.93	2.05	2.18	1.00
		(−14%)	(−4%)	(−4%)	(1%)	(10%)	(−3%)	(−4%)	(9%)	(0%)

Unit: Bilateral ratios, reference country = 1.00. Notes: For each cell, the upper figure refers to Q3 2025, the lower figure to the pre-pandemic average (2015–2019), and the value in parentheses shows the log growth relative to the pre-pandemic average, computed to preserve transitivity in bilateral comparisons. Cells in blue indicate a relative narrowing of the gap of the comparison country relative to the reference country, whereas cells in red indicate a widening.

for both Q3 2025 and the pre-pandemic average (2015–2019), together with the corresponding log-growth changes.

The left panel shows that values are generally higher in emerging economies, such as India and China, than in advanced economies. Three factors account for this outcome. First, energy prices ($P^E$) remain relatively low due to a heavy reliance on coal and the political need to restrain electricity tariffs amid weak consumer purchasing power. Second, GEP ($X/E$) is limited because the real value added per unit of energy input is small. Third, the price of output ($P^X$) is constrained by the limited international competitiveness of their products. Together, these structural elements explain why RUEC levels are persistently higher in emerging economies: low energy prices are insufficient to offset the combination of low GEP and weak output prices.

These structural features illustrate why deep decarbonization remains particularly difficult for emerging economies. First, energy prices are already held artificially low, as reflected in the Nominal PLI in Section 4.2, through tariff controls and heavy reliance on cheap coal, leaving limited room for further cost reductions and making a shift away from low-cost fossil fuels especially challenging. While energy prices may decline temporarily during the early stages of renewable deployment, such benefits are short-lived, as grid infrastructure remains underdeveloped and integration measures take time; beyond this limited window, system integration costs may offset these gains. Second, improvements in GEP have considerable potential but require replacing industrial assets and therefore materialize only gradually over the medium term. Third, raising output prices through upgrading to higher value-added industrial structures is typically a decades-long process. Taken together, these constraints underscore the importance of assessing not only the pace of technological change but also the structural conditions that determine the economic feasibility of deep decarbonization.

The center and right panels of Figure 2 compare RUEC and GEP gaps relative to the U.S. As shown in Equations (9) and (10), the RUEC gap can be expressed as the ratio of the Real PLI to the GEP gap, while the Real PLI itself equals the ratio of the nominal energy PLI to the nominal output PLI. Accordingly, cross-country differences in RUEC reflect the combined influence of price and structural factors.

In Q3 2025, India shows the highest RUEC gap—about twice the U.S. level—driven mainly by a very low output PLI, which raises its Real PLI despite a moderate energy PLI and a mid-range GEP, the latter reflecting the still-limited role of energy-intensive manufacturing. China’s large gap combines a moderately high Real PLI with relatively low GEP, reflecting the persistence of energy-intensive heavy industries. Italy’s burden, by contrast, stems primarily from high energy prices, although its GEP remains relatively strong. The UK, where deindustrialization has progressed the furthest, exhibits near parity in its RUEC gap with the U.S., as exceptionally high GEP largely offsets the effects of high energy prices. Japan, Germany, and France occupy intermediate positions among advanced economies.

These contrasts confirm that large RUEC gaps arise for different reasons—high real energy prices, low productivity, or structural composition effects—highlighting the importance of complementary indicators such as the Real PLI (Section 4.2) to isolate the pure price component of energy-cost competitiveness.

4.2. Real PLI

Figure 3 presents three indicators: (a) the quality-adjusted energy price in national currency, expressed as an index with the 2015 average set to 1.0 (left panel), (b) the nominal PLI, measured relative to the U.S. (center panel), and (c) the Real PLI, also measured relative to the U.S. (right panel). Corresponding bilateral comparisons for Figure 3b,c, using alternative reference countries, are reported in

Table 2. Bilateral Nominal and Real PLIs: Q3 2025 and pre-pandemic average (2015–2019).

(a) Nominal PLIs
		Comparison country
		CHN	IND	JPN	KOR	FRA	DEU	ITA	GBR	USA
Reference country	China (CHN)	1.00	0.85	1.42	1.27	2.04	2.43	2.41	2.09	1.04
		1.00	0.86	1.51	1.19	1.47	1.61	1.90	1.55	0.90
		(0%)	(−2%)	(−6%)	(7%)	(33%)	(41%)	(24%)	(30%)	(15%)
	India (IND)	1.18	1.00	1.68	1.50	2.41	2.87	2.85	2.47	1.23
		1.16	1.00	1.75	1.38	1.70	1.87	2.20	1.79	1.04
		(2%)	(0%)	(−4%)	(8%)	(35%)	(43%)	(26%)	(32%)	(17%)
	Japan (JPN)	0.70	0.59	1.00	0.89	1.43	1.71	1.69	1.47	0.73
		0.67	0.58	1.00	0.79	0.97	1.07	1.26	1.03	0.60
		(5%)	(3%)	(0%)	(12%)	(39%)	(47%)	(29%)	(36%)	(21%)
	Korea (KOR)	0.79	0.67	1.12	1.00	1.61	1.91	1.90	1.65	0.82
		0.84	0.73	1.27	1.00	1.24	1.36	1.60	1.31	0.76
		(−7%)	(−9%)	(−12%)	(0%)	(26%)	(34%)	(17%)	(23%)	(8%)
	France (FRA)	0.49	0.42	0.70	0.62	1.00	1.19	1.18	1.03	0.51
		0.68	0.59	1.03	0.81	1.00	1.10	1.30	1.06	0.61
		(−33%)	(−35%)	(−39%)	(−26%)	(0%)	(8%)	(−9%)	(−3%)	(−18%)
	Germany (DEU)	0.41	0.35	0.59	0.52	0.84	1.00	0.99	0.86	0.43
		0.62	0.54	0.94	0.74	0.91	1.00	1.18	0.96	0.56
		(−41%)	(−43%)	(−47%)	(−35%)	(−8%)	(0%)	(−17%)	(−11%)	(−26%)
	Italy (ITA)	0.42	0.35	0.59	0.53	0.85	1.01	1.00	0.87	0.43
		0.53	0.46	0.79	0.63	0.77	0.85	1.00	0.82	0.47
		(−24%)	(−26%)	(−29%)	(−17%)	(9%)	(17%)	(0%)	(6%)	(−9%)
	UK (GBR)	0.48	0.40	0.68	0.61	0.97	1.16	1.15	1.00	0.50
		0.65	0.56	0.98	0.77	0.95	1.04	1.23	1.00	0.58
		(−30%)	(−33%)	(−36%)	(−24%)	(2%)	(11%)	(−7%)	(0%)	(−16%)
	U.S. (USA)	0.96	0.81	1.36	1.22	1.96	2.33	2.31	2.01	1.00
		1.12	0.96	1.68	1.32	1.64	1.80	2.12	1.73	1.00
		(−15%)	(−17%)	(−21%)	(−8%)	(18%)	(26%)	(9%)	(15%)	(0%)
(b) Real PLIs
		Comparison country
		CHN	IND	JPN	KOR	FRA	DEU	ITA	GBR	USA
Reference country	China (CHN)	1.00	1.70	1.06	1.06	1.26	1.36	1.62	1.10	0.49
		1.00	1.81	0.94	0.94	1.09	1.20	1.55	1.06	0.54
		(0%)	(−7%)	(12%)	(12%)	(14%)	(13%)	(4%)	(4%)	(−8%)
	India (IND)	0.59	1.00	0.63	0.62	0.74	0.80	0.95	0.65	0.29
		0.55	1.00	0.52	0.52	0.61	0.66	0.86	0.59	0.30
		(7%)	(0%)	(18%)	(18%)	(21%)	(19%)	(11%)	(10%)	(−2%)
	Japan (JPN)	0.94	1.60	1.00	1.00	1.19	1.28	1.52	1.03	0.46
		1.06	1.93	1.00	1.00	1.16	1.27	1.65	1.12	0.57
		(−12%)	(−19%)	(0%)	(−0%)	(2%)	(1%)	(−8%)	(−8%)	(−20%)
	Korea (KOR)	0.94	1.60	1.00	1.00	1.19	1.28	1.53	1.04	0.47
		1.07	1.93	1.00	1.00	1.17	1.27	1.66	1.13	0.57
		(−12%)	(−19%)	(0%)	(0%)	(2%)	(1%)	(−8%)	(−8%)	(−20%)
	France (FRA)	0.79	1.34	0.84	0.84	1.00	1.08	1.28	0.87	0.39
		0.92	1.66	0.86	0.86	1.00	1.09	1.42	0.97	0.49
		(−15%)	(−21%)	(−2%)	(−2%)	(0%)	(−2%)	(−10%)	(−11%)	(−22%)
	Germany (DEU)	0.74	1.25	0.78	0.78	0.93	1.00	1.19	0.81	0.36
		0.84	1.52	0.79	0.79	0.92	1.00	1.30	0.89	0.45
		(−13%)	(−20%)	(−1%)	(−1%)	(1%)	(0%)	(−9%)	(−9%)	(−21%)
	Italy (ITA)	0.62	1.05	0.66	0.65	0.78	0.84	1.00	0.68	0.31
		0.64	1.17	0.61	0.60	0.70	0.77	1.00	0.68	0.34
		(−4%)	(−11%)	(8%)	(8%)	(10%)	(9%)	(0%)	(−0%)	(−12%)
	UK (GBR)	0.91	1.54	0.97	0.96	1.15	1.24	1.47	1.00	0.45
		0.95	1.71	0.89	0.89	1.03	1.13	1.47	1.00	0.51
		(−4%)	(−11%)	(8%)	(8%)	(10%)	(9%)	(0%)	(0%)	(−12%)
	U.S. (USA)	2.03	3.43	2.15	2.14	2.56	2.75	3.28	2.23	1.00
		1.87	3.39	1.76	1.76	2.05	2.24	2.91	1.98	1.00
		(8%)	(1%)	(20%)	(20%)	(22%)	(21%)	(12%)	(12%)	(0%)

Unit: Bilateral ratios, reference country = 1.00. Notes: For each cell, the upper figure refers to Q3 2025, the lower figure to the pre-pandemic average (2015–2019), and the value in parentheses shows the log growth relative to the pre-pandemic average, computed to preserve transitivity in bilateral comparisons. Cells in blue indicate a relative narrowing of the gap of the comparison country relative to the reference country, whereas cells in red indicate a widening.

for both Q3 2025 and the pre-pandemic average (2015–2019), together with the associated log-growth changes.

Across major economies, aggregate energy prices rose sharply from early 2021 to late 2022, broadly tracking movements in the global crude oil market. For reference, the West Texas Intermediate (WTI) crude oil price index in U.S. dollars is also plotted in the left panel of Figure 3. However, since mid-2024, while crude oil prices have declined, energy prices have remained elevated in most countries except the U.S. and China, partly reflecting country-specific factors such as taxes (including carbon pricing schemes like the EU ETS), subsidies, and power-mix reforms associated with decarbonization policies, as discussed in Section 5.

The nominal energy PLI captures bilateral energy price differentials but remains highly sensitive to currency fluctuations. As shown in the center panel of Figure 3, currency appreciations and depreciations during this period often produced sizable swings in nominal PLIs that did not necessarily correspond to shifts in domestic energy price levels. Over the sample period, the GBP and the euro experienced relatively modest medium-term changes against the U.S. dollar. In contrast, the Japanese yen (−31% against the dollar by Q3 2025 relative to the 2015–2019 average), Indian rupee (−30% vs. USD), Korean won (−22% vs. USD), and Chinese yuan (−8% vs. USD) underwent substantial depreciation. In such cases—most notably Japan, where widening interest rate differentials since 2021 pushed the yen to historically weak levels—the resulting decline in the nominal PLI diverges sharply from what would be inferred as international energy price differentials. For example, in Q3 2025, Japan’s nominal PLI is estimated to be approximately 21% below its pre-pandemic average, reflecting a distortion arising from the simultaneous devaluation of Japanese output when expressed in U.S. dollars. Similar declines in nominal PLIs are also observed in other Asian economies. This effect can be addressed only by the Real PLI, underscoring its importance as a more robust indicator.

Real PLI, obtained by dividing the energy PPP by the PPP for GDP, eliminates the influence of exchange rate movements and normalizes energy prices relative to overall output prices, thus reflecting international energy cost differentials in real terms. Three key patterns emerge from the data in the right panel of Figure 3. First, compared with nominal PLIs at the same quarterly frequency, Real PLIs exhibit smaller short-term fluctuations, and cross-country trajectories tend to move within a narrower range, indicating that they provide a more stable measure of international price differentials.

Second, all countries in the sample have faced a substantial real energy price disadvantage relative to the U.S., even before the pandemic, with most showing pre-pandemic Real PLI levels 1.76–2.91 times higher than the U.S. Notably, even in India and China—both recording nominal PLI levels below the U.S.—the Real PLI indicates a much larger relative gap, reflecting the relatively low value-added price per unit of output. As of Q3 2025, the Real PLIs for India and China stand at 3.43 and 2.03 times the U.S. level, respectively. The PPP for GDP used here relies on ICP 2021 (World Bank [29]), but large subnational price disparities remain, and past ICP revisions have occasionally introduced changes of several tens of percent. Specifically, in successive revisions of the ICP, India’s PPP for GDP was revised by −24% (between the 2005 ICP projection for 2011 and the 2011 ICP benchmark), +16% (between the 2011 and 2017 ICPs), and −6% (between the 2017 and 2021 ICPs), while China’s was revised by −16%, +19%, and −8%, respectively (see Box 3 in APO [36]). Measurement uncertainties may thus affect India’s PPP GDP level, which has been subject to substantial revisions across successive ICP rounds. Nevertheless, the bottom line from this international comparison is clear. As captured by the Real PLI, India and China continue to face substantially higher real energy prices relative to the U.S.

Third, in the six advanced countries—Japan, Korea, France, Germany, Italy, and the UK—the pandemic-era surge in energy prices sharply widened the real energy price gap with the U.S., peaking in Q3 2023 at 2.13–3.45 times the U.S. level. Although much of this gap was temporarily narrowed by early 2024, it has widened again in most countries, while the UK shows a more stable trajectory. In all six countries, however, the Real PLI remains well above pre-pandemic levels. This indicates that the post-pandemic energy price surge, though broadly synchronized across countries, has not merely widened but also entrenched the real energy price disadvantage relative to the U.S. Specifically, compared with their pre-pandemic levels of 1.76–2.91 times the U.S. level, the Real PLIs of these six countries had increased by 12–22% by Q3 2025, reaching 2.14–3.28 times the U.S. level, despite policy interventions such as subsidies to households and firms.

Fourth, the divergence in the six advanced countries extends beyond comparisons with the U.S.: they have also experienced further widening real energy price gaps relative to India and China. While India’s and China’s Real PLIs relative to the U.S. remained broadly stable, increasing by 1% and 8%, respectively, compared with pre-pandemic levels, the six advanced economies saw their bilateral gaps expand relative to India by 10–21% and relative to China by 4–14%. This widening relative disadvantage relative to large emerging economies is particularly relevant in light of its implications for production structures, which will be further discussed in Section 4.3.

4.3. Threshold Analysis

This section examines whether the relationship between energy Real PLI and EITE output exhibits nonlinear (and potentially discontinuous) adjustments, with recurrent regime shifts, once a country-specific critical range is crossed. Descriptive time-series trajectories of EITE output are provided in Appendix B.1 for reference. Unlike the previous subsection, which focused on country-level estimations, the panel threshold framework applied here pools observations across countries to gain statistical power while allowing for cross-country heterogeneity in threshold effects.

Threshold estimation follows Hansen [37], with bootstrap confidence intervals constructed to account for the non-standard distribution of the threshold estimator. The specification is:

$$\ln {\mathrm{E}\mathrm{I}\mathrm{T}\mathrm{E}}_{ct}={\alpha }_c+{\lambda }_t+\beta {\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l} \mathrm{P}\mathrm{L}\mathrm{I}}_{ct}+{\sum }_{c\in C^{\ast }}{\gamma }_{c}1\left({\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l} \mathrm{P}\mathrm{L}\mathrm{I}}_{ct}\ge {\widehat{\tau }}_c\right)+{\epsilon }_{ct},$$

(11)

where $c$ indexes countries, $t$ denotes quarters, and ${\alpha }_c$ and ${\lambda }_t$ are country and time fixed effects, respectively. The dependent variable is expressed in natural logarithms so that coefficients can be interpreted in percentage terms. The set $C^{\ast }$ includes countries for which thresholds were empirically identified in preliminary country-level regressions. Country-specific thresholds (${\widehat{\tau }}_c$) were first identified from single-country regressions using the same specification as in Equation (11), but without fixed effects. For these countries, the coefficient ${\gamma }_c$ captures the additional log change in EITE output once the Real PLI surpasses the country-specific threshold. For countries not in $C^{\ast }$, only the continuous effect of ${\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l} \mathrm{P}\mathrm{L}\mathrm{I}}_{ct}$ is included. This approach allows for heterogeneous adjustment dynamics across countries, as nonlinear responses may emerge at different real price levels.

Figure 4 provides a visual diagnostic of the country-specific relationship between the Real PLI and EITE output, with observations from 2021 onward shown in red to mark the onset of the post-pandemic surge in energy prices (see Figure 3), and the estimated country thresholds ${\widehat{\tau }}_c$ indicated by dashed vertical lines. Thresholds in the figure are obtained by country-by-country grid search, minimizing the profile SSR with a 5–95% trim. In Japan, Korea, France, Germany, Italy, and the UK, EITE output tends to decline once the Real PLI rises above ${\widehat{\tau }}_c$, with the cloud of points shifting downward and showing limited overlap across the threshold. In several of these countries—particularly Japan, Korea, and France—the adjustment appears more gradual rather than a distinct break, consistent with a partial rather than abrupt regime shift. It should also be noted that substantial differences exist in the overall levels of EITE across countries. In economies such as Italy, where the Real PLI has remained persistently high, past deindustrialization likely contributes to lower EITE levels and a more muted response to recent price increases. By contrast, China and India show no visible discontinuity: EITE remains relatively high or even increases in some recent observations despite higher real prices, suggesting that their recent dynamics are shaped more by stage-of-development factors than by a common break at a particular price level. These visual patterns motivate treating the six advanced economies as the set $C^{\ast }$ for which fixed-country thresholds are introduced in the panel model, while China and India are excluded from $C^{\ast }$.

Figure 5 presents bootstrap confidence intervals for the country-specific thresholds ${\widehat{\tau }}_c$. Italy exhibits the highest threshold (3.06), with a relatively narrow interval, whereas Germany’s point estimate (2.39) has a wider interval that overlaps with France’s. France and the UK fall in the middle group, with point estimates of 2.16 and 2.15, respectively, and confidence intervals spanning roughly 1.92–2.31. Japan and Korea cluster near the lower end of the distribution, with point estimates of 1.92 and 1.85, respectively. Japan’s interval is relatively tight (1.65–1.92), whereas Korea’s interval is wider (1.67–2.06), resulting in substantial overlap between the two. Given the degree of overlap in confidence intervals, these thresholds should be interpreted as indicative rather than sharply distinct. Overall, the ordering of point estimates can be summarized as ${\widehat{\tau }}_{ITA}$ > ${\widehat{\tau }}_{DEU}$ ≳ {${\widehat{\tau }}_{FRA}$, ${\widehat{\tau }}_{GBR}$} ≳ {${\widehat{\tau }}_{JPN}$, ${\widehat{\tau }}_{KOR}$}. Across the six advanced economies in $C^{\ast }$, roughly one-third of observations (median = 0.34) lie above the estimated country-specific thresholds, with post-2021 shares rising to about two-thirds (median = 0.72). The longest continuous spells above ${\widehat{\tau }}_c$ range from 13 to 15 quarters, suggesting that the sample provides adequate support on both sides of the thresholds for reliable identification. These thresholds are estimated following Hansen’s profile SSR minimization procedure, and the bootstrap confidence intervals in Figure 5 provide the appropriate inferential basis for evaluating uncertainty in ${\widehat{\tau }}_c$. Standard linear-model F-tests are not applicable in this setting because the threshold is not identified under the null hypothesis of linearity.

While these confidence intervals underscore that the exact location of ${\widehat{\tau }}_c$ is measured with error, the results from the panel estimation of Equation (11) in

Table 3. Panel threshold regression results.

Variable		Coefficient			$\mathrm{Threshold} ({\widehat{\tau }}_c$)
Real PLI	β	−0.457	(0.177)	*	—
Threshold shift: Japan	${\gamma }_{JPN}$	−0.199	(0.065)	**	1.92
Threshold shift: Korea	${\gamma }_{KOR}$	−0.179	(0.063)	**	1.85
Threshold shift: France	${\gamma }_{FRA}$	−0.073	(0.045)		2.16
Threshold shift: Germany	${\gamma }_{DEU}$	−0.125	(0.055)	*	2.39
Threshold shift: Italy	${\gamma }_{ITA}$	−0.182	(0.057)	**	3.06
Threshold shift: UK	${\gamma }_{GBR}$	−0.194	(0.058)	**	2.15
Adj. within $R^2$ = 0.578; Observations (N) = 344; Countries (C) = 8; Periods (T) = 43

Notes: Dependent variable: natural logarithm of EITE output index ($\ln {\mathrm{E}\mathrm{I}\mathrm{T}\mathrm{E}}_{ct}$). Two-way fixed effects (country and time). Robust standard errors, clustered at the country level (8 clusters), are reported in parentheses. The thresholds ${\widehat{\tau }}_c$ are fixed from single-country threshold OLS; their uncertainty is assessed with bootstrap confidence intervals (see Figure 5), computed with B = 499 replications, block length = 4, and a grid search over the 5th–95th percentile range of each country’s Real PLI. Coefficients ${\gamma }_c$ are level shifts above ${\mathrm{R}\mathrm{e}\mathrm{a}\mathrm{l} \mathrm{P}\mathrm{L}\mathrm{I}}_{ct}\ge {\widehat{\tau }}_c$ (no slope change). The U.S. is excluded from the panel because Real PLIs are measured relative to the U.S., which serves as the reference country. Sample: Q1 2015–Q3 2025. Significance: ** p < 0.05, * p < 0.1.

show that crossing the relevant price range is nevertheless associated with statistically significant level shifts in EITE output. The specification includes country- and time-fixed effects, with standard errors clustered by country. The coefficient on the continuous relative-price term (Real PLI) is negative and significant (β = −0.457, s.e. 0.177): evaluated locally, a 0.1 increase in Real PLI is associated with about a 5% decline in EITE output, holding fixed effects constant.

In macroeconomic terms, a 5% decline in EITE output is non-trivial. In advanced economies such as Japan and Germany, EITE industries account for roughly 4–5% of GDP and around 2–3% of total employment. A contraction of this magnitude, therefore, corresponds to a measurable reduction in industrial activity and labor demand, consistent with the scale of adjustments observed during past energy price shocks.

Threshold dummies are negative and statistically significant for five of the six advanced economies in $C^{\ast }$: Japan −0.199 (≈−18%), UK −0.194 (−18%), Italy −0.182 (−17%), Korea −0.179 (−16%), and Germany −0.125 (−12%), while the coefficient for France (−0.073, −7%) is smaller and not statistically significant. These magnitudes imply that once the relevant thresholds are crossed, EITE output declines by roughly 7–18% in advanced economies—a sizeable adjustment by industry-level standards. Taken together with an adjusted within R² of 0.578 (N = 344, C = 8, T = 43), these results indicate that nonlinear responses to relative energy price conditions are present and substantial, though their magnitudes differ across countries. While Real PLI is likely predetermined with respect to short-run EITE fluctuations, some reverse causality cannot be ruled out—lower EITE output could reduce energy demand, depress PPP for energy, and thereby lower Real PLI. Any such feedback would bias the coefficients toward zero, implying that the estimated negative effects represent conservative lower bounds on the true responses.

As a robustness check, the specification was re-estimated using a one-period lag of the Real PLI. The estimated coefficients on both the continuous term and the threshold dummies remain negative and statistically significant, and the ranking of country-specific thresholds is unchanged (see Appendix B.2 for full results). These findings indicate that the nonlinear effects documented above are not sensitive to contemporaneous specification and are stable across alternative timing assumptions.

5. Discussion

The empirical results have implications at three levels—global governance, industry dynamics, and structural policy design. To make these implications explicit, Section 5.1, Section 5.2 and Section 5.3 discuss how the Real PLI framework informs policy considerations across these domains. The discussion remains diagnostic rather than prescriptive, using the Real PLI primarily to characterize relative cost exposure.

5.1. Global Governance

Asymmetric cost exposure and burden-sharing have become central issues in global governance. Under the Paris Agreement, most advanced economies have pledged net-zero emissions by around 2050, whereas China and India have set targets of 2060 and 2070, respectively. The Real PLI indicates that this asymmetry is not only political but also economic: energy price differentials relative to major emerging economies widened markedly in Q3 2025 relative to 2015–2019 (by 4–14% against China and by 10–21% against India) for the six advanced economies of Japan, Korea, France, Germany, Italy, and the UK. These gaps are consistent with constraints on domestic price pass-through, given limited household purchasing power and the economy’s high marginal dependence on EITE sectors.

By contrast, notable divergences have also emerged among advanced economies, with Real PLIs relative to the U.S. widening by 12–22%. This partly reflects policy and market expectations: in 2025, the U.S. notified its intention to withdraw from the Paris Agreement, and the EPA proposed rescinding the 2009 Endangerment Finding. Regardless of the ultimate legal outcomes, these measures are likely to reduce regulatory expectations and contain domestic energy costs, thereby widening the gap relative to other advanced economies. Real PLI-based monitoring thus offers a constructive basis for discussing differentiated burden-sharing and policy sequencing beyond uniform carbon prices, while remaining agnostic about the appropriate global ambition level.

For the six advanced economies, Real PLIs relative to the U.S. have reached markedly high levels by recent standards—2.14–3.28 times the U.S. benchmark in Q3 2025, compared with 1.76–2.91 times in the pre-pandemic average (2015–2019). Given the substantial regional price dispersion within the U.S., these international gaps likely represent a conservative estimate of the true competitiveness disadvantage for industries. This suggests that widening Real PLIs may already be materializing as structural competitiveness pressures, helping to explain the weak growth performance observed in recent years. The current magnitude indicates that several economies are approaching ranges where transition-related policy trade-offs become increasingly evident. In this sense, cooperation on transition financing and measures against carbon leakage can be more effectively guided by measurable cost exposure rather than by abstract assumptions of symmetry.

5.2. Industry Dynamics

Relocation risks and early-warning signals are increasingly visible at the firm and industry level. Section 4.3 showed threshold-type responses of EITE output to adverse Real PLI conditions. Illustrative corporate decisions are consistent with these pressures, although they do not by themselves establish causality. In 2025, Nippon Steel finalized the U.S. Steel acquisition and committed roughly USD 11 billion in U.S. investments by 2028; Hyundai Steel announced a new Louisiana plant with 2.7 Mt annual capacity; and Germany’s Butting selected Alabama for its first U.S. production facility (USD 61 million). In settings where direct policy advocacy by large firms is uncommon, relocation can operate as what Hirschman [38] described as exit, reducing domestic contestation while quietly re-optimizing their production footprint. Taken together, these moves are consistent with the view that persistent real energy price gaps shape industrial geography alongside tariffs, logistics, and policy stability, and they illustrate the broader relocation dynamics highlighted by the threshold analysis.

Beyond these relocation dynamics, cross-country differences in policy style also shape how competitiveness pressures materialize. In Europe, policy interventions have tended to operate through price mechanisms: higher Real PLIs directly transmit transition costs to firms, inducing behavioral change via energy expenditure. By contrast, in Japan, Korea, and other coordinated economies, state–industry arrangements have influenced the electricity mix and investment decisions in ways that do not necessarily translate into higher energy prices. Instead, firms face implicit constraints on their production behavior, as reflected in the relatively low thresholds estimated in Section 4.3. This contrast suggests that competitiveness monitoring cannot rely solely on real prices. Complementary tracking of EITE output indices is needed to capture the broader set of mechanisms—both price-based and non-price—that condition industrial responses during the transition, underscoring the need to integrate such measures into the longer-term monitoring framework.

5.3. Structural Policy Design

Short-term interventions that mitigate nominal price increases—through levy design or tariff smoothing—may alleviate immediate burdens but do not prevent relative cost disparities from persisting. Medium-term instruments, such as capacity mechanisms, can support supply security, but they do not eliminate underlying competitiveness gaps. Likewise, subsidies can ease adjustment in the near term; however, if the Real PLI remains structurally elevated, competitive disadvantages persist. Durable improvement requires attention to fundamental determinants, including market and network design; timely investment in grids and interconnections; diversification and flexible resources that stabilize marginal costs; secure fuel-import infrastructure; and regulatory predictability that reduces capital-risk premia. Targeted support measures may have a legitimate role in addressing distributional concerns or facilitating early deployment of new technologies. Temporary price support should therefore be regarded as transitional; absent demonstrable progress in these structural domains, it risks entrenching rather than alleviating competitiveness pressures.

A different category of subsidies aims not to suppress nominal energy prices but to stimulate investment in green technologies. Such measures can foster innovation and accelerate the diffusion of clean energy. Yet, their growth effects depend critically on broader macroeconomic conditions, particularly on maintaining demand predictability under weak growth and narrowing structural energy price gaps. Moreover, the manufacturing of green technologies—such as solar panels, batteries, and other clean-energy equipment—is highly energy-intensive, making real energy price disadvantages directly relevant to competitiveness. Without progress on these fundamentals, even technology-oriented subsidies risk leaving advanced economies at a disadvantage, both in emerging clean industries and in their traditional industrial base.

Competitiveness also depends on the ability of industries to enhance the value-added price ($P^X$, value added per unit of output). Even when energy prices ($P^E$) rise, improvements in value-added prices ($P^X$) can help stabilize the Real PLI. In contrast, industrial restructuring that reduces EITE output tends to depress aggregate $P^X$ and amplify competitiveness challenges. Structural design for the transition must thus encompass both dimensions: measures that address cost disadvantages and policies that strengthen industries’ capacity to generate value added from energy inputs, particularly in emerging technology sectors, where ensuring affordable energy costs must go hand in hand with innovation.

5.4. Limitations and Further Research

Several limitations should be noted. First, the Real PLI can be measured only quarterly because GDP deflators are not available monthly, even though nominal PLIs are available at higher frequencies. Second, the analysis focuses on the aggregate EITE output because harmonized quarterly energy-use data by industry are not yet available across countries, preventing threshold estimation at the sector level. Third, although relocation indicators and corporate decisions provide suggestive evidence, industry-level output PPPs would be required to disentangle price effects from structural adjustment fully.

Finally, the Real PLI series is subject to standard statistical revisions because it integrates data sources with different update frequencies. The nominal PLI components are revised as countries update their monthly energy-related price statistics. Consistency with the national accounts is ensured through quarterly and annual SNA releases, which revise both expenditure (energy consumption) and output-side price measures (GDP deflators). Periodic benchmark-year updates further re-anchor the underlying price–quantity structure, ensuring coherence across the full system of national accounts. Such revisions are a standard feature of official statistics and do not materially alter the qualitative patterns documented in this study. However, point estimates of thresholds may shift modestly as the underlying data are updated.

Future research could extend this framework once more granular data become available, for example, by constructing energy-use-weighted industry aggregates, estimating sector-specific thresholds, or allowing for dynamic threshold behavior. These extensions would permit a richer understanding of how structural characteristics shape industrial responses to sustained energy price differentials.

6. Conclusions

This study developed PPP-consistent Real PLIs to provide a high-frequency measure of cross-country energy price disparities and examined how these conditions shape industrial adjustment. Three findings stand out. First, Real PLIs for the six major advanced economies have risen sharply relative to the U.S., China, and India, indicating a widening structural cost disadvantage. Second, the RUEC gap conflates price and composition effects, and declines in aggregate RUEC often reflect deindustrialization rather than improved competitiveness. Third, the threshold analysis shows that once country-specific price ranges are exceeded, EITE output declines by roughly 7–18%, indicating heterogeneous but economically meaningful nonlinear responses across advanced economies.

These results offer several policy implications. (i) Persistent real energy price gaps suggest that structural reforms that narrow marginal cost differentials—through market and network design, investment timing, supply diversification, and regulatory predictability—are central to sustaining industrial competitiveness. (ii) Because advanced and emerging economies face systematically different real price conditions, discussions on international burden-sharing and carbon-leakage mitigation can benefit from explicit monitoring of Real PLI dispersion rather than from assumptions of symmetric adjustment capacity. (iii) For EITE industries, competitiveness policy must balance cost relief with improvements in value-added capacity, as strengthening output prices can partially offset energy price pressures.

The Real PLI is not a comprehensive measure of transition performance, nor is it intended to be. Rather, it provides a timely and consistent reference point for assessing emerging competitiveness risks. Continued refinement of PPP methodologies and the expanded availability of harmonized industry-level data will allow future research to extend the analysis to sector-specific thresholds and to integrate energy-use-weighted indicators of industrial activity. Such developments would enable a more comprehensive understanding of how sustained real energy price differentials shape economic transitions across countries.