Application of Vis–NIR Spectroscopy and Machine Learning for Assessing Soil Organic Carbon in the Sierra Nevada de Santa Marta, Colombia

Abstract

Soil organic carbon (SOC) is an essential indicator of soil fertility, health, and carbon sequestration capacity. Its proper management improves soil structure, productivity, and resilience to climate change, making rapid and reliable SOC assessment essential for sustainable agriculture. Visible and near-infrared (Vis–NIR) spectroscopy offers a non-destructive and cost-effective alternative to conventional laboratory analyses, allowing for the simultaneous estimation of multiple soil properties from a single spectrum. This study aimed to predict SOC content using machine learning techniques applied to Vis–NIR spectra of 860 soil samples collected in the Sierra Nevada de Santa Marta, Colombia. The spectra (400–2500 nm) were acquired using a NIR spectrophotometer, and the soil organic carbon (SOC) content was quantified using a wet oxidation method that employs dichromate in an acidic medium. A hybrid modeling framework combining Random Forest (RF) with support vector regression (SVR) and XGBoost was implemented. Spectral pretreatments (Savitzky–Golay first derivative, MSC, and SNV) were compared, and spectral bands were selected every 10 nm. The 30 most relevant wavelengths were identified using RF importance analysis. Data were divided into training (80%) and test (20%) subsets using stratified random sampling, and five-fold cross-validation was applied for parameter optimization and overfitting control. The RF–XGBoost (R² = 0.86) and RF–SVR (R² = 0.85) models outperformed the individual RF and SVR models (R² < 0.7). The proposed hybrid approach, optimized through features, and advanced spectral preprocessing demonstrate a robust and scalable framework for rapid prediction of SOC and sustainable soil monitoring.

1. Introduction

Soil organic carbon (SOC) is crucial to soil fertility and the success of crop growth. It is the main component of organic matter (OM) and serves as a key indicator of soil health and productivity [1]. SOC plays a vital role in improving soil structure, enhancing its ability to retain water and nutrients, and promoting better aeration and drainage, which are essential for healthy root growth. It also supports microbial activity, enhancing nutrient cycling and making critical nutrients, such as nitrogen and phosphorus, available to plants [1]. Additionally, SOC contributes to soil aggregation, which reduces erosion and improves soil tilth, making it easier to work with during planting and cultivation [2]. Moreover, SOC contributes to soil pH stabilization and acts as a buffer against environmental stresses [3]. SOC and other fertilization parameters are analyzed in laboratories to provide accurate and reliable data on soil health and fertility [4].

Traditional soil property research methods involve collecting soil samples and performing laboratory analysis, which is expensive and time-consuming [5,6,7,8]. For this reason, different alternative techniques that have proven efficient in predicting different soil indicators are currently being explored. These alternatives include spectroscopic methods such as visible and near-infrared (Vis–NIR) spectroscopy, laser-induced breakdown spectroscopy (LIBS), near-infrared (NIR), and mid-infrared (MIR) spectroscopy; the latter encompasses Fourier transform infrared spectroscopy (FTIR) and Raman spectroscopy [9].

The Vis–NIR technique has great potential for analytical applications due to its rapid, non-destructive, and cost-effective nature [9]. This technique is based on interactions between the studied object and optical waves of different wavelengths in the visible–near-infrared (Vis–NIR) spectrum (350–2500 nm), which can occur through vibrational reflectance, transmittance, or absorbance [10]. Different soils, minerals, and plant species have been shown to reflect, absorb, and emit electromagnetic waves from various spectral regions [11]. Consequently, each soil has its unique “fingerprint” depending on its composition and state [11]. Compared to conventional chemical analysis, Vis–NIR spectroscopy enables rapid, nondestructive, and reproducible prediction of soil properties [12]. It can infer multiple components from a single spectrum [13].

The application of machine learning (ML) in soil science has increased over the past decade [14], which has also influenced the utilization of infrared spectral data to infer soil properties [15]. One of the most widely used multivariate models for estimating soil chemical properties from Vis–NIR is partial least squares regression (PLSR) [16,17]. However, it hides the nonlinear relationships between the spectrum and soil chemical properties [18]. Other alternatives include stepwise multiple regression (SMLR) [19,20], principal component regression (PCR) [21,22], backpropagation neural network (BPNN) [23,24], support vector machine regression (SVMR) [18,25,26], and random forest regression (RFR) [27].

Recent studies utilized 140 [28], 261 [29], and 523 [30] soil samples, adopting ML approaches, including support vector machines, neural networks, random forest, and Cubist, to estimate, among other indicators, SOC and OM.

Previous studies have focused on using regression models to estimate soil properties from spectral data [30]. However, the potential of classification approaches in this context is underexplored. In Colombia, Delgadillo–Durán et al. [13] categorized soil properties into three classes (low, medium, or high) based on agronomic criteria and standards. However, natural soil variability leads to unbalanced datasets that complicate modeling. To address this, merging similar classes (e.g., low and medium OM or Ca) improves prediction accuracy and supports more practical soil and crop management decisions.

In this work, we investigate the use of machine learning techniques to predict SOC using Vis–NIR regions. We evaluated the performance of various regression models, including SVR, RF, and RF–XGBoost. Additionally, we incorporated the first derivative of the Savitsky–Golay as a preprocessing technique to improve the quality and representativeness of the absorbance data. Based on this approach, we hypothesize that machine learning models calibrated with Vis–NIR spectral information can accurately predict soil organic carbon despite the high spatial and edaphic variability of the Sierra Nevada de Santa Marta.

2. Materials and Methods

2.1. Data

2.1.1. Study Area and Sample Collection Procedure

A selective sampling was carried out on farms with agroforestry–cacao systems (SAFC) in the Sierra Nevada de Santa Marta, Colombia. A total of 860 soil samples were collected across four municipalities in the region: Santa Marta, Ciénaga, Fundación, and Aracataca. Samples were taken from elevations ranging between 10 m above sea level (at coordinates N 11.249237, W 73.778825) and 2000 m above sea level (at coordinates N 10.975503, W 74.059458), across diverse SAFC systems and soils derived from various parent materials, including igneous rocks (granodiorites, quartz diorites, quartz monzonites, and granite), metamorphic rocks (ignimbrites, gneiss, schists), and colluvial–alluvial deposits. The area features a variety of landforms (ridges and beams, morainic fields, hills, knolls, and small valleys). The terrain ranges from gently sloping to steeply rugged, with slopes varying from 3% to over 75%. The soils are well-drained, shallow, and limited by bedrock, which often outcrops at the surface. Soils exhibit pH values ranging from slightly acidic to strongly acidic, with low SOC content and low fertility [31].

The sampling stage was carried out between 2023 and 2024, using a 10 cm deep ring. This depth was selected because it corresponds to the topsoil horizon (A), where the highest proportion of OM and biological activity is concentrated. Several studies have reported that between 70% and 90% of the total SOC and most of the soil macrofauna biomass are found within the first 10 cm of the soil profile, due to the accumulation of litter, fine roots, and easily decomposable organic residues [32,33,34].

However, the number of samples per municipality was not uniform, as it depended on the number and spatial extent of farms with active SAFC and on accessibility and environmental heterogeneity. The sampled farms corresponded to properties affiliated with four producer organizations in the region, and the sampling included 100% of the available farms with active agroforestry systems, meaning that the total sample represented the entire target population.

Although this resulted in unequal sampling among municipalities, the approach was methodologically justified to capture the true spatial and ecological variability of the agroforestry landscape across the Sierra Nevada. Furthermore, potential spatial bias was minimized by applying a stratified block sampling design, grouping sampling units according to slope and vegetation cover type, thus ensuring comparability among sites and maintaining the robustness of ecological and statistical analyses.

2.1.2. Chemical Measurements

The chemical method used to quantify SOC in the samples was that of Walkey and Black [35] with modifications. Between 20 and 100 mg of the sample is weighed, 2 mL of 1 N K₂Cr₂O₇ is added, and the mixture is stirred for 5 s. Then, 1 mL of concentrated sulfuric acid (H₂SO₄) is added. 7 mL of MilliQ Water is added, the reaction is left overnight, and the following day, it is centrifuged and quantified by UV–Vis at 585 nm. The method involves the wet oxidation of the soil sample using potassium dichromate in an acidic medium. The heat released during the incorporation of sulfuric acid facilitates the partial oxidation of C. In this process, a reduction of the dichromate occurs, equivalent to the oxidized C content. This method only estimates Readily Oxidizable Carbon (ROC), so a correction factor ranging from 60% to 86%, depending on soil type and horizon, is applied to estimate Total Organic Carbon (TOC) [36,37]. Numerous studies have indicated that the method typically achieves an average recovery rate of between 76% and 77%, corresponding to the application of a correction factor of 1.3 [38,39,40]. Consequently, this study adopted this correction factor to estimate total organic carbon (TOC), thus ensuring the uniformity, comparability, and standardization of the results. It is important to note that this factor represents a standardized approximation used in soil organic carbon analysis; however, the actual recovery efficiency may vary depending on soil characteristics, environmental conditions, and the nature of the OM.

2.1.3. Spectroscopy Vis–NIR

The samples passed through a humidity homogenization process; samples were dried at 40 °C (for 48–96 h, depending on the soil type). Soil samples were dried according to protocol GA-R-104 [41] and ISO 11464:2006. Drying was carried out in a forced-air oven at 40 °C until a constant weight was reached (variation < 0.1%), resulting in a soil of uniform color and free of wet aggregates. Drying time ranged from 24 to 96 h, depending on the texture and OM content, while a temperature of 40 °C preserved the organic carbon and prevented thermal alteration. Samples were placed in a 50 mm diameter annular cup and scanned from 400 to 2500 nm using a NIR spectrophotometer (FOOS-DS2500) according to the methodology proposed by Delgadillo–Durán et al. [12].

2.2. Methods

In the context of predicting SOC, several advanced machine learning techniques were explored and evaluated. The study considered the following models: RF, SVR, RF–SVR and RF–XGBoost. These methods are essential to address regression and classification tasks where data complexity and collinearity between variables are critical. The data processed for this analysis were obtained using Vis–NIR spectra and compared with results from the traditional method, which was obtained in the laboratory using the Walkey and Black method [35] with modifications.

RF uses decision trees and is trained on a random subset of features (wavelengths) and a random set of observations (sample carbon level and its absorbance levels); the decision trees grow until they reach a predetermined number of nodes [42]. It is an ensemble machine learning approach that merges thousands of decision trees, each built by bootstrapping on calibration data [43]. Moreover, the random subspace method—where the number of features considered at each node split is determined by the parameter mtry—is applied at every split in the tree [43]. The final prediction is the average of the predicted values from all the trees. RF generally has a better generalization ability, which is used for regression and classification [43].

SVR is a supervised learning algorithm derived from Support Vector Machines (SVM), explicitly designed for regression tasks. SVR seeks to find a function that approximates the relationship between input variables and a continuous output, within a specified margin of tolerance. It constructs this function by identifying a subset of training data points, support vectors, that are most relevant to defining the position of the hyperplane in a high-dimensional feature space [44].

Performs comparably well when there is a coherent margin of dissociation between classes [28]. Additionally, SVR can model nonlinear relationships. Its robustness to overfitting and ability to handle high-dimensional data make it a valuable tool in various regression applications, including time series forecasting, financial modeling, and environmental data analysis.

Extreme Gradient Boosting (XGBoost) is a very popular ensemble learning technique for structured data, as it allows solving infinite prediction problems [45]. It iteratively builds an ensemble of trees, minimizing at each step the residuals of previous models, learning from the errors of previous trees. Among its variants, XGBoost stands out as one of the most powerful and popular algorithms in machine learning, offering superior performance, scalability, and regularization techniques to avoid overfitting [46]. To achieve this, XGBoost introduces an even more efficient implementation of the gradient boosting framework, which prioritizes scalability and parallelization. It also includes regularization terms that reduce the size of the trees, allowing for successful prevention of overfitting compared to a simple decision tree or even a non-optimized boosting model.

2.2.1. Preprocessing

The first step in spectral data processing involved data cleaning to reduce the noise.

Then, the Savitsky–Golay first derivative (SG1.der), a spectral preprocessing technique that removes additive baseline effects present in the raw spectral data and highlights the most informative features of the spectrum, was applied. This transformation, applied after smoothing the data using a polynomial filter (in this study, a second-order filter with a seven-point window for the RF–SVR models and an 11-point window for the RF, SVR and RF–XGBoost models), aims to improve data quality by reducing noise and amplifying changes in spectral curvature, facilitating the identification of absorption bands relevant to soil property prediction. The number of points in each window were determined experimentally after testing multiple configurations so that no more than one inflection is included in the absorbance data at any interval of the convolution, smoothing reduces noise, and the approximation polynomial (2nd order) captures the dynamics of the data [47].

2.2.2. Training Models

The Python (version 3.10) program was used for data analysis. To generate the marching learning models, the following libraries were used: numpy (mathematical calculations), tensorflow (for model generation), matplotlib pyplot (graphics), pandas (for reading Excel), sklearn model selection (for data division), Os (for reading folders), Seaborn (statistical graphics), Sklearn ensamble (for importing random forest regressor data), sklearn.svm (for importing Support Vector Regression model), sklearn.metrics (for importing metrics), scipy.signal (for importing Savitzky–Golay filter).

For RF, the analysis path followed was first to select the number of trees using a loop, which in this case tested a total of twenty models. The next step was to choose the optimal number of features (i.e., the number of wavelengths) and a suitable stopping criterion to determine when it is prudent to continue generating trees within the RF model. Next, the stopping criterion is defined: the maximum number of leaf nodes, or max leaf nodes. Here, the maximum number of leaf nodes (nodes where a prediction will be obtained) per decision tree is defined. Once the optimal parameters of the models were obtained, they were trained with the selected characteristics from which the critical and sensitive absorbance bands were determined to predict SOC.

SVR consists of three hyperparameters: Regularization (c) that controls the balance between low training error and good generalization ability, epsilon (ε) defines a tolerance range around the prediction function within which errors are not penalized, and kernel is the function that transforms the input data into a feature space where it is easier to perform regression. To find the best values for each hyperparameter, cross-validation was performed using the GridSearchCV function from the Scikit Learn library.

For the RF–XGBoost model, spectral bands were selected every 10 nm to reduce dimensionality and noise. A RF Regressor model was then run to calculate the importance of each spectral band, selecting the 30 most relevant bands from the analysis as input for the final model. Finally, the modeling and evaluation stages were executed. The data were divided into training (80%) and testing (20%).

For the RF + XGBoost model, spectral bands were selected every 10 nm to reduce dimensionality and noise. A Random Forest Regressor model was then run to calculate the importance of each spectral band, selecting the 30 most relevant bands from the analysis as input for the final model. Finally, the modeling and evaluation stages were executed. The data were divided into training (80%) and testing (20%). This 80/20 partition was chosen to ensure a sufficient amount of data for model training while maintaining an independent portion for unbiased evaluation of predictive performance.

This ratio is widely adopted in machine learning applications involving spectral data, as it provides an appropriate balance between model learning capacity and validation reliability [48].

Additionally, a five-fold cross-validation procedure was applied within the training set to optimize hyperparameters and minimize overfitting, ensuring the robustness and generalization of the final RF + XGBoost model.

3. Results and Discussion

3.1. Descriptive Statistics of Selected Soil Properties

Table 1. Descriptive statistics for 860 soil samples taken in the Sierra Nevada de Santa Marta, Colombia.

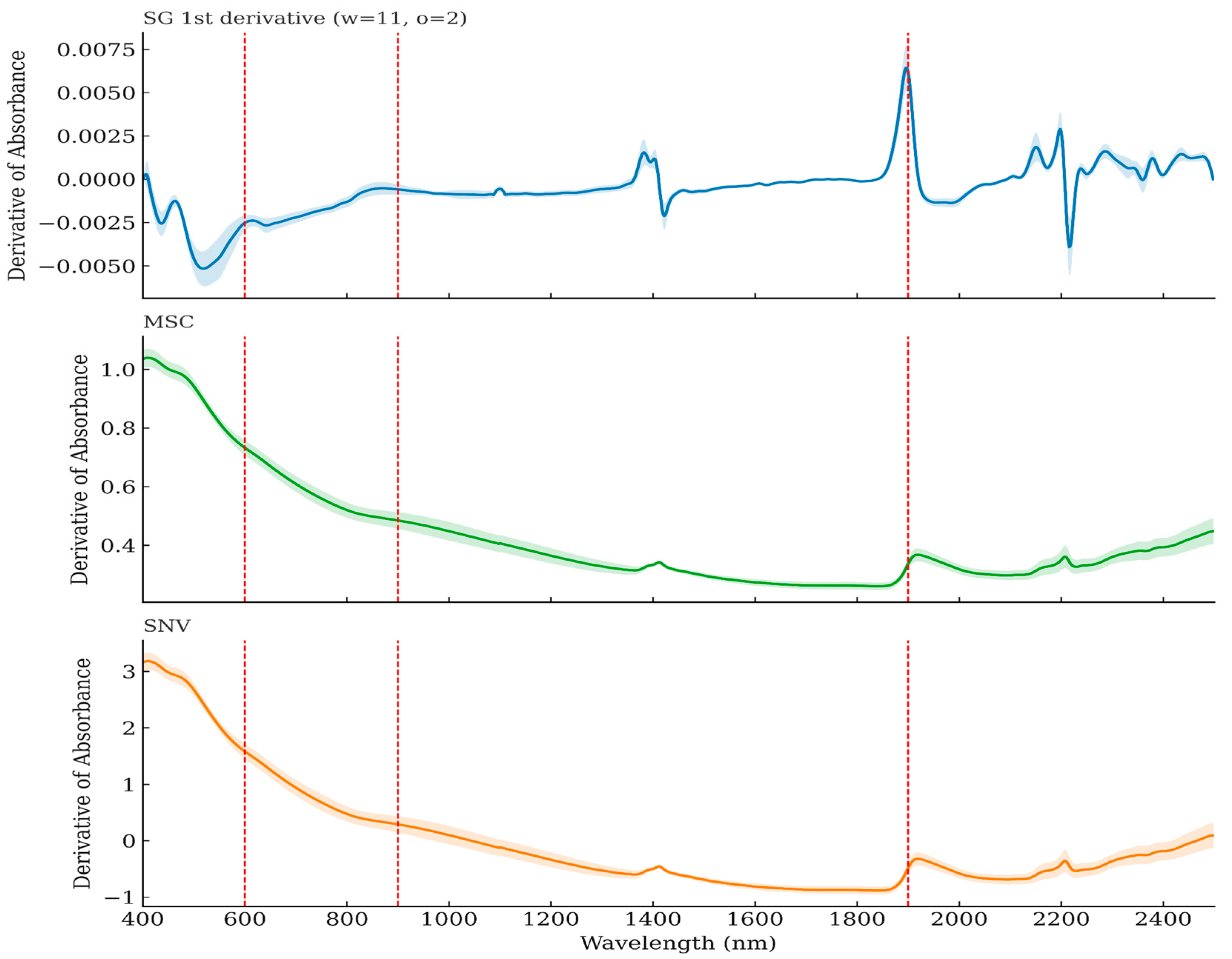
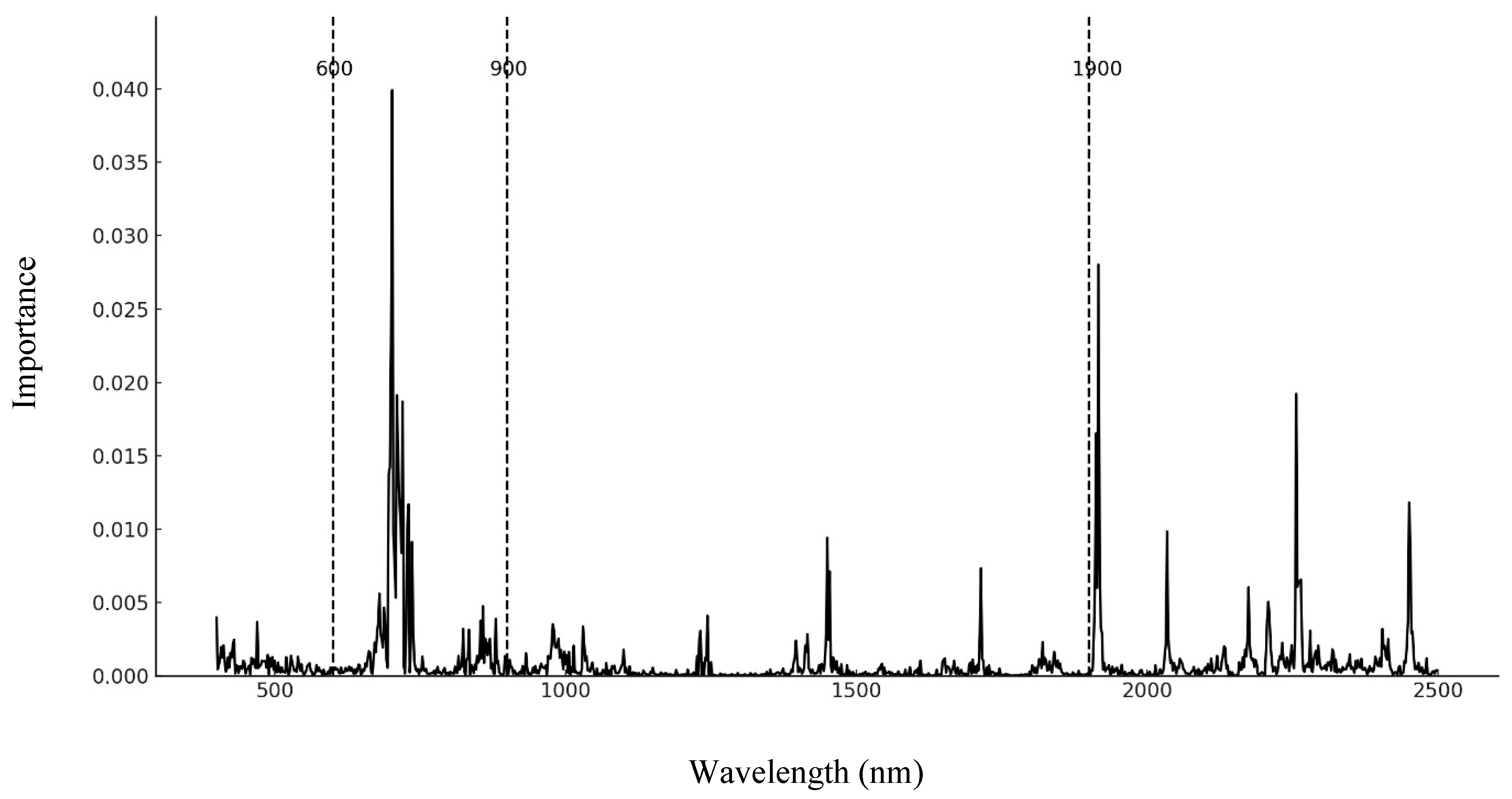
Farms	Average (g 100 g−1)	Error	SD (g 100 g−1)	CV (%)	Min (g 100 g−1)	Max (g 100 g−1)
Altamira	1.57	0.09	0.13	8.11	1.48	1.66
Brisas de Córdoba	1.51	0.19	0.32	21.32	1.25	1.87
Chukwin Chukwa	2.33	0.20	0.28	11.86	2.13	2.52
El Amparo	1.86	0.09	0.53	28.66	0.85	3.75
El Congo	1.55	0.14	0.24	15.76	1.38	1.83
El Descanso	1.67	0.14	0.24	14.12	1.41	1.87
El Diamante	2.07	0.18	0.31	14.99	1.86	2.43
El Edén	1.34	0.14	0.24	18.16	1.06	1.50
El Esfuerzo	1.22	0.15	0.26	20.91	0.97	1.48
El fraile	1.32	0.11	0.18	13.94	1.12	1.48
El Jardín	1.61	0.12	0.21	12.89	1.46	1.85
El Limón	1.69	0.33	0.58	34.07	1.03	2.09
El Manantial	3.09	0.31	1.21	39.33	0.39	4.64
El Paraíso	2.44	0.13	0.95	39.15	1.03	5.28
El Progreso	1.62	0.12	0.21	13.13	1.47	1.86
El Recuerdo	2.65	0.14	0.55	20.87	1.76	3.67
El Triunfo	1.66	0.11	0.18	11.03	1.52	1.87
Emanuel	1.24	0.07	0.13	10.18	1.10	1.34
La Arcadia	2.25	0.08	0.32	14.15	1.73	2.66
La Aurora	1.64	0.20	0.35	21.10	1.31	2.00
La Cabaña	1.90	0.15	0.60	31.50	0.96	3.24
La Carmelita	1.68	0.21	0.36	21.15	1.27	1.90
La Cascada	1.53	0.06	0.10	6.44	1.45	1.64
La Chavela	1.84	0.10	0.61	33.00	0.69	2.97
La Conquista	1.36	0.13	0.50	36.52	0.78	2.26
La Esperancita	3.67	0.44	0.75	20.57	2.87	4.37
La Esperanza	2.78	0.12	0.65	23.54	1.95	4.61
La Fortuna	1.22	0.10	0.25	20.92	0.86	1.52
La Granja	1.50	0.10	0.17	11.37	1.33	1.67
La Perla	1.40	0.12	0.20	14.49	1.27	1.63
La Vega	0.89	0.20	0.35	25.00	1.08	1.76
La Victoria	2.23	0.11	0.19	8.66	2.06	2.44
Las Tres Palmas	1.06	0.13	0.23	21.45	0.86	1.31
La Esperanza	1.39	0.21	0.37	26.33	1.05	1.78
Las Gaviotas	1.36	0.11	0.19	14.03	1.16	1.54
Las Murallas	1.89	0.09	0.55	29.14	0.84	2.92
Las Palmas 3	1.76	0.07	0.42	23.88	0.74	2.80
Las Piedritas	1.71	0.08	0.49	28.44	0.83	3.04
Los Acacios	0.91	0.07	0.42	46.43	0.11	1.77
Los Angeles	1.96	0.09	0.23	11.55	1.57	2.21
Los Cacaos	2.03	0.11	0.70	34.31	0.29	3.70
Los Jazmines	1.93	0.07	0.41	21.48	1.15	2.65
Los Mandarinos	2.24	0.10	0.60	26.93	0.95	3.53
Los Mangos	2.36	0.18	0.70	29.84	1.24	3.37
Los Naranjos	1.74	0.05	0.09	5.35	1.63	1.80
Los Potreritos	2.11	0.08	0.49	23.17	1.02	3.13
Los Recuerdos	1.71	0.08	0.14	16.83	0.69	0.97
María Bonita	1.48	0.13	0.22	14.78	1.24	1.67
Monte Carmelo	1.53	0.18	0.32	20.60	1.22	1.85
Niguakoa	2.46	0.17	0.72	29.17	1.66	4.40
No hay como tu	1.23	0.11	0.58	47.23	0.57	3.13
Nuevo Oriente	0.87	0.10	0.37	42.75	0.37	1.71
Santa Bárbara	1.86	0.22	0.86	46.23	0.90	4.50
Sinaí	2.70	0.15	0.95	35.06	0.86	5.35
Tagbi	1.24	0.14	0.24	19.33	1.01	1.49
Villa Brisa	1.05	0.02	0.04	3.62	1.02	1.09
Villa Sofia	2.05	0.10	0.40	19.66	1.29	2.70
Villa Vista	1.78	0.16	0.27	15.11	1.61	2.09
Total	1.90	0.03	0.79	41.61	0.11	5.35

summarizes the descriptive statistics (mean, error, standard deviation, coefficient of variation, minimum, and maximum) of the 860 soil samples analyzed in the Sierra Nevada de Santa Marta. SOC exhibited high variability in the observed values, with a minimum mean of 0.11 and a maximum of 5.35 g 100 g⁻¹. Notably, 57% of the samples fell within the range of 1 to 3 g 100 g⁻¹, distributed across the four sampled municipalities (Figure 1). This indicates the high variability (CV: 41.61%) of the SOC associated with agroforestry systems featuring cacao in the Sierra Nevada de Santa Marta. This is probably due, firstly, to the edaphoclimatic conditions present in the different sampled areas, which are located from sea level to 2000 masl, to the differences between forest and fruit species that make up the agroforestry arrangement on the farms, and finally to the density or number of plants that make up the forest arrangement. High variability in soil organic carbon was also present within the farm, with the most significant variability occurring on the No Hay Como Tu farms (47.23%) and Los Acacios farms (46.43%). In comparison, the least variability was found on the Billa Brisa farms (3.62%) and Los Naranjos farms (5.35%).

The variability in SOC at the farm level is attributed to farm characteristics and agronomic management practices. In the former case, a higher soil organic carbon content is found towards the lower part of the mountain, resulting from particle carryover due to rainfall and management practices associated with uneven agroforestry arrangements. In most cases, the dispersion of forest trees on the farm causes more significant litter biomass accumulation in some areas within the farm and more significant soil macrofauna activity (Figure 1).

3.2. Data Processing

Figure 2 and Figure 3 show the absorbance data after implementing the first derivative pretreatment. This pretreatment technique eliminated additive or multiplicative effects between spectra [48], which generated a positive effect on the spectral characteristics compared to the spectra obtained in the absorbance mode [log (1/R)] and on the performance of the RF–STV and RF–XGBoost models for predicting SOC. This technique also offered the advantage of showing the variation in sample reflectance in relation to the variation in wavelength and exposing the noise that could be interpreted as a signal to show where there were more marked changes between close wavelengths [49]. This principle is established by the change in reflectance (ρλ) as a function of wavelength λ at a given pointi. The derivative is numerically approximated using symmetric or central differences, as expressed in the equation presented by Rudorff et al. [50].

Figure 4 illustrates that spectral absorbance varied significantly with SOC content. The difference in absorption becomes more pronounced at higher SOC contents in the Vis region compared to the NIR region [51]. Stenberg et al. [52] also observed a decrease in the absorption rates of organic soils in the NIR region. The first derivative of the absorption spectrum further revealed a strong correlation between SOC content and absorption in the Vis region, highlighting subtle spectral variations. The absorption peaks around the wavelengths of 600, 900, and 1900 nm (Window = 7, Order = 2) in the RF–SVR model and the wavelengths of 720, 736, and 1920 nm (Window = 11, Order = 2) in the RF–XGBoost appear to be associated with SOC content (Figure 2 and Figure 3). The 7-point window used in the RF–SVR model is more sensitive to rapid variations but can introduce more variability into the data, affecting the model’s accuracy, while the 11-point window is more suitable for the RF–XGBoost model because it smooths noise better without losing relevant signals.

In addition to the Savitsky–Golay first-derivative smoothing, other commonly used scatter-correction techniques, such as Multiplicative Scatter Correction (MSC) and Standard Normal Variate (SNV), were also tested for comparison.

Although MSC and SNV effectively reduce multiplicative and additive scattering effects among spectra, the Savitsky–Golay first derivative showed a greater ability to enhance subtle spectral variations and reveal absorption features associated with SOC.

Therefore, the first-derivative Savitsky–Golay preprocessing was selected as the main spectral pretreatment method, as it improved the resolution of narrow absorption peaks around 600, 900, and 1900 nm, which are strongly correlated with SOC content, resulting in superior predictive performance of the RF–SVR and RF–XGBoost models.

Moura-Bueno et al. [53] compared the predictive performance of six preprocessing techniques and four calibration models on the SOC content of 841 samples from subtropical soil. The best preprocessing technique was the first derivative SG smoothing, and the best calibration model was PLSR.

Other preprocessing techniques have also been efficient for predicting soil indicators, including moving averages, clustering, and smoothing. Such as Savitsky–Golay filtering, normalization, continuum removal, gap derivatives, [52,54,55], for example, Savitzky–Golay is a smoothing function that reduces noise by using a weighted sum of neighboring values [52,56] clustered spectral data using unsupervised learning (UL) techniques: principal component analysis (PCA) and Fuzzy C-means (FCM) method; however, FCM clustering improved the accuracy of the PLSR model, as measured by the prediction interval (PI). However, this had little impact on the accuracy of SOC predictions, as assessed using the residual prediction deviation (RPD).

The transformed Vis–NIR spectra of the soil samples, recorded in absorbance mode as [log (1/R)], have a typical shape similar to that presented in other soils. SOC and moisture in the sample are the primary constituents that determine the shape of the spectra. In the visible region of the spectrum (400 to 780 nm), absorption is attributed to soil chromophores such as iron oxides and the dark color caused by OM. In the near-infrared region (780 to 2500 nm), absorption is attributed to water molecules, hydroxyl groups, and clay minerals [57].

3.3. Selecting the Number of Trees and Characteristics per Node in a Random Forest Model

As a result of the loop application, 20 models were tested, analyzing 20 at a time, up to a total of 400 trees. This allowed the performance of the models to be evaluated on a variety of trees, selecting the model based on the lowest “out of bag” error, which in this case was 220 trees. The “out of bag” error is a training error, which specifies that the lower the “out of bag” error value, the more stable the corresponding random forest model will be. It also shows that RF is robust to overfitting [58]. Different combinations of the number of regression trees and the number of split nodes were chosen. In this step, the number of features per node was selected based on the “out of bag” error, which for this test was 12 features and 25, the maximum number of leaves per node (Figure 5).

The RF algorithm enables predictions from multiple decision trees to be compiled into a final forecast, demonstrating an improved ability to navigate nonlinear interactions between variables and mitigate overfitting. Consequently, it has been widely used in hyperspectral soil research [59].

The above has been widely documented; for example, Meng et al. [60] employed a stratification strategy and the RF algorithm to enhance the predictive accuracy of SOC content, reducing RMSE by 4.88 g kg⁻¹ and increasing R² by 0.32. However, the RF algorithm exhibits a “step-like” behavior in predicting continuous variables, which can reduce its effectiveness in analyzing hyperspectral data. For the presented case, the RF implementation improved the predictive accuracy compared to other evaluated alternatives, such as the LSTM-trained model, which achieved an R² of 0.52, and the CNN-trained model, with an R² of 0.72. This resulted in an increased R² of 0.33 and 0.13, respectively.

3.4. Model Selection

Once the optimal parameters of the model were obtained, the model was trained with the aforementioned characteristics. The wavelengths are related to the x-axis, and the importance is on the y-axis. For the Random State 42 distribution, it can be seen that there is a more significant influence of the absorbance on the SOC around 600 nm, 900 nm and 1900 nm in the RF–SVR model and the wavelengths of 720, 736, and 1920 nm in the RF–XGBoost (Figure 4 and Figure 6). Bands with greater significance are given greater weight in the decisions of the model trees. This enables the identification of key spectral regions associated with carbon content, which can be utilized to design more efficient sensors, conduct more focused spectral analyses, or interpret chemical or biological processes related to those wavelengths.

It is worth noting that the most important bands in the RF algorithm are identified based on the Mean Decrease in Impurity (MDI), also known as Feature Importance. This criterion makes it possible to determine which spectral bands contribute most significantly to improving prediction accuracy by being used as splitting points in the decision trees. Specifically, the cumulative reduction in variance was calculated each time a band was used to split a node (in a regression context). Bands with the highest cumulative reduction were considered the most relevant.

Once these key bands were identified, the SVR and XGBoost models were trained using only the selected bands. This approach enhanced computational efficiency and helped to reduce overfitting, while maintaining high predictive performance.

This can be observed by extracting a portion of the spectrum that covers useful information from the complete spectrum data, eliminating noise, enhancing computational efficiency, and developing a concise and stable prediction model. This has been documented during the last decade in other research; for example, Stenberg [61]. published that SOC can affect spectral data ranging from 700 nm to 2450 nm. Tahmasbian et al. [62] also reported that the wavelengths important for CT prediction were primarily observed in the 740–800 and 900–1000 nm spectral regions, respectively. Also, Delgadillo–Durán et al. [13] found that the key components in the organic matter were around 400 nm and 1930 nm. In addition, there are several specific absorption features around the 950 nm wavelength and between the 2300–2400 nm wavelengths. According to Milos and Bensa [63], the most important wavelengths for clustering were in the following ranges: 1980–2025 nm, 1900, 735–775, 490–530, 1200, 2100, 2200, 2130, 2400, 485, and 440 nm.

A data cleaning process was conducted to eliminate outliers, aiming to enhance the correlation between the characteristics and the predicted variable. To achieve this, the box-and-whisker (boxplot) technique was employed, which enabled the dataset to be reduced from 860 to 842 samples, retaining only those observations that represented the overall behavior. The proposed RF model consisted of 220 trees, 12 characteristics, 25 leaves per node, and a Random state of 42, which was assigned to ensure the reproducibility of the results and to determine the data distribution during model training. Subsequently, through cross-validation using GridSearchCV, the optimal combination of hyperparameters for the SVR model was identified. The best performance was obtained using a linear kernel, with a C value of 1000 and an epsilon value of 0.151, configurations that allowed for improved model generalization capabilities. The best performance of the XGBoost model for predicting SOC was achieved using a specific combination of hyperparameters that effectively captured the nonlinear relationships between spectral bands and the target variable. A total of 200 decision trees (n_estimators = 200) were used, providing a balance between model complexity and stability, while a maximum tree depth of 5 (max_depth = 5) helped prevent overfitting and ensured good generalization. The learning rate (learning_rate = 0.1) allowed the model to make moderate optimization steps, avoiding oscillations or premature convergence. Additionally, a random seed (random_state = 42) was set to ensure result reproducibility. As a result, an RF–SVR model was generated, which, based on the sample absorbance information, presents a test prediction of R² = 0.85, while the RF–XGBoost model achieved an R² = 0.866 and an RMSE = 0.090 (Figure 7 and Figure 8). The figures illustrate the relationship between the predicted and actual values of SOC content obtained using the hybrid model (RF–SVR) or (RF–XGBoost). Each point represents a sample, and the proximity of the points to the 1:1 reference line (dashed red) indicates the accuracy of the model’s predictions. The model demonstrates a strong predictive ability, suggesting a high level of agreement between observed and estimated values. This result confirms the model’s reliability for estimating SOC based on selected spectral features, preprocessed using first derivative transformations and optimized through feature selection techniques. In contrast, the standalone models, RF and SVR, individually showed lower predictive performance, with R² values of 0.69 and 0.66, respectively (

Table 2. Predictive models for SOC.

Model	R2	RMSE	RDP
Random Forest	0.692	0.441	1.8
SVR	0.663	0.461	1.56
RF–SVR	0.853	0.380	2.6
RF-Optimized XGBoost	0.866	0.090	1.9

). This highlights the importance of the combined modeling approach and the selection of relevant spectral bands to improve prediction accuracy for estimating SOC.

The RF–SVR and RF–XGBoost model offers an alternative to SOC estimation, with greater uncertainty than traditional laboratory analyses; however, it has certain advantages (cost, time, waste) [24]. The results confirm the predictive potential of Vis–NIR spectra for SOC [64], as it has a direct spectral response related to the good indices obtained for Vis–NIR estimation [65].

This study compared and analyzed the performance of the RF–SVR model in predicting SOC. The results indicate that the RF–SVR and RF–XGBoost models outperform other models with extensive soil spectral databases in estimating SOC. The RF–SVR and RF–XGBoost models achieved the best accuracy in SOC estimation, with an R² of 0.85, an RMSE of 0.30 g/kg, and an R² of 0.86 and an RMSE of 0.09. Compared with other regression models, RF–SVR and RF–XGBoost offer wider applicability and superior performance, enabling SOC estimation across important soil spectral libraries [66]. This improvement suggests that gradient-boosting techniques benefit substantially from the reduction in input dimensionality and the elimination of noisy or redundant variables. Recent studies have shown that applying feature-selection algorithms prior to model training enhances predictive performance by reducing multicollinearity and retaining only the most informative spectral features [67,68]. Similarly, the superior performance of gradient-boosting models such as XGBoost in SOC estimation has been consistently reported, demonstrating higher accuracy and robustness compared with traditional machine learning approaches [69]. The increase in RDP values for the hybrid models also indicates greater robustness and practical applicability for soil SOC assessment. Overall, these findings demonstrate that model stacking and feature optimization not only outperform traditional single-model approaches but also provide a more reliable framework for handling complex spectral datasets in SOC estimation.

The application of the first derivative Savitsky–Golay preprocessing significantly boosted the performance metrics in all the evaluated models. Thus, the RF–SVR and RF–XGBoost models are better at predicting carbon levels from absorbance data compared to the model proposed in “Estimation of SOC in arid agricultural fields based on hyperspectral satellite images” [70] whose Ridge Regression model based on hyperspectral satellite images for carbon level estimation obtained an R² of 0.6658 and an RMSE of 0.1206, as well as the RF model of “Enhancing SOC estimation accuracy: Integrating spatial vegetation dynamics and temporal analysis with Sentinel 2 imagery” where an R² of 0.8 and an RMSE of 0.33 were obtained.

4. Conclusions

The integration of spectral preprocessing, variable selection, and hybrid machine learning models (RF–SVR and RF–XGBoost) enabled highly accurate predictions of soil organic carbon (SOC). In particular, the application of the Savitsky–Golay first derivative proved critical for enhancing spectral features and improving model performance, highlighting the importance of appropriate preprocessing in Vis–NIR-based SOC estimation.

The sequential RF–SVR and RF–XGBoost models outperformed individual models, indicating that carbon prediction based on absorbance benefits from tools capable of handling nonlinear relationships and reducing noise. Spectral band selection with RF increased efficiency by reducing dimensionality and retaining only the most relevant variables.

The results confirm that Vis–NIR spectral information is a reliable predictor of SOC and provides a fast, economical, and non-destructive alternative to traditional laboratory analyses, although it still does not match their precision. Therefore, spectroscopy should be considered a complementary technique to support soil assessment.

Field limitations include extreme climatic variability and fertilizer use, which may alter absorbance. We recommend exploring additional deep learning models, new variable combinations, and more complex architectures. The selected spectral bands may be used to design more efficient sensors and to enhance soil monitoring programs and carbon sequestration studies.