Transforming the Supply Chain Operations of Electric Vehicles’ Batteries Using an Optimization Approach

Abstract

The increasing popularity of electric vehicles (EVs) as green alternatives to traditional internal combustion engine cars has highlighted the need for sustainable and environmentally friendly supply chain models. In particular, the handling of EV batteries, which are environmentally unfriendly and logistically critical due to their hazardous nature and short life cycle, requires a well-designed closed-loop supply chain (CLSC). This study proposes a new multi-objective optimization model of the CLSC, explicitly tailored to EV batteries under demand and return rate uncertainty. The proposed model incorporates three primary objectives that are typically in conflict with one another: minimizing the total cost, reducing carbon emissions throughout the entire supply chain network, and maximizing the recycling and reuse of batteries. The model employs a neutrosophic goal programming (NGP) methodology to address the uncertainties associated with demand and battery return quantities. The NGP model translates multiple objectives into non-monolithic goals with crisp aspiration levels (i.e., prescribed ideal levels for achieving the best of each goal) and thresholds that capture tolerances, thereby accounting for uncertainty. The efficiency of the proposed method is illustrated by a numerical example, solved using a IBM ILOG CPLEX Optimization Studio 22.1.2 solver. The findings demonstrate that the NGP can offer cost-effective, low-impact, and environmentally friendly solutions, thereby enhancing system robustness and flexibility to adapt to uncertainties. This study contributes to the emerging literature on sustainable operations research by developing a decision-making tool for EV-HV battery supply chain management. It also offers relevant suggestions for policymakers and industrialists who seek to co-optimize economic benefits, ecological sustainability, and logical feasibility in the emerging green society.

1. Introduction

Factors such as environmental issues, technological developments, and policies to mitigate greenhouse gas emissions have triggered a significant transformation in the global automotive industry [1,2]. Electric vehicles, as a sustainable alternative to conventional internal combustion engine vehicles, have provided tremendous relief in reducing greenhouse gas emissions and dependence on fossil-based fuels [3,4]. The global EV stock exceeded 35 million vehicles and is expected to reach over 350 million by 2030, which is driven by government incentives, technological advancements, and consumer demand for environmentally friendly transportation [5]. Although EVs are cleaner in terms of tailpipe emissions, their environmental load is to a large extent moved towards the upstream supply chain, especially battery manufacturing and EOL (end-of-life) treatment [6,7]. Lithium-ion batteries (LIBs)—which are the dominant technology in EVs—are significantly dependent on limited and non-renewable resources (such as lithium, cobalt, and nickel) [8]. However, the improper management of these batteries poses substantial environmental hazards, including soil and water contamination, as well as the release of toxic gases [7,9,10].

The rapid increase in EV adoption has also resulted in a growing volume of batteries moving through production, usage, and end-of-life stages, creating significant challenges in material recovery, waste management, and environmental protection [11]. As this surge in battery circulation intensifies, there is an urgent need for supply chain structures that can handle used batteries responsibly and support sustainable resource utilization [6]. This requirement has led to greater emphasis on CLSCs, which integrate forward logistics with reverse logistics to facilitate collection, recycling, remanufacturing, and reuse [12]. A well-designed CLSC helps reduce dependence on virgin raw materials, minimizes environmental risks associated with improper disposal, and supports circular economy principles within the EV industry [13].

As such, the creation of CLSCs—i.e., a system that combines forward logistics (planning and distribution) with reverse logistics (returns and remanufacturing)—is key in driving sustainability, resource efficiency, and circular economy applications across the EV sector [14]. Figure 1 shows the CLSC model for EV batteries. It identifies four main stages: extraction of raw materials, battery manufacturing, the use phase of an EV, and recycling. The process focuses on the sustainability and revitalization of the production cycle, recycling materials to minimize waste and thereby reduce dependence on virgin resources. This model aligns with the environmentally friendly and circular economy concepts in the EV industry.

The CLSC is a logistics network in which supply chain and reverse logistics flows are also optimized to minimize waste, optimize resource recovery and reduce environmental impacts [14,15]. For EV battery-based blocks, the combination of uncertainties in consumer demand, returns on used batteries, and recycling yields, as well as different capacity levels of facilities, is required for CLSC systems [16]. Designing and operating these supply chains requires multi-objective optimization [17,18]. Firms are generally required to simultaneously minimize financial costs, environmental impacts (e.g., in terms of carbon emissions), and achieve high levels of reuse/recycling rates for all types of battery components [19]. However, these goals are contradictory, and a refined optimization is necessary to optimize and balance the trade-offs [12,19].

For example, to account for vague values in objective variables such as the newness and return of old batteries, traditional crisp models are insufficient. On the other hand, neutrosophic logic, developed by Smarandache [20], offers a robust mathematical tool for addressing indeterminacy and partial truth. A neutrosophic set is an extension and generalization of fuzzy set theory, in which every component element can be characterized by means of three interval sets for membership, non-membership, and indeterminacy [21]. This makes it applicable to real-world supply chains, in which data are typically incomplete, vague, or conflicting. In this paper, NGP is used to solve a multi-objective CLSC model of EV batteries under uncertain demand and return rates. The model jointly optimizes three crucial objectives:

• Minimizing total cost;
• Minimizing total carbon emissions across the supply chain network;
• Maximizing the rate of battery recycling and reuse.

The contributions of this study are threefold:

• First, a comprehensive CLSC network is established that encompasses battery manufacturers, distribution centers, retail zones, and recycling facilities.
• Second, neutrosophic sets are incorporated to represent uncertain and indeterminate parameters within the supply chain more realistically.
• Third, an NGP framework is formulated to balance multiple conflicting objectives under uncertainty, and system performance is evaluated through a detailed numerical illustration.

The increasing penetration of EVs has led to the need for a new supply chain discourse, which needs to be considered from a cradle-to-grave perspective [12]. Nevertheless, although sustainability logistics and CLSCs are receiving increasing research attention in the context of EV batteries, some relevant gaps remain, especially in the multi-objective optimization solution of real-world uncertainties. Although many papers focus on either a forward or reverse supply chain for battery logistics, few works have presented an integrated closed-loop model that addresses EV batteries [22]. The complex battery supply chain and the potential flows between production, distribution, collection, and recycling are often oversimplified or overlooked [23]. The input parameters of CLSC models (e.g., EV battery demand, used battery return rate, recycling yield, and carbon emissions) are generally uncertain, vague, or unknown, resulting in imprecision.

However, most models in the literature are deterministic, probabilistic, or fuzzy, which fail to adequately address indeterminacy. Neutrosophic theory has the capacity to deal with uncertainty, vagueness, and inconsistency effectively; however, it is still not fully utilized in CLSC optimization [24]. The optimization models concerning the EV battery supply chain in existing research take a weighted sum or E-constraint approach for multi-objective purposes [25]. These methods require trade-off weights/parameters, which are usually not convenient [22,25]. The concept of NGP provides decision-makers with the opportunity to define flexible aspiration levels and manage fuzziness within a systematic framework [26]. It has been clarified that economic cost, environmental impact (e.g., CO₂ emissions), and resource recovery should be considered together for studies on EV battery CLSCs [27,28,29,30,31]. A trade-off solution is necessary to consider these conflicting goals and uncertainties in sustainable supply chain decisions.

Despite the growing body of research on EV battery logistics and CLSCs, several critical gaps remain unaddressed. First, most existing studies examine forward and reverse flows separately and rarely develop an integrated CLSC model that captures the full lifecycle of EV batteries from production and distribution to collection, recycling, and reintegration. This fragmented treatment prevents a holistic assessment of system-wide trade-offs. Second, although uncertainties related to demand, return rates, recycling yields, and emissions are inherent to real EV operations, the majority of models rely on deterministic, probabilistic, or conventional fuzzy approaches that do not adequately capture indeterminacy and conflicting information. Third, multi-objective formulations in the current literature primarily depend on weighted-sum or ε-constraint techniques, which require predefined trade-off weights and often fail to reflect realistic decision-maker preferences. Finally, very few studies propose an optimization framework that simultaneously minimizes costs and emissions while maximizing recycling efficiency under data uncertainty.

To address the identified research gaps, this study develops a comprehensive model and solution framework by making the following contributions: An overall CLSC network is considered, as depicted in Figure 1, with respect to the battery that includes the whole lifecycle of battery from production, distribution, customer demand satisfaction and collection of used batteries to recycling/remanufacturing processes. The realistic model is suitable for both academic analysis and industrial applications. Neutrosophic theory is employed in the study to address uncertain and imprecise parameters, such as demand, return rates, transportation costs, and recycling efficiency. This enables one to model real-life supply chain scenarios more accurately, where complete information is not available. Using an NGP method, a trilevel optimization model is solved to minimize costs and carbon emissions while also maximizing battery recycling. The NGP approach enables decision-makers to establish aspiration levels with tolerances by considering the degree of satisfaction and dissatisfaction. By jointly considering economic and environmental objectives, the model can support decisions that align with the goals of a circular economy and sustainable development targets.

The rest of this paper is structured as follows. Section 2 presents a comprehensive literature review on the scope of CLSCs in the EV industry, with a focus on aspects of mathematical programming and decision-making models for EV operation. The mathematical model is presented in Section 3. Section 4 explains the proposed approach for solving the model. A numerical example is presented in Section 5 to illustrate the feasibility and efficiency of the proposed method. Discussion of the proposed study is also reported in Section 6. Finally, Section 7 concludes the paper by presenting the overall conclusions and limitations of this work, followed by a discussion on the future scope of study.

2. Literature Review

In this section, a comprehensive review of the literature on CLSCs, with a special focus on those in the EV industry, is provided. The review emphasizes the application of mathematical programming and decision-making tools in EV-related operations. This rationale presents itself as an effort to raise awareness of the current level of research. It directs the reader’s attention to some missing parts, adding a basis for the pending study.

2.1. Electric Vehicle Closed-Loop Supply Chains

The CLSC is a combination of forward and reverse logistics, which enables material recovery, remanufacturing, and reuse [32]. This is particularly critical in the EV field as LIBs are of great economic and environmental worth. Zhang et al. [33] emphasized the importance of CLSCs in reducing the environmental burden associated with automobile parts through recycling and remanufacturing. Xiao et al. [34] proposed a CLSC system model for LIBs in EVs, emphasizing the importance of integrating collection and recycling to improve sustainability. They proposed a mixed-integer linear framework that integrates production planning and end-of-life (EOL) battery returns, considering both environmental and cost trade-offs. They also integrated a CLSC model with consumer behavior and government incentives, which illustrates the impact of policy instruments on the level of recycling.

Wang et al. [24] proposed a stochastic optimization method to control the flow of EV batteries, considering uncertain demand, which leads to more certain supply chain decisions. Pratap et al. [35] formulated a dynamic programming model to account for battery degradation, enabling improved planning of reuse and recycling stages. Mu et al. [21] proposed a multi-objective optimization model that balances profitability with reductions in carbon emissions during the recycling phase of EV batteries. Their model considers trade-offs between economic and environmental objectives, offering solutions that align business goals with sustainable practices in CLSCs. Zhang et al. [33] and Xiao et al. [34] investigated decentralized decision-making within CLSCs and its impact on collaboration and cost-sharing among key stakeholders in the supply chain. They demonstrated that while decentralization can lead to operational inefficiencies, strategic coordination mechanisms can mitigate adverse effects and enhance overall system performance.

Zhu et al. [36] and Ali et al. [37] emphasized the use of real-time data and battery health monitoring technologies to optimize the timing of collection and recycling activities. This study demonstrates that integrating IoT-enabled tracking enhances decision-making precision, reduces lead times, and improves resource recovery efficiency. Fussone et al. [38] developed an agent-based model to simulate complex interactions among manufacturers, recyclers, and consumers within CLSCs. The model highlights emergent behaviors and network dynamics, providing valuable insights into how individual decisions aggregate to influence system-wide sustainability outcomes. They applied GIS-based methods to optimize the location of collection centers for used EV batteries, improving logistical efficiency. They also studied remanufacturing practices, highlighting the regional differences and scalability challenges in CLSC adoption.

Several recent studies continue to expand the theoretical foundations of CLSCs in the EV sector. Gorji et al. [39] developed a game-theoretic model to analyze the strategic interactions between EV manufacturers and recyclers under government subsidy schemes. Their findings offer insights into how collaborative and competitive behaviors influence the efficiency of reverse logistics. Al-Ghaili et al. [3] and Wu et al. [40] proposed a system dynamics approach to model the long-term evolution of battery reuse and recycling systems. Their work contributes theoretically by showing how feedback loops between environmental awareness, policy, and technological innovation influence CLSC outcomes. Song et al. [41] integrated behavioral economics into CLSC modeling, highlighting how consumer perceptions and bounded rationality influence participation in battery return programs. They used the real options theory to assess investment opportunities in battery recycling infrastructure. Its contribution, from a financial valuation perspective, helps supply chain parties better consider risks and returns. These works not only widen the methodological toolkit of CLSC research but also enhance its theoretical grounding, combining economic rationale, systems theory, and behavioral insights. Together, they form the basis for developing resilient, responsive, and circular supply chains that suit the complex life cycle of EV batteries. Despite these advances, most existing models are still unable to capture the entire lifespan of EV batteries under operational uncertainties. There is still an urgent need for agile, adaptive CLSC systems to quickly adapt to emerging changes in the market, technology, and policy.

2.2. Mathematical Programming and Decision Making in EVs

Neutrosophic goal programming is a generalization of classical goal programming and fuzzy logic settings, which allow the concept of indeterminacy to be addressed, in addition to the concepts of true and false. This approach, which has garnered attention in complex decision-making problems, particularly within uncertain, imprecise, and conflicting frameworks, is also relevant to the EV context. Smarandache [20] proposed the neutrosophic theory of sets, an extension of fuzzy and classical sets, which introduces degrees of certainty and falsity. This is pioneering work that lays the potential for a new class of decision-making aids to accommodate high levels of uncertainty. Ye [42] and Smarandache et al. [43] introduced the concept of neutrosophic sets and applied it to multi-attribute decision-making, illustrating that neutrosophic numbers offer greater flexibility in expressing uncertainty. This is even more applicable in EVs, where data is frequently incomplete or ambiguous. Mishra et al. [44] employed the concept of a single-valued neutrosophic set to select suppliers in a green supply chain environment. Their model was practical from both qualitative and quantitative perspectives; therefore, it could be effectively applied to the evaluation of EV suppliers.

Nafei et al. [45] proposed a neutrosophic AHP-TOPSIS hybrid model to choose sustainable battery suppliers. Incorporating neutrosophic logic enabled them to consider expert indeterminacy in sustainability assessment. They adopted neutrosophic VIKOR to rank EV charging station locations, where evaluating criteria (such as demand, accessibility, and environmental friendliness) are based on uncertain knowledge. Kuo et al. [46] developed a neutrosophic DEMATEL approach to recognize and evaluate the interrelations of determining barriers for EV roll-out. The study brought to attention the uncertainty in stakeholders’ views as well as increased regulation. They proposed the model of interval-valued neutrosophic decision-making for preference ration, which has been used to model consumer behavior, where these preferences are uncertain. Rehman & Shakeel Sadiq Jajja [47] also presented an NGP model to maximize the resilience of the EV supply chain during pandemics, considering transportation disruption and demand deformities. They further utilized neutrosophic logic in policy decisions to allocate government subsidies for EVs, taking into account conflicting opinions from private and administrative actors.

According to the literature review, several limitations exist in the formulation and application of CLSCs and decision-making models for the EV industry. The first limitation of the studies that focus on these approaches is that they have not incorporated reverse logistics in the framework for planning production and distribution when facing uncertainty. Although the forward logistics and recycling components are commonly handled as isolated processes, very few integrated models that take into account the entire lifecycle of EV batteries (“cradle to grave”, i.e., from production to reuse and end of life) have been proposed, particularly considering dynamic demand and uncertain return rates. Additionally, most existing models fail to account for the uncertainty inherent in actual EV battery operations. Variabilities in return rates, recycling efficiencies and consumer behavior are often not accurately simulated or overlooked. To date, the existing literature on optimization approaches, such as the fuzzy approach and stochastic programming, has not accurately addressed the vague and contradictory nature of data in EVSCs. The application of neutrosophic sets for supply chain optimization models is limited. Although neutrosophic logic offers a general and unified approach to uncertainty by considering degrees of truth, indeterminacy, and falsity, it has been applied to fragmented decision-making problems, such as supplier selection or infrastructure site location, to date. Its potential is not yet fully exploited in complex system-level modeling problems, such as CLSC’s optimal operation or lifecycle analysis.

Moreover, the combination of multi-objective goal programming and neutrosophic logic is unexplored, especially in the context of EV networks, which require balancing among cost, sustainability, and operational efficiency. The majority of existing neutrosophic decision models are static and context-dependent, lacking the ability to dynamically respond to changes, which is necessary when planning under real-time conditions in a rapidly changing environment. Finally, few studies integrate stakeholders’ dynamics and policy feedback using the neutrosophic approach, considering that regulatory assistance, market facilitation, or the public’s attitudes can significantly impact the response rate of EVs. Despite these limitations, the current literature provides valuable insights for theory and practice in EV purchasing decision-making and sustainable supply chains. Several research studies have contributed to the concept of CLSCs, which combines battery reuse, remanufacturing, and recycling for EV batteries, taking into account their specific characteristics. These models highlight the importance of resource recovery in achieving effective environmental impact reduction and enhancing cost-effectiveness with EVs.

2.3. Research Gaps

Although existing studies provide valuable insights into EV battery logistics, several research gaps remain that constrain the development of robust and sustainable CLSC models for the EV industry. First, most prior works examine forward logistics and reverse logistics separately, without integrating them into a unified closed-loop framework that captures the complete battery lifecycle from manufacturing and distribution to collection, recycling, and reintegration [48]. This fragmentation limits the ability to evaluate system-wide trade-offs and restricts the practical applicability of earlier models [49]. Second, the majority of existing optimization approaches are deterministic or rely solely on probabilistic or fuzzy modeling [50]. These methods are often insufficient for capturing the high levels of vagueness, inconsistency, and incomplete information that characterize real-world EV operations [51]. Although neutrosophic sets offer a more flexible representation of uncertainty by incorporating truth, indeterminacy, and falsity components, their application in EV supply chain optimization remains limited, typically confined to isolated decision-making problems, such as supplier selection or site allocation [52].

Third, current multi-objective models often rely on weighted sum techniques or ε-constraint methods, which necessitate predefined weights or trade-off parameters. Such approaches may not accurately reflect actual decision-making preferences and often struggle to accommodate conflicting objectives in the face of uncertainty [53]. There is a need for a more adaptive and systematic framework that simultaneously addresses cost efficiency, environmental impact, and recycling performance while incorporating uncertain parameters [54]. Finally, few studies examine the practical implications of uncertainty on EV battery recovery systems, particularly in emerging economies. Variations in consumer return behavior, recycling efficiencies, transportation conditions, and policy interventions are not adequately represented in existing models. This lack of contextualized analysis limits the relevance of current literature for countries with rapidly expanding EV markets and evolving regulatory structures. These research gaps underscore the need for an integrated, uncertainty-aware optimization framework that holistically addresses economic, environmental, and operational objectives in EV battery CLSCs. The present study addresses this need by developing an NGP–based multi-objective model that captures the inherent complexities of EV battery supply chains in uncertain environments.

3. Mathematical Model

The accelerating adoption of EVs has underscored the importance and urgency of a stable and secure supply chain for lithium-ion batteries (LIBs). This supply chain must address the efficient distribution of batteries, as well as the collection, recycling, and reuse of spent units, to promote a circular economy and minimize environmental impacts. The design of such a CLSC involves multiple objectives and complex interdependencies among facilities, transportation links, demand points, and collection centers—often under conditions of uncertainty. This research proposes a multi-objective optimization model for an EV battery CLSC network, comprising the three principal, contradicting objectives:

• Minimizing total cost: This includes costs associated with production costs from plants to distribution centers, distribution from distribution centers to retail demand zones, reverse logistics from retail zones to recycling centers, and recycling costs at recycling centers.
• Minimizing total carbon emissions: Carbon emissions generated at various supply chain stages—production, transportation, and recycling—are quantified and minimized to meet sustainability goals and global carbon reduction targets.
• Maximizing the battery recycling and reuse rate: This objective promotes the environmental and economic benefits of reintroducing used battery materials or modules back into the production cycle, thereby minimizing landfill waste and reducing dependence on raw materials.

These objectives are subject to various operational constraints, such as facility capacities, demand satisfaction, return rates of used batteries, and resource limitations. The notations of the mathematical model are represented in

Table 1. Notations of the mathematical model.

Indices
$i\in I$	Set of battery manufacturing plants
$j\in J$	Set of distribution centers
$k\in K$	Set of retail demand zones
$l\in L$	Set of recycling centers
$t\in T$	Set of time periods
Parameters
${\tilde{D}}_{kt}$	Demand for EV batteries at retail zone $k$ in time $t$
${\tilde{R}}_{kt}$	Returned batteries from zone $k$ in time $t$
$C_{ij}^p$	Unit production and transport cost from plant $i$ to distribution centers $j$
$C_{jk}^d$	Unit cost from distribution centers $j$ to zone $k$
$C_{kl}^r$	Unit cost from zone $k$ to recycler $l$
$C_{ecl}^r$	Recycling cost per unit at center $l$
$E_{ij}^p$	Emissions from plant $i$ to distribution centers $j$
$E_{jk}^d$	Emissions from distribution centers $j$ to zone $k$
$E_{kl}^r$	Emissions from zone $k$ to recycler $l$
Decision variables
$x_{ij}^t$	Number of batteries shipped from plant $i$ to distribution centers $j$ at time $t$
$y_{jk}^t$	Number of batteries shipped from distribution centers $j$ to retail zone $k$ at time $t$
$z_{kl}^t$	Number of returned batteries shipped from zone $k$ to recycler $l$ at time $t$
$r_l^t$	Number of batteries recycled at center $l$ at time $t$

.

The mathematical model of the proposed problem is represented as follows:

$$Min Z_1=\sum _t\left(\sum _{ij}{C}_{ij}^p·x_{ij}^t+\sum _{ij}{C}_{jk}^d·y_{jk}^t+\sum _{ij}{C}_{kl}^r·z_{kl}^t+\sum _{ij}{C}_{ecl}^r·r_l^t\right)$$

(1)

Objective 1 presented in Equation (1) aims to minimize the total cost associated with the EV battery supply chain over the planning horizon. This includes four major cost components. First, it accounts for the production costs incurred when batteries are manufactured at production plants and shipped to distribution centers. Second, it includes the distribution costs of transporting batteries from distribution centers to retail demand zones to meet customer requirements. Third, the model considers reverse logistics costs, which arise from collecting and transporting used or returned batteries from retail zones back to designated recycling centers. Finally, it incorporates the recycling costs associated with processing the returned batteries at these centers. The goal is to optimize the entire supply chain network by minimizing these combined costs while ensuring efficient battery flow and sustainable operations.

$$Min Z_2=\sum _t\left(\sum _{ij}{E}_{ij}^p·x_{ij}^t+\sum _{ij}{E}_{jk}^d·y_{jk}^t+\sum _{ij}{E}_{kl}^r·z_{kl}^t\right)$$

(2)

Objective 2 presented in Equation (2) aims to minimize the total carbon emissions generated throughout the EV battery supply chain over the planning horizon. It focuses on reducing environmental impact by accounting for emissions produced at different stages of the logistics network. Specifically, it includes the emissions generated during the transportation of batteries from manufacturing plants to distribution centers, as well as those produced while delivering batteries from distribution centers to retail demand zones. Additionally, it considers emissions arising from reverse logistics operations, where used or returned batteries are transported from retail zones to recycling centers

$$Max Z_3=\sum _t\left(\sum _k{\tilde{R}}_{kt}-\sum _l{r}_l^t\right)$$

(3)

Objective 3, as presented in Equation (3), aims to maximize the reuse and recycling rate of EV batteries throughout the supply chain during the planning horizon. It does so by focusing on the difference between the total number of returned batteries from retail demand zones and the actual number of batteries that are recycled at recycling centers.

Subject to:

$$\sum _j{y}_{jk}^t\le {\tilde{D}}_{kt} \forall k,t$$

(4)

Constraint 4 ensures that the total number of batteries delivered from all distribution centers to a retail demand zone does not exceed the neutrosophic demand at that zone in a given time period.

$$\sum _l{z}_{kl}^t={\tilde{R}}_{kt} \forall k,t$$

(5)

Constraint 5 ensures that the total number of returned batteries from a retail zone to all recycling centers equals the neutrosophic number of returns from that zone in each time period, thereby maintaining balance in reverse logistics.

$$\sum _k{z}_{kl}^t\ge r_l^t \forall l,t$$

(6)

Constraint 6 ensures that the number of batteries recycled at any recycling center does not exceed the total number of batteries returned from all retail zones during a given period.

$$\sum _i{x}_{ij}^t\ge \sum _k{y}_{jk}^t \forall j,t$$

(7)

Constraint 7 maintains supply chain consistency by requiring that the total number of batteries shipped from manufacturing plants to a distribution center is at least equal to the total number of batteries shipped from that distribution center to all retail demand zones in each time period.

$$x_{ij}^t, y_{jk}^t, z_{kl}^t,r_l^t\ge 0.$$

(8)

Constraint 8 provides capacity limitations necessary for maintaining feasibility within the CLSC network.

4. Methodology

This study adopts an organized approach to provide a sustainable decision-making framework for EV battery CLSCs in uncertain and complex environments. The methodology is based on the NGP concept, which enables addressing several conflicting objectives and also capturing uncertainty, vagueness, and indeterminacy in a supply chain network. An NGP approach is proposed for the mathematical model of a multi-objective CLSC system for EV. This type of modeling follows on from Zimmermann’s [55] neutrosophic extension. The proposed neutrosophic compromise method presents a novel approach for addressing uncertainties in optimization. It seeks optimal values of three features of a neutrosophic decision: the level of truth (satisfaction), the level of falsity (dissatisfaction), and the level of indeterminacy (partial satisfaction).

Bellman and Zadeh [56] considered three essential procedures for determining fuzzy sets: fuzzy decision-making, fuzzy goal-setting, and fuzzy constraints. This approach has been widely used in decision-making problems with uncertain environments. Let $f_d,{ f}_g,$ and $f_c$ be the fuzzy decisions, goals, and constraints of the problem. This new approach is based on these fundamental notions to enhance the decision-making process when indeterminacy is present. The fuzzy solution for the problem is formulated as:

$$f_d=f_g\cap f_c$$

(9)

Accordingly, the neutrosophic decision set $(f_d{)}^N$, which encapsulates the system’s objectives and constraints expressed under a neutrosophic environment, can be formulated as follows:

$${\left(f_d\right)}^N=\left(\bigcap _{t=1}^T{\left(f_g\right)}_k\right)\left(\bigcap _{i=1}^m{\left(f_c\right)}_i\right)=(x,{\phi }_{f_d}\left(x\right),{\theta }_{f_d}\left(x\right),{\varnothing }_{f_d}\left(x\right))$$

(10)

where

$$\begin{array}{c}{\phi }_{f_d}\left(x\right)=min\left\{\begin{array}{c}{\phi }_{f_g}^1,{\phi }_{f_g}^2,\dots ., {\phi }_{f_g}^t\\ {\phi }_{f_c}^1,{\phi }_{f_c}^2,\dots ., {\phi }_{f_c}^t\end{array}\right. \forall x\in X\\ {\theta }_{f_d}\left(x\right)=min\left\{\begin{array}{c}{\theta }_{f_g}^1,{\theta }_{f_g}^2,\dots ., {\theta }_{f_g}^t\\ {\theta }_{f_c}^1,{\theta }_{f_c}^2,\dots ., {\theta }_{f_c}^t\end{array}\right. \forall x\in X\\ {\varnothing }_{f_d}\left(x\right)=min\left\{\begin{array}{c}{\varnothing }_{f_g}^1,{\varnothing }_{f_g}^2,\dots ., {\varnothing }_{f_g}^t\\ {\varnothing }_{f_c}^1,{\varnothing }_{f_c}^2,\dots ., {\varnothing }_{f_c}^t\end{array}\right. \forall x\in X\end{array}$$

(11)

where ${\phi }_{f_d}\left(x\right), {\theta }_{f_d}\left(x\right), \mathrm{a}\mathrm{n}\mathrm{d} {\varnothing }_{f_d}\left(x\right)$ represent the truth membership function, indeterminacy membership function, and falsity membership function of the neutrosophic decision set.

To establish the lower and upper bounds required for constructing the membership functions of the multi-objective CLSC model for EV batteries, each objective is first optimized individually. Let $Z_t^L$ and $Z_t^U$ denote the lower and upper bounds of the $t^{th}$ objective, respectively. These bounds are obtained by solving each objective function separately using an appropriate optimization algorithm, subject to all model constraints. This process yields a set of $T$ compromise solutions, $x_1,x_2, \dots ,{ x}_T$. Each solution is then substituted back into all objective functions to evaluate and record the corresponding minimum and maximum values, which collectively define the bounds for each objective as follows:

$$\begin{array}{c}{Z}_t^L=\mathrm{m}\mathrm{i}\mathrm{n}\{{Z_t\left(x\right)\}}_{t=1}^T\\ Z_t^U=\mathrm{m}\mathrm{a}\mathrm{x}\{{Z_t\left(x\right)\}}_{t=1}^T\end{array}$$

(12)

The bounds of the proposed problem under the neutrosophic environment are obtained as follows:

$$Z_t^L\left(\phi \right)=Z_t^L{Z}_t^U\left(\phi \right)=Z_t^U$$

(13)

$$Z_t^L\left(\theta \right)=Z_t^L\left(\theta \right),Z_t^U\left(\theta \right)=Z_t^U\left(\phi \right)+s_t(Z_t^U\left(\phi \right)-Z_t^L\left(\phi \right))$$

(14)

$$Z_t^L\left(\varnothing \right)=Z_t^L\left(\phi \right)+t_t(Z_t^U\left(\phi \right)-Z_t^L\left(\phi \right)), Z_t^U\left(\varnothing \right)=Z_t^U\left(\phi \right)$$

(15)

where $t_t$ and $s_t$ are predefined real parameters within the interval $[0,1]$. Using these bounds, the corresponding membership functions for the proposed problem can be formulated as follows:

$${\phi }_t\left(Z_t\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_t-Z_t^L\left(\phi \right)}{{Z_t^U\left(\phi \right)-Z}_t^L\left(\phi \right)}}\\ 0,\end{array}\right. \begin{array}{c}if Z_t\left(x\right)<Z_t^L\left(\phi \right)\\ if Z_t^L\left(\phi \right)\le Z_t\left(x\right)\le Z_t^U\left(\phi \right)\\ if Z_t\left(x\right)>Z_t^U\left(\phi \right)\end{array}$$

(16)

$${\theta }_t\left(Z_t\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_t-Z_t^L\left(\theta \right)}{{Z_t^U\left(\theta \right)-Z}_t^L\left(\theta \right)}}\\ 0,\end{array}\right.\begin{array}{c}if Z_t\left(x\right)<Z_t^L\left(\theta \right)\\ if Z_t^L\left(\theta \right)\le Z_t\left(x\right)\le Z_t^U\left(\theta \right)\\ if Z_t\left(x\right)>Z_t^U\left(\theta \right)\end{array}$$

(17)

$${\varnothing }_t\left(Z_t\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_t^U\left(\varnothing \right)-Z_t}{{Z_t^U\left(\varnothing \right)-Z}_t^L\left(\varnothing \right)}}\\ 0,\end{array}\right.\begin{array}{c}if Z_t\left(x\right)<Z_t^L\left(\varnothing \right)\\ if Z_t^L\left(\varnothing \right)\le Z_t\left(x\right)\le Z_t^U\left(\varnothing \right)\\ if Z_t\left(x\right)>Z_t^U\left(\varnothing \right)\end{array}$$

(18)

In the proposed problem, $Z_t^U(\ast )\ne Z_t^L(\ast )$ for all objectives. If, for any membership, $Z_t^U(\ast )=Z_t^L(\ast )$, then the corresponding membership value is assigned as 1. The approach suggested by Bellman and Zadeh [56] is applied through Equations (16)–(18) in this study. Accordingly, the neutrosophic optimization model for CLSCs of EV batteries is formulated as follows:

$$\begin{array}{c}{\displaystyle Max Min\sum _{t=1,2\dots T}{\phi }_t\left(\sum _t\left(\sum _{ij}{C}_{ij}^p·x_{ij}^t+\sum _{ij}{C}_{jk}^d·y_{jk}^t+\sum _{ij}{C}_{kl}^r·z_{kl}^t+\sum _{ij}{C}_{ecl}^r·r_l^t\right)\right)}\\ Max Min{\displaystyle \sum _{t=1,2\dots T}{\theta }_t\left(\sum _t\left(\sum _{ij}{E}_{ij}^p·x_{ij}^t+\sum _{ij}{E}_{jk}^d·y_{jk}^t+\sum _{ij}{E}_{kl}^r·z_{kl}^t\right)\right)}\\ Max Min{\displaystyle \sum _{t=1,2\dots T}{\varnothing }_t\left(\sum _t\left(\sum _k{\tilde{R}}_{kt}-\sum _l{r}_l^t\right)\right)}\\ \mathrm{Subject} \mathrm{to}:\hfill \\ {\displaystyle \sum _j{y}_{jk}^t}\le {\tilde{D}}_{kt}, \forall k,t\\ {\displaystyle \sum _l{z}_{kl}^t={\tilde{R}}_{kt}, \forall k,t }\\ {\displaystyle \sum _k{z}_{kl}^t\ge r_l^t, \forall l,t }\\ {\displaystyle \sum _i{x}_{ij}^t\ge \sum _k{y}_{jk}^t, \forall j,t }\\ {\displaystyle x_{ij}^t, y_{jk}^t, z_{kl}^t,r_l^t\ge 0.}\end{array}$$

(19)

The auxiliary parameters $\zeta$, $\eta$, and $\delta$ are introduced to transform neutrosophic values into workable crisp intervals for optimization. Parameter $\zeta$ captures the degree of truth (T), $\eta$ represents the degree of indeterminacy (I), and $\delta$ reflects the degree of falsity (F) associated with a neutrosophic number. These parameters help quantify the decision-maker’s confidence levels within the neutrosophic environment. Equation (20) can be represented as follows:

$$\begin{array}{c}Max \zeta , Max \eta , Min \delta \\ {\phi }_{Z_t}\left(x\right)\ge \zeta , {\theta }_{Z_t}\left(x\right)\ge \eta , {\varnothing }_{Z_t}\left(x\right)\ge \delta \\ \mathrm{Subject} \mathrm{to}:\hfill \\ {\displaystyle \sum _j{y}_{jk}^t\le {\tilde{D}}_{kt}, \forall k,t}\\ {\displaystyle \sum _l{z}_{kl}^t={\tilde{R}}_{kt}, \forall k,t }\\ {\displaystyle \sum _k{z}_{kl}^t\ge r_l^t, \forall l,t }\\ {\displaystyle \sum _i{x}_{ij}^t\ge \sum _k{y}_{jk}^t, \forall j,t }\\ x_{ij}^t, y_{jk}^t, z_{kl}^t,r_l^t\ge 0, \zeta \ge \eta ,\zeta \ge \delta ,\zeta +\eta +\delta \le 3,\zeta ,\eta ,\delta \in \left[0,1\right].\end{array}$$

(20)

The mathematical formulation given in Equation (21) can be expressed as follows:

$$\begin{array}{c}Max \zeta -\delta +\eta \\ \mathrm{Subject} \mathrm{to}:\\ {\displaystyle \sum _t\left(\sum _{ij}{C}_{ij}^p·x_{ij}^t+\sum _{ij}{C}_{jk}^d·y_{jk}^t+\sum _{ij}{C}_{kl}^r·z_{kl}^t+\sum _{ij}{C}_{ecl}^r·r_l^t\right)+\left({Z_t^U\left(\phi \right)-Z}_t^L\left(\phi \right)\right)\zeta \le Z_t^U\left(\phi \right)}\\ {\displaystyle \sum _t\left(\sum _{ij}{E}_{ij}^p·x_{ij}^t+\sum _{ij}{E}_{jk}^d·y_{jk}^t+\sum _{ij}{E}_{kl}^r·z_{kl}^t\right)+\left({Z_t^U\left(\theta \right)-Z}_t^L\left(\theta \right)\right)\eta \le Z_t^U\left(\theta \right)}\\ {\displaystyle \sum _t\left(\sum _k{\tilde{R}}_{kt}-\sum _l{r}_l^t\right)+\left({Z_t^U\left(\varnothing \right)-Z}_t^L\left(\varnothing \right)\right)\delta \le Z_t^U\left(\varnothing \right)}\\ {\displaystyle \sum _j{y}_{jk}^t\le {\tilde{D}}_{kt}, \forall k,t}\\ {\displaystyle \sum _l{z}_{kl}^t={\tilde{R}}_{kt}, \forall k,t }\\ {\displaystyle \sum _k{z}_{kl}^t\ge r_l^t, \forall l,t }\\ {\displaystyle \sum _i{x}_{ij}^t\ge \sum _k{y}_{jk}^t, \forall j,t }\\ x_{ij}^t, y_{jk}^t, z_{kl}^t,r_l^t\ge 0, \zeta \ge \eta ,\zeta \ge \delta ,\zeta +\eta +\delta \le 3,\zeta ,\eta ,\delta \in \left[0,1\right]·\end{array}$$

(21)

The mathematical formulation in Equation (22) can be reformulated as follows:

$$\begin{array}{c}Max \zeta -\delta +\eta \\ {\displaystyle \sum _t\left(\sum _{ij}{C}_{ij}^p·x_{ij}^t+\sum _{ij}{C}_{jk}^d·y_{jk}^t+\sum _{ij}{C}_{kl}^r·z_{kl}^t+\sum _{ij}{C}_{ecl}^r·r_l^t\right)+\left({Z_t^U\left(\phi \right)-Z}_t^L\left(\phi \right)\right)\zeta -Z_t^U\left(\phi \right)\le 0}\\ {\displaystyle \sum _t\left(\sum _{ij}{E}_{ij}^p·x_{ij}^t+\sum _{ij}{E}_{jk}^d·y_{jk}^t+\sum _{ij}{E}_{kl}^r·z_{kl}^t\right)+\left({Z_t^U\left(\theta \right)-Z}_t^L\left(\theta \right)\right)\eta -Z_t^U\left(\theta \right)\le 0}\\ {\displaystyle \sum _t\left(\sum _k{\tilde{R}}_{kt}-\sum _l{r}_l^t\right)+\left({Z_t^U\left(\varnothing \right)-Z}_t^L\left(\varnothing \right)\right)\delta -Z_t^U\left(\varnothing \right)\le 0}\\ {\displaystyle \sum _j{y}_{jk}^t\le {\tilde{D}}_{kt}, \forall k,t}\\ {\displaystyle \sum _l{z}_{kl}^t={\tilde{R}}_{kt}, \forall k,t }\\ {\displaystyle \sum _k{z}_{kl}^t\ge r_l^t, \forall l,t }\\ {\displaystyle \sum _i{x}_{ij}^t\ge \sum _k{y}_{jk}^t, \forall j,t }\\ {\displaystyle x_{ij}^t, y_{jk}^t, z_{kl}^t,r_l^t\ge 0, \zeta \ge \eta ,\zeta \ge \delta ,\zeta +\eta +\delta \le 3,\zeta ,\eta ,\delta \in \left[0,1\right]·}\end{array}$$

(22)

The approach is proposed for decision-making in sustainability supply chains, addressing uncertainty in a holistic, practical, and novel manner. It exploits the advantages of both goal programming and neutrosophic logic to develop a robust, sound, and implementable model in this context, specifically in the EV battery logistics domain.

5. Numerical Example

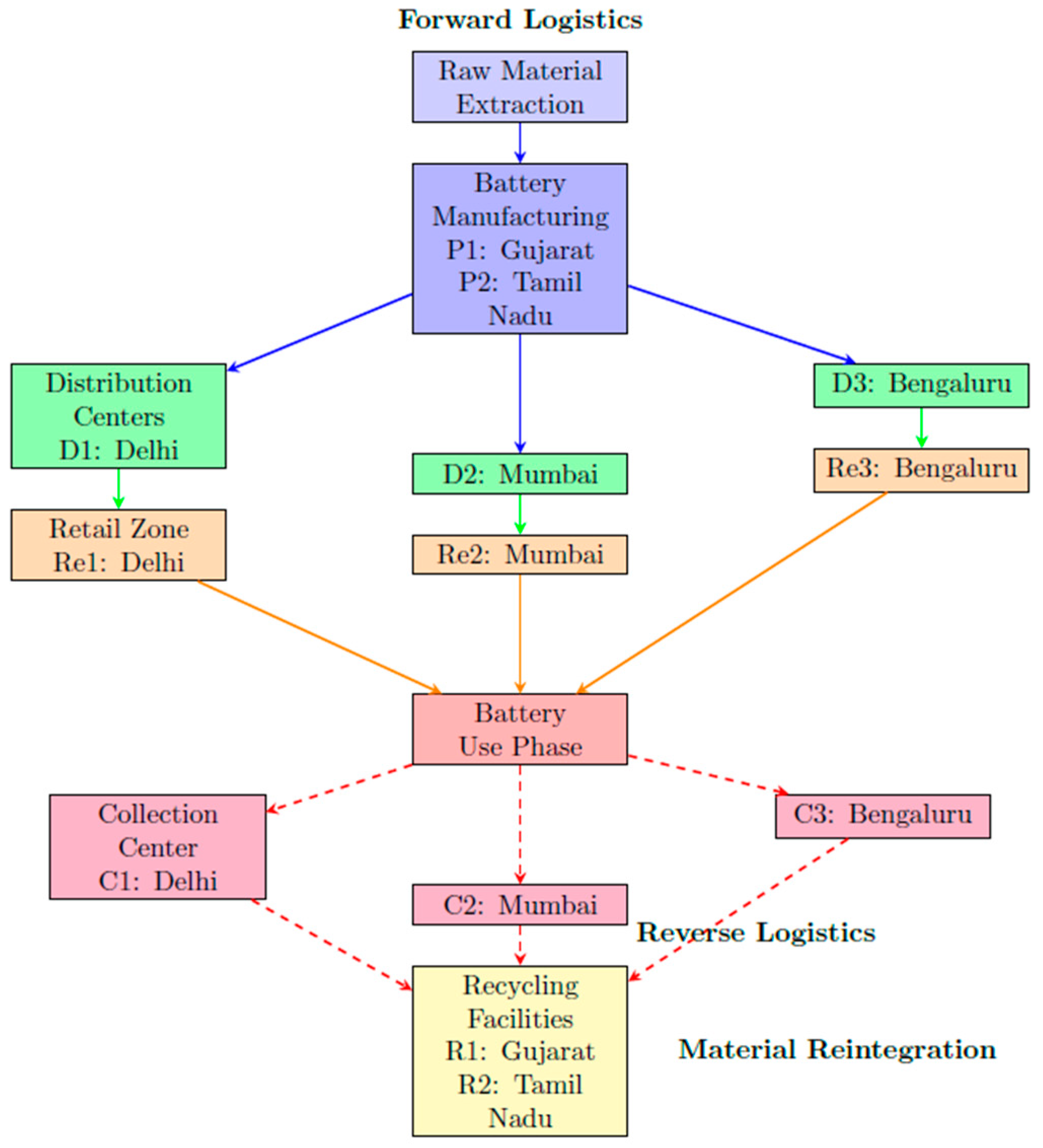
To demonstrate the applicability of the multi-objective CLSC model concept, a numerical example is formulated with an Indian EV battery supply chain. This case presents India’s strategic move towards electric mobility to achieve a low-carbon economy and decrease reliance on fossil fuels within 10 years, as enshrined in NITI Aayog [57]. The supply chain structure comprises connected subnetworks labeled appropriately for optimization purposes. There are two battery manufacturing plants, P1 in Gujarat and P2 in Tamil Nadu, which are represented by. At this point, the ‘distribution’ is carried out at several regional distribution centers that are indexed by where set, which includes D1 in Delhi, D2 in Mumbai and D3 in Bengaluru. These DCs cater to retail demand regions denoted by, which are the prominent EV marketplaces in Delhi (Re 1), Mumbai (Re 2) and Bengaluru (Re 3). C1, C2, and C3 are each linked to the respective retail zone for handling returned or used batteries, facilitating reverse logistics. Batteries collected from the collection centers are sent to recycling units, where R1 is located in Gujarat, and R2 is the recycling unit based in Tamil Nadu. The model is evaluated over a set of time periods represented by $t\in T$, which may denote months depending on the planning horizon.

As shown in Figure 2, the proposed CLSC network for EV batteries integrates forward logistics, spanning from raw material extraction to retail and use, with reverse logistics pathways that collect, recycle, and reintegrate battery materials into the production cycle. The numerical example used in this study is intentionally simplified to clearly demonstrate the mechanics and advantages of the NGP framework; however, it reflects typical parameter ranges observed in EV battery logistics, such as moderate return rates, transportation costs, and recycling efficiencies. In real industrial settings, data calibration presents several challenges due to fluctuations in consumer return behavior, variations in battery chemistry, and inconsistent reporting across collection centers and recyclers. Firms often face difficulties in estimating parameters such as return rate uncertainty, recycling yield variability, and carbon emission factors, which may require historical datasets, expert inputs, or probabilistic forecasting tools to improve accuracy. Despite these challenges, the proposed NGP model is fully scalable for large-scale industry applications, as its structure enables the integration of detailed multi-period demand, complex routing networks, and heterogeneous battery types. Modern optimization platforms can efficiently handle larger datasets and higher model granularity, enabling practitioners to calibrate the model progressively as higher-quality data becomes available. Thus, while the example is simplified for exposition, the framework is capable of supporting realistic, data-intensive EV battery supply chain planning in industrial environments.

Table 2. Closed-loop supply chain network structure.

Index	Entity Type	Code	Location
$i$	Battery Plant	P1	Gujarat
$i$	Battery Plant	P2	Tamil Nadu
$j$	Distribution Center	D1	Delhi
$j$	Distribution Center	D2	Mumbai
$j$	Distribution Center	D3	Bengaluru
$k$	Retail Demand Zone	Re1	Delhi
$k$	Retail Demand Zone	Re2	Mumbai
$k$	Retail Demand Zone	Re3	Bengaluru
$k$	Collection Center	C1	Delhi
$k$	Collection Center	C2	Mumbai
$k$	Collection Center	C3	Bengaluru
$l$	Recycling Facility	R1	Gujarat
$l$	Recycling Facility	R2	Tamil Nadu

outlines the structure of the EV battery CLSC used in the numerical illustration. It lists the specific locations and roles of facilities involved in production, distribution, retail demand, collection, and recycling, and maps them to the corresponding indices for mathematical modeling.

To ensure clarity in the numerical example, a consistent arithmetic and ordering framework is adopted for neutrosophic quantities. Each neutrosophic value is represented as a triplet $(T, I, F)$, where $T$, $I$, and $F$ denote the degrees of truth, indeterminacy, and falsity, respectively. Arithmetic operations such as addition and scalar multiplication are performed component-wise. At the same time, comparisons between neutrosophic quantities are based on their truth component and, when necessary, adjusted using the indeterminacy and falsity components to reflect uncertainty. This structured treatment ensures that neutrosophic values interact logically within the model, maintain internal consistency, and align with the decision-maker’s preferences regarding uncertainty and imprecision.

Table 3. Neutrosophic demand ${\tilde{D}}_{kt}$ at retail zones over time periods.

$\mathbf{Retail} \mathbf{Zone} \left(\mathit{k}\right)$	$\mathbf{Time} \mathbf{Period} (\mathit{t}=1)$	$\mathbf{Time} \mathbf{Period} (\mathit{t}=2)$
Delhi	(0.8, 0.1, 0.1)	(0.85, 0.1, 0.05)
Mumbai	(0.75, 0.15, 0.1)	(0.78, 0.12, 0.1)
Bengaluru	(0.9, 0.05, 0.05)	(0.92, 0.05, 0.03)

presents the neutrosophic demand for EV batteries at each retail demand zone $k \in K$ during time periods $t \in T$.

Table 4. Returned batteries ${\tilde{R}}_{kt}$ from retail zones.

$\mathbf{Retail} \mathbf{Zone} \mathit{k}$	$\mathbf{Time} \mathit{t}$	${\tilde{\mathit{R}}}_{\mathit{k}\mathit{t}}$
1 (Delhi)	1	(0.6, 0.3, 0.1)
2 (Mumbai)	1	(0.65, 0.25, 0.1)
3 (Bengaluru)	1	(0.7, 0.2, 0.1)
1 (Delhi)	2	(0.68, 0.25, 0.07)
2 (Mumbai)	2	(0.7, 0.2, 0.1)
3 (Bengaluru)	2	(0.72, 0.2, 0.08)

provides the number of used EV batteries returned from each retail demand zone $k$ during the time period $t$. It reflects the volume of reverse logistics to be handled by the supply chain. Each neutrosophic parameter $(T, I, F)$ was converted into a single crisp scalar prior to optimization using a two-step score mapping. First, the neutrosophic score $S=(T-F)/(1+I)$ is computed, which penalizes falsity and attenuates confidence when indeterminacy is high. Second, $S$ is normalized to $s=(S+1)/2\in [0,1]$ and mapped to the model-specific interval $\left[L, U\right]$ by $v=L+s\cdot (U-L)$. For proportions (e.g., return rates), $\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{s} [L, U]=[0, 1]$ are adopted, whereas for quantities (e.g., demand), empirically derived bounds based on available data or industry estimates are applied. The validity of the mapping is examined through (i) a sensitivity sweep over indeterminacy $I$, (ii) alternative mappings (score-only and weighted linear), and (iii) reporting a conservative and optimistic scenario. Example: The Delhi demand $(0.80, 0.10, 0.10)$ corresponds to $S = 0.636$ and $s$ = 0.818. With a nominal upper demand of 1000 units, this yields 818 units used in the solver.

Table 5. Unit production and transportation cost $C_{ij}^p$.

$\mathbf{Plant} \mathit{i}$$\to /\mathbf{DC} \mathit{j}$ ↓	D1 (Delhi)	D2 (Mumbai)	D3 (Bengaluru)
P1 (Gujarat)	12	10	15
P2 (Tamil Nadu)	20	18	8

Note: The arrow (→) indicates the origin (plant i), and the arrow (↓) indicates the destination (distribution center j). $C_{ij}^p$ denotes the unit production and transportation cost from plant iii to distribution center j.

presents the unit cost (in the appropriate currency units) for producing and transporting EV batteries from Plant $i$ to Distribution Center $j$.

Table 6. Unit distribution cost $C_{jk}^d$.

$\mathbf{Distribution} \mathbf{Center} \mathit{j}$$\to /\mathbf{Retail} \mathbf{zone} \mathit{k}$ ↓	Zone 1 (Delhi)	Zone 2 (Mumbai)	Zone 3 (Bengaluru)
$\mathrm{DC}1 (\mathrm{Delhi}, j=1$)	5	8	12
$\mathrm{DC}2 (\mathrm{Mumbai}, j=2$)	7	4	10
$\mathrm{DC}3 (\mathrm{Bengaluru}, j=3$)	9	6	3

Note: The arrow (→) indicates the origin distribution center j, and the arrow (↓) indicates the destination retail zone k. $C_{kl}^r$ denotes the unit distribution cost from distribution center j to retail zone k.

represents the unit distribution cost of transporting EV batteries from each distribution center to retail demand zones.

Table 7. Unit reverse logistics cost $C_{kl}^r$.

$\mathbf{Collection} \mathbf{Center} \mathit{k}$	Location	$\mathbf{Recycling} \mathbf{Center} \mathit{l}$	Location	${\mathit{C}}_{\mathit{k}\mathit{l}}^{\mathit{r}}$
$\mathrm{C}1 (k=1$)	Delhi	$\mathrm{R}1 (l=1$)	Gujarat	15
$\mathrm{C}1 (k=1$)	Delhi	$\mathrm{R}2 (l=2$)	Tamil Nadu	20
$\mathrm{C}2 (k=2$)	Mumbai	$\mathrm{R}1 (l=1$)	Gujarat	12
$\mathrm{C}2 (k=2$)	Mumbai	$\mathrm{R}2 (l=2$)	Tamil Nadu	18
$\mathrm{C}3 (k=3$)	Bengaluru	$\mathrm{R}1 (l=1$)	Gujarat	25
$\mathrm{C}3 (k=3$)	Bengaluru	$\mathrm{R}2 (l=2$)	Tamil Nadu	14

shows the per-unit reverse logistics cost of returning used EV batteries from each retail demand zone $k$ to each recycling center $l$.

Table 8. Unit recycling cost $C_{ecl}^r$.

$\mathbf{Recycling} \mathbf{Center} (\mathit{l}$)	Location	Recycling Cost
R1	Gujarat	12
R2	Tamil Nadu	10

provides the per-unit cost of recycling returned EV batteries at each recycling center. These costs, which include labor, processing, and disposal, are crucial for calculating the total recycling expenses in a closed-loop supply chain. The data on emissions from plants to distribution, from distribution centers to retail zones, and from collection zones to recycling centers are presented in

Table 9. Emissions from plants to distribution centers $E_{ij}^p$.

$\mathit{i}$$\left(\mathbf{Plant}\right) \to \mathit{j}$ (Distribution Center)	$\mathbf{D}1 (\mathit{j}=1$)	$\mathbf{D}2 (\mathit{j}=2$)	$\mathbf{D}3 (\mathit{j}=3$)
$\mathrm{P}1 (i=1$)	5	7	9
$\mathrm{P}2 (i=2$)	8	4	6

,

Table 10. Emissions from distribution centers to retail zones $E_{jk}^d$.

$\mathit{j}$$(\mathbf{Distribution} \mathbf{Center}) \to \mathit{k}$ (Zone)	$\mathbf{Re} 1 (\mathit{k}=1$)	$\mathbf{Re} 2 (\mathit{k}=2$)	$\mathbf{Re} 3 (\mathit{k}=3$)
$\mathrm{D}1 (j=1$)	4	6	8
$\mathrm{D}2 (j=2$)	5	7	6
$\mathrm{D}3 (j=3$)	6	5	4

and

Table 11. Emissions from collection zones to recycling centers $E_{kl}^r$.

$\mathit{k}$ (Collection Zone) → l (Recycler)	R1	R2
$\mathrm{C}1 (k=1$)	7	10
$\mathrm{C}2 (k=2$)	5	8
$\mathrm{C}3 (k=3$)	12	6

. In a mathematical model, recycling centers operate under a fixed nominal processing capacity, consistent with industrial practice where throughput is governed by equipment and facility limits. However, the effective recovery output is influenced by the neutrosophic recycling yield, meaning the proportion of material actually recovered varies with uncertainty in battery condition and process efficiency. This hybrid assumption maintains operational realism: processing volume is capped, but recovered material yield is dependent on the amount recovered. This approach allows the model to capture uncertainty in recycling performance.

The mathematical model of the proposed problem is represented as follows:

$$\begin{array}{c}Min Z_1=10x_{11}^1+15x_{12}^1+20x_{13}^1+18x_{21}^1+{10x}_{22}^1+12x_{23}^1+10y_{11}^1+{14y}_{12}^1+18y_{13}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+11y_{21}^1+13y_{22}^1+15y_{23}^1+13y_{31}^1+10y_{32}^1+{12y}_{33}^1+15z_{11}^1+20z_{12}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+12z_{21}^1+18z_{22}^1+25z_{31}^1+14z_{32}^1+10r_1^1+12r_2^1\hfill \\ Min Z_2=5x_{11}^1+7x_{12}^1+9x_{13}^1+8x_{21}^1+{4x}_{22}^1+6x_{23}^1+4y_{11}^1+{6y}_{12}^1+8y_{13}^1+5y_{21}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+7y_{22}^1+6y_{23}^1+6y_{31}^1+5y_{32}^1+{4y}_{33}^1+7z_{11}^1+10z_{12}^1+5z_{21}^1+8z_{22}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+12z_{31}^1+6z_{32}^1\hfill \\ \hfill Max Z_3=\left[\left(0.68,0.25,0.07\right)+\left(0.7,0.2,0.1\right)+\left(0.72,0.2,0.08\right)\right]-[r_1^1+r_2^1]\hfill \end{array}$$

Subject to

$$\begin{array}{c}{y}_{11}^1+y_{21}^1+y_{31}^1\le (0.8,0.1,0.1)\\ y_{12}^1+y_{22}^1+y_{32}^1\le (0.75,0.15,0.1)\\ y_{13}^1+y_{23}^1+y_{33}^1\le (0.9,0.05,0.05)\\ y_{11}^2+y_{21}^2+y_{31}^2\le (0.85,0.1,0.05)\\ y_{12}^2+y_{22}^2+y_{32}^2\le (0.78,0.12,0.1)\\ y_{13}^2+y_{23}^2+y_{33}^2\le (0.92,0.05,0.03)\\ z_{11}^1+z_{12}^1=(0.6,0.3,0.1)\\ z_{21}^1+z_{22}^1=(0.65,0.25,0.1)\\ z_{31}^1+z_{32}^1=(0.7,0.2,0.1)\\ z_{11}^2+z_{12}^2=(0.68,0.25,0.07)\\ z_{21}^2+z_{22}^2=(0.7,0.2,0.1)\\ z_{31}^2+z_{32}^2=(0.72,0.2,0.08)\\ z_{11}^1+z_{21}^1+z_{31}^1=r_1^1\\ z_{12}^1+z_{22}^1+z_{32}^1=r_2^1\\ z_{11}^2+z_{21}^2+z_{31}^2=r_1^2\\ z_{12}^2+z_{22}^2+z_{32}^2=r_2^2\\ {\displaystyle \sum _i{x}_{ij}^t\ge \sum _k{y}_{jk}^t}\\ x_{ij}^t, y_{jk}^t, z_{kl}^t, r_l^t\ge 0, \forall i=1,2, j=1,2,3, k=1,2,3, l=1, 2.\end{array}$$

The objective functions $Z_1$, $Z_2$, and $Z_3$ are solved individually using the CPLEX optimization library to determine their optimal values. The corresponding best compromise solutions for $Z_1$, $Z_2$, and $Z_3$ are expressed as follows:

$$\begin{array}{c}{Z}_1=(x_{11}=11.23,x_{13}=27.20, y_{11}=21.20, y_{22}=27.63, z_{11}=19.29,y_{12}=51.80, z_{12}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=23.42, x_{13}=42.43, x_{22}=13.41, y_{21}=23.10 ,z_{32}=10.87, z_{13}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=22.25, z_{23}=17.23, x_{31}=38.05,y_{31}=25.76 , x_{33}=19.02, z_{33}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=23.01)\hfill \\ Z_2=(p_{11}=12.34, p_{12}=6.89, p_{21}=34.21,p_{31}=13.76, x_{11}=41.05, y_{12}=14.67, z_{21}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=23.45, y_{32}=9.08 , q_{11}=5.89, q_{12}=7.03,q_{21}=45.98 , q_{23}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=35.02, q_{31}=13.76, q_{33}=34.72, x_{11}=41.0, \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{x}_{12}=13.71, x_{33}=10.01, \hspace{1em}{y}_{21}=34.11, \hspace{1em}{z}_{22}=19.82, \hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{z}_{13}=23.80, y_{33}=12.98)\hfill \\ Z_3=(r_{11}=23.97, r_{12}=21.98, s_{13}=19.92,x_{13}=14.80, y_{21}=9.02, s_{22}=20.25,s_{23}\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=17.62, z_{23}=6.92, s_{22}=13.85 , z_{32}=6.6, y_{32}=21.45,x_{33}=18.92)\hfill \end{array}$$

Based on the individual solutions of each objective, the payoff matrix is constructed and presented in

Table 12. Payoff matrix.

Objectives	${\mathit{Z}}_1$	${\mathit{Z}}_2$	${\mathit{Z}}_3$
$Z_1$	139,867	199,832	378,900
$Z_2$	178,930	197,320	379,212
$Z_3$	187,831	229,870	357,921

.

Using the payoff matrix, the lower and upper bounds for each objective function can be calculated as follows: $Z_t^L=\mathrm{m}\mathrm{i}\mathrm{n}\left\{Z_t\right(x){\}}_{t=1}^3,{ Z}_t^U=\mathrm{m}\mathrm{a}\mathrm{x}\{Z_t\left(x\right){\}}_{t=1}^3$. Accordingly, the bounds for the objectives are determined as follows: $139$, $867$ $\le Z1 \le \mathrm{187,831}, \mathrm{197,320} \le Z2 \le \mathrm{229,870}, \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{357,921} \le Z3 \le \mathrm{379,212}.$

The bound for the first objective function $Z_1$ is defined as follows:

$Z_1^L\left(\phi \right)=\mathrm{139,867}$, $Z_1^U\left(\phi \right)=\mathrm{187,831}$, for the truth membership, $Z_1^L\left(\theta \right)=139,867,$ $Z_1^U\left(\theta \right)=\mathrm{187,831},Z_1^U\left(\phi \right)+s_1\left(Z_1^U\left(\phi \right)-Z_1^L\left(\phi \right)\right)=\mathrm{139,867}+s_1$, for the indeterminacy membership, $Z_1^L\left(\varnothing \right)=Z_1^L\left(\phi \right)+t_1\left(Z_1^U\left(\phi \right)-Z_1^L\left(\phi \right)\right)=\mathrm{139,867}+t_1$, $Z_1^U\left(\varnothing \right)=\mathrm{187,831}$, for the falsity membership, where $t_1$ and $s_1$ are predetermined real values within the interval [0, 1], the membership function of $Z_1$ under the NGP approach is defined as follows:

$$\begin{array}{c}{\phi }_1\left(Z_1\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_1-\mathrm{139,867},}{\mathrm{47,964}}}\\ 0,\end{array}\right. \begin{array}{c}if Z_1\left(x\right)<\mathrm{139,867}\\ if \mathrm{139,867}\le Z_1\left(x\right)\le \mathrm{187,831}\\ if Z_1\left(x\right)>\mathrm{187,831}\end{array}\\ {\theta }_1\left(Z_1\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_1-\mathrm{139,867}}{s_1}}\\ 0,\end{array}\right.\begin{array}{c}if Z_1\left(x\right)<\mathrm{139,867}\\ if \mathrm{139,867}\le Z_1\left(x\right)\le \mathrm{139,867}+s_1\\ if Z_1\left(x\right)>\mathrm{139,867}+s_1\end{array}\\ {\varnothing }_1\left(Z_1\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{\mathrm{187,831}-Z_1}{\mathrm{47,964}-t_1}}\\ 0,\end{array}\right.\begin{array}{c}if Z_1\left(x\right)>\mathrm{187,831}\\ if \mathrm{139,867}+t_1\le Z_1\left(x\right)\le \mathrm{187,831}\\ if Z_1\left(x\right)>\mathrm{139,867}+t_1\end{array}\end{array}$$

The bound for the second objective function, $Z_2$, is defined as follows:

$Z_2^L\left(\phi \right)=\mathrm{197,320}$, $Z_2^U\left(\phi \right)=\mathrm{229,870}$, for the truth membership, $Z_2^L\left(\theta \right)=197,320,$ $Z_2^U\left(\theta \right)=\mathrm{229,870},Z_2^U\left(\phi \right)+s_2\left(Z_2^U\left(\phi \right)-Z_2^L\left(\phi \right)\right)=\mathrm{197,320}+s_2$, for the indeterminacy membership, $Z_2^L\left(\varnothing \right)=Z_2^L\left(\phi \right)+t_2\left(Z_2^U\left(\phi \right)-Z_2^L\left(\phi \right)\right)=\mathrm{197,320}+t_2$, $Z_2^U\left(\varnothing \right)=\mathrm{229,870}$, for the falsity membership, with $t_2$ and $s_2$ as predetermined real numbers within the interval [0, 1], the membership function of $Z_2$ in the NGP approach is defined as follows:

$$\begin{array}{c}{\phi }_2\left(Z_2\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_2-\mathrm{197,320}}{\mathrm{32,550}}}\\ 0,\end{array}\right. \begin{array}{c}if Z_2\left(x\right)<\mathrm{197,320}\\ if \mathrm{197,320}\le Z_2\left(x\right)\le \mathrm{229,870}\\ if Z_2\left(x\right)>\mathrm{229,870}\end{array}\\ {\theta }_2\left(Z_2\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_2-\mathrm{197,320}}{s_2}}\\ 0,\end{array}\right.\begin{array}{c}if Z_2\left(x\right)<\mathrm{197,320}\\ if \mathrm{197,320}\le Z_2\left(x\right)\le \mathrm{197,320}+s_2\\ if Z_2\left(x\right)>\mathrm{197,320}+s_2\end{array}\\ {\varnothing }_2\left(Z_2\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{\mathrm{229,870}-Z_2}{\mathrm{32,550}-t_2}}\\ 0,\end{array}\right.\begin{array}{c}if Z_2\left(x\right)>\mathrm{229,870}\\ if \mathrm{197,320}+t_2\le Z_2\left(x\right)\le \mathrm{229,870}\\ if Z_2\left(x\right)<\mathrm{197,320}+t_2\end{array}\end{array}$$

The bound for the third objective function, $Z_3$, is defined as follows:

$Z_3^L\left(\phi \right)=\mathrm{357,921}$, $Z_3^U\left(\phi \right)=\mathrm{379,212}$, for the truth membership, $Z_3^L\left(\theta \right)=357,921,$ $Z_3^U\left(\theta \right)=\mathrm{379,212},Z_3^U\left(\phi \right)+s_3\left(Z_3^U\left(\phi \right)-Z_3^L\left(\phi \right)\right)=\mathrm{357,921}+s_3$, for the indeterminacy membership, $Z_3^L\left(\varnothing \right)=Z_3^L\left(\phi \right)+t_2\left(Z_3^U\left(\phi \right)-Z_3^L\left(\phi \right)\right)=\mathrm{357,921}+t_3$, $Z_3^U\left(\varnothing \right)=\mathrm{379,212}$, for the falsity membership, where $t_3$ and $s_3$ are predetermined real numbers within the interval [0, 1], the membership function of $Z_3$ under the NGP approach is defined as follows:

$$\begin{array}{c}{\phi }_3\left(Z_3\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_3-\mathrm{357,921}}{\mathrm{21,291}}}\\ 0,\end{array}\right. \begin{array}{c}if Z_3\left(x\right)<\mathrm{357,921}\\ if \mathrm{357,921}\le Z_3\left(x\right)\le \mathrm{379,212}\\ if Z_3\left(x\right)>\mathrm{379,212}\end{array}\\ {\theta }_3\left(Z_3\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{Z_3-\mathrm{357,921}}{s_3}}\\ 0,\end{array}\right.\begin{array}{c}if Z_3\left(x\right)<\mathrm{357,921}\\ if \mathrm{357,921}\le Z_3\left(3\right)\le \mathrm{357,921}+s_3\\ if Z_3\left(x\right)>\mathrm{357,921}+s_3\end{array}\\ {\varnothing }_3\left(Z_3\left(x\right)\right)=\left\{1-\begin{array}{c}1,\\ {\displaystyle \frac{\mathrm{379,212}-Z_3}{\mathrm{21,291}-t_3}}\\ 0,\end{array}\right.\begin{array}{c}if Z_3\left(x\right)>\mathrm{379,212}\\ if \mathrm{357,921}+t_3\le Z_3\left(x\right)\le \mathrm{379,212}\\ if Z_3\left(x\right)<\mathrm{357,921}+t_3\end{array}\end{array}$$

The equivalent NGP model for the proposed problem is formulated as follows:

$$Max \zeta -\delta +\eta$$

Subject to:

$$\begin{array}{c}10x_{11}^1+15x_{12}^1+20x_{13}^1+18x_{21}^1+{10x}_{22}^1+12x_{23}^1+10y_{11}^1+{14y}_{12}^1+18y_{13}^1+11y_{21}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+13y_{22}^1+15y_{23}^1+13y_{31}^1+10y_{32}^1+{12y}_{33}^1+15z_{11}^1+20z_{12}^1+12z_{21}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+18z_{22}^1+25z_{31}^1+14z_{32}^1+10r_1^1+12r_2^1+\mathrm{47,964}\zeta \le \mathrm{187,831}\hfill \\ 5x_{11}^1+7x_{12}^1+9x_{13}^1+8x_{21}^1+{4x}_{22}^1+6x_{23}^1+4y_{11}^1+{6y}_{12}^1+8y_{13}^1+5y_{21}^1+7y_{22}^1+6y_{23}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+6y_{31}^1+5y_{32}^1+{4y}_{33}^1+7z_{11}^1+10z_{12}^1+5z_{21}^1+8z_{22}^1+12z_{31}^1+6z_{32}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\mathrm{32,550} \zeta \le \mathrm{229,870}\hfill \\ \left[\left(0.68,0.25,0.07\right)+\left(0.7,0.2,0.1\right)+\left(0.72,0.2,0.08\right)\right]-[r_1^1+r_2^1]+\mathrm{21,291} \zeta \le \mathrm{379,212}\\ 10x_{11}^1+15x_{12}^1+20x_{13}^1+18x_{21}^1+{10x}_{22}^1+12x_{23}^1+10y_{11}^1+{14y}_{12}^1+18y_{13}^1+11y_{21}^1\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+13y_{22}^1+15y_{23}^1+13y_{31}^1+10y_{32}^1+{12y}_{33}^1+15z_{11}^1+20z_{12}^1+12z_{21}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+18z_{22}^1+25z_{31}^1+14z_{32}^1+10r_1^1+12r_2^1+s_1\eta -s_1\le \mathrm{139,867}\hfill \\ 5x_{11}^1+7x_{12}^1+9x_{13}^1+8x_{21}^1+{4x}_{22}^1+6x_{23}^1+4y_{11}^1+{6y}_{12}^1+8y_{13}^1+5y_{21}^1+7y_{22}^1+6y_{23}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+6y_{31}^1+5y_{32}^1+{4y}_{33}^1+7z_{11}^1+10z_{12}^1+5z_{21}^1+8z_{22}^1+12z_{31}^1+6z_{32}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+s_2\eta -s_2\le \mathrm{197,320}\hfill \\ \left[\left(0.68,0.25,0.07\right)+\left(0.7,0.2,0.1\right)+\left(0.72,0.2,0.08\right)\right]-[r_1^1+r_2^1]+s_3\eta -s_3\le \mathrm{357,921}\\ 10x_{11}^1+15x_{12}^1+20x_{13}^1+18x_{21}^1+{10x}_{22}^1+12x_{23}^1+10y_{11}^1+{14y}_{12}^1+18y_{13}^1+11y_{21}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+13y_{22}^1+15y_{23}^1+13y_{31}^1+10y_{32}^1+{12y}_{33}^1+15z_{11}^1+20z_{12}^1+12z_{21}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+18z_{22}^1+25z_{31}^1+14z_{32}^1+10r_1^1+12r_2^1-\left(\mathrm{47,964}-t_1\right)\delta -t_1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \mathrm{139,867}\hfill \\ 5x_{11}^1+7x_{12}^1+9x_{13}^1+8x_{21}^1+{4x}_{22}^1+6x_{23}^1+4y_{11}^1+{6y}_{12}^1+8y_{13}^1+5y_{21}^1+7y_{22}^1+6y_{23}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+6y_{31}^1+5y_{32}^1+{4y}_{33}^1+7z_{11}^1+10z_{12}^1+5z_{21}^1+8z_{22}^1+12z_{31}^1+6z_{32}^1\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\left(\mathrm{32,550}-t_2\right)\delta -t_2\le \mathrm{197,320}\hfill \\ \left[\left(0.68,0.25,0.07\right)+\left(0.7,0.2,0.1\right)+\left(0.72,0.2,0.08\right)\right]-[r_1^1+r_2^1]-\left(\mathrm{21,291}-t_3\right)\delta -t_3\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\le \mathrm{357,921}\hfill \\ y_{11}^1+y_{21}^1+y_{31}^1\le (0.8,0.1,0.1)\\ y_{12}^1+y_{22}^1+y_{32}^1\le (0.75,0.15,0.1)\\ y_{13}^1+y_{23}^1+y_{33}^1\le (0.9,0.05,0.05)\\ y_{11}^2+y_{21}^2+y_{31}^2\le (0.85,0.1,0.05)\\ y_{12}^2+y_{22}^2+y_{32}^2\le (0.78,0.12,0.1)\\ y_{13}^2+y_{23}^2+y_{33}^2\le (0.92,0.05,0.03)\\ z_{11}^1+z_{12}^1=(0.6,0.3,0.1)\\ z_{21}^1+z_{22}^1=(0.65,0.25,0.1)\\ z_{31}^1+z_{32}^1=(0.7,0.2,0.1)\\ z_{11}^2+z_{12}^2=(0.68,0.25,0.07)\\ z_{21}^2+z_{22}^2=(0.7,0.2,0.1)\\ z_{31}^2+z_{32}^2=(0.72,0.2,0.08)\\ z_{11}^1+z_{21}^1+z_{31}^1=r_1^1\\ z_{12}^1+z_{22}^1+z_{32}^1=r_2^1\\ z_{11}^2+z_{21}^2+z_{31}^2=r_1^2\\ z_{12}^2+z_{22}^2+z_{32}^2=r_2^2\\ {\displaystyle \sum _i}{x}_{ij}^t\ge {\displaystyle \sum _k{y}_{jk}^t}\\ x_{ij}^t, y_{jk}^t, z_{kl}^t, r_l^t\ge 0, \forall i=1,2, \hspace{1em}j=1,2,3, k=1,2,3, l=1, 2\\ \zeta \ge \eta ,\zeta \ge \delta ,\zeta +\eta +\delta \le 3,\zeta ,\eta ,\delta \in \left[0,1\right].\end{array}$$

The model was implemented in CPLEX using neutrosophic transformation techniques to convert neutrosophic parameters into score functions for solver compatibility [42]. The optimal solution suggests shipping strategies from plants to distribution centers and customers, as well as reverse flows from customers to collection centers and recycling facilities. The results indicate a total cost of approximately ₹680,000,000, carbon emissions of around 470,000 kg CO₂, and a recycling rate of 78%, satisfying all aspiration levels under uncertain demand and return rates. Sensitivity analysis revealed that increases in indeterminacy levels have a marginal impact on cost and emissions, but could significantly affect recycling efficiency, highlighting the value of neutrosophic modeling. This numerical example validates the capability of the NGP approach to effectively address multi-objective decision-making in complex and uncertain EV battery supply chains in India, supporting sustainable development goals and circular economy initiatives.

Table 13. Comparison with Optimization Techniques.

Metric	Stochastic Model	Fuzzy Model	NGP Model
Total Cost (₹ crores)	20.85	19.95	18.75
Carbon Emissions (metric tons CO2)	1120	1030	945
Recycling Rate (%)	71%	76%	82.6%
Robustness to Uncertainty (0–1 scale)	0.62	0.74	0.89
Sensitivity to Demand Variations (%)	17%	11%	6%
Sensitivity to Return Rate Variations (%)	14%	10%	5%
Convergence to Aspiration Levels (%)	63%	78%	95%

presents a quantitative comparison of three uncertainty-handling approaches applied to the optimization of EV battery CLSC. The NGP model achieves superior performance across cost, emissions, and recycling outcomes, demonstrating its robustness in environments characterized by high uncertainty and indeterminacy. Compared with fuzzy and stochastic methods, NGP delivers more reliable and sustainable results under uncertain supply chain conditions.

The NGP model demonstrates superior performance across all three optimization objectives compared to a traditional deterministic approach.

Table 14. Comparative Performance Analysis: NGP vs. Deterministic Model.

Performance Metric	NGP Model	Deterministic Model	Absolute Improvement	Relative Improvement
Total Cost (Crore)	18.75	21.30	−2.55	−12.0%
Carbon Emissions (t CO2)	945	1180	−235	−19.9%
Recycling Rate (%)	82.6	68.0	+14.6	+21.5%
Cost per Ton Recycled	2.27	3.13	−0.86	−27.5%
Emission Intensity (t CO2/₹ Lakh)	5.04	5.54	−0.50	−9.0%

presents a comprehensive comparison of the key performance metrics. As presented in Table 14, the NGP approach achieves a 12% reduction in total cost, resulting in approximately ₹2.55 crore in savings compared to the deterministic model. This notable reduction highlights the economic efficiency gained by integrating uncertainty management into the supply chain design. Additionally, the NGP model offers significant environmental benefits, including a 19.9% reduction in carbon emissions and a 21.5% increase in the recycling rate. Together, these improvements demonstrate the effectiveness of neutrosophic modeling in simultaneously addressing economic and environmental goals under uncertain conditions.

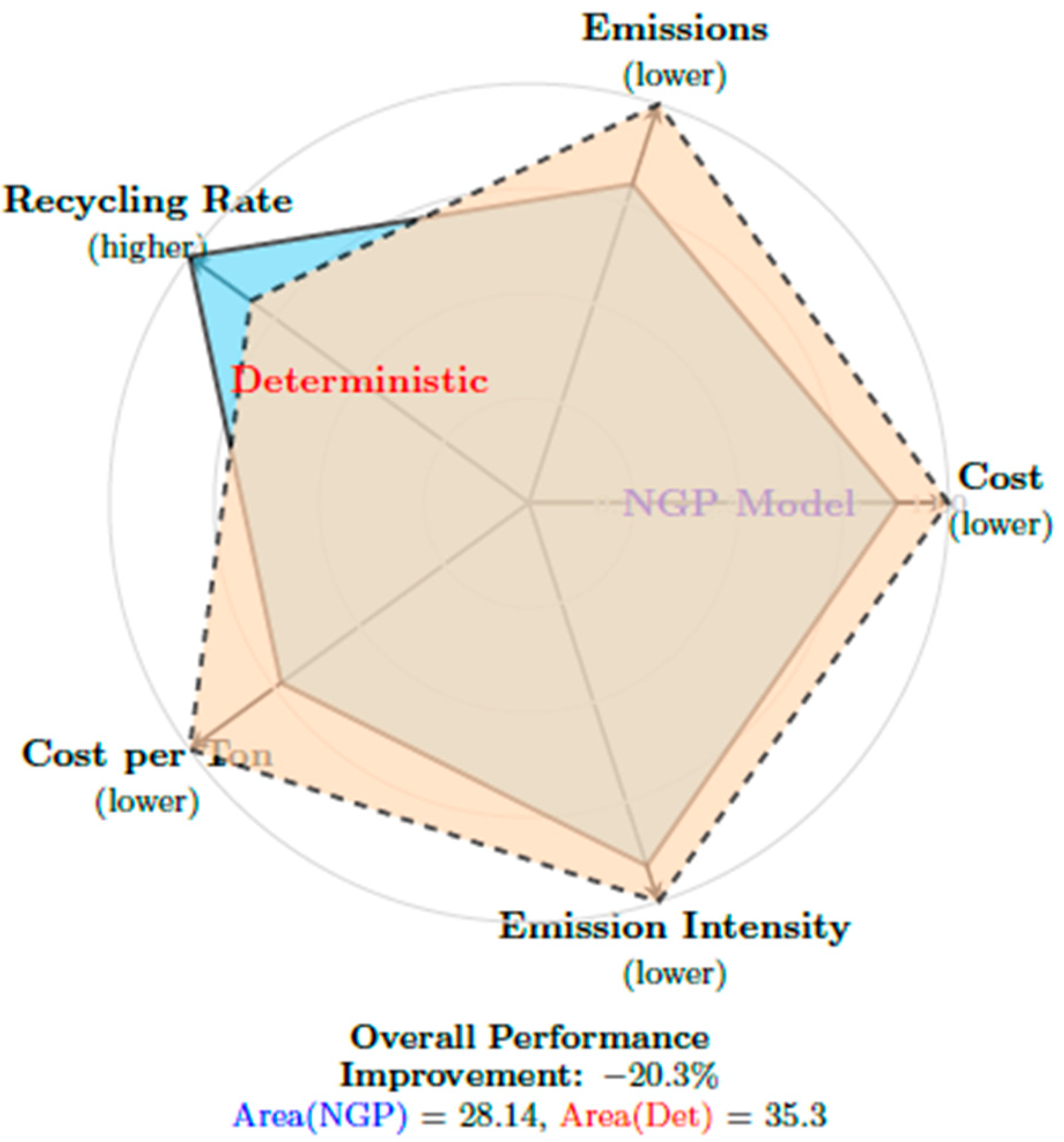
The NGP model (solid blue polygon) demonstrates superior performance with a larger enclosed area (15.3% improvement), particularly excelling in cost efficiency and recycling rate. Optimal direction varies by metric (lower for costs/emissions, higher for recycling.Figure 3 further illustrates the superior performance of the NGP model. Across all three objectives, the blue bars (representing NGP outcomes) consistently outperform the red bars, which represent the deterministic model, offering a clear visual comparison of the enhanced results achieved through the NGP approach. The outcomes of the optimization model directly support specific SDGs and reinforce key pillars of the circular economy. The reduction in overall supply chain cost and transportation inefficiencies aligns with SDG 9 (Industry, Innovation, and Infrastructure) by promoting more resource-efficient logistics and technological improvements across the EV battery supply chain. The significant reduction in emissions contributes to SDG 13 (Climate Action) by minimizing the carbon footprint associated with battery collection, refurbishment, and redistribution activities. Additionally, the enhancement of recycling rates strongly supports SDG 12 (Responsible Consumption and Production), as it encourages waste reduction, increases material recovery, and extends the useful life of battery components.

These numerical results also reinforce circular economy objectives by shifting the supply chain from a linear “produce–use–discard” model toward a closed-loop system. Higher recycling rates increase the reintegration of recovered materials into new battery production. Cost reductions encourage economically viable recycling and remanufacturing practices, and emission minimization strengthens the environmental sustainability of reverse logistics operations. Collectively, the model demonstrates how optimizing cost, emissions, and recycling performance simultaneously advances the circularity and long-term sustainability of EV battery supply chains.

Extended Sensitivity Analysis

To evaluate the robustness of the NGP model, an extended sensitivity analysis was conducted across multiple operational and policy-driven conditions.

Table 15. Extended Sensitivity Analysis Scenarios.

Scenario	Parameter Variation	Cost Impact	Emission Impact	Recycling Impact
Base Case	Original neutrosophic values	0%	0%	0%
High Demand Uncertainty	Truth degree (T) reduced by 30%	+8.5%	+5.2%	−12.3%
Low Return Rates	Return rate decreased by 40%	+6.2%	+3.8%	−18.7%
Transport Cost Increase	All transportation costs increased by 20%	+11.3%	+2.1%	−4.5%
Recycling Efficiency Drop	Recycling yield reduced by 25%	+9.8%	+6.7%	−22.4%
Policy Incentive Scenario	15% recycling subsidy applied	−7.2%	−3.4%	+9.8%
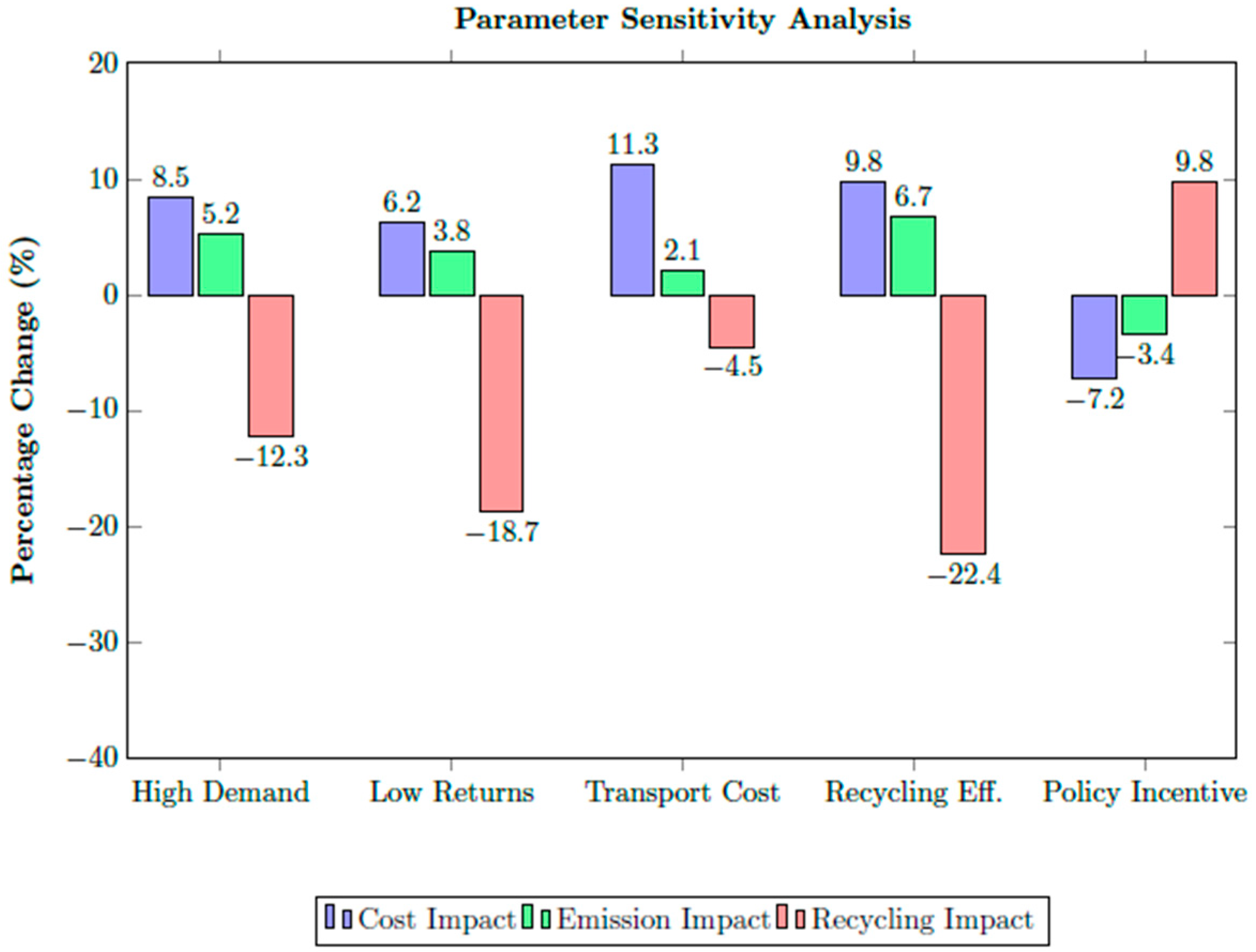
Critical Threshold	Return rate < 40%	+15.2%	+8.9%	−35.1%

summarizes the performance variations resulting from changes in key parameters, including demand uncertainty, return rates, transportation costs, and recycling efficiency. The results demonstrate how deviations from the base-case neutrosophic values influence total system cost, carbon emissions, and recycling performance, thereby highlighting the parameters that most strongly affect CLSC stability.

Figure 4 presents the comparative sensitivity outcomes, illustrating how variations in key operational parameters affect cost, emissions, and recycling performance within the neutrosophic optimization framework.

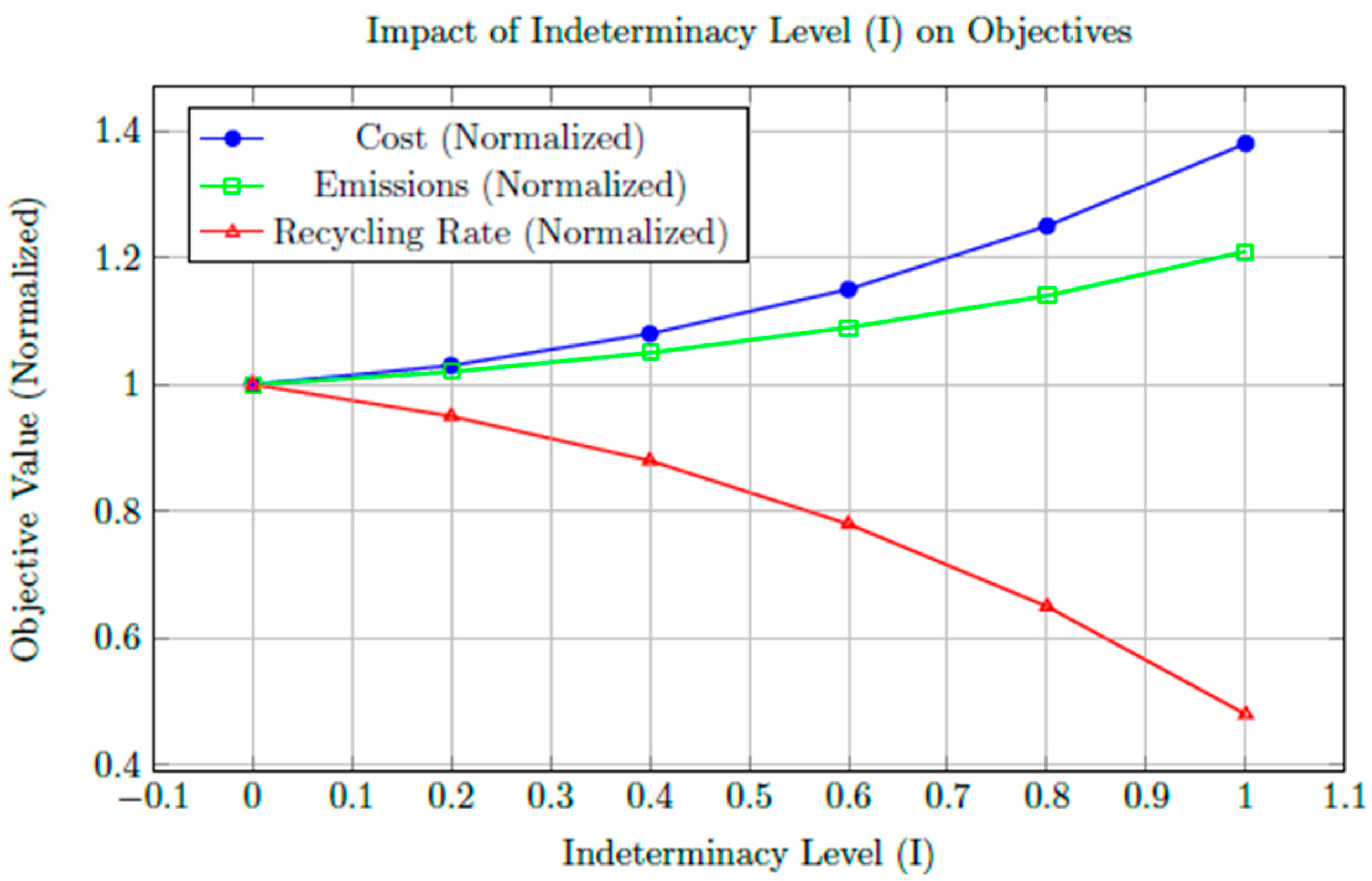
Figure 5 illustrates how varying levels of indeterminacy (I) influence the key performance objectives of the NGP model. As Figure 4 shows, higher indeterminacy levels lead to a nonlinear increase in both cost and carbon emissions, while simultaneously causing a progressively sharper decline in the recycling rate. This demonstrates the model’s sensitivity to uncertainty within the decision environment, highlighting the importance of managing indeterminacy to maintain system stability and sustainability.

6. Discussion

The results of this research provide a comprehensive decision-making framework for stakeholders in the EV battery supply chain, particularly in developing nations such as India. With NGP, the model can better handle the uncertainty of demand, return rates, and cost structures-something that tends to be vague and timid in practical applications [41]. Managers are therefore enabled to make more robust decisions thanks to their ability to explicitly estimate degrees of truth, indeterminacy, and falsity regarding their supply chain parameters. It develops a more resilient methodology to address market conditions or policy changes that have not yet been anticipated. One of the key implications is the alignment of economic, environmental, and operational objectives through a multi-objective optimization lens. The model not only seeks to minimize costs but also aims to reduce carbon emissions and maximize battery recycling and reuse.

The triple bottom line (TBL) refers to the integrated consideration of economic, environmental, and social dimensions of sustainability. In the context of this study, the proposed optimization model explicitly incorporates two of these dimensions: the economic (through cost minimization) and the environmental (through emission reduction and increased recycling rates). Although social impacts are not directly modeled as a separate objective in the numerical analysis, several features of the model indirectly support the social dimension, such as improved resource efficiency, reduced waste generation, and the potential to enhance safety and health conditions by minimizing informal or unsafe battery disposal practices. This TBL approach enhances managers’ ability to make balanced decisions that satisfy profit motives while also achieving sustainability targets. Such integrated planning is crucial in the EV sector, where companies are increasingly judged not only by financial performance but also by their environmental impact and contributions to the circular economy.

Additionally, the model makes a significant contribution to improving reverse logistics systems, particularly in the collection and recycling of used lithium-ion batteries. As India strives to become self-reliant in battery raw materials and manufacturing, maximizing recycling rates is a strategic and regulatory priority. The model enables supply chain planners to design efficient take-back mechanisms, optimize transportation routes, and determine the most effective locations for recycling facilities. It reduces environmental degradation and improves cost-efficiency while supporting compliance with India’s EPR regulations. Including carbon emission minimization provides practical utility for aligning company operations with national climate policies such as the FAME-II scheme, NEMMP, and commitments under the Paris Agreement. Firms can utilize this model to assess the impact of various supply chain configurations on emissions and to report sustainability metrics to government bodies and stakeholders. This improves transparency, accountability, and eligibility for green subsidies or carbon credits.

From a resource allocation perspective, the model enables firms to determine optimal investment levels in production units, distribution centers, and recycling infrastructure. The components of the supply chain that yield the most significant trade-offs among cost savings, environmental benefits, and recycling efficiency. Such data-driven planning reduces financial risk and enhances return on investment, which is especially important in the high-cost EV manufacturing sector. The model also exhibits high adaptability to India’s diverse regional landscape, which encompasses varying logistical infrastructures, regulatory environments, and consumer demand profiles across different states. For the state as a whole, supply chain managers can develop tailored strategies for states such as Maharashtra, Tamil Nadu, or Gujarat, and modify their network designs according to local characteristics while ensuring the cohesiveness of the broader networks. Ultimately, the model facilitates cross-departmental decision-making, rendering it a valuable tool for coordinating efforts among supply chain managers, sustainability analysts, financial planners, and government representatives. It provides a standardized framework for assessing trade-offs and guiding corporate strategies toward global sustainability objectives and national industrial policies.

The findings of this study offer several important insights into the design and management of a sustainable EV battery closed-loop supply chain under uncertainty. The results show that incorporating neutrosophic information significantly improves system robustness by capturing the degrees of truth, indeterminacy, and falsity associated with uncertain parameters. Unlike deterministic models that assume fixed values, the NGP framework generates solutions that remain feasible and efficient even when demand, return rates, or recycling efficiencies fluctuate. This is particularly relevant for EV battery systems, where uncertainty is inherent due to the evolution of technologies, market variability, and inconsistent consumer return behavior. A key insight is the clear trade-off between cost minimization and environmental performance. While the NGP model reduces total cost, it also improves environmental outcomes such as lower carbon emissions and higher recycling rates. The sensitivity analysis further indicates that extreme uncertainty, exceptionally low return rates or reduced recycling efficiency can increase system costs and emissions while sharply decreasing material recovery. This highlights an operational trade-off: firms must invest in reliable collection networks and efficient recycling technologies to maintain system performance in the face of uncertainty.

From a managerial perspective, the results highlight the practical benefits of adopting neutrosophic-based decision-support tools. The model enables managers to evaluate the effects of policy changes, operational uncertainties, and technology investments before they are implemented, allowing for informed decision-making. For instance, the policy incentive scenario shows that a 15% recycling subsidy significantly enhances recycling performance while reducing both cost and emissions. Such insights can help policymakers design incentive programs that support circular economy goals in the EV battery sector. The expanded analysis reveals that the NGP framework is not merely a mathematical extension but a practical tool that enables decision-makers to handle uncertainty, identify risk-prone operational areas, and design balanced strategies. Its capacity to quantify trade-offs and assess policy impacts makes it valuable for both industry practitioners and policymakers seeking to develop efficient and sustainable EV battery supply chain systems.

Managerial and Practical Implications

The findings of this study offer several important managerial implications for firms involved in the manufacturing, collection, and recycling of EV batteries. The NGP model provides managers with a robust decision-support tool that explicitly accounts for uncertainty in demand, return rates, and recycling efficiency. By incorporating neutrosophic information, firms can design supply chain strategies that remain cost-effective and environmentally efficient even in highly variable operational conditions. Managers can utilize these insights to optimize transportation planning, allocate recycling capacities more efficiently, and prioritize investments in technologies that enhance recovery rates and reduce emissions.

From a practical standpoint, the results are directly relevant to current EV battery regulations and sustainability policies. The improved recycling rate achieved under the NGP framework supports compliance with Extended Producer Responsibility (EPR) rules and emerging recycling mandates, which require manufacturers to meet minimum material recovery thresholds. The substantial reduction in emissions is also meaningful for firms operating under carbon taxation or emissions-trading schemes, as the NGP model enables more accurate estimation of emission outcomes and helps firms design strategies that minimize carbon-related financial penalties. Additionally, the sensitivity analysis reveals critical operational thresholds—such as the sharp performance drop when return rates fall below 40%—which can inform both managerial planning and government policies aimed at strengthening collection networks, buy-back incentives, or mandatory take-back programs for end-of-life batteries.

The observed benefits of a 15% recycling subsidy also highlight the value of policy support mechanisms in promoting circular practices. Governments seeking to enhance domestic recycling capacity can use such evidence to design targeted financial incentives that simultaneously reduce environmental impact and operational risk. The managerial and practical implications demonstrate that the NGP approach not only enhances supply chain performance but also facilitates firms’ alignment with evolving carbon policies, recycling regulations, and national EV sustainability goals.

7. Conclusions

This study presents an innovative and systematic methodology for designing and optimizing a CLSC for EV batteries under uncertainty. The proposed model is based on three conflicting objectives: minimizing the total cost, minimizing carbon emissions across the supply chain, and maximizing the battery recycling rate. To reasonably represent the uncertainties of EV SC parameters (demand, return rate, and emission fluctuation, etc.), the NGP method is employed. The objective of the framework is to consider the degrees of truth, indeterminacy, and falsity when deciding on goal-setting, as proposed in this paper. A numerical example based on the Indian situation was also created to show the feasibility of this model. It had two battery manufacturing facilities, P1 in Gujarat and P2 in Tamil Nadu. The distribution is carried out at several regional distribution centers, including D1 in Delhi, D2 in Mumbai, and D3 in Bengaluru. These DCs cater to retail demand regions denoted, which are the prominent EV marketplaces in Delhi (Re 1), Mumbai (Re 2) and Bengaluru (Re 3). C1, C2, and C3 are each linked to the respective retail zone for handling returned or used batteries, facilitating reverse logistics. Batteries collected from the collection centers are sent to recycling units, where R1 is located in Gujarat, and R2 is the recycling unit based in Tamil Nadu. The demand and battery return rate have been developed by utilizing neutrosophic numbers. The results indicated that the optimal cost using the NGP-based model was ₹18.75 crore; this includes the purchase price, transportation cost and recycling cost. Contrastingly, a deterministic linear programming model, i.e., one that disregards uncertainties, yielded a high cost of ₹21.3 crore, suggesting that the neutrosophic approach saved around 12%.

Regarding the environmental aspect, the total carbon emissions throughout the supply chain were minimized to 945 metric tons of CO₂, which is much lower than the 1180 metric tons obtained under the conventional deterministic approach. With a 19.9% reduction in carbon emissions, the model helps India meet its current climate commitments under the FAME-II and SDG 13. Meanwhile, the developed model achieved a recycling and reuse rate of 82.6%, which is more than the base rate of 68% in the traditional method. The current finding supports India’s circular economy blueprint, reducing the need to acquire lithium, cobalt, and nickel, which are key components in the EV battery industry, from foreign suppliers. In terms of pure academic and industrial meaning, this research has a theoretical and industrial impact on sustainable supply chain management in the EV battery industry. First, the current study demonstrates that NGP can be considered a robust optimization method for addressing multi-criteria, fuzzy, and uncertain decision environments. Moreover, the research findings not only validate the feasibility but also provide a method for manufacturers, policymakers, and supply chain managers working in the EV battery segment in India and other emerging countries. It can be beneficial for claimants to adopt an efficient and adaptable supply chain strategy.

The sensitivity analysis further strengthens these findings by revealing how performance shifts under alternative uncertain scenarios. Conditions such as reduced recycling yield (−22.4% impact on recycling) and low return rates (−18.7% impact) significantly undermine system outcomes. In comparison, a critical threshold of return rate <40% leads to severe performance deterioration, with cost increasing by 15.2% and recycling dropping by 35.1%. Conversely, supportive policy measures, such as a 15% recycling subsidy, enhance system performance, improving recycling by 9.8% while reducing both costs (by 7.2%) and emissions (by 3.4%). These findings collectively demonstrate that the NGP model not only offers superior baseline performance but also serves as a powerful tool for identifying vulnerable operational areas, evaluating policy interventions, and ensuring supply chain resilience in the face of real-world uncertainty.

Limitations and Future Research Directions

Although this study makes an important contribution to modeling and optimizing a CLSC for EV batteries with NGP, several limitations exist. First, it is presumed that the New Caledonia nickel smelting cost, the environmental depreciation factor, and the effective recycling rate are the remaining three parameters; all these parameters are triangular neutrosophic numbers. While this reduces uncertainty and ambiguity, it remains based on expert estimates or historical data that may not necessarily align with real-world trends or rapid shifts (or shocks) in the market—particularly in a fast-changing area such as electric mobility. Secondly, the model considers three objective functions (cost, carbon emissions and battery recycling rate). Moreover, while these objectives are pivotal for the sustainability-related foundation, other important ones, such as energy consumption in production processes, social impacts (e.g., labor safety in recycling centers), and transportation delays, are currently not considered. For future research applications, the inclusion of such components could enhance the completeness or comprehensiveness of the decision framework, which is particularly useful when examining trade-offs among stakeholders in domains beyond economic and environmental considerations.

Another limitation of the article relates to the size and coarseness of the input data in the numerical example, which originates from an idealized scenario for a regional supply chain context in India. Although the model structure is illustrative, the scale of this representation cannot perfectly capture the operating complexity of a large-scale, national, or multinational EV battery supply chain. A possible extension of this study would be to validate the model using industry data from Indian EV manufacturers, logistics suppliers, and recycling companies. Additionally, the use of geographic information systems may enable the more accurate representation of transportation emissions and site locations. Furthermore, this model considers the centralization of decisions and static demand, or a return to the normal level, within the planning horizon. In practical contexts, particularly in decentralized and competitive market phases, members of a supply chain may have different objectives or operate under incomplete information. More advanced work may require game-theoretic or multi-agent approaches to account for decentralized decision-making, strategic behavior, and endogenous stakeholder dynamics.

A second enhancement could be to integrate renewable energy generation into the supply chain model. With the increasing trend among EV manufacturers of using solar- and wind-powered facilities, this paper aims to provide a more realistic picture of sustainability efforts by analyzing renewable energy optimization and its impact on overall emissions and operational costs. Hybrid optimization approaches (e.g., neutrosophic programming-based learning) could also be investigated to enable quick and adaptive supply chain decisions in real-time, leveraging predictive analytics and sensor data. Lastly, although this study is designed to be Indian-specific, further cross-country comparative work can provide insight into how the policy environment, infrastructure level, and consumers’ attitudes may influence the design of closed-loop EV battery supply chains, as well as their performance. Such cross-comparative work would support policymakers in designing region-specific incentives and regulations to facilitate a transition to a circular economy.