Data-Driven Online State Prediction Method for the Traction Motors of Electric Multiple Units (EMUs)

Abstract

With the high-density operations of high-speed trains, predicting the health status of core components such as traction motors is crucial for enhancing the safety and sustainability of trains. Currently, traditional maintenance mechanisms such as periodic inspections and fixed-threshold alarm systems are hindered by delayed abnormality detection and inadequate real-time responsiveness. This paper proposes a dynamic prediction method for traction motor states based on an Online Gated Recurrent Unit (OGRU), which considers various influencing factors and updates model parameters in real-time. Experimental results demonstrate that the online prediction model significantly reduces the $RMSE$ compared to offline methods and exhibits increased prediction stability under different conditions and step sizes. Notably, it decreases computational time by 23.3% relative to the Online Long Short-Term Memory (OLSTM) approach. The proposed method enhances preventive maintenance strategies, optimizes resource utilization, extends equipment lifespan, and reduces costs, thereby making a substantial contribution to the sustainable operation of high-speed railways. By improving energy efficiency, safety, and economic viability, this approach supports a transition toward greener rail transportation. Based on this study, the developed method can facilitate real-time maintenance decision-making, enabling the intelligent operation and maintenance of high-speed trains.

1. Introduction

As the backbone of modern transportation, the safety and sustainability of high-speed railways are crucial to the national economy and serve as the foundation for efficient and reliable cross-regional passenger and freight transportation [1]. With the promotion of the intelligent high-speed railway development plan, an intelligent operation and maintenance system based on Beidou positioning, drone inspection, and other technologies has been gradually established, and the operation and maintenance of high-speed trains have been transformed from “planned repair” to “state repair”. As the core power unit of high-speed trains, the traction motor comprises a stator, rotor, bearings, cooling system, and other components. Traditional maintenance methods rely on frequent inspections, which waste resources and may disrupt normal train operations. State repair, however, offers significant advantages in terms of cost savings, risk reduction, efficiency enhancement, and the optimization of maintenance resource utilization, among other benefits, and has been increasingly adopted. Despite its growing application [2,3], several challenges remain in state prediction: initially, many existing predictions depend on single sensor data, limiting the ability to capture multi-dimensional state features. Secondly, the large number of parameters in traditional models such as Long Short-Term Memory (LSTM) networks limits their capacity to meet real-time prediction requirements.

With the rapid development of intelligent operation and maintenance technologies, lightweight deep learning models such as the Gated Recurrent Unit (GRU) are increasingly favored in industrial prediction tasks [4,5], with a reduced number of parameters compared to Long Short-Term Memory (LSTM) networks [6]. However, limitations persist in current research, as temperature-based univariate prediction models are unable to capture the coupling effects of operating conditions and environmental factors. Additionally, the traditional offline training modes are often inadequate in adapting to the dynamic variations of operating parameters.

This paper analyzes the traction motor dataset by examining its structural composition and working principles. Firstly, the influencing factors of temperature are integrated, followed by an investigation into the state parameter characteristics of the traction motor from a data statistical perspective. The study further explores the information embedded within the data to facilitate more accurate predictions. Based on this data analysis and background, a traction motor state prediction method for high-speed trainsets is proposed. This method employs the OGRU network, aiming to incorporate multiple influencing factors for temperature prediction, thereby enhancing maintenance efficiency, reducing costs, and ensuring the safe operation of trains.

The contribution of this paper is reflected in two aspects: (1) a multidimensional feature fusion framework is constructed to fuse 6-dimensional time series features such as temperature, current, and speed, taking into account the effects of multiple factors on the state of the traction motor; (2) a real-time prediction method based on the on-line GRU is proposed, and a dynamic parameter updating mechanism is designed, which allows the model to be learned in real time with the changes in working conditions. Experiments show that its prediction accuracy is greatly improved compared with the offline model, and it performs well under various working conditions.

The rest of the paper is organized as follows. In Section 2, the background of the study and related works in the field are reviewed. In Section 3, an online prediction model for the traction motor is constructed. In Section 4, it is presented and analyzed around a high-speed train example. Section 5 discusses the methodology and results of this paper. In Section 6, we draw conclusions.

2. Literature Review

High-speed trains have become one of the main tools for people’s transportation by virtue of their reliability, speed, comfort, and environmental protection. However, along with this come higher requirements for their safe operation [7,8]. In the process of high-speed train operation, with the traction motor being one of its core components, its stability and reliability is the key to the safe operation and sustainability of the entire train system [9].

Scholars have studied many traction motor condition prediction techniques [8,10,11], and some scholars have carried out real-time monitoring and prediction of equipment health status by formulating and optimizing on-board alarm thresholds [12]. Although such techniques can realize basic early warning, they are limited by static threshold setting and are difficult to adapt to dynamic working conditions [13]. With the gradual increase in the number of sensors arranged on intelligent high-speed railways, it has become mainstream in current research to construct a prediction model using the data collected by sensors, through which the changes in the information elements of the equipment can be sensed earlier, thus providing more timely information for train operation and maintenance [14]. The actual operation process of trains and the working environment of traction motors are complex and varied, and their states are influenced by multiple factors. Considering only a single factor or change often fails to detect and prevent potential faults in a timely manner and cannot meet the high requirements of intelligent high-speed railways for safety and fault tolerance. Multidimensional inputs can learn more information. The actual operation process of trains and the working environment of traction motors are complex and varied, and their states are affected by multiple factors. Considering only a single factor or a single change often fails to detect and prevent potential faults in a timely manner and cannot meet the high requirements of intelligent high-speed railways for safety and fault tolerance. Therefore, in-depth analysis of factors affecting motor status and the combination of predictive maintenance techniques with data collected by motor sensors have become a hot topic in current research and application [8,15,16].

In the field of intelligent high-speed rail, technologies such as fault prediction and health management (PHM) [17] and digital twins [18,19] are developing rapidly. PHM technology evaluates the health status of equipment in real time and predicts its future performance degradation and potential failures by collecting and analyzing its operational data [20]. This technology is able to detect small changes in equipment performance and signs of potential failures in a timely manner through real-time monitoring and analysis of equipment operation data [21]. At the same time, a multifactor-based fault prediction model can be constructed based on historical data and machine learning algorithms to realize the prediction and prevention of potential faults. This helps the operation and maintenance personnel to take maintenance measures in advance to avoid failures and improve the sustainability and safety of trains.

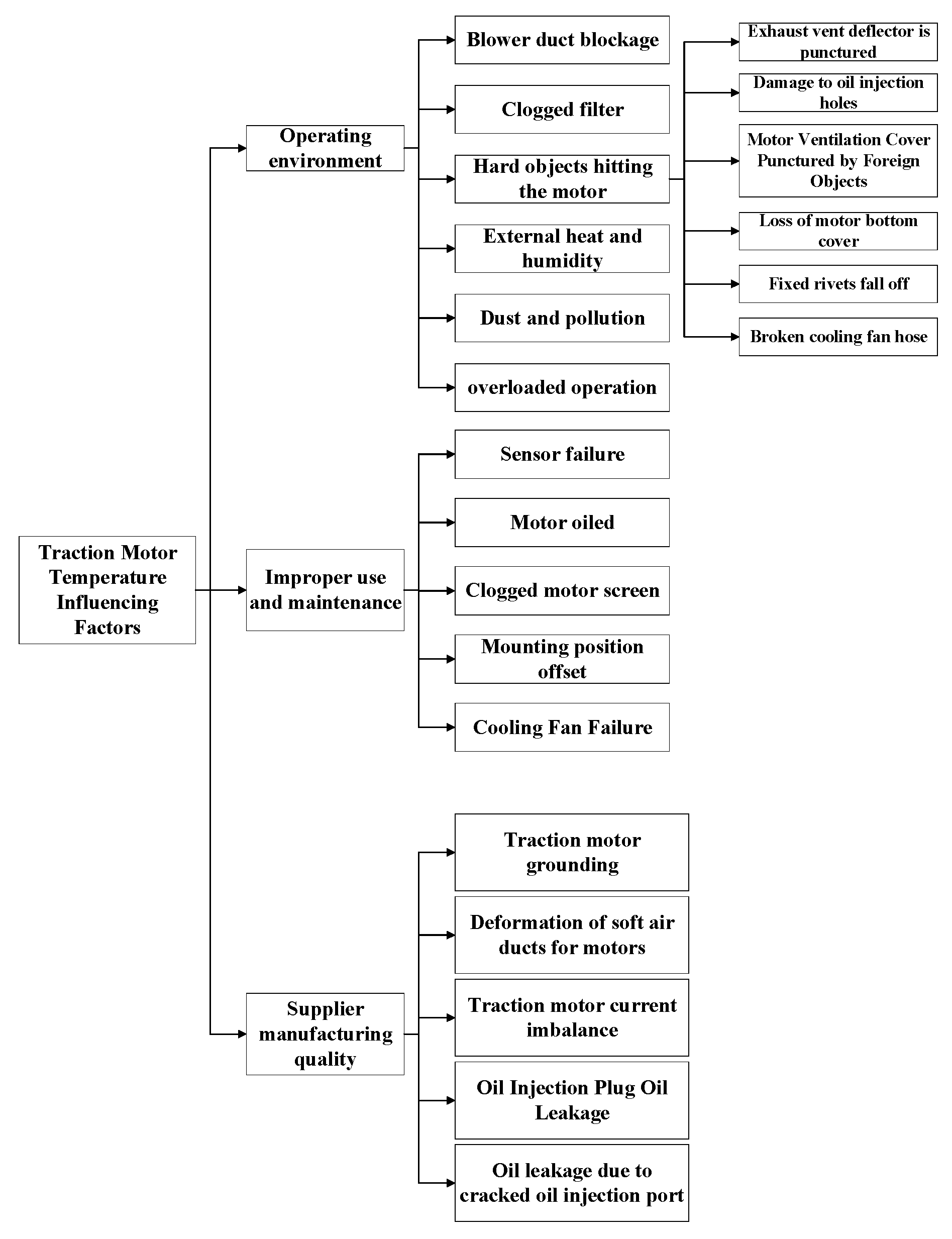
The traction motor is an important device in high-speed trains, which is mainly composed of a stator, rotor, sensor, and so on, and the stator and rotor of the traction motor are its key components [22]. Because the traction motor has a complex structure and operates in variable environments, there are many factors affecting its temperature change. For example, seasonal changes, regional differences, and other external conditions will have an impact on the operation of the traction motor, which may lead to high temperatures in the traction motor and affect the safe operation of the train. Therefore, predicting the state of traction motors based on the consideration of internal and external factors is of great significance for improving their operational efficiency and safety. In this study, various factors affecting the temperature of traction motors are investigated to provide a theoretical basis for improving the reliability and maintenance efficiency of traction motors. Based on the existing fault data, we summarize the factors affecting the temperature of traction motors into three major categories, as shown in Figure 1.

As shown in Figure 1, temperature variations can indicate numerous state abnormalities. Utilizing temperature signals as an objective function for analyzing and predicting the state changes of traction motors facilitates the early detection of potential faults, optimizes maintenance schedules, reduces risks, and enhances the safety and efficiency of the entire train system.

Due to the complexity and variability of the factors affecting the temperature of traction motors and the operating environment, data-driven methods may be more applicable than physical model-based methods for motor fault prediction [23]. Data-driven methods do not require a priori knowledge and have good scalability and generalization capabilities, which can improve the accuracy of prediction [24]. Choosing a suitable prediction method has a great impact on the accuracy of traction motor state prediction, and existing studies have explored the use of various types of fault prediction methods in a variety of fields. Wang et al. [25] utilized an improved feedforward-long short-term memory method to achieve whole-life-cycle charge state prediction of lithium-ion batteries, taking into account the variations in current, voltage, and temperature, which improves energy management and safety. Hošovský et al. [26] proposed an advanced prediction model referred to as genetic-algorithm-optimized regression wavelet neural network. This method first decomposes the temperature time series residuals via wavelet analysis. Subsequently, it constructs a multivariate nonlinear auto regressive model using an S-based neural network. Hua et al. [27] proposed a wind speed prediction method. The raw wind speed data were first decomposed into multiple subsequences using Variational Mode Decomposition. Then, feature extraction was performed using partial least squares to obtain the best test set. A simulated annealing algorithm was added to the atomic search optimization to enhance the local search capability, and then the Extreme Learning Machine was optimized using the improved atom search optimization algorithm, making the prediction more accurate. Lin et al. [28] proposed a short-term traffic flow prediction method based on the Maximal Information Coefficient feature selection, Support Vector Regression, and K-Nearest-Neighbors, which introduced a time delay to construct the time-delayed traffic volume sequence. Due to the existence of outliers and missing values in the data collected by sensors, Chen et al. [29] proposed a method combining Bayesian temporal decomposition and vector autoregressive process for modeling multidimensional time series data, especially spatio-temporal data, in the presence of missing values. By integrating the low-rank matrix tensor decomposition and the vector autoregressive process into a single probabilistic graphical model, probabilistic forecasting and generation of uncertainty estimates can be efficiently performed without the need to interpolate missing values.

The above methods are mainly offline prediction methods, while high-speed trains are equipped with multiple sensors to collect data, which can transmit some important parameters in real time for analysis, and processing these real-time data based on online models and updating the prediction model parameters in real time can improve the prediction accuracy, which is of great significance for real-time fault prediction. There are many scholars studying online learning methods. Shi Wenjun et al. [30] proposed an on-planet adaptive power control method based on online-gated recurrent unit channel prediction, which prevents the offline algorithms from generating cumulative errors by real-time training data in order to update the network parameters. Yaojian Wang et al. [31] proposed a short-term wind power probability distribution prediction model based on the online Gaussian Process (GP), which greatly improves the GP-solving efficiency while ensuring accurate GP inference. Wang F K et al. [32] proposed a bidirectional long- and short-term memory model with an attention mechanism, which predicts the online RUL by continuously updating the model parameters. Tantisripreecha T [33] proposed a Linear Discriminant Analysis (LDA) online learning method that incrementally fits a learning model using historical inventory as a training set for LDA. Thomas Bohnstingl et al. [34] proposed a biologically inspired Online Spatio-Temporal Learning algorithmic framework aimed at solving the problem of deep neural networks with traditional limitations of backpropagation through time and Real-time recursive learning (RTRL) methods when dealing with continuous data streams. Dong H et al. [8] proposed an online health monitoring framework using temperature signals to predict the health status of traction motors, where the prediction model can be optimized online to continuously extract information from historical and real-time data.

However, offline prediction models struggle to balance real-time performance and accuracy issues. In the field of railway transportation, the operation safety and efficiency of high-speed trains are crucial, while the operating environment of high-speed locomotive motors is complex and diverse, and their prediction needs to satisfy the requirements of timeliness and accuracy at the same time.

In order to ensure the optimal comprehensive efficiency of the intelligent operation and maintenance system of high-speed railways, a large number of scholars have studied the PHM technology and extended it to the railway field [35,36,37], but the research on the online state prediction technology for intelligent train equipment is still insufficient, and the online prediction model has a certain advantage over the offline model for the prediction under the intelligent high-speed railway operation scenario. Therefore, this paper is of great significance for analyzing the traction motor temperature signal and carrying out research based on a multi-factor online learning model.

3. Methods

In the online learning method, the data arrive sequentially and the prediction parameters are updated gradually, which is suitable for the case of dynamic data and time function generation [38]. High-speed trains can transmit data to the wireless data transmission device system (WTDS) in real time, so they can analyze the data in real time, input the real-time data into the model, optimize the model parameters online, and get the next prediction results; due to the high timeliness requirements of the fault prediction problem and the strict national requirements on the safety of high-speed railway transportation, it is necessary to put forward a higher requirement for the accuracy of high-speed railway fault prediction, and online learning can better satisfy the above two requirements.

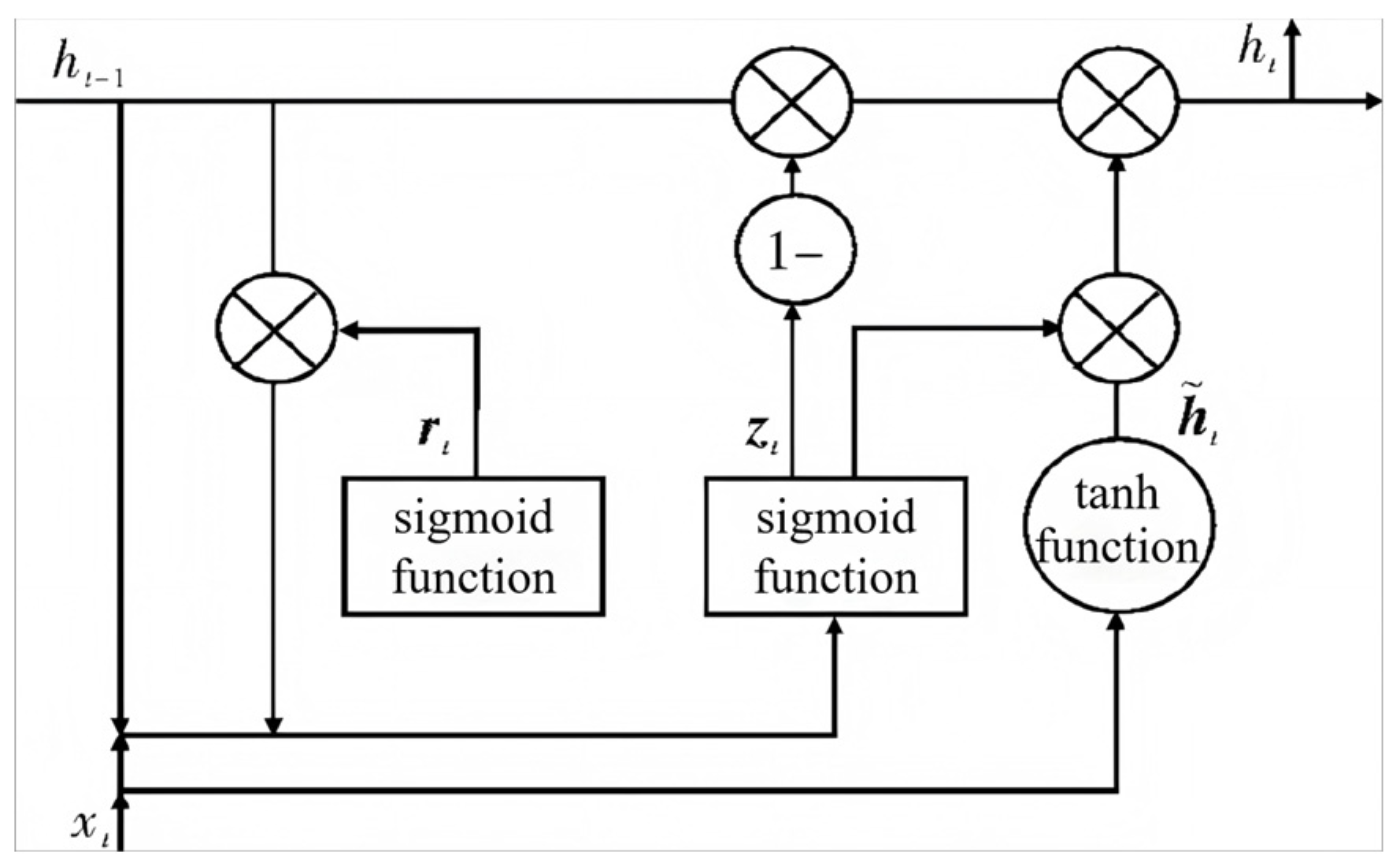
RTRL has high computational complexity and is prone to problems such as gradient vanishing or gradient explosion, and there are many algorithms investigating how to reduce its time complexity [39], but they are not sufficiently adapted to the scenario of this paper, where the interval of data transmission is 1 min. In order to ensure the timeliness and accuracy of the problem studied in this paper, this paper uses the OGRU model for prediction, and the traditional GRU is shown in Figure 2.

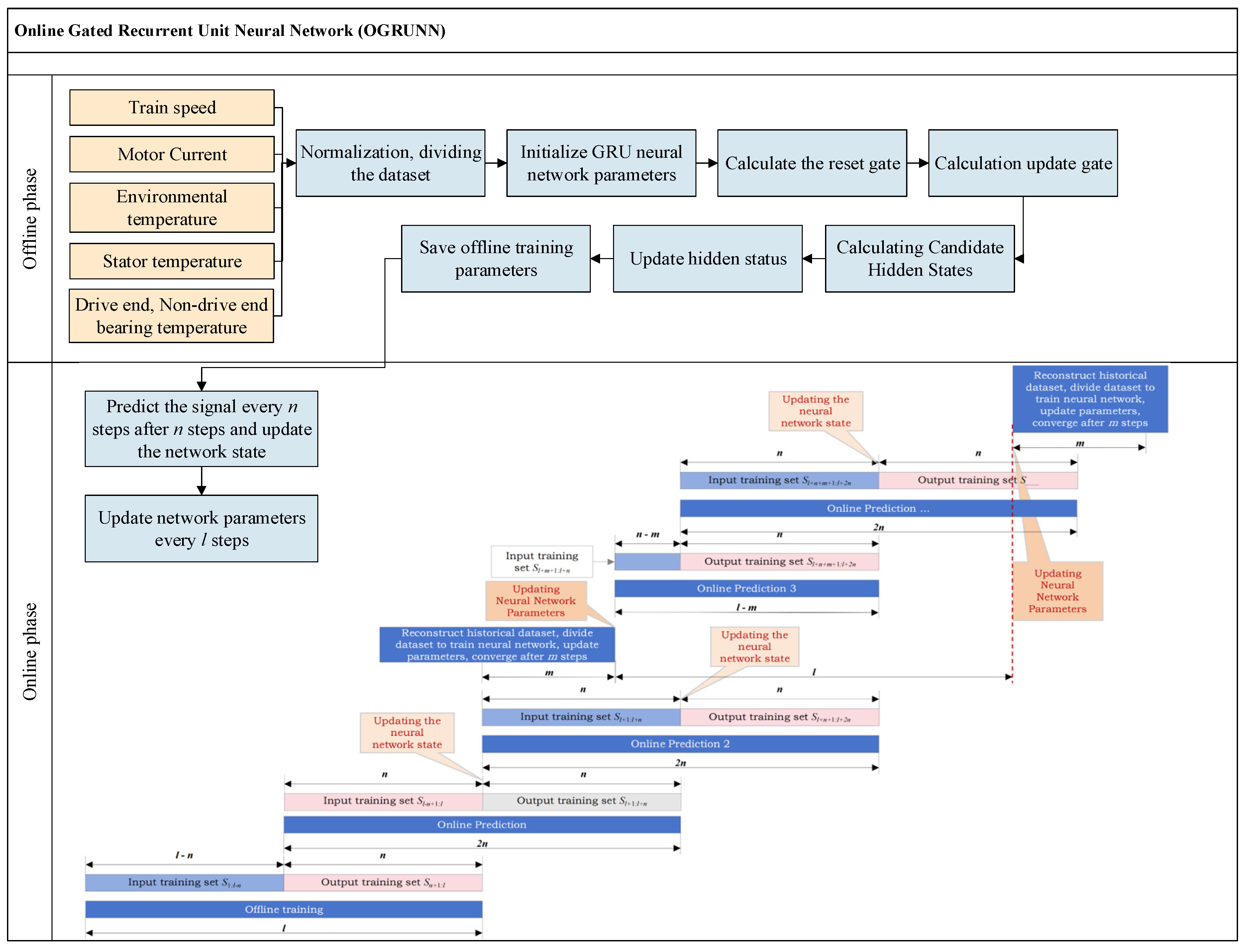
The online optimization prediction model proposed in this paper is divided into two phases. The first phase involves offline learning, where a large volume of data is fed into the neural network to train it, resulting in initial parameters for the online gated recurrent neural network at each update through offline training. The subsequent phase is the online stage, where the initial model parameters are adapted based on real-time data collected by traction motor sensors, enabling parameter updates and predictions. The online prediction results are derived, and the workflow of this online optimized prediction model is illustrated in Figure 3.

When online, the prediction results of the subsequent $n$ steps are predicted every $n$ steps, and the training results of the subsequent $n$ steps returned from the ground are used to predict the results of the further $n$ steps. At the same time, the overall parameters of the neural network are updated every $l$ steps using the data from the previous $l$ steps and converge after $m$ steps, as follows:

In the offline training part, the traction motor temperature data set is divided, and the neural network is trained offline using the input-output training set $S_{1:l-n}$ and $S_{n+1:l}$ data set, where $n$ is the signal transmission interval, and since the signal transmission interval in this paper is 1 min, and the sampling interval is also 1 min, the interval $n$ is set to be the prediction step, taking 1.

Calculate the update gate $r_t$ as in Equation (1) [40]:

$$\begin{array}{c}{r}_t=sigmoid\left(W_r\cdot \left[h_{t-1},x_t\right]\right)\end{array}$$

(1)

Calculate the reset gate $z_t$ as in Equation (2) [40]:

$$\begin{array}{c}{z}_t=sigmoid\left(W_z\cdot \left[h_{t-1},x_t\right]\right)\end{array}$$

(2)

Calculate the candidate hidden state $\widetilde{h_t}$ as in Equation (3) [40]:

$$\begin{array}{c}\widetilde{h_t}=\mathit{tanh}\left(W_{\widetilde{h_t}}\cdot \left[r_t\times h_{t-1},x_t\right]\right)\end{array}$$

(3)

Calculate the hidden state $h_t$ as in Equation (4) [40]:

$$\begin{array}{c}{h}_t=\left(1-z_t\right)\times h_{t-1}+\widetilde{h_t}\end{array}$$

(4)

Calculate the output signal $y_t$ as in Equation (5) [40]:

$$\begin{array}{c}{y}_t=sigmoid\left(W_o\cdot h_t\right)\end{array}$$

(5)

In Equations (1)–(5), [ ] denotes the vectors connected, $\times$ denotes the product of matrices, $h_{t-1}$ denotes the information of the previous time series, $x_t$ denotes the input of the current time step, which is the influencing factor of the traction motor temperature in the example of this section, and $h_t$ denotes the output of the current time step, which is the traction motor temperature signal in the example of this section. $W_r$, $W_z$, $W_{\widetilde{h_t}}$, and $W_o$ are the model parameters which denote the update gate weight, reset gate weight, candidate set weight, and output weight, respectively, and $sigmoid$ and $tanh$ denote the activation function of the neural network, which is calculated as shown in Equations (6) and (7):

$$\begin{array}{c}sigmoid\left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}\end{array}$$

(6)

$$\begin{array}{c}tanh\left(x\right)={\displaystyle \frac{e^x-e^{-x}}{e^x+e^{-x}}}\end{array}$$

(7)

The training optimization update is performed separately for the splice vectors $W_r$, $W_z$, $W_{\widetilde{h_t}}$ as in Equations (8)–(10):

$$\begin{array}{c}{W}_r=W_{rx}+W_{rh}\end{array}$$

(8)

$$\begin{array}{c}{W}_z=W_{zx}+W_{zh}\end{array}$$

(9)

$$\begin{array}{c}{W}_{\tilde{h}}=W_{\tilde{h}x}+W_{\tilde{h}h}\end{array}$$

(10)

The input of the output layer is $y_t^i=W_{o}h$, the output is $y_d=sigmoid\left(y_t^i\right)$, and $y_d$ is the final output.

$$\begin{array}{c}{E}_t={\displaystyle \frac{1}{2}}{\left(y_d-y_t^o\right)}^2\end{array}$$

(11)

Considering the error term at the current time step and setting it as ${\delta }_t=\mathsf{\partial }E/\mathsf{\partial }{h}_t$, then back propagating the error in time requires calculating the error ${\delta }_{t-1}$ at the moment $t-1$, which is as in Equation (12).

$$\begin{array}{c}{\delta }_{t-1}={\displaystyle \frac{\mathsf{\partial }E}{\mathsf{\partial }{h}_{t-1}}}={\displaystyle \frac{\mathsf{\partial }E}{\mathsf{\partial }{h}_t}}{\displaystyle \frac{\mathsf{\partial }{h}_t}{\mathsf{\partial }{h}_{t-1}}}={\delta }_t{\displaystyle \frac{\mathsf{\partial }{h}_t}{\mathsf{\partial }{h}_{t-1}}}={\delta }_{r,t}{W}_{rh}+{\delta }_{z,t}{W}_{zh}+{\delta }_{\tilde{h},t}{W}_{\tilde{h}h}+{\delta }_{y,t}{W}_o\end{array}$$

(12)

With the above equation, the partial derivatives of each weight are calculated and the learning rate is chosen, the parameters are optimized using stochastic gradient descent in order to inversely adjust the structure of the GRU network, and the trained model can be used for prediction in this paper.

The input training set $S_{l-n+1:l}$ is used as input to predict the output sequence $S_{l+1:l+n}$ after $n$ steps.

After $n$ steps, the network state is updated according to the uploaded input $S_{l+1:l+n}$ and the output sequence $S_{l+n+1:l+2n}$ is predicted after $n$ steps, and at the same time, the previous input-output dataset $S_{1:l+n}$ is reconstructed to be used for training the neural network to update all the parameters of the network, which converges after $m$ steps, and in the process of reconstructing the neural network training, in order to ensure the online prediction model runs normally, all the data transmitted during the training period are are predicted using the original GRU neural network parameters, while after the training is completed, the input training set $S_{l+m+1:l+n}$ is used to predict under the new parameters to obtain the output sequence $S_{l+n+m+1:l+2n}$.

Afterwards, the first $n$ steps of data are still used to predict the next $n$ steps of data, and the first $l$ steps of signal data are inputted every $l$ steps to train the neural network and update the overall parameters of the neural network. The above process is repeated.

The model pseudo code is shown in Algorithm 1.

Algorithm 1. Online prediction of pseudo code.

Algorithm 1 Online Gated Recurrent Neural Network Prediction

Import torch, torch.nn, GRU, pandas, numpy, scipy.io, matplotlib.pyplot, matplotlib, torch.autograd, math, csv, adabound, time

Input: The current of the motor, drive end bearing temperature, non-drive end bearing temperature, speed of the train and the external temperature are defined as data_x;

Output: Define the stator temperature of traction motor as data_y

use a sequence for offline training and save the initial parameters of GRU model

loading initial parameters of GRU model

Initialize variables list, m, data_begin, and data_end

for i in range(len(data_x)):

if (i + 1) % 1000 == 0:

train the model with data of a sequence length and update the model parameters

if (i + 1) % 1 == 0:

pred_output = gru_model(input_tensor).to(device)

For each data point, make predictions and calculate error metrics ($RMSE$, $MSE$, $MAE$, $MBE$)

update the model parameters

save the predicted results to the list, convert it to a numpy array, and save it to the Excel file ‘pred.xlsx’

calculate the code execution time

end

4. Data and Analysis

4.1. Dataset Introduction

The high-speed train set studied in this paper consists of an eight-carriage formation, comprising two trailer carriages (T1 and T2) and six motor carriages (M1–M6). Pantograph devices are installed on the roofs of carriages M3 and M6 (corresponding to vehicles 4 and 6 in

Table 1. Distribution of traction motor in the traction system of high-speed trains.

System	Component	Carriage No.1	Carriage No.2	Carriage No.3	Carriage No.4	Carriage No.5	Carriage No.6	Carriage No.7	Carriage No.8
	Traction motor		◯ × 4	◯ × 4	◯ × 4	◯ × 4	◯ × 4	◯ × 4

◯ means components, ◯ × 4 means there are 4 components.

). Carriages 2 to 7 are each equipped with four traction motors, while carriages 1 and 8 are fitted with external environmental temperature sensors. As a result, the entire train includes a total of 24 traction motors and 2 external environmental temperature sensors. The simplified diagram of the train set used in this study is shown in Figure 4, and Table 1 displays the distribution of key electrical components in the traction system.

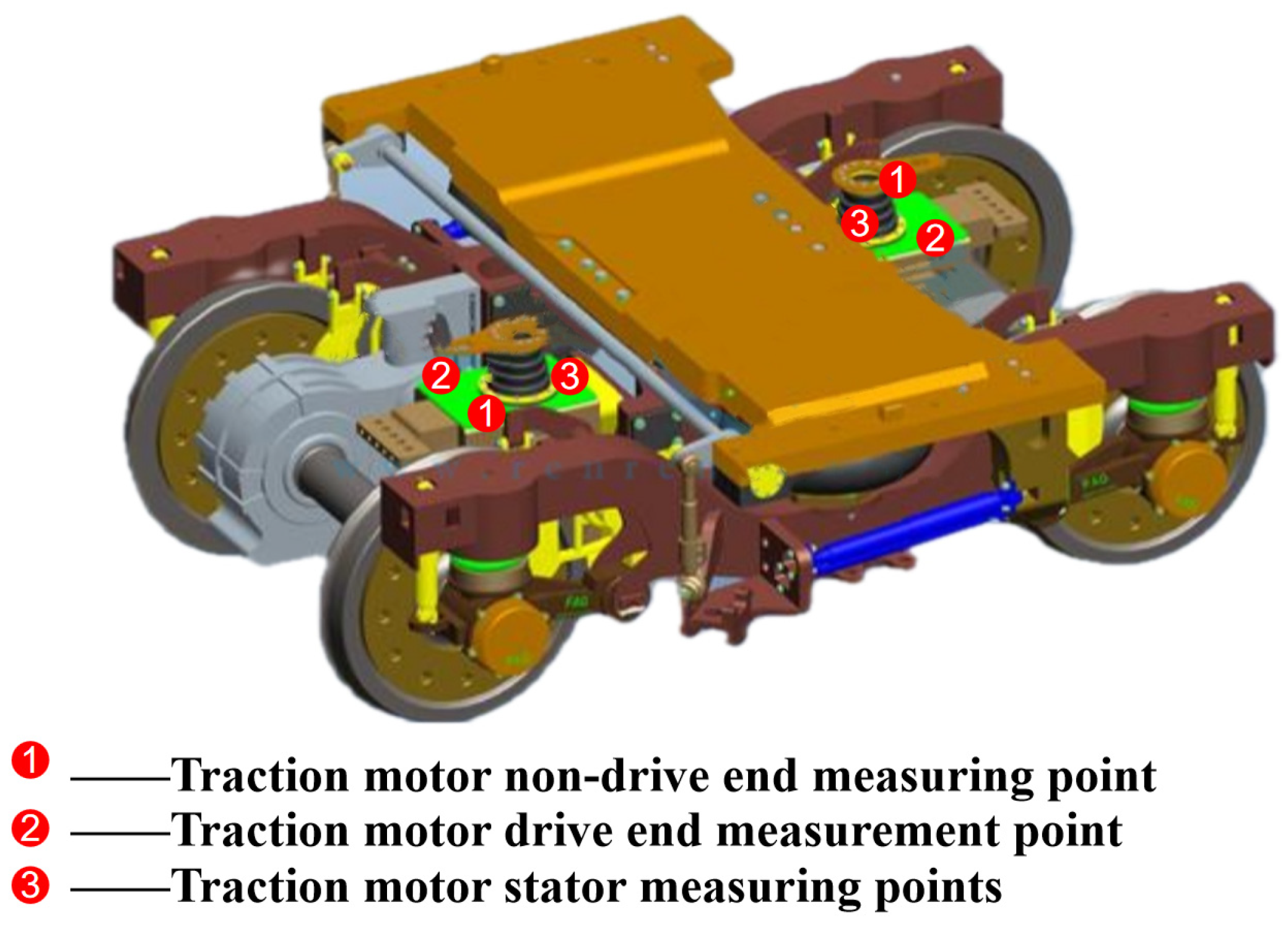
The high-speed train set analyzed in this paper is equipped with a YJ92B/YQ-365 traction motor. The locations of the temperature measurement points on the traction motor are shown in Figure 5.

The dataset comprises six-dimensional data collected from the eight-carriage high-speed train set. During real-time operation, data are sampled at a rate of 0.2 s per sample. When stored offline in the database, the data are transmitted to the data center at intervals of 1 min per sample. During online operation, data are transmitted to the data center in real time at intervals of 1 s per sample.

Data acquisition primarily relies on various advanced sensor technologies. For high-speed train sets, the number of sensors is substantial, with typical types including temperature, voltage, current, and speed sensors.

In this study, the temperature sensors mainly measure three types of temperature signals from the traction motors and external temperature signals, with units in degrees Celsius (°C). The current sensors primarily record the magnitude of the current passing through the traction motors, with units in amperes (A). The speed sensors primarily capture the train’s velocity, with units in kilometers per hour (km/h). Sensors mounted on high-speed train components collected parameters such as non-drive-end bearing temperature, drive-end bearing temperature, stator temperature, motor current, external ambient temperature, and train speed of the traction motor, which were processed and used in the data format shown in

Table 2. High-speed train parameters used in this paper.

Time	1 August 2023 10:00	1 August 2023 10:01	1 August 2023 10:02	1 August 2023 10:03	1 August 2023 10:04	1 August 2023 10:05	…
Stator temperature of shaft No. 1 (°C)	108	107	106	101	100	97	…
Bearing temperature at the drive end of shaft No. 1 (°C)	59	57	57	57	56	56	…
Non-drive end bearing temperature of shaft No. 1 (°C)	48	48	48	48	48	48	…
Stator temperature of shaft No. 2 (°C)	112	112	109	106	104	100	…
Bearing temperature at the drive end of shaft No. 2 (°C)	59	57	57	56	56	55	…
Non-drive end bearing temperature of shaft No. 2 (°C)	48	48	48	48	48	48	…
Stator temperature of shaft No. 3 (°C)	114	113	110	109	106	104	…
Bearing temperature at the drive end of shaft No. 3 (°C)	61	60	59	59	59	58	…
Non-drive end bearing temperature of shaft No. 3 (°C)	51	51	51	51	51	51	…
Stator temperature of shaft No. 4 (°C)	108	107	105	104	100	98	…
Bearing temperature at the drive end of shaft No. 4 (°C)	62	62	60	60	59	59	…
Non-drive end bearing temperature of shaft No. 4 (°C)	51	51	51	51	51	51	…
Value of current (A)	464	315	232	0	0	0	…
Temperature of the external environment (°C)	37	37	37	37	37	37	…
Train speed (km/h)	123	70	41	37	14	10	…

. The experiments involved collecting temperature and current signals from all traction motors of the high-speed train set within a single day, as well as the train set’s speed signal and external environmental temperature signal. The sampling interval was 1 min. In total, the dataset comprises sensor signals from 62 days, covering 24 motors from 6 motor carriages (M1–M6). Therefore, a one-day sequence includes a total of 72 (24 × 3)-dimensional motor temperature features, 6 (6 × 1) dimensions of motor current features, 2 (2 × 1) dimensions of external environmental temperature features, and 1 (1 × 1) dimension of the train speed feature.

Table 2 presents a subset of data from August. The dataset used for model training comprises full-day data from August and January over a 62-day period, sampled at 1 min intervals. As the train operates, all dimensional data in Table 2 continuously fluctuate: speed and current decline sharply as the train approaches a station, while temperature varies gradually.

4.2. Characterization of State Parameters of Traction Motors

Before applying deep learning techniques to learn the parameters, the traction motor state parameter dataset is first subjected to further analysis. By examining the characteristics and correlations of these data, an understanding of the train’s actual operating condition is obtained, and the specific performance and features of the traction motor under various working conditions are identified. Based on this analysis, parameters related to the influencing factors of the traction motor temperature are selected to significantly enhance the accuracy of traction motor condition prediction.

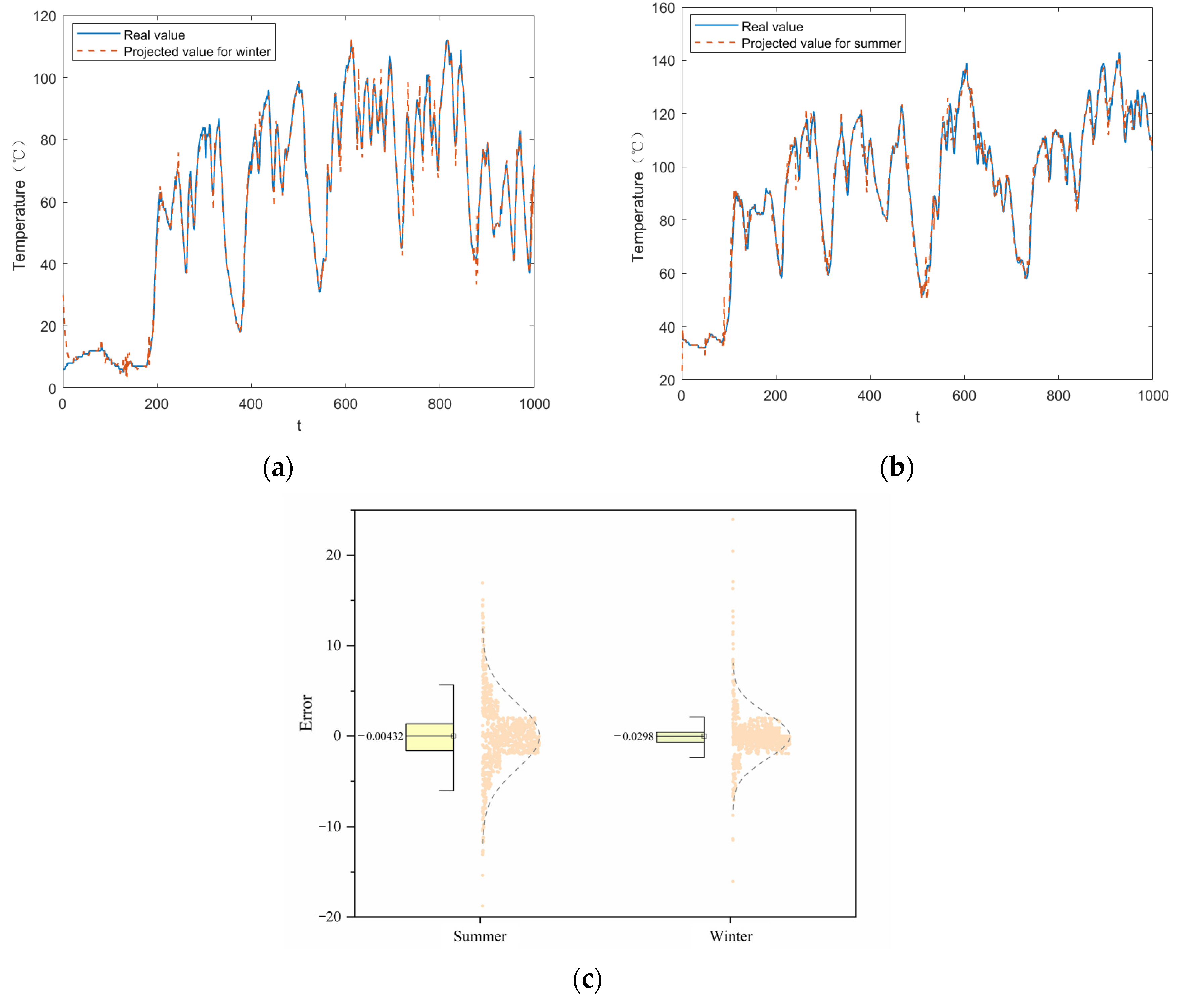
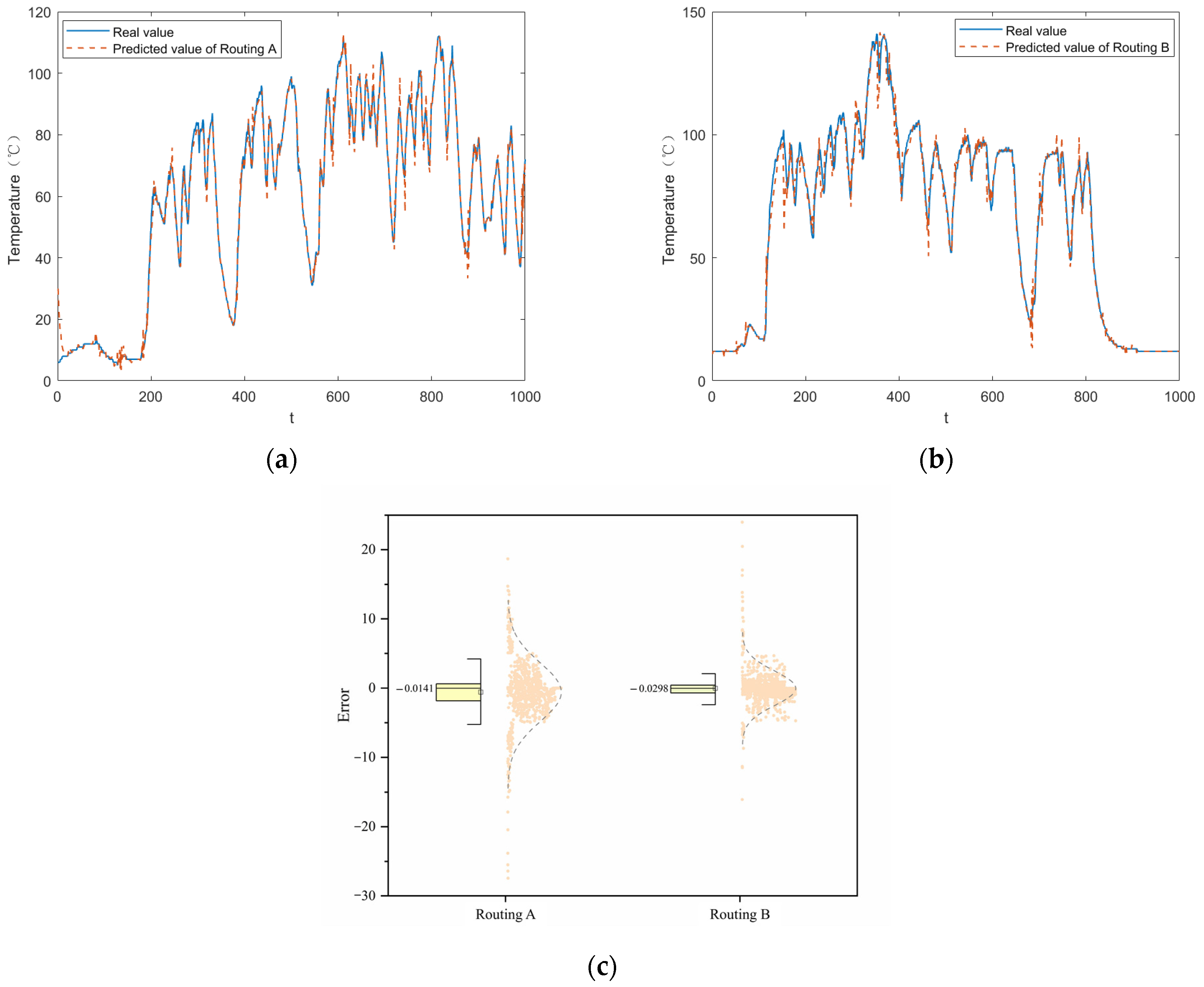
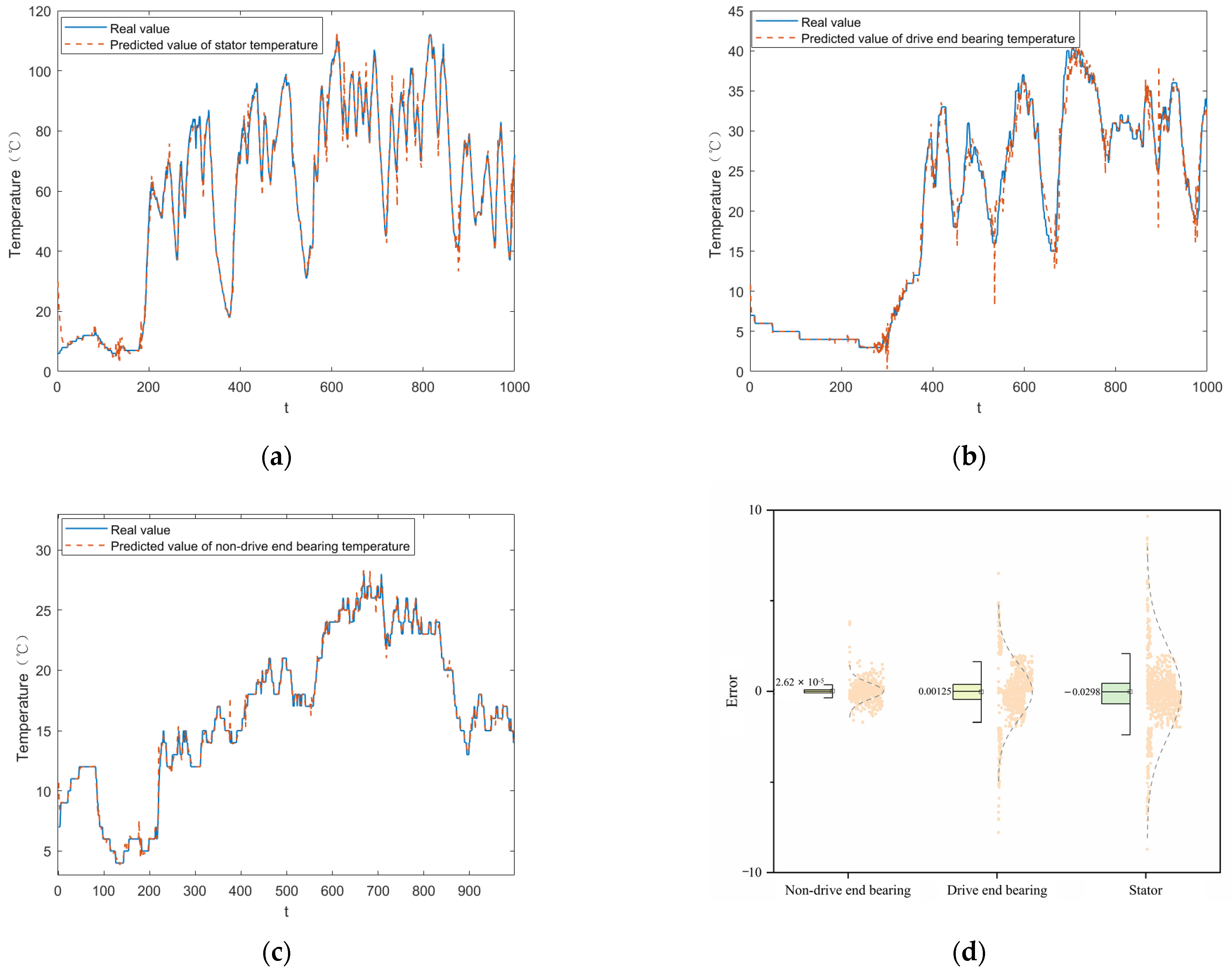
Because of the large temperature variations across different seasons for the same train routing, and because external environmental temperatures also influence the average temperature of the traction motor, these factors affect the prediction model. There are differences among the drive end bearing temperature, non-drive end bearing temperature, and stator temperature of the traction motor. The selection of different output parameters as the model’s target also impacts the effectiveness of the prediction. Moreover, train performance indices may vary across different routings at the same time due to environmental conditions such as humidity and wind, further influencing model accuracy. Therefore, to account for these factors, analyses are conducted on the same index of traction motors across different seasons, different indices of the same rolling stock on the same day, and the indexes of various routings within the same day.

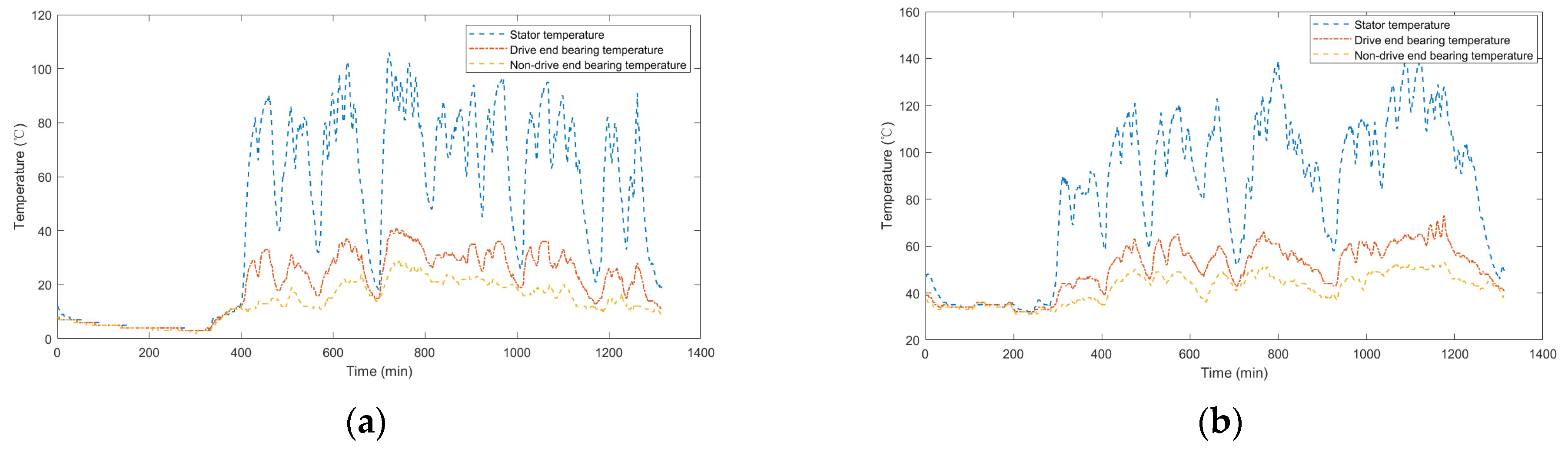
This paper begins with a comparison of various traction motor parameters across different seasons. Typically, during the train’s operation, the stator temperature exceeds the drive end temperature, which is higher than the non-drive end temperature. However, when the train is stationary, the differences among the three temperatures are minimal. Analysis of the temperature parameters for the stator, drive end, and non-drive end bearings reveals that the stator’s temperature exhibits relatively large fluctuations, decreasing most rapidly when the train stops. In August, the average values for the stator, drive end, and non-drive end bearing temperatures were 83 °C, 50 °C, and 42 °C, respectively. Given that high temperatures can easily lead to various abnormalities, this study uses the stator temperature with the highest average temperature among the three as the objective function.

Comparing the same indicator in different seasons in Figure 6, the results show that the temperature change of the stator, drive end, and non-drive end of the traction motor is not obvious when the train is not started, which is mainly related to the season. When the train starts running, the average temperature at the three measurement points is higher in August than in January due to the ambient temperature. However, during train operation, the average variation of temperature in January is greater than that in August for all the three parameters. The stator, which is inside the motor, is relatively minimized by environmental factors during operation, and its temperature change should have a greater correlation with the train operating speed, while the bearing temperature, which is relatively closer to the outside, is more significantly affected by the ambient temperature. On the same day, different train routings may be due to large differences in ambient temperature, humidity, wind, and differences in operating speeds, resulting in very different temperature averages and trends. Therefore, the specific conditions of the train routings in different seasons should be fully considered in the forecast.

During train operation, the temperature trends of the stator and drive-end bearings are generally similar. However, the temperature trend of the non-drive end differs slightly from the other two measurement points. This variation is likely caused by the fact that the stator and drive-end bearings are more strongly influenced by train operating speed, whereas the non-drive-end bearings are more significantly affected by external environmental factors. Therefore, alarm signals for the stator-end and transmission-end bearings can be more effectively issued by considering the joint trend of both parameters.

5. Discussion

This study focuses on real-time prediction of traction motor temperature. To thoroughly assess the model’s performance, five evaluation indicators—Mean Squared Error ($MSE$), Root Mean Squared Error ($RMSE$), Mean Absolute Error ($MAE$), Mean Bias Error ($MBE$), and Mean Absolute Percentage Error ($MAPE$)—are employed. These evaluation indicators, collectively, evaluate the accuracy and bias of the predictions from different perspectives, ensuring a comprehensive and justified evaluation. The specific formulas are detailed in Equations (13)–(17).

$$\begin{array}{c}MSE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\left(y_i-\widehat{y_i}\right)}^2\end{array}$$

(13)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(14)

$$\begin{array}{c}MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}\left|y_i-\widehat{y_i}\right|\end{array}$$

(15)

$$MBE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(y_i-\widehat{y_i}\right)$$

(16)

$$\begin{array}{c}MAPE={\displaystyle \frac{100\%}{n}}{\displaystyle \sum _{i=1}^n}\left|{\displaystyle \frac{{\widehat{y_i}-y}_i}{y_i}}\right|\end{array}$$

(17)

where $n$ is the number of prediction samples, $y_i$ is the true value, $\widehat{y_i}$ is the predicted value.

5.1. Comparison of Online and Offline Learning

As shown in

Table 3. Comparison of prediction error between online optimization model and offline training model in this paper.

Model	MSE	RMSE	MAE	MBE	MAPE
Our online model	7.437	2.727	1.248	0.0430	0.0495
GRU offline model	94.448	9.718	7.659	−0.409	0.234

and Figure 7 and Figure 8, the vertical axes represent temperature, while the horizontal axes denote time (t). During online prediction, 1000 data points were selected for validation, with data transmitted at 1 min intervals, amounting to a total duration of 1000 min. Compared to the method of prediction that relies entirely on pre-trained neural networks, updating the parameters using the online training optimization prediction method can solve the problem of offline prediction that results in a large accumulation of errors, ensure that the prediction effect does not diminish over time, and improve the prediction accuracy.

As shown in Figure 9, comparing the results of the error distribution of online and offline, it can be seen that the online prediction has a larger error at the beginning because it is based on the parameters of the offline training model to predict, but the effect gradually becomes better and gradually stabilizes after updating the model online; as shown in Figure 9b, most of the error is concentrated near 0, while the offline prediction error may gradually accumulate because there is no real-time updating of the model; as shown in Figure 9c, the error fluctuates between ±25 °C, and the prediction effect is poorer compared to the online prediction. Note that the hollow square “▫” in all box plots represents the mean value.

5.2. Comparison of Predicted Results for Different Working Conditions

5.2.1. Comparison of Temperature Forecasts Under Different Seasons

Under different ambient temperatures, the initial temperature of the traction motor differs from the outside temperature of the train. As a result, the temperature variation during train operation may also vary. In this study, the prediction results for the traction motor temperature are selected from trains on the same routing across different months, as shown in

Table 4. Comparison of prediction errors for different seasons.

Season	MSE	RMSE	MAE	MBE	MAPE
Winter	7.437	2.727	1.248	0.0430	0.0495
Summer	8.211	2.865	1.742	0.00253	0.0206

. By using the temperature of the motor stator as the output signal, the prediction results for January and August are found to be similar. The prediction curves are presented in Figure 10a,b. The online prediction model demonstrates good predictive performance across different months.

The error distribution of the prediction results of the online model in different seasons is shown in Figure 10c, and the median errors in summer and winter are −0.00432 and −0.0298, and more than 80% of the errors in both are near 0, with not much difference in the prediction results, so the model of this paper performs well in different seasons, and it can be adapted to the prediction scenarios of the temperature signals of the motors in different seasons.

5.2.2. Comparison of Temperature Forecasts for Different Train Routings

Since different high-speed trains have different train routings, and different train routings may have different effects on the motor temperature due to their different humidity, temperature, and wind size, in order to verify the adaptability of the method proposed in this paper to different train routings, this section selects data from another routing with identical vehicle specifications, the same travel date, and consistent data dimensions as those in Table 2. Motor temperature predictions are conducted for both routings, and the results are shown in

Table 5. Comparison of prediction errors for different train routings.

Train Routing	MSE	RMSE	MAE	MBE	MAPE
Train routing A	7.437	2.727	1.248	0.0430	0.0495
Train routing B	18.394	4.289	2.432	−0.586	0.0374

and Figure 11a,b; the error of train routings A and B is slightly different, but with the adaptation of the model to the environment and the learning situation, the error also tends to stabilize, so the method in this paper has a certain adaptability to the temperature data of different train routings.

The prediction errors of different train routings are shown in Figure 11c, which shows that although there is a certain difference in the error between different routings, the median difference between the two is only 0.01, and the median of routing B is smaller, so intersection B is not as good as routing A with the overall prediction results, but the majority of the data prediction results are also more accurate, with smaller errors, so the prediction model in this paper has a certain degree of adaptability to different routings.

5.3. Comparison of Temperature Predictions at Different Measurement Points

As can be seen from the analysis in Chapter 4, due to the different sensor measurement point locations, different measurement points of the traction motor in the train operation received the influence of internal and external factors are not the same, and the temperature change time trend is not exactly the same; in order to verify the universality of this paper’s method, this paper on the temperature of the different measurement points are predicted, and the results are shown in

Table 6. Comparison of temperature prediction errors at different measurement points.

Measurement Point	MSE	RMSE	MAE	MBE	MAPE
Stator	7.437	2.727	1.248	0.0430	0.0495
Non-drive end bearing	2.267	1.506	0.852	−0.0315	0.0584
Drive end bearing	0.445	0.198	0.242	0.00553	0.0172

and Figure 12. As the temperature of the bearings at the non-drive end and drive end fluctuates less than that of the stator temperature, the prediction effect is better, but the prediction results of the stator temperature are also good, so the method of this paper has a certain degree of universality for different measurement points.

In Figure 12d, many scattered points fall outside the normal distribution envelope. The prediction errors for the non-driving end bearing temperature do not exhibit a clear normal distribution trend. This may be due to the fact that the network parameters were not significantly adjusted during the predictions at the three measurement points. When predicting the non-driving end bearing temperature, the model parameters may not have reached optimality, leading to overfitting and other reasons, thereby causing errors.

5.4. Comparison of Temperature Predictions with Different Prediction Steps

In this paper, the data of different prediction steps are discussed, and the cases when the steps are 1, 5, and 10 are selected to verify the prediction effect of the model in this paper, and the results are shown in

Table 7. Comparison of temperature prediction errors at different prediction steps.

Prediction Steps	MSE	RMSE	MAE	MBE	MAPE
1	7.437	2.727	1.248	0.0430	0.0495
5	11.847	3.305	2.292	−0.0309	0.0660
10	32.005	5.440	3.892	−0.0929	0.0811

; with the increase in prediction steps, the $RMSE$ increases gradually, but the average error is still within the acceptable range when the prediction step is 10.

As can be seen from Figure 13, the median error increases as the step size increases, but in general, the error distributions are all normally distributed, and most of the errors of the predicted values fluctuate around 0. The overall prediction effect is better.

5.5. Comparison of Different Forecasting Methods

Real-time prediction must meet latency requirements, making time consumption one of the key evaluation indicators. In this paper, the time consumption and $RMSE$ of the proposed online GRU prediction method are compared with the OLSTM method using the same dataset, and the results are shown in

Table 8. Comparison of different forecasting methods.

Volume of Data (Groups)	Evaluation Indicators	Our Model	OLSTM
N	Time(s)	6.490	7.372
	RMSE	2.546	2.304
2 N	Time(s)	11.809	12.607
	RMSE	2.727	2.897
3 N	Time(s)	16.824	21.926
	RMSE	2.932	6.631

, where N refers to a set of data volume, which is about half a day’s worth of data.

Since the model in this paper can update the model parameters by offline learning in time, the $RMSE$ of this paper’s method has been stable, but the cumulative error of OLSM increases with the increase in data volume and the variability of the environment. And with the increase in data volume, the time taken by this paper’s method is shorter compared to OLSM, and the prediction ability is better.

6. Conclusions

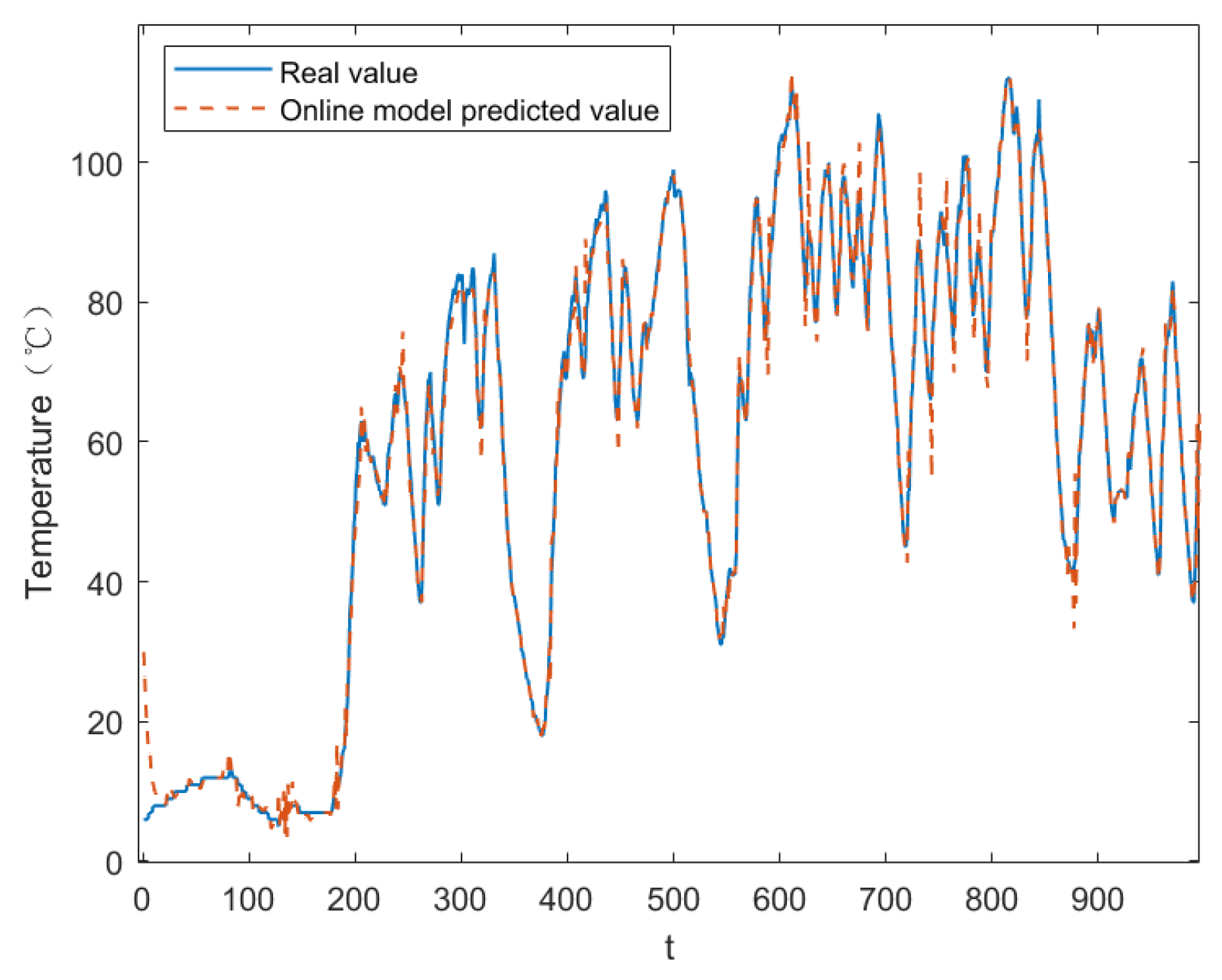
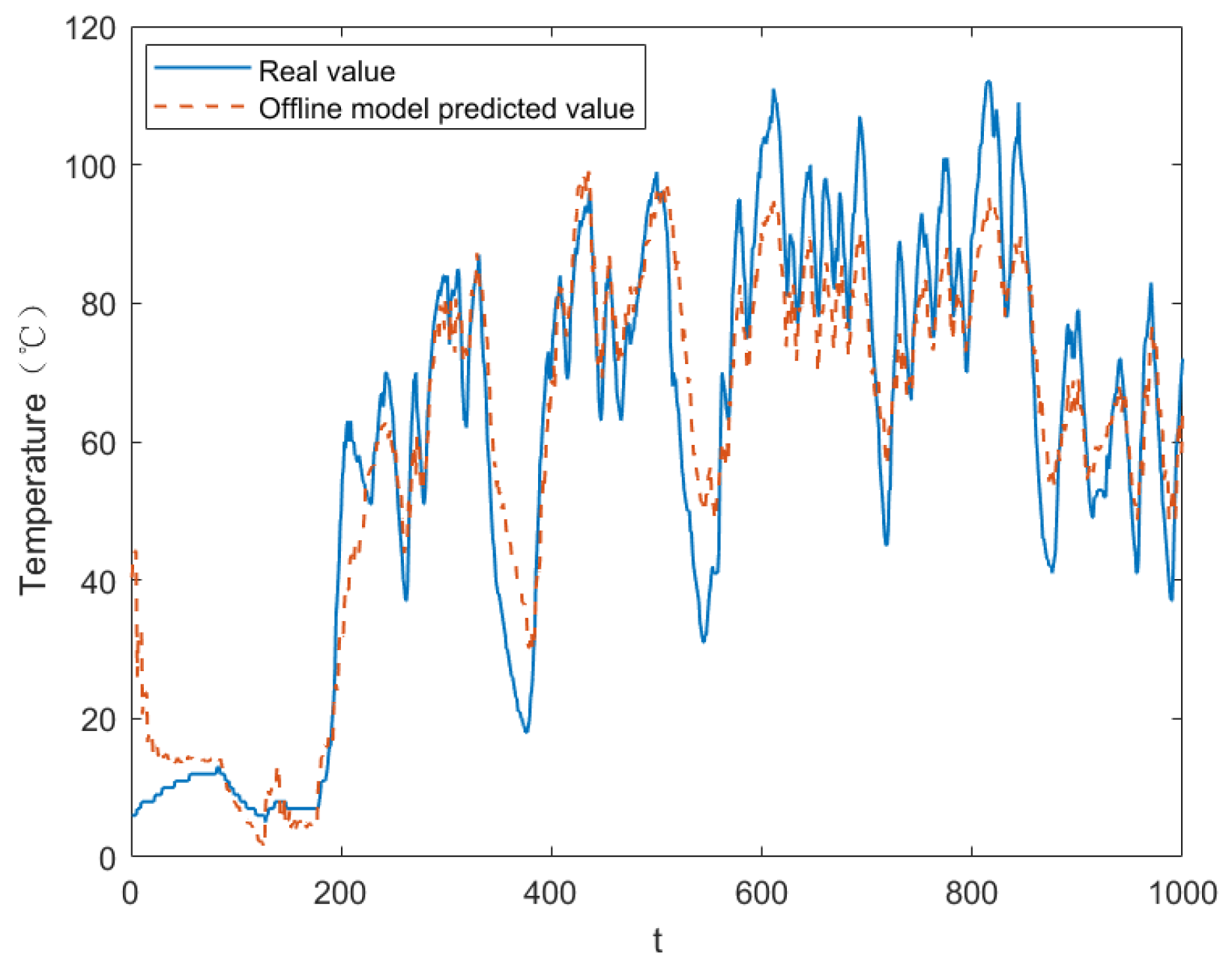
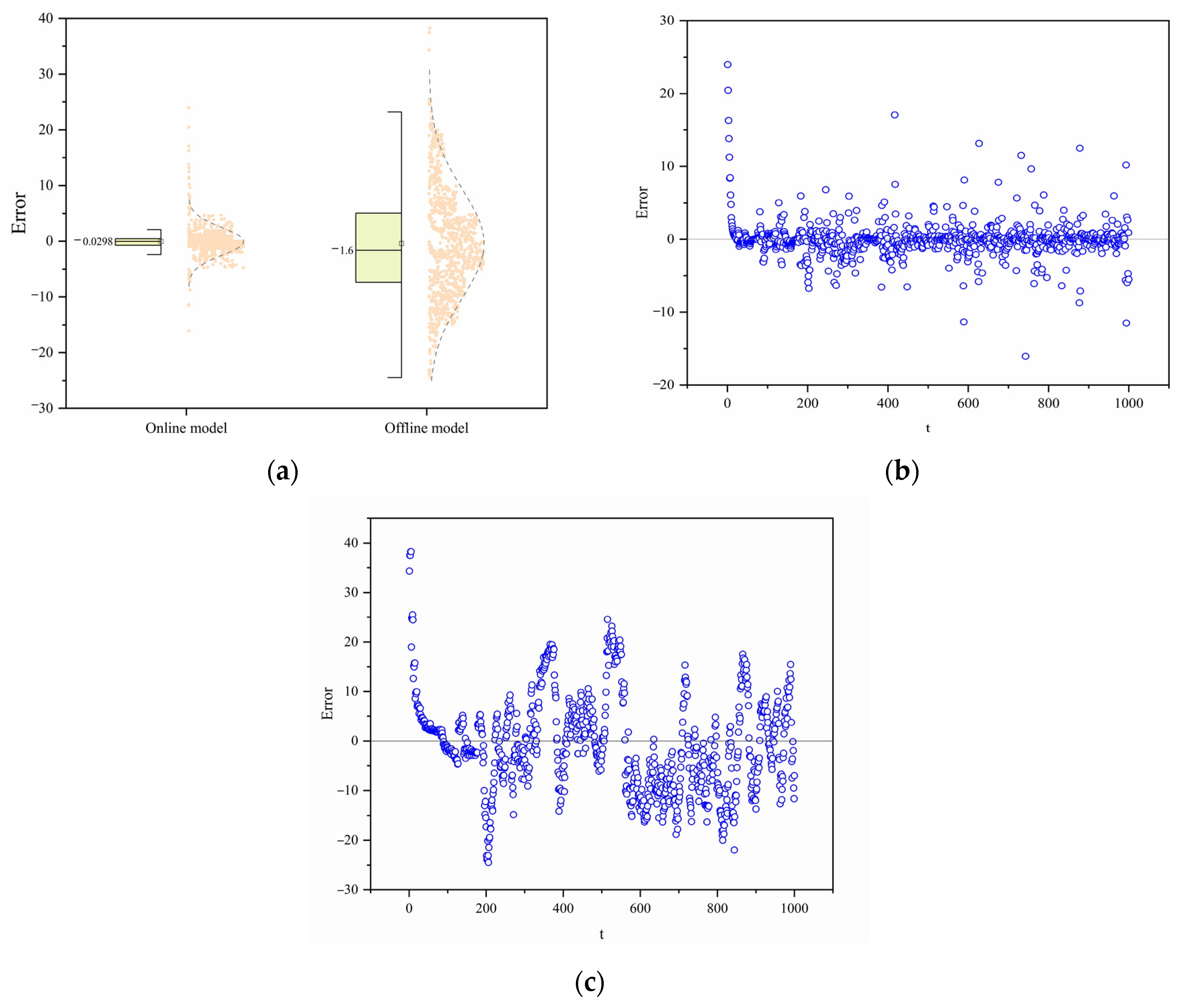
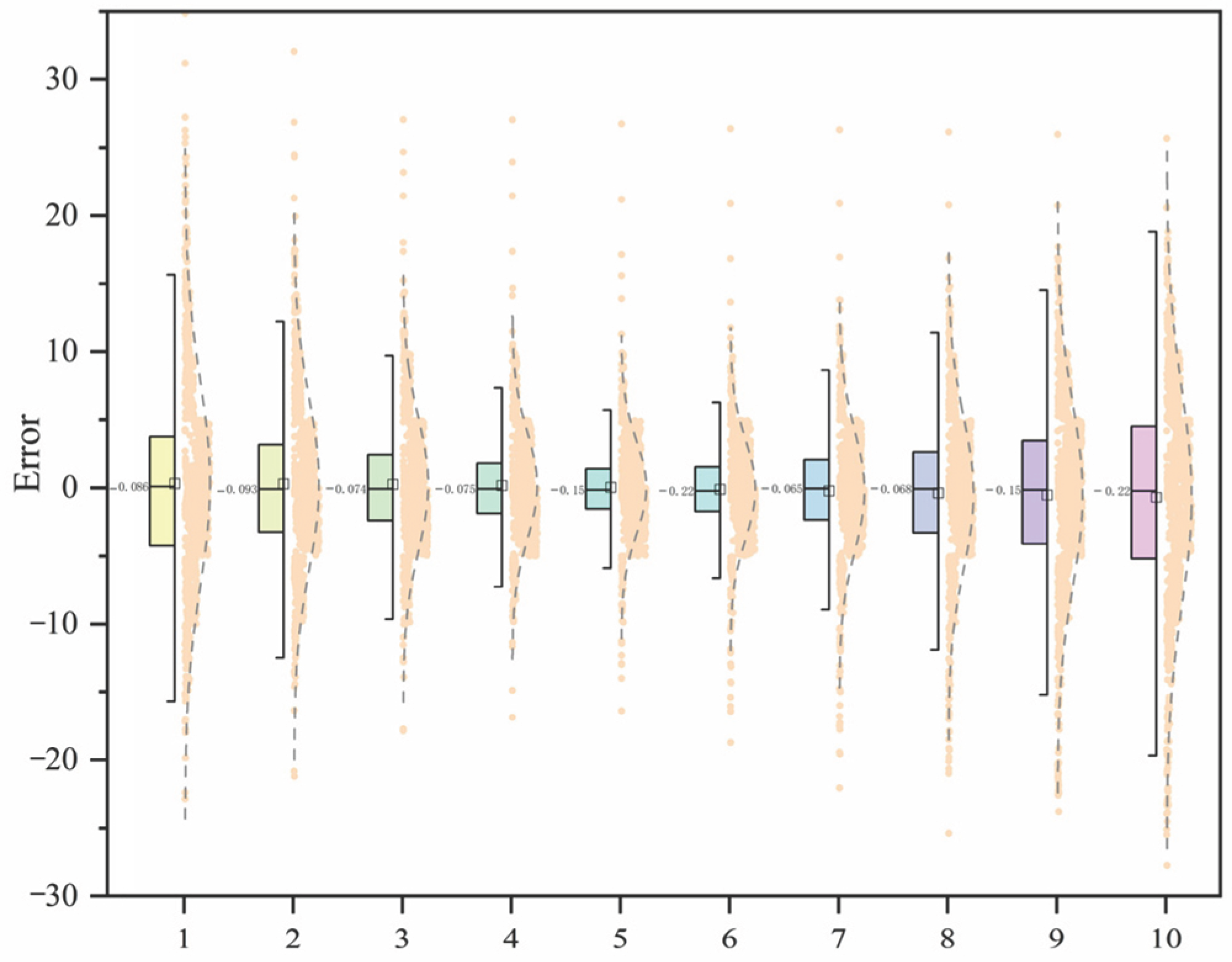
In this paper, an optimized prediction method for the traction motor temperature signal in rolling stock is proposed based on an online gated recurrent neural network. The methodology involves the following steps: collecting multidimensional time-series data via sensors and integrating environmental and operational factors to construct features, with stator temperature selected as the target variable; training a GRU model offline using historical datasets to optimize weight matrices and minimize $MSE$; in the online stage, receiving real-time data at 1 min intervals, employing multi-step rolling forecasts for future states, and dynamically updating model parameters periodically with the latest data to balance new knowledge and historical experience. Model accuracy and bias are evaluated using metrics such as $RMSE$ and $MAE$, while the model’s generalization ability is validated across different seasons, routings, and measurement points. Additionally, the computational efficiency of OGRU is compared with other online methods like OLSTM.

This method enables real-time processing of the traction motor temperature signal, allowing the online model to update its parameters and achieve real-time prediction. The approach improves prediction accuracy by approximately 70% compared to the offline method and demonstrates strong adaptability to various traction motor operating scenarios. The model’s adaptability under different working conditions is notable, although the speed of adaptation varies across environments. The offline training component of the model can be further improved to reduce prediction errors. When applied to different monitoring points, it is observed that the prediction performance for the stator temperature, which exhibits significant fluctuations, is slightly inferior to that of other measurement points. Nonetheless, the results remain stable and within acceptable ranges, confirming the model’s applicability across different scenarios and indicating its practical value.

Furthermore, when comparing the present model with OLSTM, the proposed model can reduce computation time by 23.3% or even less as the amount of data increases. Timeliness is critical for online prediction in high-speed train components, the current model essentially meets these timeliness requirements, thereby enhancing predictive maintenance efficiency and contributing to the broader goal of improving the sustainability of high-speed railways.

Future research will focus on exploring the operation mechanisms of trains and motors in greater depth, incorporating more comprehensive data such as vibration signals and historical fault records. This will aim to improve the accuracy of motor status predictions and allow for detailed fault cause analysis.