Pump Model for Drip Irrigation with Saline Water, Powered by a Photovoltaic Solar Panel with Direct and Intermittent Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Characterization
2.2. Irrigation System
2.3. Experimental Design
2.4. Experimental Procedure
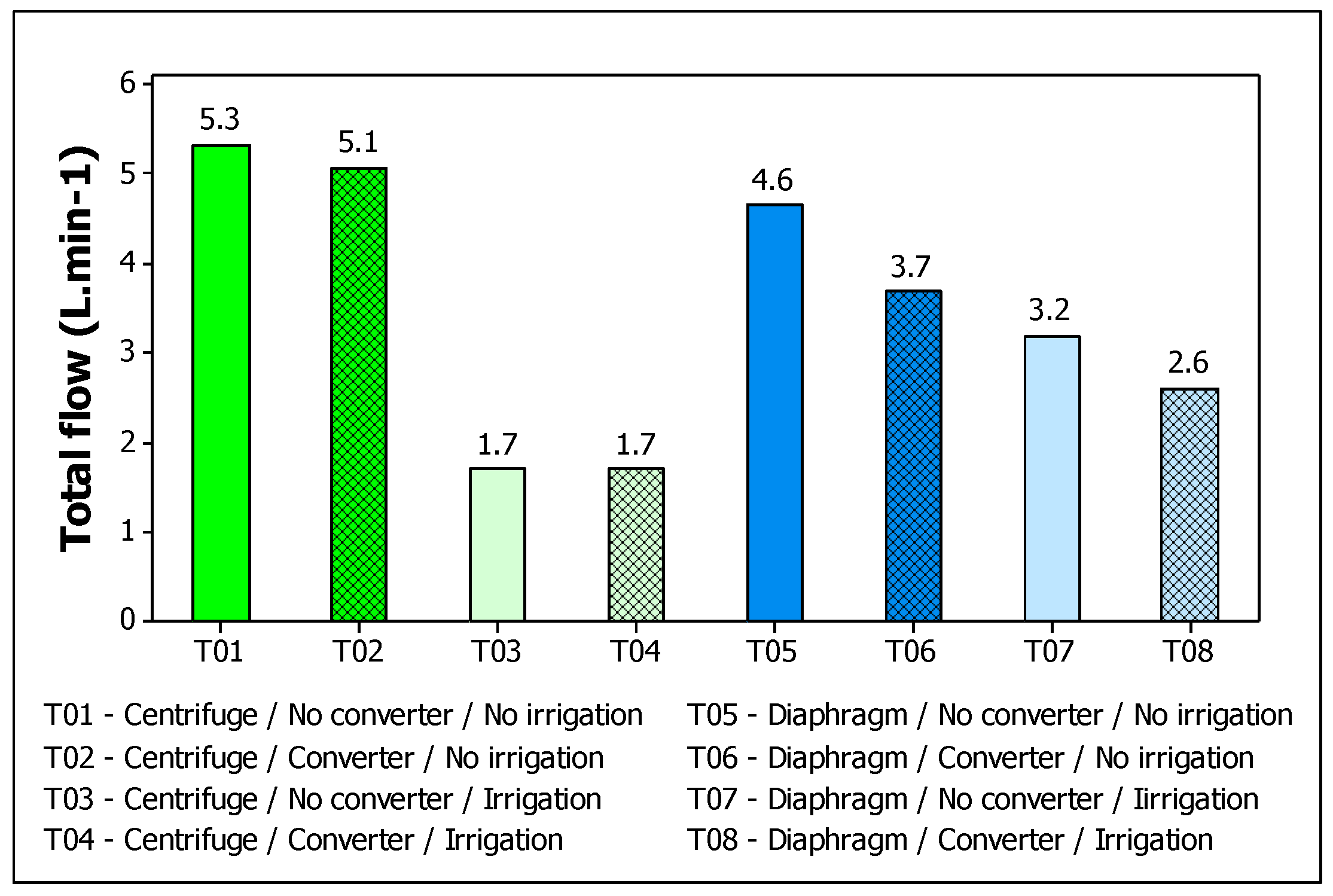
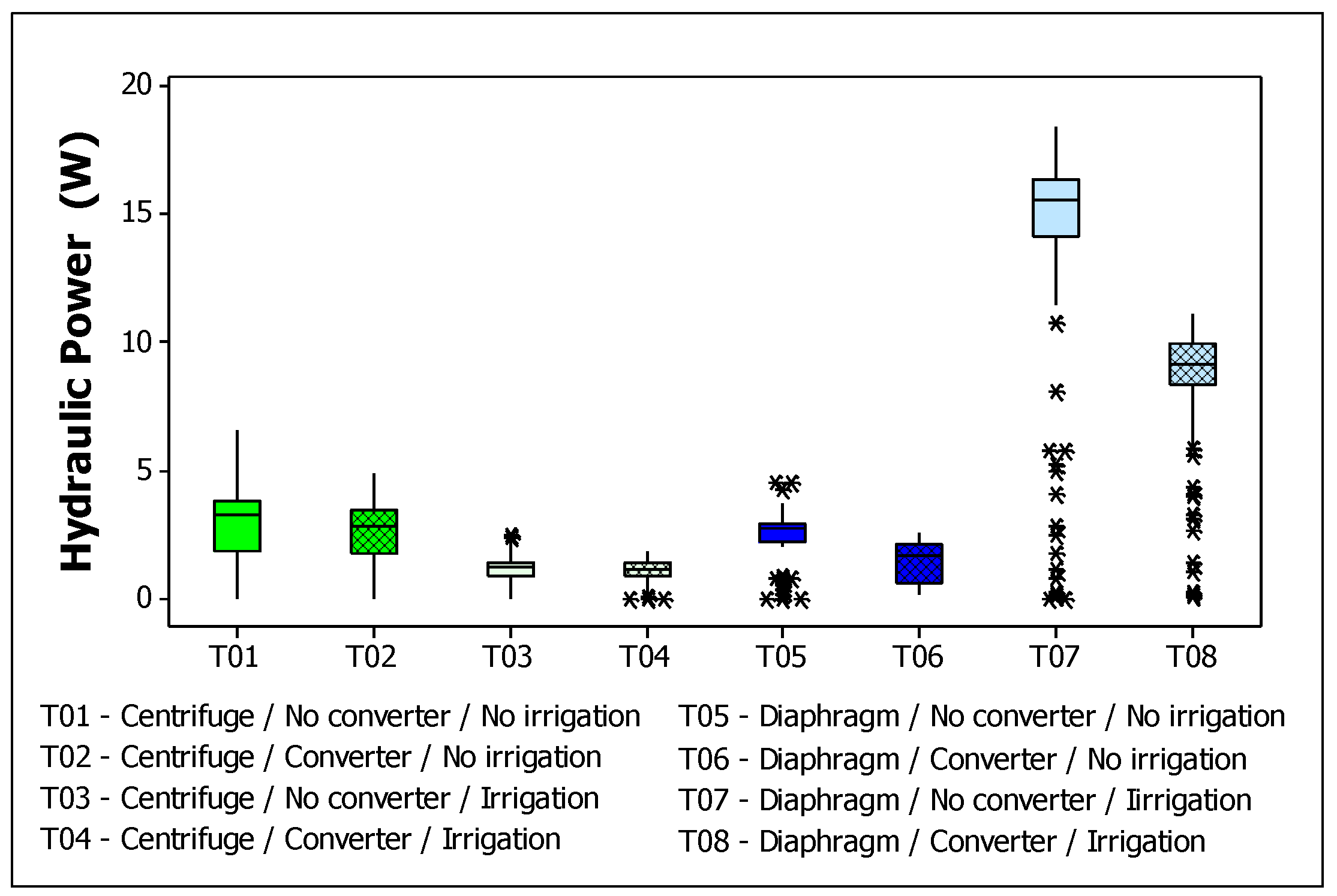
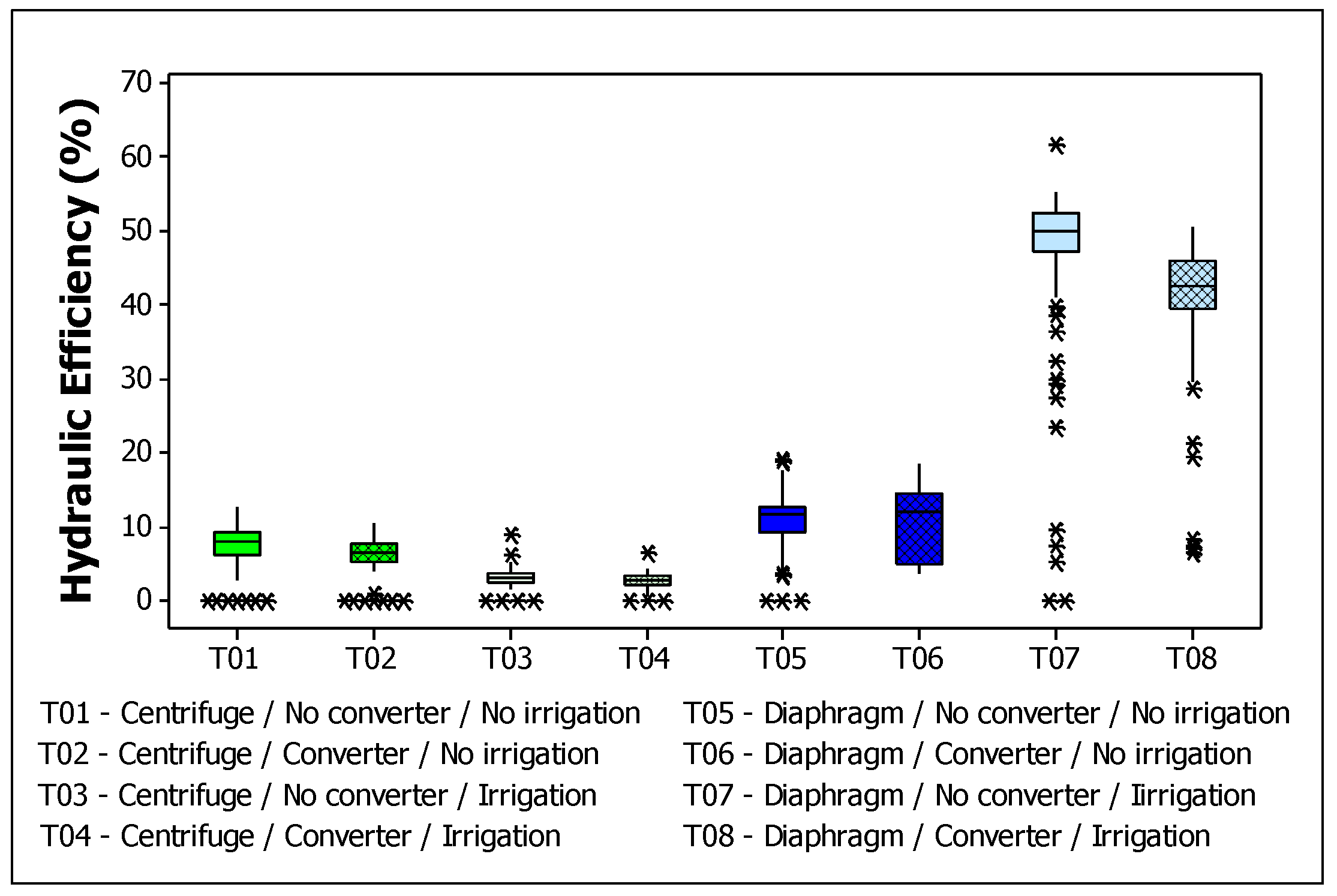
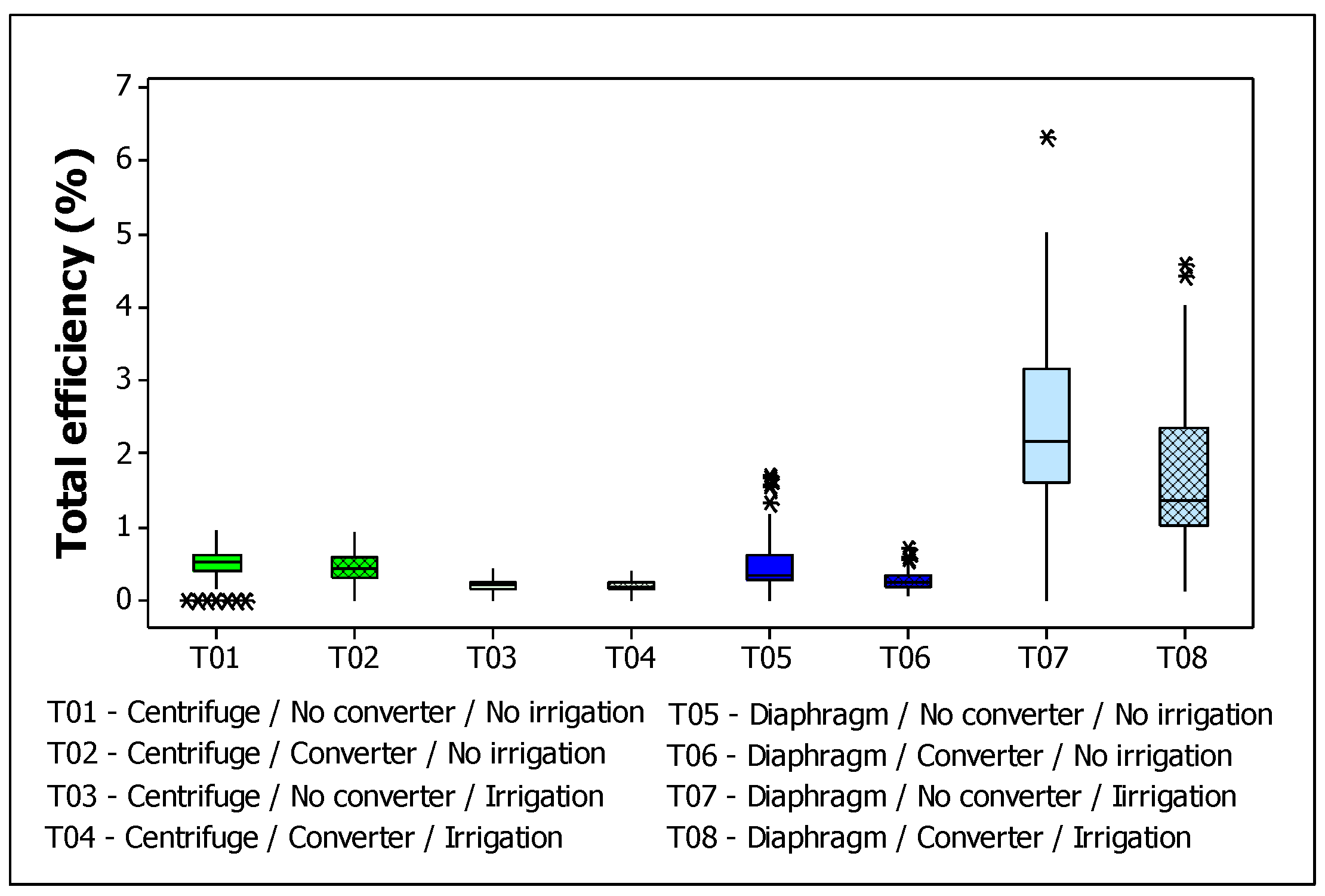
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oster, J.D.; Wichelns, D. Sustainable irrigation is necessary and achievable, but direct costs and environmental impacts can be substantial. Irrig. Sci. 2003, 22, 107–120. [Google Scholar]
- Rhoades, J.D. Drainage for salinity control. In Drainage for Agriculture; van Schilfgarde, J., Ed.; ASA Monograph. No. 17; Amer Soc Agronomy: Madison, WI, USA, 1974; pp. 433–467. [Google Scholar] [CrossRef]
- Burt, C.M.; Isbell, B. Leaching of accumulated soil salinity under drip irrigation. Trans. ASAE 2005, 48, 2115–2121. [Google Scholar] [CrossRef]
- Tanji, K.K. Nature and extent of agricultural salinity and sodicity. In Agricultural Salinity Assessment and Management; Tanji, K.K., Ed.; ASCE Manuals and Reports on Engineering Practice No. 71; American Society of Civil Engineers: New York, NY, USA, 1990; pp. 1–17. [Google Scholar]
- Kang, Y.; Chen, M.; Wan, S. Effects of drip irrigation with saline water on waxy maize (Zea mays L. var. ceratina Kulesh) in North China Plain. Agric. Water Manag. 2010, 97, 1303–1309. [Google Scholar] [CrossRef]
- Nightingale, H.I.; Hoffman, G.J.; Rolston, D.E.; Biggar, J.W. Trickle irrigation rates and soil salinity distribution in an almond (Prunus amygdalus) orchard. Agric. Water Manag. 1991, 19, 271–283. [Google Scholar] [CrossRef]
- Khan, A.A.; Yitayew, M.; Warrick, A.W. Field evaluation of water and solute distribution from a point source. J. Irrig. Drain. Eng. 1996, 122, 221–227. [Google Scholar] [CrossRef]
- Laasri, S.; El Hafidi, E.M.; Mortadi, A.; Chahid, E.G. Solar-powered single-stage distillation and complex conductivity analysis for sustainable domestic wastewater treatment. Environ. Sci. Pollut. Res. 2024, 31, 29321–29333. [Google Scholar]
- Mortadi, A.; Laasri, S. Study on a new solar-powered desalination system to alleviate water scarcity using impedance spectroscopy. Mater. Today Proc. 2024; in press. [Google Scholar]
- Meerbach, D.; Dirksen, C.; Cohen, S.; Yermiyahu, U.; Wallach, R. Influence of drip irrigation layout on salt distribution and sap flow in effluent irrigated cotton. In Proceedings of the Third International Symposium on Irrigation of Horticultural Crops, Lisbon, Portugal, 28 June–2 July 1999. [Google Scholar]
- Souza, C.F.; Folegatti, M.V.; Or, D. Distribution and storage characterization of soil solution for drip irrigation. Irrig. Sci. 2009, 27, 277–288. [Google Scholar] [CrossRef]
- Guan, H.-J.; Li, J.-S.; Li, Y.-F. Effects of drip system uniformity and irrigation amount on water and salt distributions in soil under arid conditions. J. Integr. Agric. 2013, 12, 924–939. [Google Scholar] [CrossRef]
- Chandel, S.S.; Naik, M.N.; Chandel, R. Review of solar photovoltaic water pumping system technology for irrigation and community drinking water supplies. Renew. Sustain. Energy Rev. 2015, 49, 1084–1099. [Google Scholar] [CrossRef]
- Moechtar, M.; Juwono, M.; Kantosa, E. Performance evaluation of a.c. and d.c. direct coupled photovoltaic water pumping system. Energy Convers. Manag. 1991, 31, 521–527. [Google Scholar] [CrossRef]
- Kumar, M.; Reddy, K.S.; Adake, R.V.; Rao, C.V.K.N. Solar powered micro-irrigation system for small holders of dryland agriculture in India. Agric. Water Manag. 2015, 158, 112–119. [Google Scholar] [CrossRef]
- Pande, P.C.; Singh, A.K.; Ansari, S.; Vyas, S.K.; Dave, B.K. Design development and testing of a solar PV pump-based drip system for orchards. Renew. Energy 2003, 28, 385–396. [Google Scholar]
- Reca, J.; Torrente, C.; López-Luque, R.; Martínez, J. Feasibility analysis of a standalone direct pumping photovoltaic system for irrigation in Mediterranean greenhouses. Renew. Energy 2016, 85, 1143–1154. [Google Scholar] [CrossRef]
- Zavala, V.; López-Luque, R.; Reca, J.; Martínez, J.; Lao, M.T. Optimal management of a multisector standalone direct pumping photovoltaic irrigation system. Appl. Energy 2020, 260, 114261. [Google Scholar] [CrossRef]
- Cervera-Gascó, J.; Montero, J.; del Castillo, A.; Tarjuelo, J.M.; Moreno, M.A. EVASOR, an integrated model to manage complex irrigation systems energized by photovoltaic generators. Agronomy 2020, 10, 331. [Google Scholar] [CrossRef]
- Li, Q.; Song, P.; Zhou, B.; Yang, X.; Mihammad, T.; Liu, Z.; Zhou, H.; Li, Y. Mechanism of intermittent fluctuated water pressure on emitter clogging substances formation in drip irrigation system utilizing high sediment water. Agric. Water Manag. 2019, 215, 16–24. [Google Scholar] [CrossRef]
- Liu, L.; Niu, W.Q.; Wu, Z.G. Risk and inducing mechanism of acceleration emitter clogging with fertigation through drip irrigation systems. Trans. Chin. Soc. Agric. Mach. 2017, 48, 228–236. [Google Scholar] [CrossRef]
- Protoger, C.; Pearce, S. Laboratory evaluation and system sizing charts for a second generation direct PV-powered, low-cost submersible solar pump. Solar Energy 2000, 68, 453–474. [Google Scholar]
- Resun Solar Energy. RS6E-150P. 2024. Available online: https://www.resunsolar.com/ (accessed on 5 June 2024).
- American Public Health Association—APHA. Standard Methods for the Examination of Water and Wastewater; APHA: Washington, DC, USA, 2012; 1496p. [Google Scholar]
- Gilbert, R.G.; Ford, H.W. Operational principles/emitter clogging. In Trickle Irrigation for Crop Production; Nakayama, F.S., Bulks, D.A., Eds.; Elsevier: Amsterdam, The Netherlands, 1986; pp. 142–163. [Google Scholar] [CrossRef]
- Kolhe, M.; Joshi, J.C.; Kothari, D.P. Análise de desempenho de um sistema fotovoltaico de bombeamento de água diretamente acoplado. Transações IEEE Sobre Conversão Energ. 2004, 24, 613–618. [Google Scholar] [CrossRef]
- Cossich, V.; Boas, M.A.V.; Kepp, N.C.; Lopes, A.R.; Junior, D.M. Methodology for validating autonomous and direct photovoltaic pumping in drip irrigation. Irrig. Sci. 2024, 1319–1432. [Google Scholar] [CrossRef]
- Keller, J.; Karmeli, D. Trickle irrigation design parameters. Rain Bird Sprink. Manuf. Corp. 1974, 17, 0678–0684. [Google Scholar]
- ABNT NBR ISO 9261; Equipamentos de Irrigação Agrícola-Emissores e Tubos Emissores-Especificações e Métodos de Ensaio. ISO: São Paulo, Brazil, 2006.
- Merrian, J.L.; Keller, J. Farm Irrigation System Evaluation: A Guide for Management; Civil and Environmental Engineering Faculty Publications; Utah State University: Logan, UT, USA, 1978. [Google Scholar]
- Keller, J.; Bliesner, I.D. Sprinkler and Trickle Irrigation; Van Nostrand Reinhold: NY, USA, 1990. [Google Scholar]
- Montgomery, D.C. Introdução ao Controle Estatístico de Qualidade, 7th ed.; LTC Group: Rio de Janeiro, Brazil, 2016. [Google Scholar]
- Vick, B.D.; Clark, R.N. Experimental investigation of solar powered diaphragm and helical pumps. Solar Energy 2011, 85, 945–954. [Google Scholar] [CrossRef]
- Mokeddem, A.; Midoun, A.; Kadri, D.; Hiadsi, S.; Raja, I.A. Performance of a directly coupled PV water pumping system. Energy Convers. Manag. 2011, 52, 3089–3095. [Google Scholar] [CrossRef]
- Neto, J.C.; Azevedo, T.; Salazar, A. Rastreamento de Máxima Potência em Sistemas Fotovoltaicos Baseado na Técnica One Cycle Control. 2014. Available online: https://www.researchgate.net/publication/264187930_Rastreamento_de_Maxima_Potencia_em_Sistemas_Fotovoltaicos_Baseado_na_Tecnica_One_Cycle_Control (accessed on 5 September 2024).
- Rondón, P.P.; Kriuskova, E.R.; Sobrevilla, L.P.; Hernández, R.D.; Calderín, R.C. Evaluación de dos bombas hidráulicas de engranajes de desplazamientos 32 y 50 cm3/rev. Rev. Cienc. Técnicas Agropecu. 2013, 22, 58–62. [Google Scholar]
- Seaflo. 2024. Available online: https://seaflo.com.br/ (accessed on 5 September 2024).
- Cossich, V.; Boas, M.A.V.; Kepp, N.C.; Lopes, A.R.; Machado, D. Statistical process control in pulsed drip irrigation systems. Rev. Ambiente Água 2024, 19, e2933. [Google Scholar] [CrossRef]
- Hamidat, A.; Benyoucef, B. Mathematic models of photovoltaic motor-pump systems. Renew. Energy 2008, 33, 933–942. [Google Scholar] [CrossRef]
- Benghanem, M.; Daffallah, K.O.; Joraid, A.A.; Alamri, S.N.; Jaber, A. Performances of solar water pumping system using helical pump for a deep well: A case study for Madinah, Saudi Arabia. Energy Convers. Manag. 2013, 65, 50–56. [Google Scholar] [CrossRef]
- Hilali, A.; Mardoude, Y.; Essahlaoui, A.; Rahali, A.; El Ouanjli, N. Migration to solar water pump system: Environmental and economic benefits and their optimization using genetic algorithm Based MPPT. Energy Rep. 2022, 8, 10144–10153. [Google Scholar] [CrossRef]
- Santra, P. Performance evaluation of solar PV pumping system for providing irrigation through micro-irrigation techniques using surface water resources in hot arid region of India. Agric. Water Manag. 2021, 245, 106554. [Google Scholar] [CrossRef]
- Kepp, N.C.; Boas, M.A.V.; Haupentha, S.W.; Lopes, A.R.; Cossich, V. Monitoring urea concentration at different slope angles in drip fertigation. Rev. Ambiente Água 2023, 18, e2928. [Google Scholar] [CrossRef]
- Lopes, A.R.; Boas, M.A.V.; Pazuch, F.A.; Dalla Corte, L.; Gomes, B.M.; Prates, R.T.C. Uniformity of drip irrigation system with liquid peat on different slopes. Irriga 2021, 1, 357–366. [Google Scholar] [CrossRef]
- Berwanger, D.; Haupenthal, S.W.; Siqueira, J.A.C.; Boas, M.A.V. Uniformity of drip irrigation with autonomous photovoltaic energy using solar tracker. Res. Soc. Dev. 2023, 12, e36121444496. [Google Scholar] [CrossRef]
- Lozano, D.; Ruiz, N.; Baeza, R.; Contreras, J.I.; Gavilán, P. Effect of pulse drip irrigation duration on water distribution uniformity. Water 2020, 12, 2276. [Google Scholar] [CrossRef]
- Abdelraouf, R.E. Saving 50% irrigation water, energy, reducing of soil salts accumulation and weeds growth by a new and simple method for cultivation in small pieces of pvc pipes. Plant Arch. 2019, 19 (Suppl. S2), 1912–1921. [Google Scholar]
- Arriero, S.S.; Almeida, W.F.; Paz, V.P.S.; Damasceno, L.F. Yield of eggplant using low quality water and pulse drip irrigation. Rev. Bras. Eng. Agríc. Ambient. 2020, 24, 822–826. [Google Scholar] [CrossRef]
- Al-Amoud, A.I.; Saeed, M. The effect of pulsed drip irrigation on water management. In Proceedings of the 4th International Micro-Irrigation Congress, Albury-Wodonga, Australia, 23–28 October 1988; Proceedings ICID. pp. 120–144. [Google Scholar]
- de Mélo, R.F.; Coelho, R.D.; Teixeira, M.B. Entupimento de gotejadores convencionais por precipitados químicos de carbonato de cálcio e magnésio, com quatro índices de saturação de Langelier. Irriga 2008, 13, 525–539. [Google Scholar] [CrossRef]
- Plugging, C.O.E. Causes and Prevention of Emitter Plugging in Microirrigation System; University of Florida: Gainesville, FL, USA, 1990. [Google Scholar]
- Pizarro Cabello, F. Riegos Localizados de Alta Frecuencia RLAF: Goteo, Microaspersión, Exudación; FAO: Roma, Italy, 1996. [Google Scholar]
- Hills, D.J.; Nawar, F.M.; Waller, P.M. Effects of chemical clogging on drip-tape irrigation uniformity. Trans. ASAE 1989, 32, 1202–1206. [Google Scholar] [CrossRef]
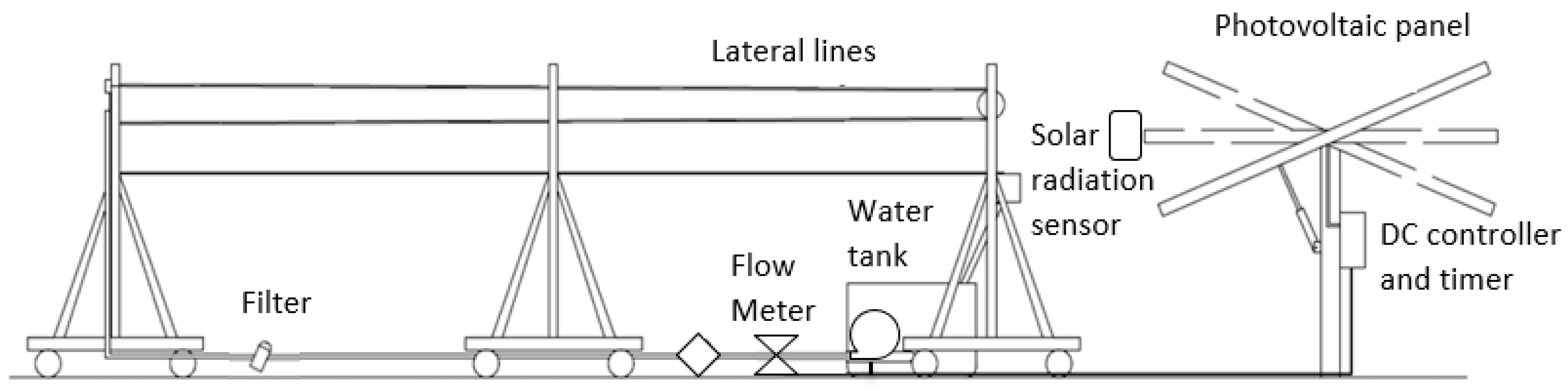
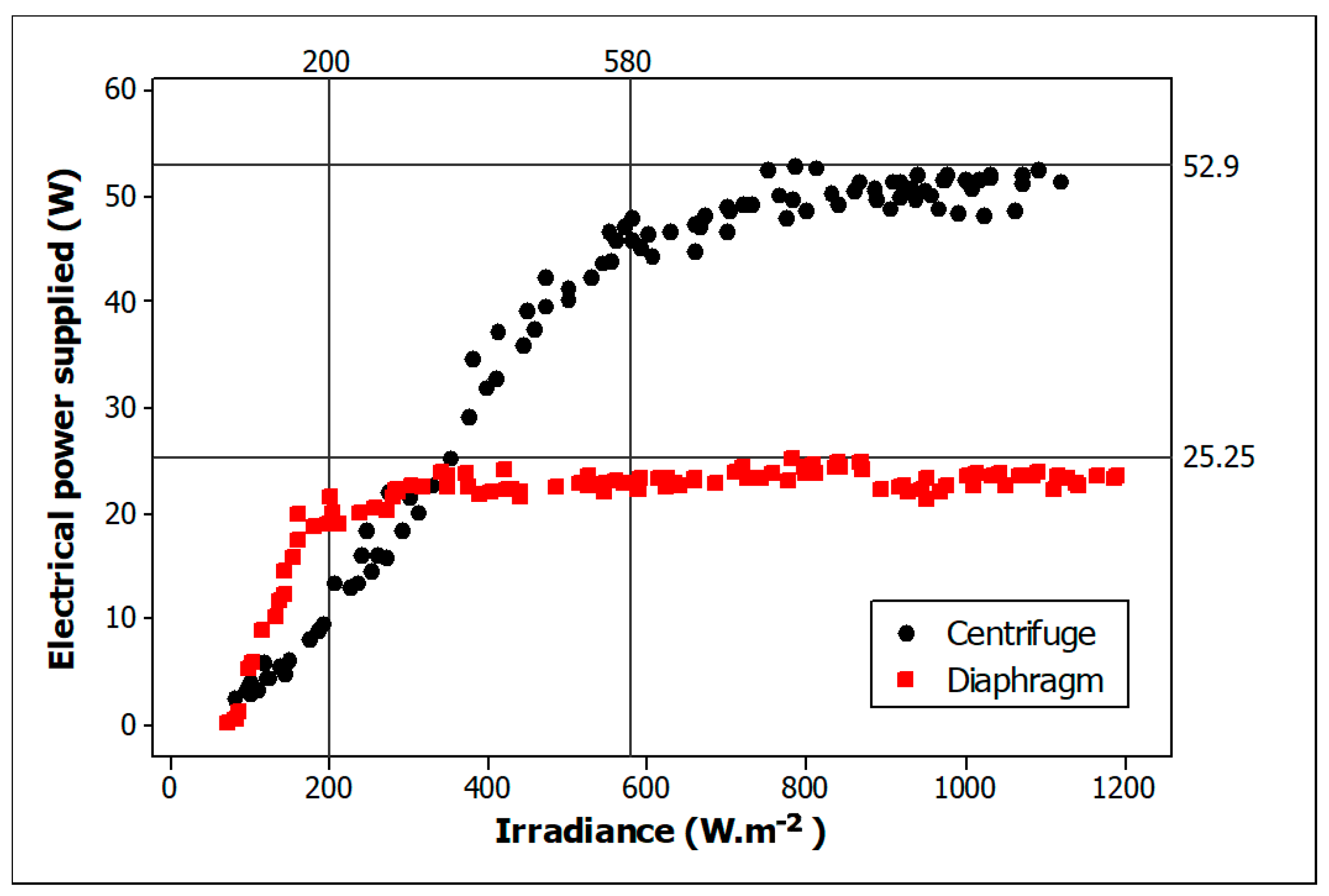
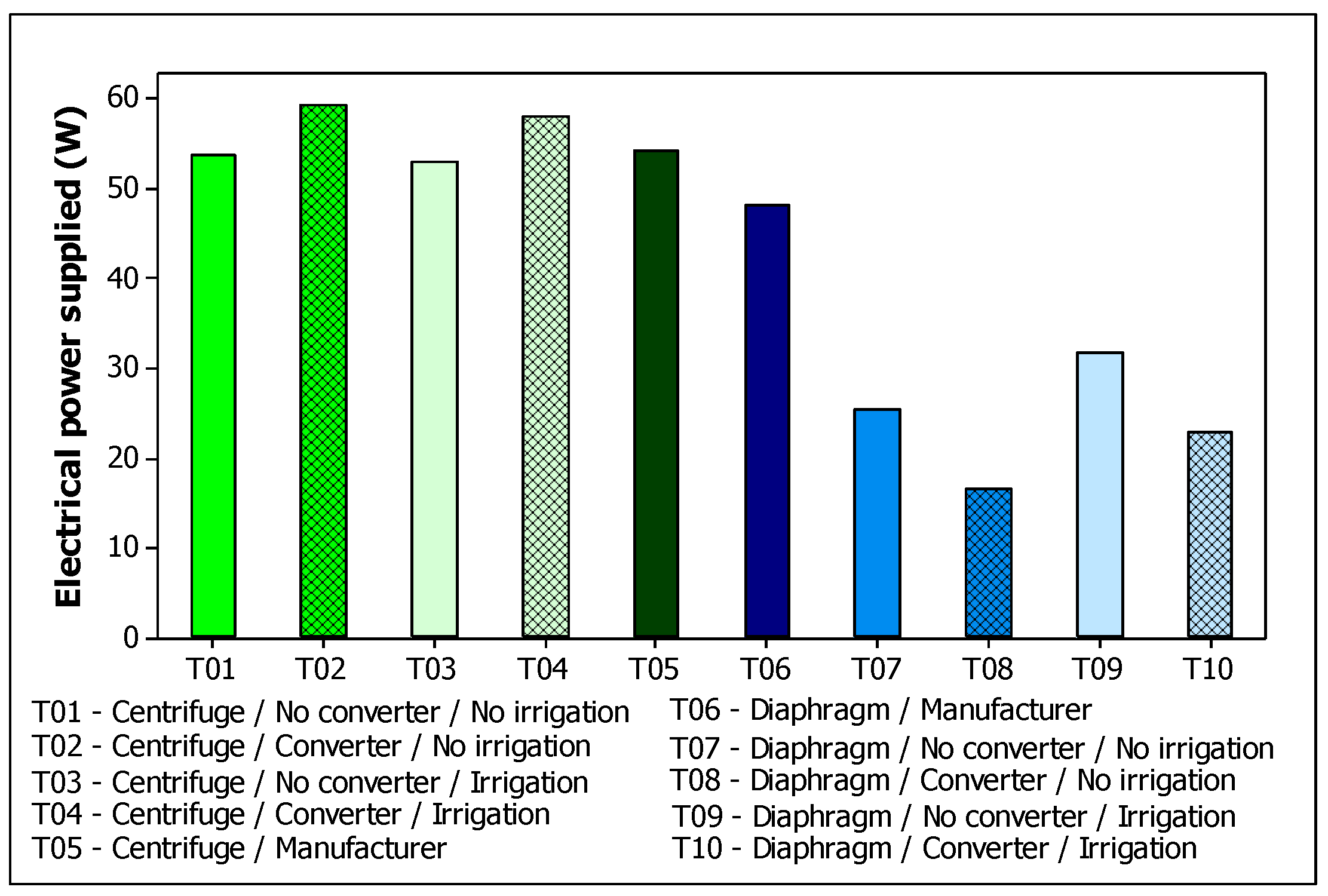
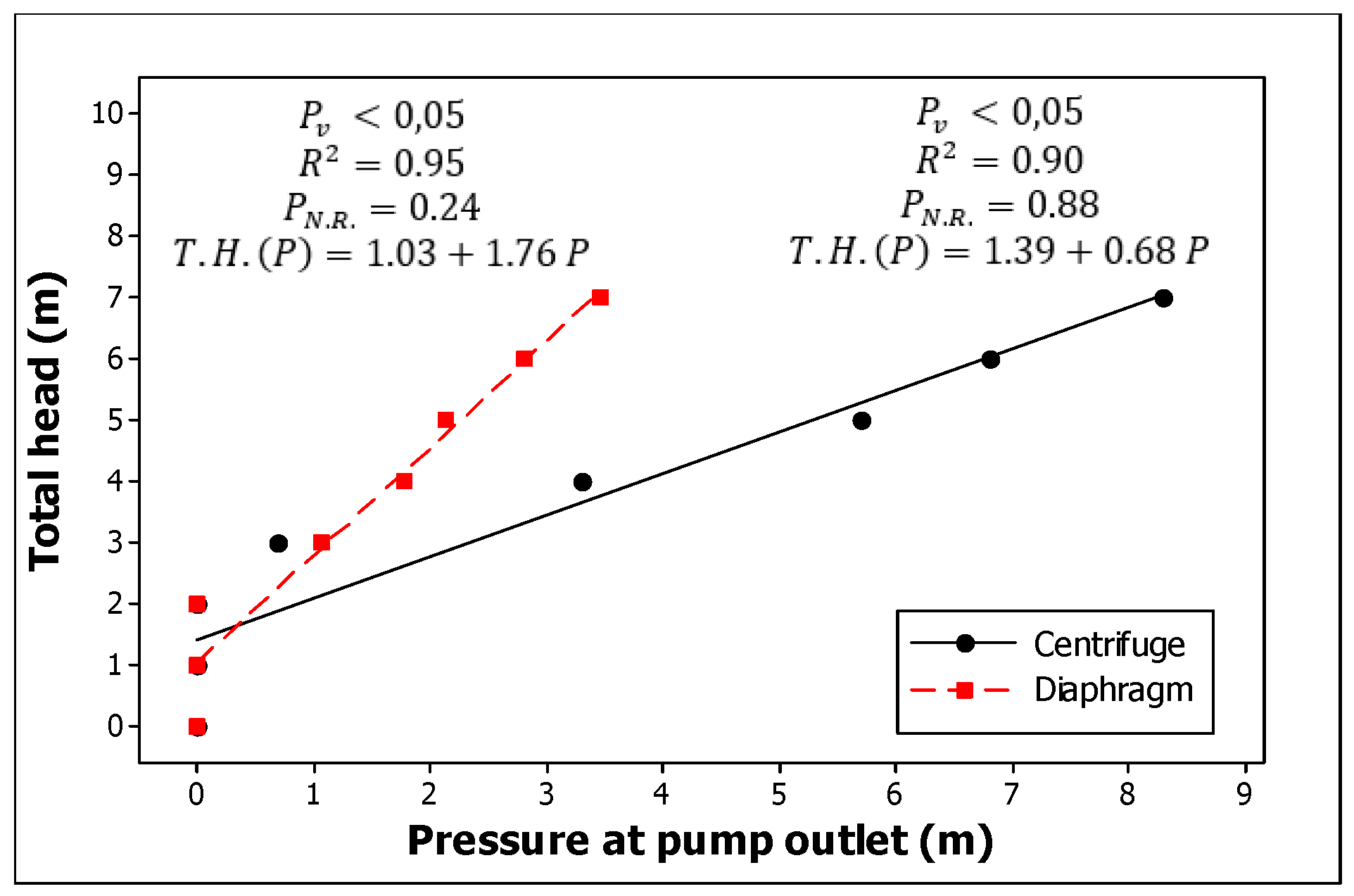


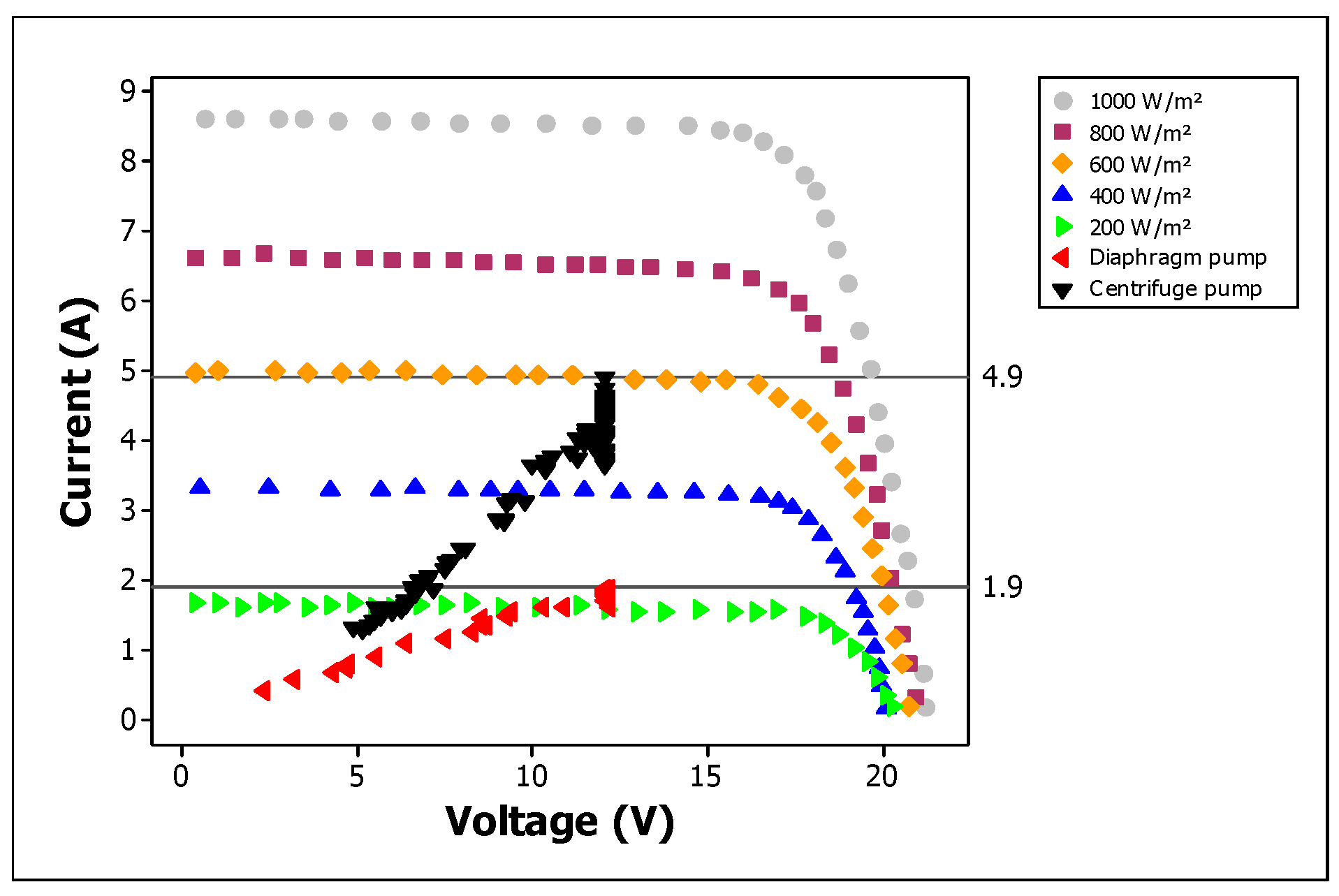

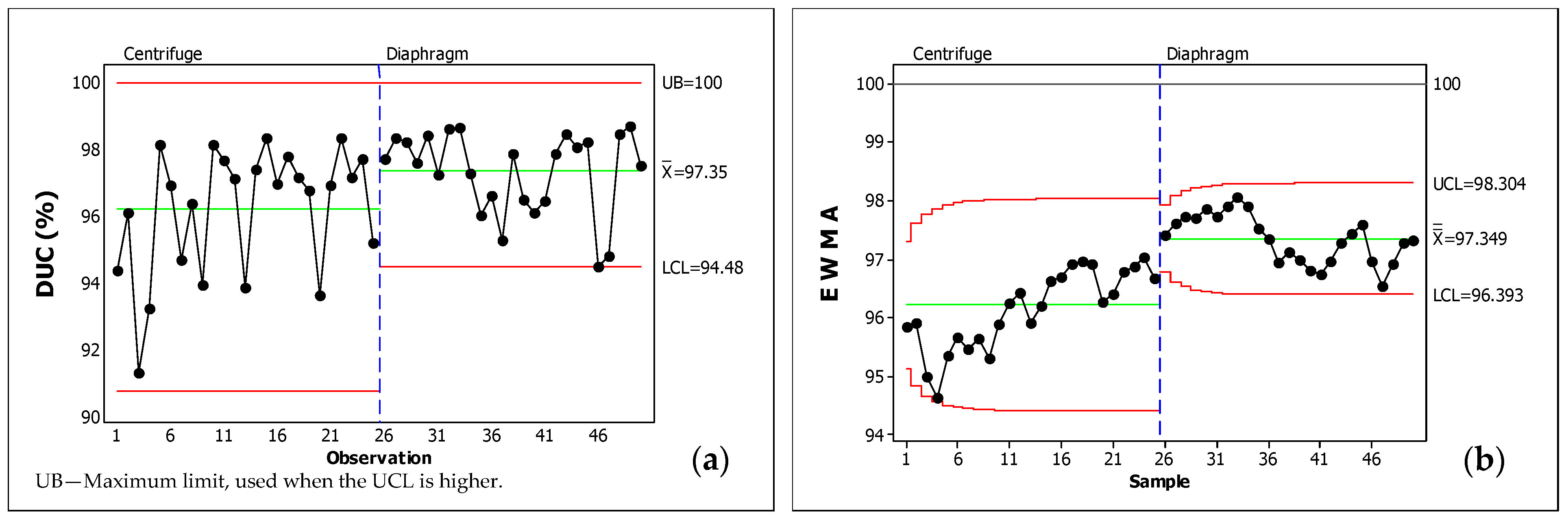
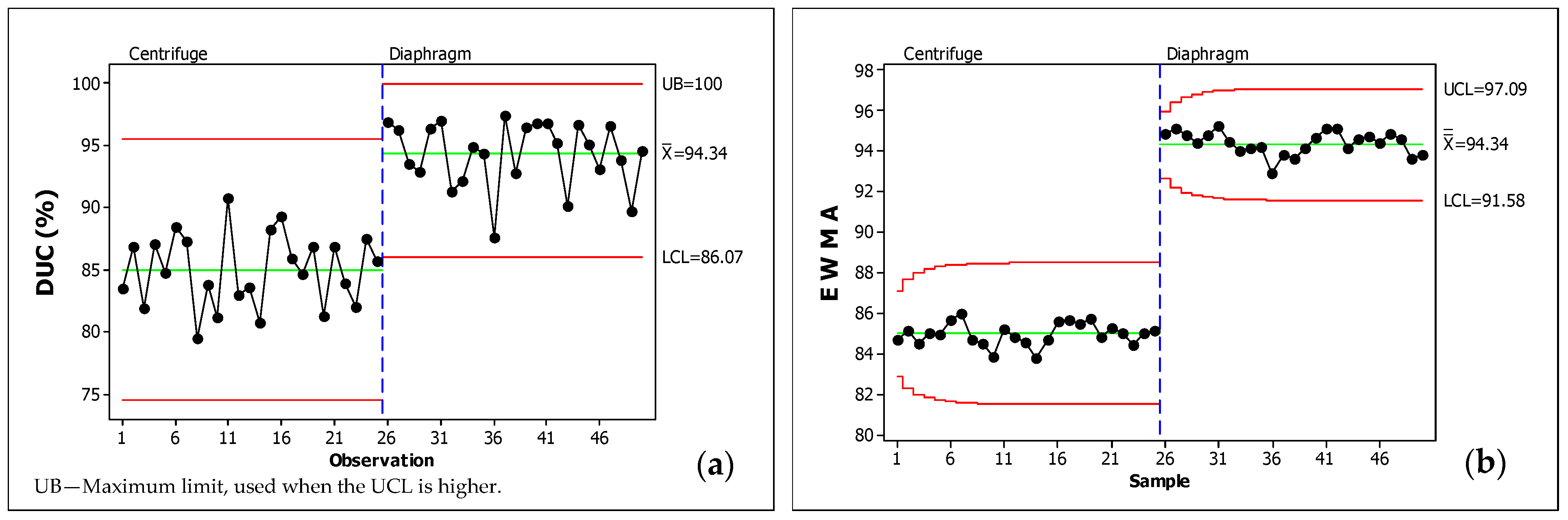

| Parameter | Instrument | Measuring Range (Accuracy) |
|---|---|---|
| Flow | HCS008 (RainPint—Santa Catarina, Brasil) | 20–2400 L· (5%) |
| Pressure | DN63 (Genebre—São Paulo, Brasil) | 0–2.5 bar (2.5%) |
| Irradiance | SM206 (IMPAC—São Paulo, Brasil) | 1–3999 W· (5%) |
| Voltage | M430 (Raidanfade—São Paulo, Brasil) | 0–100 V (1%) |
| Current | M430 (Raidanfade—São Paulo, Brasil) | 0–10 A (1%) |
| Rated Power in Watts—Pmax (Wp) | 150 W |
| Open circuit voltage—Voc (V) | 22.3 V |
| Short Circuit Current—Isc (A) | 8.82 A |
| Maximum Power Voltage—Vmp (V) | 17.91 V |
| Maximum power Current—Imp (A) | 8.38 A |
| Module Efficiency (%) | 15.29% |
| Clogging Factor | Severe Risk | Sample | Water Quality | Severe Use Restriction | Sample |
|---|---|---|---|---|---|
| Suspended solids | >100 mg· | 112 mg· | Conductivity (EC) | >3.0 dS· | 9.84 dS· |
| Dissolved solids | >2000 mg· | 5082 mg· | Nitrogen () | >3 mg· | 1280.1 mg· |
| Total iron | >1.5 mg· | 261.6 mg· | RAS | >9 | 15.4 |
| Manganese | >1 mg· | 366.8 mg· | Sodium | - | 231 mg· |
| pH | >8.0 | 4.97 | Calcium | - | 264 mg· |
| Magnesium | - | 186.8 mg· |
| Factors | Equation | Variables |
|---|---|---|
| Solar power | —solar power (W) Area of the photovoltaic panel (m2) Irr—Irradiance (W·) | |
| Electrical power | —electric power (W) I—electric current (A) U—voltage (V) | |
| Hydraulic power | —hydraulic power (W) ρ—specific mass of water (kg) g—gravitational strength (m·) Q—flow rate () H—height (m.c.a.) | |
| Motor pump efficiency | —motor pump efficiency (%) | |
| Total efficiency | —total efficiency (%) |
| Rating | DUC (%) |
|---|---|
| Excellent | >90 |
| Good | 85–90 |
| Acceptable | 65–85 |
| Poor | <65 |
| Centrifuge | Diaphragm | |||||
|---|---|---|---|---|---|---|
| Height (M) | Manufacturer | Photovoltaic Pumping | Manufacturer | Photovoltaic Pumping | ||
| Pressure * (m) | Pressure * (m) | |||||
| 0 | 31.0 | 15.5 | 0.0 | 4.1 | 4.9 | 0 |
| 1 | 25.1 | 14.0 | 0.0 | 3.9 | 4.8 | 0 |
| 2 | 23.9 | 12.1 | 0.0 | 3.75 | 4.7 | 0 |
| 3 | 20.0 | 9.9 | 0.7 | 3.63 | 4.7 | 1.07 |
| 4 | 16.0 | 8.0 | 3.3 | 3.51 | 4.6 | 1.78 |
| 5 | 10.6 | 7.0 | 5.7 | 3.42 | 4.5 | 2.14 |
| 6 | 2.0 | 2.8 | 6. | 3.35 | 4.5 | 2.80 |
| 7 | 0.0 | 0.7 | 8.3 | 3.3 | 4.4 | 3.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cossich, V.; Vilas Boas, M.A.; Alves Pereira, A.A.; Guardini, R.; Lopes, A.R.; Kepp, N.C.; Júnior, D.M.; Bertonha, A. Pump Model for Drip Irrigation with Saline Water, Powered by a Photovoltaic Solar Panel with Direct and Intermittent Application. Sustainability 2025, 17, 3981. https://doi.org/10.3390/su17093981
Cossich V, Vilas Boas MA, Alves Pereira AA, Guardini R, Lopes AR, Kepp NC, Júnior DM, Bertonha A. Pump Model for Drip Irrigation with Saline Water, Powered by a Photovoltaic Solar Panel with Direct and Intermittent Application. Sustainability. 2025; 17(9):3981. https://doi.org/10.3390/su17093981
Chicago/Turabian StyleCossich, Vinicius, Marcio Antonio Vilas Boas, Antonio Augusto Alves Pereira, Renato Guardini, Allan Remor Lopes, Naila Cristina Kepp, Dário Machado Júnior, and Altair Bertonha. 2025. "Pump Model for Drip Irrigation with Saline Water, Powered by a Photovoltaic Solar Panel with Direct and Intermittent Application" Sustainability 17, no. 9: 3981. https://doi.org/10.3390/su17093981
APA StyleCossich, V., Vilas Boas, M. A., Alves Pereira, A. A., Guardini, R., Lopes, A. R., Kepp, N. C., Júnior, D. M., & Bertonha, A. (2025). Pump Model for Drip Irrigation with Saline Water, Powered by a Photovoltaic Solar Panel with Direct and Intermittent Application. Sustainability, 17(9), 3981. https://doi.org/10.3390/su17093981






