Study on the Response of Chemical Kinetics of Fragmented Coal Under Dynamic Load
Abstract
1. Introduction
2. Experimental and Dynamic Model Construction
2.1. Basic Parameters of Experimental Samples
2.2. Preparation of Experimental Samples
2.3. Thermal Analysis Test
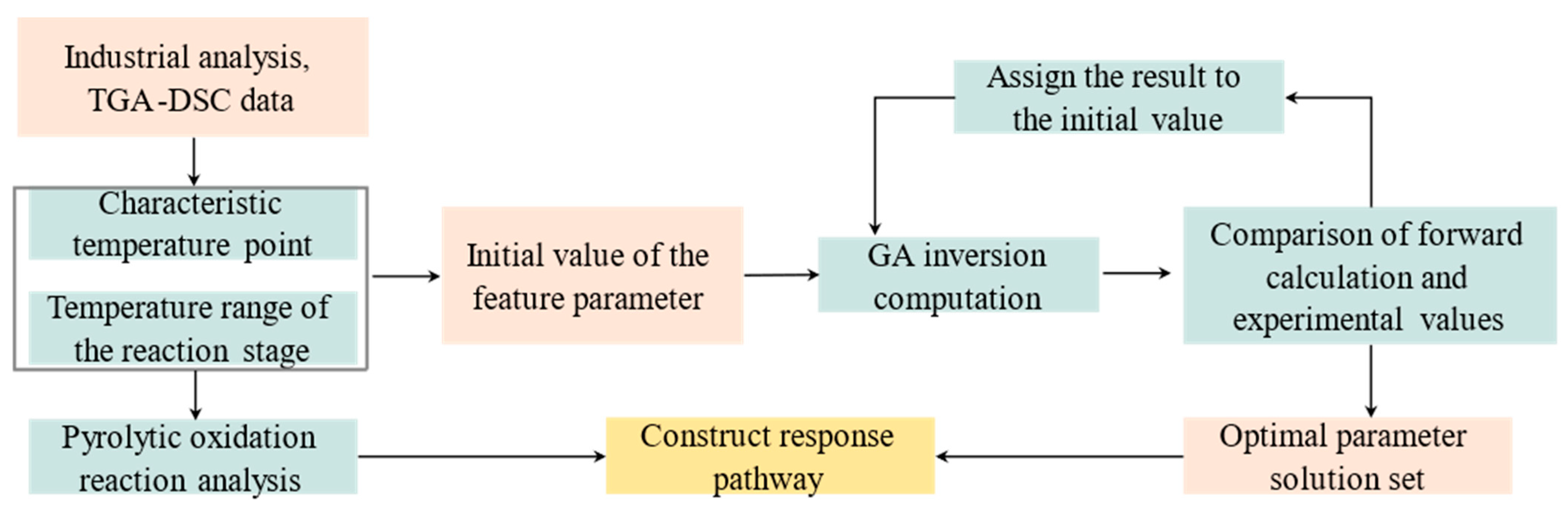
2.4. GA and Reverse Modeling
3. Results and Discussion
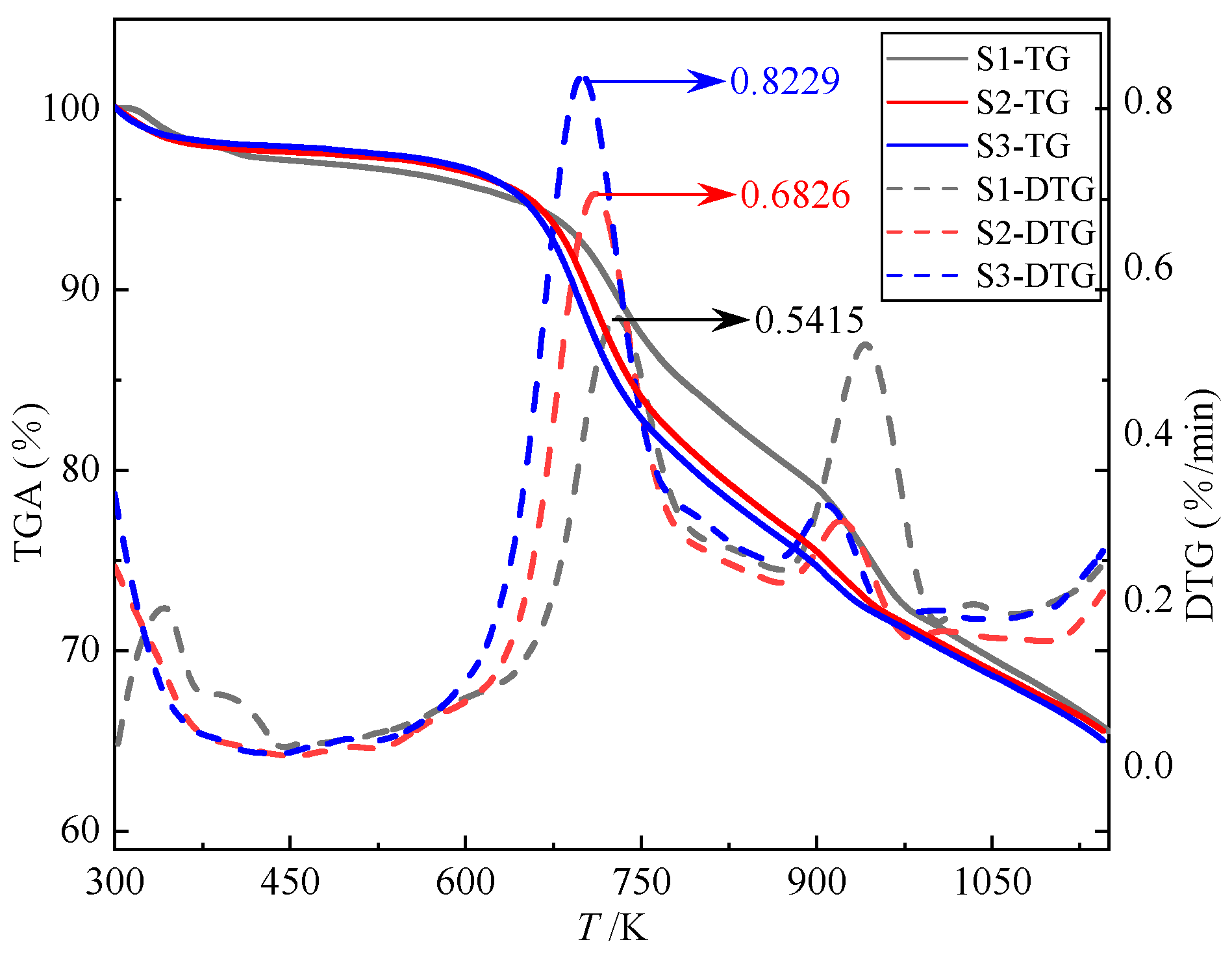
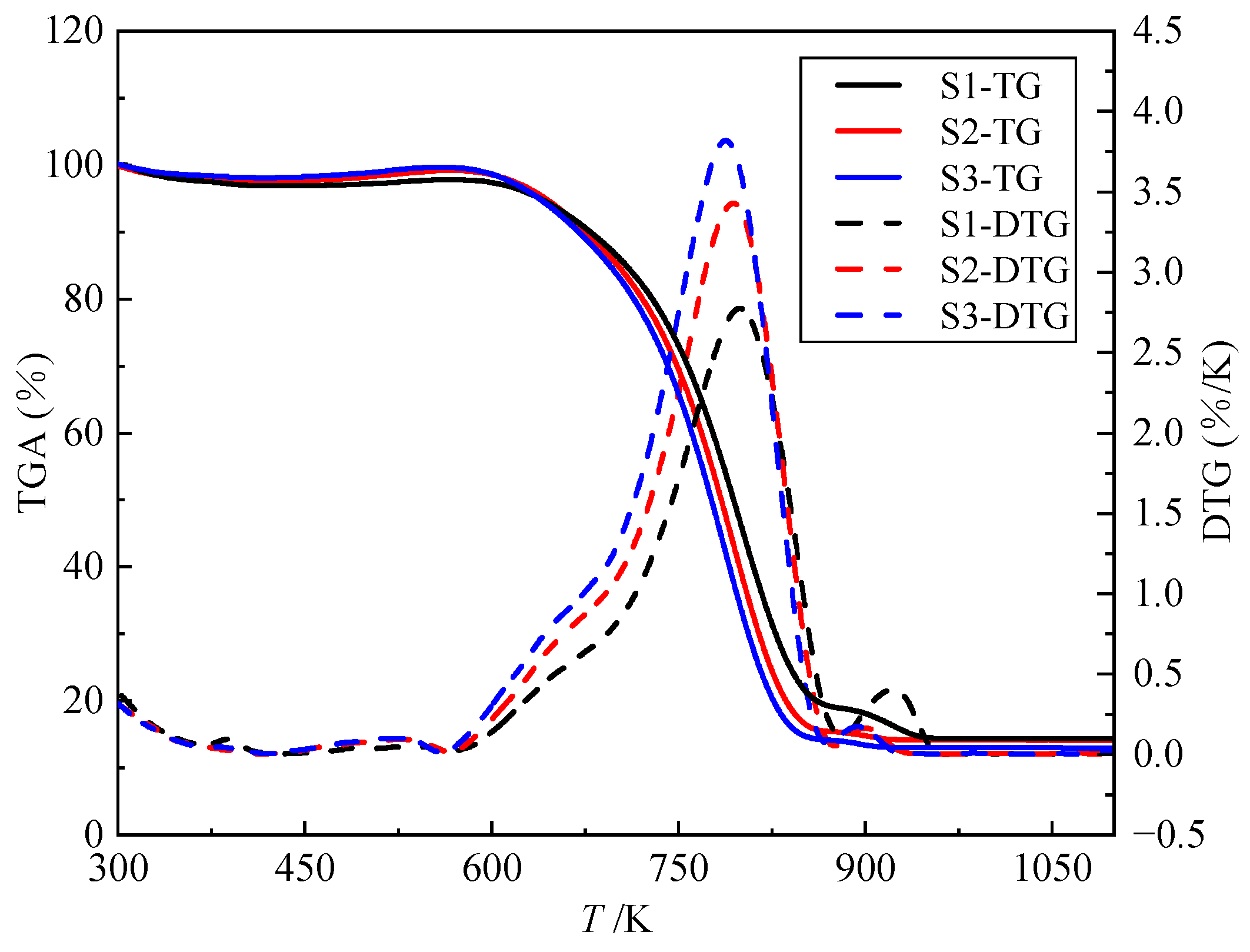
3.1. Mass Loss and Thermal Behavior in an N2 Atmosphere
3.1.1. Analysis of Pyrolysis Reaction Characteristics of Coal in Inert Gas
3.1.2. Pyrolysis Kinetics of Coal in Inert Gas
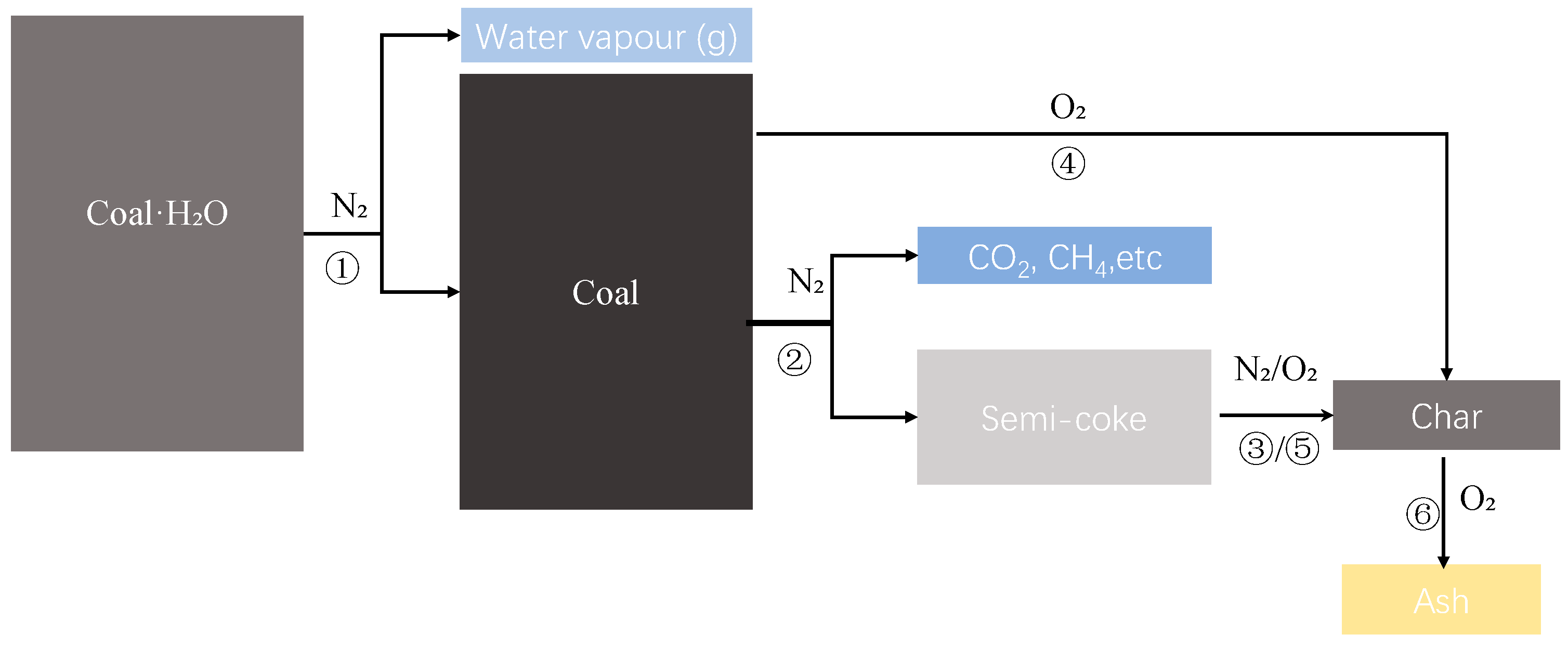
3.1.3. Pyrolysis Reaction Pathway of Coal in Inert Gas
3.2. Mass Loss and Thermal Behavior in an Air Atmosphere
3.2.1. Analysis of Coal Oxidative Pyrolysis Characteristics in an Air Atmosphere
3.2.2. Oxidative Pyrolysis Reaction Pathway of Coal in Air
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhukovskiy, Y.L.; Batueva, D.E.; Buldysko, A.D.; Gil, B.; Starshaia, V.V. Fossil Energy in the Framework of Sustainable Development: Analysis of Prospects and Development of Forecast Scenarios. Energies 2021, 14, 5268. [Google Scholar] [CrossRef]
- Ni, K.; Liu, C.; Wang, Y. Research on the Current Situation and Trends of World Coal Industry Development during the 14th Five Year Plan Period. China Coal 2024, 50, 235–245. [Google Scholar] [CrossRef]
- Yang, Y. Progress of Energy and Chemical Companies in Transition towards Green Low Carbon under Peak Carbon Dioxide Emission and Carbon Neutrality. Mod. Chem. Ind. 2023, 43, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Jiang, Y.; Qi, Y.; Liu, Z.; Cui, M.; Xia, K.; Li, Y. A Study on the Construction of the Power Demand Forecasting System under Carbon Neutrality Goal and the Development Trend of Power Demand in East China. Power Syst. Clean Energy 2024, 40, 30–36. [Google Scholar] [CrossRef]
- IEA. Coal Mid-Year Update; International Energy Agency: Paris, France, 2024; Volume 7.
- Li, X.; Cao, Z.; Xu, Y. Characteristics and Trends of Coal Mine Safety Development. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 47, 2316–2334. [Google Scholar] [CrossRef]
- Deng, J.; Li, B.; Wang, K.; Wang, C. Research Status and Outlook on Prevention and Control Technology of Coal Fire Disaster in China. Coal Sci. Technol. 2016, 44, 1–7+101. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, Z.; Sun, B. Re-Practice of Comprehensive Fire-Fighting Technology in Xinglongzhuang Coal Mine. Coal Mine Mod. 2022, 31, 40–43. [Google Scholar] [CrossRef]
- Wang, W. Current Situation and Development Trend for Coalfield Fire Exploration and Governance Technology. Saf. Coal Mines 2020, 51, 206–209+215. [Google Scholar] [CrossRef]
- Feng, X.; Ai, Z.; Zhang, X.; Wei, Q.; Du, C.; Zhang, Q.; Deng, C. Numerical Investigation of the Evolution of Gas and Coal Spontaneously Burned Composite Disaster in the Goaf of Steeply Inclined Coal Seam. Sustainability 2023, 15, 9246. [Google Scholar] [CrossRef]
- Xie, H. Research Framework and Anticipated Results of Deep Rock Mechanics and Mining Theory. Adv. Eng. Sci. 2017, 49, 1–16. [Google Scholar] [CrossRef]
- Wang, F.; Ji, Z.; Wang, H.; Chen, Y.; Wang, T.; Tao, R.; Su, C.; Niu, G. Analysis of the Current Status and Hot Technologies of Coal Spontaneous Combustion Warning. Processes 2023, 11, 2480. [Google Scholar] [CrossRef]
- Yan, Q.; Lu, Y.; Wang, Q.; Gu, W.; Wu, F. Research Progress and Development Trend of Coal Spontaneous Combustion Prevention Technology. Combust. Sci. Technol. 2024, 1–28. [Google Scholar] [CrossRef]
- Zhang, L.; Ponomarenko, T. Directions for Sustainable Development of China’s Coal Industry in the Post-Epidemic Era. Sustainability 2023, 15, 6518. [Google Scholar] [CrossRef]
- Du, B.; Liang, Y.; Tian, F.; Guo, B. Analytical Prediction of Coal Spontaneous Combustion Tendency: Pore Structure and Air Permeability. Sustainability 2023, 15, 4332. [Google Scholar] [CrossRef]
- Huang, X.; Rein, G. Smouldering Combustion of Peat in Wildfires: Inverse Modelling of the Drying and the Thermal and Oxidative Decomposition Kinetics. Combust. Flame 2014, 161, 1633–1644. [Google Scholar] [CrossRef]
- Tian, F.; Jia, D.; Chen, M.; Liang, Y.; Zhu, H.; Zhang, T. Research Progress of Spontaneous Combustion of Coal Containing Gas under the Compound Disaster Environment in the Goaf. Meitan Xuebao/J. China Coal Soc. 2024, 49, 2711–2727. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, S.; Liang, Y.; Song, S.; Ren, T. Analytical Prediction of Coal Spontaneous Combustion Tendency: Velocity Range with High Possibility of Self-Ignition. Fuel Process. Technol. 2017, 159, 38–47. [Google Scholar] [CrossRef]
- Onifade, M.; Genc, B. A Review of Research on Spontaneous Combustion of Coal. Int. J. Min. Sci. Technol. 2020, 30, 303–311. [Google Scholar] [CrossRef]
- Deng, J.; Xu, J.; Chen, X. Perspectives on Spontaneous Combustion Mechanism and Prediction Theory of Coal. J. Liaoning Tech. Univ. (Nat. Sci.) 2003, 22, 455–459. [Google Scholar] [CrossRef]
- Gong, X.; Xue, S.; Han, B.; Zheng, C.; Zhu, L.; Dong, Y.; Li, Y. Research Progress on Stress-Fracture-Seepage Characteristics for Hazard Prevention in Mine Goafs: A Review. Sustainability 2022, 14, 12107. [Google Scholar] [CrossRef]
- Carras, J.N.; Young, B.C. Self-Heating of Coal and Related Materials: Models, Application and Test Methods. Prog. Energy Combust. Sci. 1994, 20, 1–15. [Google Scholar] [CrossRef]
- Akgun, F.; Essenhigh, R.H. Self-Ignition Characteristics of Coal Stockpiles: Theoretical Prediction from a Two-Dimensional Unsteady-State Model. Fuel 2001, 80, 409–415. [Google Scholar] [CrossRef]
- Guo, X.; Xu, J.; Deng, J.; Wen, H.; Hui, S. Analyzing the Effect of Ground Temperature on Spontaneous Combustion of Coal. J. China Coal Soc. 2001, 26, 160–163. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.; Zou, Z.; Liu, Q. Study on Spontaneous Combustion Characteristics and Limit Parameters of Coal in High Geothermal Mine. Coal Technol. 2020, 39, 90–93. [Google Scholar] [CrossRef]
- Qin, J.; Li, X.; Zhou, Z.; Yu, X.; Shang, X.; Ren, W.; Jia, H. Experimental Study on the Influence of Ground Temperature on Coal Spontaneous Combustion Characteristics with Different Metamorphic Degree. China Min. Mag. 2024, 33, 186–192. [Google Scholar] [CrossRef]
- Song, S.; Qin, B.; Xin, H.; Qin, X.; Chen, K. Exploring Effect of Water Immersion on the Structure and Low-Temperature Oxidation of Coal: A Case Study of Shendong Long Flame Coal, China. Fuel 2018, 234, 732–737. [Google Scholar] [CrossRef]
- Zhong, X.; Kan, L.; Xin, H.; Qin, B.; Dou, G. Thermal Effects and Active Group Differentiation of Low-Rank Coal during Low-Temperature Oxidation under Vacuum Drying after Water Immersion. Fuel 2019, 236, 1204–1212. [Google Scholar] [CrossRef]
- Zhai, X.; Ge, H.; Wang, T.; Shu, C.-M.; Li, J. Effect of Water Immersion on Active Functional Groups and Characteristic Temperatures of Bituminous Coal. Energy 2020, 205, 118076. [Google Scholar] [CrossRef]
- Lu, W.; Li, J.; Li, J.; He, Q.; Hao, W.; Li, Z. Oxidative Kinetic Characteristics of Dried Soaked Coal and Its Related Spontaneous Combustion Mechanism. Fuel 2021, 305, 121626. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, W.; Fu, P.; Wang, J.; Gao, F. Evaluation of the Spontaneous Combustion of Soaked Coal Based on a Temperature-Programmed Test System and in-Situ FTIR. Fuel 2021, 294, 120583. [Google Scholar] [CrossRef]
- Wolf, K.-H.; Bruining, H. Modelling the Interaction between Underground Coal Fires and Their Roof Rocks. Fuel 2007, 86, 2761–2777. [Google Scholar] [CrossRef]
- Chao, J.; Chu, T.; Yu, M.; Han, X.; Hu, D.; Liu, W.; Yang, X. An Experimental Study on the Oxidation Kinetics Characterization of Broken Coal under Stress Loading. Fuel 2021, 287, 119515. [Google Scholar] [CrossRef]
- Chu, T.; Wu, C.; Jiang, B.; Zhu, T.; Zhang, X.; Chen, Y.; Li, L. Low-Temperature Oxidation Characteristics and Apparent Activation Energy of Pressurized Crushed Coal Under Stress Loading. Nat. Resour. Res. 2024, 34, 885–897. [Google Scholar] [CrossRef]
- Pan, R.; Gu, Q.; Chao, J.; Han, X.; Jia, H.; Wang, J. Study on the Spontaneous Combustion Oxidation Properties of Coal under the Coupling Effect of Stress and Temperature. Combust. Sci. Technol. 2023, 195, 1369–1385. [Google Scholar] [CrossRef]
- Niu, H.; Sun, S.; Sun, Q.; Wang, H.; Pan, H.-Y.; Yang, X.; Yu, X. Study on the Influence of Unloading Disturbance of Initial Load Stress on the Microstructure and Thermodynamic Behavior of Granular Coal. Asia-Pac. J. Chem. Eng. 2024, 19, e3130. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, C.; Guo, X.; Peng, S.; Zhao, J.; Yan, F. Experimental Investigation on the Permeability and Damage Characteristics of Raw Coal under Tiered Cyclic Unloading and Loading Confining Pressure. Powder Technol. 2021, 389, 416–429. [Google Scholar] [CrossRef]
- Dong, Z. Experimental Study on Crushing Characteristics of Lignite under Different Load Conditions. Adv. Mater. Sci. Eng. 2022, 2022, 5501501. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, Z.; Liang, Y.; Wang, J.; Cai, M.; Si, G.; Si, L.; Xu, Y. Study on Mechanism and Characteristic of CO Evolution of Loading Coal in Inert Atmosphere. Fuel 2023, 349, 128600. [Google Scholar] [CrossRef]
- Pan, R.; Li, C.; Fu, D.; Xiao, Z.; Jia, H. The Study on Oxidation Characteristics and Spontaneous Combustion Micro-Structure Change of Unloading Coal under Different Initial Stress. Combust. Sci. Technol. 2020, 192, 1053–1065. [Google Scholar] [CrossRef]
- Jia, H.; Yang, Y.; Ren, W.; Kang, Z.; Shi, J. Experimental Study on the Characteristics of the Spontaneous Combustion of Coal at High Ground Temperatures. Combust. Sci. Technol. 2022, 194, 2880–2893. [Google Scholar] [CrossRef]
- Chen, D.; Zhu, J.; Ye, Q.; Ma, X.; Xie, S.; Guo, W.; Li, Z.; Wang, Z.; Feng, S.; Yan, X. Application of Gob-Side Entry Driving in Fully Mechanized Caving Mining: A Review of Theory and Technology. Energies 2023, 16, 2691. [Google Scholar] [CrossRef]
- Qin, Y.; Song, Y.; Yang, X.; Qin, C. Experimental Study on Coal Granularity Influencing Oxidation Rate in Goaf. J. China Coal Soc. 2010, 35, 132–135. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Z.; Wang, Z. Numeral Simulation Model and Application of Temperature Rise Process Caused by Natural Burn of Lossed Coal in Goaf. J. Saf. Environ. 2004, 4, 58–61. [Google Scholar] [CrossRef]
- Li, H.; Li, X.; Fu, J.; Zhu, N.; Chen, D.; Wang, Y.; Ding, S. Experimental Study on Compressive Behavior and Failure Characteristics of Imitation Steel Fiber Concrete under Uniaxial Load. Constr. Build. Mater. 2023, 399, 132599. [Google Scholar] [CrossRef]
- Han, D.; Niu, G.; Zhu, H.; Chang, T.; Liu, B.; Ren, Y.; Wang, Y.; Song, B. Exploration and Frontier of Coal Spontaneous Combustion Fire Prevention Materials. Processes 2024, 12, 1155. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Wang, D.; Zhang, D. Investigations on the Mechanism of the Microstructural Evolution of Different Coal Ranks under Liquid Nitrogen Cold Soaking. Energy Sources Part A Recovery Util. Environ. Eff. 2025, 47, 2596–2612. [Google Scholar] [CrossRef]
- Dong, M.; Xia, W.; Xu, T. Flame Retardance and Fume Inhibition of Bio-Based Composite Flame Retardant on Bituminous Combustion and Its Numerical Models. Constr. Build. Mater. 2024, 422, 135869. [Google Scholar] [CrossRef]
- Li, X.; Chen, D.; Li, Z.; Liu, S.; Zhai, M.; Li, Y.; Gong, B.; Sun, Z.; Wang, Y.; Wang, D. Roadway Portal and Self-Moving Hydraulic Support for Rockburst Prevention in Coal Mine and Its Application. Phys. Fluids 2024, 36, 124136. [Google Scholar] [CrossRef]
- Liu, S.; Sun, H.; Zhang, D.; Yang, K.; Li, X.; Wang, D.; Li, Y. Experimental Study of Effect of Liquid Nitrogen Cold Soaking on Coal Pore Structure and Fractal Characteristics. Energy 2023, 275, 127470. [Google Scholar] [CrossRef]
- Zhang, P.; Sha, D.; Li, Q.; Zhao, S.; Ling, Y. Effect of Nano Silica Particles on Impact Resistance and Durability of Concrete Containing Coal Fly Ash. Nanomaterials 2021, 11, 1296. [Google Scholar] [CrossRef]
- Yao, Z.; Fang, Y.; Kong, W.; Huang, X.; Wang, X. Experimental Study on Dynamic Mechanical Properties of Coal Gangue Concrete. Adv. Mater. Sci. Eng. 2020, 2020, 8874191. [Google Scholar] [CrossRef]
- Yang, X.; Ren, T.; Tan, L.; Remennikov, A. Fragmentation Characteristic and Energy Dissipation of Coal under Impact Load. Int. J. Geomech. 2021, 21, 04021057. [Google Scholar] [CrossRef]
- Dodd, A.B.; Lautenberger, C.; Fernandez-Pello, A.C. Numerical Examination of Two-Dimensional Smolder Structure in Polyurethane Foam. Proc. Combust. Inst. 2009, 32, 2497–2504. [Google Scholar] [CrossRef]
- Okur, H.; Eymir, C. Dehydration Kinetics of Ulexite by Thermogravimetric Data Using the Coats-Redfern and Genetic Algorithm Method. Ind. Eng. Chem. Res. 2003, 42, 3642–3646. [Google Scholar] [CrossRef]
- Rein, G.; Lautenberger, C.; Fernandez-Pello, A.; Torero, J.; Urban, D. Application of Genetic Algorithms and Thermogravimetry to Determine the Kinetics of Polyurethane Foam in Smoldering Combustion. Combust. Flame 2006, 146, 95–108. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Yu, L.; Lu, K. The Accuracy and Efficiency of GA and PSO Optimization Schemes on Estimating Reaction Kinetic Parameters of Biomass Pyrolysis. Energy 2019, 176, 582–588. [Google Scholar] [CrossRef]
- Li, B.; Chen, G.; Zhang, H.; Sheng, C. Development of Non-Isothermal TGA-DSC for Kinetics Analysis of Low Temperature Coal Oxidation Prior to Ignition. Fuel 2014, 118, 385–391. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kissinger Method in Kinetics of Materials: Things to Beware and Be Aware of. Molecules 2020, 25, 2813. [Google Scholar] [CrossRef]
- Yang, X.; Chu, T.; Wang, L.; Li, H.; Wang, J.; Yu, M. Mechanochemical Evolution of Coal Microscopic Groups: A New Pathway for Mechanical Forces Acting on Coal Spontaneous Combustion. Sci. Total Environ. 2024, 925, 171471. [Google Scholar] [CrossRef]
- Xue, Z. Fundamental Study of Coal Pyrolysis IV. Functional Group Pyrolysis Model. J. East China Univ. Sci. Technol. 2001, 2, 113–116+120. [Google Scholar]
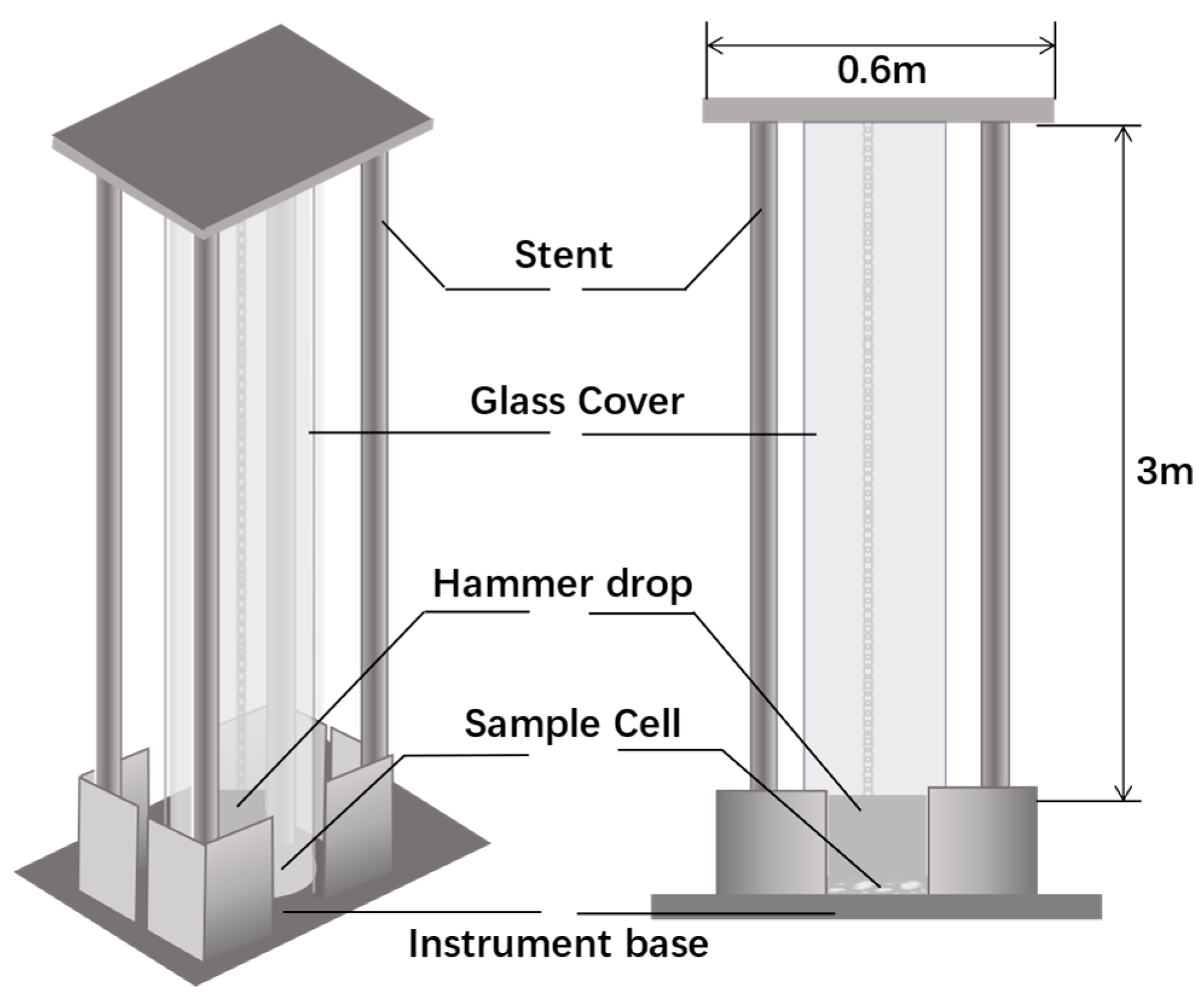
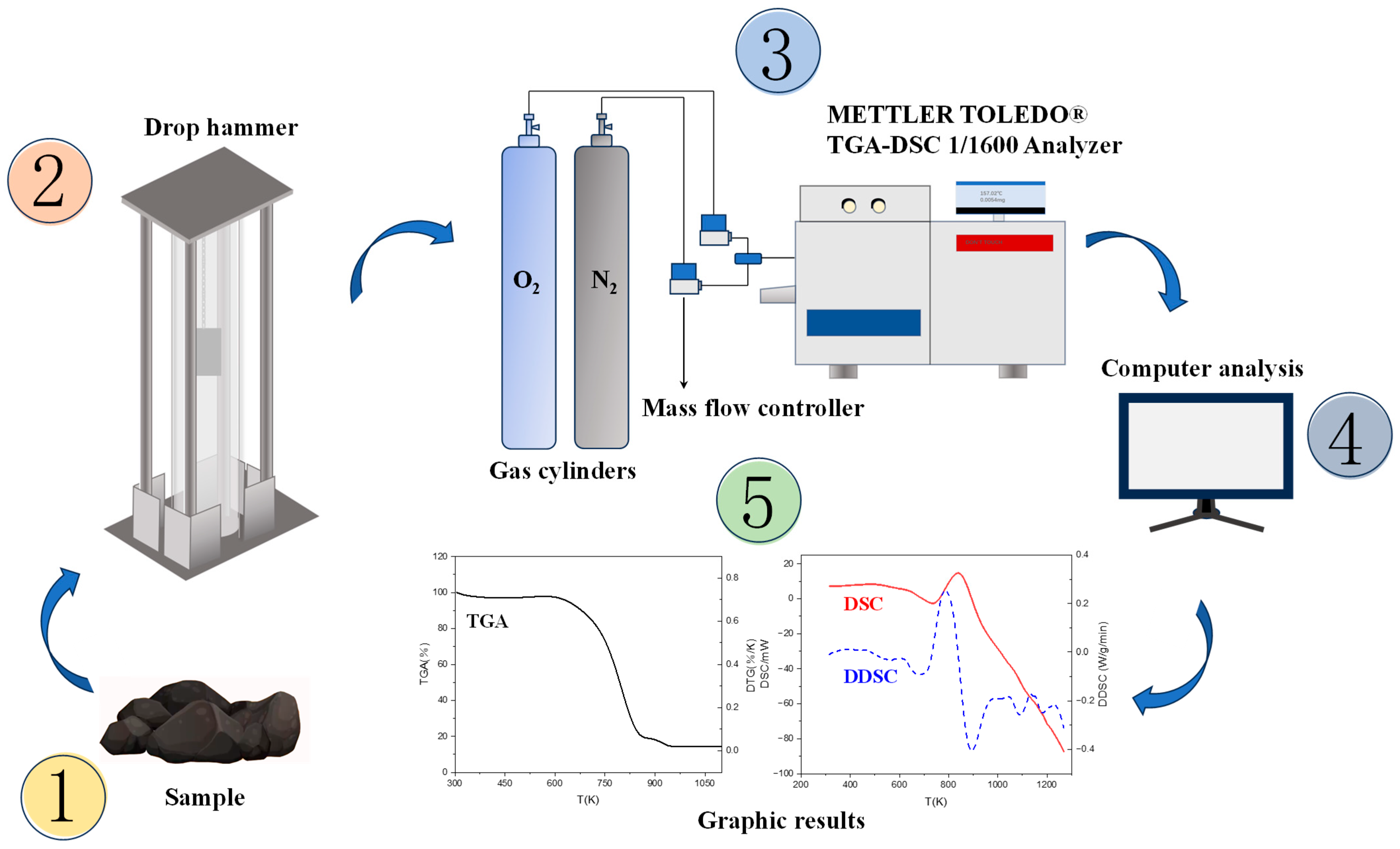



| Mad (%) | Aad (%) | Vad (%) | FCad (%) | |
|---|---|---|---|---|
| Samples | 3.16 | 9.92 | 31.20 | 55.72 |
| C (%) | H (%) | O (%) | S (%) | |
|---|---|---|---|---|
| Samples | 89.39 | 4.82 | 4,27 | 0.51 |
| Sample | S1 | S2 | S3 |
|---|---|---|---|
| Drop height | 0 m | 2 m | 3 m |
| Parameters | S1 | S2 | S3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Stage 1 | Stage 2 | Stage 3 | Stage 1 | Stage 2 | Stage 3 | Stage 1 | Stage 2 | Stage 3 | |
| Ea/(KJ mol−1) | 114.1512 | 345.7709 | 333.1087 | 64.7577 | 253.6768 | 280.8469 | 61.3986 | 202.6957 | 178.8092 |
| ln(A)/ln(s−1) | 14.1214 | 12.7739 | 13.3286 | 6.5058 | 15.2082 | 10.9504 | 7.1444 | 11.5825 | 6.3294 |
| R2 | 0.9982 | 0.9945 | 0.9765 | 0.9609 | 0.9974 | 0.9822 | 0.9882 | 0.9745 | 0.9708 |
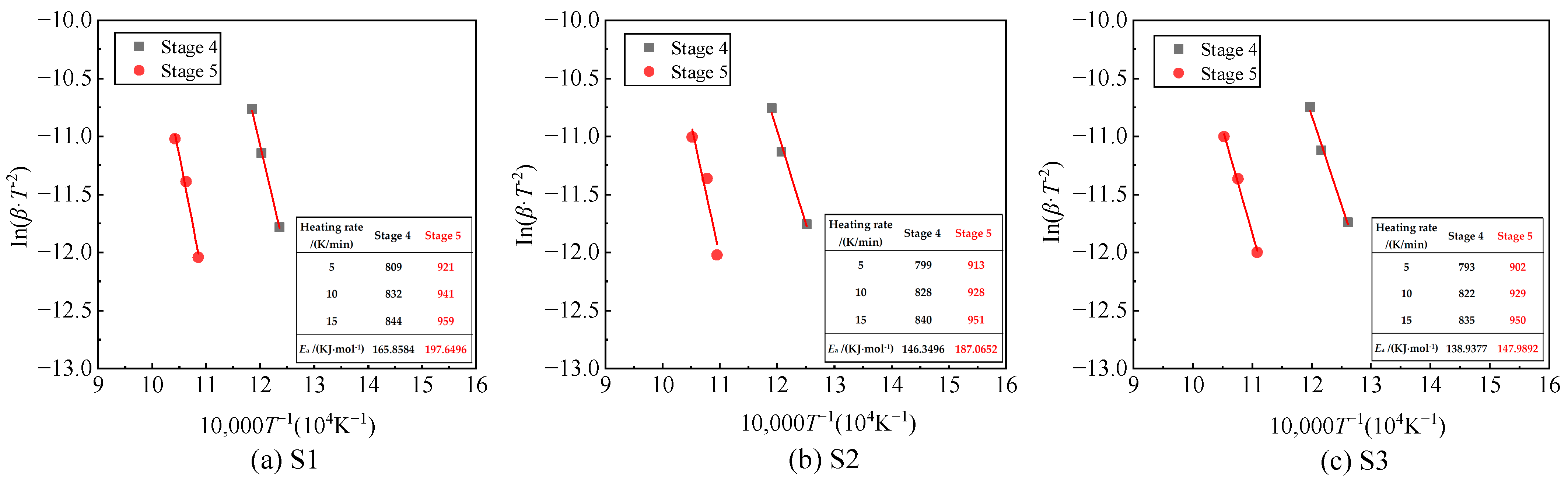
| Parameters | S1 | S2 | S3 | |||
|---|---|---|---|---|---|---|
| Stage 4 | Stage 5 | Stage 4 | Stage 5 | Stage 4 | Stage 5 | |
| Ea/(KJ mol−1) | 165.8584 | 197.6496 | 146.3496 | 187.0652 | 138.9377 | 147.9892 |
| ln(A)/ln(s−1) | 11.4256 | 10.8694 | 11.7822 | 10.4904 | 10.9027 | 8.4071 |
| R2 | 0.9863 | 0.9972 | 0.9945 | 0.9608 | 0.9963 | 0.9950 |
| Reaction step | Parameters | Unit | S1 | S2 | S3 |
|---|---|---|---|---|---|
(Coal drying dehydration) | Ea | KJ/mol | 105.7256 | 82.4857 | 63.4082 |
| ln(A) | ln(s−1) | 12.3981 | 7.4659 | 8.4220 | |
| n | 3.3301 | 3.4213 | 3.1920 | ||
| v | kg kg−1 | 0.97 | 0.97 | 0.97 | |
| nO2 | 0 | 0 | 0 | ||
(Devolatilization) | Ea | KJ/mol | 278.9330 | 248.2394 | 197.1206 |
| ln(A) | ln(s−1) | 12.4859 | 15.9821 | 11.5672 | |
| n | 4.3317 | 4.6734 | 4.1026 | ||
| v | kg kg−1 | 0.7536 | 0.7497 | 0.7442 | |
| nO2 | 0 | 0 | 0 | ||
(Semi-coke condensation to Char) | Ea | KJ/mol | 310.3451 | 291.3772 | 210.4877 |
| ln(A) | ln(s−1) | 13.2469 | 10.5918 | 6.2918 | |
| n | 2.5912 | 2.9148 | 2.5209 | ||
| v | kg kg−1 | 0.9021 | 0.9140 | 0.9098 | |
| nO2 | 0 | 0 | 0 | ||
(Oxidize to Char) | Ea | KJ/mol | 181.1491 | 176.2140 | 159.8911 |
| ln(A) | ln(s−1) | 12.3431 | 14.6920 | 11.9998 | |
| n | 3.1923 | 3.1095 | 3.7762 | ||
| v | kg kg−1 | 0.8266 | 0.8523 | 0.8014 | |
| nO2 | 5.1945 | 5.9922 | 5.8971 | ||
(Semi-coke oxidizes to Char) | Ea | KJ/mol | 153.1941 | 142.1095 | 120.2851 |
| ln(A) | ln(s−1) | 13.5491 | 11.5480 | 11.1249 | |
| n | 2.2143 | 2.1910 | 2.5091 | ||
| v | kg kg−1 | 0.8221 | 0.8022 | 0.7987 | |
| nO2 | 5.9129 | 5.1284 | 5.7980 | ||
(Char oxidizes to ash) | Ea | KJ/mol | 178.1329 | 151.4910 | 131.5494 |
| ln(A) | ln(s−1) | 9.1241 | 11.4871 | 7.1485 | |
| n | 1.2247 | 1.9471 | 1.0879 | ||
| v | kg kg−1 | 0.0923 | 0.0901 | 0.0894 | |
| nO2 | 1.7549 | 2.1042 | 1.6282 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wen, W.; Xu, W.; Zhu, K.; Guan, X. Study on the Response of Chemical Kinetics of Fragmented Coal Under Dynamic Load. Sustainability 2025, 17, 3677. https://doi.org/10.3390/su17083677
Wang L, Wen W, Xu W, Zhu K, Guan X. Study on the Response of Chemical Kinetics of Fragmented Coal Under Dynamic Load. Sustainability. 2025; 17(8):3677. https://doi.org/10.3390/su17083677
Chicago/Turabian StyleWang, Liang, Wushuang Wen, Wenjie Xu, Kai Zhu, and Xiaoqing Guan. 2025. "Study on the Response of Chemical Kinetics of Fragmented Coal Under Dynamic Load" Sustainability 17, no. 8: 3677. https://doi.org/10.3390/su17083677
APA StyleWang, L., Wen, W., Xu, W., Zhu, K., & Guan, X. (2025). Study on the Response of Chemical Kinetics of Fragmented Coal Under Dynamic Load. Sustainability, 17(8), 3677. https://doi.org/10.3390/su17083677





