Impact of Shrinking Cities on Carbon Emission Efficiency in China
Abstract
1. Introduction
2. Methods and Materials
2.1. Super-SBM DEA Model with Undesirable Outputs
2.2. Spatial Analysis
2.2.1. Spatial Autocorrelation
2.2.2. Spatial Econometric Models
2.3. Data Sources and Variable Selection
2.3.1. CO2 Emission Efficiency
2.3.2. Shrinking Cities
2.3.3. Control Variables
2.3.4. Data on the Variables
3. Results
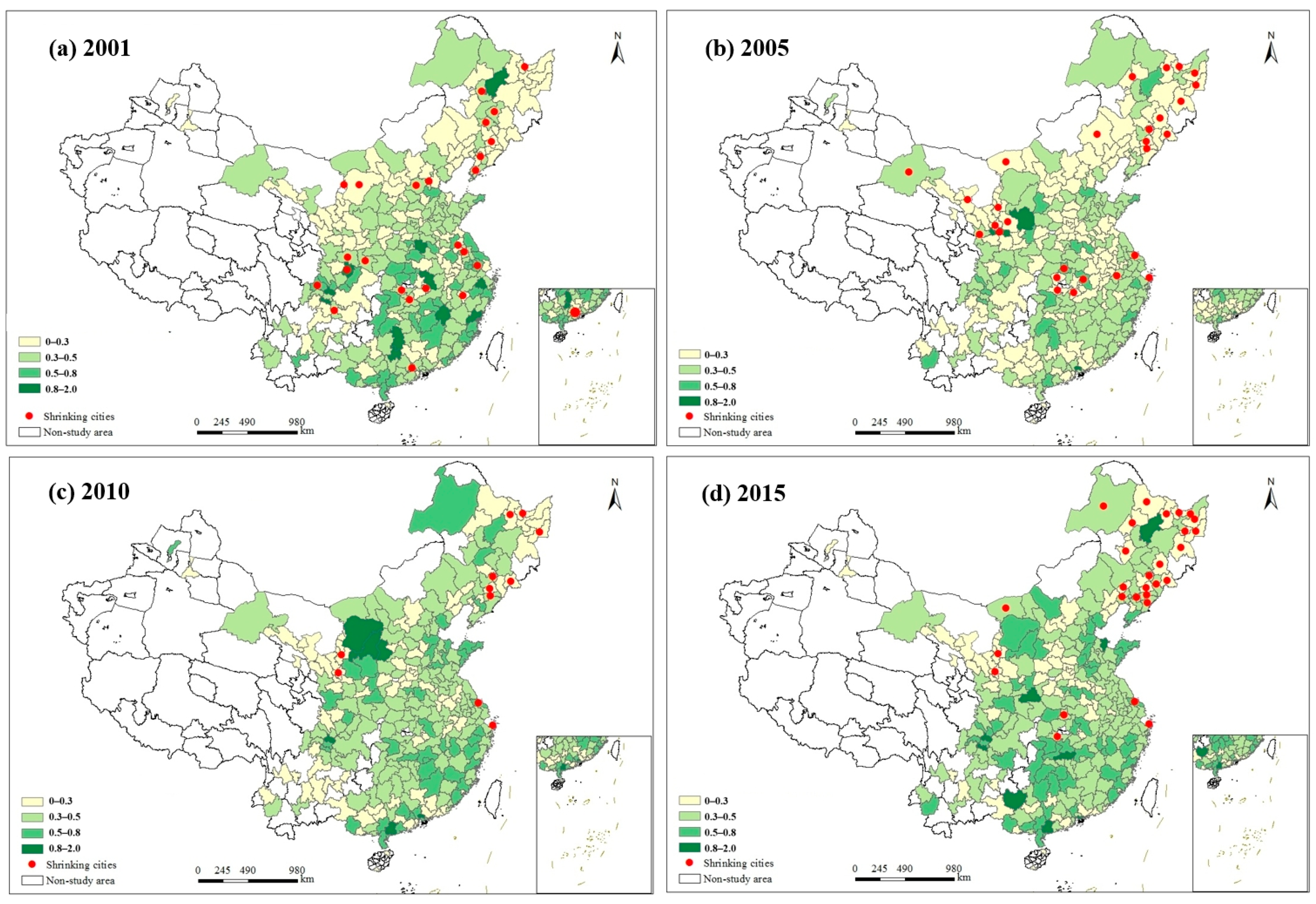
3.1. Temporal and Spatial Distribution of Urban CEE and Shrinking Cities
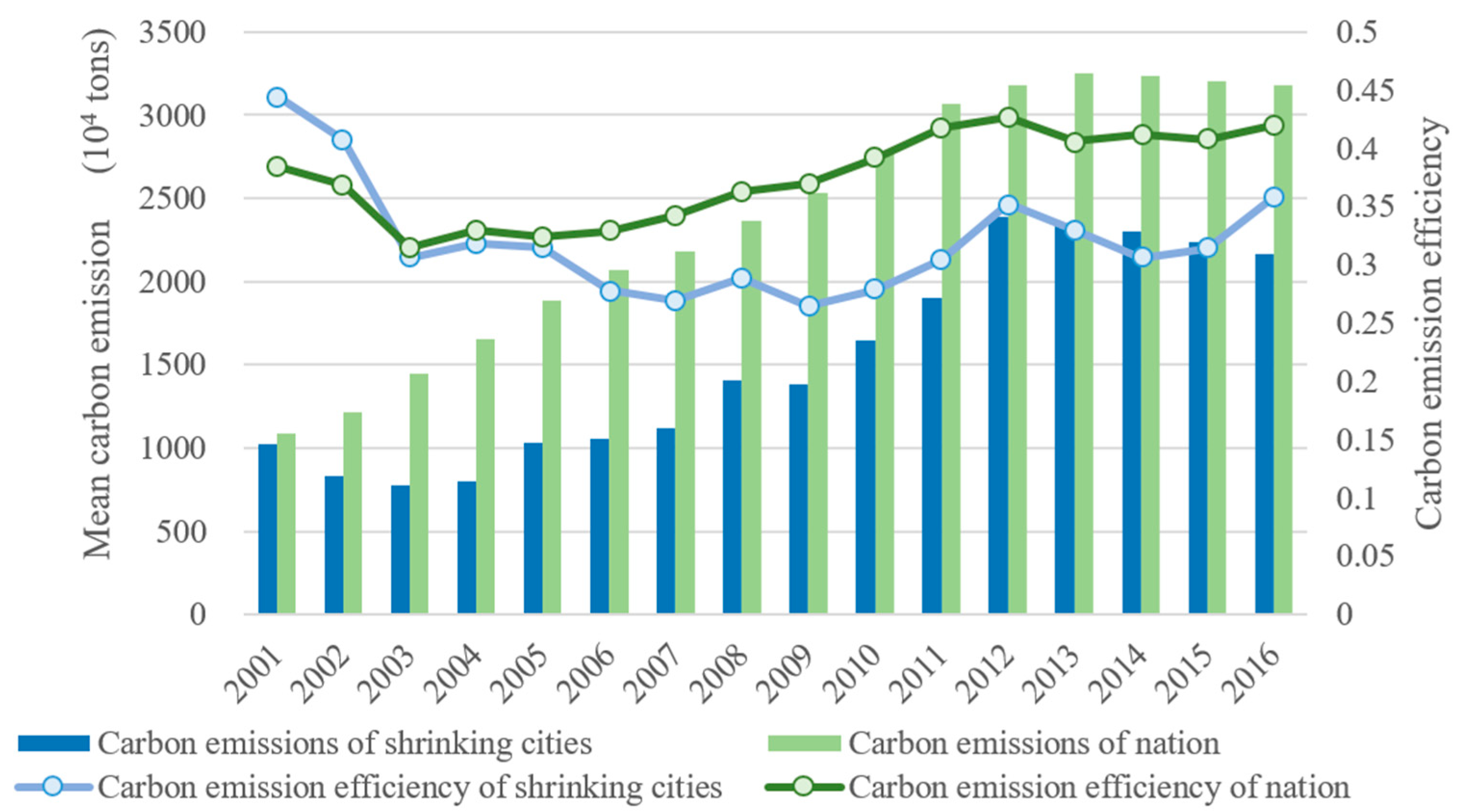
3.2. Urban CE and CEE of China
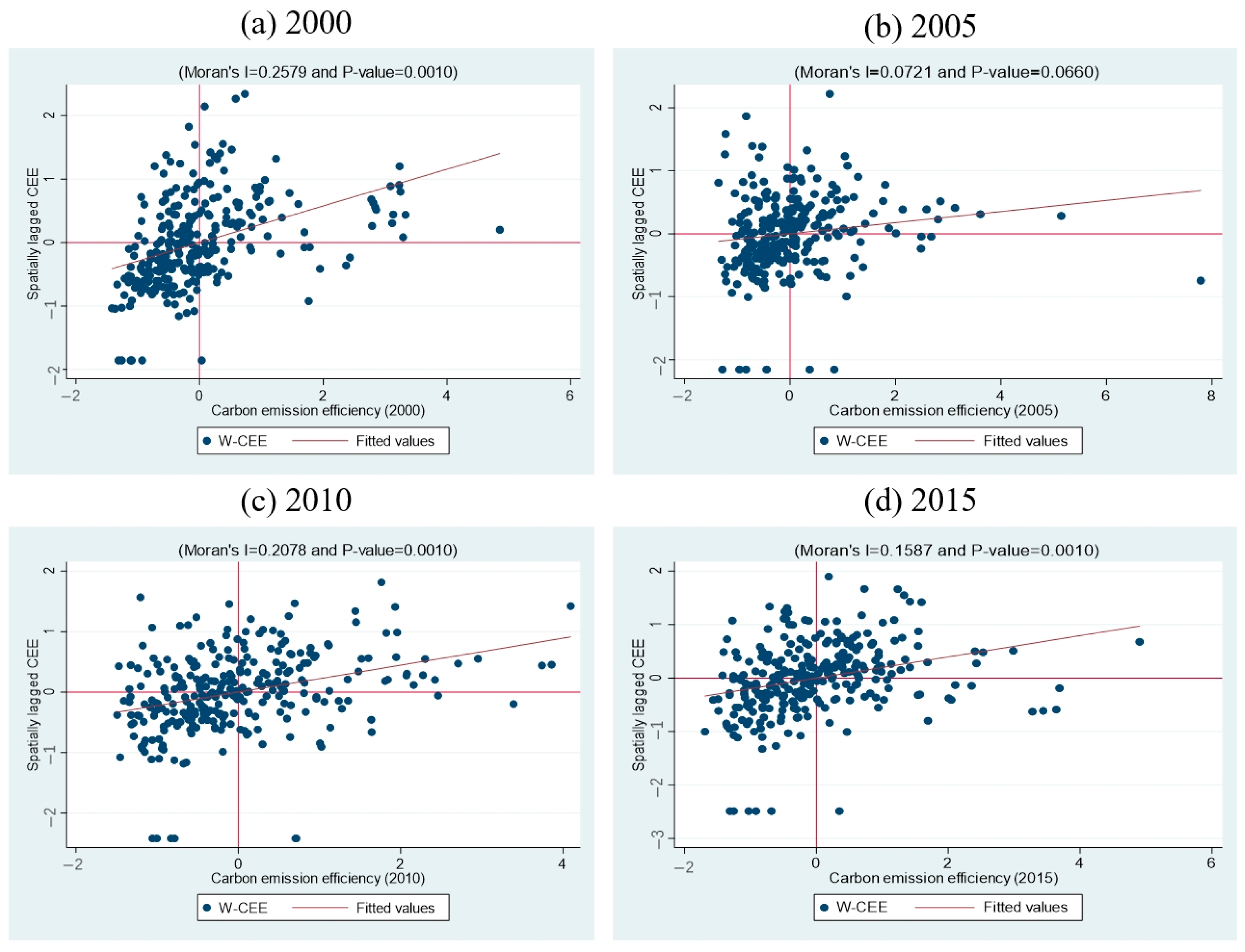
3.3. Spatial Autocorrelation of CEE
3.4. Spatial Panel Data Model Analysis
3.4.1. Effects of Shrinking Cities
3.4.2. Effects of Control Variables
4. Discussion
4.1. CEs and CEE of Chinese Cities
4.2. Impacts of Urban Shrinkage on CEE
4.3. Effects of Control Variables on CEE
4.4. Policy Implications
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CEE | Carbon Emission Efficiency |
| CE | Carbon Emission |
| SBM | Slack-Based Measure |
| DEA | Data Envelopment Analysis |
References
- Yoro, K.O.; Daramola, M.O. Chapter 1—CO2 emission sources, greenhouse gases, and the global warming effect. In Advances in Carbon Capture; Rahimpour, M.R., Farsi, M., Makarem, M.A., Eds.; Woodhead Publishing: Sawston, UK, 2020; pp. 3–28. [Google Scholar]
- Wang, Y.; Niu, Y.; Li, M.; Yu, Q.; Chen, W. Spatial structure and carbon emission of urban agglomerations: Spatiotemporal characteristics and driving forces. Sustain. Cities Soc. 2022, 78, 103600. [Google Scholar] [CrossRef]
- NBSC, National Data. 2020. Available online: https://data.stats.gov.cn/english/easyquery.htm?cn=C01 (accessed on 15 April 2025).
- Long, Y.; Wu, K. Shrinking cities in a rapidly urbanizing China. Environ. Plan. A Econ. Space 2016, 48, 220–222. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X. Does labor mobility follow the inter-regional transfer of labor-intensive manufacturing? The spatial choices of China’s migrant workers. Habitat Int. 2022, 124, 102559. [Google Scholar] [CrossRef]
- Wang, Z. The Imbalance in Regional Economic Development in China and Its Reasons. In Private Sector Development and Urbanization in China: Strategies for Widespread Growth; Wang, Z., Ed.; Palgrave Macmillan USA: New York, NY, USA, 2015; pp. 53–75. [Google Scholar]
- Liu, S.; Zhang, Y. Cities without slums? China’s land regime and dual-track urbanization. Cities 2020, 101, 102652. [Google Scholar] [CrossRef]
- Li, J.; Zhan, W.; Hong, F.; Lai, J.; Dong, P.; Liu, Z.; Wang, C.; Huang, F.; Li, L.; Wang, C.; et al. Similarities and disparities in urban local heat islands responsive to regular-, stable-, and counter-urbanization: A case study of Guangzhou, China. Build. Environ. 2021, 199, 107935. [Google Scholar] [CrossRef]
- Haase, D.; Haase, A.; Rink, D. Conceptualizing the nexus between urban shrinkage and ecosystem services. Landsc. Urban Plan. 2014, 132, 159–169. [Google Scholar] [CrossRef]
- Qiang, W.; Lin, Z.; Zhu, P.; Wu, K.; Lee, H.F. Shrinking cities, urban expansion, and air pollution in China: A spatial econometric analysis. J. Clean. Prod. 2021, 324, 129308. [Google Scholar] [CrossRef]
- Guan, D.; He, X.; Hu, X. Quantitative identification and evolution trend simulation of shrinking cities at the county scale, China. Sustain. Cities Soc. 2021, 65, 102611. [Google Scholar] [CrossRef]
- Wu, K.; Sun, D. Progress in Urban Shrinkage Research. Econ. Geogr. 2017, 37, 59–67. [Google Scholar]
- Jiang, Z.; Zhai, W.; Meng, X.; Long, Y. Identifying Shrinking Cities with NPP-VIIRS Nightlight Data in China. J. Urban Plan. Dev. 2020, 146, 04020034. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, T. Urban shrinkage and eco-efficiency: The mediating effects of industry, innovation and land-use. Environ. Impact Assess. Rev. 2023, 98, 106921. [Google Scholar] [CrossRef]
- Großmann, K.; Bontje, M.; Haase, A.; Mykhnenko, V. Shrinking cities: Notes for the further research agenda. Cities 2013, 35, 221–225. [Google Scholar] [CrossRef]
- Long, Y.; Gao, S. Shrinking Cities in China: The Overall Profile and Paradox in Planning. In Shrinking Cities in China: The Other Facet of Urbanization; Long, Y., Gao, S., Eds.; Springer: Singapore, 2019; pp. 3–21. [Google Scholar]
- Liu, X.; Wang, M.; Qiang, W.; Wu, K.; Wang, X. Urban form, shrinking cities, and residential carbon emissions: Evidence from Chinese city-regions. Appl. Energy 2020, 261, 114409. [Google Scholar] [CrossRef]
- Xiao, H.; Duan, Z.; Zhou, Y.; Zhang, N.; Shan, Y.; Lin, X.; Liu, G. CO2 emission patterns in shrinking and growing cities: A case study of Northeast China and the Yangtze River Delta. Appl. Energy 2019, 251, 113384. [Google Scholar] [CrossRef]
- Zeng, T.; Jin, H.; Geng, Z.; Kang, Z.; Zhang, Z. The Effect of Urban Shrinkage on Carbon Dioxide Emissions Efficiency in Northeast China. Int. J. Environ. Res. Public Health 2022, 19, 5772. [Google Scholar] [CrossRef]
- Danko, J.J., III; Hanink, D.M. Beyond the obvious: A comparison of some demographic changes across selected shrinking and growing cities in the United States from 1990 to 2010. Popul. Space Place 2018, 24, e2136. [Google Scholar] [CrossRef]
- Kuosmanen, T.; Kortelainen, M. Measuring eco-efficiency of production with data envelopment analysis. J. Ind. Ecol. 2005, 9, 59–72. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, W.; Wang, J.; Yang, F.; Jiang, H. Regional low-carbon economy efficiency in China: Analysis based on the Super-SBM model with CO2 emissions. J. Clean. Prod. 2017, 163, 202–211. [Google Scholar] [CrossRef]
- Li, H.; Fang, K.; Yang, W.; Wang, D.; Hong, X. Regional environmental efficiency evaluation in China: Analysis based on the Super-SBM model with undesirable outputs. Math. Comput. Model. 2013, 58, 1018–1031. [Google Scholar] [CrossRef]
- Ding, L.; Yang, Y.; Wang, W.; Calin, A.C. Regional carbon emission efficiency and its dynamic evolution in China: A novel cross efficiency-malmquist productivity index. J. Clean. Prod. 2019, 241, 118260. [Google Scholar] [CrossRef]
- Meng, F.; Su, B.; Thomson, E.; Zhou, D.; Zhou, P. Measuring China’s regional energy and carbon emission efficiency with DEA models: A survey. Appl. Energy 2016, 183, 1–21. [Google Scholar] [CrossRef]
- Wang, S.; Wang, Z.; Fang, C. Evolutionary characteristics and driving factors of carbon emission performance at the city level in China. Sci. China Earth Sci. 2022, 65, 1292–1307. [Google Scholar] [CrossRef]
- Yan, D.; Lei, Y.; Li, L.; Song, W. Carbon emission efficiency and spatial clustering analyses in China’s thermal power industry: Evidence from the provincial level. J. Clean. Prod. 2017, 156, 518–527. [Google Scholar] [CrossRef]
- Hu, S.; Yuan, Z.; Wang, A. Improving carbon emission efficiency in Chinese manufacturing: A study considering technological heterogeneity and noise. Energy 2024, 291, 130392. [Google Scholar] [CrossRef]
- Tong, X.; Guo, S.; Duan, H.; Duan, Z.; Gao, C.; Chen, W. Carbon-Emission Characteristics and Influencing Factors in Growing and Shrinking Cities: Evidence from 280 Chinese Cities. Int. J. Environ. Res. Public Health 2022, 19, 2120. [Google Scholar] [CrossRef]
- Herrmann, D.L.; Schwarz, K.; Shuster, W.D.; Berland, A.; Chaffin, B.C.; Garmestani, A.S.; Hopton, M.E. Ecology for the Shrinking City. Bioscience 2016, 66, 965–973. [Google Scholar] [CrossRef]
- Guo, S.; Tian, T.; Gong, B.; Wan, Y.; Zhou, J.X.; Wu, X. Urban shrinkage and carbon emissions: Demand-side accounting for Chinese cities. Appl. Energy 2025, 384, 125501. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Modeling undesirable factors in efficiency evaluation. Eur. J. Oper. Res. 2002, 142, 16–20. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Zhao, X.; Burnett, J.W.; Fletcher, J.J. Spatial analysis of China province-level CO2 emission intensity. Renew. Sustain. Energy Rev. 2014, 33, 1–10. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, S.; Lei, Y.; Li, S.; Li, L. Exploring spatial characteristics of city-level CO2 emissions in China and their influencing factors from global and local perspectives. Sci. Total Environ. 2021, 754, 142206. [Google Scholar] [CrossRef]
- Ni, G.; Fang, Y.; Niu, M.; Lv, L.; Song, C.; Wang, W. Spatial differences, dynamic evolution and influencing factors of China’s construction industry carbon emission efficiency. J. Clean. Prod. 2024, 448, 141593. [Google Scholar] [CrossRef]
- Moran, P.A.P. The interpretation of statistical maps. J. R. Stat. Society. Ser. B (Methodol.) 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2009. [Google Scholar]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Z.; He, G.; Wang, H.; Zhang, X.; Lin, J.; Qi, Y.; Liang, X. Challenges and opportunities for carbon neutrality in China. Nat. Rev. Earth Environ. 2022, 3, 141–155. [Google Scholar] [CrossRef]
- Mi, Z.; Meng, J.; Guan, D.; Shan, Y.; Liu, Z.; Wang, Y.; Feng, K.; Wei, Y.-M. Pattern changes in determinants of Chinese emissions. Environ. Res. Lett. 2017, 12, 074003. [Google Scholar] [CrossRef]
- Wang, S.; Gao, S.; Huang, Y.; Shi, C. Spatio-temporal evolution and trend prediction of urban carbon emission performance in China based on super-efficiency SBM model. Acta Geogr. Sin. 2020, 75, 15. [Google Scholar] [CrossRef]
- Hubacek, K.; Feng, K.; Chen, B. Changing lifestyles towards a low carbon economy: An ipat analysis for China. Energies 2012, 5, 22–31. [Google Scholar] [CrossRef]
- Feng, K.; Hubacek, K.; Guan, D. Lifestyles, technology and CO2 emissions in China: A regional comparative analysis. Ecol. Econ. 2009, 69, 145–154. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, T.; Wang, Y.; Shi, Z. Research on impacts of population-related factors on carbon emissions in Beijing from 1984 to 2012. Environ. Impact Assess. Rev. 2015, 55, 45–53. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Li, S.; Fang, C.; Feng, K. Socioeconomic driving forces and scenario simulation of CO2 emissions for a fast-developing region in China. J. Clean. Prod. 2019, 216, 217–229. [Google Scholar] [CrossRef]
- Wang, C.J.; Wang, F.; Zhang, X.L.; Yang, Y.; Su, Y.X.; Ye, Y.Y.; Zhang, H.G. Examining the driving factors of energy related carbon emissions using the extended STIRPAT model based on IPAT identity in Xinjiang. Renew. Sustain. Energy Rev. 2017, 67, 51–61. [Google Scholar] [CrossRef]
- Rocak, M.; Hospers, G.-J.; Reverda, N. Searching for Social Sustainability: The Case of the Shrinking City of Heerlen, The Netherlands. Sustainability 2016, 8, 382. [Google Scholar] [CrossRef]
- Tomohiro, O.; Shamil, M. ODIAC Fossil Fuel CO2 Emissions Dataset; National Institute for Environmental Studies: Ibaraki, Japan, 2021. [CrossRef]
- Cai, B.; Guo, H.; Ma, Z.; Wang, Z.; Dhakal, S.; Cao, L. Benchmarking carbon emissions efficiency in Chinese cities: A comparative study based on high-resolution gridded data. Appl. Energy 2019, 242, 994–1009. [Google Scholar] [CrossRef]
- Zhang, N.; Wang, B.; Chen, Z. Carbon emissions reductions and technology gaps in the world’s factory, 1990–2012. Energy Policy 2016, 91, 28–37. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, N. Low-carbon city pilot and carbon emission efficiency: Quasi-experimental evidence from China. Energy Econ. 2021, 96, 105125. [Google Scholar] [CrossRef]
- Zeng, S.; Jin, G.; Tan, K.; Liu, X. Can low-carbon city construction reduce carbon intensity? Empirical evidence from low-carbon city pilot policy in China. J. Environ. Manag. 2023, 332, 117363. [Google Scholar] [CrossRef] [PubMed]
- Schackmar, J. Smart cities as a substitute industry revitalisation approach to shrinking cities in Germany? In Handbook on Shrinking Cities; Edward Elgar Publishing: Gloucestershire, UK, 2022; pp. 381–394. [Google Scholar]
- Schackmar, J.; Fleschurz, R.; Pallagst, K. The Role of Substitute Industries for Revitalizing Shrinking Cities. Sustainability 2021, 13, 9250. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, W.; Lv, X.; Chen, X.; Shen, M. Investigating interior driving factors and cross-industrial linkages of carbon emission efficiency in China’s construction industry: Based on Super-SBM DEA and GVAR model. J. Clean. Prod. 2019, 241, 118322. [Google Scholar] [CrossRef]
- Deng, T.; Wang, D.; Yang, Y.; Yang, H. Shrinking cities in growing China: Did high speed rail further aggravate urban shrinkage? Cities 2019, 86, 210–219. [Google Scholar] [CrossRef]
- Fang, G.; Gao, Z.; Tian, L.; Fu, M. What drives urban carbon emission efficiency?—Spatial analysis based on nighttime light data. Appl. Energy 2022, 312, 118772. [Google Scholar] [CrossRef]
- Deng, T.; Liu, S.; Hu, Y. Can tourism help to revive shrinking cities? An examination of Chinese case. Tour. Econ. 2022, 28, 1683–1691. [Google Scholar] [CrossRef]
| Test | Indicator | Statistics (CEE) | |
|---|---|---|---|
| LM test | SEM | Moran’s I | 3.39 *** |
| LM | 264.79 *** | ||
| R-LM | 177.61 *** | ||
| SLM | LM | 87.18 *** | |
| R-LM | 0.21 | ||
| LR test | both to ind | 145.32 *** | |
| both to time | 4234.74 *** | ||
| Hausman test | −956.28 | ||
| Wald test | SAR | 51.42 *** | |
| SEM | 36.77 *** | ||
| LR test | SAR | 50.90 *** | |
| SEM | 36.08 *** | ||
| Indicator | Variables | Unit | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|---|
| Input | Fixed asset investment | 108 yuan | 4811 | 613 | 895 | 5 | 12,090 |
| Labor force | 104 person | 4811 | 84 | 117 | 5 | 1729 | |
| Electricity | 108 kW·h | 4811 | 66 | 121 | 1 | 1486 | |
| Desirable output | GDP | 108 yuan | 4811 | 1051 | 1659 | 18 | 19,918 |
| Undesirable output | CO2 emission | 104 ton | 4811 | 2322 | 2656 | 48 | 26,891 |
| Variable | Description | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| CEE | Carbon emission efficiency | 4811 | 0.38 | 0.17 | 0.08 | 2.67 |
| Shrinking | Dummy variable | 4811 | 0.07 | 0.26 | 0 | 1 |
| PerGDP | Per capita GDP (ln) | 4811 | 9.71 | 0.83 | 7.43 | 12.81 |
| GDPR | Annual GDP growth rate (%) | 4811 | 11.70 | 4.95 | −19.38 | 109.00 |
| Sec | Secondary industry/Total | 4811 | 0.48 | 0.11 | 0.03 | 0.91 |
| Pop | Population (ln) | 4811 | 5.84 | 0.69 | 2.77 | 8.13 |
| PopDen | Population density (ln) | 4811 | 5.71 | 0.91 | 1.55 | 9.36 |
| Area | Built-up area (ln) | 4811 | 4.19 | 0.87 | 1.61 | 8.12 |
| Rev | Local fiscal revenue (ln) | 4811 | 12.56 | 1.48 | 7.20 | 17.63 |
| Year | I | z | p Value | Year | I | z | p Value |
|---|---|---|---|---|---|---|---|
| 2000 | 0.26 | 6.56 | 0.00 | 2009 | 0.15 | 3.87 | 0.00 |
| 2001 | 0.26 | 6.68 | 0.00 | 2010 | 0.21 | 5.27 | 0.00 |
| 2002 | 0.27 | 6.84 | 0.00 | 2011 | 0.15 | 3.76 | 0.00 |
| 2003 | 0.25 | 6.31 | 0.00 | 2012 | 0.15 | 3.82 | 0.00 |
| 2004 | 0.24 | 5.98 | 0.00 | 2013 | 0.15 | 3.83 | 0.00 |
| 2005 | 0.07 | 1.94 | 0.05 | 2014 | 0.17 | 4.25 | 0.00 |
| 2006 | 0.17 | 4.41 | 0.00 | 2015 | 0.16 | 4.07 | 0.00 |
| 2007 | 0.21 | 5.20 | 0.00 | 2016 | 0.10 | 2.64 | 0.01 |
| 2008 | 0.17 | 4.25 | 0.00 |
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Main Effect | W | Direct Effect | Indirect Effect | Total Effect | |
| Shrinking | 0.0119 | 0.0242 * | 0.0132 * | 0.0312 ** | 0.0445 ** |
| (1.5310) | (1.6814) | (1.6560) | (1.9740) | (2.5148) | |
| PerGDP | 0.2355 *** | −0.0685 *** | 0.2340 *** | −0.0325 ** | 0.2015 *** |
| (22.3587) | (−4.4420) | (23.3018) | (−2.0297) | (11.7708) | |
| GDPR | −0.0007 ** | −0.0015 ** | −0.0008 ** | −0.0019 *** | −0.0026 *** |
| (−2.1269) | (−2.4555) | (−2.3086) | (−2.9041) | (−3.6604) | |
| Sec | −0.1083 *** | −0.0293 | −0.1101 *** | −0.0505 | −0.1606 *** |
| (−3.0282) | (−0.5481) | (−3.2283) | (−0.8322) | (−2.5969) | |
| Pop | 0.2201 *** | −0.1067 *** | 0.2177 *** | −0.0814 * | 0.1363 *** |
| (11.1885) | (−2.6775) | (11.2228) | (−1.8682) | (2.8000) | |
| PopDen | −0.0020 | 0.0083 | −0.0010 | 0.0101 | 0.0091 |
| (−0.1772) | (0.3821) | (−0.0948) | (0.4047) | (0.3638) | |
| Area | −0.0110 * | 0.0246 ** | −0.0102 | 0.0254 ** | 0.0152 |
| (−1.8507) | (2.1656) | (−1.6431) | (2.0931) | (1.0776) | |
| Rev | −0.0496 *** | 0.0259 *** | −0.0491 *** | 0.0200 ** | −0.0291 *** |
| (−10.8271) | (3.4833) | (−11.0716) | (2.4368) | (−3.3528) | |
| Obs | 4811 | 4811 | 4811 | 4811 | 4811 |
| Spatial rho | 0.1649 *** | ||||
| (8.4149) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, T.; Li, L.; Li, T. Impact of Shrinking Cities on Carbon Emission Efficiency in China. Sustainability 2025, 17, 3664. https://doi.org/10.3390/su17083664
Yu T, Li L, Li T. Impact of Shrinking Cities on Carbon Emission Efficiency in China. Sustainability. 2025; 17(8):3664. https://doi.org/10.3390/su17083664
Chicago/Turabian StyleYu, Tianshu, Ling Li, and Tao Li. 2025. "Impact of Shrinking Cities on Carbon Emission Efficiency in China" Sustainability 17, no. 8: 3664. https://doi.org/10.3390/su17083664
APA StyleYu, T., Li, L., & Li, T. (2025). Impact of Shrinking Cities on Carbon Emission Efficiency in China. Sustainability, 17(8), 3664. https://doi.org/10.3390/su17083664







