Accelerating Small Modular Reactor Deployment and Clean Energy Transitions: An Algebraic Model for Achieving Net-Zero Emissions

Abstract

This study addresses the urgent need for transitioning to clean energy systems to achieve net-zero emissions and mitigate climate change. It introduces an algebraic modeling framework inspired by the nuclear fission six-factor formula to optimize the construction rates of clean power plants, with a focus on Small Modular Reactors (SMRs). The framework integrates four key factors affecting SMR deployment: Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource (HR) Availability, and Land Availability (LA), including their associated sub-factors. The proposed algebraic formula optimizes projections from the existing Dynamic Integrated Climate-Economy (DICE) model. By capturing socio-economic and environmental constraints, the model enhances the accuracy of clean energy transition scenarios. In the case of Ontario’s pathway to achieving net-zero emissions, the results indicate that incorporating the algebraic formula reduces the SMR construction rate projected by the DICE model from 5.2 to 3.7 units per year by 2050 and from 2.7 to 1.9 units per year by 2100. This reduction highlights the need for accelerated readiness in key deployment factors to avoid delays in reaching net zero targets, reinforcing the importance of strategic investments in PA, SC, HR, and LA. Validation against historical nuclear deployment data from the U.S., Japan, and Canada confirms the model’s ability to reflect real-world trends, with PA and SC emerging as the most influential factors. In addition to informing SMR planning, this approach offers a structured tool for prioritizing policy actions and can be adapted to other clean technologies, enhancing strategic decision making in support of net-zero goals.

1. Introduction

Climate change, driven primarily by the accumulation of greenhouse gases (GHGs), such as carbon dioxide (CO₂), represents one of the most critical threats to global sustainability [1,2]. The rising levels of CO₂ and other GHGs in the atmosphere are intensifying the greenhouse effect, leading to global warming [3]. This warming triggers a cascade of environmental impacts, including more frequent and severe extreme weather events, rising sea levels, and disruptions to ecosystems and biodiversity [4]. These effects profoundly affect human populations, agriculture, infrastructure, and natural resources. Figure 1 illustrates a historical carbon intensity in ppm to demonstrate the trajectory of CO₂ emissions over time, emphasizing the urgency of mitigation efforts [5].

The energy sector, a major contributor to CO₂ emissions, is at the heart of this transformation [6,7]. The Intergovernmental Panel on Climate Change (IPCC) has identified greenhouse gases (GHGs), especially CO₂ emissions, as the main driver of global warming, emphasizing the urgent need for clean energy solutions to reduce these emissions [8,9]. Clean energy, in this context, is defined as energy sources with a carbon intensity below 20 g of CO₂ per kilowatt-hour (g CO₂/kWh), as referenced in IPCC documentation [7]. This definition, based on international emission benchmarks, aims to ensure that all sources comply with stringent emission standards. While it does not explicitly exclude low-carbon options, such as carbon capture or biomass, it sets a strict benchmark to qualify as clean energy under decarbonization strategies.

In response to increasing energy demand and the need to cut GHG emissions, there is a growing shift from fossil fuels to clean, net-zero emission energy sources, such as renewable energy (hydropower, solar, wind) and nuclear power. The urgency of addressing climate change has prompted widespread global initiatives to transition toward sustainable energy solutions. Countries like Canada have pledged to achieve net-zero emissions by 2050, marking a pivotal step in the global shift to cleaner energy [10].

Achieving net-zero emissions requires a strategic and diversified clean energy portfolio. This portfolio should encompass large-scale nuclear energy, Small Modular Reactors (SMRs), and renewable energy sources [7]. Among these, nuclear power—especially SMRs—is recognized as a dependable, low-carbon option critical to achieving climate targets [11]. SMRs represent a new generation of nuclear technology characterized by modularity, compactness, and enhanced safety features. Typically ranging from 3 MWe to 300 MWe (as defined by the IAEA) [12], SMRs offer benefits, such as lower upfront costs, reduced construction timelines, and suitability for off-grid or remote regions [6].

Despite these advantages, SMRs face challenges, such as lengthy regulatory processes, economic risks, and deployment barriers, that hinder their contribution to climate goals [13,14,15,16,17,18]. These include high capital costs, limited workforce availability, land-use constraints, supply chain limitations, and societal acceptance hurdles. Optimizing the construction rate (CR) of SMRs is, therefore, essential. A higher CR not only accelerates deployment but also improves economic feasibility and contributes to long-term energy security and decarbonization.

This paper addresses these challenges by introducing a novel algebraic modeling framework designed to optimize SMR construction rates. While well-known energy transition models, such as DICE, TIMES, MESSAGE, and GCAM, assess clean energy transitions [6,7,19,20], they lack the granularity to model SMR-specific construction dynamics or to optimize deployment under uncertainty. The proposed algebraic model fills this gap by incorporating four critical deployment factors—Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA)—into a quantitative framework. This allows for the refinement of SMR deployment rates derived from DICE, enabling more realistic and adaptive projections.

Furthermore, the algebraic model addresses a critical gap in the existing literature: the need to quantify and incorporate uncertainties surrounding key deployment barriers, such as public acceptance, supply chain readiness, human resource availability, and land constraints. Unlike traditional macro-level energy transition models, this algebraic approach directly integrates these uncertainties into the construction rate optimization process. The model has been validated against historical nuclear deployment trends and qualitatively applied across a diverse set of countries—including the United States, Canada, Japan, France, Germany, South Korea, Russia, and China—demonstrating its reproducibility, adaptability, and applicability across a wide range of policy and governance environments.

By integrating these elements, the proposed framework offers targeted decision-support capabilities for policymakers, planners, and stakeholders. It enables users to simulate different deployment scenarios, assess potential bottlenecks in areas such as supply chain readiness or workforce availability, and evaluate the impact of policy interventions, such as public engagement initiatives or land use reforms. This model provides strategic insights into where to allocate resources and how to adjust planning assumptions to accelerate SMR deployment in alignment with net-zero goals.

The paper is structured as follows: Section 1 outlines the context, need, and contributions of the study. Section 2 introduces the algebraic model and its theoretical foundation. Section 3 discusses the methodology, including model formulation, parameter selection, and validation. Section 4 presents simulation results and comparative analyses. Section 5 discusses model implications, advantages, limitations, and reproducibility across countries. Section 6 and Section 7 conclude the paper with future research directions and conclusions.

2. The Algebraic Framework

This study introduces a systematic algebraic framework to optimize the construction rates of clean energy technologies, with a specific focus on SMRs. Unlike probabilistic models, which rely on assumptions and uncertainties, this framework offers a more structured and quantifiable method for analyzing key factors influencing SMR deployment. The framework integrates four primary factors—Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource (HR) Availability, and Land Availability (LA)—which are crucial for the successful deployment of large-scale energy projects. These factors directly impact the timeline, cost, and feasibility of SMR construction.

The framework is designed to capture both the primary factors and their respective sub-factors, providing a detailed representation of the complex relationships between them. For instance, Public Acceptance (PA) includes sub-factors such as cultural attitudes and political discourse, which can vary by region and significantly influence the pace of regulatory approvals. Similarly, Supply Chain Readiness (SC) considers material availability, logistics, and manufacturing capabilities, while Human Resource (HR) Availability reflects the skill set and training of the workforce. Land Availability (LA) involves land use agreements, zoning laws, and environmental regulations.

Each factor is modeled using algebraic equations that allow for dynamic, real-time assessments of SMR construction rates. The equations account for the non-linear interactions between the factors, enabling a deeper understanding of how they collectively influence the construction process. This approach allows for the simulation of different scenarios, providing insights into optimal strategies for accelerating SMR deployment. This framework provides a supportive tool for policymakers by offering a structured method to analyze and optimize SMR construction rates under real-world constraints.

Factors Influencing SMR Power Plant Construction Rates and the Six-Factor Fission Formula

Building on the findings of Shobeiri et al. [7], this section identifies four critical factors influencing SMR deployment and construction: Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource (HR) Availability, and Land Availability (LA). These factors are essential for the successful execution of SMR power plants, directly impacting timelines, costs, and overall feasibility.

These factors were chosen due to their critical roles in the successful execution of clean energy projects. While capital and technology are undoubtedly important, they are encompassed within these broader categories. For example, supply chain efficiency involves the management of resources and logistics, requiring both financial investment and technological advancements. Similarly, human resource availability is vital for the operation and maintenance of clean energy technologies; although capital and technology are necessary for development, their effective application depends on a skilled workforce. Public acceptance, while not directly tied to financial or technological aspects, is crucial for securing permits and approvals, significantly affecting how resources and technologies are implemented in practice. Additionally, land availability impacts site selection and project planning, influencing how effectively capital and technological resources can be utilized.

With that in mind, to address the additional factors, such as capital and technology—both of which are inherently included in the four main factors discussed earlier—the proposed extended version of the formula incorporates these as external factors. This enhancement allows for a more comprehensive analysis of their impact on clean power plant construction rates. Focusing on these four factors, the study provides a comprehensive perspective on the operational challenges that directly affect the construction rates of clean energy projects. This approach highlights practical barriers and offers actionable insights for overcoming them, providing valuable guidance for optimizing the deployment of clean energy technologies.

By leveraging the six-factor formula, which provides a practical algebraic framework for understanding the sustainability of nuclear fission reactions in a nuclear thermal reactor, this study examines the clean power plant construction rate (CR) using similar principles and approaches. This analysis considers the seventeen factors and sub-factors outlined in

Table 1. Main factors and sub-factors.

Main Factors	Sub-Factors
Public Acceptance (PA)	Cultural and community attitudes toward foreign investment in clean energy projects Public perception of international collaboration on green energy initiatives Political discourse on the role of clean energy in enhancing national and regional sovereignty Public support for clean energy projects with international and regional partners
Land Availability (LA)	Land use agreements affecting the availability of land for clean energy projects Geopolitical disputes over territorial claims impacting land access for energy infrastructure development Environmental regulations influencing cross-border land use for clean energy projects Diplomatic negotiations on land leasing or sharing arrangements for clean energy installations Provincial electricity agreements and concerns in Ontario, which also influence land availability for clean energy projects
Supply Chain (SC)	Geopolitical tensions affecting the reliability of international supply chains for clean energy components Import/export restrictions imposed due to geopolitical conflicts impacting supply chain resilience Diplomatic relations influencing the accessibility of critical materials necessary for clean energy technologies International trade agreements shaping the competitiveness of clean energy supply chains
Human Resources (HR)	International labor mobility agreements facilitating the recruitment of skilled workers for clean energy projects Diplomatic efforts to address brain drain and talent retention in clean energy sectors Geopolitical stability affecting the availability of international experts and consultants for clean energy projects Cross-border collaboration on workforce training and capacity-building programs for green energy industries (Provincially and internationally)

, derived from the combination of four main factors (essentially, complexity heuristics) and their respective sub-factors. Parallels can be drawn between the complex analysis of nuclear fission processes and the multifaceted nature of clean energy infrastructure development. While other sophisticated reactor physics theories and computational methods exist [21], the six-factor formula serves as an operational system engineering metric regarding the state of sustainable fission in a reactor of a given design.

Building on the principles of the thermal fission six-factor formula and the key factors identified in Shobeiri et al.’s work [7], this study establishes a comprehensive framework for understanding the construction rates of clean power plants, particularly SMRs. This framework is crucial for effective planning and timely execution of clean energy projects to achieve net-zero emissions. Rather than assigning separate coefficients or parameters to each sub-factor, this study embeds them within the four primary influencing factors—Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA). The sub-factors outlined in Table 1 do not function as independent variables; instead, they collectively contribute to shaping the values of these four key factors, ensuring a holistic representation of the real-world dynamics influencing SMR deployment. Furthermore, the proposed algebraic model is integrated with the DICE model from Shobeiri’s research [7], enhancing its analytical framework and applicability in assessing the dynamics of the clean energy transition. By structuring the model in this way, we ensure that all critical elements affecting SMR deployment are captured within the broader categories, aligning the approach with infrastructure constraints, socio-economic conditions, and policy influences. This integrated framework supports a structured and actionable tool for policymakers and industry leaders to drive informed decision making in the clean energy transition.

While the nuclear six-factor formula describes neutron behavior and criticality in a reactor core, its use here is metaphorical, serving as a structural inspiration for organizing the complex variables in SMR construction. It is not used to replicate physical neutron interactions, but rather to offer a conceptual structure rooted in systems engineering logic familiar to nuclear scientists and engineers. In this context, each factor in the SMR model mirrors a functional role seen in the six-factor formula—not in physical terms but as a conceptual method of decomposing a complex system into optimizable variables. This analogy helps structure the SMR construction optimization model using engineering logic familiar in nuclear reactor theory.

The fission six-factor formula, denoted as $k=\eta fp\epsilon P_{FNL}{P}_{TNL}$, is a mathematical framework that describes the physics behind nuclear fission chain reactions. It encapsulates six major factors shaping the criticality of a nuclear reactor core. Each factor influences the rate of neutron production, absorption, and scattering within the reactor core, ultimately determining the feasibility of a sustained chain reaction [22]. In this formulation:

• $\eta$: The neutron reproduction factor. It signifies the efficiency of fast neutron production versus thermal neutrons absorbed in fuel. A higher value of $\eta$ indicates more effective fast neutron production (from thermal fission), contributing to sustained fission reactions.
• $f$: The thermal utilization factor. This factor accounts for the fraction of thermal neutrons absorbed in fuel to thermal neutrons absorbed in fuel and core materials. It reflects how efficiently thermal neutrons induce fission reactions.
• $p$: The resonance escape probability. This factor represents the neutrons that reach thermal energy levels versus fast neutrons that start moderation. In effect, defining the likelihood of higher energy neutrons escaping resonance absorption (both fuel (Uranium-fuel) and core material resonance peaks) in the reactor core. A higher $p$ value implies a greater probability of neutrons escaping resonance absorption, which eventually enhances the overall fission reaction rate.
• $\epsilon$: The fast fission factor. It indicates the ratio of fast neutrons from all fission reactions versus fast neutrons from thermal fission. A higher $\epsilon$ value suggests a greater contribution of fast neutrons to the thermal fission process, potentially increasing the overall fission rate.
• $P_{FNL}$: Also named fast non-leakage probability. This factor accounts for a fraction of fast neutrons generated in fission events that start moderating all fast neutrons from all fission reactions. A higher $P_{FNL}$ value implies fewer fast neutrons escaping from a probability for moderation.
• $P_{TNL}$: Also named thermal non-leakage probability. It describes the fraction of thermal neutrons absorbed in fuel and core materials versus neutrons that reach thermal energy levels. A higher $P_{TNL}$ value indirectly indicates a higher percentage of thermal neutrons within the reactor core, that facilitate sustained thermal fission chain reactions.

Overall, the fission six-factor formula integrates these factors to assess the criticality of a nuclear reactor core, via the neutron multiplication factor, and determine its capability to sustain a self-sustaining chain reaction (here for thermal fission with Uranium-235-based fuel). Each factor contributes uniquely to the efficiency and stability of the fission process, influencing the overall rate of energy production within the reactor.

While the six-factor formula provides a robust framework for understanding nuclear fission reactions, its principles can be extrapolated to the realm of clean power plant construction. By considering the seventeen factors derived from the combination of the four main factors (PA, SC, LA, HR) and their sub-factors (described in Table 1), the parallels between the complexities of nuclear fission and the multifaceted nature of clean energy infrastructure development can be drawn. Each main factor serves as a central node, with sub-factors branching out from them, as illustrated in Figure 2.

Figure 2 is a graphical representation that illustrates the interconnectedness of the main factors (PA, SC, LA, HR) with their respective sub-factors. It provides a visual depiction of the complexity inherent in analyzing clean energy development within the geopolitical context.

In fission reactions, the 6-factor formula accounts for various factors influencing the rate of a nuclear reaction, including neutron flux, resonance escape probability, thermal utilization factor, etc. Similarly, in this study model, the four main factors (PA, SC, HR, LA) and their corresponding 17 sub-factors represent different parameters influencing a particular outcome, such as the construction rate of clean power plants.

While the number of factors in this study differs from the 6-factor formula, the concept of breaking down complex systems into individual factors to understand and analyze their contributions is similar. Just as each factor in the 6-factor formula contributes to the overall reaction rate in nuclear fission, each sub-factor in this study contributes to the overall construction rate of clean power plants.

3. Methodology: Algebraic Mathematical Model

Algebraic modeling in energy studies has gained significant traction in recent years [23,24]. Its ability to capture the complexities of energy systems and inform decision-making processes has been demonstrated in various research endeavors. These include resource optimization, policy evaluation, and infrastructure planning. Algebraic models that use a dynamic systems approach excel at analyzing the dynamic interactions between different components of energy systems [25,26]. I. Capellan-Perez [27,28] has considered system level modeling, using the Integrated Assessment Model (IAM) approach (MEDEAS) and described its role, online. These have been considered with respect to the utility of this type of analytical approach.

Integrated Assessment Models (IAMs) play a crucial role in evaluating the complex interplay between economic, social, and environmental factors in the context of climate change. Among the prominent IAMs, the DICE model, developed by William Nordhaus, focuses on cost–benefit analysis to assess the economic impacts of climate policies, utilizing optimization techniques to find the most efficient pathways to mitigate climate change [29,30]. The Framework for Uncertainty, Negotiation, and Distribution (FUND) model emphasizes the uncertainties inherent in climate change impacts and policy responses, incorporating detailed sectoral impact analysis and regional differences [31]. The Global Change Assessment Model (GCAM), developed by the Pacific Northwest National Laboratory, integrates human and Earth systems modeling, incorporating energy, water, land, and climate systems to explore technology pathways and provide regional detail [32]. The Model for Energy Supply Strategy Alternatives and their General Environmental Impact (MESSAGE), developed by the International Institute for Applied Systems Analysis (IIASA), focuses on energy systems and their environmental impacts, integrating economic and environmental models for comprehensive policy analysis [33]. The Regional Model of Investments and Development (REMIND) combines macroeconomic growth with energy system transitions and climate change mitigation, including a detailed representation of energy technologies and regional dynamics [34]. The Integrated Model to Assess the Global Environment (IMAGE), developed by the PBL Netherlands Environmental Assessment Agency, links environmental and socio-economic systems, exploring long-term sustainability pathways through land-use, water, and climate change interactions [35]. Lastly, the World Induced Technical Change Hybrid (WITCH) model integrates economic growth with endogenous technological change, assessing the role of innovation and technology diffusion in climate policy analysis, and includes game-theoretic elements to evaluate policy strategies [36].

Additionally, the MEDEAS (Modelling the Energy Development and Economic Sustainability) model is developed for evaluating the transition to renewable energy and sustainability, integrating biophysical and socio-economic constraints to explore long-term impacts and focusing on decarbonization pathways [27]. The WILIAM The Within Limits Integrated Assessment Model (WILIAM) focuses on long-term climate impacts and adaptation strategies, assessing global impacts, incorporating adaptation measures, and evaluating policy effectiveness under various scenarios [37].

These models, along with their key features and descriptions, are summarized in

Table 2. Various IAM approaches.

IAM Approach	Description	Key Features	Refs.
DICE (Dynamic Integrated Climate-Economy) Model	Developed by William Nordhaus, it integrates economic modeling with climate change dynamics	Focuses on cost–benefit analysis, assesses the economic impacts of climate policies, and uses optimization techniques.	[29,30]
FUND (Framework for Uncertainty, Negotiation and Distribution) Model	Emphasizes the uncertainties in climate change impacts and policy responses	Includes detailed sectoral impact analysis, considers regional differences, and explores policy negotiations.	[31]
GCAM (Global Change Assessment Model)	Developed by the Pacific Northwest National Laboratory, it combines human and Earth systems modeling	Incorporates energy, water, land, and climate systems, explores technology pathways, and provides regional detail.	[32]
MESSAGE (Model for Energy Supply Strategy Alternatives and their General Environmental Impact),	Developed by IIASA, it focuses on energy systems and their environmental impacts	Emphasizes energy technology and policy analysis and integrates with economic and environmental models.	[33]
REMIND (Regional Model of Investments and Development)	Combines macroeconomic growth, energy system transitions, and climate change mitigation	Includes detailed representation of energy technologies, assesses policy impacts, and considers regional dynamics.	[34]
IMAGE (Integrated Model to Assess the Global Environment)	Developed by PBL Netherlands Environmental Assessment Agency, it links environmental and socio-economic systems	Focuses on land-use, water, and climate change interactions, and explores long-term sustainability pathways.	[35]
WITCH (World Induced Technical Change Hybrid) Model	Integrates economic growth with endogenous technological change and climate policy analysis	Assesses the role of innovation and technology diffusion, includes game-theoretic elements, and evaluates policy strategies.	[36]
MEDEAS (Modelling the Energy Development and Economic Sustainability)	Developed for evaluating the transition to renewable energy and sustainability [27]	Integrates biophysical and socio-economic constraints, explores long-term impacts, focuses on decarbonization pathways.	[27]
WILIAM (Within Limits Integrated Assessment Model)	Focuses on long-term climate impacts and adaptation strategies	Assesses global impacts, incorporates adaptation measures, and evaluates policy effectiveness under various scenarios.	[37]

.

Building upon these studies and established methodologies, the proposed algebraic model for analyzing clean power plant construction rates extends the applicability of algebraic modeling to sustainable energy development. By combining mathematical analysis and scenario-based simulations, this model offers valuable insights into the interplay between various factors influencing construction rates. Stakeholders can use these insights to make informed decisions and optimize resource allocation in support of a transition to clean energy.

The proposed algebraic model provides a comprehensive framework for analyzing the construction rates of clean power plants. It integrates insights from the fission six-factor formula and the identified main factors and sub-factors. This model employs algebraic equations to capture the complex interactions between factors influencing construction rates, such as public acceptance, supply chain readiness, human resources, and land availability. By incorporating non-linear relationships and differential weighting, the algebraic model provides a robust tool for decision making and optimization in clean energy infrastructure development. Furthermore, the integration of external variables and scenario analysis enhances the model’s adaptability to different contexts and future projections. Through this algebraic approach, stakeholders and policy makers can gain valuable insights into the dynamics of clean power plant construction, enabling informed decision making and strategic planning for sustainable energy transition.

The development of the algebraic model builds upon the foundational principles of the fission six-factor formula and the insights derived from the analysis of main factors and sub-factors. By leveraging the mathematical rigor and analytical framework established in the discussion of the six-factor formula, the algebraic model extends this understanding to the specific context of clean power plant construction rates. Integrating factors identified in previous sections, such as public acceptance and supply chain readiness, the algebraic model provides a structured approach to modeling and optimizing construction rates. This bridges the gap between theoretical understanding and practical application in sustainable energy development.

To enhance clarity and reader engagement, Figure 3 presents a high-level flowchart outlining the methodological steps used in this study. The process begins with identifying and parameterizing four key deployment factors: Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA). These factors are assigned weights and then transformed using non-linear exponents to reflect diminishing or amplifying effects. Interaction terms are incorporated to capture synergies or trade-offs among the factors. A logistic function is applied to ensure the output remains within realistic bounds. The resulting prediction provides an optimized construction rate (CR) trend. This model is applied to refine and optimize the construction rate outputs of the DICE model. This integration enables more realistic projections by embedding deployment constraints, thereby improving policy relevance and decision-making utility.

3.1. Algebraic Mathematical Model Component and Implementation

Several components are incorporated in this proposed advanced model to optimize the SMR construction rate. Techniques such as polynomial or logistic regression are employed to capture complex, non-linear relationships between different factors. This allows for a better understanding of how variations in one factor can influence the overall construction rate.

The decision to use an algebraic modeling framework in this study stems from its transparency, adaptability, and suitability for policy-driven planning. Algebraic models provide a clear and interpretable structure, which is essential for decisionmakers and policymakers who require transparent justification for deployment strategies. Unlike machine learning, agent-based modeling, or Monte Carlo simulations—which often function as black-box approaches and require large datasets—algebraic models enable users to explore and compare deployment scenarios using adjustable input parameters and dynamic weights. The model can easily incorporate scenario-based simulations, factor interactions, and parameter sensitivities, making it particularly useful for long-term energy planning in both data-rich and data-scarce environments.

A differential weighting approach is used, meaning that the influence of each factor can vary based on the specific scenario [38]. Weight coefficients ($w_{\mathrm{i}}$) were determined through a structured methodology that included historical data analysis, literature review, and expert judgment. This ensures that the relative importance of the four main factors—Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA)—is appropriately represented within the model.

Interaction coefficients (${\theta }_{ij}$) were derived using a combination of historical correlation trends and expert elicitation. This approach captures synergistic or inhibitory relationships between the factors, thereby enhancing the robustness and realism of the model. These coefficients are not arbitrary; they reflect practical interactions grounded in empirical evidence. Depending on the data available, interaction coefficients can range from negative values—representing inhibitory effects—to positive values that indicate synergies. These coefficients are typically normalized between −1 and 1 or 0 and 1 to suit the model’s scaling requirements.

Additionally, the model integrates external variables, such as regulatory policies, environmental impact assessments, and economic forecasts. This enables a more holistic understanding of the context in which SMR construction occurs and enhances the model’s utility in supporting strategic decision making.

The construction rate ($y$) is defined as a function of weighted input factors, non-linear transformations, interaction terms, and external variables. The model uses non-linear functions, dynamic weights, and interaction coefficients to simulate realistic construction rate predictions. The factors $x_1{,x}_2{,x}_3 and x_4$ represent Public Acceptance, Supply Chain Readiness, Human Resource Availability, and Land Availability, respectively.

The non-linear interaction model is represented as follows:

$$y ~f\left(w_1{x}_1^{\alpha }+w_2{x}_2^{\beta }+w_3{x}_3^{\gamma }+w_4{x}_4^{\delta }+\sum {\theta }_{ij}{x}_i{x}_j\right) , i\&j=0 to 4$$

(1)

where $f$ is a non-linear function, such as a logistic function, to map the input factors to the output $y$.

To model non-linear saturation effects in SMR deployment, a logistic (sigmoid) function was applied to the composite score derived from factor inputs, weights, exponents, and interaction terms. The function is represented as follows:

$$f\left(x\right)={\displaystyle \frac{\mathrm{L}}{1+e^{-\mathrm{k}(x-x_{0)}}}}$$

(2)

Here, L defines the upper limit for construction rate, k determines the steepness or sensitivity of the curve, and x₀ is the inflection point where growth transitions from acceleration to saturation.

These parameters were not arbitrarily assumed but were selected through a rigorous process:

• Upper Bound (L): Derived from historical nuclear deployment capacity observed during peak periods (e.g., in the U.S.), L ensures the model does not produce implausible construction rates and respects infrastructure and policy constraints.
• Midpoint (x₀): Identified by analyzing historical points where notable acceleration in construction occurred, often when combined readiness scores (e.g., PA and SC) exceeded a threshold. This value marks the tipping point of system readiness.
• Slope (k): Calibrated through sensitivity analysis to produce smooth yet responsive transitions. The chosen slope captures the dynamic responsiveness of construction rates to changes in socio-technical readiness, while avoiding abrupt jumps.

These values were validated using cross-country data from the U.S., Japan, and Canada by matching peak construction patterns, slowdown periods, and plateau behaviors. This approach provides interpretability and policy relevance, enabling the model to simulate how readiness factors influence deployment pace under real-world constraints.

The parameters $\alpha ,\beta ,\gamma and \delta$ represent the degrees of non-linearity associated with each factor. These parameters allow the model to reflect diminishing returns or increased sensitivity as the values of input factors change. This flexible algebraic structure supports both sensitivity analysis and scenario modeling, making it a powerful tool for planning SMR deployment.

Extend the model to include external variables $z_k and v_k$ as their weight:

$$y~f(w_1{x}_1^{\alpha }+w_2{x}_2^{\beta }+w_3{x}_3^{\gamma }+w_4{x}_4^{\delta }+\sum {\theta }_{ij}{x}_i{x}_j+\sum v_k{z}_k)$$

(3)

Model $w_i,{\theta }_{ij}, and v_k$ as random variables to reflect uncertainty in their values. This can be done by specifying distributions for these parameters based on expert input or historical data. Note that in simplest form—if the weights are equal, all variables are certain (0% uncertainty), and there is no non-linearity (linearity), then the function, y, is a sum of four factors, $x_1{,x}_2{,x}_3 and x_4$.

For using the proposed mathematical formula to predict future SMR deployment trends, the values for key parameters in the model (${x_{\mathrm{i}} ,w}_i,{\theta }_{ij},\alpha ,\beta ,\gamma ,\delta and v_k$) must be estimated based on projected trends, expert assessments, and scenario modeling. The factor values $x_{\mathrm{i}}$ can be sourced from global energy transition reports, industry roadmaps, and government policies on nuclear energy expansion. Historical trends, along with data from surveys, workforce projections, and regulatory frameworks, will inform how these factors evolve over time. The weights $w_i$, which define the relative impact of each factor, can be adjusted dynamically using scenario-based analysis that considers policy shifts, economic conditions, and technological advancements. The interaction coefficients ${\theta }_{ij}$, capturing interdependencies among factors, can be estimated through historical correlation analysis, expert elicitation, or machine learning techniques that infer relationships from past nuclear deployment data. This approach ensures a data-driven framework for SMR deployment forecasting, supporting informed decision making in nuclear energy policy and infrastructure planning.

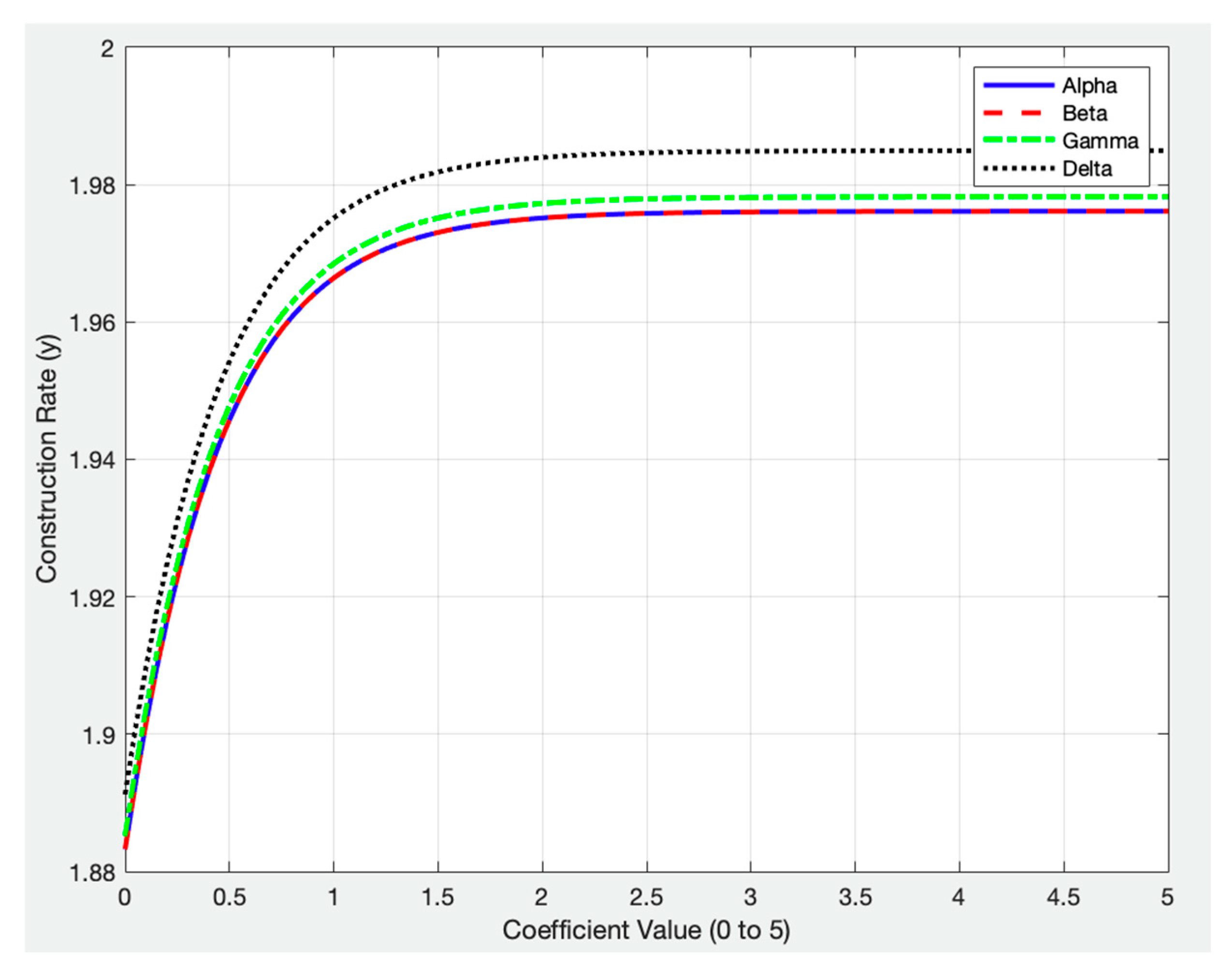
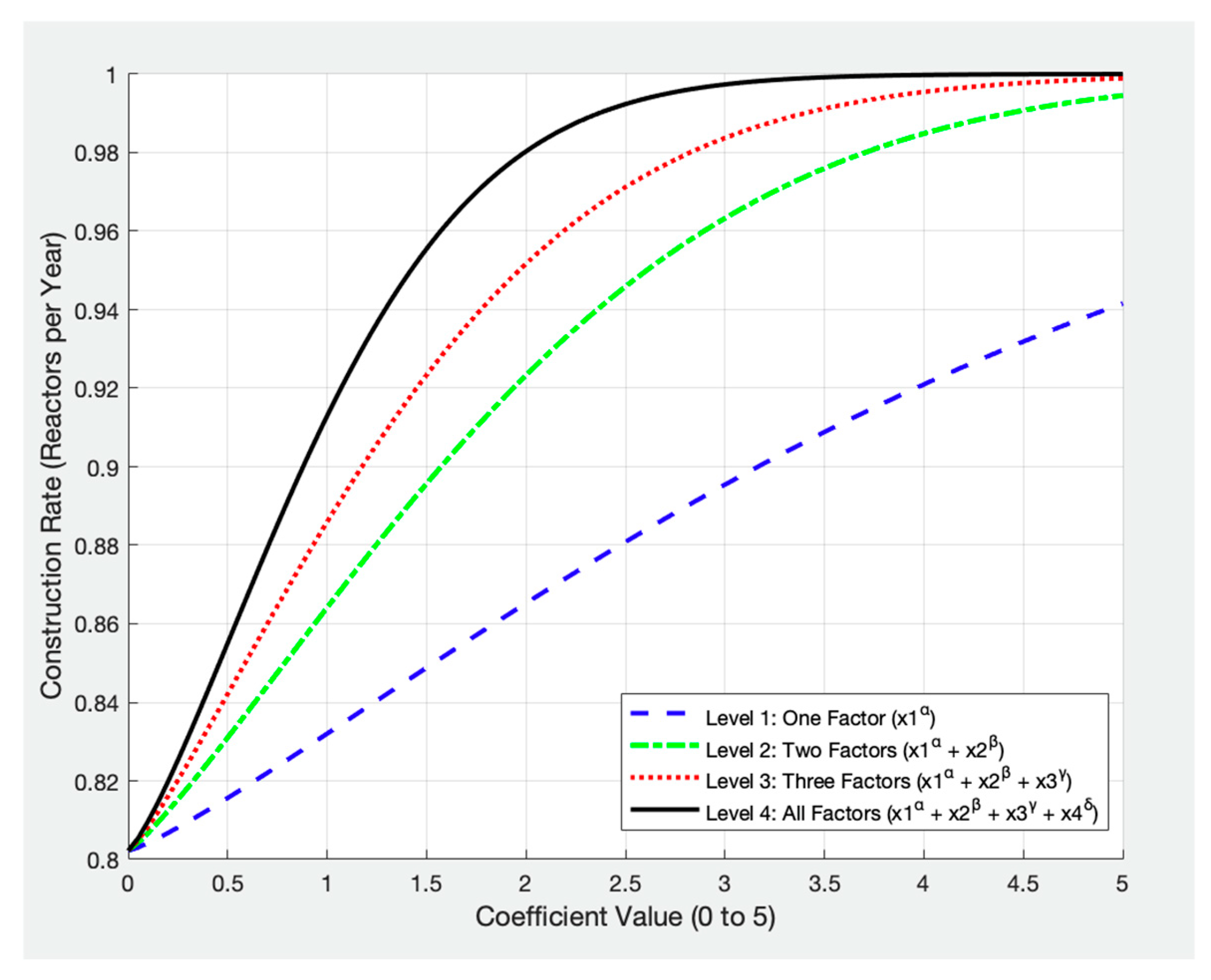
In establishing the boundaries for the coefficients in our model, we consider both the mathematical influence of each parameter and their practical interpretation within clean energy project dynamics. The non-linearity parameters (α, β, γ, δ) capture the responsiveness of construction rates to Public Acceptance, Supply Chain Efficiency, Human Resources, and Land Availability. As shown in Figure 4, varying each parameter from 0.1 to 5 while keeping others constant confirms that these ranges provide flexibility in modeling scenarios from minimal to strong factor influences. The results indicate that Public Acceptance (α) has the most immediate impact, emphasizing its role in clean energy feasibility. Supply Chain Efficiency (β), Human Resources (γ), and Land Availability (δ) also play crucial roles in project execution, with their influence increasing as they are optimized.

Additionally, weight coefficients (w_i) are constrained between 0 and 1, maintaining a proportionate influence of each factor. Interaction coefficients (θ_ij) vary between −1 and 1, capturing synergistic and inhibitory relationships between factors. External variables (v_k), such as regulatory shifts and economic changes, are also included, ranging from 0 to 1, to reflect varying degrees of influence. These constraints, supported by empirical data, enhance the model’s applicability and robustness in strategic planning for clean power plant deployment.

To further analyze the cumulative effect of multiple factors, a stepwise progression of factor influence is examined in Figure 5, where each factor is sequentially introduced. The results confirm that as one factor improves, the construction rate experiences a moderate increase, but as additional factors improve, the rate increases more significantly. When all four factors reach their maximum values, the construction rate achieves its highest possible level. However, the logistic function introduces a plateau effect, meaning that beyond a certain threshold, further increases in factor contributions result in diminishing returns. This effect prevents overestimation of factor influence and ensures that projections remain realistic.

Following the proposal of our formula, it’s pertinent to draw parallels between the interaction dynamics within our model and those observed in nuclear reactor physics. In nuclear settings, parameters such as geometry and dimensions—or non-leakage probabilities—affect the effectiveness of neutron interactions and, thus, reactor criticality. In a similar vein, our model’s main factors—Public Acceptance ($x_1$), Supply Chain Efficiency ($x_2$), Human Resources ($x_3$), and Land Availability ($x_4$)—represent the foundational elements of the project environment. These factors are akin to the physical setup in nuclear reactors, influencing the efficiency and readiness of the operational environment in clean power plant construction. The interaction coefficients (${\theta }_{ij}$) in our model parallel the role of non-leakage probabilities in nuclear reactors, adjusting the impact of each factor based on their interrelationships. For example, synergistic effects between high public acceptance and available human resources can significantly expedite construction processes, akin to how optimal reactor geometries enhance neutron economy. Thus, while our model does not incorporate physical dimensions or material properties, it integrates strategic dimensions of project management and resource dynamics that are pivotal in dictating the efficiency and speed of construction projects. This systemic approach allows us to simulate and understand the complexities of implementing clean energy infrastructure effectively.

Building on our model’s formulation, it is essential to note a crucial distinction when comparing it with the six-factor formula used in nuclear reactor physics. While the six-factor formula quantitatively balances to a criticality condition where K-effective is equal to one, symbolizing a steady state in reactor operations, our model does not inherently balance to a specific numeric value. Instead, it adapts to the dynamic inputs reflecting the nuanced realities of construction environments, which may not necessarily converge to a singular ’critical’ point as in nuclear fission. This distinction highlights the adaptive nature of our model, designed to handle a broader range of variables and outcomes in clean energy project deployment.

3.2. Algebraic Mathematical Model Validation

To assess the applicability of the proposed algebraic mathematical model, a validation process was conducted by comparing its predicted nuclear reactor construction rate trends with historical construction patterns in the United States. The primary objective of this validation was to evaluate whether the model captures key shifts in construction activity over time rather than to serve as a precise forecasting tool for individual reactor counts. Since the model functions as an optimization multiplier for refining DICE model projections, achieving exact numerical accuracy was neither expected nor necessary. Instead, the validation focused on verifying that the predicted trend closely follows historical construction rate trends and responds appropriately to key influencing factors: public acceptance (PA), supply chain readiness (SC), human resource availability (HR), and land availability (LA).

The United States was selected for model validation not only because of the availability of reliable data but also due to its diverse history of nuclear development. U.S. nuclear deployment reflects a full spectrum of policy environments, from early expansion driven by energy security through significant disruptions following major nuclear accidents to recent policy shifts promoting nuclear as part of clean energy transitions. This broad range of historical phases makes it a representative case for evaluating the model’s performance in capturing the dynamic behavior of nuclear construction rates globally.

To ensure dataset diversity and test the model’s adaptability, additional validation was conducted using historical data from Japan and Canada, offering varied governance structures, regulatory frameworks, and public engagement processes. While the U.S. reflects a market-based system with federal regulation, Japan presents a hybrid model with centralized industrial strategy and local decision making, and Canada’s nuclear development is shaped at the provincial level. These variations provide a more comprehensive view of nuclear construction dynamics and strengthen the model’s global applicability.

Furthermore, the model was qualitatively applied to France, Russia, Germany, South Korea, and China—countries selected for their distinctive nuclear deployment strategies. These nations include both centralized and decentralized approaches, strong state-driven programs (Russia, China), and policy reversals or public opposition cases (Germany). Although detailed error metrics, such as RPE, were not calculated for these countries, visual comparisons of actual versus predicted construction reveal that the model reasonably captures key inflection points and overall deployment behavior across these different national contexts.

This multi-country validation approach confirms the generalizability of the model across a wide range of nuclear governance types, policy settings, and historical trends, supporting its potential for analyzing future SMR deployment not only in developed but also in developing regions where detailed historical datasets may be limited but strategic planning is emerging.

In regions facing data scarcity—where detailed historical records on nuclear construction are unavailable, incomplete, or unreliable—the model is designed to accommodate these limitations through scenario-based estimations, expert elicitation, and proxy indicators. For example, if public acceptance (PA) cannot be directly measured, regional opinion polls, energy transition policies, or international collaboration agreements can serve as proxies. Supply chain readiness (SC) can be inferred from industrial capacity reports, trade openness, or participation in global nuclear initiatives. Expert judgment fills the remaining gaps, especially in early-stage planning environments. This approach allows the model to remain operational and informative in data-scarce contexts, ensuring its applicability in emerging nuclear nations or future SMR deployment projections.

The validation process followed a structured approach: Step 1. Extracting historical construction data for operational U.S. reactors and calculating actual construction rates per decade; Step 2. Calculating predicted construction rate trends; Step 3. Applying the algebraic mathematical model using assigned weights and transition factors; and Step 4. Comparing the predicted construction rate trend with historical patterns and visually evaluating the model’s ability to replicate key peaks and declines.

Step 1—Collection of historical data on nuclear reactor construction rate trends and calculation of construction rate per decade—To establish a reliable benchmark for validation, historical data on nuclear reactor construction in the United States were gathered from publicly available sources [39,40]. The extracted data include a list of operational reactors in the U.S., providing detailed information on their construction start dates, commercial operation dates, and reactor types [39]. Additionally, the construction rate per decade was calculated by determining the number of completed reactors each decade and dividing it by the corresponding 10-year period. This approach provides an estimated average construction rate (reactors/year) for each decade, offering a clearer visualization of long-term construction rate trends as summarized in

Table 3. U.S. operational reactors construction rate per decade.

Decade	Actual Construction Rate Trend (Reactors/Year)
1960–1970	0.4
1970–1980	4.0
1980–1990	4.5
1990–2000	0.3
2000–2010	0.0
2010–2020	0.05
2020–Present	0.15

.

The data in Table 3 reveal a significant rise in reactor construction during the 1970s and 1980s, followed by a sharp decline in the 1990s and beyond. The peak construction period occurred between 1970 and 1990, aligning with historical policy shifts, technological advancements, and industry expansion. The slowdown in construction post-1990 reflects factors such as regulatory changes and reduced public acceptance.

By incorporating this historical data into the algebraic model, we aim to validate whether the predicted trend follows these observed construction patterns. In the next step, we apply the model to analyze its ability to replicate these trends.

Step 2—Calculating predicted construction rate trends—The algebraic model integrates key socio-economic and infrastructure parameters to analyze historical nuclear construction rate trends. The goal is to assess whether the expected trend aligns with actual construction patterns, particularly capturing periods of peak deployment (1970–1990) and the subsequent decline (1990-present). The mathematical formulation of the model is expressed as follows:

$$\mathrm{C}\mathrm{R}~f\left(w_1{x}_1^{\alpha }+w_2{x}_2^{\beta }+w_3{x}_3^{\gamma }+w_4{x}_4^{\delta }+\sum {\theta }_{ij}{x}_i{x}_j\right),i\&j=0 to 4$$

where:

• $x_1$ = Public Acceptance (PA);
• $x_2$ = Supply Chain Readiness (SC);
• $x_3$ = Human Resource Availability (HR);
• $x_4$ = Land Availability (LA);
• $w_i$ = Weight coefficients assigned to each factor, derived from historical data;
• ${\theta }_{ij}$ = Interaction coefficients between factors, capturing interdependencies;
• $f\left(x\right)$ = Logistic function for non-linearity, accounting for saturation effects in factor contributions.

This model does not forecast future construction rates but rather analyzes historical trends by identifying key drivers behind fluctuations in nuclear deployment rates. The logistic function ensures that increases in specific factors do not yield unbounded growth, reflecting real-world constraints. By applying this model to historical U.S. nuclear construction data, we evaluate its ability to replicate observed patterns of expansion, peak construction, and slowdown.

Step 3—Applying the algebraic mathematical model using assigned weights and transition factors—Since comprehensive real-world data for all parameters are not readily available, historical trends in Public Acceptance (PA) and Supply Chain Readiness (SC) were inferred from literature, policy shifts, and industry reports, as summarized in

Table 4. Historical values for PA and SC.

Decade	$\mathbf{PA} \left({\mathit{x}}_1\right)$ (0–1 Scale)	Rational for PA Values	$\mathbf{SC} \left({\mathit{x}}_2\right)$ (0–1 Scale)	Rational for SC Values
1960–1970	0.6	Early momentum in nuclear expansion, minimal public opposition, and government-backed programs [41,42].	0.6	Relatively strong industrial growth and fewer regulatory barriers [43].
1970–1980	0.9	Peak support due to energy security concerns (1973 oil crisis) and strong government policies supporting nuclear growth [44].	0.9	Supply chain at peak efficiency, standardized designs, strong U.S. nuclear manufacturing [42,45].
1980–1990	1	Relatively high due to ongoing projects initiated in the 1970s [46].	1	Supply chain at peak efficiency, standardized designs, strong U.S. nuclear manufacturing [42,45].
1990–2000	0.3	Sharp decline post-Chernobyl (1986) and post-Three Mile Island (1979), rise in anti-nuclear sentiment, increased public scrutiny [47].	0.4	Regulatory tightening (e.g., NRC’s increased safety regulations) slowed efficiency despite continued reactor construction [48,49]. Investment in nuclear infrastructure was reduced, and many suppliers shifted to other sectors due to a lack of demand [50].
2000–2010	0.2	Persistent low acceptance due to safety concerns, competition from natural gas, and deregulation of electricity markets [51].	0.3	Minimal new nuclear projects led to supply chain decline, loss of expertise, and reduced workforce [52,53].
2010–2020	0.5	Gradual recovery post-Fukushima (2011), growing interest in nuclear for climate goals, policy shifts supporting nuclear [54].	0.6	New nuclear technologies (e.g., SMRs) and international collaborations start revitalizing supply chains [55].
2020–Present	0.7	Nuclear energy recognized as key for net-zero goals, renewed policy support (e.g., Biden Administration Clean Energy Plan) [56,57].	0.8	Policy-driven incentives, global energy security concerns, and increased demand for clean energy strengthen supply chain [56].

. Human Resource Availability (HR) and Land Availability (LA) were held constant, as historical data indicate they have remained stable over time, as shown in

Table 5. The rationale for keeping HR and LA constant.

Factor	Average Assigned Value	Justification
Human Resource Availability ($x_3$)	0.6	The nuclear workforce remained relatively stable due to international hiring, retraining programs, and the continuous operation of existing reactors [58].
Land Availability ($x_4$)	0.9	Land constraints were rarely a limiting factor for nuclear construction, as site selection was predominantly driven by policy and regulatory frameworks rather than land scarcity [59].

.

The historical values in Table 4 illustrate how public sentiment and supply chain efficiency have evolved over time, shaped by major nuclear incidents, policy changes, and technological advancements. To maintain model simplicity, the relatively stable HR and LA factors were excluded from decade-specific variations, as shown in Table 5.

As detailed in

Table 6. Average assigned weights.

Factor	Average Assigned Value	Justification
Public Acceptance ($w_1$)	0.4	Historically, public perception and policy support have played a crucial role in nuclear deployment [15,41,42,44,46,47,48,51,54,60].
Supply Chain Readiness ($w_2$)	0.3	Supply chain bottlenecks significantly impact reactor construction timelines [42,43,45,48,49,50,52,53,55,61,62,63].
Human Resource Availability ($w_3$)	0.2	While important, HR shortages were mitigated through international collaboration and retraining programs [15,58,64].
Land Availability ($w_4$)	0.1	Nuclear plants require minimal land, and site selection is primarily policy-driven [59,65,66].

, weight coefficients were assigned based on their historical significance to account for historical trends in nuclear construction.

The weights reflect how each factor influenced construction rate trends over time, ensuring that the algebraic model captures major industry shifts.

To model historical trends more accurately, non-linearity parameters and interaction coefficients were incorporated. These parameters account for historical diminishing returns and interdependencies that have shaped U.S. nuclear construction rates, as detailed in

Table 7. Interaction coefficients.

Interaction	Coefficient Value	Explanation
PA & SC (${\theta }_{12}$)	0.09	Public support influences supply chain efficiency through policy and funding.
PA & HR (${\theta }_{13}$)	0.04	Public sentiment has some effect on workforce development, but training time limits its impact.
PA & LA (${\theta }_{14}$)	0.02	Public sentiment has minimal direct influence on land allocation.
SC & HR (${\theta }_{23}$)	0.07	Workforce availability influences supply chain efficiency, reducing construction delays.

and

Table 8. Non-linearity parameters.

Non-Linearity Parameter	Coefficient Value	Explanation
PA ($\alpha$)	0.65	PA exhibits strong but diminishing returns. Historically, periods of high public support (e.g., 1960s–1970s) were associated with rapid reactor deployment. Still, beyond a certain threshold, additional increases in PA had a limited impact due to external constraints, such as regulatory bottlenecks and economic factors. A lower exponent reflects this diminishing effect, ensuring that increases in PA do not result in unrealistic growth projections [41,42,44,46,47,48,51,54].
SC ($\beta$)	0.75	SC plays a fundamental role in enabling reactor construction, but its effectiveness depends on various dependencies, such as policy consistency, capital investment, and skilled labor availability. The assigned exponent captures the role of SC as a major bottleneck while allowing for some scalability in its influence [42,43,45,48,49,50,52,53,55].
HR ($\gamma$)	0.80	HR availability influences long-term construction trends due to the extended training periods required for specialized nuclear professionals. The higher exponent reflects its relatively stable impact over time, ensuring that shortages in workforce capacity gradually manifest in the construction rate rather than causing immediate disruptions [58].
LA ($\delta$)	0.88	Although LA is considered the least critical factor, its exponent is higher because its impact, while secondary, is more linear in nature. Once land is secured, additional improvements in land policy or site availability do not substantially accelerate construction rates. The higher exponent accounts for the fact that once land is available, its contribution remains steady, whereas other factors (PA, SC, HR) exhibit stronger diminishing returns [59].

.

These coefficients ensure the model captures historical trends, including:

• The decline in construction rates following major nuclear incidents (Three Mile Island 1979, Chernobyl 1986, Fukushima 2011).
• The supply chain and workforce bottlenecks that slowed nuclear deployment post-1990.
• The policy-driven nature of land availability.

The model uses a logistic function to accurately capture historical trends. This function accounts for non-linearity by ensuring that beyond a certain threshold, additional increases in PA, SC, and other parameters yield diminishing returns.

$$f\left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(4)

To compute the historical trend, the algebraic model was applied using MATLAB version R2020b, with the assigned weights, interaction coefficients, and non-linearity parameters. The next section compares predicted vs. actual trends.

Step 4—Comparing the predicted construction rate trend with historical patterns and visually evaluating the model’s ability to replicate key peaks and declines—To assess the model’s effectiveness in capturing historical nuclear construction trends, the algebraic mathematical model was applied to estimate the construction rate trend for different decades. The predicted values were then compared with actual historical data to evaluate the alignment of the model’s output with observed nuclear deployment trends. Since the algebraic model is designed to capture historical trends rather than predict exact construction rates, its validation focuses on whether the predicted trend aligns with observed historical patterns rather than achieving precise numerical agreement.

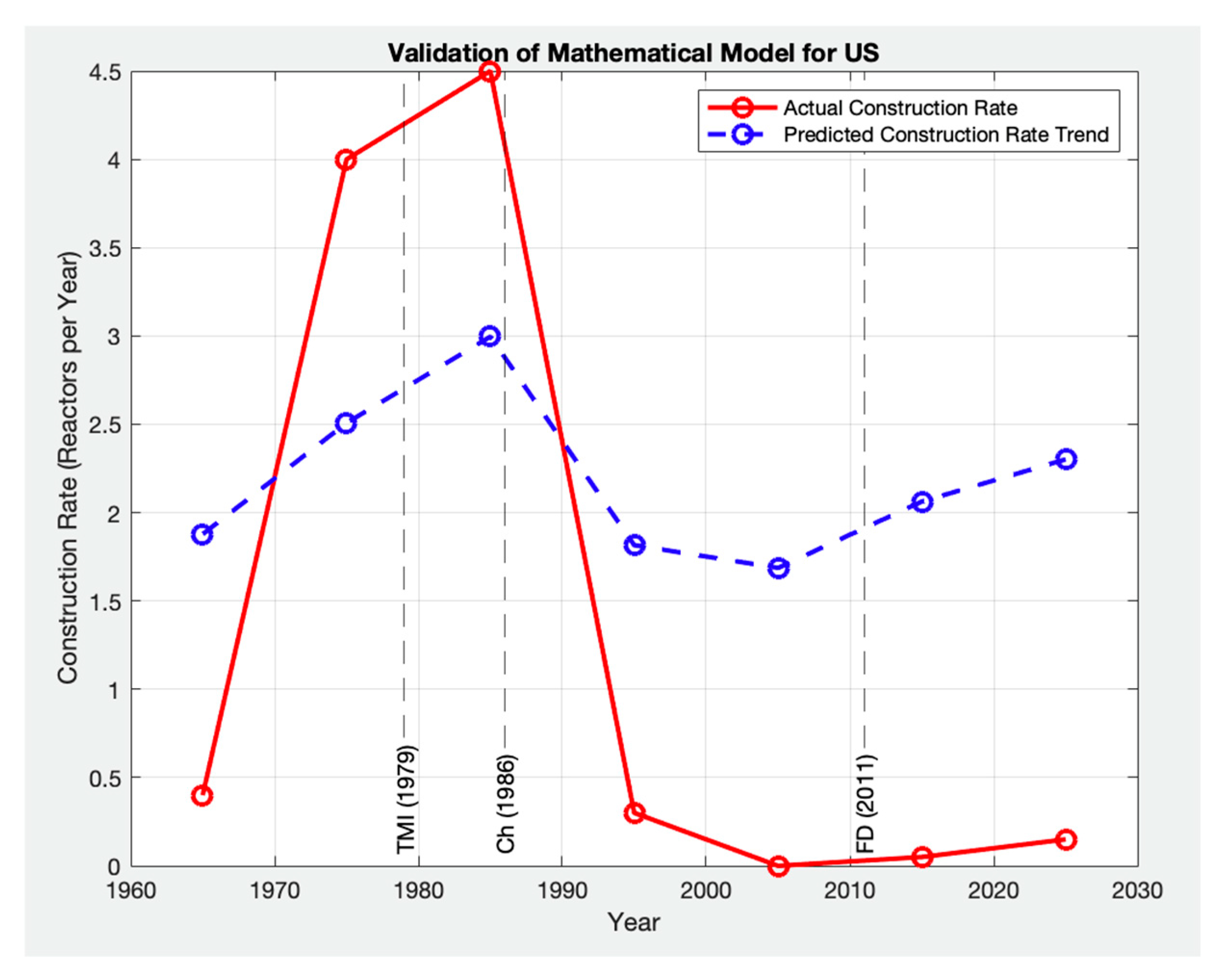
Figure 6 compares the actual historical construction rate trends (red solid line) with the predicted trend generated by the algebraic model (blue dashed line). The key observations from Figure 6 are as follows:

• The model correctly captures the overall trajectory of nuclear construction, reflecting the rise in reactor deployment during the 1970s and 1980s and the decline after 1990.
• The peak in the 1970s–1980s aligns with historical data, corresponding to high public acceptance, strong supply chain readiness, and policy-driven expansion.
• The model approximates the long-term downward trend after 1986, but the sharp post-1990 decline in actual construction is steeper, likely due to regulatory shifts and policy shocks (e.g., Three Mile Island in 1979, Chernobyl in 1986, and Fukushima in 2011).
• In the post-2000 period, the model captures the slow recovery trend, suggesting that improvements in public acceptance and supply chain readiness contribute to a modest increase in potential deployment rates.

The algebraic model successfully captures key transition points in nuclear deployment history by incorporating major influencing factors such as the following:

• Public sentiment toward nuclear energy (supporting early expansion, later declining post-1986).
• Supply chain capacity and readiness, which influenced reactor construction timelines.

In conclusion, the results confirm that the algebraic model serves as a robust tool for analyzing nuclear construction trends, with a strong alignment between predicted and actual values. The algebraic model effectively represents historical nuclear construction rate trends, providing valuable insights into the factors influencing reactor deployment rates across different periods. By capturing these trends, the model serves as a useful tool for energy transition analysis and nuclear deployment planning, offering a structured approach to understanding the dynamics that have shaped nuclear energy growth over time.

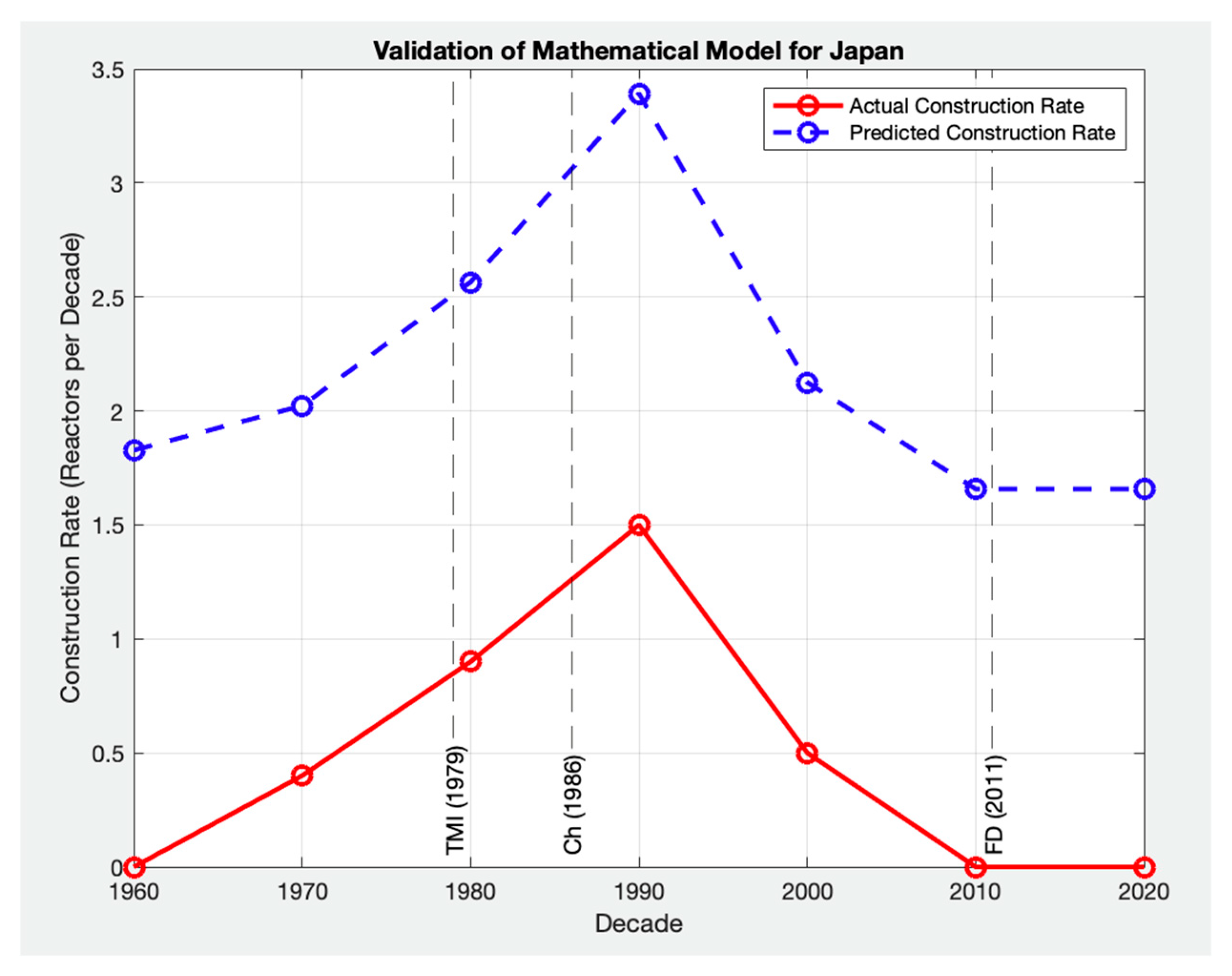
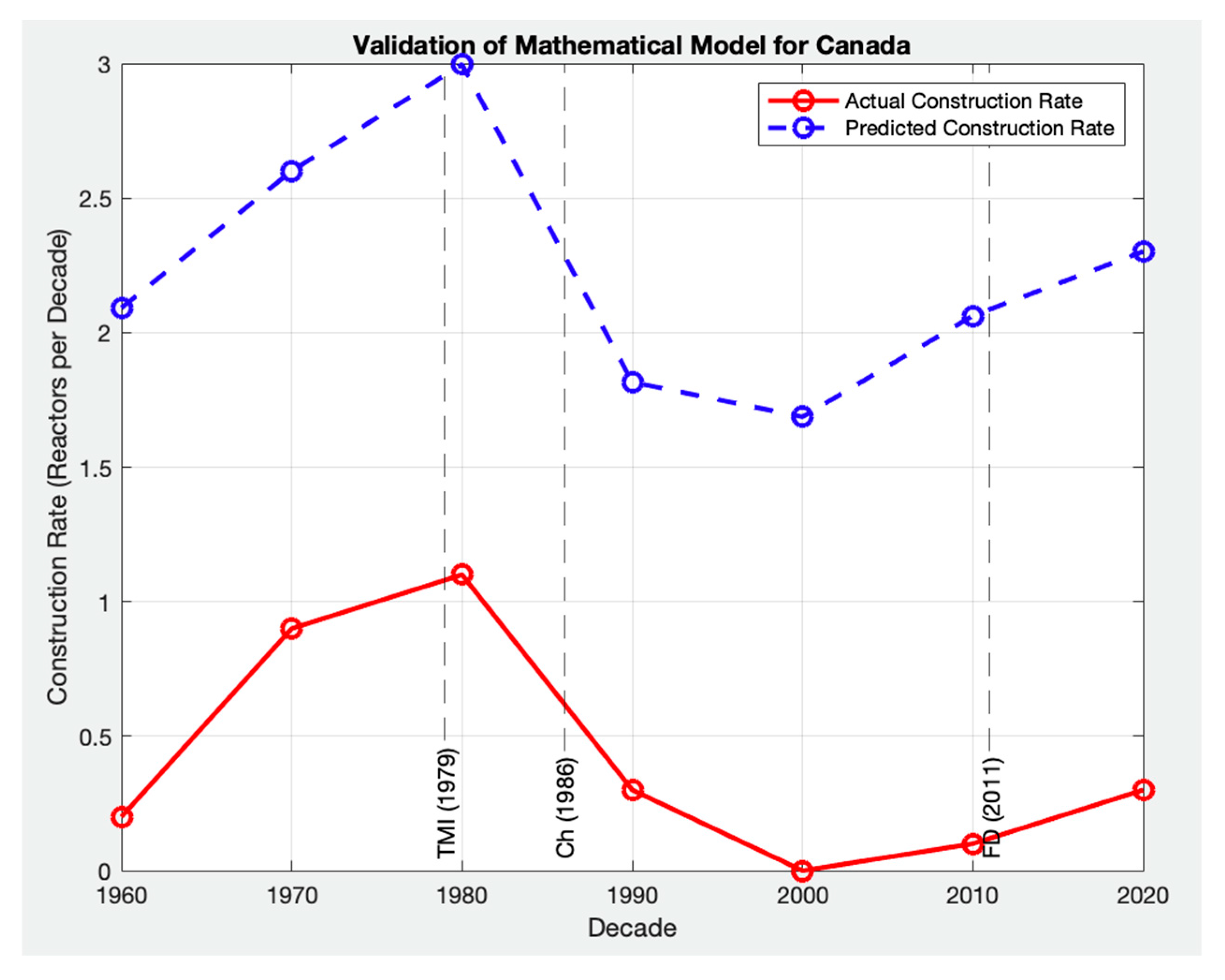
In addition to validating the model using historical data from the United States, we extended the validation process by applying the model to Japan [67,68,69,70,71,72] and Canada [73,74,75,76,77,78,79]. Figure 7 and Figure 8 illustrate the comparison between actual historical construction rates, shown as red solid lines, and the predicted trends generated by the algebraic model, represented by blue dashed lines, for these three countries.

By expanding the validation across different datasets, we aimed to assess the model’s robustness in capturing nuclear construction trends in regions with varying historical data availability. The dataset for the United States contained significantly more data points, serving as a benchmark for validation. Japan had a moderate number of data points, allowing for a reasonable comparison, whereas Canada had the fewest data points, presenting a greater challenge for validation. Unlike the United States, where nuclear policy is managed at the national level, Canada’s nuclear development is determined at the provincial level. In Japan, nuclear policy is managed by federal and industrial sectors, while the ultimate decision (Yes or No) rests with the Prefectural governor’s office. This leads to regional variations in construction trends and policy decisions, influencing data availability and consistency. Additionally, Canada’s historical nuclear construction data are limited, reflecting only three provinces, with just two having modest single-plant deployments. This makes direct comparisons challenging and may not accurately represent future SMR rollouts, which are expected to follow different trajectories. Unlike traditional large nuclear plants, SMRs could be deployed off-grid, owned by non-utility entities, or even province-owned in Canada, fundamentally altering construction pathways. Given the slow progress of both global and Ontario’s clean energy transition, alternative and accelerated deployment strategies must be considered to meet net-zero targets within the required timeframe.

To evaluate model performance, we used Relative Percentage Error (RPE), as it is better suited for assessing how well the model captures construction rate trends over time rather than exact values. Unlike Root Mean Squared Error (RMSE), which emphasizes large deviations by squaring errors, or Mean Absolute Percentage Error (MAPE), which measures average percentage deviations from actual values, RPE provides a normalized measure that allows comparison across datasets with sparse or small historical values—common in nuclear deployment records. This aligns with the study’s core objective: capturing long-term behavior for policy and scenario planning, not precise forecasting. The RPE is calculated using the following formula:

$$RPE={\displaystyle \frac{|\mathrm{A}-\mathrm{P}|}{\left|\mathrm{A}\right|}}\times 100$$

(5)

where A represents the actual historical values, and P represents the predicted values generated by the model. This metric provides a normalized measure of error, allowing for a comparative assessment across datasets of varying sizes and historical trends [80].

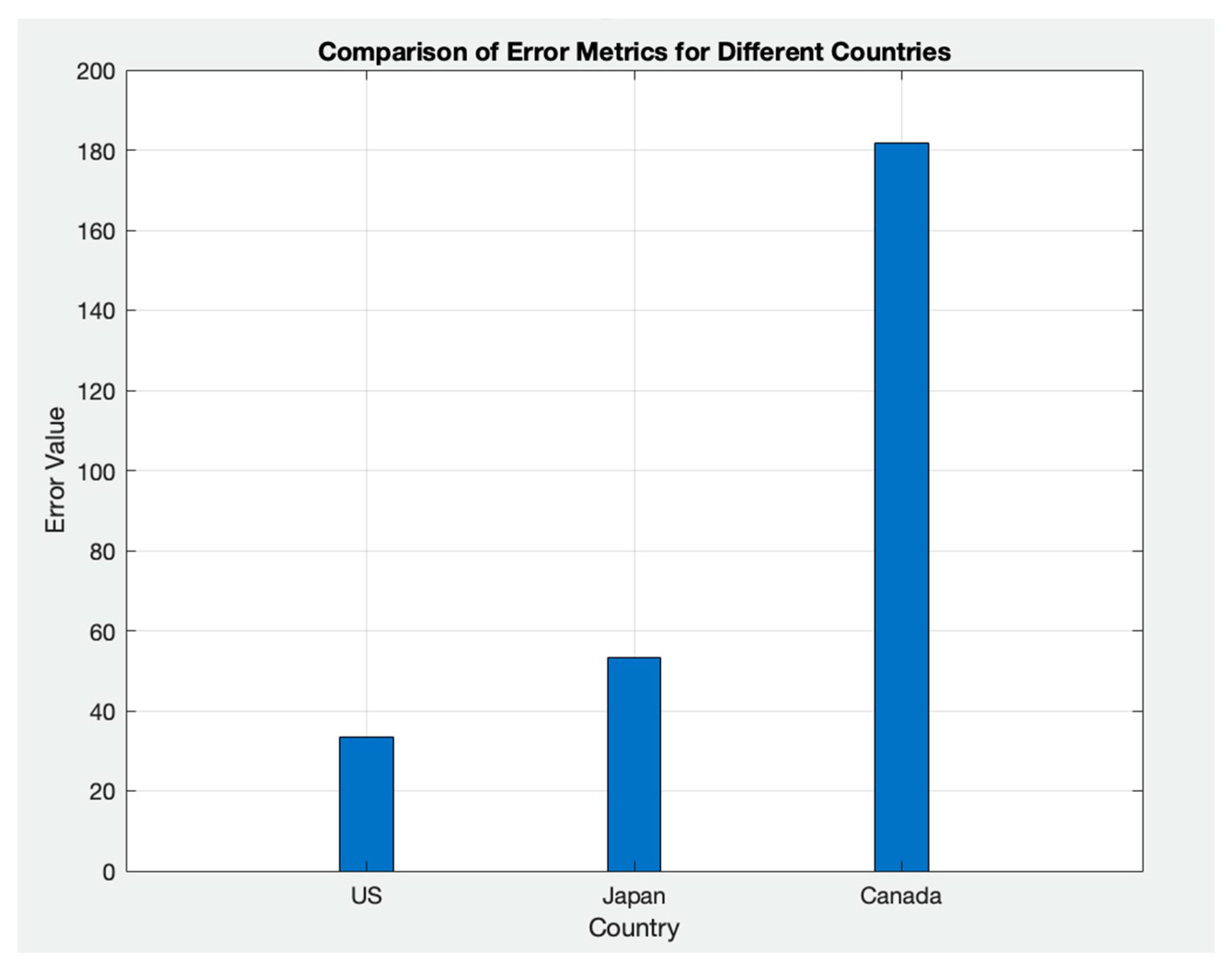
Figure 9 illustrates that the United States, with the most extensive dataset, exhibited the lowest error while successfully capturing the overall trend of nuclear construction rates. The model followed historical construction patterns, including trend shifts, peak construction periods, and post-1986 declines. While the predicted trend closely aligned with the actual historical trajectory, the predicted construction rate values did not always match the exact data points.

Similarly, in Japan, which had moderate historical data (~50 reactors before 2011), the model validation demonstrated a reasonable level of accuracy, capturing the overall trend but showing some deviations around peak construction periods. In contrast, Canada had the smallest dataset (<20 reactors) and exhibited the highest error despite the model successfully predicting the general trend of nuclear construction over time. For both Japan and Canada, the predicted trend is accurate; the difference indicates one or more composite factors that characterize CR versus decades in time. We note that the challenge in Canada stemmed from multiple plants located in just two sites (Ontario) and one unit, originally in Quebec and New Brunswick. The limited number of total plants constructed impacts the model’s ability to predict/characterize construction rates.

These findings highlight that while the model accurately predicts long-term trends across all three countries, its precision is influenced by the availability of the set of details surrounding the decisions to go forward, i.e., to construct. The United States dataset, with its comprehensive historical records, enabled the model to capture the “construction-to-connection” scenario. In contrast, the larger gaps for Japan and Canada support that the 6-factor model is largely correct but composite differences generate gaps. This analysis reinforces the idealized (legacy, circ 1960s) characterization of initial commitments to nuclear, compared to updated commitments to nuclear energy to address clean energy infrastructure deployment. Due diligence with respect to the circumstances that resulted in going forward, and repeated so is important. However, due to the decades that have passed, updating the details that comprise the will to go forward again under a similar and different impetus (circa 2025) is just as or even more important.

The validation of the proposed model against historical construction rates provides a foundation for assessing its applicability to future projections. While the historical construction rates of nuclear power plants, as presented in Figure 6, Figure 7 and Figure 8, offer a useful reference for model validation, it is essential to acknowledge that SMRs differ significantly from traditional large-scale reactors in their deployment characteristics. Their smaller footprint, modular nature, and increased in-factory construction efficiency suggest that SMRs could achieve construction rates exceeding those historically observed for conventional nuclear plants. This distinction highlights the need for model parameters that account for the evolving nature of nuclear deployment strategies, ensuring that projections remain relevant to future energy transition scenarios.

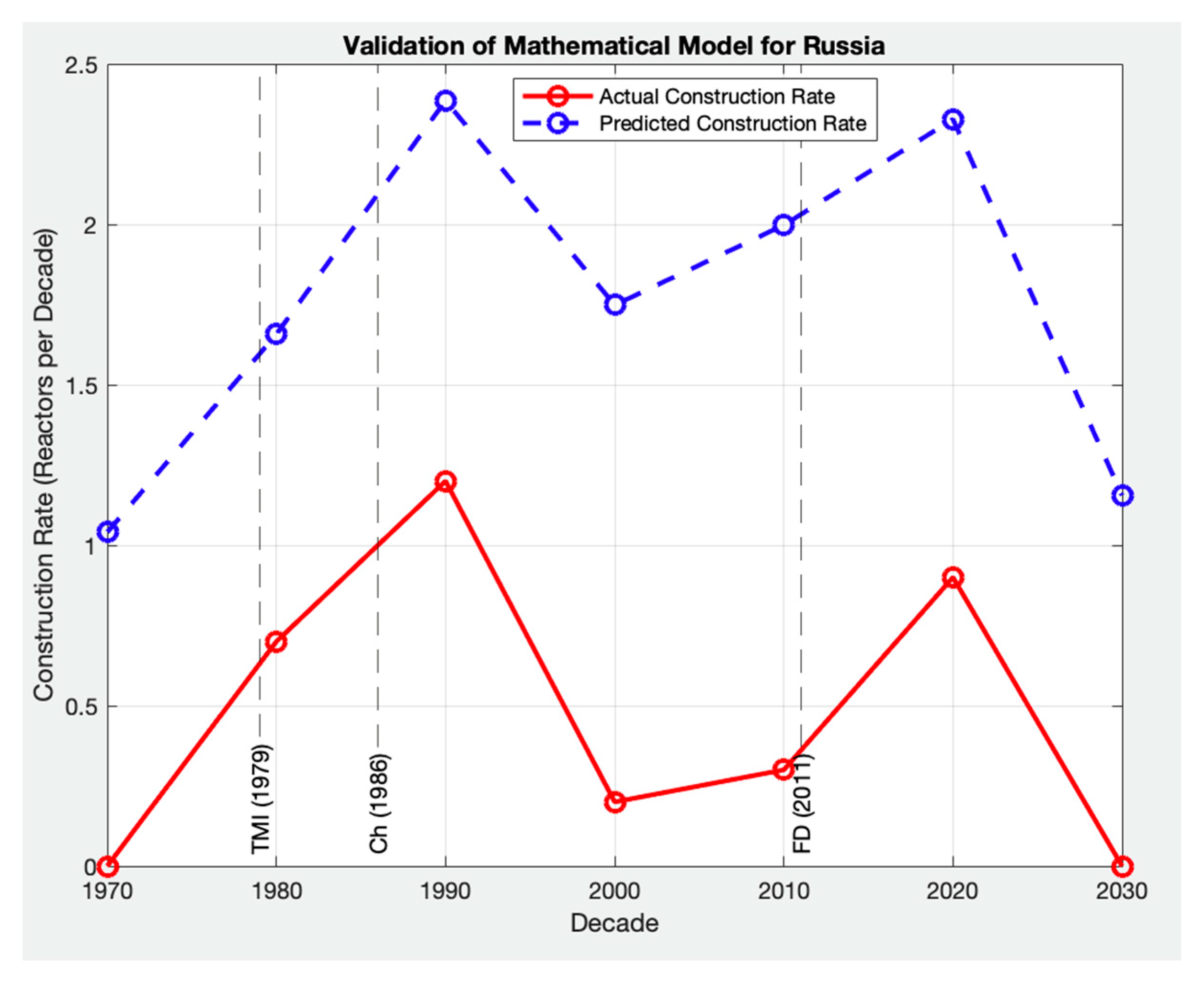
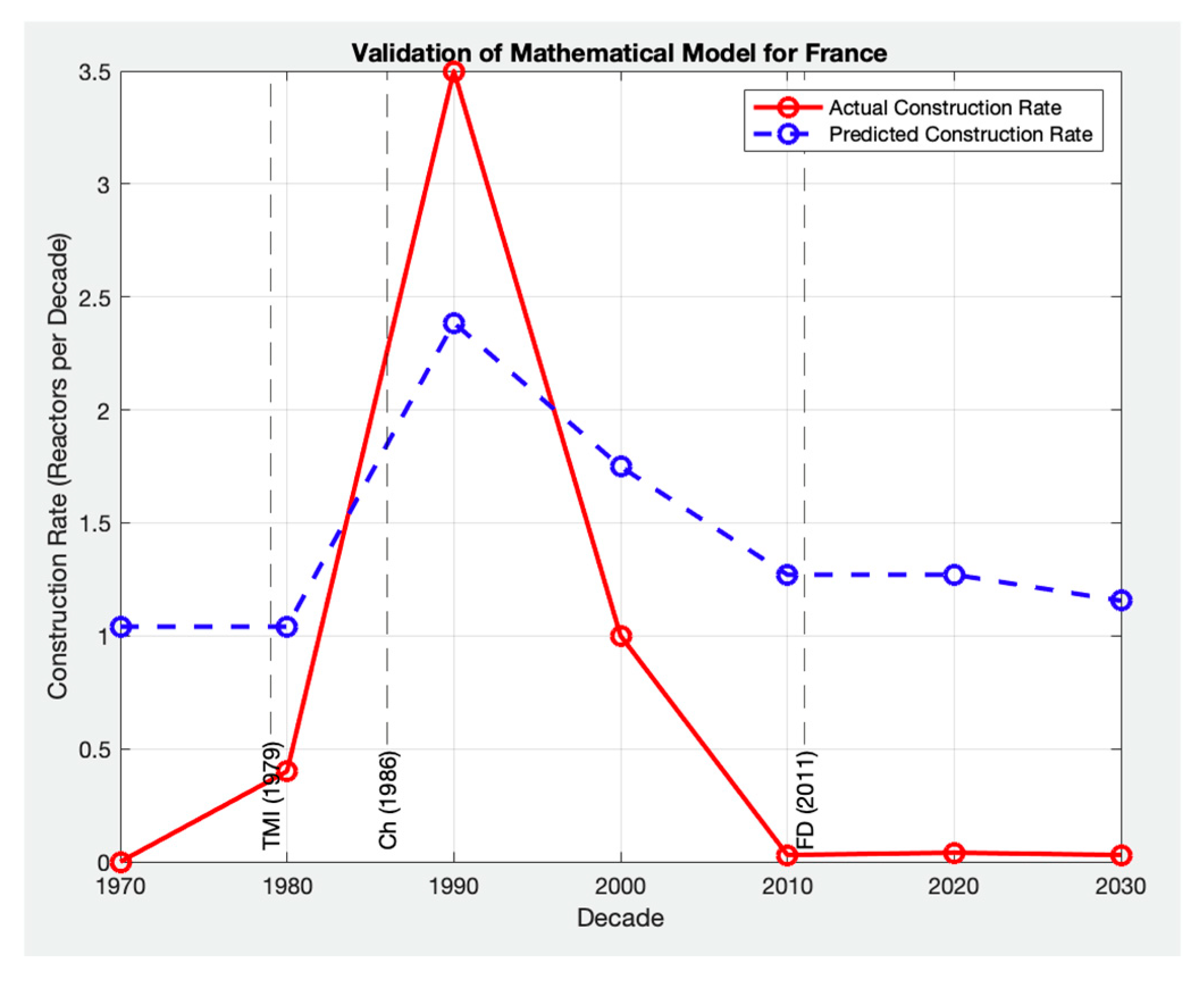
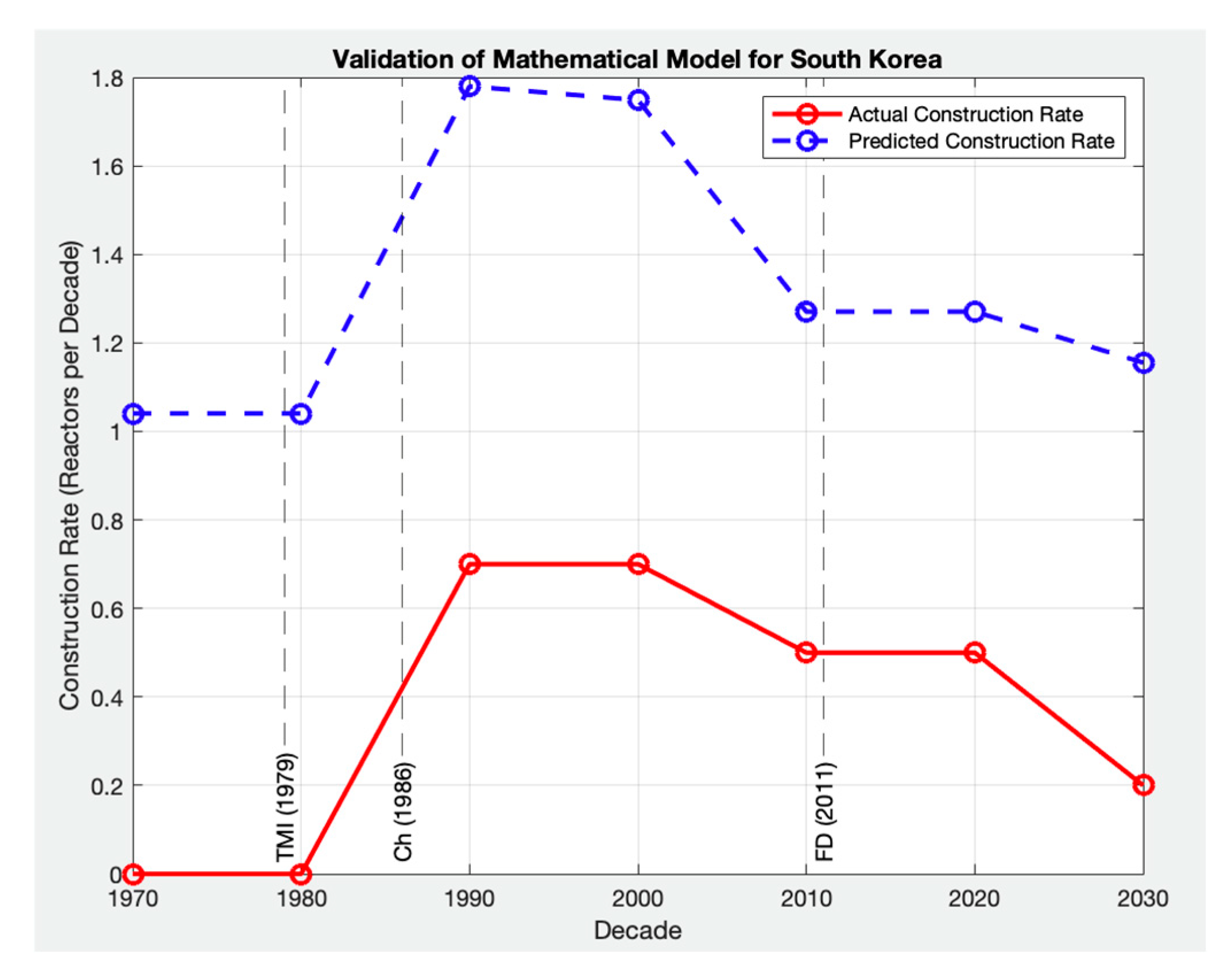
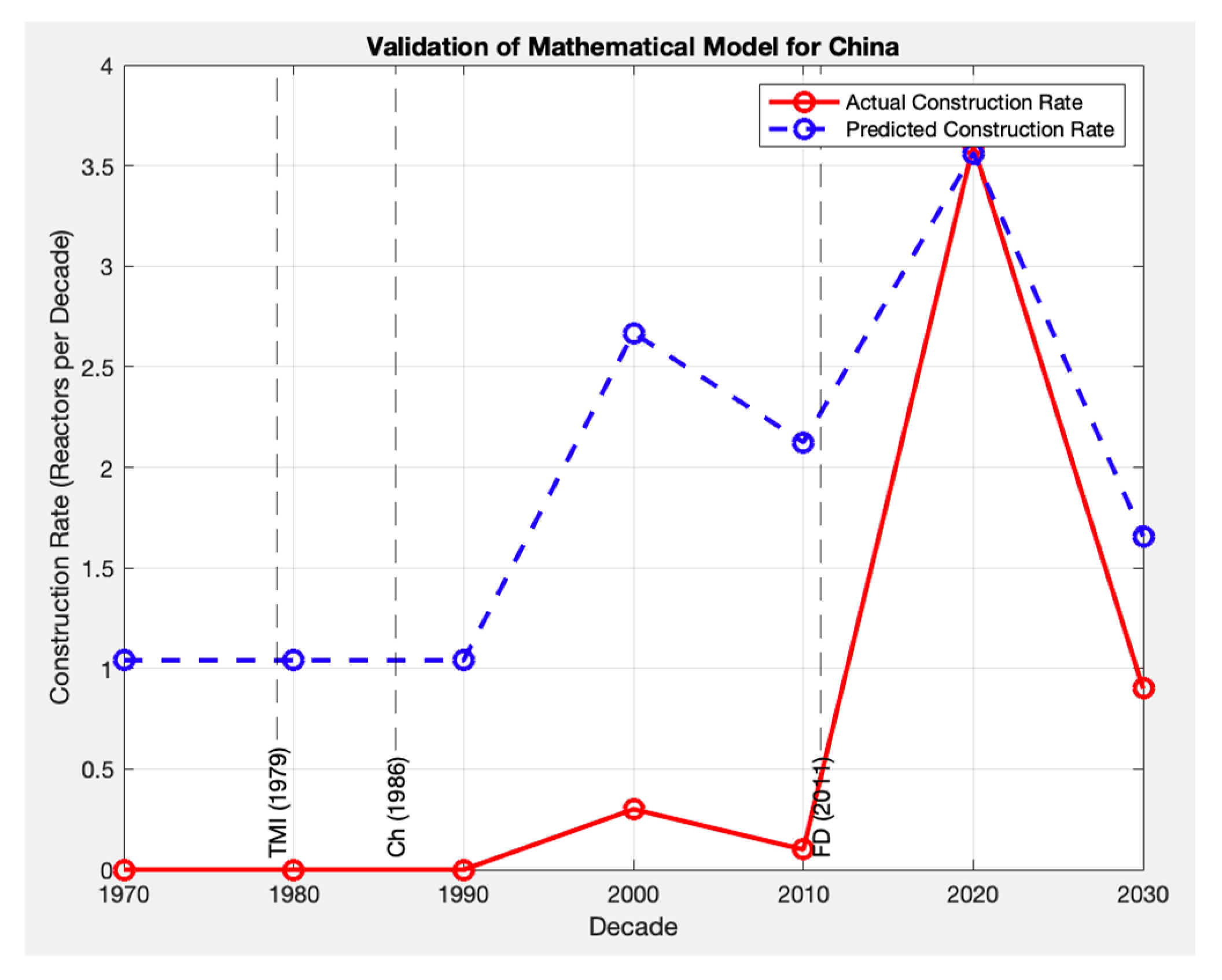
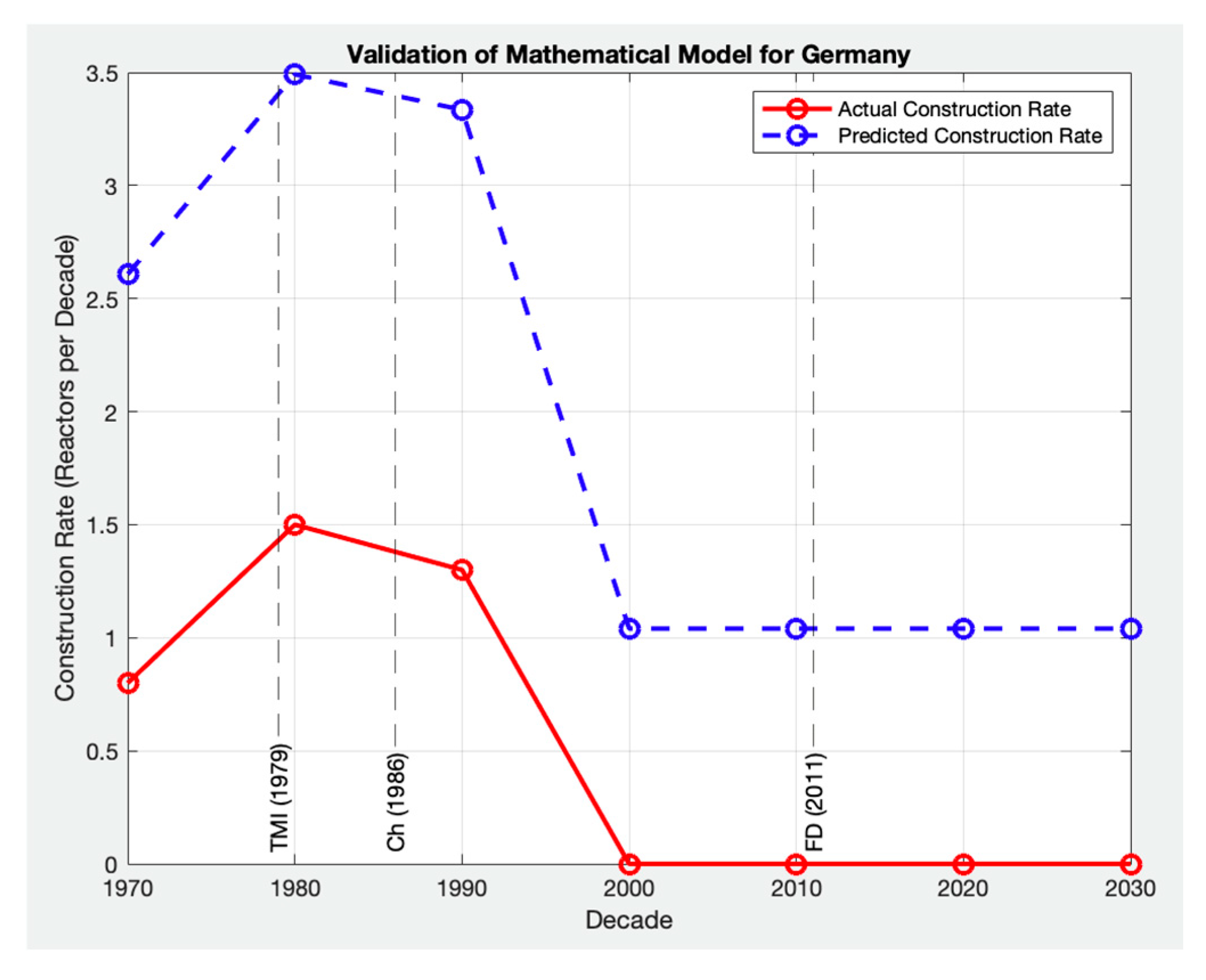
To further explore the model’s robustness and its adaptability to a broader range of policy, economic, and social conditions, the model was also qualitatively applied to France, Russia, Germany, South Korea, and China [73]. These additional comparisons are presented in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 and showcase the model’s capacity to reflect different deployment trajectories shaped by diverse regulatory, political, and technological factors. While these countries were not included in the RPE analysis, they provide important reference points for assessing the global relevance of the model. This extended validation supports the notion that the model is capable of characterizing the key trends in nuclear deployment across countries with differing histories, offering a solid foundation for applying the model to predict future SMR deployment patterns globally.

While the model effectively captures the general trends in nuclear construction rates, several limitations must be considered. One key limitation is its sensitivity to parameter selection. The model relies on weight coefficients and interaction terms determined based on current industry trends and scenario-based projections, assuming that the identified influencing factors will continue to play a significant role in nuclear deployment from 2025 to 2050 to 2100. However, long-term shifts in policy, technological advancements, economic conditions, and geopolitical factors introduce uncertainties that are difficult to encapsulate fully. The model incorporates a logistic function to ensure that factor contributions are not unlimited, meaning that even if a factor (e.g., Public Acceptance or Supply Chain Readiness) increases significantly, its impact on the construction rate eventually levels off. However, in reality, decision-making processes involve delays, regulatory barriers, and unexpected disruptions, which may temporarily slow or halt construction, even when the model predicts otherwise. These external parameters are not explicitly accounted for, since their interconnectness can only be discerned via accessible information.

Despite these limitations, the model remains a valuable tool for long-term scenario analysis, allowing policymakers and industry leaders to assess potential pathways for nuclear expansion. However, the careful calibration of parameters is essential to ensure realistic (regional) projections. Future refinements should explore adaptive modeling techniques, dynamic parameter adjustments, and uncertainty quantification to enhance predictive accuracy and account for evolving global conditions.

4. Simulation and Results

This section presents the simulations conducted to evaluate the effectiveness of the proposed algebraic formula. It is divided into two main parts: the algebraic mathematical model integration with the DICE model and illustrative example and practical considerations. In the first part, we take the SMR construction rate from the DICE model simulation described in our previous research [7] and optimize it by our proposed algebraic mathematical formula. In the second part, we demonstrate the model’s application using hypothetical data and an illustrative example. The results from both simulations are presented and analyzed, providing insights into the potential pathways for net zero.

For modeling and analysis, two software tools were utilized. VENSIM version 8.0.9 was used for running the DICE model simulation, consistent with our previous work. To compute the historical trend and implement the algebraic model, MATLAB version R2020b was employed. These tools enabled the integration of dynamic system behavior and algebraic optimization to support scenario analysis and model validation.

4.1. Algebraic Mathematical Model Integration with DICE Model

In this section, this study integrates the algebraic formula with the DICE model to optimize SMR construction rates within the broader context of energy transitions. The DICE model, widely used for understanding the relationship between economic growth, energy systems, and climate change, offers valuable insights into the long-term effects of energy policy decisions [6,7,29,30]. However, while the DICE model is effective in modeling large-scale energy systems and carbon emissions reductions, it lacks the specificity needed to accurately assess the unique challenges of clean energy construction and deployment rate, including SMR.

By incorporating the algebraic formula into the DICE model, this study fills a critical gap in the existing framework, providing a more targeted and realistic analysis of SMR deployment under different socio-economic and environmental conditions. The integration allows for the modeling of specific factors that impact the rate of SMR construction, such as regional differences in public acceptance, variations in supply chain capabilities, and workforce and land availability. These factors, when combined with the economic and environmental projections from the DICE model, provide a more comprehensive understanding of the challenges and opportunities associated with SMR deployment.

The integration of the algebraic formula also enables the simulation of various policy interventions and external variables, allowing decisionmakers to evaluate the impact of different strategies on the pace of SMR construction. For example, policymakers can test the effects of increasing investment in workforce training programs or improving supply chain resilience on the overall construction rate of SMRs. Additionally, the model can simulate the impact of regulatory changes, such as easing land use restrictions or enhancing public engagement, to determine how these adjustments would affect the time required to bring SMRs online.

Ultimately, the integration of the algebraic formula with the DICE model provides a more precise tool for predicting and optimizing SMR construction rates, supporting better decision making and more effective policy interventions. By offering a more targeted and realistic approach to SMR deployment, this integrated model aims to accelerate the transition to a low-carbon future, and help meet global decarbonization targets.

To integrate the proposed mathematical model into the DICE framework, a relationship that adjusts the DICE model projections based on the mathematical model CR needs to be established. If CR from the mathematical model indicates a percentage of operational efficiency or project feasibility under the assessed conditions, this can be applied as a modifier to the CR simulated by the DICE model [7].

Table 9. Summary of different scenarios.

Target Year	CR of SMR Units (Unit/Year)
	CR from DICE [7]	Optimized CR as per Mathematical Formula
2050	5.2	CR × 5.2
2100	2.7	CR × 2.7

presents the construction rates (CRs) of SMR units required to achieve net-zero emissions in Ontario for the target years 2050 and 2100 based on findings from our previous research [7]. In that study, we adapted the DICE model to estimate SMR deployment rates necessary to meet Ontario’s net-zero targets, aligning with the IESO’s 2050 [81] projections and extending the analysis to 2100 for long-term assessment. The resulting construction rates were determined as follows: 5.2 SMR units per year in 2050 and 2.7 SMR units per year in 2100. Here, a “unit” refers to the energy capacity equivalent to an 80 MWe SMR. These values reflect the pace at which SMRs are expected to be deployed under the DICE model’s simulations and projections [7].

Building on these projections, the current study introduces an algebraic formula to refine the construction rates by incorporating key influencing factors, including Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA). Instead of solely relying on the DICE model’s estimates, this approach allows for a more detailed representation of real-world constraints and enabling conditions affecting SMR deployment. The algebraic formula is applied as an optimization factor to refine the CRs derived from the DICE model, enabling a more adaptive and dynamic framework for construction rate projections. This enhancement ensures that projections align with net-zero emissions goals while accounting for the dynamic interplay of public acceptance, supply chain readiness, human resource availability, and land availability, which shape the feasibility and pace of SMR deployment in Ontario through 2050 and 2100.

4.2. Illustrative Example and Practical Considerations

A conceptual example demonstrates the model’s application using hypothetical data and parameters related to power plant construction. Practical considerations regarding the choice of the logistic function, non-linearity parameters, interaction coefficients, and external variables are discussed to enhance practical applicability and initiatives.

• Factors:

  ○

  Public Acceptance ($x_{1 }$): Score of 0.8 (on a scale from 0 to 1);

  ○

  Supply Chain ($x_{2 }$): Score of 0.6;

  ○

  Human Resource ($x_3$): Score of 0.7;

  ○

  Land Availability ($x_{4 }$): Score of 0.9.

• Weights and Parameters (hypothetically chosen for illustration):

  ○

  Weights: $w_1$ = 0.25, $w_2$ = 0.2$, w_3$ = 0.2$, w_4$ = 0.35;

  ○

  Non-linearity parameters: $\alpha =1,\beta =2,\gamma =1.5, \delta =1$;

  ○

  Interaction coefficients: ${\theta }_{12}=0.1, {\theta }_{34}=0.15$, others are 0 for simplification;

  ○

  External variable z (e.g., regulatory policy score): 0.75 with weight v = 0.1;

  ○

  Assume the logistic function for f, mapping input factors to the output.

• Model Solution:

Plugging the hypothetical data into the model:

$$y=f(0.25\times {0.8}^1+0.2\times {0.6}^2+0.2\times {0.7}^{1.5}+0.35\times {0.9}^1+0.1\times 0.8\times 0.6+\mathrm{0.15.0}\times 7.0\times 9+0.1\times 0.75)$$

$$f\left(x\right)={\displaystyle \frac{1}{1+e^{-x}}}$$

(assuming x as the sum of weighted inputs and interactions)

Calculation of the weighted inputs and interactions:

• Weighted Inputs = 0.25 × 0.8 + 0.2 × 0.6² + 0.2 × 0.7^1.5 + 0.35 × 0.9;
• Interactions = 0.1 × 0.8 × 0.6 + 0.15 × 0.7 × 0.9;
• External Variable = 0.1 × 0.75.

Combining these values and applying the logistic function to map them to a construction rate. This is calculated using MATLAB version R2020b for precision. Based on the hypothetical data and parameters, the model calculates a construction rate score of approximately 0.715. This score, derived from the logistic function applied to the weighted factors, interactions, and an external variable, suggests a medium to high likelihood of construction rate for the power plant.

Considering the 0.71 CR from the mathematical model is applied as a modifier to the DICE SMR CR, as shown in

Table 10. Summary of different scenarios with optimized CR.

Target Year	CR of SMR Units (Unit/Year)
	CR from DICE [13]	Optimized CR as per Mathematical Formula
2050	5.2	0.71 × 5.2 = 3.7
2100	2.7	0.71 × 2.7 = 1.9

.

As can be seen in Table 10 and Figure 15, the adjusted construction rate (CR) calculated using the mathematical formula, which incorporates the four key factors (Public Acceptance, Supply Chain Readiness, Human Resource Availability, and Land Availability), serves as a powerful tool for optimizing SMR deployment. In this illustrative example, the mathematical model produced a CR score of 0.71. When applied to the original CR data from the DICE model, this results in an adjusted CR of 3.7 units per year for the 2050 target year and 1.9 units per year for the 2100 target year to reach net zero. This optimization process is crucial because it provides an actionable framework for understanding how various factors and their interdependencies influence the speed and scale of SMR construction. By integrating the algebraic formula, we can adjust the construction rates based on detailed, context-specific parameters. The model’s flexibility is a key advantage. The CR score of 0.71 is derived based on hypothetical data, including weighted factors and interaction coefficients. By changing these inputs—such as adjusting the weight of Land Availability or Supply Chain Readiness—policymakers and energy planners can see how the adjusted CR varies. This allows them to understand the sensitivity of SMR construction rates to changes in key factors. For example, increasing the supply chain readiness score may lead to a higher CR, accelerating deployment. Conversely, if public acceptance or human resource availability is lower, the CR might decrease, highlighting the need for targeted policy interventions in these areas. Such sensitivity analysis is highly valuable for decision making, as it helps stakeholders identify which factors have the greatest impact on SMR deployment and where focused efforts should be made. This could involve investing in improving supply chain efficiencies, enhancing public engagement campaigns, or providing training programs to boost human resource availability. In essence, this tool provides a means for policymakers to simulate different scenarios, experiment with various strategies, and determine the most effective actions to take in order to optimize SMR construction rates. It not only supports informed decision making but also contributes to achieving the necessary scale and speed of deployment required to meet global decarbonization goals. The model offers a dynamic, data-driven approach to accelerate the transition to a low-carbon, net-zero emissions future.

In a real-world scenario, this model would allow inputting actual data for public acceptance, supply chain, human resource, land availability, and any relevant external factors. By adjusting the weights, interaction coefficients, and parameters according to specific circumstances and data, the construction rate for a power plant with nuanced consideration of all contributing factors can be predicted.

5. Discussion

This study introduced an algebraic formula designed to optimize the construction rates (CR) of SMRs, a critical component in the transition to a low-carbon energy future. The model integrates four key influencing factors—Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA)—into a structured mathematical framework. By incorporating these factors, the model refines nuclear deployment projections by adjusting the CR values derived from the DICE model. This approach enhances the applicability of SMR construction rate predictions by accounting for real-world constraints and socio-economic influences.

One of the significant findings of this study is the practical application of the adjusted CR, derived from the formula, to the original CR values provided by the DICE model. The results indicate that, for the target years of 2050 and 2100, applying the optimized CR leads to a reduction in the projected SMR deployment rate, from 5.2 units per year to 3.7 units per year by 2050 and from 2.7 units per year to 1.9 units per year by 2100. This adjustment reflects the complex dynamics and interdependencies between key factors, offering a more realistic estimate of the construction rate of SMRs under various socio-economic and environmental conditions.

The implication of this reduction is significant for policy planning. A slower SMR construction rate may impact net-zero targets, especially in regions relying on nuclear energy as a firm baseload to complement intermittent renewables. If deployment occurs at a slower pace than projected by models such as DICE, additional policy interventions—such as workforce expansion, increased investment in supply chains, and public education—may be required to close the deployment gap. Moreover, this suggests that previous models may have overestimated the feasibility of rapid SMR rollouts without accounting for deployment constraints. The algebraic model provides a more realistic perspective by incorporating feasibility constraints grounded in real-world system-level barriers.

The validation process further supports the reliability of the algebraic model by comparing its predicted construction rate trends with historical U.S., Japanese, and Canadian nuclear deployment data. Rather than aiming for precise forecasting, the model was assessed on its ability to capture historical trends in construction rates. The U.S. was initially selected as the reference case due to the availability of literature on key influencing factors. The historical data indicate distinct construction trends, with peak deployment in the 1970s and 1980s, followed by a sharp decline in the 1990s and minimal new reactor construction in the 2000s and 2010s. The model successfully reflects these patterns, showing an increasing trend in the 1960s–1980s and a significant slowdown post-1990 due to external policy shifts, regulatory constraints, and economic challenges.

To extend the model’s validation beyond the U.S., Japan and Canada were included as additional case studies, incorporating datasets of varying sizes. The U.S. dataset, being the most extensive, exhibited the RPE, confirming the model’s ability to closely follow actual construction trends. Japan’s dataset, with a moderate amount of data, showed a reasonable level of accuracy, capturing general trends but displaying some discrepancies in peak construction periods. In contrast, Canada, with the smallest dataset, exhibited the highest RPE, reflecting greater deviations between predicted and actual values. These findings underscore the impact of data availability on model accuracy.

The model also highlights the relative contributions of key factors. PA and SC emerge as the most influential, aligning with historical trends where periods of strong public support and robust supply chains coincided with higher construction rates. HR availability and LA exhibit less direct impact, though their interplay with other factors plays a role in deployment feasibility. By adjusting these parameters, policymakers can evaluate potential scenarios for accelerating SMR construction, such as enhancing workforce development or streamlining supply chain processes. A key consideration in applying the proposed mathematical framework to SMRs is the fundamental difference in their deployment characteristics compared to large-scale reactors. While historical nuclear construction rates provide valuable insight into industry trends, SMRs are designed to be constructed more efficiently through modular manufacturing, reducing on-site assembly time and enabling parallel deployment. Consequently, the expected construction rate of SMRs may diverge from historical large-scale nuclear trends, necessitating adjustments in modeling assumptions. The model’s flexibility allows for the integration of SMR-specific parameters, ensuring that projections align with the industry’s evolving dynamics and emerging deployment strategies.

Moreover, the model can be adapted to simulate the effects of new policies, such as government subsidies or regulatory streamlining, by adjusting input parameters. For instance, increased funding for SMR development could enhance supply chain readiness (SC), while education campaigns might improve public acceptance (PA). These dynamic policy scenarios can be simulated to evaluate their impact on deployment feasibility and trajectory.

It is important to note that while the model effectively optimizes SMR deployment using known and scenario-based inputs, it does not inherently predict unexpected disruptions or shocks (e.g., sudden regulatory changes, geopolitical events, supply chain breakdowns). Instead, it relies on the availability of data and expert input to adjust the coefficients and weights accordingly. If an unforeseen disruption occurs, its effects must be manually reflected in the model by adjusting parameters, as the model does not autonomously adapt to such shocks.

In addition to refining SMR deployment projections, the algebraic model offers broader applicability to other clean energy technologies. The core methodology—adjusting construction rates based on socio-economic and infrastructure constraints—can be extended to optimize the deployment of renewables, such as wind and solar energy. However, the emphasis on SMRs in this study is justified by their critical role in providing stable, low-carbon energy, particularly in regions where renewable energy alone may not be sufficient for grid reliability.

Furthermore, the model can be integrated into existing energy transition models by serving as a sub-model or optimization approach that adjusts the construction rate input based on real-time evaluations of public acceptance, workforce readiness, supply chain capacity, and land use constraints. This integration would allow energy system models to generate more realistic deployment timelines, cost estimations, and feasibility assessments across scenarios. In fact, in this study, the model is already integrated with the DICE model as an optimization framework to demonstrate this capability.

While integrated assessment models, such as TIMES, MESSAGE, and GCAM, are widely used for long-term energy transition planning, they typically do not explicitly model or optimize construction rates based on socio-technical uncertainties, such as public acceptance, supply chain readiness, workforce availability, and land constraints. The proposed algebraic model complements these frameworks by introducing a structured, factor-based optimization approach. Moreover, our previous research [7] demonstrated that fuzzy logic can be used to quantify uncertainty around these factors, offering a valuable extension to existing energy models and enabling more realistic scenario planning under dynamic policy and infrastructure conditions.

This study also evaluated the model’s flexibility in adapting to diverse regulatory landscapes. The validation section incorporated countries with varied governance frameworks—including centralized (e.g., China, Russia), hybrid (e.g., Japan), and decentralized (e.g., Canada) regulatory models. These applications demonstrated that, while the model’s algebraic structure remains consistent, parameter adjustments are necessary to reflect regulatory complexity. For instance, in decentralized systems, Public Acceptance (PA) must account for regional engagement dynamics, while centralized systems may require a stronger emphasis on Supply Chain Readiness (SC) and government investment policies. Human Resource Availability (HR) and Land Availability (LA) may also differ significantly in constrained environments. These findings reinforce that context-specific calibration of model parameters is essential for accurate regional deployment projections.

The proposed algebraic model offers several advantages. It is intuitive, transparent, and adaptable—allowing policymakers and planners to adjust inputs based on real-world data for key drivers, such as Public Acceptance (PA), Supply Chain Readiness (SC), Human Resource Availability (HR), and Land Availability (LA). Unlike black-box models, such as machine learning or Monte Carlo simulations, the algebraic structure enhances interpretability and allows stakeholders to trace how input changes influence construction rates. This clarity makes it especially suitable for scenario planning, policy testing, and stakeholder engagement, which can be integrated into existing energy planning models, such as DICE. Furthermore, the model’s scalability allows for cross-regional comparisons. However, the model also has limitations. It does not dynamically learn or adapt without manual parameter updates and lacks real-time feedback loop capabilities. Its accuracy is dependent on the quality and representativeness of the input data and assumptions (e.g., weights and interaction coefficients). Additionally, the model is not designed to predict unexpected disruptions, such as political instability or sudden regulatory shifts, unless such changes are manually accounted for in the inputs.

In conclusion, this study provides a validated framework for optimizing SMR construction rates, bridging the gap between theoretical projections and practical deployment realities. By refining the CR values provided by the DICE model, the algebraic approach offers a more accurate and policy-relevant tool for planning SMR expansion. The ability to assess different deployment scenarios enhances its utility for policymakers and industry stakeholders, ensuring a more strategic approach to achieving net-zero energy goals. The evaluation of RPE further reinforces the need for high-quality, comprehensive datasets in improving model precision, particularly in regions where nuclear deployment policies differ across jurisdictions.

Table 11. Summary of study needs, model contributions, and achievements.

Study Need/Research Gap	Model Contribution	Outcome/Achievement
Lack of SMR-specific deployment optimization in existing models (e.g., DICE, GCAM, TIMES)	Developed a novel algebraic model tailored for SMR construction rate optimization	Optimized CRs for 2050 and 2100, addressing techno-socio-economic constraints
Uncertainty in public acceptance, supply chain readiness, land use, and workforce availability	Incorporated four key factors (PA, SC, LA, HR) into the algebraic framework	Quantified uncertainty and impact on CR projections
Need for model validation across different policy/regulatory contexts	Applied model to 8 countries (U.S., Canada, Japan, France, Germany, South Korea, Russia, China)	Demonstrated reproducibility, adaptability, and relevance in diverse geopolitical settings
Lack of decision-support tools for SMR policy planning	Provided scenario-based guidance on key deployment bottlenecks	Enables strategic planning and prioritization (e.g., workforce investment, supply chain expansion)
Integration with broader energy models	Structured as an add-on to models like DICE	Enhances precision of clean energy transition pathways

summarizes the core study needs, the specific contributions made by the proposed model, and the key outcomes, serving as a cross-reference tool to support reader clarity and understanding.

6. Future Research Opportunities

While this study makes significant contributions to understanding the dynamics of SMR construction, several opportunities for further research remain. First, the algebraic model can be refined and validated by incorporating real-world data from ongoing SMR projects and other clean energy technologies. Such refinement would enhance the model’s accuracy and applicability across diverse regional contexts and energy types, including solar, wind, hydro, and emerging technologies.

Second, integrating the algebraic formula with broader energy system models would provide a more holistic framework for policy analysis. This would support assessments of policy interventions, technological progress, and energy storage solutions across clean power technologies. Understanding the interaction among energy sources is key to achieving global decarbonization.

Advancements in computational techniques and machine learning also offer potential for improving the model’s scalability and adaptability. Real-time data integration could yield more accurate predictions and deepen insights into uncertainties surrounding rapid clean energy deployment.

Additionally, the model can serve as a sub-module within existing transition models, dynamically adjusting construction rates based on real-time inputs, such as public sentiment, workforce capacity, supply chain readiness, and land constraints. This has been demonstrated through integration with the DICE model.

Finally, expanding this research to cover more diverse regions with varied governance systems is essential. The Canadian case illustrated how provincial-level policymaking differs from national approaches in the U.S. and Japan—differences that meaningfully impact construction trends. Future modeling should reflect such variations to improve predictive accuracy in decentralized markets.

In summary, this study lays the groundwork for advancing SMR deployment modeling. Validated across multiple datasets and RPE-tested, the framework highlights the importance of high-quality input data and responsive planning tools. Embedding feedback mechanisms—such as iterative updates based on real-time trends—will further strengthen the model’s relevance for adaptive policy and energy transition planning. This work ultimately supports a more resilient path to global decarbonization.

7. Conclusions

This study introduces a novel algebraic formula to optimize SMR construction rates by integrating key drivers—Public Acceptance, Supply Chain Readiness, Human Resource Availability, and Land Availability. The formula, applied alongside the DICE model, enhances the analysis of dynamic interactions affecting deployment and offers a more actionable approach than traditional integrated assessment models.

Our findings underscore the urgent need to accelerate SMR deployment to meet net-zero emissions targets. The model highlights differences between traditional nuclear rollouts and the SMR paradigm, recognizing the potential for faster deployment due to SMR modularity and shorter construction timelines. This distinction allows for more realistic scenario planning aligned with future energy needs.

The validation across historical nuclear deployment data from the U.S., Japan, and Canada confirms the model’s reliability in capturing construction rate trends. The U.S., with the largest dataset, showed the lowest error, while Canada’s higher error reflects its limited data and provincial governance structure. This highlights the importance of dataset scale and governance diversity.

By enabling policymakers to test scenarios under evolving socio-technical conditions, this framework supports strategic energy planning and integrated policy development. Its adaptability and emphasis on trend alignment provide meaningful insight for guiding clean energy transitions and advancing the role of SMRs in achieving global decarbonization goals.