Artificial Neural Network-Based Feedforward-Feedback Control for Parabolic Trough Concentrated Solar Field
Abstract
1. Introduction
2. Computational Methods
2.1. Concentrated Heat Collection Model
2.2. Artificial Neural Network Feedforward-Feedback Control Model for PTC Collector Circuit
2.3. PID Control Model
2.4. Numerical Algorithm
3. Results and Discussion
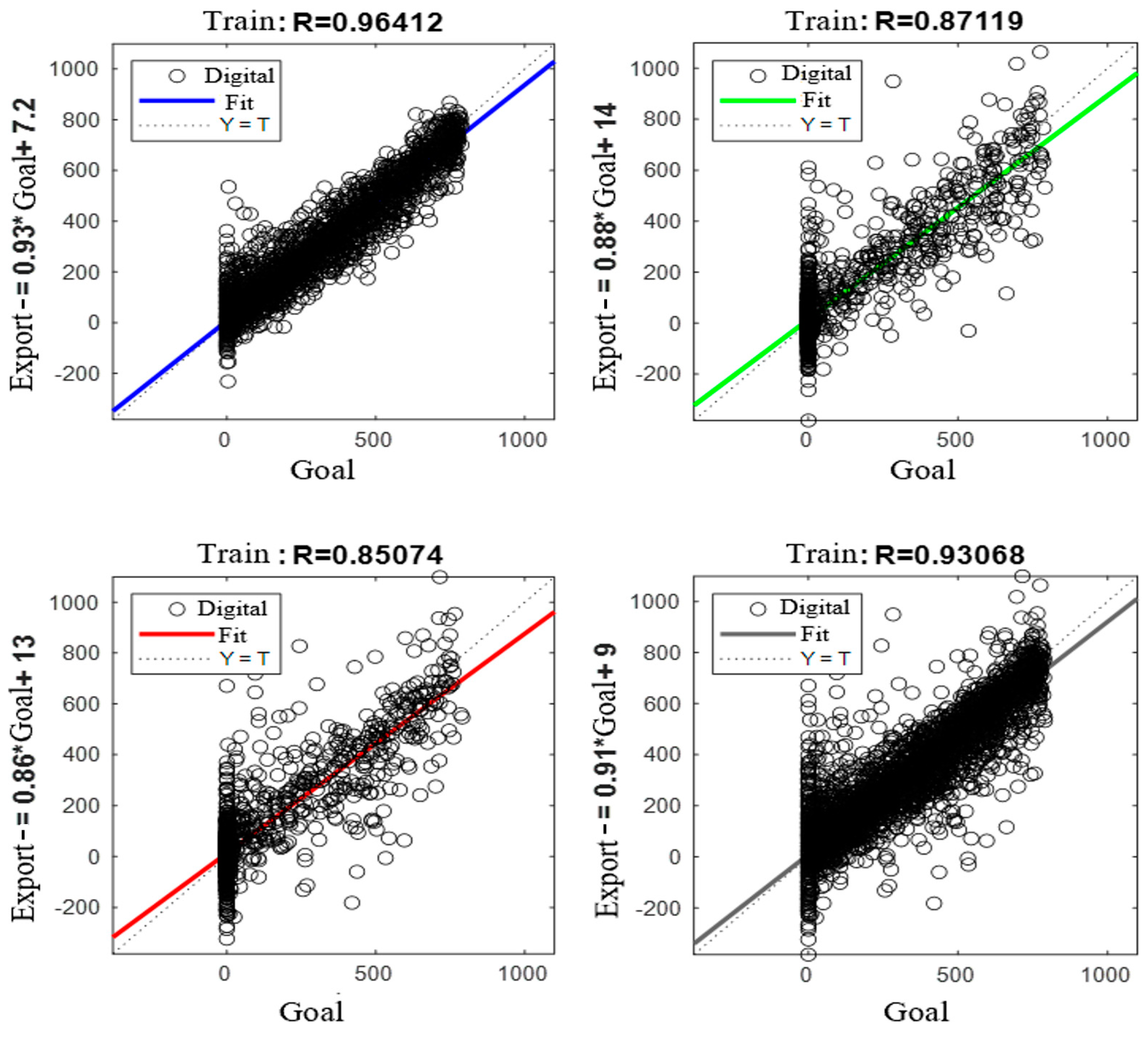
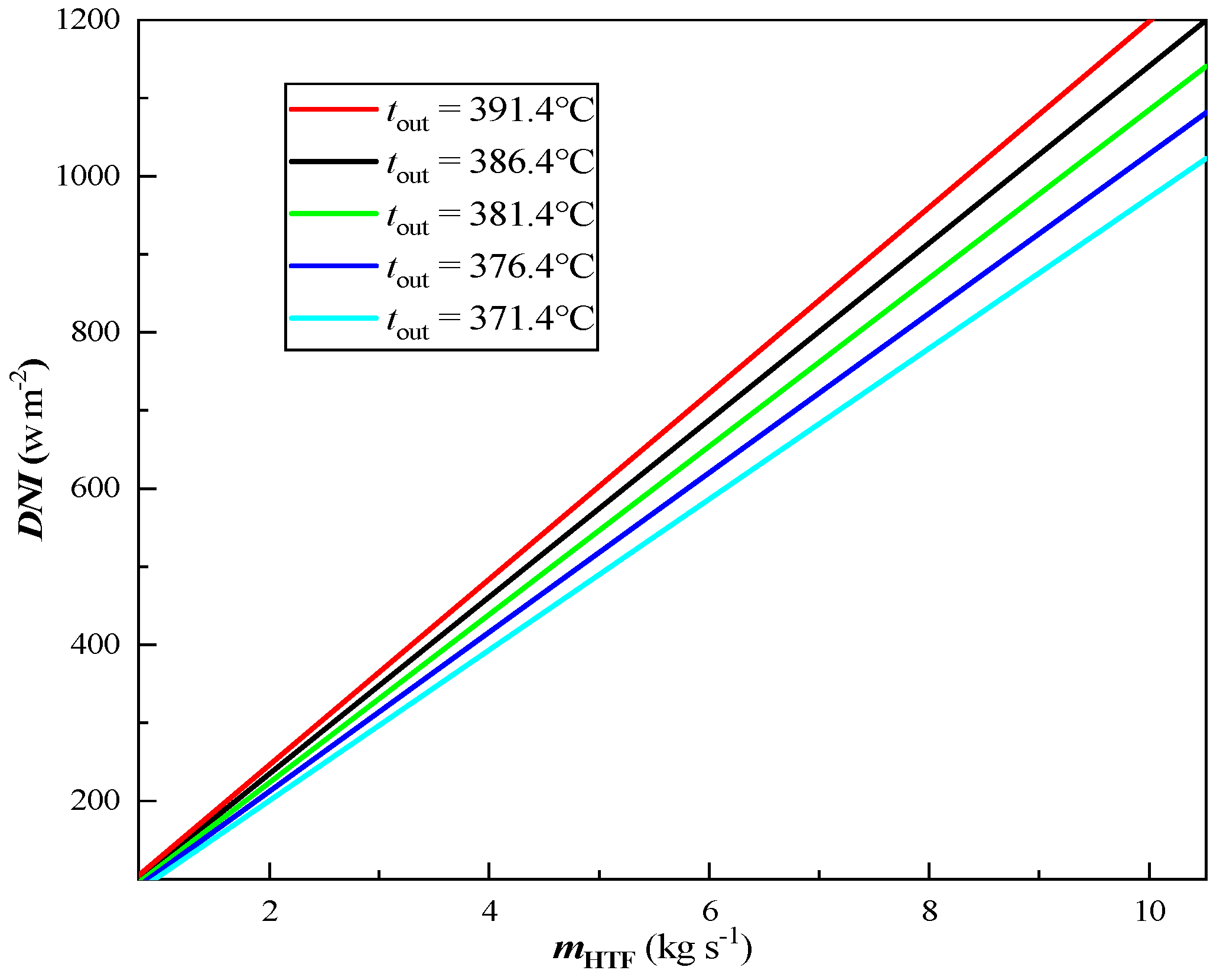
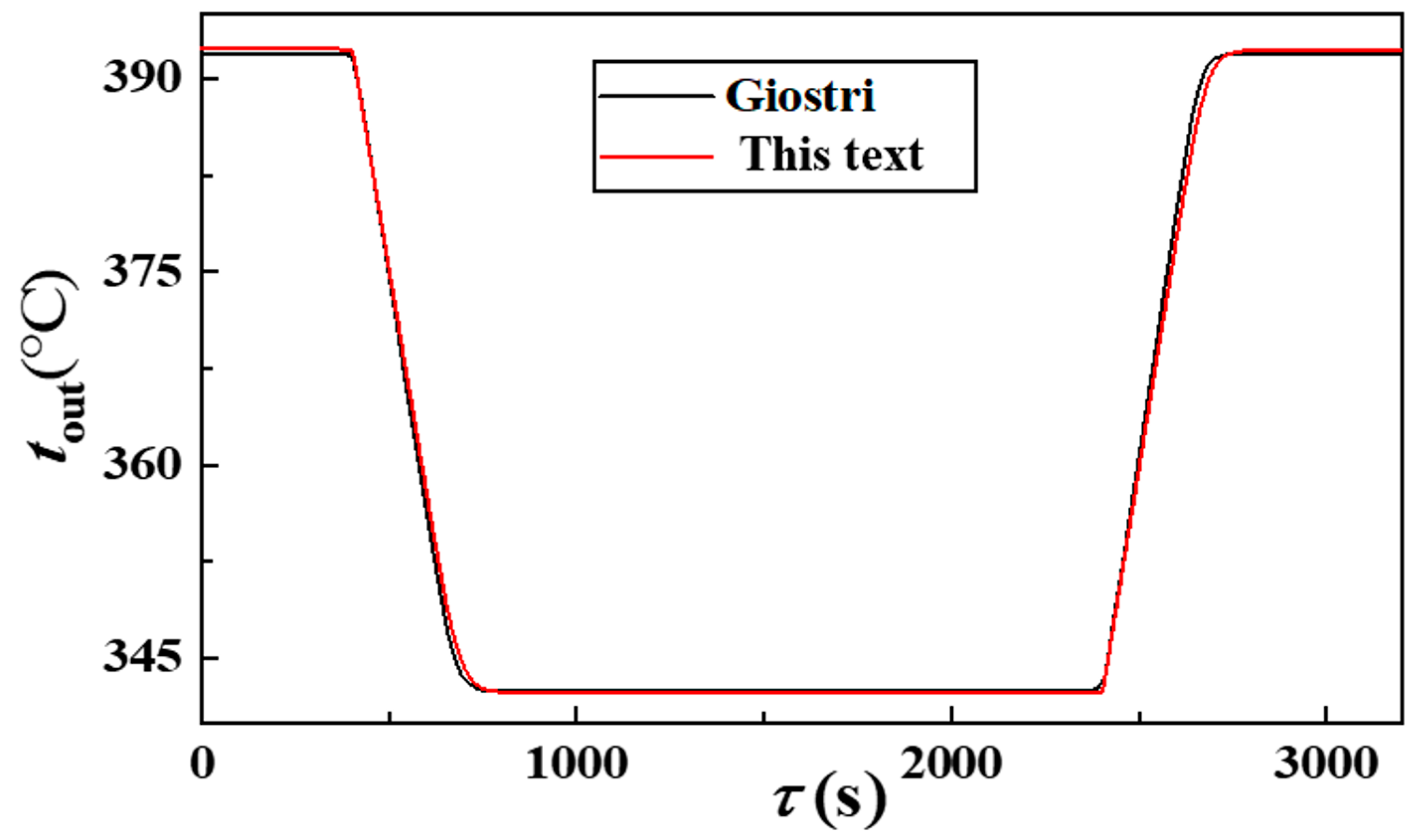
3.1. Model Validation
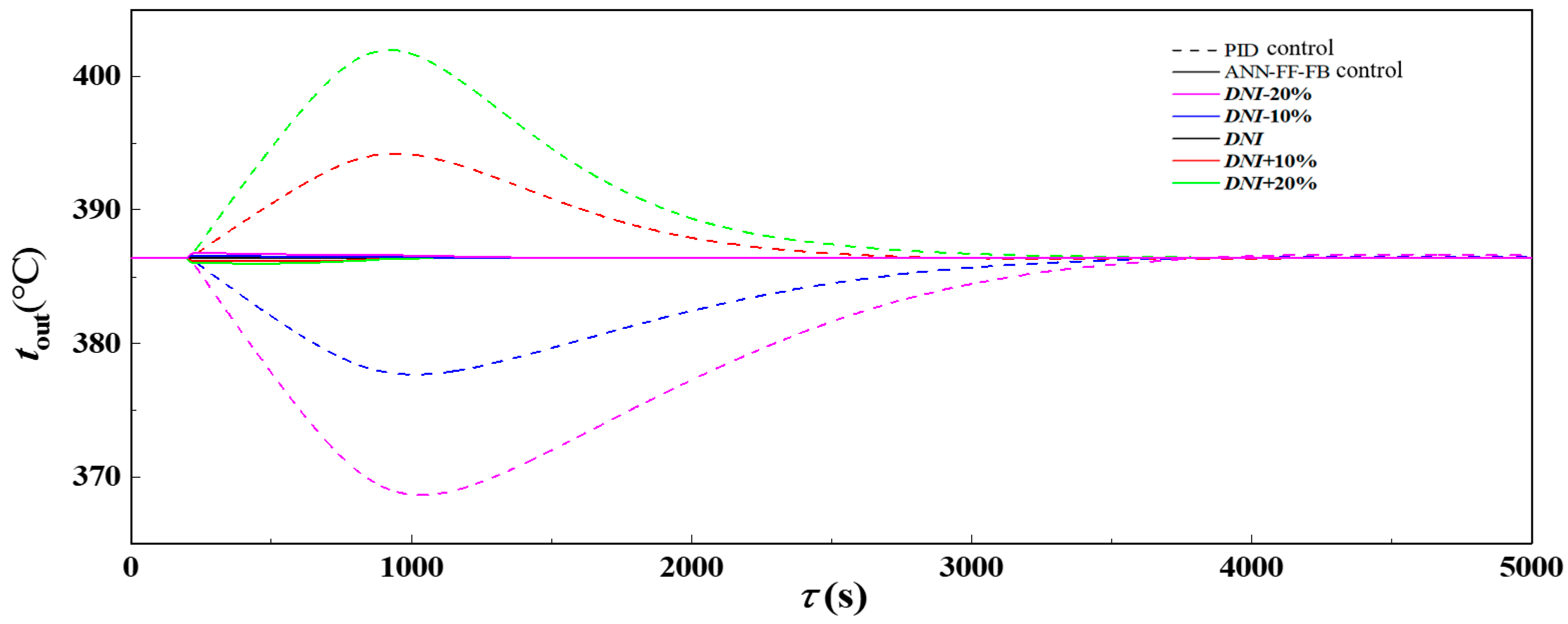
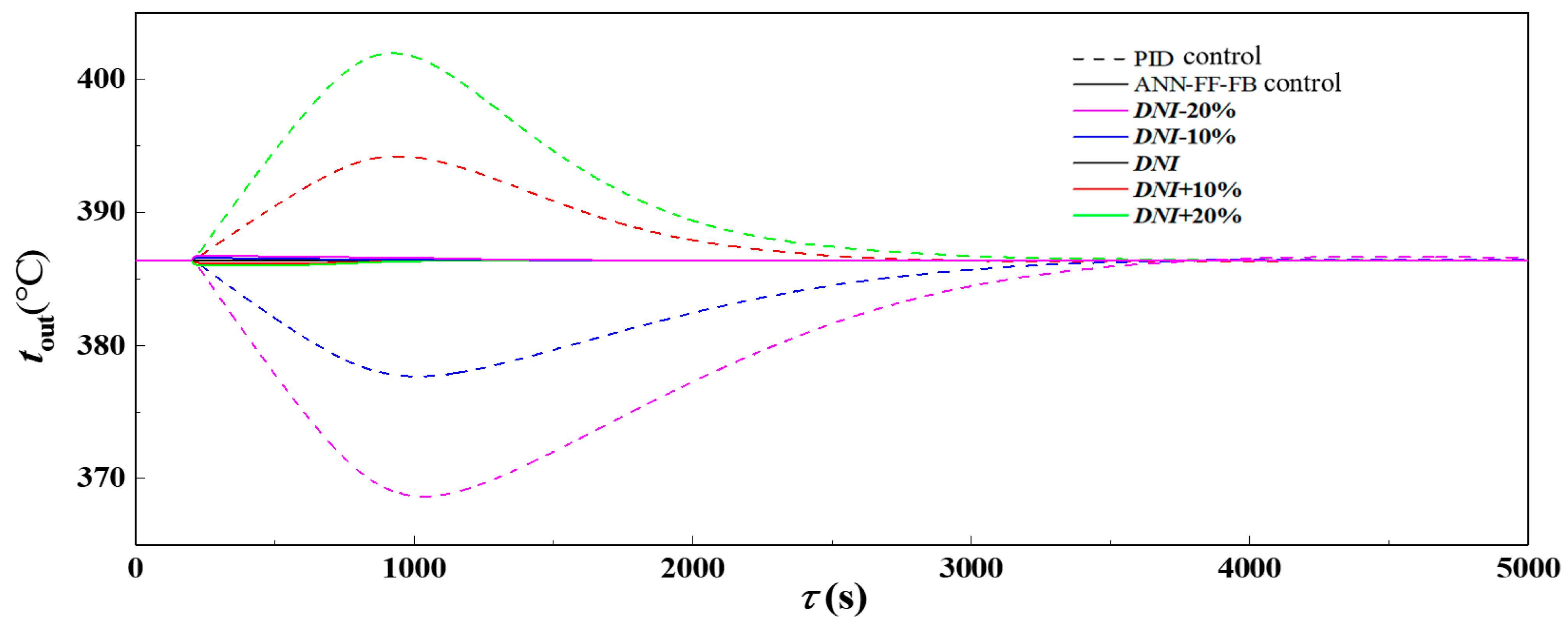
3.2. Control Performance Analysis Under Step Changes in Solar Irradiance
3.3. Analysis of Control Performance When Adjusting the Set Point of Outlet Temperature
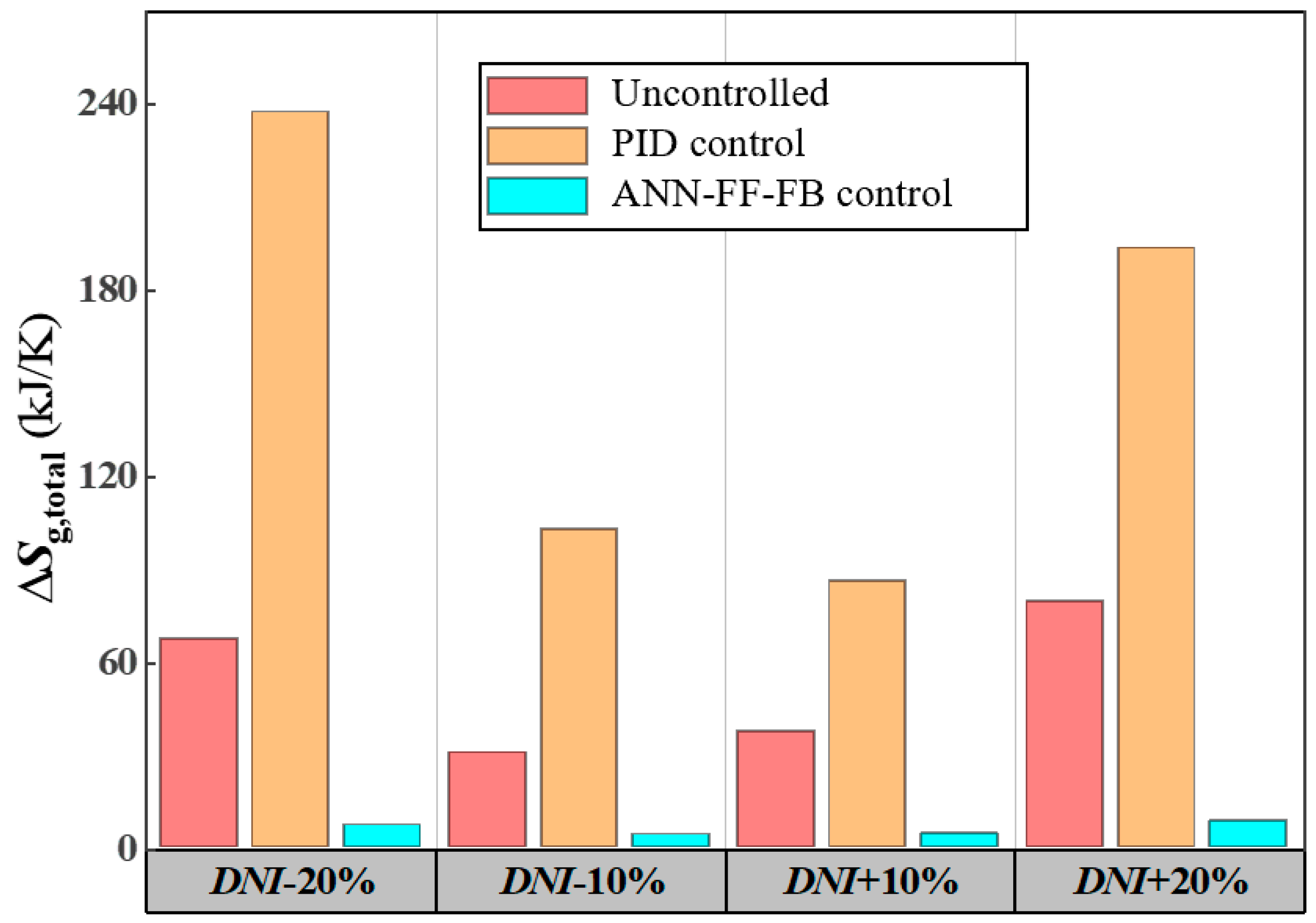
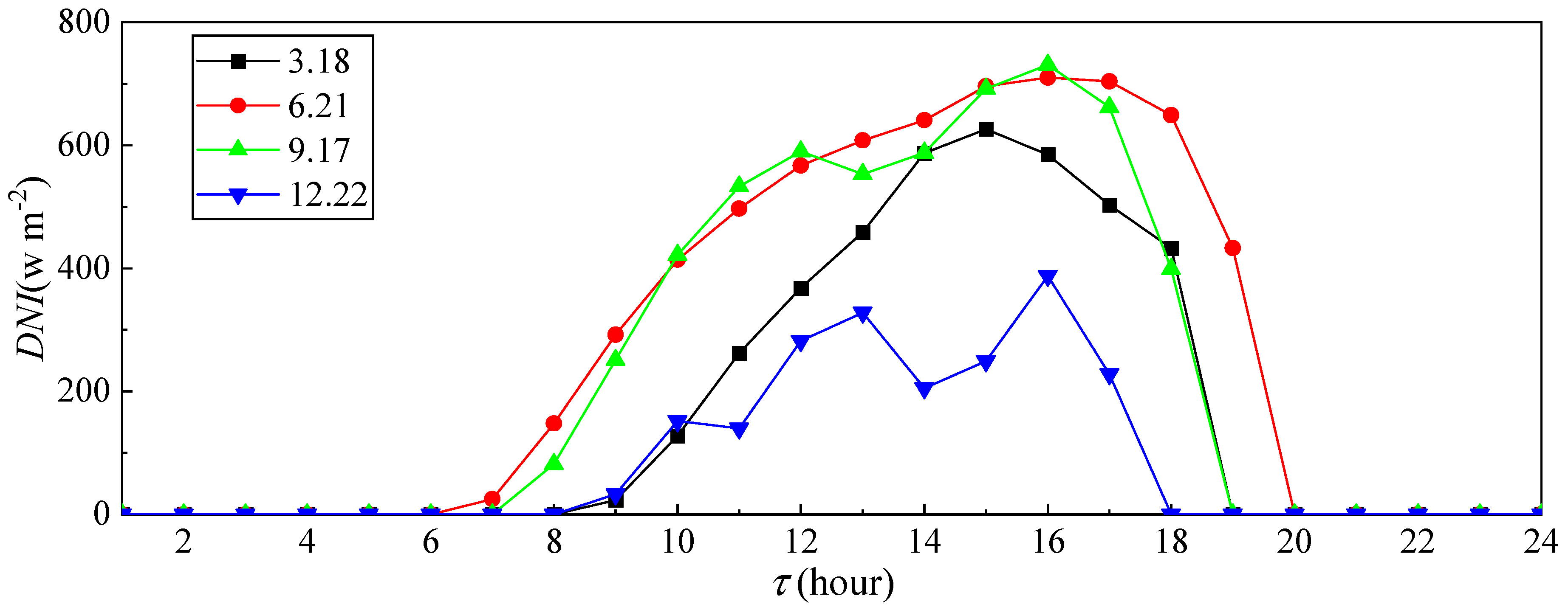
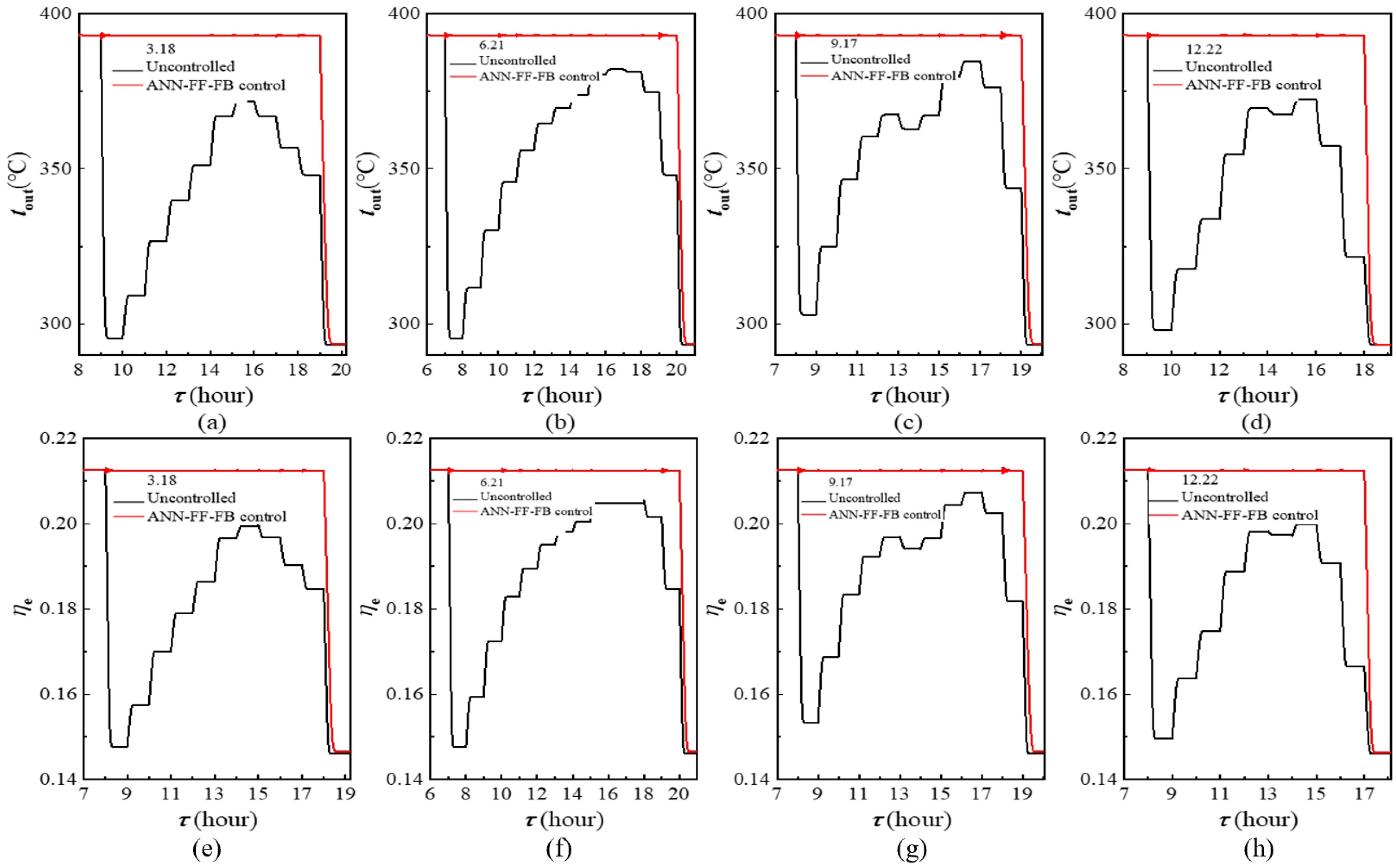
3.4. Control Performance Analysis Under Actual Meteorological Conditions
4. Conclusions
- The ANN-FF-FB control model demonstrates superior response speed, accuracy, and stability during step changes in solar irradiance. Its adjustment time is only one-quarter of that of the PID control model, with a maximum overshoot of only 0.5 °C and a steady-state error of just 0.02 °C, effectively maintaining the stable operation of the PTC collector loop outlet temperature. Furthermore, this model significantly reduces the accumulated entropy production in the absorber tube during transient processes, improving the thermodynamic performance of the PTC collector loop and ensuring its stable operation.
- When adjusting the setpoint, the ANN-FF-FB control model shows superior response speed and control accuracy in adjusting the outlet temperature setpoint of the PTC collector loop. Its adjustment time is less than one-third of the PID control model’s time, with a maximum steady-state error of only 0.03 °C. In contrast, the PID control model takes longer to adjust, while the ANN-FF-FB control model quickly calculates the required mass flow rate adjustment using a feedforward neural network, significantly improving the responsiveness of the control system.
- The ANN-FF-FB control model effectively stabilizes the outlet temperature of the PTC collector loop under actual weather condition changes, maintaining it close to the setpoint from sunrise to sunset with a maximum overshoot of less than 1 °C, while also improving energy utilization efficiency. Compared to the significant fluctuations without control, this model greatly enhances the system’s stability, which is of great significance for the stable and efficient operation of PTC power plants.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weinstein, L.A.; Loomis, J.; Bhatia, B.; Bierman, D.M.; Wang, E.N.; Chen, G. Concentrating Solar Power. Chem. Rev. 2015, 115, 12797–12838. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Fu, S.; Wan, L.; Wang, H.; Zhang, Y.; Liu, Z.; Peng, J.; Li, J.; Song, C. In-Depth Investigation of Morphology Evolution in Highly Efficient Pseudo-Planar Heterojunction All-polymer Organic Photovoltaics. Adv. Funct. Mater. 2025, 2500975. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Liu, X.; Geng, Z.; Wang, H.; Xu, Z.; Miao, Z.; Liang, Q.; Liu, J. Controlling the Third Component Distribution Toward High-Efficient Ternary Organic Solar Cells. Adv. Energy Mater. 2025, 2406136. [Google Scholar] [CrossRef]
- Wang, G.; Chao, Y.C.; Jiang, T.L.; Chen, Z.S. Facilitating developments of solar thermal power and nuclear power generations for carbon neutral: A study based on evolutionary game theoretic method. Sci. Total Environ. 2022, 814, 151927. [Google Scholar] [CrossRef]
- He, Y.-L.; Qiu, Y.; Wang, K.; Yuan, F.; Wang, W.-Q.; Li, M.-J.; Guo, J.-Q. Perspective of concentrating solar power. Energy 2020, 198, 117373. [Google Scholar] [CrossRef]
- Li, L.; Sun, J.; Li, Y.; He, Y.-L.; Xu, H. Transient characteristics of a parabolic trough direct-steam-generation process. Renew. Energy 2019, 135, 800–810. [Google Scholar] [CrossRef]
- Qiu, Y.; Xu, Y.; Li, Q.; Wang, J.; Wang, Q.; Liu, B. Efficiency enhancement of a solar trough collector by combining solar and hot mirrors. Appl. Energy 2021, 299, 117290. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, M.; Zhao, Y.; Liu, J.; Yan, J. Dynamic simulation and performance analysis of a parabolic trough concentrated solar power plant using molten salt during the start-up process. Renew. Energy 2021, 179, 1458–1471. [Google Scholar] [CrossRef]
- Camacho, E.F.; Rubio, F.R.; Berenguel, M.; Valenzuela, L. A survey on control schemes for distributed solar collector fields. Part I: Modeling and basic control approaches. Sol. Energy 2007, 81, 1240–1251. [Google Scholar] [CrossRef]
- Camacho, E.F.; Rubio, F.R.; Berenguel, M.; Valenzuela, L. A survey on control schemes for distributed solar collector fields. Part II: Advanced control approaches. Sol. Energy 2007, 81, 1252–1272. [Google Scholar] [CrossRef]
- Behera, A.R.; Mallick, R.K.; Agrawal, R.; Nayak, P.; Sinha, S. Performance Analysis of Fuzzy-PID Controller in Nuclear, dish-Stirling Solar Thermal and Reheat Thermal Energy Integrated Deregulated Power System. In Proceedings of the 2022 International Conference on Intelligent Controller and Computing for Smart Power (ICICCSP), Hyderabad, India, 21–23 July 2022; p. 6. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Yu, H.; He, Y.-L. A feedforward-feedback hybrid control strategy towards ordered utilization of concentrating solar energy. Renew. Energy 2020, 154, 305–315. [Google Scholar] [CrossRef]
- Mokhtar, M.; Zahler, C.; Stieglitz, R. Control of Concentrated Solar Direct Steam Generation Collectors for Process Heat Applications. J. Sol. Energy Eng. 2022, 144, 011005. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; He, Y.-L. Flexible and efficient feedforward control of concentrating solar collectors. Appl. Therm. Eng. 2020, 171, 115053. [Google Scholar] [CrossRef]
- Zayed, M.E.; Zhao, J.; Li, W.; Sadek, S.; Elsheikh, A.H. Chapter three—Applications of artificial neural networks in concentrating solar power systems. In Artificial Neural Networks for Renewable Energy Systems and Real-World Applications; Elsheikh, A.H., Abd Elaziz, M.E., Eds.; Academic Press: Cambridge, MA, USA, 2022; pp. 45–67. [Google Scholar]
- Moukhtar, I.; Elbaset, A.A.; El Dein, A.Z.; Qudaih, Y.; Blagin, E.; Uglanov, D.; Mitani, Y. A Developed Concentrated Solar Power Model Using Artificial Neural Network Technique. In Proceedings of the 9th International Middle East Power Systems Conference (MEPCON), Nasr City, Egypt, 19–21 December 2017; pp. 1346–1351. [Google Scholar]
- Kalogirou, S.A. Artificial neural networks in renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Vaferi, B.; Samimi, F.; Pakgohar, E.; Mowla, D. Artificial neural network approach for prediction of thermal behavior of nanofluids flowing through circular tubes. Powder Technol. 2014, 267, 1–10. [Google Scholar] [CrossRef]
- Ebrahimi-Moghadam, A.; Mohseni-Gharyehsafa, B.; Farzaneh-Gord, M. Using artificial neural network and quadratic algorithm for minimizing entropy generation of Al2O3-EG/W nanofluid flow inside parabolic trough solar collector. Renew. Energy 2018, 129, 473–485. [Google Scholar] [CrossRef]
- May Tzuc, O.; Bassam, A.; Escalante Soberanis, M.; Venegas-Reyes, E.; Jaramillo, O.; Ricalde, L.J.; Ordoñez, E.E.; El Hamzaoui, Y. Modeling and optimization of a solar parabolic trough concentrator system using inverse artificial neural network. J. Renew. Sustain. Energy 2017, 9, 013701. [Google Scholar]
- Ajbar, W.; Parrales, A.; Cruz-Jacobo, U.; Conde-Gutiérrez, R.A.; Bassam, A.; Jaramillo, O.A.; Hernández, J.A. The multivariable inverse artificial neural network combined with GA and PSO to improve the performance of solar parabolic trough collector. Appl. Therm. Eng. 2021, 189, 116651. [Google Scholar] [CrossRef]
- Cervantes-Bobadilla, M.; Hernández-Pérez, J.; Juárez-Romero, D.; Bassam, A.; García-Morales, J.; Huicochea, A.; Jaramillo, O. Control scheme formulation for a parabolic trough collector using inverse artificial neural networks and particle swarm optimization. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 176. [Google Scholar] [CrossRef]
- Qiu, Y.; Li, M.-J.; He, Y.-L.; Tao, W.-Q. Thermal performance analysis of a parabolic trough solar collector using supercritical CO2 as heat transfer fluid under non-uniform solar flux. Appl. Therm. Eng. 2017, 115, 1255–1265. [Google Scholar] [CrossRef]
- Serrano-Lopez, R.; Fradera, J.; Cuesta-Lopez, S. Molten salts database for energy applications. Chem. Eng. Process. 2013, 73, 87–102. [Google Scholar] [CrossRef]
- Cruz, J.B.; Muñoz, L.J.Y.; Bencomo, S.D.; Moya, E.Z. Modeling and Simulation of Two-Phase Flow Evaporators for Parabolic-Trough Solar Thermal Power Plants. 2013. Available online: http://documenta.ciemat.es/handle/123456789/195 (accessed on 8 March 2025).
- Kalogirou, S.A. A detailed thermal model of a parabolic trough collector receiver. Energy 2012, 48, 298–306. [Google Scholar]
- Feldhoff, J.F. Analysis of Once-Through Boiler Concepts in Parabolic Troughs. RWTH Aachen 2015. Available online: http://documenta.ciemat.es/handle/123456789/195 (accessed on 8 March 2025).
- Li, L.; Sun, J.; Li, Y. Prospective fully-coupled multi-level analytical methodology for concentrated solar power plants: General modelling. Appl. Therm. Eng. 2017, 118, 171–187. [Google Scholar] [CrossRef]
- Theodoridis, S. Neural Networks and Deep Learning. 2016. [Google Scholar]
- Available online: https://energyplus.net/weather (accessed on 1 December 2022).
- Giostri, A. Transient effects in linear concentrating solar thermal power plant. Bibl. E Arch. 2014. Available online: https://hdl.handle.net/10589/89590 (accessed on 8 March 2025).
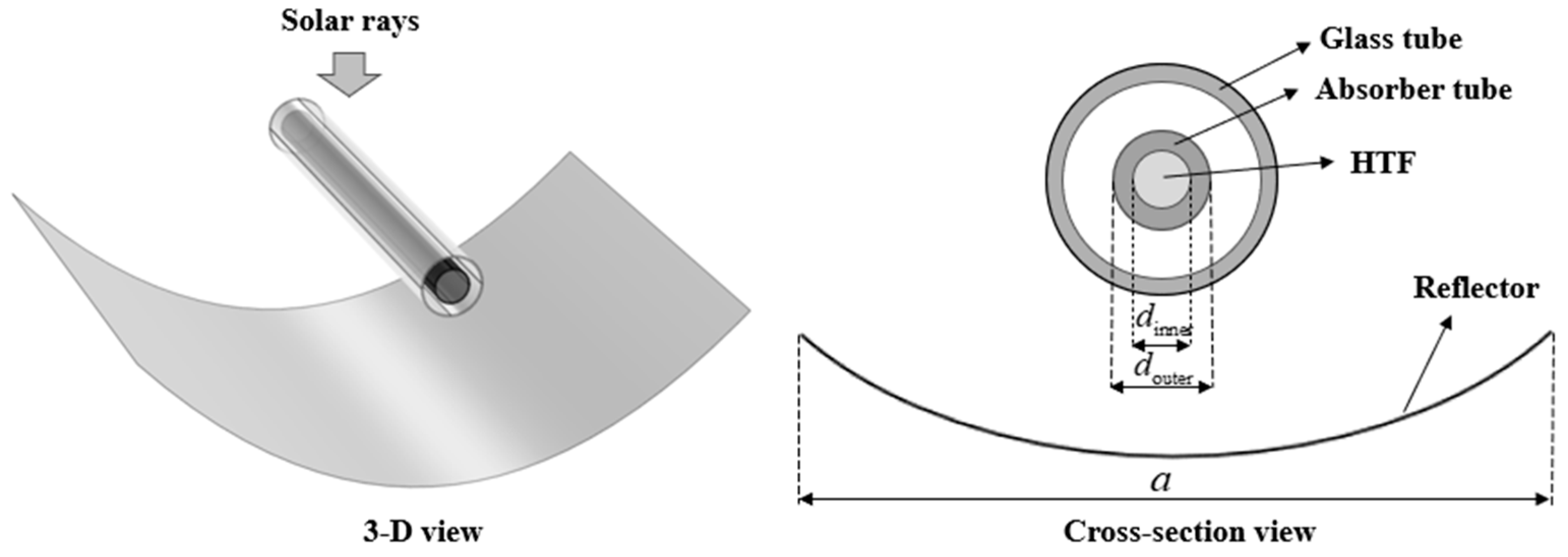
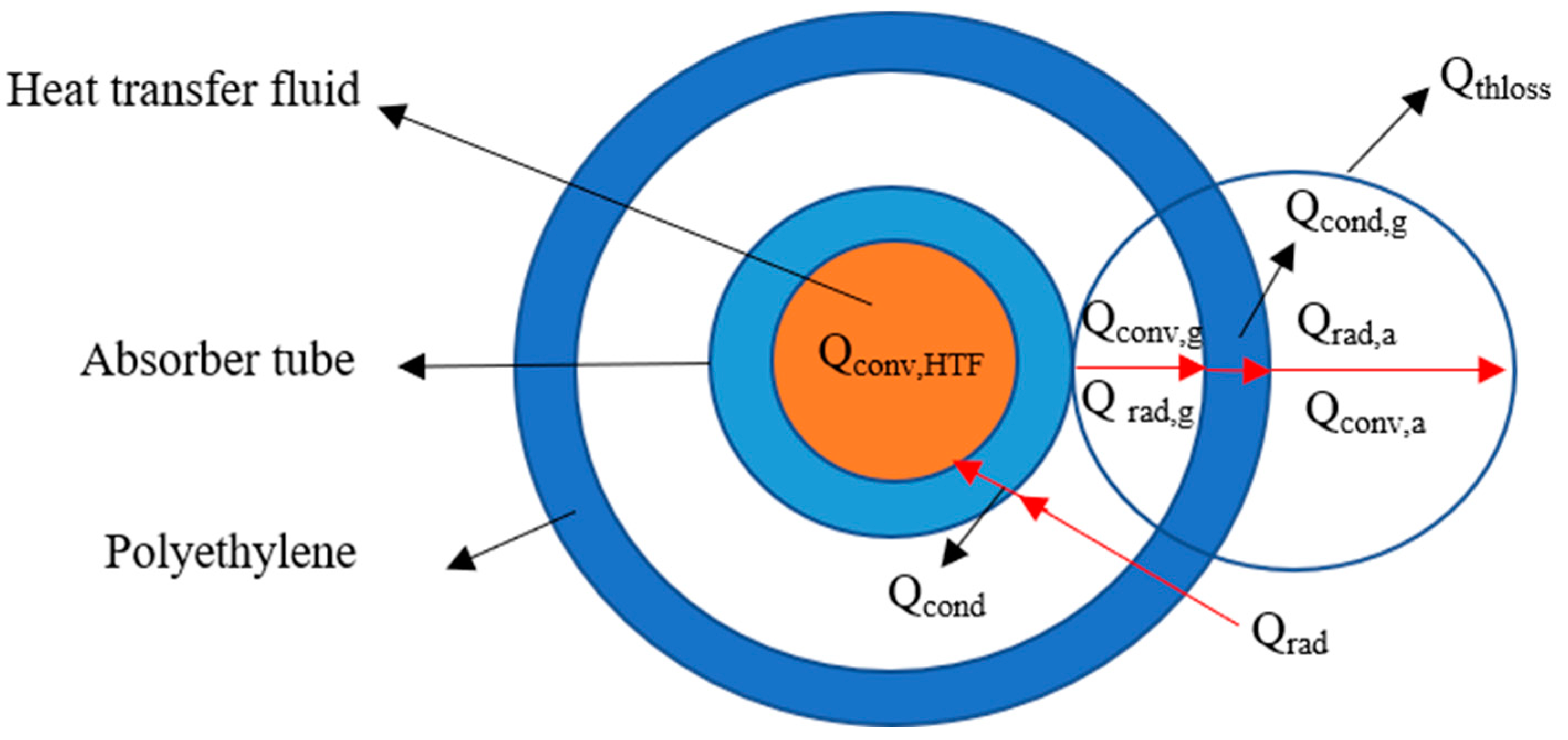

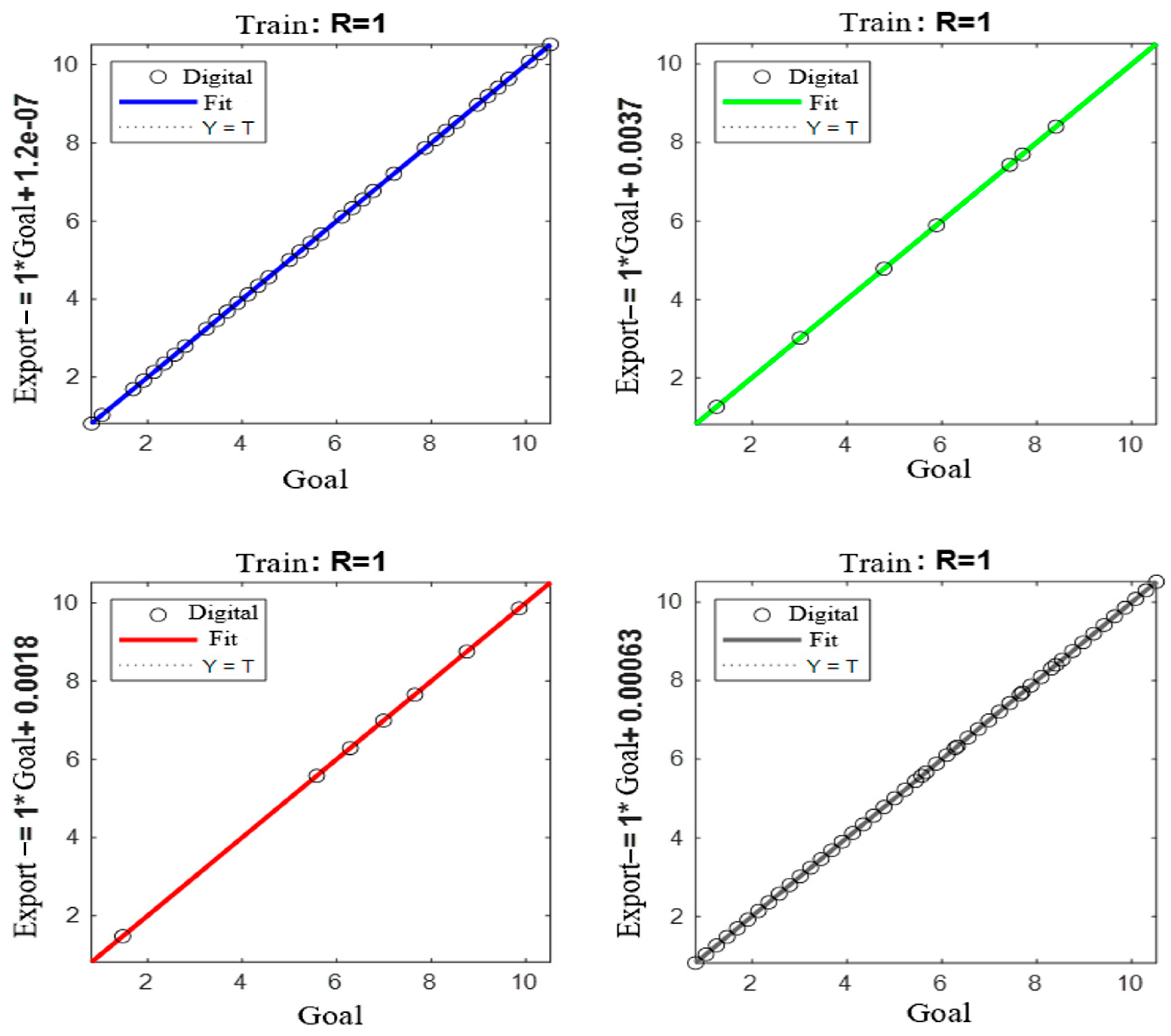


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Collector mirror width | 5.76 m | Glass tube emissivity | 0.86 |
| Focal length | 1.71 m | Absorber tube thermal conductivity | 38 W m−1 K−1 |
| Absorber tube inner diameter | 0.050 m | Glass tube thermal conductivity | 1.2 W m−1 K−1 |
| Absorber tube outer diameter | 0.070 m | Glass tube density | 2230 kg m−3 |
| Glass tube inner diameter | 0.108 m | Absorber tube relative roughness | 2.73 × 10−4 |
| Glass tube outer diameter | 0.115 m | Absorber tube density | 7763 kg m−3 |
| Parameter | Unit | Value |
|---|---|---|
| Density | kg m−3 | |
| Specific heat capacity | kJ kg−1 K−1 | |
| Thermal conductivity | W m−1 K−1 | |
| Dynamic viscosity | Pa·s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, B.; Zhang, Q.; Li, L.; Gao, F.; Wang, K.; Yang, J. Artificial Neural Network-Based Feedforward-Feedback Control for Parabolic Trough Concentrated Solar Field. Sustainability 2025, 17, 3334. https://doi.org/10.3390/su17083334
An B, Zhang Q, Li L, Gao F, Wang K, Yang J. Artificial Neural Network-Based Feedforward-Feedback Control for Parabolic Trough Concentrated Solar Field. Sustainability. 2025; 17(8):3334. https://doi.org/10.3390/su17083334
Chicago/Turabian StyleAn, Bo, Qin Zhang, Lu Li, Fan Gao, Ke Wang, and Jiaqi Yang. 2025. "Artificial Neural Network-Based Feedforward-Feedback Control for Parabolic Trough Concentrated Solar Field" Sustainability 17, no. 8: 3334. https://doi.org/10.3390/su17083334
APA StyleAn, B., Zhang, Q., Li, L., Gao, F., Wang, K., & Yang, J. (2025). Artificial Neural Network-Based Feedforward-Feedback Control for Parabolic Trough Concentrated Solar Field. Sustainability, 17(8), 3334. https://doi.org/10.3390/su17083334






