Review of Experimental Methods and Numerical Models for Hydraulic Studies in Constructed Wetlands
Abstract
1. Introduction
- (1)
- systematically summarize current hydraulic evaluation methods used in CWs;
- (2)
- compare modelling approaches in terms of their structure, assumptions, and reliability;
- (3)
- clarify the relationship between hydraulic performance and pollutant removal efficiency;
- (4)
- identify research gaps and propose future directions for integrating hydraulic and treatment models to enhance CW sustainability.
2. Experimental Methodology for Hydraulic Studies in CWs
2.1. The Methodology of Tracer Studies
2.2. Selection of Tracer
2.2.1. Sodium Chloride
2.2.2. Fluorescent Dye
2.2.3. Bromide
2.2.4. Alternative Tracer Options
2.2.5. Practical Considerations and Uncertainties in Tracer Application
2.3. Index for Hydraulic Performance Assessment in CWs
2.4. Water Quality Responses of CWs to Changing Hydrological Conditions
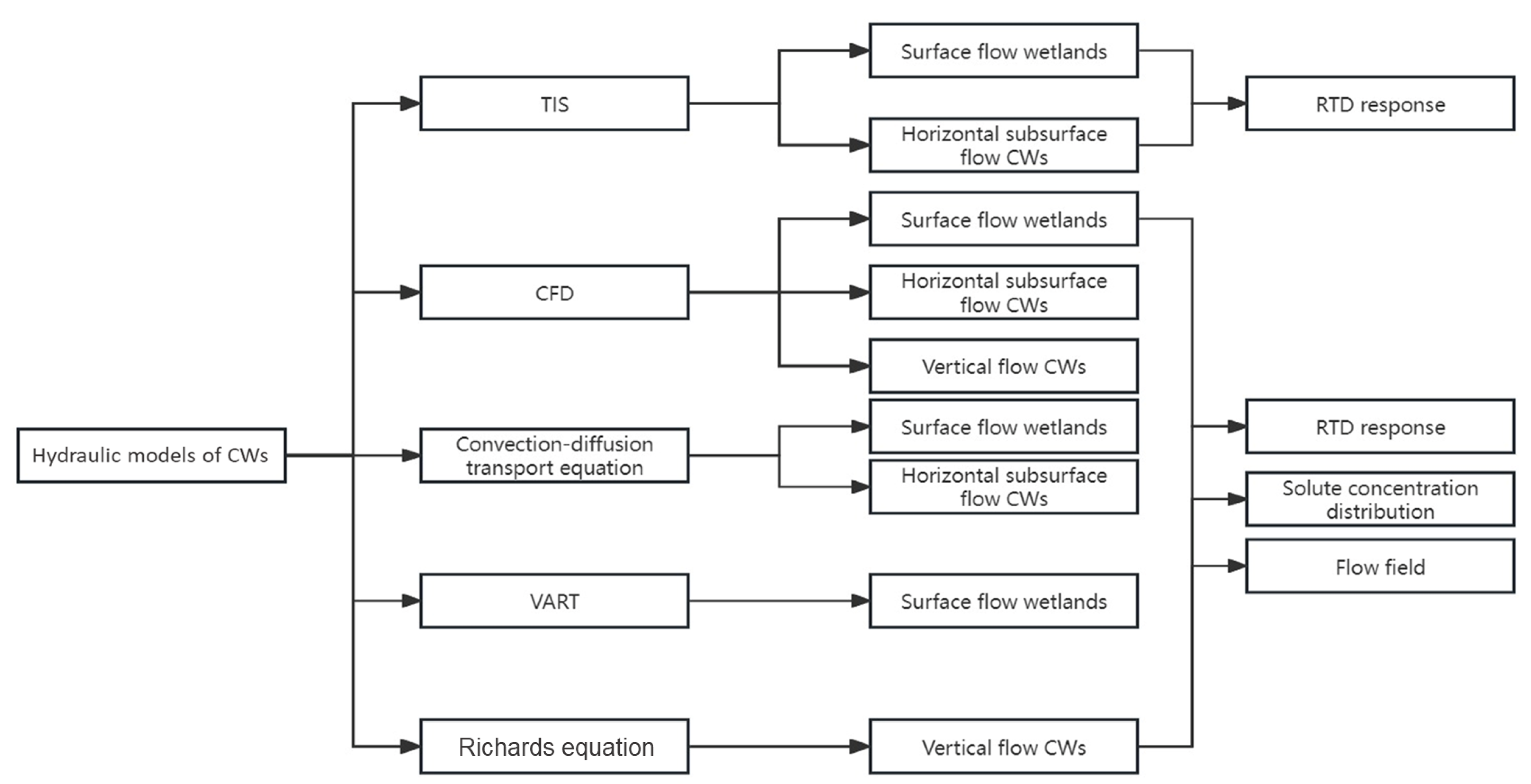
3. Numerical Models for Hydraulic Studies in CWs
3.1. Tank-in-Series Model
3.2. Computational Fluid Dynamics (CFD) Modelling
3.3. The Richards Equation
3.4. Convection–Diffusion Equation
3.5. Variable Residence Time Model (VART)
4. Discussion
- (a)
- Integration with biochemical reaction kinetic models to simulate pollutant degradation under realistic flow conditions;
- (b)
- Quantitative analysis of the relationship between hydraulic efficiency and pollutant removal efficiency for specific target parameters;
- (c)
- Development of comprehensive, multi-process models capable of simulating the coupled hydraulic–biochemical behaviour of CWs;
- (d)
- Adoption of machine learning (ML) and AI techniques (e.g., neural networks, genetic algorithms, and surrogate modelling) to improve predictive accuracy, automate parameter calibration, and identify key design variables influencing treatment performance under varying hydraulic conditions.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stottmeister, U.; Wiessner, A.; Kuschk, P.; Kappelmeyer, U.; Kastner, M.; Bederski, O.; Muller, R.A.; Moormann, H. Effects of plants and microorganisms in constructed wetlands for wastewater treatment. Biotechnol. Adv. 2003, 22, 93–117. [Google Scholar] [PubMed]
- Laurent, J.; Bois, P.; Nuel, M.; Wanko, A. Systemic models of full-scale Surface Flow Treatment Wetlands: Determination by application of fluorescent tracers. Chem. Eng. J. 2015, 264, 389–398. [Google Scholar]
- Birkigt, J.; Stumpp, C.; Maloszewski, P.; Nijenhuis, I. Evaluation of the hydrological flow paths in a gravel bed filter modeling a horizontal subsurface flow wetland by using a multi-tracer experiment. Sci. Total Environ. 2018, 621, 265–272. [Google Scholar] [PubMed]
- Stephenson, R.; Sheridan, C.; Kappelmeyer, U. A curve-shift technique for the use of non-conservative organic tracers in constructed wetlands. Sci. Total Environ. 2021, 752, 141818. [Google Scholar]
- Sabokrouhiyeh, N.; Bottacin-Busolin, A.; Savickis, J.; Nepf, H.; Marion, A. A numerical study of the effect of wetland shape and inlet-outlet configuration on wetland performance. Ecol. Eng. 2017, 105, 170–179. [Google Scholar]
- Wahl, M.D.; Brown, L.C.; Soboyejo, A.O.; Dong, B. Quantifying the hydraulic performance of treatment wetlands using reliability functions. Ecol. Eng. 2012, 47, 120–125. [Google Scholar]
- Persson, J.; Somes, N.L.G.; Wong, T.H.F. Hydraulics efficiency of constructed wetlands and ponds. Water Sci. Technol. 1999, 40, 291–300. [Google Scholar]
- Yang, M.; Lu, M.; Bian, H.; Sheng, L.; He, C. Effects of clogging on hydraulic behavior in a vertical-flow constructed wetland system: A modelling approach. Ecol. Eng. 2017, 109, 41–47. [Google Scholar] [CrossRef]
- Hua, G.; Kong, J.; Ji, Y.; Li, M. Influence of clogging and resting processes on flow patterns in vertical flow constructed wetlands. Sci. Total Environ. 2018, 621, 1142–1150. [Google Scholar]
- Wang, Y.; Song, X.; Liao, W.; Niu, R.; Wang, W.; Ding, Y.; Wang, Y.; Yan, D. Impacts of inlet–outlet configuration, flow rate and filter size on hydraulic behavior of quasi-2-dimensional horizontal constructed wetland: NaCl and dye tracer test. Ecol. Eng. 2014, 69, 177–185. [Google Scholar]
- Sun, Y.; Wang, Y.; Cao, X.; Song, X. Hydraulic performance evaluation of a quasi-two dimensional constructed wetland microcosm using tracer tests and Visual MODFLOW simulation. J. Contam. Hydrol. 2019, 226, 103537. [Google Scholar] [PubMed]
- Guo, C.; Cui, Y.; Dong, B.; Liu, F. Tracer study of the hydraulic performance of constructed wetlands planted with three different aquatic plant species. Ecol. Eng. 2017, 102, 433–442. [Google Scholar]
- Liu, H.; Hu, Z.; Zhang, J.; Ji, M.; Zhuang, L.; Nie, L.; Liu, Z. Effects of solids accumulation and plant root on water flow characteristics in horizontal subsurface flow constructed wetland. Ecol. Eng. 2018, 120, 481–486. [Google Scholar]
- Dittrich, E.; Klincsik, M.; Somfai, D.; Dolgos-Kovacs, A.; Kiss, T.; Szekeres, A. Application of divided convective-dispersive transport model to simulate variability of conservative transport processes inside a planted horizontal subsurface flow constructed wetland. Environ. Sci. Pollut. Res. Int. 2021, 28, 15966–15994. [Google Scholar]
- Bonner, R.; Aylward, L.; Harley, C.; Kappelmeyer, U.; Sheridan, C.M. Heat as a hydraulic tracer for horizontal subsurface flow constructed wetlands. J. Water Process. Eng. 2017, 16, 183–192. [Google Scholar]
- Bustillo-Lecompte, C.F.; Mehrvar, M.; Quiñones-Bolaños, E.; Castro-Faccetti, C.F. Modeling organic matter and nitrogen removal from domestic wastewater in a pilot-scale vertical subsurface flow constructed wetland. J. Environ. Sci. Health 2016, 51, 414–424. [Google Scholar]
- Deng, Z.; Sebro, D.Y.; Aboukila, A.F.; Bengtsson, L. Variable residence time-based model for BOD removal in free-water surface wetlands. Ecol. Eng. 2016, 97, 334–343. [Google Scholar]
- Martinez, C.J.; Wise, W.R. Analysis of constructed treatment wetland hydraulics with the transient storage model OTIS. Ecol. Eng. 2003, 20, 211–222. [Google Scholar]
- Holland, J.F.; Martin, J.F.; Granata, T.; Bouchard, V.; Quigley, M.; Brown, L. Effects of wetland depth and flow rate on residence time distribution characteristics. Ecol. Eng. 2004, 23, 189–203. [Google Scholar]
- Bodin, H.; Mietto, A.; Ehde, P.M.; Persson, J.; Weisner, S.E.B. Tracer behaviour and analysis of hydraulics in experimental free water surface wetlands. Ecol. Eng. 2012, 49, 201–211. [Google Scholar]
- Sheridan, C.; Hildebrand, D.; Glasser, D. Turning wine (waste) into water: Toward technological advances in the use of constructed wetlands for winery effluent treatment. AIChE J. 2013, 60, 420–431. [Google Scholar]
- Keefe, S.H.; Barber, L.B.; Runkel, R.L.; Ryan, J.N.; McKnight, D.M.; Wass, R.D. Conservative and reactive solute transport in constructed wetlands. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Cucco, A.; Umgiesser, G. Modeling the Venice Lagoon residence time. Ecol. Model. 2006, 193, 34–51. [Google Scholar]
- Aiello, R.; Bagarello, V.; Barbagallo, S.; Iovino, M.; Marzo, A.; Toscano, A. Evaluation of clogging in full-scale subsurface flow constructed wetlands. Ecol. Eng. 2016, 95, 505–513. [Google Scholar]
- Marzo, A.; Ventura, D.; Cirelli, G.L.; Aiello, R.; Vanella, D.; Rapisarda, R.; Barbagallo, S.; Consoli, S. Hydraulic reliability of a horizontal wetland for wastewater treatment in Sicily. Sci. Total Environ. 2018, 636, 94–106. [Google Scholar]
- Wang, R.; Xu, L.; Xu, X.; Xu, Z.; Zhang, X.; Cong, X.; Tong, K. Hydraulic characteristics of small-scale constructed wetland based on residence time distribution. Environ. Technol. 2023, 44, 1061–1070. [Google Scholar] [PubMed]
- Lavrnic, S.; Alagna, V.; Iovino, M.; Anconelli, S.; Solimando, D.; Toscano, A. Hydrological and hydraulic behaviour of a surface flow constructed wetland treating agricultural drainage water in northern Italy. Sci. Total Environ. 2020, 702, 134795. [Google Scholar]
- Beebe, D.A.; Castle, J.W.; Molz, F.J.; Rodgers, J.H. Effects of evapotranspiration on treatment performance in constructed wetlands: Experimental studies and modeling. Ecol. Eng. 2014, 71, 394–400. [Google Scholar]
- Kusin, F.M.; Jarvis, A.P.; Gandy, C.J. Hydraulic Performance and Iron Removal in Wetlands and Lagoons Treating Ferruginous Coal Mine Waters. Wetlands 2014, 34, 555–564. [Google Scholar]
- Liu, J.J.; Dong, B.; Guo, C.Q.; Liu, F.P.; Brown, L.; Li, Q. Variations of effective volume and removal rate under different water levels of constructed wetland. Ecol. Eng. 2016, 95, 652–664. [Google Scholar]
- Wei, J.; Cotterill, S.; Keenahan, J. Optimizing the hydraulic performance of a baffled horizontal subsurface flow constructed wetland through computational fluid dynamics modelling. J. Environ. Manag. 2024, 351, 119776. [Google Scholar] [CrossRef] [PubMed]
- Ioannidou, V.G.; Pearson, J.M. The effects of flow rate variation and vegetation ageing on the longitudinal mixing and residence time distribution (RTD) in a full-scale constructed wetland. Ecol. Eng. 2019, 138, 248–263. [Google Scholar] [CrossRef]
- Nuel, M.; Laurent, J.; Bois, P.; Heintz, D.; Mosé, R.; Wanko, A. Seasonal and ageing effects on SFTW hydrodynamics study by full-scale tracer experiments and dynamic time warping algorithms. Chem. Eng. J. 2017, 321, 86–96. [Google Scholar] [CrossRef]
- Pugliese, L.; Kusk, M.; Iversen, B.V.; Kjaergaard, C. Internal hydraulics and wind effect in a surface flow constructed wetland receiving agricultural drainage water. Ecol. Eng. 2020, 144, 105661. [Google Scholar] [CrossRef]
- Pálfy, T.G.; Gourdon, R.; Meyer, D.; Troesch, S.; Olivier, L.; Molle, P. Filling hydraulics and nitrogen dynamics in constructed wetlands treating combined sewer overflows. Ecol. Eng. 2017, 101, 137–144. [Google Scholar] [CrossRef]
- Aylward, L.; Bonner, R.; Sheridan, C.; Kappelmeyer, U. Hydraulic study of a non-steady horizontal sub-surface flow constructed wetland during start-up. Sci. Total Environ. 2019, 646, 880–892. [Google Scholar] [CrossRef]
- Ávila, C.; García, J.; Garfí, M. Influence of hydraulic loading rate, simulated storm events and seasonality on the treatment performance of an experimental three-stage hybrid constructed wetland system. Ecol. Eng. 2016, 87, 324–332. [Google Scholar] [CrossRef]
- Latrach, L.; Ouazzani, N.; Hejjaj, A.; Zouhir, F.; Mahi, M.; Masunaga, T.; Mandi, L. Optimization of hydraulic efficiency and wastewater treatment performances using a new design of vertical flow Multi-Soil-Layering (MSL) technology. Ecol. Eng. 2018, 117, 140–152. [Google Scholar] [CrossRef]
- Munavalli, G.R.; Sonavane, P.G.; Koli, M.M.; Dhamangaokar, B.S. Field-scale decentralized domestic wastewater treatment system: Effect of dynamic loading conditions on the removal of organic carbon and nitrogen. J. Environ. Manag. 2022, 302 Pt A, 114014. [Google Scholar] [CrossRef]
- Stephenson, R.; Sheridan, C. Review of experimental procedures and modelling techniques for flow behaviour and their relation to residence time in constructed wetlands. J. Water Process. Eng. 2021, 41, 102044. [Google Scholar] [CrossRef]
- Rodrigues, A.E. Residence time distribution (RTD) revisited. Chem. Eng. Sci. 2021, 230, 116188. [Google Scholar] [CrossRef] [PubMed]
- Persson, J. The hydraulic performance of ponds of various layouts. Urban Water 2000, 2, 243–250. [Google Scholar] [CrossRef]
- Vonortas, A.; Hipolito, A.; Rolland, M.; Boyer, C.; Papayannakos, N. Fluid Flow Characteristics of String Reactors Packed with Spherical Particles. Chem. Eng. Technol. 2011, 34, 208–216. [Google Scholar] [CrossRef]
- Huang, Y.; Seinfeld, J.H. A note on flow behavior in axially-dispersed plug flow reactors with step input of tracer. Atmos. Environ. X 2019, 1, 100006. [Google Scholar] [CrossRef]
- Flury, M.; Wai, N.N. Dyes as tracers for vadose zone hydrology. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Lin, A.Y.-C.; Debroux, J.-F.; Cunningham, J.A.; Reinhard, M. Comparison of rhodamine WT and bromide in the determination of hydraulic characteristics of constructed wetlands. Ecol. Eng. 2003, 20, 75–88. [Google Scholar] [CrossRef]
- Rana, S.M.M.; Scott, D.T.; Hester, E.T. Effects of in-stream structures and channel flow rate variation on transient storage. J. Hydrol. 2017, 548, 157–169. [Google Scholar] [CrossRef]
- Živančev, N.; Vojt, P.; Mitrinović, D.; Radišić, M.; Kovačević, S. Tracer test and behavior of selected pharmaceuticals. Water Supply 2017, 17, 1043–1052. [Google Scholar]
- Guo, C.; Cui, Y.; Shi, Y.; Luo, Y.; Liu, F.; Wan, D.; Ma, Z. Improved test to determine design parameters for optimization of free surface flow constructed wetlands. Bioresour. Technol. 2019, 280, 199–212. [Google Scholar] [CrossRef]
- Gerke, K.M.; Sidle, R.C.; Mallants, D. Criteria for selecting fluorescent dye tracers for soil hydrological applications using Uranine as an example. J. Hydrol. Hydromech. 2013, 61, 313–325. [Google Scholar] [CrossRef]
- Decezaro, S.T.; Wolff, D.B.; Pelissari, C.; Ramirez, R.; Formentini, T.A.; Goerck, J.; Rodrigues, L.F.; Sezerino, P.H. Influence of hydraulic loading rate and recirculation on oxygen transfer in a vertical flow constructed wetland. Sci. Total Environ. 2019, 668, 988–995. [Google Scholar] [PubMed]
- Angeloudis, A.; Stoesser, T.; Gualtieri, C.; Falconer, R.A. Contact Tank Design Impact on Process Performance. Environ. Model. Assess. 2016, 21, 563–576. [Google Scholar]
- Liu, J.; Dong, B.; Zhou, W.; Qian, Z. Optimal selection of hydraulic indexes with classical test theory to compare hydraulic performance of constructed wetlands. Ecol. Eng. 2020, 143, 105687. [Google Scholar]
- Thackston, E.L.; Schroeder, P.R.; Shields, F.D., Jr. Residence time distributions of shallow basins. J. Environ. Eng. 1987, 113, 1319–1332. [Google Scholar]
- Teixeira, E.C.; Siqueira, R.d.N. Performance Assessment of Hydraulic Efficiency Indexes. J. Environ. Eng. 2008, 134, 851–859. [Google Scholar]
- Wahl, M.D.; Brown, L.C.; Soboyejo, A.O.; Martin, J.; Dong, B. Quantifying the hydraulic performance of treatment wetlands using the moment index. Ecol. Eng. 2010, 36, 1691–1699. [Google Scholar]
- Konyha, K.D.; Shaw, D.T.; Weiler, K.W. Hydrologic design of a wetland: Advantages of continuous modeling. Ecol. Eng. 1995, 4, 99–116. [Google Scholar]
- Cakir, R.; Gidirislioglu, A.; Cebi, U. A study on the effects of different hydraulic loading rates (HLR) on pollutant removal efficiency of subsurface horizontal-flow constructed wetlands used for treatment of domestic wastewaters. J. Environ. Manag. 2015, 164, 121–128. [Google Scholar]
- Tee, H.C.; Lim, P.E.; Seng, C.E.; Nawi, M.A. Newly developed baffled subsurface-flow constructed wetland for the enhancement of nitrogen removal. Bioresour. Technol. 2012, 104, 235–242. [Google Scholar]
- Jiang, L.; Chui, T.F.M. A review of the application of constructed wetlands (CWs) and their hydraulic, water quality and biological responses to changing hydrological conditions. Ecol. Eng. 2022, 174, 106459. [Google Scholar]
- Xing, C.; Xu, X.; Xu, Z.; Wang, R.; Xu, L. Study on the Decontamination Effect of Biochar-Constructed Wetland under Different Hydraulic Conditions. Water 2021, 13, 893. [Google Scholar] [CrossRef]
- Wei, J.; Cotterill, S.; Keenahan, J. Investigating the treatment efficiency of a baffled horizontal subsurface flow constructed wetland with diverse hydraulic efficiency. J. Environ. Manag. 2025, 379, 124864. [Google Scholar]
- Małoszewski, P.; Wachniew, P.; Czupryński, P. Study of hydraulic parameters in heterogeneous gravel beds: Constructed wetland in Nowa Słupia (Poland). J. Hydrol. 2006, 331, 630–642. [Google Scholar]
- Seeger, E.M.; Maier, U.; Grathwohl, P.; Kuschk, P.; Kaestner, M. Performance evaluation of different horizontal subsurface flow wetland types by characterization of flow behavior, mass removal and depth-dependent contaminant load. Water Res. 2013, 47, 769–780. [Google Scholar]
- Zhang, B.; Cui, Y.; Shu, Y.; Liao, B.; Yang, M.; Tang, C. Comparative analysis and selection criteria for residence time distribution models in free water surface constructed wetlands. J. Hydrol. 2024, 629, 130620. [Google Scholar]
- Manenti, S.; Todeschini, S.; Collivignarelli, M.C. Integrated RTD − CFD Hydrodynamic Analysis for Performance Assessment of Activated Sludge Reactors. Environ. Process. 2018, 5, 23–42. [Google Scholar]
- Alvarado, A.; Vedantam, S.; Goethals, P.; Nopens, I. A compartmental model to describe hydraulics in a full-scale waste stabilization pond. Water Res. 2012, 46, 521–530. [Google Scholar]
- Karpinska, A.M.; Bridgeman, J. CFD-aided modelling of activated sludge systems—A critical review. Water Res. 2016, 88, 861–879. [Google Scholar]
- Rengers, E.E.; Silva, J.B.d.; Paulo, P.L.; Janzen, J.G. Hydraulic performance of a modified constructed wetland system through a CFD-based approach. J. Hydro-Environ. Res. 2016, 12, 91–104. [Google Scholar]
- Fan, L.; Hai, R.; Lu, Z. CFD study on hydraulic performance of subsurface flow constructed wetland: Effect of distribution and catchment area. Korean J. Chem. Eng. 2010, 26, 1272–1278. [Google Scholar]
- Wang, R.; Xu, L.; Xu, X.; Xu, Z.; Cong, X. Simulation and optimization of hydraulic performance of small baffled subsurface flow constructed wetland. Water Sci. Technol. 2021, 84, 632–643. [Google Scholar]
- Savickis, J.; Bottacin-Busolin, A.; Zaramella, M.; Sabokrouhiyeh, N.; Marion, A. Effect of a meandering channel on wetland performance. J. Hydrol. 2016, 535, 204–210. [Google Scholar]
- Giraldi, D.; de’Michieli Vitturi, M.; Zaramella, M.; Marion, A.; Iannelli, R. Hydrodynamics of vertical subsurface flow constructed wetlands: Tracer tests with rhodamine WT and numerical modelling. Ecol. Eng. 2009, 35, 265–273. [Google Scholar]
- Genuchten, M.T.v. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar]
- Günter Langergraber, J.Š. Modeling Variably Saturated Water Flow and Multicomponent Reactive Transport in Constructed Wetlands. Vadose Zone J. 2005, 4, 924–938. [Google Scholar]
- Samso, R.; Garcia, J.; Molle, P.; Forquet, N. Modelling bioclogging in variably saturated porous media and the interactions between surface/subsurface flows: Application to Constructed Wetlands. J. Environ. Manag. 2016, 165, 271–279. [Google Scholar]
- Langergraber, G. Applying Process-Based Models for Subsurface Flow Treatment Wetlands: Recent Developments and Challenges. Water 2016, 9, 5. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N.; Poultsidis, V.G.; Papaspyros, J.N.E.; Tsihrintzis, V.A. Simulation of hydrodynamics and nitrogen transformation processes in HSF constructed wetlands and porous media using the advection–dispersion-reaction equation with linear sink-source terms. Ecol. Eng. 2011, 37, 1407–1415. [Google Scholar]
- Abrantes, J.R.C.B.; Moruzzi, R.B.; de Lima, J.L.M.P.; Silveira, A.; Montenegro, A.A.A. Combining a thermal tracer with a transport model to estimate shallow flow velocities. Phys. Chem. Earth Parts A/B/C 2019, 109, 59–69. [Google Scholar]
- Deng, Z.Q.; Jung, H.S. Variable residence time–based model for solute transport in streams. Water Resour. Res. 2009, 45, W03415. [Google Scholar]
- Aboukila, A.F.; Elhawary, A. BOD5 dynamics in three vertical layers in free-water surface wetlands. Egypt. J. Aquat. Res. 2022, 48, 115–121. [Google Scholar]
- Wanko, A.; Tapia, G.; Mosé, R.; Gregoire, C. Adsorption distribution impact on preferential transport within horizontal flow constructed wetland (HFCW). Ecol. Model. 2009, 220, 3342–3352. [Google Scholar]
- Llorens, E.; Saaltink, M.W.; Poch, M.; Garcia, J. Bacterial transformation and biodegradation processes simulation in horizontal subsurface flow constructed wetlands using CWM1-RETRASO. Bioresour. Technol. 2011, 102, 928–936. [Google Scholar]
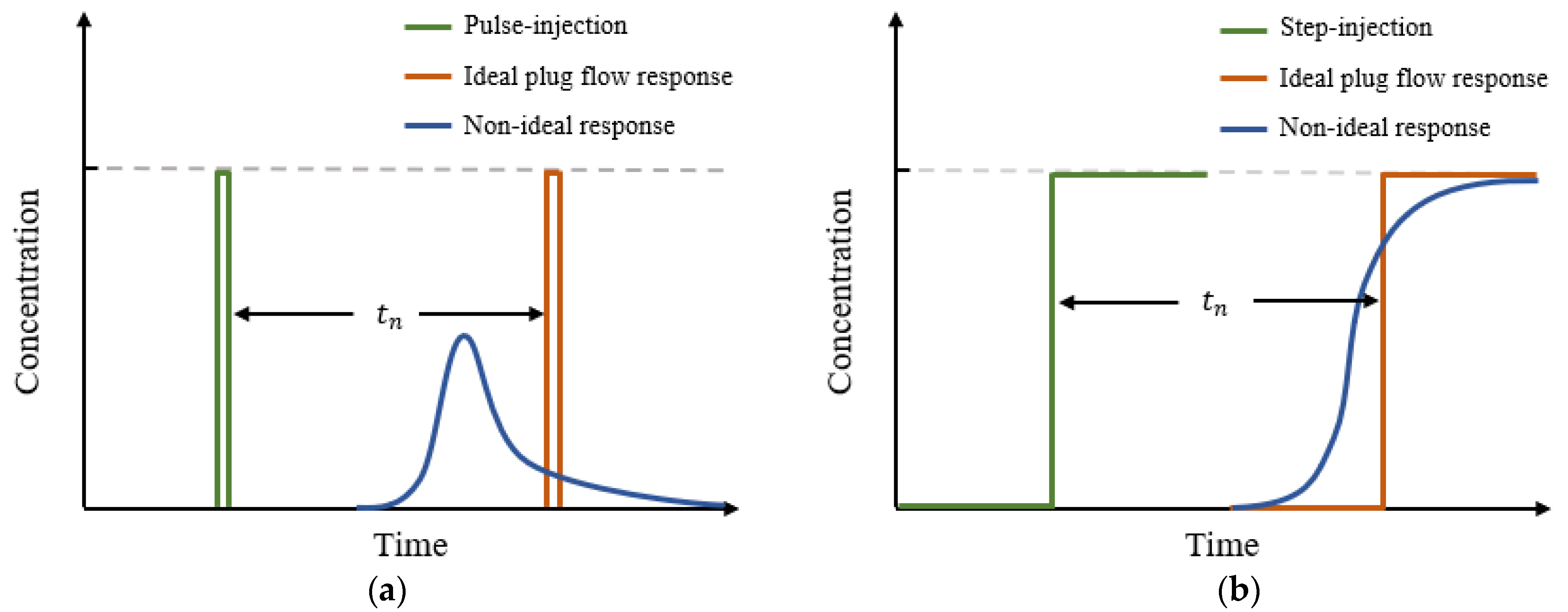
| No. | Injection Method | CW Type * | Tracer Material | Changing Hydraulic Conditions | Hydraulic Indicators | Reference |
|---|---|---|---|---|---|---|
| 1 | Pulse injection | VSFCW | Sodium chloride (NaCl) | Clogging (porosity) | [8] | |
| 2 | Pulse injection | HSFCW | NaCl | Clogging (porosity) | [24] | |
| 3 | Pulse injection | VSFCW | NaCl | Clogging effects | [9] | |
| 4 | Pulse injection | Hybrid-VSFCW | NaCl | Clogging effects and Hydraulic Loading Rate (HLR) | [25] | |
| 5 | Pulse injection | SFW, HSFCW (baffled), VSFCW | NaCl | Baffle and Flow direction | [26] | |
| 6 | Pulse injection | SFW | NaCl | [27] | ||
| 7 | Pulse injection | SFW | NaCl | Evapotranspiration effects, water depth | [28] | |
| 8 | Pulse injection | SFW | NaCl, Sodium bromide, and sodium-fluorescein | [29] | ||
| 9 | Pulse injection | Quasi-two-dimensional HSFCW | NaCl and Dye (Acid Red 315) | Filter size, inflow rate, and inlet–outlet configuration | S | [10] |
| 10 | Pulse injection | Quasi-two-dimensional HSFCW | NaCl and Dye (Acid Red 315) | Flow rate and inlet–outlet configuration | [11] | |
| 11 | Pulse injection | SFW | Rhodamine WT (RWT) | Water depth | , MDI | [30] |
| 12 | Pulse injection | Baffled HSFCW | RWT | Length and number of baffles | [31] | |
| 13 | Pulse injection | SFW | RWT | Flow rate, seasonal vegetation variation | [32] | |
| 14 | Pulse injection | SFW | RWT | Vegetation effects (Vegetation type and planting density) | [12] | |
| 15 | Pulse injection | SFW | Fluorescent dye (Sulforhodamine B) | Seasonal and ageing effects | [33] | |
| 16 | Pulse injection | HSFCW | Fluorescein sodium | Clogging effects, vegetation root | [13] | |
| 17 | Pulse injection | SFW | Uranine and sodium bromide | Wind effects | [34] | |
| 18 | Pulse injection | Combined sewer overflow CW | Uranine | [35] | ||
| 19 | Pulse injection | HSFCW | Uranine | Flow rate, climatic factors | [36] | |
| 20 | Pulse injection | Three SFWs | Uranine and sulforhodamine B | HRT, HLR | [2] | |
| 21 | Pulse injection | HSFCW | Deuterium oxide, Bromide, Uranine | Water depth | [3] | |
| 22 | Pulse injection | three-stage hybrid CW | Potassium bromide | HLR | [37] | |
| 23 | Pulse injection | VSFCW | Dicalcium chloride | Layer distribution | [38] | |
| 24 | Pulse injection | Hybrid-CW | Fluoride | HLR | [39] | |
| 25 | Pulse injection | HSFCW | Uranine, Benzoate | [4] | ||
| 26 | Step injection | HSFCW | Heat | [15] |
| Tracer Type | Advantages | Limitations | Typical Applications |
|---|---|---|---|
| Dye tracer (e.g., Rhodamine WT) | Easy to detect; cost-effective; low toxicity; widely available | Subject to photodegradation; adsorption to media may occur | Small- to medium-scale CWs |
| Salt tracer (e.g., NaCl) | Inexpensive; chemically stable; easy to measure via conductivity | Affected by background salinity; less suitable in saline environments | Field studies; systems with low background conductivity |
| Bromide (e.g., KBr) | Conservative tracer; minimal interaction with substrate or biota | Requires laboratory analysis (ion chromatography); more costly | Research-grade CW studies |
| Heat mapping (e.g., thermal tracer) | Non-invasive; visualizes temperature-based flow patterns | Low spatial resolution; affected by ambient temperature | Surface or shallow subsurface CWs |
| Model | Key Features | Advantages | Limitations | Computational Complexity |
|---|---|---|---|---|
| TIS | Series of CSTRs approximating RTD | Good fit for RTD; low data requirement | Lacks internal spatial detail | Low |
| CFD | Solves Navier–Stokes or Darcy–Forchheimer in discretized domain | High spatial resolution; visualizes flow field | High computational demand; needs validation | High |
| Convection–diffusion | Models transport using advection and dispersion equations | Captures key processes; analytical foundation | Assumes steady-state; limited for 3D, variable flows | Medium |
| The Richards equation | Governs unsaturated flow through porous media | Suitable for variably saturated zones | Complex parameters; computationally intensive | High |
| VART | Allows variable residence time in system compartments | Flexible representation of non-ideal flow | Limited availability; calibration challenging | Medium–High |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Keenahan, J.; Cotterill, S. Review of Experimental Methods and Numerical Models for Hydraulic Studies in Constructed Wetlands. Sustainability 2025, 17, 3303. https://doi.org/10.3390/su17083303
Wei J, Keenahan J, Cotterill S. Review of Experimental Methods and Numerical Models for Hydraulic Studies in Constructed Wetlands. Sustainability. 2025; 17(8):3303. https://doi.org/10.3390/su17083303
Chicago/Turabian StyleWei, Jiahao, Jennifer Keenahan, and Sarah Cotterill. 2025. "Review of Experimental Methods and Numerical Models for Hydraulic Studies in Constructed Wetlands" Sustainability 17, no. 8: 3303. https://doi.org/10.3390/su17083303
APA StyleWei, J., Keenahan, J., & Cotterill, S. (2025). Review of Experimental Methods and Numerical Models for Hydraulic Studies in Constructed Wetlands. Sustainability, 17(8), 3303. https://doi.org/10.3390/su17083303








