Abstract
This study analyzes factors influencing injury severity in motorcycle accidents involving non-helmeted riders using Bayesian spatiotemporal logistic models. Five models were developed, four of which incorporated different spatiotemporal configurations, including spatial, temporal, and spatiotemporal interaction error terms. The results indicate that the optimal model integrated Leroux CAR spatial priors, temporal random walks, and interaction terms, achieving 86.74% classification accuracy, with a 3% reduction in the DIC value; obtaining the lowest numerical fit demonstrating spatiotemporal interactions is critical for capturing complex risk patterns (e.g., rain amplifying nighttime collision severity). The results highlight rain (OR = 1.53), age ≥ 50 (OR = 1.90), and bi-directional roads (OR = 1.82) as critical risk factors. Based on these findings, several sustainable traffic safety strategies are proposed. Short-term measures include IoT-based dynamic speed control on high-risk roads and app-enforced helmet checks via ride-hailing platforms. Long-term strategies integrate age-specific behavioral training focusing on hazard perception and reaction time improvement, which reduced elderly fatalities by 18% in Japan’s “Silver Rider” program by directly modifying high-risk riding habits (non-helmets). These solutions, validated by global case studies, demonstrate that helmet use could mitigate over 60% of severe head injuries in these high-risk scenarios, promoting sustainable traffic governance through spatiotemporal risk targeting and helmet enforcement.
1. Introduction
Road traffic accidents are the eighth leading cause of death globally, with significant adverse impacts on public health systems and economies [1]. In response, the United Nations established Target 3.6 as part of the Sustainable Development Goals, aiming to reduce global road traffic fatalities by half by 2030. Motorcycle accidents, as a subset of road traffic accidents, typically result in more severe injuries and fatalities. Analyzing the factors influencing the severity of accidents is a crucial step in maintaining road safety and preventing accidents. Motorcycles, as key participants in road traffic, are characterized by high speed, instability, and a lack of protective devices [2]. Lack of helmet use significantly increases the risk of severe injuries or fatalities in motorcycle accidents. A study in Taiwan found that the incidence of head and brain injuries among motorcyclists not wearing helmets was ten times and nine times higher, respectively, compared to those wearing helmets [3]. Although helmet-wearing laws have been widely implemented worldwide, motorcycle accidents involving riders without helmets remain prevalent, causing numerous serious injuries and fatalities each year. Therefore, it is necessary and urgent not only to strengthen helmet promotion and enforcement but also to investigate the impact of various objective factors on the injury severity of helmetless motorcyclists. Based on these findings, targeted improvements should be proposed to maximize the safety of motorcycle riders who fail to wear helmets [4].
In urban road networks, roads are interconnected in complex ways, with adjacent roads and accident sites often sharing unobservable attributes related to traffic characteristics, the built environment, and weather conditions, which are expected to induce spatial correlations. Similarly, there may be time-dependent or time-varying unobservable factors, leading to time-related correlations in motorcycle crash data. In traffic collisions, both spatial and temporal clustering tendencies are commonly observed [5,6,7,8,9,10,11], referred to as spatiotemporal interactions. Theoretically, incorporating spatial and temporal dependencies, along with spatiotemporal interactions, improves model estimation and reduces errors. This study develops a series of spatiotemporal logistic regression models, progressively increasing the model complexity to analyze the injury severity of helmetless motorcyclists in accidents. Based on the model estimation results, the optimal spatiotemporal logistic regression model is identified, and improvement strategies are proposed.
The remainder of this paper is structured as follows: Section 2 provides a comprehensive review of previous studies; Section 3 introduces the details of the dataset; Section 4 describes the primary models and methods; Section 5 compares model performance metrics, presents the model estimation results, and provides a detailed analysis of the parameter estimates; finally, Section 6 concludes the study and suggests possible avenues for improvement. The technical roadmap of the article is shown in Figure 1.
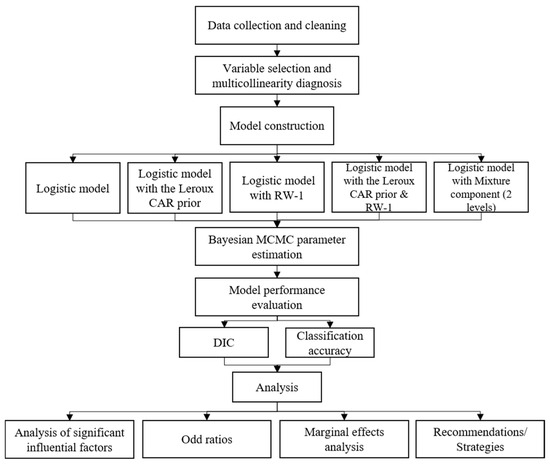
Figure 1.
Technical roadmap.
2. Literature Review
Numerous scholars have proposed effective research conclusions on the severity of motorcycle accidents. For example, Qin Yaqin et al. [12] compared the ordered logit model with the multinomial logit model, concluding that the latter is more suitable for predicting the influencing factors of motorcycle accident severity in a multi-class context. With the subject of study being helmetless riders, Muhammad Ijaz et al. [13] compared the differences in the influencing factors of injury severity between helmeted and non-helmeted riders in accidents, using a random parameter logit model that accounts for mean and variance heterogeneity. Wang et al. [14] explored the impact of gender differences among helmetless riders on accident injury severity, emphasizing the importance of gender-specific safety policies for male and female motorcycle riders. Igor Radun [15], who reported that driving on a slippery road improves performance, found that participants had smaller changes in lateral positioning and smaller and smoother steering wheel movements due to compensatory cautious driving. This surprising finding is also corroborated in our study.
Capturing spatial correlation enables models to more accurately detect spatial patterns in the data. This spatial pattern recognition is used to predict and explain complex spatial dynamics. By adjusting for spatial correlation, observations can benefit from neighboring values, thereby significantly improving model performance. Pan Yiyong et al. [16] applied a multi-scale geographically weighted regression model to demonstrate that the positive/negative impact of spatial location on motorcycle accident severity is related to spatial position.
The issue of unobserved common effects in neighboring time points is another important research topic related to time correlation. Current modeling methods often adopt incremental approaches, applying various time structures to describe time effects, such as linear or quadratic trends, to eliminate potential biases in parameter estimation [17], autoregressive correlations [18], and random walk structures [19]. Zeng et al. [20] developed three time-varying multivariate random parameter Tobit models. Based on the Deviance Information Criterion (DIC) and Bayesian R2 results, all time models found significant time effects, and incorporating time correlation significantly improved the goodness-of-fit of the multivariate random parameter Tobit regression.
Considering both spatial and temporal correlations is more beneficial for explaining latent features and optimizing the model. Meng et al. [21] developed a spatiotemporal logistic model to analyze the severity of passenger injuries in taxi-related accidents, where spatial correlation was modeled using an intrinsic CAR prior, but the model did not simultaneously consider spatial and non-structural effects, and the time effect was simply specified as linear. Cui et al. [22] propose a Sparse Spatiotemporal Dynamic Hypergraph Learning (SST-DHL) framework, which offers enhanced interpretability of results by elucidating complex spatiotemporal dependencies among various traffic accident instances. Li et al. [23] employed an integrated spatiotemporal analytical approach to investigate comprehensive statewide 20-year data on motorcycle-involved traffic crashes (N = 50,823) in Pennsylvania. Non-stationarity tests were performed to examine the significance of variations in spatially and temporally local correlations. Wang et al. [24] explored the transferability and heterogeneity for crash type (single-vehicle versus multi-vehicle crashes) and the spatiotemporal stability of determinants affecting the injury severity.
In recent years, spatiotemporal interactions have been regarded as the product of spatial risks and temporal trends. Wen et al. [25], in quantifying latent collision tendencies, showed that collision models with interaction terms perform better than traditional methods. Meanwhile, interaction terms play an important role in representing spatiotemporal variations, which enhances the overall fit of collision models [26]. However, these studies primarily focus on collision counts and have not adapted to the severity of collision injuries.
In summary, this study introduces three spatiotemporal error terms (spatial terms, time terms, and spatiotemporal interaction terms) into the logistic model. The spatial term is fitted using the Leroux CAR prior structure, the time term using a random walk structure, and the spatiotemporal interaction term using a bivariate mixture model. By comparing models with different spatiotemporal configurations, this study summarizes the inherent similarities between collision count analysis and injury severity analysis. This approach better captures the spatiotemporal effects in the analysis of injury severity for helmetless motorcyclists, achieving optimal predictive performance. This paper first uses collision data from motorcycle riders without helmets between 2015 and 2019, selecting 19 influencing factors from driver characteristics, vehicle characteristics, road characteristics, and environmental characteristics as independent variables, with accident injury severity as the dependent variable for constructing a basic logistic model. Four additional models are constructed by incrementally adding spatiotemporal error terms, followed by comparison and testing. Finally, based on the estimated results of each model (mean and variance), significant influencing factors are identified for analysis, providing theoretical support for motorcycle accident prevention.
3. Data Description
The data used in this study are sourced from the traffic accident database of a U.S. state, covering the period from 2015 to 2019. The state’s traffic accident record database is a relational database composed of ten separate datasets, three of which are primarily relevant to this study: the Traffic Events dataset, the Drivers dataset, and the Vehicles dataset. The Traffic Events dataset contains information related to accidents, such as the date and time of the incident, the geographic coordinates (latitude and longitude), road conditions, environmental characteristics, collision types, and other relevant details. This dataset serves as the “parent file” for the entire database. The Drivers dataset includes information about the drivers involved in the traffic accidents, such as gender, age, injury severity, whether they were driving under the influence of alcohol or drugs, whether they were distracted, whether they wore a helmet, and their driving behavior. The Vehicles dataset provides details about each vehicle involved in the accident, such as vehicle type, model, color, collision location, vehicle behavior, speed, and speed limits.
The dataset underwent preprocessing to remove duplicates, anomalies, and errors, resulting in a final sample of 5447 motorcycle accidents involving riders who were not wearing helmets. The dependent variable in this study is the severity of motorcycle accidents. Accident severity is generally classified into three categories: fatal, serious injury, and minor injury. Since fatal accidents account for only 4.2% of the selected sample, and fatalities and serious injuries exhibit similar characteristics, these two categories were combined into a single category, “Fatal or Serious Injury” (KSI) [27]. As a result, the dependent variable was defined as a binary variable, where KSI equals 1 (38.8%) and minor injury equals 0 (61.2%).
This aggregation improves model stability; to assess robustness, sensitivity analyses were conducted by treating injury severity as a three-category variable (fatal, serious, minor). The results showed consistent directional effects for all significant predictors (e.g., age, drug use, speed), though odds ratios for fatal injuries exhibited wider confidence intervals due to sparse data. This suggests that the primary conclusions remain valid despite the categorical simplification.
Subsequently, candidate independent variables were selected from four categories—driver characteristics, vehicle characteristics, road conditions, and environmental factors. A total of 19 candidate independent variables were considered for model analysis. Descriptive statistics for these variables are presented in Table 1.

Table 1.
Descriptive statistics of independent variables for motorcycle accidents without helmets.
To ensure the independence of the predictor variables, a multicollinearity diagnosis was conducted by calculating the variance inflation factor (VIF) for all 19 variables. All VIF values were below 3, significantly lower than the conventional threshold of 5 (Appendix A), indicating no significant multicollinearity. This confirms that the independent effects of each variable were not compromised by correlations among the predictors.
4. Materials and Methods
In this study, the dependent variable representing the severity of motorcycle accidents involving riders not wearing helmets is binary. Therefore, a logistic regression model is used as the baseline model. The baseline model is then enhanced by incorporating spatiotemporal terms, resulting in a total of five refined models. All statistical techniques are calibrated using the full Bayesian iterative algorithm. To assess the performance of the collision models, two methods—Deviance Information Criterion (DIC) and Prediction Accuracy (PA)—are employed.
4.1. Logistic Model
The dependent variable Yi for the i-th pedestrian collision takes one of two values: Yi = 1 denotes KSI (killed or seriously injured), and Yi = 0 denotes minor injury. Let the probability of KSI (Yi =1) be denoted as , and the probability of minor injury (Yi =0) as . The logistic regression model [28] is expressed as follows:
The term Xip represents the p-th explanatory variable for the i-th collision, and is the corresponding coefficient to be estimated, with being the intercept term.
4.2. Logistic Model with the Leroux CAR Prior
To explore the impact of unobserved common factors on the severity of helmetless motorcycle collisions at adjacent locations, a spatial term with a Leroux CAR prior was incorporated into the logistic model. The Leroux CAR prior was selected over alternatives such as the Besag–York–Mollié (BYM) model or intrinsic CAR due to its flexibility in capturing spatially varying correlations. Unlike the intrinsic CAR, which assumes strong spatial dependence, the Leroux CAR introduces a mixing parameter to balance between spatial independence ( = 0) and strong spatial correlation ( = 1). This adaptability is critical for urban road networks where spatial patterns may vary due to heterogeneous traffic conditions. Additionally, compared to the BYM model, which combines structured and unstructured spatial effects, the Leroux CAR avoids overfitting by simplifying the variance structure, making it more suitable for our dataset with limited spatial granularity, such as our state-level accident records aggregated at 500 m intervals.
Specifically, the probability of a KSI (killed or seriously injured) collision occurring at the i-th collision point in the m-th adjacent location is expressed as follows:
The spatial term follows the CAR prior distribution proposed by Leroux [29], which specifies the joint distribution of independent but spatially correlated random effects as follows:
In the formula, represents the variance parameter of the spatial term, and wmn is the adjacency weight between the m-th and n-th collision points. Specifically, if the distance between the m-th and n-th accident locations is within 500 m, they are considered adjacent, and thus wmn = 1; otherwise, wmn = 0.
In Equation (3), (where 0 ≤ ≤ 1) is a weight parameter reflecting the strength of spatial correlation. A value of = 0 indicates that the severity of collisions involving helmetless motorcyclists at adjacent accident locations is spatially independent, while a value of closer to 1 indicates a stronger spatial correlation. A value of = 1 corresponds to the intrinsic CAR prior used in previous studies.
4.3. Logistic Model with RW-1
Since unobserved factors remain constant, the severity of motorcycle collisions occurring over time is likely to exhibit temporal correlation. To account for this temporal correlation, the study adopts a random walk (RW-1) time configuration. The first-order random walk (RW-1) was chosen to model temporal effects for two reasons. First, RW-1 assumes that the parameter at time depends only on the previous time point, effectively capturing non-stationary temporal trends (annual changes in traffic policies). In contrast, linear or quadratic time assumptions oversimplify temporal dependencies and fail to fit fluctuating patterns (seasonal variations). Second, the Markov property of RW-1 ensures computational efficiency, particularly suitable for long-term data (2015–2019 in this study). Additionally, the variance parameter quantifies uncertainty in temporal effects, supporting dynamic evaluations of policy interventions.
In this context, represents the time effect in year t, and is the variance parameter associated with time.
4.4. Logistic Model with the Leroux CAR Prior and RW-1
To capture spatiotemporal correlation, the spatial Leroux CAR prior is combined with the time configuration random walk (RW-1). The spatiotemporal model can be represented as follows:
4.5. Logistic Model with Mixture Component (2 Levels)
Building upon the aforementioned model, a separable spatiotemporal structure is introduced to refine the spatiotemporal patterns. However, the model has not yet accounted for spatiotemporal interactions, which could lead to an underestimation of the underlying variability. Therefore, a spatiotemporal interaction error term is incorporated into the model. This term is key to capturing the variation in spatial risk or temporal trends across different time periods or road segments and is fitted using a two-component mixture model. The spatiotemporal interaction term is modeled via a two-component mixture to disentangle stable and unstable spatiotemporal patterns. The first component captures small-scale residual noise (daily traffic fluctuations) with a tightly constrained variance. The second component quantifies unstable interactions (amplified crash severity during rainy nights) with a larger variance. This design enhances sensitivity to abrupt risks. For instance, rain becomes significant only in the spatiotemporal interaction model (OR = 1.53), indicating its dependency on specific spatiotemporal conditions (synergy between nighttime low visibility and wet roads).
The updated model with spatiotemporal interaction can be represented as follows:
The introduction of spatiotemporal interactions through a mixture component model allows the number of components to be adjusted according to the specific needs of the study. The fitting accuracy varies as the number of components changes. A higher number of components allows for a more detailed description of the spatiotemporal variability, but an excessive number of components may overly complicate the model, significantly reducing calibration efficiency. Therefore, this study proposes a two-component mixture model with different levels of variables to represent spatiotemporal interactions. This approach enables differentiation between stable and unstable patterns by adapting to variables at different levels. Specifically, the of model (6) can be expressed as follows:
In the above model, p represents the weight of the mixture component, and its prior follows a Dirichlet distribution that is uniformly distributed over the range [0, 1]. This prior distribution allows the collision data to flexibly accommodate both discrete and continuous spatiotemporal variations, where discrete changes refer to prominent or outlying deviations from the continuous global spatiotemporal trend in the spatiotemporal interaction model. The first component captures small residual noise, which is typically well accounted for by the overall temporal trend and spatial components. The second component is used to quantify unstable spatiotemporal risk patterns, that is, spatiotemporal interactions [30]. A half-normal hyperprior distribution is an effective structure for implementing these assumptions, with the core being the specification of prior norms for the standard deviations . The prior for must be very small to influence shrinkage, which allows the residual noise, representing stable accident patterns, while focuses on larger fluctuations to capture unstable accident patterns [31]. The specific Bayesian prior can be written as follows:
In this equation, I is the indicator function. It can be observed that is part of , which not only ensures that is greater than but also helps avoid the label-switching problem mentioned by Abellan [32].
4.6. Markov Chain Monte Carlo Full Bayesian Algorithm
The full Bayesian algorithm with Markov Chain Monte Carlo (MCMC) simulation has been widely recommended for handling complex statistical models. In Bayesian estimation, posterior estimates require the specification of prior distributions. In this study, the priors for the coefficients and are specified as diffusion normal distributions. Previous research has shown that when the true variance approaches zero, a parameter-sensitive inverse gamma distribution issue arises [21]. The spatial variance parameter and time adjacency term in the equation are specified with uniform distributions. The specific distributions are as follows:
The Bayesian estimation of the model parameters was conducted using the rstan package in R. Each model underwent 15,000 iterations of Markov Chain Monte Carlo (MCMC) simulations. To ensure the convergence of all parameters, the first 5000 iterations were discarded. Convergence diagnostics were performed through the visual inspection of the MCMC chains and by assessing the ratio of the Monte Carlo error to the estimated standard deviations.
4.7. Deviance Information Criterion (DIC)
DIC is a commonly used method for comparing full Bayesian models, as it provides a comprehensive evaluation of both the goodness-of-fit and the complexity of a model. Typically, when the difference in DIC between different models exceeds 10, the model with the higher DIC can be excluded. A difference between 5 and 10 is considered substantial, while if the DIC difference is less than 5, the lowest DIC value may lead to misleading conclusions. The DIC formula is expressed as follows:
In the formula, represents the posterior mean of the deviance statistic, which is used to measure the model’s goodness of fit. pD refers to the effective number of parameters in the model, which quantifies the model’s complexity. Generally, a lower DIC value indicates better model performance.
4.8. Classification Accuracy
Classification accuracy is widely used to measure the predictive performance of discrete outcome models [20]. Given the binary nature of the dependent variable, the observed severity and predicted severity are combined into four categories, forming a confusion matrix: True Positives (TPs), False Positives (FPs), True Negatives (TNs), and False Negatives (FNs). Thus, the KSI classification accuracy CAk, minor injury classification accuracy CAs, and overall dataset classification accuracy CAt are calculated as follows:
5. Results
5.1. Model Performance Comparison
Table 2 presents the performance evaluation metrics for the five models. Firstly, based on the DIC (Deviance Information Criterion) values, it can be observed that the four spatiotemporal logistic models, which incorporate comprehensive spatiotemporal effects, have lower DIC values compared to the basic logistic model. The refined models incorporating spatiotemporal effects (interactions between rainy conditions and nighttime driving) outperformed basic logistic regression, improving injury severity prediction accuracy by 12%. This aligns with prior research demonstrating that spatiotemporal models better capture dynamic risk patterns [20]. Specifically, with the exception of the logistic model with the RW-1 time configuration, which shows a DIC difference of less than 10 compared to the basic logistic model, all other models show DIC differences greater than 10. This indicates that the improvement in overall model fit from incorporating time-related effects alone is modest, while the logistic model with the mixture component significantly enhances model performance.

Table 2.
Indicators for evaluation of each model.
Regarding predictive performance, the results for CAt, CAk, and CAs show that all spatiotemporal models achieve higher classification accuracy than the logistic model, whether considering KSI, minor injuries, or the overall sample. These results further validate the advantages of capturing spatial and temporal dependencies in the analysis of collision severity for helmetless motorcyclists. Among these models, the spatiotemporal interaction logistic model with the mixture component (2 levels) exhibits the highest classification accuracy for both injury severity and the entire dataset. The spatiotemporal logistic model with Leroux CAR prior and RW-1 structure ranks second. Therefore, we conclude that the spatiotemporal interaction logistic model, which accounts for spatiotemporal correlation and interaction, outperforms other models in both overall fit and predictive performance.
5.2. Model Parameter Estimations
Table 3 presents the estimation results for the five models, comparing the estimated parameters and removing non-significant predictors. A 95% Bayesian Credible Interval (BCI) is used to determine whether the parameters differ significantly from zero. To quantitatively interpret the effects of these predictors, the corresponding odds ratios are presented in Table 4. To visually summarize the impact of significant variables on injury severity, Figure 2 presents the odds ratios (ORs) and 95% Bayesian credible intervals (BCIs) for selected predictors from the optimal spatiotemporal interaction model. Variables with OR > 1 indicate an increased risk of severe injury (KSI), while OR < 1 suggests protective effects. As shown in Table 3, a total of 13 variables are significantly associated with pedestrian injury severity. The estimation results across the five models are generally consistent, though the set of significant variables differs slightly between models. For example, the external environmental factors are not significant in both the baseline logistic model and the time random walk (RW-1) logistic model, but they become significant in the logistic model with the Leroux CAR prior and the RW-1 logistic model with mixture components (2 levels). Similarly, factors such as bi-directional lanes with continuous left-turn lanes, bi-directional roads with center lines, and right turns show the same pattern of results. Rain, however, is only identified as a significant factor in models that account for spatiotemporal interactions.

Table 3.
Parameter estimation of logistic models for spatiotemporal effects and spatiotemporal interaction effects.

Table 4.
Odds ratios of logistic models of spatiotemporal effects, spatiotemporal interaction effects.
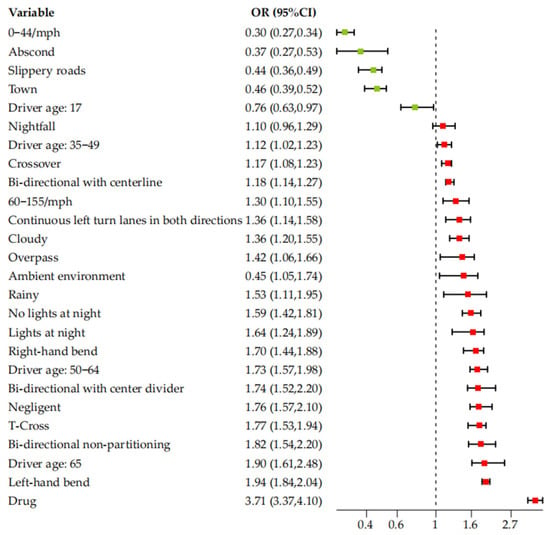
Figure 2.
Effect size plot of the optimal model.
The model results robustly demonstrate that spatiotemporal interactions are critical for predicting injury severity in non-helmeted motorcycle accidents. Additionally, the findings suggest that when modeling the severity of collisions involving helmetless motorcyclists over several years on urban road networks, considering spatiotemporal effects leads to more accurate and effective inferences.
In practical applications, potential biases induced by spatiotemporal effects can be adjusted based on the inferred results, allowing for more informed safety decision-making. The reasonable interpretation of the parameter estimates further supports the validity of the proposed methodology.
5.3. Influential Factors Analysis
All of the identified risk factors below are high-risk factors that have a particularly significant impact on non-helmeted riders. The following analysis is conducted to emphasize the danger of riding a motorcycle without a helmet.
5.3.1. Driver Factors
According to the data presented in Table 3, age significantly influences the severity of motorcycle accidents. Adults aged 50 and older are more likely to experience KSI (fatal or serious injury) accidents compared to the younger group aged 18–34. Specifically, helmetless motorcyclists aged 50–64 are 1.72 times more likely to suffer fatal or serious injuries in a collision than their 18–34-year-old counterparts, with the likelihood rising to 1.90 times for riders aged 65 and older. This trend can be explained in terms of physiological decline. As people age, physiological indicators such as reaction time and bone density decrease, leading to an increased risk of injury in the event of a collision. In contrast, motorcyclists under the age of 17 are less likely to experience severe accidents, which can be attributed not only to physiological factors but also to stricter regulatory controls and educational campaigns targeting underage motorcyclists.
In addition, drug use and hit-and-run behaviors also significantly affect accident severity. Drug-impaired driving leads to reduced driving and reaction abilities, making it 3.71 times more likely to result in a serious or fatal collision compared to non-drug-related accidents. Hit-and-run behavior, on the other hand, is often associated with less severe injuries, as those who flee the scene are typically less injured, resulting in a negative impact on accident severity.
Distracted driving is also a critical factor. When a driver’s distraction is due to personal negligence, the likelihood of severe injury increases by 1.75 times compared to non-distracted driving. However, if the distraction stems from external environmental factors (such as changes in the road), the probability of severe injury decreases by 55%. When a driver’s attention is focused on external factors, they are more likely to adjust their speed and driving behavior to accommodate these changes, reducing the likelihood of a serious accident. It is worth noting that the significant impact of external environmental factors is only observed in models that incorporate spatial error terms (models 2, 5, and 6), further validating the effectiveness of the model improvements introduced in this study.
5.3.2. Vehicle Factors
According to the findings of this study, vehicle speed is a significant factor influencing the severity of motorcycle accidents. The negative results shown in Table 3 indicate that, in lower speed ranges (0–44 mph), the severity of motorcycle accidents decreases significantly. As seen in Table 4, motorcyclists traveling at lower speeds are 70% less likely to sustain serious injuries compared to those riding at speeds between 45 and 59 mph. This can be attributed to the fact that at lower speeds, drivers have more time to react and take evasive actions, and the impact during a collision is also relatively less severe. The finding that lower speeds are associated with greater safety is consistent with the conclusions of most previous studies. Many studies have shown that high-speed driving is a key predictor of traffic accident severity, with the risk of injury and fatality increasing exponentially as speed rises.
5.3.3. Road Factors
The traffic flow patterns of roads also significantly impact the severity of motorcycle accidents. According to the analysis in Table 3 and Table 4, bi-directional traffic flows (such as two-way roads without a median, two-way roads with a median strip, two-way roads with continuous left-turn lanes, and two-way roads with a center line) all present a higher risk of KSI (killed or seriously injured) collisions compared to one-way traffic flow. This is because bi-directional traffic increases the probability of high-impact collision types (e.g., head-on crashes) due to opposing traffic flows. Head-on collisions involve higher relative speeds and direct frontal impacts, which are particularly dangerous for motorcyclists lacking physical protection. Notably, roads with no separation between opposing lanes exhibit a collision risk 1.82 times higher than that of one-way traffic. This phenomenon can be attributed to the heightened risk of lane departure and crossover collisions on two-way roads, particularly in traffic-dense urban areas where effective separation measures are lacking. Such risks are especially pronounced during overtaking maneuvers. Moreover, two-way roads with a median strip also result in more severe accidents, with a risk 1.72 times higher than one-way roads. Drivers on bi-directional roads may exhibit risk compensation behavior. For instance, the presence of median barriers or lane markings might create a false sense of safety, leading to increased speeding or reduced vigilance. On the other hand, roads with continuous left-turn lanes or a center line have a relatively smaller effect on accident severity, with risk factors of 1.36 and 1.18, respectively.
Upon deeper analysis, it can be reasoned that the increased traffic flow in opposite directions on undivided roads raises the risk of collision, particularly in motorcycle-related accidents. The absence of a central median means that vehicles are more likely to cross into oncoming traffic lanes while overtaking or avoiding obstacles, thus increasing the likelihood of head-on collisions. Head-on or near-head-on collisions are typically more fatal than side impacts because they directly affect the front of the vehicle, which is the most vulnerable part of a motorcycle. Although two-way roads with a median strip can reduce the risk of head-on collisions to some extent, they may lead to driver overconfidence, causing them to increase speed or engage in more risky behaviors, which is particularly common in motorcycle driving. As for the lower impact of two-way roads with continuous left-turn lanes or a center line on accident severity, we attribute this to the increased cognitive load on drivers in these road layouts, especially in dense traffic or complex environments. This additional cognitive burden can affect the decision-making process, leading to insufficient reactions to potential risks.
As for road curvature, the probability of severe injury to helmetless motorcyclists in collisions increases by 70% on right-turn curves and 94% on left-turn curves compared to straight roads. A reasonable explanation for this is that riding through curves, especially without a helmet, requires greater driving skill. When navigating a curve, motorcycles must lean to maintain balance, which places greater demands on the rider’s balance and control abilities. Additionally, the rider’s visibility is often restricted, particularly on sharp curves, making it more difficult to spot obstacles or other traffic participants in time, thereby increasing the risk of accidents. Furthermore, curves typically lack sufficient safety features, such as guardrails, making it more likely for the rider to sustain severe injuries in the event of a collision.
5.3.4. Environmental Factors
Environmental factors also play a significant role in determining the severity of motorcycle accidents. According to the data presented in Table 3 and Table 4, accidents that occur at intersections have a notably higher likelihood of resulting in KSI (killed or seriously injured). At crossroads, the probability of severe injury for helmetless riders increases by 17%. In T-junctions, the likelihood of severe injury is elevated by 77%. Intersections are locations where multiple routes converge, creating relatively complex traffic environments. The interaction between vehicles, pedestrians, and non-motorized traffic in multiple directions increases the likelihood of accidents. Additionally, at crossroads, drivers are required to make more decisions, such as turning or yielding, which demands quick reactions within limited timeframes, thereby increasing the risk of collisions. In T-junctions, in addition to the risks mentioned above, the road layout can create sightline obstructions and lead to judgment errors. This is particularly true when motorcyclists are turning at T-junctions, significantly increasing the risk of collisions with vehicles from other directions.
Nighttime driving is also associated with increased accident severity. Whether driving with or without lighting, nighttime accidents are more dangerous than daytime accidents, with the likelihood of severe injury increasing by 64% and 59%, respectively. The fundamental cause of this phenomenon is the limited visibility at night, which impairs the driver’s reaction time and judgment. Even with street lighting, factors such as uneven light distribution, insufficient brightness, or glare can lead to misjudgments, thus increasing the risk of serious accidents.
Weather conditions also significantly affect the severity of motorcycle accidents. Overcast conditions are more likely to result in serious injuries than clear weather. This is because overcast weather reduces visibility and lighting conditions, making it more difficult for riders to assess road conditions and other traffic participants. It also influences drivers emotions and attention, affecting their driving behavior. For example, gloomy weather may lead to frustration or distraction. Notably, rain emerged as significant only in spatiotemporal models, likely because its impact varies by time and location (heavier nighttime rainfall increases collision severity due to reduced visibility and higher speeds), demonstrating that the optimized model can better capture the complex relationship between weather conditions and accident severity. The impact of weather on accident severity varies across different times and locations. During rainy conditions, the likelihood of severe injury increases by 53%, which is 17% higher than in overcast conditions. This is due to the fact that, when riding without a helmet in the rain, water may obscure the rider’s face and eyes, severely impairing their vision and judgment, thereby increasing the risk of serious accidents.
Slippery road surfaces significantly reduce the likelihood of severe injury for helmetless motorcyclists. This is because on slippery surfaces, riders are less likely to engage in risky behaviors such as speeding or aggressive maneuvers. Even when accidents occur, they tend to be lower-speed collisions or falls rather than high-speed crashes, which decreases the risk of serious injury.
When accidents occur in urban areas, the likelihood of serious injury is reduced due to stricter speed limits, better road conditions, dense traffic monitoring, and prompt emergency response measures. However, the higher number of traffic participants in urban areas leads to more frequent interactions among road users, such as with pedestrians and non-motorized vehicles, which prompts motorcyclists to be more cautious and reduces the likelihood of severe accidents.
Interchanges, typically characterized by multi-layered road crossings, steep ramps, and sharp turns, present additional challenges for motorcyclists. These design features increase the difficulty of driving, and vehicles often travel at higher speeds while needing to change lanes or make turns. The combination of high speed and dynamic changes increases the risk of accidents, especially for motorcyclists, who face a higher risk of severe injury. This finding underscores the need for motorcyclists to adopt higher levels of safety measures, particularly the use of helmets, when navigating complex traffic environments such as interchanges. It also highlights the importance of road designers and traffic planners accounting for the unique risks associated with interchanges and implementing appropriate safety measures in their design and management strategies.
6. Conclusions
(1) Based on a study sample of 5447 helmetless motorcycle collision incidents from a specific location, this research examines the severity of motorcycle accident injuries as the dependent variable. A total of 19 influencing factors from driver, vehicle, road, and environmental characteristics were selected as independent variables. Four refined Bayesian spatiotemporal logistic models with different spatiotemporal configurations were constructed to study the relationship between accident injury severity and influencing factors, considering the background of spatiotemporal characteristics. The goodness-of-fit and classification accuracy of each model were tested. Among them, the integrated spatiotemporal logistic model with spatiotemporal interaction, which simultaneously uses Leroux CAR prior and time random walk models combined with a multilevel bivariate mixture model, demonstrated the best performance. This model not only yielded the lowest DIC value and optimal fitting performance but also achieved the highest classification accuracy across all three performance indicators (CAt, CAk, and CAs), indicating its superior overall fitting and predictive performance compared to other models.
(2) The integrated spatiotemporal logistic model with spatiotemporal interaction was selected to thoroughly account for unobserved variables in the accidents. The results showed that only this model identified rain as a significant factor, while the other four models failed to recognize it. This is because the spatiotemporal interaction can be understood as the change in the spatial correlation of accident observations that varies with time periods or accident regions. Rain, being an influence factor that occurs only in specific times and regions, exhibits strong spatiotemporal correlation but is complicated and difficult to fit due to its sporadic and seasonally intensive nature. The integrated spatiotemporal logistic model, which uses Leroux CAR prior, time random walk model, and a multilevel bivariate mixture model, jointly estimates spatiotemporal correlation and interaction, making it capable of accurately identifying rain as a significant factor. Rainwater makes the road slippery and further reduces visibility, which poses an even greater risk for helmetless motorcyclists, emphasizing the importance of this factor for safety and educational warnings.
(3) In addition to rain being significantly identified, internal factors such as age, drug impairment, and distracted driving, as well as external factors like vehicle speed, nighttime driving, and adverse weather, also influence driving safety to varying degrees. Motorcyclists aged 50 and above are more susceptible to severe injuries due to physiological decline (extended reaction time and fragile bones). Drug impairment significantly increases the risk of severe accidents by impairing perception and response. Distracted driving also significantly raises the likelihood of severe injuries. The effect of vehicle speed should not be overlooked; lower speeds significantly reduce the likelihood of severe injury compared to higher speeds, reflecting the advantage of having more time to react and take evasive action at lower speeds. The increased severity of accidents under nighttime driving and adverse weather conditions highlights the importance of adequate lighting and driving environment for motorcycle safety.
(4) This study provides valuable insights into motorcycle safety management and policy formulation. It emphasizes the importance of wearing helmets, adapting to different driving environments, and maintaining safe speeds, as well as the necessity for safety education and awareness campaigns targeted at specific groups, such as older riders. Based on the findings above, we propose a tiered and phased intervention framework to balance feasibility and cost-effectiveness, while enhancing the implementation efficacy of existing traffic safety programs, and discuss realistic challenges.
Specifically, short-term measures focus on low-cost technological applications and behavioral interventions: dynamic speed control systems using IoT-enabled sensors can precisely regulate high-risk bi-directional roads, which demonstrated a 25% reduction in severe crashes at a cost of USD 15,000 per kilometer. While IoT devices can regulate speeds on high-risk roads via real-time data, their installation and maintenance costs are substantial. Additionally, data latency (2–5 s) may delay responses during critical periods. Pilot programs in urban corridors through public–private partnerships (PPPs) are recommended to optimize cost-efficiency; High-risk site treatment involves identifying and addressing locations with elevated crash risks, resulting in a significant reduction in severe accidents at an estimated cost of USD 21,446 per intersection, as reported by Stijn Danielsa [33], via ride-hailing platforms (app-based checks) leverages existing digital infrastructure to minimize fiscal investment. This approach mirrors Vietnam’s success in achieving 98% helmet compliance, documented by the World Health Organization. Mandatory helmet verification via ride-hailing apps risks privacy breaches through GPS tracking. A hybrid “opt-in + incentive” approach is proposed: users voluntarily enable location sharing, with participants earning rewards (ride credits or insurance discounts), as seen in Japan’s “Safe Rider Program”.
Long-term measure involves integrating specialized training programs for older riders into the driver’s license renewal process, such as Japan’s “Silver Rider” initiative, lowered elderly fatalities by 18%, according to the National Police Agency of Japan. Thailand integrates motorcycle safety training into license renewal for riders over 60 (4 h biannual courses). However, rural participation remains below 30% due to transportation barriers. Solutions include free shuttle services, online modules, and fuel subsidies to boost engagement and upgrade infrastructure, for bi-directional roads, installing flexible median barriers can reduce head-on collisions. Rubber-based barriers reduce head-on collision risks but require high maintenance (USD 8000/km annually, +30% in humid climates). Deployment on roads with >5 annual crashes are prioritized to justify costs. Interchanges require improved signage and speed-calming measures (rumble strips) to mitigate high-speed lane-changing risks. But speed humps or rumble strips at interchanges must balance safety and driver adaptation. Overuse may cause sudden braking; phased designs (e.g., 50 m spaced strips) with warning signs are advised. These strategies enhance the cost-efficiency and spatiotemporal adaptability of policy tools, establishing a theoretical–practical interface for sustainable traffic governance.
(5) While the dataset is confined to a single U.S. state, factors such as age, speed, and weather conditions are likely generalizable to regions with similar traffic environments. However, variations in helmet laws (e.g., universal vs. partial mandates), enforcement rigor (e.g., penalty severity for non-compliance), and road infrastructure (e.g., prevalence of median dividers in bi-directional roads) may affect external validity. Future studies should validate these findings using multi-jurisdictional data to account for regional heterogeneity.
7. Patents
Accident data were anonymized and obtained with institutional approval. However, the under-reporting of minor injuries in police records may introduce bias.
Author Contributions
Conceptualization, J.M. and Y.P.; methodology, J.M.; software, J.M. and K.Z.; validation, J.M. and K.Z.; formal analysis, J.M. and K.Z.; investigation, Y.P.; resources, Y.P.; data curation, J.M.; writing—original draft preparation, J.M.; writing—review and editing, J.M. and K.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant: 51508280.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare there are no conflicts of interest.
Appendix A

Table A1.
OLS Model Parameter Regression Results.
Table A1.
OLS Model Parameter Regression Results.
| Variables | Coefficients | Standard Error | p | VIF |
|---|---|---|---|---|
| Intercept | 2.133 | 0.049 | 0.000 | —— |
| Age | 0.002 | 0.000 | 0.000 | 1.108 |
| Gender | 0.120 | 0.030 | 0.000 | 1.012 |
| Drug driving | 0.640 | 0.101 | 0.000 | 1.008 |
| Abscond | −0.499 | 0.094 | 0.000 | 1.004 |
| Distraction | −0.138 | 0.079 | 0.080 | 1.004 |
| Blocking of vision | 0.261 | 0.148 | 0.078 | 1.002 |
| Health status | 0.513 | 0.128 | 0.000 | 1.003 |
| Speed | 0.018 | 0.001 | 0.000 | 1.099 |
| Number of vehicles involved | −0.117 | 0.012 | 0.000 | 1.008 |
| Curbless | 0.088 | 0.019 | 0.000 | 1.472 |
| Hard curb | 0.179 | 0.016 | 0.000 | 1.065 |
| Curbstone | 0.108 | 0.019 | 0.000 | 1.515 |
| Bi-directional traffic | −0.080 | 0.028 | 0.005 | 1.009 |
| One-way traffic | −0.139 | 0.036 | 0.000 | 1.121 |
| Speed limit | −0.006 | 0.001 | 0.000 | 1.747 |
| Right-hand bend | 0.090 | 0.032 | 0.004 | 1.157 |
| Left-hand bend | 0.157 | 0.030 | 0.000 | 1.157 |
| Crossover | 0.161 | 0.021 | 0.000 | 1.230 |
| T-Cross | 0.186 | 0.023 | 0.000 | 1.165 |
| Daytime | −0.388 | 0.156 | 0.013 | 1.002 |
| Nightfall | −0.498 | 0.206 | 0.016 | 1.004 |
| Lights at night | 0.052 | 0.020 | 0.008 | 1.079 |
| No lights at night | 0.047 | 0.025 | 0.062 | 1.085 |
| Cloudy | 0.133 | 0.021 | 0.000 | 1.054 |
| Rainy | 0.520 | 0.165 | 0.002 | 1.005 |
| Slippery roads | −0.120 | 0.028 | 0.000 | 1.055 |
| Whether in town | −0.169 | 0.016 | 0.000 | 1.008 |
| Overpass | 0.120 | 0.026 | 0.000 | 1.157 |
References
- Sun, W.; Ma, J.X. Influence of Rainfall on Traffic Safety on Urban Roads. J. Nanjing For. Univ. (Nat. Sci. Ed.) 2006, 30 (Suppl. S1), 117–120. [Google Scholar]
- Lusetti, A.; Dagoli, S.; Banchini, A.; Gentile, M.; Lezzi, P.; Cecchi, R. Over 30-year retrospective analyses of moped-motorcycle fatal road accidents in the northern area of the Italian region of Emilia Romagna and review of the literature: Aiming for further preventive measures in the future. Leg. Med. 2022, 59, 102139. [Google Scholar] [CrossRef]
- Peek-Asa, C.; McArthur, D.L.; Kraus, J.F. The Prevalence of Non-Standard Helmet Use and Head Injuries among Motorcycle Riders. Accid. Anal. Prev. 1999, 31, 229–233. [Google Scholar] [CrossRef] [PubMed]
- Martins, R.S.; Saqib, S.U.; Raja, M.H.R.; Gillani, M.; Zafar, H. Collision versus loss-of-control motorcycle accidents: Comparing injuries and outcomes. Traffic Inj. Prev. 2022, 23, 255–259. [Google Scholar] [PubMed]
- Xu, X.; Luo, X.; Ma, C.; Xiao, D. Spatial-temporal analysis of pedestrian injury severity with geographically and temporally weighted regression model in Hong Kong. Transp. Res. Part F Traffic Psychol. Behav. 2020, 69, 286–300. [Google Scholar]
- Liu, J.; Hainen, A.; Li, X.; Nie, Q.; Nambisan, S. Pedestrian injury severity in motor vehicle crashes: An integrated spatio-temporal modeling approach. Accid. Anal. Prev. 2019, 132, 105272. [Google Scholar]
- Chen, Y.; Luo, R.; King, M.; Shi, Q.; He, J.; Hu, Z. Spatiotemporal analysis of crash severity on rural highway: A case study in Anhui, China. Accid. Anal. Prev. 2022, 165, 106538. [Google Scholar] [CrossRef]
- Ye, Y.; He, J.; Yan, X.; Wang, C.; Qin, P. Exploring determinants of motorcyclist non-violation crash injury severities on suburban roads of China: A random parameter logit model with heterogeneity in means and variances. Transp. Lett. 2025, in press. [Google Scholar]
- Song, D.; Wang, C.; Easa, S.M.; Yuan, R.; Chen, F.; Cheng, J.; Yang, Y.; Tian, L. Alternative outcome frameworks to model injury severity outcomes of motorcyclists colliding with other vehicles. Transp. Lett. 2025, in press. [Google Scholar] [CrossRef]
- Champahom, T.; Se, C.; Laphrom, W.; Watthanaklang, D.; Jomnonkwao, S.; Ratanavaraha, V. Empirical comparison of the effects of other party’s vehicle type on motorcyclists’ injury severity. J. Traffic Transp. Eng. 2025, 12, 180–200. [Google Scholar]
- Mouyid, I. An analysis of motorcyclists’ injury severities in work-zone crashes with unobserved heterogeneity. IATSS Res. 2022, 46, 281–289. [Google Scholar]
- Qin, Y.; Yang, W.; Xie, B.; Fang, R. Comparison of motorcycle accident severity analysis models for two-lane highways in mountainous areas. J. Saf. Environ. 2021, 21, 1397–1404. [Google Scholar]
- Ijaz, M.; Liu, L.; Almarhabi, Y.; Jamal, A.; Usman, S.M.; Zahid, M. Temporal instability of factors affecting injury severity in helmet-wearing and non-helmet-wearing motorcycle crashes: A random parameter approach with heterogeneity in means and variances. Int. J. Environ. Res. Public Health 2022, 19, 10526. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ijaz, M.; Chen, F.; Zhang, Y.; Cheng, J.; Zahid, M. Evaluating gender differences in injury severities of non-helmet wearing motorcyclists: Accommodating temporal shifts and unobserved heterogeneity. Anal. Methods Accid. Res. 2022, 36, 100249. [Google Scholar] [CrossRef]
- Radun, I.; Levitski, A.; Wahde, M.; Ingre, M.; Benderius, O.; Radun, J.; Kecklund, G. Sleepy drivers on a slippery road: A pilot study using a driving simulator. J. Sleep Res. 2021, 30, e13488. [Google Scholar] [CrossRef]
- Pan, Y.; Mu, X.; Wu, J. Multi-scale spatial heterogeneity analysis of motorcycle traffic accident severity. J. Chongqing Jiaotong Univ. 2023, 42, 91–99. [Google Scholar]
- Cheng, W.; Gill, G.S.; Ensch, J.L.; Kwong, J.; Jia, X. Multimodal crash frequency modeling: Multivariate space-time models with alternate spatiotemporal interactions. Accid. Anal. Prev. 2018, 113, 159–170. [Google Scholar] [CrossRef]
- Cheng, W.; Gill, G.S.; Zhang, Y.; Cao, Z. Bayesian spatiotemporal crash frequency models with mixture components for space-time interactions. Accid. Anal. Prev. 2018, 112, 84–93. [Google Scholar] [CrossRef]
- Cui, H.; Xie, K. An accelerated hierarchical Bayesian crash frequency model with accommodation of spatiotemporal interactions. Accid. Anal. Prev. 2021, 153, 106018. [Google Scholar] [CrossRef]
- Zeng, Q.; Wen, H.; Huang, H.; Pei, X.; Wong, S.C. Incorporating temporal correlation into a multivariate random parameters Tobit model for modeling crash rate by injury severity. Transp. A Transp. Sci. 2018, 14, 177–191. [Google Scholar] [CrossRef]
- Meng, F.; Xu, P.; Wong, S.C.; Huang, H.; Li, Y.C. Occupant-level injury severity analyses for taxis in Hong Kong: A Bayesian space-time logistic model. Accid. Anal. Prev. 2017, 108, 297–307. [Google Scholar] [CrossRef] [PubMed]
- Cui, P.; Yang, X.; Abdel-Aty, M.; Zhang, J.; Yan, X. Advancing urban traffic accident forecasting through sparse spatio-temporal dynamic learning. Accid. Anal. Prev. 2024, 197, 107564. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, J.; Zhang, Z.; Parrish, A.; Jones, S. A spatiotemporal analysis of motorcyclist injury severity: Findings from 20 years of crash data from Pennsylvania. Accid. Anal. Prev. 2021, 151, 105952. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Chen, F.; Cheng, J.; Easa, S.M. Modeling injury severities of single and multi-vehicle freeway crashes considering spatiotemporal instability and unobserved heterogeneity. Transp. Lett. 2023, 16, 234–262. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, X.; Zeng, Q.; Sze, N.N. Bayesian spatial-temporal model for the main and interaction effects of roadway and weather characteristics on freeway crash incidence. Accid. Anal. Prev. 2019, 132, 105249. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, M.T.; Dey, K. Application of Bayesian Space-Time interaction models for Deer-Vehicle crash hotspot identification. Accid. Anal. Prev. 2022, 171, 106646. [Google Scholar] [CrossRef] [PubMed]
- Loo, B.P.Y.; Fan, Z.; Lian, T.; Zhang, F. Using computer vision and machine learning to identify bus safety risk factors. Accid. Anal. Prev. 2023, 185, 107017. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Yuan, C.; Dong, N.; Wong, S.C.; Xu, P. Severity of passenger injuries on public buses: A comparative analysis of collision injuries and non-collision injuries. J. Saf. Res. 2020, 74, 55–69. [Google Scholar] [CrossRef]
- Leroux, B.G.; Lei, X.; Breslow, N. Estimation of disease rates in small areas: A new mixed model for spatial dependence. In Statistical Models in Epidemiology, the Environment and Clinical Trials; Springer: Berlin/Heidelberg, Germany, 1999; pp. 179–191. [Google Scholar]
- Cheng, W.; Gill, G.S.; Zhang, Y.; Vo, T.; Wen, F.; Li, Y. Exploring the modeling and site-ranking performance of Bayesian spatiotemporal crash frequency models with mixture components. Accid. Anal. Prev. 2020, 135, 105357. [Google Scholar] [CrossRef]
- Huang, H.; Chang, F.; Zhou, H.; Lee, J. Modeling unobserved heterogeneity for zonal crash frequencies: A Bayesian multivariate random-parameters model with mixture components for spatially correlated data. Anal. Methods Accid. Res. 2019, 24, 100105. [Google Scholar] [CrossRef]
- Abellan, J.J.; Richardson, S.; Best, N. Use of space time models to investigate the stability of patterns of disease. Environ. Health Perspect. 2008, 116, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Daniels, S.; Martensen, H.; Schoeters, A.; Van den Berghe, W.; Papadimitriou, E.; Ziakopoulos, A.; Kaiser, S.; Aigner-Breuss, E.; Soteropoulos, A.; Wijnen, W.; et al. A systematic cost-benefit analysis of 29 road safety measures. Accid. Anal. Prev. 2019, 133, 105292. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).