Numerical Investigation of the Opto-Electric and Thermal Performance of a Newly Enhanced Double V-Trough Low Concentration Photovoltaic System for Sustainable Solar Energy Utilization
Abstract
1. Introduction
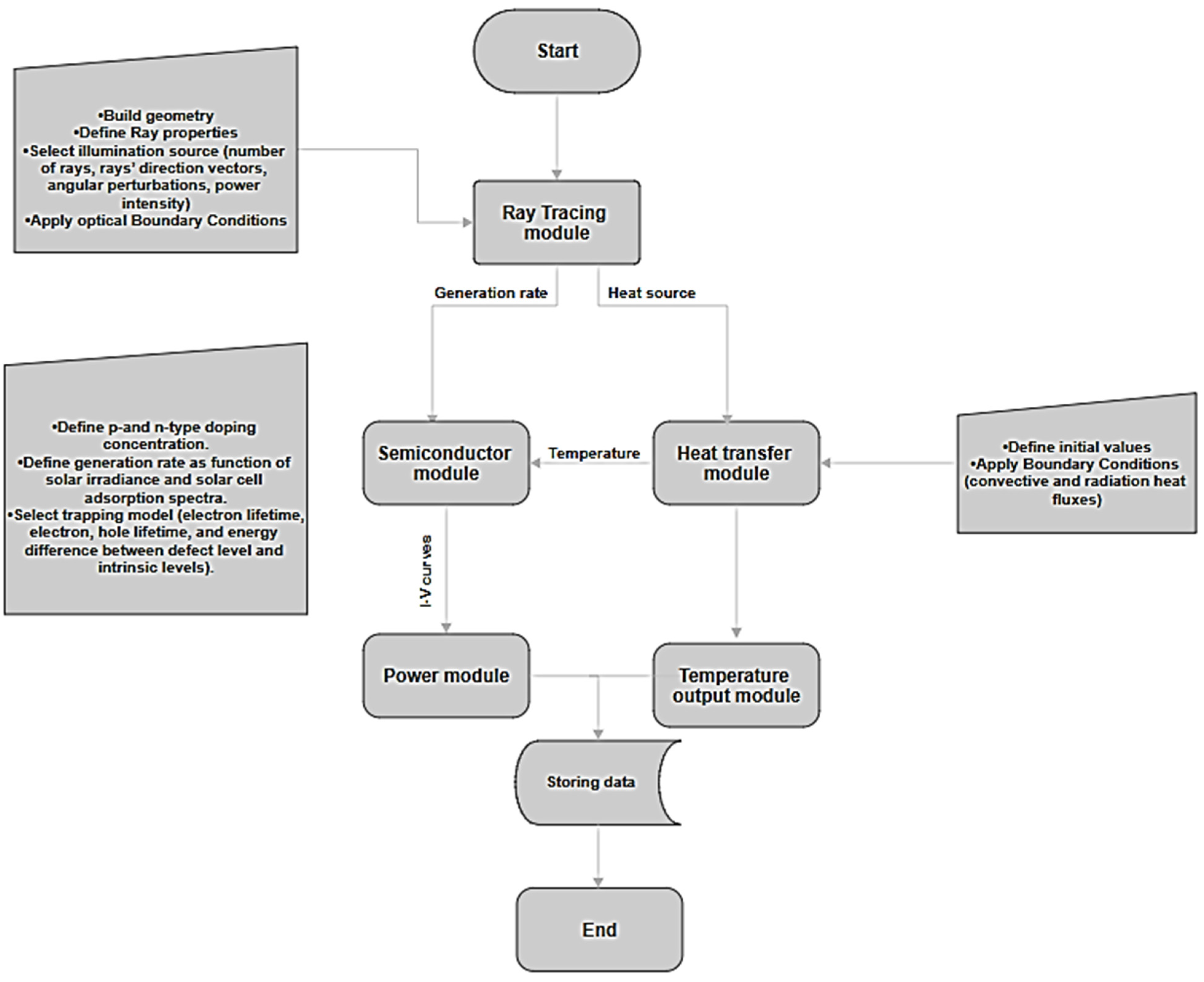
2. Numerical Modeling
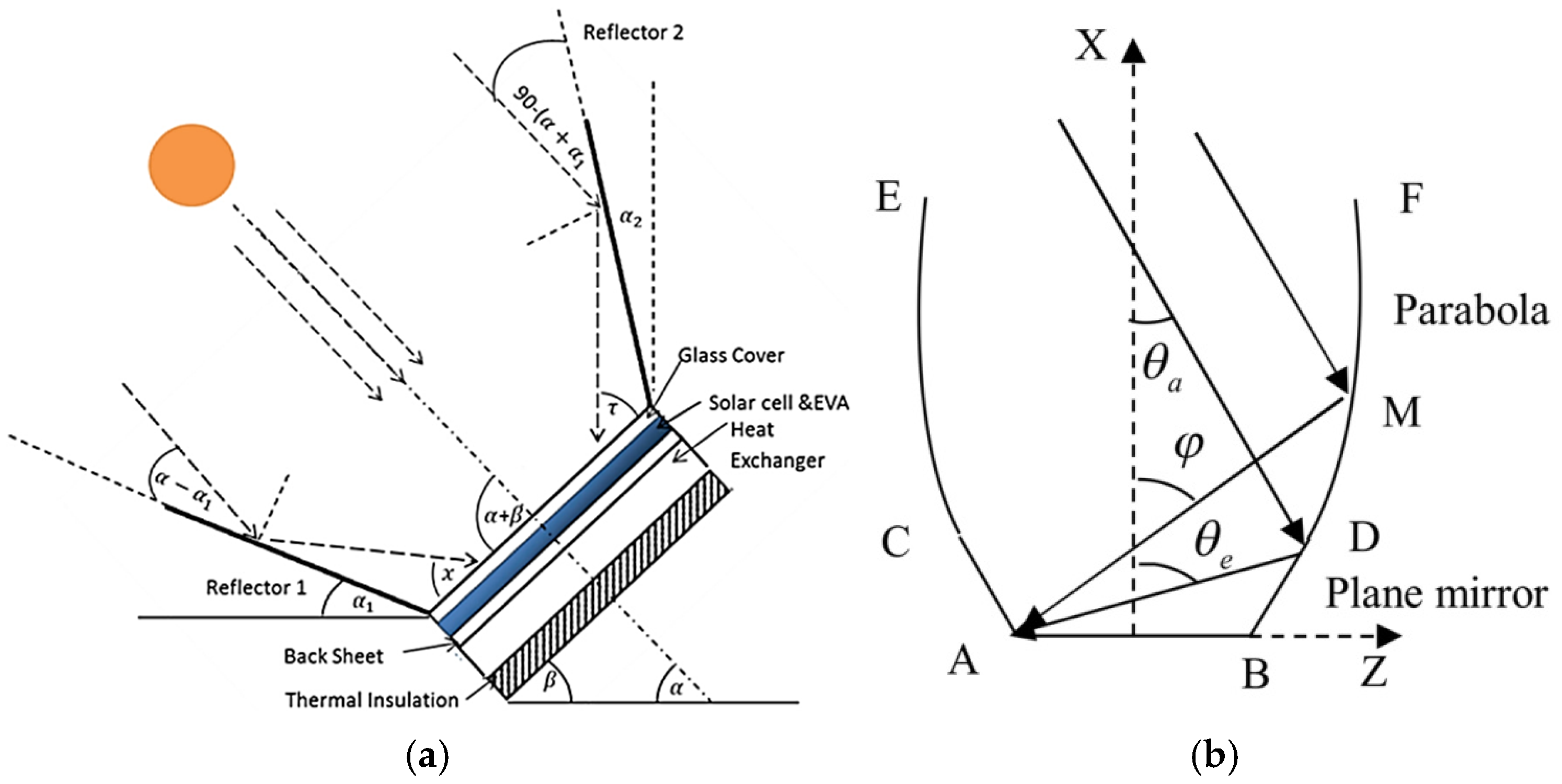
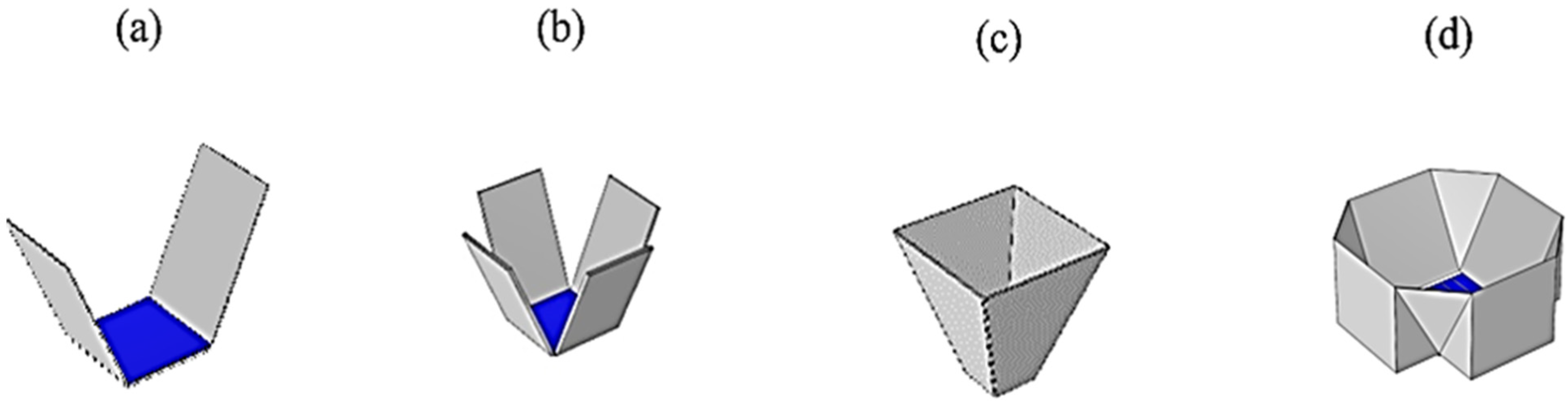
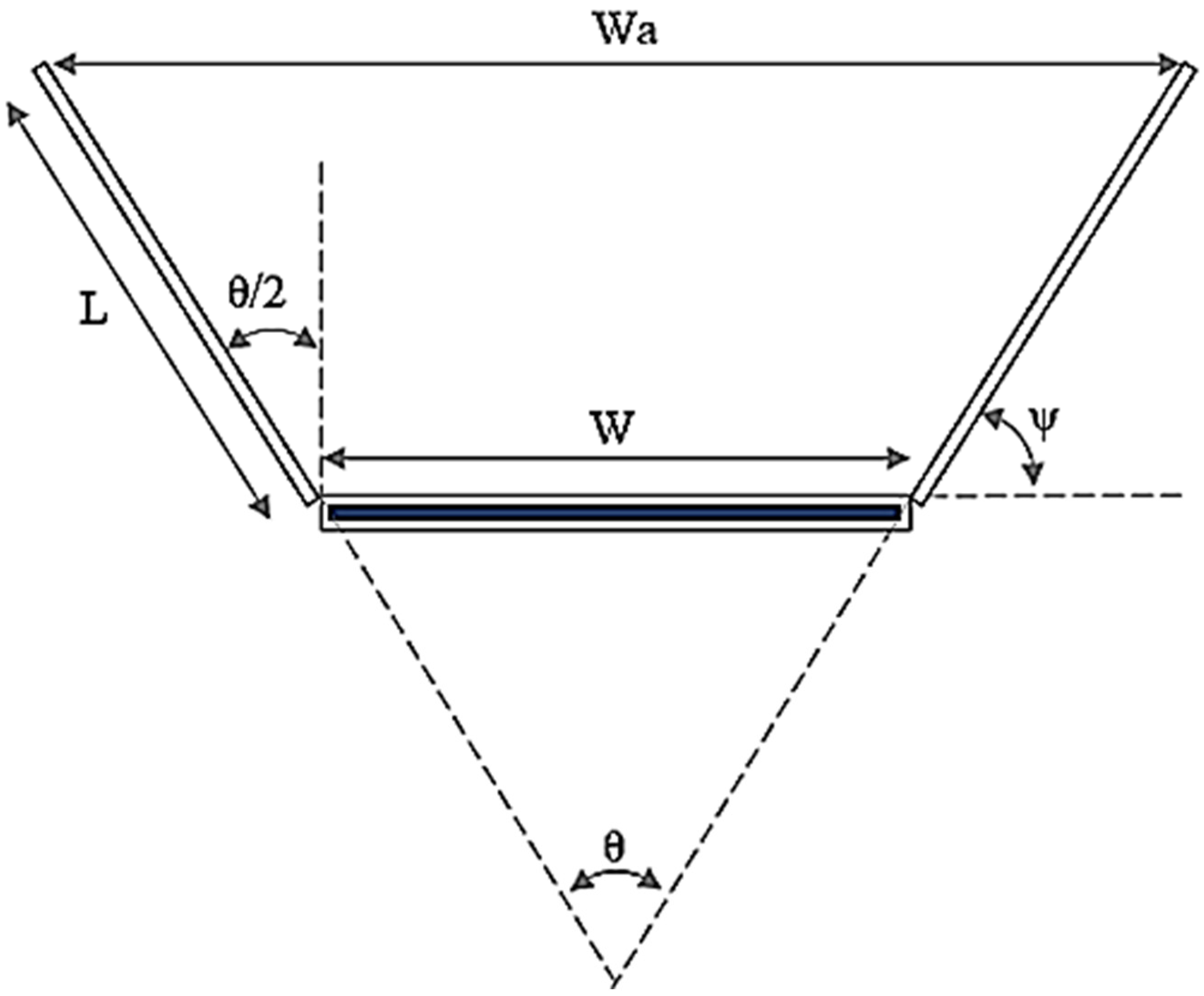
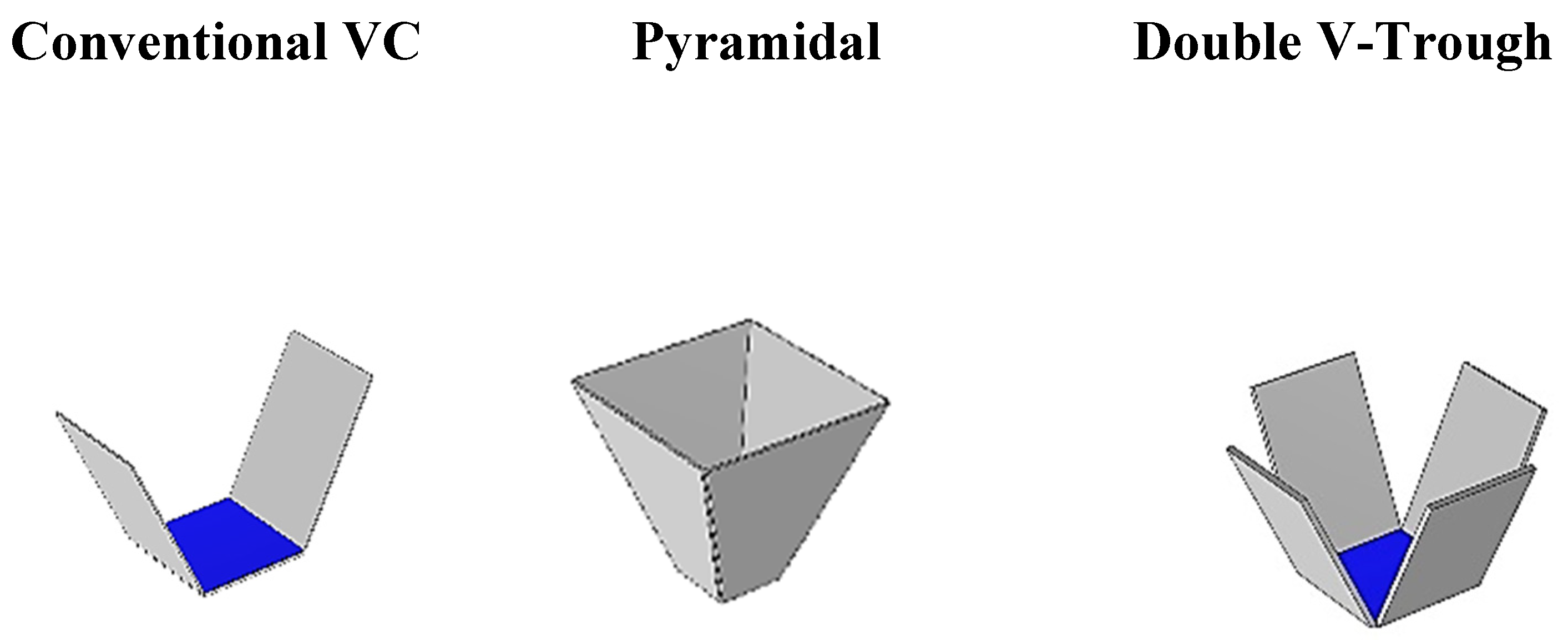
2.1. Geometric Modeling
2.2. Heat Transfer Model
2.3. Solar Cell Model
2.4. Assumptions
- i.
- Direct normal irradiance of 1000 W/m2.
- ii.
- The maximum sun disc angle is assumed to be 4.65 mrad.
- iii.
- The number of released rays is set to 100,000 rays per release.
- iv.
- Absorption coefficient of 0 and 0.3 for ideal case and real case, respectively.
- v.
- Air density is kept at 1 kg/m3.
- vi.
- Wind velocity is set to 1 m/s.
- vii.
- Ambient temperature of 25 °C.
- viii.
- Absolute pressure is kept at 1 a.m.
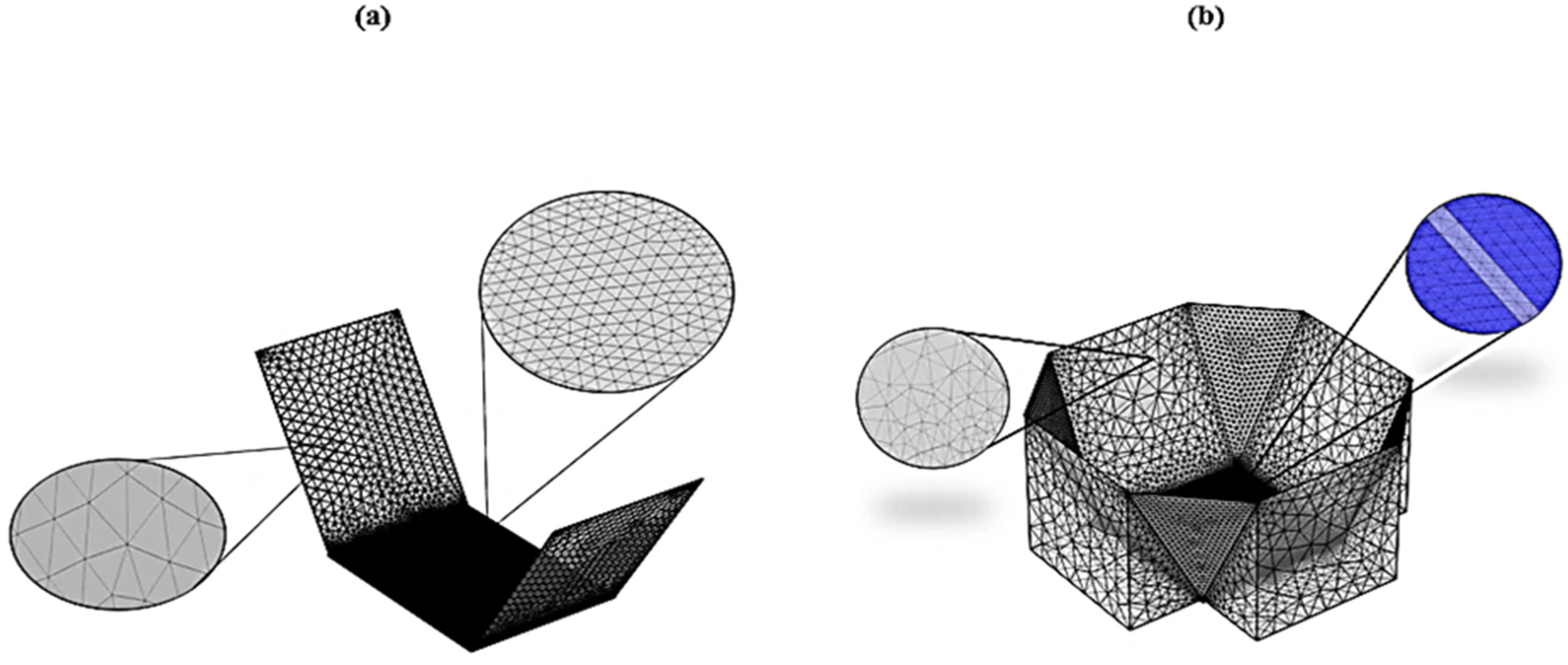
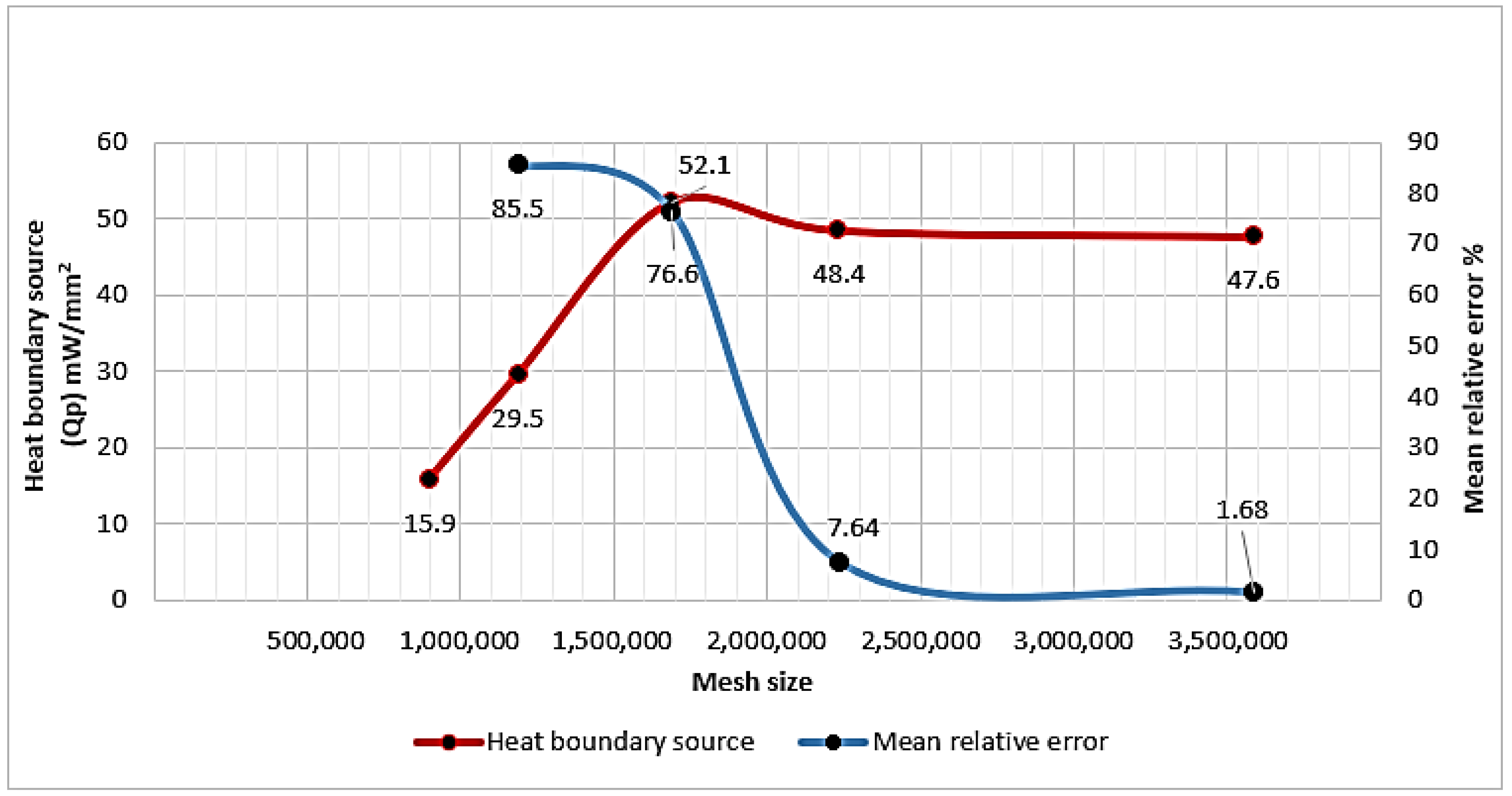
2.5. Generated Mesh
3. Results and Analysis
3.1. Optical Model Validation
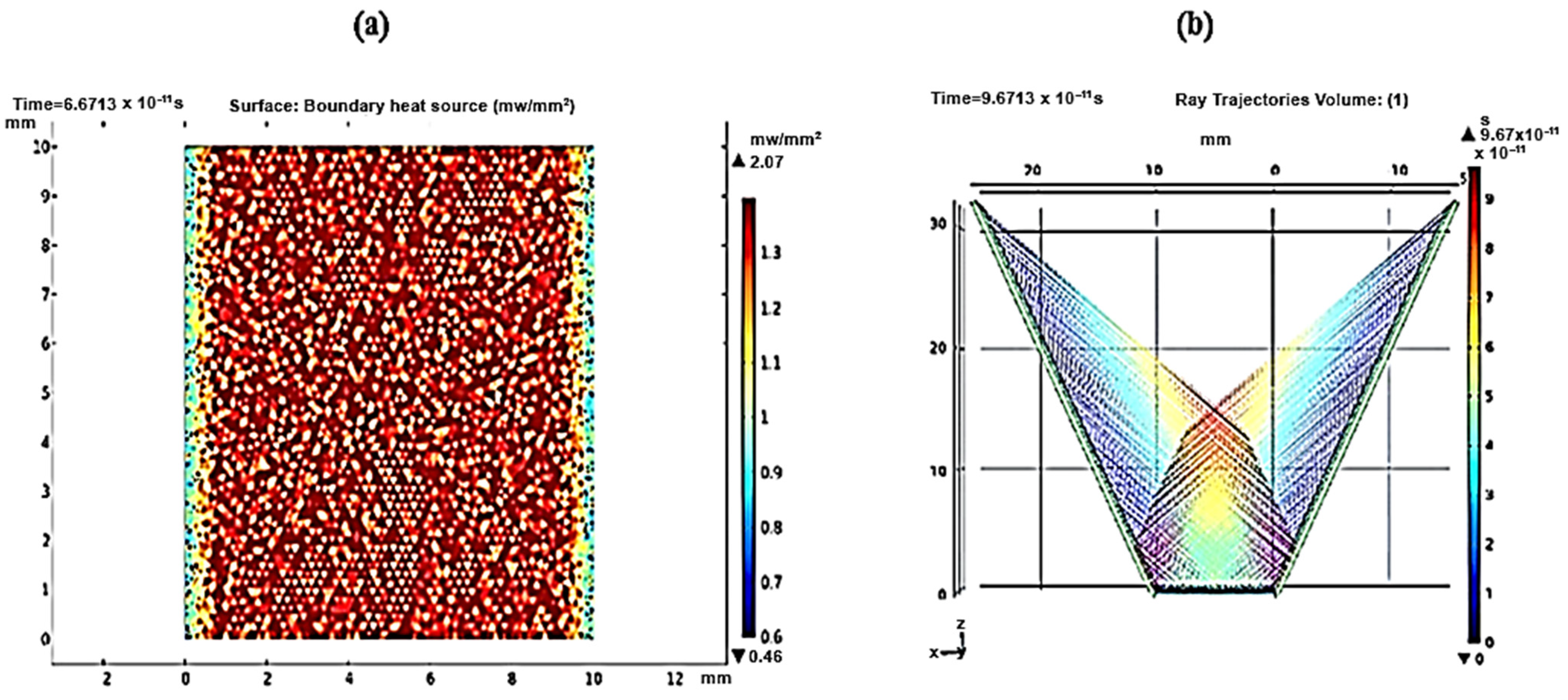
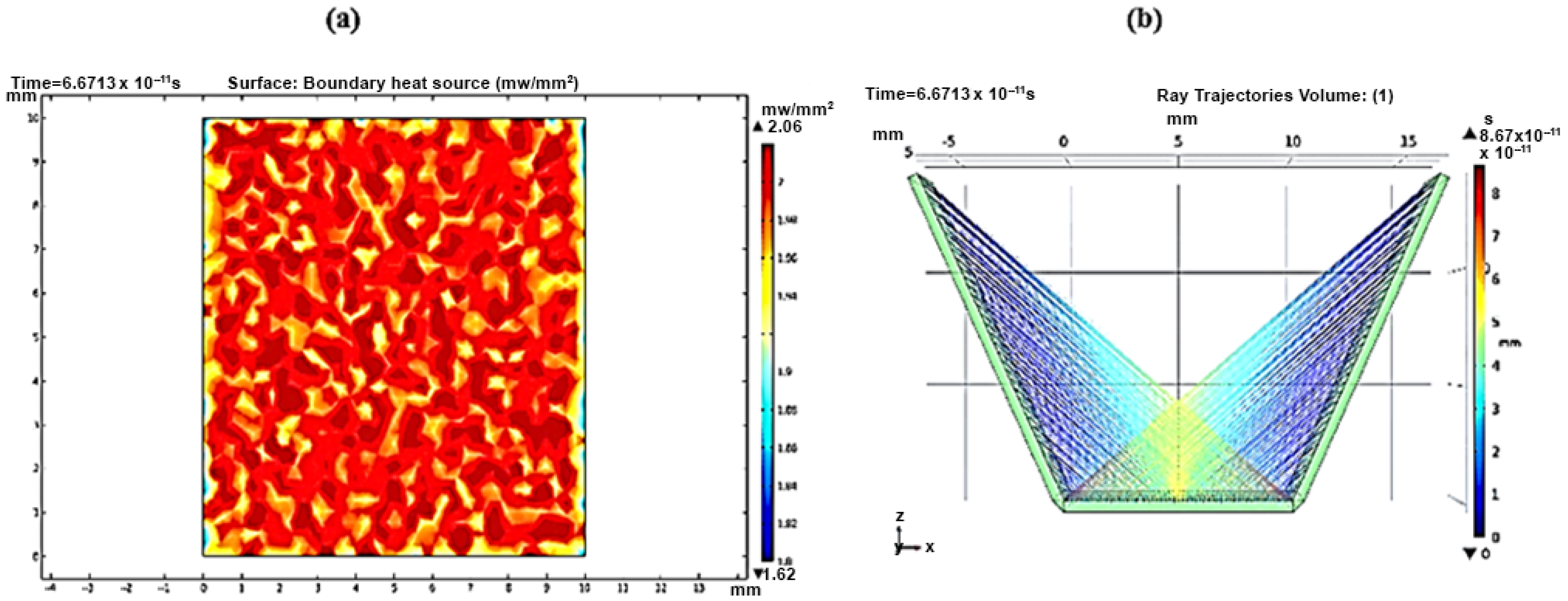
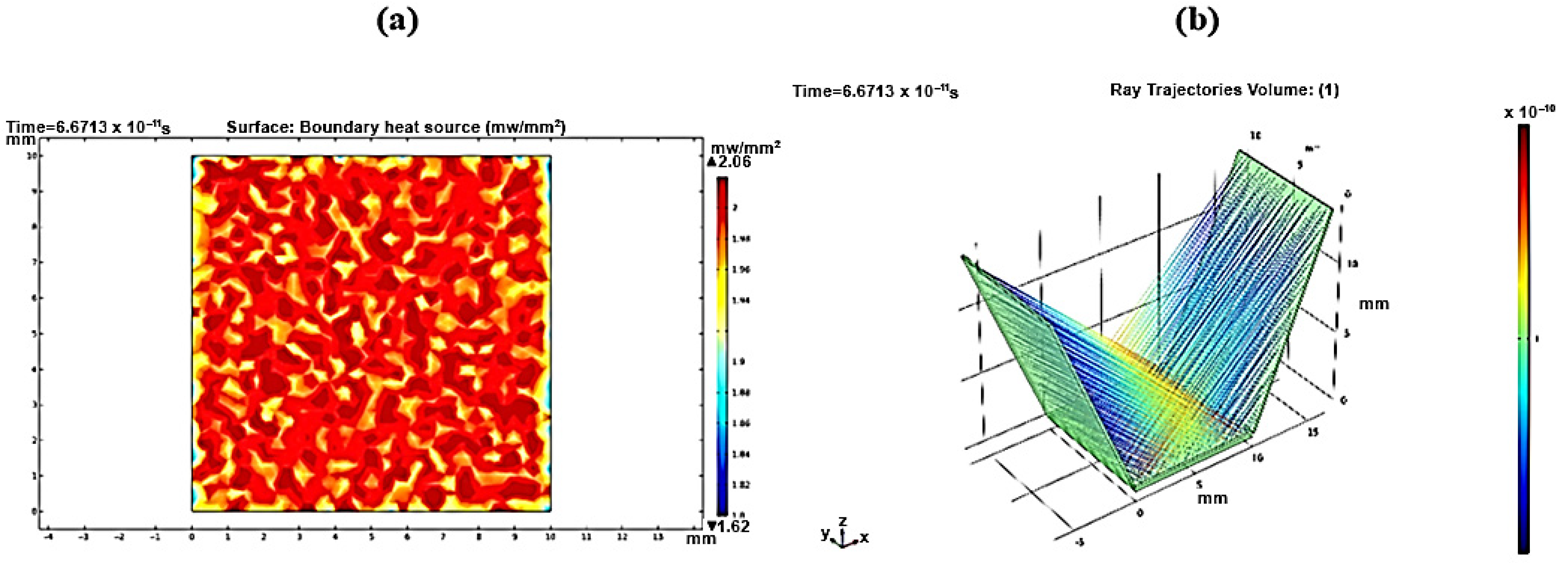
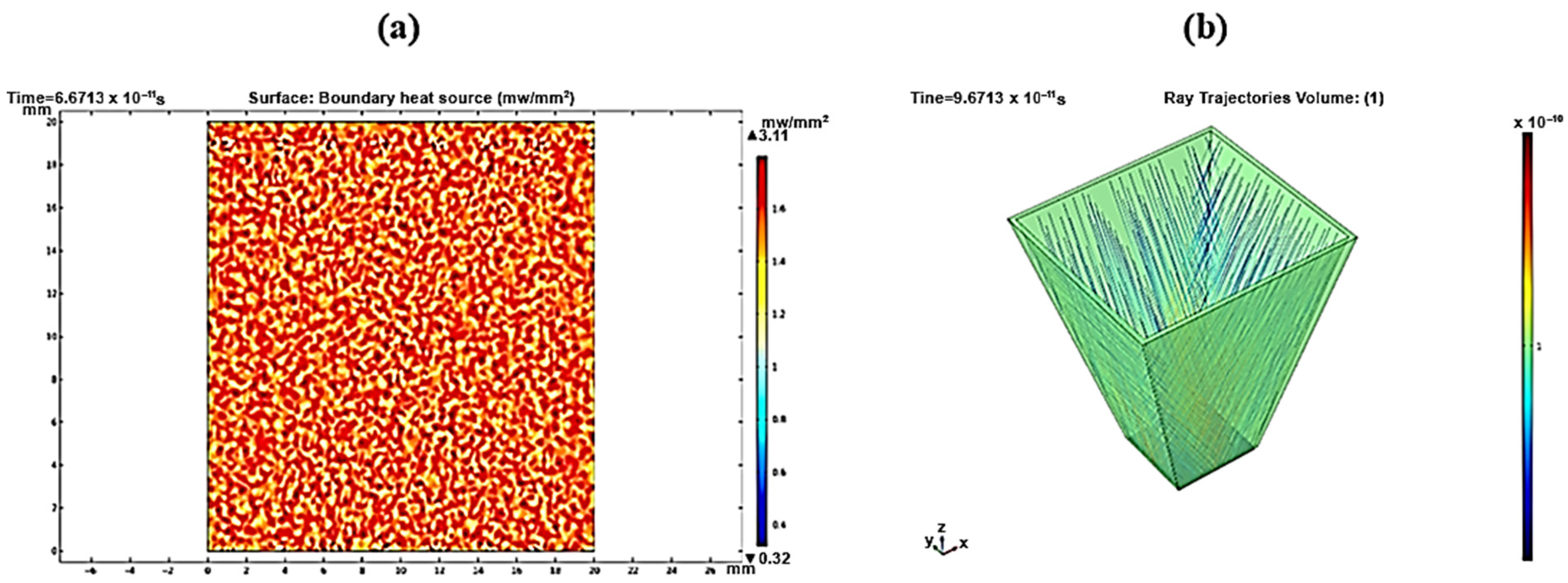
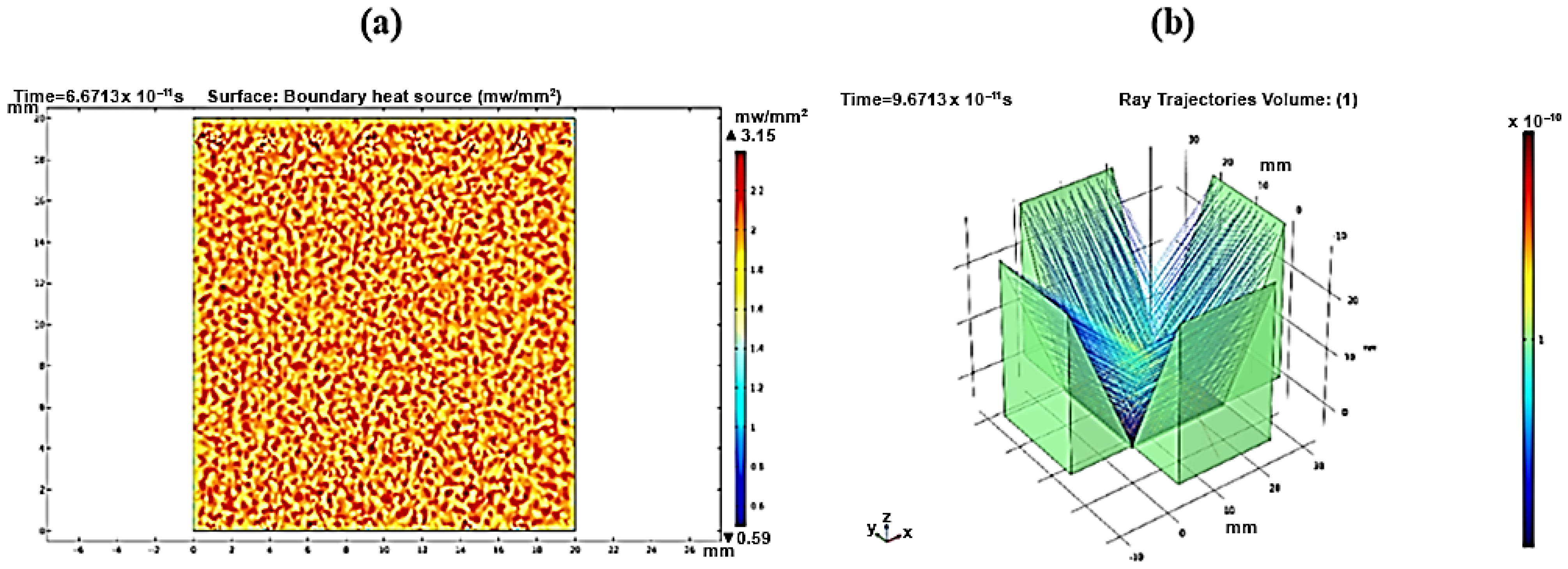
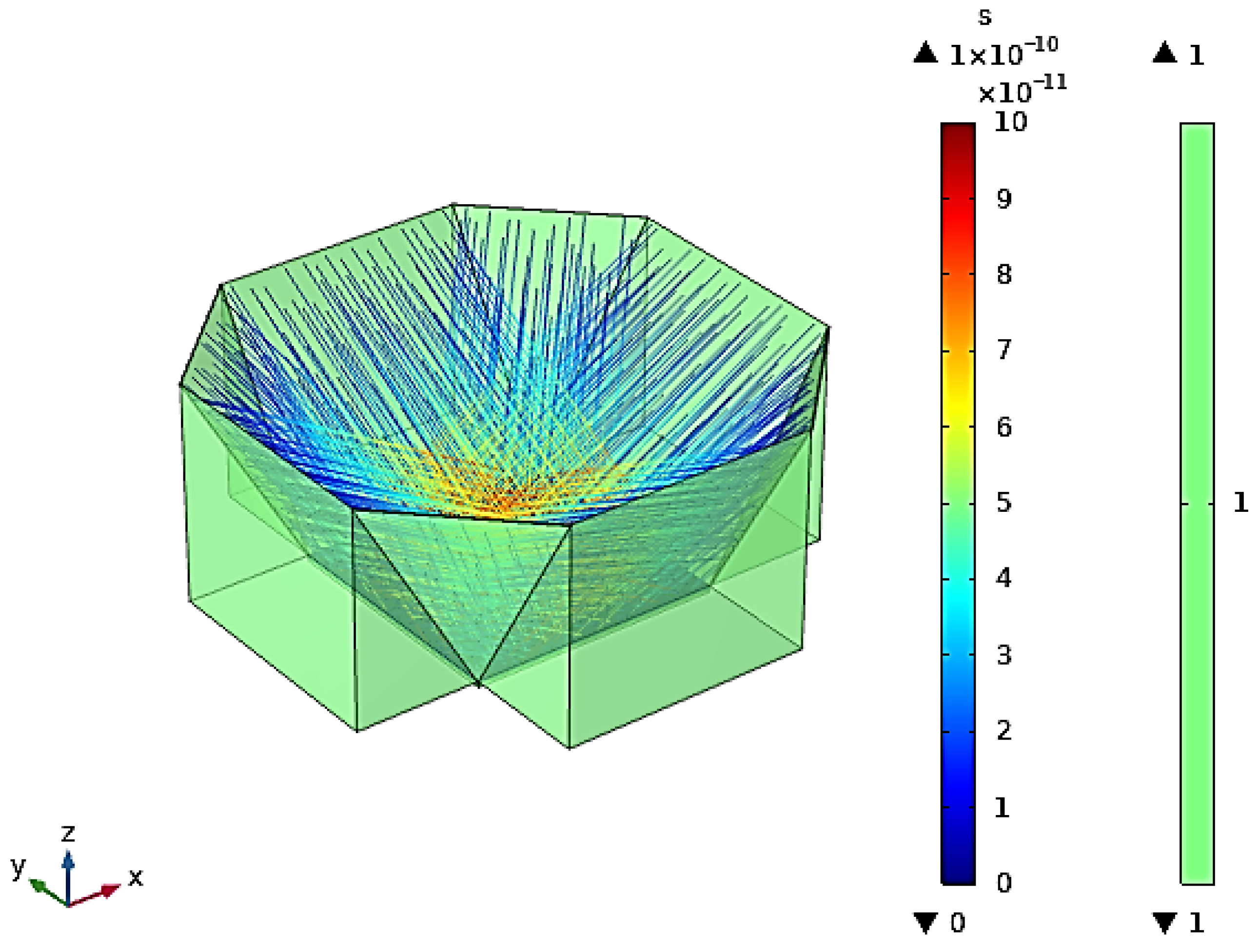
3.2. Ray Trajectories
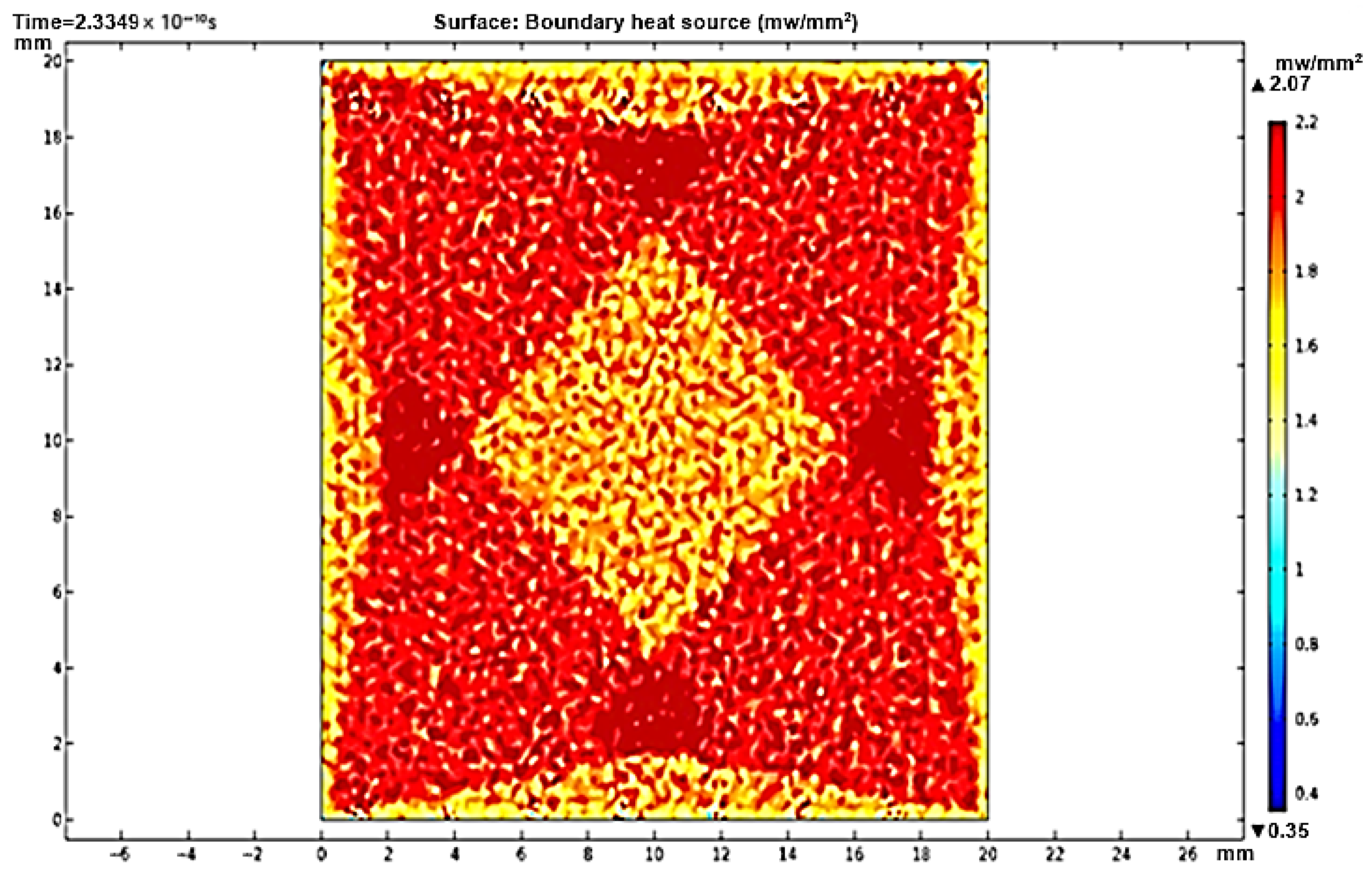
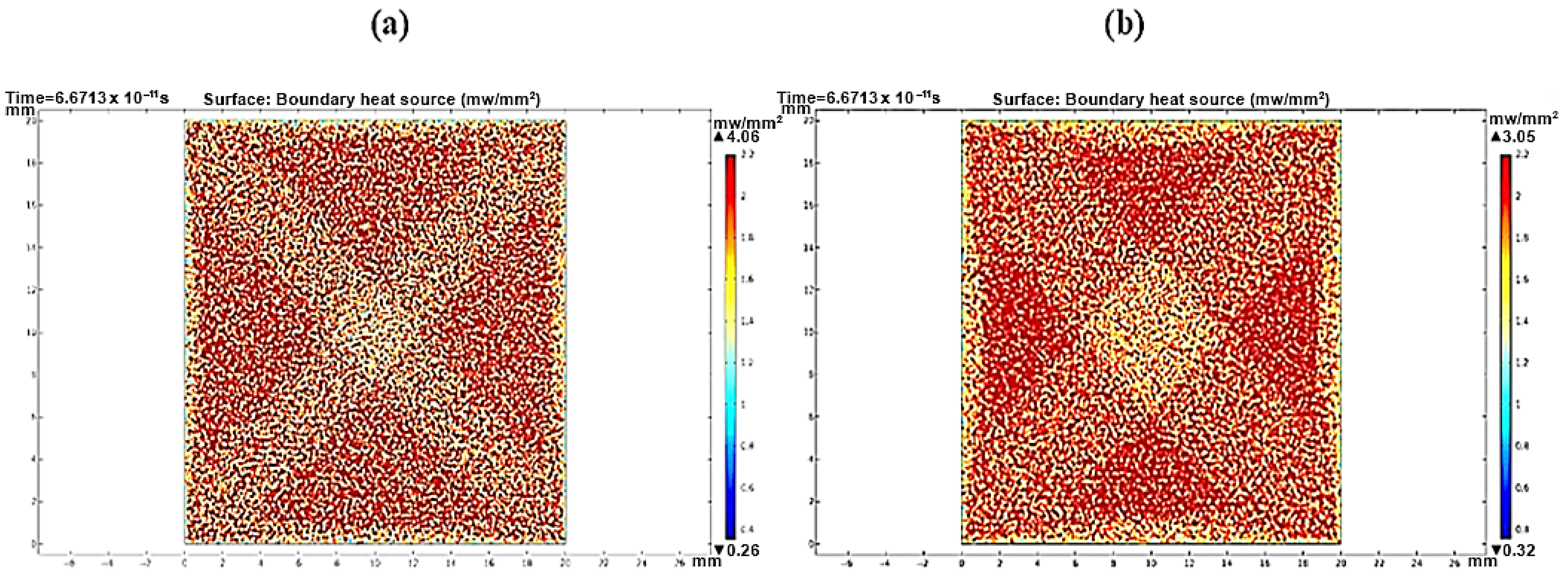
3.3. Local Sun Power Intensity Distribution
3.4. Optical Concentration Ratio and Optical Efficiency Analysis
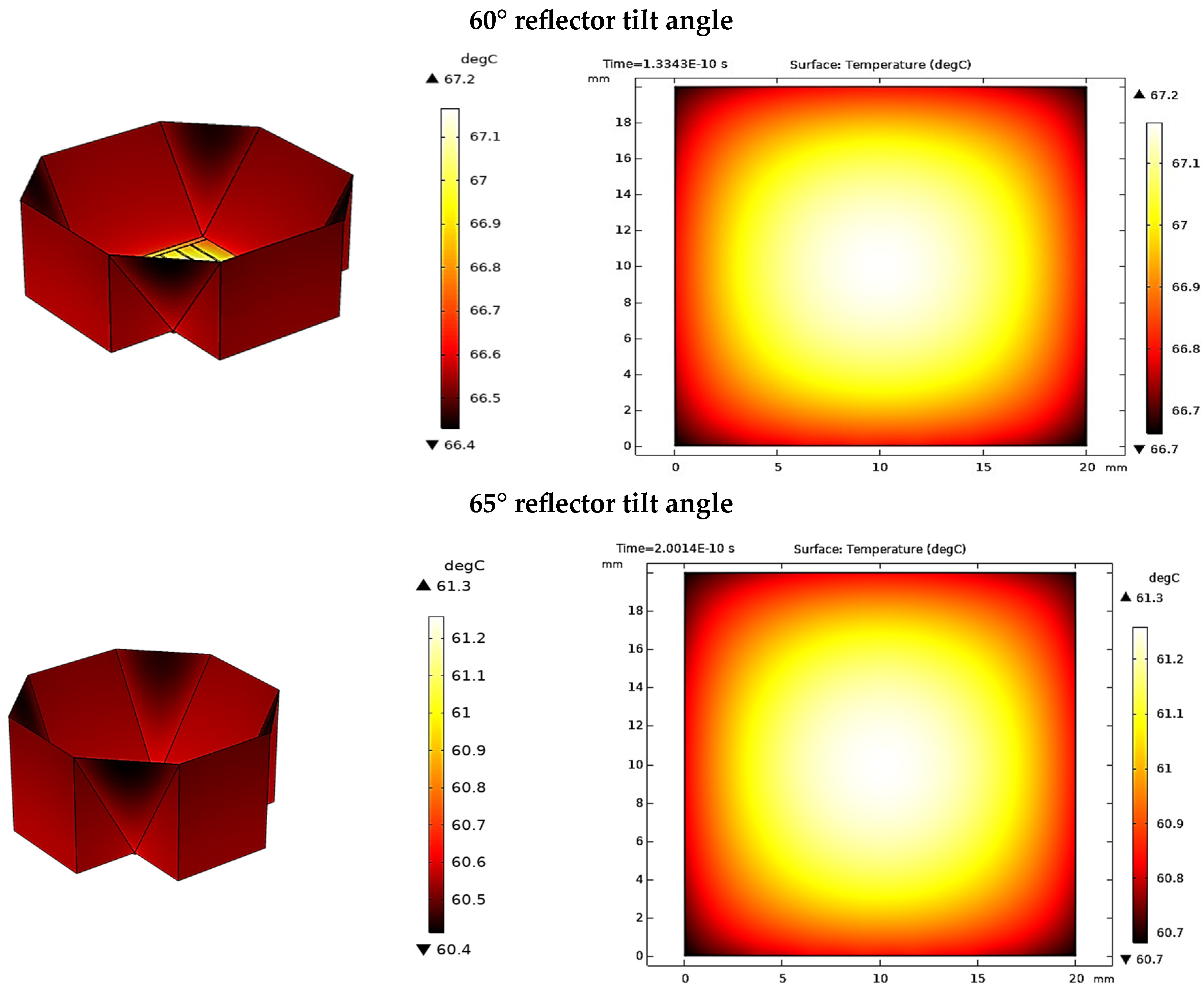
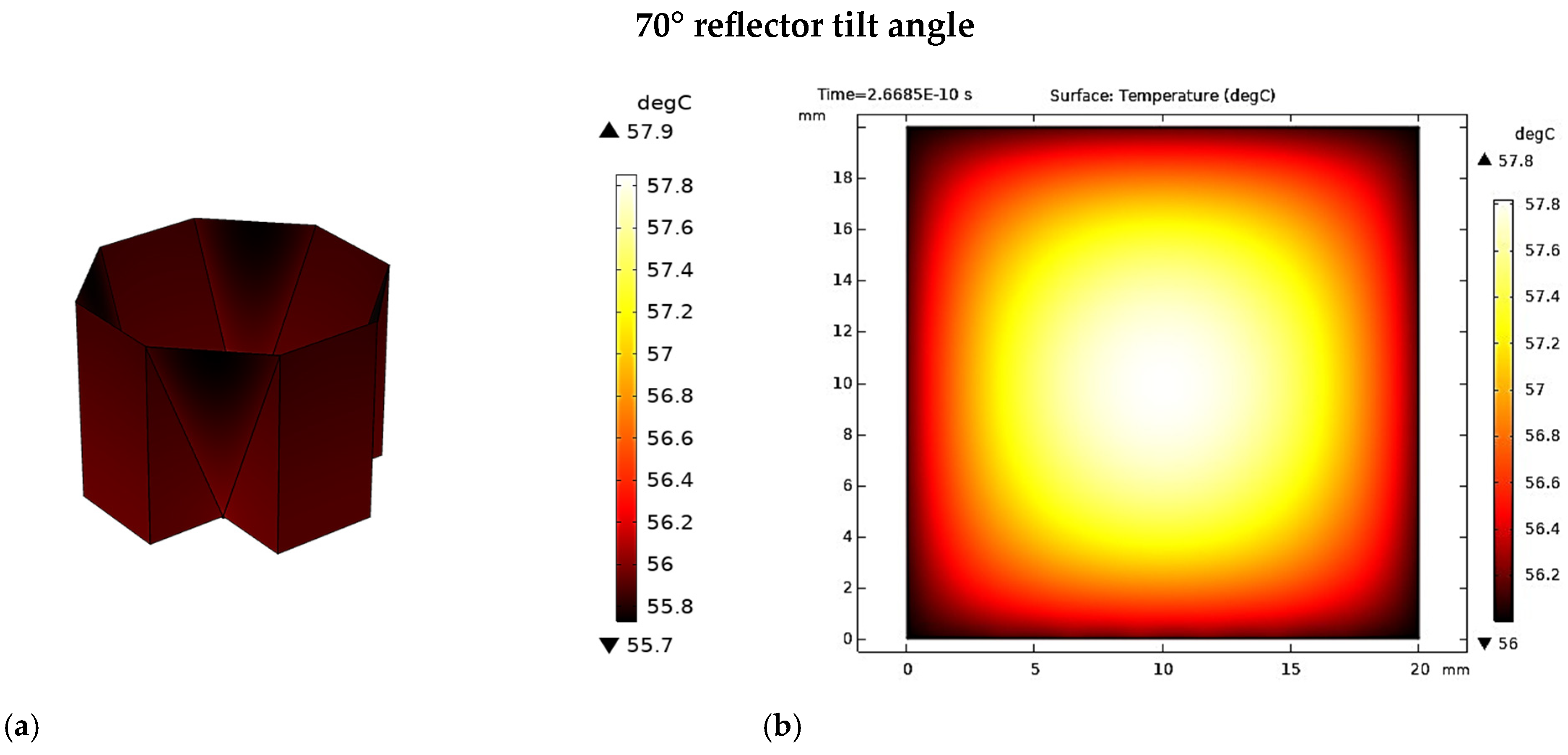
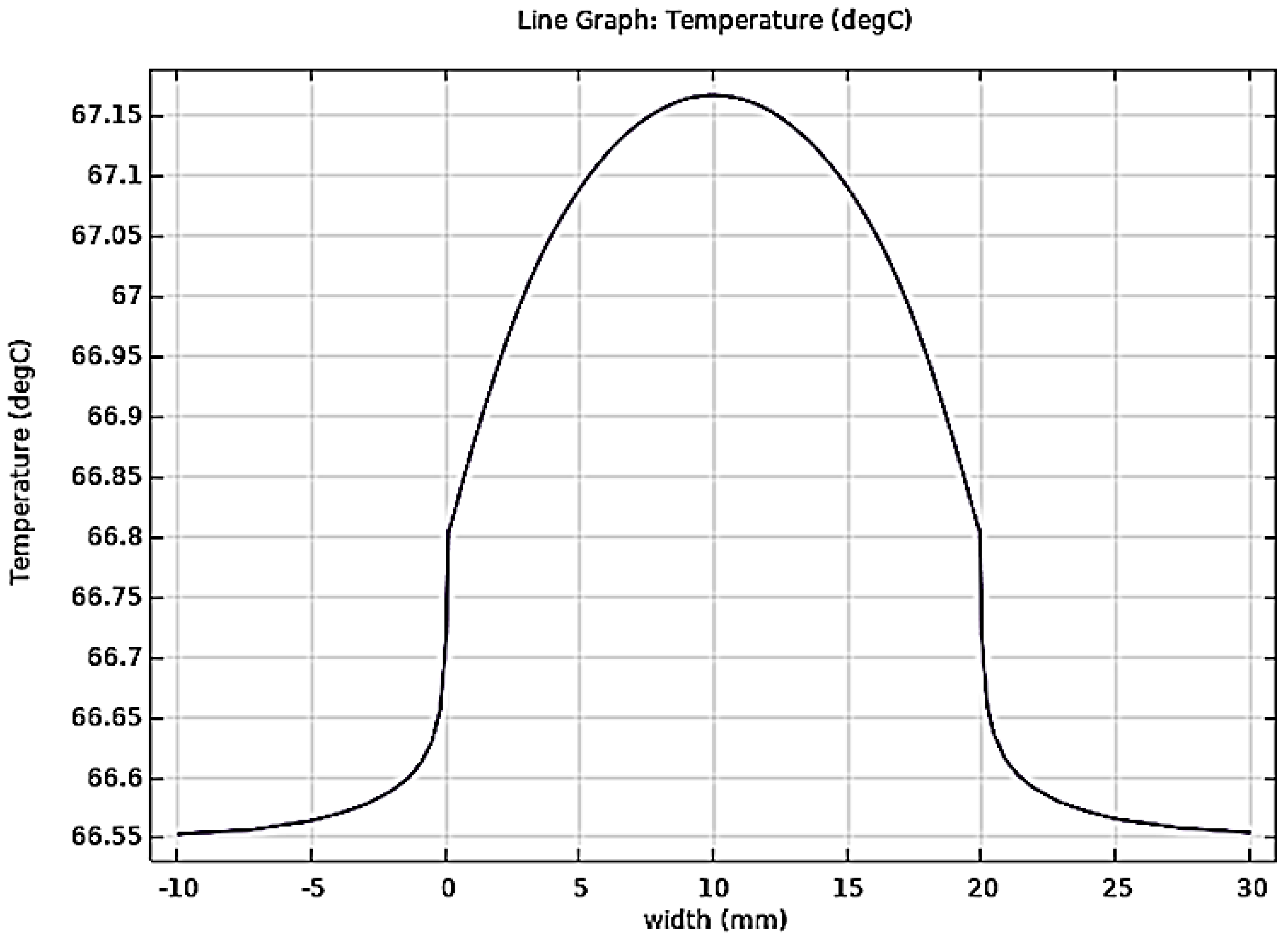
3.5. Heat Transfer Analysis
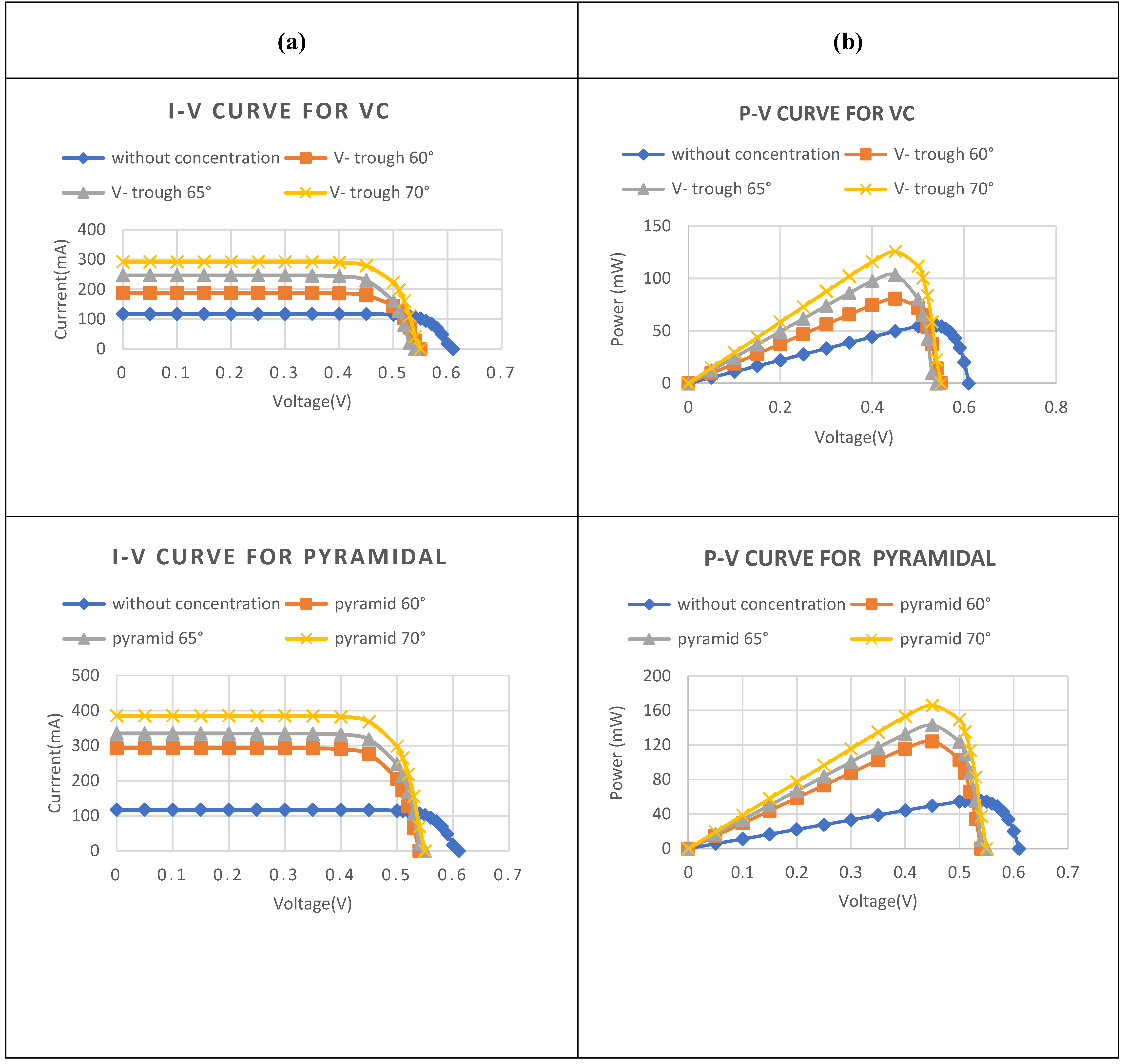
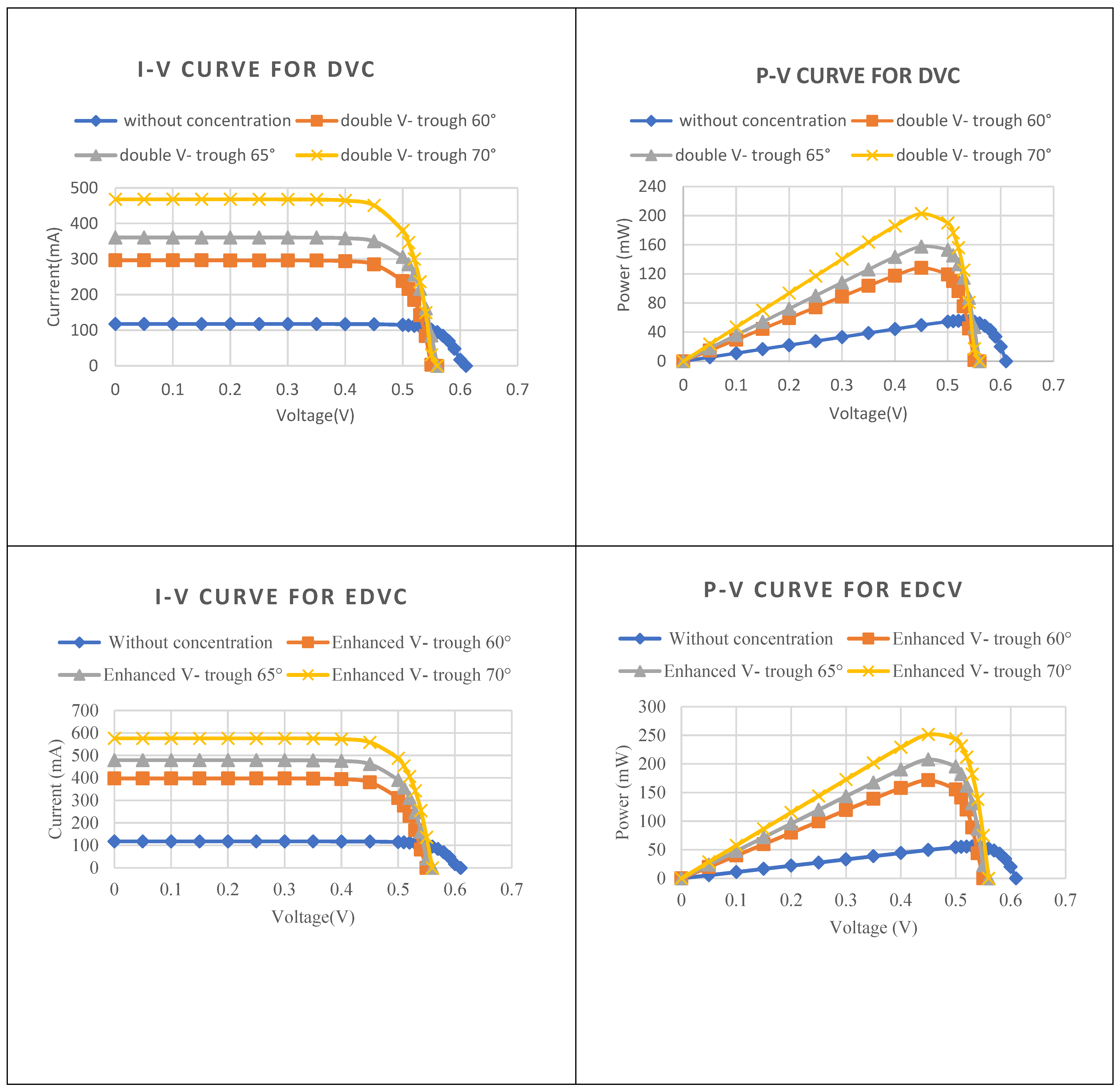
3.6. Electrical Analysis
4. Conclusions
- The present research establishes a complete numerical methodology for modeling, simulating, and evaluating the electric and opto-thermal behavior of the different configurations of V-trough-based low concentrating photovoltaic systems. These systems have the advantage of working in passive modes and ensuring uniform illumination distribution over cells without the risk of high thermal strains that may be applied to the entire system, and especially to the primary optics.
- The developed optical model is validated, and the ray-tracing module shows a high precision compared to the literature.
- The Enhanced Double V-trough design shows its superiority over all the existing designs. At an optimum tilt angle of 70°, this new design recorded the highest optical concentration ratio of 4.77 suns, with an optical efficiency of 89%.
- The short-circuit current of the Enhanced Double V-trough increased by 488% and had a drop of 11% compared to the design without concentration.
- The output power of the Enhanced Double V-trough recorded a spike of 452% compared to the design without concentration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamid, S.A.; Othman, M.Y.; Sopian, K.; Zaidi, S.H. An overview of photovoltaic thermal combination (PV/T combi) technology. Renew. Sustain. Energy Rev. 2014, 38, 212–222. [Google Scholar] [CrossRef]
- El Alimi, S.; Maatallah, T.; Ben Nasrallah, S. Break-even analysis and optimization of a stand-alone hybrid system with battery storage for residential load consumption—A case study. Renew. Sustain. Energy Rev. 2014, 37, 408–423. [Google Scholar] [CrossRef]
- Date, A.; Date, A.; Dixon, C.; Akbarzadeh, A. Progress of thermoelectric power generation systems: Prospect for small to medium scale power generation. Renew. Sustain. Energy Rev. 2014, 33, 371–381. [Google Scholar] [CrossRef]
- Byrne, J.; Taminiau, J.; Kurdgelashvili, L.; Kim, K.N. A review of the solar city concept and methods to assess rooftop solar electric potential, with an illustrative application to the city of Seoul. Renew. Sustain. Energy Rev. 2015, 41, 830–844. [Google Scholar] [CrossRef]
- Kumar, A.; Baredar, P.; Qureshi, U. Historical and recent development of photovoltaic thermal (PVT) technologies. Renew. Sustain. Energy Rev. 2015, 42, 1428–1436. [Google Scholar] [CrossRef]
- Tang, R.; Liu, X. Optical performance and design optimization of V-trough concentrators for photovoltaic applications. Sol. Energy 2011, 85, 2154–2166. [Google Scholar] [CrossRef]
- Tyagi, V.; Kaushik, S.; Tyagi, S. Advancement in solar photovoltaic/thermal (PV/T) hybrid collector technology. Renew. Sustain. Energy Rev. 2012, 16, 1383–1398. [Google Scholar] [CrossRef]
- Daghigh, R.; Ruslan, M.; Sopian, K. Advances in liquid based photovoltaic/thermal (PV/T) collectors. Renew. Sustain. Energy Rev. 2011, 15, 4156–4170. [Google Scholar] [CrossRef]
- Zondag, H. Flat-plate PV-Thermal collectors and systems: A review. Renew. Sustain. Energy Rev. 2008, 12, 891–959. [Google Scholar] [CrossRef]
- Hasan, M.A.; Sumathy, K. Photovoltaic thermal module concepts and their performance analysis: A review. Renew. Sustain. Energy Rev. 2010, 14, 1845–1859. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.; Smith, S.; Xu, J.; Yu, X. Review of R&D progress and practical application of the solar photovoltaic/thermal (PV/T) technologies. Renew. Sustain. Energy Rev. 2012, 16, 599–617. [Google Scholar]
- Chemisana, D. Building integrated concentrating photovoltaics: A review. Renew. Sustain. Energy Rev. 2011, 15, 603–611. [Google Scholar] [CrossRef]
- Zahedi, A. Review of modelling details in relation to low-concentration solar concentrating photovoltaic. Renew. Sustain. Energy Rev. 2011, 15, 1609–1614. [Google Scholar] [CrossRef]
- Vivar, M.; Clarke, M.; Pye, J.; Everett, V. A review of standards for hybrid CPV-thermal systems. Renew. Sustain. Energy Rev. 2011, 16, 443–448. [Google Scholar] [CrossRef]
- Singh, B.; Othman, M.Y. A review on photovoltaic thermal collectors. J. Renew. Sustain. Energy 2009, 1, 062702. [Google Scholar] [CrossRef]
- Chong, K.-K.; Lau, S.-L.; Yew, T.-K.; Tan, P.C.-L. Design and development in optics of concentrator photovoltaic system. Renew. Sustain. Energy Rev. 2013, 19, 598–612. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.; Tanweer, B.; Gandhidasan, P.; Rehman, S. A Combined Optical, Thermal and Electrical Performance Study of a V-Trough PV System—Experimental and Analytical Investigations. Energies 2015, 8, 2803–2827. [Google Scholar] [CrossRef]
- Xu, S.-J.; Wu, S.-Y.; Xiao, L.; Chen, Z.-L. Performance Assessment of Compound Parabolic Concentrating Photovoltaic System Based on Optical-Thermal-Electrical-Environmental Coupling. Energy 2023, 284, 129241. [Google Scholar] [CrossRef]
- Orynbassar, S.; Almen, D.; Mekhilef, S.; Kapparova, A.; Dosymbetova, G.; Nurgaliyev, M.; Saymbetov, A.; Ibraimov, M.; Kuttybay, N.; Yershov, E.; et al. Minimum Solar Tracking System for a Fresnel Lens-Based LCPV. Renew. Energy 2024, 237, 121607. [Google Scholar] [CrossRef]
- Benecke, M.; Van Dyk, E.; Vorster, F. Optical design of low concentrator photovoltaic modules. J. Energy S. Afr. 2013, 24, 46–50. [Google Scholar] [CrossRef]
- Ağbulut, Ü.; Gürel, A.E.; Ergün, A.; Ceylan, İ. Performance assessment of a V-trough photovoltaic system and prediction of power output with different machine learning algorithms. J. Clean. Prod. 2020, 268, 122–269. [Google Scholar] [CrossRef]
- Li, G.; Hua, Q.; Sun, L.; Khosravi, A.; Pabon, J.J.G. Thermodynamic Modeling and Optimization of Hybrid Linear Concentrating Photovoltaic and Mechanically Pumped Two-Phase Loop System. Appl. Energy 2022, 333, 120547. [Google Scholar] [CrossRef]
- Elsheniti, M.B.; Zaheer, S.; Zeitoun, O.; Alshehri, H.; AlRabiah, A.; Almutairi, Z. Experimental Evaluation of a Solar Low-Concentration Photovoltaic/Thermal System Combined with a Phase-Change Material Cooling Technique. Appl. Sci. 2022, 13, 25. [Google Scholar] [CrossRef]
- Parupudi, R.V.; Singh, H.; Kolokotroni, M.; Tavares, J. Long term performance analysis of low concentrating photovoltaic (LCPV) systems for building retrofit. Appl. Energy 2021, 300, 117412. [Google Scholar] [CrossRef]
- Parupudi, R.V.; Singh, H.; Kolokotroni, M. Low Concentrating Photovoltaics (LCPV) for buildings and their performance analyses. Appl. Energy 2020, 279, 115839. [Google Scholar] [CrossRef]
- Muhammad-Sukki, F.; Farooq, H.; Abu-Bakar, S.H.; Ardila-Rey, J.A.; Sellami, N.; Kilpatrick, C.; Muhtazaruddin, M.N.; Bani, N.A.; Zulkipli, M. Mathematical Modelling of a Static Concentrating Photovoltaic: Simulation and Experimental Validation. Appl. Sci. 2021, 11, 3894. [Google Scholar] [CrossRef]
- Ustaoglu, A.; Ozbey, U.; Torlaklı, H. Numerical investigation of concentrating photovoltaic/thermal (CPV/T) system using compound hyperbolic –trumpet, V-trough and compound parabolic concentrators. Renew. Energy 2020, 152, 1192–1208. [Google Scholar] [CrossRef]
- Taniguchi, T.; Ishibe, T.; Naruse, N.; Mera, Y.; Alam, M.; Sawano, K.; Nakamura, Y. High Thermoelectric Power Factor Realization in Si-Rich SiGe/Si Superlattices by Super-Controlled Interfaces. ACS Appl. Mater. Interfaces 2020, 12, 25428–25434. [Google Scholar] [CrossRef]
- Basset, P.; Galayko, D.; Paracha, A.M.; Marty, F.; Dudka, A.; Bourouina, T. A Batch-Fabricated and Electret-Free Silicon Electrostatic Vibration Energy Harvester. J. Micromech. Microeng. 2009, 19, 115025. [Google Scholar] [CrossRef]
- Hollands, K. A concentrator for thin-film solar cells. Sol. Energy 1971, 13, 149–163. [Google Scholar] [CrossRef]
- Amanlou, Y.; Hashjin, T.T.; Ghobadian, B.; Najafi, G.; Mamat, R. A comprehensive review of Uniform Solar Illumination at Low Concentration Photovoltaic (LCPV) Systems. Renew. Sustain. Energy Rev. 2016, 60, 1430–1441. [Google Scholar] [CrossRef]
- Al-Najideen, M.; Al-Shidhani, M.; Min, G. Optimum design of V-trough solar concentrator for photovoltaic applications. In Proceedings of the 15th International Conference on Concentrator Photovoltaic Systems (CPV-15), Fes, Morocco, 25–27 March 2019. [Google Scholar]
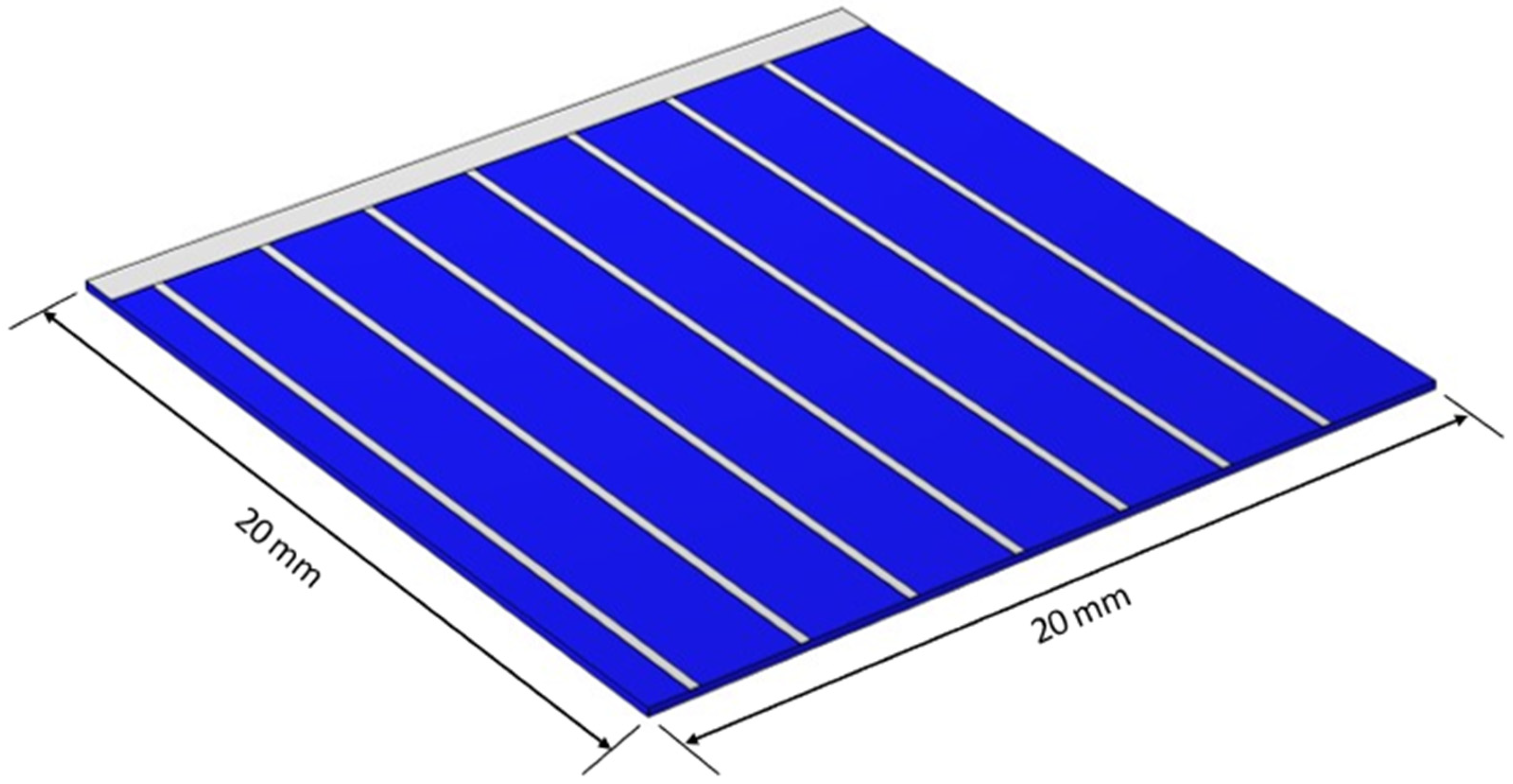
| Layer | Material | Dimensions (mm) | Thickness (mm) | Thermal Conductivity (W/mk) | Density (kg/m3) | Real Refractive Index | Imaginary Refractive Index |
|---|---|---|---|---|---|---|---|
| Cell | Silicon | 20 × 20 | 0.2 | 130 | 2330 | 3.723 | 7.59 × 10−3 |
| Busbar | Aluminum | 33 × 2 | 0.015 | 202.4 | 2719 | 1.1978 | 7.617 |
| Reflector | Aluminum | 20 × 20 | 2 | 202.4 | 2719 | 1.1978 | 7.617 |
| ψ | |||||
|---|---|---|---|---|---|
| CVC | DVC | Pyramidal | EDVC | ||
| 60° | 1 | 2× | 3× | 4× | 3.5× |
| 65° | 1.521 | 2.29× | 3.57× | 5.22× | 4.39× |
| 70° | 2.24 | 2.56× | 4.06× | 6.41× | 5.23× |
| ψ | ||||
|---|---|---|---|---|
| CVC | Pyramidal | DVC | ||
| 60° | 1 | 2× | 4× | 3× |
| 65° | 1.521 | 2.29× | 5.22× | 3.57× |
| 68° | 2.013 | 2.51× | 6.29× | 4.02× |
| 71° | 3.164 | 3.06× | 9.36× | 5.12× |
| Types | [31] | Validation | |
|---|---|---|---|
| (%) | (%) | Absolute Mean Relative Error (%) | |
| V-trough | 0.36 | 90.8 | 90.44 |
| Pyramidal | 1.57 | 49.41 | 50.2 |
| Double V-trough | 0.011 | 88.8 | 88.81 |
| Tilt Angle [%] | Geometrical Cr [x] | Optical Cr [suns] | Optical Efficiency [%] |
|---|---|---|---|
| 60 | 3.5 | 3.21 | 91.7% |
| 65 | 4.39 | 3.86 | 87.9% |
| 70 | 5.23 | 4.66 | 89.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maatallah, T.; Ali, S. Numerical Investigation of the Opto-Electric and Thermal Performance of a Newly Enhanced Double V-Trough Low Concentration Photovoltaic System for Sustainable Solar Energy Utilization. Sustainability 2025, 17, 2537. https://doi.org/10.3390/su17062537
Maatallah T, Ali S. Numerical Investigation of the Opto-Electric and Thermal Performance of a Newly Enhanced Double V-Trough Low Concentration Photovoltaic System for Sustainable Solar Energy Utilization. Sustainability. 2025; 17(6):2537. https://doi.org/10.3390/su17062537
Chicago/Turabian StyleMaatallah, Taher, and Sajid Ali. 2025. "Numerical Investigation of the Opto-Electric and Thermal Performance of a Newly Enhanced Double V-Trough Low Concentration Photovoltaic System for Sustainable Solar Energy Utilization" Sustainability 17, no. 6: 2537. https://doi.org/10.3390/su17062537
APA StyleMaatallah, T., & Ali, S. (2025). Numerical Investigation of the Opto-Electric and Thermal Performance of a Newly Enhanced Double V-Trough Low Concentration Photovoltaic System for Sustainable Solar Energy Utilization. Sustainability, 17(6), 2537. https://doi.org/10.3390/su17062537