Leveraging the GEV Model to Estimate Flood Due to Extreme Rainfall in Ungauged Dry Catchments of the Gobi Region
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Dataset
2.2. Methods
2.2.1. Trend Analysis
2.2.2. GEV Model for Extreme Precipitation
2.2.3. Rainfall Intensity Method for Flood Calculation
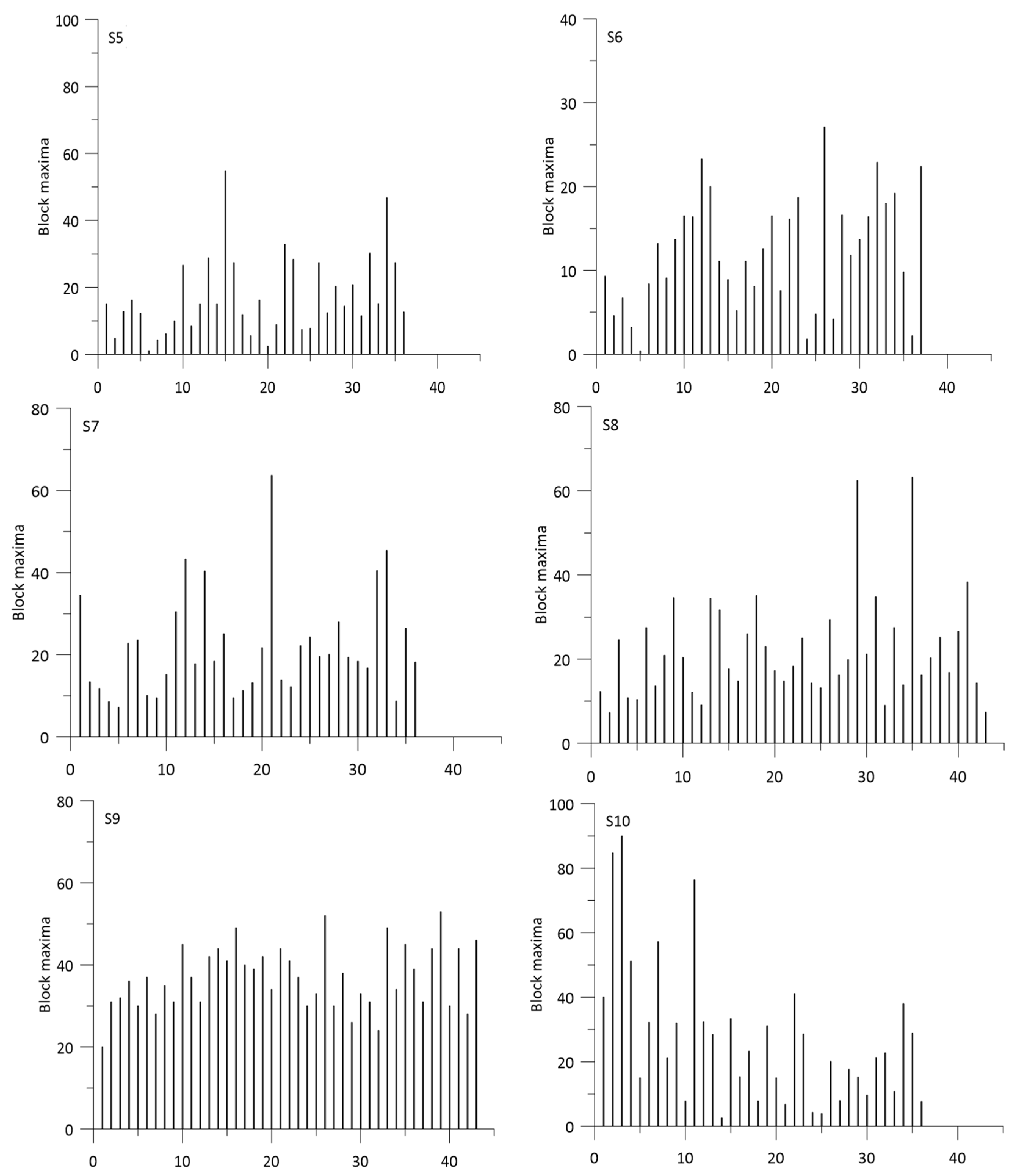
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loyeh, N.S.; Bavani, A.M. Daily Maximum Runoff Frequency Analysis under Non-Stationary Conditions Due to Climate Change in the Future Period: Case Study Ghareh Sou Basin. J. Water Clim. Change 2021, 12, 1910–1927. [Google Scholar] [CrossRef]
- Fan, M. Making Water Available in Mongolia at the Right Time, at the Right Place, and in the Right Quality; ADB Brief No. 140; Asian Development Bank: Mandaluyong, Philippines, 2020. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- National Statistical Office. Baseline study of Umnugobi aimag report, 2018. In Changes in the Environmental Indicators of Umnugobi in 2008–2018; National Statistical Office: Ulaanbaatar, Mongolia, 2018. [Google Scholar]
- Baldi, M.; Amin, D.; Al Zayed, I.S.; Dalu, G. Climatology and Dynamical Evolution of Extreme Rainfall Events in the Sinai Peninsula—Egypt. Sustainability 2020, 12, 6186. [Google Scholar] [CrossRef]
- Henny, L.; Thorncroft, C.D.; Hsu, S.S.; Bosart, L.F. Extreme Rainfall in Taiwan: Seasonal Statistics and Trends. J. Clim. 2021, 34, 4711–4731. [Google Scholar] [CrossRef]
- Li, X.; Zhang, K.; Gu, P.; Feng, H.; Yin, Y.; Chen, W.; Cheng, B. Changes in precipitation extremes in the Yangtze River Basin during 1960–2019 and the association with global warming, ENSO, and local effects. Sci. Total Environ. 2021, 760, 144244. [Google Scholar] [CrossRef] [PubMed]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2023: Synthesis Report. In Contribution of Working Groups I, II, and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2023; Available online: https://www.ipcc.ch/report/ar6/syr/ (accessed on 5 December 2024).
- Kartal, V.; Nones, M. Assessment of Meteorological, Hydrological and Groundwater Drought in the Konya Closed Basin, Türkiye. Environ. Earth Sci. 2024, 83, 285. [Google Scholar] [CrossRef]
- Antokhina, O.; Antokhin, P.; Gochakov, A.; Zbirannik, A.; Gazimov, T. Atmospheric Circulation Patterns Associated with Extreme Precipitation Events in Eastern Siberia and Mongolia. Atmosphere 2023, 14, 480. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Liu, Y. Hydroclimatic Variability over Eurasia during the 21st Century: A Review. Earth Sci. Rev. 2019, 199, 102972. [Google Scholar] [CrossRef]
- Zorigt, M.; Gankhuu, B.; Ganjuur, S.; Kenner, S.; Nergui, S.; Markus, H. Runoff dynamics of the upper Selenge basin, a major water source for Lake Baikal, under a warming climate. Reg. Environ. Change 2019, 19, 2609–2619. [Google Scholar] [CrossRef]
- Ying, H.; Zhang, H.; Zhao, J.; Shan, Y.; Zhang, Z.; Guo, X.; Rihan, W.; Deng, G. Effects of spring and summer extreme climate events on the autumn phenology of different vegetation types of Inner Mongolia, China, from 1982 to 2015. Ecol. Indic. 2020, 111, 105974. [Google Scholar] [CrossRef]
- Gong, D.Y.; Shi, P.J.; Wang, J.A. Daily precipitation changes in the semi-arid region over northern China. J. Arid Environ. 2004, 59, 771–784. [Google Scholar] [CrossRef]
- Zhai, P.; Zhang, X.; Wan, H.; Pan, X. Trends in Total Precipitation and Frequency of Daily Precipitation Extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Liu, B.; Xu, M.; Henderson, M.; Gong, D. Changes in precipitation over China during the past half-century. Int. J. Climatol. 2011, 31, 111–123. [Google Scholar]
- Hiraga, Y.; Tahara, R.; Meza, J. A methodology to estimate Probable Maximum Precipitation (PMP) under climate change using a numerical weather model. J. Hydrol. 2025, 652, 132659. [Google Scholar] [CrossRef]
- Rai, P.; Bangelesa, F.; Abel, D.; Ziegler, K.; Huang, J.; Schaffhauser, T.; Polinger, F.; Disse, M.; Paeth, H. Extreme precipitation and temperature indices under future climate change in central Asia based on CORDEX-CORE. Theor. Appl. Climatol. 2024, 155, 6015–6039. [Google Scholar] [CrossRef]
- Vandandorj, S.; Munkhjargal, E.; Boldgiv, B.; Gantsetseg, B. Changes in event number and duration of rain types over Mongolia from 1981 to 2014. Environ. Earth Sci. 2016, 76, 70. [Google Scholar] [CrossRef]
- Davi, N.; Jacoby, G.; Fang, K.; Li, J.; D’Arrigo, R.; Baatarbileg, N.; Robinson, D. Reconstructing drought variability for Mongolia based on a large- scale tree ring network:1520–1993. J. Geophys. Res. 2010, 115, D22103. [Google Scholar] [CrossRef]
- Kang, S.; Huang, J.; Zhang, F. Projections of future precipitation changes in Central Asia based on CMIP5 climate models. Environ. Res. Lett. 2015, 10, 064016. [Google Scholar]
- Mijiddorj, T.; Davaa, G.; Tumenjargal, E. Assessment of hydroclimatic variability in Mongolia using observational data. Water 2020, 12, 2392. [Google Scholar]
- World Bank. Climate Risk Profile: Central Asia; World Bank Group Publications: Chicago, IL, USA, 2021. [Google Scholar]
- Tanprayoon, E.; Tonggumnead, U.; Aryuyuen, S. A new extension of generalized extreme value distribution: Extreme value analysis and return level estimation of the rainfall data. Trends Sci. 2023, 20, 4034. [Google Scholar] [CrossRef]
- Cavanaugh, N.R.; Gershunov, A.; Panorska, A.K.; Kozubowski, T.J. The probability of distribution of intense daily precipitation. Geophys. Res. Lett. 2015, 42, 1560–1567. [Google Scholar] [CrossRef]
- Paula, F.D.; Giugni, M.; Pugliese, F.; Annis, A.; Nardi, F. EV Parameter Estimation and Stationery vs. Non-Stationary Analysis of Extreme Rainfall in African Test Cities. Hydrology 2018, 5, 28. [Google Scholar] [CrossRef]
- Ulrich, J.; Faur, F.S.; Rust, H.W. Modeling seasonal variations of extreme rainfall on different time scales in Germany. Hydrol. Earth Syst. Sci. 2021, 25, 6133–6149. [Google Scholar] [CrossRef]
- Hossain, I.; Khastagir, A.; Aktar, M.N.; Imteaz, M.A. Comparison of estimation techniques for generalized extreme value (GEV) distribution parameters: A case study with Tasmanian rainfall. Int. J. Environ. Sci. Technol. 2022, 19, 7737–7750. [Google Scholar] [CrossRef]
- Belhiri, A.; Kim, J.H. Advanced frequency analysis techniques in modeling extreme rainfall events. J. Hydrol. Res. 2023, 78, 12–25. [Google Scholar]
- Gründemann, G.J.; Zorzetto, E.; Hylke, E.; Bec, H.E.; Schleiss, M.; van de Giesen, N.; Marani, M.; Ruud, J.; van der Ent, R. Extreme precipitation return levels for multiple durations on a global scale. J. Hydrol. 2023, 621, 129558. [Google Scholar] [CrossRef]
- Back, A.J.; Bonfante, F.M. Evaluation of generalized extreme value and Gumbel distributions for estimating maximum daily rainfall. Braz. J. Environ. Sci. 2021, 56, 654–664. [Google Scholar] [CrossRef]
- Hanum, H.; Djuraidah, A.H.W.; Mangku, I.W. Modeling extreme rainfall with Gamma-Paretto distribution. Appl. Math. Sci. 2015, 9, 6029–6039. [Google Scholar] [CrossRef]
- Min, J.L.; Halim, S.A. Rainfall modelling using generalized extreme value distribution with cyclic covariate. Math. Stat. 2020, 8, 762–772. [Google Scholar] [CrossRef]
- Salinas, J.L.; Castellarin, A.; Kohnová, S.; Kjeldsen, T.R. Regional parent flood frequency distributions in Europe-Part 2: Climate and scale controls. Hydrol. Earth Syst. Sci. 2014, 18, 4391–4401. [Google Scholar] [CrossRef]
- He, S.; Li, Z.; Liu, X. An improved GEV boosting method for imbalanced data classification with application to short-term rainfall prediction. J. Hydrol. 2023, 617 Pt B, 128882. [Google Scholar] [CrossRef]
- Chaudhuri, R.R.; Sharma, P. Addressing uncertainty in extreme rainfall intensity for semi-arid urban regions: Case study of Delhi, India. Nat. Hazards 2020, 104, 2307–2324. [Google Scholar] [CrossRef]
- Nguyen, V.T.V.; Nguyen, T.H. Statistical Modeling of Extreme Rainfall Processes (SMExRain): A Decision Support Tool for Extreme Rainfall Frequency Analyses. Procedia Eng. 2016, 154, 624–630. [Google Scholar] [CrossRef]
- Das, S.; Zhu, D.; Yin, Y. Comparison of mapping approaches for estimating extreme precipitation of any return period at ungauged locations. Stoch. Environ. Res. Risk Assess. 2020, 34, 1175–1196. [Google Scholar] [CrossRef]
- Roslan, S.N.; Siadatmousavi, S.M.; Naderi, A. Extreme value analysis for waves in the Persian Gulf: Skill assessment of different methods for a fetch-limited basin. Reg. Stud. Mar. Sci. 2023, 57, 102576. [Google Scholar]
- National Statistical Office. Social Indicator Sample Survey 2018; National Statistical Office: Ulaanbaatar, Mongolia, 2018.
- Chepelianskaia, O. Mongolia—Climate Change and Disaster Risk Profile; United Nations Economic and Social Commission for Asia and the Pacific (ESCAP): Bangkok, Thailand, 2022. [Google Scholar]
- Dagvadorj, D.; Batjargal, Z.; Natsagdorj, L. Mongolian Second Assessment Report on Climate Change 2014; Ministry of Environment and Tourism: Ulaanbaatar, Mongolia, 2014.
- Mann, H.B. Non-Parametric Test against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, UK, 1975. [Google Scholar]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Embrechts, P.; Klüppelberg, C.; Mikosch, T. Modelling Extremal Events for Insurance and Finance; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- McNeil, A.J.; Frey, R.; Embrechts, P. Quantitative Risk Management: Concepts, Techniques, and Tools; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- National Construction Committee. Norms and Rules for Calculating Hydrological Definitions; National Construction Committee: Ulaanbaatar, Mongolia, 1986.
- Davaa, G. Surface Water Regime and Resources of Mongolia; Admon Printing: Ulaanbaatar, Mongolia, 2015; ISBN 978-99973-0-767-5. [Google Scholar]
- Batima, P.; Dagvadorj, D. Climate Change and Its Impacts in Mongolia; JEMR Publication; National Agency for Meteorology, Hydrology, and Environmental Monitoring: Ulaanbaatar, Mongolia, 2000; 227p.
- Dashdorj, B. Peak flow frequency analysis of the Orkhon River, Mongolia. In Proceedings of the Second International Conference on Resources and Technology (RESAT 2023), Ulaanbaatar, Mongolia, 19–20 June 2023; Lkhamsuren, A., Dashdorj, B., Tsend, C., Eds.; Advances in Engineering Research. Atlantis Press: Dordrecht, The Netherlands, 2023; pp. 133–145. [Google Scholar]
- Trenberth, K.E. The impact of climate change and variability on heavy precipitation, floods, and droughts. Encycl. Hydrol. Sci. 2005, 17, 1–11. [Google Scholar]
- Pilgrim, D.H.; Cordery, I. Flood Runoff. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; Chapter 9; pp. 1–42. [Google Scholar]
- Tong, S.; Li, X.; Zhang, J.; Bao, Y.; Bao, Y.; Li, N.; Si, A. Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci. Total Environ. 2019, 649, 75–89. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.; Yang, X. Recent changes in heavy rainfall events in East Asia: A response to anthropogenic climate change. Clim. Change 2021, 166, 78. [Google Scholar]
- Kharin, V.V.; Zwiers, F.W. Estimating Extremes in Transient Climate Change Simulations. J. Clim. 2005, 18, 1156–1173. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Selection of the best fit flood frequency distribution and parameter estimation procedure: A case study for Tasmania in Australia. Stoch. Environ. Res. Risk Assess. 2011, 25, 415–428. [Google Scholar] [CrossRef]
- Fu, G.; Yu, J.; Yu, X.; Ouyang, R.; Zhang, Y.; Wang, P.; Liu, W.; Min, L. Temporal variation of extreme rainfall events in China, 1961–2009. J. Hydrol. 2013, 487, 48–59. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions: A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
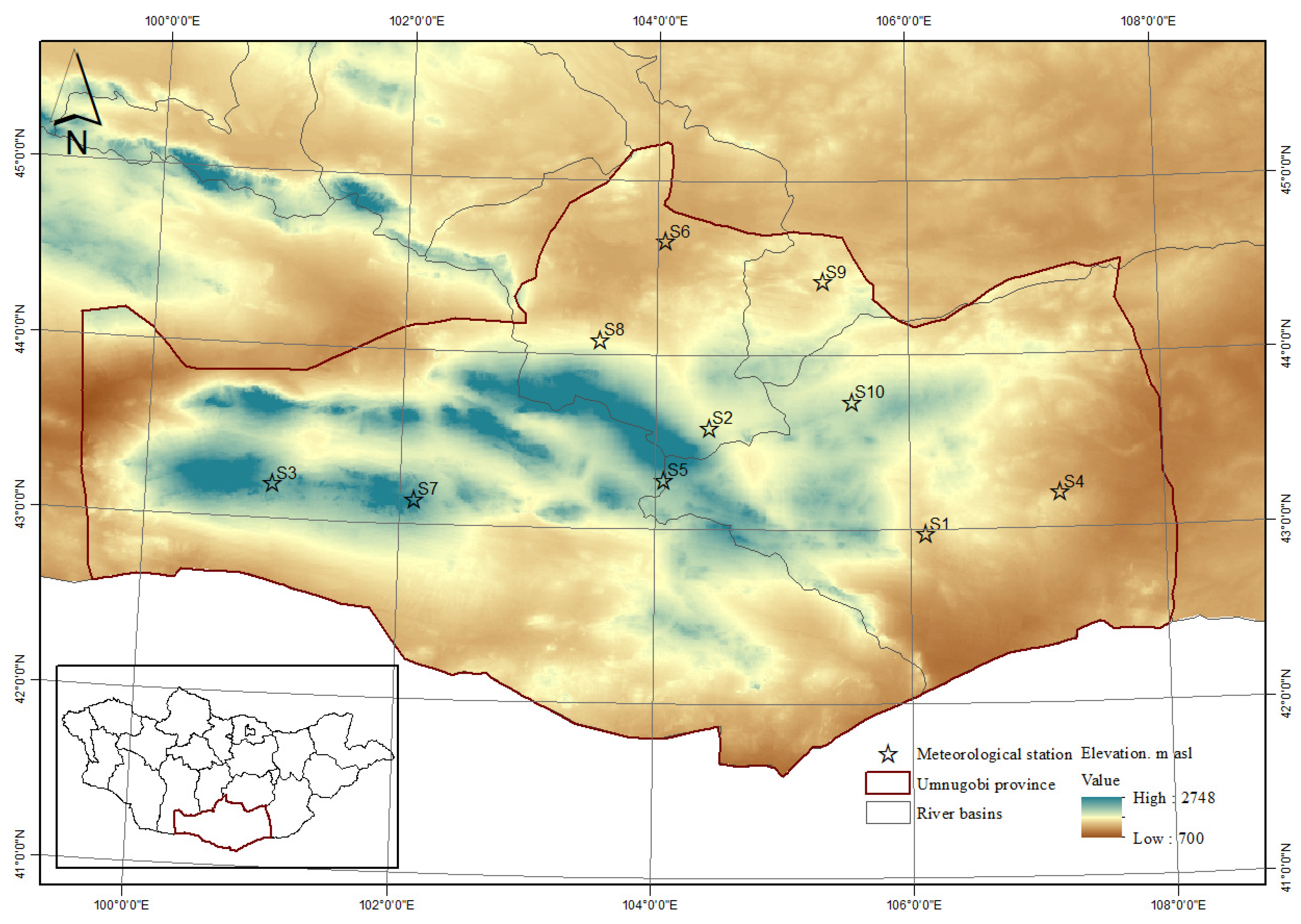




| No. | Station Name | Station Code | Elevation, m asl | Natural Zone |
|---|---|---|---|---|
| 1 | Bayan-Ovoo | S1 | 1179 | Desert |
| 2 | Dalanzadgad | S2 | 1465 | Desert |
| 3 | Gurvantes | S3 | 1726 | Desert steppe |
| 4 | Khanbogd | S4 | 1115 | Desert |
| 5 | Khurmen | S5 | 1701 | Desert steppe |
| 6 | Mandal-Ovoo | S6 | 1084 | Desert steppe |
| 7 | Noyon | S7 | 1960 | Desert steppe |
| 8 | Saikhan | S8 | 1328 | Desert steppe |
| 9 | Tsogt-Ovoo | S9 | 1287 | Desert steppe |
| 10 | Tsogttsetsii | S10 | 1480 | Desert steppe |
| No. | Code of the Dry Beds | Coordinates | Catchment Area | Length | Slope | |
|---|---|---|---|---|---|---|
| Longitude | Latitude | S, km2 | L, km | J, ‰ | ||
| 1 | OP1 | 105.57018 | 43.64322 | 16.9 | 7.9 | 12.4 |
| 2 | OP2 | 105.60599 | 43.64468 | 5.0 | 2.5 | 1.26 |
| 3 | OP3 | 105.63950 | 43.63189 | 9.4 | 4.9 | 16.2 |
| 4 | OP4 | 105.69949 | 43.57616 | 21.1 | 6.1 | 10.4 |
| 5 | OP5 | 105.70716 | 43.56900 | 30.6 | 7.8 | 6.88 |
| 6 | OP6 | 105.79048 | 43.52828 | 31.0 | 16.6 | 10.4 |
| 7 | OP7 | 106.15165 | 43.08921 | 27.9 | 7.6 | 6.20 |
| 8 | OP8 | 106.41030 | 43.02717 | 1.0 | 1.4 | 17.8 |
| 9 | OP9 | 106.41524 | 43.02572 | 1.4 | 1.9 | 10.2 |
| 10 | OP10 | 106.49008 | 43.01194 | 21.6 | 5.1 | 5.82 |
| 11 | OP11 | 106.52481 | 43.01148 | 1.1 | 1.4 | 21.4 |
| 12 | OP12 | 106.56545 | 43.01076 | 6.1 | 3.8 | 9.39 |
| 13 | OP13 | 106.58033 | 43.01038 | 1.9 | 1.8 | 16.2 |
| 14 | OP14 | 106.61200 | 43.01063 | 7.8 | 5.6 | 10.7 |
| 15 | OP15 | 106.61437 | 43.01077 | 5.9 | 4.9 | 12.3 |
| 16 | OP16 | 106.64359 | 43.01625 | 2.5 | 1.1 | 10.8 |
| 17 | OP17 | 106.64596 | 43.01674 | 3.0 | 1.5 | 12.8 |
| 18 | OP18 | 106.70157 | 43.01905 | 8.3 | 3.2 | 7.8 |
| 19 | OP19 | 106.73463 | 43.00953 | 24.3 | 6.2 | 7.3 |
| 20 | OP20 | 106.94933 | 42.93028 | 9.7 | 4.3 | 6.9 |
| 21 | OP21 | 106.98352 | 42.84089 | 3.4 | 2.2 | 8.3 |
| 22 | OP22 | 107.02945 | 42.77521 | 1.5 | 1.8 | 8.6 |
| 23 | OP23 | 107.13343 | 42.66283 | 80 | 17.9 | 9.5 |
| 24 | OP24 | 107.36268 | 42.48558 | 49.4 | 7.8 | 4.5 |
| 25 | OP25 | 107.43750 | 42.46302 | 95.2 | 16.9 | 4.3 |
| 26 | OP26 | 107.55582 | 42.44049 | 26.8 | 9.2 | 6.0 |
| 27 | OP27 | 107.61814 | 42.41307 | 11.5 | 3.5 | 6.1 |
| Stations Code | Z-Value | Sen’s Slope | p-Value |
|---|---|---|---|
| S1 | 1.08 | 0.12 | 0.27 |
| S2 | −0.41 | −0.03 | 0.68 |
| S3 | −0.88 | −0.07 | 0.37 |
| S4 | 1.42 | 0.09 | 0.14 |
| S5 | 2.05 | 0.30 | 0.04 |
| S6 | 1.68 | 0.19 | 0.09 |
| S7 | 1.37 | 0.23 | 0.16 |
| S8 | 1.04 | 0.12 | 0.29 |
| S9 | 0.67 | 0.06 | 0.53 |
| S10 | −2.18 | −0.62 | 0.02 |
| Station Code | Maximum Livelihood | ||
|---|---|---|---|
| Location (µ) | Scale (σ) | Shape (ξ) | |
| S1 | 11.5 | 5.5 | 0.1 |
| S2 | 27.9 | 5.1 | −0.1 |
| S3 | 33.7 | 7.3 | −0.2 |
| S4 | 27.9 | 5.1 | −0.1 |
| S5 | 11.3 | 8.1 | 0.2 |
| S6 | 9.4 | 6.2 | −0.2 |
| S7 | 15.4 | 7.3 | 0.2 |
| S8 | 16.1 | 8.0 | 0.1 |
| S9 | 33.7 | 7.2 | −0.2 |
| S10 | 16.5 | 12.7 | 0.2 |
| No. | Station Code | Return Level 100-Years |
|---|---|---|
| 1 | S1 | 44.6 |
| 2 | S2 | 63.1 |
| 3 | S3 | 68.4 |
| 4 | S4 | 46.5 |
| 5 | S5 | 79.1 |
| 6 | S6 | 27.8 |
| 7 | S7 | 79.4 |
| 8 | S8 | 71.1 |
| 9 | S9 | 54.1 |
| 10 | S10 | 130.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bat-Erdene, M.; Zorigt, M.; Dambaravjaa, O.; Dechinlkhundev, D.; Sumiya, E.; Nones, M. Leveraging the GEV Model to Estimate Flood Due to Extreme Rainfall in Ungauged Dry Catchments of the Gobi Region. Sustainability 2025, 17, 2500. https://doi.org/10.3390/su17062500
Bat-Erdene M, Zorigt M, Dambaravjaa O, Dechinlkhundev D, Sumiya E, Nones M. Leveraging the GEV Model to Estimate Flood Due to Extreme Rainfall in Ungauged Dry Catchments of the Gobi Region. Sustainability. 2025; 17(6):2500. https://doi.org/10.3390/su17062500
Chicago/Turabian StyleBat-Erdene, Myagmarsuren, Munkhtsetseg Zorigt, Oyunbaatar Dambaravjaa, Dorjsuren Dechinlkhundev, Erdenesukh Sumiya, and Michael Nones. 2025. "Leveraging the GEV Model to Estimate Flood Due to Extreme Rainfall in Ungauged Dry Catchments of the Gobi Region" Sustainability 17, no. 6: 2500. https://doi.org/10.3390/su17062500
APA StyleBat-Erdene, M., Zorigt, M., Dambaravjaa, O., Dechinlkhundev, D., Sumiya, E., & Nones, M. (2025). Leveraging the GEV Model to Estimate Flood Due to Extreme Rainfall in Ungauged Dry Catchments of the Gobi Region. Sustainability, 17(6), 2500. https://doi.org/10.3390/su17062500








