Public Transport Planning Using Modified Ant Colony Optimization

Abstract

Planning sustainable public transport is a crucial aspect of the efficient performance of the entire transport network. This paper presents a method for planning public transport routes using modified ant colony optimization. The individual objective function is created, which determines the effort needed to cover the route. This function takes into account real-world parameters such as driving time, route length, delays, and attractiveness more dynamically and flexibly. The application of the tool is described using an example of one of the most energy-efficient means of transport. The results made it possible to reduce the effort needed for the same line by 11.5% compared to the current route.

1. Introduction

The transport planning process, especially for public transport, is a very important element in the functioning of entire transport networks and aims for the correct development of transport supply systems [1,2]. In urban agglomerations, sustainable public transport planning is particularly important. The main characteristics of efficient and sustainable public transport include speed, reliability, convenience, cost-effectiveness, and minimal environmental impact. Using these characteristics, it is possible to travel efficiently within agglomeration.

However, despite continuous research and various measures to improve traffic conditions, public transport still faces numerous challenges. These issues are often experienced during daily trips to school, work, medical appointments, and other destinations. The problem is often more visible and perceptible as the network becomes larger and more complex. As a result, many people choose individual transport, leading to increased car traffic in cities and causing severe congestion during peak hours. It is worth adding that an increase in the number of cars in cities does not only mean more congestion on the roads, but also an increase in air pollution, which has a negative impact on the health of residents [3,4,5,6].

Therefore, as mentioned, the issue of improving transport networks is the subject of many studies and much research. The public transport planning process can take place through an initial assessment of current technical and economic solutions [7,8,9,10,11] or via the implementation of a multi-criteria coordinated model based on economic, social, and environmental data [12]. It is important to keep mobility policy in mind, understood as a correction of the modal split to a balanced ratio between car travel and public transport [13]. An integral part of mobility policy is the idea of mobility hubs as facilities with more functions than just transport [14]. Another potential solution to increasing urban congestion is the integration of different modes of transport [15]. The paper [16] describes a practical solution to the underground metro line planning problem by integrating existing bus and metro networks into a single interconnected transit network.

In this paper, the authors present a tool for efficient public transport route planning based on a heuristic approach. Heuristic methods are already widely used in transport-related problems, particularly in cases where solving the problem requires a large number of calculations. Using heuristics, it is possible to eliminate certain areas of calculation, which speeds up the process. This is important currently, particularly in an age with a very large increase in various types of data [17]. The authors of [18] point out that, regarding transport planning issues, the trips required to cover a service at the desired frequency are most often determined in advance of establishing the vehicles needed to serve those trips. As a result, this potentially leads to the acquisition of more vehicles than needed. The authors propose a model that integrates vehicle scheduling and planning using a metaheuristic diving approach. The results show that this method can help even experienced schedulers to develop better solutions or develop them faster and with less effort. Similarly, in [19], the author also considers the integration of the entire transport planning process. To this end, the author proposes his own iteration model integrating line planning, scheduling, and vehicle planning. These approaches demonstrate how heuristics can be used to solve complex, integrated transport planning problems. The public transport planning process can take place, for example, through an initial assessment of current technical and economic solutions [10,11]. In [20], a metaheuristic based on the harmonic optimization technique is used to improve the travel and departure times of city buses. The results achieved a reduction in travel time of approximately 10%. A genetic algorithm (GA) is used for the transit route network design problem (TRNDP). The authors in [21,22,23] used a GA to design urban bus route networks. In the [24] paper, a huge pool of candidate routes is created to reflect the design objectives, and then the set coverage problem is formulated at the selection stage.

In this paper, one of the heuristic methods used is ant colony optimization (ACO). In the ‘classic’ version of the algorithm, the goal is to find the shortest path [25]. Therefore, the algorithm is often used to solve the traveling salesman problem (TSP) [26,27] or the vehicle routing problem (VRP) [28,29]. It is possible to optimize the entire transportation network [30,31] and plan multimodal routes [32]. In [33,34], the authors use ACO for train traffic planning. In the case where the optimization goal is only length, the classic version is sufficient. On the other hand, if the optimization problem is complex, the classical ACO is insufficient. The authors in [35] point out that route optimization with a complex approach is complicated in real applications, mainly due to the huge number of variables and constraints. Additionally, various types of data are required. The algorithm proposed in the paper provides reasonably optimal solutions in cases where volume-dependent and length-dependent costs are the main components of the objective function. In cases where the optimization criteria, i.e., total trip length, time, energy consumed, are determined deterministically, the approach used yields satisfactory solutions. In contrast, the authors in [36] used ACO to determine the optimal route of electric cars when the optimization criteria were deterministic.

Researchers choose to modify the algorithm to benefit from the advantages of ACO, while adapting the algorithm to the problem under consideration to obtain meaningful results. In [37,38,39], the authors use an improved ACO to solve the VRP. To increase the algorithm’s convergence speed and improve the quality of the optimal solution, the authors of [40] modified an algorithm that takes into account the length, safety, and smoothness of the path during pheromone updates to plan a safer navigation path. In [41], an improved ant colony algorithm is developed for path planning based on a weight matrix. This allows the algorithm to avoid repeatedly selecting paths with lower weights. It is also possible, with modifications, to optimize an urban bus network based on existing bus routes [42]. If modifications to the algorithm are not enough, it is possible to create proprietary tools, using heuristics, that can help with complex optimization problems. An example of such a method is the NOAH algorithm, inspired by the behavior of monkeys in nature, which can be used to model commuter rail systems [43].

2. Methodology

2.1. Ant Colony Optimization

In this paper, the authors use a modified ACO for public transport route planning. The proposed algorithm serves as a novel computational model that shifts away from traditional control, pre-programming, and centralization. Instead, it emphasizes autonomy and distributed operation. These structures prove to be flexible and resilient, able to adapt quickly to changing conditions and to continue functioning even when individual components fail.

The algorithm is inspired by the observation of ants, which in nature, as individuals, are unable to communicate or successfully hunt for food. However, as a group, ants have the ability to solve complex problems and successfully find and collect food for their colony. Ants, as they have very little vision, communicate with each other using a chemical called a pheromone. As the ant migrates, it emits a constant quantity of pheromones that other ants can follow. Each ant moves at random, but when it encounters a pheromone, it must decide whether or not to follow it. If it follows the pheromone, the ant’s own pheromone reinforces the existing path, and the increase in pheromone increases the probability that the next ant will take the same path. Therefore, the more ants move along the path, the more attractive the path becomes to subsequent ants. In addition, an ant using a short path to a food source will return to the nest faster, and so it will mark its path twice before the ants that took the longer path have time to return. This has a direct impact on the probability of path selection for the next ant leaving the nest. Over time, as more ants use the shorter route, pheromones accumulate more rapidly on these paths, while longer routes receive less reinforcement and gradually become less favorable.

The mathematical description of the algorithm is as follows. Ants move at random, choosing a path with probability $p_{ij}^k$, determined by the following formula:

$$p_{ij}^k={\displaystyle \frac{\left({\tau }_{ij}^{\alpha }\right)\left({\eta }_{ij}^{\beta }\right)}{{\sum }_{zϵ{allowed}_i}\left({\tau }_{ij}^{\alpha }\right)\left({\eta }_{ij}^{\beta }\right)}}$$

(1)

where $p_{ij}^k$—probability of a k-ant crossing through section ij; ${\tau }_{ij}$—the amount of pheromone at section ij; and η_ij—the attractiveness of section ij.

In transportation issues, η_ij is determined by the following formula:

$${\eta }_{ij}={\displaystyle \frac{1}{L}}$$

(2)

where $L$—the total route to be taken.

Coefficient α is the parameter increasing ${\tau }_{ij}$. The larger α is, the more we ‘trust’ the information left by other ants. It is assumed that α ≥ 0. Coefficient β is the parameter increasing η_ij. The larger β is, the more we ’trust’ our own experience. It is assumed that β ≥ 1. The user of the algorithm can freely control the parameters $\alpha$ and β. During migration, ants secrete a constant amount of pheromone for other ants to follow. The amount of pheromone left behind can be determined by the following formula:

$$\Delta {\tau }_{ij}^k=\left\{\begin{array}{c}Q/L_k\\ 0\end{array}\right.$$

(3)

where $Q$—a fixed value indicating the amount of pheromone; $L_k$—the length of route traveled by the k-ant.

If the k-ant passes through segment ij, the value of the coefficient ${∆\tau }_{ij}^k$ takes the value $Q/L_k$. In other cases, where the ant has not walked the path and has left no pheromone, the coefficient ${∆\tau }_{ij}^k$ takes the value 0. When determining the route, it is necessary to update the amount of pheromone. The pheromone update process can be divided into two parts. The first part is the reduction in the pheromone located along section ij due to the natural evaporation of the pheromone. The second part is the increase in pheromone due to the following ants crossing in the next iteration. The amount of pheromone located along section ij after the update can be described by the following formula:

$${\tau \prime }_{ij}=\left(1-\rho \right){\tau }_{ij}+\sum _k∆{\tau }_{ij}^k$$

(4)

where ${\tau \prime }_{ij}$—the existing amount of pheromone at section ij; ${∆\tau }_{ij}^k$—the amount of pheromone left by k-ant in the next iteration; $\rho$—the evaporation coefficient of the pheromone.

The evaporation coefficient takes a value from 0 to 1. When ρ = 1, the pheromone evaporates completely after each iteration. Therefore, the more ants move along the path, the more attractive it becomes to subsequent ants. This affects the probability that the next ant leaving the nest will choose the path.

When applying ACO in the methodology described, it is necessary to make a network model in the form of a graph. The graph is described in such a way that obtaining the solution to the problem corresponds to the paths in the graph. Additionally, incorporating directed edges into the graph allows for the separate analysis of routes in both directions. This is particularly useful in urban traffic, where one-way sections may exist. By including directed edges, such sections can be accurately represented within the model. The mathematical description of the network model is a cost matrix C, given in the following form:

$$C=\left[\begin{array}{ccc}{c}_{11}& \cdots & c_{1j}\\ ⋮& \ddots & ⋮\\ c_{i1}& \cdots & c_{ij}\end{array}\right]$$

(5)

The coefficient $c_{ij}$ determines the cost required to cover section ij. If there is no direct connection between nodes, the cost is 0. The cost matrix is the same as the objective function on which the ACO is based. The structure of the cost matrix allows it to be freely modified according to the needs under consideration. This makes it possible to carry out the public transport route planning process as efficiently as possible.

The authors implemented ACO in the Python programming language version 3.10, into which the determined C matrices are input. The program determines the best route and provides the value of cost C. The resulting values allow you to proceed to step two of the evaluation. The algorithm works based on the following pseudocode.

Ant Colony Optimization
1.	Input:		cost matrix C
			number of iteration N
			number of ants M
			number of nodes (stops) n
			$\mathrm{evaporation} \mathrm{rate} \rho$
2.	For $i=1$ to N
3.		For $k=1$ to M
4.				Repeat until k-ant has completed a route
5.					Select the nodes n to be visited next
6.					$\mathrm{With} \mathrm{probability} p_{ij}^k$ given by C
7.				Calculate the cost for the route
8.		$\mathrm{Update} \mathrm{the} \mathrm{pheromone} \left(\mathrm{evaporation}\right) \mathrm{according} \mathrm{to} \rho$
9.	End

2.2. Determination of the Objective Function

This paper presents a proprietary objective function that modifies the operation of the ACO. As a result, the effort required to travel between nodes (stops) is determined. As a result, the cost matrix is an effort matrix with the following formula:

$$E=\left[\begin{array}{ccc}{e}_{11}& \cdots & e_{1j}\\ ⋮& \ddots & ⋮\\ e_{i1}& \cdots & e_{ij}\end{array}\right]$$

(6)

The coefficients of the $e_{ij}$ matrix are determined according to the formula:

$$e_{ij}={\displaystyle \frac{t_{R,ij}}{t_{S,ij}}}·{\displaystyle \frac{L_{ij}}{L_c}}·{\displaystyle \frac{V_o}{V_{\mathrm{ś}r,ij}}}·D_{ij}·A_{ij}·I_{ij}$$

(7)

where $t_{R,ij}$—real (average) time between nodes ij; $t_{S, ij}$—scheduled time between nodes ij; $L_{ij}$—length between nodes ij; $L_c$—total network length; $V_o$—expected average operating speed of vehicles planned on the network; $V_{śr,ij}$—average real speed of vehicles between nodes ij; $D_{ij}$—time uncertainty coefficient between nodes ij; $A_{ij}$—attractiveness coefficient between nodes ij; $I_{ij}$—passenger potential coefficient between nodes ij.

Each coefficient of Equation (7) is a separate element, and each enters the formula as a dimensionless value. In addition, a weight can be assigned to each element to change its impact on the value of the effort. The paper assumes that each element has the same weight because each of the aspects addressed is equally important. The ratio $t_{R,ij}/t_{S, ij}$ is a parameter that checks to the extent to which the scheduled time and the actual time are compatible. The greater the real time is relative to the scheduled one, the greater the effort value obtained. The value of real time can be obtained through your own measurements. Then, it is advisable to take more measurements on a given section and draw an average value from them. It is possible to obtain such a database, for example, from the operator. In the case of scheduled times, it should be read from the timetable, usually available from the carrier. The expected average operating speed of vehicles planned on the network should be adopted depending on the agglomeration mobility policy adopted in the city. The average real speed of vehicles between nodes is determined by the known value of the real travel time and the distance between nodes. The distance between stops can be read directly from the map. The time uncertainty factor is a parameter that allows discrepancies in the actual travel time between given nodes to be taken into account. The greater the discrepancy, the less certain it is that a given vehicle will be able to travel the section in the scheduled time, and this can translate into the generation of delays on that section. The value of $D_{ij}$ is calculated using the following formula:

$$D_{ij}=\left\{\begin{array}{c}1 for d_{ij}<60\\ {\displaystyle \frac{d_{ij}}{60}} for d_{ij}\ge 60\end{array}\right.$$

(8)

where $d_{ij}$—the difference between the measured real-time largest and lowest times between nodes ij [s].

To determine the value of $d_{ij}$, it is necessary to take a minimum of three measurements in real time between stops. From the times obtained, we choose the maximum and the minimum value. The difference in these times is the value searched for. It is assumed that discrepancies of up to 60 s are acceptable and will not increase the effort. Above this value, the parameter $D_{ij}$ will increase the value of effort. The attractiveness factor $A_{ij}$ is determined by the following formula:

$$A_{ij}=1-{\displaystyle \frac{n_{T,ij}}{n_{T,c}}}$$

(9)

where $n_{T, ij}$—number of public transport lines routed between nodes ij; $n_{T,c}$—the total number of public transport lines on the entire network.

It has been assumed that existing network layouts are dictated by different conditions. Therefore, if a number of public transport lines run through a given section, that section is attractive to users. This assumption can be applied if all lines have the same frequency. Otherwise, the attractiveness of sections should be equated with the frequency of vehicles. The passenger potential coefficient is related to the area of influence of public transport stops and has the following formula:

$$I_{ij}=1-P_{ij}$$

(10)

where $P_{ij}$ is the parameter defining the common part of the population between nodes ij and is determined by the formula:

$$P_{ij}=\left(I_i+I_j\right)·{\displaystyle \frac{L_{ij}}{R_{ij}}}$$

(11)

where: $I_i$, $I_j$—population within the area of influence of node i and j; $R_{ij}$—sum of the values of the radii of influence for node i and j.

When comparing the classic ACO approach to the modified version of the algorithm proposed in the paper, the higher computational complexity is evident. First of all, in the classical version, the objective function is only the length of the route. In contrast, in the modified version, length is one of the six parameters included, as shown in Equation (7). This modification is an advantage of the proposed method, because in the optimization we take into account both travel time, travel delays, travel speed, the attractiveness of areas, and passenger potential. The choice of these coefficients is motivated by the problems that are present in public transportation and reduce its attractiveness. A major challenge is the total travel time, which is often longer than that seen using individual transportation. In addition, there are delays in running, which further increase this time. The length of the route is related to the energy needed to cover the route, and so the shorter the route, the better. The consideration of attractiveness and passenger potential allows for the creation of modified routes with high attractiveness and accessibility.

A potential challenge with this method is the need to obtain all the necessary data to determine the effort value. However, if some data cannot be obtained, the effort can be abandoned. Then, one of the elements will be eliminated, but it will still be possible to perform optimization. On the other hand, this makes it possible to add more parameters to the formula, which will increase or decrease the value of effort. It should be remembered that the subsequent coefficients should also be dimensionless. This is also a great advantage of the presented objective function, which allows the tool to be freely modified and adjusted depending on the problem being analyzed.

The authors in paper [44] already used the effort matrix for the design of underground railway routes. At that time, the formula defining the coefficients of the $e_{ij}$ matrix had a different form. The previous work analyzed the routing of new infrastructure. In addition, a cost matrix was used in [45], but only to improve tram journey times. In this work, the description of the formula is adapted to the needs of public transport planning involving the planning of routes.

3. Case Study

The authors chose the tramway network in Wrocław for their research. The city is located in south-western Poland and the agglomeration has a population of around 1 million. In Figure 1, the entire network is shown as a graph. A graph is built from nodes and inter-node segments (edges). The nodes represent individual stops on the network, and each stop is assigned a number. The work uses directed edges. This means that each track and the possible direction of travel on it are modeled separately in the model. This makes it possible to take into account the one-way sections that are on the network. The entire network is greatly expanded, especially in the downtown area. This causes chronic problems with the proper planning of routes. In addition, the current traffic flow problems motivate an attempt at optimization. The methodology presented in this paper allows the better planning of tram line routes. One tram line is selected for the study, namely line no. 12. The line has a route between the Sępolno residential area (node no. 75) and the Kozanów residential area (node no. 192). The line has the character of a cross-city route, runs through the city center, and is important for the functioning of the entire network. The line under consideration and its route are shown in Figure 1 using a bold line.

In order to perform optimization, an effort matrix must be prepared for the entire network under consideration. For this, it is necessary to draw up intermediate matrices for the parameters included in Equation (7). The authors prepared a dataset comprising the intermediate matrices based on their own measurements and calculations. All data will be made available to readers upon request.

For the selected line, an ACO is applied to validate that it is planned better than the current route. The validation take places for two objective functions. The first objective function is the effort, described in Section 2.2. The second function is the ‘classic’ version of the algorithm, i.e., it is determined using a distance matrix of the following formula:

$$L=\left[\begin{array}{ccc}{l}_{11}& \cdots & l_{1j}\\ ⋮& \ddots & ⋮\\ l_{i1}& \cdots & l_{ij}\end{array}\right]$$

(12)

The coefficients of the matrix $l_{ij}$ determine the distance between the nodes (stops). This means that the shortest route between a specified start and end point is determined. The results from the study are shown in the next section.

4. Results

Table 1. Summary of results.

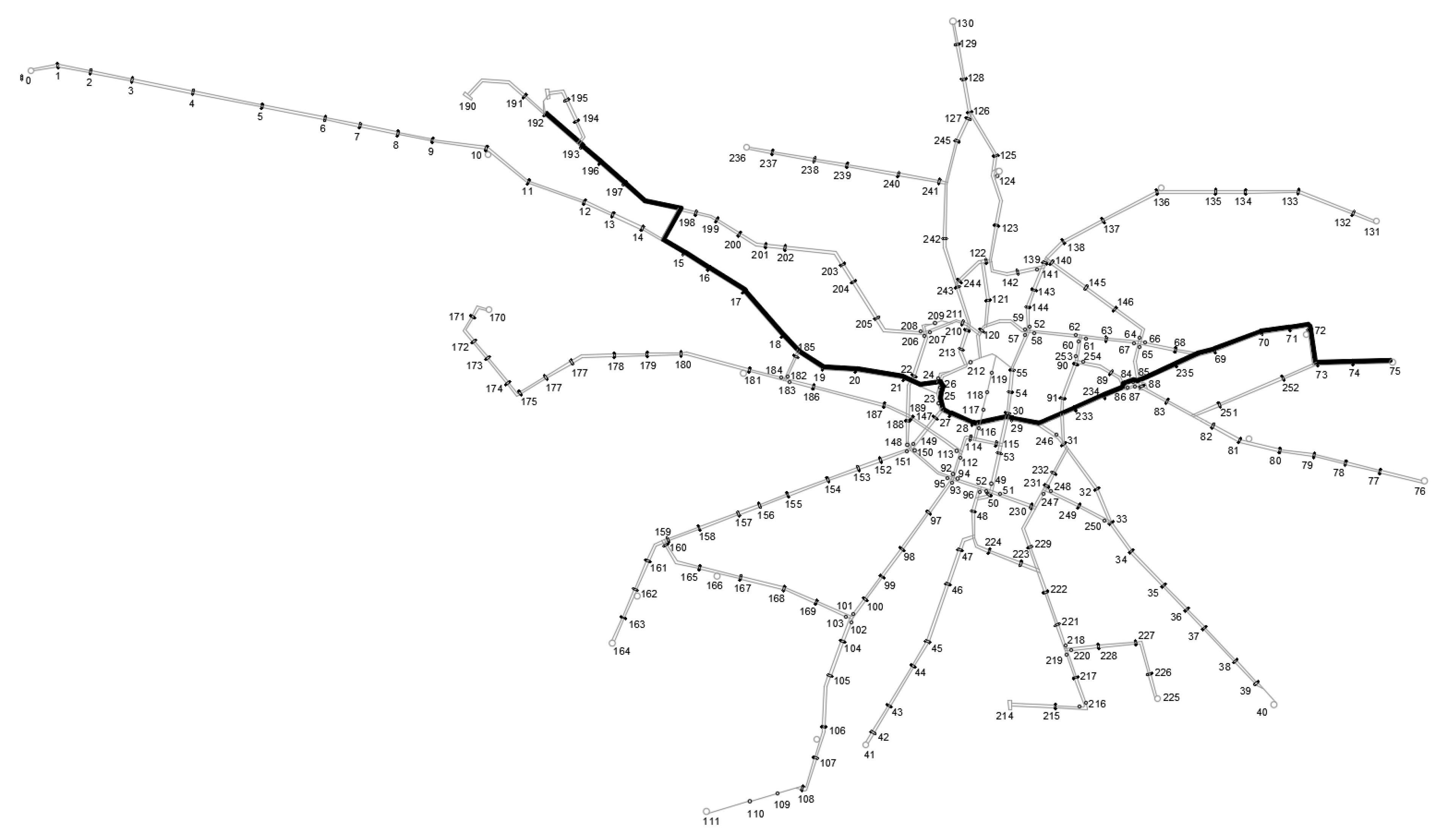
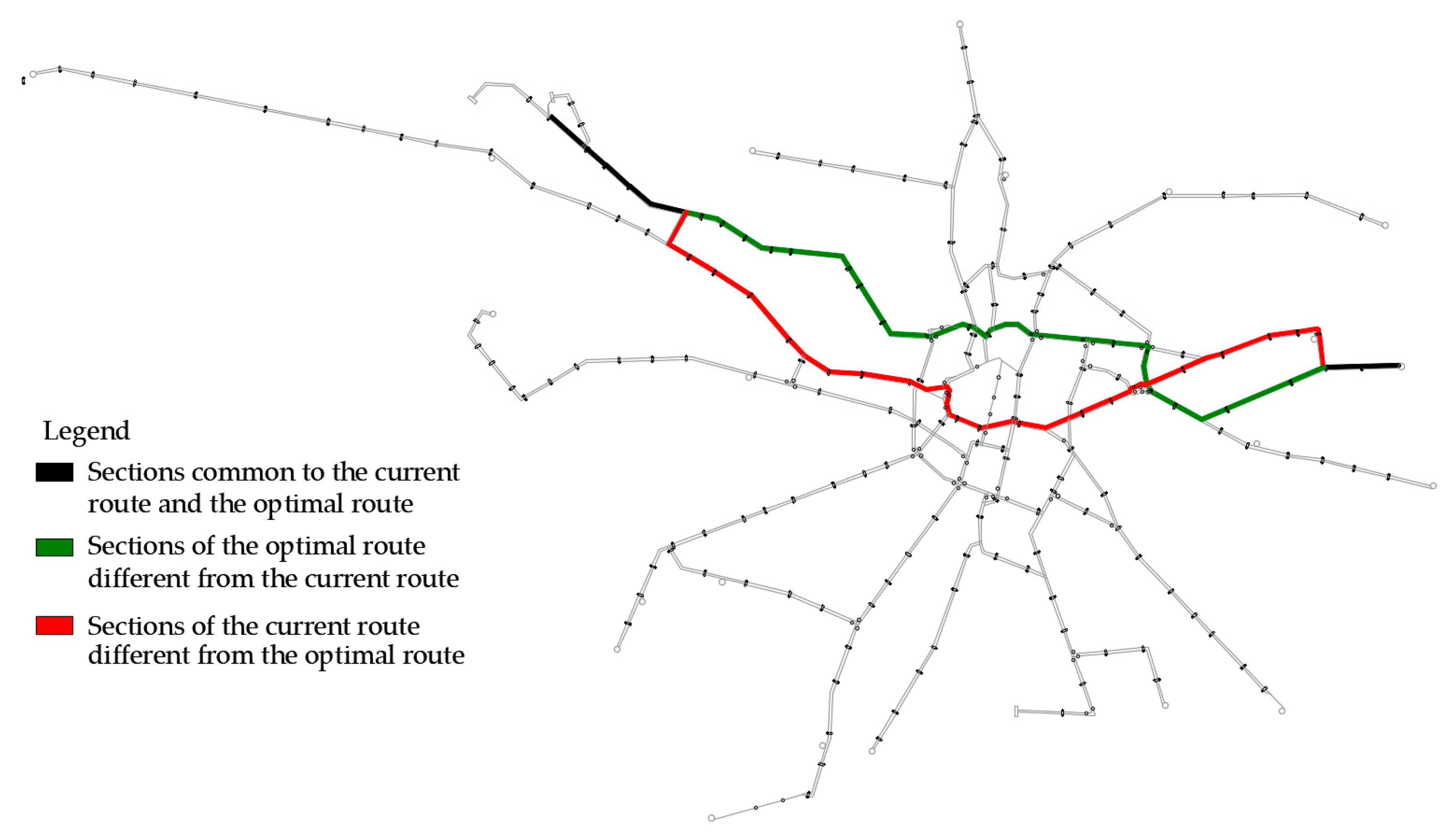
	Current Route	Optimal Route
Number of stops	26	26
Effort [-]	55.9265	50.1512
Length [m]	12,717	12,092
Scheduled time [s]	2400 (40 min)	2520 (42 min)
Real-time (average) [s]	2684 (44.73 min)	2505 (41.75 min)

summarizes the results obtained for the current route and the optimal route relative to the effort value. Figure 2 illustrates the current and optimal route. The sections common to the current route and the optimized route are marked in black. Red shows the sections of the current route that are different from the optimal route and green shows the sections of the optimal route that are different from the current route. In addition to the effort value obtained, Table 1 compares the selected intermediate factors needed to calculate effort. The number of stops, real time, scheduled time, and route length are compared.

A significant difference is the route. The route was only optimized for the common section at the beginning and at the end. The rest of the route changed. It is important that the line is crossing at an important traffic generator in the city. As a result, the optimized route does not lose the character of a trunk route. The results obtained for the optimal route are better than the current route, except for the schedule time, which is higher. The effort value obtained for the optimized route, 50.1512, is lower than that of the current route at 55.9265. The same is true for the length of the route, which is 12,092 m for the optimized route and 12,717 m for the current route. In terms of real-time value, it is 2.505 s (41.75 min) for the optimal route, which is less than for the current route, which stands at 2684 s (44.73 min). Only in terms of scheduled time, the current route has a lower value than the optimal route and is 2400 s (40 min), while for the optimal route this time is 2520 s (42 min). A detailed discussion of the results is presented in the next section.

5. Discussion

In this paper, the authors consider a tool for sustainable public transport planning. By using ACO, it is possible to define the objective function freely, depending on the problem under consideration. In this way, the author’s objective function is defined, which determines the effort needed to cover a route. The effort value takes into account parameters such as route length, scheduled and real time, vehicle delays, travel speed, the attractiveness of areas, and the number of residents in the immediate neighborhood of the line. These are parameters that have a significant impact on sustainable public transport in the city. To demonstrate the practical application of the developed tool, an example is provided using one of the largest tramway networks in Poland.

The results show that the current tram route is not optimal in terms of the effort value considered. Moreover, the length of the current route and the real time are also worse than the optimal route. Comparing the two routes on a map shows a big difference between the routes. This indicates that the current route is suboptimal and needs to be changed. The same procedure can be carried out for any existing tram line, but also for any other means of public transport. Alternatively, a completely new network of connections between stops can be proposed.

Comparing the current route with the optimal route, the effort value obtained for the current route is 11.5% worse than the effort value of the optimal route. The length of the current route is close to the optimal route, being only 5% worse. The real-time value for the current route is 7% worse compared to the optimal route. Only the scheduled time for the optimal route is 5% worse relative to the current route. Regarding scheduled time, it is worth noting the differences between the obtained schedule time and real-time results for both routes. For the current route, the difference is 284 s (4.73 min), while for the optimal route, it is only 15 s. This may indicate a poorly planned timetable, resulting in tramway delays. Therefore, when analyzing optimal travel time, it is more reliable to consider real-time data, which reflect actual traffic conditions, rather than scheduled time, which is predetermined by the operator. Importantly, the obtained route meets the basic conditions, runs through the main locations in the city, and does not change the character of the tramway line.

The differences obtained may seem insignificant, but it is important to bear in mind that these values apply to a single tramway run. When considering the entire network, the savings in travel time, distance traveled, and effort required can be substantial, particularly in the context of sustainable public transportation.

6. Conclusions

In this paper, the authors use a modified ACO to plan public transport routes. The results obtained allow for the comparison of routes and the identification of differences between them. The modification of the tool has resulted in a route requiring less effort than the current one. This means that better planning of the network is possible, which confirms the performance of the presented method. Due to the complexity of the effort values, it is also possible to compare the routes in terms of the individual effort elements, such as scheduled and real travel time, length, number of stops, and more. Using this methodology, it is possible to improve the performance of the entire network, which is important for sustainable urban development.

The results indicate several issues that should be considered in future studies. The main issue is how to determine the real travel time, which is a closed database consisting of its own measurements. This is a potential factor that can affect the results obtained, especially when it regards delay issues. Random occurrences can happen on the network that will significantly affect the measurements received. Examples of such events include accidents, rolling stock breakdowns, etc. Another variable is the time of passenger exchange, which is a component of real time. Further modification of Equation (7) with additional elements can also be considered, which will allow the even more accurate optimization of routes and the network as a whole. It would also be beneficial to analyze how removing specific components from Equation (7) affects the effort value and overall results. Furthermore, comparing the proposed methodology with other heuristic methods would allow for more comprehensive verification of the tool and could lead to potential improvements.