Frequency and Time Domain Simulations of a 15 MW Floating Wind Turbine Integrating with Multiple Flap-Type WECs
Abstract
1. Introduction
2. Materials and Methods
2.1. Hydrodynamic Load Calculation Theory
2.1.1. Frequency Domain Motion Equation
2.1.2. Time Domain Motion Equation
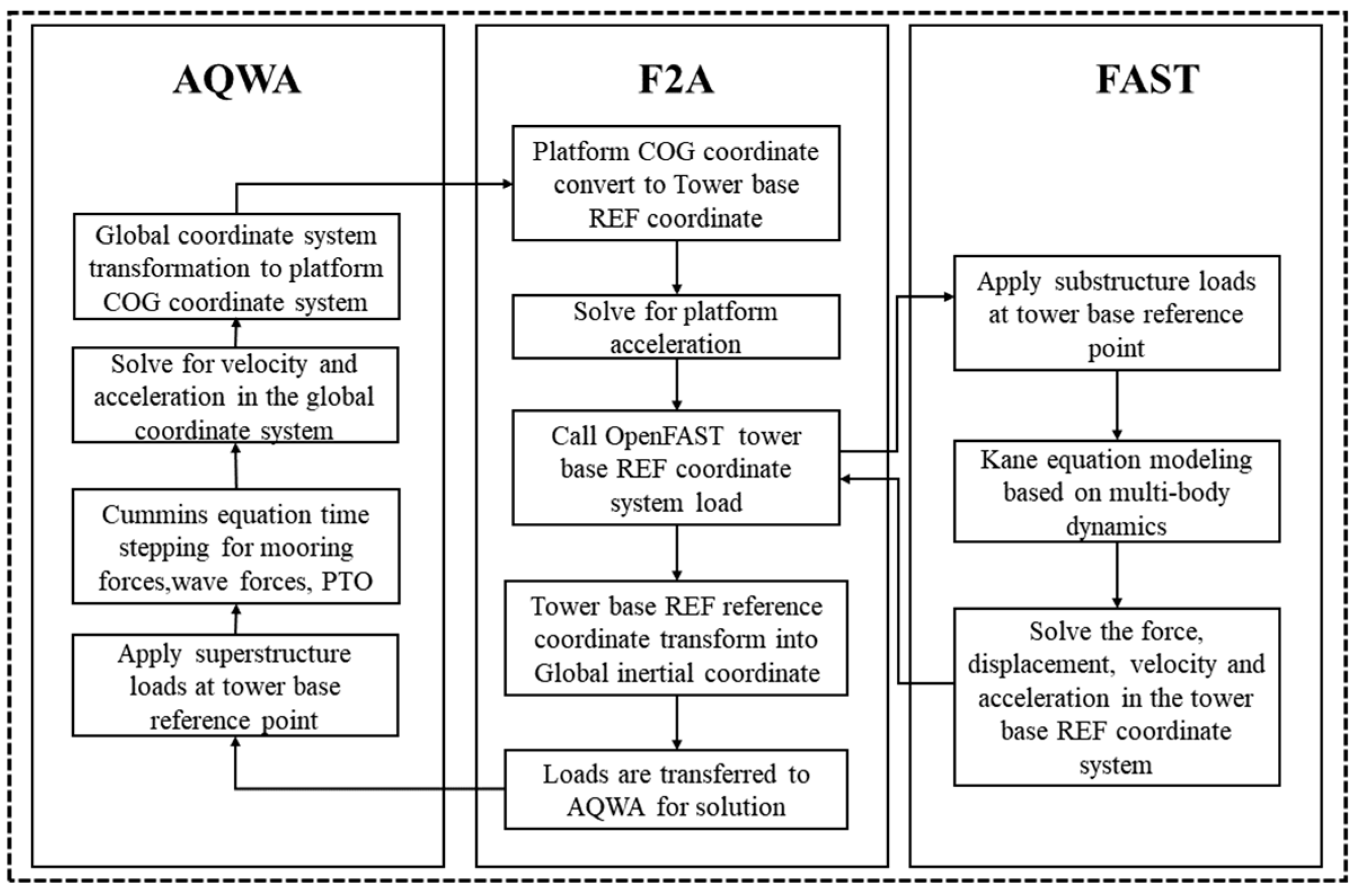
2.2. Time-Domain Coupled Analysis of Flap-Type Wave Energy Converter Combined Platform
3. Wind and Wave Combined Power Generation Platform System Model
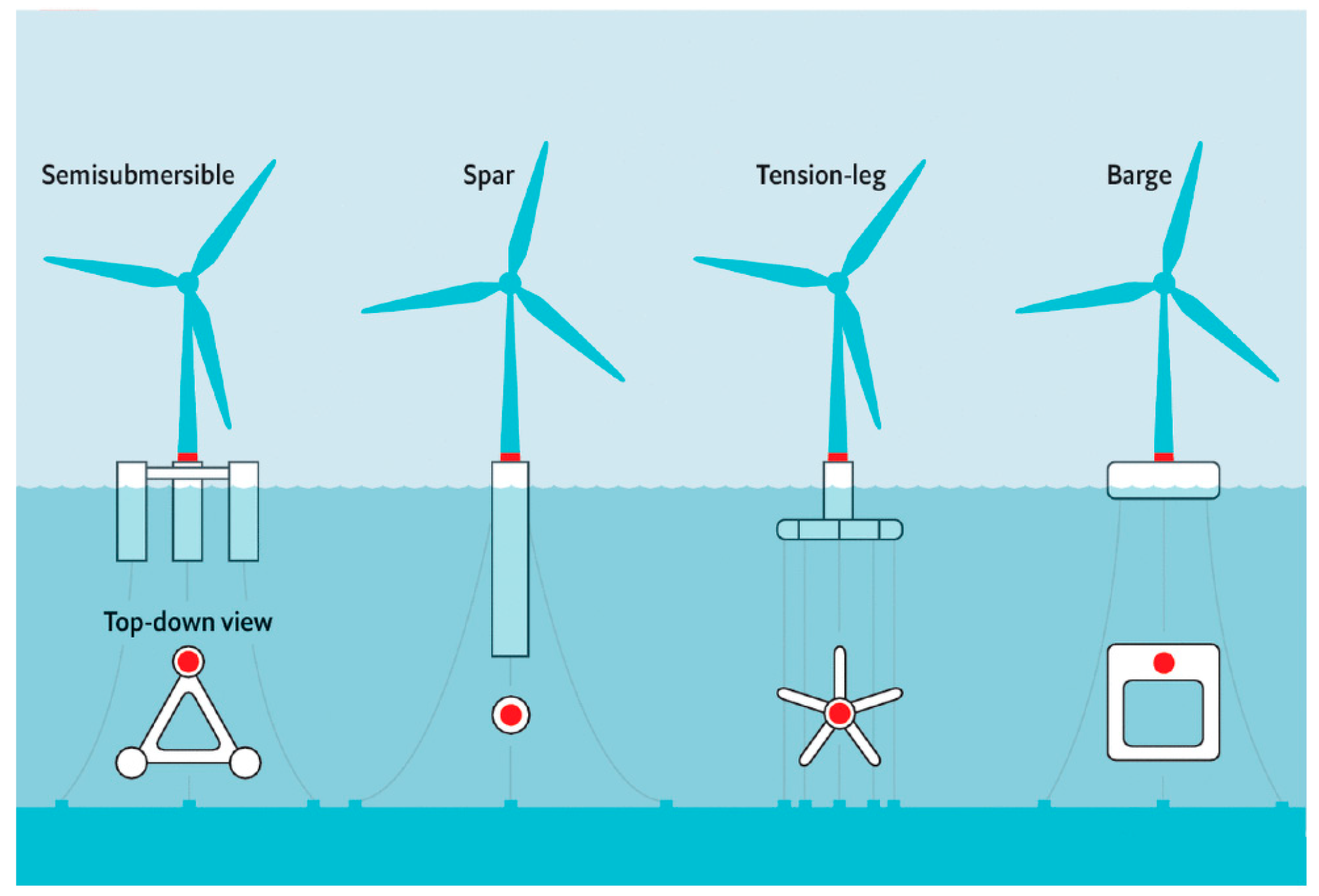
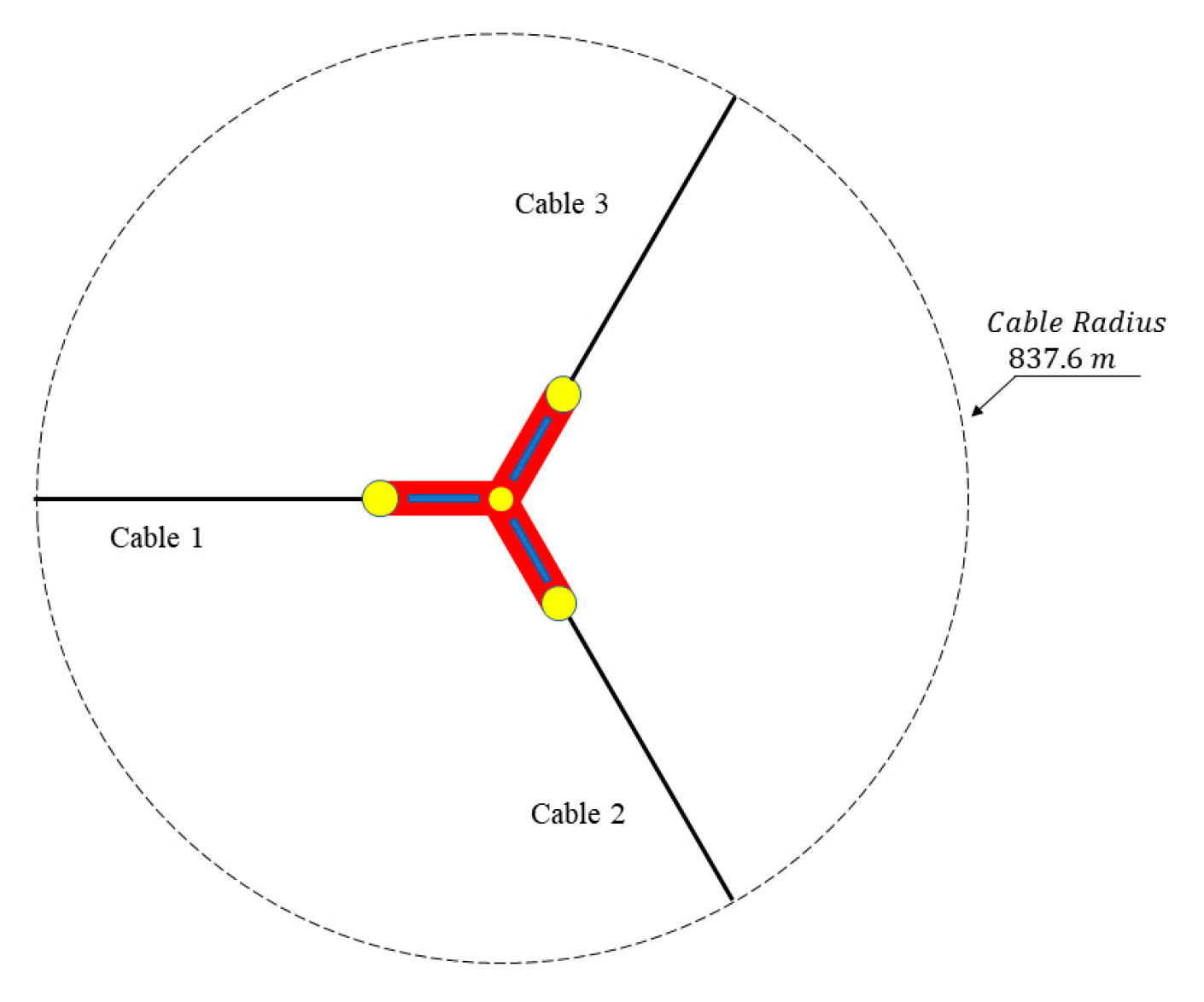
3.1. Semi-Submersible Platform and Mooring Design Parameters
3.2. Wind Turbine and Oscillating Flap-Type Design Model
3.3. Array Oscillating Wind-Wave Combined Platform Model
4. Result
4.1. Parameter Analysis of Flap-Type Wave Energy Converter
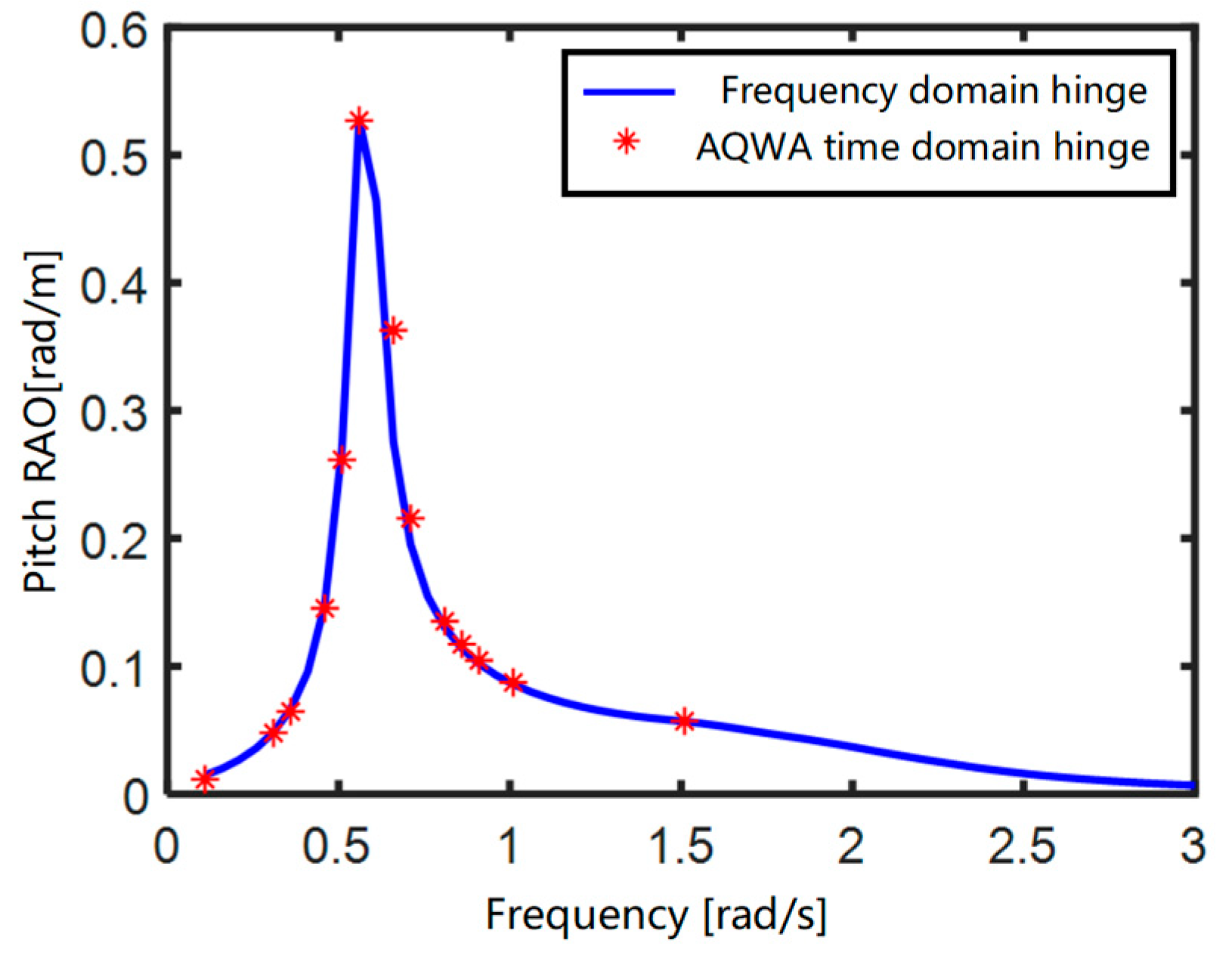
4.1.1. Comparative Validation of the Frequency-Domain Analysis Method for a Flap-Type Wave Energy Converter
4.1.2. Hydrodynamic Analysis of Flap-Type Wave Energy Converter
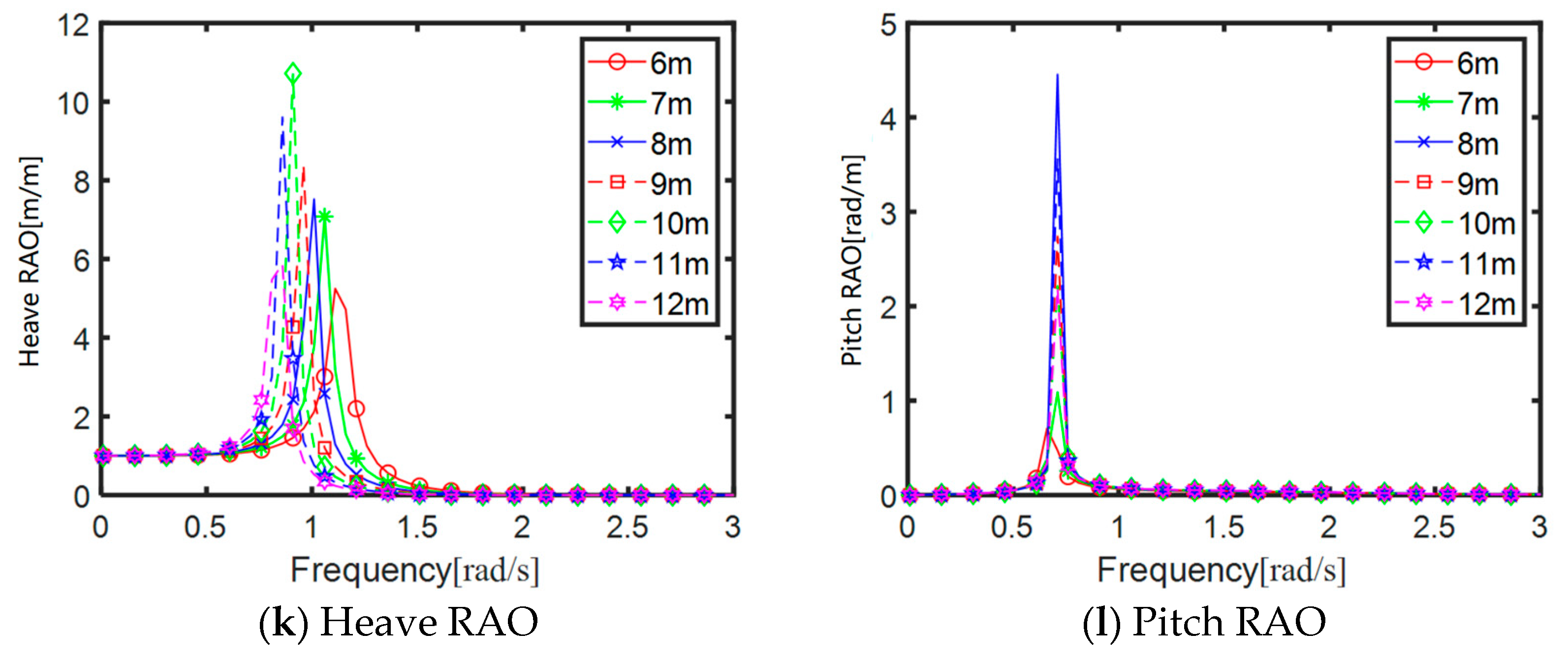
4.1.3. Parameter Optimization of Flap-Type Wave Energy Converter
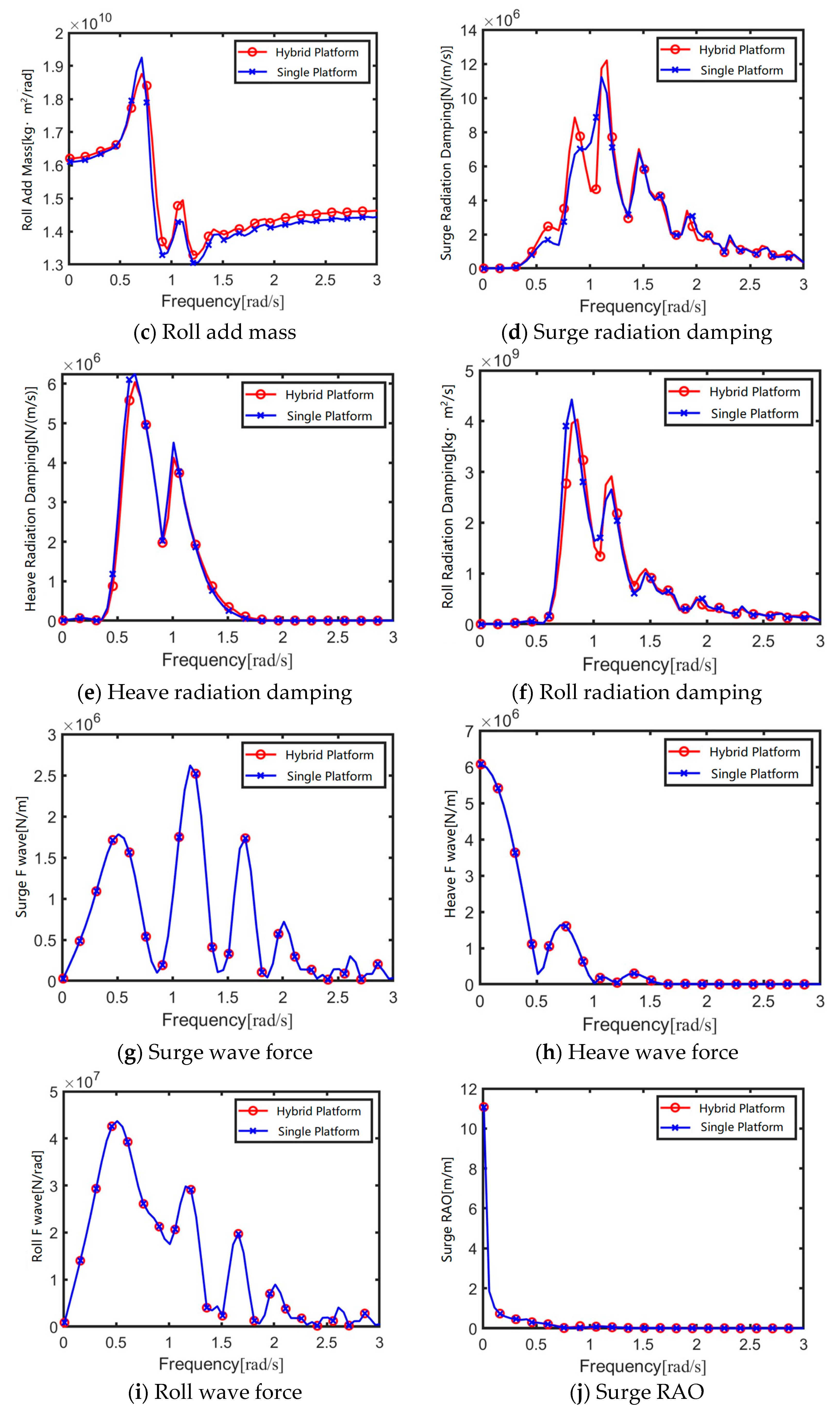
4.2. Hydrodynamic Analysis of Array Flap-Type WEC Combined Platform
4.3. Time Domain Coupling Analysis of Array Flap-Type WEC Combined Platform
4.3.1. Verification of Time Domain Analysis Method for Array Flap-Type Wave Energy Converter Combined Platform
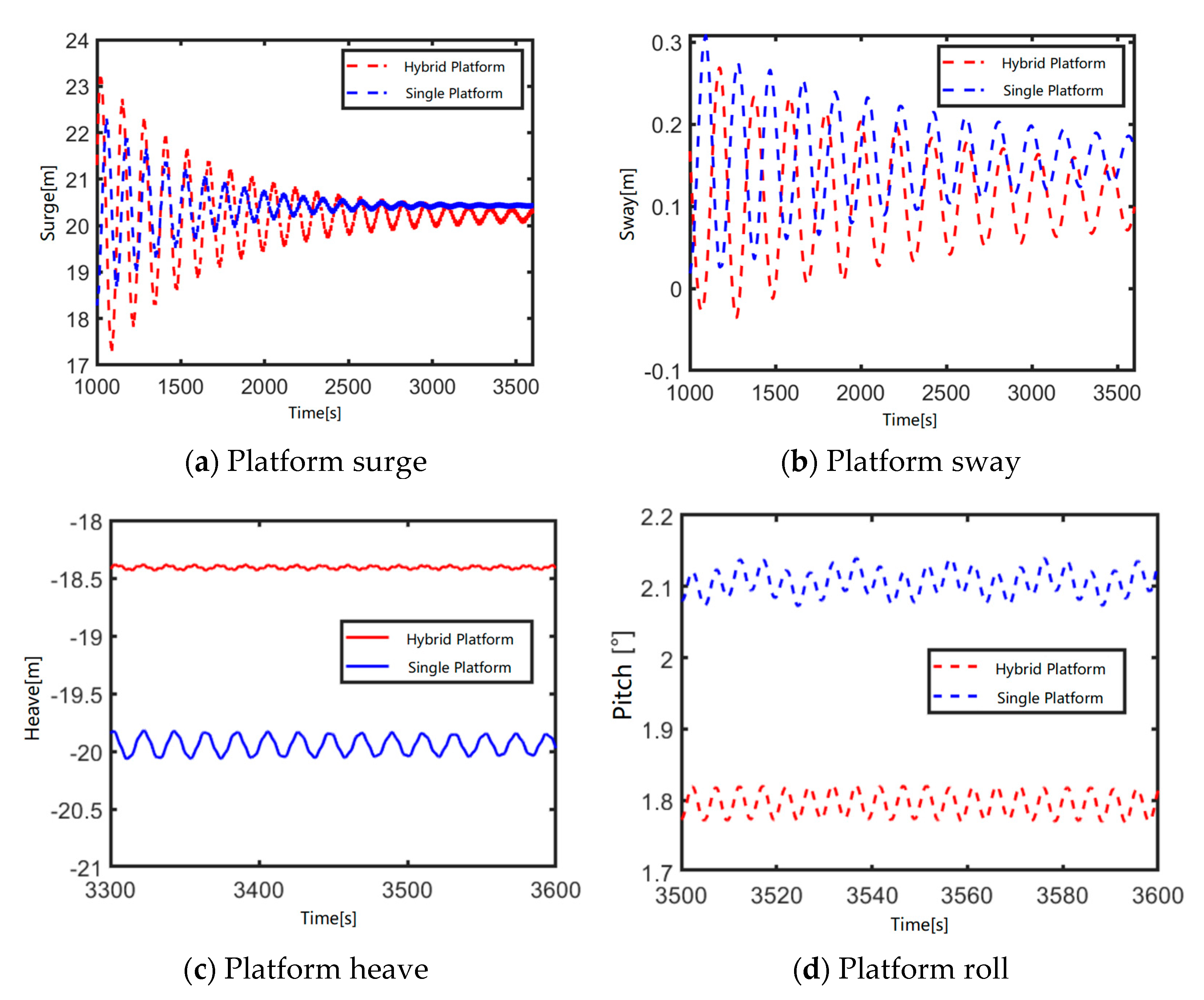
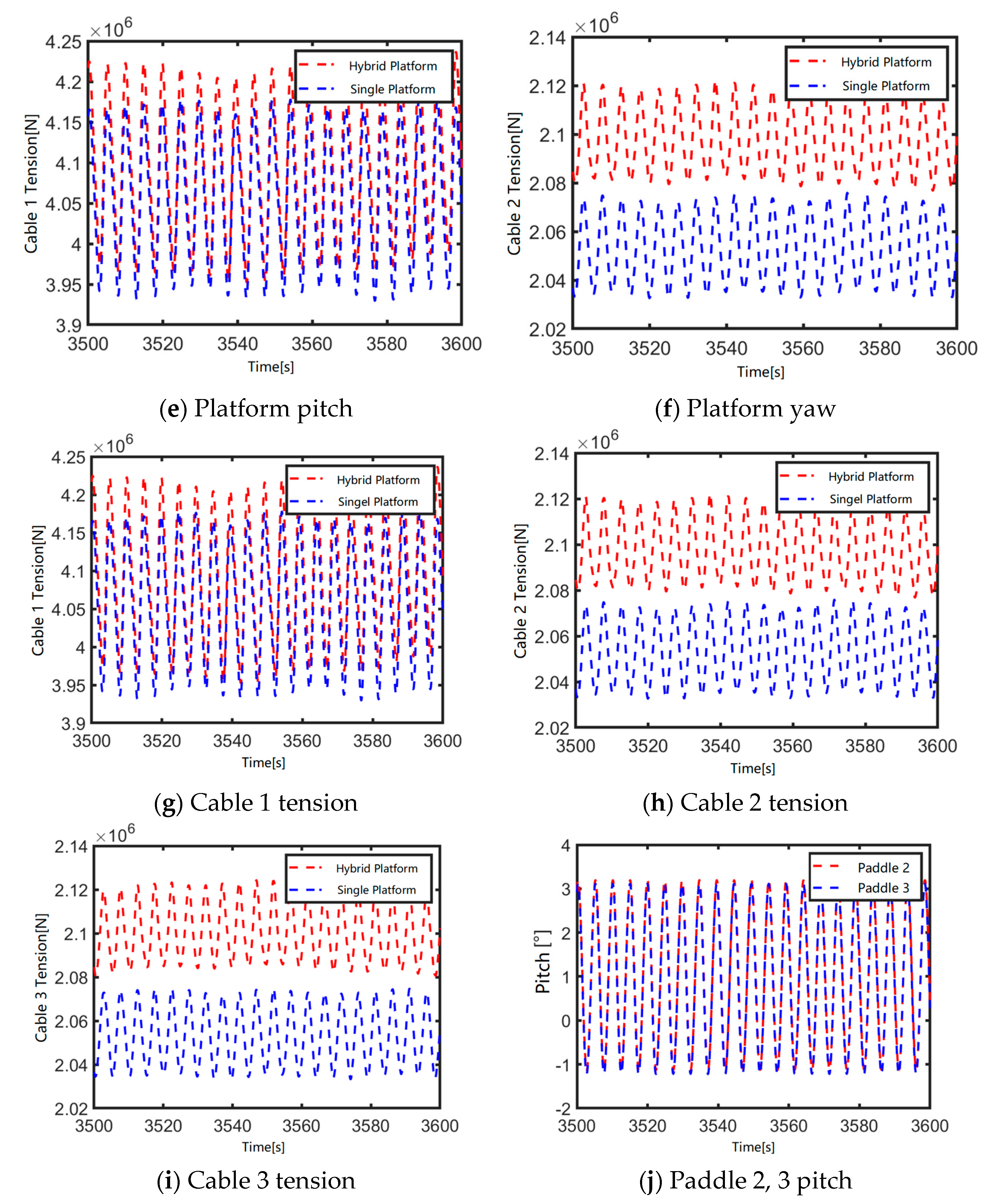
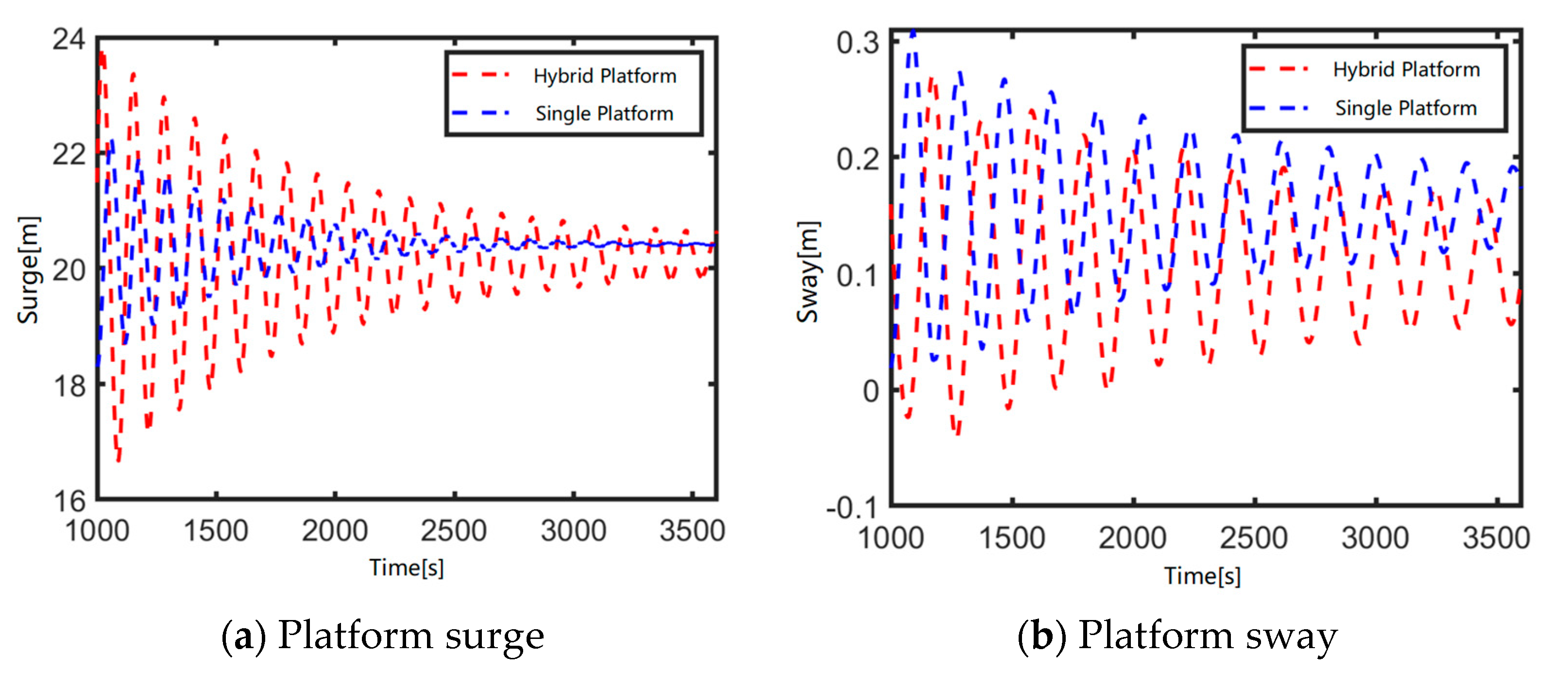
4.3.2. Motion and Mooring Analysis of an Array Flap-Type Wave Energy Converter Combined Platform
4.3.3. Fully Coupled Motion Response of an Array Flap-Type Wave Energy Converter Combined Platform
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rebecca Williams, F.Z. Global Offshore Wind Report 2023; Global Wind Energy Council: Brussels, Belgium, 2023. [Google Scholar]
- Bossler, A. Floating Offshore Wind Foundations: Industry Projects in the USA, Europe and Japan; Technical Report; Maine International Consulting, Inc.: Bremen, USA, 2011. [Google Scholar]
- Lefebvre, S.; Collu, M. Preliminary design of a floating support structure for a 5 MW offshore wind turbine. Ocean Eng. 2012, 40, 15–26. [Google Scholar] [CrossRef]
- Ahn, H.; Ha, Y.-J.; Cho, S.-G.; Lim, C.-H.; Kim, K.-H. A Numerical Study on the Performance Evaluation of a Semi-Type Floating Offshore Wind Turbine System According to the Direction of the Incoming Waves. Energies 2022, 15, 5485. [Google Scholar] [CrossRef]
- Johannessen, M. Concept Study and Design of Floating Offshore Wind Turbine Support Structure. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018. [Google Scholar]
- Liu, Y.; Hu, C.; Sueyoshi, M.; Yoshida, S.; Iwashita, H.; Kashiwagi, M. Motion response characteristics of a Kyushu-University semi-submersible floating wind turbine with trussed slender structures: Experiment vs. numerical simulation. Ocean Eng. 2021, 232, 109078. [Google Scholar] [CrossRef]
- Meng, H.; Liu, Y.; Tian, D.; Long, K.; Su, Y.; Li, B.; Sun, K. A novel conceptual design of a semi-submersible foundation for a 15 MW floating wind turbine. Ocean Eng. 2024, 294, 116726. [Google Scholar] [CrossRef]
- Psomas, P.M.; Platis, A.N.; Koutras, V.P.; Dagkinis, I.K. Intermittent system utilization for an efficient maintenance planning of offshore wind turbine rotor blades. Ocean Eng. 2025, 318, 120181. [Google Scholar] [CrossRef]
- Chatterjee, S.; Byun, Y.-C. Leveraging generative adversarial networks for data augmentation to improve fault detection in wind turbines with imbalanced data. Results Eng. 2025, 25, 103991. [Google Scholar] [CrossRef]
- Zou, Q.; Lu, Z.; Shen, Y. Short-term prediction of hydrodynamic response of a novel semi-submersible FOWT platform under wind, current and wave loads. Ocean Eng. 2023, 278, 114471. [Google Scholar] [CrossRef]
- Hu, Y.; Luo, P.; Yao, W.; Zhou, L.; Shi, P.; Yang, W.; Han, H. Power increase and lifespan extension control strategy of wind turbine yaw system based on power loss. Sustain. Energy Technol. Assess. 2025, 74, 104172. [Google Scholar] [CrossRef]
- Wan, L.; Moan, T.; Gao, Z.; Shi, W. A review on the technical development of combined wind and wave energy conversion systems. Energy 2024, 294, 130885. [Google Scholar] [CrossRef]
- Chen, M.; Deng, J.; Yang, Y.; Zhou, H.; Tao, T.; Liu, S.; Sun, L.; Hua, L. Performance Analysis of a Floating Wind–Wave Power Generation Platform Based on the Frequency Domain Model. J. Mar. Sci. Eng. 2024, 12, 206. [Google Scholar] [CrossRef]
- Chen, M.; Yun, Q.; Hallak, T.; Zhou, H.; Zhang, K.; Yang, Y.; Tao, T.; Liu, S.; Jiang, W.; Li, C. Comparative Study on the Performances of a Hinged Flap-Type Wave Energy Converter Considering Both Fixed and Floating Bases. J. Mar. Sci. Eng. 2024, 12, 1416. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B.; Hu, Z.; Deng, J.; Xiao, P.; Chen, M. Research on Size Optimization of Wave Energy Converters Based on a Floating Wind-Wave Combined Power Generation Platform. Energies 2022, 15, 8681. [Google Scholar] [CrossRef]
- Tian, Z.; Shi, W.; Li, X.; Park, Y.; Jiang, Z.; Wu, J. Numerical simulations of floating offshore wind turbines with shared mooring under current-only conditions. Renew. Energy 2025, 238, 121918. [Google Scholar] [CrossRef]
- Michailides, C.; Gao, Z.; Moan, T. Experimental and numerical study of the response of the offshore combined wind/wave energy concept SFC in extreme environmental conditions. Mar. Struct. 2016, 50, 35–54. [Google Scholar] [CrossRef]
- Michailides, C.; Luan, C.; Gao, Z.; Moan, T. Effect of Flap Type Wave Energy Converters on the Response of a Semi-Submersible Wind Turbine in Operational Conditions. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Wang, T.; Zhu, K.; Cao, F.; Li, D.; Gong, H.; Li, Y.; Shi, H. A coupling framework between OpenFAST and WEC-Sim. Part I: Validation and dynamic response analysis of IEA-15-MW-UMaine FOWT. Renew. Energy 2024, 225, 120249. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T.; Lugni, C. Experimental and numerical comparisons of hydrodynamic responses for a combined wind and wave energy converter concept under operational conditions. Renew. Energy 2016, 93, 87–100. [Google Scholar] [CrossRef]
- Wan, L.; Gao, Z.; Moan, T.; Lugni, C. Comparative experimental study of the survivability of a combined wind and wave energy converter in two testing facilities. Ocean Eng. 2016, 111, 82–94. [Google Scholar] [CrossRef]
- Luan, C.; Michailides, C.; Gao, Z.; Moan, T. Modeling and Analysis of a 5 MW Semi-Submersible Wind Turbine Combined with Three Flap-Type Wave Energy Converters. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Li, C.B.; Zhang, Z.; Zhang, J.; Li, X.; Choung, J.; Chen, M. Investigation on local mooring stresses of floating offshore wind turbines considering mooring chain geometrical and material nonlinearity. Ocean Eng. 2024, 312, 119166. [Google Scholar] [CrossRef]
- Bachynski, E.E.; Moan, T. Point Absorber Design for a Combined Wind and Wave Energy Converter on a Tension-Leg Support Structure. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, 8–13 June 2013. [Google Scholar]
- Yang, Y.; Bashir, M.; Michailides, C.; Li, C.; Wang, J. Development and application of an aero-hydro-servo-elastic coupling framework for analysis of floating offshore wind turbines. Renew. Energy 2020, 161, 606–625. [Google Scholar] [CrossRef]
- Yang, Y.; Bashir, M.; Wang, J.; Yu, J.; Li, C. Performance evaluation of an integrated floating energy system based on coupled analysis. Energy Convers. Manag. 2020, 223, 113308. [Google Scholar] [CrossRef]
- Chen, M.; Xiao, P.; Zhou, H.; Li, C.B.; Zhang, X. Fully coupled analysis of an integrated floating wind-wave power generation platform in operational sea-states. Front. Energy Res. 2022, 10, 931057. [Google Scholar] [CrossRef]
- Chen, M.; Huang, W.; Liu, H.; Hallak, T.S.; Liu, S.; Yang, Y.; Tao, T.; Jiang, Y. A novel SPM wind-wave-aquaculture system: Concept design and fully coupled dynamic analysis. Ocean Eng. 2025, 315, 119798. [Google Scholar] [CrossRef]
- Jiang, W.; Liang, C.; Tao, T.; Yang, Y.; Liu, S.; Deng, J.; Chen, M. Fully Coupled Analysis of a 10 MW Floating Wind Turbine Integrated with Multiple Wave Energy Converters for Joint Wind and Wave Utilization. Sustainability 2024, 16, 9172. [Google Scholar] [CrossRef]
- Tian, W.; Wang, Y.; Shi, W.; Michailides, C.; Wan, L.; Chen, M. Numerical study of hydrodynamic responses for a combined concept of semisubmersible wind turbine and different layouts of a wave energy converter. Ocean Eng. 2023, 272, 113824. [Google Scholar] [CrossRef]
- Jin, P.; Zheng, Z.; Zhou, Z.; Zhou, B.; Wang, L.; Yang, Y.; Liu, Y. Optimization and evaluation of a semi-submersible wind turbine and oscillating body wave energy converters hybrid system. Energy 2023, 282, 128889. [Google Scholar] [CrossRef]
- Zhang, D.; Chen, Z.; Liu, X.; Sun, J.; Yu, H.; Zeng, W.; Ying, Y.; Sun, Y.; Cui, L.; Yang, S.; et al. A coupled numerical framework for hybrid floating offshore wind turbine and oscillating water column wave energy converters. Energy Convers. Manag. 2022, 267, 115933. [Google Scholar] [CrossRef]
- Cao, F.; Yu, M.; Han, M.; Liu, B.; Wei, Z.; Jiang, J.; Tian, H.; Shi, H.; Li, Y. WECs microarray effect on the coupled dynamic response and power performance of a floating combined wind and wave energy system. Renew. Energy 2023, 219, 119476. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Fatikow, S. Design and analysis of a high-accuracy flexure hinge. Rev. Sci. Instrum. 2016, 87, 055106. [Google Scholar] [CrossRef]
- ANSYS. AQWA Theory Manual; AQWA: Canonsburg, PA, USA, 2023. [Google Scholar]
- Cummins, W.E. The Impulse Response Function and Ship Motions; Department of the Navy, David Taylor Model Basin: West Bethesda, MD, USA, 2010. [Google Scholar]
- Taghipour, R.; Perez, T.; Moan, T. Hybrid frequency–time domain models for dynamic response analysis of marine structures. Ocean Eng. 2008, 35, 685–705. [Google Scholar] [CrossRef]
- Zou, M.; Chen, M.; Zhu, L.; Yun, Q.; Zhao, W.; Liang, Q.; Zhao, Y. Experimental and numerical investigation of gap resonances between side-by-side fixed barges under beam sea excitation. Ocean Eng. 2024, 297, 117150. [Google Scholar] [CrossRef]
- Zou, M.; Chen, M.; Zhu, L.; Li, L.; Zhao, W. A constant parameter time domain model for dynamic modelling of multi-body system with strong hydrodynamic interactions. Ocean Eng. 2023, 268, 113376. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, J.; Zhang, W.; Li, C.B.; Zhou, H.; Jiang, Y.; Sun, X. Study on Mooring Design of 15 MW Floating Wind Turbines in South China Sea. J. Mar. Sci. Eng. 2024, 12, 33. [Google Scholar] [CrossRef]
- Liang, H.; Qiao, D.; Wang, X.; Zhi, G.; Yan, J.; Ning, D.; Ou, J. Energy capture optimization of heave oscillating buoy wave energy converter based on model predictive control. Ocean Eng. 2023, 268, 113402. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, J.; Lin, X. Effects of mooring line failure on semi-submersible wind turbine and the study of its mitigation measures. Ocean Eng. 2024, 311, 118889. [Google Scholar] [CrossRef]
- Allen, C.K.; Viscelli, A.; Dagher, H.J.; Goupee, A.J.; Gaertner, E.; Abbas, N.J.; Hall, M.; Barter, G.E. Definition of the UMaine VolturnUS-S Reference Platform Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2020.
- Zhou, Y.; Ye, Q.; Shi, W.; Yang, B.; Song, Z.; Yan, D. Wave characteristics in the nearshore waters of Sanmen bay. Appl. Ocean Res. 2020, 101, 102236. [Google Scholar] [CrossRef]
- Hongxia, C.; Feng, H.; Ye-li, Y. Seasonal Characteristics and Temporal Variations of Ocean Wave in the Chinese Offshore Waters and Adjacent Sea Areas. Adv. Mar. Sci. 2006, 24, 407. [Google Scholar]



















| Parameter | Value |
|---|---|
| Total mass (t) | 17,854 |
| Distance from the center of mass to the water surface line (m) | 14.94 |
| Ixx (kg·m2) | 1.251 × 1010 |
| Iyy (kg·m2) | 1.251 × 1010 |
| Izz (kg·m2) | 2.367 × 1010 |
| Parameter | Value |
|---|---|
| Frequency/MW | 15 |
| Number of Blades | 3 |
| Rotor Diameters/m | 240 |
| Hub Height/m | 150 |
| Cut-in Wind Speed/(m/s) | 3 |
| Cutting Wind Speed/(m/s) | 25 |
| Rated Wind Speed/(m/s) | 10.59 |
| Parameter | Value |
|---|---|
| Width (m) | 30 |
| Height (m) | 13 |
| Thickness (m) | 3 |
| Ixx (kg·m2) | 1.362 × 107 |
| Iyy (kg·m2) | 6.957 × 107 |
| Izz (kg·m2) | 8.182 × 107 |
| Paddle | Parameter | Value |
|---|---|---|
| Paddle 1 | Distance from oscillating axis to water plane | 13 m |
| Geometric center coordinates of paddle | (24.625, 0, −1.5) | |
| Deflection angle | 0° | |
| Paddle 2 | Distance from oscillating axis to water plane | 13 m |
| Geometric center coordinates of paddle | (12.3125, 21.326, −1.5) | |
| Deflection angle | 0° | |
| Paddle 3 | Distance from oscillating axis to water plane | 13 m |
| Geometric center coordinates of paddle | (12.3125, −21.326, −1.5) | |
| Deflection angle | 0° |
| Draft (m) | PTO Stiffness (N·m/rad) | Natural Frequency (rad/s) | Optimal Damping (N·m (rad/s)) |
|---|---|---|---|
| 8 | 3.0 × 107 | 0.51 | 1.3 × 107 |
| 5.0 × 107 | 0.56 | 2.3 × 107 | |
| 8.0 × 107 | 0.61 | 3.5 × 107 | |
| 1.1 × 108 | 0.66 | 4.8 × 107 |
| Parameter | Value |
|---|---|
| Number of mooring lines | 3 |
| Length of mooring line in an unstretched state | 850 m |
| Mooring line diameter | 0.185 m |
| Equivalent density | 685 kg/m |
| Equivalent ductile stiffness | 3270 MN |
| Transverse drag coefficient | 2 |
| Tangential drag coefficient | 1.15 |
| Additional mass coefficient | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Liang, C.; Liu, S.; Jiang, J.; Huang, Z.; Liang, C.; Ou, W.; Tao, T.; Chen, M. Frequency and Time Domain Simulations of a 15 MW Floating Wind Turbine Integrating with Multiple Flap-Type WECs. Sustainability 2025, 17, 2448. https://doi.org/10.3390/su17062448
Yang Y, Liang C, Liu S, Jiang J, Huang Z, Liang C, Ou W, Tao T, Chen M. Frequency and Time Domain Simulations of a 15 MW Floating Wind Turbine Integrating with Multiple Flap-Type WECs. Sustainability. 2025; 17(6):2448. https://doi.org/10.3390/su17062448
Chicago/Turabian StyleYang, Yi, Chenyu Liang, Shi Liu, Jiale Jiang, Zheng Huang, Chonggan Liang, Wenjun Ou, Tao Tao, and Mingsheng Chen. 2025. "Frequency and Time Domain Simulations of a 15 MW Floating Wind Turbine Integrating with Multiple Flap-Type WECs" Sustainability 17, no. 6: 2448. https://doi.org/10.3390/su17062448
APA StyleYang, Y., Liang, C., Liu, S., Jiang, J., Huang, Z., Liang, C., Ou, W., Tao, T., & Chen, M. (2025). Frequency and Time Domain Simulations of a 15 MW Floating Wind Turbine Integrating with Multiple Flap-Type WECs. Sustainability, 17(6), 2448. https://doi.org/10.3390/su17062448








