Abstract
Freeway transportation safety issues have attracted public concern in China for decades. This study aims to identify the factors influencing the injury severity of freeway crashes and to quantify their effects on the likelihood of various crash severity levels, with consideration of heterogeneity and interactions. The empirical analysis is based on three years of crash data from two mountainous freeways in Guangdong, China, covering the years of 2021 to 2023. A random parameters logit model with interaction terms is developed for the analysis. Goodness-of-fit indicators reveal that accommodating the interactive effects can significantly improve model fit performance. The estimation results of the parameters and marginal effects indicate that the factors related to vehicle type, time of day, crash season and cause, 3D curvature, and traffic volume have significant effects on crash severity. Notably, interactive effects are revealed between spring and evening, autumn and fixed objects, and non-local vehicles and improper driving. According to the findings, some countermeasures on safety education, traffic management, and freeway design are provided for preventing freeway crash injury, which is helpful for the development of sustainable transportation systems.
1. Introduction
From the perspectives of energy consumption and greenhouse gas emission, other transport modes (e.g., rail, air, or sea transport) may be more sustainable than roadway transport [1]. In China, however, most passengers and cargo are transported by roadways, of which freeways are the primary type. The total length of freeways in China has ranked the first worldwide for over ten years. As an important aspect of sustainability in freeway transportation, traffic safety issues have raised the concerns of freeway designers, operation managers, and safety scholars for a long time. While the design and construction standards for freeways are higher than those for other types of roadways, freeway traffic crashes are more likely to result in severe casualties [2], given that the vehicle speeds on freeways are usually higher. The safety situation of mountainous freeways may be more serious, since poor roadway geometry alignments (e.g., small curve radius, great grades, and combinations of horizontal and vertical curves) on certain sections can lead to limited sight distances and driver misperception [3,4]. In addition, the high proportion of heavy vehicles is also expected to increase the risk and injury severity of freeway crashes, due to their lower speeds relative to passenger cars (leading to greater speed variance) and greater crash aggressivity (that imposes more hazards on other vehicles) [5].
In the literature, a large number of studies have analyzed the factors influencing freeway crash frequency [6,7], real-time crash risk [8,9], and crash injury severity [2,10], which aim to design effective countermeasures for improving freeway safety performance. With regard to freeway crash severity analysis, researchers in the U.S. [10,11,12,13,14,15,16,17,18,19], China [2,20,21,22,23,24,25,26,27,28,29,30,31], and other countries [32] have investigated the effects of the observed factors pertaining to human factors (e.g., driver age and gender, airbag deployment, and driving behavior), vehicle (e.g., vehicle type and year), roadway (e.g., pavement condition, horizontal curvature, vertical grade, number and width of lanes, and speed limit), environment (e.g., weather conditions, lighting conditions, and traffic volume), emergency medical service (e.g., its response time, on-scene time, and transport time), and crash configuration (e.g., crash type, number of vehicles involved, and crash time, day, and season) on the injury severity of freeway crashes, freeway tunnel crashes, or certain types of freeway crashes (e.g., single-vehicle crashes, rear-end crashes, truck crashes, median crashes, tire failure-related crashes, and secondary crashes). Parametric methods, including Bayesian logistic regression, ordered logit models, generalized ordered logit models, spatial generalized ordered logit/probit models, and random parameters logit models, and non-parametric or machine learning methods, including random forest, support vector machine, and classification regression trees, have been adopted in the above research. The parametric models (especially random parameters models) are more prevalent, because of their strong abilities of interpretation and addressing certain issues (e.g., unobserved heterogeneity) of crash data [33]. Nonetheless, these models assume that the effects of factors are mutually independent. The interactions between various factors are omitted, which may not comprehensively or precisely reveal the contributing factors to freeway crash severity and quantify their effects on the probabilities of each severity level.
Interactive effects are defined as the cumulative effects of two or more explanatory variables on the response variable. In the realm of traffic safety, a limited number of studies [34,35,36,37,38,39,40] have taken factor interactions into consideration. In particular, Jung et al. [34] investigated the injury severity of two-vehicle crashes in rainy weather and found that it is significantly affected by the interactions of upgrade class with left shoulder width and lane number. Based on a binary logit analysis of wrong-way driving crashes, Ponnaluri [35] found that the interactions between facility type and lighting condition, and between facility type and urban/rural location, have significant effects on fatality likelihood. Ahmed et al. [36] adopted a Bayesian logistic model for analyzing the injury severity of rural highway crashes in Wyoming State. The results suggested that there were various interactive effects (e.g., speeding and horizontal curves, truck involvement and vertical grade) on crash severity. In an analysis of pedestrian crash severity in Hong Kong, significant interactive effects of weather conditions (including rain and temperature) and driver/pedestrian behaviors (e.g., driver inattention, pedestrian jaywalking, pedestrians running onto the road) were uncovered [38]. Sun et al. [39] proposed a hybrid method of using random forest and random parameters logit models for analyzing the injury severity of crashes involving vulnerable road users and found that the likelihood of fatality was increased by primary roads and rural areas, while it was decreased by their interaction. These works all concluded that accounting for the interactions between the observed factors provided deeper insights into the mechanisms of crash injuries. To our knowledge, there is no reported research which investigates the interactive effects on freeway crash injury severity in the parametric modeling paradigm.
To this end, the current research aims to reveal the factors influencing the injury severity of freeway crashes with consideration of their interactive and heterogeneous effects, using a random parameters logit model incorporating interaction terms between various factors. The three-year (2021–2023) crash data from two mountainous freeways with high proportions of heavy vehicles in Guangdong Province, China, is employed for the empirical analysis. To demonstrate the benefits of capturing the interactive effects, the random parameters models with and without interaction terms are compared.
The rest of the article is structured as follows: Section 2 describes the collected crash data. Section 3 introduces the formulation of the random parameters logit model and the methods for model comparison. The model results are summarized and analyzed in Section 4. The conclusions and practical implications are provided in Section 5.
2. Data
In this study, a three-year (2021–2023) crash dataset from two mountainous freeways in Guangdong Province, China: Shantou–Kunming Freeway (from the kilometer marker K45 to K114) and Meizhou–Shanwei Freeway (from the kilometer marker K0 to K28) is employed for the crash injury severity analysis. Figure 1 illustrates the locations of the freeway sections under investigation. The two freeway sections are spatially adjacent and are operated and managed by the same agency—the Luda Constituent Company of Guangdong Road and Bridge Construction Development Co. Ltd. The dataset was assembled with information from four different data sources: (i) crash records, (ii) roadway designs, (iii) traffic flow, and (iv) meteorological conditions. Given that the data were sourced from a third party and do not contain the private information of the involved persons, ethical review was not required in the present study.
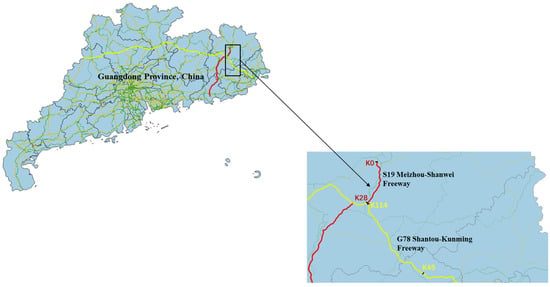
Figure 1.
Illustration of the freeway sections under investigation.
2.1. Crash Record
The traffic crash data were retrieved from the Freeway Maintenance and Administration Management System, which is maintained by the freeway management agency. According to the system, 664 crashes occurred on the selected sections of the two freeways from 2021 to 2023. By removing the crash records with incomplete information, the data of 617 crashes were extracted and processed for the study. In the raw crash records, crash injury severity is categorized into four levels: no injury, slight injury, severe injury, and fatality, in accordance with the rules of the Ministry of Public Security. Among the extracted data, only one and nine crashes resulted in severe injuries and fatalities, respectively. Due to this sparseness, the two severity levels were combined to constitute the “fatal and severe injury (FSI)” category.
In addition to crash injury severity, the system also provides information on the types and license numbers of the involved vehicles, and the dates, time, types, and causes of crashes. These vehicle and crash attributes are categorized based on the original definitions in the system and their classifications in similar works [2,29].
2.2. Roadway Design
The profiles of the two freeway sections which are designed by the Guangdong Provincial Highway Survey, Planning and Design Institute were also obtained from the management agency. The quantities of roadway attributes (e.g., the number and width of lanes, the type and width of shoulders, speed limit) are constant along the two freeway sections. Although it is fixed, noticeably, the speed limit is only 80 km/h, which is significantly lower than the counterparts (100 or 120 km/h) on other freeways in China. Three geometric design attributes of crash locations, including vertical grade, three-dimensional (3D) curvature, and 3D torsion, were extracted from the freeway profiles. The two 3D highway attributes were selected because they determine the geometric morphology of freeways, whose alignments are 3D in nature. The 3D curvature measures the bending of a freeway, and the 3D torsion measures its twisting. Please refer to Wang et al. [41] for more detailed descriptions and computing formulas of the attributes. While Wang et al. [41] found that freeway crash rate is significantly associated with 3D attributes, their effects on freeway crash severity have not been investigated. In addition, in the two mountainous freeway sections, the minimum grade of down-slopes reaches −4.67%, and the maximum grade of up-slopes reaches 4.8%.
2.3. Traffic Flow and Meteorological Condition
The monthly traffic data recorded by the Electronic Toll Collection (ETC) units along the two freeway sections from 2021 to 2023 were also collected. According to the data, the number of truck vehicles accounts for over 60% in the mixed traffic flow. Each crash was matched to the nearest upstream ETC unit. The monthly traffic volume from the nearest ETC unit was used as an explanatory variable for the analysis of freeway crash severity.
The meteorological observation data at a municipal-level weather station near the two freeway sections were obtained from the National Oceanic and Atmospheric Administration, which is an official website of the United States government. Information on the temperature, wind speed, and precipitation on the day of each crash are available.
The definitions/categorizations of the above variables and their descriptive statistics in the prepared dataset are summarized in Table 1.

Table 1.
Definitions and descriptive statistics of the variables for modeling freeway crash injury severity.
3. Method
3.1. Random Parameters Logit Model
Unobserved heterogeneity is one of the most important characteristics of traffic crash data [33]. A random parameters logit model (also called a “mixed logit model”) is a very prevalent method of analyzing crash injury severity with three or more levels while accommodating for the heterogeneity in it. In our random parameters logit model, to measure the propensity of the injury severity level for crash , a latent variable is defined as follows [42]:
where is a vector of observed factors specific to crash that may affect injury severity , and is a vector of random parameters which correspond to the vector of observed factors and are allowed to vary across the observations. is a residual term which is assumed to follow an extreme value Type I distribution that is independent and identical across the observed crashes and divided severity levels.
To reveal the interactive effects of the observed factors on crash injury severity, noticeably, the interaction terms of the factors in Table 1 are also incorporated into the vector . While the interactions among three or more factors is possible, only those between two factors (i.e., their products, such as rollover × grade) are considered in the analysis, which is consistent with previous studies [34,35,36,37,38,39].
The vector of random parameters is structured as follows:
where is a vector of fixed parameters corresponding to the means of the random parameters specific to the injury severity . represents the random components unique to each crash and severity level, which are assumed to follow a distribution, such as normal distribution.
The probability of a crash leading to a particular injury severity level is thus formulated as:
where is the density function of and is a vector of parameters describing the density function of distribution for .
To estimate the random parameters logit models with and without interactions, a simulation-based maximum likelihood approach with Halton draws was adopted [43]. A total of 500 Halton draws was set, as some previous research [44,45] has shown that this is appropriate for the estimation of random parameters models. The model estimation was conducted via programming in the econometric software NLOGIT 6.0. Additionally, to quantify the effects of significant factors on each crash injury severity, their marginal effects were also estimated. For a continuous variable , its marginal effect on is computed by its first-order derivative with respect to . For a dummy variable , the marginal effect on is calculated as:
Since the marginal effect of a certain variable may vary across the observations, its average for the entire dataset is quantified and reported.
3.2. Model Comparison Criteria
To compare the random parameters logit models with and without interactions in terms of goodness-of-fit, the widely used Akaike Information Criterion (AIC), McFadden Pseudo R2, and the likelihood ratio test are adopted. According to the likelihood performance of a model and its number of parameters, the AIC provides a measure of the information loss amount in it. The AIC is defined as [46]:
where is the number of estimable parameters in the model, and is its log-likelihood at convergence. Generally, a model with a lower AIC is preferred.
The McFadden Pseudo R2 is calculated as:
where is the log-likelihood of the null model (i.e., the model with constant only). A greater value of McFadden Pseudo R2 indicates better fit performance.
Based on the definition in [43], the likelihood ratio test statistic for models A and B is computed as:
where and represents the log-likelihood at convergence of models A and B, respectively. The statistic is assumed to follow a chi-square distribution, whose degree of freedom is the difference in the number of estimable parameters between the two models.
4. Result Analysis
4.1. Model Comparison
The estimation and comparison results of the random parameters logit models with and without interactions are shown in Table 2, where only those factors with significant effects (i.e., the corresponding parameters different from zero at least at the 0.1 significance level) on crash injury severity are included. According to the results, the AIC value (=540) of the random parameters logit model with interactions is smaller than that (=552) of the random parameters logit model (without interactions), which indicates the better fit performance of the former model. It is also demonstrated by the higher value of the McFadden Pseudo R2 for the model with interactions. The findings are reasonable, because there are three pairs of factors (i.e., spring × evening, fixed object × autumn, and non-local vehicle × improper driving) with significant interactive effects on crash injury severity. They are also consistent with the conclusions in previous studies [34,36,37,38]: capturing the interactions among the observed factors is able to improve the goodness-of-fit of models. The findings can be further validated by the results of the likelihood ratio test. Specifically, the likelihood ratio test statistic between the two models equals 12, which is bigger than the chi-squared critical value at the 0.05 significance level (=7.81). That is, the two models are significantly different from each other.

Table 2.
The estimation and comparison results of the random parameters logit models with and without interactions.
4.2. Interpretation of Model Estimation and Marginal Effects
Due to the superiority of the random parameters logit model with interactions, the effects (including the main effects and interactive effects) of significant factors on the injury severity of freeway crashes are interpreted according to the results of its parameter estimation (shown in Table 2) and the corresponding marginal effects (shown in Table 3).

Table 3.
The marginal effects of significant factors on freeway crash severity.
Vehicle type is an important characteristic of the involved vehicles with significant influence on crash injury severity. Specifically, the parameters of buses and heavy trailers for minor injury and FSI are all significantly positive, which indicate that the involvement of buses and heavy trailers in freeway traffic crashes increases the injury severity level of freeway crashes. According to the estimated marginal effects, compared to passenger car-only crashes (the reference category), the involvement of buses and heavy trailers would increase the probability of minor injury by 2.35% and 0.61%, respectively, and increase the probability of FSI by 1.32% and 0.79%, respectively. These results are anticipated because the crash aggressivity of these vehicles is stronger (given their bigger sizes and masses and higher stiffness) than passenger cars [2,5,29], which would result in greater damage to the other vehicles colliding to them. The coefficient of trucks for minor injury is a random parameter with a mean of 0.14 and a standard deviation of 2.30, which suggests that the involvement of trucks would increase the probability of minor injury for 52.4% of freeway crashes and decrease the probability of minor injury for the remaining 47.6%. On average, the involvement of trucks would decrease the probability of no injury by 4.64% and increase the probability of minor injury by 4.71%, as revealed by the estimated marginal effects. It is interesting to find that the coefficient of other vehicles for FSI are significantly negative, which suggests that the involvement of other types of vehicles would decrease the probability of FSI. This is possibly due to the vehicles mostly being specialized, such as road sweepers, which are usually driven at very low speeds.
With regard to the time of day, the time being before dawn had positive effects on both minor injury and FSI. According to the marginal effects, the probabilities of minor injury and FSI crashes occurring before dawn are 1.25% and 1.34% higher, respectively, relative to those occurring in the afternoon (the reference category). Evening also has a significantly positive effect on KSI, which indicates that freeway crashes in the evening are more likely to result in severe outcomes. The results are generally in line with the previous findings [30,47], which argued that they may be attributed to the limited visual field and lower mental alertness of vehicle drivers in the evening and before dawn.
While the main effects of the seasonal variables are not statistically significant, the interactive effects between some of them and other factors are significant. Specifically, the interaction between spring and evening was found to be positively associated with minor injury. There is a sharp rise in freeway traffic volume during the Spring Festival, which is the most important festival in China, and many people will return to their hometown from big cities by driving cars along freeways, because freeways are free of charge during the festival. This increased traffic volume usually results in traffic congestion on freeways, while the limited visual field in the evening might bring about vehicle collisions. The interactive effects between autumn and fixed objects on minor injury is also significantly positive, which means that fixed-object crashes are more likely to result in minor injuries in autumn.
Curvature was the only roadway factor found to have a significant effect on freeway crash injury severity. According to its marginal effects, a one-unit increase in the 3D curvature would increase the probability of minor injury by 0.52% and decrease the probabilities of no injury and FSI by 0.50% and 0.02%, respectively. This finding is generally consistent with [41], in which the authors concluded that 3D curvature is significantly associated with the safety performance of freeways. It is also similar to the effect of horizontal curvature on freeway crash severity: a greater curvature requires stronger force for vehicles negotiating the curve, and therefore reduces vehicle control [29,47].
The parameter of traffic for minor injuries is positive at the 0.05 significance level, which indicates that freeway sections with higher traffic volumes are more likely to experience minor injury crashes. Specifically, a 105 PCU increase in the monthly traffic volume is expected to increase the probability of minor injuries by 0.85% and decrease the probabilities of no injury and FSI by 0.84% and 0.01%, respectively. This conforms to transportation intuitions and the extant literature [2,47]: a higher traffic volume would bring about severer traffic congestion and lower vehicle speed. The traffic congestion may make some aggressive drivers change lanes frequently and thus increase traffic conflicts. The lower vehicle speed would decrease the probability of severe outcomes.
Regarding the causes of crashes, the negative coefficient of improper driving for FSI suggests that improper driving is less likely to result in FSI than insufficient safety distance (the reference category). Its marginal effects reveal that the probability of FSI caused by improper driving is 1.45% lower than that caused by insufficient safety distance. Additionally, the interactive effect between improper driving and non-local vehicles on the propensity of minor injury is positive at the 0.05 significance level, which means that the improper driving behavior of non-local vehicle drivers is more likely to result in minor injury. This may be attributed to the drivers of non-local vehicles being unfamiliar with mountainous freeways [29]. When encountering an upcoming crash, they may not take proper actions to avoid crash injury.
While interaction and heterogeneity were found in the effects of the observed factors, there are some limitations in this research. First, information related to human factors (e.g., the age and gender of drivers involved) and emergency medical services (e.g., its response time and on-scene time) was not recorded in the crash data. Therefore, their main and interactive effects on freeway crash injury severity were not investigated. Second, the crash data were from two freeways in Guangdong Province, China. The transferability of the analysis results to freeways in other regions or countries is not verified. Third, the random parameters logit model was formulated in the standard form. More complicated versions, such as a model with heterogeneity in means and variances, may further reveal heterogeneous effects, although they were not found in the random parameters used in the current research.
5. Conclusions and Future Research
This research investigates the heterogeneous and interactive effects of vehicle characteristics (i.e., vehicle type and registration location), roadway design attributes (i.e., vertical grade, 3D curvature and torsion), traffic volume, meteorological conditions (i.e., temperature, wind speed, and precipitation), crash time (i.e., time of day, day of week, and season), type, and causes on the injury severity of freeway crashes, using a three-year (2021–2023) crash dataset from Shantou–Kunming Freeway and Meizhou–Shanwei Freeway in China, which are featured by mountainous terrain and high proportions of heavy vehicles. A random parameters logit model with interaction terms was developed for the empirical investigation.
The results of the model estimation indicate that there is unobserved heterogeneity in the effect of trucks on crash injury severity. Three pairs of explanatory variables, including spring and evening, autumn and fixed objects, and non-local vehicles and improper driving, significantly increase the likelihood of minor injury. It is also increased by traffic volume and the 3D curvature of freeway sections. Compared with passenger car-only crashes, the involvement of buses and heavy trailers would increase the likelihoods of minor injury and FSI, and the involvement of other vehicles (e.g., road sweepers) would decrease the likelihood of FSI. Freeway crashes in the evening and before dawn, and those caused by insufficient safety distance, are more likely to result in severe outcomes. The marginal effects of these significant variables on the probabilities of each injury severity level are quantified. In addition, the results of DIC, McFadden Pseudo R2, and the likelihood ratio test suggest that the random parameters logit model with interactions outperforms the counterpart without interactions. The findings justify the necessity and advantage of capturing the heterogeneity and interaction in crash data.
The analysis results provide some suggestions for designing countermeasures for the prevention of freeway traffic injury (especially severe injuries and fatalities), which is a key goal of developing a safe and sustainable freeway transportation system. For example, more safety education/campaigns and more frequent police patrols during the evening (especially in spring) and before dawn are suggested to regulate drivers to obey the traffic rules, especially those for intercity buses, heavy vehicles, and hazardous material vehicles; (1) the drivers of these vehicle types are prohibited from continuously driving for over 4 h during daytime (6:00 a.m. to 10:00 p.m.) or over 2 h during nighttime (10:00 p.m. to 6:00 a.m.), and the rest time of each vehicle stop should be not less than 20 min; (2) the cumulative driving time of bus drivers within 24 h should be no more than 8 h; and (3) the driving speed of intercity buses during nighttime should be under 80% of the posted speed limit. Adding vehicle distance confirmation markers to the hotspots of crashes attributed to insufficient safety distance is helpful for reducing crashes of this type and mitigate their crash injury severity. Setting solid lines in freeway sections with high traffic volume is expected to reduce lane-changing behaviors and the potential traffic crashes and injuries caused by them. Reducing the 3D curvature of freeway geometry alignments is encouraged during their reconstruction projects to improve safety performance.
Due to the limitations in the crash data collection and methodology, some directions for future research are provided. The effects of human factors, emergency medical services, and their interactions with other factors on crash injury severity should be examined, and the spatial transferability and temporal stability of the findings should be validated if more crash data are available. In addition, extending the random parameters logit model to further account for heterogeneity in means and variances is also worth exploration.
Author Contributions
Conceptualization, K.S. and Y.L.; methodology, Q.Z.; software, Q.Z.; validation, Y.L. and Q.Z.; formal analysis, K.S.; investigation, K.S.; resources, K.S.; data curation, Y.L.; writing—original draft preparation, K.S. and Y.L.; writing—review and editing, Q.Z. and X.W.; visualization, Y.L.; supervision, X.W.; project administration, X.W.; funding acquisition, Q.Z. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
The authors declare that this study received funding from the Open Fund of the Key Laboratory of Highway Engineering of Ministry of Education (Changsha University of Science & Technology), grant number kfj230301; the Natural Science Foundation of Guangdong Province, grant number 2024A1515011177; and the Guangdong S&T programme, grant number 2024A1111120009. The funders were not involved in the study design; the collection, analysis, or interpretation of data; the writing of this article; or the decision to submit it for publication.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are not publicly available due to privacy restrictions.
Conflicts of Interest
Keqiang Sun and Yongquan Li were employed by the company Guangdong Road and Bridge Construction Development Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FSI | fatal and severe injury |
| MI | minor injury |
| 3D | three-dimensional |
| ETC | Electronic Toll Collection |
| PCU | passenger car unit |
| AIC | Akaike Information Criterion |
References
- Macioszek, E.; Ahac, S. Analysis of the transport volume of passengers and cargo on the example of the Warsaw-Okęcie international airport (Poland). Sci. J. Silesian Univ. Technol. Ser. Transp. 2023, 120, 151–164. [Google Scholar] [CrossRef]
- Zeng, Q.; Gu, W.; Zhang, X.; Wen, H.; Lee, J.; Hao, W. Analyzing freeway crash severity using a Bayesian spatial generalized ordered logit model with conditional autoregressive priors. Accid. Anal. Prev. 2019, 127, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.; Sayed, T.; Hassan, Y. Influence of vertical alignment on horizontal curve perception: Effect of spirals and position of vertical curve. Can. J. Civ. Eng. 2005, 32, 204–212. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Li, X.; Wang, Y.; Zeng, Q. Effects of geometric attributes of horizontal and sag vertical curve combinations on freeway crash frequency. Accid. Anal. Prev. 2023, 186, 107056. [Google Scholar] [CrossRef]
- Huang, H.; Siddiqui, C.; Abdel-Aty, M. Indexing crash worthiness and crash aggressivity by vehicle type. Accid. Anal. Prev. 2011, 43, 1364–1370. [Google Scholar] [CrossRef]
- Ahmed, M.; Huang, H.; Abdel-Aty, M.; Guevara, B. Exploring a Bayesian hierarchical approach for developing safety performance functions for a mountainous freeway. Accid. Anal. Prev. 2011, 43, 1581–1589. [Google Scholar] [CrossRef]
- Hou, Q.; Meng, X.; Leng, J.; Yu, L. Application of a random effects negative binomial model to examine crash frequency for freeways in China. Phys. A Stat. Mech. Appl. 2018, 509, 937–944. [Google Scholar] [CrossRef]
- Xu, C.; Wang, W.; Liu, P.; Li, Z. Calibration of crash risk models on freeways with limited real-time traffic data using Bayesian meta-analysis and Bayesian inference approach. Accid. Anal. Prev. 2015, 85, 207–218. [Google Scholar] [CrossRef]
- Wu, Y.; Abdel-Aty, M.; Lee, J. Crash risk analysis during fog conditions using real-time traffic data. Accid. Anal. Prev. 2018, 114, 4–11. [Google Scholar] [CrossRef]
- Alnawmasi, N.; Mannering, F. The impact of higher speed limits on the frequency and severity of freeway crashes: Accounting for temporal shifts and unobserved heterogeneity. Anal. Methods Accid. Res. 2022, 34, 100205. [Google Scholar] [CrossRef]
- Dzinyela, R.; Alnawmasi, N.; Adanu, E.K.; Dadashova, B.; Lord, D.; Mannering, F. A multi-year statistical analysis of driver injury severities in single-vehicle freeway crashes with and without airbags deployed. Anal. Methods Accid. Res. 2024, 41, 100317. [Google Scholar] [CrossRef]
- Haq, M.T.; Zlatkovic, M.; Ksaibati, K. Investigating occupant injury severity of truck-involved crashes based on vehicle types on a mountainous freeway: A hierarchical Bayesian random intercept approach. Accid. Anal. Prev. 2020, 144, 105654. [Google Scholar] [CrossRef] [PubMed]
- Haq, M.T.; Zlatkovic, M.; Ksaibati, K. Assessment of tire failure related crashes and injury severity on a mountainous freeway: Bayesian binary logit approach. Accid. Anal. Prev. 2020, 145, 105693. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.; Bertini, R. Exploring the effect of COVID-19 on driver injury severities in freeway single-vehicle crashes accounting for unobserved heterogeneity. Transp. Lett. 2024, 16, 612–627. [Google Scholar] [CrossRef]
- Russo, B.J.; Savolainen, P.T. A comparison of freeway median crash frequency, severity, and barrier strike outcomes by median barrier type. Accid. Anal. Prev. 2018, 117, 216–224. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Abdel-Aty, M.; Han, L. Effects of speed difference on injury severity of freeway rear-end crashes: Insights from correlated joint random parameters bivariate probit models and temporal instability. Anal. Methods Accid. Res. 2024, 42, 100320. [Google Scholar] [CrossRef]
- Yu, R.; Abdel-Aty, M. Analyzing crash injury severity for a mountainous freeway incorporating real-time traffic and weather data. Saf. Sci. 2014, 63, 50–56. [Google Scholar] [CrossRef]
- Gonzalez, R.P.; Cummings, G.R.; Phelan, H.A.; Mulekar, M.S.; Rodning, C.B. Does increased emergency medical services prehospital time affect patient mortality in rural motor vehicle crashes? A statewide analysis. Am. J. Surg. 2009, 197, 30–34. [Google Scholar] [CrossRef]
- Lee, J.; Abdel-Aty, M.; Cai, Q.; Wang, L. Effects of emergency medical services times on traffic injury severity: A random effects ordered probit approach. Traffic Inj. Prev. 2018, 19, 577–581. [Google Scholar] [CrossRef]
- Hou, Q.; Huo, X.; Leng, J.; Cheng, Y. Examination of driver injury severity in freeway single-vehicle crashes using a mixed logit model with heterogeneity-in-means. Phys. A Stat. Mech. Its Appl. 2019, 531, 121760. [Google Scholar] [CrossRef]
- Huang, H.; Peng, Y.; Wang, J.; Luo, Q.; Li, X. Interactive risk analysis on crash injury severity at a mountainous freeway with tunnel groups in China. Accid. Anal. Prev. 2018, 111, 56–62. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Ding, X.; Yuan, C.; Liu, X.; Tang, J. Jointly analyzing freeway primary and secondary crash severity using a copula-based approach. Accid. Anal. Prev. 2023, 180, 106911. [Google Scholar] [CrossRef]
- Ma, Z.; Steven, I.; Chien, J.; Dong, C.; Hu, D.; Xu, T. Exploring factors affecting injury severity of crashes in freeway tunnels. Tunn. Undergr. Space Technol. 2016, 59, 100–104. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Shi, C.; Huang, Y.; Yang, Y.; Ke, R.; Zhao, J. Sensing data supported traffic flow prediction via denoising schemes and ANN: A comparison. IEEE Sens. J. 2020, 20, 14317–14328. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, J.; Li, C.; Wu, B.; Wu, H.; Montewka, J. Maritime traffic situation awareness analysis via high-fidelity ship imaging trajectory. Multimed. Tools Appl. 2024, 83, 48907–48923. [Google Scholar] [CrossRef]
- Pervez, A.; Lee, J.; Huang, H. Exploring factors affecting the injury severity of freeway tunnel crashes: A random parameters approach with heterogeneity in means and variances. Accid. Anal. Prev. 2022, 178, 106835. [Google Scholar] [CrossRef]
- Wang, C.; Chen, F.; Cheng, J.; Easa, S.M. Modeling injury severities of single and multi-vehicle freeway crashes considering spatiotemporal instability and unobserved heterogeneity. Transp. Lett. 2024, 16, 234–262. [Google Scholar] [CrossRef]
- Wen, H.; Ma, Z.; Chen, Z.; Luo, C. Analyzing the impact of curve and slope on multi-vehicle truck crash severity on mountainous freeways. Accid. Anal. Prev. 2023, 181, 106951. [Google Scholar] [CrossRef]
- Zeng, Q.; Wang, Q.; Wang, F.; Sze, N.N. Revisiting spatial correlation in crash injury severity: A Bayesian generalized ordered probit model with Leroux conditional autoregressive prior. Transp. A Transp. Sci. 2022, 18, 1084–1102. [Google Scholar] [CrossRef]
- Zeng, Q.; Xu, Z.; Liang, Y.; Lee, J.; Wang, X. Incorporating spatio-temporal correlation and interaction into a generalized ordered logit model for examining injury severities of traffic accidents. J. Transp. Saf. Secur. 2024, 16, 1237–1258. [Google Scholar] [CrossRef]
- Zhou, Z.; Meng, F.; Song, C.; Sze, N.N.; Guo, Z.; Ouyang, N. Investigating the uniqueness of crash injury severity in freeway tunnels: A comparative study in Guizhou, China. J. Saf. Res. 2021, 77, 105–113. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.; Kim, J.J.; Hong, J.G. Factors Affecting Injury Severity in Tunnel Crashes Observed over a Long Period on Korean Freeway Systems. KSCE J. Civ. Eng. 2024, 29, 100001. [Google Scholar] [CrossRef]
- Savolainen, P.T.; Mannering, F.L.; Lord, D.; Quddus, M.A. The statistical analysis of highway crash-injury severities: A review and assessment of methodological alternatives. Accid. Anal. Prev. 2011, 43, 1666–1676. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.; Jang, K.; Yoon, Y.; Kang, S. Contributing factors to vehicle to vehicle crash frequency and severity under rainfall. J. Saf. Res. 2014, 50, 1–10. [Google Scholar] [CrossRef]
- Ponnaluri, R.V. The odds of wrong-way crashes and resulting fatalities: A comprehensive analysis. Accid. Anal. Prev. 2016, 88, 105–116. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Franke, R.; Ksaibati, K.; Shinstine, D.S. Effects of truck traffic on crash injury severity on rural highways in Wyoming using Bayesian binary logit models. Accid. Anal. Prev. 2018, 117, 106–113. [Google Scholar] [CrossRef]
- Wen, H.; Zhang, X.; Zeng, Q.; Sze, N.N. Bayesian spatial-temporal model for the main and interaction effects of roadway and weather characteristics on freeway crash incidence. Accid. Anal. Prev. 2019, 132, 105249. [Google Scholar] [CrossRef]
- Zhai, X.; Huang, H.; Sze, N.N.; Song, Z.; Hon, K.K. Diagnostic analysis of the effects of weather condition on pedestrian crash severity. Accid. Anal. Prev. 2019, 122, 318–324. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, D.; Gu, X.; Abdel-Aty, M.; Xing, Y.; Wang, J.; Lu, H.; Chen, Y. A hybrid approach of random forest and random parameters logit model of injury severity modeling of vulnerable road users involved crashes. Accid. Anal. Prev. 2023, 192, 107235. [Google Scholar] [CrossRef]
- Sun, Z.; Ai, Z.; Wang, Z.; Wang, J.; Gu, X.; Wang, D.; Lu, H.; Chen, Y. Considering multi-scale built environment in modeling severity of traffic violations by elderly drivers: An interpretable machine learning framework. Accid. Anal. Prev. 2024, 207, 107740. [Google Scholar] [CrossRef]
- Wang, J.; He, S.; Zhai, X.; Wang, Z.; Fu, X. Estimating mountainous freeway crash rate: Application of a spatial model with three-dimensional (3D) alignment parameters. Accid. Anal. Prev. 2022, 170, 106634. [Google Scholar] [CrossRef] [PubMed]
- Mannering, F.L.; Shankar, V.; Bhat, C.R. Unobserved heterogeneity and the statistical analysis of highway accident data. Anal. Methods Accid. Res. 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Washington, S.P.; Karlaftis, M.G.; Mannering, F. Statistical and Econometric Methods for Transportation Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Song, D.; Yang, X.; Anastasopoulos, P.C.; Zu, X.; Yue, X.; Yang, Y. Temporal stability of the impact of factors determining drivers’ injury severities across traffic barrier crashes in mountainous regions. Anal. Methods Accid. Res. 2023, 39, 100282. [Google Scholar] [CrossRef]
- Yu, M.; Zheng, C.; Ma, C. Analysis of injury severity of rear-end crashes in work zones: A random parameters approach with heterogeneity in means and variances. Anal. Methods Accid. Res. 2020, 27, 100126. [Google Scholar] [CrossRef]
- Akaike, H. Maximum likelihood identification of Gaussian autoregressive moving average models. Biometrika 1973, 60, 255–265. [Google Scholar] [CrossRef]
- Christoforou, Z.; Cohen, S.; Karlaftis, M.G. Vehicle occupant injury severity on highways: An empirical investigation. Accid. Anal. Prev. 2010, 42, 1606–1620. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).