Abstract
In this work, a new method to analyze the drought episodes based on the annual precipitation time series and utilizing complex networks theory is proposed. The precipitation time series is transformed into a complex network using the visibility algorithm.Then, several network measures are computed to characterize the underlying connectivity. The proposed analysis identifies important nodes which correspond to the low annual precipitation volume, providing a way to assess drought intensity without the use of the mean value and standard deviation, which are sensitive to climate change. Additionally, using community detection algorithms and network centrality measures, the method identifies ∼10-year and ∼4-year cycles within a period of 57 years. Using macroscopic measures like network distributions, we can identify rare high-intensity drought events. Finally, network analysis shows that the closeness centrality measure is in very good agreement with the well-known Standardised Precipitation Index (SPI) and thus can be used to characterize drought intensity.
1. Introduction
Drought remains a serious threat to the livelihoods of millions worldwide. Combating drought is essential for achieving sustainable development goals, as it supports the preservation of ecosystem services and enhances the quality of life for millions in regions vulnerable to drought (E/CN.17/2009/19) [1]. According to the same source, encouraging the establishment of scientifically based drought- and desertification-related local, national, and, where appropriate, regional indicators remains a challenge in combating drought.
Climate change, as well as other trends such as rapid urbanization, changes the water regime; hence, the sustainability concept is becoming an essential challenge for the scientific community. The impacts of emerging global climate change threats are very serious for urban areas due to the potentially high population density [2], as well as threats to food security, ecosystems, and more. An interesting occurrence of climate change is that water flows are becoming more unpredictable due to the increased frequency of extreme weather events and changes in rainfall patterns over time and space. This results in more intense floods and droughts, severe wildfires, rising sea levels, polar ice melt, catastrophic storms, flooding, and a decline in biodiversity [3]. Therefore, climate change is expected to increase the risk of hydrometeorological events with significant social, environmental, and economic impacts [4,5].
As the frequency of droughts is expected to increase in the coming years, their reliable detection, in combination with other indices, is a valuable tool for mapping drought-prone areas to mitigate the impact on water resources. This, in conjunction with the construction of suitable infrastructure (e.g., dams, rainwater harvesting systems) and legislative modifications, facilitates the sustainable management of water resources in accordance with the Sustainable Development Goals (SDGs) and circular economy principles.
Over the last few years, complex networks theory has been utilized to study the complicated environmental interactions for climate dynamics [6,7]. Spatial correlated climatic observables, such as heatwaves, drought or extreme floods, are modelled as complex networks highlighted as ‘teleconnections’ [6,8]. Complex network analysis explores the topological climate characteristics, aspiring to reveal the underlying mechanisms and contributing to weather forecasting of extreme events under climate change. Furthermore, the topological analysis can be used to identify hotspot regions of extreme events (extreme drought [8] or rainfall [6]).
In this work, we propose a method to analyze and characterize the intensity of meteorological drought by transforming the ‘inverted’ precipitation time series of an area into a complex network. This transformation is achieved using the visibility algorithm proposed by Lacassa et al. [9]. Then, the structural properties of the network are studied, and the severity of the drought is evaluated. Thus, complex network measures (e.g., closeness centrality measure) can serve as indices for drought characterization.
The visibility method of Lacasa et al. [9] has many applications, e.g., in physics and mechanics [10,11,12], medicine [13,14] and finance [15,16]. For instance, in Charakopoulos et al. [11], the authors use the visibility algorithm to analyze the magnetohydrodynamic channel flow. Additionally, John R. and John M. [17] apply the visibility algorithm to investigate the time lag between rainfall and water level fluctuations in Lake Okeechobee. Nevertheless, this is the first time (to our knowledge) that the visibility algorithm is combined with complex networks theory to estimate the characteristics of drought events, similar to well-known indices, e.g., Standardised Precipitation Index (SPI).
We highlight here that the well-known drought indicators (RDI, SDI, SPI; RDI: Reconnaissance Drought Index, SDI: Standardized Discharge Index [18,19,20]) use either mean values or the median and standard deviation based on historical data [18,21]. However, accurately estimating the mean value is challenging due to either limited data or climate change. Our method proposes a different approximation to characterize drought severity, liberated from the low-order statistics (e.g., mean and variance). The paper is organized as follows. In Section 2, we present the methodological steps and the network measures that characterize the topological structure. In Section 3, a description of the areas under study is given, and in Section 4, we represent the results for the Arnaia and Florina areas. Finally, we conclude in Section 5.
2. Materials and Methods
Initially, we present the construction of a complex network from a time series based on the visibility algorithm in [9,11]. According to the visibility algorithm, nodes correspond to time (years in our case), and edges are created in proportion to the intensity of the yearly drought value. Thus, high-intensive drought years (i.e., nodes with high visibility) are expected to play a central role in the network structure.
Consequently, one can study and analyze the topological properties (the structure of the network) and characterize the drought years using an arsenal of network measures. For instance, by utilizing centrality measures, one can characterize which year is important in the evolution of droughts. These measures are degree centrality, closeness centrality, and betweenness centrality.
Another important marker for drought organization is the modularity index (i.e., the detection of network communities), which serves as an alternative method to define the meteorological drought cyclicity. Different communities correspond to different cycles of drought. In total, network analysis can be used to study the organization of drought and to identify rare (extreme) drought events, offering valuable information for the sustainability of water resources.
2.1. Network Construction Using Visibility Algorithm
We let a given discrete time series. Each data point constitutes a node i in the network. Two nodes are connected, i.e., if they satisfy the visibility criterion: Any intermediate point between and does not obstruct the view line of . To be more specific, we express the visibility principle using the slope of line segment. We let be the slope of line segment with ending points which is defined as . We let , with , any intermediate point of . Then, the point C is visible from A if for each :
Solving Equation (1) with respect to we obtain the visibility condition:
Equation (2) simply says that there is a ‘visibility line’ between A and C, which does not intersect any intermediate data height [9]. A concrete example is given in Figure 1. The time series is depicted in Figure 1A, which contains 8 points, from 1 to 8. Point A (for x = 1) has visibility at Point B but does not have visibility at Point C. This is explained as follows: the intermediate Point B between A and C ‘blocks’ the view (the grey line from A to C). Using the mathematical definition of the slope of the segment, we determine for the intermediate Point B, , that is, the visibility property of Equation (1) is not satisfied.

Figure 1.
From drought time series to complex network representation and analysis. (A) The visibility algorithm, (B) Transformation of time series into a complex network, (C) Adjacency or connectivity matrix, (D) Network measures that characterize connectivity.
Employing the visibility algorithm, we transform the time series into a complex network; see Figure 1B. The numbering represents the abscissa points (e.g., the years sequentially). The network can be represented using the adjacency or connectivity matrix A. If nodes are connected, then , otherwise . For example, Node 1 is connected with Node 2, which implies , while Nodes 1 and 3 are not connected; thus, . In Figure 1C, we show the corresponding adjacency matrix of the example network in Figure 1D.
The aforementioned procedure defines a complex network which can be presented as graph , where N is the set of nodes and E is the the set of edges. The network connectivity is ‘stored’ in the adjacency matrix A. The elements of the adjacency matrix A have values 1 and 0 according to connectivity, i.e.,
where indicates that the nodes are connected. Using the adjacency matrix, we compute important network measures that characterize the connectivity. A representative set of network measures contains the degree centrality, the betweenness centrality, the man path length and the community detection or modularity.
2.2. Measures Characterizing the Drought Network Connectivity
Network measures are used to obtain information about the connectivity structure of the network. The main categories are centralities, which characterize the importance of a node, clustering measures which describe motifs and how they appear in the networks, and community detection, which is a partition of the network into different subgroups [22,23,24,25,26,27,28,29].
Network quantities can be separated into local, when the quantity describes a node property, and global (or macroscopic), when results are obtained from statistics over all the members of the network. For example, the statistical distribution of a network property and its first-order statistics, i.e., the mean value, are obtained as global measures.
2.2.1. Degree Centrality
The degree of a node i or degree centrality refers to the number of links connected to it [22]. In the case of undirected network (i node connected with j and vice versa), the degree centrality is defined as
where is the element of the adjacency matrix A (i.e., iff ). A high degree of connectivity (increased numbers of links) of the ith node defines the importance of a node in the network (called degree centrality). The degree distribution defines the probability of a randomly selected node having a specific degree k.
2.2.2. Path Lengths, Closeness Centrality and Clustering Coefficient
A path between nodes with a minimum number of successive edges (steps) constitutes a geodesic path. The minimum number of steps between these two nodes in the network defines the shortest path length or distance between node i and j. Averaging over the set of all shortest paths, we obtain the mean path length of the network [22,30]:
The mean path length shows how fast the information can be spread in the network. A low mean shortest path length shows that any two random nodes can interact very fast. A similar phenomenon is known: the six-degree social connectedness of Kevin Bacon [31]).
A centrality measure which estimates the importance of a node with respect to distance from other nodes is closeness centrality. Nodes that are in a central position in the network are closer to all other nodes. Closeness centrality is defined as
and it computes the inverse sum of the shortest paths with respect to the ith node. A central node i in the network, form short distances from the other nodes, which implies the denominator , is small; thus, the closeness centrality is expected to admit a high value.
Another important measure which characterizes connectivity is the clustering coefficient. It measures the proportion of triangle loops that exist in a node. Specifically, the clustering coefficient of node i is defined as the following ratio:
The higher the number of triangles (that exist) with respect to the ith node, the higher the clustering coefficient.
2.2.3. Betweenness Centrality
Another important measure, which quantifies the significance of a node, is betweenness centrality. Betweenness centrality measures the amount of influence which a node has with respect to the total information flow in the network. Important nodes that connect different subgraphs in the network (i.e., act as a bridge) show high betweenness centrality. The betweenness centrality of the ith node is mathematically defined as the fraction of all shortest paths in the network that pass through the node; that is,
where is the number of shortest paths from j to k passing over i, and is the number of shortest paths between nodes j and k. Bridging nodes that connect different subsets of the network often have high betweenness centrality. Higher values of indicate that the node acts as a central hub.
2.3. Detection of Communities and Modularity
In many cases, networks can be partitioned into subsets (subgraphs) such that there are dense internal connectivity (connectivity among nodes in the subset) and sparse connections to other subgraphs [24]. The partition of the network into densely connected subgraphs (or communities) plays a significant role in information processing within the network since it offers a modular view of the process on the network [32,33].
From graph theory, it is proven that the expected number of edges (if edges were positioned at random) is [24,34], where the number is the total number of edges in the network. Quantity
expresses the deviation of the subgraph K connectivity from an equivalent random network (with the same degrees of nodes); not, however, when it is constructed randomly, i.e., using the configuration model ([35], Chapter 13).
According to [24], quantity Q is extended as follows: (a) The modality index assigns a community number to each node. For example, if there are two communities, then . Then, the term if have the same sign (i.e., belong to the same community) and 0 otherwise. (b) The modularity (or modality) is given by
Using matrix multiplication, the last sum is written as follows:
where is the resultant modularity matrix. Here, we seek the best network partition, i.e., we separate the network into subgraphs in order to maximize the modularity function . The matrix B has the form of a graph Laplacian matrix, and in such matrices, the optimizations can be achieved using graph partitioning or spectral partitioning (eigenvalue–eigenvector decomposition) of B [24,36].
2.4. Data and Drought Time Series Preprocess
For the drought analysis, the precipitation data are transformed as follows:
an then, we normalize as follows:
Clearly, , where value corresponds to the case of maximum precipitation, and , in the case of minimum precipitation, which implies that expresses the drought evolution as ‘inverse’ precipitation.
3. Case Study
Rainfall data from the Arnea and Florina rain gauge stations were provided by the Decentralized Administration Unit of Macedonia and Thrace, Greek minister of Decentralization www.m-t.gov.gr and the Hellenic National Meteorological Service www.emy.gr (accessed 10 February 2020), respectively, and then evaluated at the Laboratory of Engineering Geology and Hydrogeology of Aristotle University. The rain gauge at the Arnaia station is located at an elevation of +590 m. The average annual rainfall at the Arnaia station for the period of 1954–2019 ranges from 416.5 (1992) to 1238.7 (2014) with an average of 755.6 mm.
The meteorological station of Florina is located at an altitude of 637 m above sea level. The average annual rainfall is 644.2 mm, with a maximum of 1090.4 mm (1966) and a minimum of 279.1 mm (1990). According to the Köppen climate classification, the climate of Florina belongs to the Dfb type (continental humid with dry summers) and that of Arnaia to the Cfa type (temperate with very dry summers). Both areas have been affected by episodes of severe drought. This has been documented by previous research [37]; see also Figure 2.

Figure 2.
Area under study. With a red star, we depict the Arnaia, and with a green star the Florina area.
4. Results
We apply the the visibility algorithm to transform the data into a complex network. We examine two cases: (a) the Arnaia (Chalkidiki area) precipitation data and (b) the Florina area precipitation data.
4.1. Localized Important Network Nodes: The Case of Arnaia
Initially, the precipitation time series of Arnaia area is transformed according to Equations (12) and (13) a drought . Both data sets are depicted in Figure 3A. The resulting drought network of Arnaia is shown in Figure 3B. The color code in Figure 3B shows different communities in the network, and it is explained in detail in the next paragraph. We characterize the importance of nodes using network measures such as betweenness centrality, degree centrality, clustering coefficient and closeness centrality.

Figure 3.
(A) The annual precipitation time series of the north Greece city Arnaia is depicted with blue color. The transformed with red one. (B) Transformation of into a complex network. The color code shows the existence of different communities in the network.
Figure 4 presents the betweenness centrality and the degree centrality for each node. The abscissa corresponds to time in years. The betweenness centrality in Figure 4A possesses three dominant local maxima at 1984–1985, 1999–2000 and 2011–2012, while there are few less important maxima in 1964–1965, 1976–1977, 1992–1993, 2016–2017. The corresponding number of these nodes in the network (in Figure 3A) are 4 → 1964–1965, 16 → 1976–1977, 24 → 1984–1985, 32 → 1992–1993, 39 → 1999–2000, → 51 → 2011–2012 and 56 → 2016–2017. A more detailed view in the network, i.e., Figure 3B reveals that these are ‘bridge’ nodes that connect different communities (subnetworks with different colors). Furthermore, these nodes are important in the network since they control the information flow.

Figure 4.
The is depicted with red color. (A) Node’s betweenness centrality (BC). (B) Degree centrality (Deg).
Similar results are obtained in Figure 4B (but not so clear compared to Figure 4A), e.g., the highest three maxima of degree centrality coincide with the three maxima of drought time series at the same positions as in betweenness centrality.
Finally, we depict the clustering coefficient and the closeness centrality in Figure 5A,B, respectively. The majority of clustering coefficients correspond to nodes with a small number of connections (i.e., small degree of centrality). These nodes have Clustering Coefficient 1 (trivial nodes which form only one triagle). However, we can observe in Figure 5A that the extreme maximun values of correspond to extreme minima of clustering values.

Figure 5.
The is depicted with red color. (A) Clustering coefficient of each node. (B) Closeness centrality (Cl) for each node.
The closeness centrality of nodes Figure 5B is in a very good agreement with the drought evolution: both closeness centrality and have the same monotonic properties. In particular, computing the correlation coefficient, we obtain , ( is covariance and stands for standard deviation). Again, the three maxima of drought correspond to the three maxima of closeness centrality.
4.2. Macroscopic Network Measures: The Case of Arnaia
In the previous section, we localized important nodes according to the values of the network measures (e.g., betweenness centrality). Constructing the normalized histogram for one network measure, we obtained the density or the distribution of this quantity. The distribution of a network measure characterizes the whole network and is refered to as macroscopic description. Furthermore, the low order statistics of the distribution, i.e., the mean value and variance, are global measures that describe the network structure.
The first global measure we depict is the degree distribution in Figure 6A. The degree distribution expresses the probability of a randomly selected node to have k edge connections. The distribution is skewed right (the tail of the distribution is more pronounced on the right side) with a mean value of 5.42. It can be approximated with Gamma Distribution , with with confidence intervals for distribution parameters CI and .
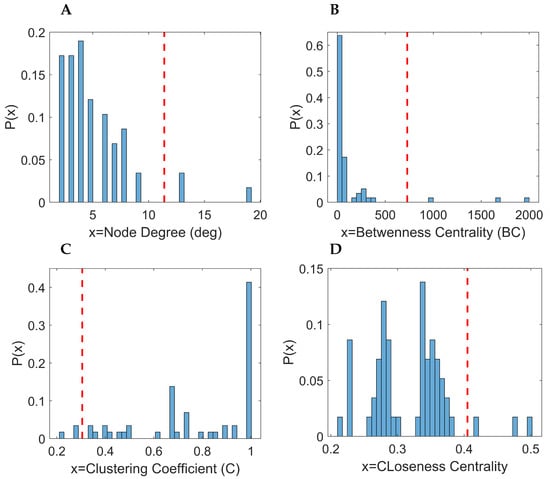
Figure 6.
Distributions of the computed network measures. The red vertical line indicates the 95% percentile value of the distribution. (A) Degree centrality. (B) Betweenness centrality. (C) Clustering coefficient. (D) Closeness centrality.
The distribution of betweenness centrality is depicted in Figure 6B. It has a power law form with approximated. Most nodes show a low number of BC, less than 500, while there are few nodes with high BC values. These nodes serve as bridges between different subsets of the network. Figure 6C,D show the clustering coefficient and the mean geodesic distance from each node, respectively. The clustering coefficient counts the relative number of triangle motifs. The distribution of the clustering coefficient shows a uniform structure. The mean geodesic distance shows a normal distribution with a mean value around three.
The distributions of degrees and betweenness centrality highlight a heterogeneous network structure, i.e., there are nodes with a higher number of connections; furthermore, few nodes are acting as a bridge (these nodes are with high ; see Figure 6B).
4.3. The Case of Florina
In this section, we apply the network construction and analysis for the data of the Florina area. Similar to the previous section, we transform the precipitation data into drought evolution using Equations (12) and (13); see Figure 7A. The resulting drought network of Florina is depicted in Figure 7B. The color code in Figure 3B shows different communities in the network.
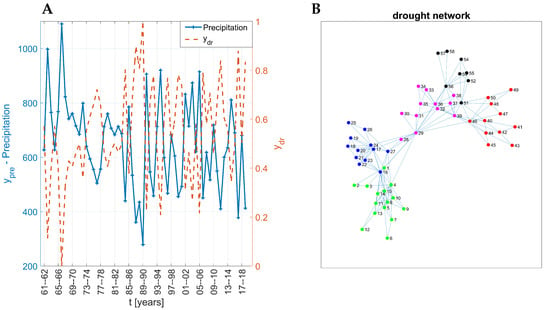
Figure 7.
(A) The annual precipitation time series (blue line) of the north Greece city Florina. On the right axis, is depicted. (B) Transformation of into a complex network. The color code shows the existence of different communities in the network.
4.4. Localized Important Network Nodes: The Case of Florina
The betweenness centrality and the degree centrality for each node are presented in Figure 8A,B, respectively. Clearly, in Figure 8A, betweenness centrality BC admits one dominated maximum value, which appears together with a maximum value of . It is of interest that all other local maxima of BC in Figure 8A coincide with extreme drought values of and specifically the following years: 1964–1965, 1976–1977, 1989–1990, 2006–2007, 2011–2012, 2016–2017. These nodes are localized in the network as 4 → 1964–1965, 16 → 1976–1977, 29 → 1989–1990, 46 → 2006–2007, 51 → 2011–2012 and 56 → 2016–2017. A detailed view of the network structure in Figure 7B confirms that these nodes are the central hubs in the structure. Similarly, in Figure 8B, the degree centrality follows the drought , i.e., the local maxima coincide with the local maxima of drought time series (however, not so clear compared to Figure 8A).
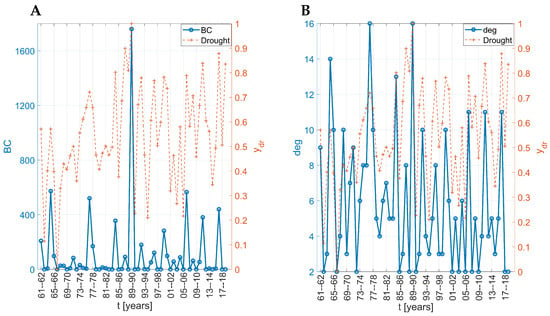
Figure 8.
The is always depicted with red line on the right axis. (A) Betweenness centrality of each node. (B) Degree centrality.
Finally, we depict the clustering coefficient and the local mean path length in Figure 9A,B, respectively. The clustering coefficients show variability, with high deep nodes coinciding with the high drought nodes. Furthermore, the clustering coefficient time series depicts rhythmicity, with a period of ≈T = 5 years (observe that the sharp deeps appear every 4–6 nodes in Figure 9A).
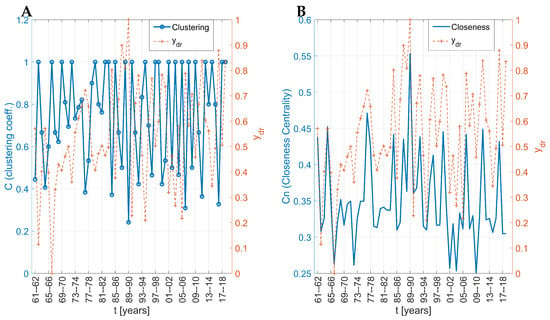
Figure 9.
(A) Clustering coefficient centrality of each node. (B) Closeness centrality of each node.
The closeness centrality in Figure 9B of nodes follows the drought evolution, and similarly to the Arnaia case, it has a high positive correlation (). Again, the local maxima of drought coincide with the maxima of the closeness centrality.
4.5. Macroscopic Network Measure for the Florina Case
The global measures that characterize the whole network structure are depicted in Figure 10. The degree distribution in Figure 10A shows the probability of a randomly selected node to have k edge links. The distribution is skewed right with the mean value of 5.8. Similar to the Arnaia case, it can be approximated with a Gamma distribution, i.e., , with and .
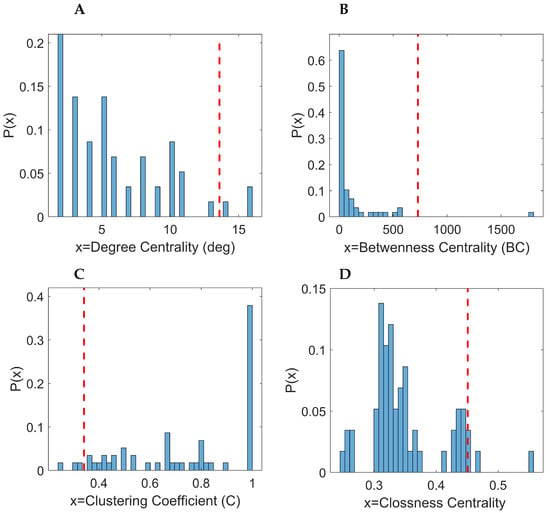
Figure 10.
Distributions of the computed network measures. The red vertical line indicates the 95% percentile value of distribution. (A) Degree distribution. (B) Betweenness centrality. (C) Clustering coefficient. (D) Closeness centrality.
Betweenness centrality distribution is depicted in Figure 10B. It has a power law form with approximated. The majority of the nodes show a low number of BC, less than 500, while there exist few nodes with high BC values (). Figure 10C,D show the clustering coefficient and the mean path length from each node, respectively. The distribution of clustering coefficient shows a uniform structure. The mean path distance shows a normal distribution with a mean value of around three.
Similar to the Arnaia case, the distributions of degree centrality and betweenness centrality highlight a heterogeneous network structure, where few nodes act as central nodes (nodes with high , see Figure 10B, connecting different part of the network. These nodes are central in the network, and we expect them to be in agreement with high drought nodes.
4.6. Community Detection (Modularity) and Cyclicity of Drought Time Series in the Cases of Arnaia and Florina
The cases under study, i.e., Arnaia and Florina, show similarities in community structure (see Figure 3 and Figure 7). The network structure is organized into a few communities: six communities in the Arnaia case and five in Florina case (see color codes in Figure 3 and Figure 7). Inside the communities, the members (nodes) follow an almost successive time pattern (Arnaia: 47–58 months with green, 40–46 black, 32–39 blue and in Florina: 1–15 green, 16–27 blue, etc.). The mean value of the number of members in the team is 9 in the case of Arnaia and 11.6 in Florina. We conclude that there is a critical periodical component of ≈10 years of mild drought. This mild period is interrupted by a strong drought event. Consequently, this event (or node) has high visibility, and the connectivity is organized with respect to this extreme event. As a result, this event-node shows high centrality in the network (e.g., 24 → 1984–1985, 39 → 1999–2000 and 51 → 2011–2012 in the Arnaia case).
5. Discussion
In this study, a new approximation to investigate and analyze the meteorological drought is proposed. Drought severity is characterized by network measures such as degree, betweenness and closeness centrality. One advantage of the network method is that it is not based on the mean value and standard deviation as opposed to classical indicators of drought (RDI, SPI, and SDI), which are dependent on low-order statistics.
Both cases (Arnaia and Florina regions) show structural network similarities; in particular, both networks display high centrality nodes. As we show in Figure 4 and Figure 8, these nodes are the extreme drought years. The other computed network measures (degree centrality, closeness centrality) confirm the localization of these extreme drought events.
5.1. Utilizing Network Measure Distributions to Characterize Drought Rare Events
The computed distributions of the network measures offer a macroscopic view of network connectivity, i.e., the distributions show the properties of the entire connectivity (in a period of 57 years). The main macroscopic characteristic that is revealed is the heterogeneous structure of the networks: in both cases (Arnaia and Florina), there are few nodes acting as ‘Hubs’, i.e., nodes with high centrality (degree, betweenness and closeness centrality). These are identified as extreme drought years. Indeed, in Figure 6 and Figure 10, the 95% percentile value is also depicted, i.e., the value which indicates that the 95% of all measurements are below this value. In the case of Arnaia, these are nodes 24 → 1984–1985, 39 → 1999–2000 and 51 → 2011–2012. Similarly, in the case of Florina, the extreme-rare drought years are 4 → 1964–1965, 29 → 1989–1990 and 46 → 2006–2007.
Regarding the results, they are compatible with previous studies [5,38]. Indeed, in Kourtis et al. [5], the case of Chrysoupoli station is reported (Figure 9 in [5], 100 km distance from Arnaia). As measured in [5] (Figure 9 therein), the drought patterns are in very good agreement with our results. Specifically, the following major drought events are reported in [5]: 1984–1985, 1989–1990, 1991–1992 and 1999–2000. Regarding the severe drought in the whole Greek area, the results are not identical concerning the spatial distribution. For instance, a severe drought took place in the Cyclades and Athens during the hydrological year 1999–2000 (based on the RDI, ) according to [38], which is compatible with our results regarding both the Arnaia and the Florina stations. However, in this year, the intensity of drought cannot be characterized as severe in the case of Thessaly [38]. During 1989–1999, a severe drought occurred in Athens and Cyclades, as well as in our study in Florina, but this does not hold true for Thessaly [38].
In conclusion, our analysis characterizes rare (extreme) events: nodes (or years) as the values above 95% percentile of betweenness centrality. Our probabilistic approach has similarities with other statistical methods for drought identification. For example, one of the most widely used methodologies is the statistical Theory of Runs (ToR) proposed by Yevjevich [39]. Although ToR is not a drought index or indicator, it can be used to analyze hydrometeorological time series in order to differentiate drought as a feature [40]. A ‘run’, according to this theory, is a segment of a drought time series, in which each value is either above or below the prescribed truncation level [41].
5.2. Comparison with the Standardized Precipitation Index-SPI
The annual Standardized Precipitation Index (SPI) was calculated for both examined areas. The SPI is based on a standardization method [18,20], where if SPI values are below −2 (SPI ), an extreme drought event takes place. Subsequently, the linear correlation was determined by comparing the SPI annual values with degree centrality, closeness centrality, betweenness centrality and the clustering coefficient. For both cases, the linear correlation was closest to −1 when applying the closeness coefficient. More specifically, in the case of the Arnaia station, the linear correlation coefficients were equal to −0.55, −0.71, 0.64 and −0.8 when comparing the annual SPI with the annual values of betweenness centrality, degree centrality, clustering coefficient and closeness centrality, respectively. In the case of the Florina station, the linear correlation coefficients were −0.57, −0.59, 0.66, and −0.78 for the same comparisons.
In summary, closeness centrality can be used to describe the intensity of drought, producing results comparable to the existing methodology for assessing the intensity of meteorological drought. For illustration purposes, in Figure 11, we depict the closeness centrality measure multiplied by (−1) to achieve the same monotony with the annual SPI (then the correlation becomes positive). In the cases of both Arnaia and Florina, the annual SPI is in very good agreement with closeness centrality.

Figure 11.
For comparison reasons, we depict the annual SPI and closeness centrality inverted (multiplied by −1, i.e., -Cl). (A) The case of Arnaia. (B) The case of Florina.
5.3. Emergent Cyclicity or Periodicity from Network Analysis
The modularity algorithm [24,36] (i.e., the network communities detection) revealed the organization of the drought into these extreme events. The networks of Arnaia and Florina were partitioned into successive periods with central nodes and extreme drought events. The successive periods are highlighted in the color code in Figure 3B and Figure 7B. Consequently, the network-proposed method can be used to define meteorological mild drought periods, which are separated due to new strong drought extreme events. These periods have ten members on average (in the case of Arnaia, we found a periodicity of 9 years, while in Florina’s case there was a periodicity of 11 years).
In a second, careful view of the network measures, we observe two cyclicity behaviors. Counting the period between local maxima in all network measures, we observe a periodicity or cyclicity of approximately ∼4 years. Concluding, the network approximations reveal two cycles. The first one is almost 10 years whilst the second appears between 3 and 4 years. Remarkably, the authors in [42,43] studied the Mediterranean drought and concluded with similar results. Specifically, they reported two periods of cyclicity, one of almost 10 years (9.4) and a second short-term cyclicity behavior (in the Iberian Peninsula). Moreover, by using Fourier analysis, Moreira et al. [43] suggested the existence of the two most frequent cycles, with periods of 6 years and 9.4 years, respectively, in Portugal.
One future network approximation topic is using the network features in a machine learning (ML) framework. The network features can be used to create a model for predicting or classifying drought. For example, betweenness centrality has a power law form with . Furthermore, including a higher number of drought data regions, one could study spatial correlations of climatic observables in future work, e.g., drought or extreme floods. Thus, complex network analysis could be applied to explore and reveal possible mechanisms of weather observables (flood or precipitation).
6. Conclusions
A challenge for sustainable development is adaptation to climate change. One advantage of the proposed method is the fact that it has less tolerance to climate change conditions since it is not dependent on the mean value and standard deviation estimation. Two case studies were examined with similar but not identical results. By exploiting several measures from complex network theory, several conclusions can be justified. For instance, the annual drought episodes can be distinguished based on the measure of degree centrality (Deg), whilst betweenness centrality highlights extreme events. Community detection (modularity) shows a cyclicity of ∼10 years, while all other network measures indicate a second shortest cyclicity of ∼4 years. Another interesting point is that for both cases, closeness centrality can be used to describe the intensity of drought, producing results comparable to the existing methodology of annual SPI, which is widely used in drought studies.
Author Contributions
Conceptualization, K.S., M.S., H.V. and K.V.; methodology, K.S. and M.S.; data software, K.V. and K.S.; validation, M.S. and H.V.; formal analysis, M.S., K.V. and H.V.; supervision M.S., H.V. and K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available from authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nations, U. Drought Sustainability. Available online: https://sdgs.un.org/documents/e200929-ecn17200919-report-17th-ses-18614 (accessed on 1 September 2024).
- Mugume, S.N.; Diao, K.; Astaraie-Imani, M.; Fu, G.; Farmani, R.; Butler, D. Enhancing resilience in urban water systems for future cities. Water Supply 2015, 15, 1343–1352. [Google Scholar] [CrossRef][Green Version]
- Tsakiris, G.; Loucks, D. Adaptive Water Resources Management Under Climate Change: An Introduction. Water Resour Manag. 2019, 37, 2221–2233. [Google Scholar] [CrossRef]
- Tabari, H.; Willems, P. Sustainable development substantially reduces the risk of future drought impacts. Commun. Earth Environ. 2023, 4, 180. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Vangelis, H.; Tigkas, D.; Mamara, A.; Nalbantis, I.; Tsakiris, G.; Tsihrintzis, V. Drought Assessment in Greece Using SPI and ERA5 Climate Reanalysis Data. Sustainability 2023, 15, 15999. [Google Scholar] [CrossRef]
- Boers, N.; Goswami, B.; Rheinwalt, A.; Bookhagen, B.; Hoskins, B.; Kurths, J. Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature 2019, 566, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Donges, J.F.; Zou, Y.; Marwan, N.; Kurths, J. Complex networks in climate dynamics. Eur. Phys. J. Spec. Top. 2009, 174, 157–179. [Google Scholar] [CrossRef]
- Mondal, S.; Mishra, A.K.; Leung, R.; Cook, B. Global droughts connected by linkages between drought hubs. Nat. Commun. 2023, 14, 144. [Google Scholar] [CrossRef]
- Lacasa, L.; Luque, B.; Ballesteros, F.; Luque, J.; Carlos Nuno, J. From time series to complex networks: The visibility graph. Proc. Natl. Acad. Sci. USA 2008, 105, 4972–4975. [Google Scholar] [CrossRef]
- Liu, C.; Zhou, W.; Yuan, W. Statistical properties of visibility graph of energy dissipation rates in three-dimensional fully developed turbulence. Phys. A Stat. Mech. Its Appl. 2010, 389, 2675–2681. [Google Scholar] [CrossRef]
- Charakopoulos, A.; Karakasidis, T.; Sarris, I. Analysis of magnetohydrodynamic channel flow through complex network analysis. Chaos Interdiscip. J. Nonlinear Sci. 2021, 31, 043123. [Google Scholar] [CrossRef] [PubMed]
- Telesca, L.; Lovallo, M. Analysis of seismic sequences by using the method of visibility graph. Europhys. Lett. 2012, 97, 50002. [Google Scholar] [CrossRef]
- Ahmadlou, M.; Adeli, H.; Adeli, A. Improved visibility graph fractality with application for the diagnosis of Autism Spectrum Disorder. Phys. A Stat. Mech. Its Appl. 2012, 391, 4720–4726. [Google Scholar] [CrossRef]
- Gao, Z.; Cai, Q.; Yang, Y.; Dong, N.; Zhang, S. Visibility Graph from Adaptive Optimal Kernel Time-Frequency Representation for Classification of Epileptiform EEG. Int. J. Neural Syst. 2017, 27, 1750005. [Google Scholar] [CrossRef]
- Zhuang, E.; Small, M.; Feng, G. Time series analysis of the developed financial markets’ integration using visibility graphs. Phys. A Stat. Mech. Its Appl. 2014, 410, 483–495. [Google Scholar] [CrossRef]
- Qian, M.C.; Jiang, Z.Q.; Zhou, W.X. Universal and nonuniversal allometric scaling behaviors in the visibility graphs of world stock market indices. J. Phys. A Math. Theor. 2010, 43, 335002. [Google Scholar] [CrossRef]
- John, R.; John, M. Adaptation of the visibility graph algorithm for detecting time lag between rainfall and water level fluctuations in Lake Okeechobee. Adv. Water Resour. 2019, 134, 103429. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional Drought Assessment Based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of Hydrological Drought Revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- McKee, T.; Doesken, N.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Latifoğlu, L.; Özger, M. A Novel Approach for High-Performance Estimation of SPI Data in Drought Prediction. Sustainability 2023, 15, 14046. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J.; Reijneveld, J.C. Graph theoretical analysis of complex networks in the brain. Nonlinear Biomed. Phys. 2007, 1, 1753–4631. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Daskalaki, E.; Papadopoulos, G.A.; Spiliotis, K.; Siettos, C. Analysing the topology of seismicity in the Hellenic arc using complex networks. J. Seismol. 2014, 18, 37–46. [Google Scholar] [CrossRef]
- Daskalaki, E.; Spiliotis, K.; Siettos, C.; Minadakis, G.; Papadopoulos, G.A. Foreshocks and short-term hazard assessment of large earthquakes using complex networks: The case of the 2009 L’Aquila earthquake. Nonlinear Process. Geophys. 2016, 23, 241–256. [Google Scholar] [CrossRef]
- Spiliotis, K.; Siettos, C. A timestepper-based approach for the coarse-grained analysis of microscopic neuronal simulators on networks: Bifurcation and rare-events micro- to macro-computations. Neurocomputing 2011, 74, 3576–3589. [Google Scholar] [CrossRef]
- Papana, A.; Kyrtsou, C.; Kugiumtzis, D.; Diks, C. Financial networks based on Granger causality: A case study. Phys. A Stat. Mech. Its Appl. 2017, 482, 65–73. [Google Scholar] [CrossRef]
- Chorozoglou, D.; Papadimitriou, E.; Kugiumtzis, D. Investigating small-world and scale-free structure of earthquake networks in Greece. Chaos Solitons Fractals 2019, 122, 143–152. [Google Scholar] [CrossRef]
- Watts, D.; Strogatz, S. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Wikipedia. Six Degrees of Kevin Bacon. Available online: https://en.wikipedia.org/wiki/Six_Degrees_of_Kevin_Bacon (accessed on 29 October 2022).
- Betzel, R.F.; Medaglia, J.D.; Papadopoulos, L.; Baum, G.L.; Gur, R.; Gur, R.; Roalf, D.; Satterthwaite, T.D.; Bassett, D.S. The modular organization of human anatomical brain networks: Accounting for the cost of wiring. Netw. Neurosci. 2017, 1, 42–68. [Google Scholar] [CrossRef] [PubMed]
- Marcoux, M.; Lusseau, D. Network modularity promotes cooperation. J. Theor. Biol. 2013, 324, 103–108. [Google Scholar] [CrossRef]
- Barabási, A.L.; Pósfai, M. Network Science; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Newman, M. Networks, An Introductions; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Leicht, E.A.; Newman, M.E.J. Community Structure in Directed Networks. Phys. Rev. Lett. 2008, 100, 118703. [Google Scholar] [CrossRef] [PubMed]
- Karavitis, C.; Alexandris, S.; Tsesmelis, D.E.; Athanasopoulos, G. Application of the Standardized Precipitation Index (SPI) in Greece. Water 2011, 3, 787–805. [Google Scholar] [CrossRef]
- Tigkas, D. Drought Characterisation and Monitoring in Regions of Greece. Eur. Water EWRA 2008, 23/24, 29–39. [Google Scholar]
- Yevjevich, V. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts; Hydrology Papers No. 23; Colorado State University: Fort Collins, CO, USA, 1967. [Google Scholar]
- Burka, A.; Biazin, B.; Bewket, W. Drought characterization using different indices, theory of run and trend analysis in bilate river watershed, rift valley of Ethiopia. Front. Environ. Sci. 2023, 11, 1098113. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Spatio-temporal Changes and Frequency Analysis of Drought in the Wei River Basin, China. Water Resour. Manag. 2014, 28, 3095–3110. [Google Scholar] [CrossRef]
- Merino, A.; López, L.; Hermida, L.; Sánchez, J.; García-Ortega, E.; Gascón, E.; Fernández-González, S. Identification of drought phases in a 110-year record from Western Mediterranean basin: Trends, anomalies and periodicity analysis for Iberian Peninsula. Glob. Planet. Change 2015, 133, 96–108. [Google Scholar] [CrossRef]
- Moreira, E.E.; Martins, D.S.; Pereira, L.S. Assessing drought cycles in SPI time series using a Fourier analysis. Nat. Hazards Earth Syst. Sci. 2015, 15, 571–585. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).