Charging Scheduling of Electric Vehicles Considering Uncertain Arrival Times and Time-of-Use Price
Abstract
1. Introduction
- In line with charging practices, the EV charging scheduling problem considering uncertain EV arrival times, the TOU mechanism, and the nonlinear charging function is first introduced in this work;
- For addressing this problem, a K-means enhanced SAA (Sample Average Approximation) approach and distribution-free approaches are, respectively, established by this work;
- To the best of our knowledge, the BP neural network is applied for the first time to enhance the distribution-free approach for addressing the EV charging scheduling problem. Numerical experiments are conducted to demonstrate the effectiveness of our approaches.
2. Literature Review
2.1. Optimization of Charging Costs
2.2. Mitigation of Power Grid Constraints
2.3. Reduction in Electric Vehicle Waiting Time
2.4. Management of Charging Station Capacity
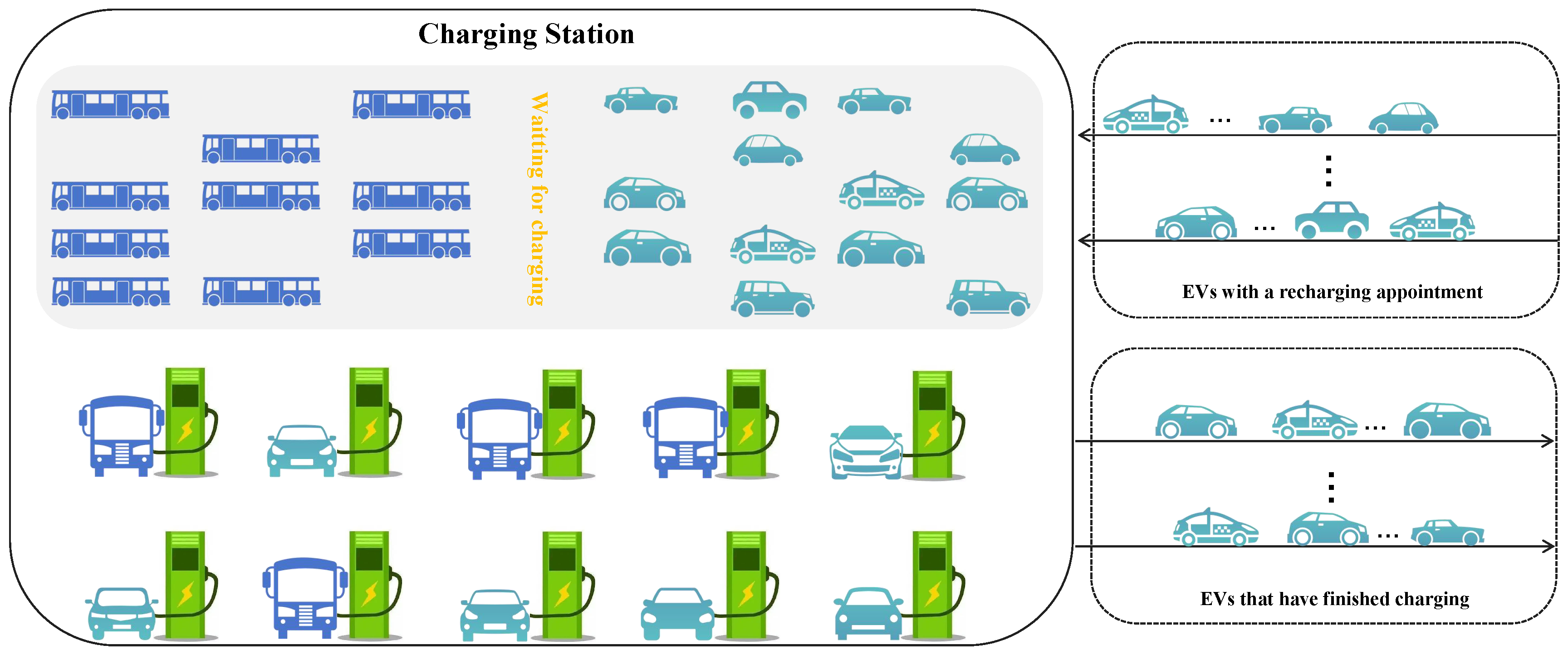
3. Problem Description
- In line with effective charging protocols, the charging duration of any EV is continuous, and preemption is not allowed;
- In this work, continuous charging of EVs fails to account for the time needed to switch between charging stations during the charging process;
- Each EV charger is designed to maintain a constant power output;
- The time horizon covers three types of electricity prices, i.e., peak price, off-peak price, and valley price.
3.1. Mathematical Model
3.1.1. Input Parameters
- :
- Set of EV chargers, indexed by i, i.e., ;
- :
- Set of appointed EVs, indexed by j, i.e., ;
- :
- Set of time points, indexed by t, i.e., ;
- :
- Uncertain arrival time of EV ;
- :
- A binary parameter, equal to 1 indicates that EV charger is available at time , 0 otherwise;
- :
- Initial SoC of EV ;
- :
- Charging level of EV ;
- :
- Charging duration time of EV ;
- :
- Charging speed () associated with less than or equal to 80 SoC;
- :
- Charging speed () associated with large than 80 SoC;
- :
- Electricity price at time ;
- P:
- Power of each EV charger (in );
- :
- Given maximum waiting time for each EV;
- :
- Given risk level;
- :
- Discrete time interval (in minutes);
- M:
- A sufficiently large positive integer.
3.1.2. Decision Variables
- :
- A binary variable, when equal to 1 indicates that EV is charged at time , 0 otherwise;
- :
- A binary variable, when equal to 1 indicates that start charging time of EV is time point , 0 otherwise;
- :
- Start charging time of EV .
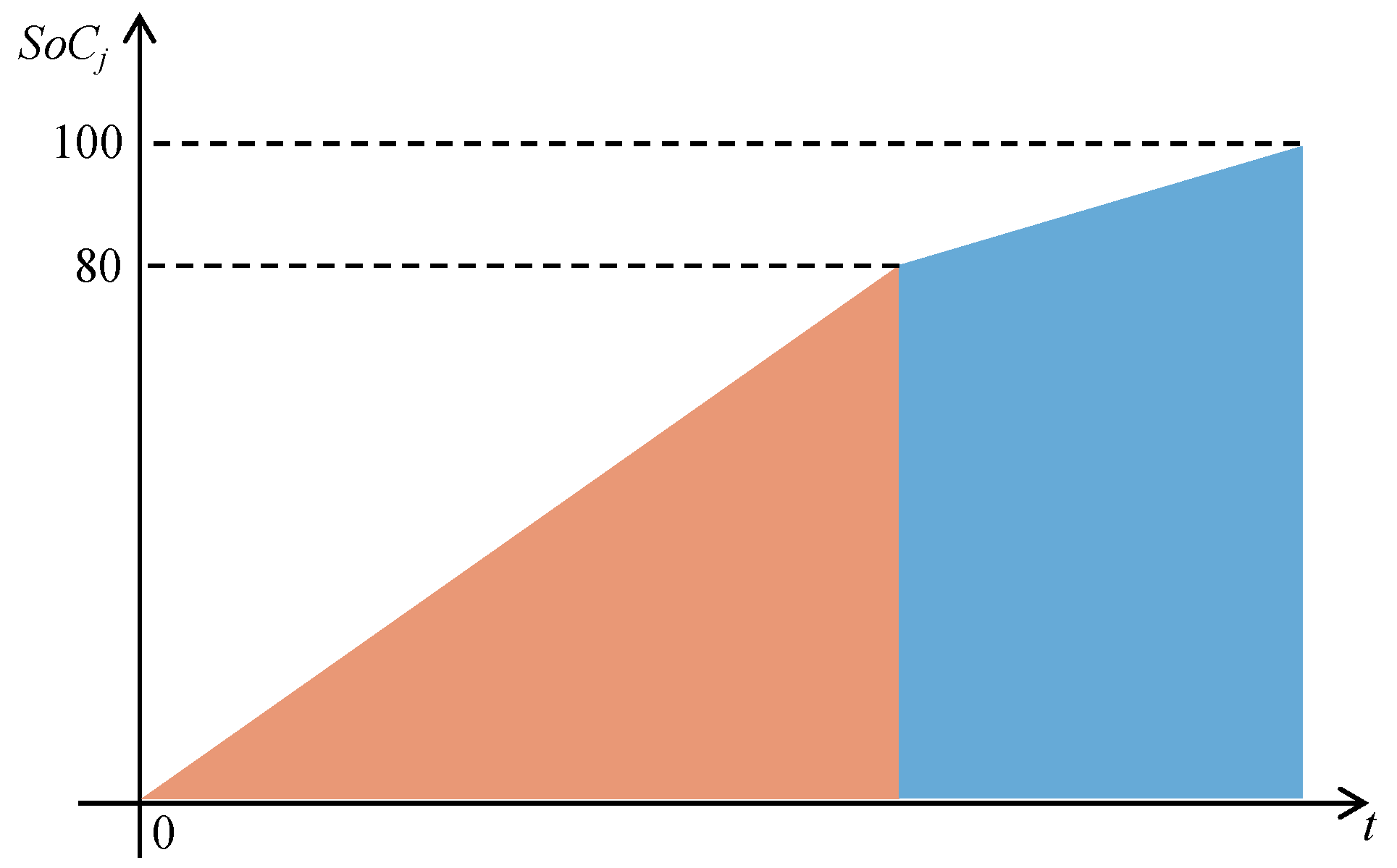
3.2. Nonlinear Charging Function
- :
- A binary auxiliary parameter, equal to 1 indicates that , 0 otherwise.
4. Solution Approaches
4.1. K-Means Enhanced SAA Approach
- Step 1: Given the original sample set, initialize centers in a random manner.
- Step 2: Assign each scenario to the closest cluster by utilizing a classifier based on the smallest Euclidean distance.
- Step 3: Update the cluster centers iteratively, and repeat Step 2 until convergence is achieved, defined as all the cluster centers remaining unchanged in the last two iterations.
4.2. Distribution-Free Approaches
4.2.1. Case 4.2.1: Cantelli’s Inequality-Based Distribution-Free Method
4.2.2. Case 4.2.2: Markov Inequality-Based Distribution-Free Method
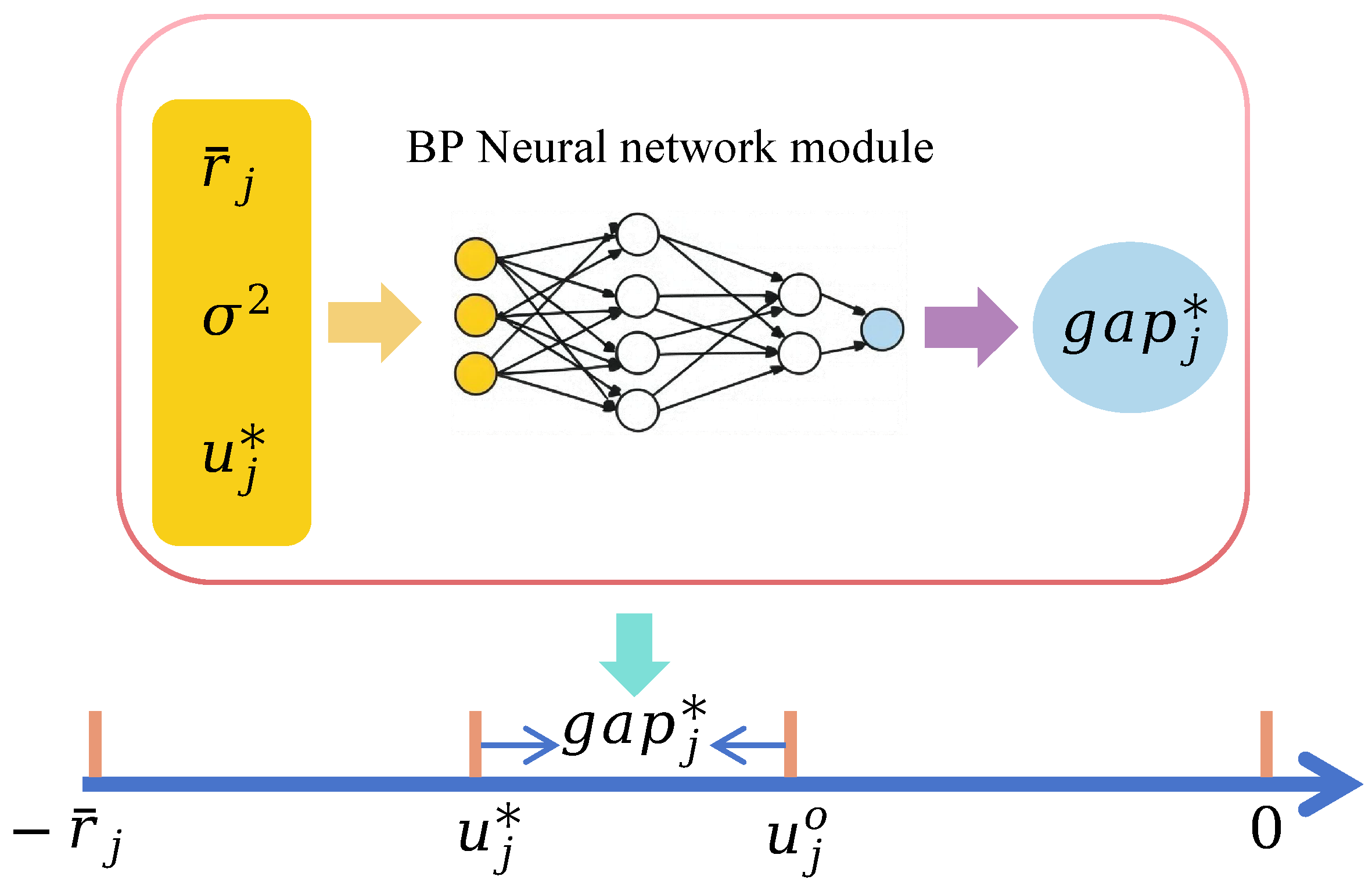
4.2.3. BP Neural Network-Enhanced Distribution-Free Approach
5. Numerical Experiments
5.1. Experiment Settings
- represents the relative error between Cantelli’s inequality-based distribution-free approach and the KSAA model.
- represents the relative error between the Markov inequality-based distribution-free approach and the KSAA model.
- represents the relative error between the BP neural network-enhanced distribution-free approach and the KSAA model.
5.2. Numerical Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The SAA Model
- :
- A binary auxiliary variable, when equal to 1 indicates that , or 0 otherwise.
Appendix B. Numerical Results
| Instances () | KSAA | DF1a | DF2 | DF1b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| time(s) | time(s) | (%) | time(s) | (%) | time(s) | (%) | IRL (%) | |||||
| Normal distribution | ||||||||||||
| (2,3) | 106.21 | 243 | 119.24 | 4 | 12.27 | 119.24 | 4 | 12.27 | 111.46 | 9 | 4.94 | 0.13 |
| (2,5) | 237.17 | 617 | 248.84 | 7 | 4.92 | 260.51 | 7 | 9.84 | 241.06 | 8 | 1.64 | 0.00 |
| (2,7) | 325.89 | 1559 | 352.54 | 12 | 8.18 | 371.99 | 12 | 14.15 | 344.76 | 14 | 5.79 | 0.47 |
| (3,5) | 236.78 | 742 | 248.84 | 8 | 5.09 | 252.73 | 8 | 6.74 | 241.06 | 10 | 1.81 | 0.00 |
| (3,7) | 303.53 | 1523 | 336.98 | 13 | 11.02 | 340.87 | 13 | 12.30 | 325.31 | 15 | 7.18 | 0.47 |
| (3,9) | 379.34 | 3257 | 395.29 | 18 | 4.20 | 403.07 | 18 | 6.26 | 383.62 | 20 | 1.13 | 0.30 |
| (4,7) | 301.58 | 2739 | 317.53 | 13 | 5.29 | 329.20 | 13 | 9.16 | 305.86 | 15 | 1.42 | 0.47 |
| (4,9) | 378.95 | 2382 | 395.29 | 20 | 4.31 | 403.07 | 20 | 6.36 | 383.62 | 21 | 1.23 | 0.30 |
| (4,11) | 501.87 | 3389 | 518.41 | 21 | 3.29 | 526.19 | 21 | 4.84 | 506.74 | 23 | 0.97 | 0.10 |
| (5,9) | 379.54 | 4363 | 395.29 | 18 | 4.15 | 403.07 | 18 | 6.20 | 383.62 | 26 | 1.08 | 0.30 |
| (5,11) | 501.88 | 2991 | 518.41 | 19 | 3.29 | 526.19 | 19 | 4.84 | 506.74 | 21 | 0.97 | 0.10 |
| (5,13) | 540.37 | 7159 | 553.40 | 21 | 2.41 | 561.18 | 21 | 3.85 | 545.62 | 23 | 0.97 | 0.51 |
| Lognormal distribution | ||||||||||||
| (2,3) | 104.07 | 326 | 115.35 | 4 | 10.84 | 119.24 | 4 | 14.58 | 107.57 | 6 | 3.36 | 0.13 |
| (2,5) | 233.28 | 620 | 244.95 | 6 | 5.00 | 256.62 | 6 | 10.01 | 237.17 | 18 | 1.67 | 0.00 |
| (2,7) | 319.48 | 1562 | - | 12 | - | - | 12 | - | 340.87 | 12 | 6.70 | 0.50 |
| (3,5) | 233.28 | 670 | 244.95 | 8 | 5.00 | 248.84 | 8 | 6.67 | 237.17 | 9 | 1.67 | 0.00 |
| (3,7) | 301.58 | 1546 | 329.20 | 13 | 9.16 | 333.09 | 13 | 10.45 | 305.86 | 14 | 1.42 | 0.50 |
| (3,9) | 376.03 | 2399 | 391.40 | 18 | 4.09 | 395.29 | 18 | 5.12 | 379.73 | 20 | 0.98 | 0.30 |
| (4,7) | 298.47 | 1536 | 309.75 | 13 | 3.78 | 313.64 | 13 | 5.08 | 301.97 | 15 | 1.17 | 0.50 |
| (4,9) | 376.23 | 2786 | 387.51 | 19 | 3.00 | 391.40 | 19 | 4.03 | 379.73 | 21 | 0.93 | 0.30 |
| (4,11) | 499.35 | 3666 | 510.63 | 22 | 2.26 | 518.41 | 21 | 3.82 | 502.85 | 24 | 0.70 | 0.11 |
| (5,9) | 375.84 | 2876 | 387.51 | 17 | 3.11 | 391.40 | 17 | 4.14 | 379.73 | 19 | 1.04 | 0.30 |
| (5,11) | 499.35 | 6589 | 510.63 | 20 | 2.26 | 514.52 | 20 | 3.04 | 502.85 | 22 | 0.70 | 0.11 |
| (5,13) | 537.84 | 7421 | 545.62 | 104 | 1.45 | 549.51 | 106 | 2.17 | 541.73 | 101 | 0.72 | 0.57 |
| Average | 347.83 | 2623 | 364.24 | 18 | 5.15 | 370.83 | 18 | 7.21 | 354.03 | 20 | 2.09 | 0.27 |
| Instances () | KSAA | DF1a | DF2 | DF1b | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| time(s) | time(s) | (%) | time(s) | (%) | time(s) | (%) | IRL (%) | |||||
| Normal distribution | ||||||||||||
| (2,3) | 139.78 | 256 | 151.64 | 4 | 8.49 | 155.53 | 4 | 11.27 | 143.86 | 6 | 2.92 | 0.13 |
| (2,5) | 269.57 | 1547 | 281.24 | 9 | 4.33 | 292.91 | 7 | 8.66 | 273.46 | 9 | 1.44 | 0.00 |
| (2,7) | 355.70 | 1390 | 378.46 | 12 | 6.40 | 401.80 | 12 | 12.96 | 378.46 | 13 | 6.40 | 0.47 |
| (3,5) | 269.18 | 678 | 281.24 | 7 | 4.48 | 285.13 | 7 | 5.93 | 273.46 | 9 | 1.59 | 0.00 |
| (3,7) | 332.95 | 1403 | 362.90 | 13 | 9.00 | 366.79 | 13 | 10.17 | 355.12 | 14 | 6.66 | 0.47 |
| (3,9) | 445.50 | 3661 | 471.76 | 16 | 5.89 | 487.32 | 16 | 9.39 | 452.31 | 18 | 1.53 | 0.30 |
| (4,7) | 329.06 | 1168 | 343.45 | 10 | 4.37 | 355.12 | 10 | 7.92 | 331.78 | 20 | 0.83 | 0.47 |
| (4,9) | 443.75 | 3494 | 460.09 | 108 | 3.68 | 467.87 | 105 | 5.44 | 448.42 | 79 | 1.05 | 0.30 |
| (4,11) | 579.64 | 4394 | 607.84 | 25 | 4.87 | - | 24 | - | 596.17 | 24 | 2.85 | 0.10 |
| (5,9) | 444.34 | 2609 | 460.09 | 19 | 3.55 | 467.87 | 19 | 5.30 | 448.42 | 23 | 0.92 | 0.30 |
| (5,11) | 579.64 | 4028 | 596.17 | 27 | 2.85 | 607.84 | 27 | 4.87 | 584.50 | 29 | 0.84 | 0.10 |
| (5,13) | 670.36 | 5808 | 686.89 | 28 | 2.47 | - | 28 | - | 675.22 | 28 | 0.72 | 0.51 |
| Lognormal distribution | ||||||||||||
| (2,3) | 136.47 | 287 | 147.75 | 4 | 8.27 | 151.64 | 4 | 11.12 | 139.97 | 5 | 2.57 | 0.13 |
| (2,5) | 266.65 | 726 | 281.24 | 7 | 5.47 | 289.02 | 8 | 8.39 | 269.57 | 9 | 1.09 | 0.00 |
| (2,7) | 348.31 | 1402 | - | 12 | - | - | 12 | - | 370.68 | 12 | 6.42 | 0.50 |
| (3,5) | 266.26 | 773 | 281.24 | 8 | 5.62 | 281.24 | 8 | 5.62 | 269.57 | 9 | 1.24 | 0.00 |
| (3,7) | 331.00 | 1765 | 359.01 | 13 | 8.46 | 362.90 | 13 | 9.64 | 335.67 | 15 | 1.41 | 0.50 |
| (3,9) | 440.83 | 3371 | 456.20 | 18 | 3.49 | 471.76 | 18 | 7.02 | 448.42 | 20 | 1.72 | 0.30 |
| (4,7) | 326.33 | 1788 | 339.56 | 13 | 4.05 | 343.45 | 13 | 5.24 | 331.78 | 15 | 1.67 | 0.50 |
| (4,9) | 441.03 | 2601 | 452.31 | 19 | 2.56 | 456.20 | 19 | 3.44 | 444.53 | 23 | 0.79 | 0.30 |
| (4,11) | 577.10 | 2992 | - | 17 | - | - | 17 | - | - | 16 | - | 0.11 |
| (5,9) | 440.64 | 2760 | 452.31 | 19 | 2.65 | 456.20 | 19 | 3.53 | 444.53 | 21 | 0.88 | 0.30 |
| (5,11) | 577.11 | 3809 | 588.39 | 25 | 1.95 | 596.17 | 25 | 3.30 | 580.61 | 27 | 0.61 | 0.11 |
| (5,13) | 667.44 | 8469 | 683.00 | 26 | 2.33 | 683.00 | 25 | 2.33 | 671.33 | 27 | 0.58 | 0.57 |
| Average | 403.28 | 2549 | 414.67 | 19 | 4.78 | 398.99 | 19 | 7.08 | 402.95 | 20 | 2.03 | 0.27 |
References
- Roy, S.; Lam, Y.F.; Hung, N.T.; Chan, J.C.L. Development of on-road emission inventory and evaluation of policy intervention on future emission reduction toward sustainability in Vietnam. Sustain. Dev. 2021, 29, 1072–1085. [Google Scholar] [CrossRef]
- Park, K.; Moon, I. Multi-agent deep reinforcement learning approach for EV charging scheduling in a smart grid. Appl. Energy 2022, 328, 120111. [Google Scholar] [CrossRef]
- Yin, W.J.; Qin, X. Cooperative optimization strategy for large-scale electric vehicle charging and discharging. Energy 2022, 258, 124969. [Google Scholar] [CrossRef]
- Shahmoradi, H.; Esmaelian, M.; Karshenas, H. An EDA-based method for solving electric vehicle charging scheduling problem under limited power and maximum imbalance constraints. Comput. Ind. Eng. 2022, 172, 108544. [Google Scholar] [CrossRef]
- Huang, Q.L.; Yang, L.; Hou, C.; Zeng, Z.Y.; Qi, Y.W. Event-based EV charging scheduling in a microgrid of buildings. IEEE Trans. Transp. Electrif. 2023, 9, 1784–1796. [Google Scholar] [CrossRef]
- Shao, S.P.; Sartipizadeh, H.; Gupta, A. Scheduling EV charging having demand with different reliability constraints. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11018–11029. [Google Scholar] [CrossRef]
- Lampon, J.F. Efficiency in design and production to achieve sustainable development challenges in the automobile industry: Modular electric vehicle platforms. Sustain. Dev. 2023, 31, 26–38. [Google Scholar] [CrossRef]
- Ullah, Z.; Wang, S.R.; Wu, G.; Hasanien, H.M.; Rehman, A.U.; Turky, R.A.; Elkadeem, M.R. Optimal scheduling and techno-economic analysis of electric vehicles by implementing solar-based grid-tied charging station. Energy 2023, 267, 126560. [Google Scholar] [CrossRef]
- Wu, J.; Su, H.; Meng, J.H.; Lin, M.Q. Electric vehicle charging scheduling considering infrastructure constraints. Energy 2023, 278, 127806. [Google Scholar] [CrossRef]
- de Sa, A.L.S.; Lavieri, P.S.; Cheng, Y.T.; Hajhashemi, E.; Oliveira, G.J.M. Modelling driver’s response to demand management strategies for electric vehicle charging in Australia. Energy Res. Soc. Sci. 2023, 103, 103218. [Google Scholar] [CrossRef]
- Montoya, A.; Gueret, C.; Mendoza, J.E.; Villegas, J.G. The electric vehicle routing problem with nonlinear charging function. Transp. Res. Part B 2017, 103, 87–110. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q. Fleet sizing for one-way electric carsharing services considering dynamic vehicle relocation and nonlinear charging profile. Transp. Res. Part B 2019, 128, 23–49. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, S.; Qu, X. Optimal electric bus fleet scheduling considering battery degradation and non-linear charging profile. Transp. Res. Part E 2021, 154, 102445. [Google Scholar] [CrossRef]
- Zheng, F.F.; Wang, Z.J.; Liu, M. Charging scheduling of battery electric buses with uncertain charging time. Oper. Res. 2022, 22, 4865–4903. [Google Scholar] [CrossRef]
- Luo, Y.G.; Feng, G.X.; Wan, S.; Zhang, S.W.; Li, V.; Kong, W.W. Charging scheduling strategy for different electric vehicles with optimization for convenience of drivers, performance of transport system and distribution network. Energy 2020, 194, 116807. [Google Scholar] [CrossRef]
- Wu, F.Z.; Yang, J.; Zhan, X.P.; Liao, S.Y.; Xu, J. The online charging and discharging scheduling potential of electric vehicles considering the uncertain responses of users. IEEE Trans. Power Syst. 2021, 36, 1794–1806. [Google Scholar] [CrossRef]
- Xie, D.F.; Yu, Y.P.; Zhou, G.J.; Zhao, X.M.; Chen, Y.J. Collaborative optimization of electric bus line scheduling with multiple charging modes. Transp. Res. Part D 2023, 114, 103551. [Google Scholar] [CrossRef]
- Sassi, O.; Oulamara, A. Electric vehicle scheduling and optimal charging problem: Complexity, exact and heuristic approaches. Int. J. Prod. Res. 2017, 55, 519–535. [Google Scholar] [CrossRef]
- Koufakis, A.M.; Rigas, E.S.; Bassiliades, N.; Ramchurn, S.D. Offline and online electric vehicle charging scheduling with V2V energy transfer. IEEE Trans. Intell. Transp. Syst. 2020, 21, 2128–2138. [Google Scholar] [CrossRef]
- Kakkar, R.; Gupta, R.; Agrawal, S.; Tanwar, S.; Altameem, A.; Altameem, T.; Sharma, R.; Turcanu, F.E.; Raboaca, M.S. Blockchain and IoT-driven optimized consensus mechanism for electric vehicle scheduling at charging stations. Sustainability 2022, 14, 12800. [Google Scholar] [CrossRef]
- Cao, Y.S.; Wang, Y.Q.; Li, D.M.; Chen, X.M. Joint routing and wireless charging scheduling for electric vehicles with shuttle services. IEEE Internet Things J. 2023, 10, 14810–14819. [Google Scholar] [CrossRef]
- Wang, W.L.; Wu, L. A semi-decentralized real-time charging scheduling scheme for large EV parking lots considering uncertain EV arrival and departure. IEEE Trans. Smart Grid 2024, 15, 5871–5884. [Google Scholar] [CrossRef]
- Hossain, M.B.; Pokhrel, S.R.; Vu, H.L. Efficient and private scheduling of wireless electric vehicles charging using reinforcement learning. IEEE Trans. Intell. Transp. Syst. 2023, 24, 4089–4102. [Google Scholar] [CrossRef]
- Wang, H.; Shi, M.G.; Xie, P.; Lai, C.S.; Jia, Y.W. Electric vehicle charging scheduling strategy for supporting load flattening under uncertain electric vehicle departures. J. Mod. Power Syst. Clean Energy 2023, 11, 1634–1645. [Google Scholar] [CrossRef]
- Nimalsiri, N.I.; Ratnam, E.L.; Smith, D.B.; Mediwaththe, C.P.; Halgamuge, S.K. Coordinated charge and discharge scheduling of electric vehicles for load curve shaping. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7653–7665. [Google Scholar] [CrossRef]
- Frendo, O.; Gaertner, N.; Stuckenschmidt, H. Open source algorithm for smart charging of electric vehicle fleets. IEEE Trans. Ind. Inform. 2021, 17, 6014–6022. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Lee, C.K.M.; Ren, J.Z. A two-level charging scheduling method for public electric vehicle charging stations considering heterogeneous demand and nonlinear charging profile. Appl. Energy 2024, 355, 122278. [Google Scholar] [CrossRef]
- Aljohani, T.; Mohamed, M.A.; Mohammed, O. Tri-level hierarchical coordinated control of large-scale EVs charging based on multi-layer optimization framework. Electr. Power Syst. Res. 2024, 226, 109923. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, Y.; Bai, H.; Wang, S.; Li, Q.; Hua, Y. Electric vehicles participate in the economic optimal scheduling method of virtual power plant considering time-of-use tariff. In Proceedings of the 2023 IEEE Power Electronics and Power Systems Conference (PEPSC), Chongqing, China, 24–26 November 2023; pp. 267–275. [Google Scholar] [CrossRef]
- Tan, M.; Ren, Y.L.; Pan, R.; Wang, L.; Chen, J. Fair and efficient electric vehicle charging scheduling optimization considering the maximum individual waiting time and operating cost. IEEE Trans. Veh. Technol. 2023, 72, 9808–9820. [Google Scholar] [CrossRef]
- Arikumar, K.S.; Prathiba, S.B.; Moorthy, R.S.; Srivastava, G.; Gadekallu, T.R. Software defined networking assisted electric vehicle charging: Towards smart charge scheduling and management. IEEE Trans. Netw. Sci. Eng. 2024, 11, 163–173. [Google Scholar]
- de Vos, M.H.; van Lieshout, R.N.; Dollevoet, T. Electric vehicle scheduling in public transit with capacitated charging stations. Transp. Sci. 2024, 58, 279–294. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.Q.; Cao, Y.J.; Li, L.Y.; Yan, K.; Wu, L.; Liang, K. Electric vehicle charging schedule considering shared charging pile based on Generalized Nash Game. Int. J. Electr. Power Energy Syst. 2022, 136, 107579. [Google Scholar] [CrossRef]
- Diefenbach, H.; Emde, S.; Glock, C.H. Multi-depot electric vehicle scheduling in in-plant production logistics considering non-linear charging models. Eur. J. Oper. Res. 2023, 306, 828–848. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, D.; Ji, B.; Zhou, S.; Li, S.; Zhou, L. A MILP model and heuristic method for the time-dependent electric vehicle routing and scheduling problem with time windows. J. Clean. Prod. 2024, 434, 140188. [Google Scholar] [CrossRef]
- Ke, B.; Chung, Y.C.; Chen, Y.C. Minimizing the costs of constructing an all plug-in electric bus transportation system: A case study in Penghu. Appl. Energy 2016, 177, 649–660. [Google Scholar] [CrossRef]
- Emelogu, A.; Chowdhury, S.; Marufuzzaman, M.; Bian, L.; Eksioglu, B. An enhanced sample average approximation method for stochastic optimization. Int. J. Prod. Econ. 2016, 182, 230–252. [Google Scholar] [CrossRef]
- Ng, M. Distribution-free vessel deployment for liner shipping. Eur. J. Oper. Res. 2014, 238, 858–862. [Google Scholar] [CrossRef]
- Liu, X.; Chu, F.; Zheng, F.F.; Chu, C.B.; Liu, M. Parallel machine scheduling with stochastic release times and processing times. Int. J. Prod. Res. 2021, 59, 6327–6346. [Google Scholar] [CrossRef]



| Study | Nonlinear Charging Function | Uncertain Arrival Times | TOU | EV Charger Unavailability | Solution Method |
|---|---|---|---|---|---|
| Ref. [18] | ✓ | MILP, Heuristics | |||
| Ref. [19] | MILP, OFA, ONA | ||||
| Ref. [20] | Heuristic | ||||
| Ref. [21] | ✓ | RCBD | |||
| Ref. [22] | ✓ | ✓ | SDRCSS | ||
| Ref. [24] | ✓ | ADMM | |||
| Ref. [25] | MILP, C-VF, C-VF-PS | ||||
| Ref. [26] | ✓ | Heuristic | |||
| Ref. [28] | ✓ | MIQP | |||
| Ref. [29] | ✓ | MILP | |||
| Ref. [30] | ✓ | ONA | |||
| Ref. [31] | SEVC | ||||
| Ref. [32] | CG, Heuristic | ||||
| Ref. [9] | ✓ | AGA | |||
| Ref. [33] | QPSA | ||||
| Ref. [4] | EDA | ||||
| Ref. [34] | ✓ | B&C | |||
| Ref. [2] | ✓ | ✓ | RL | ||
| Ref. [23] | ✓ | ✓ | RL, GA | ||
| Ref. [27] | ✓ | ✓ | RL, MDP | ||
| Ref. [35] | ✓ | VNS-PM | |||
| this work | ✓ | ✓ | ✓ | ✓ | MILP, DFA |
| Parameters: | P | |||||
| Values: | 100 | 1 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zheng, F.; Liu, M. Charging Scheduling of Electric Vehicles Considering Uncertain Arrival Times and Time-of-Use Price. Sustainability 2025, 17, 1100. https://doi.org/10.3390/su17031100
Wang Z, Zheng F, Liu M. Charging Scheduling of Electric Vehicles Considering Uncertain Arrival Times and Time-of-Use Price. Sustainability. 2025; 17(3):1100. https://doi.org/10.3390/su17031100
Chicago/Turabian StyleWang, Zhaojie, Feifeng Zheng, and Ming Liu. 2025. "Charging Scheduling of Electric Vehicles Considering Uncertain Arrival Times and Time-of-Use Price" Sustainability 17, no. 3: 1100. https://doi.org/10.3390/su17031100
APA StyleWang, Z., Zheng, F., & Liu, M. (2025). Charging Scheduling of Electric Vehicles Considering Uncertain Arrival Times and Time-of-Use Price. Sustainability, 17(3), 1100. https://doi.org/10.3390/su17031100








