Building Disaster Resilience: A Sustainable Approach to Integrated Road Rehabilitation and Emergency Logistics Optimization in Extreme Events

Abstract

The increasing frequency and intensity of extreme disasters, exacerbated by climate change, pose significant challenges to sustainable development by disrupting critical infrastructure and hampering relief efforts. Enhancing disaster resilience—a core objective of sustainable development—requires integrated approaches that simultaneously address infrastructure restoration and efficient resource allocation. This study proposes a sustainable optimization framework for post-disaster response, integrating road rehabilitation decisions with emergency logistics planning within a three-tier supply chain network. We develop a mathematical model that synergistically optimizes repair crew scheduling, depot location, and vehicle routing, with the objective of maximizing a comprehensive satisfaction index that balances timely delivery (time satisfaction) and fulfillment of material needs (demand satisfaction). This integrated approach directly contributes to sustainable disaster management by ensuring more reliable and equitable access to vital resources in affected communities. A tailored variable neighborhood search algorithm is designed to solve the model efficiently, as demonstrated through large-scale numerical experiments. Our findings highlight several policy-relevant insights for sustainable emergency planning: adequate budgeting is crucial for uninterrupted relief operations; strategic investments in rapid road repair capabilities or vehicle fleets significantly enhance system efficiency; and prioritizing time satisfaction (rapid response) yields greater overall benefits than merely increasing delivered quantities. Furthermore, restoring critical road infrastructure is shown to mitigate transportation uncertainties, thereby strengthening the resilience of the entire relief system. This work provides a quantifiable methodology and practical decision support tools for building more sustainable and resilient communities in the face of disasters.

1. Introduction

In recent years, the intensification of global climate change has led to the frequent occurrence of extreme natural disasters, such as earthquakes, floods, hurricanes, and other catastrophic events, which not only cause major casualties and property damage but also cause devastating damage to infrastructure systems. After a disaster, the large-scale destruction of road networks often leads to the interruption of the ‘lifeline’, which seriously hampers the transport of emergency supplies and the implementation of rescue operations. According to the statistics, in the 2008 Wenchuan earthquake, the damage rate of roads in the disaster area was as high as 70% or more, and as a result, about 30% of the affected area during the 72 h golden rescue period could not get timely rescue; the tsunami triggered by the 2011 Tohoku earthquake in Japan caused more than 4000 road damages, which reduced the efficiency of post-disaster distribution of materials by 60%. The 2023 earthquake in Turkey led to the destruction of 100,000 km of roads, and the 2021 earthquake in Henan Province led to the destruction of 100,000 km of roads. Cases such as the destruction of 100,000 km of roads caused by the 2023 Turkey earthquake and the paralysis of the transport network caused by the heavy rainfall in Henan province in 2021 show that the post-disaster emergency response system is facing the dual challenges of road infrastructure destruction and surging demand for materials. In this context, determining how to achieve the synergistic optimization of road repair and emergency material distribution through scientific decision-making methods has become a key scientific issue to enhance the timeliness of emergency rescue and safeguard the lives and properties of affected people. In extreme disaster situations, the emergency logistics system mainly faces three core challenges: (1) the sharp decline in traffic accessibility due to damaged road networks; (2) the dynamic spatial and temporal characteristics of the demand for materials at the disaster site; and (3) the severe shortage of rescue resources (including maintenance teams, transport vehicles, etc.). Existing studies tend to treat the road rehabilitation problem and the material distribution problem separately, ignoring the dynamic coupling relationship between the two. Specifically, the road rehabilitation decision directly affects the connectivity of the transport network, which, in turn, constrains the choice of material distribution paths; while the urgency of material distribution in turn determines the priority of road rehabilitation. This complex interaction makes it difficult to optimize either link individually to maximize the overall rescue efficiency. Therefore, it is of great theoretical and practical significance to establish a synergistic optimization framework for road rehabilitation and emergency material distribution to improve the emergency rescue efficiency at the system level.

In the field of emergency logistics research, many scholars have carried out an in-depth exploration of the emergency warehouse location path problem (LRP). Existing studies mainly focused on key factors such as material demand [1,2,3], transport time uncertainty [4,5], and road condition uncertainty [6,7]. Aliakbari and Komijan [8] constructed a scenario-based robust optimization model by considering the uncertainty of demand and transport time; Khanchehzarrin et al. [9] addressed the uncertainty of rescue material demand, inventory level, and priority uncertainties and built a multi-objective two-layer stochastic planning model. In terms of emergency supplies distribution, Vidal et al. [10] constructed an optimization model with the objective of the shortest dispatch distance, while Rahafrooz and Alinaghian [11] proposed a multi-objective robust optimization model that takes into account fairness, distribution risk, and logistics cost. These studies provide an important theoretical foundation for coping with material distribution problems in extreme disasters. However, there are obvious limitations in traditional emergency logistics research. Generally speaking, the main shortcomings of the existing studies are as follows: (1) road repair and material distribution are regarded as independent decision-making processes, resulting in insufficient spatial and temporal synergy between the repair scheme and the transport path; (2) there is a lack of an in-depth exploration of the differentiated treatment of ‘soft and hard time windows’ under the constraints of the time window; and (3) the mechanism of the influence of the degree of road repair on the uncertainty of the transport time has not yet been analyzed in a systematic way. These limitations seriously restrict the overall efficiency of emergency resource allocation.

This study addresses the above theoretical gaps and innovatively proposes a synergistic optimization framework for road rehabilitation and emergency material distribution. The breakthroughs that distinguish it from the existing literature are reflected in three dimensions: (1) constructing a three-level emergency material distribution network (emergency material reserve depot-transit center-disaster site), embedding road rehabilitation decision variables into a site-path optimization model, and realizing integrated decision-making between infrastructure rehabilitation and logistics resource allocation; (2) introducing a time satisfaction function to quantify the urgency differences of the constraints in different time windows and combining the demand for materials to establish a bi-objective optimization model, which balances timeliness and fairness by weighting the comprehensive satisfaction index; (3) develop an improved variable neighborhood search algorithm (VNS), which adopts an initial solution generation strategy based on cluster analysis and is combined with an adaptive neighborhood switching mechanism to enhance the solution efficiency of large-scale arithmetic cases. These innovations effectively solve the key problems of traditional methods, such as the fragmentation of the ‘repair-distribution’ decision, the single satisfaction evaluation, and the lack of algorithm scalability. This study adopts the methodological system of ‘problem modeling–algorithm development–experimental analysis’. First, a mixed-integer planning model is constructed with the goal of maximizing comprehensive satisfaction, which innovatively introduces the coupling constraints between road repair state variables and material distribution path variables. Then, a variable neighborhood search algorithm integrating a greedy initialization strategy is designed, which dynamically adjusts the neighborhood structure to balance the breadth and depth of the search. Finally, sensitivity analysis is conducted via orthogonal experiments to systematically investigate the influence of key parameters—such as budget constraints, maintenance capacity, and the number of vehicles—on system performance. In particular, this study will verify the important hypothesis that ‘road repair progress is negatively correlated with transport time uncertainty’, thereby providing a scientific basis for the formulation of hierarchical rescue strategies.

The subsequent chapters of this study are arranged as follows: Section 2 provides a review of the related research progress; Section 3 elaborates upon the construction process of the collaborative optimization model; Section 4 introduces the design principle of the variable neighborhood search algorithm; Section 5 verifies the validity of the model and algorithm through numerical experiments; Section 6 analyzes the degree of influence of each uncertain parameter on the target value through sensitivity analysis; and Section 7 summarizes the research results and highlights future directions. Through this systematic research, we expect to contribute new solutions to enhance the emergency rescue capability under extreme disasters.

2. Literature Review

In recent years, with the intensification of global climate change, extreme natural disasters (e.g., earthquakes, floods, hurricanes, etc.) have been occurring frequently, causing serious damage to human society and infrastructure. After a disaster occurs, road damage and material shortages often become the key factors restricting the efficiency of emergency relief. Determining how to efficiently repair damaged roads and optimize the distribution path of emergency materials under limited time and resource conditions has become an important research topic in the field of emergency logistics management. In this paper, we systematically sort out the existing research on the two aspects of road repair under extreme disasters and optimization of emergency material distribution and point out the shortcomings of the existing research and the innovations of this research.

2.1. Research on Road Repair Under Extreme Disasters

The destructive impact of extreme disasters on roads often leads to serious traffic disruption, affecting the timely distribution of rescue materials. To address the problem of emergency material distribution, the introduction of road rehabilitation research under extreme disasters can ensure the timely delivery of relief materials to the victims. Rawls and Turnquist [12] proposed a two-phase emergency facility siting model in response to the uncertainty of the material demand and road damage in earthquake disasters. Du and Yi [13] believed that the timeliness of the emergency logistics is crucial and, therefore, proposed the emergency logistics vehicle path model based on road network failure and solved it using a genetic algorithm. Bruni et al. [14] conducted a risk assessment of the road network access state after a disaster in order to improve the safety and reliability of the vehicle path scheme and proposed an emergency logistics model with the objective of minimizing the distribution time, which was solved using an iterative greedy heuristic algorithm. Qiuping et al. [15] proposed a hybrid meta-heuristic algorithm for assessing the reliability of road networks with different levels of damage. Sanci and Daskin [16] proposed a two-level stochastic planning model for emergency response with the objective of minimizing the total cost, considering the uncertainty in demand, road damage rate, and repair time and solved it using an integer L-shape algorithm. Aslan and Çelik [17] assumed infinite repair resources and preset a subset of path candidates to describe the road access state using probability distributions, proposed a two-stage stochastic planning model with the objective of minimizing the total relief time, and solved it using the Sample Average Approximation (SAA) method. Yuan and Wang [18], also taking into account the traveling time factor, constructed a single-objective path selection model that pursues the shortest traveling time, incorporating a time-varying speed constraint to reflect traffic congestion. Khorsi et al. [19] constructed a mixed-integer planning model to study the distribution of emergency rescue resources under damaged road conditions and the path optimization and decision-making of the emergency logistics distribution path and path selection problem, taking into account the three aspects of rescue efficiency, rescue fairness, and effectiveness. Huang and Song [20] pointed out that in the study of emergency logistics problems, the variables that are difficult to determine are usually estimated by experts, and in view of the unavailability of historical data of some parameters in emergency events, an emergency logistics distribution path optimization model is constructed based on the uncertainty theory. Ozdamar et al. [21] presented a constructive heuristic method for generating roadside debris cleanup plans in post-disaster road recovery, which aimed to maximize cumulative network accessibility throughout the cleanup operation and minimize the makespan. Chang et al. [22] studied the emergency logistics problem with information uncertainty in the context of flooding in order to achieve a reasonable distribution of rescue materials, using ArcGIS Desktop (version 10.8) software, based on the potential map of the flooded area to obtain an estimate of the possible location of the affected points and the number of emergency resources, to construct two stochastic planning models that can be effectively used in the actual rescue, and to improve the work of the relevant departments of the emergency relief to provide a reference basis.

2.2. Research on the Optimization of Emergency Material Distribution

Emergency logistics is a special logistics activity that emphasizes time efficiency and relatively weak economic efficiency, distinguishing it from ordinary commercial logistics. Rescue operations in sudden natural disasters, social hazards, epidemics, and other catastrophic events need to rely on the support of emergency logistics. The emergency logistics path problem is a research hotspot in the field of emergency management. It was first proposed by Dantzig and Ramser [23], and its main research objective is to transport materials from a distribution center to customer points with different needs by vehicles and to plan a reasonable route for each transport vehicle under the premise of meeting all transport requirements. Vahdani et al. [24] and others constructed a multi-vehicle yard path optimizing the minimization of the transport time of the materials with the maximization of the safety optimization model and used a meta-heuristic algorithm with good results to solve this multi-objective optimization problem. Chang [25] constructed an emergency logistics vehicle path optimization model with the objective function of maximizing time satisfaction and verified the effectiveness of the model by combining a hybrid approach of a genetic algorithm and an ant colony algorithm. Gao [26] defined the ‘cost of unsatisfactory’ as an unsatisfied demand and an oversupply of materials and designed a two-level hybrid material scheduling model with the shortest total time and the smallest unsatisfied cost as the optimization objectives. Liu and Xie [27] carried out an exhaustive analysis of the available information and the road network after the earthquake disaster to construct a dynamic optimization model, based on which the corresponding resource performance can be derived and the purpose of which is to achieve the maximum rescue efficiency. Qin et al. [28] also studied the distribution problem of limited rescue resources, focusing on the impact of an insufficient supply of materials and uncertain demand on the rescue effect within 72 h after a disaster, considering both an insufficient quantity of materials and uncertain demand in the model, focusing on the rational planning of rescue routes, and improving the utilization rate of limited materials. Ahmadi-Javid [29] proposed a mixed-integer planning LRP model with the objective of minimizing the total cost and solved it using a two-stage heuristic algorithm. Lars et al. [30] proposed a three-stage stochastic optimization model for emergency logistics siting distribution, in which the first stage is for the siting study and the second and third stages are designed for the scheduling of the materials under the uncertainty conditions. Shen et al. [31] proposed an emergency logistics siting-path optimization model considering the environmental cost of carbon emission and used a two-stage hybrid algorithm of particle swarm and forbidden search to solve the problem. Xu et al. [32] proposed an emergency logistics siting-path model under multiple constraints for the urban evacuation siting problem in an earthquake disaster.

2.3. Research Gaps

This study provides a systematic review and comparative analysis of the existing literature, as detailed in

Table 1. Differences in the literature.

Ref.	Reference	Uncertainty Factors					Decision		Model Type	Algorithm
		AT	AL	DR	RC		C	UC
[12]	Rawls and Turnquist.			√	√		√		LP	TS
[13]	Du and Yi	√			√			√	LP	ACO
[14]	Bruni et al.	√			√			√	MILP	GA
[15]	Qiuping et al.	√		√	√			√	LP	GA
[16]	Sanci and Daskin		√	√			√		MILP	BD
[17]	Aslan and Çelik		√		√			√	MILP	B&P
[18]	Yuan and Wang	√		√	√			√	MILP	ASM
[19]	Khorsi et al.	√		√	√		√		MINLP	GA
[20]	Huang and Song	√					√		FMO	GA
[21]	Chang et al.	√	√	√			√		LP	ASM
[23]	Dantzig and Ramser	√	√					√	LP	ASM
[24]	Vahdani et al.	√		√	√			√	LP	TS
[25]	Chang	√	√	√			√		LP	ACO
[26]	Gao	√		√			√		MILP	ASM
[27]	Liu and Xie	√	√	√			√		MILP	TS
[28]	Qin et al.	√	√	√				√	MILP	ACO
[29]	Ahmadi-Javid	√	√					√	MILP	VNS
[30]	Lars et al.	√		√				√	MILP	ASM
[31]	Shen et al.	√	√	√				√	BLPM	GA
[32]	Xu et al.	√		√	√			√	MINLP	GA
-	This study	√	√	√	√			√	MILP	VNS

Note: AT: Accident time; AL: Accident location; DR: Demand resources; RC: Road condition; C: Certain; UC: Uncertain; LP: Linear programming; MILP: Mixed-integer linear programming; MINLP: Mixed-integer non-linear programming; FMO: Fuzzy multi-objective; BLPM: Bi-level programming model; TS: Tabu search; ACO: Ant colony optimization; GA: Genetic algorithm; BD: Benders decomposition; B&P: Branch-and-price; ASM: Active set method; VNS: Variable neighborhood search.

. It identifies the following three limitations in the current research: (1) in terms of model construction, existing studies tend to separate road repair decisions and emergency material distribution network design, lacking a dynamic integrated framework for their collaborative optimization; (2) in terms of optimization objectives, the interactive influence mechanism between time satisfaction and demand satisfaction has not been fully considered; and (3) in terms of algorithm design, existing solution methods face computational efficiency bottlenecks when dealing with large-scale post-disaster emergency logistics problems.

To address these research gaps, this paper makes the following innovative contributions:

(1)

It proposes a three-level emergency material collaborative optimization model integrating road repair decisions, innovatively incorporating repair path selection, transfer warehouse location selection, and multi-vehicle routing planning into a unified framework for joint optimization, breaking through the limitations of subsystem separation optimization in traditional research;

(2)

It constructs a dual satisfaction-driven multi-objective optimization function, quantifying the differential contributions of time satisfaction (material delivery timeliness) and demand satisfaction (material allocation fairness) to overall rescue effectiveness by introducing a weight adjustment mechanism;

(3)

It designs a hybrid intelligent algorithm based on improved variable neighborhood search (VNS), combining a parameter sensitivity analysis method to systematically reveal the impact mechanisms of key parameters, such as budget constraints and repair capacity, on system performance.

The VNS algorithm has been widely applied in research on combinatorial optimization and vehicle routing problems. Currently, there is limited research on emergency material distribution path optimization for road repair under extreme disasters. Moreover, when considering the uncertainty caused by disasters, many studies assume that it follows a probability distribution and use stochastic programming methods. However, actual disasters are more complex, making it difficult to accurately characterize the precise probability distribution of uncertain parameters. Based on the above analysis, this paper studies a secondary emergency material distribution network, considering limited repair resources and all transportation paths, and explores the emergency logistics distribution path optimization problem under the damaged state of the road network due to natural disasters. This paper constructs a distribution path optimization model with the comprehensive satisfaction of the material distribution process as the objective, and based on the actual disaster situation at demand points, it achieves a reasonable distribution of emergency materials to maximize satisfaction. A variable neighborhood search (VNS) algorithm is designed to solve the model, providing new insights for emergency logistics path optimization research.

3. Model Construction

3.1. Problem Description

During extreme disasters, the emergency material distribution in affected areas faces significant challenges due to a high uncertainty in material demand, transportation times, and distribution route selection, which substantially impacts the efficiency and timeliness of rescue operations, particularly as road conditions become a key influencing factor with three main post-disaster scenarios. To systematically address these uncertainties, the proposed model is designed primarily for pre-disaster strategic planning, while its structure allows for rapid post-disaster operational adjustments tailored to different road condition scenarios. After a disaster, the road conditions are usually classified into the following three main situations:

(1)

Severe road damage: Disasters may cause bridges to break, roadbeds to collapse, or other situations, rendering some or all roads impassable. In this case, vehicles cannot follow the original routes, and rescue efforts may stall, requiring either repairs or alternative paths. The repair time and the feasibility of alternative paths add unpredictability, further prolonging the distribution time of materials.

(2)

Surge in traffic volume: After a disaster, affected populations need to evacuate quickly, and rescue teams need to enter urgently, all of which may lead to a dramatic increase in traffic volume. In particular, in urban or densely populated areas, traffic may become severely congested, causing a significant reduction in vehicle speeds and potentially leading to gridlock. This situation directly impacts the efficiency of material transportation and delays the initiation of rescue operations.

(3)

Good road conditions: In some cases, the roads may not be severely damaged after the disaster, and traffic volume may remain relatively low. In this case, vehicles can follow the planned routes quickly, and the transportation of materials faces no obstacles. This scenario represents an ideal condition, ensuring that rescue materials can be delivered to disaster sites in a timely and effective manner.

Therefore, in the face of different road conditions, the transport routes, scheduling, and resource deployment of emergency supplies need to be flexibly adjusted according to the specific conditions of the disaster to ensure that the rescue efficiency is maximized. In this context, the establishment of a flexible, efficient, and real-time response to the emergency supply transport program is particularly important. In this case, vehicle b is required to transport emergency materials p from supply point k and emergency warehouse s to disaster point d through the material distribution network. Figure 1 shows the schematic diagram of the distribution of emergency supplies. Some of the roads between the supply point, the emergency warehouse, and the disaster site need to be repaired due to damage, which makes the transport time of vehicle b uncertain. These uncertainty parameters are characterized by a series of values that reflect the likelihood of the parameters in different scenarios. Scenario-based parameter and decision variables that may lead to scenarios in stochastic planning models are introduced. Scenario probabilities are used to describe the uncertainty of demand, and the uncertainty of transport time is portrayed using the opportunity constrained planning method. The uncertainty of demand and transport time of emergency supplies directly affects the satisfaction of emergency supplies distribution at the disaster site due to the disaster situation.

In summary, the core problem of decision-making is how to properly arrange the repair of damaged roads, plan the service paths of emergency vehicles in combination with the road network connectivity information, and ensure the distribution of emergency materials to the affected points within the specified time, so as to maximize the comprehensive satisfaction of the whole distribution system while meeting the constraints of supply capacity of the supply points, the capacity of the emergency warehouses, and the number of transport vehicles.

3.2. Problem Assumption

Assumption (1): The amount of material stored at each supply point is known.

Assumption (2): The quantity of supplies required at each disaster site is known.

Assumption (3): The coordinates of the locations of the supply points and the disaster site are known.

Assumption (4): The capacity of all emergency warehouses is measured using a unified standard spatial unit. Additionally, each supply type possesses a predefined spatial conversion factor. This factor converts the quantity of a unit supply into the number of standard spatial units it occupies. Consequently, the total capacity constraint of a warehouse refers to the aggregate spatial occupancy of all stored supplies, converted via these factors, which must not exceed the warehouse’s rated capacity.

3.3. Model Construction

3.3.1. Sets

$K$	The set of all supply points, $k\in K$.
$k$	The index of the supply point.
$S$	The set of all candidate contingency warehouses, $s \in S$.
$s$	The index of candidate contingency warehouses.
$D$	The set of all affected points, $d\in D$.
$d$	The index of affected points.
$\mathit{\Omega }$	The set of all scenarios, $\omega \in \mathit{\Omega }$.
$\omega$	The index of scenarios.
$P$	The set of all material types, $p\in P$.
$p$	The index of the type of material.
Q	The set of all emergency warehouse sizes, $q\in Q$.
$q$	The index of the size of the emergency warehouse.
$N$	The set of all nodes, $i,j\in N$, where $N=K\cup S\cup D$.
$i,j$	The index of nodes in the emergency material distribution network, including all supply points, emergency warehouses, and disaster points.

3.3.2. Parameters

$\xi \left(\omega \right)$	Denotes the probability of scenario $\omega$ occurring.
$M$	Denotes a sufficiently large positive number.
$C$	Indicates the total budget.
$r$	Indicates the number of road rehabilitation teams.
${oc}_r$	Denotes the cost of rehabilitating the road per unit of rehabilitation team $r$.
${oc}_{s,q}$	Denotes the cost of building scale $q$ at node $s$.
${oc}_{i,j}$	Denotes the cost of transporting from node $i$ to node $j$.
$z_{k,p}^{\omega }$	Quantity of material $p$ that supply point $k$ can supply under scenario $\omega$.
$y_{s,p}^{\omega }$	Scenario $\omega$, the amount of material $p$ that is initially stored in emergency warehouse s.
$g_{d,p}^{\omega }$	Scenario $\omega$, the demand for emergency supplies $p$ at disaster point $d$.
${\eta }_{i,j}^{\omega }$	Scenario $\omega$, if the road from node $i$ to node $j$ is not damaged, it is 1; otherwise it is 0.
$a_1$	Indicates the maximum demand factor at the affected site.
$a_2$	Denotes the minimum demand coefficient of the affected point.
$\lambda$	Denotes the impact coefficient of the disaster on the distribution route.
${rt}_{i,j}^{\omega }$	Scenario $\omega$, the time to repair the road from node $i$ to node $j$.
$l{t}_{i,j}$	Denotes the latest time for material distribution from point $i$ to point $j$.
$e{t}_{i,j}$	Denotes the earliest time for material distribution to reach point $j$ from point $i$.
${xt}_{i,j}$	Denotes the distribution time from node $i$ to point $j$ when the road is intact.

3.3.3. Decision Variables

${\alpha }_{i,q}$	Binary variable, 1 if an emergency warehouse of size $q$ is established at candidate point $i$, 0 otherwise.
${\delta }_{i,j}^{\omega }$	Binary variable, scenario $\omega$, the road from node $i$ to node $j$ needs to be repaired is 1, 0 otherwise.
${\beta }_{i,j}^{\omega }$	Binary variable, scenario $\omega$, 1 if node $j$ is reached from node $i$, 0 otherwise.
${\zeta }_{k,d,p}^{\omega }$	Floating variable, scenario $\omega$, the amount of material $p$ delivered from supply point $k$ to disaster point $d$.
${\zeta }_{k,s,p}^{\omega }$	Float variable, scenario $\omega$, with the number of deliveries of material $p$ from supply point $k$ to emergency depot $s$.
${\zeta }_{s,d,p}^{\omega }$	Float variable, scenario $\omega$, with the number of deliveries of material $p$ from emergency depot $s$ to disaster point $d$.

3.3.4. Comprehensive Satisfaction

The three decision scenarios described in this section all employ the variable, where the range of indices i and j follows the definition in Section 3.3.1.

• Time satisfaction

The soft time window is used to construct the fuzzy affiliation function, where $t_{i,j}^{\omega }=\lambda \times {xt}_{i,j} + {\delta }_{i,j}^{\omega }\times {rt}_{i,j}^{\omega }$; because of the different types of damage to the road, a road impact coefficient $\lambda (\lambda \ge 1)$ is introduced. Therefore, the timeliness of emergency material distribution is portrayed as the time satisfaction function, and the time satisfaction $f\left(t_{i,j}^{\omega }\right)$ of material distribution at the affected point is as follows:

$$f\left(t_{i,j}^{\omega }\right)=\left\{\begin{array}{ll}1,& 0<t_{i,j}^{\omega }⩽e{t}_{i,j}\\ {\displaystyle \frac{l{t}_{i,j}-t_{i,j}^{\omega }}{l{t}_{i,j}-e{t}_{i,j}}},& e{t}_{i,d}<t_{i,j}^{\omega }⩽l{t}_{i,j}\\ 0,& l{t}_{i,j}<t_{i,j}^{\omega }\end{array}\right.$$

(1)

The overall time satisfaction function $f_1$ for the emergency material distribution system at each disaster site is as follows:

$$f_1={\displaystyle \frac{1}{n}}f\left(t_{i,j}^{\omega }\right)$$

(2)

2.

Demand satisfaction

The degree of satisfaction with the demand for emergency supplies at the affected sites is as follows:

$$f\left({\zeta }_{i,j,p}^{\omega }\right)=\sum _{i\in N}\sum _{p\in P}{\beta }_{i,j}^{\omega }(g_{j,p}^{\omega }-{\zeta }_{i,j,p}^{\omega })$$

(3)

The satisfaction function $f_2$ for the overall demand for the emergency distribution system at each disaster site is as follows.

$$f_2={\displaystyle \frac{1}{n}}f\left({\zeta }_{i,j,p}^{\omega }\right)$$

(4)

3.

Comprehensive satisfaction

The function sets the weight of the time satisfaction of the affected point $\theta$ and the weight of demand satisfaction $1-\theta$, followed by the comprehensive satisfaction function of the affected point on the distribution of rescue materials of the emergency logistics system:

$$f_3=\theta f_1 + (1-\theta )f_2$$

(5)

3.3.5. Objective Function

$$Max f={\displaystyle \frac{1}{\mathsf{\Omega }}}\sum _{\omega \in \mathsf{\Omega }}\xi \left(\omega \right)f_3$$

(6)

s.t.

$${\sum }_{q\in Q}{\alpha }_{i,q}\le 1 \forall i\in S$$

(7)

$${\sum }_{p\in P}{\zeta }_{s,d,p}^{\omega }\le {M\beta }_{s,d}^{\omega } \forall d\in D,\forall s\in S,\forall \omega \in \mathsf{\Omega }$$

(8)

$${\sum }_{p\in P}{\zeta }_{k,d,p}^{\omega }\le {M\beta }_{k,d}^{\omega } \forall k\in K,\forall d\in D,\forall \omega \in \mathsf{\Omega }$$

(9)

$${\sum }_{p\in P}{\zeta }_{k,s,p}^{\omega }\le {M\beta }_{k,s}^{\omega } \forall k\in K,\forall s\in S,\forall \omega \in \mathsf{\Omega }$$

(10)

$${\sum }_{i\in S\cup D}{\zeta }_{k,i,p}^{\omega }\le z_{k,p}^{\omega } \forall k\in K,\forall p\in P,\forall \omega \in \mathsf{\Omega }$$

(11)

$${\sum }_{i\in N}{\sum }_{j\in N}{\delta }_{i,j}^{\omega }\le r \forall \mathsf{\omega }\in \mathsf{\Omega }$$

(12)

$${\sum }_{p\in P}{\sum }_{d\in D}{\zeta }_{s,d,p}^{\omega }\le {\sum }_{p\in P}{y}_{s,p}^{\omega }+{\sum }_{p\in P}{\sum }_{k\in K}{\zeta }_{k,s,p}^{\omega } \forall s\in S,\forall \omega \in \mathsf{\Omega }$$

(13)

$${a_{1}g}_{d,p}^{\omega }\le {\sum }_{i\in K\cup S}{\zeta }_{i,d,p}^{\omega }\le {a_{2}g}_{d,p}^{\omega } \forall d\in D,\forall p\in P,\forall \omega \in \mathsf{\Omega }$$

(14)

$${\sum }_{i\in K\cup S}{\beta }_{i,d}^{\omega }\ge 1 \forall d\in D,\forall \omega \in \mathsf{\Omega }$$

(15)

$${\delta }_{i,j}^{\omega }\le 1-{\eta }_{i,j}^{\omega } \forall i,j\in N,\forall \omega \in \mathsf{\Omega }$$

(16)

$${\beta }_{i,j}^{\omega }\le 1-\left(1-{\eta }_{i,j}^{\omega }\right)\left(1-{\delta }_{i,j}^{\omega }\right) \forall i,j\in N,\forall \omega \in \mathsf{\Omega }$$

(17)

$${\sum }_{k\in K}{\zeta }_{k,s,p}^{\omega }-M{\sum }_{q\in Q}{\alpha }_{i,q}\le 0 \forall s\in S,\forall p\in P,\forall \omega \in \mathsf{\Omega }$$

(18)

$${\sum }_{i\in N}{\sum }_{j\in N}{oc}_{i,j}{\beta }_{i,j}^{\omega }+{\sum }_{i\in N}{\sum }_{j\in N}{\delta }_{i,j}^{\omega }{oc}_r+{\sum }_{q\in Q}{\sum }_{s\in S}{oc}_{s,q}{\alpha }_{s,q}\le C \forall \omega \in \mathsf{\Omega }$$

(19)

$${\zeta }_{i,j,p}^{\omega }\ge 0 \forall i,j\in N,p\in P,\forall \omega \in \mathsf{\Omega }$$

(20)

$${rt}_{i,j}^{\omega }\ge 0 \forall i,j\in N$$

(21)

$${\epsilon }_{b,i,p}^{\omega }\ge 0 \forall j\in N,p\in P,\omega \in \mathsf{\Omega }$$

(22)

$${\beta }_{i,j}^{\omega },{\delta }_{i,j}^{\omega },{\eta }_{i,j}^{\omega },{\alpha }_{i,q}\in \left\{\mathrm{0,1}\right\} \forall i,j\in N,\omega \in \mathsf{\Omega }$$

(23)

The objective function (6) denotes the maximization of the overall satisfaction. Constraint (7) denotes that, at most, one size of emergency depot can be established at any emergency depot candidate. Constraints (8)–(10) denote that the transport of supplies occurs only at nodes where the routes are connected. Constraint (11) denotes the supply capacity constraint of the material supply provider. Constraint (12) denotes the road team repair quantity constraint. Constraint (13) denotes the constraint on the distribution of materials from the emergency warehouse. Constraint (14) indicates that the total amount of each type of emergency supply transported to the disaster site can meet the minimum demand in different scenarios while not exceeding the maximum demand. Constraint (15) indicates that each affected point is served by at least one vehicle. Constraint (16) indicates that the repair team only repairs the damaged roads. Constraint (17) indicates that the repaired road is restored to traffic. Constraint (18), on the other hand, ensures that no supply point will send emergency supplies to an emergency warehouse candidate point if no warehouse is established at that point. Constraint (19) indicates the total budget limit. Constraints (20)–(23) denote the range of values for the decision variables.

4. Algorithm Design

Variable neighborhood search (VNS) algorithms have been widely used to solve combinatorial optimization problems [33] and vehicle path problems [34]. In this paper, we focus on the joint path problem of road rehabilitation and emergency warehouse siting. As the problem size continues to grow, the time required for computation will increase exponentially. To cope with this challenge, this paper adopts two different initial solution generation strategies (VNS-RandomStart and VNS-GreedyStart) and combines the VNS algorithm with the CPLEX solver to propose a new solution model. This study aims to conduct an in-depth analysis of the differences between CPLEX and VNS algorithms with different initial solution generation strategies, as well as the effects of different initial solution generation strategies (VNS-RandomStart and VNS-GreedyStart) on the solution efficiency of the VNS algorithm.

4.1. Solution

Based on the analysis, it can be seen that the variables ${\alpha }_{i,q}$ and ${\beta }_{i,j}^{\omega }$, ${\zeta }_{i,j,p}^{\omega }$ are the main decision variables in the model proposed in this study, and the rest of the decision variables depend on these three decision variables. Therefore, this study uses VNS to perform a neighborhood search for these three decision variables, and each time a new neighborhood is generated, the commercial solver CPLEX is invoked to solve the model and determine whether the value of the objective function has improved. If a better solution is found, it is necessary to jump out of the current neighborhood to go back to the first neighborhood and start the search again. When a better solution cannot be found within one iteration, a neighborhood perturbation is performed on the current incumbent solution, after which it proceeds to the next iteration to continue searching until no shaking is possible.

According to the basic framework, the key issues in solving the model include (i) initialization: how to give a good and feasible solution, including alternatives, and the size of the contingency store; (ii) neighborhood structure: how to set up a suitable neighborhood structure, which can find the incumbent solution in a very short period of time; and (iii) neighborhood shaking process: how to avoid falling into local optimality.

4.2. Initial Solution Generation

A better initial solution may be located in a better region of the solution space, which helps the VNS algorithm to find a high-quality solution faster. Conversely, a poorer initial solution may cause the algorithm to spend more time in a poorer region of the solution space early in the search. Starting from a better initial solution, the VNS algorithm may converge to a better solution faster because it may be closer to the global incumbent solution. For this reason, two solution methods with different initial solutions (VNS-RandomStart and VNS-GreedyStart) are proposed in this study.

4.2.1. VNS-RandomStart

The randomly generated initial solution algorithm (hereinafter referred to as VNS-R) first calculates the total demand for all types of materials at all affected sites, and based on the total demand quantity among all warehouse sizes that can satisfy the demand, it selects the largest one as the size of the warehouse, whose location is known. In this way, the value of ${\alpha }_{i,q}$ can be determined; for ${\beta }_{i,j}^{\omega }$, because of the complexity of the route deployment problem, the supplies are randomly distributed from the first supply point (K) or emergency warehouse (S) to any disaster-stricken point (D) until the storage capacity of the supplies at the supply point (K) or emergency warehouse (S) is distributed. Thus, a set of initial solutions for ${\beta }_{i,j}^{\omega }$ is obtained; the pseudo-code is shown in Algorithm 1.

Algorithm 1: Random Strategy for Generating Initial Solution
1:	Input: $D;K;S;$ $g_{d,p}^{\omega }$ $z_{i,p}^{\omega }$; {1,2, ..., Q}; {1,2, ..., P}
2:	Output: ${\alpha }_{i,q}$; ${\beta }_{i,j}^{\omega }$
3:	Procedure:
4:	Initialize all ${\alpha }_{i,q}$ = 0; ${\beta }_{i,j}^{\omega }$ = 0
5:	For each commodity P:
6:	Calculate total demand: TotalDemand = $\sum _{d\in D}{g}_{d,p}^{\omega }$
7:	For each warehouse size option Q: If Q ≥ TotalDemand, mark Q as feasible
8:	Select the largest feasible Q, set ${\alpha }_{i,q}=1$
9:	For each commodity $\mathit{P}$:
10:	Combine sources: $Sources=K\cup S$.
11:	While there exists unmet demand in D and available supply in Sources:
12:	Randomly select a Source$i\in Sources$ with $y_{s,p}^{\omega }$> 0
13:	Randomly select a disaster point $j\in D$ with $g_{d,p}^{\omega }$> 0
14:	Compute transport amount:$amount=Min(y_{s,p}^{\omega },z_{k,p}^{\omega },g_{d,p}^{\omega }-\sum _{k\in K}{\beta }_{k,j}^{\omega })$
15:	Assign ${\beta }_{i,j}^{\omega }$ = amount
16:	Update capacity: $z_{i,p}^{\omega }$←$z_{i,p}^{\omega }$−amount
17:	Update demand: $g_{d,p}^{\omega }$←$g_{d,p}^{\omega }$−amount
18:	If $z_{i,p}^{\omega }$ = 0, remove i from Sources
19:	Return ${\alpha }_{i,q};{\beta }_{i,j}^{\omega }$

4.2.2. VNS-GreedyStart

The initial solution algorithm generated by the greedy strategy (hereinafter referred to as VNS-G) is a method of constructing a global incumbent solution by selecting a local incumbent solution. First, the total demand $g_{d,p}^{\omega }$ of all the affected points for various types of supplies is calculated, and according to the number of the total demand among all the warehouse sizes that can satisfy the demand, the one with the largest scale is selected as the warehouse size, and the warehouse’s location is known. This enables a set of initial solutions for ${\alpha }_{i,q}$ to be obtained; for ${\beta }_{i,j}^{\omega }$, the closest supply point (K) or emergency warehouse (S) is selected based on the location of the affected point to provide the supplies until there is no storage capacity for the supplies at this supply point (K) or emergency warehouse (S). Then, the second closest supply point (K) or emergency warehouse (S) is changed to distribute the supplies. Thus, a series of initial solutions of ${\beta }_{i,j}^{\omega }$ are generated. The pseudo-code is shown in Algorithm 2.

Algorithm 2: Function greedy Algorithm (Problem, Strategy)
1:	Input: $D;K;S;$ $g_{d,p}^{\omega }$; $z_{i,p}^{\omega }$; {1,2, ..., Q}; P; $Distance\left(i,j\right)$; {1,2, ..., P}
2:	$\mathbf{O}\mathbf{u}\mathbf{t}\mathbf{p}\mathbf{u}\mathbf{t}:$${\alpha }_{i,q}; {\beta }_{i,j}^{\omega }$
3:	$\mathbf{P}\mathbf{r}\mathbf{o}\mathbf{c}\mathbf{e}\mathbf{d}\mathbf{u}\mathbf{r}\mathbf{e}:$
4:	Initialize all ${\alpha }_{i,q}$ = 0; ${\beta }_{i,j}^{\omega }$ = 0
5:	$\mathbf{F}\mathbf{o}\mathbf{r} \mathbf{e}\mathbf{a}\mathbf{c}\mathbf{h} \mathbf{c}\mathbf{o}\mathbf{m}\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{i}\mathbf{t}\mathbf{y} \mathbf{P}:$
6:	Calculate total demand: TotalDemand = $\sum _{d\in D}{g}_{d,p}^{\omega }$.
7:	$\mathit{F}\mathit{o}\mathit{r} \mathit{e}\mathit{a}\mathit{c}\mathit{h} \mathit{w}\mathit{a}\mathit{r}\mathit{e}\mathit{h}\mathit{o}\mathit{u}\mathit{s}\mathit{e} \mathit{s}\mathit{i}\mathit{z}\mathit{e} \mathit{o}\mathit{p}\mathit{t}\mathit{i}\mathit{o}\mathit{n}$Q: If Q ≥ TotalDemand, mark Q as feasible
8:	Select the largest feasible Q, set ${\alpha }_{i,q}=1$
9:	$\mathbf{F}\mathbf{o}\mathbf{r} \mathbf{e}\mathbf{a}\mathbf{c}\mathbf{h} \mathbf{c}\mathbf{o}\mathbf{m}\mathbf{m}\mathbf{o}\mathbf{d}\mathbf{i}\mathbf{t}\mathbf{y} \mathbf{P}:$
10:	Combine sources: $Sources=K\cup S$
	For each disaster point $j\in D$: Sort Sources by $\mathit{D}\mathit{i}\mathit{s}\mathit{t}\mathit{a}\mathit{n}\mathit{c}\mathit{e}(\mathit{i},\mathit{j})$ in ascending order
11:	While $g_{d,p}^{\omega }>0$and $\exists i\in \mathit{Sources}\mathit{with}{z}_{i,p}^{\omega }>0$
12:	Select the closest source i from the sorted list
13:	Compute transport amount:
14:	amount = $Min(z_{i,p}^{\omega },g_{d,p}^{\omega }-\sum _{k\in K}{\beta }_{k,j}^{\omega })$
15:	Assign ${\beta }_{i,j}^{\omega }$ = amount
16:	Update capacity: $z_{i,p}^{\omega }$←$z_{i,p}^{\omega }$−amount
17:	Update demand: $g_{d,p}^{\omega }$←$g_{d,p}^{\omega }$−amount
18:	If $z_{i,p}^{\omega }$ = 0, remove i from Sources
19:	Return ${\alpha }_{i,q};{\beta }_{i,j}^{\omega }$

4.3. Neighborhood Structure

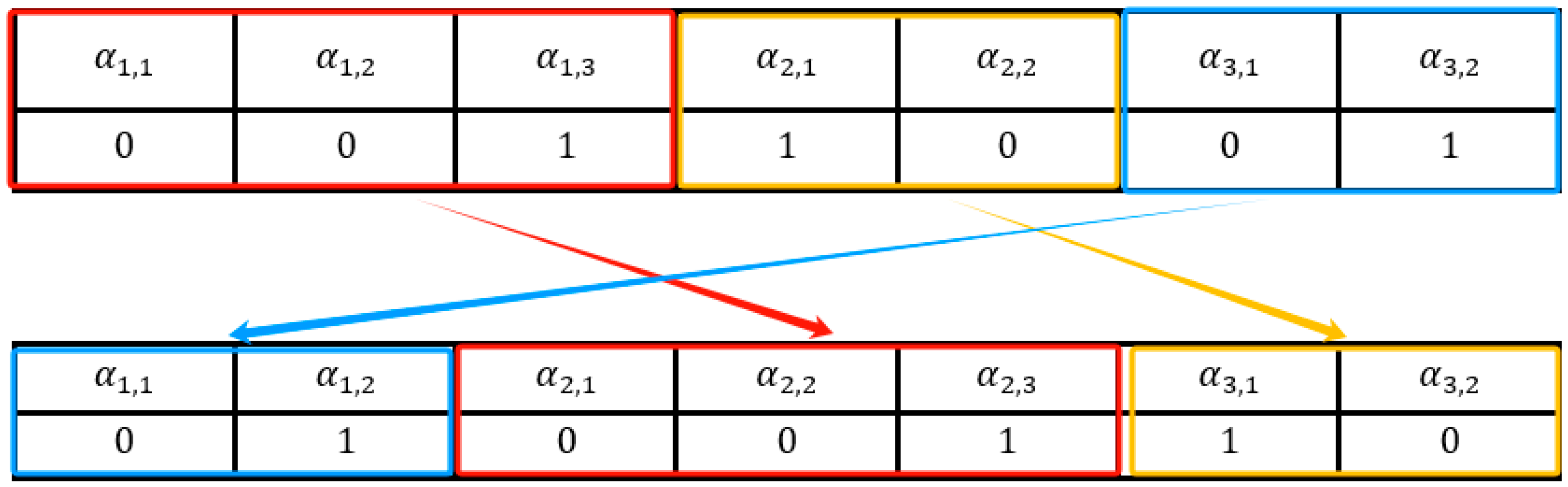
Since the model in this study is a mixed-integer programming model, the decision variables searched in the VNS contain binary variables and float variables, and a suitable neighborhood structure is designed according to the decision variables involved in the algorithm. This study can encode the neighborhood selection of ${\alpha }_{i,q}$, which is the decision variable for the location of the emergency stockpile, according to the dimensionality of the decision variable after expanding it, with 1 representing the establishment of the warehouse and 0 representing the non-establishment of the warehouse. Neighborhoods can be generated by mutation, exchange, and insertion, but after performing the above operations, it is necessary to determine whether the site selection of the warehouse meets the restrictions of constraint (3). For the decision variable ${\beta }_{i,j}^{\omega }$, 1 means that under scenario ω, the point from node i reaches node j, and 0 means that the affected point is served by other nodes, and the decision variable ${\beta }_{i,j}^{\omega }$, needs to satisfy the requirements of constraint (2).

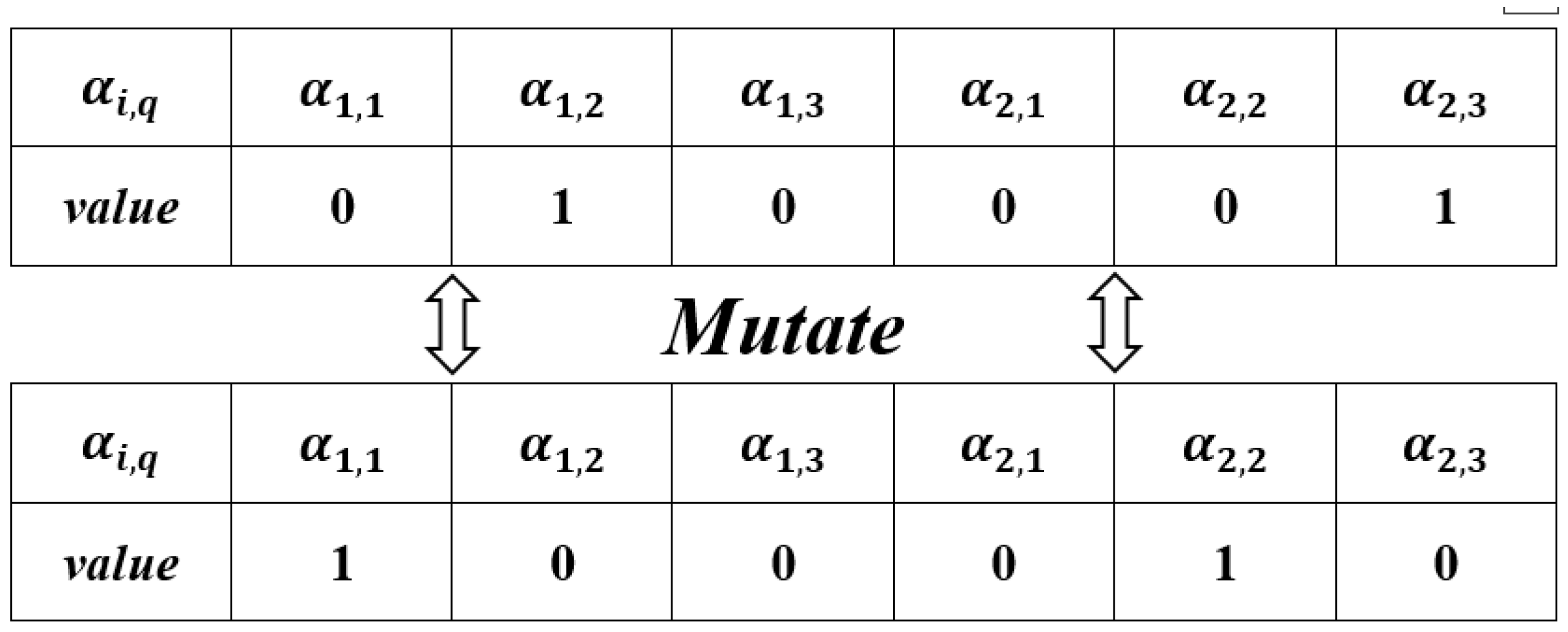
4.3.1. Domain Structure 1: Mutation

Randomly select ${\alpha }_{i,q}$, if its original value is 0 and then change it to 1; if it is 1, then change it to 0. Subsequently, the feasibility of the solution must be verified. Specifically, if a candidate point is selected to host a new warehouse of a certain size, but our solution has already assigned a different-sized warehouse to that same point, an adjustment is required. To enforce the constraint that each candidate point can accommodate at most one warehouse, the codes for all other warehouse sizes at this point must be set to 0, while the code for the newly selected warehouse size is set to 1. This adjustment process, which ensures the feasibility of the neighborhood solution generated by the mutation operator, is illustrated in Figure 2.

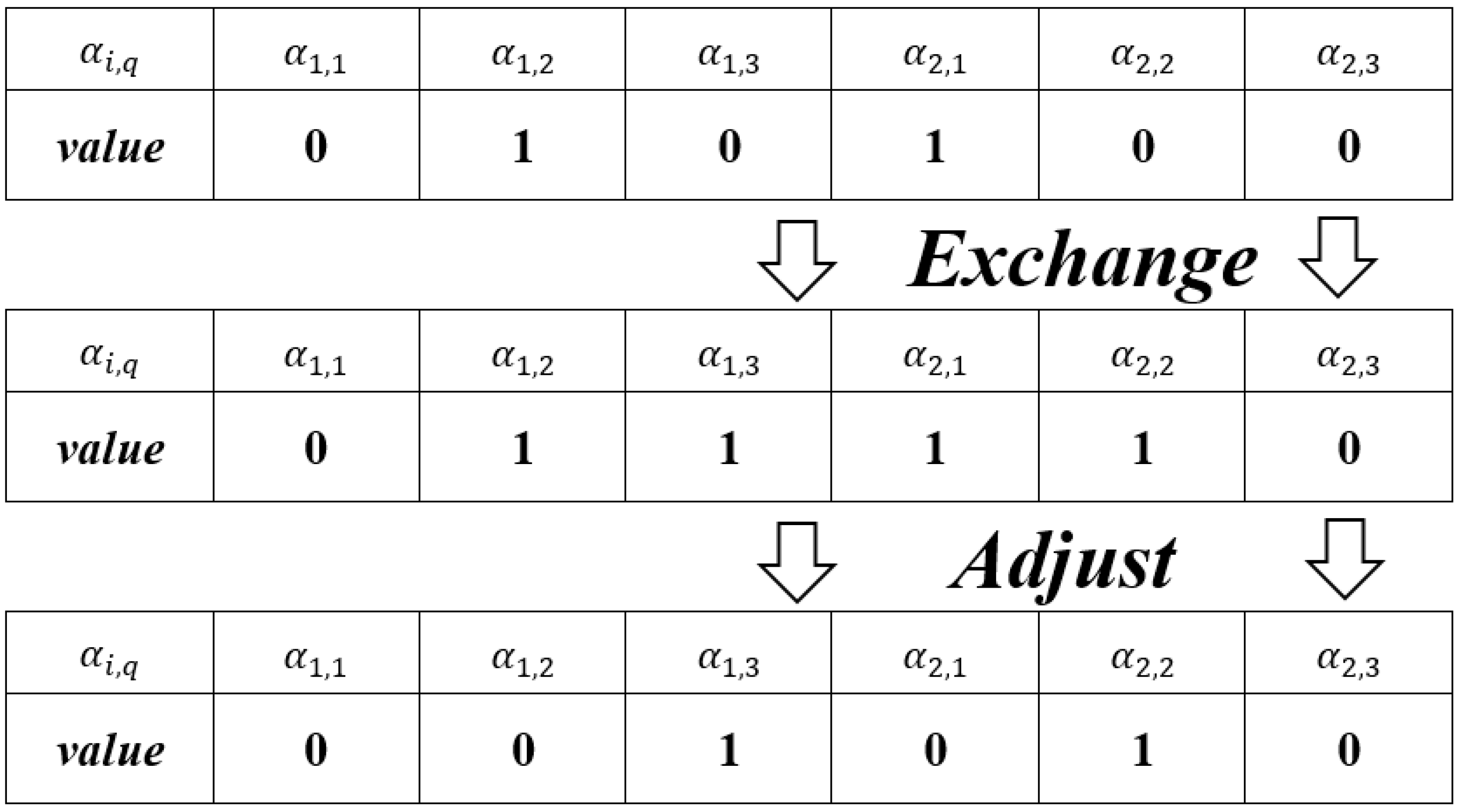
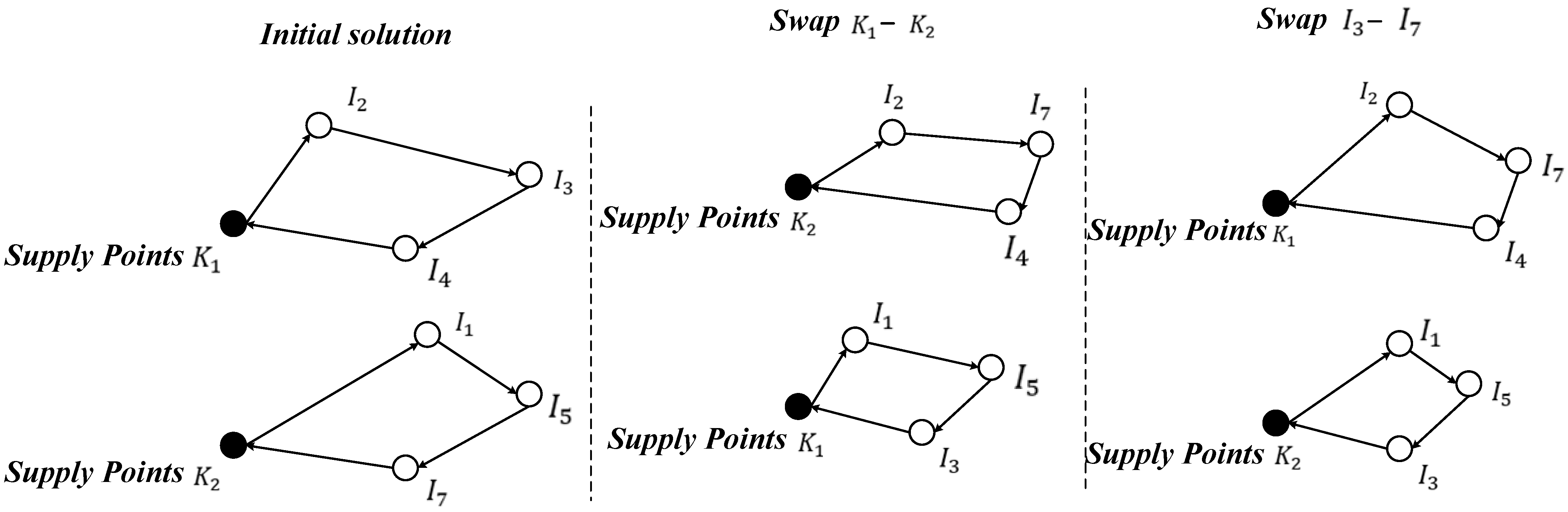
4.3.2. Domain Structure 2: Exchange

The process of exchange is shown in Figure 3; first, two values of ${\alpha }_{i,q}$ are randomly selected from the initial solution array of ${\alpha }_{i,q}$ = 1, which can only be the values corresponding to different supply points or emergency warehouses distributing emergency supplies to the affected points. Swap the values corresponding to the two points. Again, it is necessary to judge whether it is feasible or not after doing the swap. The same strategy, as shown in Figure 4, exchanges the distribution of two supply points or the affected points served by two supply points.

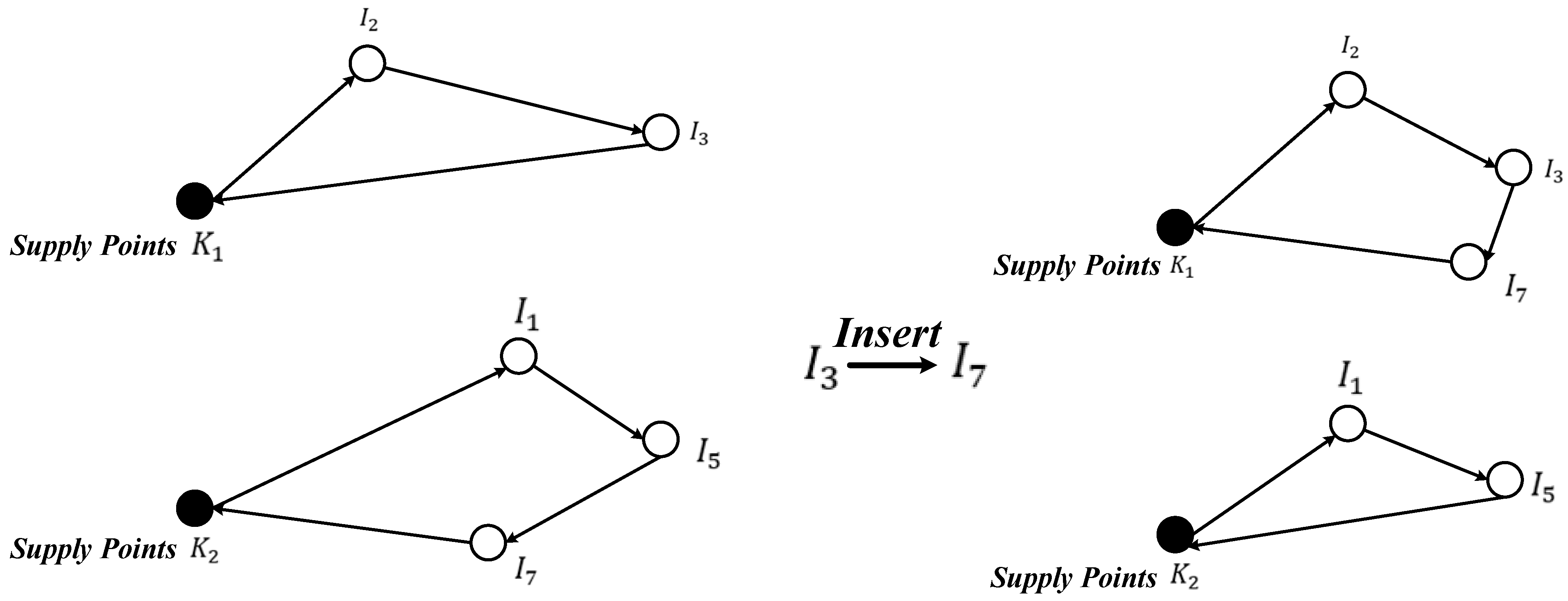
4.3.3. Domain Structure 3: Insertion

The process of insertion is shown in Figure 5; for two different supply points k, one of them, ${\beta }_{i,j}^{\omega }$ = 1, is brought to the other supply point. After doing the insertion, it is again necessary to judge whether it is feasible or not.

4.3.4. Domain Structure 4: Addition and Subtraction

For the continuous decision variable ${\zeta }_{s,d,p}^{\omega }$, this study employs fixed-step neighborhood search. Specifically, we preset a reasonable step size $\mathit{\Delta }\zeta$. The neighborhood of this variable is defined as $\{\zeta -\mathit{\Delta }\zeta ,\zeta + \mathit{\Delta }\zeta \}$. To avoid excessive computational resource consumption during local search on a single variable, we limit the number of consecutive searches in either direction (increase or decrease) to a maximum of K steps (K = 20 in this study). This approach approximates the continuous problem as a combinatorial one through discretized search. While it introduces minor precision errors due to step size and search depth constraints, these errors remain within manageable limits and are offset by a significant improvement in computational efficiency.

4.4. Basic Variable Neighborhood Descent

Variable neighborhood descent is the framework of the algorithm, which searches in the neighborhood structure. The algorithm will completely explore a neighborhood structure and then move to the next neighborhood structure if a better solution cannot be found; the flow of VNS is shown in Algorithm 3.

Algorithm 3: Variable Neighborhood Descent (VND)
Input:	incumbent_sol, candidate_sol, k ← 1 // incumbent_sol is the current best solution, candidate_sol is for neighborhood exploration, k is the index of the neighborhood structure
1:	candidate_sol ← incumbent_sol
2:	While (true) do
3:	switch (k)
4:	case 1:
	apply_NH_1(candidate_sol) // Apply the first neighborhood operator
5:	if candidate_sol.fitness > incumbent_sol.fitness then
6:	incumbent_sol ← candidate_sol
7:	k ← 0
8:	end if
9:	break
10:	case 2:
11:	apply_NH_2(candidate_sol) // Apply the second neighborhood operator
12:	if candidate_sol.fitness > incumbent_sol.fitness then
13:	incumbent_sol ← candidate_sol
14:	k ← 0
15:	end if
16:	break
17:	case 3:
18:	apply_NH_3(candidate_sol) // Apply the third neighborhood operator
19:	if candidate_sol.fitness > incumbent_sol.fitness then
20:	incumbent_sol ← candidate_sol
21:	k ← 0
22:	end if
23:	break
24:	case 4:
25:	apply_NH_4(candidate_sol) // Apply the fourth neighborhood operator
26:	if candidate_sol.fitness > incumbent_sol.fitness then
27:	incumbent_sol ← candidate_sol
28:	k ← 0
29:	end if
30:	break
31:	default:
32:	return
33:	end switch
34:	k ← k + 1
35:	end while
36:	candidate_sol ← incumbent_sol

4.5. Neighborhood Perturbation Process

In variable neighborhood search algorithms, a neighborhood perturbation process must be executed after each iteration to prevent getting stuck in local optima. This study employs a structured block perturbation strategy: first, the current incumbent solution is divided into multiple decision blocks based on candidate warehouse locations, with each block containing all configuration variables for a specific location; Based on each block’s contribution to the objective function, a quality-oriented probabilistic selection mechanism determines the block to be perturbed, prioritizing blocks with a lower contribution. Subsequently, the selected block is reassigned to an unused candidate location in the current solution. The new location is determined following a diversity-first principle, prioritizing candidate points farther from the original location. Since the internal structure of each block (particularly warehouse size attributes) remains unchanged during perturbation, the new solution inherently satisfies all warehouse configuration constraints. This ensures solution feasibility while enabling effective search space transfer. By systematically altering the spatial layout structure of the solution, the algorithm escapes the current attractor region. The specific operational flow is illustrated in Figure 6.

4.6. Steps of Variable Neighborhood Search Algorithm

The variable neighborhood search (VNS) algorithm begins by generating a feasible initial solution. This solution is then refined using a local search component called variable neighborhood descent (VND), which leverages predefined neighborhood structures to find a locally improved solution. To avoid becoming trapped in local optima, a shaking procedure is applied. This step strategically perturbs the current solution within the feasible region, providing a new starting point for subsequent iterations. The algorithm terminates when either the maximum number of iterations is reached or when no improvement is observed for a specified number of consecutive cycles. The complete framework is outlined in Algorithm 4.

Algorithm 4: Variable Neighborhood Search (VNS)
Input:	max_iterations, global_best, current_sol, stagnation_count←0, max_iterations←10// max_iterations is the maximum stagnation count, global_best is the best solution, current_sol is the working solution
Output:	Objective value
1:	global_best ← GenerateInitialSolution()
2:	While (stagnation_count < max_iterations) do
3:	current_sol ← global_best
4:	shaking_phase(current_sol) // Apply shaking to escape local optimum
5:	Variable_Neighborhood_Descent(current_sol) // Call Algorithm 3 for local search
6:	If (current_sol.fitness > global_best.fitness) then
7:	global_best ← current_sol
8:	stagnation_count ← 0 // Reset counter on improvement
9:	End if
10:	stagnation_count ← stagnation_count + 1
11:	End while
12:	Return global_best.fitness

5. Numerical Experiments

In order to verify the effectiveness of the proposed models and algorithms for practical applications, this study implements two algorithms, VNS-R and VNS-G, using the C# programming language in the Visual Studio 2022 environment. The hardware configurations used for the experiments include a computer with 16 GB of RAM, an AMD R7-4680H processor, and a Windows 10 operating system. The emergency warehouse siting problem in this study is a stochastic planning model that considers different scenarios of demand at the disaster site. The scenarios are generated based on historical disaster data, the demand at the affected points obeys a Poisson distribution, and the probability of road damage is set to be uniformly distributed from 20% to 40%. The number of scenarios has a significant impact on the experimental results: too few scenarios cannot fully reflect the robustness of the model, while too many scenarios will lead to a decrease in computational efficiency. In the case of optimizing the model size to A5-10-25-3-3, the meaning of the example ID A5-10-25-3-3 is 5 supply points, 10 emergency warehouses, 25 affected points, 3 different sizes of warehouses with different capacities, and 3 different types of emergency supplies. We designed experiments to determine the number of scenarios for the system. As shown in

Table 2. Test model run under a different number of scenarios.

Number of Scenarios	Maximum Value	Minimum Value	Difference	Mean	Standard Deviation	Average CPU Runtime (s)
10	0.9877	0.9241	0.0636	0.9550	0.0209	17.12
20	0.9851	0.9341	0.0510	0.9549	0.0162	20.55
50	0.9963	0.9501	0.0462	0.9749	0.0156	34.88
100	0.9975	0.9557	0.0418	0.9730	0.0124	71.22
200	0.9887	0.9688	0.0199	0.9743	0.0055	178.99
400	0.9883	0.9689	0.0194	0.9752	0.0054	485.33
800	0.9888	0.9702	0.0186	0.9750	0.0050	1547.22

, we tested seven groups of scenario quantities (10, 20, 50, 100, 200, 400, and 800), with 10 randomly generated instances for each group and all scenarios using the equal probability assumption ($1/|\mathit{\Omega }|$).

As shown in Table 2, the standard deviation of the objective function decreases with the number of scenarios and stabilizes after $|\mathit{\Omega }| \ge 100 (<0.0125)$; the running time increases approximately linearly with the number of scenarios, and when $|\mathit{\Omega }| \ge 200$, the magnitude of the objective function improvement (<0.1%) is no longer significant. Based on the convergence-efficiency trade-off analysis, we choose 100 scenarios as the criterion for subsequent experiments. This number ensures the stability of the results (standard deviation < 1.25%) and keeps the time of a single experiment within a reasonable range (about 71 s). At the same time, 100 scenarios can adequately cover the demand fluctuations under typical disaster situations. Therefore, we use 100 scenarios in the subsequent numerical experiments. We randomly generated a set of scenarios, each reflecting a specific disaster situation. As shown in

Table 3. Relevant parameter settings.

Parameter	Value	Parameter	Value	Parameter	Value
$z_{k,p}^{\omega }$	[3000, 7000]	$g_{d,p}^{\omega }$	[1000, 3000]	${oc}_r$	[800, 1500]
$\xi \left(\omega \right)$	$1/\left|\mathsf{\Omega }\right|$	${xt}_{i,j}$	[360, 720]	${oc}_{s,q}$	[10,000, 30,000]
$\lambda$	[1, 3]	${rt}_{i,j}^{\omega }$	[60, 120]	${oc}_{i,j}$	[20, 80]
$a_1$	0.8	$a_2$	0.5	$r$	[30, 50]

, it contains deterministic information such as the location of the disaster site, the supply site, the location of the emergency warehouse, and the damage to the road.

5.1. Performance Comparison of Two Different Initial Solution Algorithms

Table 4. Comparison of the two algorithms and CPLEX in small-scale arithmetic cases.

Case ID	CPLEX		VNS-R		Comparison		VNS-G		Comparison
	${\mathit{f}}_{\mathit{C}}$	${\mathit{T}}_{\mathit{C}}$	${\mathit{f}}_{\mathit{R}}$	${\mathit{T}}_{\mathit{R}}$	$\frac{{\mathit{T}}_{\mathit{R}}}{{\mathit{T}}_{\mathit{C}}}$	${\mathit{G}\mathit{A}\mathit{P}}_{\mathit{R}}$	${\mathit{f}}_{\mathit{G}}$	${\mathit{T}}_{\mathit{G}}$	$\frac{{\mathit{T}}_{\mathit{G}}}{{\mathit{T}}_{\mathit{C}}}$	${\mathit{G}\mathit{A}\mathit{P}}_{\mathit{G}}$
A2-3-5-3-3-1	0.8721	3.2	0.8721	12.7	3.97	0.00%	0.8721	10.5	3.28	0.00%
A2-3-5-3-3-2	0.8786	4.2	0.8786	11.9	2.83	0.00%	0.8786	11.0	2.61	0.00%
A2-3-5-3-3-3	0.8749	5.8	0.8749	11.1	1.91	0.00%	0.8749	10.3	1.78	0.00%
A2-3-5-3-3-4	0.8812	5.2	0.8811	12.3	2.37	0.00%	0.8812	10.6	2.04	0.00%
Avg.	0.8773	4.2	0.8773	12	2.86	0.00%	0.8773	10.6	2.52	0.00%
A3-3-5-3-3-1	0.8846	6.9	0.8846	22.4	3.25	0.00%	0.8846	12.4	1.80	0.00%
A3-3-5-3-3-2	0.8721	7.6	0.8721	20.8	2.74	0.00%	0.8721	14.8	1.95	0.00%
A3-3-5-3-3-3	0.8785	10.4	0.8785	18.9	1.82	0.00%	0.8785	13.9	1.34	0.00%
A3-3-5-3-3-4	0.8812	9.9	0.8812	21.5	2.17	0.00%	0.8812	15.3	1.55	0.00%
Avg.	0.8793	8.7	0.8793	20.9	2.40	0.00%	0.8793	14.1	1.62	0.00%
A2-4-10-3-3-1	0.8819	8.2	0.8819	12.3	1.50	0.00%	0.8819	10.1	1.23	0.00%
A2-4-10-3-3-2	0.8968	5.6	0.8968	14.1	2.52	0.00%	0.8968	10.8	1.93	0.00%
A2-4-10-3-3-3	0.9066	7.5	0.9066	13.2	1.76	0.00%	0.9066	10.6	1.41	0.00%
A2-4-10-3-3-4	0.9102	8.3	0.9102	15.2	1.83	0.00%	0.9102	12.1	1.46	0.00%
Avg.	0.8963	7.4	0.8963	13.7	1.85	0.00%	0.8963	11.9	1.61	0.00%
A3-4-10-3-3-1	0.8812	15.1	0.8812	21.2	1.40	0.00%	0.8812	15.6	1.03	0.00%
A3-4-10-3-3-2	0.8888	19.5	0.8888	21.4	1.10	0.00%	0.8888	16.3	0.84	0.00%
A3-4-10-3-3-3	0.8745	22.7	0.8745	21.6	0.95	0.00%	0.8745	15.8	0.70	0.00%
A3-4-10-3-3-4	0.8778	22.7	0.8778	21.6	0.95	0.00%	0.8778	17.1	0.75	0.00%
Avg.	0.8826	20	0.8826	21.45	1.07	0.00%	0.8826	16.2	0.81	0.00%
A2-5-15-3-3-1	0.8821	20.1	0.8821	11.4	0.57	0.00%	0.8821	10.8	0.54	0.00%
A2-5-15-3-3-2	0.8797	22.2	0.8797	11.9	0.54	0.00%	0.8797	10.1	0.45	0.00%
A2-5-15-3-3-3	0.8971	22.8	0.8971	10.6	0.46	0.00%	0.8971	10.9	0.48	0.00%
A2-5-15-3-3-4	0.9052	23.3	0.9052	12.1	0.52	0.00%	0.9052	11.9	0.51	0.00%
Avg.	0.889	22.1	0.889	11.5	0.52	0.00%	0.889	10.8	0.49	0.00%
A3-5-15-3-3-1	0.8977	32.4	0.8977	22.4	0.69	0.00%	0.8977	18.2	0.56	0.00%
A3-5-15-3-3-2	0.8959	29.6	0.8959	22.8	0.77	0.00%	0.8959	17.9	0.60	0.00%
A3-5-15-3-3-3	0.8992	25.3	0.8992	24.7	0.98	0.00%	0.8992	19.7	0.78	0.00%
A3-5-15-3-3-4	0.9013	35.1	0.9013	24.7	0.70	0.00%	0.9013	19.7	0.56	0.00%
Avg.	0.8983	30.6	0.8983	23.3	0.76	0.00%	0.8983	18	0.59	0.00%

Note: (1) ${\mathrm{f}}_{\mathrm{C}},{\mathrm{f}}_{\mathrm{R}},{\mathrm{f}}_{\mathrm{G}}$ denote the objective values solved by the CPLEX, VNS-R, and VNS-G algorithms; (2) ${\mathrm{T}}_{\mathrm{C}},{\mathrm{T}}_{\mathrm{R}},{\mathrm{T}}_{\mathrm{G}}$ denote the time consumed by the solution of CPLEX, VNS-R, and VNS-G algorithms; (3) ${\mathrm{G}\mathrm{A}\mathrm{P}}_{\mathrm{R}}=\left({\mathrm{f}}_{\mathrm{C}}-{\mathrm{f}}_{\mathrm{R}}\right)/{\mathrm{f}}_{\mathrm{C}}$; ${\mathrm{G}\mathrm{A}\mathrm{P}}_{\mathrm{G}}=\left({\mathrm{f}}_{\mathrm{C}}-{\mathrm{f}}_{\mathrm{G}}\right)/{\mathrm{f}}_{\mathrm{C}.}$

and

Table 5. Comparison of the two algorithms and CPLEX in the medium-sized case.

Case ID	CPLEX		VNS-R		Comparison		VNS-G		Comparison
	${\mathit{f}}_{\mathit{C}}$	${\mathit{T}}_{\mathit{C}}$	${\mathit{f}}_{\mathit{R}}$	${\mathit{T}}_{\mathit{R}}$	$\frac{{\mathit{T}}_{\mathit{R}}}{{\mathit{T}}_{\mathit{C}}}$	${\mathit{G}\mathit{A}\mathit{P}}_{\mathit{R}}$	${\mathit{f}}_{\mathit{G}}$	${\mathit{T}}_{\mathit{G}}$	$\frac{{\mathit{T}}_{\mathit{G}}}{{\mathit{T}}_{\mathit{C}}}$	${\mathit{G}\mathit{A}\mathit{P}}_{\mathit{G}}$
A5-5-20-3-3-1	0.8997	326.8	0.8997	103.8	0.32	0.00%	0.8997	59.6	0.18	0.00%
A5-5-20-3-3-2	0.8984	278.7	0.8984	98.6	0.35	0.00%	0.8984	54.4	0.20	0.00%
A5-5-20-3-3-3	0.8932	263.6	0.8932	97.3	0.37	0.00%	0.8932	57.6	0.22	0.00%
A5-5-20-3-3-4	0.9047	287.3	0.9047	105.9	0.37	0.00%	0.9047	61.6	0.21	0.00%
Avg.	0.899	289.1	0.899	101.4	0.35	0.00%	0.899	58.3	0.20	0.00%
A5-10-25-3-3-1	0.8779	783.8	0.8779	111.3	0.14	0.00%	0.8779	57.4	0.07	0.00%
A5-10-25-3-3-2	0.8699	812.1	0.8699	105.6	0.13	0.00%	0.8699	62.4	0.08	0.00%
A5-10-25-3-3-3	0.8322	804.1	0.8211	104.1	0.13	1.33%	0.8322	57.5	0.07	0.00%
A5-10-25-3-3-4	0.8484	798.8	0.8363	115.4	0.14	1.43%	0.8392	57.5	0.07	1.08%
Avg.	0.8571	799.7	0.8513	109.1	0.14	0.68%	0.8548	58.7	0.07	0.27%
A5-15-30-3-3-1	0.8447	2224.2	0.8311	129.5	0.06	1.61%	0.8447	59.2	0.03	0.00%
A5-15-30-3-3-2	0.8515	2483.5	0.8379	112.3	0.05	1.60%	0.8503	67.7	0.03	0.14%
A5-15-30-3-3-3	0.8442	2560.7	0.8376	116.4	0.05	0.78%	0.8442	58.8	0.02	0.00%
A5-15-30-3-3-4	0.8612	2760.4	0.8486	125	0.05	1.46%	0.8452	64.1	0.02	1.86%
Avg.	0.8504	2507.2	0.8388	120.8	0.05	1.36%	0.8461	62.45	0.02	0.51%

Note: (1) ${\mathrm{f}}_{\mathrm{C}},{\mathrm{f}}_{\mathrm{R}},{\mathrm{f}}_{\mathrm{G}}$ denote the objective values solved by the CPLEX, VNS-R, and VNS-G algorithms; (2) ${\mathrm{T}}_{\mathrm{C}},{\mathrm{T}}_{\mathrm{R}},{\mathrm{T}}_{\mathrm{G}}$ denote the time consumed by the solution of CPLEX, VNS-R, and VNS-G algorithms; (3) ${\mathrm{G}\mathrm{A}\mathrm{P}}_{\mathrm{R}}=\left({\mathrm{f}}_{\mathrm{C}}-{\mathrm{f}}_{\mathrm{R}}\right)/{\mathrm{f}}_{\mathrm{C}}$; ${\mathrm{G}\mathrm{A}\mathrm{P}}_{\mathrm{G}}=\left({\mathrm{f}}_{\mathrm{C}}-{\mathrm{f}}_{\mathrm{G}}\right)/{\mathrm{f}}_{\mathrm{C}.}$

show the experimental results for the small- and medium-sized algorithms, respectively. Here, the variable Z represents the valuation of the objective function, while T refers to the computational time of the algorithm. The subscripts C, R, and G correspond to the three solution methods, i.e., CPLEX, VNS-R, and VNS-G, respectively. The GAP metric in the table is used to quantify the deviation between the solution obtained by the algorithm and the exact solution of CPLEX, which is calculated as $\left(f_C-f\right)/f_C$. Here, the subscripts C, R, and G also refer to the CPLEX, VNS-R, and VNS-G algorithms, respectively. According to the test data, neither algorithm terminates the iterative process when the preset maximum number of iterations is reached or when no further exploration for a better solution is possible.

In Table 4, this study conducts an exhaustive test on 6 out of 18 sets of small-scale arithmetic cases and compares the performance of three different algorithms in terms of solution and computation time. The meanings of the algorithm IDs A2-3-5-3-3-1 are as follows: two supply points, three emergency warehouses, five affected points, three different sizes of warehouses with different capacities, three different types of emergency supplies, and the index of the calculated cases. The difference between the four cases in each group of scales lies mainly in the stochastic demand of supplies at the affected points. The CPLEX method solves the model directly, whereas the other two methods, VNS-R and VNS-G, search for the best solution. As shown in Table 4, both heuristic algorithms found the same solution as CPLEX. In all 24 cases, the average difference in the incumbent solutions is 0.0%, showing the very high solution quality of the VNS-R and VNS-G algorithms. In terms of computation time, CPLEX shows great efficiency when dealing with small-scale cases, with a solution time of less than 10 s for CPLEX when the case size contains only 5 scenarios, while the solution time of VNS-R and VNS-G is more than 10 s. However, as the case size increases, the VNS-R and VNS-G algorithms begin to outperform CPLEX. With the case configuration of 4 candidate warehouses, 10 affected regions, and more than 10 scenarios, both VNS-R and VNS-G can complete the computation in about 25 s, with VNS-G having a slightly better solving speed and being able to keep the solving time under 20 s. In contrast, the solution time of CPLEX gradually decreases.

Table 5 shows the experimental results for medium-sized arithmetic cases, in which 12 configurations from three sets of arithmetic cases are selected in this study and combined with other relevant parameters. The VNS-R and VNS-G algorithms significantly outperform CPLEX in terms of solution time for medium-sized problems. For medium-sized problems, CPLEX appears to be time-consuming in finding the incumbent solution. In the first set of examples, A5-5-20-3-3-1, A5-5-20-3-3-2, A5-5-20-3-3-3, and A5-5-20-3-3-4, the solution time of CPLEX is about three times that of VNS-R and five times that of VNS-G. This time gap is further widened in the following two sets of examples due to the exponential increase in the solution time of CPLEX. In terms of solution quality, the VNS-R and VNS-G algorithms are able to find the best solution matching CPLEX in most cases. Only in a few cases was the incumbent solution not reached, but the average difference was still less than 2 per cent. This finding confirms that the VNS-R and VNS-G algorithms developed in this study can improve the efficiency of solving complex models while ensuring the accuracy of the solutions. VNS-G demonstrates better performance than VNS-R in terms of solution quality and solution time. This result is consistent with the findings of other researchers. In the application of the mixed-integer programming model, VNS-G outperforms VNS-R in overall performance, especially in the location allocation problem in supply chain management, where VNS-G not only exhibits better behavioral characteristics but also requires less solution time.

5.2. Large-Scale Experiments

In order to verify the effectiveness of the VNS-R and VNS-G algorithms proposed in this study in depth, we conducted extended tests on the value of the schemes. Most of the variables in

Table 6. Comparison of the two algorithms and CPLEX in large-scale cases.

Case ID	CPLEX		VNS-R		VNS-G		Comparison
	${\mathit{f}}_{\mathit{C}}$	${\mathit{T}}_{\mathit{C}}$	${\mathit{f}}_{\mathit{R}}$	${\mathit{T}}_{\mathit{R}}$	${\mathit{f}}_{\mathit{G}}$	${\mathit{T}}_{\mathit{G}}$	$\frac{{\mathit{T}}_{\mathit{R}}}{{\mathit{T}}_{\mathit{G}}}$	${\mathit{G}\mathit{A}\mathit{P}}_{\mathit{G}\mathit{R}}$
A10-10-40-3-3-1	-	>7200	0.8225	1886.8	0.8325	1186.8	1.59	1.20%
A10-10-40-3-3-2	-	>7200	0.8123	1788.7	0.8422	1188.7	1.50	3.55%
A10-10-40-3-3-3	-	>7200	0.8099	1906.6	0.8399	1206.2	1.58	3.57%
A10-10-40-3-3-4	-	>7200	0.8245	1906.3	0.8514	1087.5	1.75	3.16%
Avg.	-	>7200	0.8173	1872.1	0.8415	1167.3	1.60	2.88%
A10-10-40-3-3-1	-	>7200	0.8122	2084.9	0.8322	1584.6	1.32	2.40%
A10-10-40-3-3-2	-	>7200	0.8187	2030.4	0.8387	1430.2	1.42	2.38%
A10-10-40-3-3-3	-	>7200	0.8012	2017.6	0.8212	1577.6	1.28	2.44%
A10-10-40-3-3-4	-	>7200	0.8271	2118.7	0.8411	1442.4	1.47	1.66%
Avg.	-	>7200	0.8148	2062.9	0.8333	1508.7	1.37	2.22%
A10-10-50-3-3-1	-	>7200	0.8191	1925.8	0.8511	1225.8	1.57	3.76%
A10-10-50-3-3-2	-	>7200	0.8191	1897.3	0.8531	1197.3	1.58	3.99%
A10-10-50-3-3-3	-	>7200	0.8101	1812.4	0.8503	1212.3	1.50	4.73%
A10-10-50-3-3-4	-	>7200	0.8073	1978.1	0.8487	1198.2	1.65	4.88%
Avg.	-	>7200	0.8139	1903.4	0.8508	1208.4	1.58	4.34%
A10-10-50-3-3-1	-	>7200	0.8099	2071.2	0.8499	1871.2	1.11	4.71%
A10-10-50-3-3-2	-	>7200	0.8304	2123.7	0.8603	1823.7	1.16	3.48%
A10-10-50-3-3-3	-	>7200	0.8209	2073	0.8509	1973	1.05	3.53%
A10-10-50-3-3-4	-	>7200	0.8484	2217.3	0.8673	1845.3	1.20	2.18%
Avg.	-	>7200	0.8274	2121.3	0.8571	1878.3	1.13	3.47%

Note: (1) ${\mathrm{f}}_{\mathrm{C}},{\mathrm{f}}_{\mathrm{R}},{\mathrm{f}}_{\mathrm{G}}$ denote the objective values solved by the CPLEX, VNS-R, and VNS-G algorithms; (2) ${\mathrm{T}}_{\mathrm{C}},{\mathrm{T}}_{\mathrm{R}},{\mathrm{T}}_{\mathrm{G}}$ denote the time consumed by the solution of CPLEX, VNS-R, and VNS-G algorithms; (3) ${\mathrm{G}\mathrm{A}\mathrm{P}}_{\mathrm{G}\mathrm{R}}={\displaystyle \frac{\left({\mathrm{f}}_{\mathrm{G}}-{\mathrm{f}}_{\mathrm{R}}\right)}{{\mathrm{f}}_{\mathrm{G}}}}.$

have the same meanings as those in Table 5. The only difference lies in the GAP metric, which represents the difference between the VNS-G and VNS-R solutions and is calculated as $(f_G-f_R)/f_G$; the subscripts R and G also refer to the VNS-R and VNS-G algorithms, respectively. It is obvious that the average computation time shows an upward trend as the scale of the algorithm increases. According to the data summarized in Table 6, CPLEX fails to find a feasible solution in 7200 s, which limits its feasibility in practical applications. When comparing these two algorithms with different initial solutions, we find that VNS-G is always able to find the same or better solutions as VNS-R. The computation time of VNS-G shows a linear increase as the size of the algorithm increases, and its performance is superior to that of CPLEX and VNS-R. This result further proves the efficiency and robustness of the VNS-G algorithm in dealing with large-scale problems and also shows that different initial solutions can affect the efficiency of the VNS algorithm.

Through the comparative analysis of VNS-G and VNS-R in different scale problems, as shown in Table 6, in the same VNS structure, the objective values (comprehensive satisfaction) solved by using the VNS-G algorithm are all better than the results of using the VNS-R algorithm ($f_G$ ≥ $f_R$), and the values of ${GAP}_{GR}$ are all controlled within 5%. Thus, we draw the following conclusions:

(1)

A well-designed complex mixed-integer planning model plays a key role in constructing a scientific resource transmission network in the case of a sudden disaster.

(2)

A high-quality initial solution can accelerate the convergence of the algorithm. If the initial solution is already close to the incumbent solution, the VNS algorithm may only need a small number of local search and perturbation steps to reach the incumbent or near-incumbent solution.

(3)

By optimizing the resource allocation and transmission strategies, the model aims to maximize the overall satisfaction and ensure that the demand in each affected region is fully satisfied.

(4)

The quality of the initial solution directly affects the quality of the final solution, and a good initial solution can improve the optimization of the final solution, especially in problems with a large solution space and high search difficulty.

(5)

Different initial solutions may cause the algorithm to take different paths in the search process, and a stable initial solution can make the algorithm produce more consistent results in multiple runs. In the VNS algorithm, the initial solution generated by the greedy algorithm usually provides a starting point that is closer to the incumbent solution because it is based on locally incumbent decisions. Such an initial solution helps the VNS algorithm to explore the solution space more efficiently during subsequent searches, which may increase the probability of finding a globally incumbent solution.

6. Sensitivity Analysis

The optimization of emergency rescue systems is influenced by variations in multiple parameters. To explore the impact of these changes, we conducted a sensitivity analysis of the total budget, number of repair teams, and demand coefficient. The configurations A3-5-15-3-3, A5-5-20-3-3, and A10-10-40-3-3 represent small, medium, and large instances, respectively. Beyond comparing changes in objective function values based on sensitivity analysis, we also documented variations in different metrics of the obtained solutions, particularly those reflecting service quality: service coverage and average delay time.

6.1. Analysis of Total Budget Impact on Decision-Making

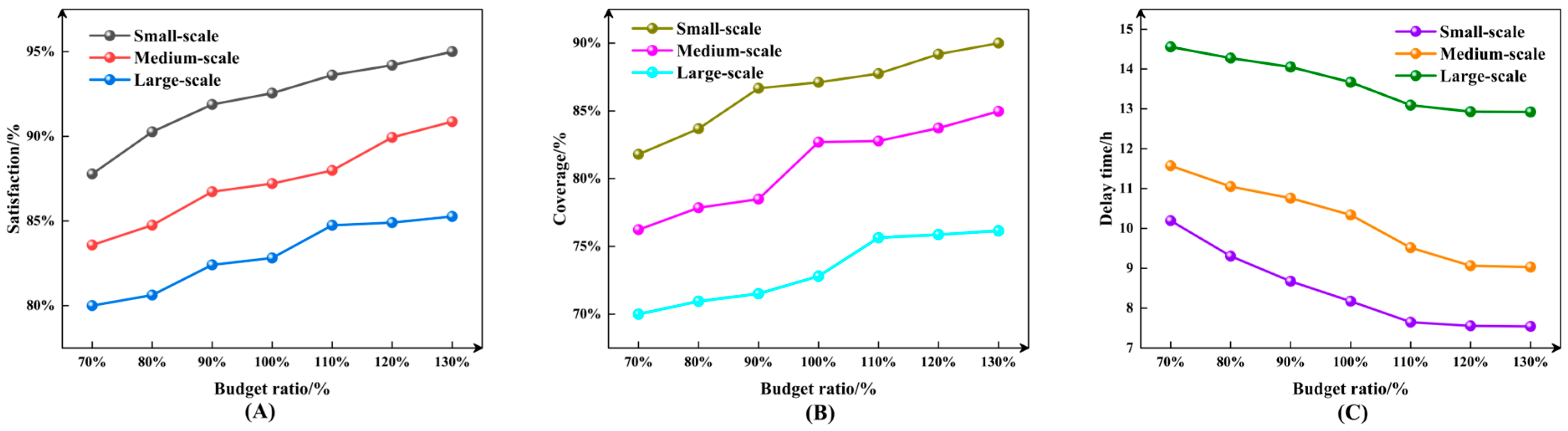
The first sensitivity analysis examines the influence of the system’s total budget. To evaluate the impact of the total budget on various metrics, this section conducts sensitivity analysis using different total budgets. Based on the selected calculation examples, the budget proportion for each example is scaled. By uniformly increasing the C parameter representing the total budget for each scaled example, the changes in the target value f (comprehensive satisfaction), service coverage rate, and average delay time are analyzed. The results are shown inFigure 7.

As shown in Figure 7A–C, sensitivity analysis of budget variations reveals that increasing the budget generally enhances the overall satisfaction and service coverage of the emergency rescue system while effectively reducing the average delay time. However, improvements in all performance metrics exhibit diminishing marginal returns, meaning that beyond 1.1 times the baseline budget, the rate of benefit growth slows significantly. The analysis also reveals pronounced scale differences: the small-scale case study (A3-5-15-3-3) exhibits incumbent absolute performance and the highest sensitivity to budget changes (delay reduction up to 26%), while the medium-scale scenario (A5-5-20-3-3) shows the greatest magnitude of performance improvement. Conversely, the large-scale scenario (A10-10-40-3-3) exhibits a relatively sluggish response and requires substantially higher budgets to achieve noticeable gains. Collectively, these findings indicate that budget allocation strategies should prioritize small-to-medium-scale emergency scenarios and maintain budgets within the 1.0–1.1 times benchmark range to achieve incumbent cost-effectiveness.

6.2. Sensitivity Analysis of the Number of Repair Teams

To examine the impact of the number of repair teams on the target value $f$ (overall satisfaction), this section conducts a sensitivity analysis using a different number of repair teams. Under the same case study scale, it analyzes changes in the target value f (overall satisfaction), service coverage rate, and average delay time. The results are shown in Figure 8.

As shown in Figure 8, the impact of the number of repair teams on the performance of emergency systems of varying scales is revealed, characterized by pronounced scale effects and diminishing marginal returns. Emergency systems of different scales exhibit distinctly different responses to variations in the number of repair teams. As illustrated in Figure 8A, small-scale experiments demonstrate highly sensitive responses. Increasing teams from 1 to 4 reduces the delay time by 40% (from 14.73 h to 8.83 h) while steadily improving satisfaction and coverage. This indicates that adding teams directly and effectively resolves bottlenecks in small systems. As shown in Figure 8B, medium-scale experiments exhibit noticeable responses but face a threshold for activation. Increasing teams from 2 to 5 reduced latency by 24.5% (from 14.87 h to 11.22 h), with satisfaction and coverage showing significant improvement only after reaching 4 teams. This indicates that a critical mass of teams is required for noticeable effects. As shown in Figure 8C, the large-scale case exhibited sluggish response with the fastest diminishing returns. Increasing teams from 3 to 7 reduced latency by only 17.8% (from 16.61 h to 13.66 h), with minimal gains in satisfaction and coverage. This suggests that for large and complex networks, adding repair teams alone yields limited overall performance improvements, potentially requiring more comprehensive optimization. All systems exhibit diminishing marginal returns. As the number of teams increases, the performance improvement per additional team—particularly in reducing the delay time—gradually diminishes. For instance, in small systems, adding the second team slashes the delay by nearly 3 h, while the fourth team contributes less than 1.3 h of reduction. The number of repair teams directly determines the road network’s capacity, making its impact on delay time the most immediate and significant. Satisfaction and coverage rates exhibit relatively delayed responses to the number of teams, especially in medium-to-large systems. These metrics typically begin improving only after reaching a “critical threshold” (e.g., 4 teams in the medium-scale simulation), indicating that overall logistics efficiency undergoes qualitative improvement only after critical paths are cleared.

The impact of the number of repair teams on emergency system performance exhibits pronounced scale effects and diminishing marginal returns: small systems respond most sensitively, where increasing teams from 1 to 4 drastically reduces delay by 40% while simultaneously boosting satisfaction and coverage. Medium-sized systems face a noticeable activation threshold, requiring 4–5 teams to achieve a 24.5% delay reduction and performance enhancement. Large systems respond relatively sluggishly, where increasing teams from 3 to 7 yields only a 17.8% delay improvement with minimal satisfaction growth. This indicates that adding repair teams significantly benefits small-to-medium systems, but complex large systems require complementary optimization strategies. All systems exhibit diminishing returns with each additional team.

6.3. Analysis of Demand Coefficient Impact on Decision-Making

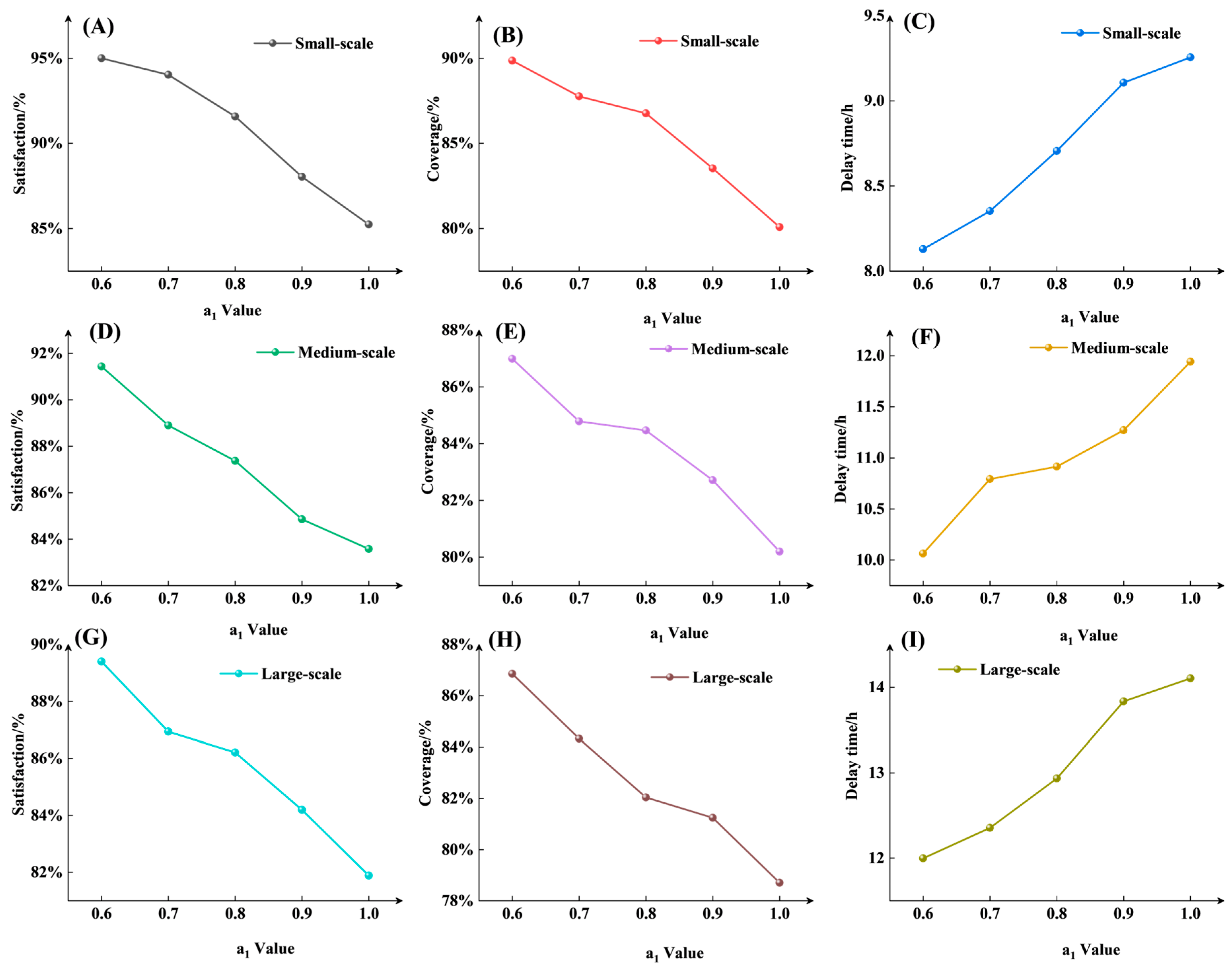
To examine the influence of the minimum demand coefficient a₁ at the disaster-affected point on the objective value f (comprehensive satisfaction), this section analyzes changes in $f$ (comprehensive satisfaction), service coverage rate, and average delay time under different calculation scenarios. The results are shown in Figure 9.

As shown in Figure 9, sensitivity analysis of variations in the minimum demand coefficient ($a_1$) reveals that this coefficient exerts a systemic influence on the performance of the emergency rescue system. As depicted in Figure 9A,D,G, increasing $a_1$ from 0.6 to 1.0 leads to a decline in overall satisfaction across all scaled experiments. Satisfaction only exhibits a significant surge once the number of teams exceeds a critical threshold. This indicates that a certain scale of team deployment is necessary to effectively initiate and substantially enhance rescue outcomes. As depicted in Figure 9B,E,H, the three coverage rate line charts similarly exhibit consistent downward trends, with patterns highly analogous to the satisfaction curves. This occurs because the coverage rate forms a crucial foundation for satisfaction; the inability to meet higher demand standards inevitably reduces the number of disaster points that can be covered. The charts reveal that no system size achieves 100% coverage, with all falling to approximately 0.8 or lower under the highest standard ($a_1$ = 1.0). This visually demonstrates that pursuing 100% fulfillment of all disaster sites’ maximum demands is unrealistic in emergency logistics, ultimately diminishing the system’s overall coverage efficiency. As shown in Figure 9C,F,I, the three delay timeline charts exhibit a clear upward trend. This represents one of the most critical findings of this analysis: increasing demand standards directly leads to higher average system delay times. The delay curves for large-scale systems consistently occupy the highest positions, with their deterioration (slope) becoming more pronounced as $a_1$ increases. This further demonstrates the vulnerability of large-scale systems when confronting high-standard demands. All trendlines converge on the same conclusion: setting the minimum demand coefficient $a_1$ constitutes a critical strategic decision. Higher a_1 values come at the cost of reduced overall system efficiency (decreased satisfaction and coverage) and performance (increased latency).

7. Conclusions

This study constructs a secondary emergency relief network model that takes road rehabilitation into account and aims to optimize the efficiency of emergency material distribution. This study proposes a material distribution model with the optimization objective of comprehensive satisfaction in the context of uncertainty in demand and transport time. In this study, the VNS-R and VNS-G algorithms are used to solve the model, and the effects of different initial solutions on the performance of the VNS algorithm are analyzed. The results of the algorithms show that the initial solution quality of the VNS-G algorithm is better than that of the VNS-R algorithm, and both algorithms are able to solve the large-scale problem efficiently in a reasonable time. We summarize the following literature contributions.

(1)

Distribution and scheduling decisions in emergency logistics are closely related. Arranging distribution vehicles according to specific demands and deploying them from supply points and emergency warehouses to reach the disaster-stricken points usually needs to be synchronized with scheduling optimization to ensure that sufficient transport resources are available to meet the demands. Therefore, our model aims to solve an emergency logistics distribution and scheduling problem involving long- and short-term discontinuities. This study takes into account more uncertainties in real-world environments than the existing literature, especially the special needs of emergency logistics and distribution. We also consider the stochastic nature of the location and time of the disaster, the uncertain demand for various emergency supplies, and the uncertainty of the status of the distribution paths between the supply points, emergency warehouses, and the disaster sites.

(2)

The relationship between the VNS algorithmic process and the model characteristics needs to be emphasized when developing the model solution tool. Since the decision variables in the two stages of the model interact with each other, in the VND process, we nested the neighborhood structure of decision variables belonging to different stages. Unlike the independent neighborhood structures in most studies, this method effectively prevents the algorithm from losing potential incumbent solutions in the local search. The numerical experimental results show that the solution time of the VNS-G algorithm is reduced by about 30% compared to the VNS-R algorithm, and it is more effective.

(3)

We conducted a comprehensive sensitivity analysis to reveal how different parameters are influenced by the total budget C, the number of repair teams r, and the minimum demand coefficient at affected points. This analysis provides valuable insights for practical management. Specifically, to reduce rescue costs, road rescue managers should rationally allocate material supplies and ensure the number of repair teams aligns with the minimum demand coefficient at affected points. Furthermore, they should recognize that determining the number of repair teams and scheduling arrangements requires balancing economic efficiency (i.e., controlling total budget C) with timeliness (i.e., enhancing affected site satisfaction and demand response speed). The marginal effect of additional resources (such as repair teams and supplies) diminishes progressively until it reaches zero.

This study has some limitations. Scenario-based optimization requires identifying the location and rescue needs of each accident-prone roadway in order to build the scenarios. In future studies, attempts should be made to consider robust optimization under dynamic road conditions. In this paper, the focus of solving the emergency logistics and distribution problem, considering road conditions, is to define a suitable uncertainty set for different hazards. The model can be applied to situations where there are not enough data to calibrate the stochastic planning model. In addition, although we extend our model to cases where extreme disasters may arise dynamically to propose a simple dynamic scheduling mechanism in the future, alternative approaches, such as predictive path algorithms, can be used to improve the performance of emergency logistics distribution in real-world environments. The capability of material supply services is crucial in the emergency response system. Future research could focus on the integration of emergency material supply and distribution and explore the application of multimodal transport modes such as helicopters, drones, and vehicles. In addition, in emergency rescue operations, there may be contradictions between objectives, such as the shortest transport time, the lowest cost, and the maximum coverage. Future research could be devoted to the trade-off problem in multi-objective optimization, aiming to achieve rapid response and maximize the effect of emergency rescue based on a careful consideration of various factors.