Dual-Layer Optimization Control for Furnace Temperature Setting and Tracking in Municipal Solid Waste Incineration Process
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
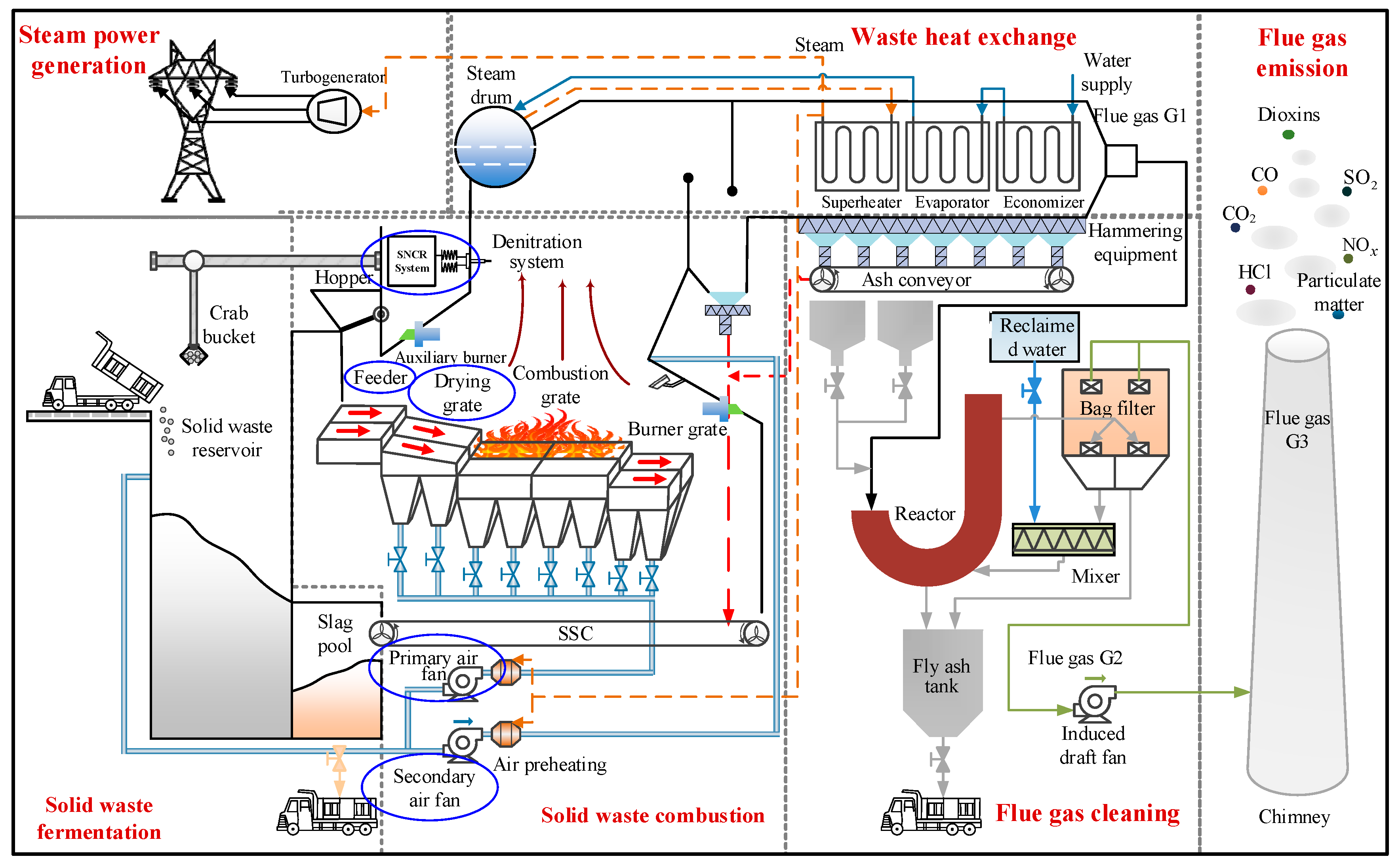
2.1.1. Description of the MSWI Process
2.1.2. Optimization Control Characteristics Analysis
Optimization Control Analysis for Minimizing Pollutant Emission Concentrations
Optimization Control Analysis for Minimizing FT Tracking Performance
Control Performance Evaluation Indicators
2.1.3. Description of Experimental Data
2.2. Methods
- (1)
- Difficulty in setpoint optimization: Determining the optimal FT setpoints that minimize combined emissions of NOx and CO2 is difficult, and external condition changes (such as seasonal climate fluctuations) cause variations in output, which affects manual adjustments;
- (2)
- Difficulty in control parameter tuning: Multi-loop PID controllers have strong parameter coupling, making manual tuning inefficient and unable to guarantee tracking performance. Additionally, internal factors (such as waste calorific value changes) result in discrepancies between the controlled object model and the actual process, preventing dynamic adjustment of model parameters to adapt to changes in system characteristics;
- (3)
- Difficulty in judgment and coordination between the two layers: Current offline optimization methods cannot adapt to changes in the actual control process, leading to suboptimal optimization results. Furthermore, unnecessary repeated optimizations between layers cause computational resource waste.
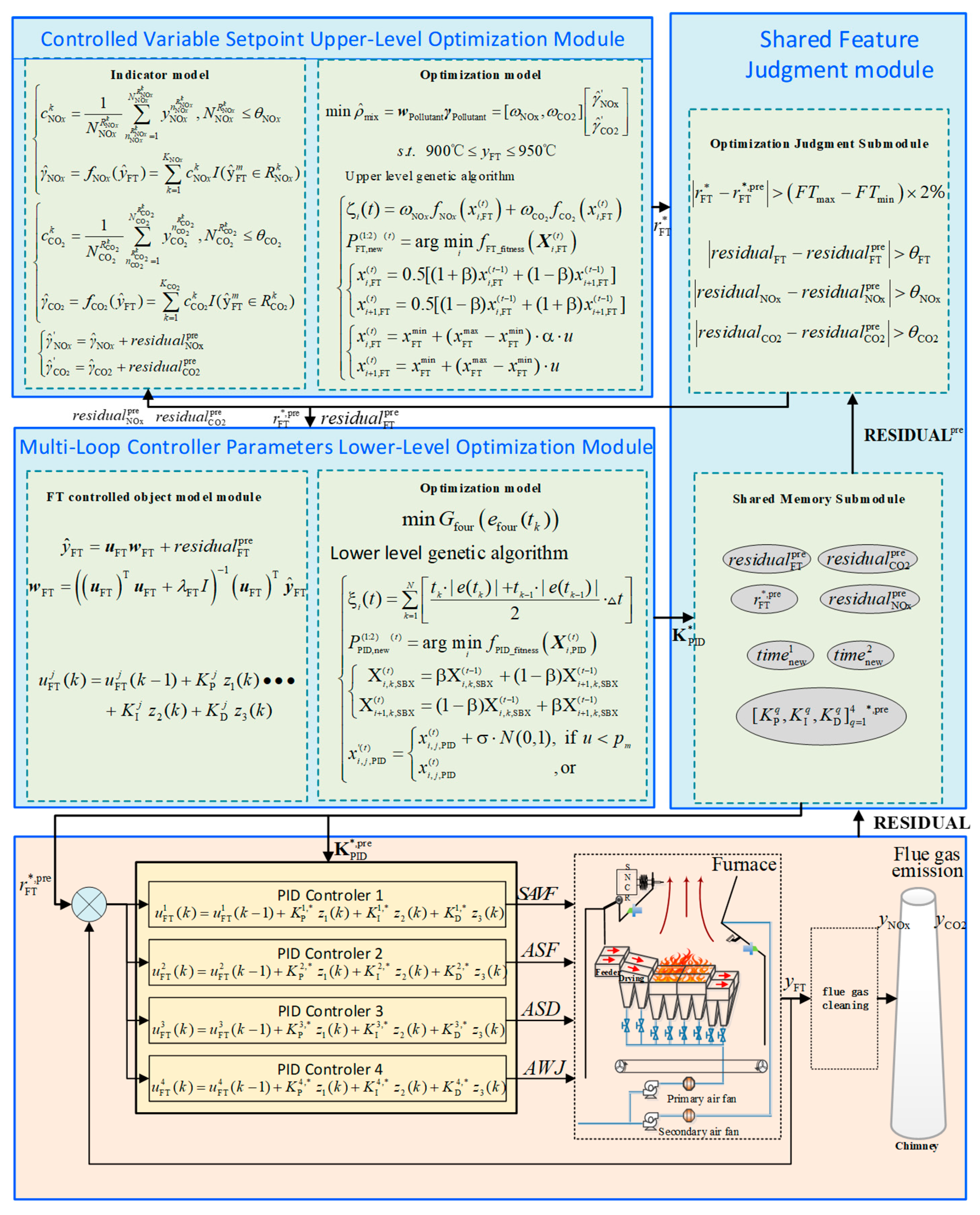
- (1)
- Controlled Variable Setpoint Upper-Level Optimization Module: The optimal FT setpoint () that minimizes pollutant concentration is solved using the genetic algorithm (GA), based on the pollutant emission model.
- (2)
- Multi-Loop Controller Parameters Lower-Level Optimization Module: The optimal multi-loop PID parameters () are determined using GA, with as input and the goal of minimizing ITAE, achieving rapid and precise setpoint tracking.
- (3)
- Shared Feature Judgment module: Shared memory is used as the parameter transmission medium between the optimization layer and the control layer, and the decision to execute the optimization program again is made based on intermediate parameters.
2.2.1. Controlled Variable Setpoint Upper-Level Optimization Module
- (1).
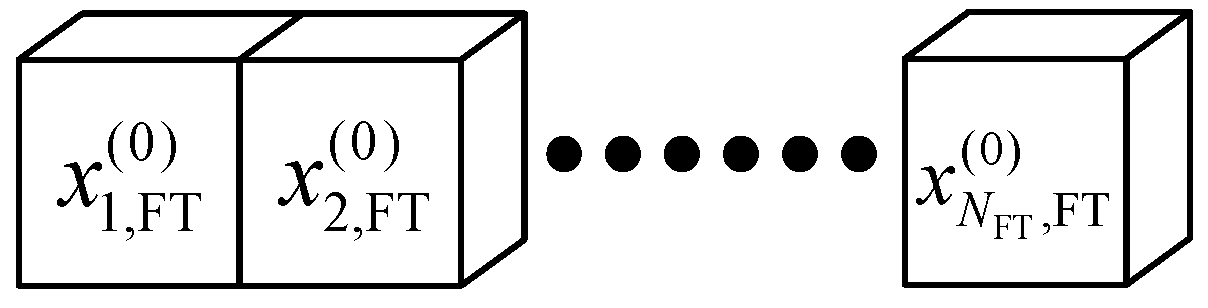
- Initialization of the population
- (2).
- Fitness function design
- (3).
- Selection operator
- (4).
- Crossover Operator
- (5).
- Mutation Operator
2.2.2. Multi-Loop Controller Parameters Lower-Level Optimization Module
- (1).
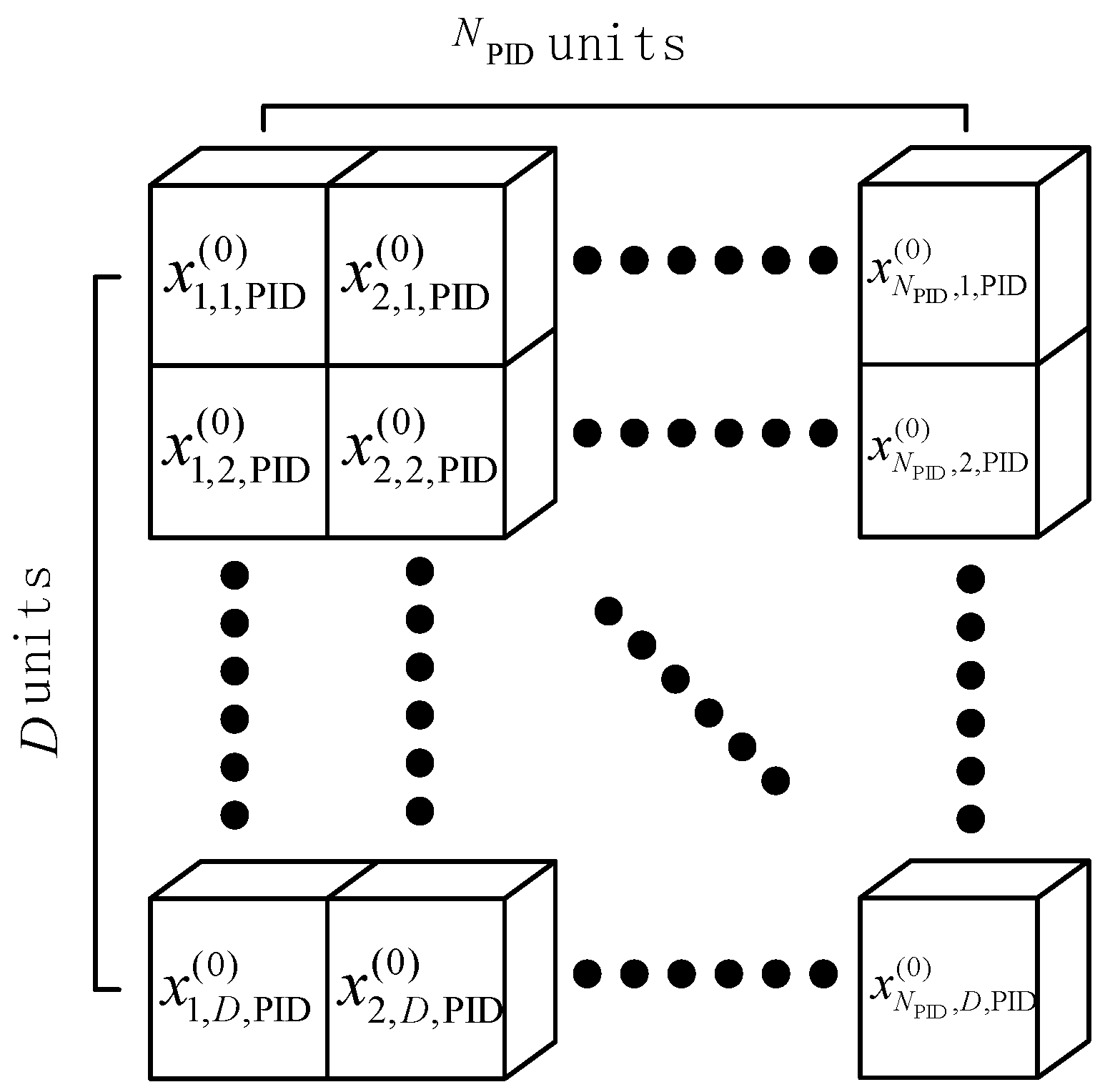
- Initialization of the population
- (2).
- Fitness function design
- (3).
- Selection Operator
- (4).
- Crossover Operator
- (5).
- Mutation Operator
2.2.3. Shared Feature Judgment Module
Optimization Judgment Submodule
2.2.4. Pseudocode
Upper-Level Optimization Algorithm
| Algorithm 1: Upper-Level Optimization Algorithm | |
| Input: | Population size , maximum iterations , crossover rate , mutation rate , model historical residual value , ; |
| Step 1: | Initialize the algebraic counter , randomly generate the initial population individual genes according to Formula (12), and finally produce the upper-level initial population ; |
| Step 2: | Calculate the fitness of the initial population according to Equations (13) and (14); |
| Step 3: | Record the current optimal solution of the population and save it as the global best individual; |
| Step 4: | Iteration begins, while ; |
| Step 5: | Use tournament selection to choose parent individuals from the current population; |
| Step 6: | According to Formulas (16) and (17), for the selected parent individuals, simulation two is performed with probability ; |
| Step 7: | Perform crossover; according to Formulas (18) and (19), for the individuals after crossover, execute the hybrid mutation operation with probability ; |
| Step 8: | Calculate the fitness of the new population according to Equations (13) and (14); |
| Step 9: | if global optimal individual fitness < new population worst individual fitness; |
| Step 10: | The globally optimal individual replaces and eliminates the worst individual in the new population; |
| Step 11: | end if; |
| Step 12: | If the fitness of the new population’s optimal individual < the fitness of the global optimal individual; |
| Step 13: | Save the best individual in the new population to the global best individual; |
| Step 14: | end if; |
| Step 15: | end while; |
| Output: | The optimal FT setting . |
Lower-Level Optimization Algorithm
| Algorithm 2: Lower-Level Optimization Algorithm | |
| Input: | Population size , maximum number of iterations , crossover rate , mutation rate , model historical residual value ; the historically optimal |
| Step 1: | Initialize the algebraic counter , randomly generate the initial population individual genes according to Formula (22), and finally produce the initial lower-level population ; |
| Step 2: | Calculate the fitness of the initial population according to Equations (23) and (24); |
| Step 3: | Record the current optimal solution of the population and save it as the global best individual; |
| Step 4: | Iteration begins, while ; |
| Step 5: | Using tournament selection and elitist selection according to Formula (25), select parent individuals from the current population; |
| Step 6: | According to Formulas (26) and (27), for the selected parent individuals, perform grouping simulation binary crossover with probability . |
| Step 7: | According to Equations (28) and (29), adaptive Gaussian mutation is performed on the crossed individuals with a probability of . |
| Step 8: | Calculate the fitness of the new population according to Equations (23) and (24); |
| Step 9: | If optimal individual fitness of the new population< global optimal individual fitness; |
| Step 10: | Save the optimal individual from the new population as the global optimal individual; |
| Step 11: | end if |
| Step 12: | If fitness reaches the threshold |
| Step 13: | break while |
| Step 14: | end if |
| Step 15: | end while |
| Output: | The optimal PID parameter settings value for this optimization. |
3. Results
3.1. Parameter Settings
3.2. Experimental Results
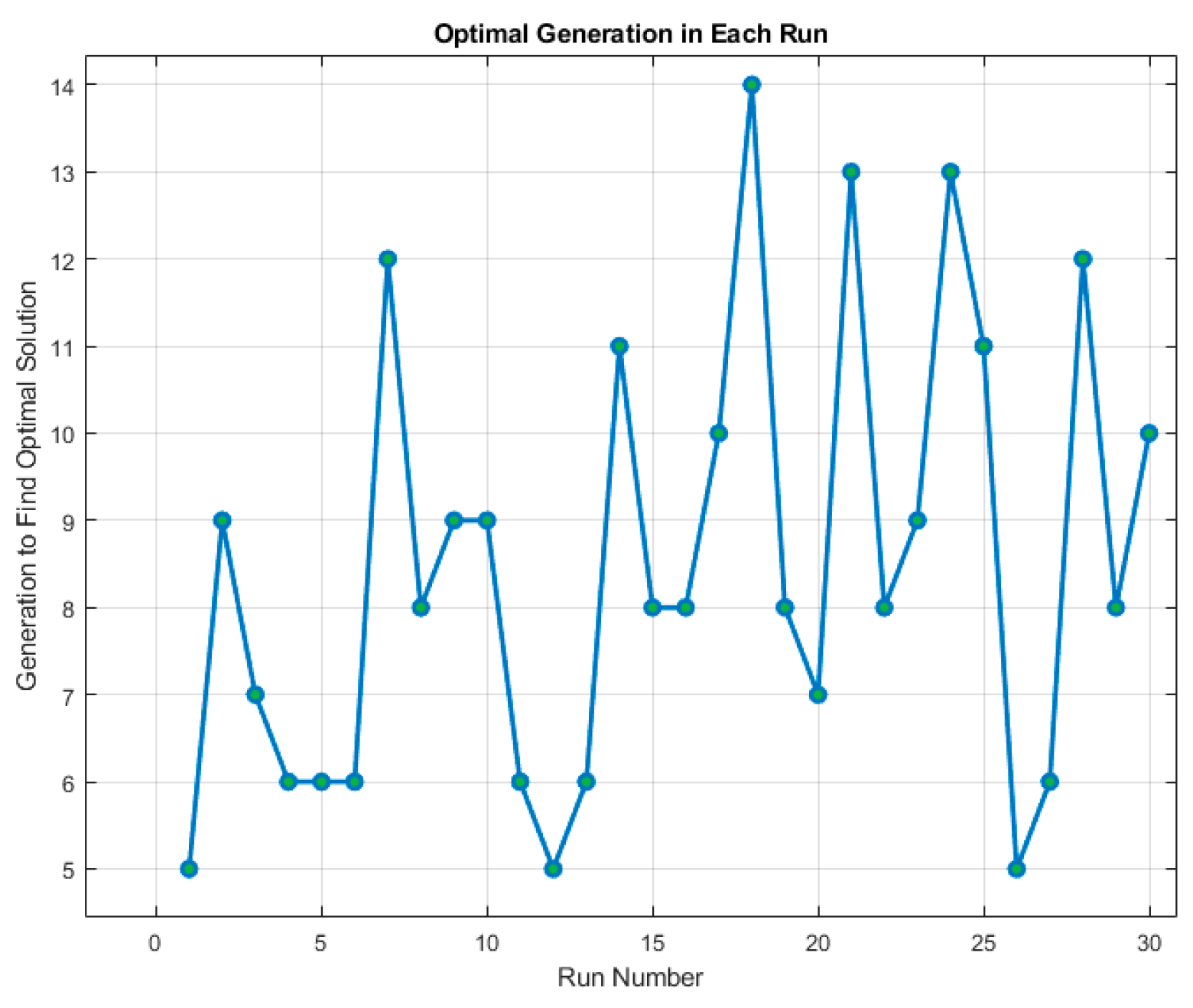
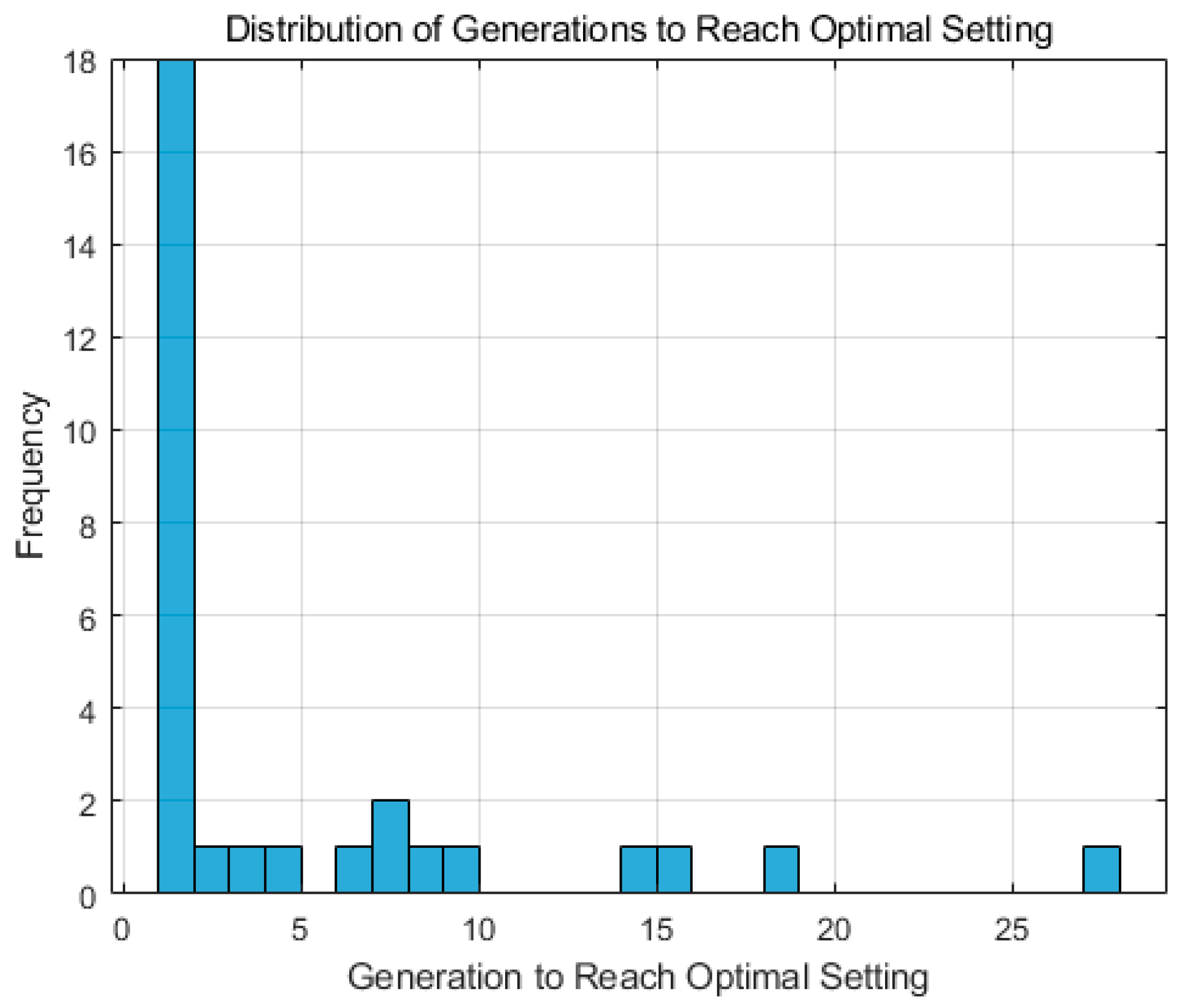
3.2.1. Upper-Layer GA Optimization Results
3.2.2. Lower-Level GA Optimization Results
3.2.3. Shared Judgment Results
3.3. Method Comparison
3.3.1. PID Performance Perspective
3.3.2. Pollutant Emissions Perspective
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MSW | Municipal solid waste |
| MSWI | Municipal solid waste incineration |
| FT | FT |
| ITAE | Integral of Time-weighted Absolute Error |
| GA | Genetic algorithm |
| IMOPSO | Improved multi-objective particle swarm optimization |
| ALMOCSO | Adaptive large-scale multi-objective competitive swarm optimization algorithm |
| PID | Proportional-Integral-Derivative |
| 3T+E | Temperature, Turbulence, Time, and Excess Oxygen |
| PAVF | Primary air volumetric flowrate |
| SAVF | Secondary air volumetric flowrate |
| ASF | Average speed of the feeder grate |
| ASD | Average speed of the drying grate |
| AWJ | Ammonia water injection |
| SNCR | Selective Non-Catalytic Reduction |
| TR-LRDT | Tikhonov regularization-least regression decision tree |
| CART | Classification and regression tree |
| SBX | Simulated binary crossover |
Appendix A
| Num | Symbol | Actual Meaning |
|---|---|---|
| 1. | Objective function vector | |
| 2. | The l-th indicator model | |
| 3. | Equality constraint | |
| 4. | Inequality constraint | |
| 5. | Decision variable vector | |
| 6. | Pollutant emission concentration unitless vector | |
| 7. | The n-th pollutant model normalized output | |
| 8. | The combined pollutant emission concentration | |
| 9. | Weight vector | |
| 10. | Compensated pollutant emission concentration output unitless vector | |
| 11. | Weight of the emission concentration of the n-th pollutant | |
| 12. | Compensated emission model normalized output of the n-th pollutant | |
| 13. | Normalized compensation value of the n-th pollutant model | |
| 14. | Optimal FT setpoint for minimum pollutant concentration | |
| 15. | Historical optimal FT setpoint for minimum pollutant concentration | |
| 16. | Trapezoidal method discrete time-weighted absolute error integral function | |
| 17. | Total step length of ITAE | |
| 18. | PID intelligent controller calculation process | |
| 19. | Time variable in the PID controller computation process | |
| 20. | Time step | |
| 21. | FT controlled object model | |
| 22. | The controller output value at the next time step after the PID computation of the q-th manipulated variable | |
| 23. | Optimal multivariable PID controller setpoint parameter vector | |
| 24. | Optimal multivariable PID parameters | |
| 25. | Residual value unitless vector | |
| 26. | Historical residual value unitless vector | |
| 27. | FT residual value | |
| 28. | NOx residual normalized value | |
| 29. | CO2 residual normalized value | |
| 30. | Historical FT residual value | |
| 31. | Historical NOx residual normalized value | |
| 32. | Historical CO2 residual normalized value | |
| 33. | FT residual value update threshold | |
| 34. | NOx residual value update threshold | |
| 35. | CO2 residual value update threshold | |
| 36. | Actual output value of NOx | |
| 37. | Actual output value of CO2 | |
| 38. | Actual output value of the FT | |
| 39. | Output value of the FT controlled object model | |
| 40. | Setpoint value of the secondary air volumetric flowrate rate output to the actuator after PID intelligent controller computation | |
| 41. | Setpoint value of the feeder output to the actuator after PID intelligent controller computation | |
| 42. | Setpoint value of the dryer flow rate output to the actuator after PID intelligent controller computation | |
| 43. | Setpoint value of the ammonia water injection amount output to the actuator after PID intelligent controller computation | |
| 44. | Comprehensive emission concentration of NOx and CO2 | |
| 45. | Weight vector of NOx and CO2 | |
| 46. | Output vector of the emission concentrations of NOx and CO2 | |
| 47. | Weight of NOx emission concentration | |
| 48. | Weight of CO2 emission concentration | |
| 49. | Compensated normalized output of the NOx model | |
| 50. | Compensated normalized output of the CO2 model | |
| 51. | Normalized output of the NOx model | |
| 52. | Normalized output of the CO2 model | |
| 53. | Value of the i-th individual gene (FT) in the 0th generation population (initial population) of the upper-level optimization algorithm | |
| 54. | Maximum value of the individual gene (FT) | |
| 55. | Minimum value of the individual gene (FT) | |
| 56. | Population size of the upper-level optimization algorithm | |
| 57. | Fitness of the i-th individual in the upper-level optimization algorithm at the t-th iteration | |
| 58. | FT fitness function in the upper-level optimization algorithm | |
| 59. | The -dimensional gene vector of the i-th individual at the t-th iteration, where | |
| 60. | The value of the gene (FT) of the i-th individual at the t-th iteration | |
| 61. | Normalization function of the NOx pollutant index model | |
| 62. | Normalization function of the CO2 pollutant index model | |
| 63. | Compensated NOx pollutant index model function | |
| 64. | Compensated CO2 pollutant index model function | |
| 65. | Maximum value of NOx emissions | |
| 66. | Minimum value of NOx emissions | |
| 67. | Maximum value of CO2emissions | |
| 68. | Minimum value of CO2 emissions | |
| 69. | The first two individuals in the population at the t-th iteration | |
| 70. | The two individuals that minimize the objective function | |
| 71. | FT gene of the i-th individual in the parent generation of the upper-level optimization algorithm | |
| 72. | FT gene of the (i + 1)-th individual in the parent generation of the upper-level optimization algorithm | |
| 73. | FT gene of the i-th individual in the offspring generated by the upper-level optimization algorithm | |
| 74. | FT gene of the (i + 1)-th individual in the offspring generated by the upper-level optimization algorithm | |
| 75. | Upper-level mutation decay factor | |
| 76. | Random number in the range (0, 1) | |
| 77. | Maximum number of iterations in the upper-level optimization | |
| 78. | Upper-level optimization generation count | |
| 79. | Time-weighted absolute error integral (ITAE) calculation process under the selected manipulated variable | |
| 80. | Calculation process of the PID intelligent controller under the selected manipulated variable | |
| 81. | Controlled object model under the selected manipulated variable | |
| 82. | Represents the next-time-step controller output values of the ASF, ASD, AWJ, and PAVF manipulated variables after PID calculation | |
| 83. | Value of the j-th gene (one of the parameters in the 4 PID controllers) of the i-th individual in the 0-th generation population (initial population) of the lower-level optimization algorithm | |
| 84. | Maximum value of the j-th gene of an individual in the lower-level optimization | |
| 85. | Minimum value of the j-th gene of an individual in the lower-level optimization | |
| 86. | Population size of the lower-level optimization | |
| 87. | Number of genes per individual in the lower-level optimization | |
| 88. | Fitness of the i-th individual in the t-th iteration of the lower-level optimization | |
| 89. | Multi-loop PID controller parameter gene vector of the i-th individual in the t-th generation | |
| 90. | Calculation process using the PID intelligent controller of the i-th individual in the t-th generation | |
| 91. | The first two individuals in the population of the t-th iteration | |
| 92. | The two individuals that minimize the objective function | |
| 93. | Gaussian distribution disturbance factor | |
| 94. | The k-th genome of the i-th individual in the parent generation of the lower-level optimization algorithm | |
| 95. | The k-th genome of the (i + 1)-th individual in the parent generation of the lower-level optimization algorithm | |
| 96. | The k-th genome of the i-th individual in the offspring generation produced by the lower-level optimization algorithm | |
| 97. | The k-th genome of the (i + 1)-th individual in the offspring generation produced by the lower-level optimization algorithm | |
| 98. | Mutation strength in the lower-level optimization algorithm, used as a scaling factor to control the magnitude of the random disturbance | |
| 99. | Standard normal distribution | |
| 100. | Gene before mutation in the lower-level optimization | |
| 101. | Gene after mutation in the lower-level optimization | |
| 102. | Gene after boundary reflection when it exceeds the range in the lower-level optimization | |
| 103. | The maximum value of the optimal FT setpoint | |
| 104. | The minimum value of the optimal FT setpoint | |
| 105. | The error at step | |
| 106. | The error at step |
References
- Tang, J.; Xia, H.; Yu, F.; Qiao, J. Research Status and Prospects of Intelligent Optimization Control for Municipal Solid Waste Incineration Process. Acta Autom. Sin. 2023, 49, 2019–2059. [Google Scholar] [CrossRef]
- Gómez-Sanabria, A.; Kiesewetter, G.; Klimont, Z.; Schoepp, W.; Haberl, H. Potential for Future Reductions of Global GHG and Air Pollutants from Circular Waste Management Systems. Nat. Commun. 2022, 13, 106. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Chen, J.; Cui, J.; Fan, C.; Han, W. The study on the “Risk of Garbage Surrounding Cities” in 31 Municipalities and Provincial Capitals of China and Countermeasures—An Empirical Study Based on the DIIS Method. Bull. Chin. Acad. Sci. 2019, 34, 797–806. [Google Scholar] [CrossRef]
- Vilardi, G.; Verdone, N. Exergy Analysis of Municipal Solid Waste Incineration Processes: The Use of O2-Enriched Air and the Oxy-Combustion Process. Energy 2022, 239, 122147. [Google Scholar] [CrossRef]
- Bajić, B.Ž.; Dodić, S.N.; Vučurović, D.G.; Dodić, J.M.; Grahovac, J.A. Waste-to-Energy Status in Serbia. Renew. Sustain. Energy Rev. 2015, 50, 1437–1444. [Google Scholar] [CrossRef]
- Walser, T.; Limbach, L.K.; Brogioli, R.; Erismann, E.; Flamigni, L.; Hattendorf, B.; Juchli, M.; Krumeich, F.; Ludwig, C.; Prikopsky, K.; et al. Persistence of Engineered Nanoparticles in a Municipal Solid-Waste Incineration Plant. Nat. Nanotechnol. 2012, 7, 520–524. [Google Scholar] [CrossRef]
- Chen, B.; Perumal, P.; Aghabeyk, F.; Adediran, A.; Illikainen, M.; Ye, G. Advances in Using Municipal Solid Waste Incineration (MSWI) Bottom Ash as Precursor for Alkali-Activated Materials: A Critical Review. Resour. Conserv. Recycl. 2024, 204, 107516. [Google Scholar] [CrossRef]
- Yang, D.; Kow, K.-W.; Wang, W.; Meredith, W.; Zhang, G.; Mao, Y.; Xu, M. Co-Treatment of Municipal Solid Waste Incineration Fly Ash and Alumina-/Silica-Containing Waste: A Critical Review. J. Hazard. Mater. 2024, 479, 135677. [Google Scholar] [CrossRef]
- Kammen, D.M.; Sunter, D.A. City-Integrated Renewable Energy for Urban Sustainability. Science 2016, 325, 922–928. [Google Scholar] [CrossRef]
- Kumar, A.; Samadder, S.R. A Review on Technological Options of Waste to Energy for Effective Management of Municipal Solid Waste. Waste Manag. 2017, 69, 407–422. [Google Scholar] [CrossRef]
- Long, J.; Du, H.; Zou, X.; Huang, J. A Systematic Study on Carbon Emission Reduction in Urban Household Waste Management. Bull. Chin. Acad. Sci. 2022, 37, 1143–1153. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, W.; Liu, J. Greenhouse Gas Emissions from Different Municipal Solid Waste Management Scenarios in China: Based on Carbon and Energy Flow Analysis. Waste Manag. 2017, 68, 653–661. [Google Scholar] [CrossRef]
- Asri, R.; Baxter, D. Process Control in Municipal Solid Waste Incinerators: Survey and Assessment. Waste Manag. Res. 2004, 22, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Khandelwal, H.; Dhar, H.; Thalla, A.K.; Kumar, S. Application of Life Cycle Assessment in Municipal Solid Waste Management: A Worldwide Critical Review. J. Clean. Prod. 2019, 209, 630–654. [Google Scholar] [CrossRef]
- Yu, T.; Ding, H.; Qiao, J. Ensemble Self-Organizing Recursive Neural Network for Modeling Furnace Temperature in Municipal Solid Waste Incineration. Appl. Soft Comput. 2025, 178, 113170. [Google Scholar] [CrossRef]
- Wang, J.; Nketiah, E.; Cai, X.; Obuobi, B.; Adu-Gyamfi, G.; Adjei, M. What Establishes Citizens’ Household Intention and Behavior Regarding Municipal Solid Waste Separation? A Case Study in Jiangsu Province. J. Clean. Prod. 2023, 423, 138642. [Google Scholar] [CrossRef]
- Lu, M.; Xia, Y.; Yan, J.; Wang, L. Wet Carbonation of MSWI Fly Ash for Sustainable Limestone Calcined Clay Cement-Type Composites. Cem. Concr. Compos. 2025, 156, 105866. [Google Scholar] [CrossRef]
- Zhou, H.; Wei, L.; Wang, D.; Zhang, W. Environmental Impacts and Optimizing Strategies of Municipal Sludge Treatment and Disposal Routes in China Based on Life Cycle Analysis. Environ. Int. 2022, 166, 107378. [Google Scholar] [CrossRef]
- Hunsinger, H.; Jay, K.; Vehlow, J. Formation and Destruction of PCDD/F inside a Grate Furnace. Chemosphere 2002, 46, 1263–1272. [Google Scholar] [CrossRef]
- Yao, X.; Jiao, F.; Gao, S.; Hu, Y.; Liu, T.; Zhang, Y.; Mao, L.; Wu, C.; Li, H.; Dong, Z. Co-Melting Mechanisms for Municipal Solid Waste Incineration Fly Ash with Fine Slag from Coal Gasification and Coal Gangue. J. Environ. Manag. 2024, 367, 122035. [Google Scholar] [CrossRef]
- Kolekar, K.A.; Hazra, T.; Chakrabarty, S.N. A Review on Prediction of Municipal Solid Waste Generation Models. Procedia Environ. Sci. 2016, 35, 238–244. [Google Scholar] [CrossRef]
- Qiao, J.; Sun, Z.; Meng, X. A Comprehensively Improved Interval Type-2 Fuzzy Neural Network for NOx Emissions Prediction in MSWI Process. IEEE Trans. Ind. Inform. 2023, 19, 11286–11297. [Google Scholar] [CrossRef]
- Tang, J.; Wang, T.; Xia, H.; Cui, C. An Overview of Artificial Intelligence Application for Optimal Control of Municipal Solid Waste Incineration Process. Sustainability 2024, 16, 2042. [Google Scholar] [CrossRef]
- Wang, T.; Tang, J.; Xia, H.; Yang, C.; Yu, W.; Qiao, J. Data-Driven Multi-Objective Intelligent Optimal Control of Municipal Solid Waste Incineration Process. Eng. Appl. Artif. Intell. 2024, 137, 109157. [Google Scholar] [CrossRef]
- Huang, W.; Ding, H.; Qiao, J. Large-Scale and Knowledge-Based Dynamic Multiobjective Optimization for MSWI Process Using Adaptive Competitive Swarm Optimization. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 379–390. [Google Scholar] [CrossRef]
- Qiao, J.; Cui, Y.; Meng, X. Dynamic Multi-Objective Operation Optimization of Municipal Solid Waste Incineration Process Based on Transfer Learning. IEEE Trans. Autom. Sci. Eng. 2025, 22, 9338–9352. [Google Scholar] [CrossRef]
- Samad, T.; Bauer, M.; Bortoff, S.; Di Cairano, S.; Fagiano, L.; Odgaard, P.F.; Rhinehart, R.R.; Sánchez-Peña, R.; Serbezov, A.; Ankersen, F.; et al. Industry Engagement with Control Research: Perspective and Messages. Annu. Rev. Control 2020, 49, 1–14. [Google Scholar] [CrossRef]
- Cui, Y.; Meng, X.; Qiao, J. Multi-Condition Operational Optimization with Adaptive Knowledge Transfer for Municipal Solid Waste Incineration Process. Expert Syst. Appl. 2024, 238, 121783. [Google Scholar] [CrossRef]
- Wang, T.; Tang, J.; Xia, H.; Aljerf, L.; Zhang, R.; Tian, H.; Akele, M.L. Intelligent Optimal Control of FT for the Municipal Solid Waste Incineration Process Using Multi-Loop Controller and Particle Swarm Optimization. Expert Syst. Appl. 2024, 257, 125015. [Google Scholar] [CrossRef]
- Tao, J.; Li, Z.; Chen, C.; Liang, R.; Wu, S.; Lin, F.; Cheng, Z.; Yan, B.; Chen, G. Intelligent Technologies Powering Clean Incineration of Municipal Solid Waste: A System Review. Sci. Total Environ. 2024, 935, 173082. [Google Scholar] [CrossRef]
- Tian, H.; Tang, J.; Aljerf, L.; Wang, T.; Qiao, J. FT Control Based on Interval Type-2 Fuzzy Broad Learning System for Municipal Solid Waste Incineration Process. Expert Syst. Appl. 2025, 280, 127530. [Google Scholar] [CrossRef]
- Li, Z.; Yao, S.; Chen, D.; Li, L.; Lu, Z.; Yu, Z. Modelling Nitrogen Oxide Emission Trends from the Municipal Solid Waste Incineration Process Using an Adaptive Bi-Directional Long and Short-Term Memory Network. Can. J. Chem. Eng. 2024, 102, 1225–1237. [Google Scholar] [CrossRef]
- Sanoj, K.P.; Dhanya Ram, V. Optimal PID Controller Tuning for Multivariable Unstable Systems by Minimizing ITAE Criteria. IFAC Pap. 2024, 57, 391–396. [Google Scholar] [CrossRef]

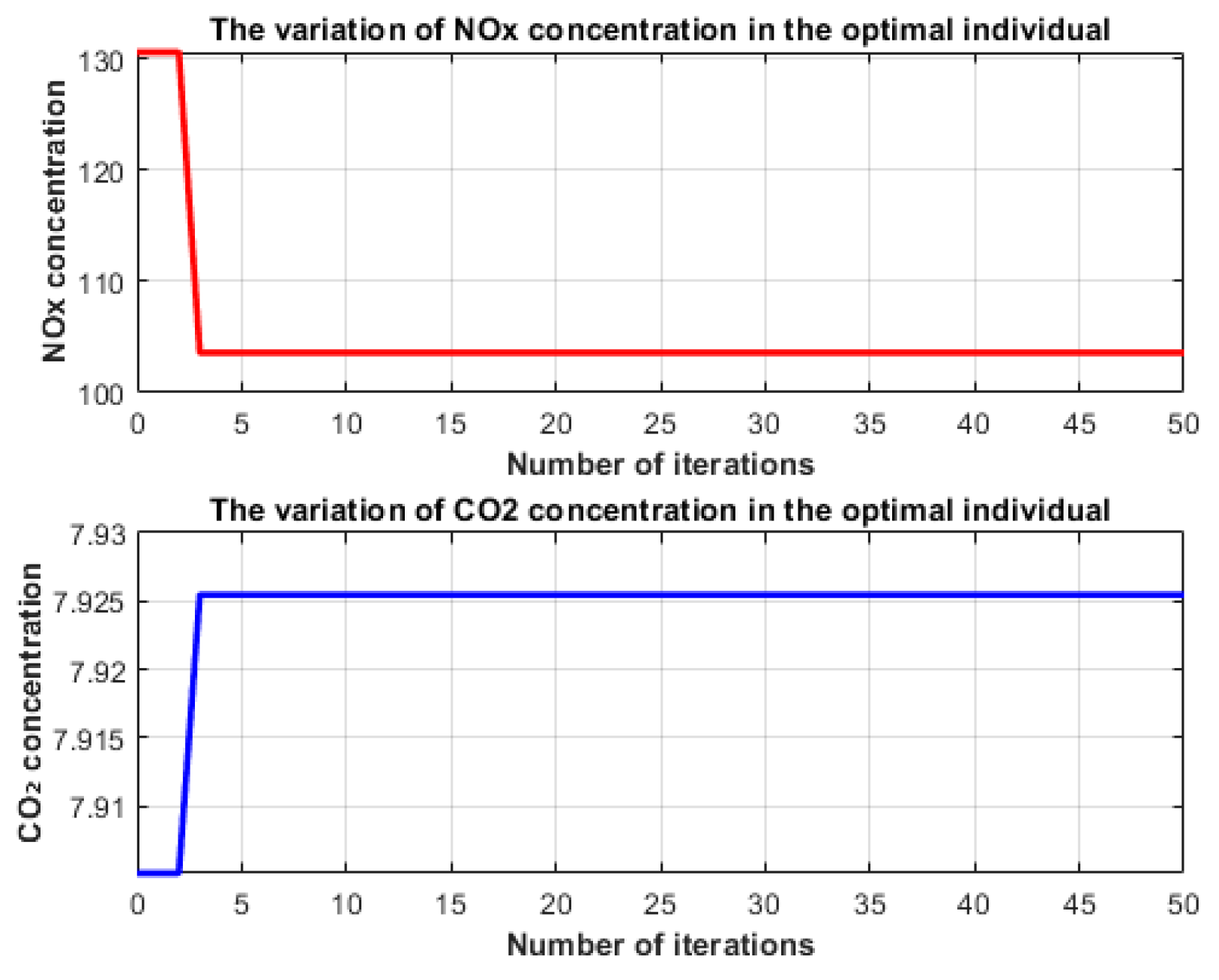
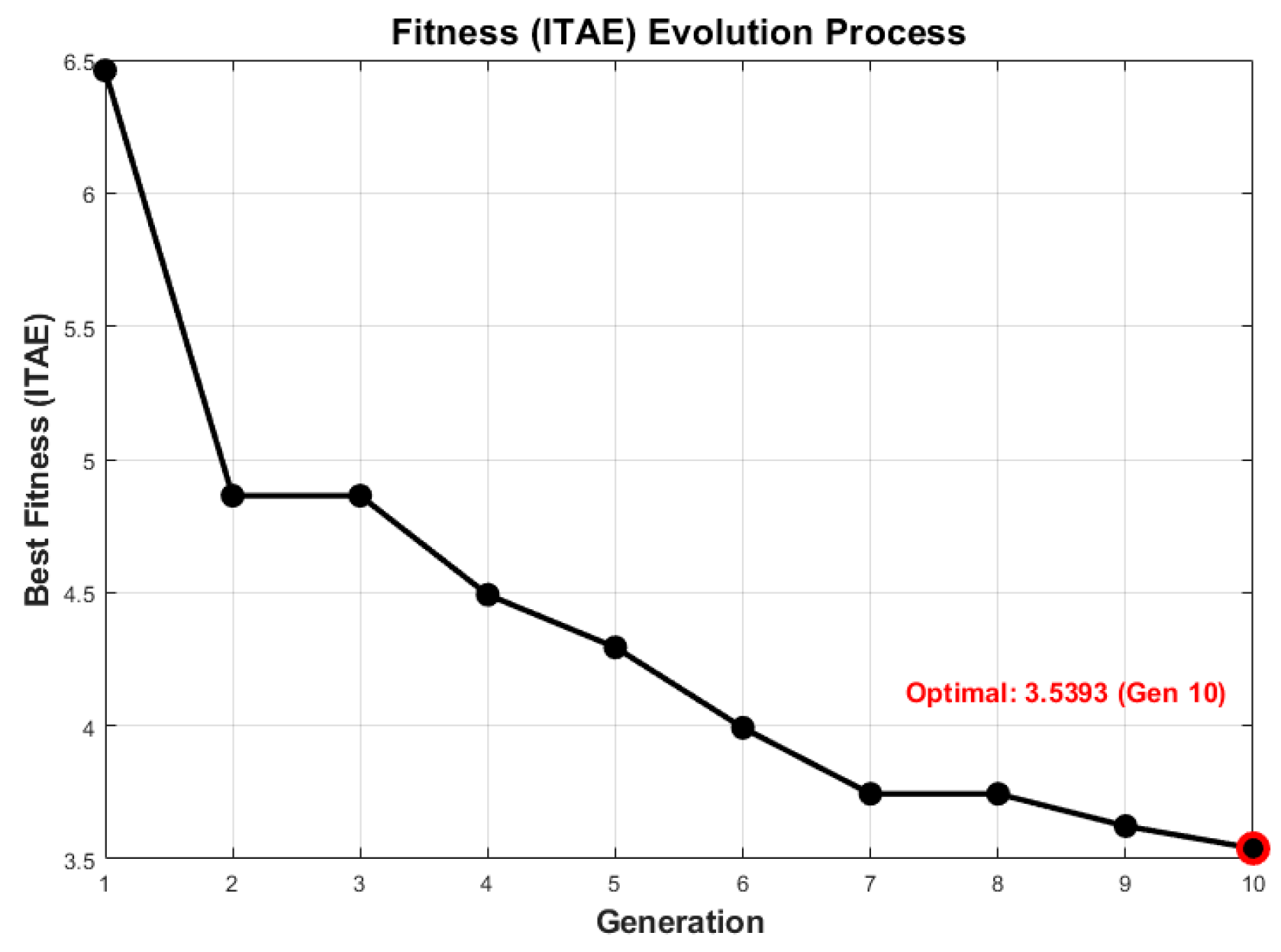
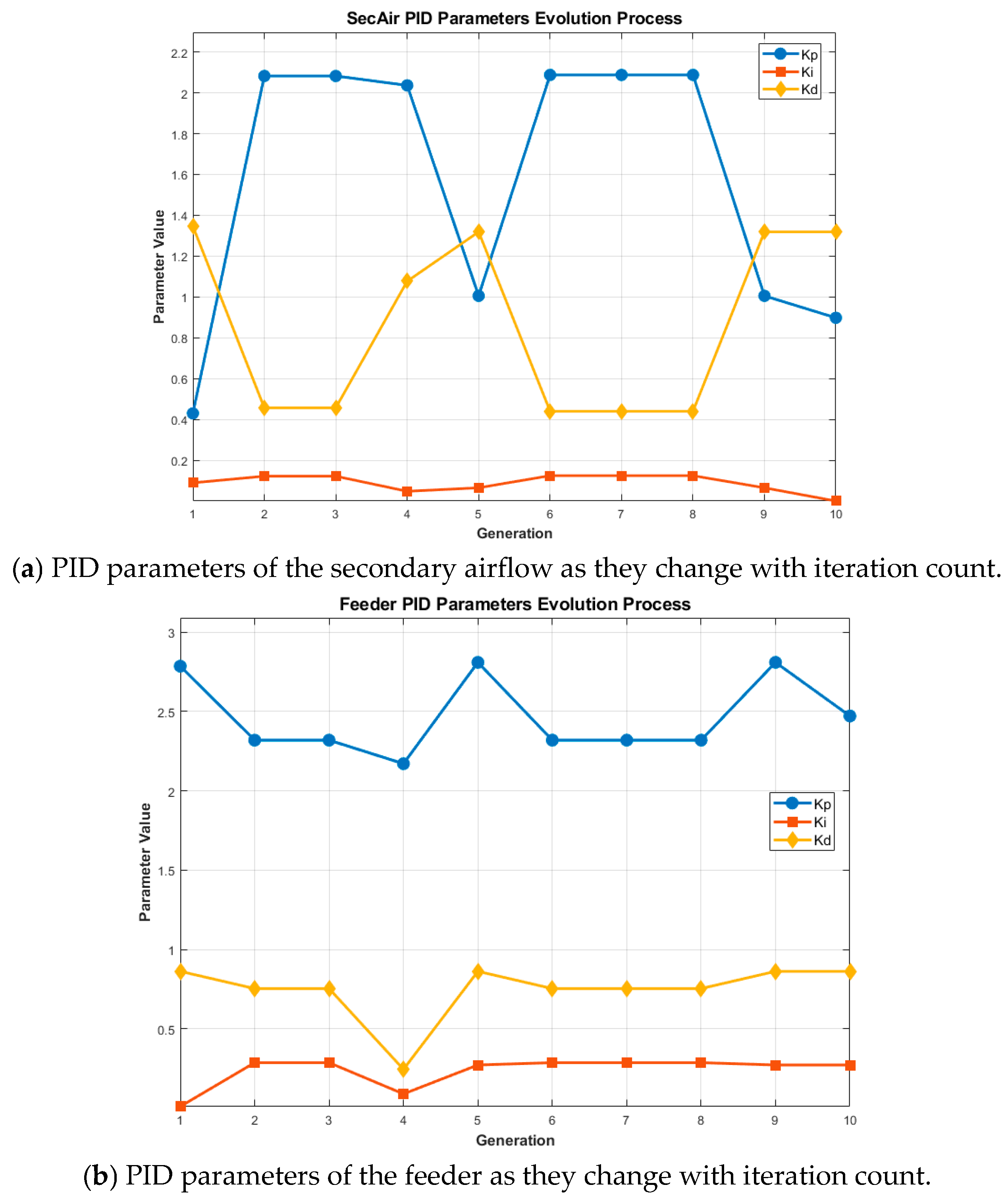
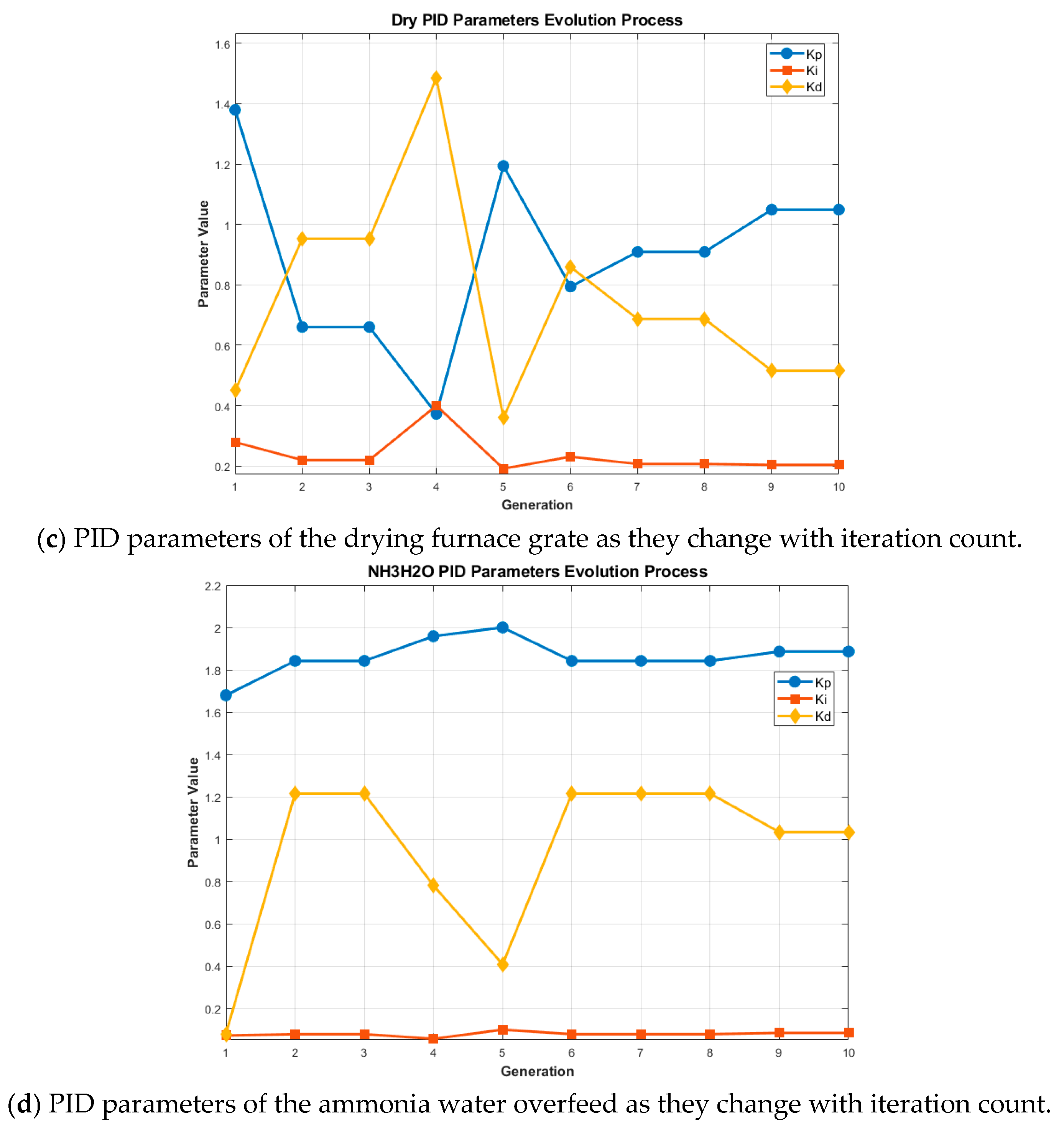

| Parameters | Upper-Level | Lower-Level |
|---|---|---|
| Population Size | 30 | 50 |
| Maximum Number of Iterations | 50 | 20 |
| Crossover Probability | 0.8 | 0.8 |
| Mutation Probability | 0.2 | 0.1 |
| Maximum Emission Concentration | Minimum Emission Concentration | |
|---|---|---|
| NOx | 245.3532 mg/m3 | 51.0312 mg/m3 |
| CO2 | 10.1750% | 6.4454% |
| Maximum Set Value | Minimum Set Value | |
|---|---|---|
| 950 °C | 900 °C |
| Upper-Level | |
|---|---|
| Runtime (s) | 1.9051 ± 0.0115 |
| Optimal Fitness | 0.3869 ± 0.0000 |
| Generations to Optimal Solution | 50 ± 0 |
| Control Loop | Scope | Scope | Scope |
|---|---|---|---|
| SAVF | (0,5) | (0,0.2) | (0,2) |
| ASF | (0,3) | (0,0.3) | (0,1) |
| ASD | (0,4) | (0,0.4) | (0,2) |
| AWJ | (0,2) | (0,0.1) | (0,1.5) |
| Control Loop | Value | Value | Value |
|---|---|---|---|
| SAVF | 0.8979 | 0 | 1.3187 |
| ASF | 2.472 | 0.2728 | 0.863 |
| ASD | 1.048 | 0.2036 | 0.5158 |
| AWJ | 1.8862 | 0.0849 | 1.0332 |
| Parameters | Values |
|---|---|
| 1 | |
| 2.5 | |
| 0.5 |
| Average ± Variance | |
|---|---|
| Optimal Fitness | 0.4622 ± 0.3263 |
| NOx Concentration | 60.9998 ± 7.6801 |
| CO2 Concentration | 8.3003 ± 1.6351 |
| Optimal Temperature Setting | 935.77 ± 1.57 °C |
| Residual Value | Optimal Fitness |
|---|---|
| −5 | 3.523 |
| 0 | 3.586 |
| 5 | 3.629 |
| Control Loop | |||
|---|---|---|---|
| SAVF | 1.5383 | 0.5692 | 0.3721 |
| ASF | 2.1913 | 0.4234 | 0.4889 |
| ASD | 0.9816 | 0.1512 | 0.5805 |
| AWJ | 0.5018 | 0.0806 | 0.7386 |
| Control Loop | |||
|---|---|---|---|
| SAVF | 2.8728 | 0.1504 | 0.5397 |
| ASF | 1.9408 | 0 | 0.5493 |
| ASD | 1.1752 | 0.0451 | 0.1085 |
| AWJ | 0.6091 | 0.0708 | 0.6325 |
| Control Loop | |||
|---|---|---|---|
| SAVF | 1.5671 | 0.1510 | 0.0566 |
| ASF | 2.9907 | 0.1603 | 0.7423 |
| ASD | 0.9866 | 0.2033 | 0.1268 |
| AWJ | 0.0972 | 0.0358 | 1.4827 |
| ITAE | GA_PID | ISNA_PID | PID |
|---|---|---|---|
| Stage 1(Original–900 °C) | 14.91 | 502.38 | 1606.15 |
| Stage 2(900 °C–925 °C) | 29.76 | 1331.65 | 4898.39 |
| Stage 3(925 °C–910 °C) | 28.98 | 926.97 | 2939.92 |
| Stage 4(915 °C–920 °C) | 14.92 | 564.24 | 1959.58 |
| Stage 5(920 °C–940 °C) | 25.89 | 1075.30 | 3918.86 |
| Stage 6(940 °C–930 °C) | 18.50 | 601.55 | 1959.87 |
| Stage 7(930 °C–925 °C) | 8.82 | 295.55 | 979.9 |
| Algorithm | ISE | IAE | DEVmax |
|---|---|---|---|
| GA_PID | 0.1542 | 0.0113 | 25 |
| ISNA_PID | 0.4258 | 0.0612 | 25 |
| PID | 1.1148 | 0.1301 | 25 |
| GA | PSO | |
|---|---|---|
| Average Computation Time (s) | 1.9051 | 5.0388 |
| Variance of Computation Time (s) | 0.0115 | 0.1209 |
| Average Generations to Find Optimum | 4.63 | 2.33 |
| Variance of Generations to Optimum | 41.75 | 4.82 |
| Minimum Generations to Optimum | 1 | 1 |
| Maximum Generations to Optimum | 28 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; Wang, W.; Tang, J.; Li, Z.; Rong, J. Dual-Layer Optimization Control for Furnace Temperature Setting and Tracking in Municipal Solid Waste Incineration Process. Sustainability 2025, 17, 10577. https://doi.org/10.3390/su172310577
Wu Y, Wang W, Tang J, Li Z, Rong J. Dual-Layer Optimization Control for Furnace Temperature Setting and Tracking in Municipal Solid Waste Incineration Process. Sustainability. 2025; 17(23):10577. https://doi.org/10.3390/su172310577
Chicago/Turabian StyleWu, Yicong, Wei Wang, Jian Tang, Zenan Li, and Jian Rong. 2025. "Dual-Layer Optimization Control for Furnace Temperature Setting and Tracking in Municipal Solid Waste Incineration Process" Sustainability 17, no. 23: 10577. https://doi.org/10.3390/su172310577
APA StyleWu, Y., Wang, W., Tang, J., Li, Z., & Rong, J. (2025). Dual-Layer Optimization Control for Furnace Temperature Setting and Tracking in Municipal Solid Waste Incineration Process. Sustainability, 17(23), 10577. https://doi.org/10.3390/su172310577







