Multi-Objective Optimization of Electric–Gas–Thermal Systems via the Hippo Optimization Algorithm: Low-Carbon and Cost-Effective Solutions
Abstract
1. Introduction
2. Framework and Model of Integrated Electricity–Gas–Heat Energy System
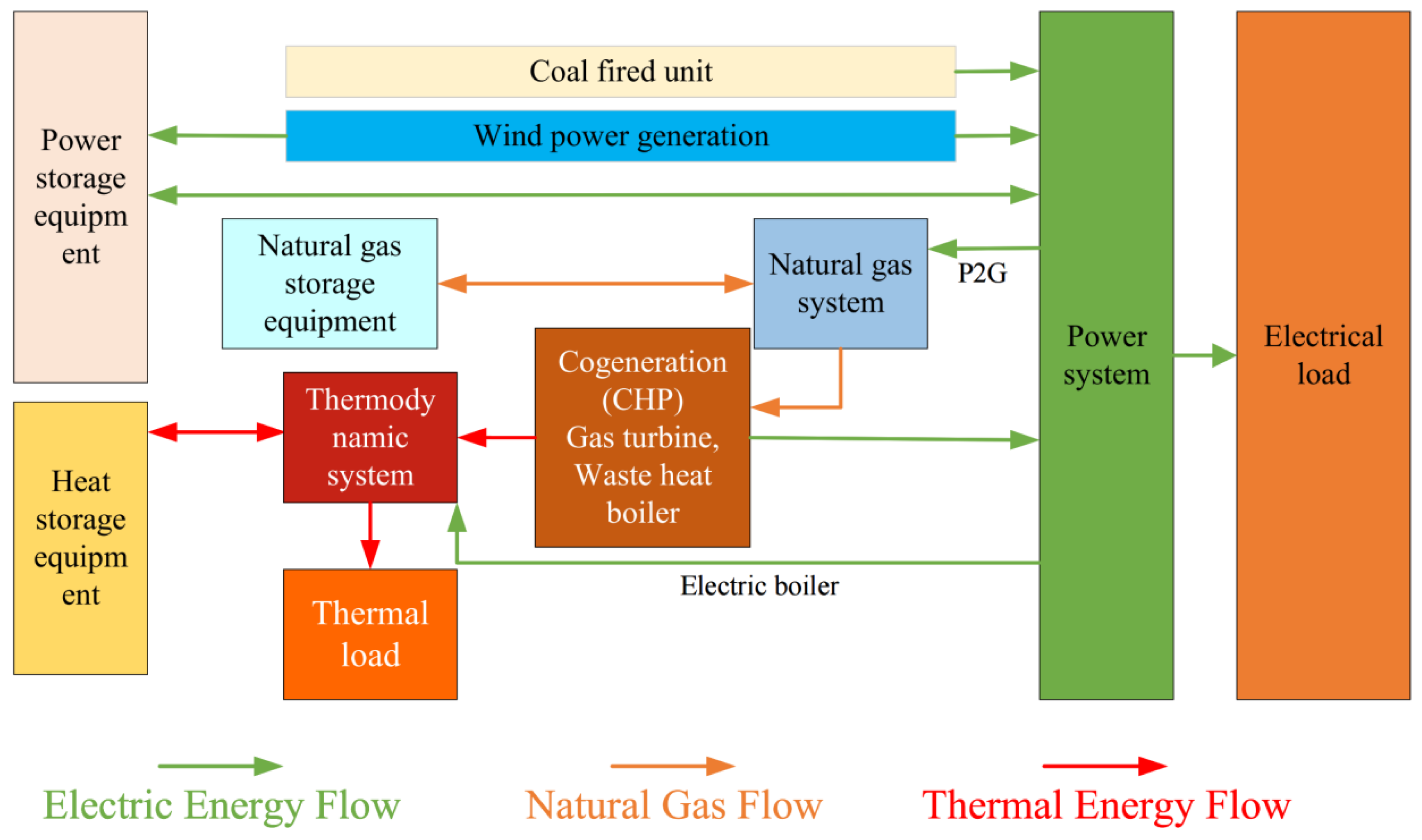
2.1. Framework of Integrated Electric–Gas–Thermal Energy System
2.2. Power System Model
2.2.1. DC Power Flow Model
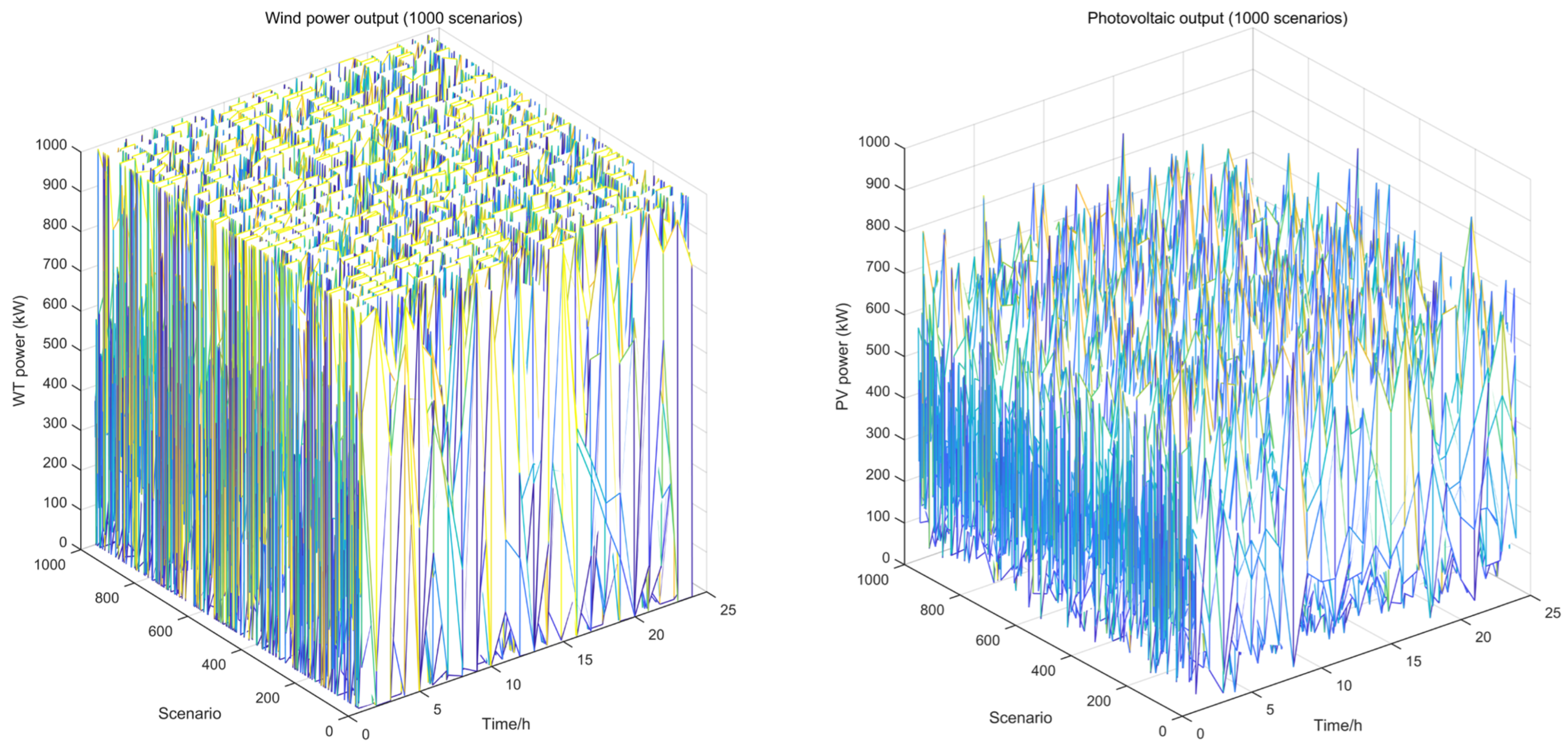
2.2.2. Wind Turbine Generator Model
2.2.3. Coal-Fired Unit Model
2.3. Natural Gas System Model
2.3.1. Natural Gas Subsystem Model
- 1.
- Natural gas source
- 2.
- Natural gas pipeline flow
- 3.
- Compressor
2.3.2. Natural Gas Pipeline Model
2.4. Thermodynamic System Model
2.4.1. Heat Source Model
2.4.2. Heat Supply Network Model
2.4.3. Pipeline Flow Loss Conversion
2.5. Optimization Model
2.5.1. Objective Function
2.5.2. Carbon Emissions
2.5.3. Constraint Condition
- 1.
- Wind turbine generator set output constraint
- 2.
- Climbing constraint of wind turbine generator set
- 3.
- Electric Boiler
- 4.
- P2G
- 5.
- Energy Storage
- 6.
- Branch power flow constraint
- 7.
- Node power balance constraints
- 8.
- Nodal pressure constraint
- 9.
- Thermodynamic system equilibrium constraint
2.6. Chapter Summary
3. Model Solving
3.1. The Connection Between the Hippopotamus Optimization Algorithm and Energy System Optimization
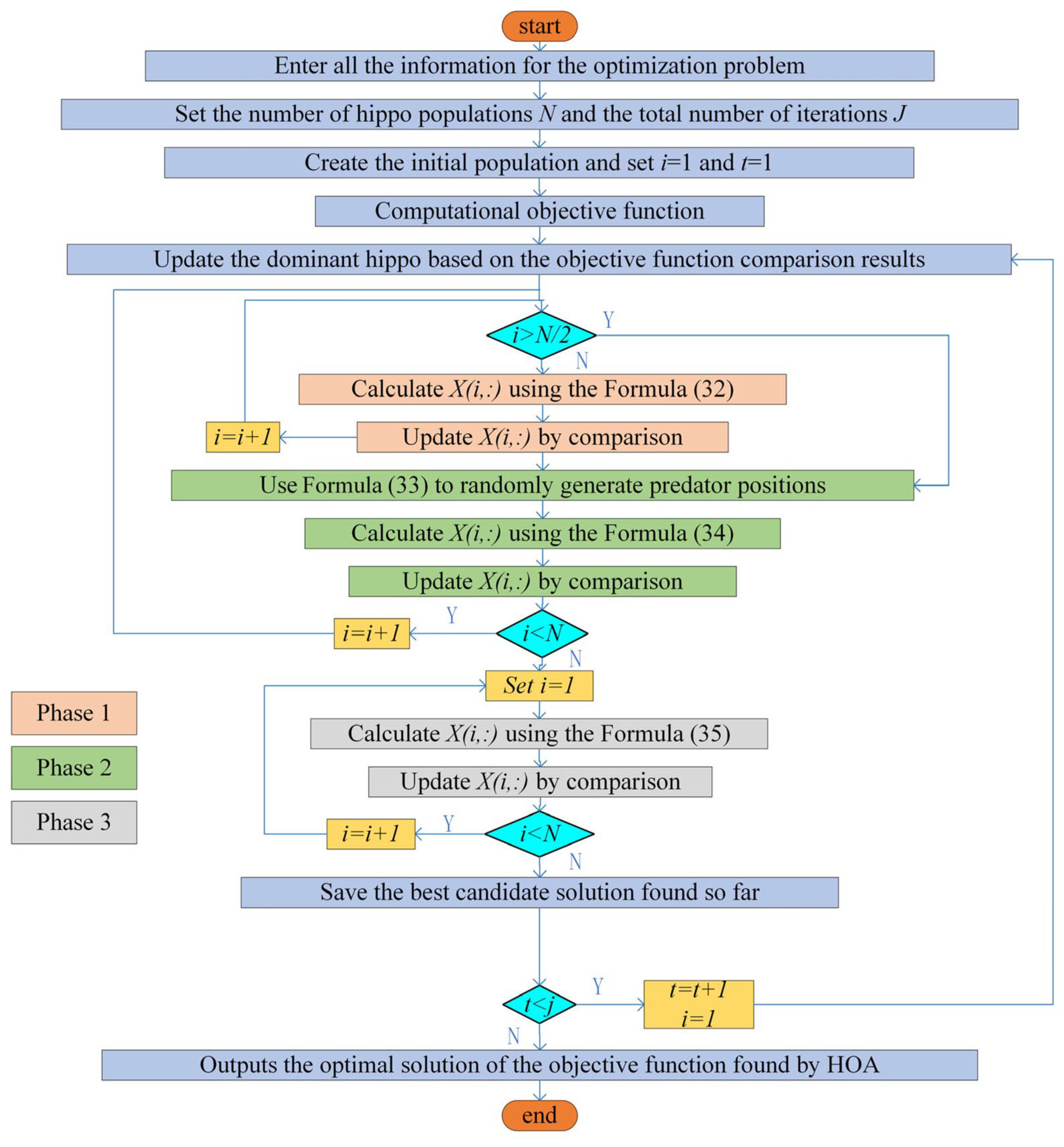
3.1.1. Hippopotamus Optimization Algorithm
- 1.
- Objective Function Formulation
- 2.
- Multi-objective Optimization Method
- 3.
- HOA for Multi-objective Problem Solving
- 1.
- Exploration stage (the hippopotamus’ position update in the river or pond): mimic the aggregation behavior of the hippo herd and guide the population search through the position of the dominant hippo. The calculation formula is as follows:
- 2.
- Defense phase (hippopotamus defense against predators): describes response to potential threats, such as predators, by making loud calls and turns to avoid attack, using the following formula:
- 3.
- Escape from predator phase (hippopotamus escaping from the predator): simulate the behavior of the hippo away from danger area during threat using the following formula:
3.1.2. Correspondence Between HOA Phases and Energy System Scheduling
- Exploration Phase: In this phase, the algorithm conducts a broad search across the solution space, analogous to exploring various operational modes in system scheduling (e.g., different combinations of unit start-ups and shutdowns, P2G absorption strategies, and energy storage charge–discharge schemes). This stage helps identify diverse candidate operating plans and prevents premature convergence to local minima.
- Defense Phase: Here, the algorithm performs local refinement of promising individuals while maintaining diversity. This corresponds to fine-tuning the system under operational constraints (e.g., unit ramping limits, pipeline pressure minimums, thermal network temperature requirements) to ensure that solutions remain technically and safely feasible.
- Escape Phase: When the search is trapped in a local optimum or encounters suboptimal “predator-like” solutions, HOA employs large-step jumps to escape the local region. In scheduling terms, this is equivalent to introducing aggressive operational strategy adjustments (e.g., temporarily increasing P2G absorption or changing power allocation to avoid high-cost zones), thereby seeking superior system-level solutions.
3.1.3. Influence of HOA Phases on the Optimization Process
3.2. Chapter Summary
4. Example Results and Analysis
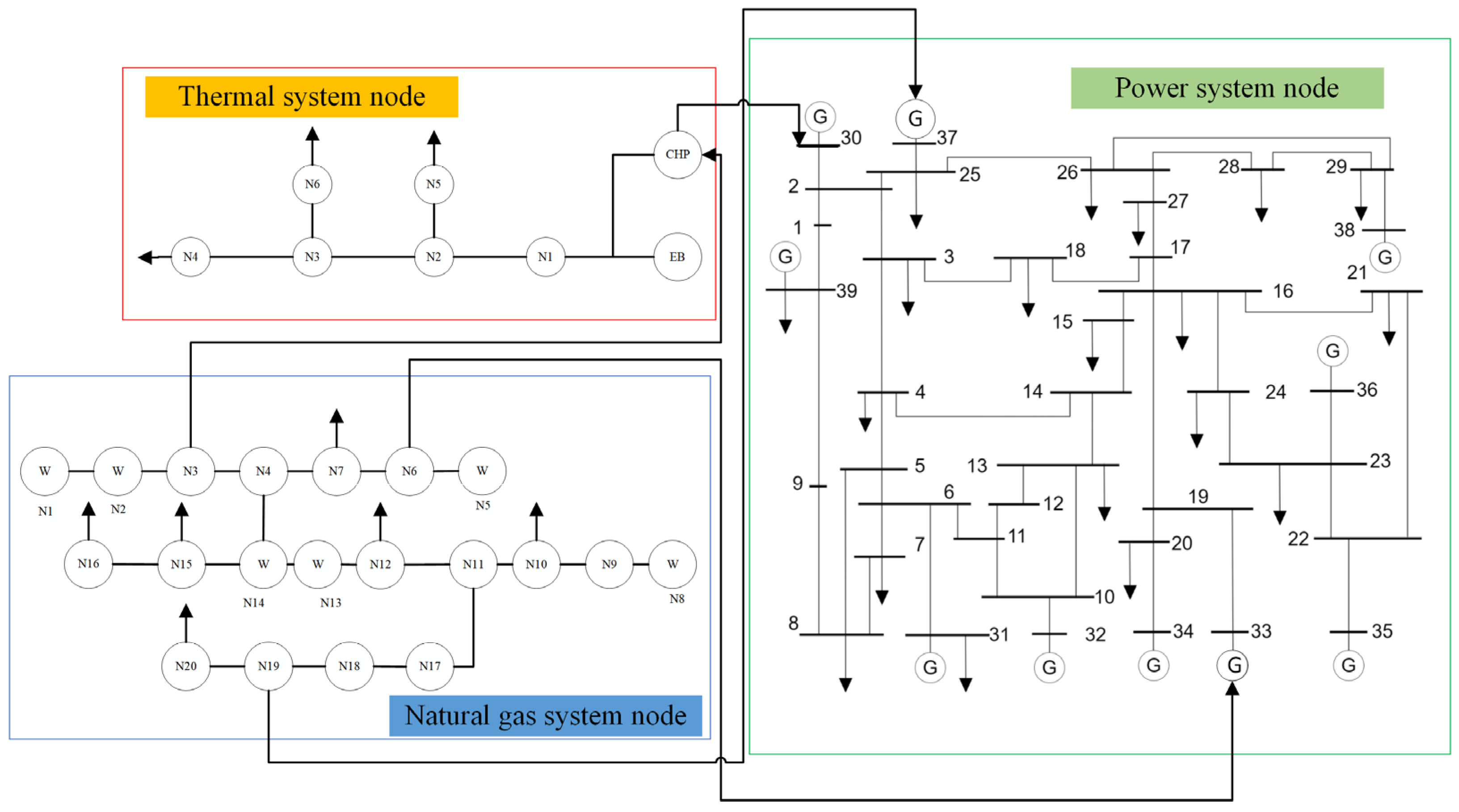
4.1. Example Parameters
4.1.1. Power System Data
4.1.2. Natural Gas System Data
4.1.3. Thermal System Data
4.2. Result Analysis
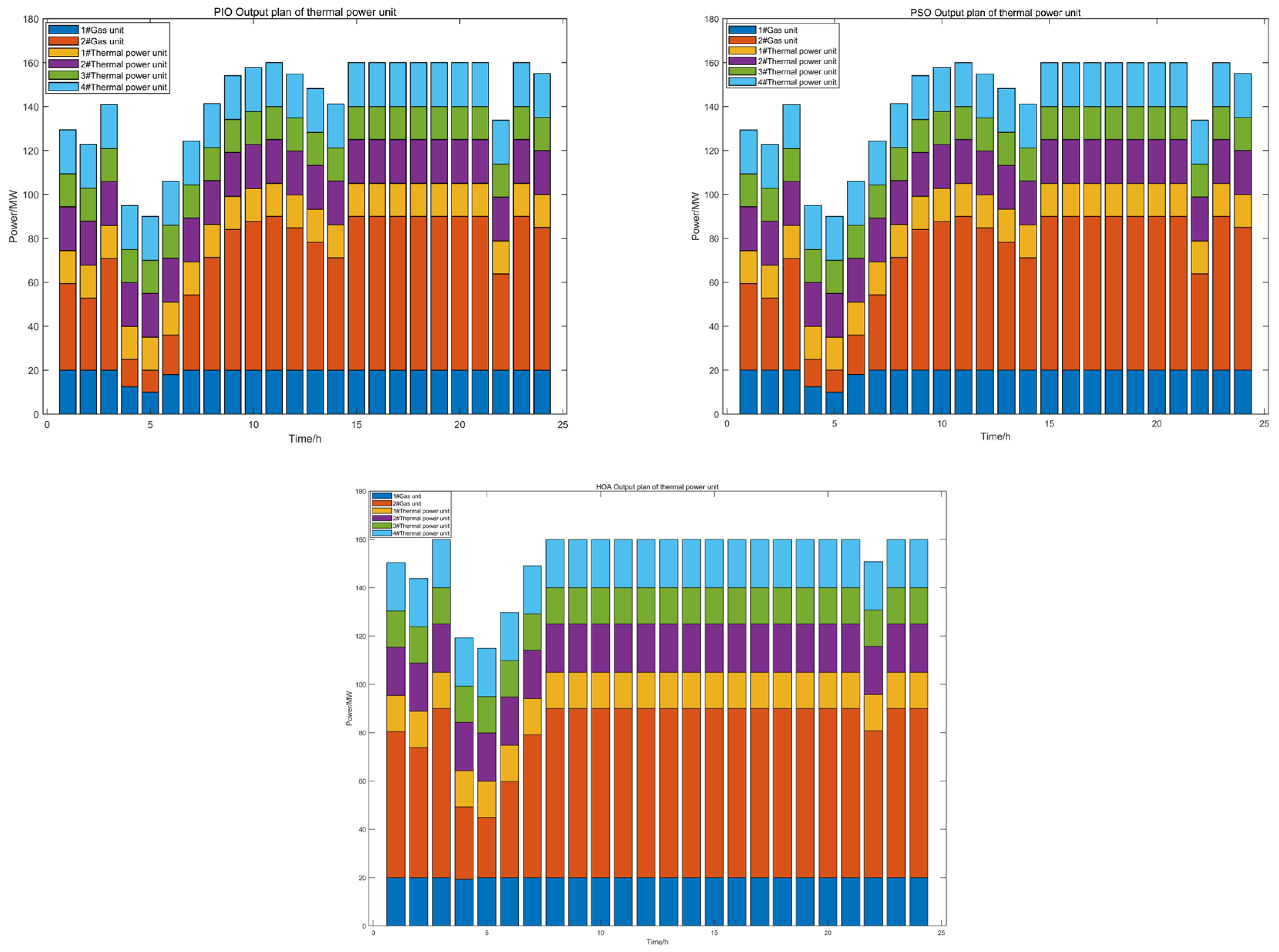
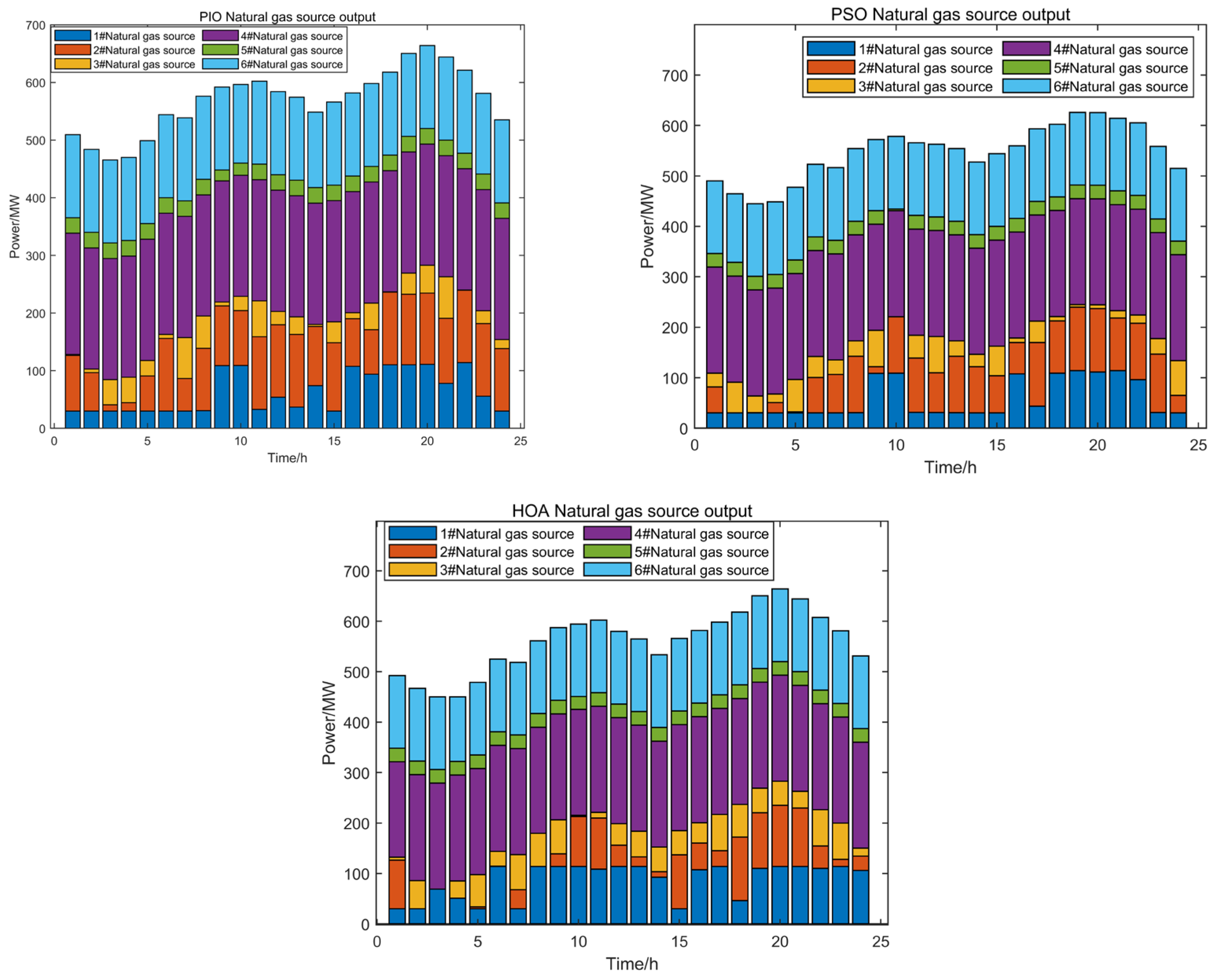
4.2.1. Comparative Analysis of Optimization Algorithms
4.2.2. Comparative Analysis of Objective Function
4.2.3. Payback Period Analysis
- (1)
- Investment cost composition and annualisation.
- (2)
- Based on the data in Table 8, the investment cost of HOA increased by yuan compared with PIO, while the annual operational cost saving is 4.85 × 108 yuan/year. Substituting into the formula yields the following:
4.3. Limitations and Scope of Applicability
4.3.1. Limitations
4.3.2. Scope of Applicability
4.4. Chapter Summary
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, M.; Wang, J.; Zhi, H.; Zhao, J.; Chang, X.; Zhang, S.; Guo, X.; Wang, T. An Integrated Electricity–Gas–Heat Energy System Based on the Synergy of Long-and Short-Term Energy Storage. Energies 2025, 18, 55. [Google Scholar] [CrossRef]
- Amiri, M.H.; Mehrabi Hashjin, N.; Montazeri, M.; Mirjalili, S.; Khodadadi, N. Hippopotamus optimization algorithm: A novel nature-inspired optimization algorithm. Sci. Rep. 2024, 14, 5032. [Google Scholar] [CrossRef] [PubMed]
- Faisal, S.; Gao, C. A Comprehensive Review of Integrated Energy Systems Considering Power-to-Gas Technology. Energies 2024, 17, 4551. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Ji, X.; Yang, M.; Ye, P. Optimal scheduling of electricity–gas–heat integrated energy system with coordination of flexibility and reliability. Sustain. Energy Technol. Assess. 2024, 71, 103968. [Google Scholar] [CrossRef]
- Clegg, S.; Mancarella, P. Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans. Sustain. Energy 2015, 6, 1234–1244. [Google Scholar] [CrossRef]
- Qin, L.; Ma, H.; Huang, C.; Li, H.; Wu, S.; Wang, G. Low-carbon operation optimization of integrated energy system considering CCS-P2G and multi-market interaction. Front. Energy Res. 2024, 11, 1337164. [Google Scholar] [CrossRef]
- Fambri, G.; Diaz-Londono, C.; Mazza, A.; Badami, M.; Weiss, R. Power-to-Gas in gas and electricity distribution systems: A comparison of different modeling approaches. J. Energy Storage 2022, 55, 105454. [Google Scholar] [CrossRef]
- Alizad, E.; Rastegar, H.; Hasanzad, F. Dynamic planning of Power-to-Gas integrated energy hub considering demand response programs and future market conditions. Int. J. Electr. Power Energy Syst. 2022, 143, 108503. [Google Scholar] [CrossRef]
- Tao, J.; Duan, J.; Tuo, L.; Gao, Q.; Tian, Q.; Lu, W. Exergy efficiency based multi-objective configuration optimization of energy hubs in the multi-energy distribution system. Energy 2025, 329, 136554. [Google Scholar] [CrossRef]
- Ming, M.; Wang, R.; Zha, Y.; Zhang, T. Multi-objective optimization of hybrid renewable energy system using an enhanced multi-objective evolutionary algorithm. Energies 2017, 10, 674. [Google Scholar] [CrossRef]
- Zhang, Z. Multi-objective optimization method for building energy-efficient design based on multi-agent-assisted NSGA-II. Energy Inform. 2024, 7, 90. [Google Scholar] [CrossRef]
- Mokaramian, E.; Shayeghi, H.; Younesi, A.; Shafie-Khah, M.; Siano, P. Energy hubs components and operation: State-of-the-art review. Renew. Sustain. Energy Rev. 2025, 212, 115395. [Google Scholar] [CrossRef]
- Ghaemifard, S.; Ghannadiasl, A. A comparison of metaheuristic algorithms for structural optimization: Performance and efficiency analysis. Adv. Civ. Eng. 2024, 2024, 2054173. [Google Scholar] [CrossRef]
- Zhang, J.; Kong, X.; Shen, J.; Sun, L. Day-ahead optimal scheduling of a standalone solar-wind-gas based integrated energy system with and without considering thermal inertia and user comfort. J. Energy Storage 2023, 57, 106187. [Google Scholar] [CrossRef]
- Shang, K.; Ishibuchi, H.; He, L.; Pang, L.M. A survey on the hypervolume indicator in evolutionary multiobjective optimization. IEEE Trans. Evol. Comput. 2020, 25, 1–20. [Google Scholar] [CrossRef]
- Wang, Z.; Younesi, A.; Liu, M.V.; Guo, G.C.; Anderson, C.L. AC optimal power flow in power systems with renewable energy integration: A review of formulations and case studies. IEEE Access 2023, 11, 102681–102712. [Google Scholar] [CrossRef]
- Mirzaei, M.A.; Oskouei, M.Z.; Mohammadi-Ivatloo, B.; Loni, A.; Zare, K.; Marzband, M.; Shafiee, M. Integrated energy hub system based on power-to-gas and compressed air energy storage technologies in the presence of multiple shiftable loads. IET Gener. Transm. Distrib. 2020, 14, 2510–2519. [Google Scholar] [CrossRef]
- Mao, Y.; Cai, Z.; Jiao, X.; Long, D. Multi-timescale optimization scheduling of integrated energy systems oriented towards generalized energy storage services. Sci. Rep. 2025, 15, 8549. [Google Scholar] [CrossRef]
- Wang, L. Building Energy Efficiency Design and Energy Consumption Analysis Based on MOEA/D Algorithm. IEEE Access 2024, 12, 187313–187328. [Google Scholar] [CrossRef]
- Fambri, G.; Diaz-Londono, C.; Mazza, A.; Badami, M.; Sihvonen, T.; Weiss, R. Techno-economic analysis of Power-to-Gas plants in a gas and electricity distribution network system with high renewable energy penetration. Appl. Energy 2022, 312, 118743. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, H.; Hong, F.; Yang, J.; Chen, Z.; Cui, H.; Feng, J. Modeling and optimization of combined heat and power with power-to-gas and carbon capture system in integrated energy system. Energy 2021, 236, 121392. [Google Scholar] [CrossRef]
- Fan, G.; Peng, C.; Wang, X.; Wu, P.; Yang, Y.; Sun, H. Optimal scheduling of integrated energy system considering renewable energy uncertainties based on distributionally robust adaptive MPC. Renew. Energy 2024, 226, 120457. [Google Scholar] [CrossRef]
- Alonso, A.M.; Costa, D.; Messagie, M.; Coosemans, T. Techno-economic assessment on hybrid energy storage systems comprising hydrogen and batteries: A case study in Belgium. Int. J. Hydrogen Energy 2024, 52, 1124–1135. [Google Scholar] [CrossRef]
- Liang, T.; Zhang, X.; Tan, J.; Jing, Y.; Liangnian, L. Deep reinforcement learning-based optimal scheduling of integrated energy systems for electricity, heat, and hydrogen storage. Electr. Power Syst. Res. 2024, 233, 110480. [Google Scholar] [CrossRef]
- Wang, W.; Tian, J. An improved hippopotamus optimization algorithm utilizing swarm-elite learning mechanism’s levy flight and quadratic interpolation operators for optimal parameters extraction in photovoltaic models. In Proceedings of the International Conference on Intelligent Computing, Tianjin, China, 5–8 August 2024; Springer Nature: Singapore, 2024; pp. 264–277. [Google Scholar]
- Zhang, Y.; Zhang, P.; Du, S.; Dong, H. Economic optimal scheduling of integrated energy system considering wind–solar uncertainty and power to gas and carbon capture and storage. Energies 2024, 17, 2770. [Google Scholar] [CrossRef]
- Duan, Y.; Gao, C.; Xu, Z.; Ren, S.; Wu, D. Multi-Objective Optimization for the Low-Carbon Operation of Integrated Energy Systems Based on an Improved Genetic Algorithm. Energies 2025, 18, 2283. [Google Scholar] [CrossRef]
- Tang, D.; Zheng, Z.; Guerrero, J.M. A hybrid multi-criteria dynamic sustainability assessment framework for integrated multi-energy systems incorporating hydrogen at ports. Int. J. Hydrogen Energy 2025, 99, 540–552. [Google Scholar] [CrossRef]
- Xie, Q.; Huang, C.; Zhou, Y.; Shen, Z.; Fu, Q.; Wang, X. Improved hippo algorithm optimization strategy for heliostat field layout with dynamic time weighting. Appl. Therm. Eng. 2025, 279, 127598. [Google Scholar] [CrossRef]
- Mao, Y.; Li, X.; Liu, J.; Yu, M.; Kim, M.K.; Yang, K. Multi-objective optimization of integrated energy systems in natural gas industrial zones: Enhancing performance through variable hydrogen blending ratios. Appl. Therm. Eng. 2025, 268, 125942. [Google Scholar] [CrossRef]
- Han, T.; Wang, H.; Li, T.; Liu, Q.; Huang, Y. MHO: A Modified Hippopotamus Optimization Algorithm for Global Optimization and Engineering Design Problems. Biomimetics 2025, 10, 90. [Google Scholar] [CrossRef]
- Zhao, Y.; Wei, Y.; Zhang, S.; Guo, Y.; Sun, H. Multi-objective robust optimization of integrated energy system with hydrogen energy storage. Energies 2024, 17, 1132. [Google Scholar] [CrossRef]
- Krishna Meera, V.; Balasubramanian, C.; Praveen, R. Hybrid Hippopotamus Optimization Algorithm–Based Energy-Efficient Stable Cluster Construction Protocol for Data Routing in VANETs. Int. J. Commun. Syst. 2025, 38, e70171. [Google Scholar] [CrossRef]
- Asim, A.M.; Awad, A.S.A.; Attia, M.A. Integrated optimization of energy storage and green hydrogen systems for resilient and sustainable future power grids. Sci. Rep. 2025, 15, 25656. [Google Scholar] [CrossRef] [PubMed]
- Lu, M.; Teng, Y.; Chen, Z.; Song, Y. A bi-level optimization strategy of electricity-hydrogen-carbon integrated energy system considering photovoltaic and wind power uncertainty and demand response. Sci. Rep. 2025, 15, 18. [Google Scholar] [CrossRef]
- Zheng, Z.; Xiwang, A.; Sun, Y. Optimal scheduling of integrated energy system considering hydrogen blending gas and demand response. Energies 2024, 17, 1902. [Google Scholar] [CrossRef]
- Lei, Y. Application of improved hippopotamus optimization algorithm integrating multi-strategy. Nat. Sci. Hainan Univ. 2025, 43, 289–296. [Google Scholar]
- Wang, Y.; Wu, Z.; Ni, D. Real-time optimization of heliostat field aiming strategy via an improved swarm intelligence algorithm. Appl. Sci. 2024, 14, 416. [Google Scholar] [CrossRef]
- Wang, R.; Wang, J. Multi-objective collaborative optimization of system configurations and energy scheduling of integrated energy system with electricity-fuel-heat storage systems. J. Energy Storage 2025, 132, 117846. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, L.; He, K.; Gong, Y.; Zhang, Z.; Chen, K. Optimization of the Joint Operation of an Electricity–Heat–Hydrogen–Gas Multi-Energy System Containing Hybrid Energy Storage and Power-to-Gas–Combined Heat and Power. Energies 2024, 17, 3144. [Google Scholar] [CrossRef]
- Liu, X.; Mancarella, P. Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 2016, 167, 336–352. [Google Scholar] [CrossRef]
- Liu, S.; Mu, T.; Guo, Y.; Lei, K.; An, D. Research and Application of Network Structure Optimization Method Based on DC Power Flow Model. Inn. Mong. Electr. Power 2022, 40, 45–49. [Google Scholar]
- Deng, H.W. Evaluating Nodal Energy Price of Carbon Emission-Embedded Electricity-Gas-Heat Integrated Energy System. Master’s Thesis, Northeast Electric Power University, Jilin, China, 2019. [Google Scholar]
- Benonysson, A.; Bohm, B.; Ravn, H.F. Operational optimiz ion in a district heating system. Energy Convers. Manag. 1995, 36, 297–314. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, G.; Pan, H.; Hu, R.; Zou, Y.; Yi, J. Day-ahead Scheduling of Integrated Energy System Considering Districted Heating System and Uncertain Factors. Proc. CSU-EPSA 2019, 32, 83–90. [Google Scholar]
- Modu, B.; Abdullah, P.; Bukar, A.L.; Hamza, M.F.; Adewolu, M.S. Operational strategy and capacity optimization of standalone solar-wind-biomass-fuel cell energy system using hybrid LF-SSA algorithms. Int. J. Hydrogen Energy 2024, 50, 92–106. [Google Scholar] [CrossRef]
- Yu, X.; Duan, Y.; Cai, Z. Sub-population improved grey wolf optimizer with Gaussian mutation and Lévy flight for parameters identification of photovoltaic models. Expert Syst. Appl. 2023, 232, 120827. [Google Scholar] [CrossRef]
- Schneider, K.; Phanivong, P.; Lacroix, J.S. IEEE 342-node low voltage networked test system. In Proceedings of the 2014 IEEE PES General Meeting|Conference & Exposition, National Harbor, MD, USA, 27–31 July 2014; IEEE: New York, NY, USA, 2014; pp. 1–5. [Google Scholar]
- Goel, S. Pigeon optimization algorithm: A novel approach for solving optimization problems. In Proceedings of the 2014 International Conference on Data Mining and Intelligent Computing (ICDMIC), Delhi, India, 5–6 September 2014; IEEE: New York, NY, USA, 2014; pp. 1–5. [Google Scholar]
- Borge-Diez, D.; Rosales-Asensio, E.; Açıkkalp, E.; Alonso-Martínez, D. Analysis of power to gas technologies for energy intensive industries in European Union. Energies 2023, 16, 538. [Google Scholar] [CrossRef]


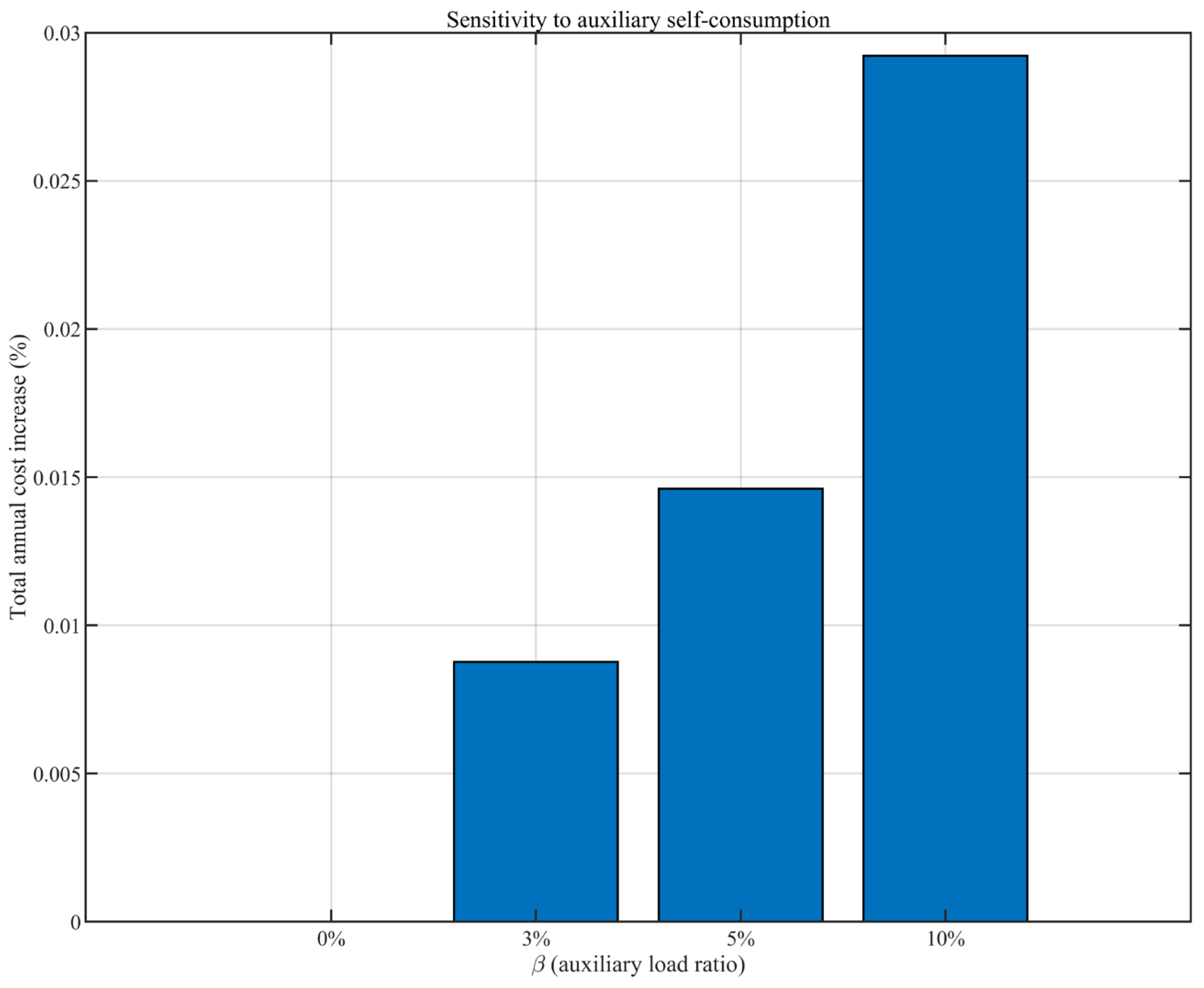

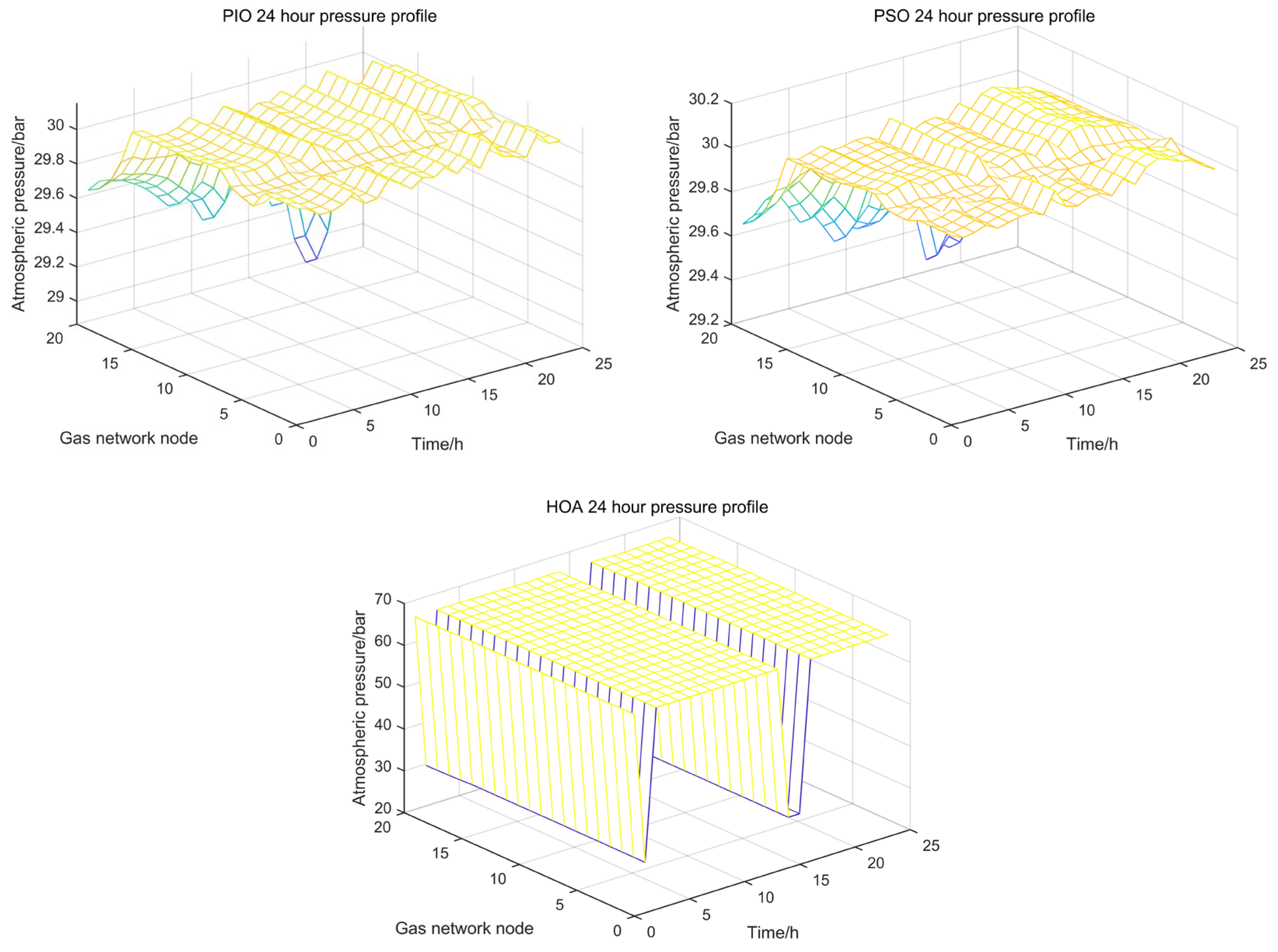
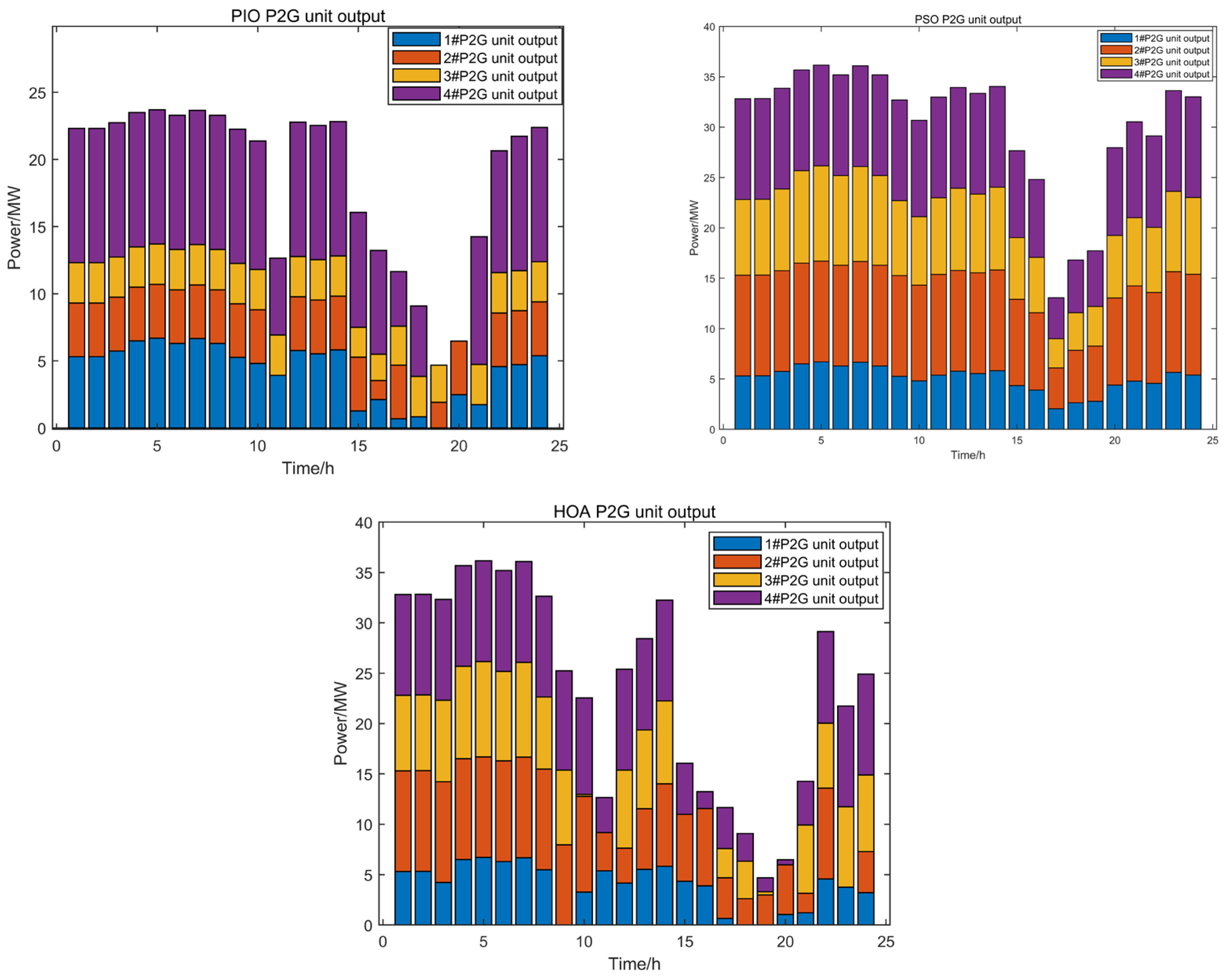


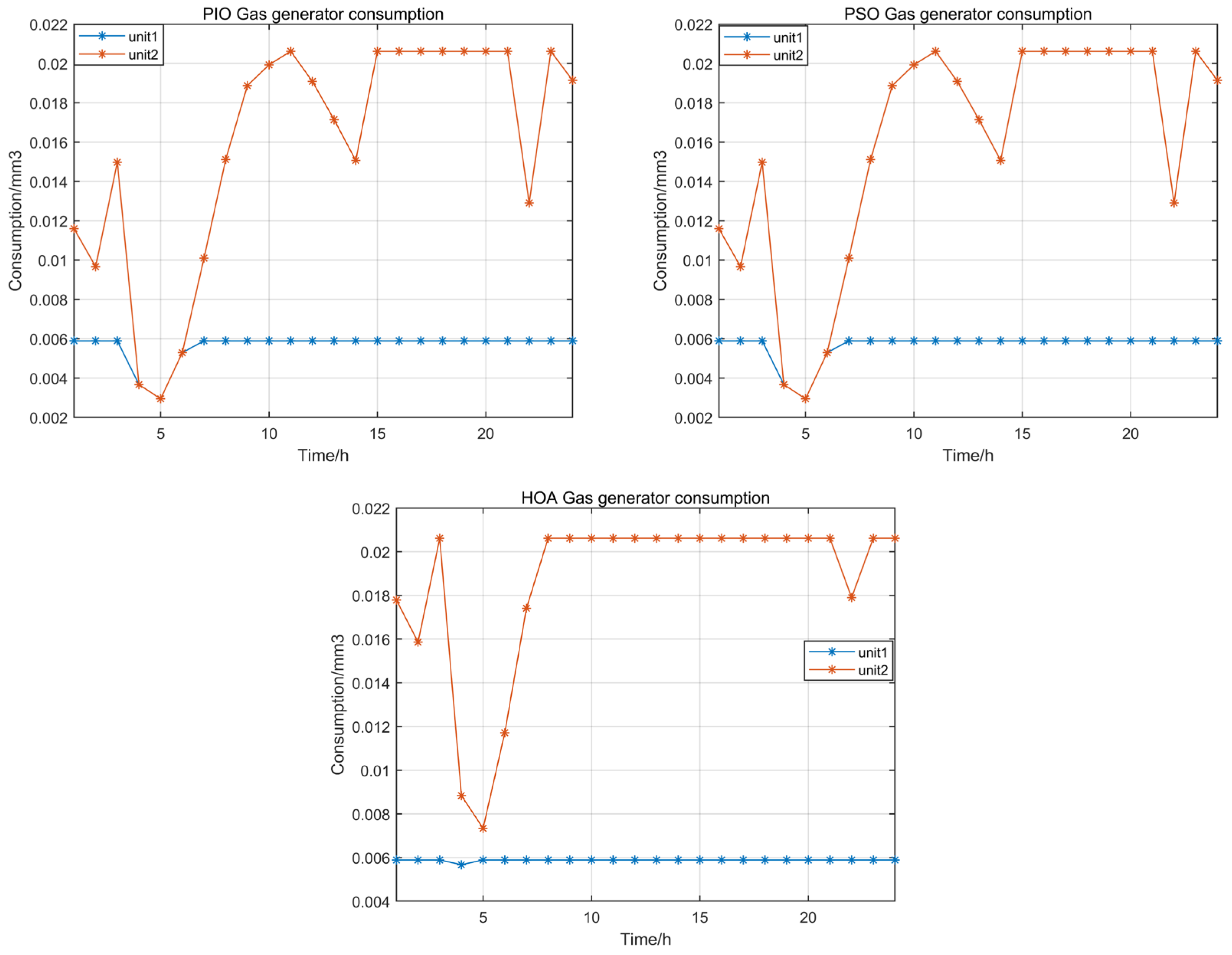
| Node Number | Machine Type | Gas Input Source | Remark |
|---|---|---|---|
| Grid node 33 | gas turbine | Node 6 of the air network supplies gas | none |
| Grid node 37 | gas turbine | Node 19 of the air network supplies gas | none |
| Grid node 30 | CHP units | Node 3 of the air network supplies gas | Heat source of the heat network node 1 |
| The remaining 7 power supply nodes | Coal-fired units | none | none |
| Node ID | Cost Factor | Upper Output Limit/MW | Lower Output Limit/MW | ||
|---|---|---|---|---|---|
| 30 | 1469 | 19.71 | 0.077 | 1040 | 0 |
| 31 | 2639 | 21.02 | 0.009 | 646 | 0 |
| 32 | 2639 | 21.02 | 0.009 | 725 | 0 |
| 33 | 1469 | 20.31 | 0.030 | 652 | 0 |
| 34 | 2839 | 24.02 | 0.077 | 108 | 0 |
| 35 | 2639 | 21.02 | 0.009 | 687 | 0 |
| 36 | 2639 | 21.02 | 0.009 | 580 | 0 |
| 37 | 1469 | 20.31 | 0.030 | 564 | 0 |
| 38 | 1469 | 19.71 | 0.077 | 865 | 0 |
| 39 | 1469 | 19.71 | 0.077 | 1100 | 0 |
| Gas Source Number | Lower Flow Limit/mm3 | Traffic Upper Limit/mm3 |
|---|---|---|
| 1 | 0.90 | 1.7391 |
| 2 | 0 | 1.26 |
| 3 | 0 | 0.72 |
| 4 | 1.00 | 2.3018 |
| 5 | 0 | 0.27 |
| 6 | 0 | 1.44 |
| Pipeline Number | First Node | End Node | Pipeline Number | First Node | End Node | ||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 9.070 | 11 | 11 | 12 | 0.860 |
| 2 | 2 | 3 | 6.040 | 12 | 12 | 13 | 0.910 |
| 3 | 3 | 4 | 1.390 | 13 | 13 | 14 | 7.260 |
| 4 | 5 | 6 | 0.100 | 14 | 14 | 15 | 3.630 |
| 5 | 6 | 7 | 0.150 | 15 | 15 | 16 | 1.450 |
| 6 | 7 | 4 | 0.220 | 16 | 11 | 17 | 0.050 |
| 7 | 4 | 14 | 0.660 | 17 | 17 | 18 | 0.006 |
| 8 | 8 | 9 | 7.260 | 18 | 18 | 19 | 0.002 |
| 9 | 9 | 10 | 1.810 | 19 | 19 | 20 | 0.030 |
| 10 | 10 | 11 | 1.450 |
| Node Number | Upper Pressure Limit (Bar) | Lower Pressure Limit (Bar) | Node Number | Upper Pressure Limit (Bar) | Lower Pressure Limit (Bar) |
|---|---|---|---|---|---|
| 1 | 77.0 | 0 | 11 | 66.2 | 0 |
| 2 | 77.0 | 0 | 12 | 66.2 | 0 |
| 3 | 80.0 | 30.0 | 13 | 66.2 | 0 |
| 4 | 80.0 | 0 | 14 | 66.2 | 0 |
| 5 | 77.0 | 0 | 15 | 66.2 | 0 |
| 6 | 80.0 | 30.0 | 16 | 66.2 | 0 |
| 7 | 80.0 | 30.0 | 17 | 66.2 | 0 |
| 8 | 66.2 | 0 | 18 | 80.0 | 0 |
| 9 | 66.2 | 0 | 19 | 66.2 | 0 |
| 10 | 66.2 | 30.0 | 20 | 66.2 | 25.0 |
| CHP Number | CHP Cost Factor | ||
|---|---|---|---|
| 1 | 24.2 | 0.31 | 2.40 |
| 2 | 24.2 | 0.31 | 2.40 |
| Moment (h) | Temperature (°C) | Moment (h) | Temperature (°C) | Moment (h) | Temperature (°C) |
|---|---|---|---|---|---|
| 1 | −10.00 | 9 | −7.10 | 17 | −5.94 |
| 2 | −10.00 | 10 | −6.52 | 18 | −6.52 |
| 3 | −8.84 | 11 | −5.94 | 19 | −6.52 |
| 4 | −9.42 | 12 | −5.35 | 20 | −6.52 |
| 5 | −9.42 | 13 | −4.77 | 21 | −7.10 |
| 6 | −9.42 | 14 | −4.77 | 22 | −7.68 |
| 7 | −8.84 | 15 | −4.77 | 23 | −8.26 |
| 8 | −8.26 | 16 | −5.35 | 24 | −8.26 |
| Hyper-Parameter | HOA (Nominal) | PSO (Nominal) | PIO (Nominal) | Planned Perturbation |
|---|---|---|---|---|
| Population size N | 6 | 6 | 6 | ±20% |
| Iterations T | 30 | 30 | T1 = 30; T2 = 5 | ±20% |
| Learning/interaction factors | Lévy = 0.05 | c1 = 1.49445, c2 = 1.49445, ω = 0.729 | R = 0.3 (geomagnetic factor) | ±10–20% |
| Randomness and implementation | Fixed seed/unified init/elitism/constraints | Fixed seed/unified init/elitism/constraints | Fixed seed/unified init/elitism/constraints | — |
| Pigeon-Inspired Optimization Algorithm | Particle Swarm Optimization Algorithm | Hippopotamus Optimization Algorithm | |
|---|---|---|---|
| Investment cost (Yuan) | 139,600,000.0000 | 187,400,000.0000 | 206,608,000.0000 |
| Operation cost of thermal power unit (Yuan/day) | 541,983.3137 | 563,482.2677 | 574,552.2387 |
| Operation cost of wind turbine (Yuan/day) | 21,952,737.0990 | 13,170,759.0173 | 13,783,126.4225 |
| Natural gas output cost (Yuan/day) | 66,513,243.0420 | 65,409,457.8785 | 65,342,420.3912 |
| P2G unit operation cost (Yuan/day) | 27,864,853.2895 | 45,245,191.2159 | 35,424,791.5274 |
| Optimal objective function (Yuan/year) | 42,798,178,111.6442 | 42,712,635,496.6322 | 42,227,193,061.6362 |
| Subsystem | Simplified Model Used | Unsimplified Alternative | Captured Effects | Missed Effects | Typical Use Cases |
|---|---|---|---|---|---|
| Power network | DC power flow (linear, P–θ) | AC power flow (full P–Q–V–θ) | Active-power dispatch, line loading | Voltage/reactive limits, losses, voltage stability margins | Day-ahead scheduling, planning under moderate loading |
| Gas network | Steady-state algebraic flow (Weymouth-type, constant compression ratio) | Transient gas with linepack and compressor maps | Average pressures/flows, capacity usage | Linepack dynamics, fast ramping feasibility, compressor efficiency curves | Planning, hourly operation without fast ramps |
| Coupling | Linear energy links (CHP/P2G in steady state) | Dynamic unit/efficiency curves, start/stop | Average production, energy balance | Cycling losses, start-up penalties | Same as above |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Lu, L.; Yang, Q.; Feng, Y.; Wang, B. Multi-Objective Optimization of Electric–Gas–Thermal Systems via the Hippo Optimization Algorithm: Low-Carbon and Cost-Effective Solutions. Sustainability 2025, 17, 9970. https://doi.org/10.3390/su17229970
Hu K, Lu L, Yang Q, Feng Y, Wang B. Multi-Objective Optimization of Electric–Gas–Thermal Systems via the Hippo Optimization Algorithm: Low-Carbon and Cost-Effective Solutions. Sustainability. 2025; 17(22):9970. https://doi.org/10.3390/su17229970
Chicago/Turabian StyleHu, Keyong, Lei Lu, Qingqing Yang, Yang Feng, and Ben Wang. 2025. "Multi-Objective Optimization of Electric–Gas–Thermal Systems via the Hippo Optimization Algorithm: Low-Carbon and Cost-Effective Solutions" Sustainability 17, no. 22: 9970. https://doi.org/10.3390/su17229970
APA StyleHu, K., Lu, L., Yang, Q., Feng, Y., & Wang, B. (2025). Multi-Objective Optimization of Electric–Gas–Thermal Systems via the Hippo Optimization Algorithm: Low-Carbon and Cost-Effective Solutions. Sustainability, 17(22), 9970. https://doi.org/10.3390/su17229970






