Prediction of Thermal and Oxidative Degradation of Amines to Improve Sustainability of CO2 Absorption Process
Abstract
1. Introduction
1.1. State of the Art for Predictive Models
1.2. Motivation and Objectives of the Current Study
2. Methodology
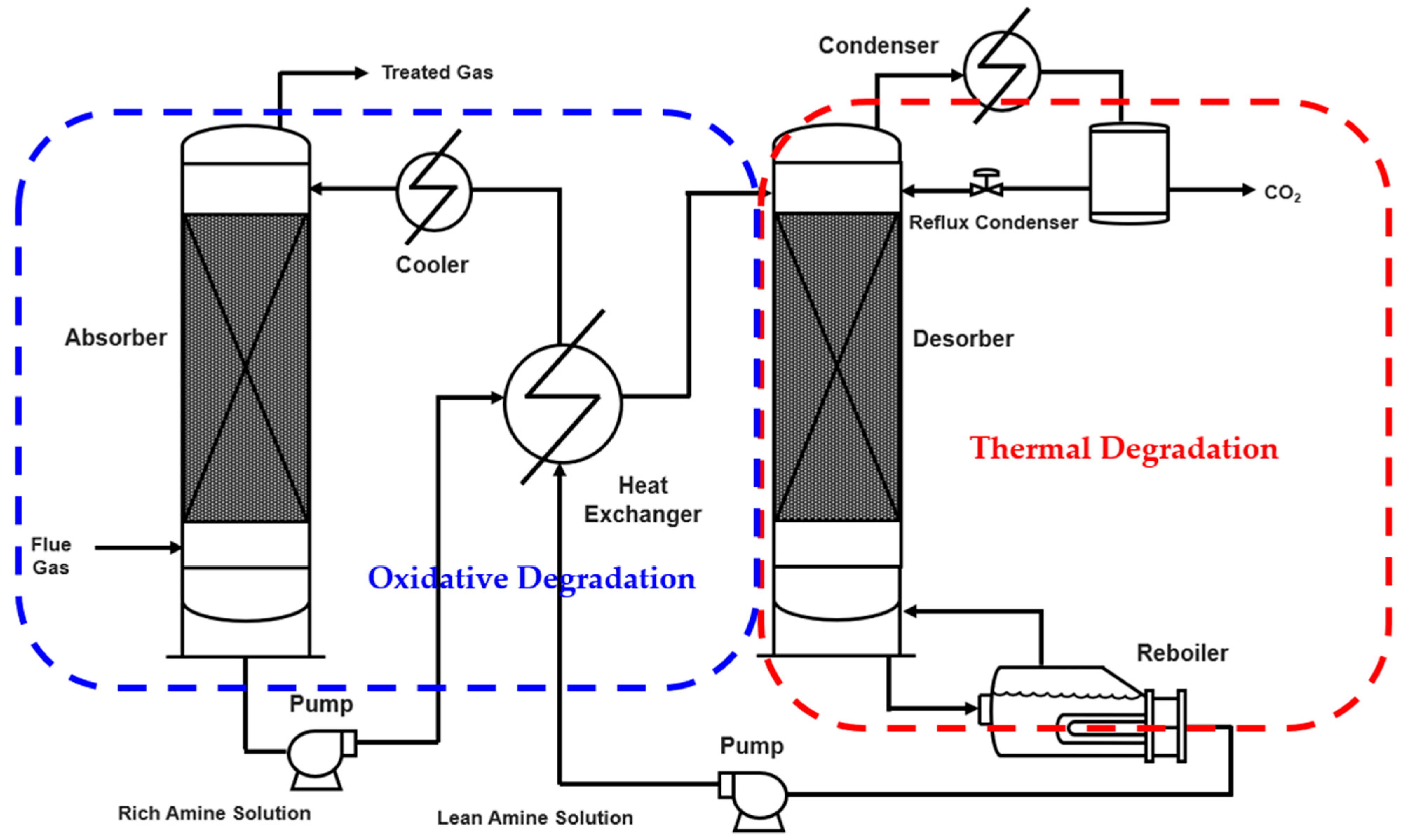
2.1. Experimental Data
2.1.1. Thermal Degradation Data
2.1.2. Oxidative Degradation Data
2.2. Model Development
2.2.1. Thermal Degradation Models
Artificial Neural Network (ANN)
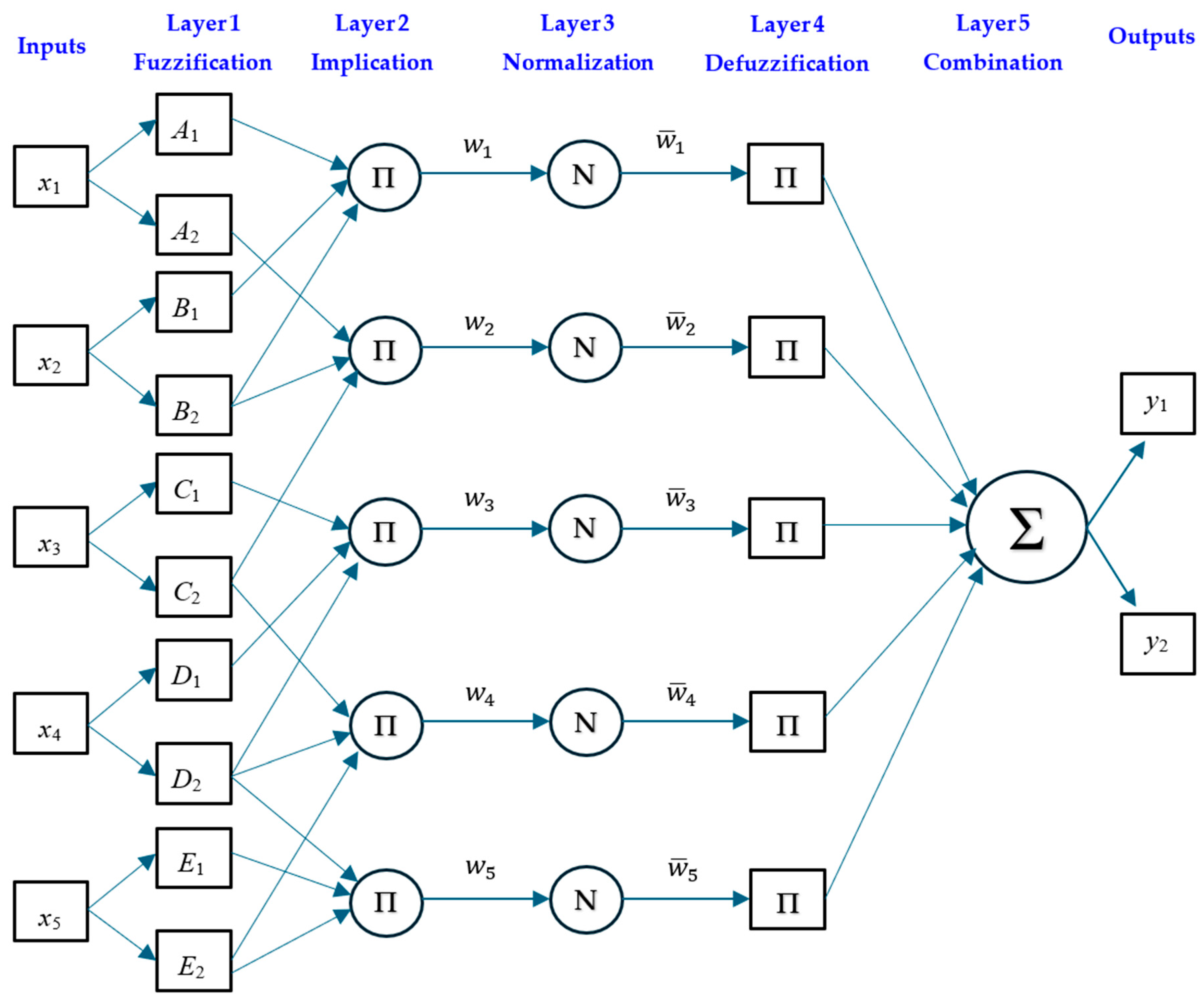
Adaptive Neuro-Fuzzy Inference System (ANFIS)
2.2.2. Oxidative Degradation Models
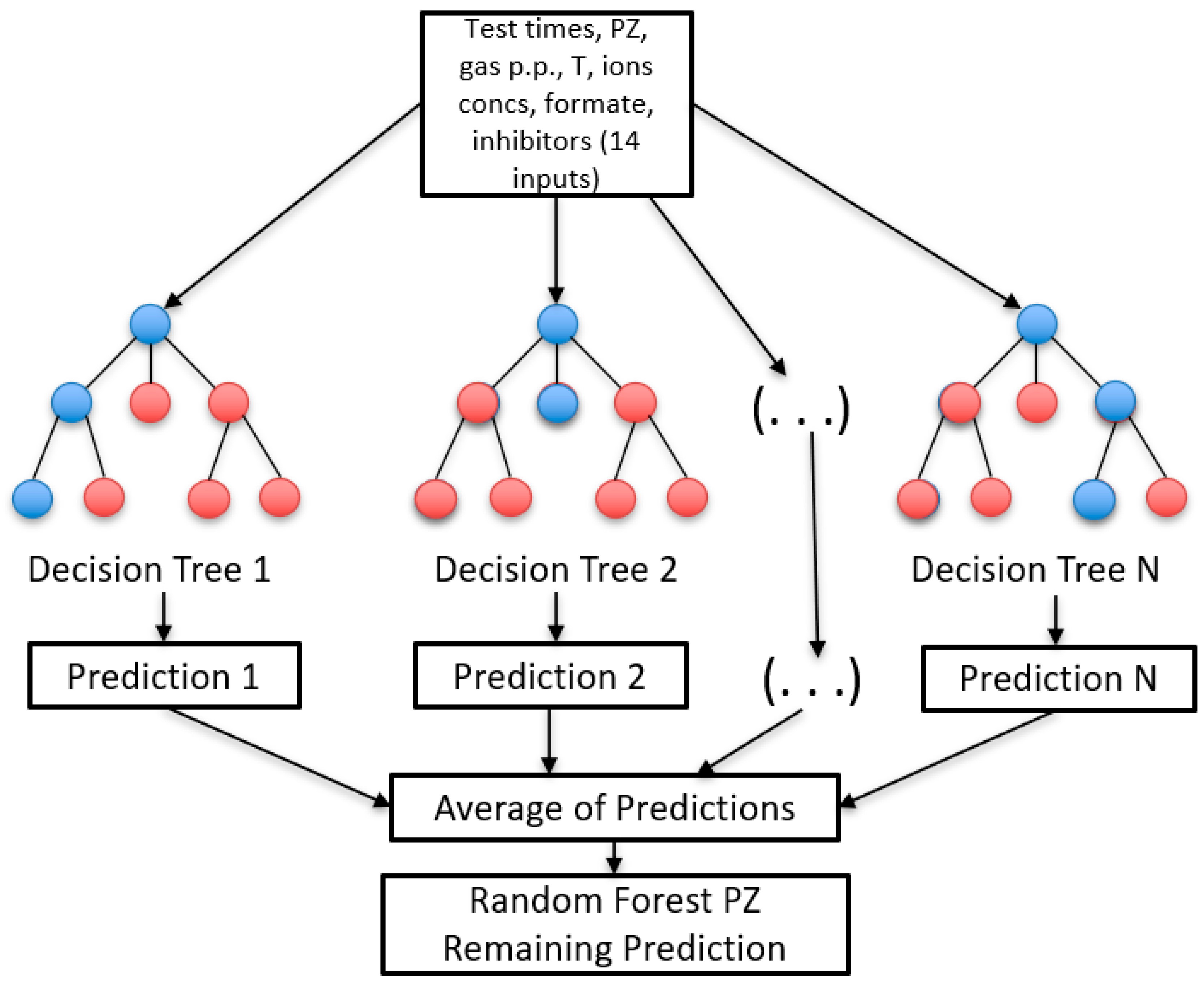
Random Forest Regression (RFR)
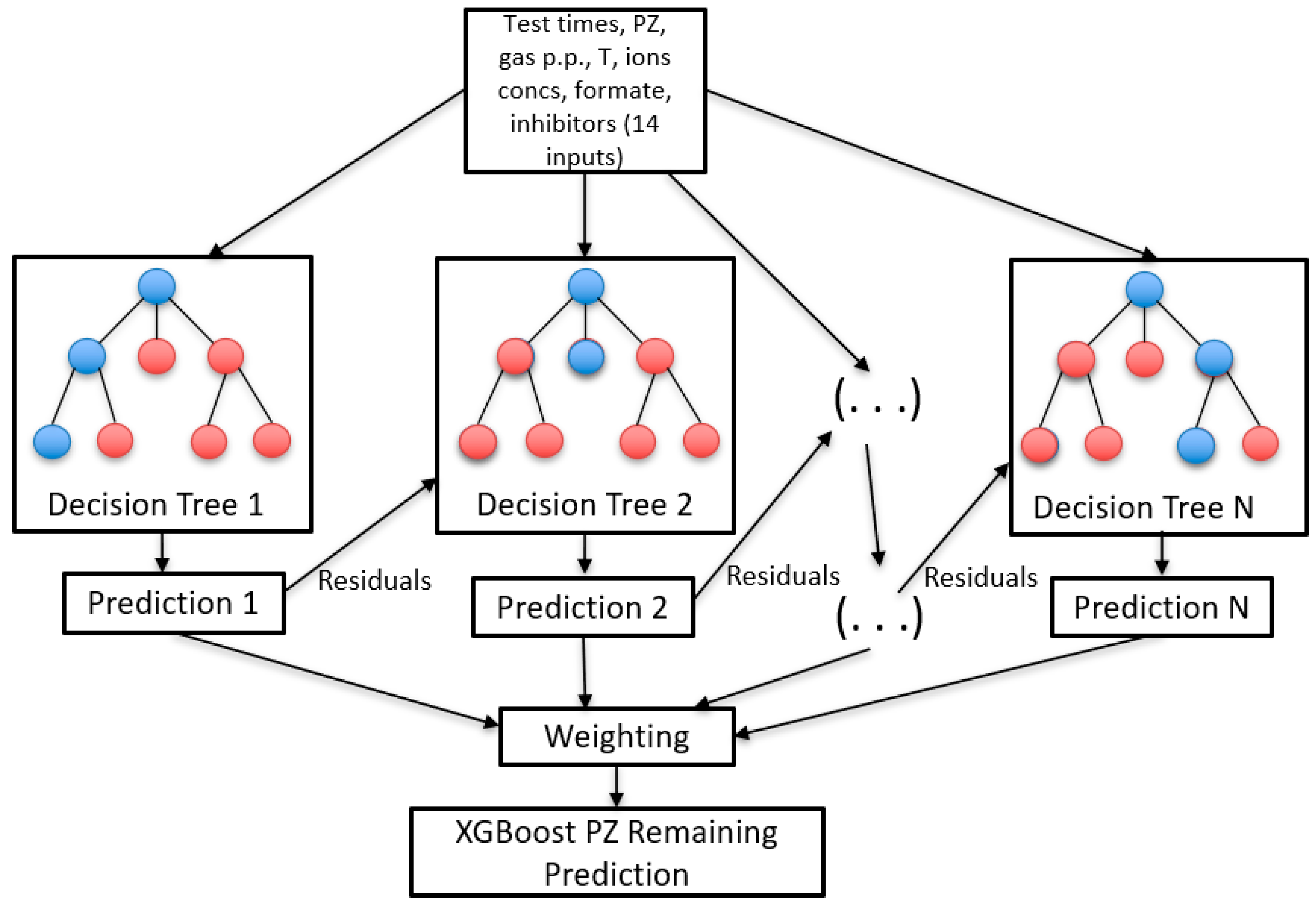
XGBoost
2.3. Model Performance Evaluation
3. Results and Discussion
3.1. Thermal Degradation Results
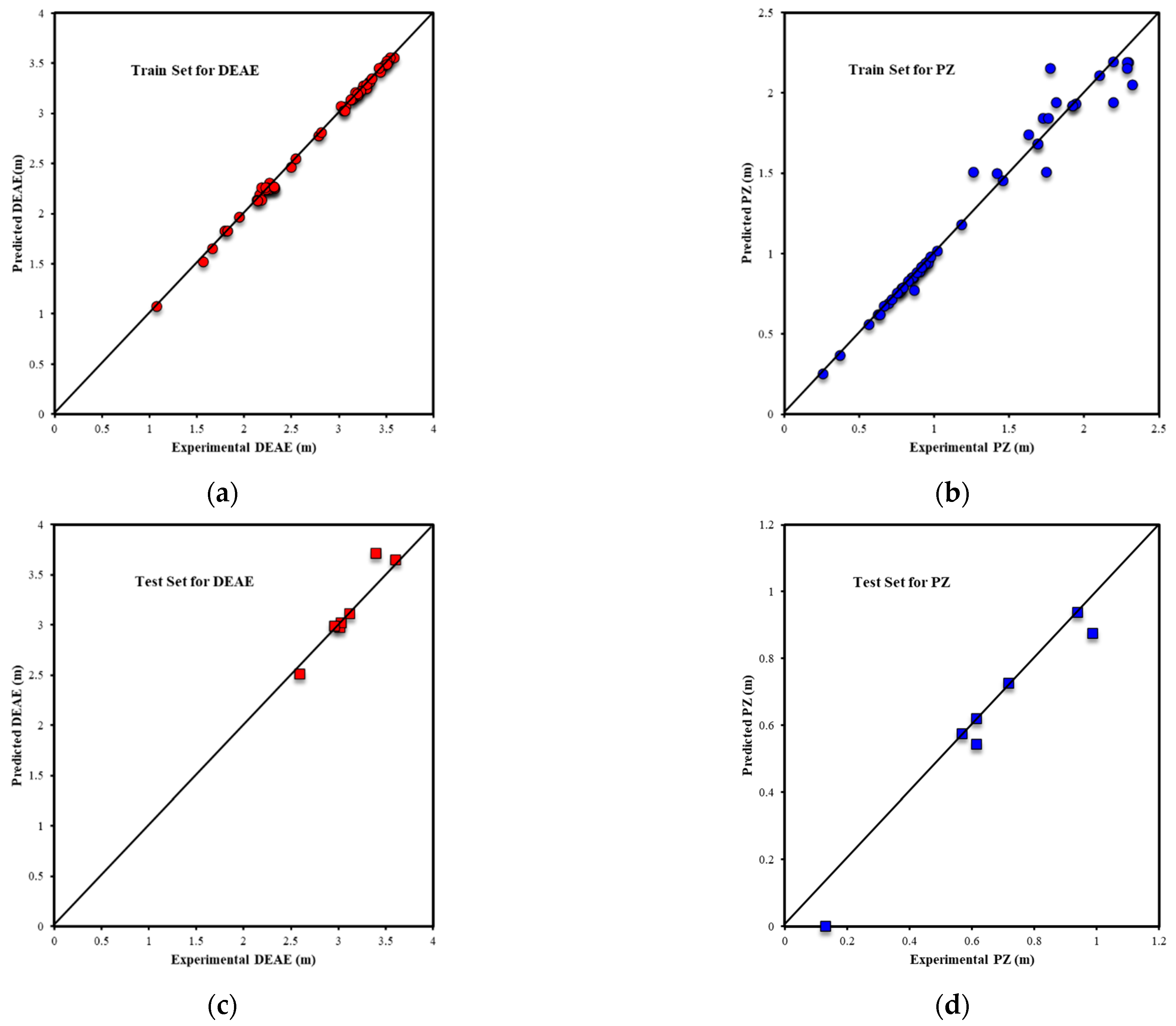
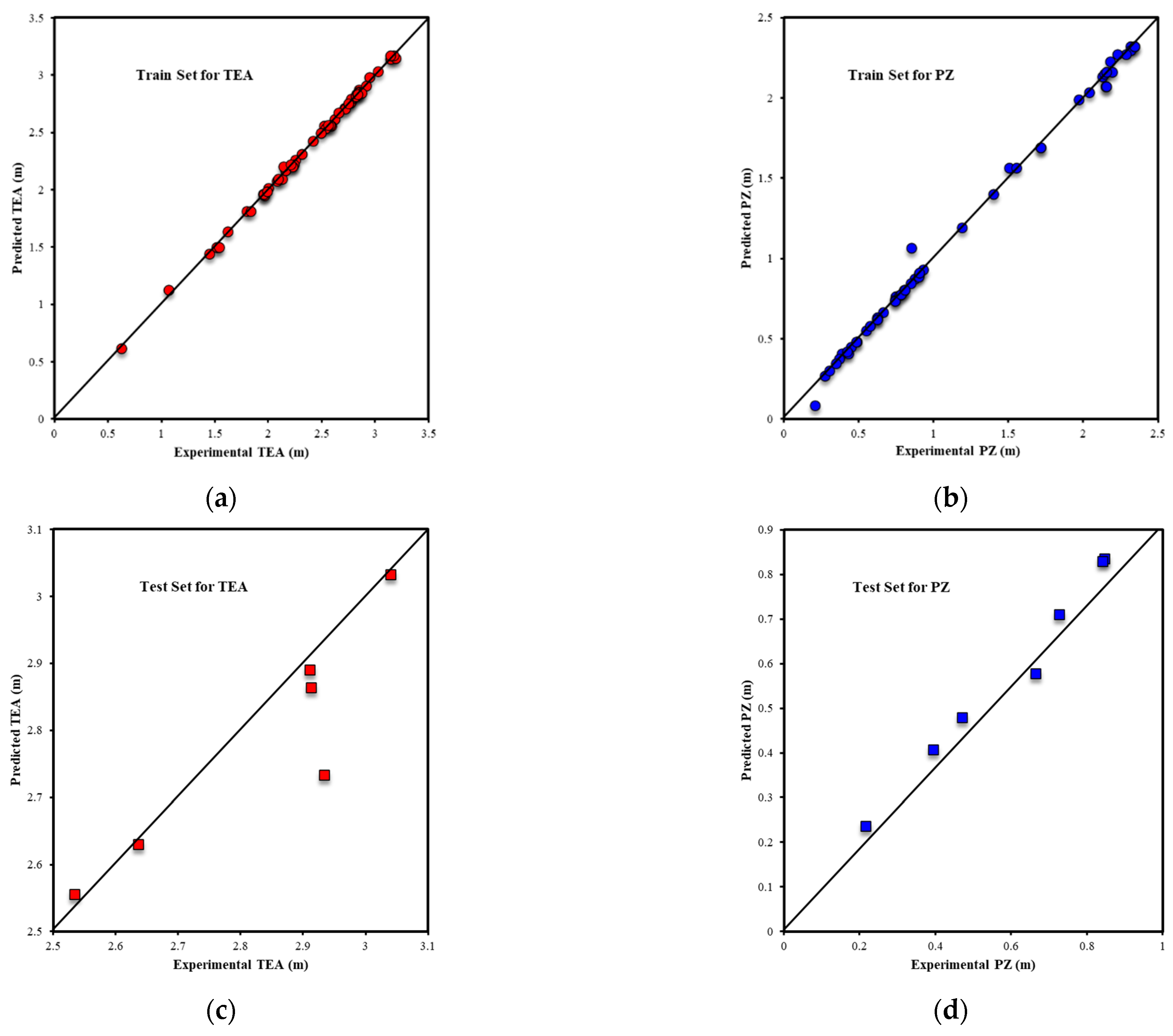
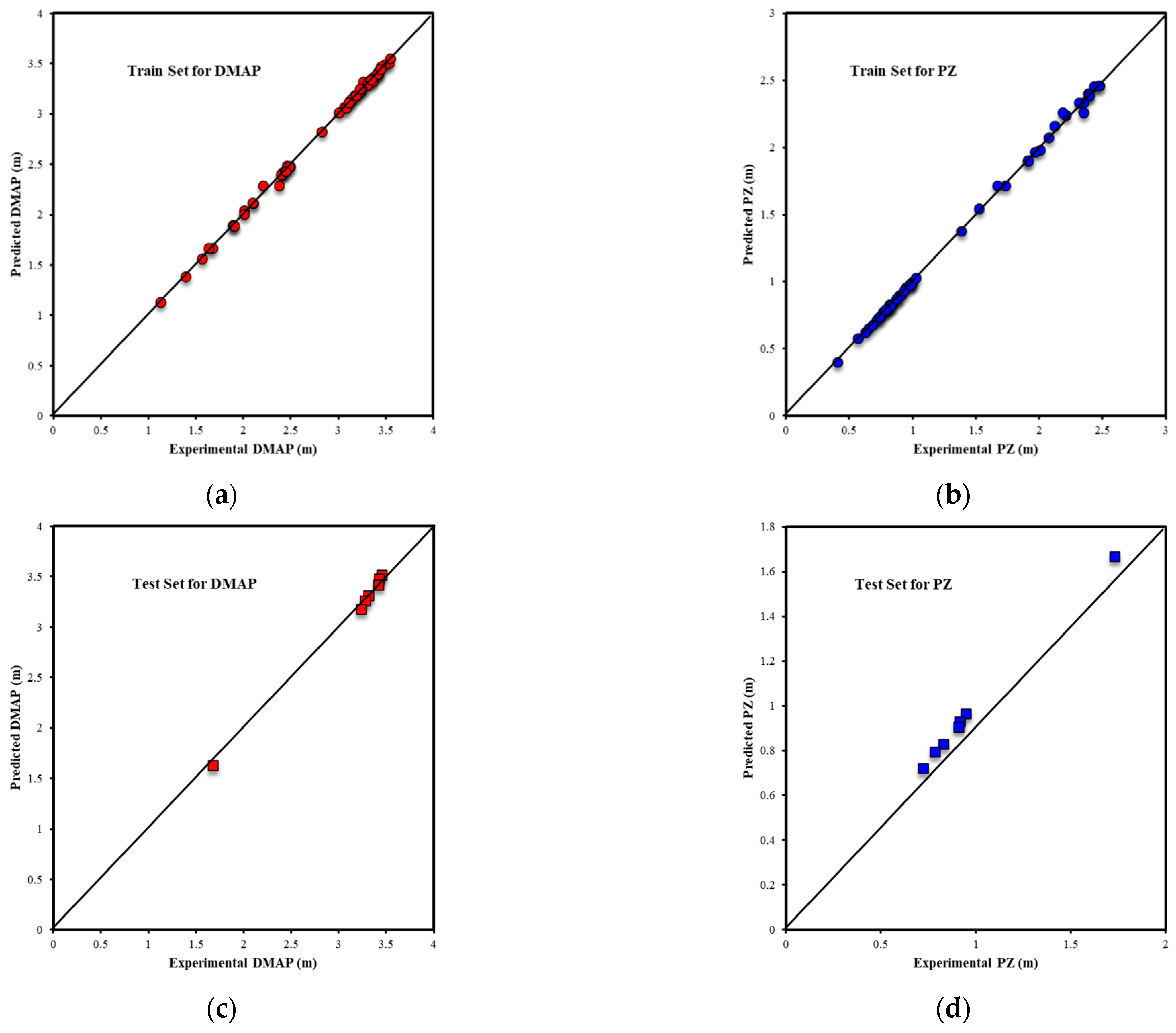
3.1.1. ANN Model Results
3.1.2. ANFIS Model Results
3.2. Oxidative Degradation Results
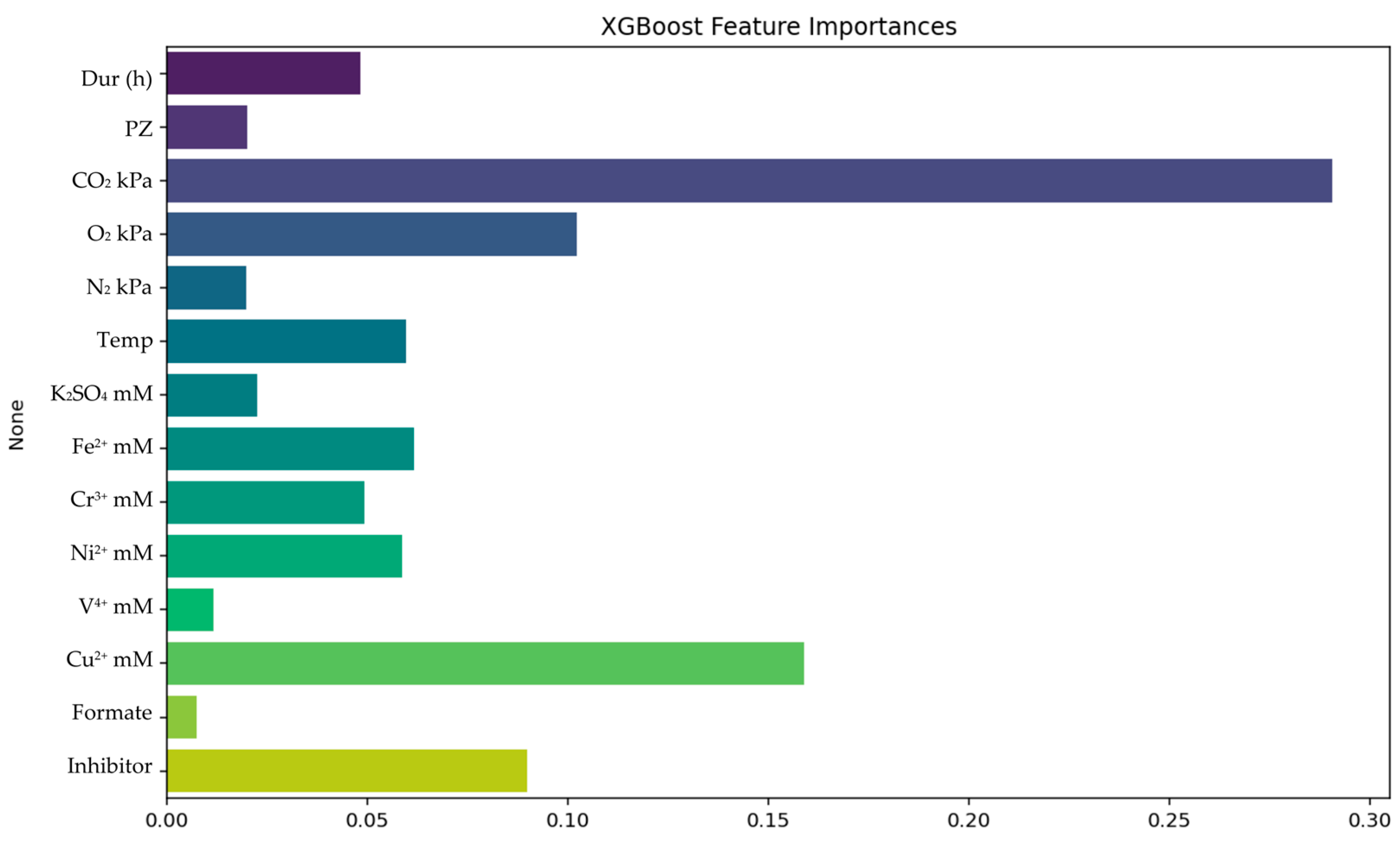
3.2.1. Random Forest Results
3.2.2. XGBoost Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elmarghni, S.; Ansarpour, M.; Borhani, T.N. Effect of Different Amine Solutions on Performance of Post-Combustion CO2 Capture. Processes 2025, 13, 2521. [Google Scholar] [CrossRef]
- Gouedard, C.; Picq, D.; Launay, F.; Carrette, P.L. Amine degradation in CO2 capture. I. A review. Int. J. Greenh. Gas Control 2012, 10, 244–270. [Google Scholar] [CrossRef]
- Namjoshi, O.A. Thermal Degradation of PZ-Promoted Tertiary Amines for CO2 Capture. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2015. [Google Scholar]
- Thompson, J.G.; Gao, X.; Toma, S.; Abad, K.; Bhatnagar, S.; Landon, J.; Liu, K. Decomposition of N-nitrosamines formed in CO2 capture systems through electrochemically-mediated reduction on carbon xerogel electrode. Int. J. Greenh. Gas Control 2019, 83, 83–90. [Google Scholar] [CrossRef]
- Hatchell, D.; Namjoshi, O.; Fischer, K.; Rochelle, G.T. Thermal Degradation of Linear Amines for CO2 Capture. Energy Procedia 2014, 63, 1558–1568. [Google Scholar] [CrossRef]
- Vega, F.; Sanna, A.; Navarrete, B.; Maroto-Valer, M.M.; Cortés, V.J. Degradation of amine-based solvents in CO2 capture process by chemical absorption. Greenh. Gases Sci. Technol. 2014, 4, 707–733. [Google Scholar] [CrossRef]
- Liu, H.; Namjoshi, O.A.; Rochelle, G.T. Oxidative Degradation of Amine Solvents for CO2 Capture. Energy Procedia 2014, 63, 1546–1557. [Google Scholar] [CrossRef]
- Peeters, W.; Neerup, R.; Fosbøl, P.L. Solvent degradation & influences on amine-based carbon capture operations. Int. J. Greenh. Gas Control 2025, 147, 104500. [Google Scholar] [CrossRef]
- Vevelstad, S.J.; Buvik, V.; Knuutila, H.K.; Grimstvedt, A.; da Silva, E.F. Important Aspects Regarding the Chemical Stability of Aqueous Amine Solvents for CO2 Capture. Ind. Eng. Chem. Res. 2022, 61, 15737–15753. [Google Scholar] [CrossRef]
- Borhani, T.N.; García-Muñoz, S.; Vanesa Luciani, C.; Galindo, A.; Adjiman, C.S. Hybrid QSPR models for the prediction of the free energy of solvation of organic solute/solvent pairs. Phys. Chem. Chem. Phys. 2019, 21, 13706–13720. [Google Scholar] [CrossRef] [PubMed]
- Martin, S.; Lepaumier, H.; Picq, D.; Kittel, J.; De Bruin, T.; Faraj, A.; Carrette, P.L. New Amines for CO2 Capture. IV. Degradation, Corrosion, and Quantitative Structure Property Relationship Model. Ind. Eng. Chem. Res. 2012, 51, 6283–6289. [Google Scholar] [CrossRef]
- Azarpour, A.; Zendehboudi, S. Hybrid Smart Strategies to Predict Amine Thermal Degradation in Industrial CO2 Capture Processes. ACS Omega 2023, 8, 26850–26870. [Google Scholar] [CrossRef]
- Davis, J.D. Thermal Degradation of Aqueous Amines used for Carbon Dioxide Capture. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2009. [Google Scholar]
- Kottala, R.K.; Chigilipalli, B.K.; Mukuloth, S.; Shanmugam, R.; Kantumuchu, V.C.; Ainapurapu, S.B.; Cheepu, M. Thermal Degradation Studies and Machine Learning Modelling of Nano-Enhanced Sugar Alcohol-Based Phase Change Materials for Medium Temperature Applications. Energies 2023, 16, 2187. [Google Scholar] [CrossRef]
- Muchan, P.; Supap, T.; Narku-Tetteh, J.; Lisawadi, S.; Idem, R. The relationship between oxidative degradation and ammonia emission of carbon capture amines based on their chemical structures. Clean Energy 2024, 8, 134–152. [Google Scholar] [CrossRef]
- Wagaarachchige, J.D.; Idris, Z.; Khatibzadeh, A.; Drageset, A.; Jens, K.J.; Halstensen, M. Demonstration of CO2 Capture Process Monitoring and Solvent Degradation Detection by Chemometrics at the Technology Centre Mongstad CO2 Capture Plant. Ind. Eng. Chem. Res. 2023, 62, 9747–9754. [Google Scholar] [CrossRef]
- Wagaarachchige, J.D.; Idris, Z.; Khatibzadeh, A.; Drageset, A.; Jens, K.J.; Halstensen, M. Demonstration of CO2 Capture Process Monitoring and Solvent Degradation Detection by Chemometrics at the Technology Centre Mongstad CO2 Capture Plant: Part II. Ind. Eng. Chem. Res. 2024, 63, 10704–10712. [Google Scholar] [CrossRef]
- Buvik, V.; Høisæter, K.K.; Vevelstad, S.J.; Knuutila, H.K. A review of degradation and emissions in post-combustion CO2 capture pilot plants. Int. J. Greenh. Gas Control 2021, 106, 103246. [Google Scholar] [CrossRef]
- Chen, P.; Wang, D.; Yi, N.; Jiang, J.; Herraiz, L.; Zhou, X.; Chen, J.; Ren, Y.; Xu, S.; Garcia, S.; et al. Amine-based carbon capture through an environmental lens: Amine emissions and associated implications. J. Environ. Chem. Eng. 2025, 13, 119605. [Google Scholar] [CrossRef]
- Muchan, P.; Kruthasoot, S.; Kongton, T.; Supap, T.; Narku-Tetteh, J.; Lisawadi, S.; Srisuradetchai, P.; Idem, R. Development of a Predictive Model to Correlate the Chemical Structure of Amines with Their Oxidative Degradation Rate in a Post-Combustion Amine-Based CO2 Capture Process Using Multiple Linear Regression and Machine Learning Regression Approaches. ACS Omega 2024, 9, 6669–6683. [Google Scholar] [CrossRef] [PubMed]
- Irvin, B.D.; Jones, T.; Pelgen, J.V.; Fan, Z.; Abad, K.; Bhatnagar, S.; Frimpong, R.A.; Nikolic, H.; Thompson, J.; Liu, K. Determining alkalinity, carbon loading, and degradation of aqueous amine in CO2 capture processes using heuristic methods. Int. J. Greenh. Gas Control 2025, 145, 104394. [Google Scholar] [CrossRef]
- Braakhuis, L.; Høisæter, K.K.; Knuutila, H.K. Modeling the Formation of Degradation Compounds during Thermal Degradation of MEA. Ind. Eng. Chem. Res. 2022, 61, 2867–2881. [Google Scholar] [CrossRef]
- Braakhuis, L.; Knuutila, H.K. Predicting solvent degradation in absorption–based CO2 capture from industrial flue gases. Chem. Eng. Sci. 2023, 279, 118940. [Google Scholar] [CrossRef]
- Dickinson, J.; Percy, A.; Puxty, G.; Verheyen, T.V. Oxidative degradation of amine absorbents in carbon capture systems—A dynamic modelling approach. Int. J. Greenh. Gas Control 2016, 53, 391–400. [Google Scholar] [CrossRef]
- Yoon, B.; Stowe, H.M.; Hwang, G.S. Molecular mechanisms for thermal degradation of CO2-loaded aqueous monoethanolamine solution: A first-principles study. Phys. Chem. Chem. Phys. 2019, 21, 22132–22139. [Google Scholar] [CrossRef]
- Parks, C.; Alborzi, E.; Akram, M.; Pourkashanian, M. DFT Studies on Thermal and Oxidative Degradation of Monoethanolamine. Ind. Eng. Chem. Res. 2020, 59, 15214–15225. [Google Scholar] [CrossRef]
- Parks, C.; Hughes, K.J.; Pourkashanian, M. Furthering the understanding of product formation in monoethanolamine degradation: A mechanistic DFT study. Int. J. Greenh. Gas Control 2022, 119, 103732. [Google Scholar] [CrossRef]
- Yu, J.; Patel, D.; Hwang, G.S. First-Principles Prediction of the Critical Role of Superoxide Anions in Oxidative Degradation of Aqueous Amine Solvents for Carbon Dioxide Capture. Ind. Eng. Chem. Res. 2025, 64. [Google Scholar] [CrossRef]
- He, Z.; He, L.; Wang, L.; Wang, W.; Ma, D.; Yao, Q.; Sun, M. Thermal oxidation degradation mechanism under the rust-catalyzed condition of CO2 absorbent monoethanolamine and the DFT analysis of pathway. J. Environ. Chem. Eng. 2025, 13, 116189. [Google Scholar] [CrossRef]
- Freeman, S.A. Thermal Degradation and Oxidation of Aqueous Piperazine for Carbon Dioxide Capture. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2011. [Google Scholar]
- Yan, Y.; Borhani, T.N.; Clough, P.T. Chapter 14: Machine Learning Applications in Chemical Engineering. In Machine Learning in Chemistry: The Impact of Artificial Intelligence; RSC Theoretical and Computational Chemistry Series; Royal Society of Chemistry: London, UK, 2020; pp. 340–371. [Google Scholar] [CrossRef]
- Han, S.-H.; Kim, K.W.; Kim, S.; Youn, Y.C. Artificial Neural Network: Understanding the Basic Concepts without Mathematics. Dement. Neurocogn. Disord. 2018, 17, 83–89. [Google Scholar] [CrossRef]
- Ramadan, A.; Kamel, S.; Hamdan, I.; Agwa, A.M. A Novel Intelligent ANFIS for the Dynamic Model of Photovoltaic Systems. Mathematics 2022, 10, 1286. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Zhang, J.; Gu, J.; Zhang, S.; Li, G.; Shao, J.; He, Y.; Yang, H.; Zhang, S.; et al. Applied machine learning to analyze and predict CO2 adsorption behavior of metal-organic frameworks. Carbon Capture Sci. Technol. 2023, 9, 100146. [Google Scholar] [CrossRef]
- Orhan, I.B.; Le, T.C.; Babarao, R.; Thornton, A.W. Accelerating the prediction of CO2 capture at low partial pressures in metal-organic frameworks using new machine learning descriptors. Commun. Chem. 2023, 6, 214. [Google Scholar] [CrossRef]
- Burns, T.D.; Pai, K.N.; Subraveti, S.G.; Collins, S.P.; Krykunov, M.; Rajendran, A.; Woo, T.K. Prediction of MOF Performance in Vacuum Swing Adsorption Systems for Postcombustion CO2 Capture Based on Integrated Molecular Simulations, Process Optimizations, and Machine Learning Models. Environ. Sci. Technol. 2020, 54, 4536–4544. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2016, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Yang, A.; Sun, S.; Mi, H.; Wang, W.; Liu, J.; Kong, Z.Y. Interpretable Feedforward Neural Network and XGBoost-Based Algorithms to Predict CO2 Solubility in Ionic Liquids. Ind. Eng. Chem. Res. 2024, 63, 8293–8305. [Google Scholar] [CrossRef]
- Longe, P.O.; Davoodi, S.; Mehrad, M.; Wood, D.A. Robust machine-learning model for prediction of carbon dioxide adsorption on metal-organic frameworks. J. Alloys. Compd. 2025, 1010, 177890. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining 2019, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar] [CrossRef]
- Gharamaleki, S.B.; Ruiz, S.C.; Reina, T.R.; Michael Short, S.; Duyar, M. Effect of adsorbent loading on NaNiRu-DFMs’ CO2 capture and methanation: Finding optimal Na-loading using Bayesian optimisation guided experiments. Ind. Chem. Mater. 2025. [Google Scholar] [CrossRef]








| Model | Solvent | Key Remarks | Descriptors/Inputs of the Model | References |
|---|---|---|---|---|
| QSPR model for degradation (not clear that it is oxidative or thermal) | 22 different amine solutions | PLS model is used for this model R2 value of 0.85 | dipole moment, calculated pKa value, and topological and Jurs descriptors | [11] |
| Machine learning model for thermal degradation | 135 data points for MEA solution | ANN-PSO, Coupled simulated annealing-least squares support vector machine (CSA-LSSVAM), GEP and ANFIS used. The most accurate model was ANFIS with R2, MSE, and AARE% of 0.992, 0.066, and 2.745. | CO2 loading, temperature, initial concentration of MEA, and duration | [12] |
| Chemometric models for total inorganic carbon (TIC) and total alkalinity (TA) | MEA | PLS model is developed. TIC-1 model was based on 1 latent variable (LV) with RMSE of 0.0415 mol/kg and R2 of 0.985. TA-1 model was based on 2 LV with RMSE of 0.0953 mol/kg and R2 of 0.882. TIC-2 model was based on 3 LV with RMSE of 0.0206 mol/kg and R2 of 0.992. TA-2 model was based on 3 LV with RMSE of 0.0514 mol/kg and R2 of 0.920. | FTIR spectra data of the solvent samples | [16] |
| Chemometric models to detect heat-stable salts (HSS) and amine degradation products (ADPs) | MEA | PLS model is developed. HSS model was based on 1 LV with RMSE of 0.0144 mol/kg and R2 of 0.933. Another HSS model was based on 2 LVs with RMSE of 0.0117 mol/kg and R2 of 0.952. ADO model was obtained with RMSE of 4621 mg/L and R2 of 0.916 | FTIR spectra data of the solvent samples Residual FTIR spectra | [17] |
| QSPR model for Oxidative degradation | 30 amines in 4 categories (cyclic and non-cyclic) | Multiple Linear Regression (MLR) and CatBoost Regression (ML + MLR hybrid) used in the study. Based only on structural groups and substituents of amines with 22.2% average absolute deviations (AAD) for the training set and 7.0% AAD for validation set. Using CatBoost machine learning approach the degradation rate prediction accuracy improved to 0.3% AAD for the training set and 3.2% for validation. | Structural descriptors (e.g., NH, CH, OH groups), electron-withdrawing groups (EWG), electron-donating groups (EDG), steric (S) variables, and interaction terms | [20] |
| ANN model | CAER-solvent | ANN for real-time estimation of alkalinity, carbon loading, and solvent degradation in amine-based CO2 capture. The key parameters used were pH, temperature, density, viscosity, and C/N ratio, all of which influence solvent performance | Amine concentration, temperature, CO2 exposure/flow, reaction time, measured alkalinity | [21] |
| XGBoost | RF | ||
|---|---|---|---|
| Parameter | Definition/Value | Parameter | Definition/Value |
| Number of inputs | 14 | Number of inputs | 14 |
| Number of outputs | 1 | Number of outputs | 1 |
| n_estimators | 1316 | n_estimators | 444 |
| Max depth | 10 | Max depth | 10 |
| Learning Rate | 0.0116 | Min samples split | 3 |
| Subsample | 0.6711 | Min samples leaf | 1 |
| Colsample_bytree | 0.9006 | Max_features | Log2 |
| gamma | 0.0013 | ||
| Min_child_weight | 2 | ||
| Reg_alpha | 0.5034 | ||
| Reg_lambda | 0.5924 | ||
| ANFIS | ANN | ||
|---|---|---|---|
| Parameter | Definition/Value | Parameter | Definition/Value |
| Number of inputs | 5 | Number of inputs | 5 |
| Number of outputs | 2 | Number of outputs | 2 |
| Fuzzy type | Sugeno | Hidden layer size | 5 |
| FIS generation Grid | Partition | Training algorithm | Levenberg–Marquardt |
| Optimisation method | Hybrid | performance function | MSE |
| Membership function | Gaussian | Transfer functions | Tansig and purelin |
| Number of fuzzy rules | 9 | Max fail | 20 |
| Maximum number of epochs | 300 | Number of epochs | 100 |
| Initial step size | 0.01 | Initial Mu | 0.001 |
| Increase rate of step size | 1.05 | Stopped Value Mu | 0.0001 |
| Decrease rate of step size | 0.7 | ||
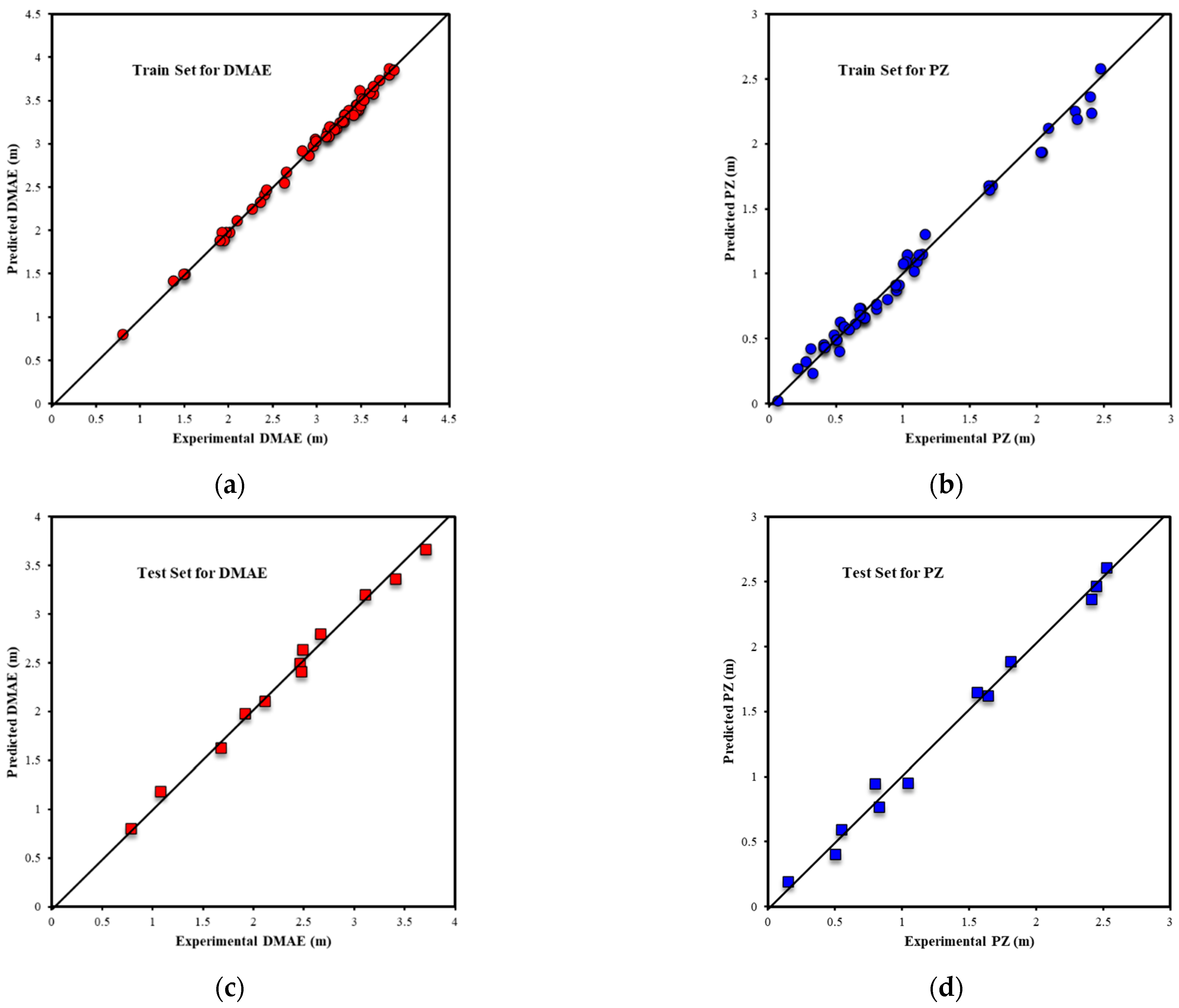
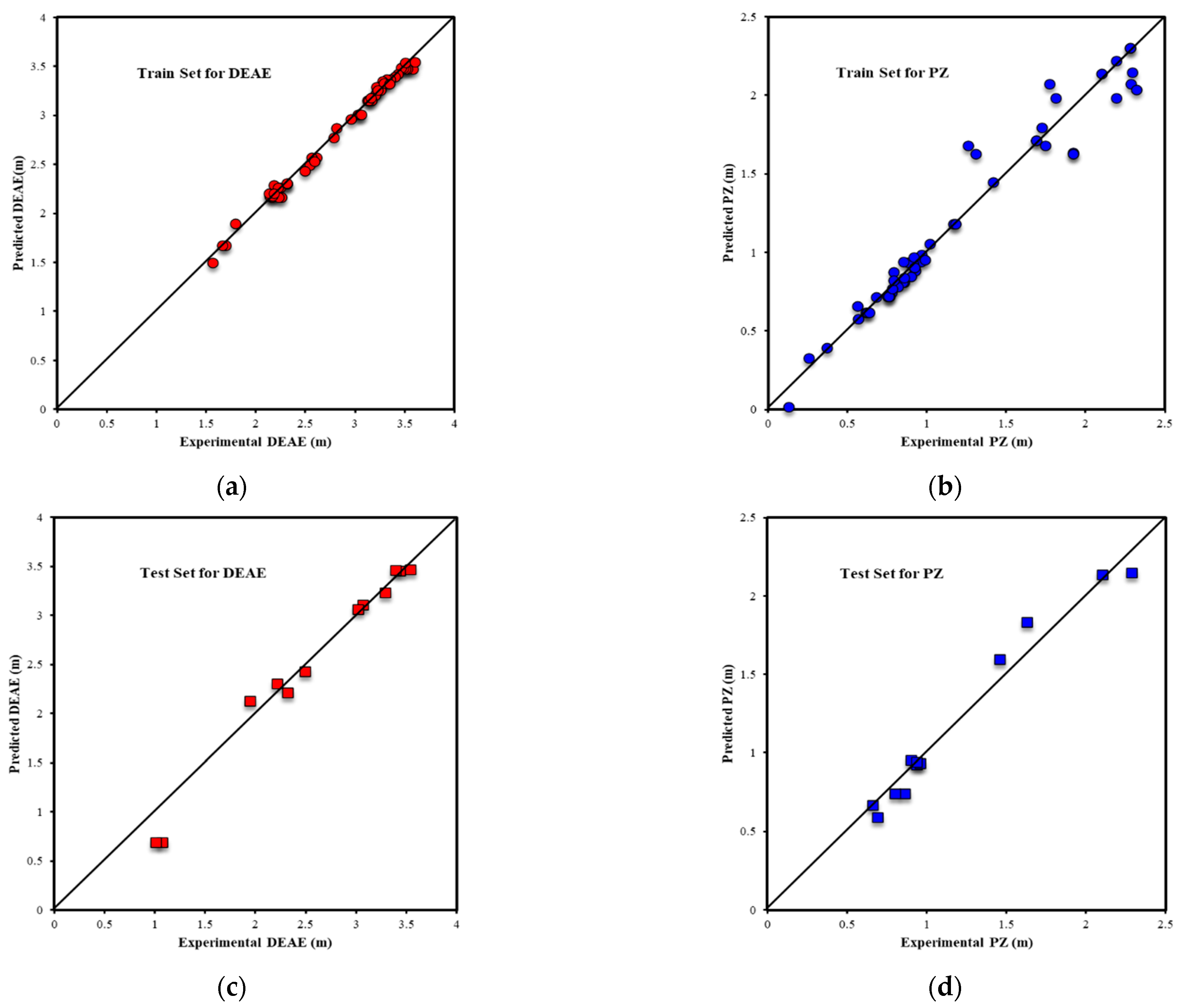
| Metrics | PZ-MDEA | PZ-TEA | PZ-DMAE | PZ-DEAE | PZ-DMAP |
|---|---|---|---|---|---|
| R2All-Output1 | 0.9803 | 0.9717 | 0.9939 | 0.9853 | 0.9969 |
| R2All-Output2 | 0.9750 | 0.9626 | 0.9864 | 0.9593 | 0.9950 |
| R2Train-Output1 | 0.9812 | 0.9688 | 0.9962 | 0.9938 | 0.9970 |
| R2Train-Output2 | 0.9814 | 0.9690 | 0.9734 | 0.9558 | 0.9943 |
| R2Validation-Output1 | 0.9809 | 0.9854 | 0.9878 | 0.9916 | 0.9977 |
| R2Validation-Output2 | 0.9226 | 0.9570 | 0.9906 | 0.9734 | 0.9962 |
| R2Test-Output1 | 0.9739 | 0.9695 | 0.9910 | 0.9624 | 0.9949 |
| R2Test-Output2 | 0.9282 | 0.9272 | 0.9906 | 0.9658 | 0.9960 |
| RMSEAll-Output1 | 0.0933 | 0.0967 | 0.0639 | 0.0789 | 0.0394 |
| RMSEAll-Output2 | 0.0993 | 0.1349 | 0.0819 | 0.1148 | 0.0447 |
| RMSETrain-Output1 | 0.0907 | 0.1069 | 0.0440 | 0.0458 | 0.0389 |
| RMSETrain-Output2 | 0.0920 | 0.1279 | 0.0677 | 0.1261 | 0.0461 |
| RMSEValidation-Output1 | 0.1026 | 0.0591 | 0.1064 | 0.0606 | 0.0368 |
| RMSEValidation-Output2 | 0.0867 | 0.1143 | 0.1300 | 0.0693 | 0.0415 |
| RMSETest-Output1 | 0.0950 | 0.0776 | 0.0795 | 0.1642 | 0.0438 |
| RMSETest-Output2 | 0.1358 | 0.1774 | 0.0769 | 0.0977 | 0.0415 |
| AARE%All-Output1 | 3.04% | 3.84% | 2.24% | 2.53% | 1.38% |
| AARE%All-Output2 | 9.82% | 11.06% | 10.17% | 7.26% | 2.42% |
| AARE%Train-Output1 | 2.90% | 4.48% | 1.23% | 1.39% | 1.38% |
| AARE%Train-Output2 | 9.24% | 11.98% | 10.02% | 7.95% | 2.32% |
| AARE%Validation-Output1 | 3.69% | 2.00% | 5.60% | 1.99% | 1.54% |
| AARE%Validation-Output2 | 11.64% | 9.92% | 11.63% | 5.07% | 2.71% |
| AARE%Test-Output1 | 3.00% | 2.88% | 3.34% | 8.09% | 1.21% |
| AARE%Test-Output2 | 10.57% | 8.15% | 9.37% | 6.38% | 2.58% |
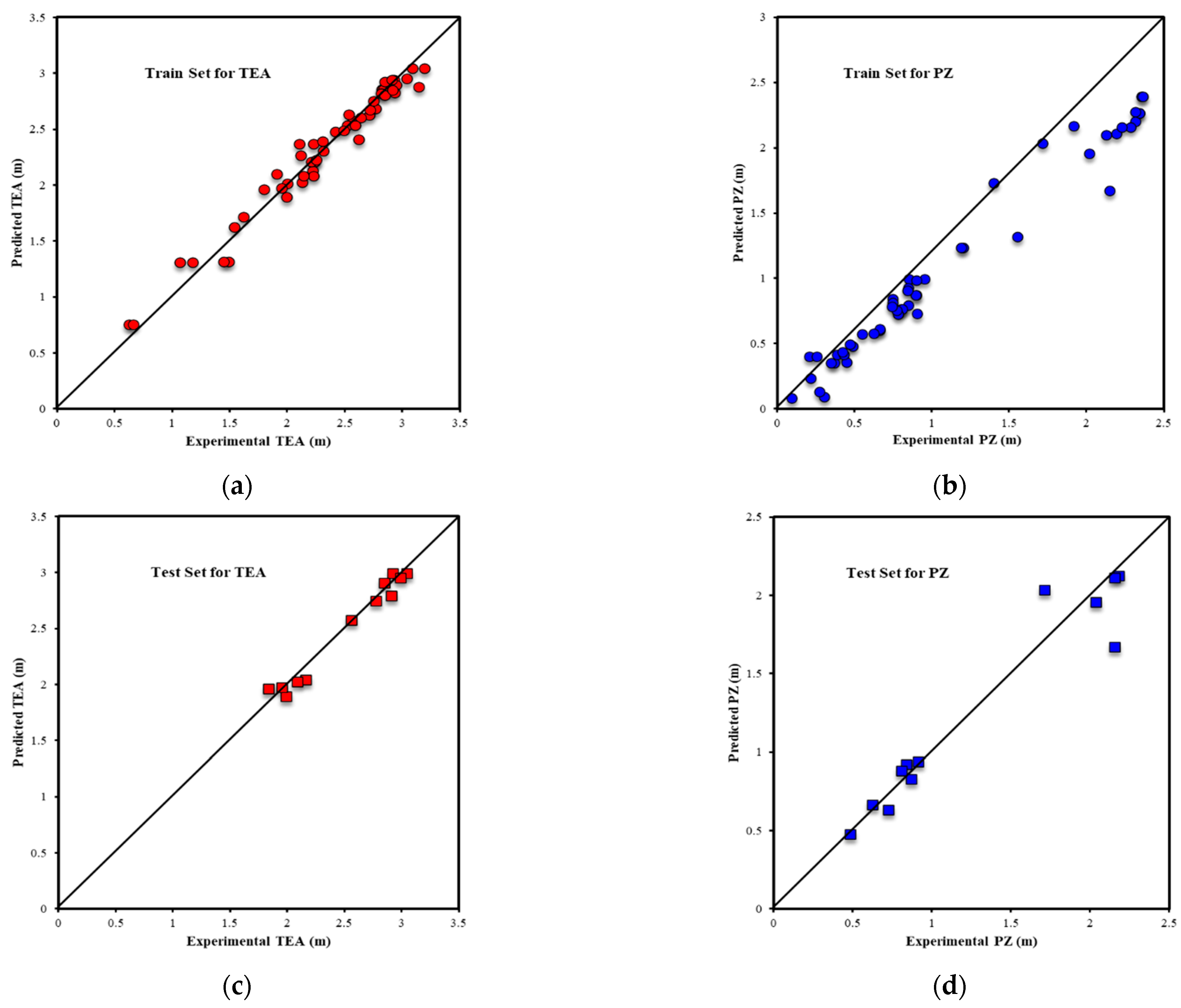
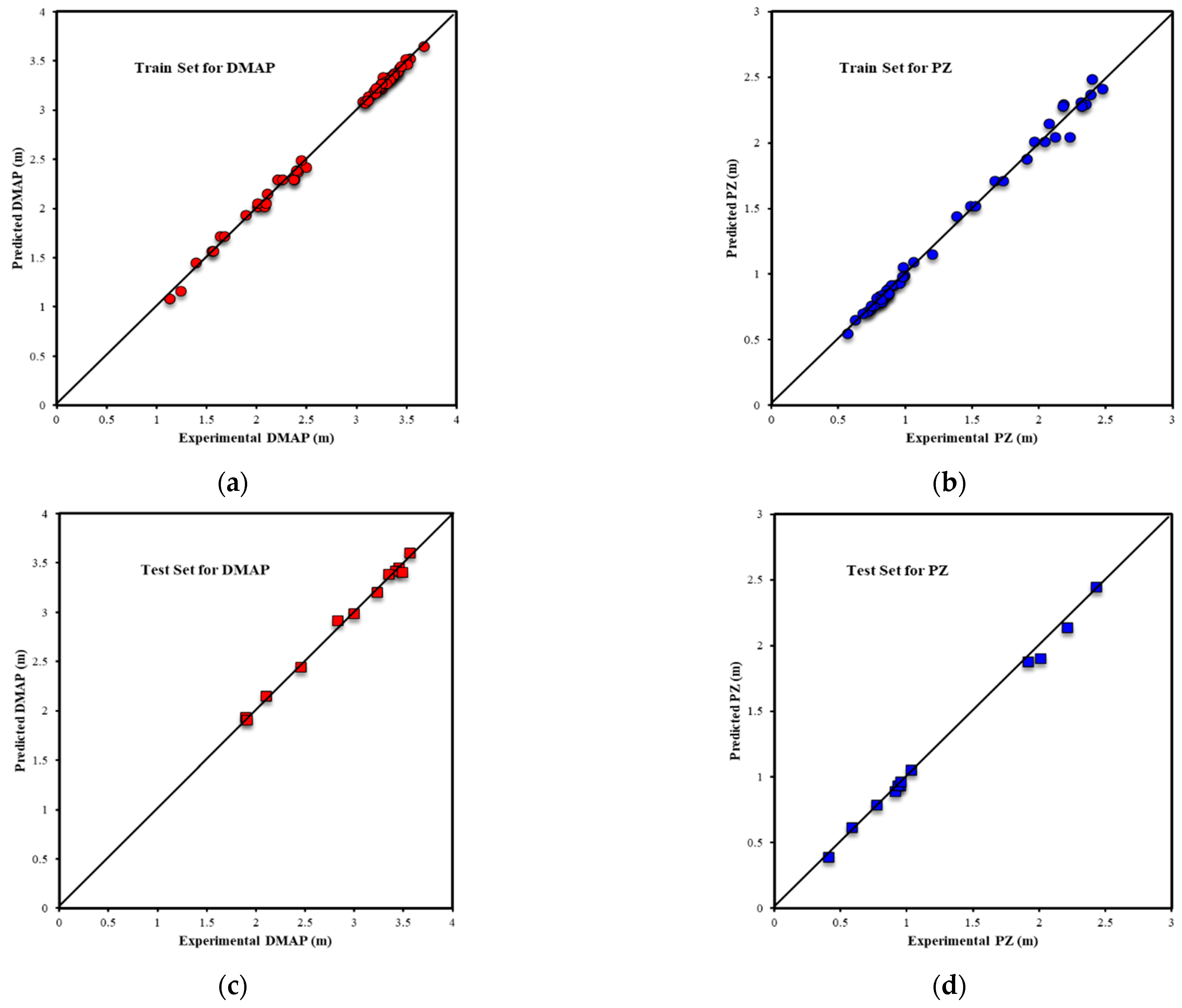
| Metrics | PZ-MDEA | PZ-TEA | PZ-DMAE | PZ-DEAE | PZ-DMAP |
|---|---|---|---|---|---|
| R2All-Output1 | 0.9679 | 0.9810 | 0.9893 | 0.9938 | 0.9975 |
| R2All-Output2 | 0.9572 | 0.9936 | 0.9977 | 0.9604 | 0.9971 |
| R2Train-Output1 | 0.9942 | 0.9987 | 0.9965 | 0.9980 | 0.9988 |
| R2Train-Output2 | 0.9964 | 0.9971 | 0.9995 | 0.9728 | 0.9989 |
| R2Validation-Output1 | 0.7919 | 0.9419 | 0.9915 | 0.9943 | 0.9936 |
| R2Validation-Output2 | 0.7906 | 0.9734 | 0.9914 | 0.8820 | 0.9824 |
| R2Test-Output1 | 0.9772 | 0.8913 | 0.7211 | 0.8256 | 0.9330 |
| R2Test-Output2 | 0.9909 | 0.9755 | 0.9785 | 0.9310 | 0.9852 |
| RMSEAll-Output1 | 0.1193 | 0.0792 | 0.0844 | 0.0513 | 0.0357 |
| RMSEAll-Output2 | 0.1300 | 0.0557 | 0.0338 | 0.1132 | 0.0339 |
| RMSETrain-Output1 | 0.0523 | 0.0195 | 0.0459 | 0.0282 | 0.0221 |
| RMSETrain-Output2 | 0.0365 | 0.0386 | 0.0158 | 0.0932 | 0.0214 |
| RMSEValidation-Output1 | 0.2778 | 0.1858 | 0.0931 | 0.0619 | 0.0739 |
| RMSEValidation-Output2 | 0.3185 | 0.1096 | 0.0674 | 0.1935 | 0.0708 |
| RMSETest-Output1 | 0.0208 | 0.0814 | 0.2145 | 0.1257 | 0.0273 |
| RMSETest-Output2 | 0.0173 | 0.0348 | 0.0525 | 0.0688 | 0.0092 |
| AARE%All-Output1 | 2.35% | 1.62% | 2.15% | 1.25% | 0.91% |
| AARE%All-Output2 | 3.26% | 3.92% | 2.98% | 4.93% | 1.27% |
| AARE%Train-Output1 | 1.35% | 0.65% | 1.37% | 0.85% | 0.52% |
| AARE%Train-Output2 | 2.09% | 2.38% | 1.02% | 2.71% | 0.79% |
| AARE%Validation-Output1 | 7.94% | 6.19% | 4.17% | 2.60% | 2.97% |
| AARE%Validation-Output2 | 9.39% | 10.90% | 2.90% | 8.12% | 3.82% |
| AARE%Test-Output1 | 0.66% | 1.84% | 5.20% | 2.26% | 0.68% |
| AARE%Test-Output2 | 2.88% | 4.69% | 19.34% | 17.90% | 1.03% |
| Metrics | RF | XGBoost |
|---|---|---|
| R2Train | 0.9722 | 0.9487 |
| R2Test | 0.8655 | 0.8900 |
| R2Validation | 0.8800 | 0.8890 |
| RMSETrain | 0.0997 | 0.1354 |
| RMSETest | 0.2177 | 0.2085 |
| RMSEValidation | 0.2454 | 0.2230 |
| AARE%Train | 1.65% | 2.61% |
| AARE%Test | 3.90% | 3.97% |
| AARE%Validation | 5.35% | 5.15% |
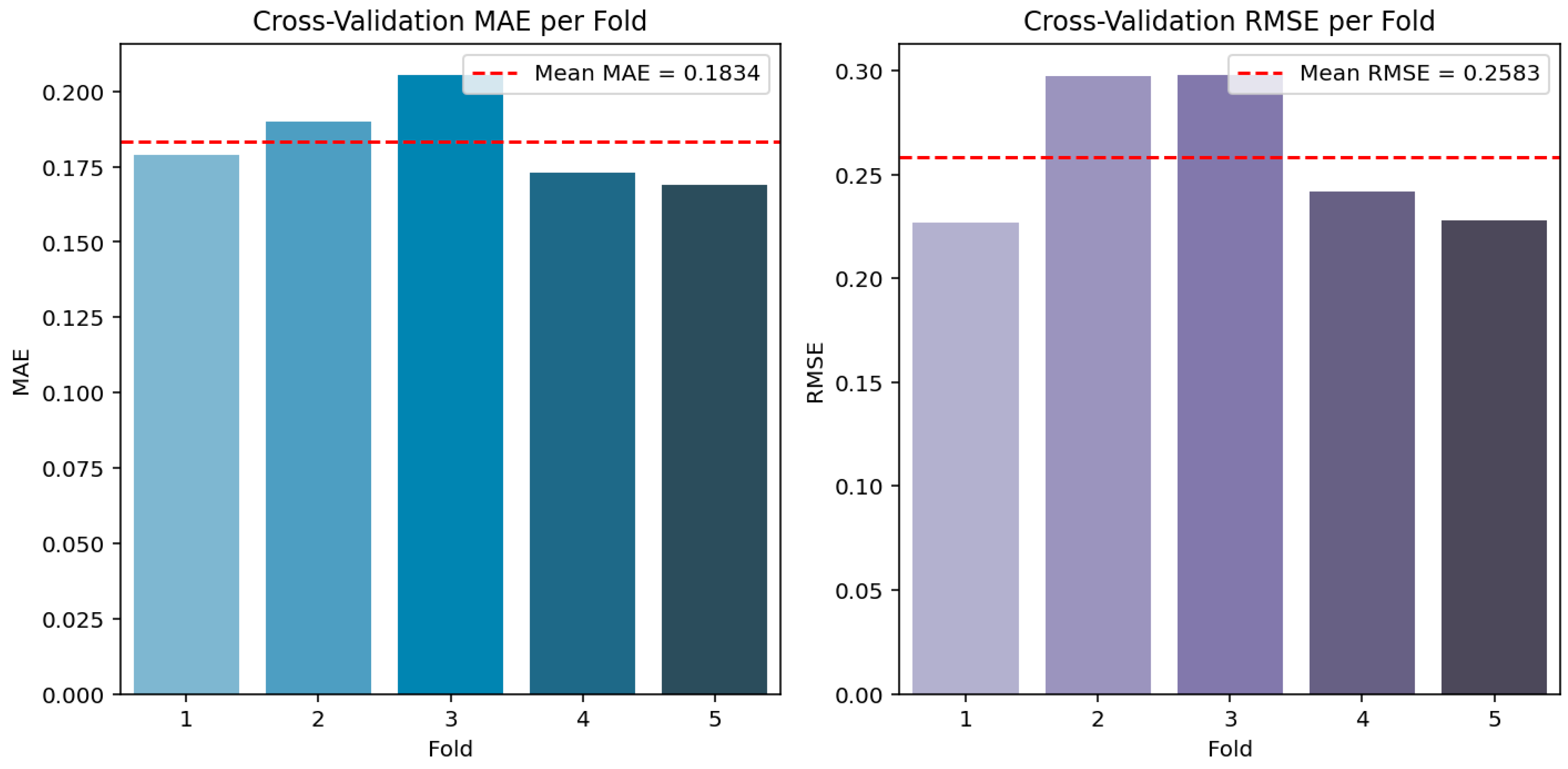
| 5-fold cross validation (mean MAE) | 0.1735 | 0.1834 |
| 5-fold cross validation (std dev) | 0.0208 | 0.0132 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borhani, T.N.; Short, M. Prediction of Thermal and Oxidative Degradation of Amines to Improve Sustainability of CO2 Absorption Process. Sustainability 2025, 17, 10311. https://doi.org/10.3390/su172210311
Borhani TN, Short M. Prediction of Thermal and Oxidative Degradation of Amines to Improve Sustainability of CO2 Absorption Process. Sustainability. 2025; 17(22):10311. https://doi.org/10.3390/su172210311
Chicago/Turabian StyleBorhani, Tohid N., and Michael Short. 2025. "Prediction of Thermal and Oxidative Degradation of Amines to Improve Sustainability of CO2 Absorption Process" Sustainability 17, no. 22: 10311. https://doi.org/10.3390/su172210311
APA StyleBorhani, T. N., & Short, M. (2025). Prediction of Thermal and Oxidative Degradation of Amines to Improve Sustainability of CO2 Absorption Process. Sustainability, 17(22), 10311. https://doi.org/10.3390/su172210311







