A Dynamic Urban Waterlogging Risk Assessment Framework Using RAGA-Optimized Projection Pursuit and Scenario Simulation
Abstract
1. Introduction
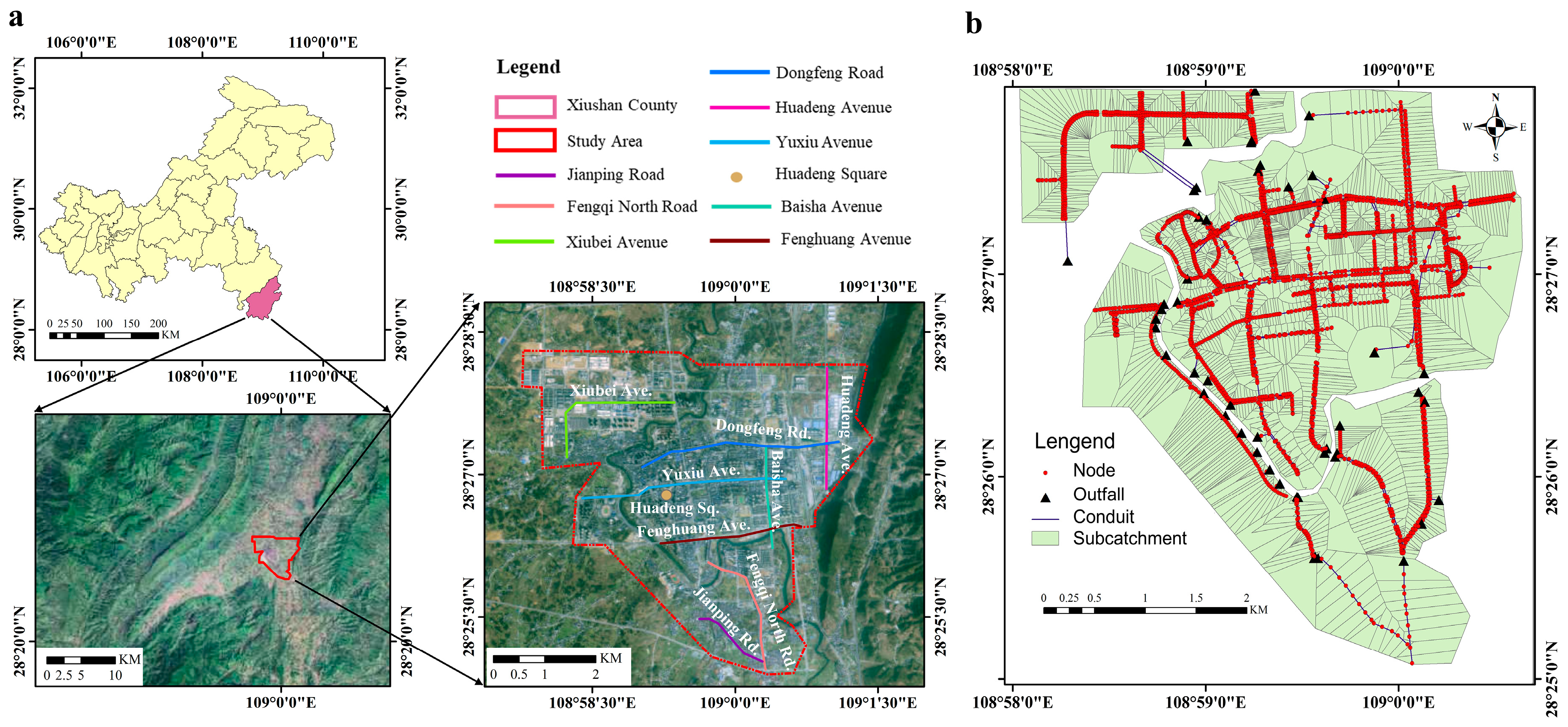
2. Description of Study Area
3. Methodology
3.1. Development of the Indicator System
3.2. Projection Pursuit Model
- Step 1: Data standardization for evaluation indicators
- Step 2: Projection index function construction
- Step 3: Optimize the projection index function
- Step 4: Optimal projection direction and indicator weight calculation
- Step 5: Component-specific weight allocation
- Step 1: Chromosome representation
- Step 2: Population initialization
- Step 3: Fitness evaluation
- Step 4: Adaptive parent selection
- Step 5: Crossover operation
- Step 6: Mutation process
- Step 7: Iterative evolution
- Step 8: Adaptive range acceleration
3.3. Calibration and Validation of the Waterlogging Model
3.4. Urban Waterlogging Scenario Design
4. Urban Waterlogging Risk Assessment
4.1. Risk Level Threshold for Urban Waterlogging
4.2. Indicator Weighting System for Urban Waterlogging Risk
4.3. Urban Waterlogging Risk Assessment Results
4.3.1. Disaster-Causing Factor Hazard Analysis
4.3.2. Disaster-Pregnant Environment Sensitivity Analysis
4.3.3. Disaster-Affected Body Vulnerability Analysis
4.3.4. Comprehensive Assessment of Urban Waterlogging Risk
5. Urban Waterlogging Risk Mitigation Strategies
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cao, Y.; Zhou, B.; Chung, C.Y.; Wu, T.; Zheng, L.; Shuai, Z. A coordinated emergency response scheme for electricity and watershed networks considering spatio-temporal heterogeneity and volatility of rainstorm disasters. IEEE Trans. Smart Grid 2024, 15, 3528–3541. [Google Scholar] [CrossRef]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef]
- Tang, X.; Shu, Y.; Lian, Y.; Zhao, Y.; Fu, Y. A spatial assessment of urban waterlogging risk based on a Weighted Naïve Bayes classifier. Sci. Total Environ. 2018, 630, 264–274. [Google Scholar] [CrossRef]
- Sun, D.; Wang, H.; Huang, J.; Zhang, J.; Liu, G. Urban road waterlogging risk assessment based on the source–pathway–receptor concept in Shenzhen, China. J. Flood Risk Manag. 2023, 16, e12873. [Google Scholar] [CrossRef]
- Li, J.; Zeng, J.; Huang, G.; Chen, W. Urban Flood Mitigation Strategies with Coupled Gray–Green Measures: A Case Study in Guangzhou City, China. Int. J. Disaster Risk Sci. 2024, 15, 467–479. [Google Scholar] [CrossRef]
- Chiu, Y.-J.; Chang, L.-C.; Lin, Y.-T.; Lin, Y.-T.; Liu, C.-W.; Lee, J.-J. Hydrologic performance assessment of low impact development facilities based on monitoring data and SWMM modeling in an urban catchment in Taiwan. Sci. Rep. 2025, 15, 27251. [Google Scholar] [CrossRef]
- Li, S.; Wang, Z.; Wu, X.; Zeng, Z.; Shen, P.; Lai, C. A novel spatial optimization approach for the cost-effectiveness improvement of LID practices based on SWMM-FTC. J. Environ. Manag. 2022, 307, 114574. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Li, J.; Gao, X.; Yao, Y.; Jiang, C. Comprehensive analysis of waterlogging control and carbon emission reduction for optimal LID layout: A case study in campus. Environ. Sci. Pollut. Res. 2022, 29, 87802–87816. [Google Scholar] [CrossRef]
- Tan, Y.; Cheng, Q.; Lyu, F.; Liu, F.; Liu, L.; Su, Y.; Yuan, S.; Xiao, W.; Liu, Z.; Chen, Y. Hydrological reduction and control effect evaluation of sponge city construction based on one-way coupling model of SWMM-FVCOM: A case in university campus. J. Environ. Manag. 2024, 349, 119599. [Google Scholar] [CrossRef]
- Soares, J.A.J.P.; Ozelim, L.C.S.M.; Bacelar, L.; Ribeiro, D.B.; Stephany, S.; Santos, L.B.L. ML4FF: A machine-learning framework for flash flood forecasting applied to a Brazilian watershed. J. Hydrol. 2025, 652, 132674. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, C.; Su, M.; Xu, Z.; Lu, W.; Teng, Y.; Huang, Q. Urban spatial layout optimization from the “Double E” perspective to mitigate urban flooding in the context of urban expansion. J. Hydrol. Reg. Stud. 2025, 62, 102790. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, Z.; Xin, K.; Liao, Z.; Yuan, Z. Enhancing the resilience of urban drainage system using deep reinforcement learning. Water Res. 2025, 281, 123681. [Google Scholar] [CrossRef]
- McGauley, M.W.; Amur, A.; Shakya, M.; Wadzuk, B.M. A Complete Water Balance of a Rain Garden. Water Resour. Res. 2023, 59, e2023WR035155. [Google Scholar] [CrossRef]
- Zoghi, A.; Bilodeau, É.; Khaliq, M.N.; Kim, Y.; Martel, J.-L.; Drake, J. Nature-based solutions for flood mitigation in Canadian urban centers: A review of the state of research and practice. J. Hydrol. Reg. Stud. 2025, 60, 102460. [Google Scholar] [CrossRef]
- Jamali, B.; Bach, P.M.; Deletic, A. Rainwater harvesting for urban flood management—An integrated modelling framework. Water Res. 2020, 171, 115372. [Google Scholar] [CrossRef]
- Javan, K.; Banihashemi, S.; Nazari, A.; Roozbahani, A.; Darestani, M.; Hossieni, H. Coupled SWMM-MOEA/D for multi-objective optimization of low impact development in urban stormwater systems. J. Hydrol. 2025, 656, 133044. [Google Scholar] [CrossRef]
- Ramadan, M.S.; Almurshidi, A.H.; Razali, S.F.M.; Ramadan, E.; Tariq, A.; Bridi, R.M.; Rahman, M.A.; Albedwawi, S.; Alshamsi, M.; Alshamisi, M.; et al. Spatial decision-making for urban flood vulnerability: A geomatics approach applied to Al-Ain City, UAE. Urban Clim. 2025, 59, 102297. [Google Scholar] [CrossRef]
- Feng, J.; Yang, Y.; Li, J. Optimization of the Low-Impact Development Facility Area Based on a Surrogate Model. Water Resour. Manag. 2023, 37, 5789–5806. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Huang, Q.; Xia, J.; Li, J. Surrogate-based multiobjective optimization to rapidly size low impact development practices for outflow capture. J. Hydrol. 2023, 616, 128848. [Google Scholar] [CrossRef]
- Black, A.R.; Burns, J.C. Re-assessing the flood risk in Scotland. Sci. Total Environ. 2002, 294, 169–184. [Google Scholar] [CrossRef]
- Lin, Y.C.; Jenkins, S.F.; Chow, J.R.; Biass, S.; Woo, G.; Lallemant, D. Modeling downward counterfactual events: Unrealized disasters and why they matter. Front. Earth Sci. 2020, 8, 575048. [Google Scholar] [CrossRef]
- Nasiri, H.; Yusof, M.J.M.; Ali, T.A.M.; Hussein, M.K.B. District flood vulnerability index: Urban decision-making tool. Int. J. Environ. Sci. Technol. 2019, 16, 2249–2258. [Google Scholar] [CrossRef]
- Xie, S.; Liu, W.; Yuan, Z.; Zhang, H.; Lin, H.; Wang, Y. Integrated risk assessment of waterlogging in Guangzhou based on runoff modeling, AHP, GIS and scenario analysis. Water 2022, 14, 2899. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, D.; Zhang, L.; Guo, H.; Ma, J.; Gao, W. Flood risk assessment of Wuhan, China, using a multi-criteria analysis model with the improved AHP-Entropy method. Environ. Sci. Pollut. Res. 2023, 30, 96001–96018. [Google Scholar] [CrossRef]
- Wang, L.; Hou, H.; Li, Y.; Pan, J.; Wang, P.; Wang, B.; Chen, J.; Hu, T. Investigating relationships between landscape patterns and surface runoff from a spatial distribution and intensity perspective. J. Environ. Manag. 2023, 325, 116631. [Google Scholar] [CrossRef]
- Ahmad, S.; Peng, X.; Ashraf, A.; Yin, D.; Chen, Z.; Ahmed, R.; Israr, M.; Jia, H. Building resilient urban drainage systems by integrated flood risk index for evidence-based planning. J. Environ. Manag. 2025, 374, 124130. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Wang, Y.; Jin, N.; Zhang, S.; Giustozzi, F.; Ma, T. Assessing flood risk to urban road users based on rainfall scenario simulations. Transp. Res. Part D Transp. Environ. 2023, 123, 103919. [Google Scholar] [CrossRef]
- Löwe, R.; Urich, C.; Domingo, N.S.; Mark, O.; Deletic, A.; Arnbjerg-Nielsen, K. Assessment of urban pluvial flood risk and efficiency of adaptation options through simulations—A new generation of urban planning tools. J. Hydrol. 2017, 550, 355–367. [Google Scholar] [CrossRef]
- Hlodversdottir, A.O.; Bjornsson, B.; Andradottir, H.O.; Eliasson, J.; Crochet, P. Assessment of flood hazard in a combined sewer system in Reykjavik city centre. Water Sci. Technol. 2015, 71, 1471–1477. [Google Scholar] [CrossRef]
- Wei, H.; Wu, H.; Zhang, L.; Liu, J. Urban flooding simulation and flood risk assessment based on the InfoWorks ICM model: A case study of the urban inland rivers in Zhengzhou, China. Water Sci. Technol. 2024, 90, 1338–1358. [Google Scholar] [CrossRef]
- Liu, Y.; Eckert, C.M.; Earl, C. A review of fuzzy AHP methods for decision-making with subjective judgements. Expert Syst. Appl. 2020, 161, 113738. [Google Scholar] [CrossRef]
- Aggarwal, M. Decision aiding model with entropy-based subjective utility. Inf. Sci. 2019, 501, 558–572. [Google Scholar] [CrossRef]
- Xu, H.; Ma, C.; Lian, J.; Xu, K.; Chaima, E. Urban flooding risk assessment based on an integrated k-means cluster algorithm and improved entropy weight method in the region of Haikou, China. J. Hydrol. 2018, 563, 975–986. [Google Scholar] [CrossRef]
- Yang, C.; Li, H.; Huang, X.; Li, X.; Liu, Y.; Hong, W.; Zou, Y. Research on extraction and evaluation of ecological corridor based on remote sensing and GIS. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3464–3467. [Google Scholar]
- Sarkar, A.; Vulimiri, A.; Paul, S.; Iqbal, J.; Banerjee, A.; Chatterjee, R.; Ray, S.S. Unsupervised and supervised classification of hyperspectral imaging data using projection pursuit and Markov random field segmentation. Int. J. Remote Sens. 2012, 33, 5799–5818. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, J.; Guo, Q.; Liu, L.; Chen, Y.; Pan, M. Dynamic risk assessment model for flood disaster on a projection pursuit cluster and its application. Stoch. Environ. Res. Risk Assess. 2014, 28, 2175–2183. [Google Scholar] [CrossRef]
- Wu, S.; Tian, C.; Li, B.; Wang, J.; Wang, Z. Ecological environment health assessment of lake water ecosystem system based on simulated annealing-projection pursuit: A case study of plateau lake. Sustain. Cities Soc. 2022, 86, 104131. [Google Scholar] [CrossRef]
- Cheng, D.; Zhang, X.; Li, H. Application of the deformed Thiessen polygon in the analysis of layout influence factors for rural express delivery points. J. Geo-Inf. Sci. 2024, 26, 2140–2160. [Google Scholar] [CrossRef]
- Chen, W.; Huang, G.; Zhang, H.; Wang, W. Urban inundation response to rainstorm patterns with a coupled hydrodynamic model: A case study in Haidian Island, China. J. Hydrol. 2018, 564, 1022–1035. [Google Scholar] [CrossRef]
- Waghwala, R.K.; Agnihotri, P.G. Flood risk assessment and resilience strategies for flood risk management: A case study of Surat City. Int. J. Disaster Risk Reduct. 2019, 40, 101155. [Google Scholar] [CrossRef]
- Zheng, C.; Yang, W.; Jiang, X.; Lian, J.; Hu, D.; Yan, X.; Yan, L. A novel integrated Urban flood risk assessment approach coupling GeoDetector-Dematel and clustering method. J. Environ. Manag. 2024, 354, 120308. [Google Scholar] [CrossRef] [PubMed]
- Kruskal, J.B. Toward a practical method which helps uncover the structure of a set of multivariate observations by finding the linear transformation which optimizes a new “index of condensation”. In Statistical Computation; Academic Press: Cambridge, MA, USA, 1969; pp. 427–440. [Google Scholar] [CrossRef]
- Wang, L.; Wan, J.; Gao, X. Toward the Health Measure for Open Source Software Ecosystem Via Projection Pursuit and Real-Coded Accelerated Genetic. IEEE Access 2019, 7, 87396–87409. [Google Scholar] [CrossRef]
- Niu, H.; Liu, Z. Measurement on carbon lock-in of China based on RAGA-PP model. Carbon Manag. 2021, 12, 451–463. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, L. Assessing the sustainability of renewable energy: An empirical analysis of selected 18 European countries. Sci. Total Environ. 2019, 692, 529–545. [Google Scholar] [CrossRef]
- Liu, B.I.N.; Duan, T.; Li, Y. One improved agent genetic algorithm—Ring-like agent genetic algorithm for global numerical optimization. Asia-Pac. J. Oper. Res. 2009, 26, 479–502. [Google Scholar] [CrossRef]
- Lin, F.; Chen, X.; Yao, H. Evaluating the Use of Nash-Sutcliffe Efficiency Coefficient in Goodness-of-Fit Measures for Daily Runoff Simulation with SWAT. J. Hydrol. Eng. 2017, 22, 05017023. [Google Scholar] [CrossRef]
- GB/T 22482-2008; Standard for Hydrological Information and Hydrological Forecasting. Chinese Standard: Beijing, China, 2008.
- T/CUWA 40058-2025; Technical Standards for Urban Waterlogging Risk Assessment. China Urban Water Association: Beijing, China, 2025.
- Lin, L.; Wu, Z.; Liang, Q. Urban flood susceptibility analysis using a GIS-based multi-criteria analysis framework. Nat. Hazards 2019, 97, 455–475. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, L. Assessing the sustainability of the shale gas industry by combining DPSIRM model and RAGA-PP techniques: An empirical analysis of Sichuan and Chongqing, China. Energy 2019, 176, 353–364. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, J.; Ou, S.; Gao, C.; Zhou, Y.; Shi, L.; Zhou, K. Impact of effective impervious surface disconnection on urban hydrographs: A multi-scenario modeling study at the catchment scale. J. Hydrol. 2024, 630, 130656. [Google Scholar] [CrossRef]
- Jarecke, K.M.; Zhang, X.; Keen, R.M.; Dumont, M.; Li, B.; Sadayappan, K.; Moreno, V.; Ajami, H.; Billings, S.A.; Flores, A.N.; et al. Woody encroachment modifies subsurface structure and hydrological function. Ecohydrology 2025, 18, e2731. [Google Scholar] [CrossRef]
- He, Z.; Jia, G.; Liu, Z.; Zhang, Z.; Yu, X.; Xiao, P. Field studies on the influence of rainfall intensity, vegetation cover and slope length on soil moisture infiltration on typical watersheds of the Loess Plateau, China. Hydrol. Process. 2020, 34, 4904–4919. [Google Scholar] [CrossRef]
- Gao, Y.-q.; Liu, Y.-p.; Lu, X.-h.; Luo, H.; Liu, Y. Change of stream network connectivity and its impact on flood control. Water Sci. Technol. 2020, 13, 253–264. [Google Scholar] [CrossRef]
- Gunnell, K.; Mulligan, M.; Francis, R.A.; Hole, D.G. Evaluating natural infrastructure for flood management within the watersheds of selected global cities. Sci. Total Environ. 2019, 670, 411–424. [Google Scholar] [CrossRef]
- Mediero, L.; Soriano, E.; Oria, P.; Bagli, S.; Castellarin, A.; Garrote, L.; Mazzoli, P.; Mysiak, J.; Pasetti, S.; Persiano, S.; et al. Pluvial flooding: High-resolution stochastic hazard mapping in urban areas by using fast-processing DEM-based algorithms. J. Hydrol. 2022, 608, 127649. [Google Scholar] [CrossRef]
- Peinado Guevara, H.J.; Espinoza Ortiz, M.; Peinado Guevara, V.M.; Herrera Barrientos, J.; Peinado Guevara, J.A.; Delgado Rodríguez, O.; Pellegrini Cervantes, M.D.; Sánchez Morales, M. Potential flood risk in the city of Guasave, Sinaloa, the effects of population growth, and modifications to the topographic relief. Sustainability 2022, 14, 6560. [Google Scholar] [CrossRef]
- Moraga, J.S.; Peleg, N.; Fatichi, S.; Molnar, P.; Burlando, P. Revealing the impacts of climate change on mountainous catchments through high-resolution modelling. J. Hydrol. 2021, 603, 126806. [Google Scholar] [CrossRef]
- Abenayake, C.; Jayasinghe, A.; Kalpana, H.N.; Wijegunarathna, E.E.; Mahanama, P.K.S. An innovative approach to assess the impact of urban flooding: Modeling transportation system failure due to urban flooding. Appl. Geogr. 2022, 147, 102772. [Google Scholar] [CrossRef]
- El Baida, M.; Chourak, M.; Boushaba, F. Flood mitigation and water resource preservation: Hydrodynamic and SWMM simulations of nature-based solutions under climate change. Water Resour. Manag. 2025, 39, 1149–1176. [Google Scholar] [CrossRef]
- Razguliaev, N.; Flanagan, K.; Muthanna, T.; Viklander, M. Urban stormwater quality: A review of methods for continuous field monitoring. Water Res. 2024, 249, 120929. [Google Scholar] [CrossRef]
- Peng, H.-Q.; Liu, Y.; Wang, H.-W.; Ma, L.-M. Assessment of the service performance of drainage system and transformation of pipeline network based on urban combined sewer system model. Environ. Sci. Pollut. Res. 2015, 22, 15712–15721. [Google Scholar] [CrossRef]
- Liang, C.-Y.; You, G.J.-Y.; Lee, H.-Y. Investigating the effectiveness and optimal spatial arrangement of low-impact development facilities. J. Hydrol. 2019, 577, 124008. [Google Scholar] [CrossRef]
- Abduljaleel, Y.; Salem, A.; ul Haq, F.; Awad, A.; Amiri, M. Improving detention ponds for effective stormwater management and water quality enhancement under future climate change: A simulation study using the PCSWMM model. Sci. Rep. 2023, 13, 5555. [Google Scholar] [CrossRef] [PubMed]
- Avila, H.; Avila, L.; Sisa, A. Dispersed Storage as Stormwater Runoff Control in Consolidated Urban Watersheds with Flash Flood Risk. J. Water Resour. Plann. Manag. 2016, 142, 04016056. [Google Scholar] [CrossRef]
- Duan, H.-F.; Li, F.; Yan, H. Multi-Objective Optimal Design of Detention Tanks in the Urban Stormwater Drainage System: LID Implementation and Analysis. Water Resour. Manag. 2016, 30, 4635–4648. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Appropriate resolution timescale to evaluate water saving and retention potential of rainwater harvesting for toilet flushing in single houses. J. Hydroinform. 2015, 17, 331–346. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Rainwater harvesting as source control option to reduce roof runoff peaks to downstream drainage systems. J. Hydroinform. 2015, 18, 23–32. [Google Scholar] [CrossRef]







| Target Layer | Criterion Layer | Indicator Layer |
|---|---|---|
| Urban waterlogging risk | Hazard of disaster-causing factors (H) | Waterlogging depth (m) |
| Waterlogging duration (min) | ||
| Waterlogging recession time (min) | ||
| Surface flow velocity (m/s) | ||
| Sensitivity of disaster-pregnant environments (S) | Elevation (m) | |
| Slope (%) | ||
| Terrain ruggedness index | ||
| Topographic wetness index | ||
| Vegetation coverage | ||
| Vulnerability of disaster-affected bodies (V) | Road density | |
| Population density (hundred persons/hm2) | ||
| GDP density (million RMB/km2) |
| Risk Level Thresholds | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Waterlogging depth (m) | [0, 0.05] | (0.05, 0.15] | (0.15, 0.3] | (0.3, 0.5] | (0.5, ∞) |
| Waterlogging duration (min) | [0, 30] | (30, 60] | (60, 90] | (90, 120] | (120, ∞) |
| Waterlogging recession time (min) | [0, 15] | (15, 30] | (30, 45] | (45, 60] | (60, ∞) |
| Surface flow velocity (m/s) | [0, 0.05] | (0.05, 0.15] | (0.15, 0.3] | (0.3, 0.5] | (0.5, ∞) |
| Elevation (m) | (389, 451] | (369, 389] | (358, 369] | (347, 358] | [297, 347] |
| Slope (%) | (14.35, 21.6] | (7.48, 14.35] | (3.98, 7.48] | (1.69, 3.98] | [0, 1.69] |
| Terrain ruggedness index | (27, 47] | (15, 27] | (8, 15] | (4, 8] | [0, 4] |
| Topographic wetness index | (14.3, 19.46] | (11.3, 14.3] | (8.9, 11.3] | (7.1, 8.9] | [0, 7.1] |
| Vegetation coverage | (0.67, 1] | (0.61, 0.67] | (0.56, 0.61] | (0.5, 0.56] | [0, 0.5] |
| Road density | [0, 0.027] | (0.027, 0.085] | (0.085, 0.131] | (0.131, 0.165] | (0.165, 0.200] |
| Population density (hundred persons/hm2) | [0, 1.47] | (1.47, 3.29] | (3.29, 5.73] | (5.73, 8.56] | (8.56, 12.39] |
| GDP Density (million RMB/km2) | [0, 136] | (136, 262] | (262, 417] | (417, 603] | (603, 924] |
| Indicator Name | Optimal Projection Direction (wp) | Weight (Wj) |
|---|---|---|
| Waterlogging depth (h1) | 0.335 | 0.112 |
| Waterlogging duration (h2) | 0.292 | 0.085 |
| Waterlogging recession time (h3) | 0.336 | 0.113 |
| Surface flow velocity (h4) | 0.255 | 0.065 |
| Elevation (s1) | 0.272 | 0.074 |
| Slope (s2) | 0.338 | 0.114 |
| Terrain ruggedness index (s3) | 0.351 | 0.123 |
| Topographic wetness index (s4) | 0.249 | 0.062 |
| Vegetation coverage (s5) | 0.205 | 0.042 |
| Road density (v1) | 0.155 | 0.024 |
| Population Density (v2) | 0.345 | 0.119 |
| GDP density (v3) | 0.259 | 0.067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rao, Y.; Cheng, Q.; Zhu, J.; Liu, L.; Mu, Y.; Zhou, Y.; Su, D.; Liu, Z.; Chen, Y. A Dynamic Urban Waterlogging Risk Assessment Framework Using RAGA-Optimized Projection Pursuit and Scenario Simulation. Sustainability 2025, 17, 10305. https://doi.org/10.3390/su172210305
Rao Y, Cheng Q, Zhu J, Liu L, Mu Y, Zhou Y, Su D, Liu Z, Chen Y. A Dynamic Urban Waterlogging Risk Assessment Framework Using RAGA-Optimized Projection Pursuit and Scenario Simulation. Sustainability. 2025; 17(22):10305. https://doi.org/10.3390/su172210305
Chicago/Turabian StyleRao, Ye, Qiming Cheng, Jiayue Zhu, Linhao Liu, Yixin Mu, Yuanhan Zhou, Dingjiang Su, Zhen Liu, and Yao Chen. 2025. "A Dynamic Urban Waterlogging Risk Assessment Framework Using RAGA-Optimized Projection Pursuit and Scenario Simulation" Sustainability 17, no. 22: 10305. https://doi.org/10.3390/su172210305
APA StyleRao, Y., Cheng, Q., Zhu, J., Liu, L., Mu, Y., Zhou, Y., Su, D., Liu, Z., & Chen, Y. (2025). A Dynamic Urban Waterlogging Risk Assessment Framework Using RAGA-Optimized Projection Pursuit and Scenario Simulation. Sustainability, 17(22), 10305. https://doi.org/10.3390/su172210305






