1. Introduction
With the growing global attention to green development and sustainability, the number of new energy vehicles continues to increase, and the recycling of end-of-life electric vehicle batteries (EVBs) has become increasingly important and urgent [
1,
2]. EVBs contain rare metals such as lithium, which possess high recycling value. Efficient recovery of these materials not only helps to alleviate resource constraints [
3] but also significantly reduces environmental pollution and promotes the development of a circular economy [
4,
5,
6]. Improper disposal of waste batteries may release hazardous substances that cause long-term damage to water and soil environments and even trigger safety incidents. Therefore, the establishment of efficient and reliable EVB recycling networks has become a key requirement for ensuring the sustainable development of the new energy vehicle industry [
7,
8].
The systematic planning of EVB recycling networks is a central issue within the recycling system. Proper network design (ND) optimizes facility configuration, enhances operational efficiency, and strengthens the system’s ability to coordinate resources and respond to risks [
9,
10,
11,
12]. However, most existing studies focus predominantly on the location of recycling facilities, whereas the optimization of network topology has received comparatively little attention, despite its potential to generate greater economic benefits [
13]. Against this background, the fourth-party logistics (4PL) framework provides a new perspective for electric vehicle battery recycling network design (EVBRND). Compared with traditional third-party logistics (3PL), 4PL integrates multiple logistics resources and supports collaborative decision-making, thereby strengthening system-level optimization and responsiveness. This enables joint optimization between facility location and logistics service provider selection, ultimately improving overall network performance [
14,
15].
Although the 4PL framework improves network efficiency, conventional EVB recycling networks are typically designed with little attention to potential disruption risks. Such risks may arise from natural hazards (e.g., extreme weather, hurricanes, earthquakes), human-induced events (e.g., terrorist attacks), or unexpected accidents (e.g., industrial incidents, equipment failures), all of which can impair the functionality of network nodes or links [
16]. These disruptions are typically characterized by sudden occurrence and wide-ranging effects, with consequences of business suspension far more severe than ordinary operational risks [
17]. Once critical recycling facilities are disrupted, a large volume of waste batteries may accumulate, leading to higher operational costs as well as environmental and safety risks. Incorporating resilience-oriented design into EVB recycling network construction has thus emerged as a vital research direction.
Following the COVID-19 pandemic, resilience strategies have been increasingly acknowledged as effective measures for managing disruptions. According to the summary by Govindan et al. [
18], such strategies can generally be categorized into mitigation and contingency approaches, including temporary outsourcing, capacity backups, and facility fortification. Fortification strategies improve facility reliability and disaster resistance, thereby reducing the probability of disruption, while capacity backup strategies rely on backup resources to maintain system operation after disruption occurs. Building on this foundation, this study integrates several strategies: multi-source allocation, multiple transportation routes, diversified 3PL selection, facility fortification, and capacity backup, to systematically enhance the stability and resilience of EVB recycling networks.
This study addresses the design of resilient EVB recycling networks under disruption risks within a 4PL framework. The proposed approach simultaneously considers the location of remanufacturing centers, collection centers, and disposal centers, and incorporates multi-source allocation, multiple transportation routes, multi-3PL collaboration, facility fortification, and capacity backup to counter potential disruptions. A two-stage stochastic programming model is formulated to describe the problem, which is subsequently reformulated into a mixed-integer linear programming (MILP) model through a scenario-based method. To address the computational challenges caused by large-scale scenario sets, a scenario reduction and decomposition-based heuristic (SRDBH), combining scenario reduction (SR), conditional relaxation, Lagrangian relaxation (LR), and an adaptive subgradient (AS) algorithm, is developed, following the idea of Zhang et al. [
19]. A real-world case study is conducted to validate the proposed model and algorithm. Numerical results reveal that the proposed algorithm exhibits superior efficiency compared with the commercial solver CPLEX. Furthermore, the findings indicate that flexible configuration of risk-mitigation strategies plays a crucial role in achieving both cost control and network resilience. The main contributions of this study are summarized as follows:
The influence of facility disruption risk on EVBRND decisions is rarely investigated. This study addresses a novel resilient EVBRND problem under disruption risk.
The 4PL concept is incorporated into the EVBRND process to enhance network resilience. Multiple 3PL providers, multi-source allocation, multiple transportation routes, facility fortification, and capacity backup strategies are integrated to mitigate facility disruption risks.
A novel two-stage stochastic EVBRND model under a 4PL framework with integrated hybrid risk-mitigation strategies is proposed. To address the computational challenges caused by the significant increase in binary decision variables due to logistics provider selection and the large number of disruption scenarios, a SRDBH algorithm is developed by combining SR, conditional relaxation, LR, and an AS algorithm.
Validation of the proposed model and algorithm is conducted using a real-world case study.
This study offers several key research contributions. The research expands the body of knowledge on resilient supply chain ND by integrating disruption risks and corresponding mitigation strategies into EVB recycling models. In addition, the incorporation of a 4PL framework into EVBRND clarifies the function of logistics coordination under uncertainty. The proposed SRDBH algorithm further advances methodological development for large-scale stochastic optimization in supply chain management. Collectively, these contributions provide a solid foundation for future studies that aim to integrate resilience, sustainability, and logistics management.
The remainder of this paper is structured as follows.
Section 2 reviews the relevant literature.
Section 3 outlines the problem and formulates the model.
Section 4 details the SRDBH algorithm developed for its solution.
Section 5 presents a case study to indicate the model’s applicability, and
Section 6 concludes the study.
2. Literature Review
Circular economy has been recognized as a key pathway to achieving sustainable development, playing a significant role in promoting resource efficiency and environmental protection [
20,
21,
22]. In the field of EVB recycling, extensive research efforts have been devoted to establishing efficient, green, and resilient recycling networks to mitigate resource waste and environmental pollution. This study focuses on the design of EVB recycling networks under disruption risks from a 4PL perspective. Related studies can be broadly classified into two categories: (1) EVBRND; (2) 4PLND.
(1) EVBRND
In the modeling and optimization of EVBRND, research has mainly concentrated on facility configuration, transportation route optimization, and uncertainty parameters. Harper et al. [
23] systematically reviewed and evaluated major recycling and reuse methods for lithium-ion batteries, highlighting future research directions. Jafari et al. [
24] employed trapezoidal fuzzy numbers to handle uncertainties in facility capacity and recovery rates, formulating a closed-loop location model to optimize both costs and environmental impacts. Wang et al. [
25] developed a multi-level recycling network model by refining three battery treatment strategies, significantly reducing total system costs and carbon emissions. Du et al. [
26] conducted a life cycle assessment to compare different allocation methods in battery recycling, providing insights for path selection. Fan et al. [
27] developed an interactive fuzzy programming model to simultaneously consider economic and environmental objectives in reverse logistics networks. Li et al. [
28] emphasized the role of inter-firm cooperation in improving recycling efficiency, demonstrating that collaboration between incumbent and new firms effectively reduces configuration costs. In terms of scheduling and allocation strategies, Tan et al. [
29] established an integer programming model to optimize urban-level recycling scheduling, ensuring customer satisfaction while reducing operational costs. Fu et al. [
30] investigated multi-period EVB recycling planning with demand prediction, demonstrating that data-driven models enhance long-term network adaptability. Mahdiraji et al. [
31] proposed a stochastic programming framework for resilient recycling networks, emphasizing the role of fortification and redundancy strategies in mitigating disruption risks. Haynes et al. [
32] adopted geographic clustering algorithms to optimize facility spatial layout, thereby improving recycling efficiency and reducing transportation costs. Some studies have further highlighted the impact of uncertainty in the quantity and capacity of retired batteries on network stability. For example, Du et al. [
33] and Yan et al. [
34] applied scenario simulation and robust optimization methods, respectively, to enhance system reliability. He et al. [
11] incorporated cascade utilization and urban development weights into a fuzzy chance-constrained model, constructing a multi-level reverse logistics network aligned with urban sustainability. Qi et al. [
35] developed a robust optimization model for EVB recycling networks under uncertain demand, showing that the proposed approach improves system resilience and cost efficiency. Ai et al. [
36] introduced a green supply chain design integrating carbon emission constraints, highlighting the effectiveness of carbon reduction strategies in sustainable EVB recycling. Zhang et al. [
37] proposed a bi-objective model for disassembly–assembly line balancing that optimizes profit and worker learning, solved using a multi-objective fruit fly optimization algorithm with superior performance.
(2) 4PLND
Since the introduction of the 4PL concept, research has evolved from service evaluation to network structure optimization. Early studies, such as Krakovics et al. [
38] and Büyüközkan et al. [
39], primarily focused on the establishment of evaluation indicator systems for 4PL providers, laying the foundation for subsequent ND studies. Li et al. [
40] introduced a robust optimization-based framework for ND under disruptive events, thereby improving system resilience. Wang et al. [
41] and Huang et al. [
42] explored the influence of customer behavior on network decision-making, constructing supply chain network models that incorporated psychological factors of customers. In recent years, disruption risk management has emerged as a major focus in 4PL research. Yin et al. [
43] employed two-stage stochastic programming, multi-period optimization, and temporary outsourcing mechanisms to systematically analyze the impact of disruptions and demand uncertainty on network structures, significantly enhancing the resilience and service continuity of 4PL networks. Zhang et al. [
44] proposed a 4PL ND that integrates both defensive and recovery mechanisms, strengthening survivability under supply disruptions. Jiang et al. [
45] investigated resource leasing strategies under sudden demand, proving that dynamic deployment is more cost-effective than static configuration. Vidal et al. [
46] examined collaboration mechanisms among logistics providers in recycling networks, revealing that 4PL-led coordination significantly enhances operational performance. Bo et al. [
47] focus on the 4PL routing optimization problem in complex environments, particularly under infection and delay risks.
In summary, existing research on EVBRND primarily emphasizes facility location, cost control, and uncertainty parameters modeling, while discussions on system responses to disruption risks remain insufficient. Meanwhile, although the 4PL model indicates significant advantages in integrating logistics resources and enhancing supply chain resilience, its application in EVBRND has not been systematically explored, particularly in terms of multi-strategy collaborative optimization under disruption scenarios. The distinctions of this study from the existing literature are reflected in the following aspects:
From the innovative perspective of 4PL, this paper investigates the EVBRND. Decision results extend from discrete facility location to network topology optimization for enhancing operational efficiency.
Disruption risks are incorporated into the EVBRND. Fortification, capacity backups, multi-3PL collaboration, multi-route transportation, and multi-source allocation are integrated to effectively address uncertainties and challenges caused by disruptions.
A novel EVBRND model is developed by integrating fortification, capacity backups, multi-3PL, multi-route, and multi-source strategies, providing new insights into the application of 4PL under disruptive events.
To address the computational challenges posed by the significant increase in binary decision variables introduced by logistics provider selection and the large number of disruption scenarios, a SRDBH algorithm is developed.
Validation of the proposed model and algorithm is conducted using a real-world case study.
3. Problem Description and Mathematical Model
3.1. Problem Description
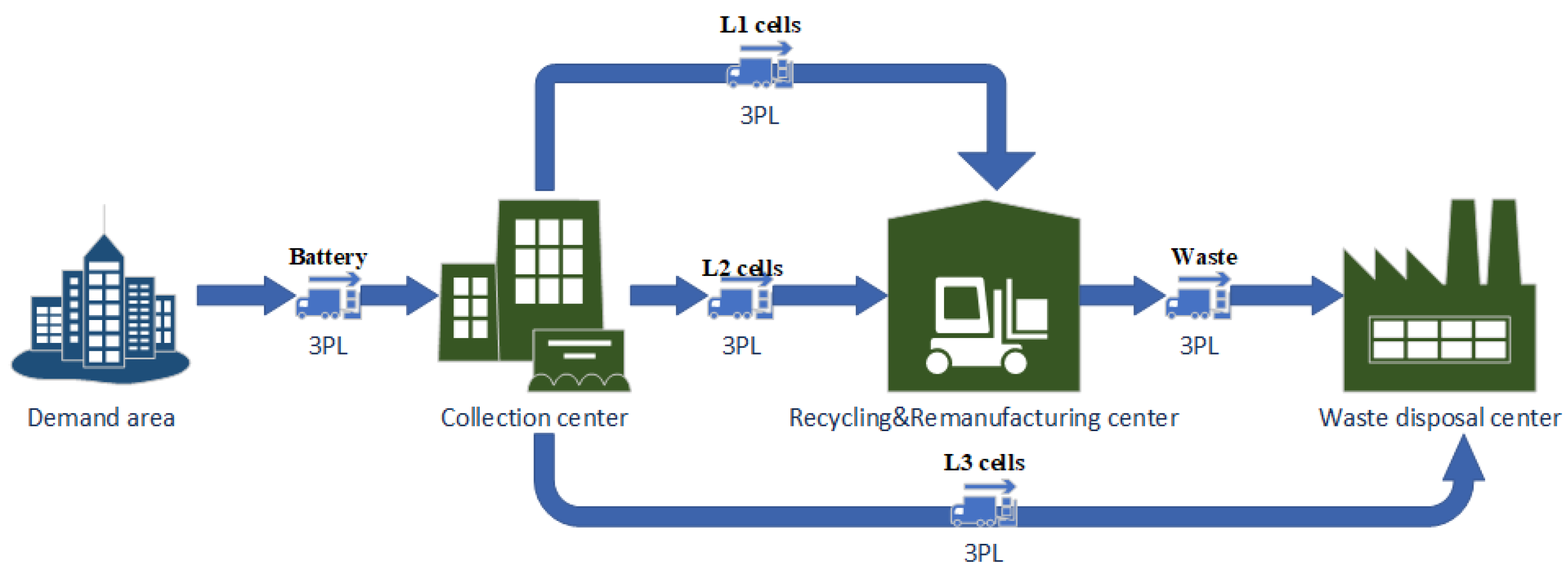
In the recycling system of EVBs, the construction of an efficient, reliable, and resilient network is essential for achieving resource circulation and environmental protection. From the perspective of integrated optimization under 4PL, this study proposes a resilient EVBRND model under multiple disruption risks. The network is represented as a directed graph
, where the node set
S consists of demand regions (
D), collection centers (
C), remanufacturing centers (
R), and disposal centers (
W), while the edge set
E denotes the logistics connections between facilities, as illustrated in
Figure 1.
Facility location decisions in the network are controlled by binary variables . Each facility is subject to capacity limitations and is associated with construction costs, capacity backups costs, and fortification expenses. A demand region generates a certain amount of EVB , which is transported to collection centers for preliminary disassembly and classification. The processing capacity of a collection center is determined by its basic capacity and backup capacity, with a unit processing cost of . In this stage, EVBs are classified into three categories (L1, L2, L3) according to their technical condition, with proportions , , , serving as the basis for subsequent resource allocation. Classified EVBs are assigned to differentiated pathways: L1 and L2 batteries are sent to remanufacturing centers R for material recovery, where the maximum processing capacity is given by the sum of basic capacity and backup capacity, and the unit processing costs differ by category, denoted as and . L3 batteries and a fraction of waste flows are directed to disposal centers W, with unit processing cost , subject to capacity constraints similar to other facilities. Flow balance and mass conservation constraints are enforced during logistics operations to ensure rational flows among nodes. In terms of transportation organization, multiple 3PL providers are introduced to undertake the transport tasks between nodes, coordinated and integrated by the 4PL operator for system-wide cost optimization. Transportation route selection is represented by decision variables , , , . Each 3PL provider is subject to maximum transport capacities , , , and charges corresponding unit transportation costs , , , .
To mitigate facility and transportation disruptions, multiple resilience strategies are integrated into the EVBRND. These strategies include fortifying facilities, establishing backup capacities to enhance recovery flexibility, and introducing redundancy through multi-3PL collaboration and multi-route allocation. Preventive investment, which represents the enterprise’s expenditures on fortification and backup measures, is subject to a budget
, as suggested by Yin et al. [
43]. This
as a key control parameter for resilience design. The specific allocation of fortification and backup resources across facilities is determined by the optimization results, which reflect the trade-offs among facility vulnerability, reinforcement costs, and system-wide recovery efficiency.
In summary, the proposed EVBRND problem, whose key notations are defined in
Table 1, systematically integrates location-allocation-routing decisions with disruption risk management. A multi-layer optimization framework is developed to achieve synergy among economic efficiency, environmental sustainability, and operational resilience, thereby providing theoretical support and decision-making tools for closed-loop EVB recycling management.
3.2. Mathematical Model
To address potential disruption scenarios, facilities can be fortified and reserved to enhance facilities resilience under disruptions. The fortification decisions are controlled by binary variables . The costs incurred from fortification are determined by the fortification cost parameters . The backup decisions are governed by binary variables , which represent the reserved capacities of the corresponding facilities. The costs of backup are determined by the backup cost parameters . After fortification and backup, facilities can retain partial or full processing capacity under disruption scenarios, thereby ensuring the stable operation of the recycling network.
When collection centers, remanufacturing centers, or disposal centers fail to fully meet the recycling demand, penalty costs arise from the uncollected batteries. The quantity of uncollected batteries
is determined by the amount of batteries left untreated, and the penalty cost is given by the product of the unit penalty
and the number of uncollected batteries. In addition, a recycling compensation
is paid to users to incentivize them to supply waste batteries for recycling. To achieve the minimization of the cost, the decision vector is defined as
The scenario-based method is employed to characterize facility disruptions. Specifically, under disruption scenario , “” implies operational availability of collection center c, while “” reflects a failure. As an illustration, with , scenario describes a case where nodes and are disrupted, whereas and remain functional. Accordingly, a two-stage stochastic programming model can be constructed as follows.
(P1):where
=
(P1) is developed with the objective of minimizing the total cost of the EVB recycling network. The objective function consists of the following four components:
Facility construction and fortification costs: Including the fixed construction costs of collection centers, remanufacturing centers, and disposal centers, as well as the corresponding fortification expenditures;
Capacity backup costs: Expenditures related to the additional reserved capacity at each type of facility to hedge against disruption risks;
Third-party logistics (3PL) construction costs: Fixed costs associated with the selection of transportation paths among demand regions, collection centers, remanufacturing centers, and disposal centers;
Network operating costs: Covering facility processing costs, transportation costs, penalty costs for unsatisfied recovery demand, and reimbursement costs paid to customers for returning used batteries. This component is evaluated under multiple disruption scenarios.
The model is limited by the following constraints:
Fortification logic: Constraint (
2) stipulates that a facility may be fortified only if it is selected for construction;
Reservation capacity: Constraint (3) restricts the backup capacity at each facility to remain within its specified upper bound;
Budget limitation: Constraint (4) requires that the total preventive investment—including both fortification and backup costs—does not exceed the available budget;
Binary variables: Constraints (5)–(10) specify that the facility location, fortification, and logistics provider selection decisions are binary;
Backup capacity non-negativity: Constraint (11) defines the backup capacities of facilities as non-negative continuous variables;
Flow balance: Constraint (
13) guarantees that, under any disruption scenario, the recovery demand at each collection center equals the sum of recovered and unrecovered quantities;
Processing capacity: Constraints (14)–(16) ensure that, under disruption conditions, the processed quantity at each facility does not exceed its available capacity, given by the sum of basic and reserved capacity;
Material conservation: Constraint (17) enforces the balance between the outflow of each grade of batteries from collection centers and their inflow to remanufacturing centers; Constraint (18) relates the third-grade outflow to disposal centers; and Constraint (19) maintains consistency between the waste generated by remanufacturing and the inflow to disposal facilities;
Transportation capacity: Constraints (20)–(23) require that the transported volume along each path by a 3PL service provider does not exceed its carrying capacity;
Transportation and shortage non-negativity: Constraints (24)–(28) impose non-negativity on transportation flows and the number of unrecovered batteries.
The computation of constitutes the main difficulty in solving the above two-stage stochastic program, and the calculation of the disruption probability under scenario is a key issue. To theoretically characterize possible disruptions, the following assumptions are made:
- (a)
Disruptions among facilities are assumed to be independent;
- (b)
The disruption probability of each facility is known;
- (c)
Each facility exposed to disruption risk has a binary state—disrupted or non-disrupted.
Assumptions (a)–(c) are commonly adopted in the existing literature. For example, Losada et al. [
48], Baghalian et al. [
49], and Fattahi et al. [
50] assumed that the facility states follow a known probability distribution. Similarly, Fattahi and Govindan [
51] modeled each facility as having two possible states, non-disrupted or disrupted. Based on these assumptions and following the method proposed by Snyder and Daskin [
52], the probability of each disruption scenario is calculated as follows:
where
denotes the disruption probability under scenario
,
S denotes the set of all collection centers that may experience disruptions,
denotes the subset of collection centers disrupted in scenario
, and
denotes the disruption probability of collection center
. Based on
, problem (P1) can be reformulated into the following deterministic form (P2).
s.t. (2)–(28)
Notably, model (P2) is formulated as an MILP, which can in principle be solved using commercial optimization packages such as CPLEX. Nevertheless, as the number of disruption scenarios grows, the computational burden on these solvers increases considerably, often leading to severe efficiency limitations. To address the computational burden, the subsequent section introduces a heuristic algorithm based on SR and decomposition to effectively solve the proposed model.
4. A Scenario Reduction and Decomposition-Based Heuristic
In this section, an SRDBH algorithm is proposed by integrating SR, conditional relaxation, LR, and an AS algorithm. Specifically, the SR technique is employed to shrink the disruption scenario set, which allows the upper bound of model (P2) to be estimated more efficiently. In parallel, conditional relaxation, LR, and the AS algorithm are employed to derive the corresponding lower bound. The detailed procedure of the algorithm is presented as follows.
First, the SR method is applied to derive an upper bound of the model. Its core idea is to replace the original full scenario set with a carefully selected subset of scenarios. The goal is to retain a representative yet smaller scenario set, reducing computational complexity while preserving solution accuracy.
Let denote the set of potentially disrupted facilities. Define as the uncertainty vector indicating whether facility experiences disruption. Each takes values from a finite set with , where indicates no disruption, and indicates disruption. The probability associated with each is given by , where and .
By applying the SR method described above, we can generate a new reduced scenario subset to replace the original full set, thereby achieving a more tractable approximation of the disruption environment.
Here,
represents the probability of each scenario in the reduced subset. The objective function (
31) is designed to prioritize the inclusion of scenarios with relatively high probabilities from the original set. Constraints (32)–(34) preserve the disruption probabilities of facilities within the reduced subset. Constraint (35) requires that the total probability of all reduced scenarios equals 1, while Constraint (36) restricts the assigned probabilities of individual scenarios to the interval
.
Applying the SR method yields a reduced scenario set with probabilities , upon which model (P2) is reformulated as follows:
Solve problem (P3) using CPLEX and record the corresponding optimal solution . By substituting into (P2), the problem (P2) degenerates into the following linear form (P4):
s.t. (2)–(28)
(P4):where
is a fixed constant. It should be noted that (P4) can be decomposed into multiple independent subproblems, where the
-th subproblem can be expressed as (P4s):
By solving the corresponding (P4s) problem, an upper bound of P2 can be obtained as . The advantage of the SR method lies in its ability to significantly reduce the number of disruption scenarios, thereby improving computational efficiency. However, its limitation is that it cannot evaluate the quality of the obtained solution. To address this issue, we employ two relaxation approaches—based on LR and conditional relaxation—to provide lower bounds for model P2.
s.t. (13)–(28)
First, by setting , we can derive a conditional relaxation model (P2v) of model P2, which is formulated as follows (P2v):
Theorem 1. Let denote the optimal objective value of (P2v), and let denote its corresponding optimal solution. Then, constitutes a valid lower bound for problem (P2).
Proof of Theorem 1. Let represent the optimal objective value of (P2), with being its associated optimal solution. Since (P2v) is formulated as an MILP independent of specific disruption scenarios, any optimal solution of (P2) is guaranteed to be feasible for (P2v). Consequently, we have , which establishes that serves as a lower bound of (P2). □
The conditional relaxation method can quickly provide a lower bound for P2; however, due to its global relaxation nature, the quality of the lower bound may be poor. To address this, we propose an approach based on LR and the adaptive subgradient algorithm to obtain a higher-quality lower bound.
The main challenge in solving model P2 lies in the fact that the decision variables are independent of disruption scenarios. To facilitate decomposition, scenario-dependent decision variables are introduced for each scenario in : , so that P2 can be decomposed into N independent subproblems (with ). To preserve equivalence with the original formulation, the following non-anticipativity constraints are imposed: . Accordingly, we obtain the following decomposition formulation (P2n):
Based on Yin et al. [
43], formulas (46) and (47) can be transformed into
where
is a transformation matrix composed of identity and zero matrices.
Given
as the vector of Lagrangian multipliers, by relaxing the above constraints, the LR is formulated as follows
:
s.t. (2)–(28)
The LR problem can be decomposed into several independent subproblems, and its lower bound is obtained through the solution of the corresponding Lagrangian dual model.
The Lagrangian dual problem, being a concave maximization problem with a non-differentiable objective function, is solved by applying the subgradient method with an adaptive step size, following the approach suggested by Yin et al. [
43]. The algorithmic steps are described below:
Step 1. Initialize the iteration counter and the initial value .
Step 2. Given , compute the corresponding subgradient , update the current best objective function value, and denote it as .
Design the update formula for the step size
:
where
,
, and both
and
are linearly and monotonically decreasing functions of
k with positive values. If the current best solution
remains unchanged for three consecutive iterations, the step size is adaptively adjusted according to
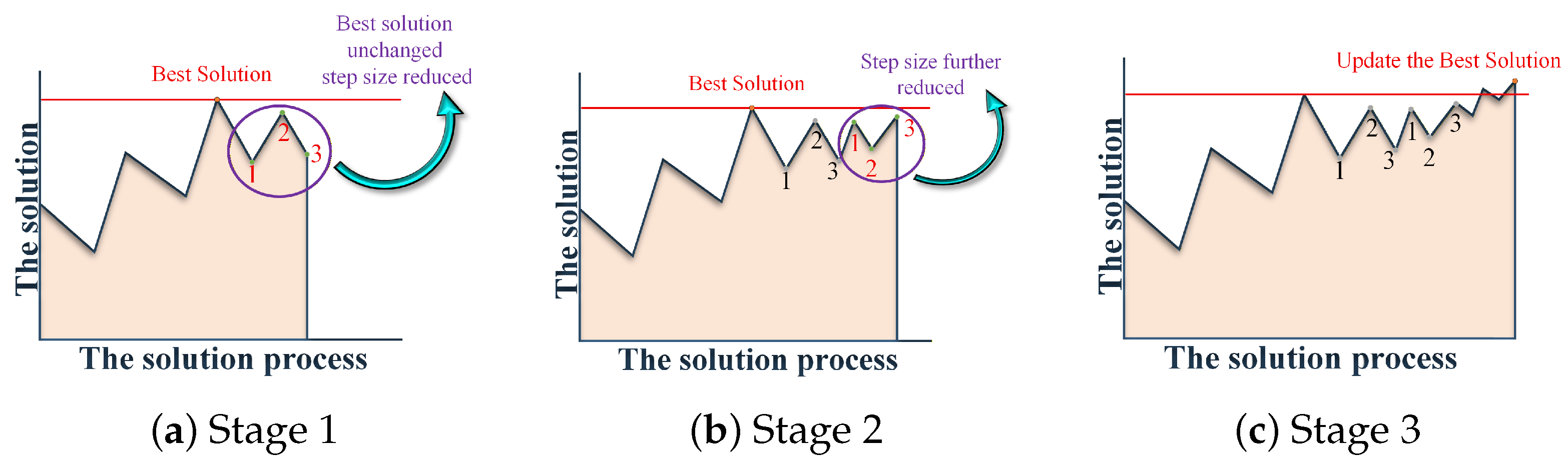
to accelerate the convergence process. Since the Lagrangian dual problem is a concave and unconstrained optimization problem, a global optimum exists, and the subgradient method is adopted to solve it. The iterative process of this method resembles that of the steepest descent algorithm but relies on subgradient directions instead of exact gradients. By adaptively reducing the step size when stagnation occurs, the proposed scheme improves convergence stability and computational efficiency. An illustrative example of this process is shown in
Figure 2.
Step 4. Termination condition:
where
is a sufficiently small positive number. Otherwise, set
and return to Step 2. In the P2 problem, when the network structure includes
c collection centers,
r remanufacturing centers,
w disposal centers, and
d demand nodes, the numbers of decision variables and constraints are
and
, respectively. It can be observed that both quantities increase by
and
as the number of scenarios
grows, which significantly amplifies the computational complexity of the model. To address this issue, the proposed decomposition algorithm divides the original problem into multiple independent scenario subproblems, thereby reducing the numbers of decision variables and constraints in each subproblem by a factor of
. This decomposition strategy effectively alleviates computational burden and enhances solution efficiency.
Furthermore, the proposed algorithm indicates general applicability to multi-scenario stochastic programming problems, extending beyond the specific context of recycling ND.
5. Numerical Experiments
To systematically validate the feasibility and overall performance of the proposed EVB recycling network model in practical settings, this study conducts data-driven simulation experiments based on a real-world case from an EVB recycling enterprise. Several groups of comparative tests are designed to comprehensively evaluate system performance under different strategies. The experiments are analyzed from three perspectives: algorithmic performance, computational efficiency, and parameter sensitivity. The structure of this chapter is organized as follows:
Section 5.1 introduces the sources of experimental data;
Section 5.2 evaluates the solution performance and computational efficiency of the proposed SRDBH algorithm;
Section 5.3 analyzes the impact of key parameters—such as unit penalty cost and fortification budget limits—on system behavior;
Section 5.4 summarizes managerial insights derived from the experimental results, providing theoretical support and decision-making references for industry practice.
5.1. Experimental Data
The recycling network is based on the infrastructure jointly established by Jiangling Electric Vehicle Limited (Nanchang, China) and Dongfeng Electric Vehicle Co., Ltd. (Wuhan, China) drawing on reports from Jiangxi Province and Dongfeng Motor (2019–2021). The experimental parameters are primarily obtained from Wang et al. [
25], and the corresponding values are summarized in
Table 2. For parameters not reported in Wang’s study, including facility processing capacities, 3PL construction costs, 3PL transportation capacities, 3PL unit transportation costs, maximum reservation levels, and unit reservation costs, reasonable estimates were made with reference to Wang’s data. These estimated values are presented in the
Table A1 to facilitate reproducibility.
5.2. Algorithm Performance and Solution Efficiency
For each facility subject to potential disruption, two possible states are considered: disrupted or non-disrupted. A total of ten facilities are assumed to face potential disruption, resulting in 1024 possible disruption scenarios. The disruption probability of each facility is assumed to be known, as listed in
Table 3, and the probability of each disruption scenario is calculated using Equation (
29). These probabilities are determined with reference to prior studies, ensuring that the parameter settings remain within a realistic range typically encountered in recycling networks.
Under these 1024 disruption scenarios, the proposed SRDBH algorithm is compared with the commercial solver CPLEX to indicate that the proposed model and algorithm are more suitable than mainstream commercial solvers for disruption-prone and resource-constrained environments. Experiments are conducted on a computer equipped with a 2.60 GHz quad-core processor and 8 GB of RAM, with the runtime limited to 3600 s. By applying the SR technique, the original 1024 scenarios are reduced to four representative ones, which are then solved by both SRDBH and CPLEX.
Since this study focuses on a strategic engineering management problem, solution quality is of greater importance than computation time. Specifically, the quality of solutions is evaluated by calculating the lower bound and assessing the upper–lower bound gap as a key indicator of algorithmic performance. A small gap indicates that SRDBH consistently yields near-optimal solutions with high reliability—an essential property for managerial decision-making under uncertainty.
To further assess the scalability and practical value of SRDBH, we divide the test instances into two categories: small-scale networks (47 nodes, denoted SRDBH-S) and large-scale networks (71 nodes, denoted SRDBH-L). This classification allows us to evaluate the adaptability of the algorithm to different network sizes commonly encountered in engineering practice. The choice of 47 and 71 nodes is consistent with the assumptions proposed by Yin et al. [
43], which suggest that the number of network nodes in practical EVB recycling systems generally does not exceed 100.
The experimental results are summarized in
Table 4 and
Table 5 (TCRN denotes the total cost, LB represents the lower bound, and N/A indicates termination due to memory overflow). The main findings are as follows:
Computational efficiency: SRDBH successfully solves all test cases within the 3600-s time limit, with runtimes significantly shorter than those of CPLEX.
Memory robustness: CPLEX frequently terminates due to insufficient memory, while SRDBH consistently produces stable outputs, demonstrating superior applicability in engineering contexts.
Solution accuracy: Even when CPLEX produces results, the gaps remain close to 100%, indicating infeasible lower bounds. By contrast, SRDBH achieves gaps below 3.5% in SRDBH-S and below 1.3% in SRDBH-L, highlighting its capability to deliver high-quality near-optimal solutions.
Scalability: SRDBH maintains low gaps and stable performance in both small- and large-scale networks, confirming its adaptability to various network sizes in engineering management practice.
In summary, the SRDBH algorithm efficiently and reliably addresses large-scale EVBRND problems under multiple uncertainties and complex constraints. It effectively overcomes the computational bottlenecks of traditional commercial solvers in resource-limited environments and indicates strong engineering management value, particularly for enterprises that must make rapid and resilient network optimization decisions under disruption risks and budget constraints.
5.3. Sensitivity Analysis
Based on the 1024 disruption scenarios, this study applies the SR technique to extract four representative scenarios with occurrence probabilities of 0.15, 0.70, 0.05, and 0.10, respectively. On this reduced scenario set, we further conduct a parameter sensitivity analysis, focusing on the impacts of the and the fortification budgets on the performance of the recycling network. The parameter settings are as follows: increases from 7000 to 9000 in increments of 500, while increases from 10,000 to 60,000 in increments of 10,000. System behavior is analyzed from multiple dimensions, including total network cost (TCRN), total penalty cost (TPFN), and unrecycled battery volume (URB), based on which managerial insights are proposed.
5.3.1. Impacts of Unit Penalty Cost and Fortification Budget on Total Cost
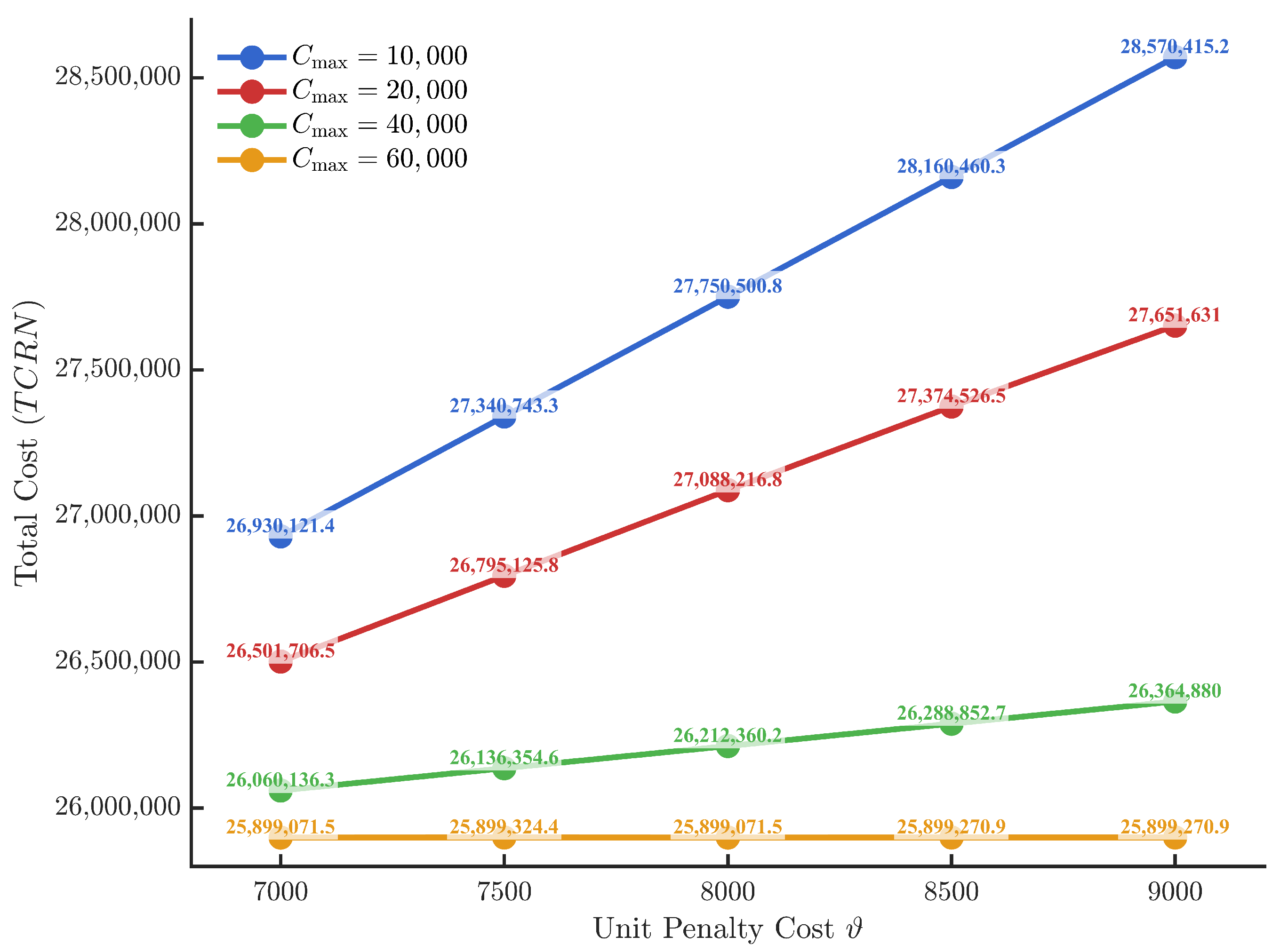
The experimental results are presented in
Table 6 and
Figure 3, from which the following conclusions can be drawn:
When the is fixed, the TCRN shows a steady upward trend as increases. For example, when = 10,000, TCRN rises from 26,930,121.4 to 28,570,415.2, reflecting a notable increase. However, when is raised to 60,000, TCRN remains largely stable across different levels, with only minor fluctuations. This indicates that under sufficient budget, the marginal effect of increasing becomes saturated, and its influence on total cost weakens significantly.
When is fixed, TCRN generally decreases as increases. Numerically, the cost reduction is most significant when rises from 20,000 to 40,000. Moreover, the cost-saving effect of increasing varies across levels: the higher the penalty cost, the greater the marginal cost reduction achieved through the same budget increase. For instance, when , increasing from 10,000 to 60,000 reduces total cost by approximately 2,671,144.3, whereas under , the reduction is only 1,031,049.9. This suggests that under high penalty cost pressure, relaxing the is more effective in mitigating total system costs.
The primarily drives up short-term operational costs by incentivizing recycling, influencing 3PL routing decisions, and intensifying processing center operations. In contrast, the reduces long-term risks and recovery costs by enhancing the resilience of the recycling network against disruptions. Therefore, enterprises should jointly consider both parameters in practice: on the one hand, setting an appropriate penalty cost helps constrain unrecycled behavior without excessively inflating costs; on the other hand, carefully evaluating the risk mitigation and cost-saving benefits of fortification investments is essential. Particularly in highly uncertain environments, moderately relaxing budget constraints can significantly improve system-level economic performance.
5.3.2. Impacts of Unit Penalty Cost and Fortification Budget on Penalty Costs
To further examine the mechanisms through which the unit penalty cost
and the fortification budget
affect the TPFN within the recycling network,
Table 7 and
Figure 4 reports TPFN values under different parameter combinations. From the experimental findings, the following observations can be made:
When is fixed, TPFN increases with . For instance, at = 10,000, TPFN rises from 5,762,010.4 to 7,374,842.5, representing an increase of about 28%. A similar pattern is observed at = 40,000, where the increase is around 29%. This indicates that raising the directly drives up total penalty expenditure. However, when = 60,000, TPFN consistently equals zero, implying that under a sufficiently large budget the system can entirely avoid penalty costs, rendering ineffective. Therefore, if firms are highly sensitive to TPFN, adopting excessively high penalty costs should be approached with caution, particularly considering their interaction with budget constraints.
When is fixed, TPFN decreases substantially as increases, exhibiting a clear nonlinear pattern. For example, under , raising from 10,000 to 20,000 reduces TPFN by about 29%; further increasing from 20,000 to 40,000 reduces TPFN by approximately 74%. Once reaches 60,000, TPFN drops to zero. This trend holds across all levels, suggesting that larger budgets enhance system robustness, thereby reducing the number of unrecycled batteries and substantially lowering or even eliminating penalty costs. Notably, the marginal reduction effect of on TPFN is strongest within the 20,000–40,000 range, identifying this interval as a sensitive zone for cost control.
In summary, exerts a direct and nearly linear upward pressure on TPFN, while indicate s a strong nonlinear suppressive effect with a distinct threshold property. The former increases cost burden by raising the penalty per unit of unrecycled battery, whereas the latter reduces penalties fundamentally by strengthening the network’s resilience against disruptions. From a managerial perspective, if minimizing penalty expenditure is the primary objective, firms should prioritize securing an adequate and then complement it with a moderate penalty cost policy. This dual approach enables the simultaneous optimization of both economic efficiency and environmental responsibility.
5.3.3. Impacts of Unit Penalty Cost and Fortification Budget on Unrecycled Batteries
The URBN is a key performance indicator for assessing the system’s ability to withstand disruptions and fulfill recycling tasks.
Table 8 reports URBN results under different combinations of
and
, leading to the following conclusions:
is fixed, increasing has only a limited suppressive effect on URBN. For example, at = 10,000, URBN remains constant at 819, with no improvement in system recovery capability. When = 20,000, URBN decreases only slightly from 587 to 543, indicating marginal optimization. This suggests that relying solely on penalty mechanisms cannot systematically enhance recycling completion rates.
URBN decreases significantly with higher , particularly within the range of 10,000–40,000, where the reduction is most pronounced. Once reaches 60,000, URBN drops to zero, indicating that the network has achieved full resilience against disruption. This indicates that expanding the can unlock scheduling potential and fundamentally improve task completion capability.
A clear substitution effect exists between and . When is insufficient (e.g., 10,000), raising has virtually no impact on URBN. Conversely, when is sufficiently large, URBN remains at very low or even zero levels regardless of whether is set high or low (e.g., 7000). This highlights that a sufficient can largely substitute for the pressure imposed by high penalty costs, providing a more fundamental physical basis for system optimization.
In conclusion, the control of URBN is highly dependent on the resource adequacy determined by , while plays only an auxiliary role. From a managerial perspective, firms are advised to prioritize fortification investment and adopt resilience-oriented network optimization strategies, rather than relying excessively on ex-post economic penalties.
5.4. Managerial Implications
Through a series of numerical experiments, the effectiveness of the proposed model and solution algorithm is validated. Based on these results, the following managerial recommendations are offered for practitioners:
First, from the perspective of computational efficiency and solution feasibility, the proposed SRDBH algorithm exhibits strong stability in addressing complex scenarios. Practical optimization strategies for ND under frequent disruption risks or stringent constraints are thereby enabled. For decision makers who are required to adjust network configurations within limited time horizons, such a heuristic approach can be regarded as an effective means of mitigating unexpected risks and resource fluctuations.
Second, the sensitivity analysis indicates that and exert considerable influence on network performance, but their effects differ in nature. From the enterprise perspective, serves as a controllable investment decision. An increase in consistently reduces both TCRN and URBN; for example, increasing in the sensitive range yields substantial reductions in TPFN: raising from 10,000 to 20,000 reduces TPFN by about 29%, and further increasing from 20,000 to 40,000 reduces TPFN by approximately 74%. Moreover, in the example where = 10,000, increasing leads to only a modest increase in TCRN of about 6.09%, whereas the corresponding increase in penalty expenditures TPFN is approximately 28.0%. These results indicate that expanding —when affordable—can more effectively and fundamentally lower URBN and penalty expenditures than simply raising .
However, for firms with limited resources, directly increasing may not be feasible. In such cases, enhancing redundancy through multi-3PL collaboration and diversified routing offers an alternative. For instance, when is moderate, increasing redundancy and operational flexibility can reduce URBN by an additional 7.5% compared with changes driven primarily by penalty adjustments, providing a cost-effective way to improve recovery without large upfront fortification budgets.
From the policy perspective, represents a regulatory lever controlled by governments. Higher levels encourage recycling behavior, but their marginal effects diminish when is sufficiently large. For example, under low settings, raising substantially increases penalty spending (TPFN rises by 28% in one tested scenario) while yielding limited improvements in completion rates; conversely, under sufficiently large , penalty costs can be driven to zero and URBN approaches zero regardless of . This implies that, from a public-policy viewpoint, calibrated combinations of regulatory pressure and support for preventive investment (e.g., subsidies, cost-sharing, or co-investment schemes that effectively increase firms’ available ) are likely to be more effective and efficient than relying only on high punitive charges.
In conclusion, the SRDBH algorithm is indicated to be a reliable decision-support instrument for enterprises operating under uncertainty and resource constraints. Managerial strategies should therefore avoid excessive dependence on ex-post penalty mechanisms and instead prioritize preventive investments when feasible. At the same time, governments should design with caution, ensuring that they motivate compliance without imposing unnecessary costs. A balanced coordination between enterprise-driven preventive investment and government-designed policy incentives can achieve the dual goals of cost efficiency and sustainable recovery.
7. Conclusions
This study examines the EVBRND under disruption risks within the framework of the 4PL management model. To strengthen system resilience, strategies such as multi-source allocation, multi-route transportation, multi-3PL collaboration, facility fortification, and capacity backup are incorporated into the EVBRND. A two-stage resilient optimization model is established, in which facility construction costs, fortification expenditures, unit processing costs, battery classifications and proportions, 3PL capacity, transportation costs, and are considered as key parameters. To address the computational challenges of large-scale stochastic optimization, a SRDBH algorithm is developed, which integrates SR, conditional relaxation, LR, and an adaptive subgradient method.
The results of case experiments indicate that the proposed model and algorithm effectively control total costs while significantly reducing both unrecycled batteries and penalty expenditures, thereby enhancing recycling efficiency and improving network robustness. Sensitivity analyses further reveal the following insights:
Although exerts an incentive effect on recycling behavior, its marginal benefits diminish as the penalty level increases.
Moderate increases in contribute to cost reduction; however, careful calibration of investment levels is necessary to prevent diminishing returns.
Despite the comprehensive exploration of model formulation and algorithmic design, several avenues remain open for future research. First, the current framework assumes that disruption probabilities are independent and known in advance, which enables the problem to be reformulated as an MILP. This assumption improves computational tractability but may not fully capture the complexities of real-world disruption patterns. Future studies may relax this assumption and extend the framework to account for correlated or uncertain disruption probabilities. Second, the model does not incorporate carbon emission constraints. The integration of mechanisms such as carbon trading or carbon taxation could enhance the policy relevance of the model by introducing carbon quota constraints and incorporating carbon emission costs into the objective function. Third, the impact of stochastic recycling demand has not yet been considered. Extending the framework to capture EVBRND problems under dual sources of uncertainty could further advance the practical applicability of resilient recycling systems. Fourth, collaborative optimization of EVB echelon utilization and recycling could be investigated. Specifically, the inclusion of echelon utilization centers in the ND may affect facility location decisions and support the full-lifecycle management of EVBs, which aligns with current industry trends and expands the potential application scenarios of this research.