Sustainable Reduced-Order Thermal Modeling for Energy-Efficient Real-Time Control of Grid-Scale Energy Storage Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. System Configuration and Specifications
2.2. Detailed Thermal Model Development
2.3. Reduced-Order Thermal Model Formulation
2.4. Operational Scenario Definition
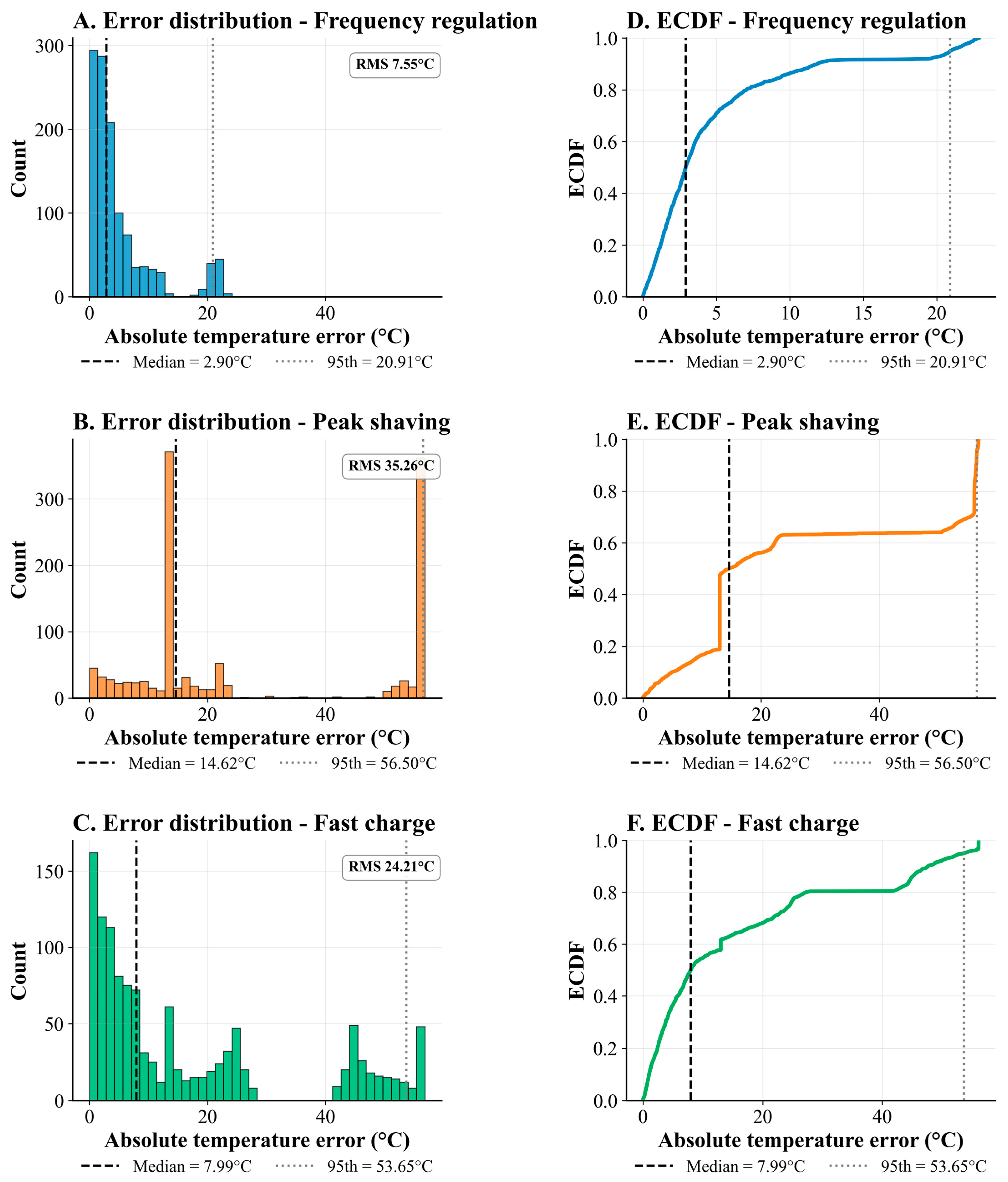
2.5. Model Validation and Error Quantification
2.6. Performance Metrics and Sustainability Assessment
2.7. Real-Time Control Implementation
2.8. Computational Implementation and Analysis
2.9. Data Processing and Statistical Analysis
3. Results
3.1. System Thermal Dynamics and Load Response
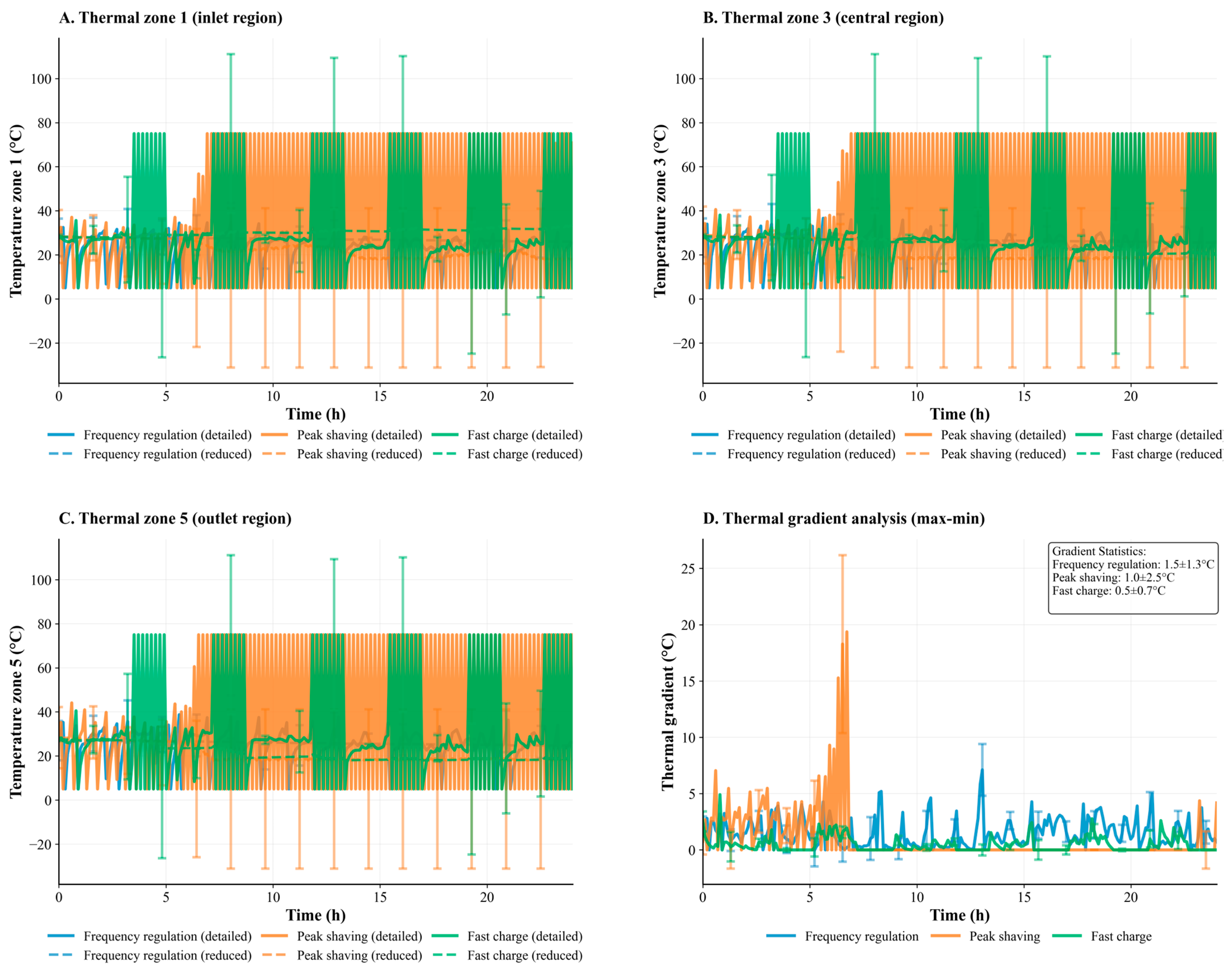
3.2. Spatial Thermal Distribution Analysis
3.3. Performance and Sustainability Assessment
3.4. Comparative Analysis Against Existing Reduced-Order Modeling Approaches
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Definition |
| BESS | Battery Energy Storage System |
| BMS | Battery Management System |
| BTMS | Battery Thermal Management System |
| CFD | Computational Fluid Dynamics |
| DoE | Design of Experiments |
| ECM | Equivalent Circuit Model |
| ECDF | Empirical Cumulative Distribution Function |
| FEM | Finite Element Method |
| MPC | Model Predictive Control |
| POD | Proper Orthogonal Decomposition |
| RMS | Root Mean Square |
| ROM | Reduced-Order Model |
| SOC | State of Charge |
| SOH | State of Health |
| TEGS | Thermal Energy Grid Storage |
Appendix A
References
- Rajendran, G.; Raute, R.; Caruana, C. A Comprehensive Review of Solar PV Integration with Smart-Grids: Challenges, Standards, and Grid Codes. Energies 2025, 18, 2221. [Google Scholar] [CrossRef]
- Rabbi, M.F.; Popp, J.; Máté, D.; Kovács, S. Energy Security and Energy Transition to Achieve Carbon Neutrality. Energies 2022, 15, 8126. [Google Scholar] [CrossRef]
- Abdolrasol, M.G.M.; Ansari, S.; Sarker, I.A.; Tiong, S.K.; Hannan, M.A. Lithium-Ion to Sodium-Ion Batteries Transitioning: Trends, Analysis and Innovative Technologies Prospects in EV Application. Prog. Energy 2025, 7, 022007. [Google Scholar] [CrossRef]
- Maher, K.; Boumaiza, A. Thermal Challenges in Lithium-Ion Battery Technology: Investigating Performance and Thermal Stability. J. Energy Storage 2025, 111, 115396. [Google Scholar] [CrossRef]
- Rabbi, M.F. Optimizing Carbon Emissions and SDG-12 Performance in the EU Food System. Carbon Res. 2025, 4, 54. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K.T. Health-Conscious Energy Management for Fuel Cell Vehicles: An Integrated Thermal Management Strategy for Cabin and Energy Source Systems. Energy 2025, 333, 137330. [Google Scholar] [CrossRef]
- Rabbi, M.F. Cross-Framework Hybrid Artificial Intelligence for High-Penetration Renewable Energy Integration: Multi-Regional Forecasting and Adaptive Control. Appl. Energy 2025, 401, 126834. [Google Scholar] [CrossRef]
- Rufino Júnior, C.A.; Sanseverino, E.R.; Gallo, P.; Amaral, M.M.; Koch, D.; Kotak, Y.; Diel, S.; Walter, G.; Schweiger, H.-G.; Zanin, H. Unraveling the Degradation Mechanisms of Lithium-Ion Batteries. Energies 2024, 17, 3372. [Google Scholar] [CrossRef]
- Murashko, K.; Pyrhonen, J.; Laurila, L. Three-Dimensional Thermal Model of a Lithium Ion Battery for Hybrid Mobile Working Machines: Determination of the Model Parameters in a Pouch Cell. IEEE Trans. Energy Convers. 2013, 28, 335–343. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D. Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts. Energies 2025, 18, 1302. [Google Scholar] [CrossRef]
- Söderäng, E.; Hautala, S.; Mikulski, M.; Storm, X.; Niemi, S. Development of a Digital Twin for Real-Time Simulation of a Combustion Engine-Based Power Plant with Battery Storage and Grid Coupling. Energy Convers. Manag. 2022, 266, 115793. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Z.; Ji, H.; Gong, H. Application and Comparison of Several Adaptive Sampling Algorithms in Reduced Order Modeling. Heliyon 2024, 10, e34928. [Google Scholar] [CrossRef]
- Samadiani, E.; Joshi, Y. Reduced Order Thermal Modeling of Data Centers via Proper Orthogonal Decomposition: A Review. Int. J. Numer. Methods Heat Fluid Flow 2010, 20, 529–550. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-Order Modeling: New Approaches for Computational Physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef]
- Jiang, G.; Kang, M.; Cai, Z.; Liu, Y.; Wang, W. Data-Driven Temperature Estimation of Non-Contact Solids Using Deep-Learning Reduced-Order Models. Int. J. Heat. Mass. Transf. 2022, 185, 122383. [Google Scholar] [CrossRef]
- Coccato, S.; Barhmi, K.; Lampropoulos, I.; Golroodbari, S.; van Sark, W. A Review of Battery Energy Storage Optimization in the Built Environment. Batteries 2025, 11, 179. [Google Scholar] [CrossRef]
- Eltamaly, A.M.; Almutairi, Z.A. Adaptive Real-Time Degradation Modeling for Lithium-Ion Batteries in Grid Energy Storage Systems. IEEE Access 2025, 13, 148203–148218. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Sun, F.; Wang, Z. An Overview on Thermal Safety Issues of Lithium-Ion Batteries for Electric Vehicle Application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Xu, L.; Wang, S.; Xi, L.; Li, Y.; Gao, J. A Review of Thermal Management and Heat Transfer of Lithium-Ion Batteries. Energies 2024, 17, 3873. [Google Scholar] [CrossRef]
- Chen, C.-H.; Brosa Planella, F.; O’Regan, K.; Gastol, D.; Widanage, W.D.; Kendrick, E. Development of Experimental Techniques for Parameterization of Multi-Scale Lithium-Ion Battery Models. J. Electrochem. Soc. 2020, 167, 080534. [Google Scholar] [CrossRef]
- Li, R.; Kirkaldy, N.D.; Oehler, F.F.; Marinescu, M.; Offer, G.J.; O’Kane, S.E.J. The Importance of Degradation Mode Analysis in Parameterising Lifetime Prediction Models of Lithium-Ion Battery Degradation. Nat. Commun. 2025, 16, 2776. [Google Scholar] [CrossRef]
- Adaikkappan, M.; Sathiyamoorthy, N. Modeling, State of Charge Estimation, and Charging of Lithium-ion Battery in Electric Vehicle: A Review. Int. J. Energy Res. 2022, 46, 2141–2165. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.J.; Zhao, J. Development of Efficient Air-Cooling Strategies for Lithium-Ion Battery Module Based on Empirical Heat Source Model. Appl. Therm. Eng. 2015, 90, 521–529. [Google Scholar] [CrossRef]
- Duffy, A.; Hand, M.; Wiser, R.; Lantz, E.; Dalla Riva, A.; Berkhout, V.; Stenkvist, M.; Weir, D.; Lacal-Arántegui, R. Land-Based Wind Energy Cost Trends in Germany, Denmark, Ireland, Norway, Sweden and the United States. Appl. Energy 2020, 277, 114777. [Google Scholar] [CrossRef]
- Yin, S.; Wang, H.; Wang, L.; Liu, C.; Tong, L. Influencing Factors and Evaluation System for Carbon–Calcium Pellet Performance in a Pyrolysis Furnace. Energy 2021, 214, 118991. [Google Scholar] [CrossRef]
- dos Santos-Gómez, L.; Porras-Vázquez, J.M.; Losilla, E.R.; Martín, F.; Ramos-Barrado, J.R.; Marrero-López, D. Stability and Performance of La0.6Sr0.4Co0.2Fe0.8O3-δ Nanostructured Cathodes with Ce0.8Gd0.2O1.9 Surface Coating. J. Power Sources 2017, 347, 178–185. [Google Scholar] [CrossRef]
- Ruiz, P.L.; Damianakis, N.; Mouli, G.R.C. Physics-Based and Data-Driven Modeling of Degradation Mechanisms for Lithium-Ion Batteries—A Review. IEEE Access 2025, 13, 21164–21189. [Google Scholar] [CrossRef]
- Hosseininasab, S.; Lin, C.; Pischinger, S.; Stapelbroek, M.; Vagnoni, G. State-of-Health Estimation of Lithium-Ion Batteries for Electrified Vehicles Using a Reduced-Order Electrochemical Model. J. Energy Storage 2022, 52, 104684. [Google Scholar] [CrossRef]
- Roy, P.K.; Shahjalal, M.; Shams, T.; Fly, A.; Stoyanov, S.; Ahsan, M.; Haider, J. A Critical Review on Battery Aging and State Estimation Technologies of Lithium-Ion Batteries: Prospects and Issues. Electronics 2023, 12, 4105. [Google Scholar] [CrossRef]
- Zhao, X.; Bi, Y.; Choe, S.-Y.; Kim, S.-Y. An Integrated Reduced Order Model Considering Degradation Effects for LiFePO4/Graphite Cells. Electrochim. Acta 2018, 280, 41–54. [Google Scholar] [CrossRef]
- Rodríguez-Iturriaga, P.; García, V.M.; Rodríguez-Bolívar, S.; Valdés, E.E.; Anseán, D.; López-Villanueva, J.A. A Coupled Electrothermal Lithium-Ion Battery Reduced-Order Model Including Heat Generation Due to Solid Diffusion. Appl. Energy 2024, 367, 123327. [Google Scholar] [CrossRef]
- Ansari, A.B.; Esfahanian, V.; Torabi, F. Thermal-Electrochemical Simulation of Lead-Acid Battery Using Reduced-Order Model Based on Proper Orthogonal Decomposition for Real-Time Monitoring Purposes. J. Energy Storage 2021, 44, 103491. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference (SciPy 2010), Austin, TX, USA, 28 June–3 July 2010; pp. 56–61. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array Programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Asgari, S.; Hu, X.; Tsuk, M.; Kaushik, S. Application of POD plus LTI ROM to Battery Thermal Modeling: SISO Case. SAE Int. J. Commer. Veh. 2014, 7, 278–285. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, H.; Chen, J.; Ding, R.; Luo, D. Modeling and Model Predictive Control of a Battery Thermal Management System Based on Thermoelectric Cooling for Electric Vehicles. Energy Technol. 2024, 12, 2301205. [Google Scholar] [CrossRef]
- Tang, M.; Wu, C.; Peng, W.; Han, R.; Zhang, S.; Wang, D. Numerical Simulation Study on the Impact of Convective Heat Transfer on Lithium Battery Air Cooling Thermal Model. Appl. Therm. Eng. 2024, 257, 124220. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Liu, Y.; Sun, F.; Qiao, J.; Xu, T. Review on Degradation Mechanism and Health State Estimation Methods of Lithium-Ion Batteries. J. Traffic Transp. Eng. 2023, 10, 578–610. [Google Scholar] [CrossRef]
- Vedhanarayanan, B.; Seetha Lakshmi, K.C. Beyond Lithium-Ion: Emerging Frontiers in next-Generation Battery Technologies. Front. Batter. Electrochem. 2024, 3, 1377192. [Google Scholar] [CrossRef]
- Xu, C.; Chen, Q.; Liu, S.; Zhong, C.; Wan, C.; Yu, X. Study on Optimization Control of Thermal Management System for Lithium-Ion Battery Pack. Appl. Therm. Eng. 2025, 282, 128800. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| Battery capacity | 100 kWh | kWh |
| Nominal voltage | 400 V | V |
| Operating temp range | 15–45 °C | °C |
| Cooling system type | Liquid cooling | - |
| Thermal zones | 5 zones | - |
| Computational time step | 0.1 s | s |
| Simulation duration | 24 h | h |
| Grid frequency regulation | ±2% frequency | Hz |
| Peak shaving power | 50 kW peak | kW |
| Fast charge rate | 2 C rate | C |
| Scenario | Max Temp (°C) | Avg Temp (°C) | Cooling Energy (kWh) | Thermal Energy (kWh) | Cooling Efficiency (%) |
|---|---|---|---|---|---|
| Frequency regulation | 38.73 | 24.16 | 5.44 | 0.32 | 17.27 |
| Peak shaving | 75.00 | 35.31 | 309.25 | 26.55 | 11.65 |
| Fast charge | 75.00 | 30.62 | 162.60 | 18.19 | 8.94 |
| Scenario | RMS Error (°C) | Cooling Efficiency (%) | Max Temperature (°C) | Avg Temperature (°C) |
|---|---|---|---|---|
| Frequency regulation | 7.8 | 17.27 | 38.73 | 24.16 |
| Peak shaving | 34.4 | 11.65 | 75.00 | 35.31 |
| Fast charge | 23.3 | 8.94 | 75.00 | 30.62 |
| Criterion | Prior POD-Based Studies | Present Framework | Advancement |
|---|---|---|---|
| Computational speedup | 7–17× versus detailed models | 15.2–22.3× across all scenarios | 1.3–2.2× improvement in efficiency |
| Application scale | Laboratory cells (0.1–5 kWh) | Grid-scale systems (100 kWh) | 20–1000× capacity scaling |
| Operational scenarios | Single scenario (typically constant current) | Three distinct grid services (frequency regulation, peak shaving, fast charging) | Multi-scenario validation framework |
| Validation approach | High-fidelity simulation only | High-fidelity simulation with spatial gradient analysis and cooling energy quantification | Integrated sustainability metrics |
| Spatial resolution | Single-zone or 2-zone models | 5-zone thermal architecture | 2.5× spatial granularity |
| Real-time control integration | Not evaluated or limited to feed-forward | Model predictive control with <0.1 s response | Closed-loop feasibility demonstrated |
| Sustainability metrics | Energy efficiency only (if reported) | Energy efficiency + cooling efficiency + parasitic load analysis | Comprehensive environmental assessment |
| Temperature error (RMS) | 2–5 °C (single scenario) | 7.8–34.4 °C (three scenarios, varying load intensity) | Accuracy maintained across operational diversity |
| Thermal gradient analysis | Not reported | Inter-zone gradients quantified (0.5–2.5 °C) | Spatial heterogeneity characterized |
| Deployment readiness | Laboratory demonstration | Industrial BMS integration pathway defined | Technology transfer framework |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rabbi, M.F. Sustainable Reduced-Order Thermal Modeling for Energy-Efficient Real-Time Control of Grid-Scale Energy Storage Systems. Sustainability 2025, 17, 9839. https://doi.org/10.3390/su17219839
Rabbi MF. Sustainable Reduced-Order Thermal Modeling for Energy-Efficient Real-Time Control of Grid-Scale Energy Storage Systems. Sustainability. 2025; 17(21):9839. https://doi.org/10.3390/su17219839
Chicago/Turabian StyleRabbi, Mohammad Fazle. 2025. "Sustainable Reduced-Order Thermal Modeling for Energy-Efficient Real-Time Control of Grid-Scale Energy Storage Systems" Sustainability 17, no. 21: 9839. https://doi.org/10.3390/su17219839
APA StyleRabbi, M. F. (2025). Sustainable Reduced-Order Thermal Modeling for Energy-Efficient Real-Time Control of Grid-Scale Energy Storage Systems. Sustainability, 17(21), 9839. https://doi.org/10.3390/su17219839








