Multi-Field Coupled Numerical Simulation of Geothermal Extraction and Reinjection in the Sandstone Reservoir
Abstract
1. Introduction
2. Background and Methods
2.1. Establishment of Numerical Model
2.1.1. Multi-Field Coupling Computing Theory
- (1)
- Fluid flow equation
- (2)
- Heat transfer equation
- (3)
- Solid deformation equation
2.1.2. Model Geometry and Computational Parameters
2.1.3. Geothermal Extraction and Reinjection Conditions
2.1.4. Model Discretization
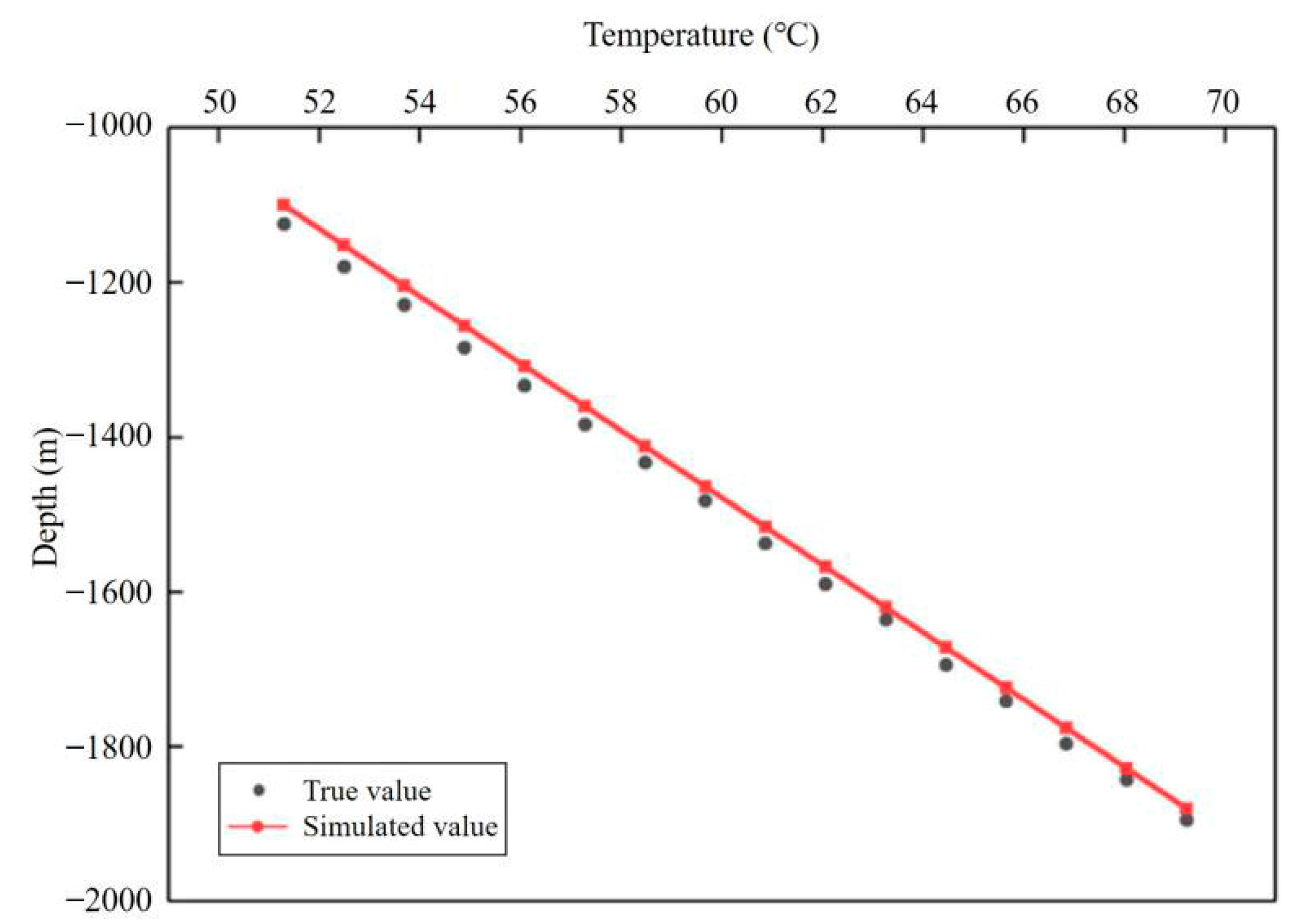
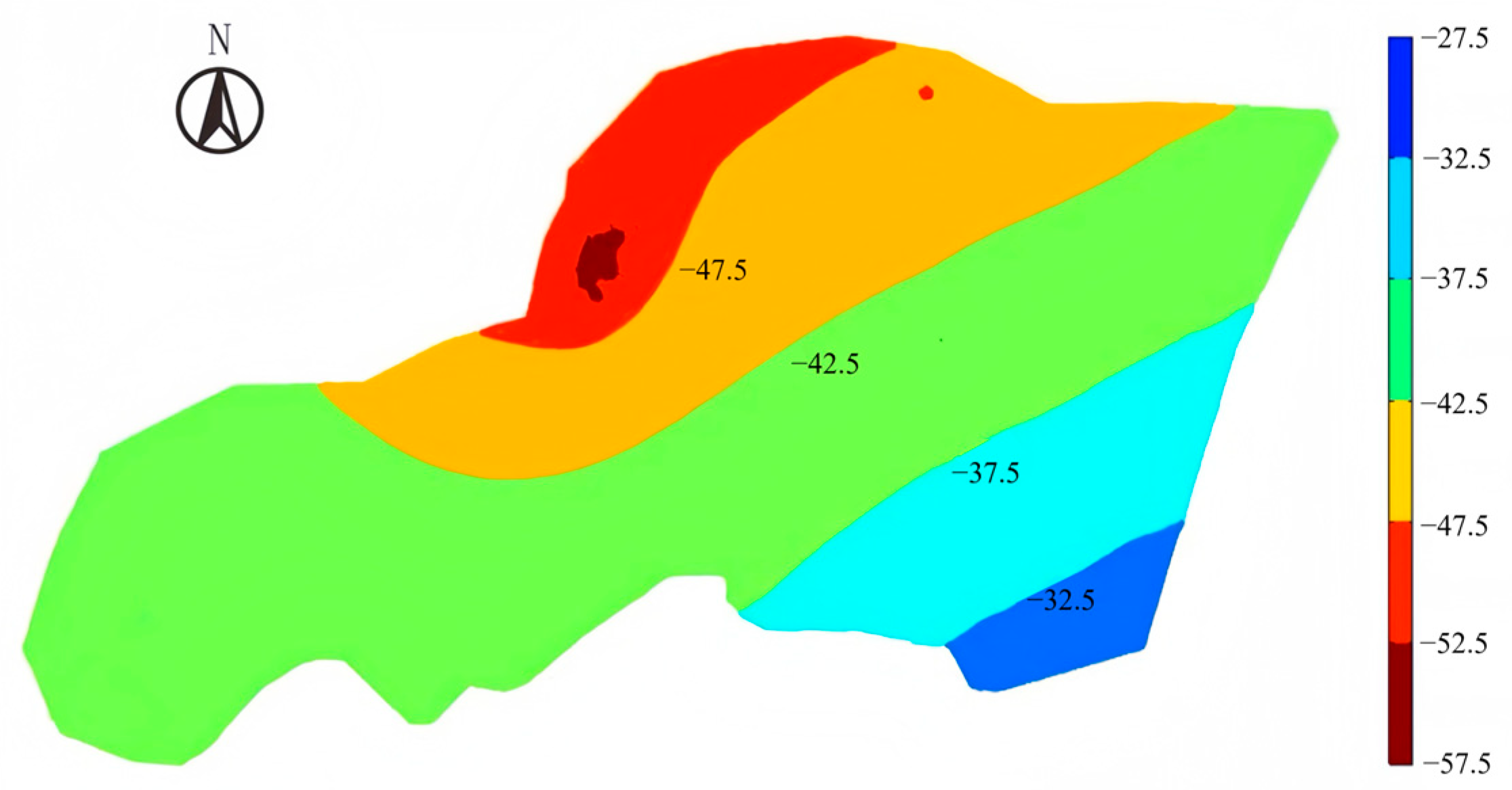
2.1.5. Model Identification and Verification
- (1)
- Water level verification
- (2)
- Temperature fitting
3. Results
3.1. Reservoir Evolution Under Current Conditions
3.1.1. Flow Field Evolution
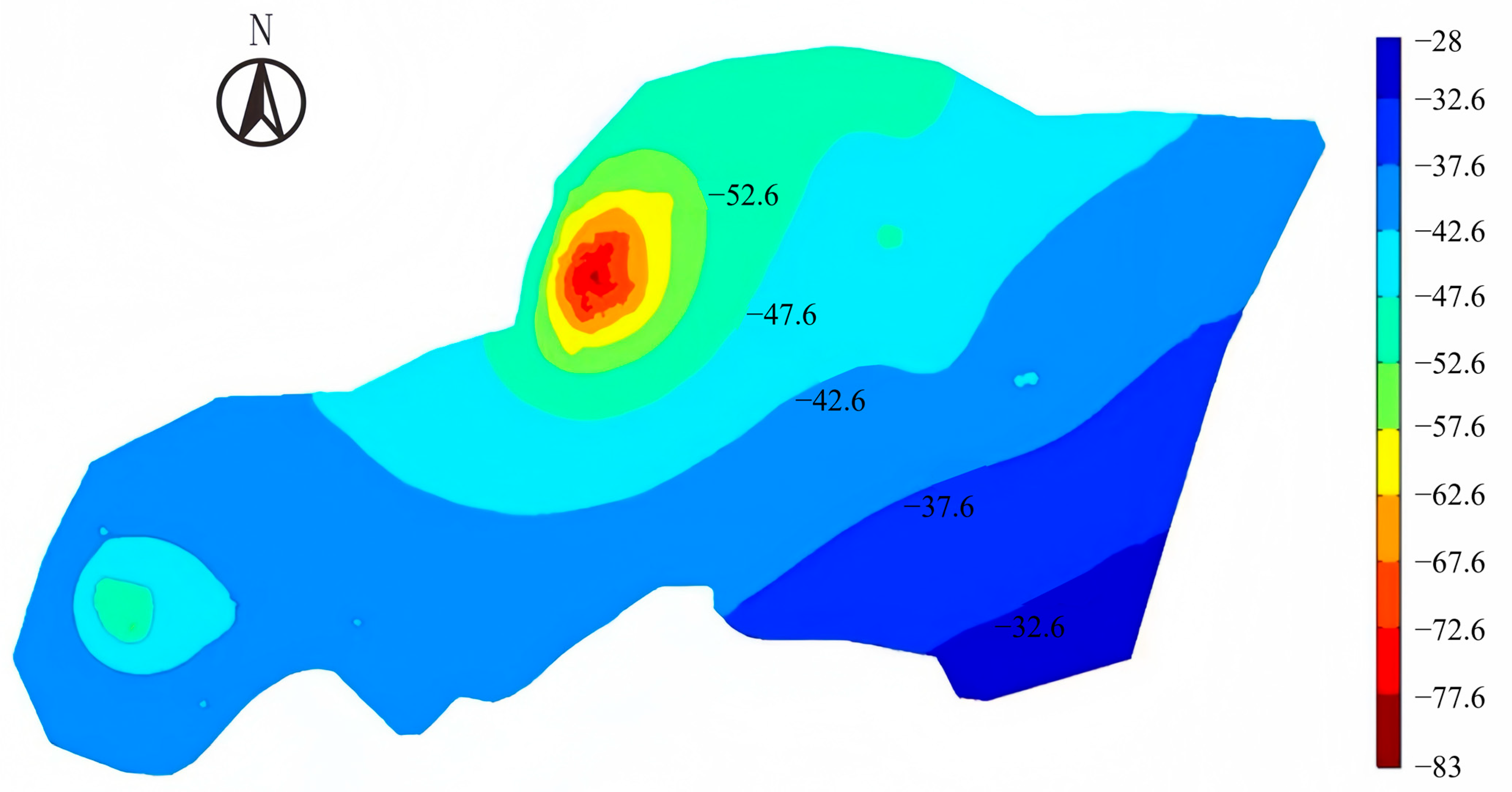
3.1.2. Temperature Field Evolution
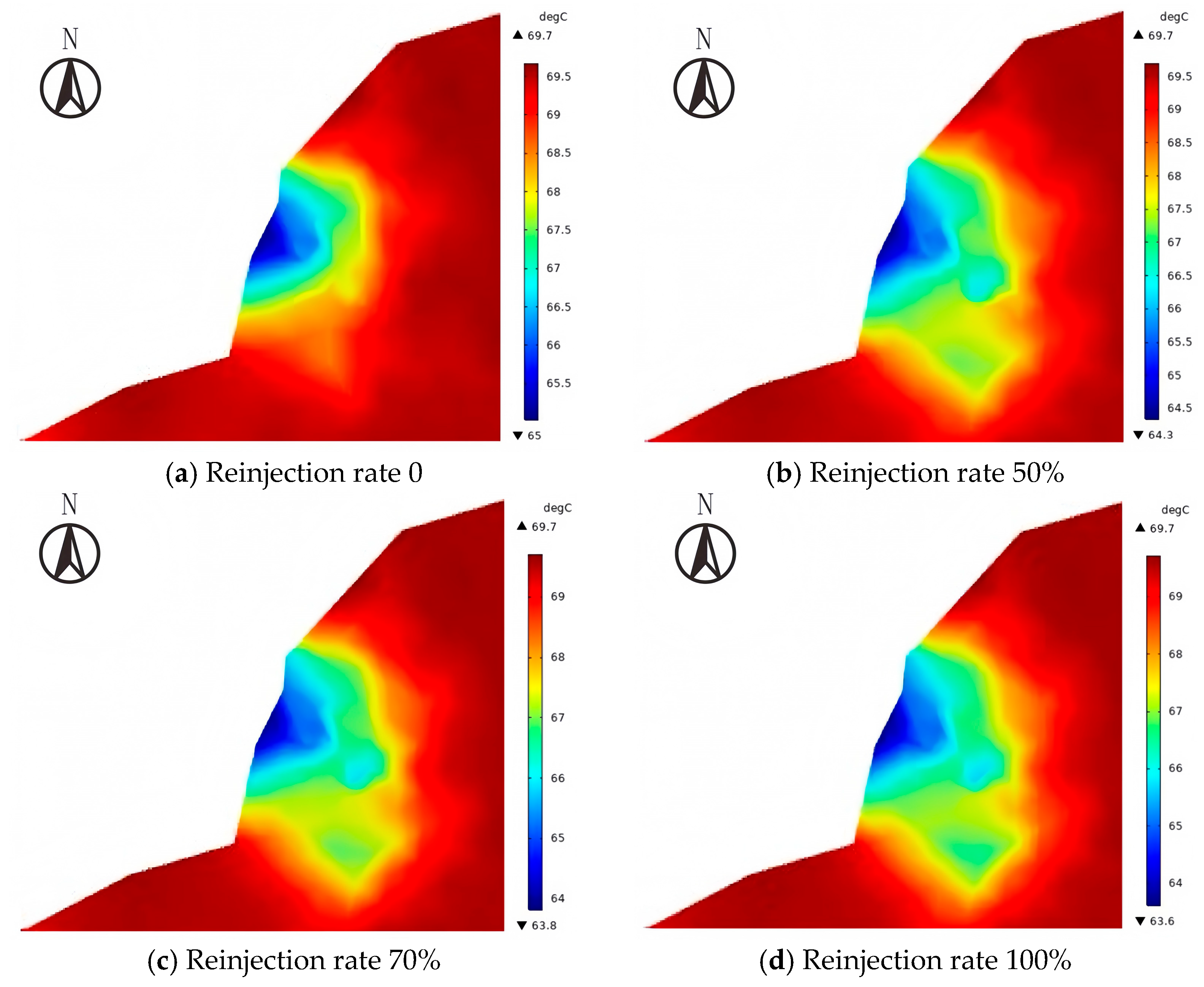
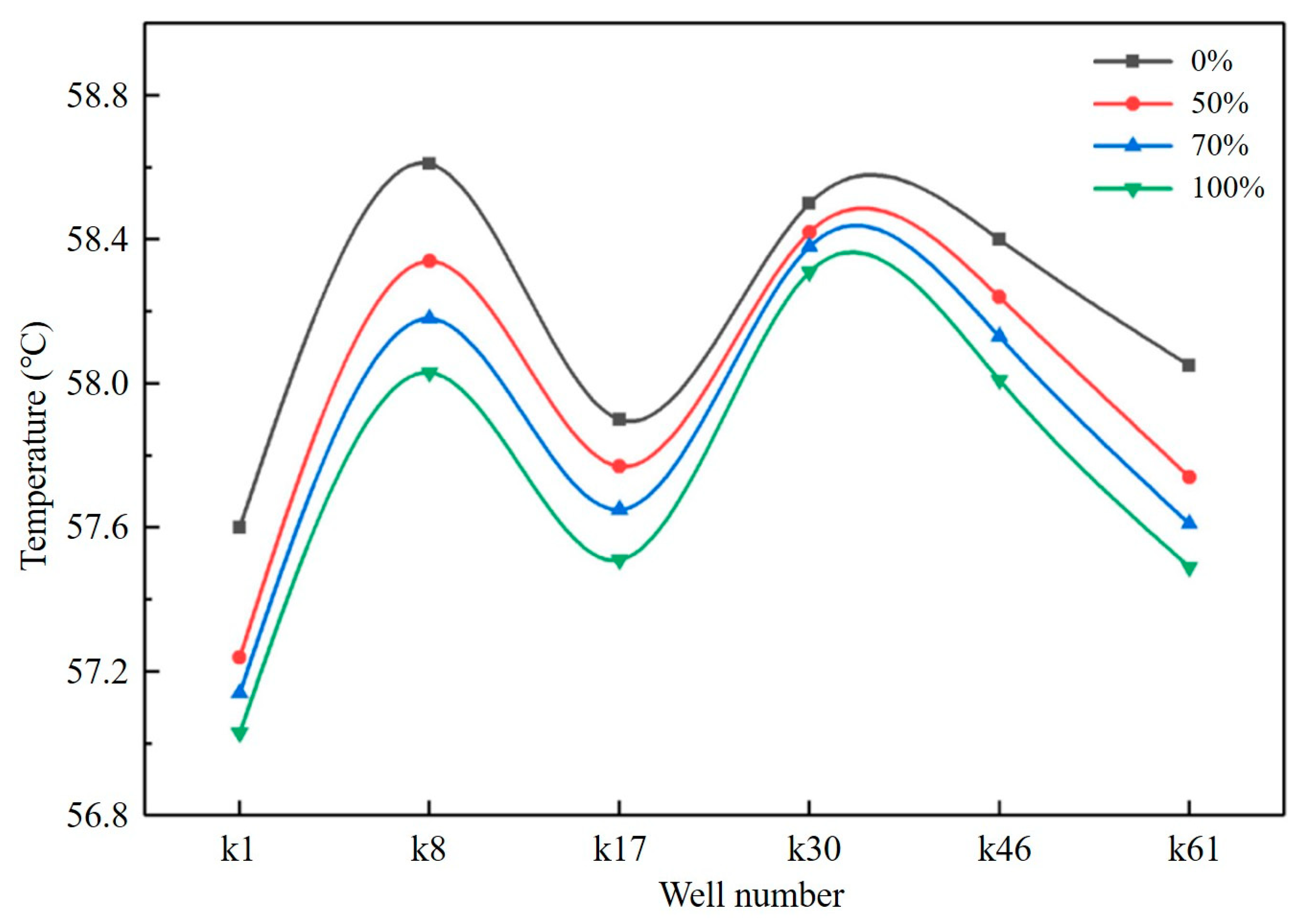
3.2. Impacts of Reinjection Rate
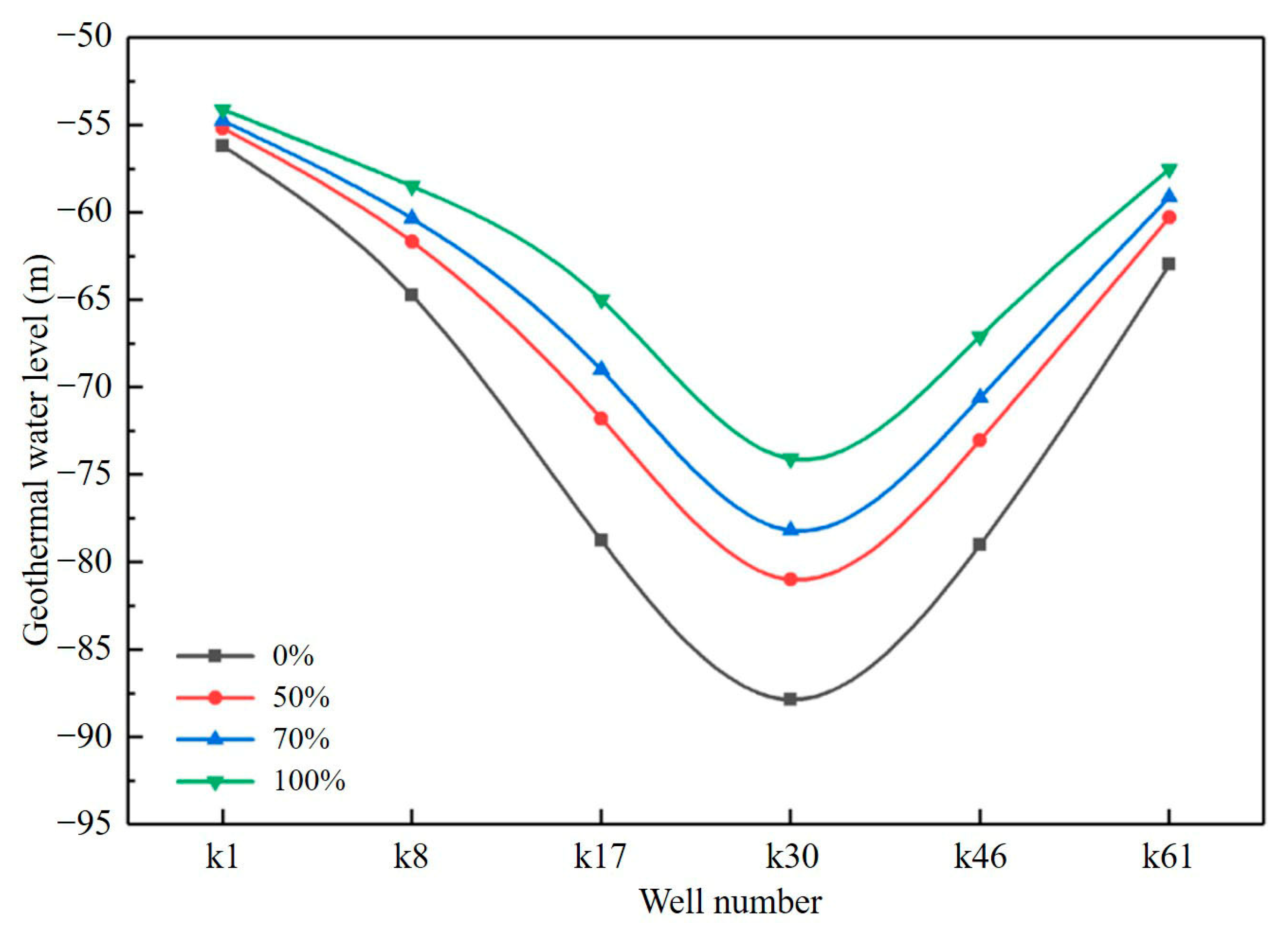
3.2.1. Flow Field Response
3.2.2. Temperature Field Response
4. Discussion
5. Conclusions
- (1)
- Under current conditions, a pronounced geothermal water-level depression funnel has developed in the urban area of Linqing. The water level declines by approximately 7.4 m within one year and by 32.7 m at the center of the funnel within ten years, while the affected area gradually expands. Without effective reinjection, the reservoir experiences continuous pressure attenuation, which threatens the long-term stability of the system.
- (2)
- The reinjection rate exerts opposite effects on the flow field and the temperature field. When the reinjection rate increases from 0% to 100%, the water-level decline at the center of the depression funnel slows from 36.4 m to 19.3 m over a ten-year period. However, the minimum reservoir temperature decreases from 65.0 °C to 63.6 °C, and the extent of the low-temperature zone expands from 2.24 km2 to 11.61 km2.
- (3)
- Over a ten-year forecast period, moderate reinjection maintains reservoir pressure stability and delays water-level decline while preventing rapid thermal breakthrough, making it a relatively reasonable operational strategy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, A.; Rezaie, B. Geothermal Technology: Trends and Potential Role in a Sustainable Future. Appl. Energy 2019, 248, 18–34. [Google Scholar] [CrossRef]
- Zheng, T.; Axelsson, G.; Kang, F.; Zhao, J.; Zhang, P.; Bai, T.; Yang, X.; Zhou, Q.; Luo, Y. Sustainable Geothermal Yield through Effective Reinjection: Reservoir Engineering Case Study of the Dezhou Sandstone Geothermal Reservoir, North Shandong Plain, China. Geotherm. Energy 2025, 13, 36. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Huang, L.; Li, B.; Yan, J.; Zhang, P.; Liu, Z. Life Cycle Dynamic Formation Temperature Response and Thermal Energy Extraction of Mine Geothermal System Considering Groundwater Flow. Int. J. Min. Sci. Technol. 2025, 35, 1–17. [Google Scholar] [CrossRef]
- Wu, D.; Kong, L.; Kong, G.; Fang, J.; Wang, C.; Wang, Y. Thermo-Mechanical Behavior of an Energy Retaining Pile for Geothermal Extraction. Geomech. Energy Environ. 2024, 40, 100587. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Li, T.; Tang, C. Numerical Investigation of Heat Extraction Performance Affected by Stimulated Reservoir Volume and Permeability Evolution in the Enhanced Geothermal System. Appl. Therm. Eng. 2024, 250, 123515. [Google Scholar] [CrossRef]
- Pruess, K. The TOUGH Codes—A Family of Simulation Tools for Multiphase Flow and Transport Processes in Permeable Media. Vadose Zone J. 2004, 3, 738–746. [Google Scholar] [CrossRef]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K. TOUGHREACT—A Simulation Program for Non-Isothermal Multiphase Reactive Geochemical Transport in Variably Saturated Geologic Media: Applications to Geothermal Injectivity and CO2 Geological Sequestration. Comput. Geosci. 2006, 32, 145–165. [Google Scholar] [CrossRef]
- Liu, S.; Yan, Y.; Zhang, L.; Song, W.; Feng, Y.; Feng, G.; Chen, J. Study on Reasonable Well Spacing for Geothermal Development of Sandstone Geothermal Reservoir—A Case Study of Dezhou, Shandong Province, China. Energies 2025, 18, 4149. [Google Scholar] [CrossRef]
- Rutqvist, J. Status of the TOUGH-FLAC Simulator and Recent Applications Related to Coupled Fluid Flow and Crustal Deformations. Comput. Geosci. 2011, 37, 739–750. [Google Scholar] [CrossRef]
- Kolditz, O. Thermo-Hydro-Mechanical-Chemical Processes in Porous Media; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wang, B.; Zhao, Y.; Cai, Y.; Zhang, S.; Yang, B.; Liu, F. Feasibility Research on Surface Water Reinjection into the Sandstone Geothermal Reservoir of the Guantao Formation in Tianjin Based on Laboratory Experiments. Water 2024, 16, 2475. [Google Scholar] [CrossRef]
- Shi, H.; Wang, G.; Lu, C. Numerical Investigation on Delaying Thermal Breakthrough by Regulating Reinjection Fluid Path in Multi-Aquifer Geothermal System. Appl. Therm. Eng. 2022, 221, 119692. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Bian, K.; Zhang, H.; Wang, X.; Zhang, H.; Wang, W.; Qin, S. Influence of Low Temperature Tail Water Reinjection on Seepage and Heat Transfer of Carbonate Reservoirs. Energy Explor. Exploit. 2021, 39, 2062–2079. [Google Scholar] [CrossRef]
- Cao, Q.; Fang, C.; Li, Y.; Wang, H.; Fang, Q.; Shi, X. Development Status of Geothermal Reinjection at Home and Abroad and Its Enlightenment. Oil Drill. Prod. Technol. 2021, 43, 203–211. [Google Scholar] [CrossRef]
- Xia, Y.; Wang, B.; Zhang, F.; Jia, Z. Optimization and Transformation of Water Treatment Technology for Surface Water Reinjection into Geothermal Reservoir in Dongli Lake Area of Tianjin. Energy Rep. 2023, 9, 25–29. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, X.; Chen, R.; Shen, Y.; Shang, Z.; Hai, K. Numerical Simulation of Deep Thermal Groundwater Exploitation in the Beijing Plain Area. Water 2019, 11, 1494. [Google Scholar] [CrossRef]
- Ganguly, S.; Tan, L.; Date, A.; Kumar, M.S.M. Effect of Heat Loss in a Geothermal Reservoir. Energy Procedia 2017, 110, 77–82. [Google Scholar] [CrossRef]
- Sato, K.; Firoozabadi, A. Prediction of Thermal Front Movement in Geothermal Reservoirs Containing Distributed Natural Fractures. Geoenergy Sci. Eng. 2024, 236, 212763. [Google Scholar] [CrossRef]
- Zhao, W.; Liu, L.; Li, J.; Shi, Z.; Cheng, Z.; Jing, T.; Yin, Y.; Zhu, M. Reinjection Modeling in Sandstone Geothermal Reservoirs: A Case Study of Dezhou Geothermal Heating Demonstration Project. Nat. Gas Ind. B 2024, 11, 106–120. [Google Scholar] [CrossRef]
- Memon, A.R.; Makauskas, P.; Kaminskaitė-Baranauskienė, I.; Pal, M. Repurposing Depleted Hydrocarbon Reservoirs for Geothermal Energy: A Case Study of the Vilkyčiai Cambrian Sandstone in Lithuania. Energy Rep. 2025, 14, 243–253. [Google Scholar] [CrossRef]
- Axelsson, G. Sustainable Geothermal Utilization—Case Histories; Definitions; Research Issues and Modelling. Geothermics 2010, 39, 283–291. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Song, X.; Shi, Y.; Li, G.; Yang, R.; Wang, G.; Zheng, R.; Li, J.; Lyu, Z. Numerical Simulation of Heat Extraction Performance in Enhanced Geothermal System with Multilateral Wells. Appl. Energy 2018, 218, 325–337. [Google Scholar] [CrossRef]
- Liu, D.; Yang, X.; Han, L.; Jia, C.; Qi, S.; Wang, H.; Yang, S. Research on the Changes of Sandstone Thermal Storage RechargeCharacteristics Based on Time Series Parameters Analysis:A Case Studyof Linging City in Shandong Province. Geol. Explor. 2024, 60, 610–621. [Google Scholar]
- Wang, K.; Yang, D.; Song, X.; Liu, P.; Ma, X. Chemical Characteristics and Encrustment and Erosion of Geothermawater in the Guantao Formation in Linging. Hydrogeol. Eng. Geol. 2010, 37, 130–134. [Google Scholar]
- Yang, X.; Yao, Y.; Jia, C.; Yang, T. Spatiotemporal Prediction of Land Subsidence and Its Response Patterns to Different Aquifers in Coastal Areas. Ocean Coast. Manag. 2024, 253, 107148. [Google Scholar] [CrossRef]
- Dong, X.; Liu, H.; Wei, R.; Liu, L.; Jia, C.; Sun, H.; Chu, W. A Hybrid Physics-Constrained Interpretable Machine Learning Framework for Stability Assessment of Natural Gas Hydrate-Bearing Submarine Slopes. Eng. Anal. Bound. Elem. 2025, 179, 106371. [Google Scholar] [CrossRef]
- Lesmana, A.; Pratama, H.B.; Ashat, A.; Saptadji, N.M. Sustainability of Geothermal Development Strategy Using a Numerical Reservoir Modeling: A Case Study of Tompaso Geothermal Field. Geothermics 2021, 96, 102170. [Google Scholar] [CrossRef]
- Kaya, E.; Zarrouk, S.J.; O’Sullivan, M.J. Reinjection in Geothermal Fields: A Review of Worldwide Experience. Renew. Sustain. Energy Rev. 2011, 15, 47–68. [Google Scholar] [CrossRef]
- Zinsalo, J.M.; Lamarche, L.; Raymond, J. Design and Optimization of Multiple Wells Layout for Electricity Generation in a Multi-Fracture Enhanced Geothermal System. Sustain. Energy Technol. Assess. 2021, 47, 101365. [Google Scholar] [CrossRef]
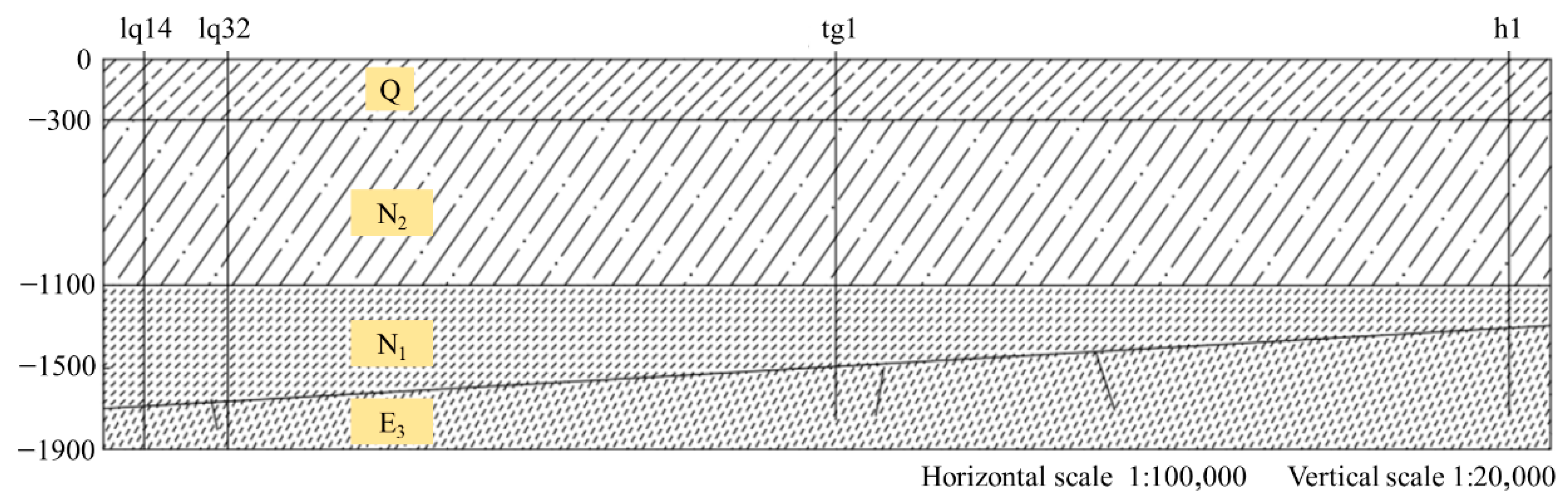
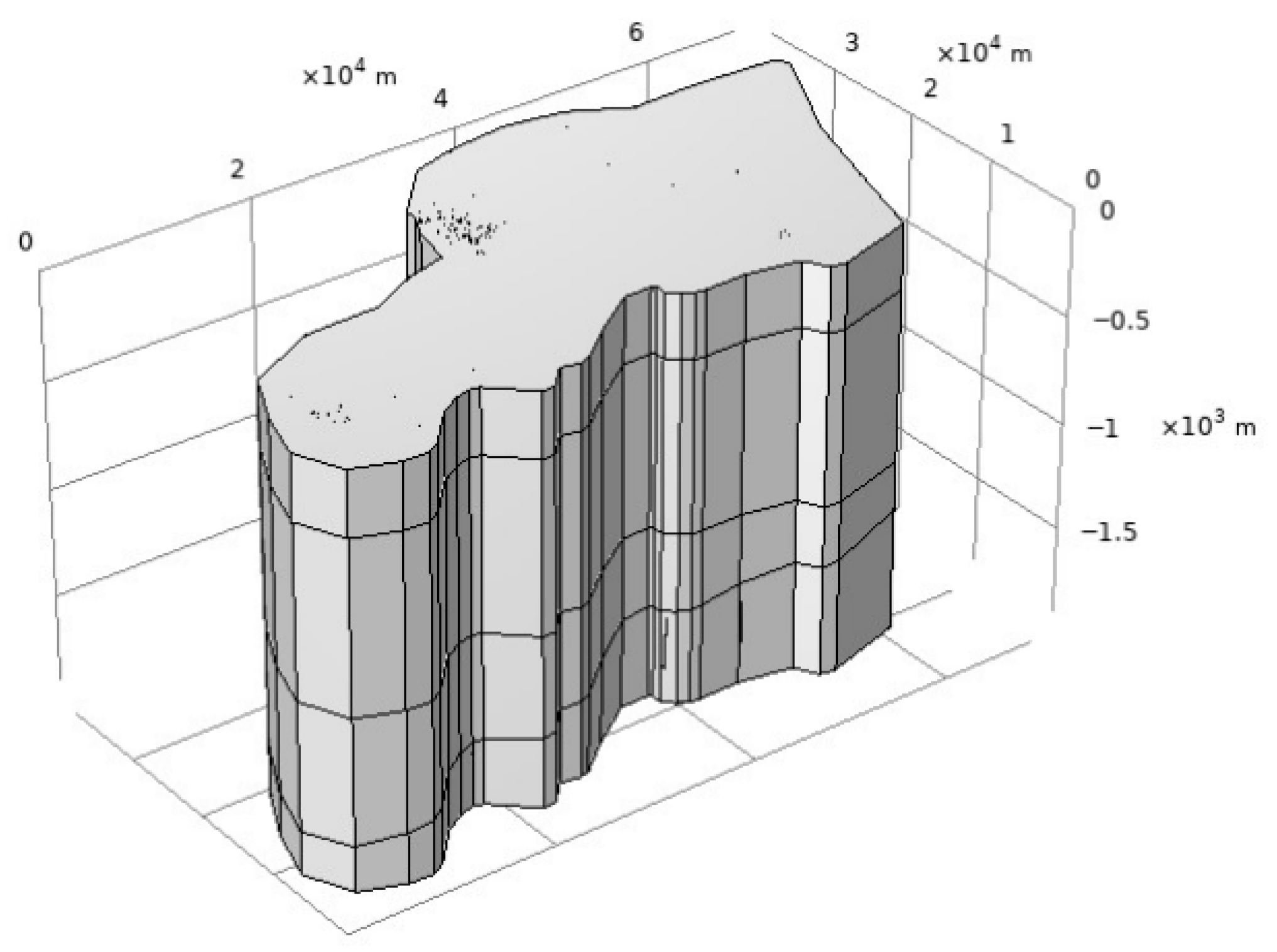


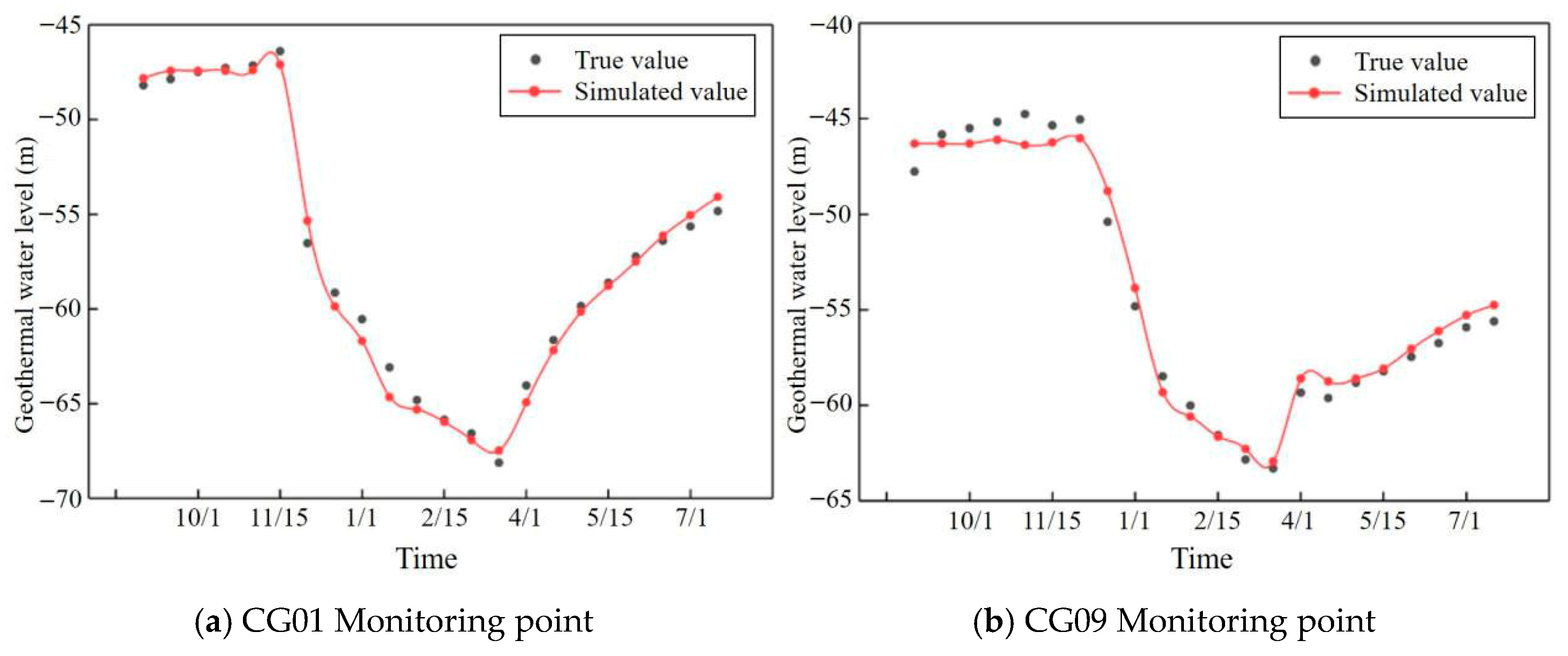
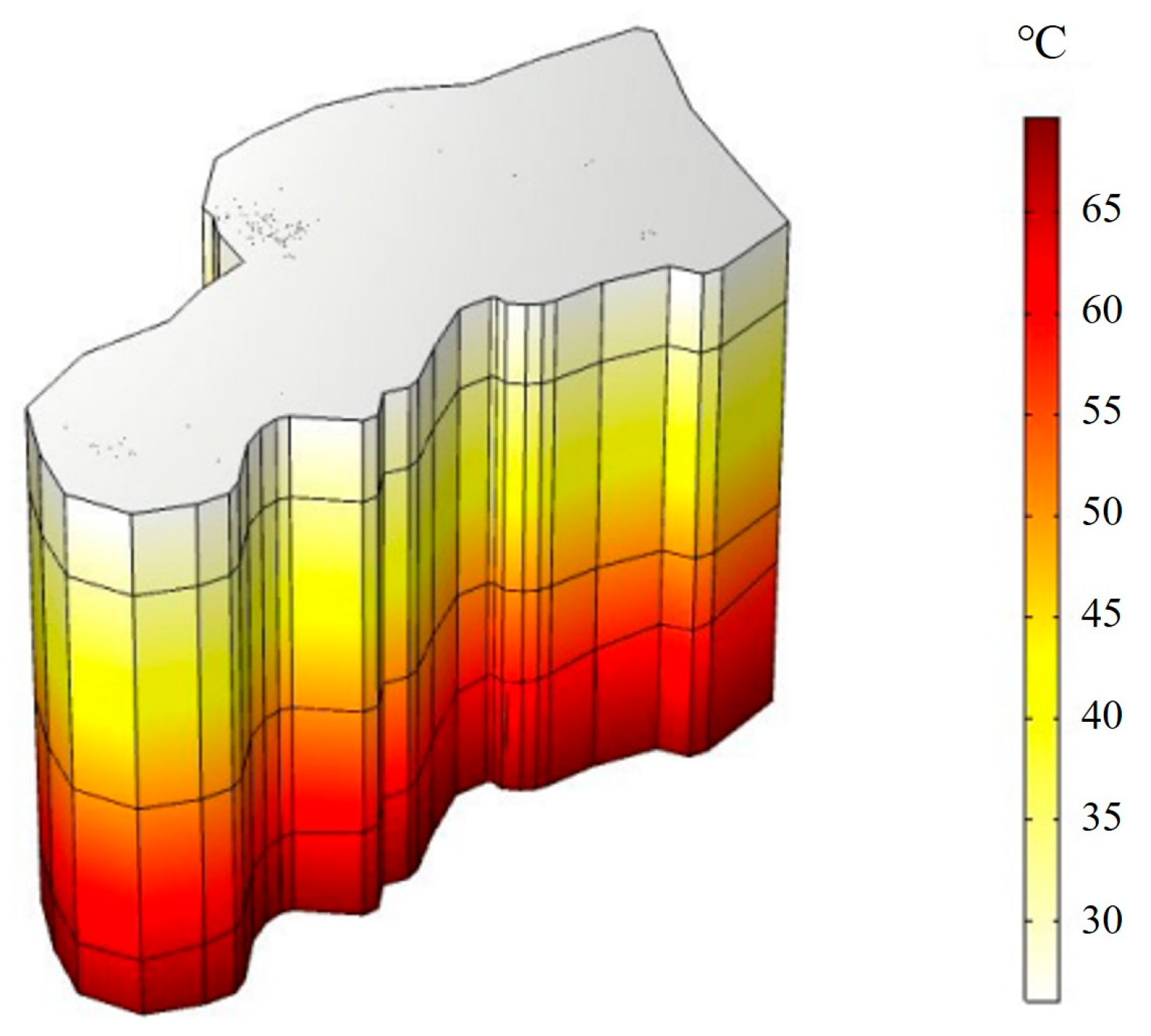






| Stratum | Elastic Modulus (MPa) | Density (Kg/m3) | Poisson | Porosity | Permeability (m2) | Thermal Conductivity (W/(M·k)) | Constant Pressure Heat Capacity (J/(Kg·K)) | Coefficient of Thermal Expansion (1/K) |
|---|---|---|---|---|---|---|---|---|
| Q | 80 | 1.97–2.02 | 0.22–0.25 | 0.28–0.37 | 4.79 × 10−15–1.61 × 10−14 | 1.03–1.35 | 820–870 | 1.0 × 10−5 |
| N2 | 180 | 1.99–2.20 | 0.31–0.40 | 0.114–0.236 | 6.3 × 10−14–7.2 × 10−14 | 1.48–1.77 | 820–900 | 1.3 × 10−5 |
| N1 | 350 | 1.88–2.18 | 0.30–0.35 | 0.148–0.350 | 2.3 × 10−14–4.53 × 10−13 | 1.74–1.91 | 850–948 | 8.5 × 10−6 |
| E3 | 370 | 2.03–2.22 | 0.30–0.33 | 0.132–0.310 | 1.4 × 10−14–3.80 × 10−13 | 1.80–1.91 | 850–950 | 7.1 × 10−6 |
| Serial Number | Mining Well Number | Mining Location (m) | Production Volume (kg/s) | Corresponding to the Number of the Reinjection Well | Reinjection Volume (kg/s) |
|---|---|---|---|---|---|
| 1 | K4 | −1475~−1714 | 21.22 | h18 | 15.55 |
| 2 | K5 | −1543~−1894 | 22.22 | h5 | 31.1 |
| 3 | K6 | −1477~−1789 | 22.22 | ||
| 4 | K12 | −1359~−1802 | 30.56 | h6 | 21.39 |
| 5 | K15 | −1480~−1700 | 30.56 | h1 | 21.39 |
| 6 | K17 | −1476~−1786 | 20.30 | h2 | 14.21 |
| 7 | K20 | −1450~−1710 | 33.33 | h7 | 23.33 |
| 8 | K21 | −1450~−1710 | 32.40 | h8 | 22.68 |
| 9 | K23 | −1490~−1708 | 21.67 | h3, h9 | 7.85 |
| 10 | K24 | −1465~−1880 | 23.15 | h10, h11 | 8.10 |
| 11 | K28 | −1517~−1709 | 30.56 | h12 | 21.39 |
| 12 | K37 | −1469~−1800 | 23.15 | h13 | 16.20 |
| 13 | K38 | −1407~−1720 | 40.00 | h14, h22 | 14.00 |
| 14 | K39 | −1407~−1700 | 22.22 | h15 | 15.56 |
| 15 | K41 | −1409~−1710 | 21.78 | h16 | 19.44 |
| 16 | K45 | −1478~−1725 | 30.56 | h17 | 21.39 |
| 17 | K51 | −1481~−1710 | 30.56 | h4 | 21.39 |
| 18 | K52 | −1481~−1710 | 19.44 | h19 | 13.61 |
| 19 | K53 | −1481~−1751 | 26.39 | h20 | 18.47 |
| 20 | K56 | −1481~−1710 | 16.67 | h21 | 11.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Dong, X.; Liu, H.; He, Y.; Li, S.; Jia, C.; Qin, P.; Li, B.; Ding, P. Multi-Field Coupled Numerical Simulation of Geothermal Extraction and Reinjection in the Sandstone Reservoir. Sustainability 2025, 17, 9646. https://doi.org/10.3390/su17219646
Liu Z, Dong X, Liu H, He Y, Li S, Jia C, Qin P, Li B, Ding P. Multi-Field Coupled Numerical Simulation of Geothermal Extraction and Reinjection in the Sandstone Reservoir. Sustainability. 2025; 17(21):9646. https://doi.org/10.3390/su17219646
Chicago/Turabian StyleLiu, Zhizheng, Xiao Dong, Huafeng Liu, Yunhua He, Shuang Li, Chao Jia, Peng Qin, Bo Li, and Pengpeng Ding. 2025. "Multi-Field Coupled Numerical Simulation of Geothermal Extraction and Reinjection in the Sandstone Reservoir" Sustainability 17, no. 21: 9646. https://doi.org/10.3390/su17219646
APA StyleLiu, Z., Dong, X., Liu, H., He, Y., Li, S., Jia, C., Qin, P., Li, B., & Ding, P. (2025). Multi-Field Coupled Numerical Simulation of Geothermal Extraction and Reinjection in the Sandstone Reservoir. Sustainability, 17(21), 9646. https://doi.org/10.3390/su17219646







