Multi-Objective Optimization Method for Flexible Distribution Networks with F-SOP Based on Fuzzy Chance Constraints
Abstract
1. Introduction
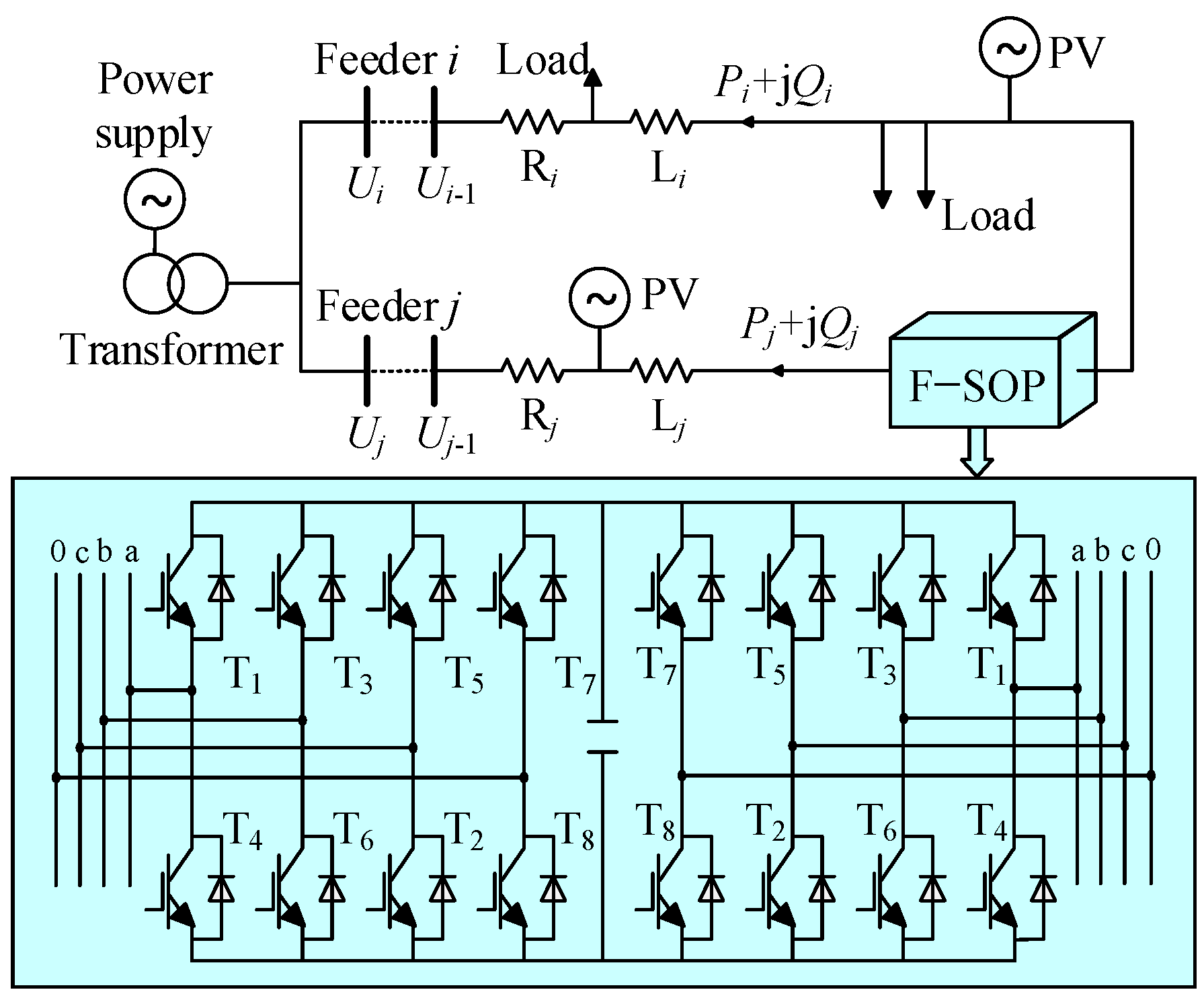
2. F-SOP Working Principle
2.1. F-SOP Structure
2.2. F-SOP Loss Model
2.3. F-SOP Mathematical Model
2.3.1. F-SOP Operational Constraint
2.3.2. F-SOP Capacity Constraint
3. Multi-Objective Optimization Model for Flexible Distribution Networks Incorporating F-SOP Based on Fuzzy Chance Constraints
3.1. Multi-Objective Model Objective Function
3.1.1. Distribution Network Losses
3.1.2. Overall Voltage Deviation
3.1.3. Three-Phase Imbalance
3.2. Multi-Objective Model Constraints
3.2.1. System Trend Constraint
3.2.2. Safety Constraint
3.2.3. PV Active Power Output Constraint
3.2.4. CB Constraint
3.2.5. SVG Constraint
3.2.6. F-SOP Constrain
3.2.7. Power Balance Constraint
4. Multi-Objective Model Solving
4.1. SOCP Linearization
4.2. Fuzzy Chance Constraint Processing
5. Example Simulation and Analysis
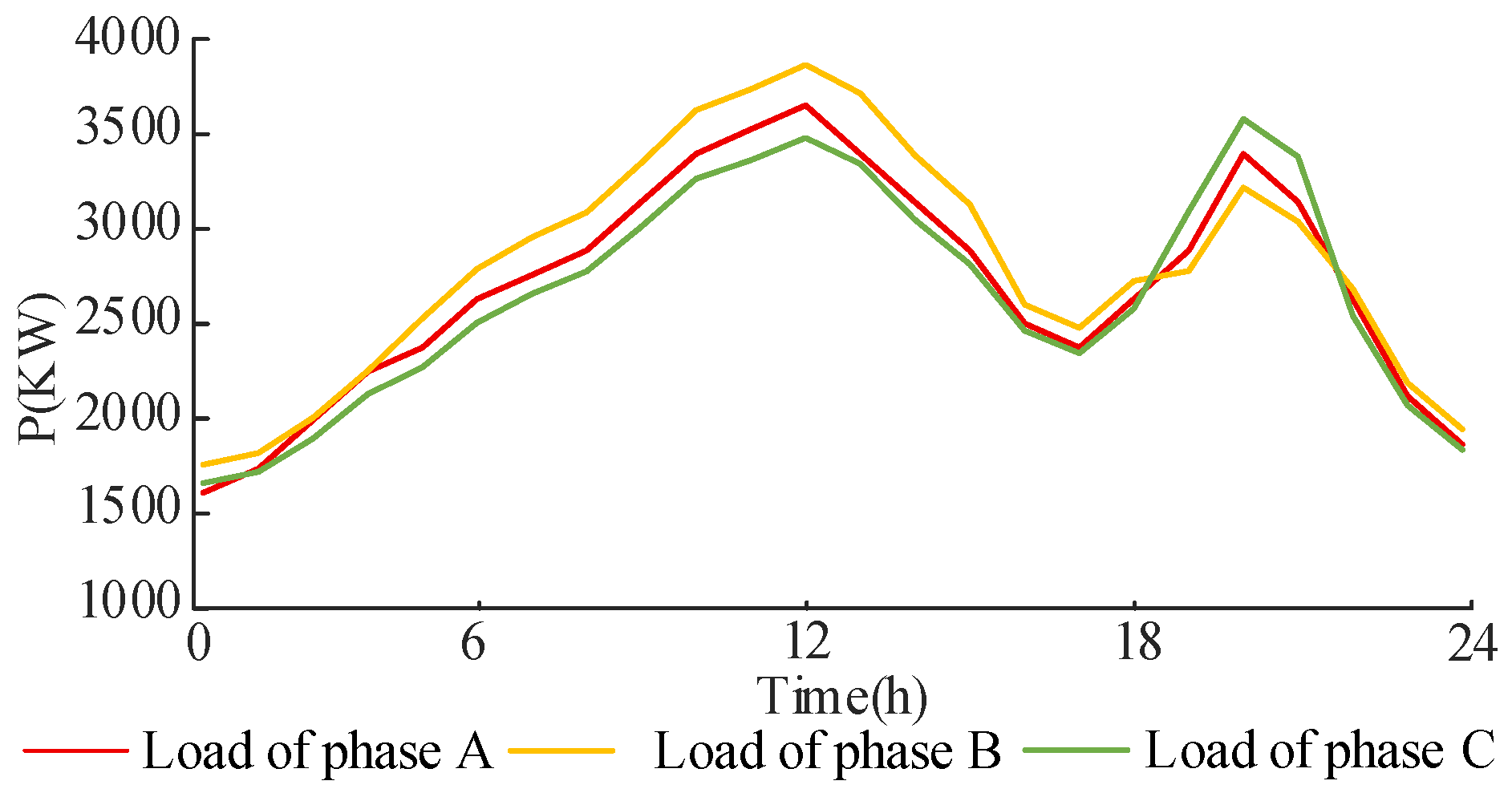
5.1. Example Overview and Parameterization
5.2. Simulation Results Analysis
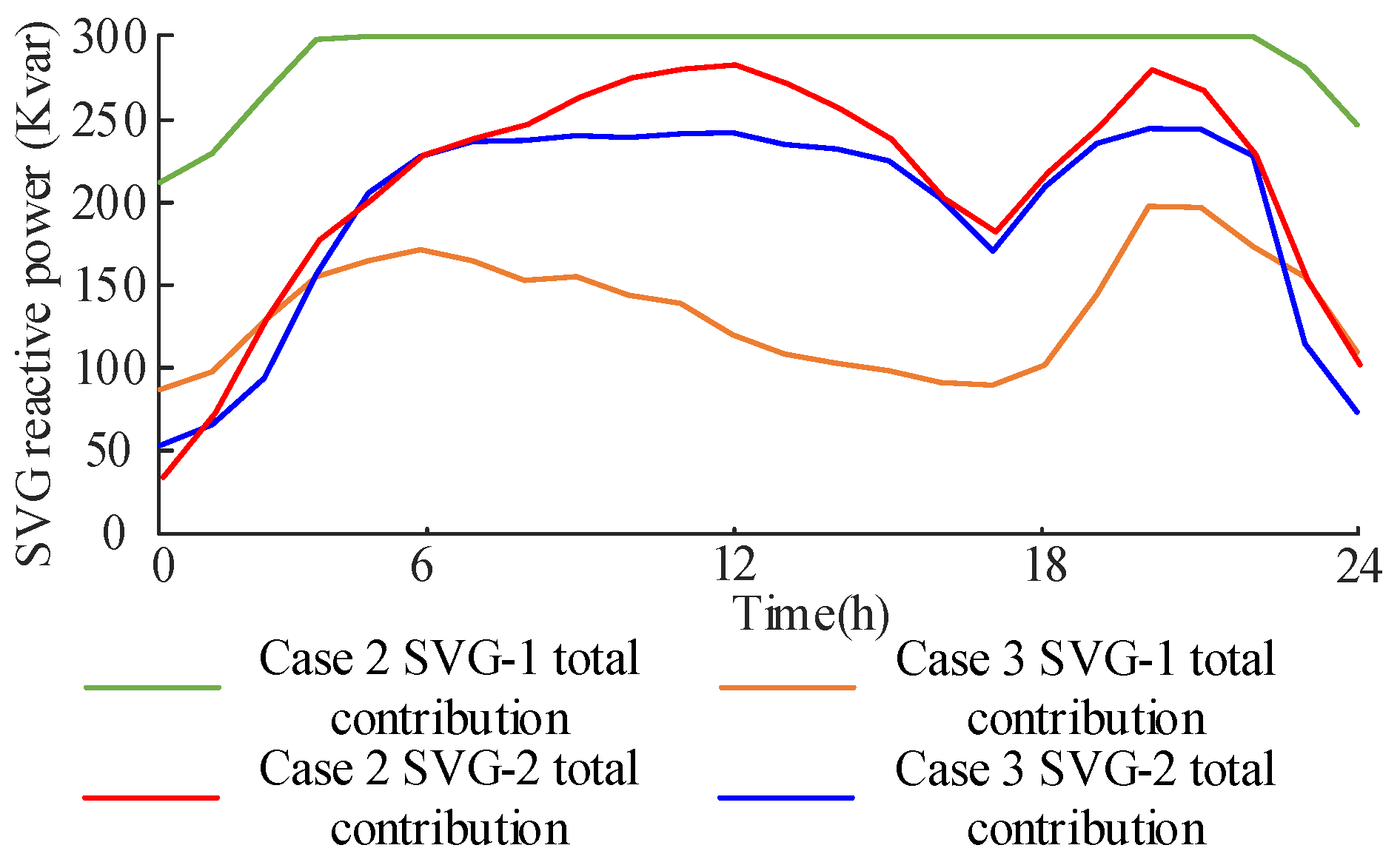
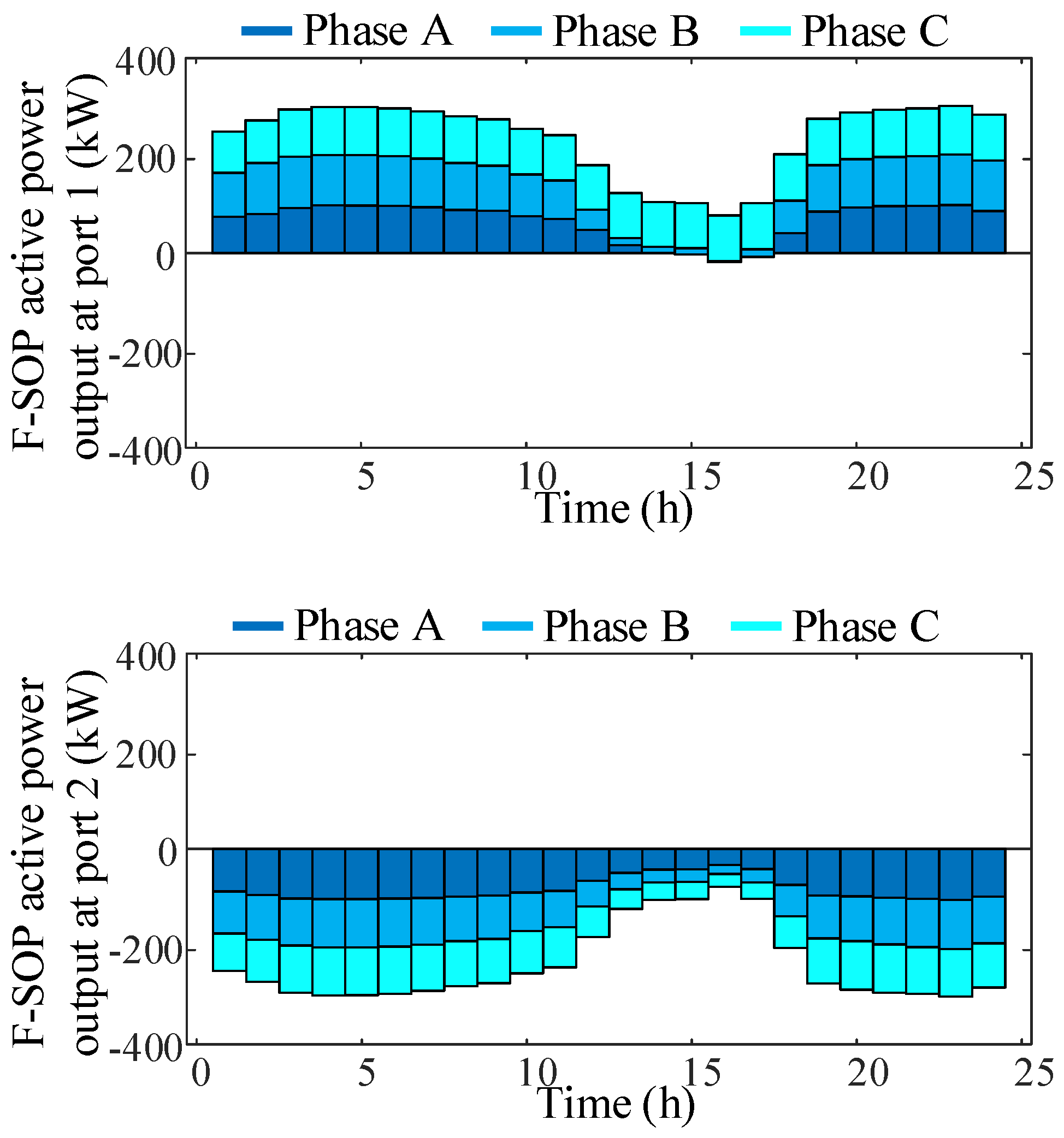
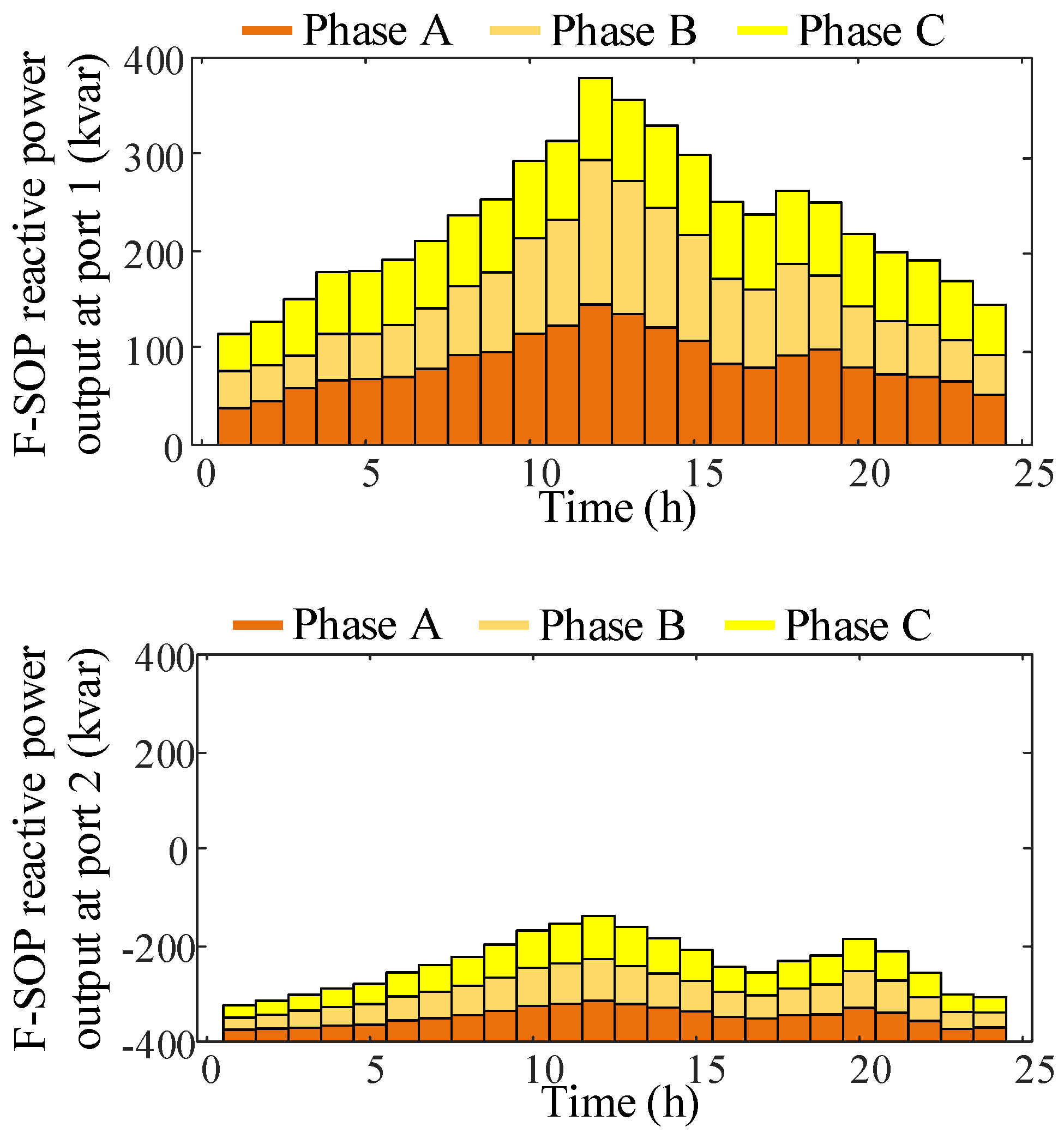
5.2.1. Analysis of Critical Equipment
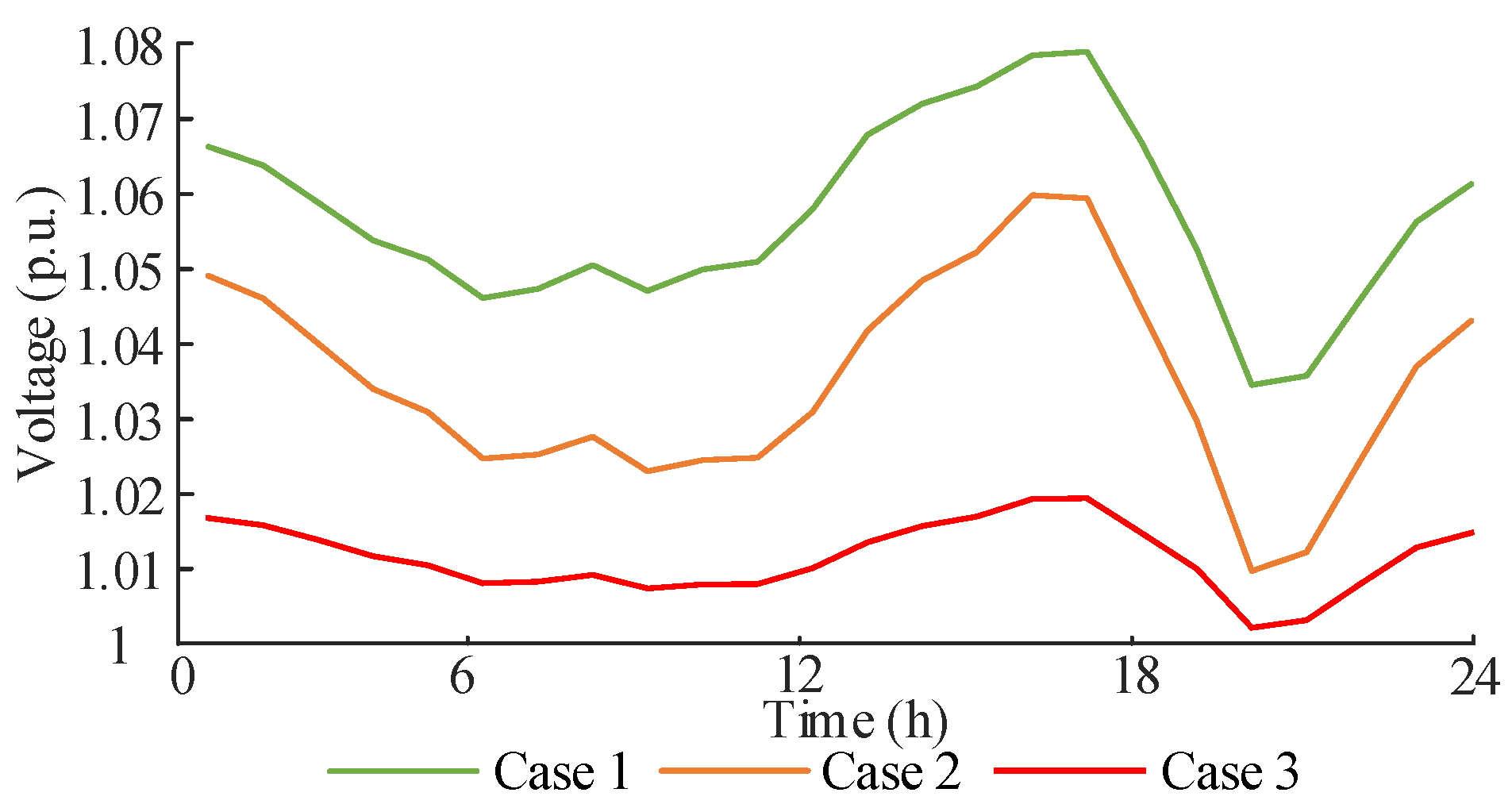
5.2.2. Analysis of Key Indicators
5.2.3. The Influence of Various Objective Weights
6. Conclusion
- (1)
- Regarding system network losses, compared to conventional three-phase imbalance mitigation methods, the approach proposed in this paper can significantly reduce both distribution network losses and reactive power output from reactive power compensation devices. Case study analysis indicates that the network losses in the proposed model decreased by 30.17% relative to traditional methods, while the utilization rate of reactive power compensation devices dropped from 84.85% to 68.19%.
- (2)
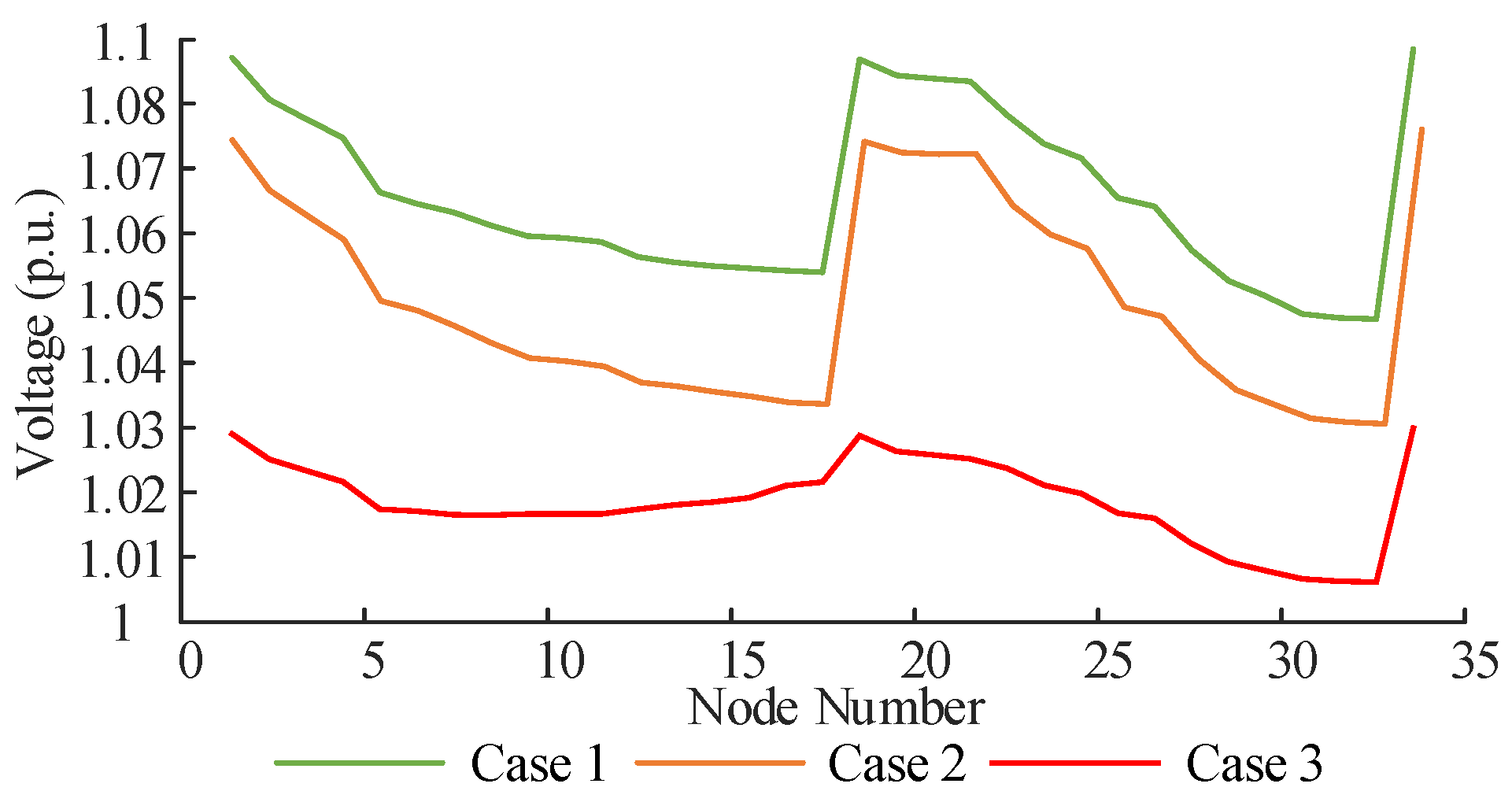
- Regarding voltage deviation, the maximum three-phase voltage in the distribution network was reduced to 1.029 p.u. in the method described herein. The minimum value of the three-phase voltage in the distribution network is 0.998 p.u. This method eliminates voltage over-limit conditions in the distribution network. Simultaneously, the overall three-phase voltage deviation in the distribution network under this approach is 192.95 p.u., meeting the ±7% range specified by national standards. Compared to unregulated and traditional regulation methods, this represents reductions of 46.32% and 21.39%, respectively.
- (3)
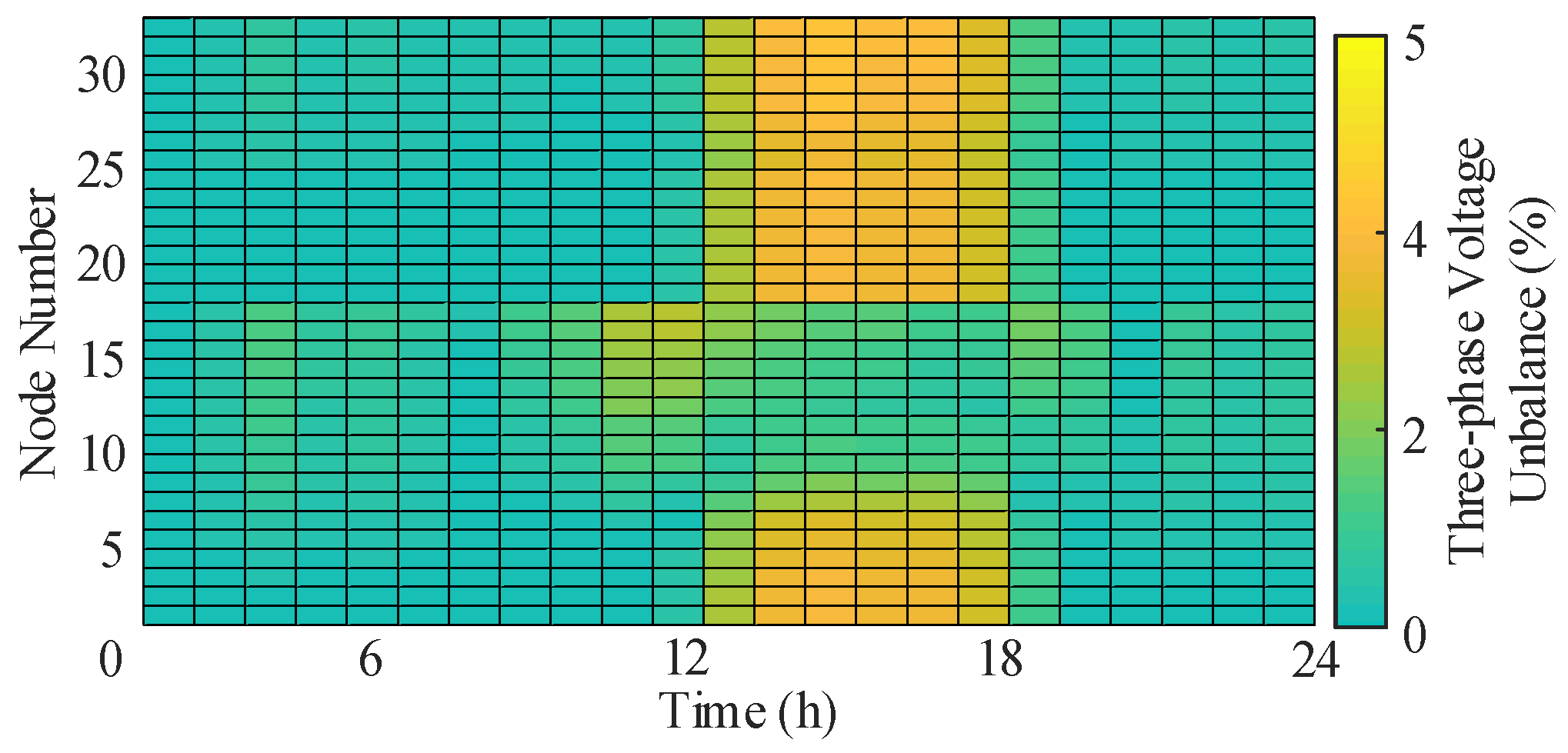
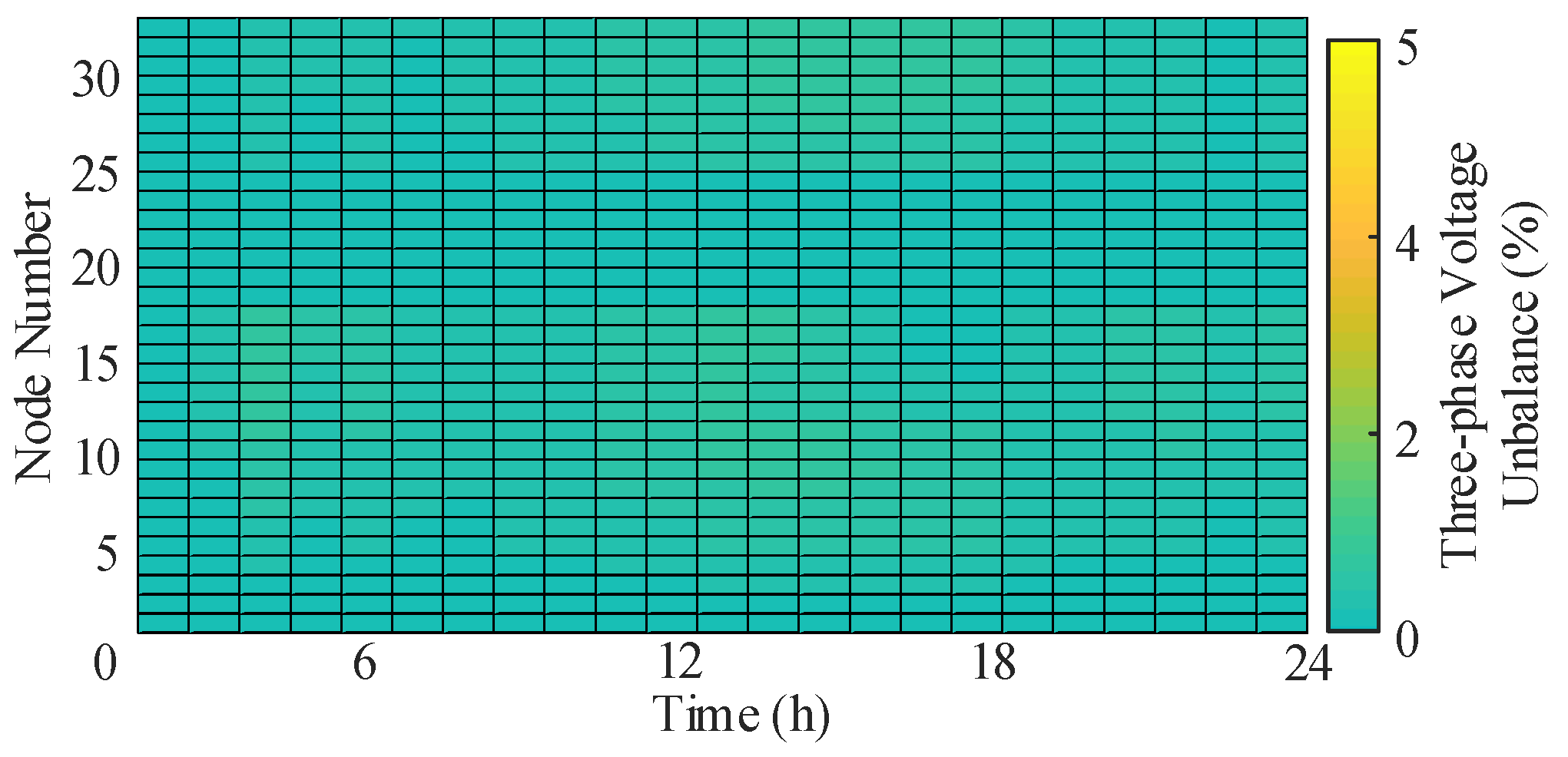
- Regarding three-phase imbalance, this method utilizes F-SOP’s intra-phase and inter-phase power transfer characteristics to achieve power exchange between relative phases at a single node. This effectively mitigates three-phase imbalance across node voltages. The three-phase imbalance achieved by this method is 7.43, representing reductions of 57.86% and 10.82% compared to Cases 1 and 2, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| F-SOP | Four-leg soft open point |
| PV | photovoltaic |
| SVG | Static VAR generator |
| CB | Capacitor banks |
| VSC | Voltage source converters |
| SOP | Soft open point |
| SOCP | Second-order conic programming |
| Active power loss generated in phase e by the VSC of F-SOP access node i at time t | |
| F-SOP power loss coefficient | |
| Active power transmitted by the VSC of F-SOP access node i in phase e at time t | |
| Reactive power transmitted by the VSC of F-SOP access node i in phase e at time t | |
| Capacity of the VSC for F-SOP access node i | |
| Weighting factors for the network loss target | |
| Weighting factors for the overall voltage deviation target | |
| Weighting factors for the three-phase imbalance target | |
| Actual measured distribution network loss target | |
| Overall voltage deviation target | |
| Three-phase imbalance target | |
| Weight for the network loss target | |
| Weight for the overall voltage deviation target | |
| Weight for the voltage imbalance target | |
| Initial values of the network loss target | |
| Initial values of the overall voltage deviation target | |
| Initial values of the three-phase imbalance target | |
| The number of nodes in the distribution network | |
| Branch current between nodes i and j in phase e | |
| Resistance between nodes i and j in phase e | |
| The duration of a single time interval | |
| The node voltage of node j in phase e | |
| Reference voltage of the distribution network | |
| Three-phase imbalance degree of the voltage at node j | |
| Average value of the amplitude of the three-phase voltage at node j | |
| Active power injected by node j into the e phase | |
| Reactive power injected by node j into the e phase | |
| Active power flowing out from node j to its downstream node k in the direction of e | |
| Reactive power flowing out from node j to its downstream node k in the direction of e | |
| Active power flowing out from node i to its downstream node j in the direction of e | |
| Reactive power flowing out from node i to its downstream node j in the direction of e | |
| Reactance of link e between nodes i and j | |
| Conductance of link e between nodes i and j | |
| Admittance of link e between nodes i and j | |
| The upper limits of node voltage for node j | |
| The lower limits of node voltage for node j | |
| The upper limits of the branch current between nodes i and j | |
| The lower limits of the branch current between nodes i and j | |
| Active power exchanged between the distribution network and the higher-level grid on phase e | |
| Reactive power exchanged between the distribution network and the higher-level grid on phase e | |
| The maximum values of active power exchanged between the distribution network and the higher-level grid on phase e | |
| The maximum values of reactive power exchanged between the distribution network and the higher-level grid on phase e | |
| The minimum values of active power exchanged between the distribution network and the higher-level grid on phase e | |
| The minimum values of reactive power exchanged between the distribution network and the higher-level grid on phase e | |
| Actual output of the photovoltaic power station assembled at node j at time t in phase e | |
| Predicted output of the photovoltaic power station assembled at node j at time t in phase e | |
| Error in photovoltaic output | |
| Reactive power compensation delivered by CB connected to node j at time t in phase e | |
| The number of operational units for CB | |
| Compensation power for each group of CBs | |
| The upper limit of the number of groups connecting node j to CB | |
| The upper limit for the number of CB operations | |
| Reactive power compensation delivered by SVG connected to node j at time t in phase e | |
| The lower limits of the SVG compensation power | |
| The upper limits of the SVG compensation power | |
| Active loads of the distribution network | |
| Reactive loads of the distribution network | |
| Active power is injected at each node of the distribution network | |
| Reactive power is injected at each node of the distribution network | |
| The square of the branch current between node i and node j in phase e | |
| The square of the node voltage at node i in phase e | |
| PV membership degree parameter | |
| load membership degree parameter |
References
- Elsayed, A.M.; El-Rifaie, A.M.; Areed, M.F.; Shaheen, A.M.; Atallah, M.O. Allocation and control of multi-devices voltage regulation in distribution systems via rough set theory and grasshopper algorithm: A practical study. Results Eng. 2025, 25, 103860. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, W.; He, G.; Wang, J. A new shared module soft open point for power distribution network. IEEE Trans. Power Electron. 2022, 38, 3363–3374. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Xiao, F.; Chen, Z.; Luo, J.; Hou, Y. A hybrid advanced traction power supply equipment based on triple-port high-frequency isolated converter with its control strategy. IEEE Trans. Power Electron. 2025, 40, 10038–10048. [Google Scholar] [CrossRef]
- Liu, D.; Wang, W.; Wang, L.; Jia, H.; Shi, M. Dynamic pricing strategy of electric vehicle aggregators based on DDPG reinforcement learning algorithm. IEEE Access 2021, 9, 21556–21566. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Ellien, A.R.; El-Rifaie, A.M.; El-Ela, A.A.; Ali, E.S. Performance assessment of modern distribution networks conjoined with electric vehicles in normal and faulty conditions. Sci. Afr. 2025, 28, e02630. [Google Scholar] [CrossRef]
- Nasef, A.F.; Alqahtani, M.H.; Shaheen, A.M. Technical and optimization insights into PV penetration in power distribution systems-based wild horse algorithm: Real cases on Egyptian networks. Results Eng. 2025, 25, 104603. [Google Scholar] [CrossRef]
- Aljumah, A.S.; Alqahtani, M.H.; Ginidi, A.R.; Shaheen, A.M. Improved Artificial Hummingbird Algorithm for Optimal Allocation of SVCs in Distribution Networks to Maximize Energy Efficiency. J. Mod. Power Syst. Clean Energy, 2025; early access. [Google Scholar]
- Zhang, D.; You, X.; Liu, S.; Pan, H. Dynamic multi-role adaptive collaborative ant colony optimization for robot path planning. IEEE Access 2020, 8, 129958–129974. [Google Scholar] [CrossRef]
- Liu, S.; Lin, Z.; Li, J.; Wen, F.; Ding, Y.; Wang, Q.; Lu, F.; Yang, L. Bi-level optimal placement model of phase switch devices for mitigating three-phase unbalance in low-voltage areas. IEEE Trans. Power Syst. 2022, 37, 3149–3152. [Google Scholar] [CrossRef]
- Razmi, D.; Lu, T.; Papari, B.; Akbari, E.; Fathi, G.; Ghadamyari, M. An overview on power quality issues and control strategies for distribution networks with the presence of distributed generation resources. IEEE Access 2023, 11, 10308–10325. [Google Scholar] [CrossRef]
- Zhang, J.; Chang, X.; Xue, Y.; Bai, X.; Li, Z.; Wang, P.; Sun, H. Optimal planning for electricity-gas-hydrogen integrated energy systems considering intertemporal long-term hydrogen storage and multiple uncertainties. IEEE Trans. Power Syst. 2025, 40, 4660–4674. [Google Scholar] [CrossRef]
- Luo, R.; He, Y.; Liu, J. Research on the unbalanced compensation of delta-connected cascaded H-bridge multilevel SVG. IEEE Trans. Ind. Electron. 2018, 65, 8667–8676. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H. Analytical modeling and design of capacitor bank considering thermal coupling effect. IEEE Trans. Power Electron. 2020, 36, 2629–2640. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Li, J.; Xiao, F.; Wan, D. A two-stage optimal strategy for flexible interconnection distribution network considering the loss characteristic of key equipment. Int. J. Electr. Power Energy Syst. 2023, 152, 109232. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Che, L.; Yang, W.; Xiao, F.; Hou, Y. A two-layer control strategy for soft open points considering the economical operation area of transformers in active distribution networks. IEEE Trans. Sustain. Energy 2022, 13, 2184–2195. [Google Scholar] [CrossRef]
- Hong, L.; Qizhe, L.; Qiang, Z.; Zhengyang, X.; Shaohan, L. Optimal dispatch of unbalanced distribution networks with phase-changing soft open points based on safe reinforcement learning. Sustain. Energy Grids Netw. 2024, 40, 101521. [Google Scholar] [CrossRef]
- Lou, C.; Yang, J.; Li, T.; Vega-Fuentes, E. New phase—changing soft open point and impacts on optimising unbalanced power distribution networks. IET Gener. Transm. Distrib. 2020, 14, 5685–5696. [Google Scholar] [CrossRef]
- Lou, C.; Yang, J.; Vega-Fuentes, E.; Meena, N.K.; Min, L. Multi-terminal phase-changing soft open point SDP modeling for imbalance mitigation in active distribution networks. Int. J. Electr. Power Energy Syst. 2022, 142, 108228. [Google Scholar] [CrossRef]
- Cui, X.; Ruan, G.; Vallée, F.; Toubeau, J.F.; Wang, Y. A two-level coordination strategy for distribution network balancing. IEEE Trans. Smart Grid 2023, 15, 529–544. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Q.; Tu, C.; Che, L.; Xu, Z.; Xiao, F.; Li, T.; Chen, L. A comprehensive control strategy for F-SOP considering three-phase imbalance and economic operation in ISLDN. IEEE Trans. Sustain. Energy 2024, 15, 149–159. [Google Scholar] [CrossRef]
- Chowdhury, M.M.U.T.; Biswas, B.D.; Kamalasadan, S. Second-order cone programming (SOCP) model for three phase optimal power flow (OPF) in active distribution networks. IEEE Trans. Smart Grid. 2023, 14, 3732–3743. [Google Scholar] [CrossRef]
- Han, T.; Chen, Y.; Ma, J.; Zhao, Y.; Chi, Y.Y. Surrogate modeling-based multi-objective dynamic VAR planning considering short-term voltage stability and transient stability. IEEE Trans. Power Syst. 2017, 33, 622–633. [Google Scholar] [CrossRef]
- Han, T.; Chen, Y.; Ma, J. Multi—objective robust dynamic VAR planning in power transmission girds for improving short—term voltage stability under uncertainties. IET Gener. Transm. Distrib. 2018, 12, 1929–1940. [Google Scholar] [CrossRef]


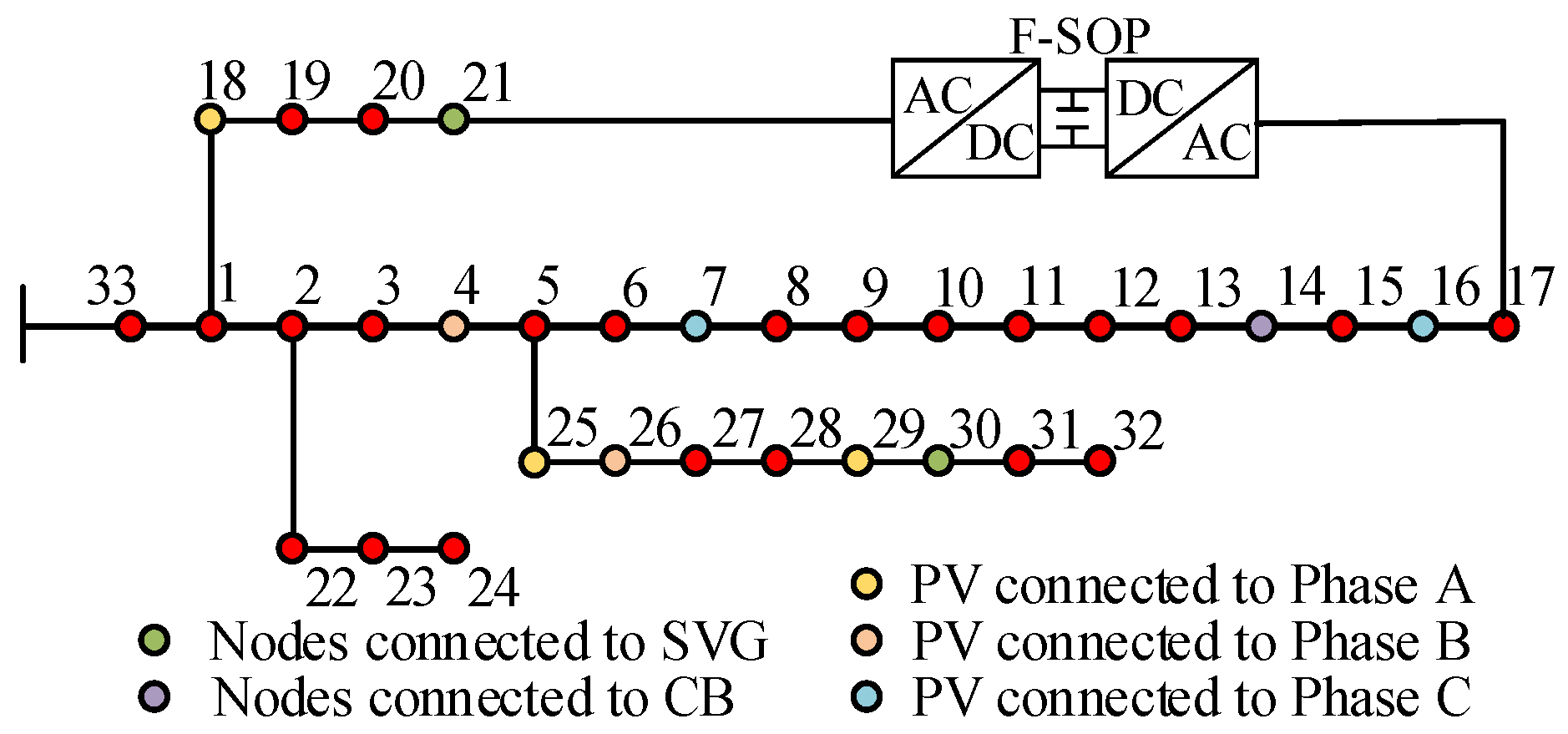
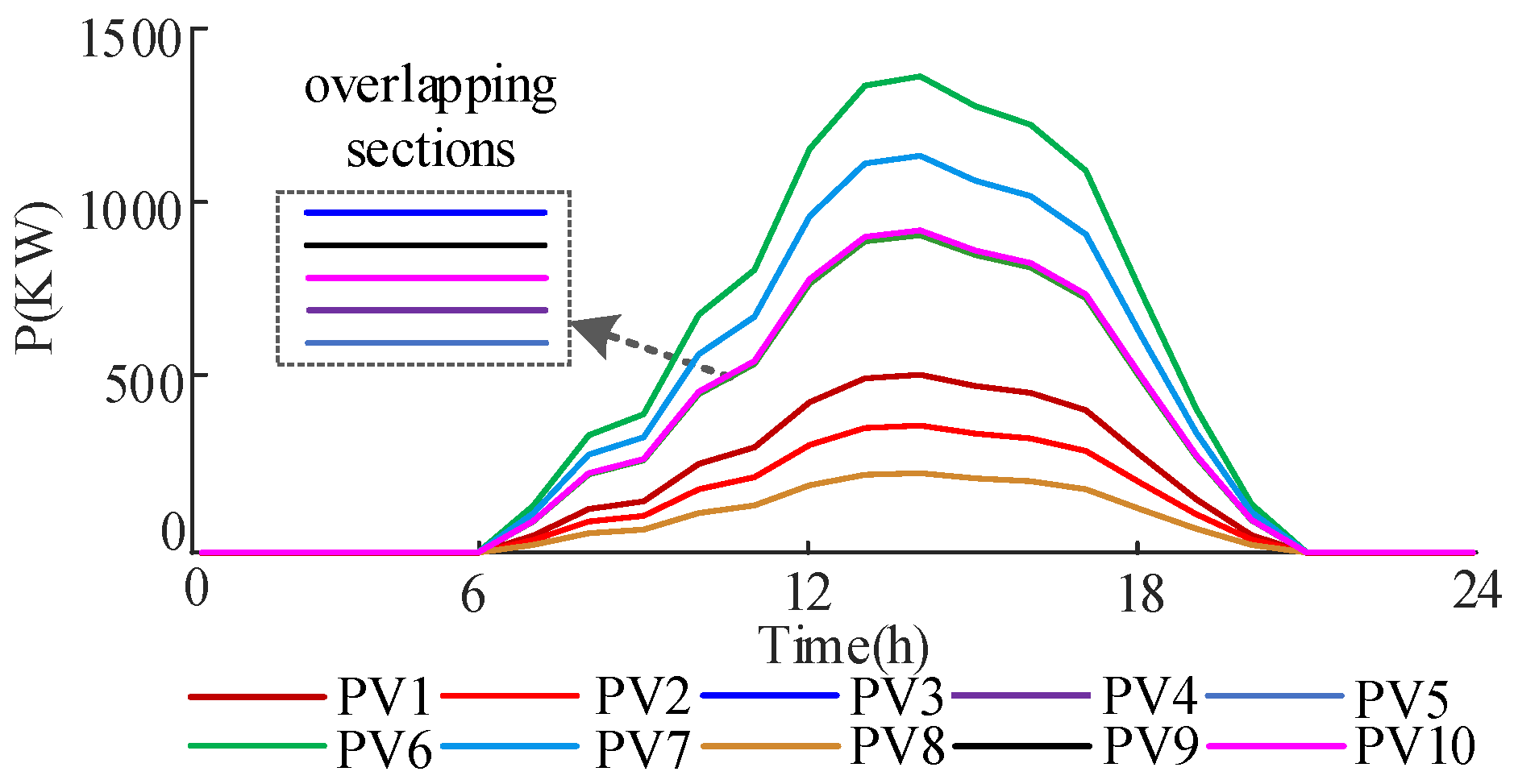

| PV Number | Connected Nodes | Phase | Grid-Connected Inverter Capacity/kVA |
|---|---|---|---|
| 1 | 2 | A | 500 |
| 2 | 4 | A | 400 |
| 3 | 7 | B | 800 |
| 4 | 9 | A | 800 |
| 5 | 13 | B | 800 |
| 6 | 16 | B | 1300 |
| 7 | 18 | C | 1100 |
| 8 | 25 | C | 300 |
| 9 | 26 | A | 800 |
| 10 | 29 | C | 850 |
| Case | Network Losses/kW | Overall Voltage Deviation/p.u. | Three-Phase Imbalance |
|---|---|---|---|
| 1 | 6013.57 | 359.43 | 17.63 |
| 2 | 5237.43 | 245.45 | 8.33 |
| 3 | 4199.32 | 192.95 | 7.43 |
| Case | Network Losses/kW | Overall Voltage Deviation/p.u. | Three-Phase Imbalance |
|---|---|---|---|
| 1 | 6013.57 | 359.43 | 17.63 |
| 2 | 5237.43 | 245.45 | 8.33 |
| 3 | 4199.32 | 192.95 | 7.43 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, Z.; Tan, R.; Yang, C.; Peng, X.; Zhao, K. Multi-Objective Optimization Method for Flexible Distribution Networks with F-SOP Based on Fuzzy Chance Constraints. Sustainability 2025, 17, 9510. https://doi.org/10.3390/su17219510
Lan Z, Tan R, Yang C, Peng X, Zhao K. Multi-Objective Optimization Method for Flexible Distribution Networks with F-SOP Based on Fuzzy Chance Constraints. Sustainability. 2025; 17(21):9510. https://doi.org/10.3390/su17219510
Chicago/Turabian StyleLan, Zheng, Renyu Tan, Chunzhi Yang, Xi Peng, and Ke Zhao. 2025. "Multi-Objective Optimization Method for Flexible Distribution Networks with F-SOP Based on Fuzzy Chance Constraints" Sustainability 17, no. 21: 9510. https://doi.org/10.3390/su17219510
APA StyleLan, Z., Tan, R., Yang, C., Peng, X., & Zhao, K. (2025). Multi-Objective Optimization Method for Flexible Distribution Networks with F-SOP Based on Fuzzy Chance Constraints. Sustainability, 17(21), 9510. https://doi.org/10.3390/su17219510







