Hydrogen Strategies Under Uncertainty: Risk-Averse Choices for Green Hydrogen Pathways
Abstract
1. Introduction
- The development of a complete optimization-based methodological framework for the design of an HES. The coordinated system differs from traditional energy systems in its holistic, flexible, and interconnected approach.
- Most of the literature has focused on uncertainties in renewable energy production or load variability, overlooking the effects of the uncertainty on system costs. In contrast, we consider economic model parameters uncertain in the design stage allowing for a more realistic assessment of risk, particularly when gas/energy prices can fluctuate significantly.
- The incorporation of a non-scenario-based risk measure within a comprehensive multi-energy system design model. Unlike traditional scenario-based approaches, this formulation does not rely on a finite set of sampled scenarios.
- The application of the framework to a case study to illustrate the insights that can be generated and to highlight the importance of uncertainty considerations.
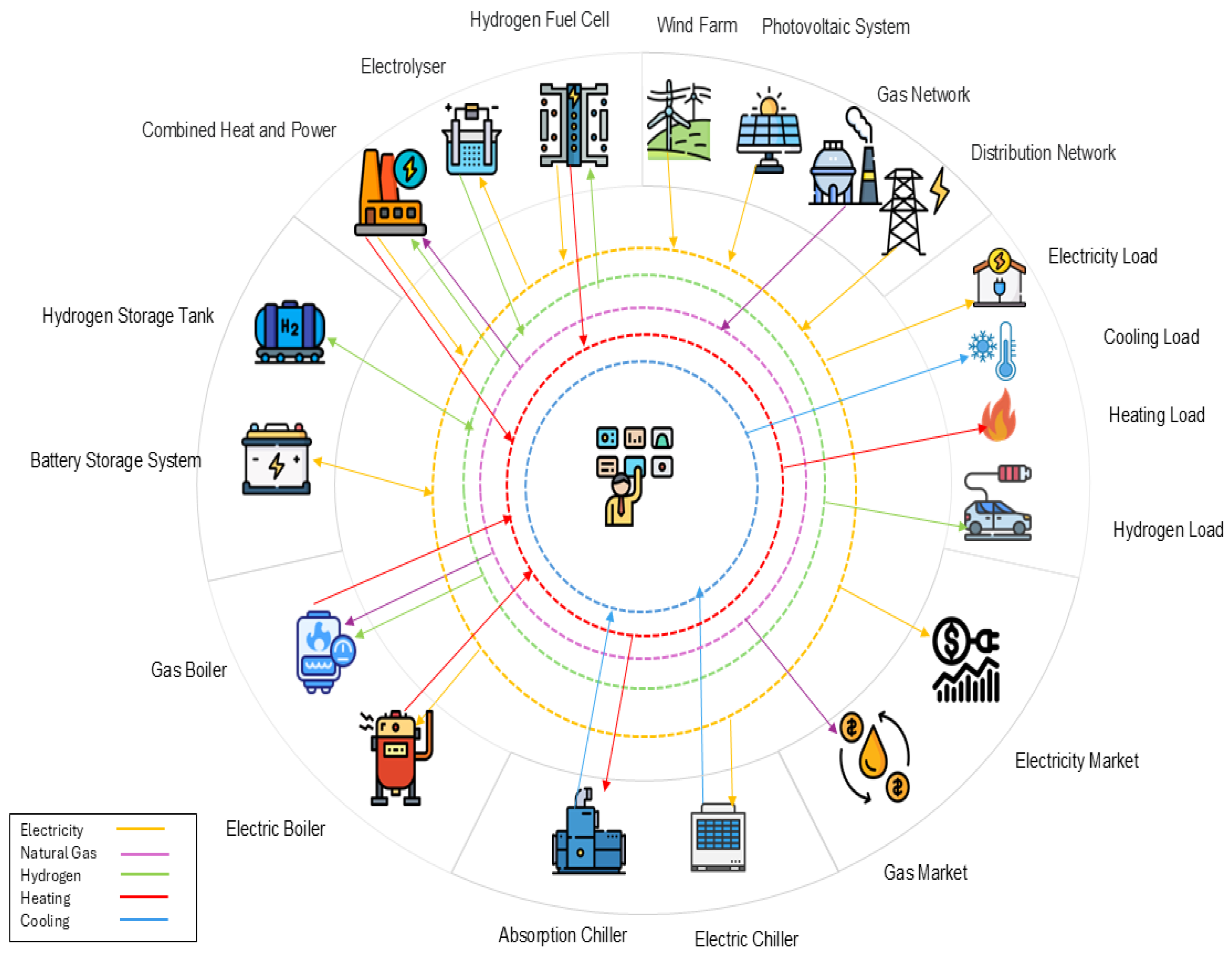
2. The Integrated Hybrid Energy System: Problem Description and Mathematical Formulation
Mathematical Formulation
- Photovoltaic System: The Photovoltaic (PV) system consists of solar panels that convert the sunlight into electric power. The area that can be dedicated to the solar panels, (), is bounded by the parameter , which is the maximum available area. The electric power output of the PV system on the nominal day of month m at time instant t, (kW), is defined aswhere and (kW/m2) are, respectively, the PV panel efficiency and the solar radiation intensity on the nominal day of month m at time instant t; also, denotes the nominal peak power of the PV system. The low energy density is among the greatest limitations of this technology, which requires considerable areas for the production of modest powers. In our case, we set the efficiency of the photovoltaic module equal to that is in line with an average monocrystalline module.
- Combined Heat and Power Plant: The Combined Heat and Power (CHP) plant converts the fuel into electric power. Utilizing H2-NG technology, the fuel consumption in the CHP can incorporate both hydrogen and natural gas. This approach notably decreases methane usage and the overall carbon emissions. The proportion of hydrogen in the mixed gas must remain within a certain range, typically not exceeding 20% of the total volume. The following equation describes the relationship between fuel usage and electric power output in the CHP.where and (kW) denote, respectively, the hydrogen and natural gas fuel consumption in the CHP on the nominal day of month m at time t; (kW) denotes the electric power output; the binary variable is set to one or zero depending on the state of the CHP (either on or off). Parameters and represent the conversion of fuel to electric power in the CHP. In addition, parameter displays the hydrogen blending ratio that is set to 20%.Constraint (6) describes the relation between CHP state and the electric power output where M is a sufficiently large constant , and parameter (kW) in constraint (7) denotes the maximum electrical output in the CHP.In addition, waste heat from combustion can be exploited to produce thermal power to cover the thermal load. The thermal output of the CHP on the nominal day of month m at time t ( in kW) is expressed aswhere and , respectively, represent the power generation efficiency and heat dissipation loss coefficient.
- Electrolyzer: The electrolyzer unit is the critical component in the power-to-gas process converting the electric power into hydrogen. The operation of the electrolyzer is modeled aswhere and are the power input and hydrogen output of the electrolyzer on the nominal day of month m at time t; under the hourly discretization (), denotes the kilograms of hydrogen produced during time instant t (kg). Since has units of kg h−1, multiplying by yields kg per step. For a generic , the right-hand side of (9) would be .The Lower Heating Value (LHV) is set to 33.33 kWh/kg.Constraint (10) shows the relation between the amount hydrogen production and consumption where (kW) represents the available hydrogen fuel in the system.Clearly, the electrolyzer power input is bounded by the installed capacity
- Gas Boiler: The natural gas blended with the hydrogen (produced by the electrolyzer) was injected as the fuel into the GB which is a thermal equipment supplying thermal power. This process is modeled aswhere variables (kW) represent the energy rate equivalent of natural gas and hydrogen consumption; (kW) is the thermal power generated by GB on the nominal day of month m at time t, and displays the installation capacity of GB. Finally, parameter describes the GB efficiency. Similar to the case of CHP, the percentage of hydrogen blended with natural gas should be below a maximum value of .
- Electric Boiler: The Electric Boiler (EB) is another thermal device taking the electric power as the input and produces the heating power
- Electric Chiller: In order to supply the cooling load, the HES operates an electric chiller (EC) working on a reversed-cycle machines aimed to satisfy a cooling load, which is primarily present in but not limited to the summer season.The operation of the EC is described aswhere and (kW) are, respectively, the cooling output and the electric power input in the EC. Variable represents the capacity of EC.
- Absorption Chiller: The Absorption Chiller (AC) absorbs the wasted heat and turns it into cooling power. The following constraints describe the AC operationswhere and (kW) are the cooling power output and the heating input in the AC with the efficiency parameter . The variable denotes the capacity installation of AC.
- Hydrogen Fuel Cell: Hydrogen can be injected into the Hydrogen fuel cell (HFC) to produce electric and thermal power.The HFC operation are described by the following constraints:where and () are, respectively, the hydrogen input and power (thermal) output of HFC, all in kW. Parameters and represent the electricity and thermal generation efficiency of the HFC, and variable is the HFC installed capacity.
- Hydrogen Storage Tank: The hydrogen produced by the EL can be stored into the hydrogen storage tank (HST) to be utilized by the GB, the CHP, and the HFC, or to satisfy the hydrogen load of the fuel cell electric vehicles. The operation of the HST is modeled by constraints (24)–(29).where , is the installed capacity of the HST; is the state of the charge; variables and show the hydrogen charging and discharging in the HST. The input parameter denotes the initial state of the charge in HST.
- Battery Storage System: When the total power generation is greater than the total load or the electricity price drastically drops, and it is very convenient to purchase some extra power, electricity can be stored in a Battery Storage System (BSS). From the battery, electric energy can be used in times of need, to make up for any peaks not covered by intermittent power generation from renewable energy sources. To model the operation of the BSS, we introduce non-negative variables (kWh) and (kW) indicating, respectively, the state of the battery on the nominal day of month m at time t and the installation capacity of BSS, and the power charging and discharging of the BSS on the nominal day of month m at time t. We also should add the set of constraints (30)–(33).where . Constraint (30) expresses the connection between the state of the charge within every two consecutive time instants with the amount of charging and discharging power. Parameters and () display, respectively, the energy loss rate and the charging (discharging) efficiency. Constraint (31) expresses the relation between the state of the charge and the installed capacity. Constraints (32) and (33) express the logical bounds on the power charge and discharge. Since the technology in BSS does not allow simultaneous power charge and discharge, we introduced binary variables and added the set of constraints in (34) and (35) where M is an arbitrary big number.
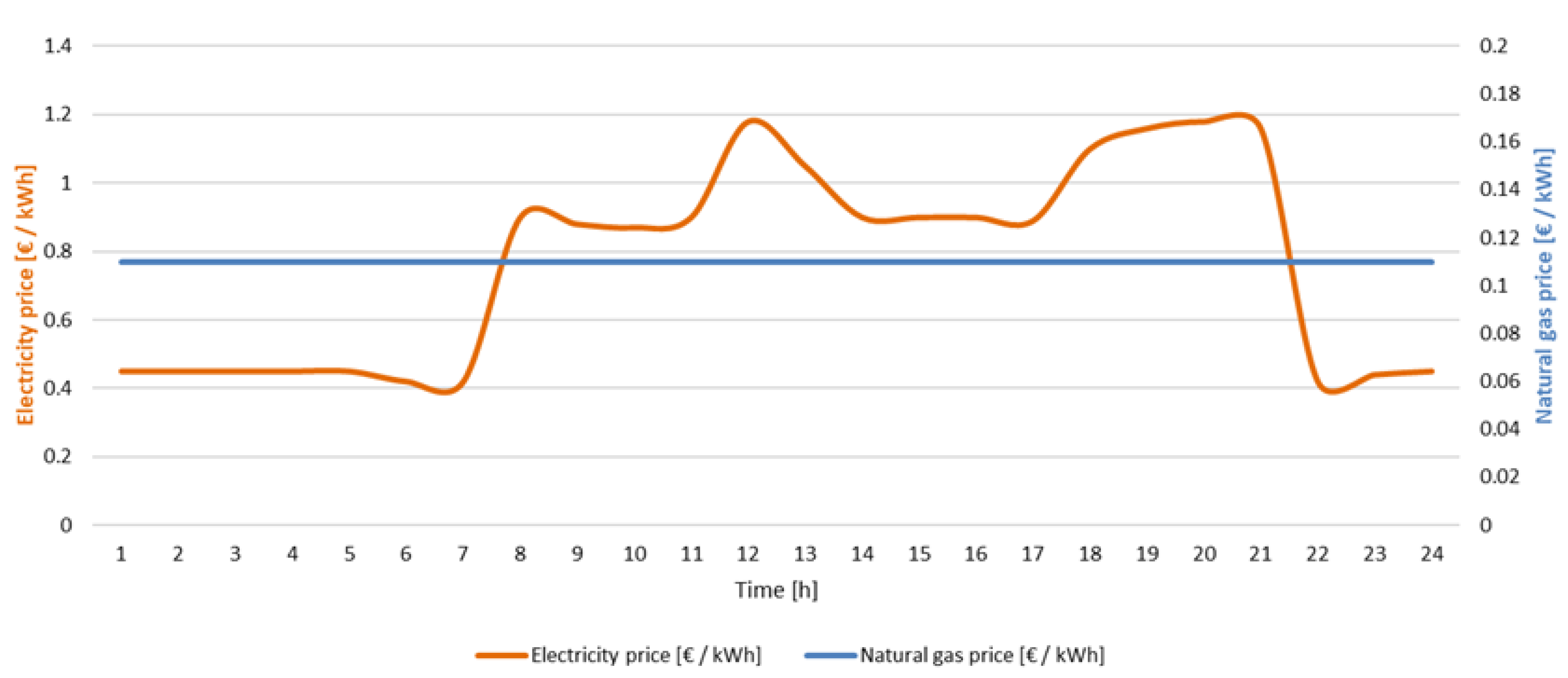
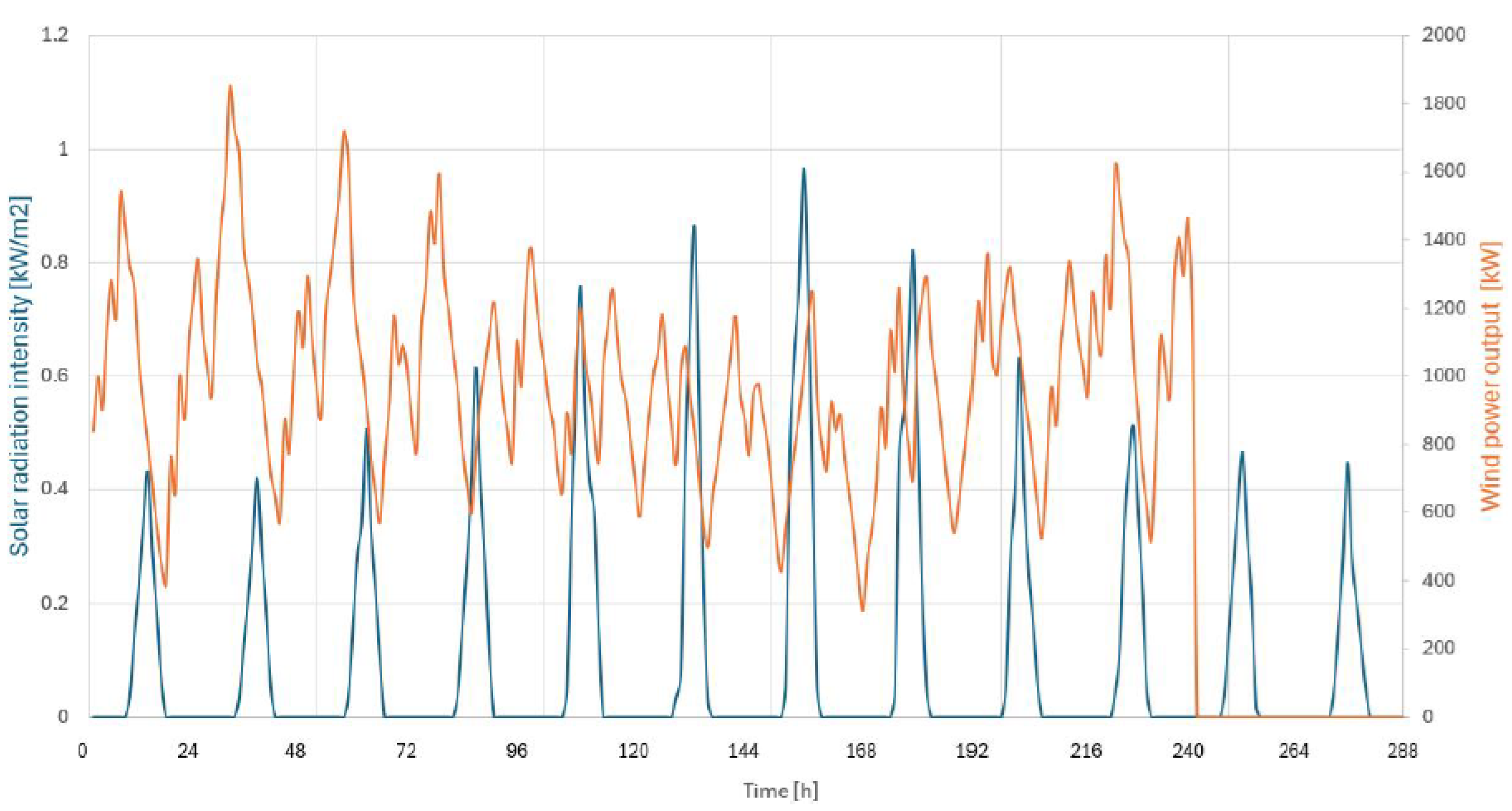
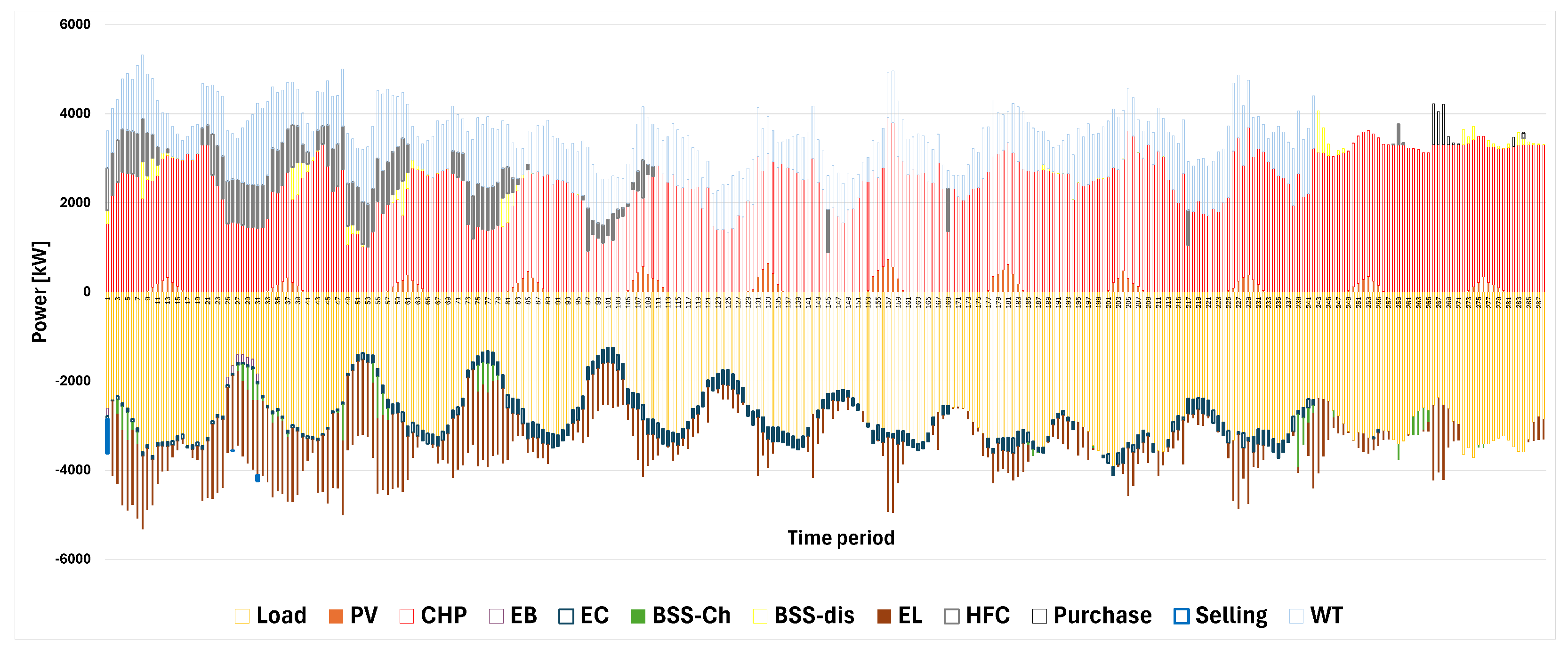
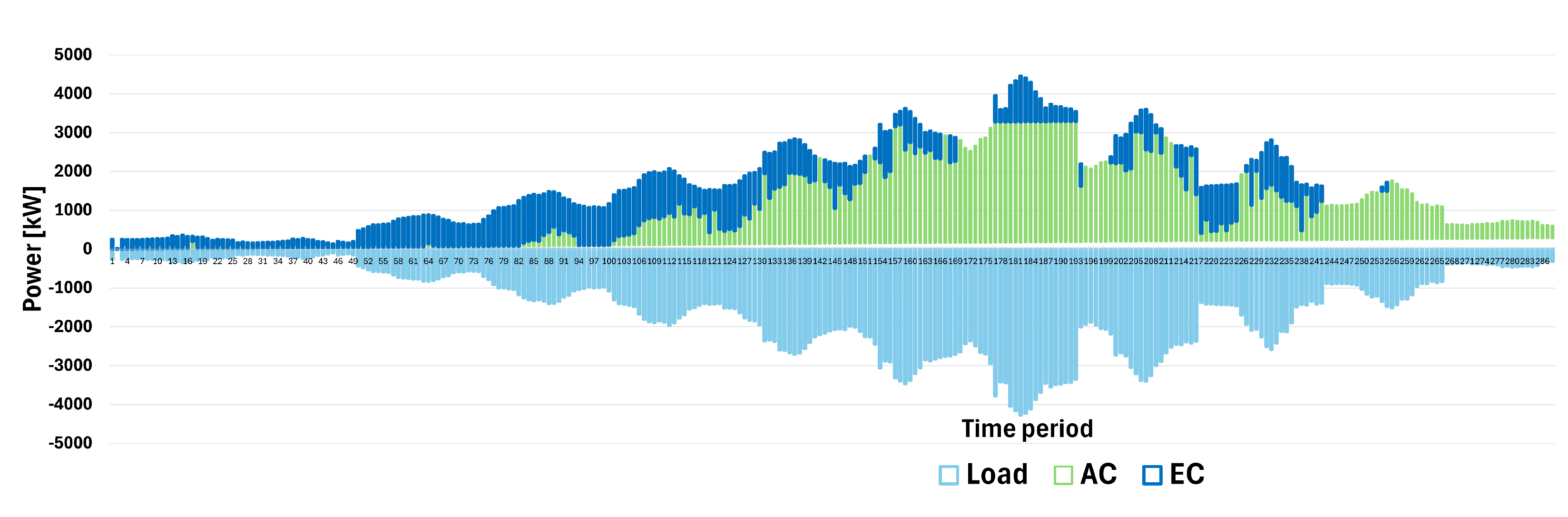
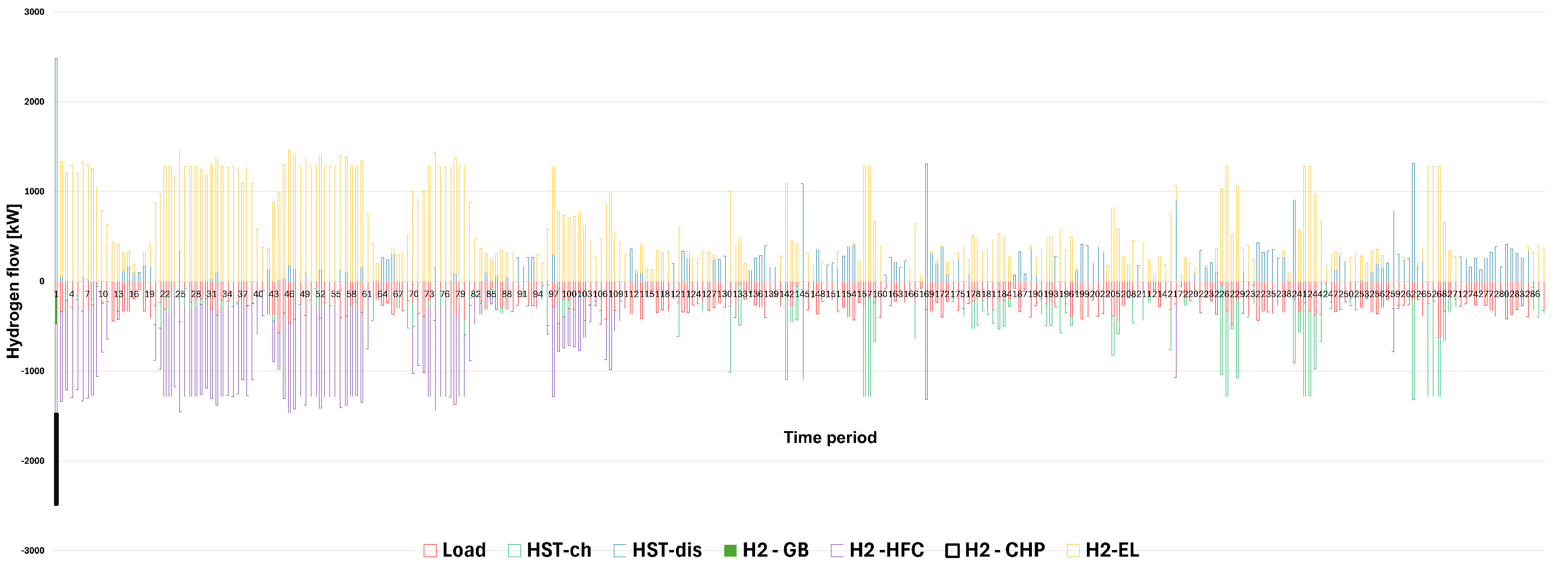
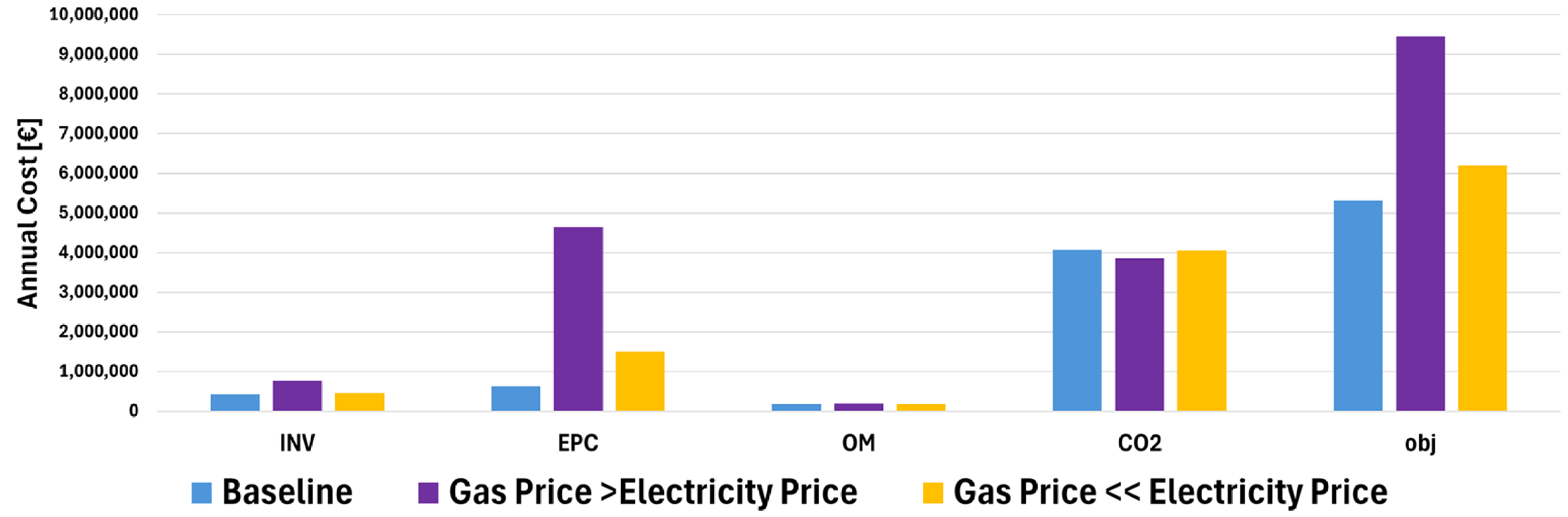
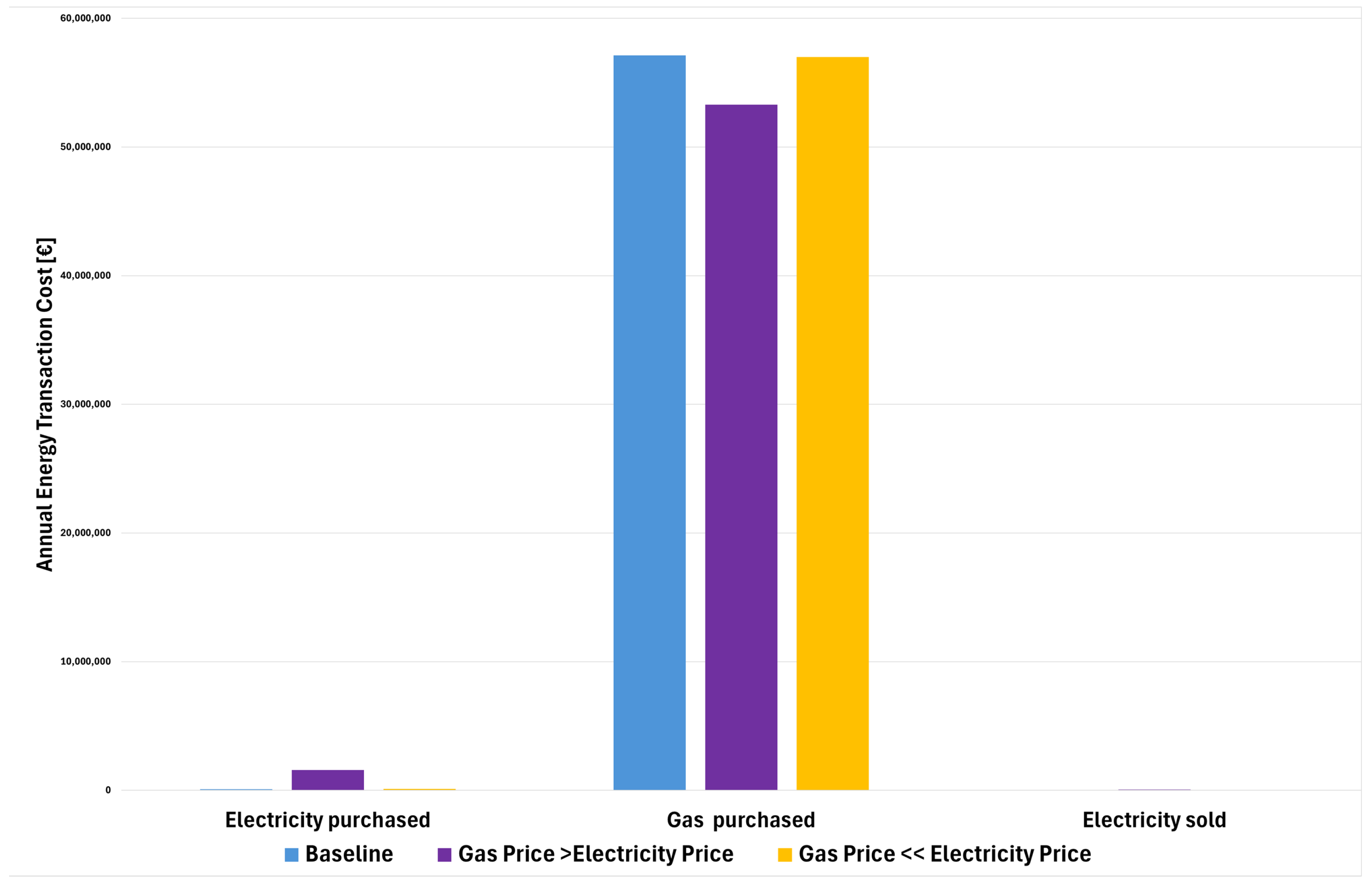
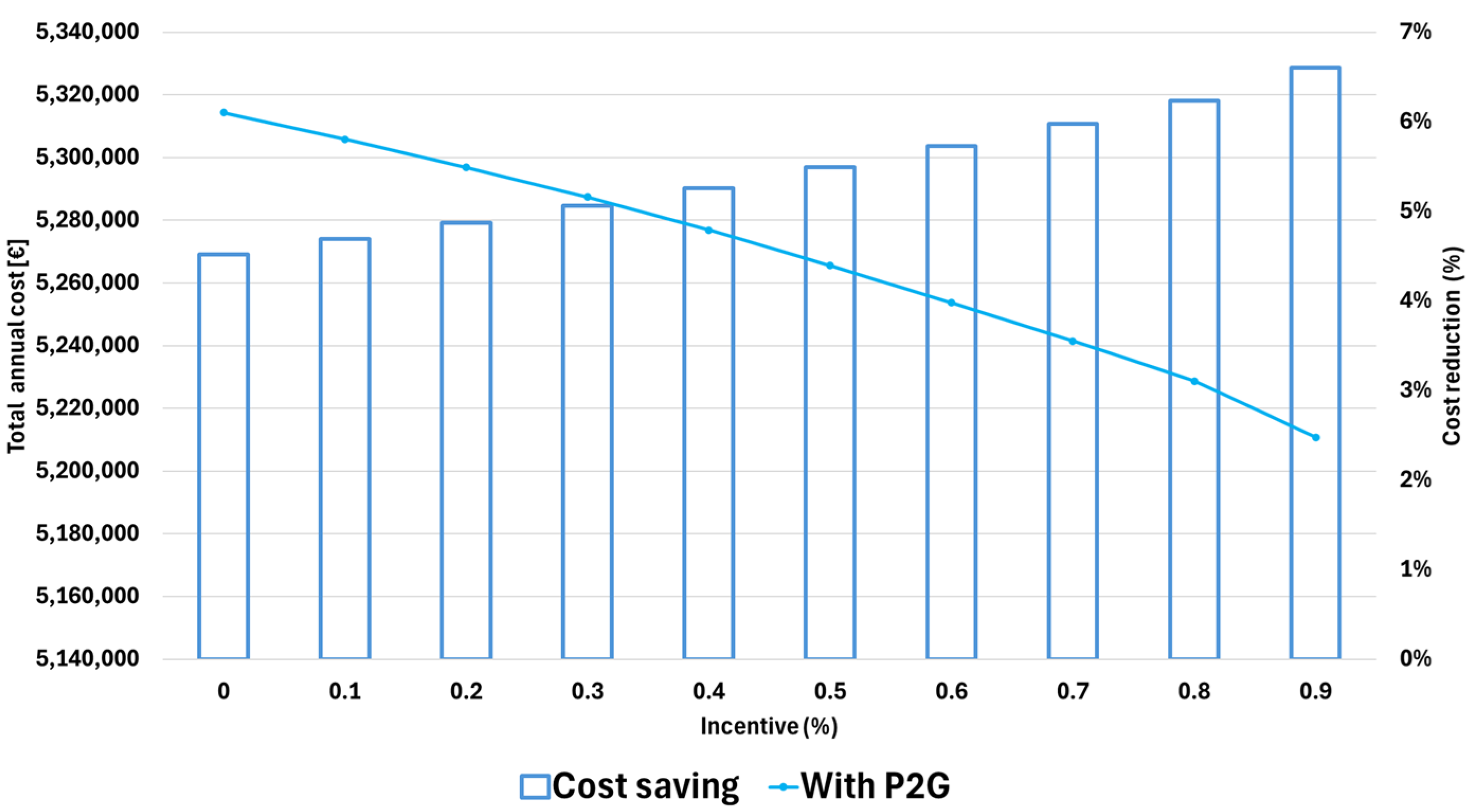
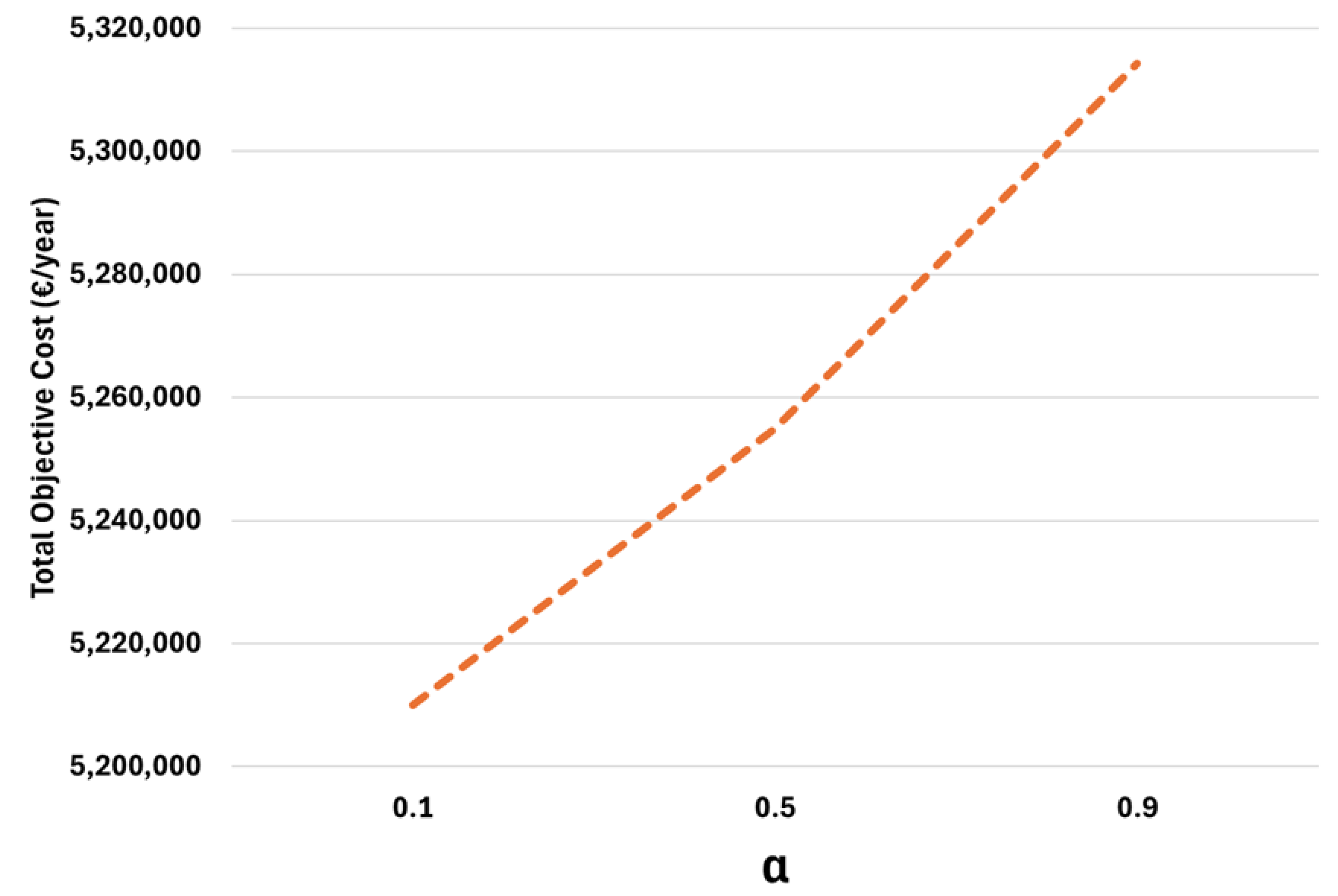
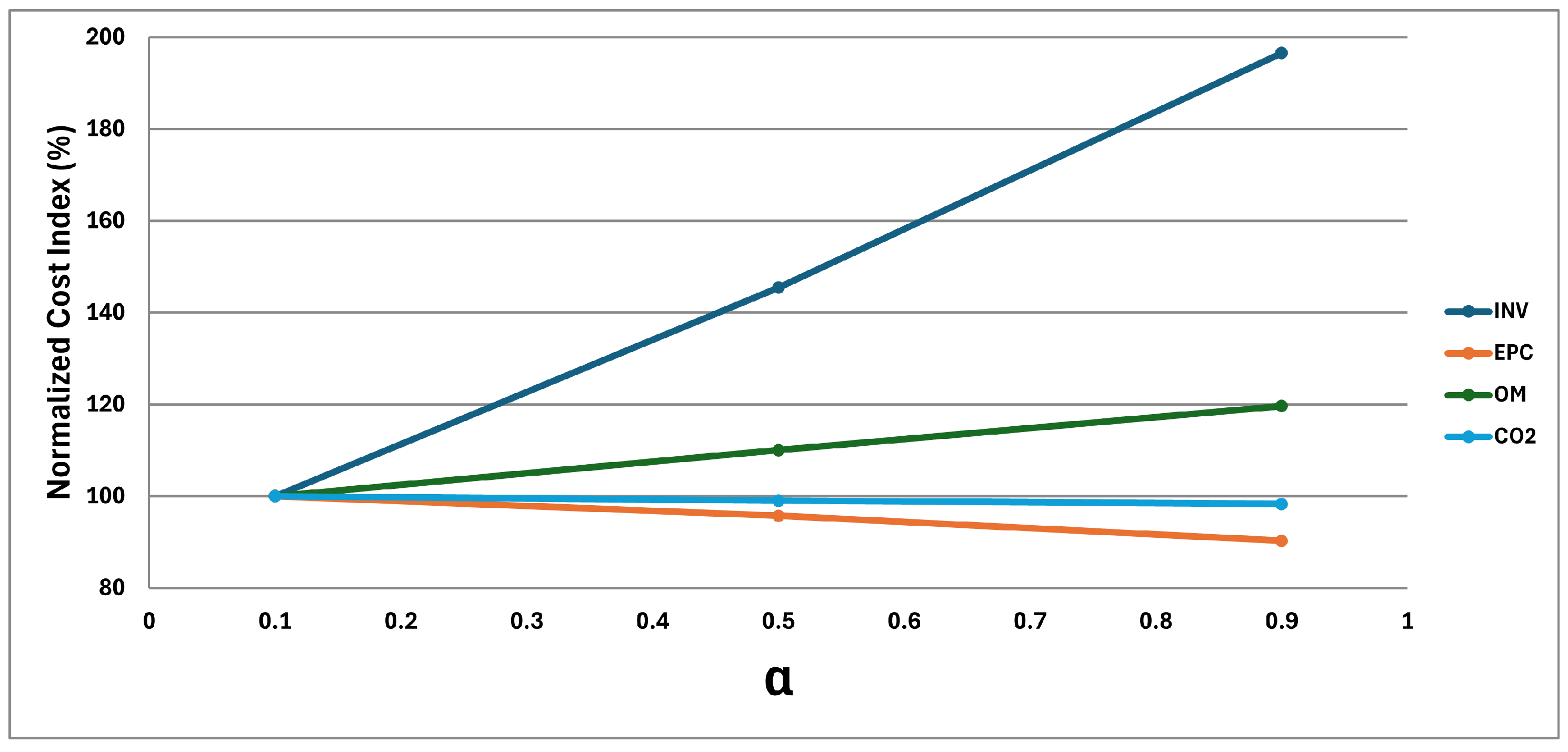
3. Computational Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter | Description | Value | Unit |
|---|---|---|---|
| M | Number of months | 12 | months |
| T | Hourly periods per representative day | 24 | hours/day |
| Number of days represented by month m | – | days | |
| Time-step length | 1 | hour | |
| PV panel efficiency (module) | 0.20 | – | |
| Solar irradiance at | – | kW/m2 | |
| Maximum available area for PV | 5000 | m2 | |
| CHP fuel-to-electric slope | 2.5 | kW fuel/kW el | |
| CHP minimum fuel offset when ON | 2.6 | kW fuel | |
| Max H2 blending ratio (grid/appliance) | 0.2 | – | |
| CHP electric efficiency | 0.40 | – | |
| CHP heat dissipation loss coefficient | 0.15 | – | |
| Electrolyzer efficiency (LHV basis) | 0.70 | – | |
| Hydrogen lower heating value | 33.33 | kWh/kg | |
| Gas boiler efficiency | 0.92 | – | |
| Electric boiler efficiency | 1.00 | – | |
| Electric chiller coefficient of performance (COP) | 3.5 | – | |
| Absorption chiller coefficient of performance (COP) | 0.7 | – | |
| Hydrogen fuel cell electric efficiency | 0.55 | – | |
| Hydrogen fuel cell thermal efficiency | 0.35 | – | |
| Battery standing loss per hour (self-discharge rate) | 0.001 | – per hour | |
| Battery charging efficiency | 0.97 | – | |
| Battery discharging efficiency | 0.97 | – | |
| Economic lifetime of device k | – | years | |
| i | Annual real discount/interest rate | 0.05 | 1/year |
References
- Menniti, D.; Pinnarelli, A.; Bruni, M.E.; Sorrentino, N.; Brusco, G.; Bilotta, V.; Vizza, P. The Sizing of a Smart Microgrid Integrating Hydrogen Technology for a Power to Power Scenario. In Proceedings of the 2024 AEIT International Annual Conference (AEIT), Trento, Italy, 25–27 September 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Cambini, C.; Congiu, R.; Soroush, G. Regulation, innovation, and systems integration: Evidence from the EU. Energies 2020, 13, 1670. [Google Scholar] [CrossRef]
- Cambini, C.; Congiu, R.; Jamasb, T.; Llorca, M.; Soroush, G. Energy Systems Integration: Implications for public policy. Energy Policy 2020, 143, 111609. [Google Scholar] [CrossRef]
- Zhou, Y.; Min, C.; Wang, K.; Xie, L.; Fan, Y. Optimization of integrated energy systems considering seasonal thermal energy storage. J. Energy Storage 2023, 71, 108094. [Google Scholar] [CrossRef]
- Yang, D.; He, Z.; Sun, Y.; Li, B.; Li, D.; Liu, X.; Jiang, C. Optimised operation of integrated community energy system considering integrated energy pricing strategy: A two-layer Stackelberg game approach. J. Energy Storage 2024, 87, 111383. [Google Scholar] [CrossRef]
- Beraldi, P.; Khodaparasti, S. Designing electricity tariffs in the retail market: A stochastic bi-level approach. Int. J. Prod. Econ. 2023, 257, 108759. [Google Scholar] [CrossRef]
- Beraldi, P.; Khodaparasti, S. A bi-level model for the design of dynamic electricity tariffs with demand-side flexibility. Soft Comput. 2023, 27, 12925–12942. [Google Scholar] [CrossRef]
- Fan, L.; Tu, Z.; Chan, S.H. Recent development of hydrogen and fuel cell technologies: A review. Energy Rep. 2021, 7, 8421–8446. [Google Scholar] [CrossRef]
- Tostado-Véliz, F.; Contreras, J.; Rider, M.J. Risk-averse electrolyzer sizing in industrial parks: A hybrid stochastic–robust optimization approach. Appl. Energy 2022, 306, 118095. [Google Scholar]
- Wang, X.; Li, Y.; Zhao, H.; Chen, M.; Zhang, T.; Liu, Q.; Xu, L.; Huang, J.; Yang, D.; Sun, P.; et al. Multi-objective distributionally robust optimization for hydrogen-renewable energy-coupled CCHP systems. Energy Convers. Manag. 2022, 261, 115648. [Google Scholar]
- Zheng, Y.; You, S.; Wang, J.; Li, X.; Bindner, H.W.; Münster, M. Data-driven robust chance-constrained optimization for optimal operation of a wind/hydrogen system. In Proceedings of the 13th International Conference on Applied Energy (ICAE 2021), Bangkok, Thailand, 29 November–2 December 2021. [Google Scholar]
- Liu, Y.; Li, J.; Zhang, H. Distributionally robust scheduling of port energy systems with hydrogen production and storage. Appl. Energy 2023, 340, 120923. [Google Scholar]
- Aramoon, A.; Khodabakhshian, A.; Siano, P. Risk-averse techno-economic analysis of off-grid PV/diesel/fuel cell systems using IGDT. Renew. Energy 2023, 205, 722–735. [Google Scholar]
- Xuan, A.; Shen, X.; Guo, Q.; Sun, H. A conditional value-at-risk based planning model for integrated energy systems with energy storage and renewables. Appl. Energy 2021, 294, 116971. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. Resolution Adopted by the General Assembly on 25 September 2015. A/RES/70/1. 2015. Available online: https://sdgs.un.org/2030agenda (accessed on 10 June 2025).
- Li, J.Y.M. Technical note—Closed-form solutions for worst-case law invariant risk measures with application to robust portfolio optimization. Oper. Res. 2018, 66, 1533–1541. [Google Scholar] [CrossRef]
- Mazarrón, F.R.; Álvarez, J.; Cervera-Gascó, J.; López-Santiago, J. Impact of Electricity Price Reductions on the Profitability and Sizing of Photovoltaic Systems in Agri-Food Industries. Agriculture 2025, 15, 631. [Google Scholar] [CrossRef]
- Mallapragada, D.S.; Junge, C.; Wang, C.; Pfeifenberger, H.; Joskow, P.L.; Schmalensee, R. Electricity pricing challenges in future renewables-dominant power systems. Energy Econ. 2023, 126, 106981. [Google Scholar] [CrossRef]
- Fagerström, J.; Das, S.; Klyve, Ø,S.; Olkkonen, V.; Marstein, E.S. Profitability of battery storage in hybrid hydropower–solar photovoltaic plants. J. Energy Storage 2024, 77, 109827. [Google Scholar] [CrossRef]


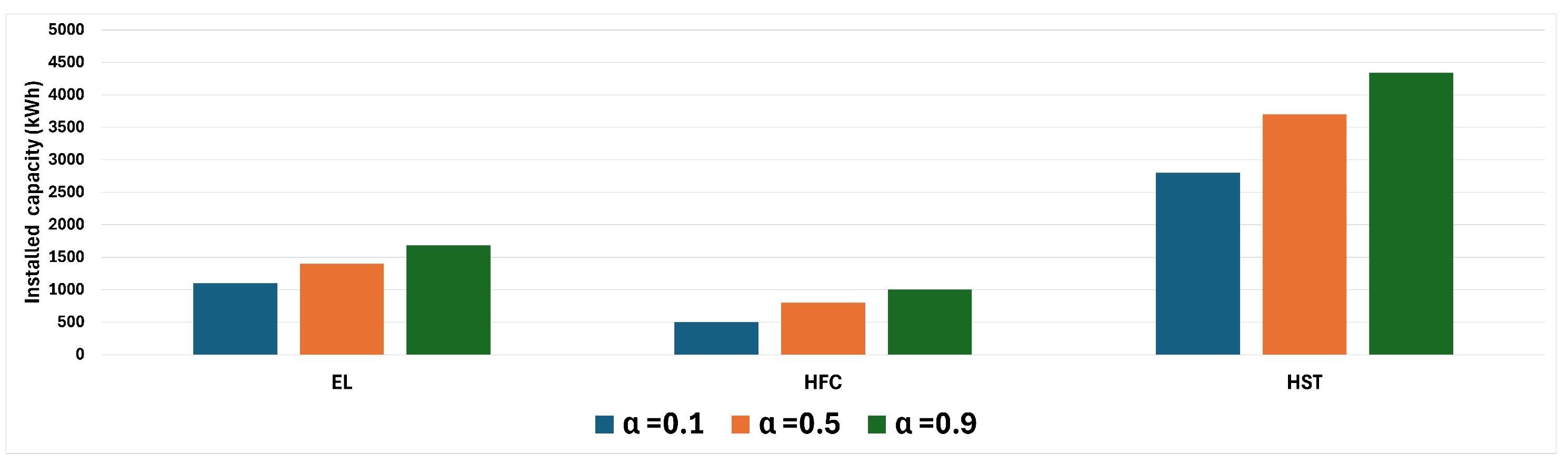
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khodaparasti, S.; Cosma, A.; Pinnarelli, A.; Bruni, M.E. Hydrogen Strategies Under Uncertainty: Risk-Averse Choices for Green Hydrogen Pathways. Sustainability 2025, 17, 9475. https://doi.org/10.3390/su17219475
Khodaparasti S, Cosma A, Pinnarelli A, Bruni ME. Hydrogen Strategies Under Uncertainty: Risk-Averse Choices for Green Hydrogen Pathways. Sustainability. 2025; 17(21):9475. https://doi.org/10.3390/su17219475
Chicago/Turabian StyleKhodaparasti, Sara, Antonio Cosma, Anna Pinnarelli, and Maria Elena Bruni. 2025. "Hydrogen Strategies Under Uncertainty: Risk-Averse Choices for Green Hydrogen Pathways" Sustainability 17, no. 21: 9475. https://doi.org/10.3390/su17219475
APA StyleKhodaparasti, S., Cosma, A., Pinnarelli, A., & Bruni, M. E. (2025). Hydrogen Strategies Under Uncertainty: Risk-Averse Choices for Green Hydrogen Pathways. Sustainability, 17(21), 9475. https://doi.org/10.3390/su17219475







