Seismic Performance of a Modular Steel Building with Glass Curtain Walls: Shaking Table Tests
Abstract
1. Introduction
2. Experimental Design
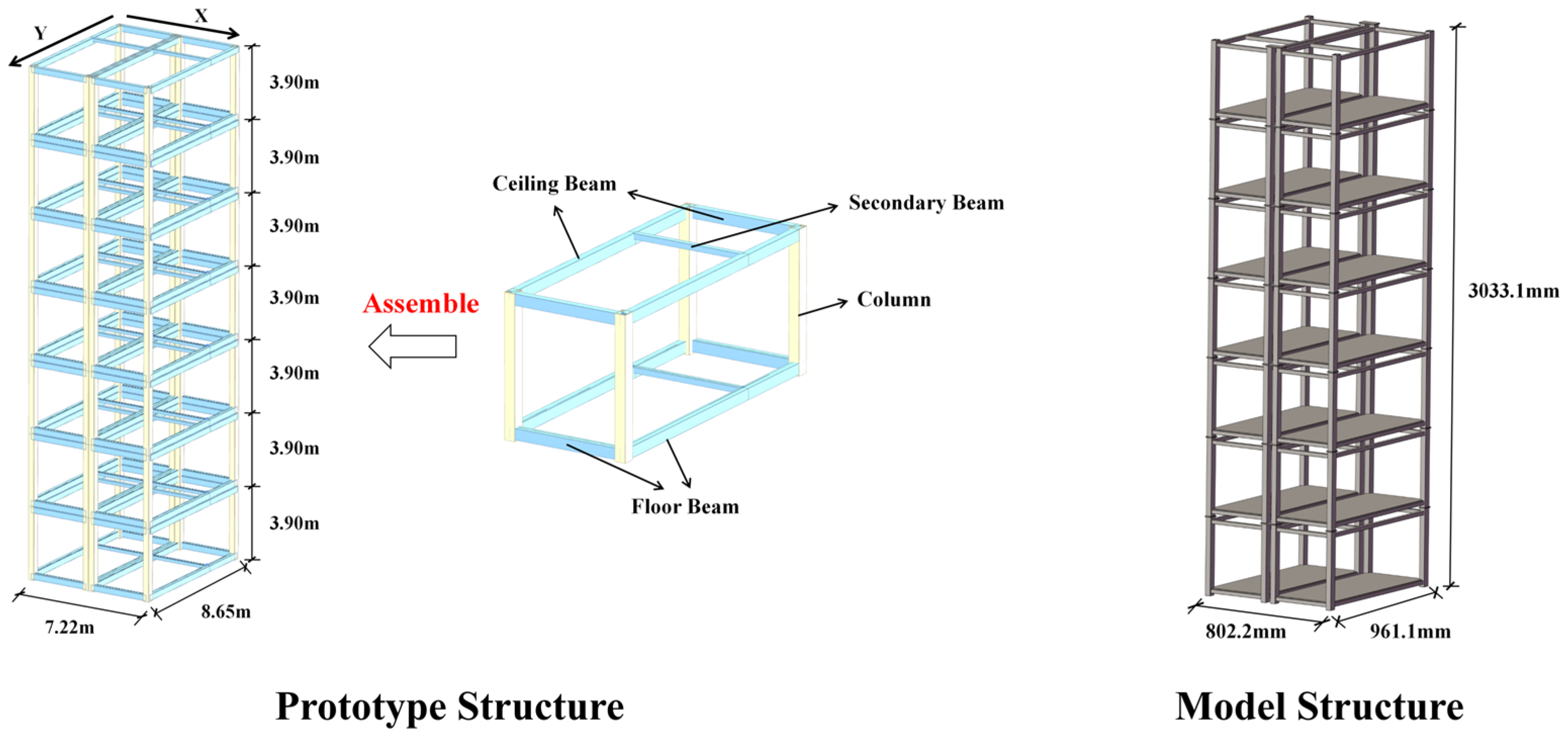
2.1. The Prototype
2.2. Similitude Relationship
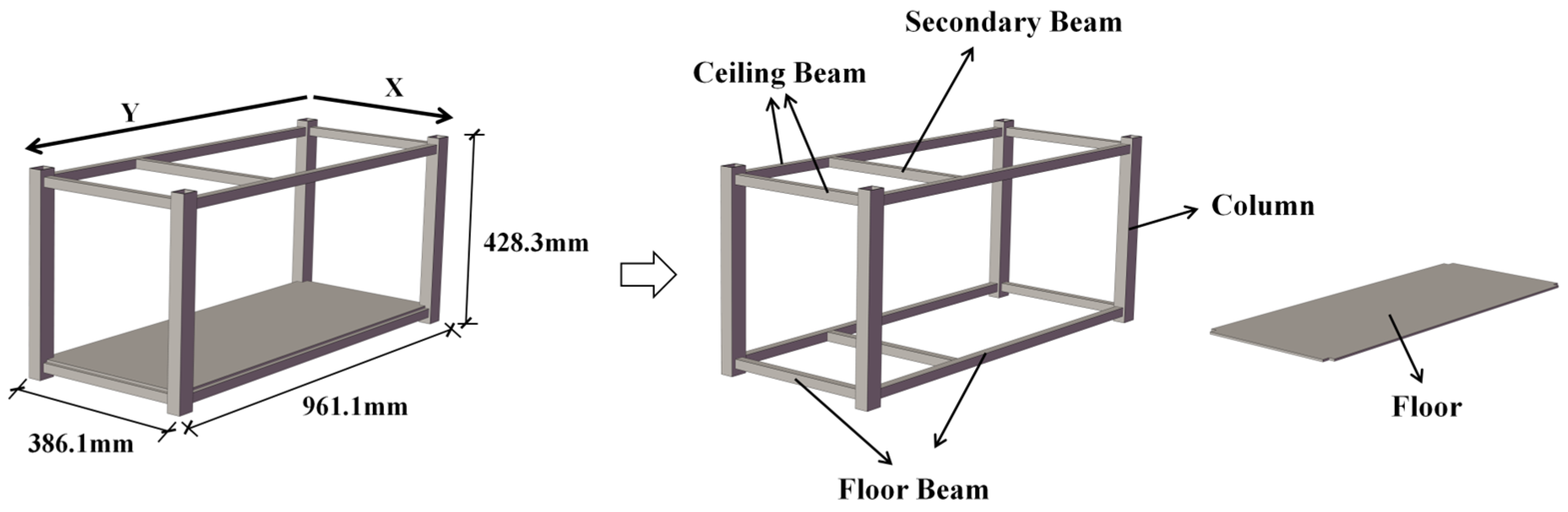
2.3. The Physical Model
2.3.1. Structural Component Design
2.3.2. Main Frame Design
2.3.3. Glass Curtain Wall Design
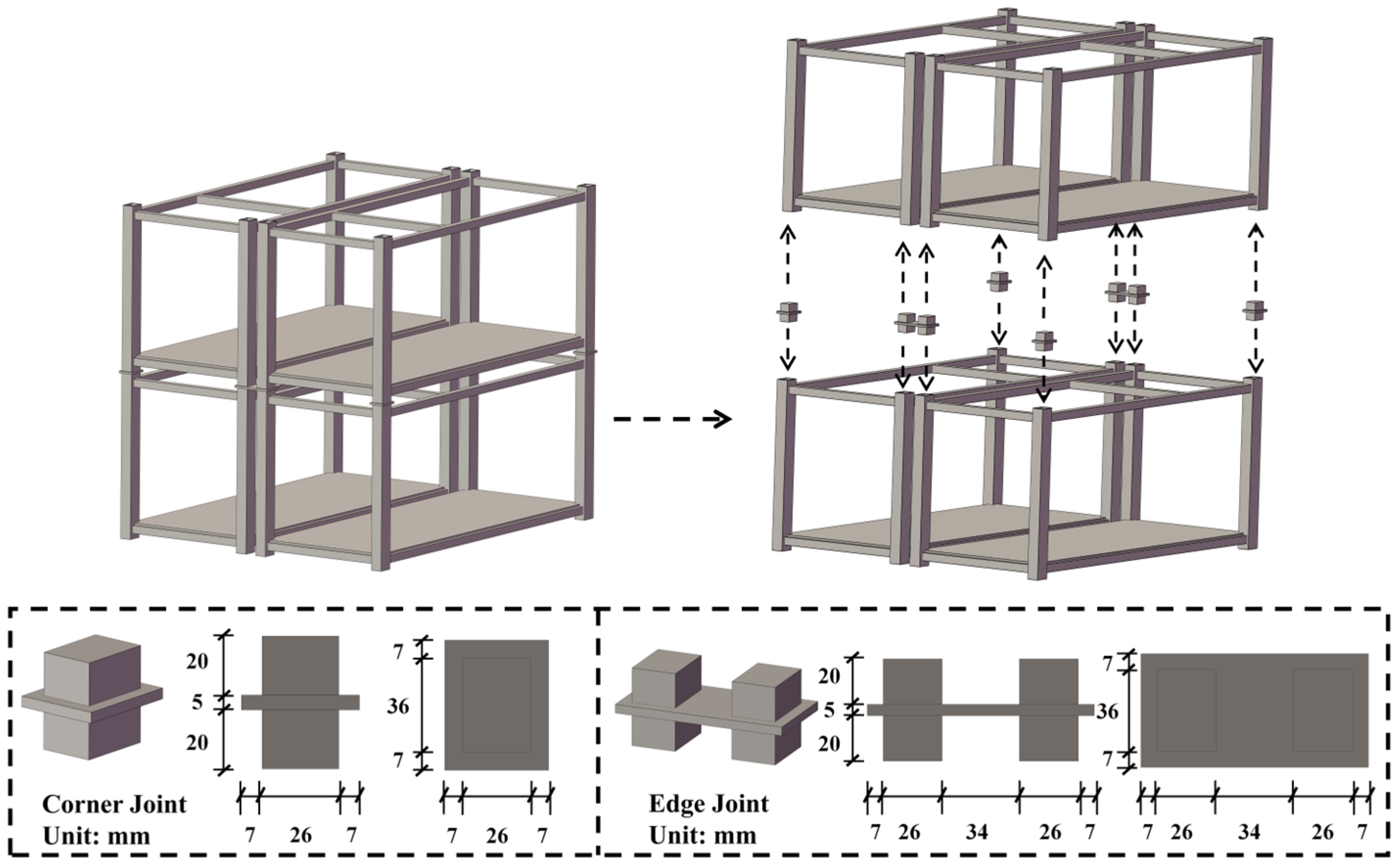
2.3.4. Fabrication of the Model Structure
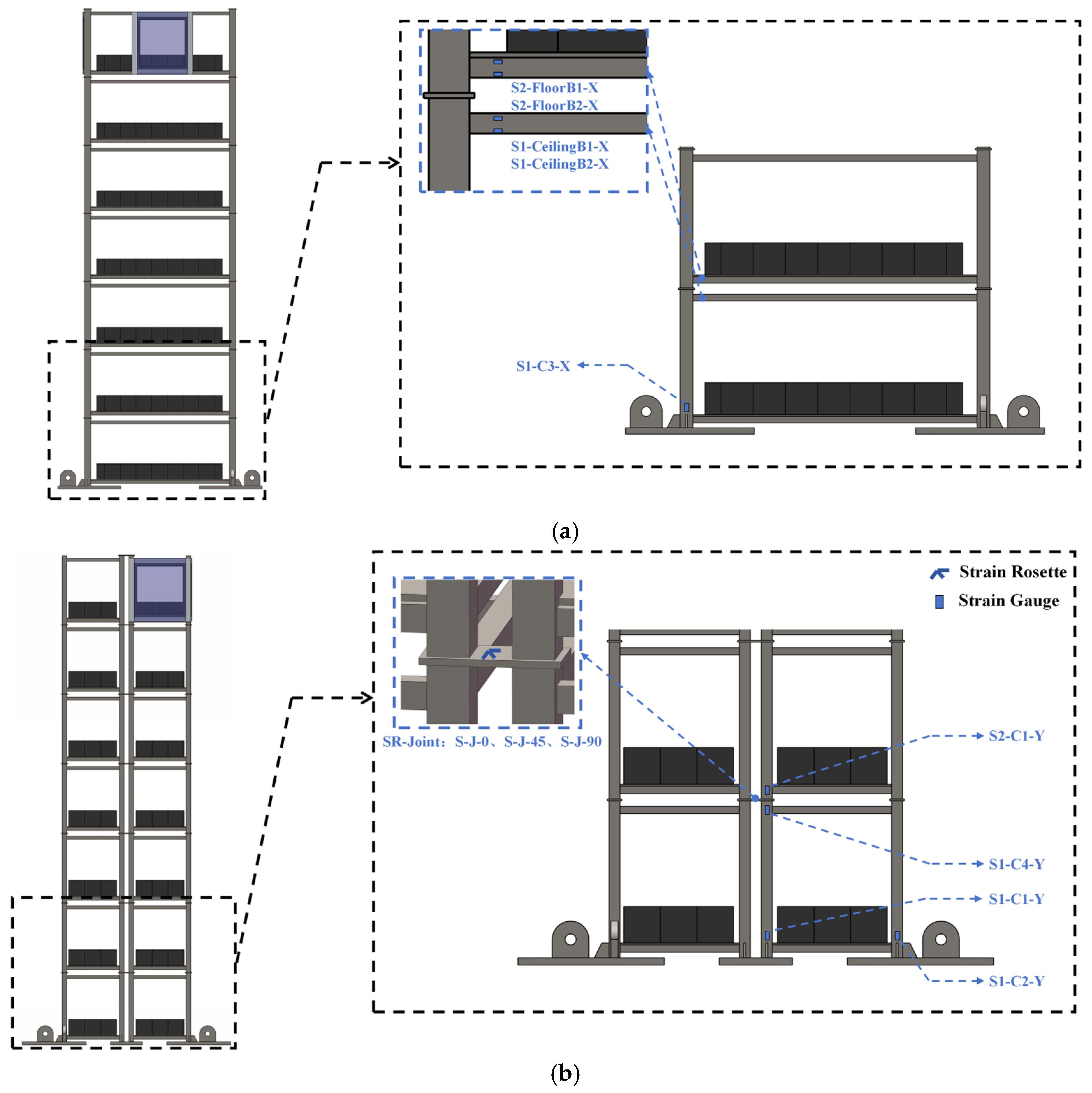
2.4. Measurement
2.4.1. Sensors
2.4.2. Sensor Arrangement
2.5. Dynamic Similarity Verification
2.6. Load Scheme
2.6.1. Shaking Table
2.6.2. Selection of Seismic Waves
2.6.3. Test Loading Scheme
3. Test Results and Discussion
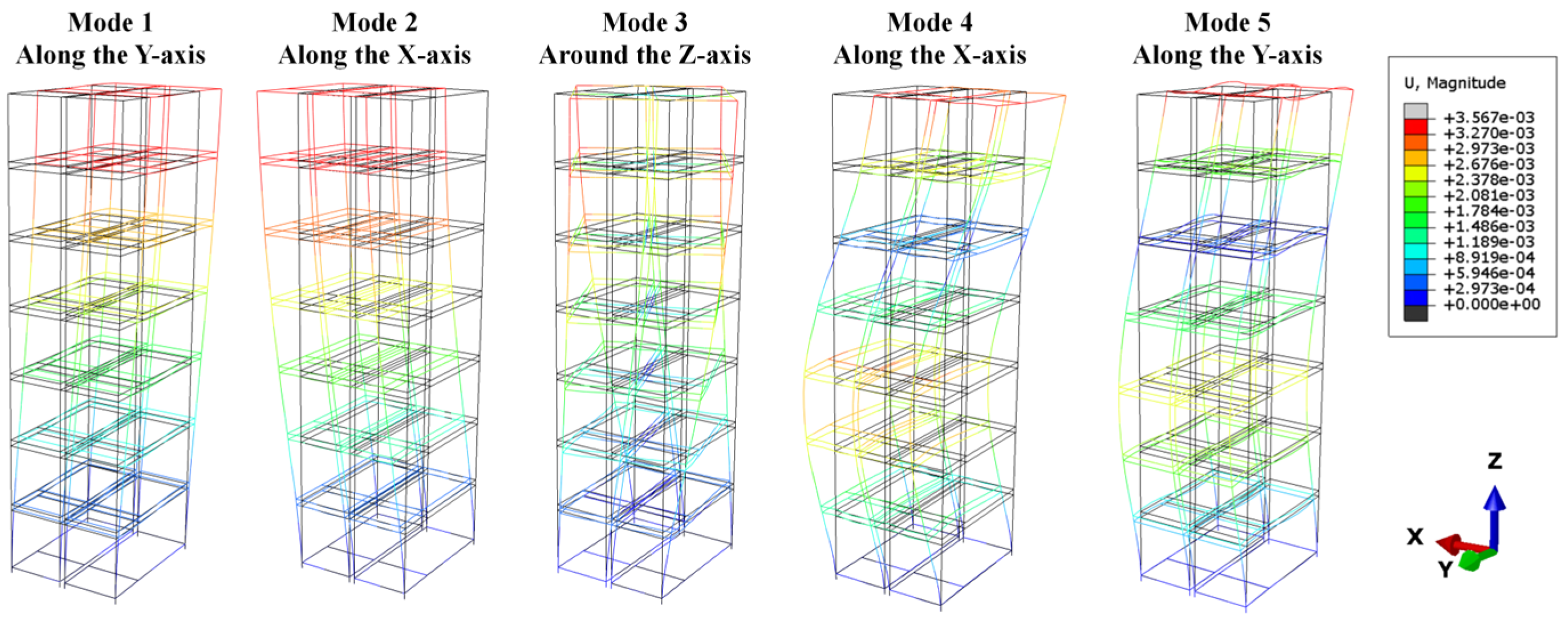
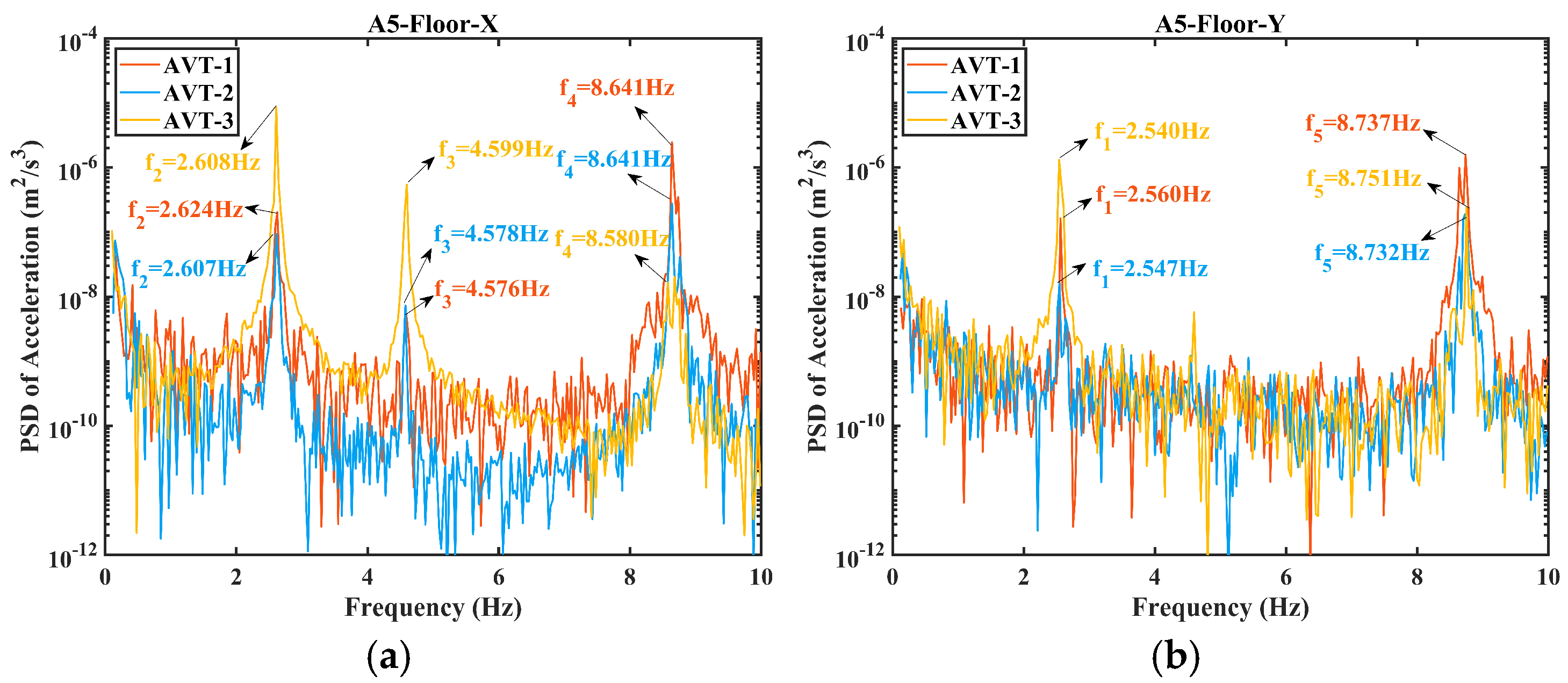
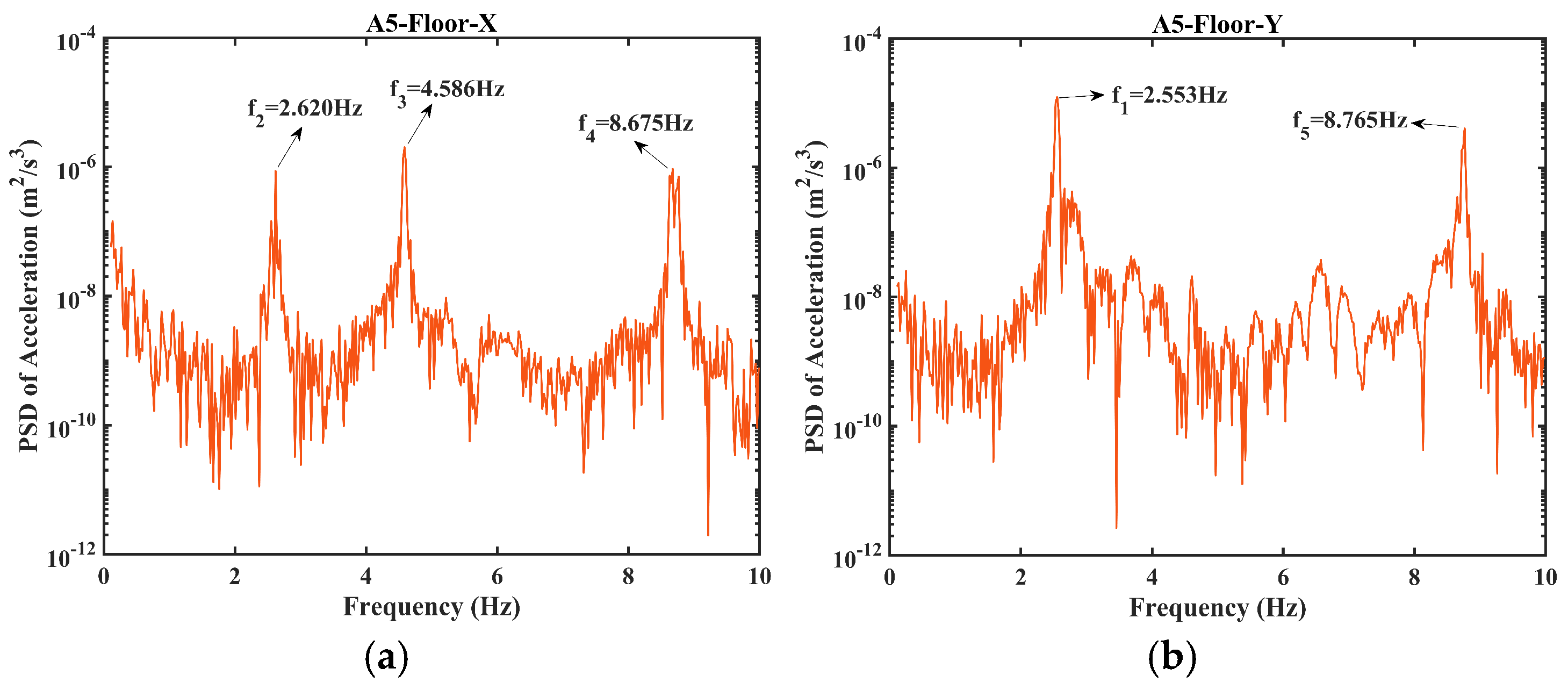
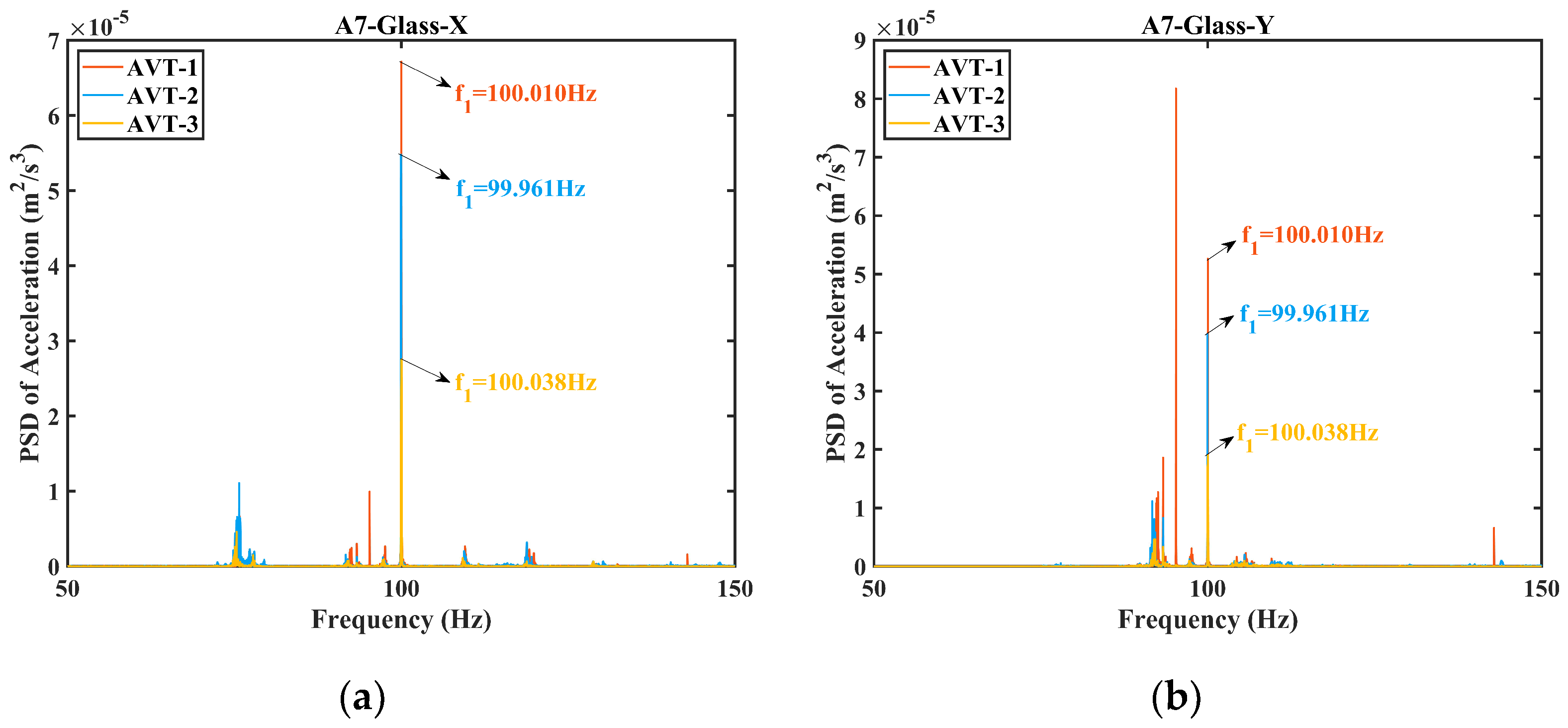
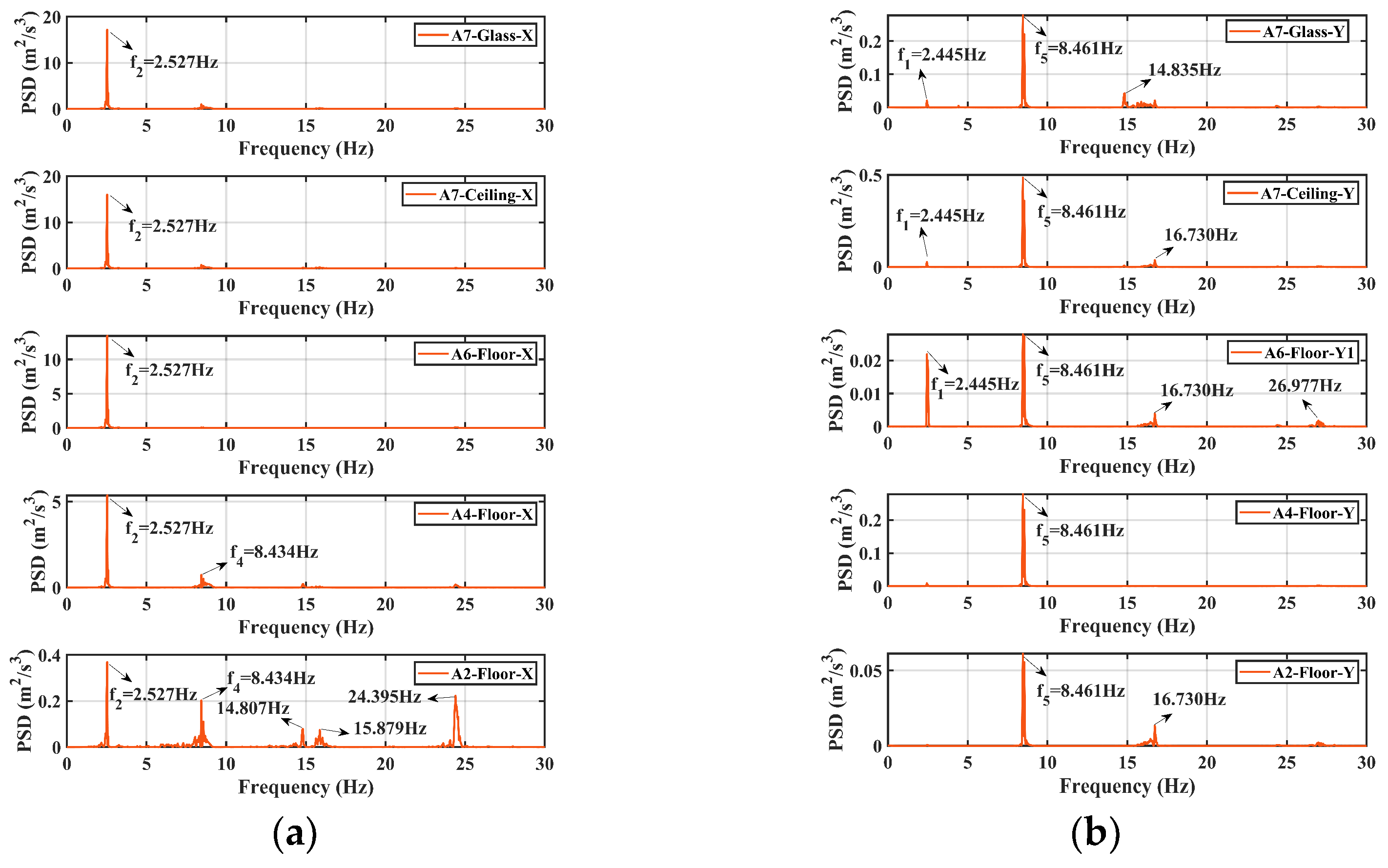
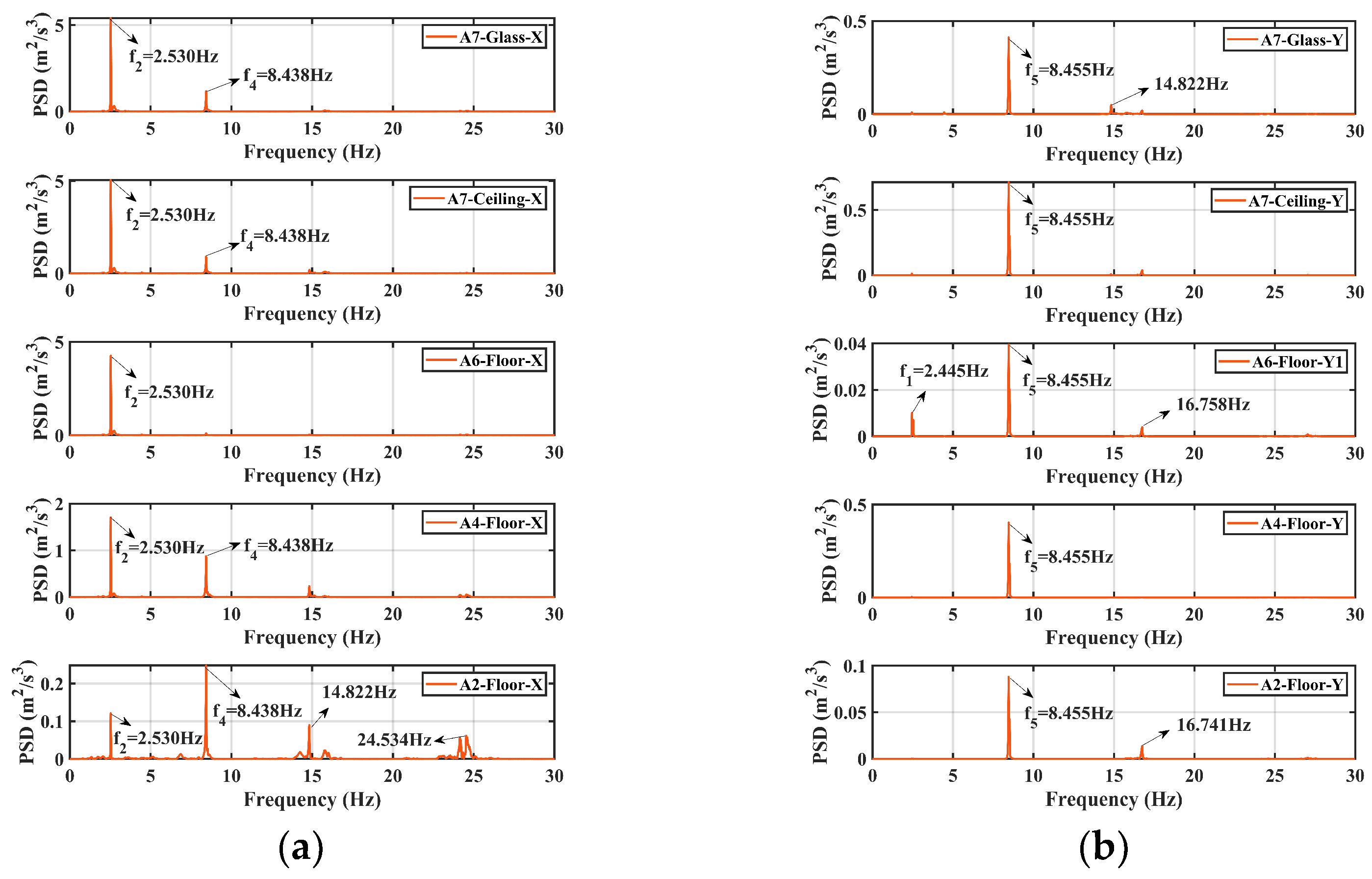
3.1. Dynamic Characteristics
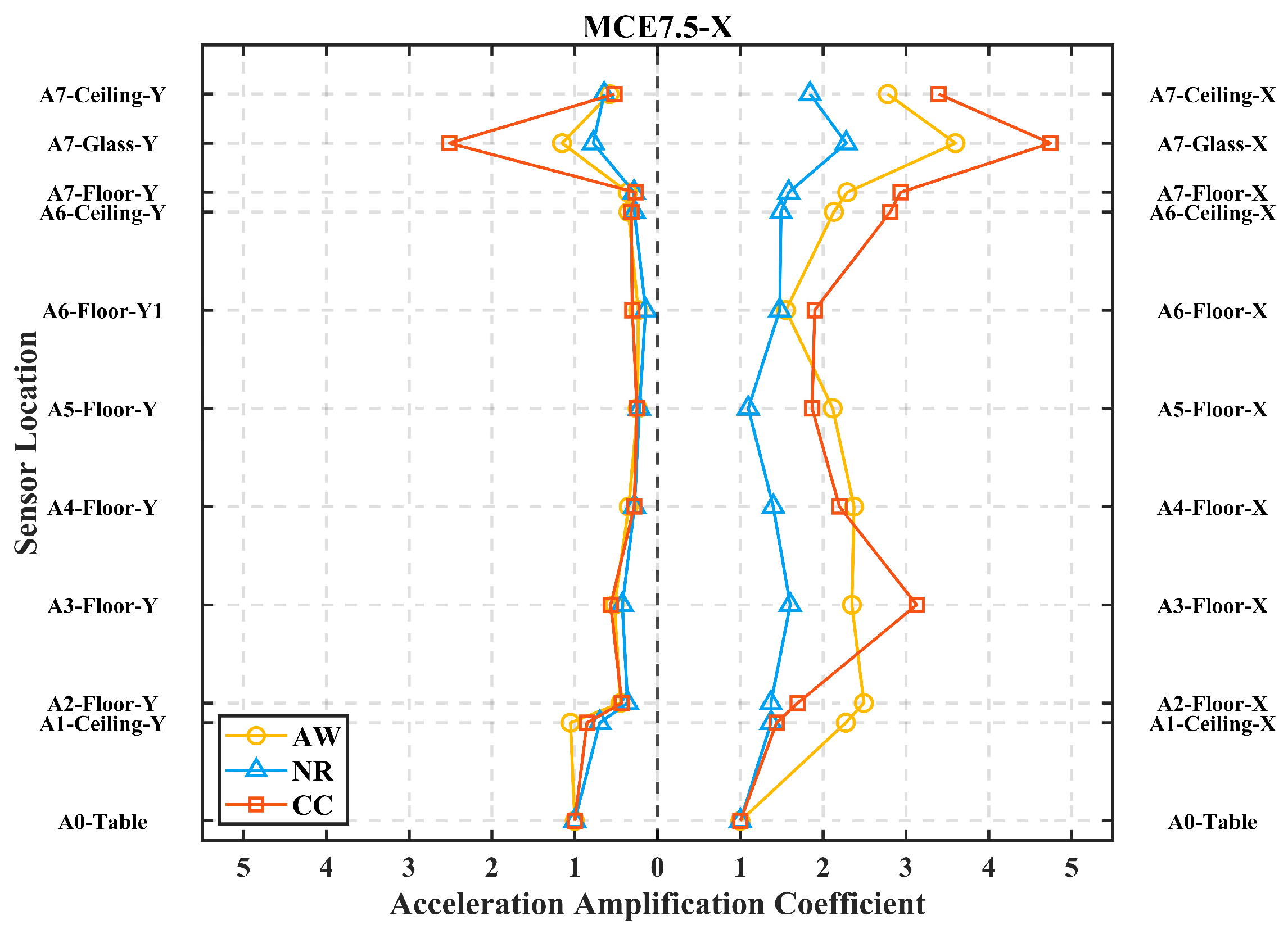
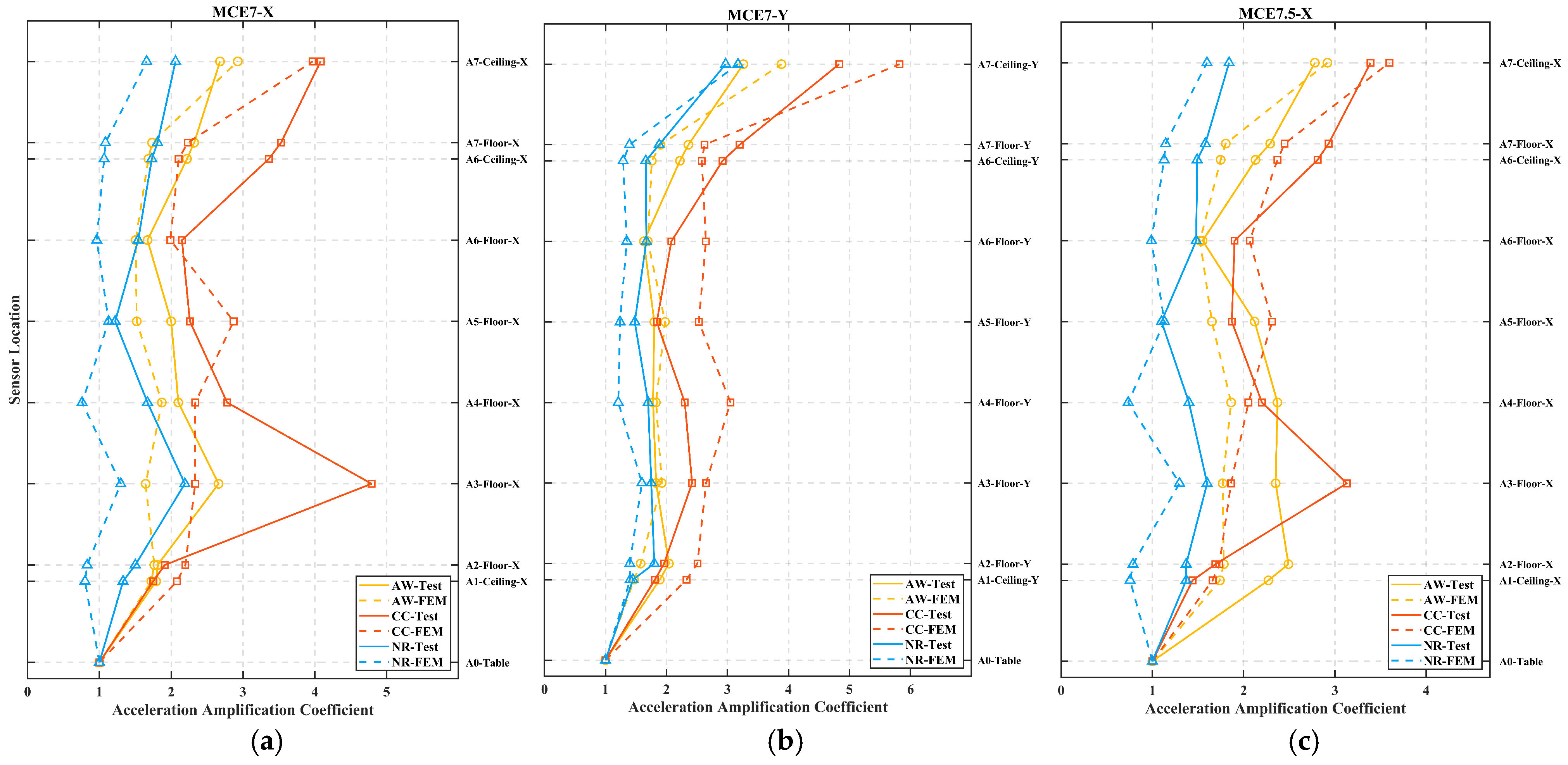
3.2. Acceleration Amplification Coefficient
3.3. Acceleration Response Spectrum Analysis
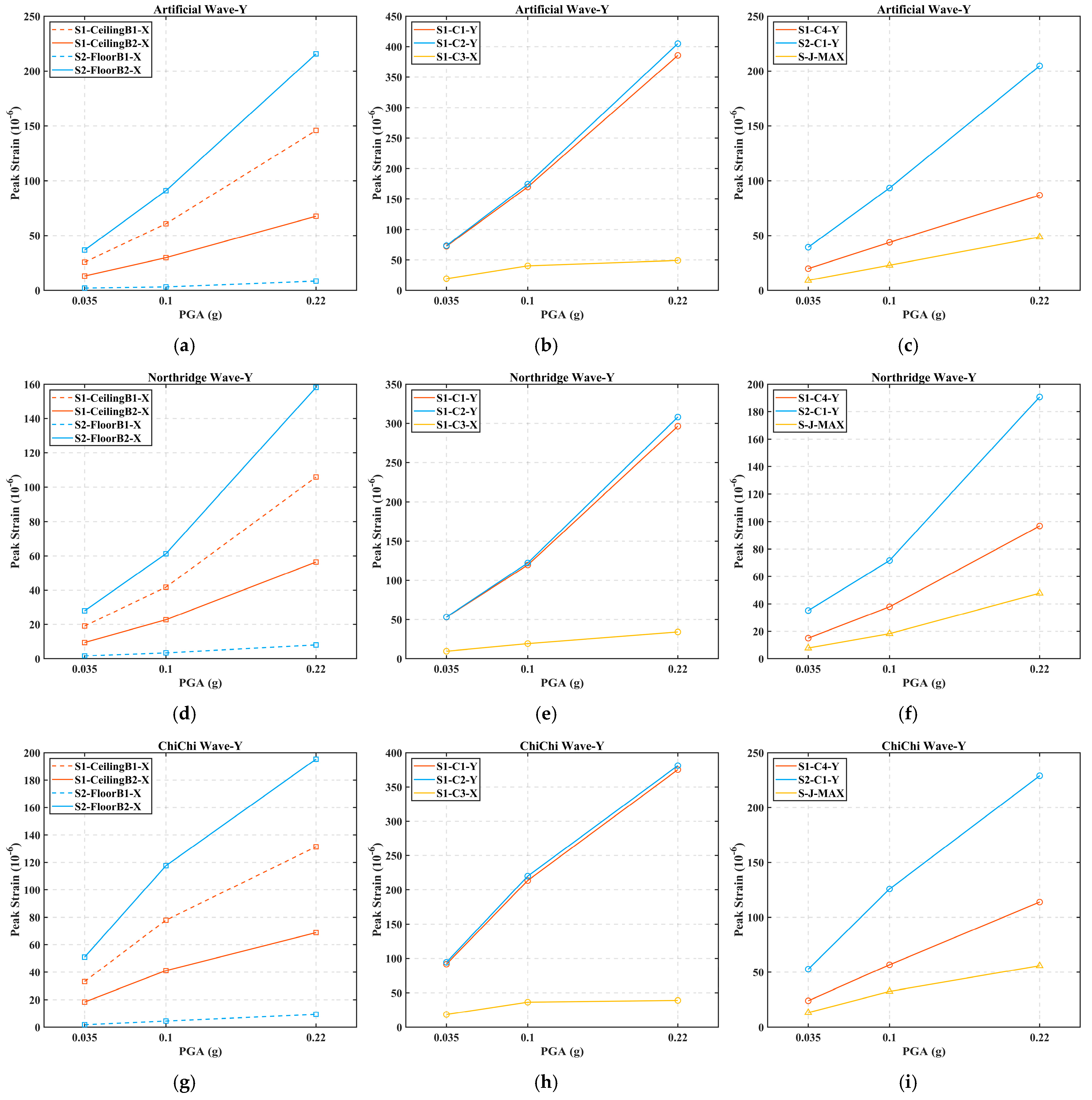
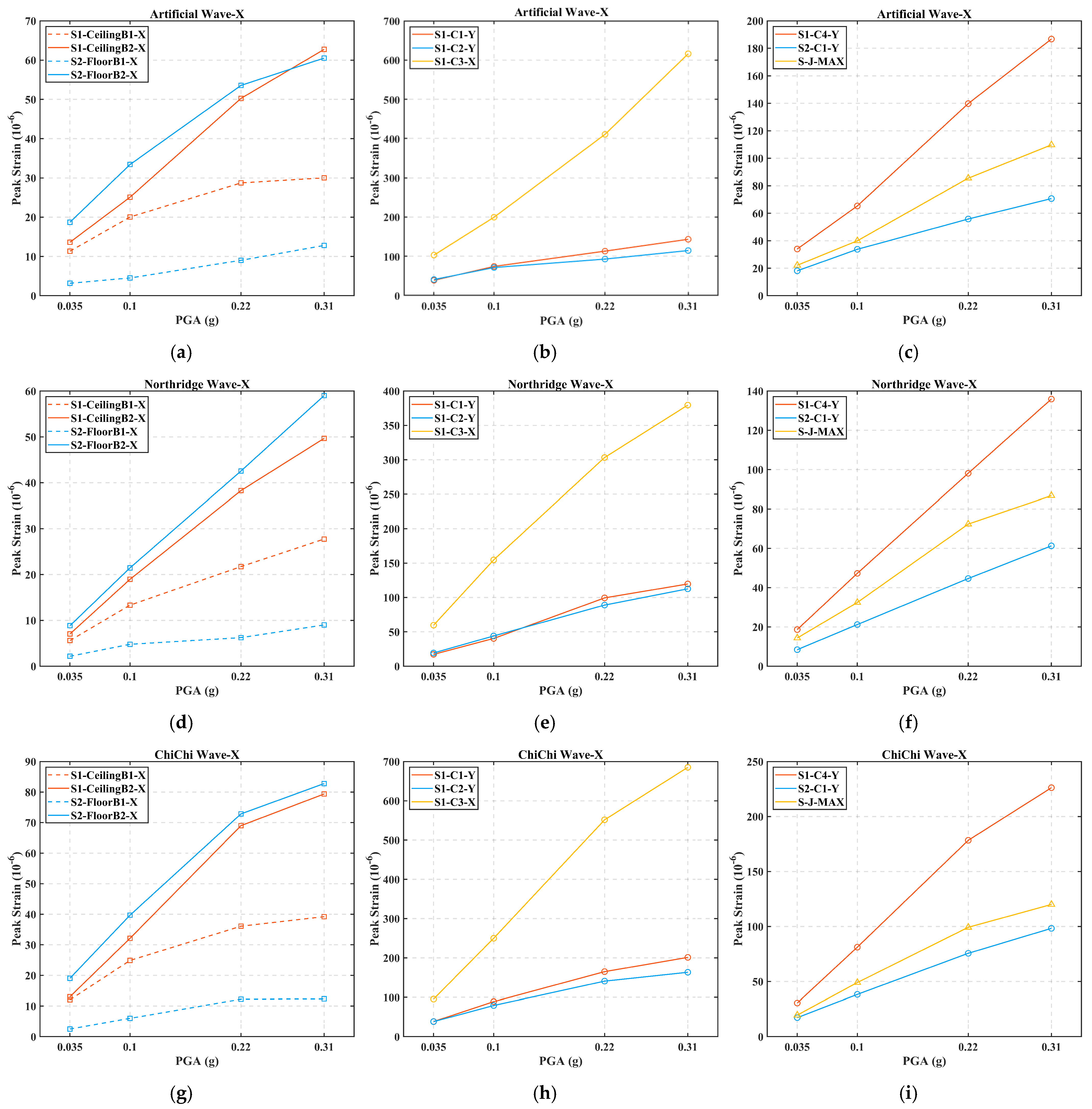
3.4. Strain Response
4. Finite Element Model Validation
4.1. Finite Element Modeling
4.2. Comparison of Acceleration Response: Tests vs. FEM
5. Conclusions
- (1)
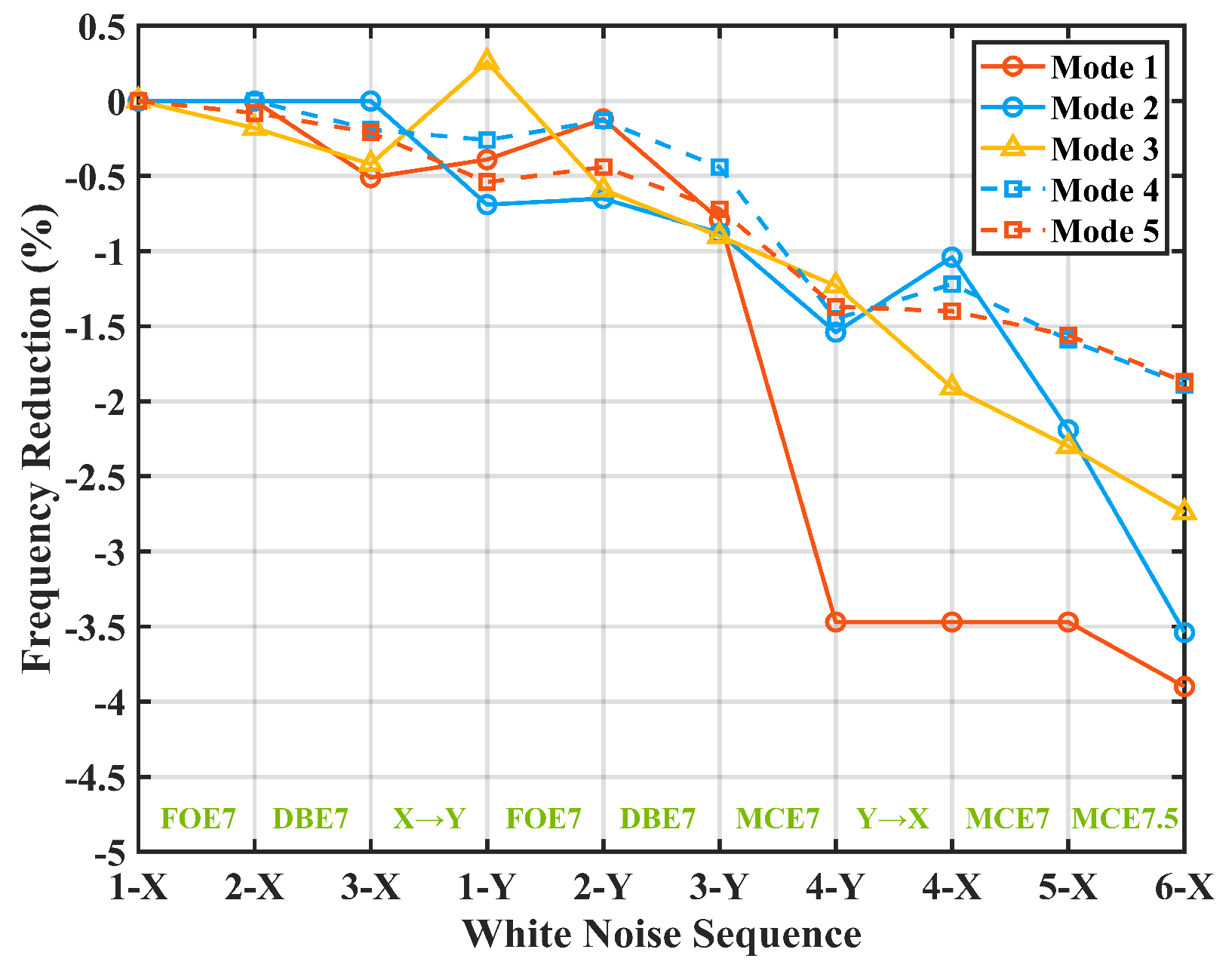
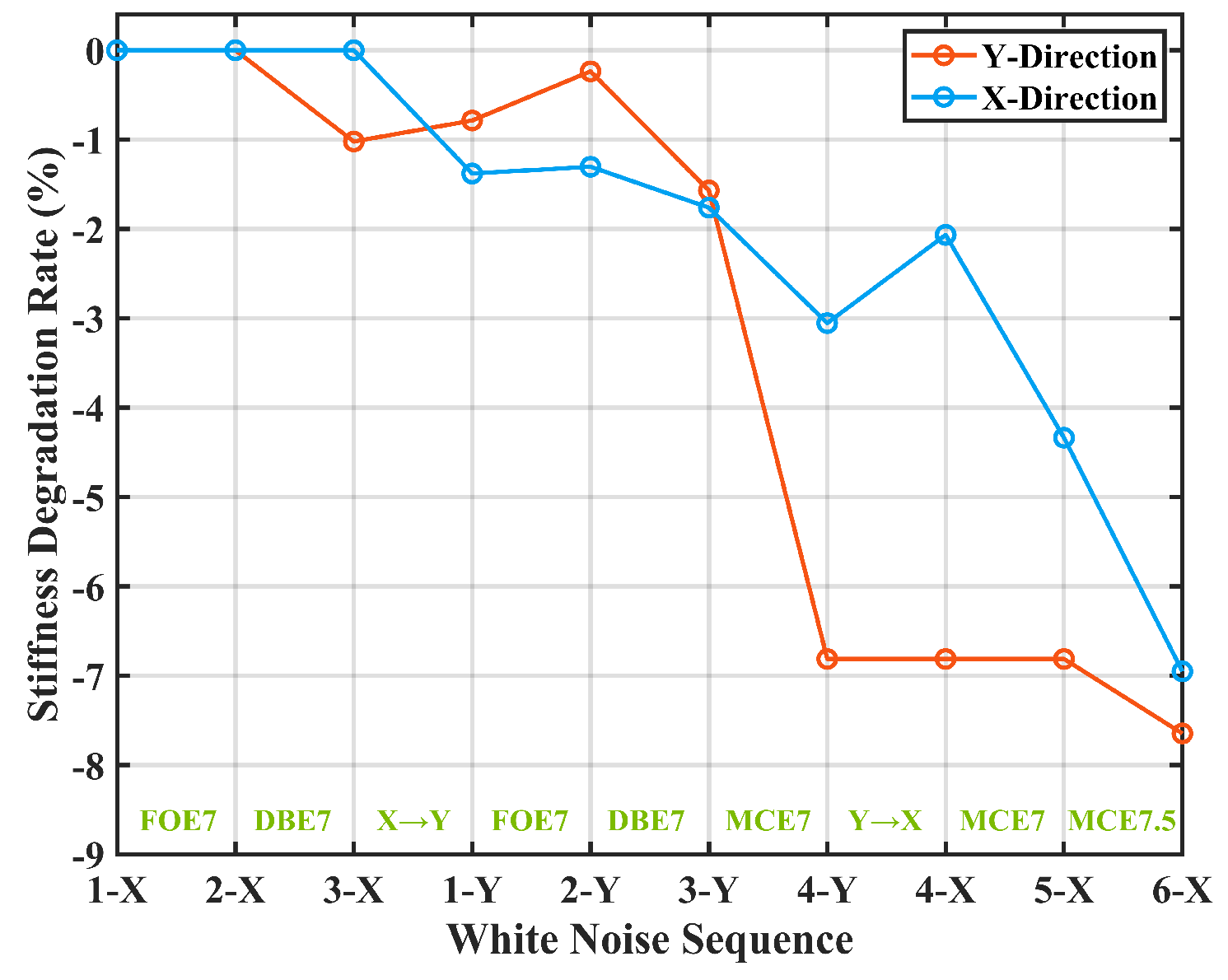
- The ambient vibration test, hammer test, and white noise test are all able to identify the natural frequencies of the structure, with discrepancies of less than 1.0%. The natural frequency decreases progressively with the intensity of seismic waves, especially earthquakes of MCE7 intensity or higher. The lower-order natural frequencies (f1 and f2) decrease by approximately 3.7%, while the higher-order natural frequencies (f4 and f5) decrease by about 1.9%. Thus, the structure has experienced a stiffness degradation, with the degradation rate in both principal directions being approximately 7.3%.
- (2)
- However, the strain values of all types of structural members remain below the yield strain, and the whole building is still in the elastic state. In the double-beam system, the floor beams bear approximately 50% greater seismic loads compared to the ceiling beams below them. The corner and edge columns exhibit good structural coordination in load resistance, because their strain amplitudes and variation trends are nearly consistent.
- (3)
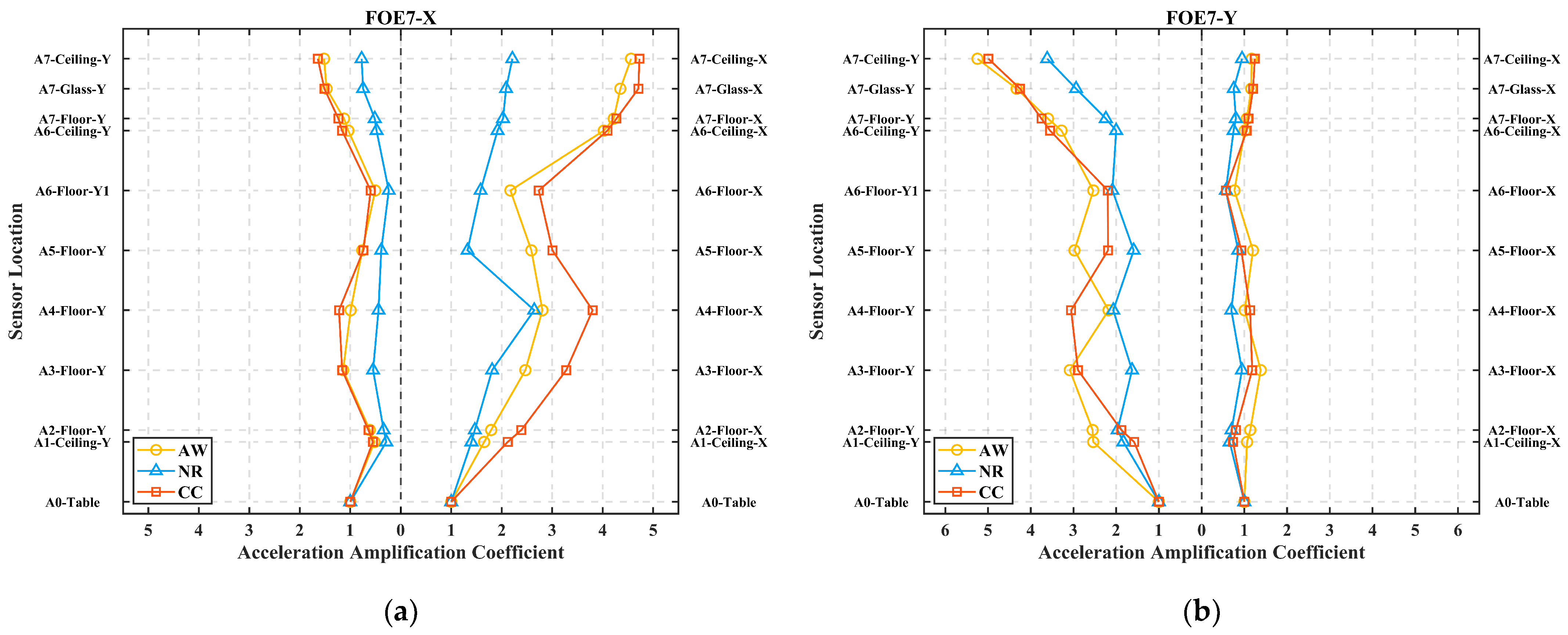
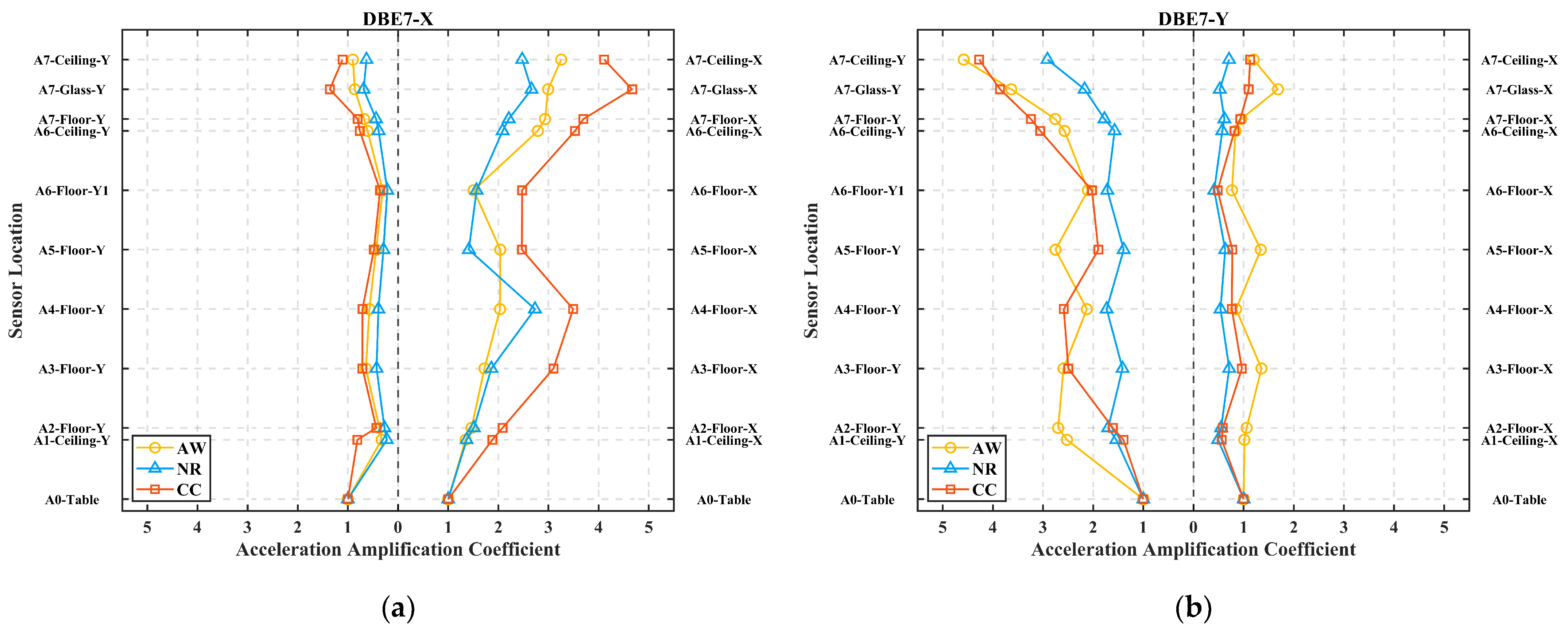
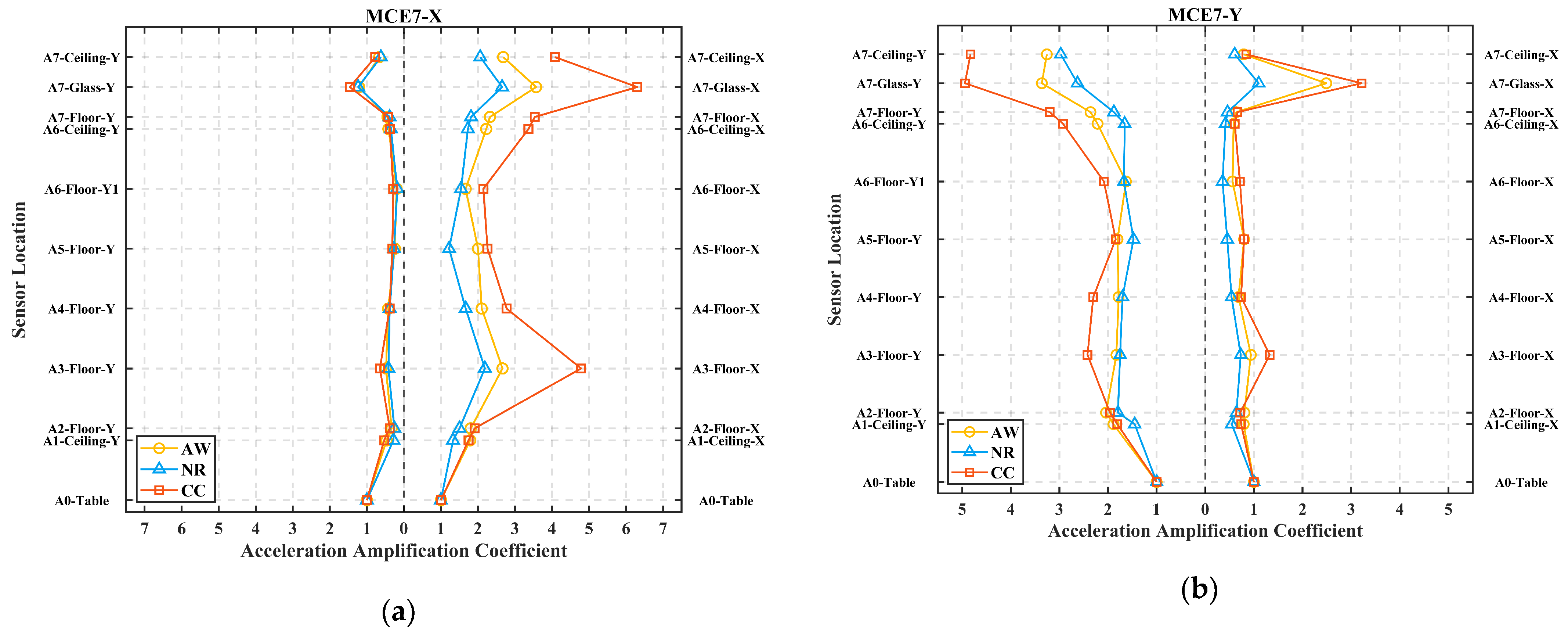
- In the global sense, the AACs exhibit an overall increasing trend with altitudes. However, this trend is not strictly monotonic, as certain upper locations exhibit smaller AAC values than the lower locations. S-shape amplification curves are observed under certain conditions. This phenomenon is also validated in the finite element simulations. In addition, the acceleration responses of the lower stories contain more modal components, while the acceleration responses of the upper stories are primarily governed by lower-order modes (f1 or f2). In the orthogonal direction across all stories, the responses are dominated by higher-order modes (f4 or f5).
- (4)
- In terms of the local response of glass curtain walls, as the seismic intensity increases, the AACs become more pronounced. This suggests that the glass curtain walls are more susceptible to intense vibration than the main structure. Even out-of-plane excitation can induce significant in-plane responses. Although the glass curtain walls inherently have high natural frequencies, their dynamic responses are dominated by the main structure.
- (a)
- On one hand, modular steel buildings exhibit relatively large PSA values. In design, it is advisable to consider adding lateral force-resisting members [33] or energy dissipation devices [29,43] to reduce the PSA. On the other hand, when applied to modular steel buildings, existing codes tend to underestimate the acceleration amplification effect (Section 3.2, about 9.3–23.2%). Additionally, the acceleration responses in the mid-to-lower stories of the structure also warrant attention.
- (b)
- Compared to the main steel frame, the glass curtain walls exhibit higher PSA values under strong seismic waves, posing a higher safety risk.
- (c)
- The structural seismic response is sensitive to the direction of input. For example, when the structure is excited by MCE7-CC but in different directions (X and Y), the measured strain data at gauge S1-C3-X vary by more than one order of magnitude. Therefore, it is recommended to use box-shaped sections in the design of modular steel structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, X.M. Research on Seismic Behavior and Design Method of Self-Lock Plug-in Joints in Modular Steel Construction. Ph.D. Thesis, Tianjin University, Tianjin, China, 21 May 2019. [Google Scholar]
- Deng, E.F.; Zong, L.; Ding, Y.; Zhang, Z.; Zhang, J.F.; Shi, F.W.; Cai, L.M.; Gao, S.C. Seismic performance of mid-to-high rise modular steel construction—A critical review. Thin-Walled Struct. 2020, 155, 106924. [Google Scholar] [CrossRef]
- Ding, Y.; Deng, E.F.; Zong, L.; Dai, X.M.; Li, Y.M.; Wang, H.P.; Bi, J.X. State-of-the-art on connection in modular steel construction. J. Build. Struct. 2019, 40, 33–40. [Google Scholar]
- Yang, C.; Wang, S.; Wang, X.; Zhao, B.; Wang, Q.; Ou, J. Seismic behavior of full-scale T-shaped joints connected by through-tie rod in MIC. J. Constr. Steel Res. 2022, 197, 107498. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Zhang, Z.; Wu, W. Experimental study on seismic cyclic behavior of an innovative blind bolted connection joint between modules in modular steel frame. Structures 2023, 52, 158–174. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. A comprehensive experimental-numerical investigation on the bending response of laminated double channel beams in modular buildings. Eng. Struct. 2019, 200, 109737. [Google Scholar] [CrossRef]
- Xu, B.; Xia, J.; Chang, H.; Ma, R.; Zhang, L. Flexural behaviour of pairs of laminated unequal channel beams with different interfacial connections in corner-supported modular steel buildings. Thin-Walled Struct. 2020, 154, 106792. [Google Scholar] [CrossRef]
- Ding, Y.; Deng, E.F.; Zong, L.; Dai, X.M.; Lou, N.; Chen, Y. Cyclic tests on corrugated steel plate shear walls with openings in modularized constructions. J. Constr. Steel Res. 2017, 138, 675–691. [Google Scholar] [CrossRef]
- Deng, E.F.; Zong, L.; Wang, H.P.; Shi, F.W.; Ding, Y. High efficiency analysis model for corrugated steel plate shear walls in modular steel construction. Thin-Walled Struct. 2020, 156, 106963. [Google Scholar] [CrossRef]
- Hou, J.; Wang, X.; Liu, J.; Chen, Z.; Zhong, X. Study on the stability bearing capacity of multi-column wall in modular steel building. Eng. Struct. 2020, 214, 110648. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, W. A hybrid coupled wall system with replaceable steel coupling beams for high-rise modular buildings. J. Build. Eng. 2020, 31, 101355. [Google Scholar] [CrossRef]
- Annan, C.D.; Youssef, M.A.; El Naggar, M.H. Seismic overstrength in braced frames of modular steel buildings. J. Earthq. Eng. 2008, 13, 1–21. [Google Scholar] [CrossRef]
- Annan, C.D.; Youssef, M.A.; El Naggar, M.H. Experimental evaluation of the seismic performance of modular steel-braced frames. Eng. Struct. 2009, 31, 1435–1446. [Google Scholar] [CrossRef]
- Annan, C.D.; Youssef, M.A.; El Naggar, M.H. Seismic vulnerability assessment of modular steel buildings. J. Earthq. Eng. 2009, 13, 1065–1088. [Google Scholar] [CrossRef]
- Hong, S.G.; Cho, B.H.; Chung, K.S.; Moon, J.H. Behavior of framed modular building system with double skin steel panels. J. Constr. Steel Res. 2011, 67, 936–946. [Google Scholar] [CrossRef]
- Fathieh, A.; Mercan, O. Three-Dimensional, Nonlinear, Dynamic Analysis of Modular Steel Buildings. In Structures Congress; ASCE: Boston, MA, USA, 2014. [Google Scholar]
- Fathieh, A.; Mercan, O. Seismic evaluation of modular steel buildings. Eng. Struct. 2016, 122, 83–92. [Google Scholar] [CrossRef]
- Landolfo, R.; Iuorio, O.; Fiorino, L. Experimental seismic performance evaluation of modular lightweight steel buildings within the ELISSA project. Earthq. Eng. Struct. Dyn. 2018, 47, 2921–2943. [Google Scholar] [CrossRef]
- Jing, J.; Clifton, G.C.; Roy, K.; Lim, J.B. Three-storey modular steel building with a novel slider device: Shake table tests on a scaled down model and numerical investigation. Thin-Walled Struct. 2020, 155, 106932. [Google Scholar] [CrossRef]
- Jing, J.; Clifton, G.C.; Roy, K.; Lim, J.B. Performance of a novel slider device in multi-storey cold-formed steel modular buildings under seismic loading. Structures 2020, 27, 212–246. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Z.; Liu, Y.; Bai, Y.; Zhong, X. Full-scale corner-supported modular steel structures with vertical inter-module connections under cyclic loading. J. Build. Eng. 2021, 44, 103269. [Google Scholar] [CrossRef]
- Sanches, R.; Tao, J.; Fathieh, A.; Mercan, O. Investigation of the seismic performance of braced low-, mid- and high-rise modular steel building prototypes. Eng. Struct. 2021, 234, 111986. [Google Scholar] [CrossRef]
- Zhai, X.; Zha, X.; Wang, K.; Wang, K.; Wang, H. Shake table tests of a full-scale two-story plate-type modular composite building with semi-rigid corner connections. Eng. Struct. 2023, 289, 116325. [Google Scholar] [CrossRef]
- Zhai, X.; Zha, X.; Chen, D. Shaking table tests on 0.5-scale multistory models of plate-type modular steel and composite buildings with semi-rigid corner connections. Thin-Walled Struct. 2023, 188, 110833. [Google Scholar] [CrossRef]
- Wang, C.; Chan, T.M. Seismic design and parametric study of steel modular frames with distributed seismic resistance. Thin-Walled Struct. 2023, 182, 110325. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, Y.; Qian, K.; Xie, X.; Zhao, M.; Zhao, Z.; Zheng, X.Y. Experimental investigation of the seismic behavior of a multi-story steel modular building using shaking table tests. Buildings 2025, 15, 2661. [Google Scholar] [CrossRef]
- Ye, Z.; Bu, H.; Liu, Z.; Lu, D.; Min, D.; Shan, H. Seismic resilience design of prefabricated modular pressurized buildings. Resilient Cities Struct. 2025, 4, 53–70. [Google Scholar] [CrossRef]
- Mata, R.; Nuñez, E.; Forcellini, D. Seismic resilience of composite moment frame buildings with slender built-up columns. J. Build. Eng. 2025, 111, 113532. [Google Scholar] [CrossRef]
- Mo, Z.; Lai, B.; Shu, G.; Yang, T.Y.; Ventura, C.E.; Liew, J.R. Enhancing seismic resilience in modular steel buildings through three-dimensional isolation. Eng. Struct. 2025, 323, 119269. [Google Scholar] [CrossRef]
- Zhou, X.; Yao, X.; Xu, L.; Shi, Y.; Ke, K.; Liu, L. Shake table tests on a full-scale six-storey cold-formed thin-walled steel-steel plate shear wall structure. Thin-Walled Struct. 2022, 181, 110009. [Google Scholar] [CrossRef]
- Wu, F.W.; Li, Y.Q. Large-scale shaking table tests of a six-story floor-by-floor assembled CFS frame-framing shear wall structure. Eng. Struct. 2023, 293, 116608. [Google Scholar] [CrossRef]
- Feng, L.Q.; Li, F.; Niu, C.L.; Wei, H.L.; Ji, S.Y.; Yang, P.; Wang, G.J. Design and shaking table test of a ten-storey building with steel plate shear walls partially connected to columns. J. Build. Eng. 2022, 49, 103982. [Google Scholar] [CrossRef]
- SJG 129-2023; Technical Specification for Steel Modular Buildings. Housing and Construction Bureau of Shenzhen Municipality: Shenzhen, China, 2023.
- GB 50017-2017; Standard for Design of Steel Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2017.
- GB 50009-2012; Load Code for the Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2012.
- GB/T 50018-2025; Technical Standard of Cold-Formed Steel Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2025.
- GB 50352-2019; Code for Design of Civil Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Chi, S.C.; Lin, S.S. Validation of Similitude Laws for Dynamic Structural Model Test. World Earthq. Eng. 2004, 20, 10. [Google Scholar]
- JGJ/T 101-2015; Specification for Seismic Test of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- Bakarji, J.; Callaham, J.; Brunton, S.L.; Kutz, J.N. Dimensionally consistent learning with Buckingham Pi. Nat. Comput. Sci. 2022, 2, 834–844. [Google Scholar] [CrossRef]
- Li, Z.Y. Shaking Table Test and Finite Element Optimization of Steel Frame Bent Structure with Buckling Restrained Brace. Master’s Thesis, Beijing University of Technology, Beijing, China, 22 June 2022. [Google Scholar]
- He, H.Q. Shaking Table Test and Simulation Analysis of High-Rise Steel Frame-Steel Plate Shear Wall Structure. Master’s Thesis, Chongqing University, Chongqing, China, 24 May 2021. [Google Scholar]
- Liu, L. Research on TMD Vibration Reduction and Vibration Table Test of High-Rise Structure. Master’s Thesis, Guangzhou University, Guangzhou, China, May 2019. [Google Scholar]
- Shi, F.; Wang, H.; Zong, L.; Ding, Y.; Su, J. Seismic behavior of high-rise modular steel constructions with various module layouts. J. Build. Eng. 2020, 31, 101396. [Google Scholar] [CrossRef]
- Yang, C.; Ou, J. Buckling Restrained Brace Steel Frame Modular Assembly Structure and Its Seismic Performance Analysis. J. Disaster Prev. Mitig. 2021, 41, 917–927+953. [Google Scholar]
- Wu, B.; Zhang, Y.; Zhang, A.; Wang, X.; Wang, N. RSF-SIFS limit state study and quantitative parametric analysis of miniature rubber bearings. Structures 2025, 76, 108955. [Google Scholar] [CrossRef]
- JGJ 102-2003; Technical Code for Glass Curtain Wall Engineering. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2003.
- GB/T 14683-2017; Silicone and Modified Silicone Sealants for Building. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China; China National Standardization Administration: Beijing, China, 2017.
- GB 50011-2010; Code for Seismic Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2016.
- GB 50981-2014; Code for Seismic Design of Mechanical and Electrical Equipment. Ministry of Housing and Urban-Rural Development of the People’s Republic of China; General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2014.
- JGJ 339-2015; Code for Seismic Design of Non-Structural Components. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2015.
- ASCE/SEI 7-16; Minimum Design Loads for Buildings and Other Structures. American Society of Civil Engineers: Reston, VA, USA, 2016.
- Eurocode 8; Design of Structures for Earthquake Resistance–Part 1: General Rules, Seismic Actions and Rules for Buildings. Commission of the European Communities; European Committee for Standardization: Brussels, Belgium, 2004.
- Shang, Q.X.; Zheng, J.Y.; Li, J.C.; Wang, T. Comparative study of relevant specifications on peak floor acceleration in current codes of different countries. Eng. Mech. 2020, 37, 91–96. [Google Scholar]
- Huang, B.; Hua, X.; Lu, W.; Zhang, Q. Floor acceleration amplification factor in the instrumented buildings under historical earth-quake excitations. China. Civ. Eng. J. 2020, 53, 16–27. [Google Scholar]
- Wang, D.; Lu, X.; Liu, Z. Shaking table test and comparison analysis for base-isolated high-rise buildings with different aspect ratios. J. Vib. Shock 2015, 34, 109–118. [Google Scholar]
- Zhang, Y.X.; Wu, B.L.; Zhang, A.L.; Li, Y.L.; Zhang, H.; Xiao, C.Y. Shaking table test and structural dynamic analysis for resilient steel frames with seismically isolated floor under bi-directional seismic action. J. Build. Eng. 2025, 46, 30–50. [Google Scholar]
- Montuori, R.; Nastri, E.; Piluso, V. Theory of plastic mechanism control: A new approach for the optimization of seismic resistant steel frames. Earthquake Eng. Struct. Dyn. 2022, 51, 3598–3619. [Google Scholar] [CrossRef]
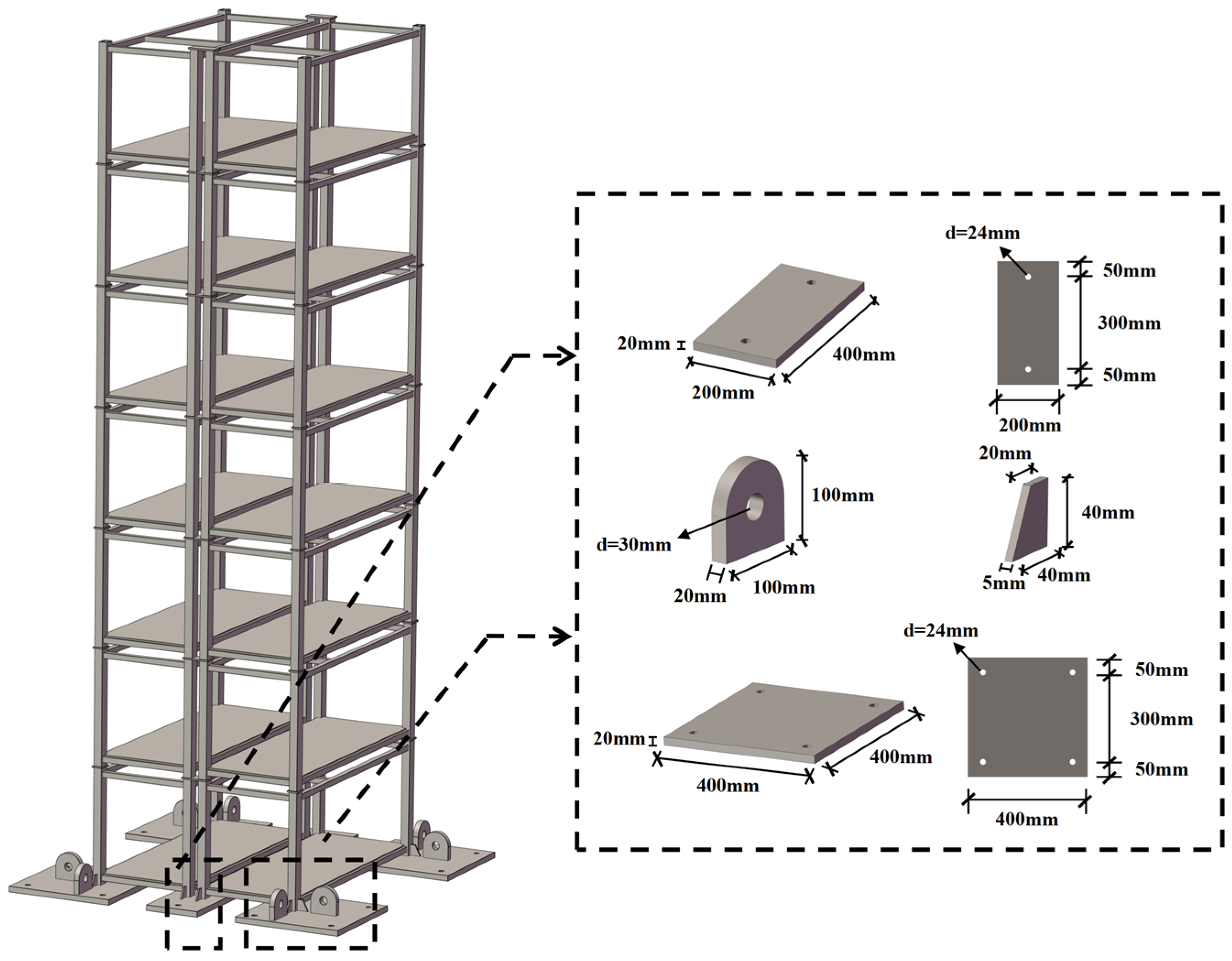

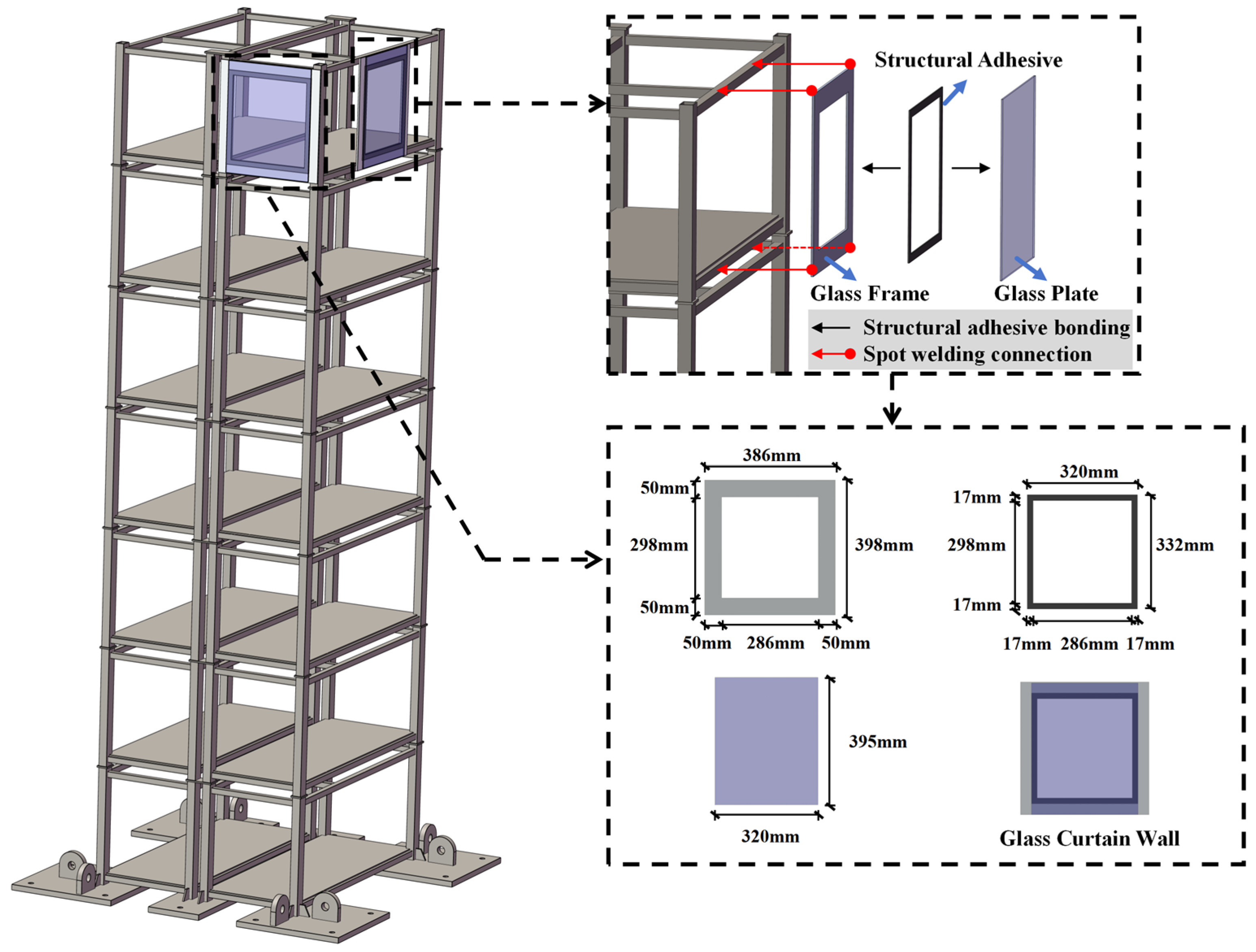
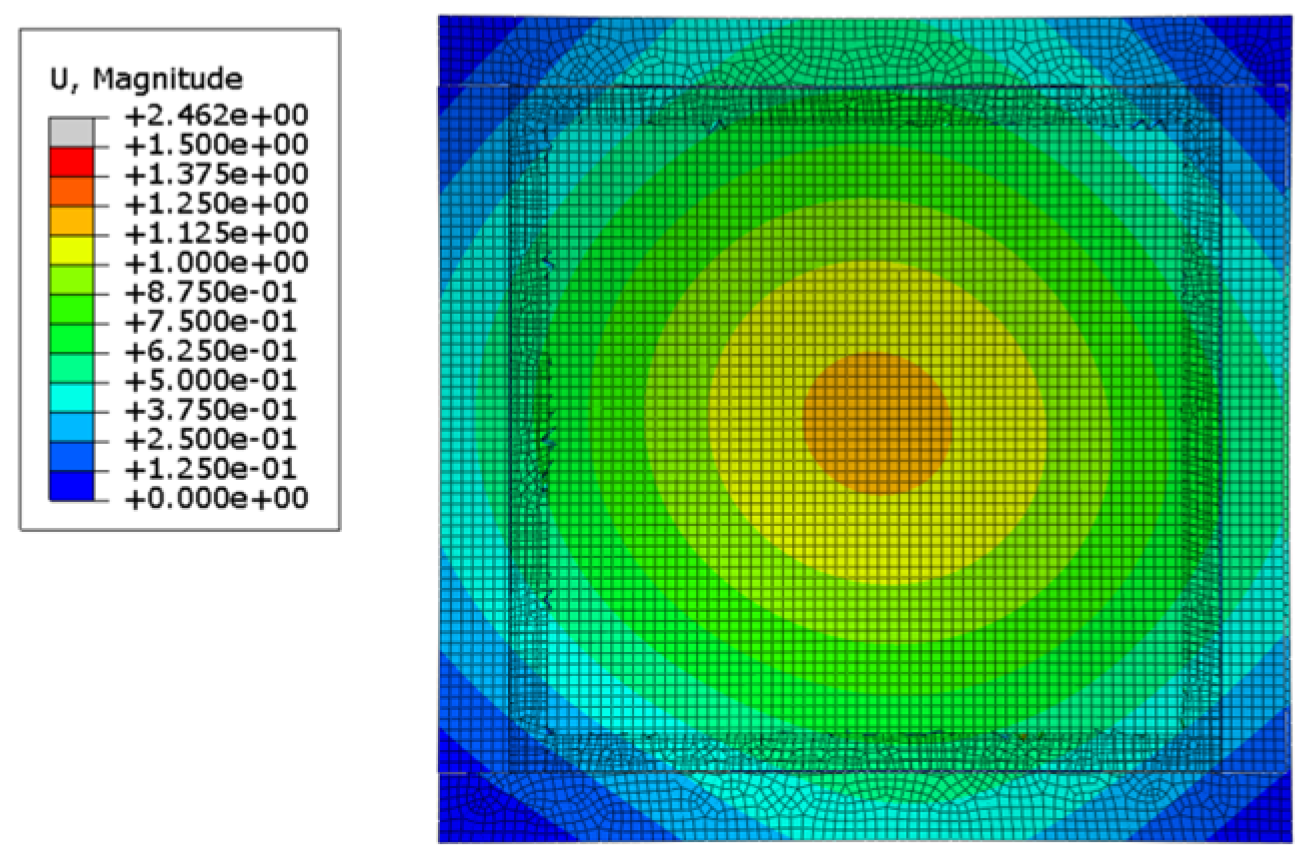



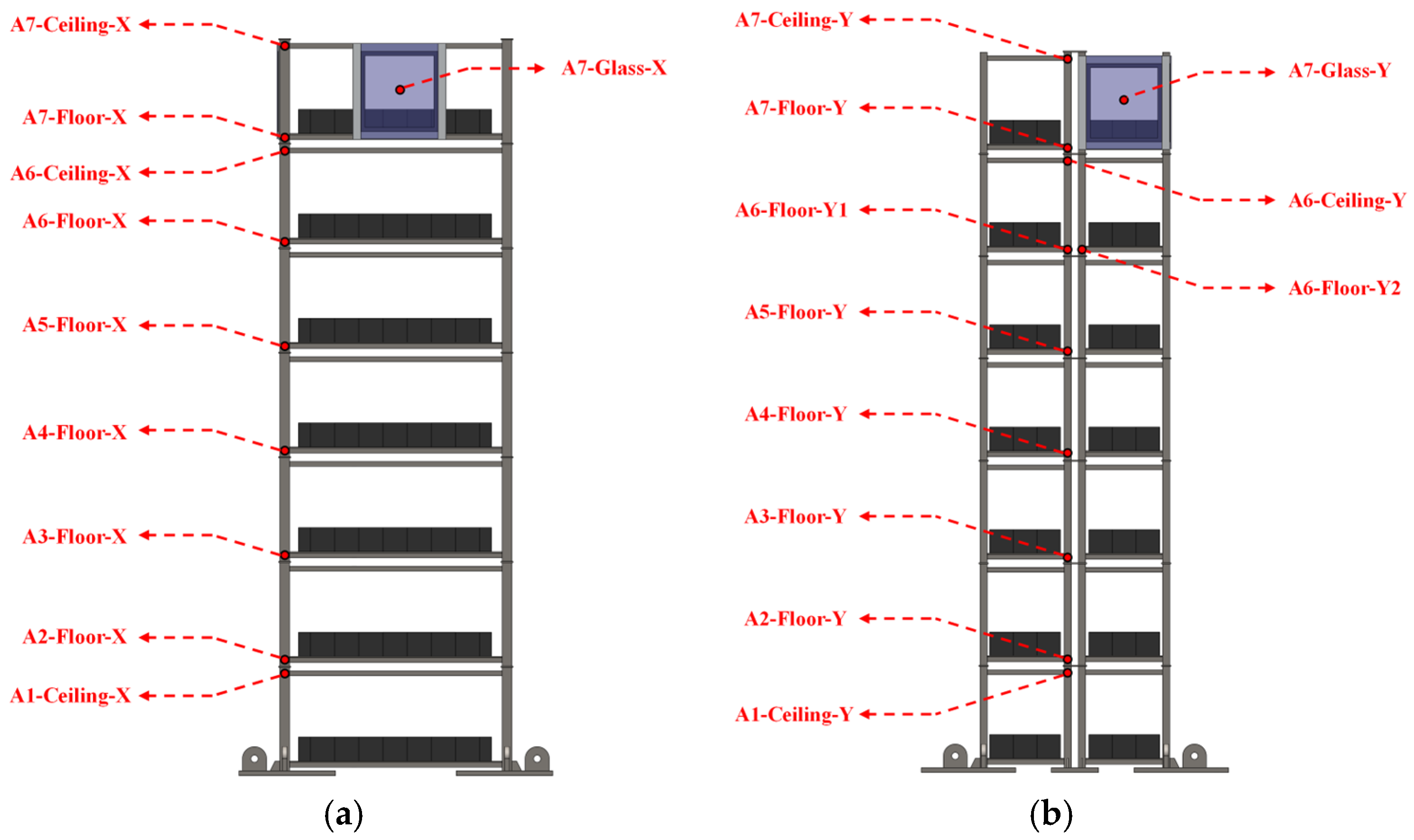

| Component Type | Prototype Section | Model Section |
|---|---|---|
| Column | Box-shaped, 250 × 450 × 16 | Box-shaped, 30 × 40 × 2.0 |
| Main beam—X | Box-shaped, 200 × 200 × 10 | Box-shaped, 20 × 20 × 2.0 |
| Main beam—Y | Box-shaped, 200 × 250 × 10 | Box-shaped, 20 × 20 × 2.0 |
| Secondary beam | Box-shaped, 150 × 200 × 10 | Box-shaped, 20 × 20 × 1.2 |
| Natural Frequency (Hz) | YJK | ABAQUS | Error | Mode Shape |
|---|---|---|---|---|
| Mode 1: f1 | 0.848 | 0.854 | 0.70% | Translation along the Y-axis |
| Mode 2: f2 | 0.873 | 0.877 | 0.46% | Translation along the X-axis |
| Mode 3: f3 | 1.117 | 1.213 | 7.91% | Torsion around the Z-axis |
| Mode 4: f4 | 2.691 | 2.668 | 0.86% | Translation along the X-axis |
| Mode 5: f5 | 2.833 | 2.868 | 1.22% | Translation along the Y-axis |
| Physical Parameter | Relationship | Scale Factor |
|---|---|---|
| Length | 1/9 | |
| Mass density | 9 | |
| Elastic modulus | 1 | |
| Poisson’s ratio | 1 | |
| Stress | 1 | |
| Mass | 1/81 | |
| Time | 1/3 | |
| Frequency | 3 | |
| Displacement | 1/9 | |
| Velocity | 1/3 | |
| Acceleration | 1 |
| Parameters | Scale Factor | Model | Prototype |
|---|---|---|---|
| X-direction length (m) | 1/9 | 0.802 | 7.22 |
| Y-direction length (m) | 1/9 | 0.961 | 8.65 |
| Height (m) | 1/9 | 3.033 | 27.30 |
| Elastic modulus (GPa) | 1/1 | 210 | 210 |
| Poisson’s ratio | 1/1 | 0.3 | 0.3 |
| Total mass (kg) | 1/81 | 2730.86 | 221,200.00 |
| Natural frequency—f1 (Hz) | 3/1 | 2.562 | 0.854 |
| Acceleration of gravity (m/s2) | 1/1 | 9.81 | 9.81 |
| Material | Elastic Modulus (MPa) | Density (kg/m3) | Poisson’s Ratio |
|---|---|---|---|
| Glass plate | 70,000 | 2500 | 0.20 |
| Structural adhesive | 0.8 | 1240 | 0.49 |
| Glass frame | 206,000 | 7800 | 0.30 |
| Design Value | Size (mm) | Mass (kg) | 1st Mode in ABAQUS (Hz) |
|---|---|---|---|
| Prototype | 2100 × 1200 × 15.5 | 97.65 | 34.85 |
| Scale calculation | - | 1.21 | 104.55 |
| Model | 395 × 320 × 3.85 | 1.22 | 107.01 |
| Error | - | 0.83% | 2.35% |
| Type | Design (kg) | Actual (kg) | Error |
|---|---|---|---|
| Main steel frame | 322.75 | 319.97 | 0.86% |
| Added mass | 2402.39 | 2415.00 | 0.52% |
| Glass curtain wall | 5.72 | 5.82 | 2.10% |
| Entire model | 2730.86 | 2740.79 | 0.36% |
| Type | Sensitivity (mv/g) | Amplitude Range (g) | Frequency Range (Hz) |
|---|---|---|---|
| AI-050 | 500 | 10 | 0.2–2500 |
| AI-100 | 1000 | 5 | 0.2–2000 |
| AI-500 | 5000 | 1 | 0.2–2000 |
| CA-YD-188T | 500 | 10 | 0.6–5000 |
| Type | Resistance (Ω) | Coefficient of Sensitivity | Limiting Strain (μm/m) |
|---|---|---|---|
| BMB120-5AA | 120 ± 0.5 | 2.11 ± 1% | 20,000 |
| BMB120-3CA | 120 ± 0.5 | 2.11 ± 1% | 20,000 |
| Specification | Parameter | Specification | Parameter |
|---|---|---|---|
| Voltage range | ±100 Mv~±10 V | Max sampling rate | 256 kHz |
| Voltage display error | ≤0.2% | Number of collection cards | 16 |
| Display stability | 0.05%/h | Number of data channels | 64 |
| Natural Frequency (Hz) | AVT-1 | AVT-2 | AVT-3 | AVT Mean Values | Hammer Test | Error |
|---|---|---|---|---|---|---|
| Mode 1: f1 | 2.560 | 2.547 | 2.540 | 2.549 | 2.553 | 0.16% |
| Mode 2: f2 | 2.624 | 2.607 | 2.608 | 2.613 | 2.620 | 0.27% |
| Mode 3: f3 | 4.576 | 4.578 | 4.599 | 4.584 | 4.586 | 0.04% |
| Mode 4: f4 | 8.641 | 8.641 | 8.580 | 8.621 | 8.675 | 0.62% |
| Mode 5: f5 | 8.737 | 8.732 | 8.751 | 8.740 | 8.765 | 0.29% |
| Parameter | Proto Design | Model Design | Model Measured | Error |
|---|---|---|---|---|
| Total mass (kg) | 221,200.00 | 2730.86 | 2740.79 | 0.36% |
| Mode 1: f1 (Hz) | 0.854 | 2.562 | 2.549 | 0.51% |
| Mode 2: f2 (Hz) | 0.877 | 2.631 | 2.613 | 0.68% |
| Mode 3: f3 (Hz) | 1.213 | 3.639 | 4.584 | 20.62% |
| Mode 4: f4 (Hz) | 2.668 | 8.004 | 8.621 | 7.16% |
| Mode 5: f5 (Hz) | 2.868 | 8.604 | 8.740 | 1.56% |
| Parameter | Proto Design | Model Design | Model Measured | Error |
|---|---|---|---|---|
| Mass (kg) | 97.65 | 1.21 | 1.23 | 1.65% |
| Mode 1: f1 (Hz) | 34.85 | 104.55 | 100.00 | 4.45% |
| Specification | Parameter Value | Specification | Parameter Value |
|---|---|---|---|
| Shaking direction | Unidirectional horizontal | Operating frequency | 0.1–50 Hz |
| Table size | 3 m × 3 m | Driving method | Electro-hydraulic |
| Load-bearing capacity | 15,000 kg | Max displacement | 150 mm |
| Overturning moment | 450 kN × m | Full load acceleration | 1.5 g |
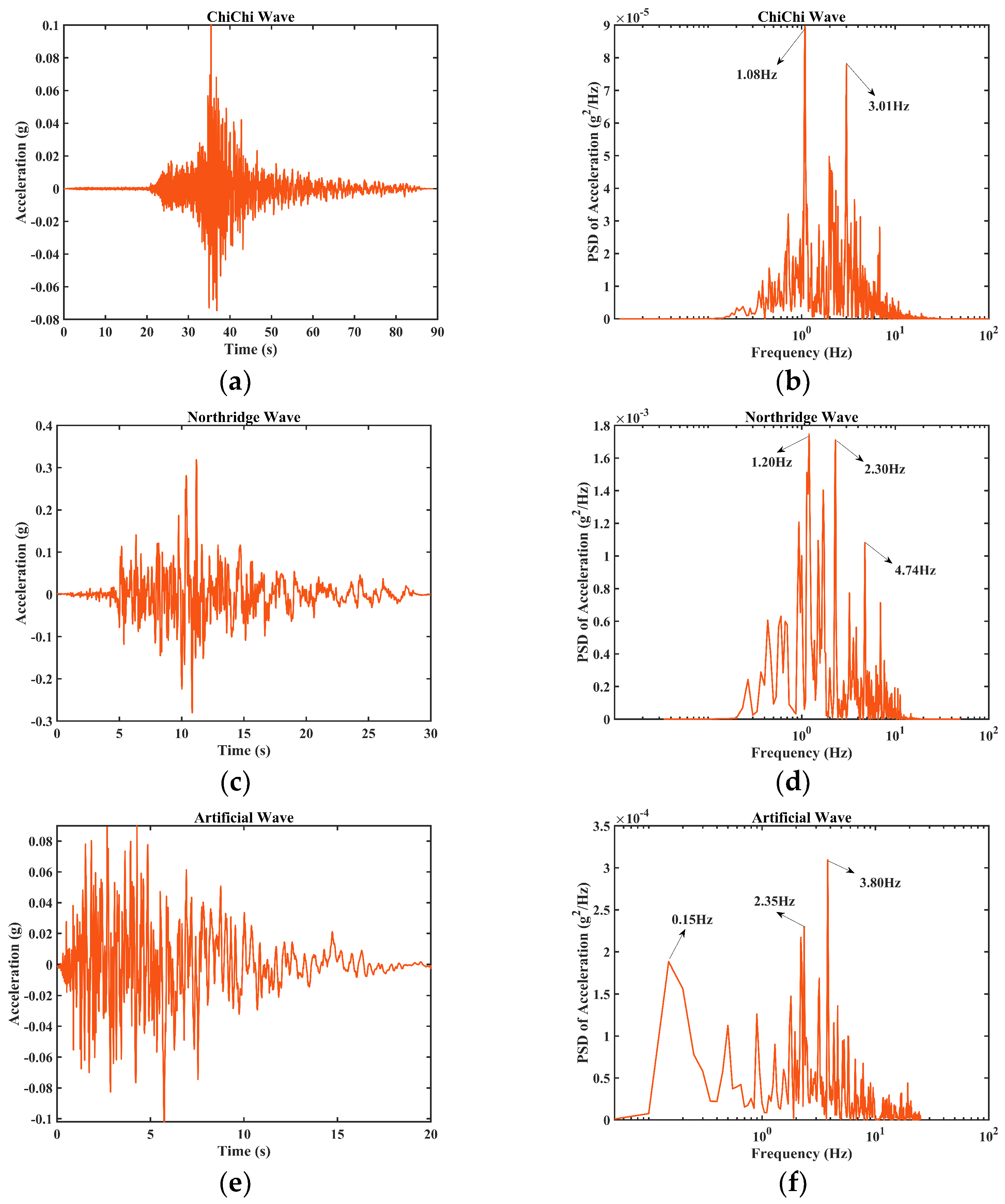
| Name | Magnitude | Duration (s) | Step Size (s) | Peak Frequency (Hz) | PGA (m/s2) |
|---|---|---|---|---|---|
| ChiChi wave (CC) | 7.6 | 88.985 | 0.005 | 0.100 | 1.08 |
| Northridge wave (NR) | 6.6 | 29.98 | 0.01 | 0.319 | 1.20 |
| Artificial wave (AW) | - | 20.00 | 0.02 | 0.102 | 3.80 |
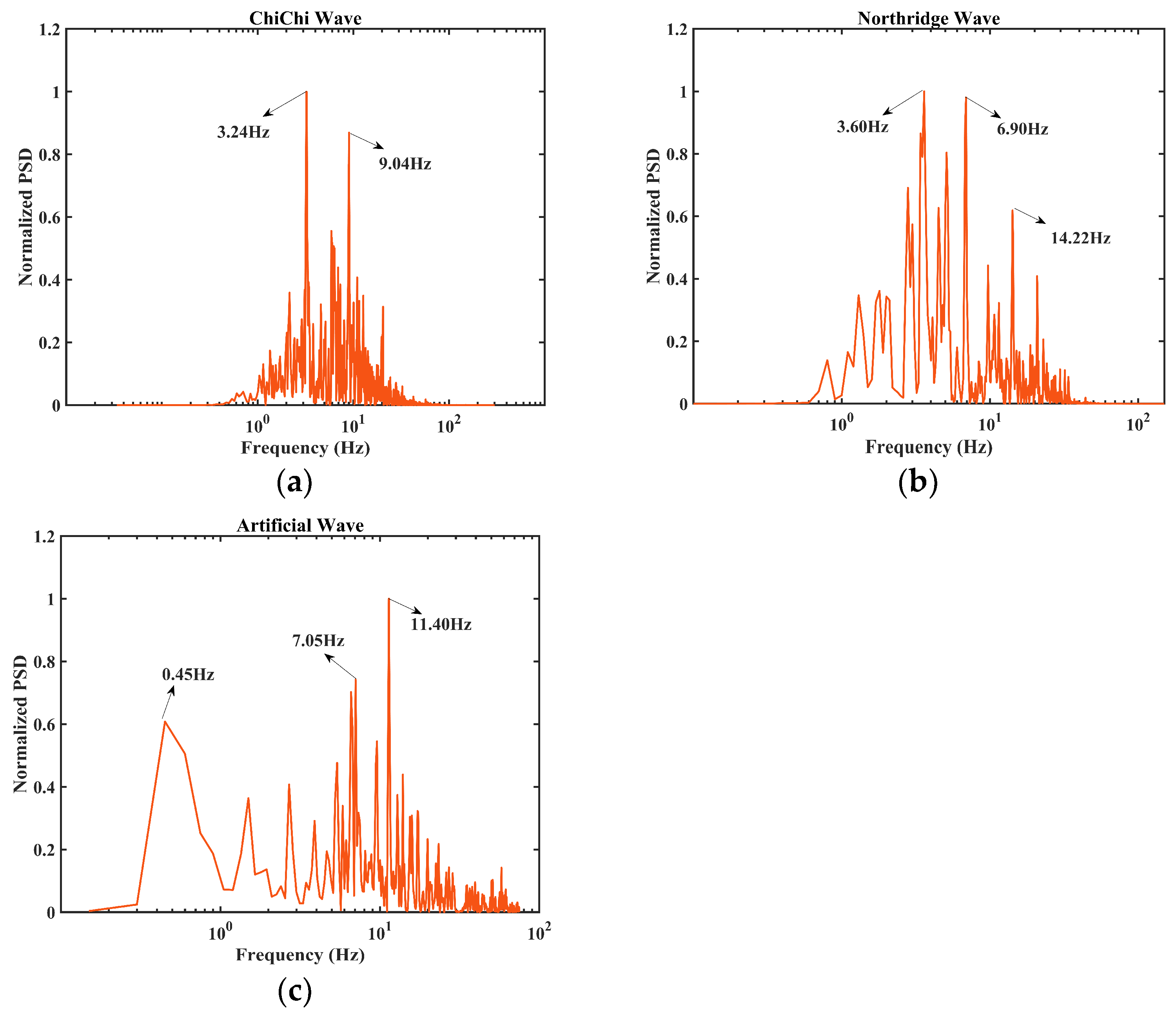
| Name | Effective Duration (s) | Entire Duration (s) | Step Size (s) | Spectral Peak Frequency (Hz) |
|---|---|---|---|---|
| ChiChi wave (CC) | 29.66 | 30.00 | 0.001 | 3.24 |
| Northridge wave (NR) | 9.99 | 10.00 | 0.001 | 3.60 |
| Artificial wave (AW) | 6.67 | 10.00 | 0.001 | 11.40 |
| Sequence | Loading Label | Seismic Wave | Input Direction | Intensity | PGA (g) |
|---|---|---|---|---|---|
| 1 | WN1-X | White Noise | X | - | - |
| 2 | AW-FOE7-X | Artificial Wave | X | FOE7 | 0.035 |
| 3 | NR-FOE7-X | Northridge Wave | X | FOE7 | 0.035 |
| 4 | CC-FOE7-X | ChiChi Wave | X | FOE7 | 0.035 |
| 5 | WN2-X | White Noise | X | - | - |
| 6 | AW-DBE7-X | Artificial Wave | X | DBE7 | 0.1 |
| 7 | NR-DBE7-X | Northridge Wave | X | DBE7 | 0.1 |
| 8 | CC-DBE7-X | ChiChi Wave | X | DBE7 | 0.1 |
| 9 | WN3-X | White Noise | X | - | - |
| 10 | WN1-Y | White Noise | Y | - | - |
| 11 | AW-FOE7-Y | Artificial Wave | Y | FOE7 | 0.035 |
| 12 | NR-FOE7-Y | Northridge Wave | Y | FOE7 | 0.035 |
| 13 | CC-FOE7-Y | ChiChi Wave | Y | FOE7 | 0.035 |
| 14 | WN2-Y | White Noise | Y | - | - |
| 15 | AW-DBE7-Y | Artificial Wave | Y | DBE7 | 0.1 |
| 16 | NR-DBE7-Y | Northridge Wave | Y | DBE7 | 0.1 |
| 17 | CC-DBE7-Y | ChiChi Wave | Y | DBE7 | 0.1 |
| 18 | WN3-Y | White Noise | Y | - | - |
| 19 | AW-MCE7-Y | Artificial Wave | Y | MCE7 | 0.22 |
| 20 | NR-MCE7-Y | Northridge Wave | Y | MCE7 | 0.22 |
| 21 | CC-MCE7-Y | ChiChi Wave | Y | MCE7 | 0.22 |
| 22 | WN4-Y | White Noise | Y | - | - |
| 23 | WN4-X | White Noise | X | - | - |
| 24 | AW-MCE7-X | Artificial Wave | X | MCE7 | 0.22 |
| 25 | NR-MCE7-X | Northridge Wave | X | MCE7 | 0.22 |
| 26 | CC-MCE7-X | ChiChi Wave | X | MCE7 | 0.22 |
| 27 | WN5-X | White Noise | X | - | - |
| 28 | AW-MCE7.5-X | Artificial Wave | X | MCE7.5 | 0.31 |
| 29 | NR-MCE7.5-X | Northridge Wave | X | MCE7.5 | 0.31 |
| 30 | CC-MCE7.5-X | ChiChi Wave | X | MCE7.5 | 0.31 |
| 31 | WN6-X | White Noise | X | - | - |
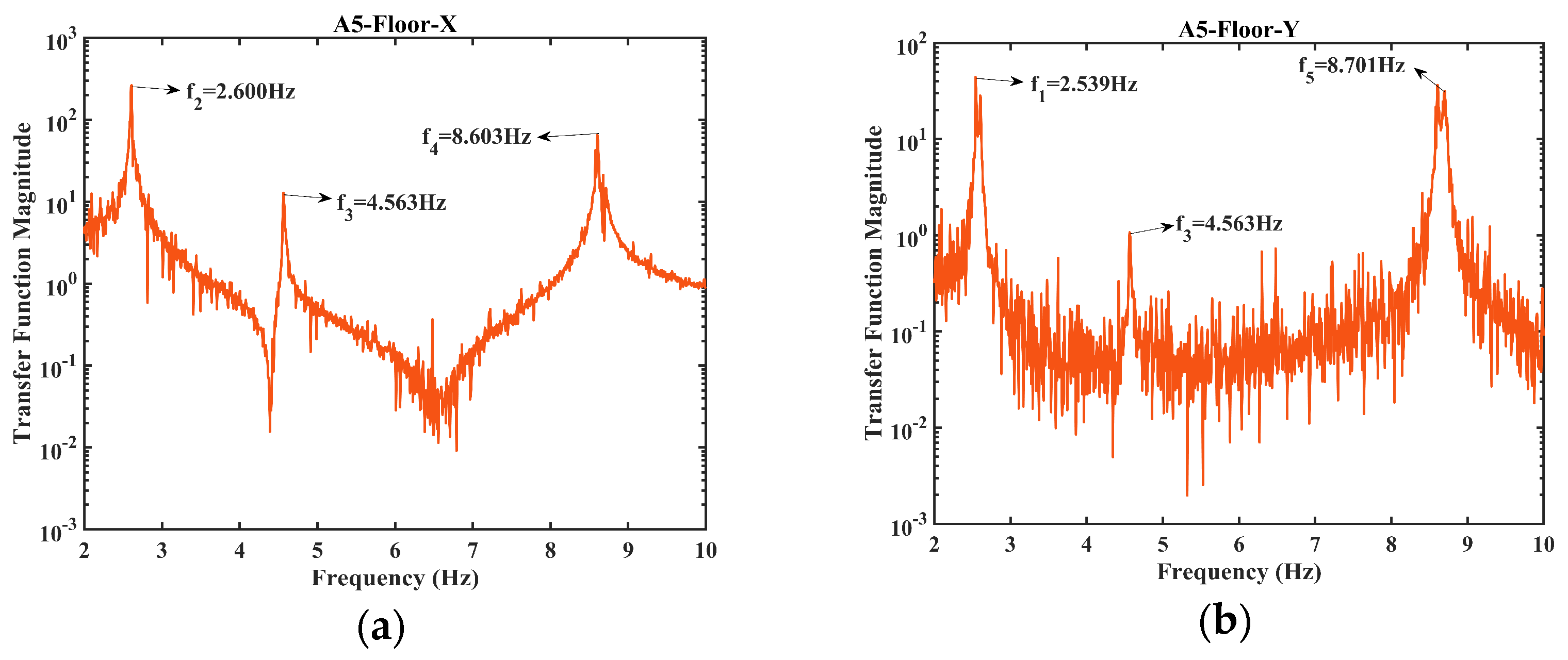
| Natural Frequency (Hz) | White Noise | AVT | Error | Hammer Test | Error |
|---|---|---|---|---|---|
| Mode 1: f1 | 2.539 | 2.549 | 0.39% | 2.553 | 0.55% |
| Mode 2: f2 | 2.600 | 2.613 | 0.50% | 2.620 | 0.77% |
| Mode 3: f3 | 4.563 | 4.584 | 0.46% | 4.586 | 0.50% |
| Mode 4: f4 | 8.603 | 8.621 | 0.21% | 8.675 | 0.84% |
| Mode 5: f5 | 8.701 | 8.740 | 0.45% | 8.765 | 0.74% |
| Natural Frequency (Hz) | Mode Shape | WN1-X | WN2-X | Reduction | |||
| Mode 1: f1 | Translation along the Y-axis | 2.539 | 2.539 | 0.00% | |||
| Mode 2: f2 | Translation along the X-axis | 2.600 | 2.600 | 0.00% | |||
| Mode 3: f3 | Torsion around the Z-axis | 4.563 | 4.555 | −0.18% | |||
| Mode 4: f4 | Translation along the X-axis | 8.603 | 8.603 | 0.00% | |||
| Mode 5: f5 | Translation along the Y-axis | 8.701 | 8.694 | −0.08% | |||
| WN3-X | Reduction | WN1-Y | Reduction | WN2-Y | Reduction | WN3-Y | Reduction |
| 2.526 | −0.51% | 2.529 | −0.39% | 2.536 | −0.12% | 2.519 | −0.79% |
| 2.600 | 0.00% | 2.582 | −0.69% | 2.583 | −0.65% | 2.577 | −0.88% |
| 4.544 | −0.42% | 4.575 | +0.26% | 4.536 | −0.59% | 4.522 | −0.90% |
| 8.587 | −0.19% | 8.581 | −0.26% | 8.592 | −0.13% | 8.565 | −0.44% |
| 8.683 | −0.21% | 8.654 | −0.54% | 8.663 | −0.44% | 8.638 | −0.72% |
| WN4-Y | Reduction | WN4-X | Reduction | WN5-X | Reduction | WN6-X | Reduction |
| 2.451 | −3.47% | 2.451 | −3.47% | 2.451 | −3.47% | 2.440 | −3.90% |
| 2.560 | −1.54% | 2.573 | −1.04% | 2.543 | −2.19% | 2.508 | −3.54% |
| 4.507 | −1.23% | 4.476 | −1.91% | 4.458 | −2.30% | 4.438 | −2.74% |
| 8.478 | −1.45% | 8.498 | −1.22% | 8.466 | −1.59% | 8.440 | −1.89% |
| 8.582 | −1.37% | 8.579 | −1.40% | 8.565 | −1.56% | 8.538 | −1.87% |
| Seismic Wave | A1-Ceiling | A2-Floor | A3-Floor | A4-Floor | A5-Floor | A6-Floor | A6-Ceiling | A7-Floor | A7-Glass | A7-Ceiling | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FOE7-X | AW | 1.65 | 1.79 | 2.47 | 2.81 | 2.59 | 2.17 | 4.02 | 4.22 | 4.35 | 4.56 |
| NR | 1.40 | 1.47 | 1.81 | 2.64 | 1.32 | 1.58 | 1.92 | 2.03 | 2.09 | 2.21 | |
| CC | 2.12 | 2.39 | 3.28 | 3.80 | 3.00 | 2.73 | 4.09 | 4.27 | 4.71 | 4.73 | |
| FOE7-Y | AW | 1.06 | 1.14 | 1.38 | 1.01 | 1.20 | 0.77 | 1.01 | 1.06 | 1.16 | 1.17 |
| NR | 0.66 | 0.70 | 0.94 | 0.70 | 0.86 | 0.57 | 0.75 | 0.80 | 0.75 | 0.95 | |
| CC | 0.73 | 0.80 | 1.18 | 1.13 | 0.93 | 0.57 | 1.05 | 1.10 | 1.20 | 1.25 | |
| DBE7-X | AW | 1.35 | 1.46 | 1.72 | 2.03 | 2.04 | 1.51 | 2.79 | 2.93 | 2.99 | 3.25 |
| NR | 1.37 | 1.51 | 1.86 | 2.73 | 1.41 | 1.57 | 2.09 | 2.21 | 2.66 | 2.48 | |
| CC | 1.88 | 2.08 | 3.10 | 3.49 | 2.47 | 2.47 | 3.53 | 3.70 | 4.67 | 4.11 | |
| DBE7-Y | AW | 1.01 | 1.06 | 1.36 | 0.85 | 1.34 | 0.77 | 0.84 | 0.95 | 1.68 | 1.20 |
| NR | 0.49 | 0.55 | 0.71 | 0.54 | 0.63 | 0.41 | 0.57 | 0.62 | 0.52 | 0.71 | |
| CC | 0.56 | 0.59 | 0.97 | 0.76 | 0.77 | 0.48 | 0.82 | 0.93 | 1.10 | 1.13 | |
| MCE7-X | AW | 1.79 | 1.81 | 2.66 | 2.10 | 2.00 | 1.67 | 2.22 | 2.32 | 3.57 | 2.68 |
| NR | 1.33 | 1.50 | 2.19 | 1.67 | 1.22 | 1.54 | 1.73 | 1.81 | 2.65 | 2.06 | |
| CC | 1.75 | 1.91 | 4.79 | 2.78 | 2.26 | 2.15 | 3.36 | 3.53 | 6.30 | 4.08 | |
| MCE7-Y | AW | 0.79 | 0.80 | 0.94 | 0.68 | 0.80 | 0.56 | 0.58 | 0.64 | 2.49 | 0.79 |
| NR | 0.54 | 0.64 | 0.73 | 0.54 | 0.45 | 0.36 | 0.42 | 0.46 | 1.10 | 0.60 | |
| CC | 0.74 | 0.72 | 1.32 | 0.74 | 0.80 | 0.71 | 0.61 | 0.66 | 3.21 | 0.85 | |
| MCE7.5-X | AW | 2.27 | 2.49 | 2.35 | 2.37 | 2.12 | 1.55 | 2.13 | 2.29 | 3.60 | 2.78 |
| NR | 1.37 | 1.37 | 1.60 | 1.40 | 1.10 | 1.48 | 1.49 | 1.58 | 2.28 | 1.84 | |
| CC | 1.44 | 1.69 | 3.13 | 2.20 | 1.87 | 1.90 | 2.81 | 2.93 | 4.74 | 3.39 | |
| Seismic Wave | A1-Ceiling | A2-Floor | A3-Floor | A4-Floor | A5-Floor | A6-Floor | A6-Ceiling | A7-Floor | A7-Glass | A7-Ceiling | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FOE7-X | AW | 0.52 | 0.61 | 1.14 | 0.99 | 0.76 | 0.51 | 1.04 | 1.12 | 1.47 | 1.52 |
| NR | 0.29 | 0.34 | 0.55 | 0.44 | 0.39 | 0.24 | 0.48 | 0.51 | 0.75 | 0.77 | |
| CC | 0.55 | 0.64 | 1.16 | 1.22 | 0.74 | 0.60 | 1.16 | 1.23 | 1.51 | 1.64 | |
| FOE7-Y | AW | 2.54 | 2.55 | 3.09 | 2.18 | 2.98 | 2.54 | 3.28 | 3.60 | 4.33 | 5.25 |
| NR | 1.83 | 1.97 | 1.63 | 2.07 | 1.59 | 2.09 | 2.00 | 2.24 | 2.94 | 3.61 | |
| CC | 1.58 | 1.88 | 2.89 | 3.05 | 2.19 | 2.20 | 3.55 | 3.75 | 4.25 | 4.99 | |
| DBE7-X | AW | 0.33 | 0.37 | 0.64 | 0.57 | 0.44 | 0.31 | 0.61 | 0.68 | 0.86 | 0.90 |
| NR | 0.22 | 0.27 | 0.43 | 0.39 | 0.29 | 0.21 | 0.39 | 0.44 | 0.69 | 0.63 | |
| CC | 0.81 | 0.43 | 0.71 | 0.71 | 0.48 | 0.36 | 0.76 | 0.80 | 1.36 | 1.11 | |
| DBE7-Y | AW | 2.52 | 2.70 | 2.59 | 2.13 | 2.75 | 2.10 | 2.57 | 2.76 | 3.63 | 4.58 |
| NR | 1.54 | 1.70 | 1.41 | 1.73 | 1.39 | 1.72 | 1.57 | 1.78 | 2.17 | 2.91 | |
| CC | 1.40 | 1.61 | 2.50 | 2.59 | 1.90 | 2.02 | 3.06 | 3.24 | 3.86 | 4.27 | |
| MCE7-X | AW | 0.47 | 0.33 | 0.48 | 0.42 | 0.25 | 0.20 | 0.42 | 0.44 | 1.21 | 0.66 |
| NR | 0.28 | 0.26 | 0.42 | 0.38 | 0.27 | 0.18 | 0.35 | 0.38 | 1.24 | 0.62 | |
| CC | 0.53 | 0.38 | 0.65 | 0.39 | 0.31 | 0.29 | 0.38 | 0.42 | 1.46 | 0.77 | |
| MCE7-Y | AW | 1.89 | 2.04 | 1.83 | 1.78 | 1.80 | 1.63 | 2.22 | 2.36 | 3.36 | 3.26 |
| NR | 1.45 | 1.80 | 1.75 | 1.70 | 1.48 | 1.67 | 1.66 | 1.88 | 2.63 | 2.97 | |
| CC | 1.81 | 1.96 | 2.42 | 2.30 | 1.84 | 2.08 | 2.92 | 3.20 | 4.94 | 4.83 | |
| MCE7.5-X | AW | 1.05 | 0.45 | 0.52 | 0.35 | 0.24 | 0.23 | 0.35 | 0.36 | 1.15 | 0.58 |
| NR | 0.70 | 0.36 | 0.43 | 0.28 | 0.22 | 0.14 | 0.28 | 0.28 | 0.78 | 0.65 | |
| CC | 0.85 | 0.43 | 0.57 | 0.28 | 0.25 | 0.30 | 0.32 | 0.27 | 2.51 | 0.52 | |
| Current Codes | A1-Ceiling | A2-Floor | A3-Floor | A4-Floor | A5-Floor | A6-Floor | A6-Ceiling | A7-Floor | A7-Glass | A7-Ceiling |
|---|---|---|---|---|---|---|---|---|---|---|
| GB 50011-2010 [49]; GB 50981-2014 [50]; JGJ 339-2015 [51] AAC = 1 + z/h | 1.14 | 1.16 | 1.30 | 1.44 | 1.58 | 1.73 | 1.85 | 1.87 | 1.94 | 2.00 |
| ASCE 7-16 [52] AAC = 1 + 2z/h | 1.28 | 1.32 | 1.60 | 1.88 | 2.16 | 2.46 | 2.70 | 2.74 | 2.88 | 3.00 |
| Eurocode 8 [53] AAC = 1 + 3z/2h | 1.21 | 1.24 | 1.45 | 1.66 | 1.87 | 2.10 | 2.28 | 2.31 | 2.41 | 2.50 |
| AAC | Modular Steel Structure | Conventional Steel Structure [56] | Difference |
|---|---|---|---|
| 1st ceiling | 1.81 | 1.25 | 44.8% |
| 4th floor | 2.30 | 1.65 | 39.4% |
| 5th floor | 2.08 | 1.40 | 48.6% |
| 7th ceiling | 4.83 | 2.40 | 101.3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nie, Y.; Zhang, X.; Zheng, X.Y.; Xie, X.; Qian, K.; Li, Y.; Zhao, Z.; Xu, W. Seismic Performance of a Modular Steel Building with Glass Curtain Walls: Shaking Table Tests. Sustainability 2025, 17, 9443. https://doi.org/10.3390/su17219443
Nie Y, Zhang X, Zheng XY, Xie X, Qian K, Li Y, Zhao Z, Xu W. Seismic Performance of a Modular Steel Building with Glass Curtain Walls: Shaking Table Tests. Sustainability. 2025; 17(21):9443. https://doi.org/10.3390/su17219443
Chicago/Turabian StyleNie, Yucong, Xinxin Zhang, Xiang Yuan Zheng, Xinyu Xie, Kehao Qian, Yuanting Li, Zhan Zhao, and Wenjun Xu. 2025. "Seismic Performance of a Modular Steel Building with Glass Curtain Walls: Shaking Table Tests" Sustainability 17, no. 21: 9443. https://doi.org/10.3390/su17219443
APA StyleNie, Y., Zhang, X., Zheng, X. Y., Xie, X., Qian, K., Li, Y., Zhao, Z., & Xu, W. (2025). Seismic Performance of a Modular Steel Building with Glass Curtain Walls: Shaking Table Tests. Sustainability, 17(21), 9443. https://doi.org/10.3390/su17219443






