Characterizing the Evolution of Multi-Scale Communities in Urban Road Networks
Abstract
1. Introduction
2. Data and Methodology
2.1. Study Area and Data
2.2. Traffic-Data-Driven Urban Road Network Modeling
2.2.1. Dual-Graph Representation of Urban Road Networks
2.2.2. Data Matching of Road Segments
2.2.3. Dynamic Time Warping Weighting
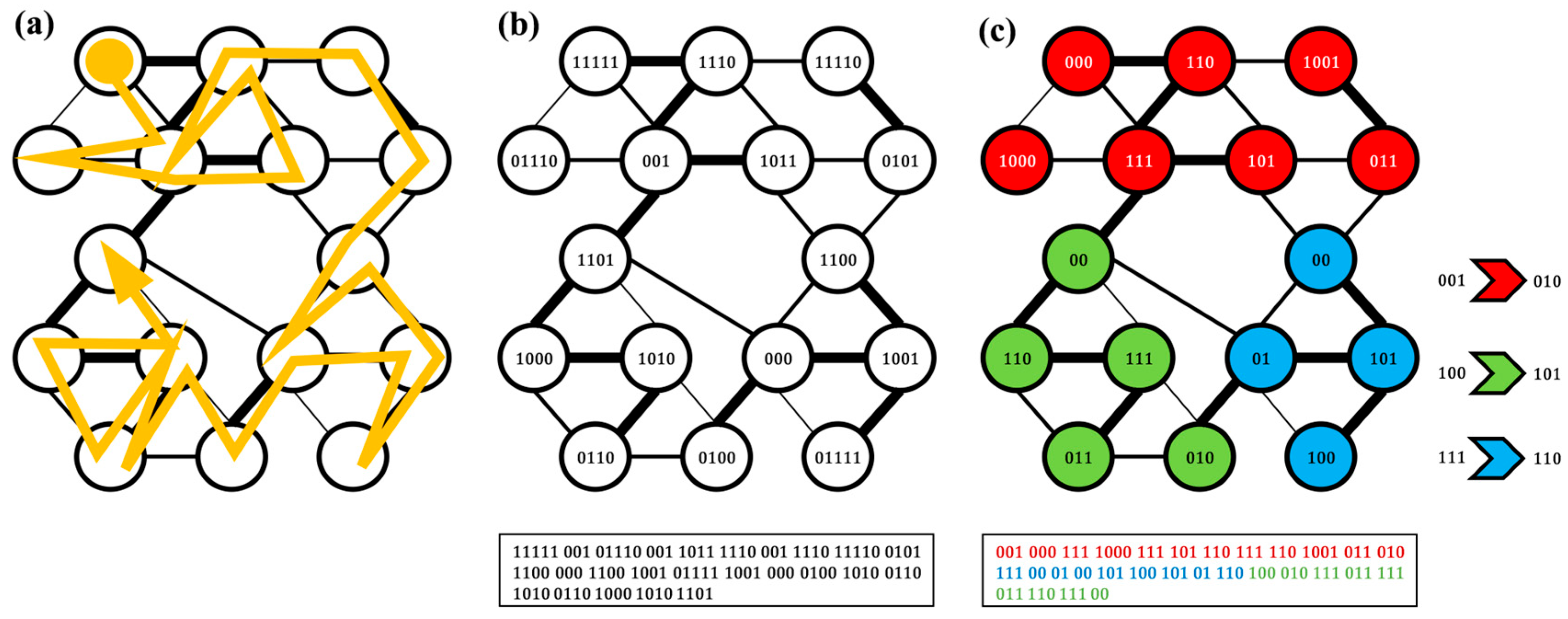
2.3. Multi-Scale Community Detection
- (1)
- In the initial stage of the first phase, each node is assigned to a separate module.
- (2)
- Then, in a random order, nodes are reassigned to the adjacent module that can reduce to the greatest extent.
- (3)
- Step 2 is repeated in a new random order each time until no further reduction in the value of is achievable through node movement, thereby obtaining one-level community detection results.
- (4)
- Based on the results of step 3, a new network is constructed. Each node in the new network represents a community from the original network. The weight of each new edge is calculated as the sum of the weights of the corresponding original edges. Steps 1 to 3 are then repeated on the new network to obtain more level community detection results.
- (5)
- Step 4 is repeated until the value of in the new network can no longer be reduced. Finally, the algorithm outputs the multi-scale hierarchical community detection results of the network, as illustrated in Figure 6.
3. Results and Discussion
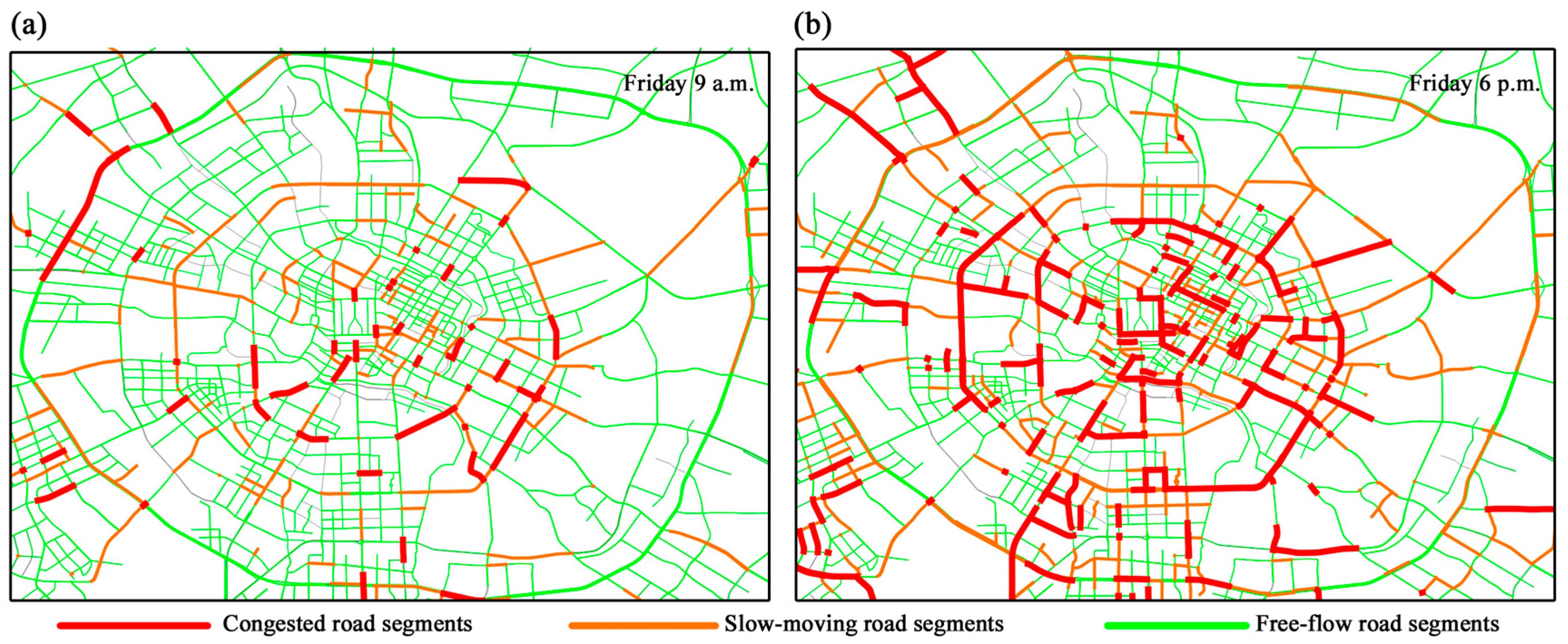
3.1. Statistical Characteristics of Urban Road Traffic
3.2. Multi-Scale Community Detection Results for the Chengdu Road Network
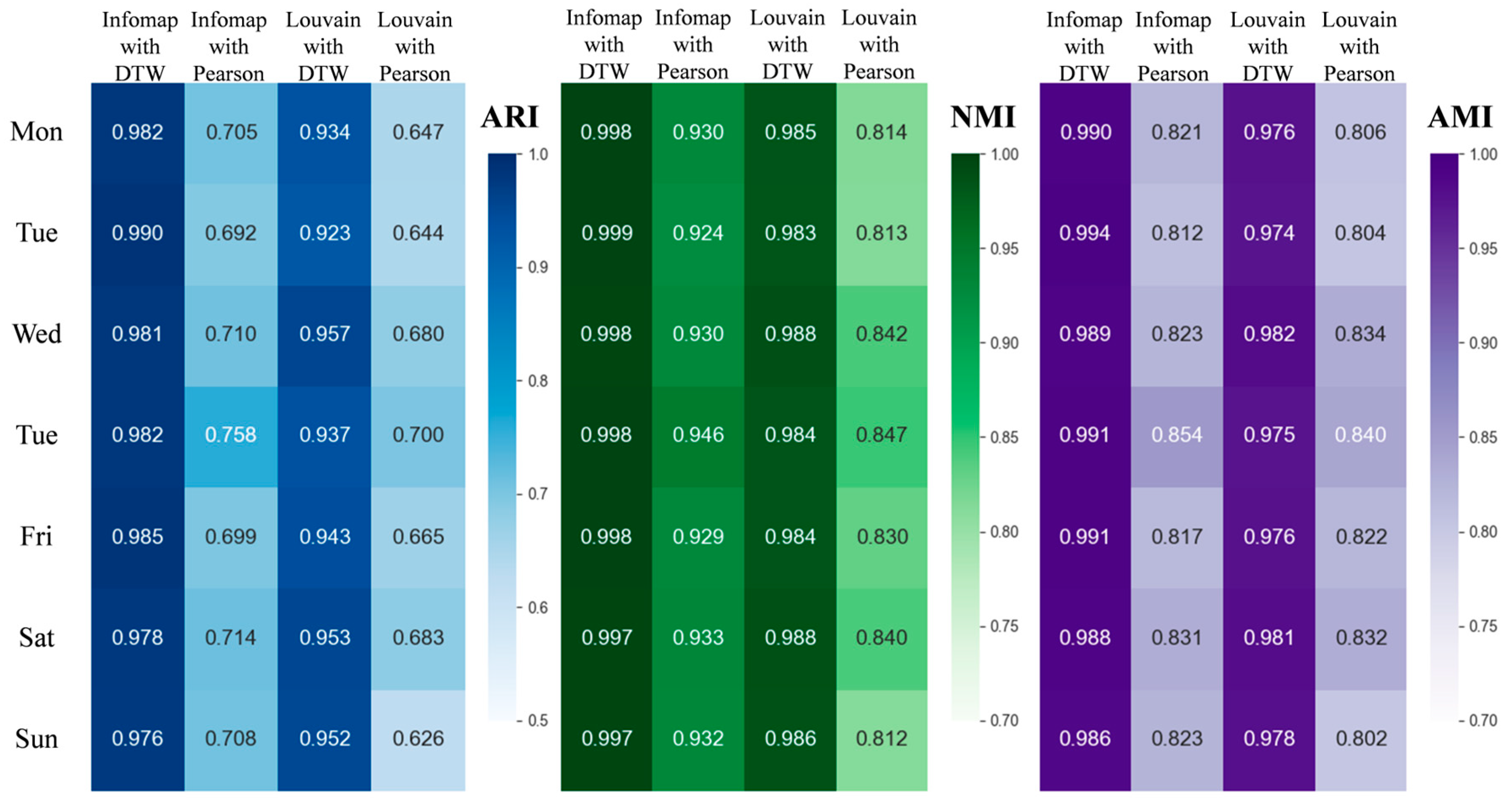
3.3. Robustness of Community Detection Results
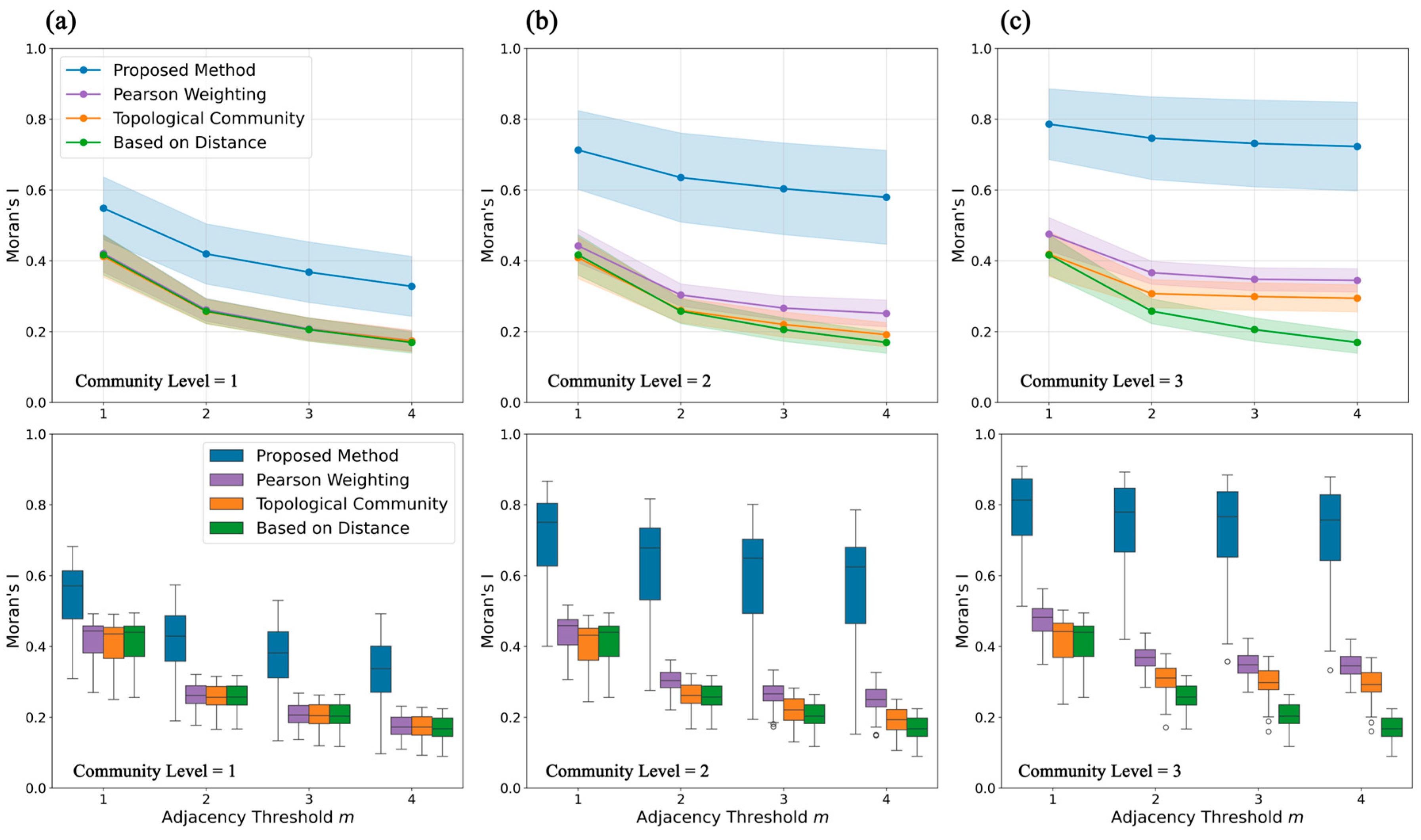
3.4. Spatial Autocorrelation of the Multi-Scale Community
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Chen, B.Y.; Gao, F.; Zhu, X. Dynamic community detection considering daily rhythms of human mobility. Travel Behav. Behav. Behav. Soc. 2023, 31, 209–222. [Google Scholar] [CrossRef]
- Zhou, H.; Hirasawa, K. Spatiotemporal traffic network analysis: Technology and applications. Knowl. Inf. Syst. 2019, 60, 25–61. [Google Scholar] [CrossRef]
- Fang, Y.; Zhao, F.; Qin, Y.; Luo, H.; Wang, C. Learning all dynamics: Traffic forecasting via locality-aware spatio-temporal joint transformer. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23433–23446. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Yu, Q.; Yang, H. Taxi global positioning system data in urban road network: A methodology to identify key road clusters based on travel speed–traffic volume correlation. Transp. Res. Rec. 2022, 2676, 487–498. [Google Scholar] [CrossRef]
- Liang, J.; Xie, S.; Bao, J. Analysis of a Multiple Traffic Flow Network’s Spatial Organization Pattern Recognition Based on a Network Map. Sustainability 2024, 16, 1300. [Google Scholar] [CrossRef]
- Wang, L.; Yang, M.; Li, X.; Qian, Y. A Microcirculation Optimization Model for Public Transportation Networks in Low-Density Areas Considering Equity—A Case of Lanzhou. Sustainability 2025, 17, 5679. [Google Scholar] [CrossRef]
- Almaliki, M.; Bamaqa, A.; Badawy, M.; Farrag, T.A.; Balaha, H.M.; Elhosseini, M.A. Adaptive Traffic Light Management for Mobility and Accessibility in Smart Cities. Sustainability 2025, 17, 6462. [Google Scholar] [CrossRef]
- Si, R.; Lin, Y. Exploring the Spatiotemporal Associations Between Ride-Hailing Demand, Visual Walkability, and the Built Environment: Evidence from Chengdu, China. Sustainability 2025, 17, 5441. [Google Scholar] [CrossRef]
- Qiang, D.; Xiaoyi, Z.; Yi, L.; Xiqian, G.; Zhongnan, Y.; Shasha, L.; Libiao, B. Resilience optimization of bus-metro double-layer network against extreme weather events. Transp. Res. Part D Transp. Environ. 2024, 135, 104378. [Google Scholar]
- Feng, Z.T.; Zhang, L.; Wu, Y.H.; Hu, M.B. Dynamic partition of urban network considering congestion evolution based on random walk. Chin. Phys. B 2025, 34, 018902. [Google Scholar] [CrossRef]
- Gao, Y.; Meng, H.; Pei, T.; Liu, Y. Understanding Spatial Dependency Among Spatial Interactions. In International Conference on Spatial Data and Intelligence; Springer Nature: Singapore, 2024; pp. 28–43. [Google Scholar]
- Owais, M.; Ahmed, A.S.; Moussa, G.S.; Khalil, A.A. An Optimal Metro Design for Transit Networks in Existing Square Cities Based on Non-Demand Criterion. Sustainability 2020, 12, 9566. [Google Scholar] [CrossRef]
- Owais, M.; Ahmed, A.S.; Moussa, G.S.; Khalil, A.A. Integrating underground line design with existing public transportation systems to increase transit network connectivity: Case study in Greater Cairo. Expert Syst. Appl. 2021, 167, 114183. [Google Scholar] [CrossRef]
- Bramson, A.; Hori, M.; Zha, B.; Inamoto, H. Social and economic flows across multimodal transportation networks in the Greater Tokyo Area. Appl. Netw. Sci. 2020, 5, 7. [Google Scholar] [CrossRef]
- Wu, D.; Ma, L.; Yan, X. Applying and Evaluating Data-Driven Fine Grid Partitioning Methods for Traffic Analysis Zones. J. Urban Plan. Dev. 2024, 150, 04024004. [Google Scholar] [CrossRef]
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. Part C Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Wang, J.; Tsapakis, I.; Zhong, C. A space–time delay neural network model for travel time prediction. Eng. Appl. Artif. Intell. 2016, 52, 145–160. [Google Scholar] [CrossRef]
- Lu, F.; Liu, K.; Duan, Y.; Cheng, S.; Du, F. Modeling the heterogeneous traffic correlations in urban road systems using traffic-enhanced community detection approach. Phys. A Stat. Mech. Its Appl. 2018, 501, 227–237. [Google Scholar] [CrossRef]
- Chen, W.; Gu, Y.; Chen, X.; Cheng, L.; De Vos, J. Optimal location of free-floating bike-sharing dispatching hubs: A multi-scale perspective. J. Transp. Geogr. 2025, 127, 104264. [Google Scholar] [CrossRef]
- Nagy, V.; Horváth, B. Automatic Definition of Traffic Analysis Zones Based on Big Data. Appl. Sci. 2024, 14, 5964. [Google Scholar] [CrossRef]
- Gao, Y.; Liao, Y. Urban Tourism Traffic Analysis Zone Division Based on Floating Car Data. Promet-Traffic Transp. 2023, 35, 395–406. [Google Scholar] [CrossRef]
- Yang, Y.; Cao, J.; Qin, Y.; Jia, L.; Dong, H.; Zhang, A. Spatial correlation analysis of urban traffic state under a perspective of community detection. Int. J. Mod. Phys. B 2018, 32, 1850150. [Google Scholar] [CrossRef]
- Chen, S.; Wu, N.; Fu, H.; Wang, Y.; Qiao, Y. Urban road network partitioning based on bi-modal traffic flows with multiobjective optimization. IEEE Trans. Intell. Transp. Syst. 2022, 23, 20664–20680. [Google Scholar] [CrossRef]
- Javed, M.A.; Younis, M.S.; Latif, S.; Qadir, J.; Baig, A. Community detection in networks: A multidisciplinary review. J. Netw. Comput. Appl. 2018, 108, 87–111. [Google Scholar] [CrossRef]
- Chen, X.J.; Zhao, Y.; Kang, C.; Xing, X.; Dong, Q.; Liu, Y. Characterizing the temporally stable structure of community evolution in intra-urban origin-destination networks. Cities 2024, 150, 105033. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Yu, Q.; Li, W.; Yang, D.; Zhang, H. Partitioning urban road network based on travel speed correlation. Int. J. Transp. Sci. Technol. 2021, 10, 97–109. [Google Scholar] [CrossRef]
- Dong, Q.F.; Chen, D.K.; Wang, T. Urban community structure detection based on the OD of traffic analysis zones. Mod. Phys. Lett. B 2019, 33, 1950164. [Google Scholar] [CrossRef]
- Petri, G.; Expert, P.; Jensen, H.J.; Polak, J.W. Entangled communities and spatial synchronization lead to criticality in urban traffic. Sci. Rep. 2013, 3, 1798. [Google Scholar] [CrossRef]
- Leibon, G.; Pauls, S.; Rockmore, D.; Savell, R. Topological structures in the equities market network. Proc. Natl. Acad. Sci. USA 2008, 105, 20589–20594. [Google Scholar] [CrossRef]
- Newman, M.E. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA 2006, 103, 8577–8582. [Google Scholar] [CrossRef]
- Rosvall, M.; Axelsson, D.; Bergstrom, C.T. The map equation. Eur. Phys. J. Spec. Top. 2009, 178, 13–23. [Google Scholar] [CrossRef]
- Konstantinos, S.; Petros, P.; Dora, S.; Aris, P. Overlapping community detection using graph attention networks. Future Gener. Comput. Syst. 2025, 163, 107529. [Google Scholar]
- Chen, J.; Gao, J.; Cui, B. ICS-GNN+: Lightweight interactive community search via graph neural network. VLDB J. 2023, 32, 447–467. [Google Scholar] [CrossRef]
- Hussein, N.A.; Mokhtar, H.M.O.; El-Sharkawi, M.E. Influential Attributed Communities via Graph Convolutional Network (InfACom-GCN). Information 2022, 13, 462. [Google Scholar] [CrossRef]
- Yue, Y.; Guodong, L.; Dongxu, L.; Jun, Z.; Pengwei, H.; Lun, H. Integrating Fuzzy Clustering and Graph Convolution Network to Accurately Identify Clusters from Attributed Graph. IEEE Trans. Netw. Sci. Eng. 2025, 12, 1112–1125. [Google Scholar]
- He, H.; Enjian, Y.; Yang, Y.; Shasha, L.; Long, P.; Yue, W. How to build vibrant communities by utilizing functional zones? A community-detection-based approach for revealing the association between land use and community vibrancy. Cities 2024, 155, 105431. [Google Scholar]
- Zhao, J.; Itti, L. shapeDTW: Shape dynamic time warping. Pattern Recognit. 2018, 74, 171–184. [Google Scholar] [CrossRef]
- Emmons, S.; Mucha, P.J. Map equation with metadata: Varying the role of attributes in community detection. Phys. Rev. E 2019, 100, 022301. [Google Scholar] [CrossRef]
- Macioszek, E.; Kurek, A. Road traffic distribution on public holidays and workdays on selected road transport network elements. Transp. Probl. 2021, 16, 127–138. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, Z.; Ma, H.; Hu, G.; Guo, R. Identification of Urban Spatial Form Based on Multimode Transit Travel Features. J. Urban Plan. Dev. 2023, 149, 04023025. [Google Scholar] [CrossRef]
- Wang, N.; Yuen, K.F.; Gao, X.; Nie, Y. Resilience assessment of global container shipping network via port communities. Transp. Res. Part D Transp. Environ. 2025, 141, 104649. [Google Scholar] [CrossRef]
- Liu, M.; Liu, Y.; Wong, C.W.; Lai, K.H.; Tu, E. The impacts of geopolitics on global Liquefied Natural Gas (LNG) shipping network: Evidence from two geopolitical events. Ocean Coast. Manag. 2025, 267, 107706. [Google Scholar] [CrossRef]
- Chan, H.Y.; Ma, H.; Zhou, J. Resilience of socio-technical transportation systems: A demand-driven community detection in human mobility structures. Transp. Res. Part A Policy Pract. 2024, 190, 104244. [Google Scholar] [CrossRef]
- Huffman, D.A. A Method for the Construction of Minimum-Redundancy Codes. Proc. IRE 1952, 40, 1098–1101. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Zang, J.; Jiao, P.; Liu, S.; Zhang, X.; Song, G.; Yu, L. Identifying Traffic Congestion Patterns of Urban Road Network Based on Traffic Performance Index. Sustainability 2023, 15, 948. [Google Scholar] [CrossRef]









| Weighting Type | Average ARI | Average NMI | Average AMI |
|---|---|---|---|
| No Weight | 0.626 | 0.897 | 0.766 |
| One-Week data | 0.973 | 0.997 | 0.985 |
| Monday data | 0.982 | 0.998 | 0.990 |
| Tuesday data | 0.990 | 0.999 | 0.994 |
| Wednesday data | 0.981 | 0.998 | 0.989 |
| Thursday data | 0.982 | 0.998 | 0.991 |
| Friday data | 0.985 | 0.998 | 0.991 |
| Saturday data | 0.978 | 0.997 | 0.988 |
| Sunday data | 0.976 | 0.997 | 0.986 |
| Weighting Type | Average ARI | Average NMI | Average AMI |
|---|---|---|---|
| No Weight | 0.444 | 0.849 | 0.726 |
| One-Week data | 0.829 | 0.983 | 0.937 |
| Monday data | 0.950 | 0.995 | 0.977 |
| Tuesday data | 0.977 | 0.997 | 0.988 |
| Wednesday data | 0.963 | 0.996 | 0.982 |
| Thursday data | 0.981 | 0.998 | 0.990 |
| Friday data | 0.960 | 0.995 | 0.980 |
| Saturday data | 0.939 | 0.994 | 0.974 |
| Sunday data | 0.941 | 0.994 | 0.972 |
| Weighting Type | Average ARI | Average NMI | Average AMI |
|---|---|---|---|
| No Weight | 0.516 | 0.737 | 0.713 |
| One-Week data | 0.706 | 0.924 | 0.854 |
| Monday data | 0.731 | 0.964 | 0.889 |
| Tuesday data | 0.858 | 0.979 | 0.941 |
| Wednesday data | 0.758 | 0.972 | 0.908 |
| Thursday data | 0.961 | 0.996 | 0.982 |
| Friday data | 0.845 | 0.978 | 0.935 |
| Saturday data | 0.790 | 0.968 | 0.910 |
| Sunday data | 0.762 | 0.961 | 0.900 |
| Methods | Scales | m = 1 | m = 2 | m = 3 | m = 4 | p |
|---|---|---|---|---|---|---|
| Proposed Method | Level = 1 | 31.61% | 62.74% | 78.78% | 93.51% | all < 0.001 |
| Level = 2 | 71.05% | 146.34% | 193.20% | 241.95% | all < 0.001 | |
| Level = 3 | 88.58% | 189.49% | 255.37% | 326.55% | all < 0.001 | |
| Pearson Weighting | Level = 1 | 0.94% | 1.47% | 0.92% | 2.89% | all < 0.001 |
| Level = 2 | 6.14% | 17.68% | 29.48% | 48.38% | all < 0.001 | |
| Level = 3 | 14.08% | 42.11% | 69.01% | 103.48% | all < 0.001 | |
| Topological Communities | Level = 1 | −1.08% | −0.47% | 0.15% | 2.42% | all < 0.001 |
| Level = 2 | −1.94% | 1.01% | 6.99% | 12.98% | all < 0.001 | |
| Level = 3 | 0.48% | 19.19% | 45.31% | 73.63% | all < 0.001 |
| Data Length | Constrained | Cost Time (Seconds) | Improvement Rate | Similarity Results | MAD Results |
|---|---|---|---|---|---|
| One-day traffic data | None constrained | 1.48 | - | - | - |
| = 0.20 | 0.54 | 63.51% | 0.9954 | 9.34 | |
| = 0.15 | 0.44 | 70.27% | 0.9941 | 11.90 | |
| = 0.10 | 0.33 | 77.70% | 0.9922 | 15.66 | |
| = 0.05 | 0.22 | 85.14% | 0.9895 | 21.76 | |
| Full-week traffic data | None constrained | 71.74 | - | - | - |
| = 0.20 | 26.12 | 63.59% | 0.9960 | 27.61 | |
| = 0.15 | 20.48 | 71.45% | 0.9944 | 40.32 | |
| = 0.10 | 13.72 | 80.88% | 0.9915 | 60.44 | |
| = 0.05 | 7.46 | 89.60% | 0.9875 | 108.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, Y.; Song, X.; Wang, S.; Wang, N. Characterizing the Evolution of Multi-Scale Communities in Urban Road Networks. Sustainability 2025, 17, 9355. https://doi.org/10.3390/su17209355
Wang Y, Li Y, Song X, Wang S, Wang N. Characterizing the Evolution of Multi-Scale Communities in Urban Road Networks. Sustainability. 2025; 17(20):9355. https://doi.org/10.3390/su17209355
Chicago/Turabian StyleWang, Yifan, Yi Li, Xingwa Song, Shilong Wang, and Ning Wang. 2025. "Characterizing the Evolution of Multi-Scale Communities in Urban Road Networks" Sustainability 17, no. 20: 9355. https://doi.org/10.3390/su17209355
APA StyleWang, Y., Li, Y., Song, X., Wang, S., & Wang, N. (2025). Characterizing the Evolution of Multi-Scale Communities in Urban Road Networks. Sustainability, 17(20), 9355. https://doi.org/10.3390/su17209355





