Effect of Rock Structure on Seismic Wave Propagation
Abstract
1. Introduction
2. Methodology: Integrated Experimental and Analytical Framework
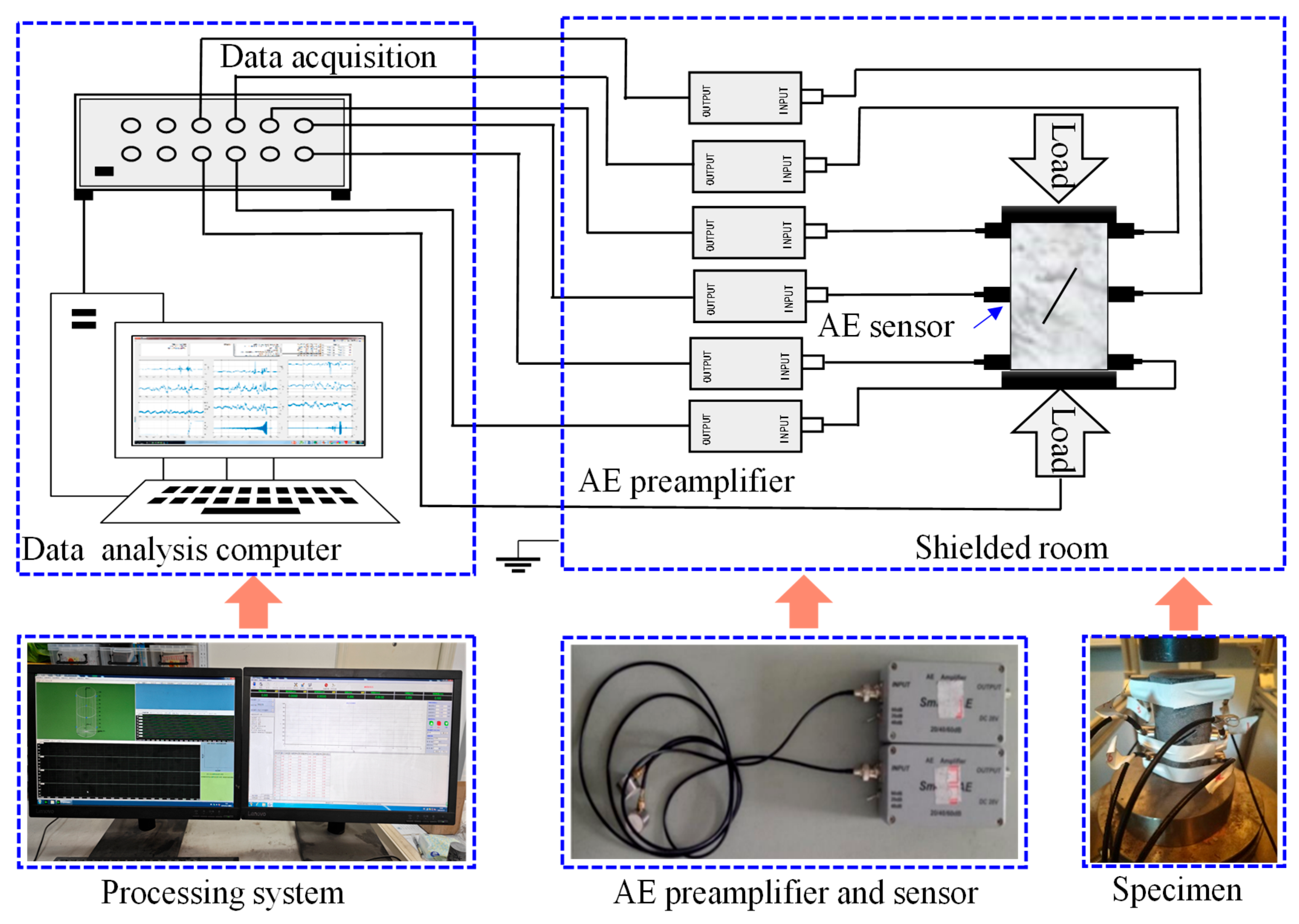
2.1. Experimental Equipment
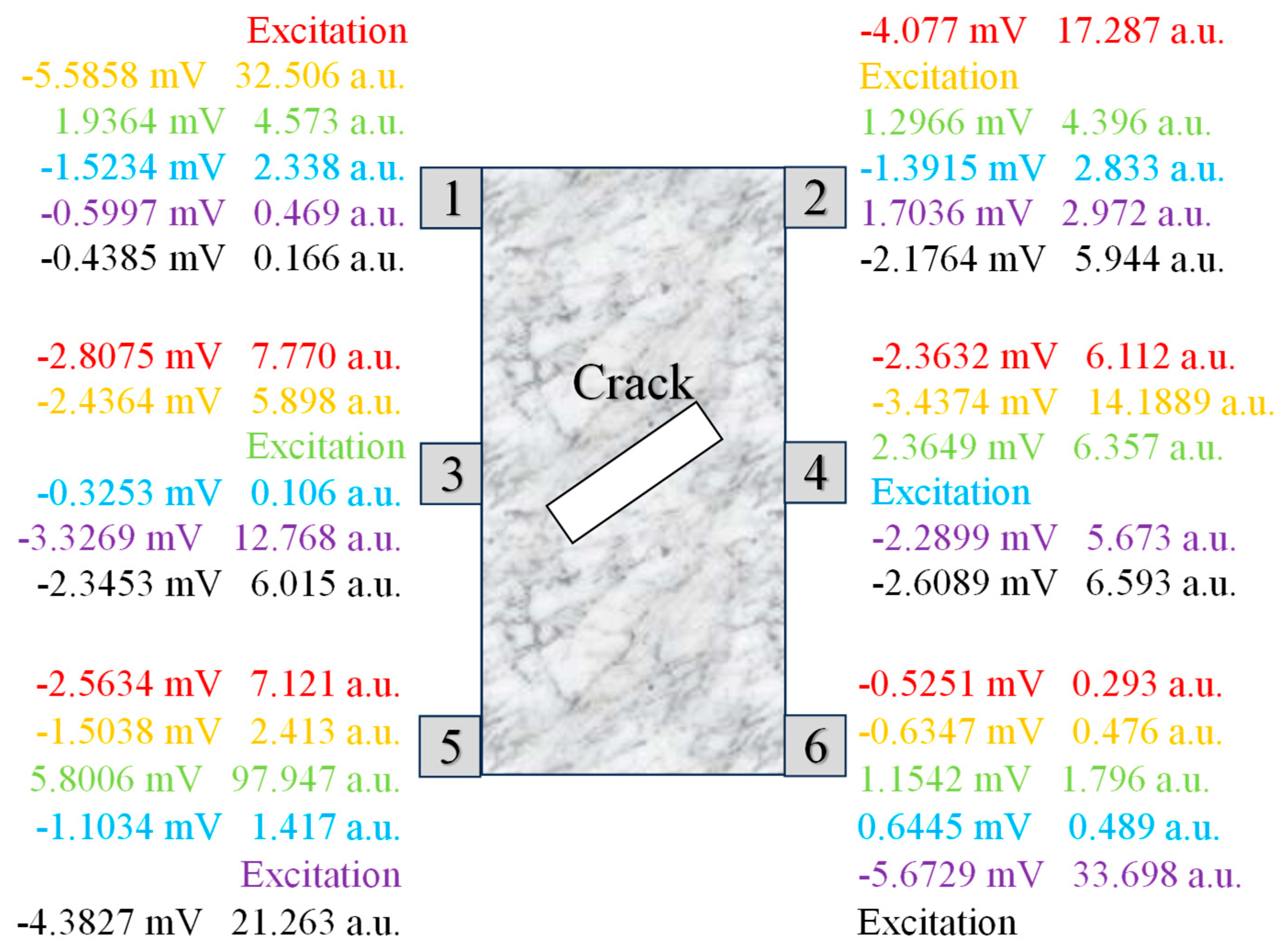
2.2. Experimental Scheme
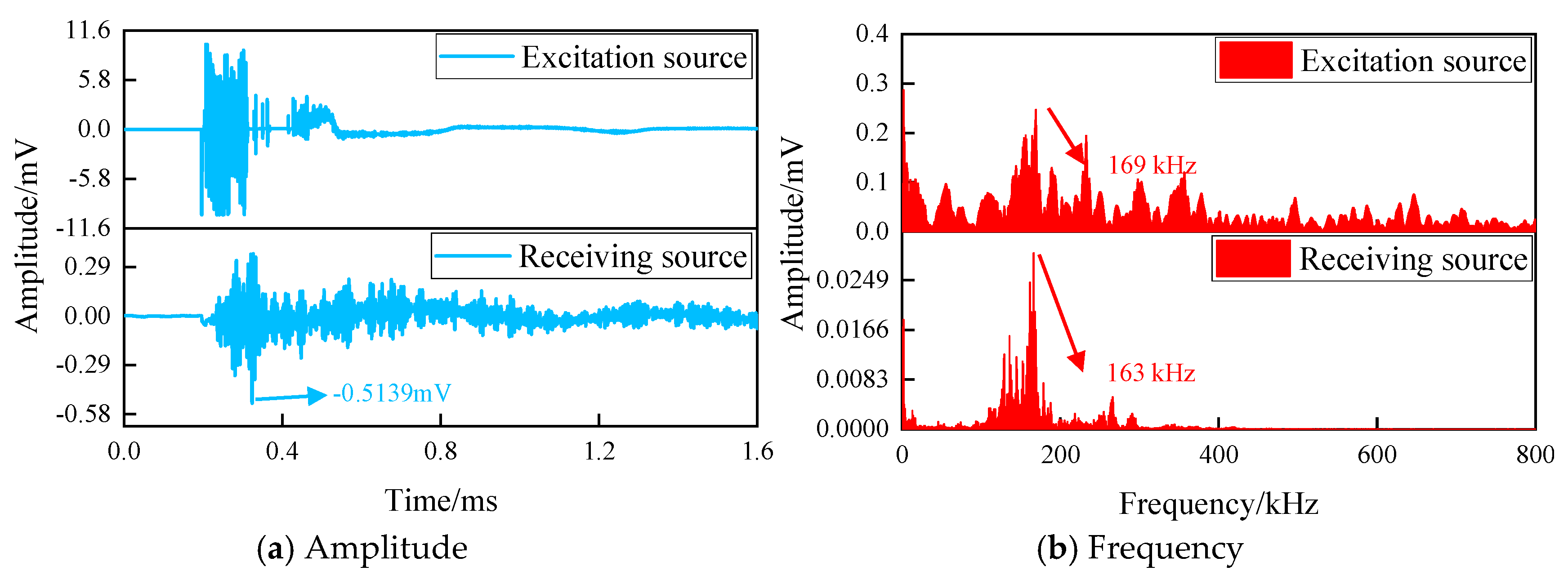
2.3. Signal Processing Methodology
- Pre-processing:
- 2.
- Analysis and Parameter Extraction:
3. Effect of Seismic Wave Characteristic Parameters by Rock Structure
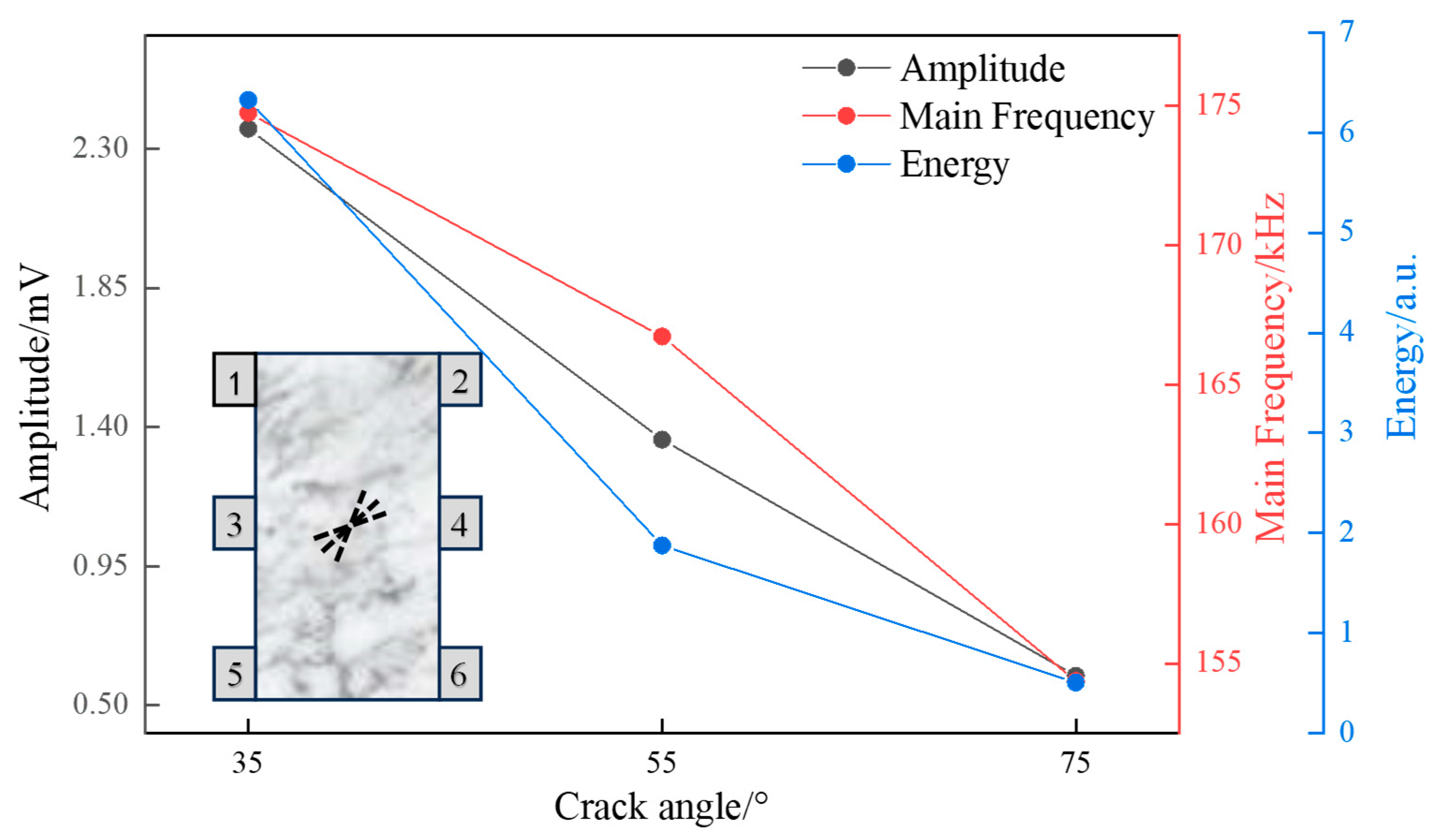
3.1. Effect of Crack Angle to the Characteristic Parameters of Seismic Waves
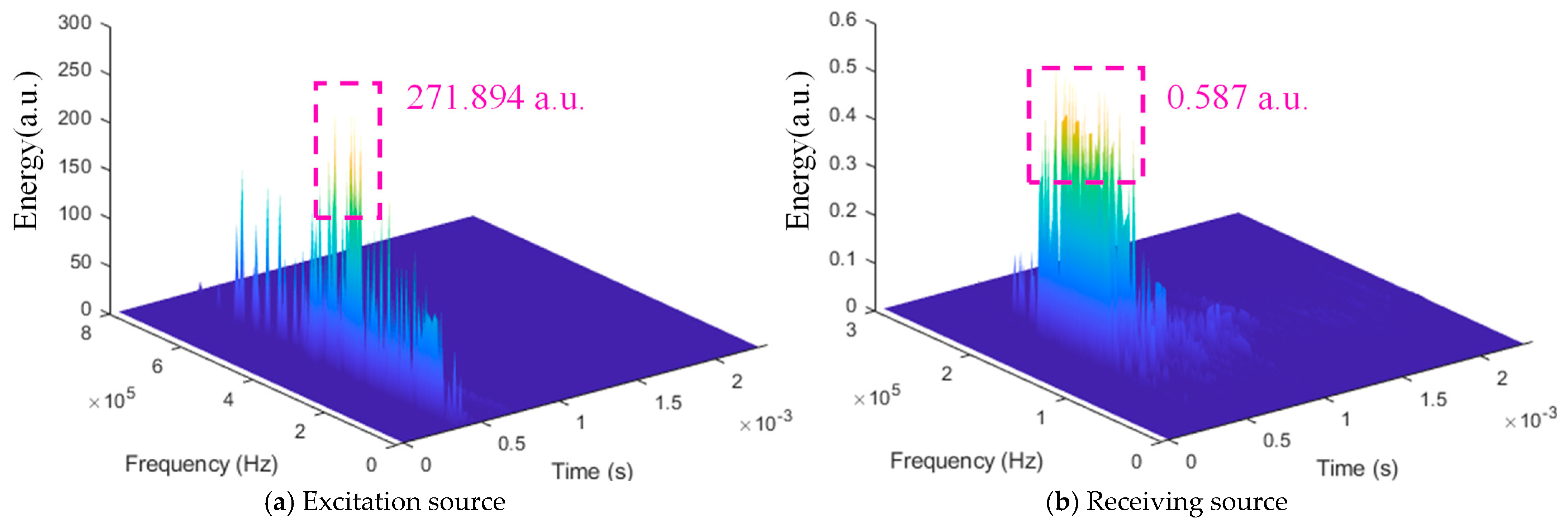
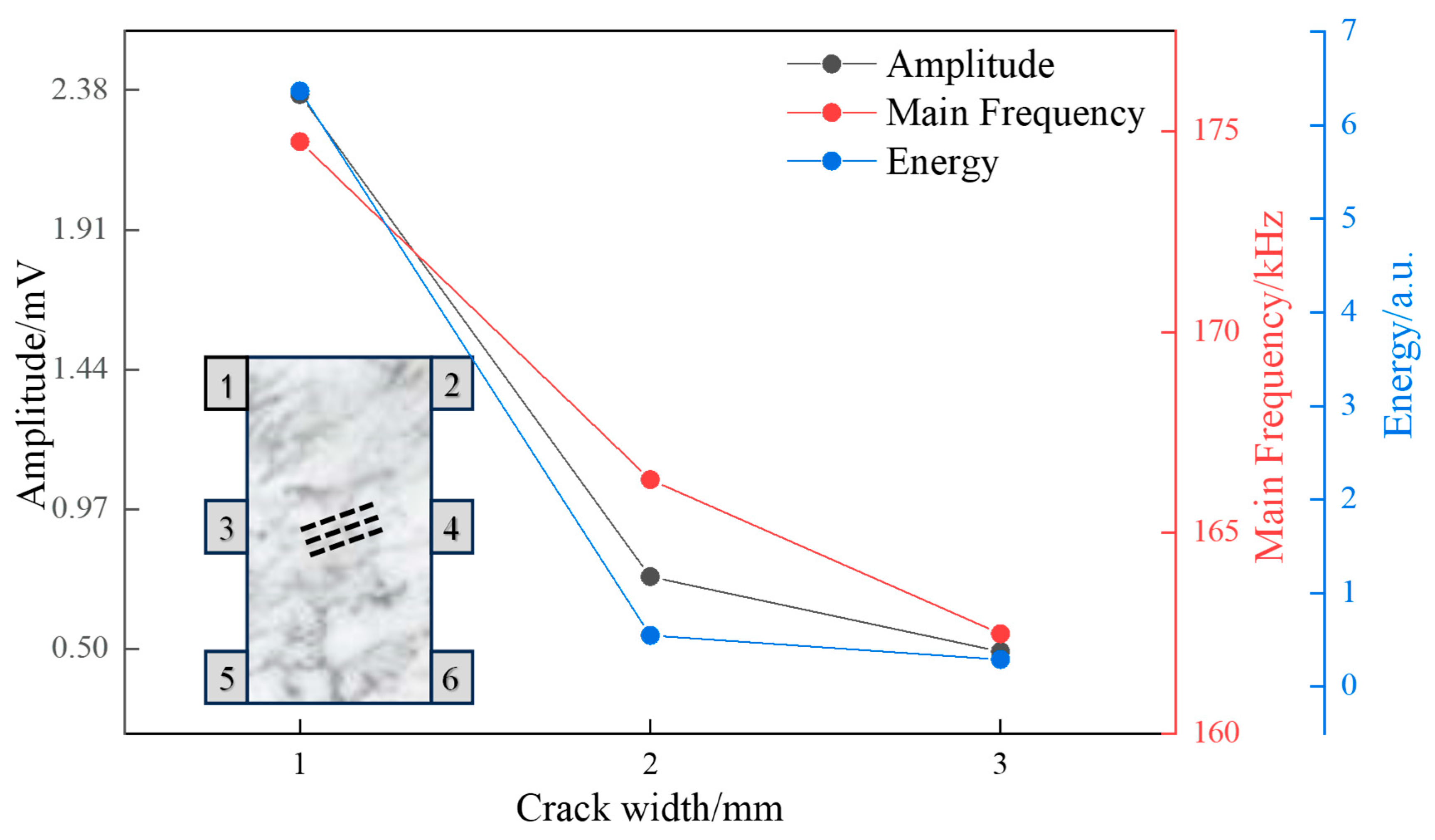
3.2. Effect of Crack Width on Characteristic Parameters of Seismic Waves
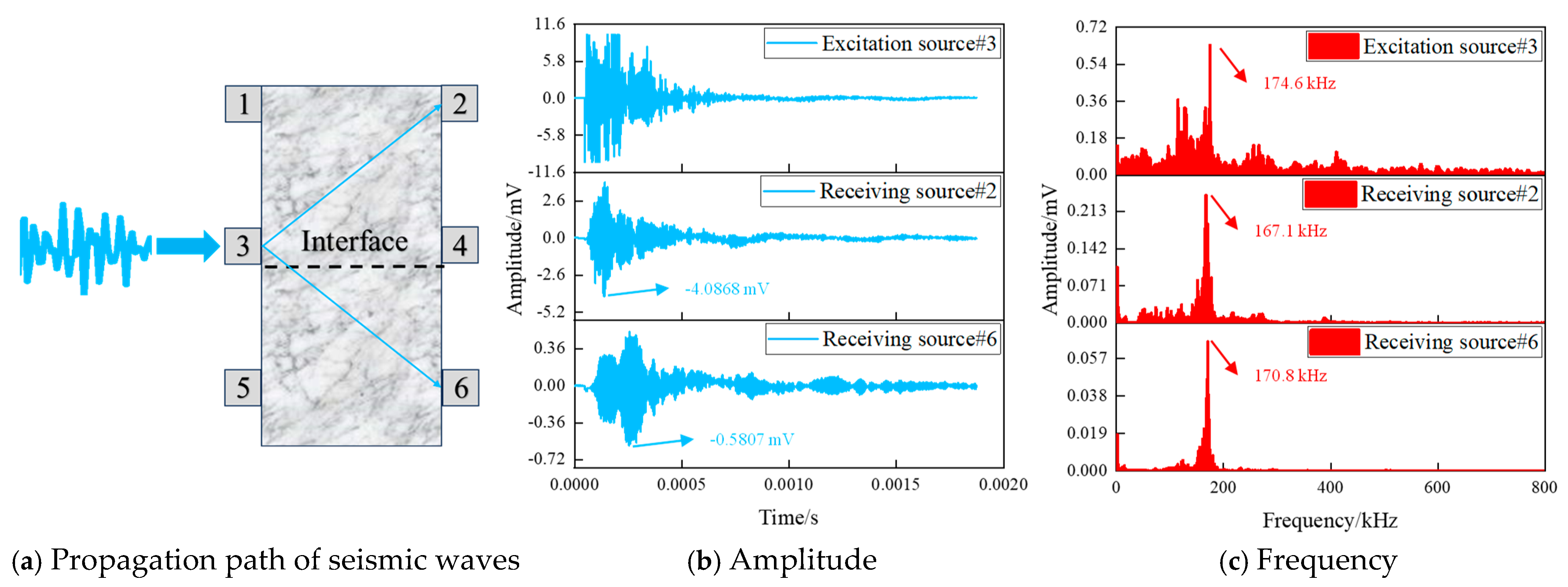
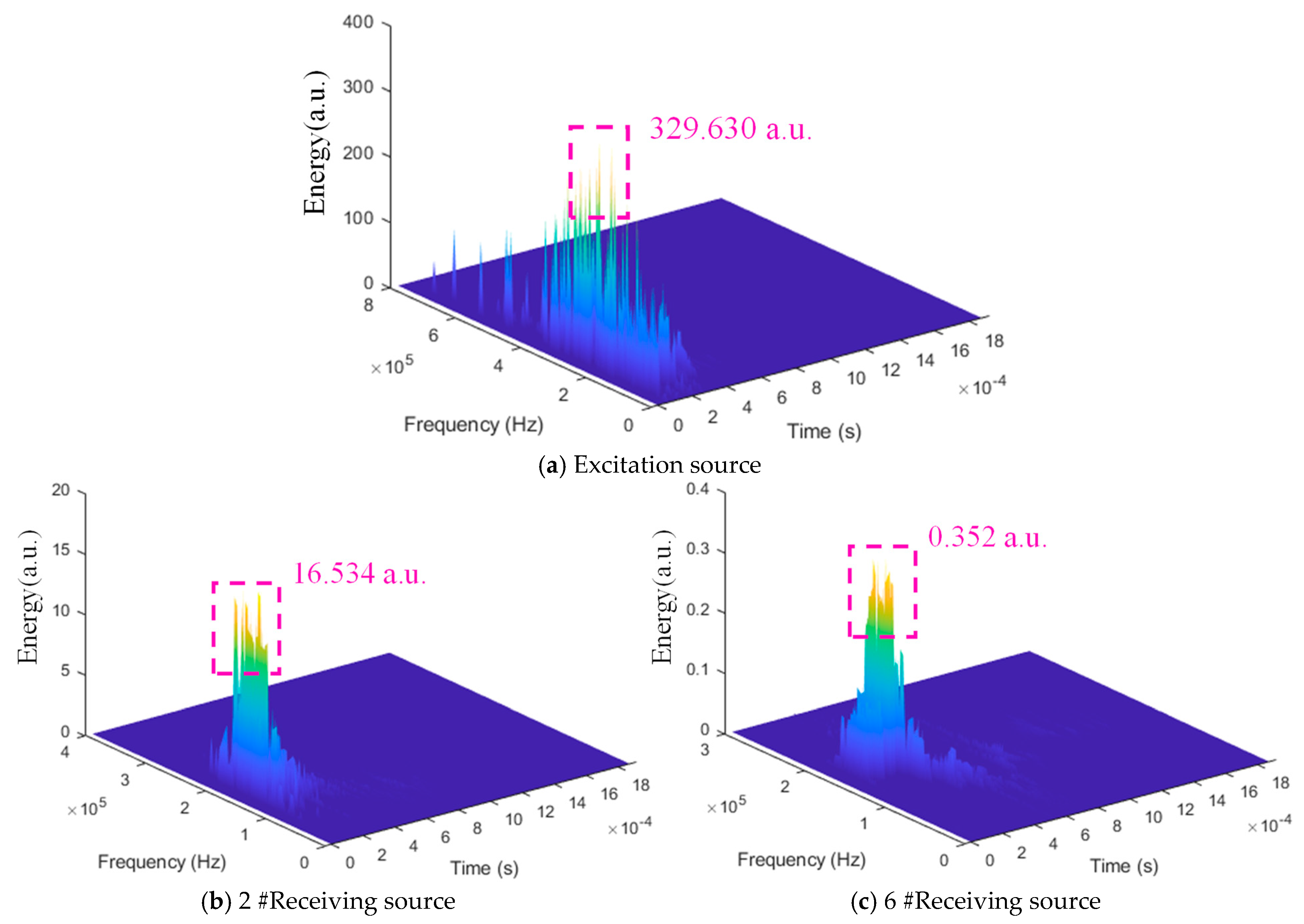
3.3. Effect of Rock Interface on Characteristic Parameters of Seismic Wave
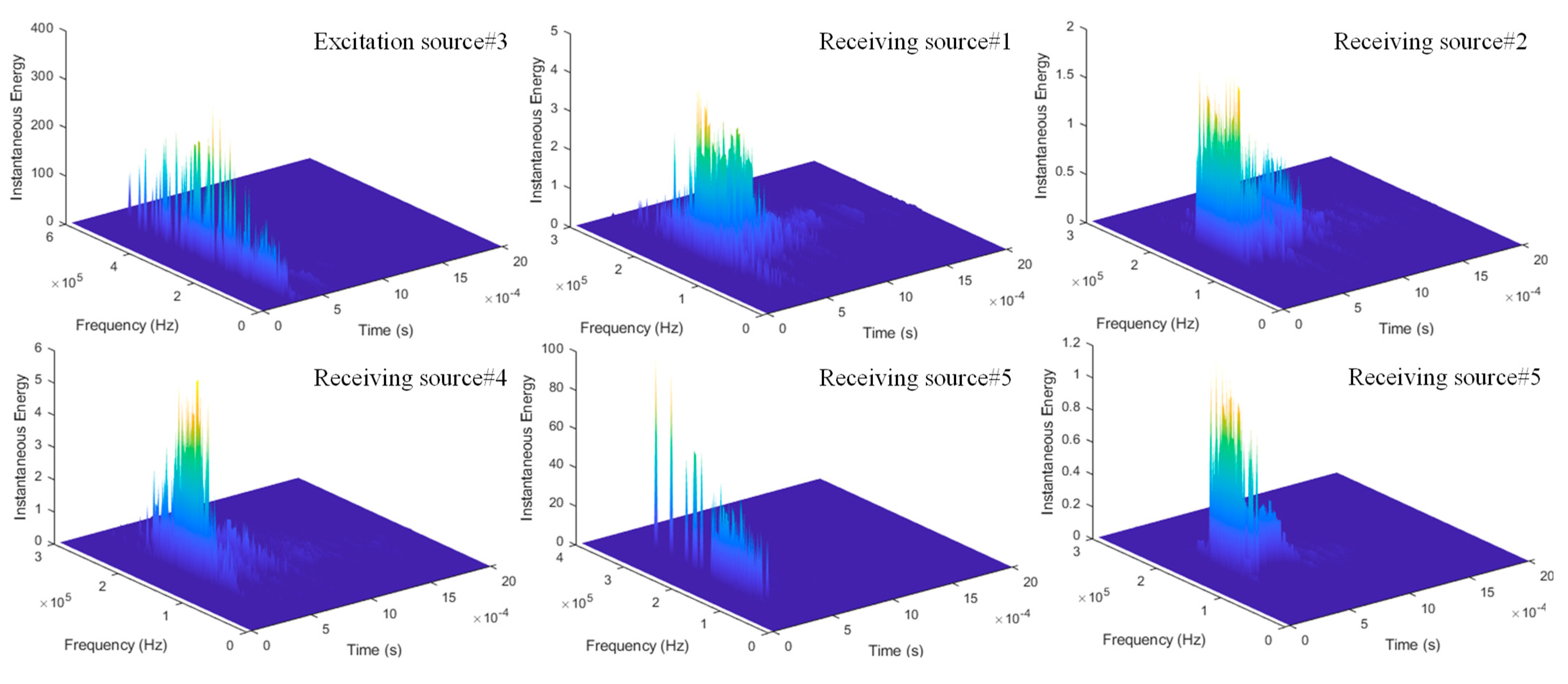
4. Difference in Characteristic Parameters of Seismic Wave Along Different Propagation Paths of the Same Rock Structure
5. Discussion
5.1. Limitations and Implications for In Situ Conditions
5.2. Practical Applications
5.3. Robustness of Time–Frequency Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, R.; Wang, J.; Li, H.; Cui, H.; Tang, M.; Zhao, J. A study on the acquisition technology for weak seismic signals from deep geothermal reservoirs. Energies 2023, 16, 2751. [Google Scholar] [CrossRef]
- Um, E.S.; Commer, M.; Gritto, R.; Peacock, J.R.; Alumbaugh, D.L.; Jarpe, S.P.; Hartline, C. Cooperative joint inversion of magnetotelluric and microseismic data for imaging The Geysers geothermal field, California, USA. Geophysics 2023, 88, WB45–WB54. [Google Scholar] [CrossRef]
- Tunç, S.; Selek, B.; Koca, B.; Selek, Ü.S.; Balcı, K.; Yıldırım, A.; Kaypak, B. Installation of microseismic monitoring networks in geothermal fields. J. Fac. Eng. Archit. Gazi Univ. 2023, 38, 1307–1319. [Google Scholar] [CrossRef]
- Li, J.; Wu, W.; Li, H.; Zhu, J.; Zhao, J. A thin-layer interface model for wave propagation through filled rock joints. J. Appl. Geophys. 2013, 91, 31–38. [Google Scholar] [CrossRef]
- Lu, G.; Tao, Y. Experimental study into the propagation and attenuation of blasting seismic waves in porous rock-like materials. Front. Mater. 2023, 10, 1284158. [Google Scholar] [CrossRef]
- Fan, L.; Jiang, F.; Wang, M.; Chen, S. Oblique incident seismic P wave propagation through joints containing saturated fluids with different media on both sides. J. Appl. Geophys. 2024, 222, 105316. [Google Scholar] [CrossRef]
- Yu, C.; Li, H.; Yue, H.; Wang, X.; Xia, X. A case study of blasting seismic attenuation based on wave component characteristics. J. Rock Mech. Geotech. Eng. 2023, 15, 1298–1311. [Google Scholar] [CrossRef]
- Tartoussi, N.; Lataste, J.-F.; Rivard, P.; Barbosa, N.D. Effects of a filled discontinuity in a rock mass on transmission losses of compressional and shear wave of full-waveform sonic log data. J. Appl. Geophys. 2023, 217, 105179. [Google Scholar] [CrossRef]
- Tartoussi, N.; Lataste, J.-F.; Rivard, P.; Barbosa, N.D. Analysis of P-wave propagation in filled jointed rock mass with viscoelastic properties. Geomech. Geophys. Geo-Energy Geo Resour. 2023, 9, 102. [Google Scholar] [CrossRef]
- Wu, W.; Li, C.; Zhao, J. Seismic response of adjacent filled parallel rock fractures with dissimilar properties. J. Appl. Geophys. 2013, 96, 33–37. [Google Scholar] [CrossRef]
- Zhao, X.B.; Zhao, J.; Hefny, A.M.; Cai, J.G. Normal transmission of S-wave across parallel fractures with Coulomb slip behavior. J. Eng. Mech. 2006, 132, 641–650. [Google Scholar] [CrossRef]
- Syu, S.-Y.; Hutchings, L.; Lee, C.-S.; Jarpe, S. The implications of S-wave attenuation in geothermal reservoirs. Geothermics 2024, 117, 102861. [Google Scholar] [CrossRef]
- Toksoz, M.N.; Johnston, D.H.; Timur, A. Attenuation of seismic waves in dry and saturated rocks—1. laboratory measurements. Geophysics 2012, 44, 681–690. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, C.; Jiang, N.; Xu, X. Effect of excavation blasting in an under-cross tunnel on airport runway. Geotech. Geol. Eng. 2015, 33, 973–981. [Google Scholar] [CrossRef]
- Li, J.; Ma, G.; Jian, Z. Analysis of stochastic seismic wave interaction with a slippery rock fault. Rock Mech. Rock Eng. 2011, 44, 85–92. [Google Scholar] [CrossRef]
- Li, J.; Ma, G.; Zhao, J. An equivalent viscoelastic model for rock mass with parallel joints. J. Geophys. Res. Atmos. 2010, 115, 1923–1941. [Google Scholar] [CrossRef]
- Chapman, S.; Borgomano, J.V.M.; Quintal, B.; Benson, S.M.; Fortin, J. Seismic wave attenuation and dispersion due to partial fluid saturation: Direct measurements and numerical simulations based on X-ray CT. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021643. [Google Scholar] [CrossRef]
- Borgomano, J.V.M.; Pimienta, L.X.; Fortin, J.; Guéguen, Y. Seismic dispersion and attenuation in fluid-saturated carbonate rocks: Effect of microstructure and pressure. J. Geophys. Res. Solid Earth 2019, 124, 12498–12522. [Google Scholar] [CrossRef]
- Batzle, M.L.; Han, D.H.; Hofmann, R. Fluid mobility and frequency-dependent seismic velocity—Direct measurements. Geophysics 2006, 71, N1–N9. [Google Scholar] [CrossRef]
- Sun, C.; Tang, G.Y.; Fortin, J.; Borgomano, J.V.M.; Wang, S. Dispersion and attenuation of elastic wave velocities: Impact of microstructure heterogeneity and local measurements. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020132. [Google Scholar] [CrossRef]
- Yin, H.; Zhao, J.; Tang, G.; Zhao, L.; Ma, X.; Wang, S. Pressure and fluid effect on frequency-dependent elastic moduli in fully saturated tight sandstone. J. Geophys. Res. Solid Earth 2017, 122, 8925–8942. [Google Scholar] [CrossRef]
- Guo, J.; Shuai, D.; Wei, J.; Ding, P.; Gurevich, B. P-wave dispersion and attenuation due to scattering by aligned fluid saturated fractures with finite thickness: Theory and experiment. Geophys. J. Int. 2018, 215, 2114–2133. [Google Scholar] [CrossRef]
- Song, Y.; Hu, H.; Han, B. Elastic wave scattering by a fluid-saturated circular crack and effective properties of a solid with a sparse distribution of aligned cracks. J. Acoust. Soc. Am. 2019, 146, 470–485. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Rudnicki, J.W.; Hu, H.; Han, B. Dynamics anisotropy in a porous solid with aligned slit fractures. J. Mech. Phys. Solids 2020, 137, 103865. [Google Scholar] [CrossRef]
- Fu, B.; Guo, J.; Fu, L.; Glubokovskikh, S.; Galvin, R.J.; Gurevich, B. Seismic dispersion and attenuation in saturated porous rock with aligned slit cracks. J. Geophys. Res. Solid Earth 2018, 123, 6890–6910. [Google Scholar] [CrossRef]
- Tan, Y.; Li, X.Y.; Wu, T.H. Dynamic stress intensity factor of a rectangular crack in an infinite saturated porous medium: Mode I problem. Eng. Fract. Mech. 2020, 223, 106737. [Google Scholar] [CrossRef]
- Song, Y.; Hu, H.; Han, B. Effective properties of a porous medium with aligned cracks containing compressible fluid. Geophys. J. Int. 2020, 221, 60–76. [Google Scholar] [CrossRef]
- Song, Y.; Hu, H.; Han, B. P-wave attenuation and dispersion in a fluid-saturated rock with aligned rectangular cracks. Mech. Mater. 2020, 147, 103409. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Hu, H.; Han, B. Attenuation and dispersion of P-waves in fluid-saturated porous rocks with a distribution of coplanar cracks—Scattering approach. Geophysics 2021, 86, 81–93. [Google Scholar] [CrossRef]
- GB/T 23561.7-2009; Methods for Determining the Physical and Mechanical Properties of Coal and Rock—Part 7: Methods for Determining the Uniaxial Compressive Strength and Counting Softening Coefficient. China National Standardization Administration: Beijing, China, 2009.









| No. | Structure Type | Crack Length, mm | Crack Width, mm | Angle of Crack, ° |
|---|---|---|---|---|
| 1 | Crack | 30 | 1 | 35 |
| 2 | 2 | 35 | ||
| 3 | 3 | 35 | ||
| 4 | 1 | 55 | ||
| 5 | 1 | 75 |
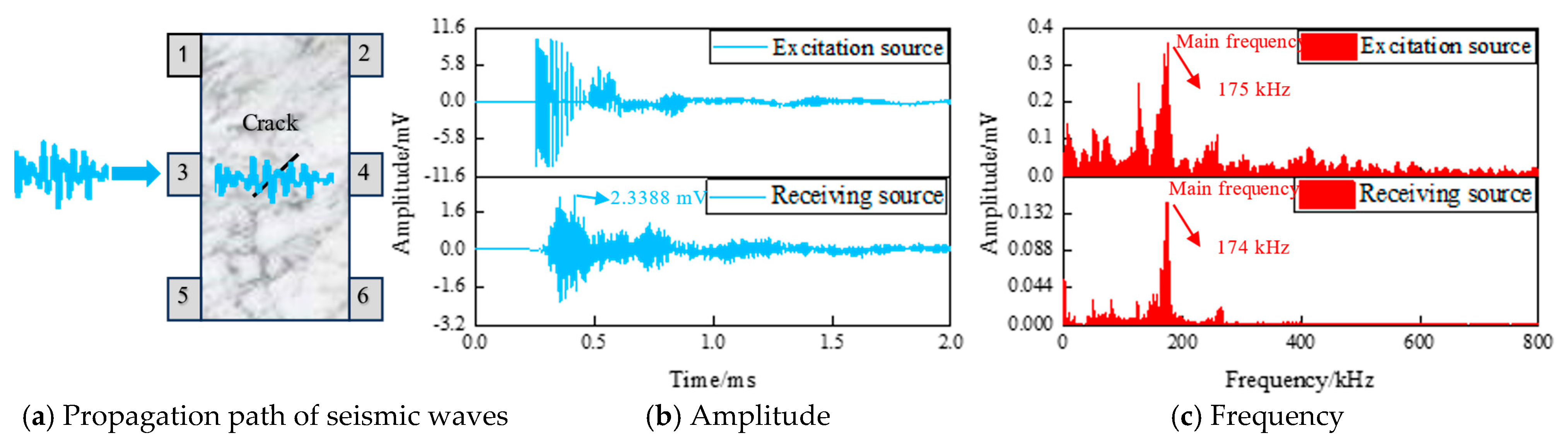
| Crack Angle, ° | Parameter | Excitation Source (Mean) | Receiving Source (Mean ± SD) | 95% CI | Decay (%) |
|---|---|---|---|---|---|
| 35 | Amplitude (mV) | 10.0 | 2.36 ± 0.15 | [2.25, 2.47] | 76.35 |
| Main Frequency (kHz) | 175.50 | 174.74 ± 0.52 | [174.37, 175.11] | 0.44 | |
| Energy (a.u.) | 315.03 | 6.36 ± 0.41 | [6.06, 6.66] | 97.98 | |
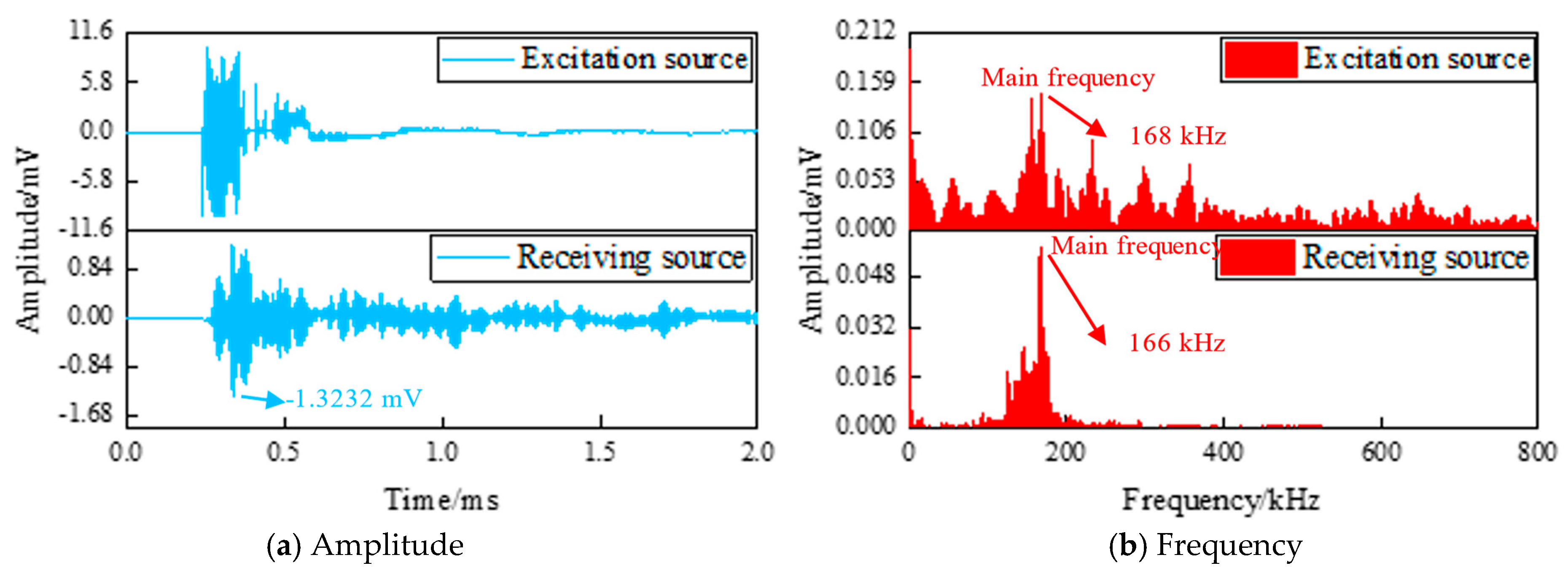
| 55 | Amplitude (mV) | 10.0 | 1.36 ± 0.11 | [1.28, 1.44] | 86.42 |
| Main Frequency (kHz) | 167.78 | 166.72 ± 0.65 | [166.25, 167.19] | 0.63 | |
| Energy (a.u.) | 297.33 | 1.88 ± 0.23 | [1.71, 2.05] | 99.37 | |
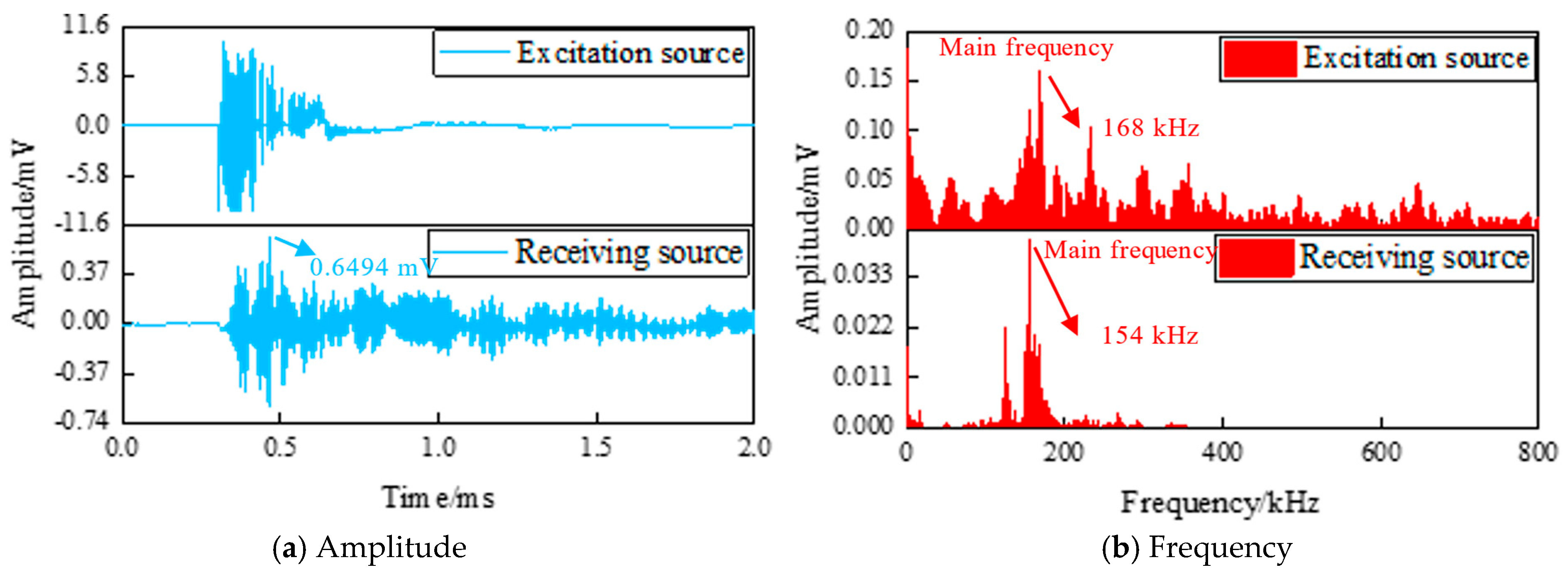
| 75 | Amplitude (mV) | 10.0 | 0.60 ± 0.08 | [0.54, 0.66] | 94.04 |
| Main Frequency (kHz) | 168.61 | 154.36 ± 1.21 | [153.49, 155.23] | 8.45 | |
| Energy (a.u.) | 265.80 | 0.51 ± 0.07 | [0.46, 0.56] | 99.81 |
| Equation | y = a + b × x | ||
|---|---|---|---|
| Parameter | Energy | Amplitude | Main Frequency |
| Intercept | 10.95942 ± 2.56548 | 3.87283 ± 0.20106 | 193,287.29167 ± 3593.16331 |
| Slope | −0.14625 ± 0.04472 | −0.04424 ± 0.0035 | −509.375 ± 62.62807 |
| R2 | 0.91451 | 0.99376 | 0.98511 |
| Symbol | Definition | SI Unit |
|---|---|---|
| RPP, TPP | Reflection and transmission coefficients for P-wave | Dimensionless |
| RSS, TSS | Reflection and transmission coefficients for S-wave | Dimensionless |
| KN | Normal specific stiffness | Pa/m (or N/m3) |
| KT | Tangential specific stiffness | Pa/m (or N/m3) |
| ω | Angular frequency (2πf) | rad/s |
| ZP | P-wave acoustic impedance (pvP) | kg/(m2s) |
| ZS | S-wave acoustic impedance (pvS) | kg/(m2s) |
| P | Rock density | kg/m3 |
| vP | P-wave velocity in the rock | m/s |
| US | S-wave velocity in the rock | m/s |
| i | Imaginary unit () | Dimensionless |
| Crack Width, mm | Parameter | Excitation Source (Mean) | Receiving Source (Mean ± SD) | 95% CI | Decay (%) |
|---|---|---|---|---|---|
| 1 | Amplitude (mV) | 10.0 | 2.36 ± 0.15 | [2.25, 2.47] | 76.35 |
| Main Frequency (kHz) | 175.50 | 174.74 ± 0.52 | [174.37, 175.11] | 0.44 | |
| Energy (a.u.) | 315.03 | 6.36 ± 0.41 | [6.06, 6.66] | 97.98 | |
| 2 | Amplitude (mV) | 10.0 | 0.74 ± 0.09 | [0.68, 0.80] | 92.56 |
| Main Frequency (kHz) | 169.96 | 166.33 ± 0.71 | [165.82, 166.84] | 2.14 | |
| Energy (a.u.) | 289.49 | 0.55 ± 0.08 | [0.49, 0.61] | 99.81 | |
| 3 | Amplitude (mV) | 10.0 | 0.49 ± 0.06 | [0.45, 0.53] | 95.08 |
| Main Frequency (kHz) | 169.70 | 162.49 ± 0.88 | [161.86, 163.12] | 4.25 | |
| Energy (a.u.) | 275.07 | 0.29 ± 0.04 | [0.26, 0.32] | 99.89 |
| Equation | y = a·eb·x | ||
|---|---|---|---|
| Parameter | Energy | Amplitude | Main Frequency |
| Fitting results | y = 11.8398·e−1.8848x | y = 4.5428·e−1.0287x | y = 167·e−0.0076x |
| R2 | 0.9702 | 0.9822 | 0.9490 |
| Parameter Type | Parameter Value | Experimental Attenuation (%) | Theoretical Prediction (%) |
|---|---|---|---|
| Angle (°) | 35 | 97.98 | 98.7 (DDM) |
| 55 | 99.37 | 99.5 (DDM) | |
| 75 | 99.81 | 99.94 (DDM) | |
| Width (mm) | 1 | 97.98 | 98.1 (scattering) |
| 2 | 99.81 | 99.7 (scattering) | |
| 3 | 99.89 | 99.92 (scattering) | |
| Interface (receiving source #6) | - | 99.89 | 99.82 (stiffness) |
| No. | Peak Amplitude, mV | Peak Amplitude Time, ×10−4 s | Main Frequency, kHz | Energy Peak, a.u. |
|---|---|---|---|---|
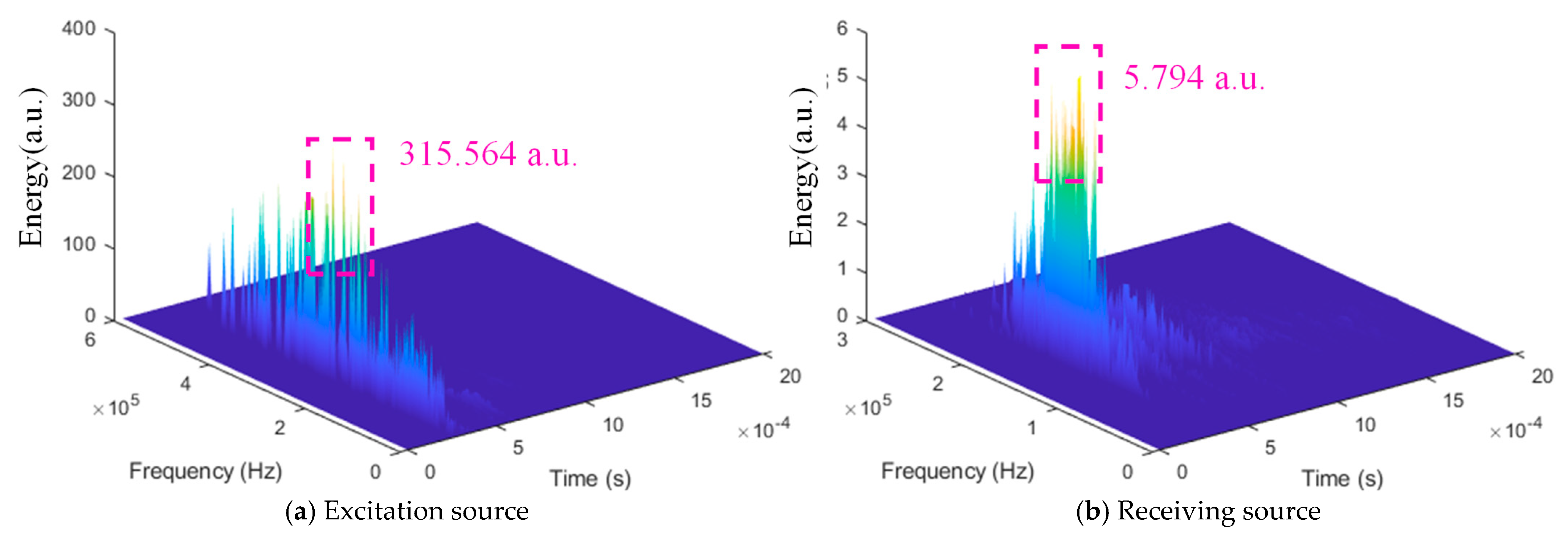
| Excitation source 3 | 10 | 2.60 | 175.029 | 315.564 |
| Receiving source 1 | −1.9189 | 3.24 | 171.528 | 4.178 |
| Receiving source 2 | −1.2743 | 4.34 | 171.028 | 1.769 |
| Receiving source 4 | 2.3388 | 4.18 | 174,529 | 5.794 |
| Receiving source 5 | −5.8202 | 3.35 | 170,028 | 98.037 |
| Receiving source 6 | 1.0058 | 3.96 | 169,028 | 1.110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Z.; He, S.; Jiang, H.; Shen, F.; Quan, C. Effect of Rock Structure on Seismic Wave Propagation. Sustainability 2025, 17, 9325. https://doi.org/10.3390/su17209325
Kang Z, He S, Jiang H, Shen F, Quan C. Effect of Rock Structure on Seismic Wave Propagation. Sustainability. 2025; 17(20):9325. https://doi.org/10.3390/su17209325
Chicago/Turabian StyleKang, Zhongquan, Shengquan He, Huiling Jiang, Feng Shen, and Chengzhu Quan. 2025. "Effect of Rock Structure on Seismic Wave Propagation" Sustainability 17, no. 20: 9325. https://doi.org/10.3390/su17209325
APA StyleKang, Z., He, S., Jiang, H., Shen, F., & Quan, C. (2025). Effect of Rock Structure on Seismic Wave Propagation. Sustainability, 17(20), 9325. https://doi.org/10.3390/su17209325





