AI-Driven Ensemble Learning for Spatio-Temporal Rainfall Prediction in the Bengawan Solo River Watershed, Indonesia
Abstract
1. Introduction
2. Methods
2.1. Study Area
2.2. Data
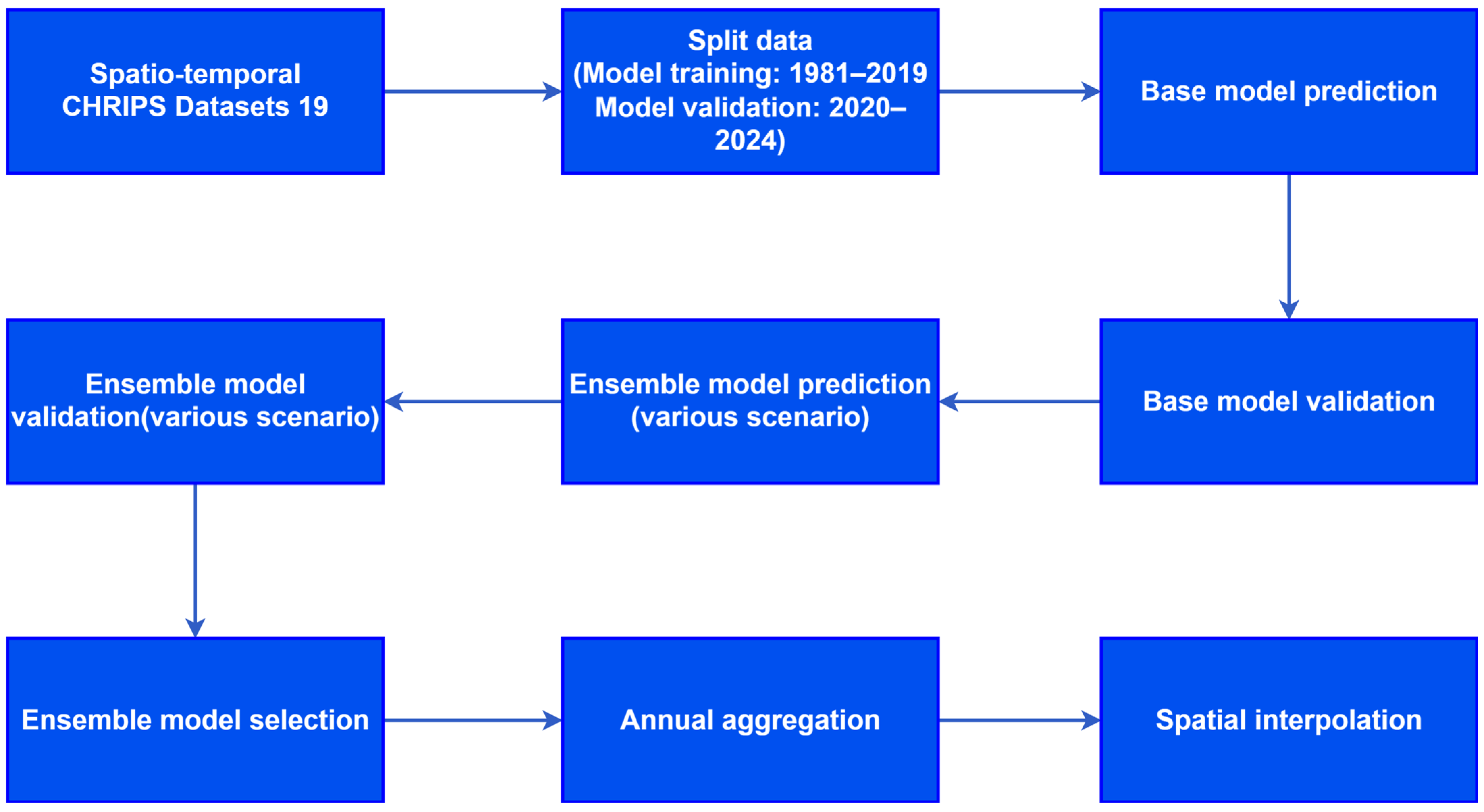
2.3. Research Framework
2.3.1. Preprocessing
- Training set: includes data from January 1981 to December 2019. This data is used to train the model, extract seasonal patterns and long-term trends, and tune parameters.
- Validation set: includes data from January 2020 to December 2024. This data serves to evaluate the model’s ability to make out-of-sample predictions, thereby measuring the model’s accuracy in the most recent period.
2.3.2. Development of Prediction Models
- Machine Learning (ML) Models
- 2.
- Deep Learning (DL) Models
- 3.
- Prediction and Evaluation Process
2.3.3. Ensemble Stacking and Scenario Evaluation
2.3.4. Data Aggregation (Monthly to Annual)
2.3.5. Spatial Interpolation
2.3.6. Visualization and Analysis of Results
3. Results
3.1. Evaluation of Individual Model Performance
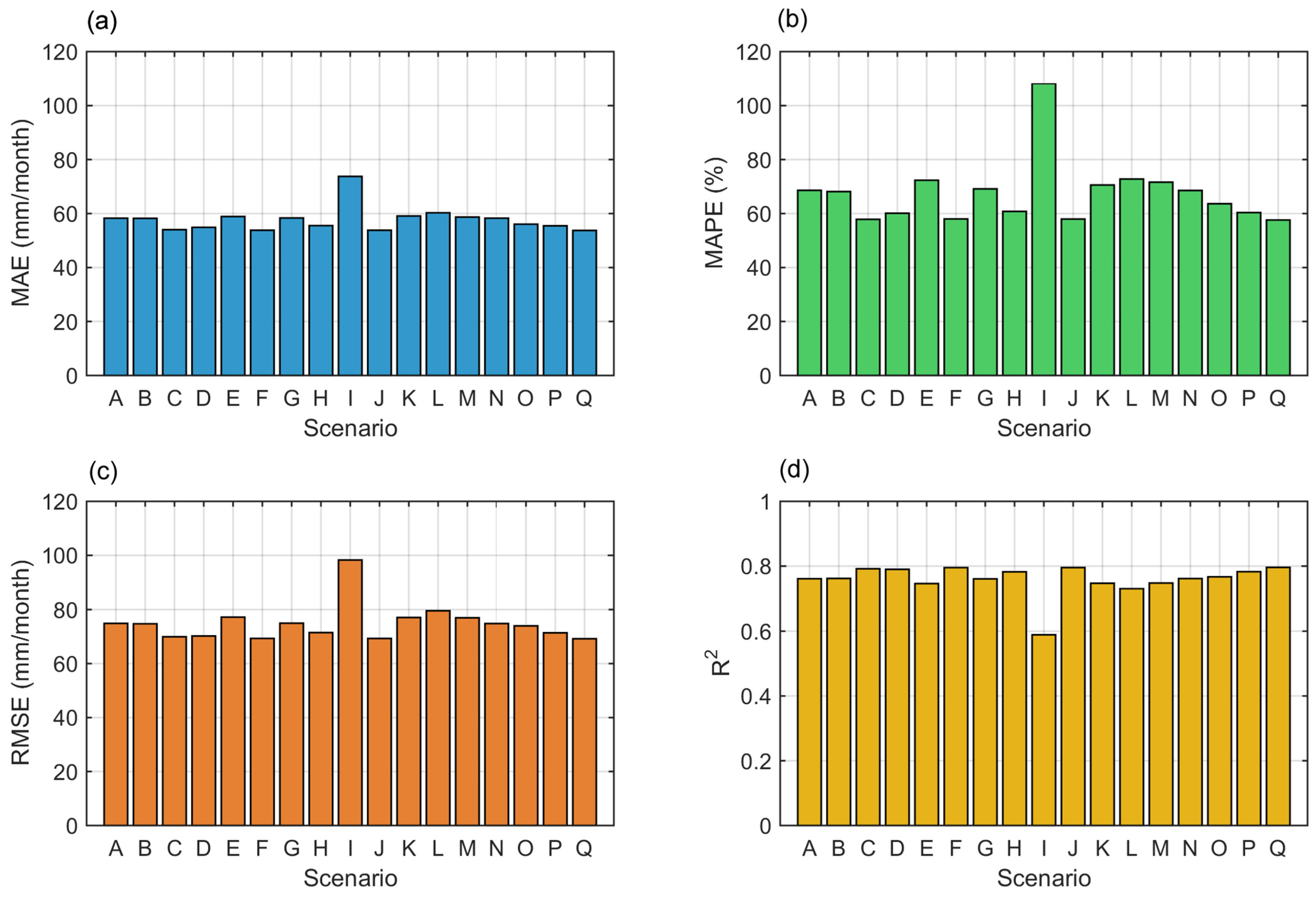
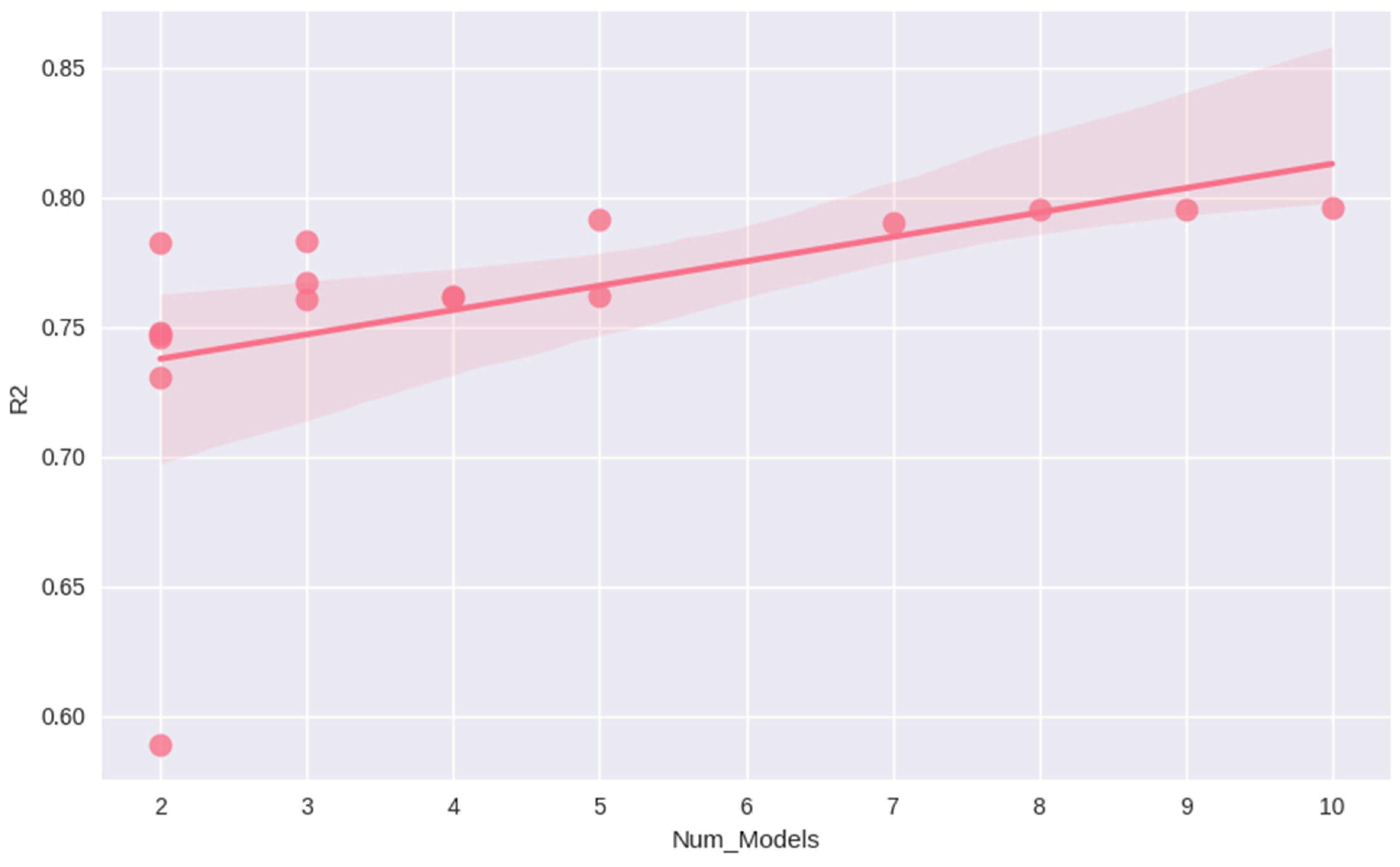
3.2. Analysis of Ensemble Stacking Performance in Various Scenarios
3.3. Comparative Analysis Between Scenarios
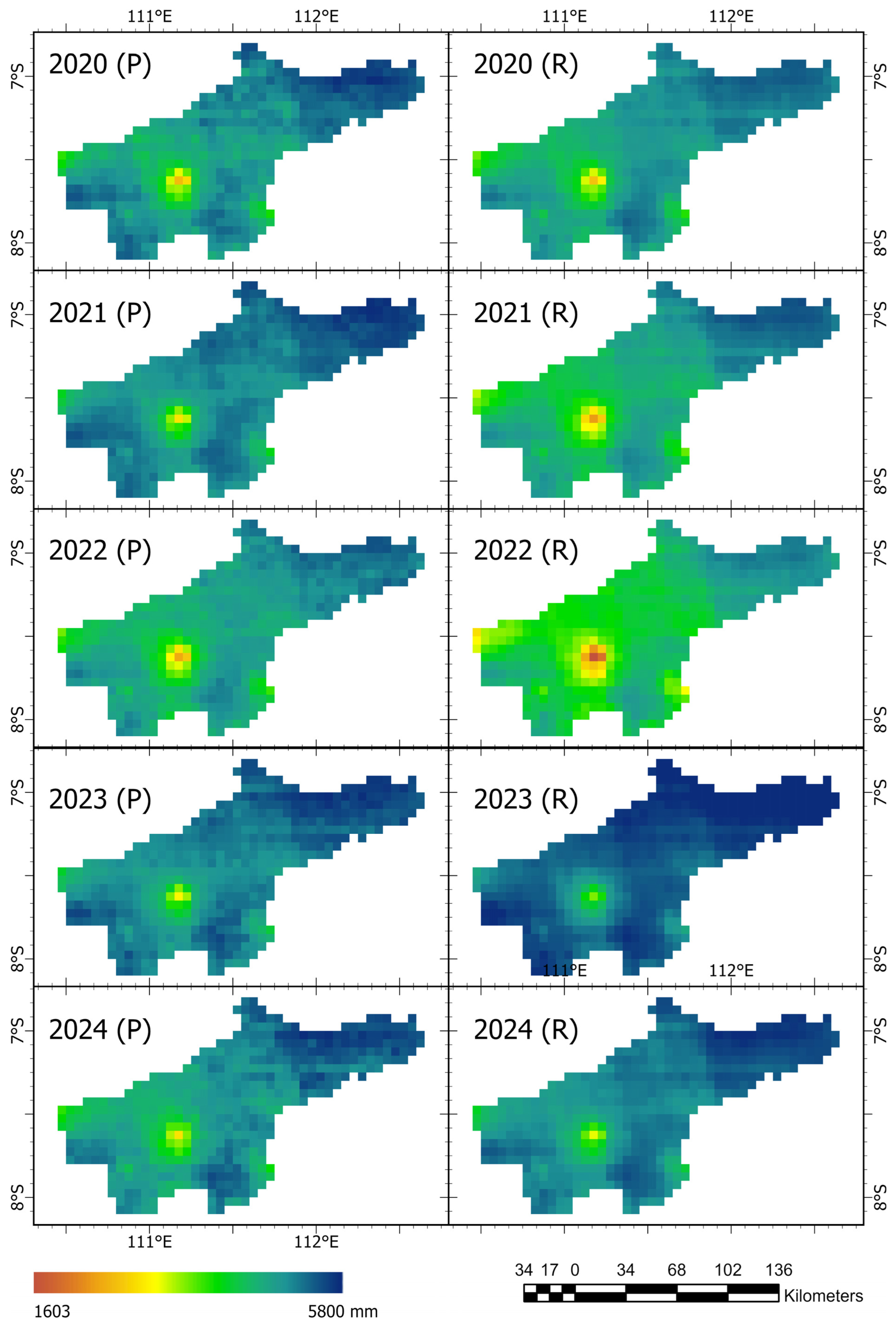
3.4. Spatial and Temporal Error Analysis
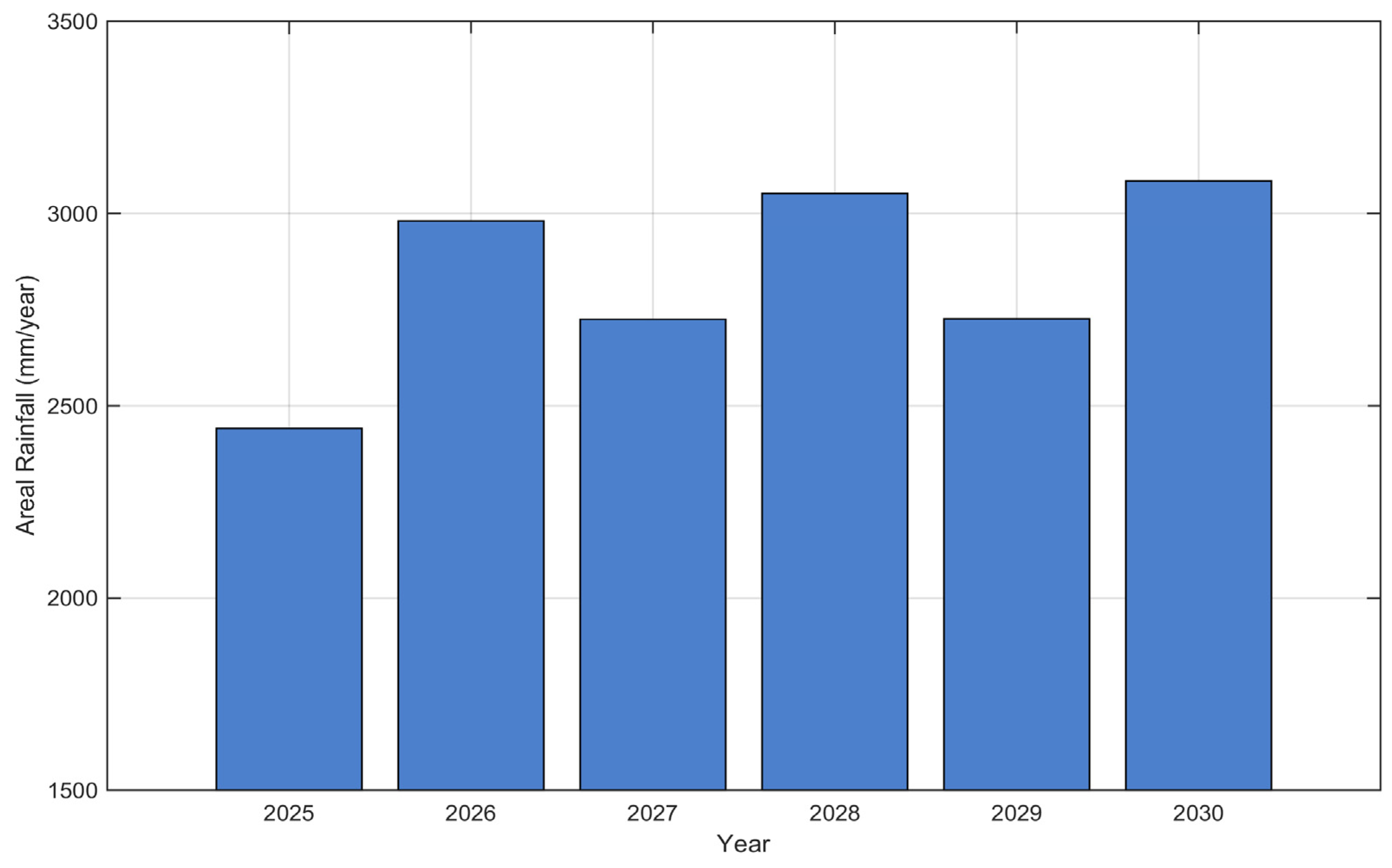
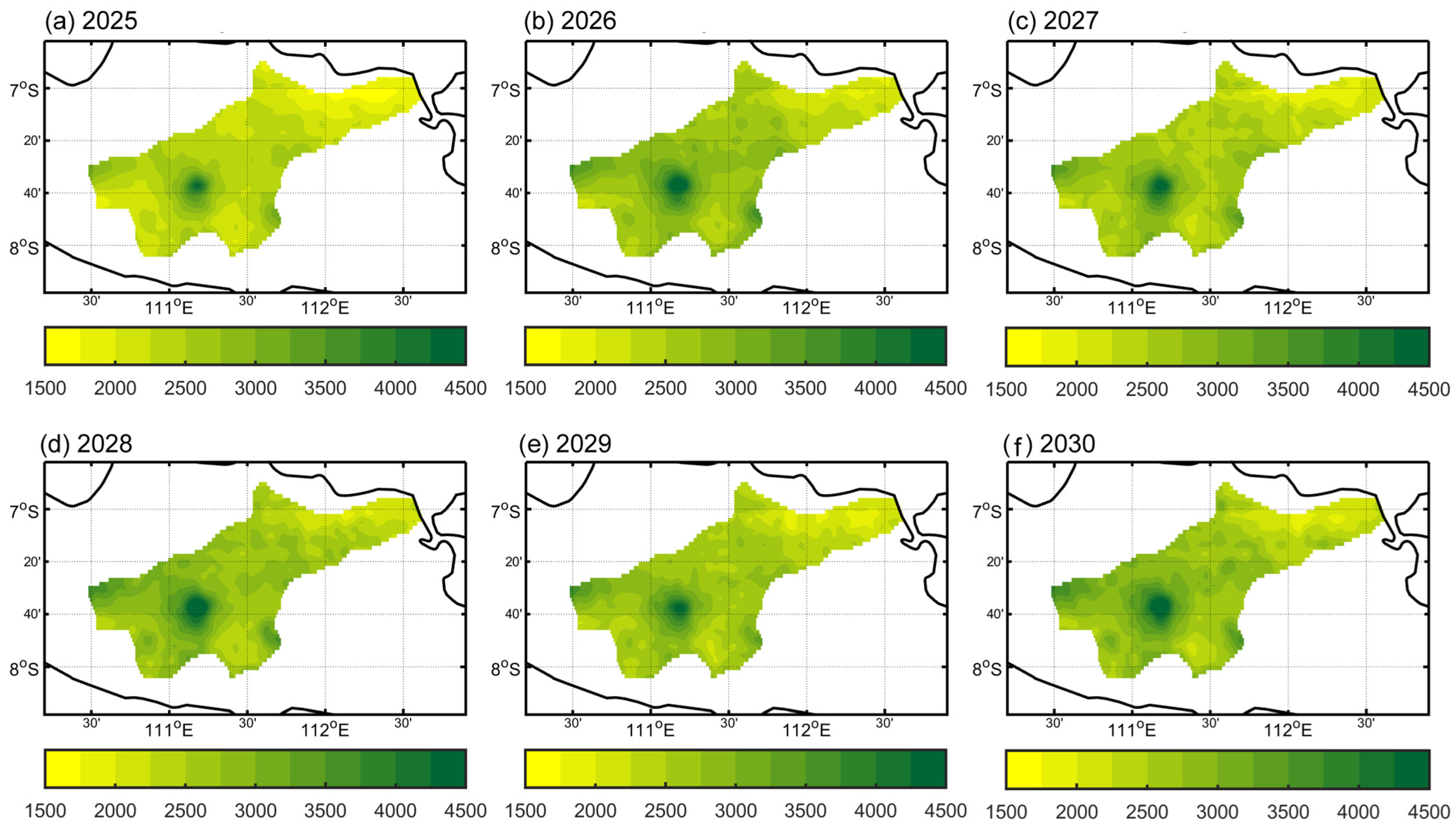
3.5. Analysis of Spatio-Temporal Rainfall Patterns
4. Discussion
4.1. Evaluation of Findings
4.2. Limitations and Future Works
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Alikhanov, B.; Pulatov, B.; Samiev, L. Impact of Climate Change on the Cryosphere of the Ugam Chatkal National Park, Bostonliq District, Uzbekistan, During the Post-Soviet Period, Based on Remote Sensing and Statistical Analysis. Forum Geogr. 2024, 38, 302–316. [Google Scholar] [CrossRef]
- Haq, D.Z.; Novitasari, D.C.R.; Hamid, A.; Ulinnuha, N.; Farida, Y.; Nugraheni, R.D.; Nariswari, R.; Rohayani, H.; Pramulya, R.; Widjayanto, A. Long Short-Term Memory Algorithm for Rainfall Prediction Based on El-Nino and IOD Data. Procedia Comput. Sci. 2021, 179, 829–837. [Google Scholar] [CrossRef]
- Ward, P.J.; Van Pelt, S.C.; De Keizer, O.; Aerts, J.C.J.H.; Beersma, J.J.; Van Den Hurk, B.J.J.M.; Te Linde, A.H. Including Climate Change Projections in Probabilistic Flood Risk Assessment. J. Flood Risk Manag. 2014, 7, 141–151. [Google Scholar] [CrossRef]
- Kasihairani, D.; Hidayat, R.; Supari, S. Assessing the Reliability of Predicted Decadal Surface Temperatures in Southeast Asia. Forum Geogr. 2024, 38, 413–425. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Aerts, J.C.; Van Beek, L.P.; Bierkens, M.F.; Bouwman, A.; Jongman, B.; Kwadijk, J.C.; Ligtvoet, W.; Lucas, P.L.; Van Vuuren, D.P. Global Drivers of Future River Flood Risk. Nat. Clim. Change 2016, 6, 381–385. [Google Scholar] [CrossRef]
- Gu, J.; Liu, S.; Zhou, Z.; Chalov, S.R.; Zhuang, Q. A Stacking Ensemble Learning Model for Monthly Rainfall Prediction in the Taihu Basin, China. Water 2022, 14, 492. [Google Scholar] [CrossRef]
- Praveen, B.; Talukdar, S.; Shahfahad; Mahato, S.; Mondal, J.; Sharma, P.; Islam, A.R.M.T.; Rahman, A. Analyzing Trend and Forecasting of Rainfall Changes in India Using Non-Parametrical and Machine Learning Approaches. Sci. Rep. 2020, 10, 10342. [Google Scholar] [CrossRef]
- Schaffer, A.L.; Dobbins, T.A.; Pearson, S.-A. Interrupted Time Series Analysis Using Autoregressive Integrated Moving Average (ARIMA) Models: A Guide for Evaluating Large-Scale Health Interventions. BMC Med. Res. Methodol. 2021, 21, 58. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhang, Q.; Kashani, M.H.; Jun, C.; Bateni, S.M.; Band, S.S.; Dash, S.S.; Chau, K.-W. Forecast of Rainfall Distribution Based on Fixed Sliding Window Long Short-Term Memory. Eng. Appl. Comput. Fluid Mech. 2022, 16, 248–261. [Google Scholar] [CrossRef]
- Ni, L.; Wang, D.; Singh, V.P.; Wu, J.; Wang, Y.; Tao, Y.; Zhang, J. Streamflow and Rainfall Forecasting by Two Long Short-Term Memory-Based Models. J. Hydrol. 2020, 583, 124296. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Miao, Q.; Pan, B.; Wang, H.; Hsu, K.; Sorooshian, S. Improving Monsoon Precipitation Prediction Using Combined Convolutional and Long Short Term Memory Neural Network. Water 2019, 11, 977. [Google Scholar] [CrossRef]
- Fang, L.; Shao, D. Application of Long Short-Term Memory (LSTM) on the Prediction of Rainfall-Runoff in Karst Area. Front. Phys. 2022, 9, 790687. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W. Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Slater, L.J.; Arnal, L.; Boucher, M.-A.; Chang, A.Y.-Y.; Moulds, S.; Murphy, C.; Nearing, G.; Shalev, G.; Shen, C.; Speight, L. Hybrid Forecasting: Blending Climate Predictions with AI Models. Hydrol. Earth Syst. Sci. 2023, 27, 1865–1889. [Google Scholar] [CrossRef]
- Espeholt, L.; Agrawal, S.; Sønderby, C.; Kumar, M.; Heek, J.; Bromberg, C.; Gazen, C.; Carver, R.; Andrychowicz, M.; Hickey, J. Deep Learning for Twelve Hour Precipitation Forecasts. Nat. Commun. 2022, 13, 5145. [Google Scholar] [CrossRef]
- Koya, S.R.; Roy, T. Temporal Fusion Transformers for Streamflow Prediction: Value of Combining Attention with Recurrence. J. Hydrol. 2024, 637, 131301. [Google Scholar] [CrossRef]
- Lim, B.; Zohren, S. Time-Series Forecasting with Deep Learning: A Survey. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2021, 379, 20200209. [Google Scholar] [CrossRef]
- Laptev, N.; Yosinski, J.; Li, L.E.; Smyl, S. Time-Series Extreme Event Forecasting with Neural Networks at Uber. In Proceedings of the International conference on machine learning, Sydney, Australia, 6–11 August 2017; Volume 34, pp. 1–5. [Google Scholar]
- Avand, M.; Moradi, H.R.; Ramazanzadeh Lasboyee, M. Spatial Prediction of Future Flood Risk: An Approach to the Effects of Climate Change. Geosciences 2021, 11, 25. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating Physics-Based Modeling with Machine Learning: A Survey. arXiv 2020, arXiv:2003.04919. [Google Scholar]
- Kundu, S.; Biswas, S.K.; Tripathi, D.; Karmakar, R.; Majumdar, S.; Mandal, S. A Review on Rainfall Forecasting Using Ensemble Learning Techniques. E-Prime-Adv. Electr. Eng. Electron. Energy 2023, 6, 100296. [Google Scholar] [CrossRef]
- Nelson, B.K. Time Series Analysis Using Autoregressive Integrated Moving Average (ARIMA) Models. Acad. Emerg. Med. 1998, 5, 739–744. [Google Scholar] [CrossRef] [PubMed]
- Das, P.; Posch, A.; Barber, N.; Hicks, M.; Duffy, K.; Vandal, T.; Singh, D.; van Werkhoven, K.; Ganguly, A.R. Hybrid Physics-AI Outperforms Numerical Weather Prediction for Extreme Precipitation Nowcasting. npj Clim. Atmos. Sci. 2024, 7, 282. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Doulamis, N.; Doulamis, A. Ensemble Learning for Uncertainty Estimation with Application to the Correction of Satellite Precipitation Products. Mach. Learn. Earth 2025, 1, 015004. [Google Scholar] [CrossRef]
- Baig, F.; Ali, L.; Faiz, M.A.; Chen, H.; Sherif, M. How Accurate Are the Machine Learning Models in Improving Monthly Rainfall Prediction in Hyper Arid Environment? J. Hydrol. 2024, 633, 131040. [Google Scholar] [CrossRef]
- El Hafyani, M.; El Himdi, K.; El Adlouni, S.-E. Improving Monthly Precipitation Prediction Accuracy Using Machine Learning Models: A Multi-View Stacking Learning Technique. Front. Water 2024, 6, 1378598. [Google Scholar] [CrossRef]
- Shetty, S.; Dharmendra, D.; Bankapur, S.; Prasad, P. HydroStack: A Hybrid Meta-Ensemble Machine Learning Framework for Accurate Annual Rainfall Prediction. In Proceedings of the 2024 8th International Conference on I-SMAC (IoT in Social, Mobile, Analytics and Cloud)(I-SMAC), Biratnagar, Nepal, 3–5 October 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1926–1934. [Google Scholar]
- Kim, S.; Shin, J.-Y.; Heo, J.-H. Assessment of Future Rainfall Quantile Changes in South Korea Based on a CMIP6 Multi-Model Ensemble. Water 2025, 17, 894. [Google Scholar] [CrossRef]
- Priyana, Y.; Jumadi; Anna, A.N.; Rudiyanto. Farmer’s Adaptation Strategies in Facing Drought Disasters (A Case Study in Some Areas of Bengawan Solo Watershed). AIP Conf. Proc. 2023, 2727, 050026. [Google Scholar] [CrossRef]
- Anna, A.N.; Priyana, Y.; Rudiyanto; Fikriyah, V.N. Water Resources Management Model Based Area (A Case Study in Some Areas of Bengawan Solo Watershed). AIP Conf. Proc. 2023, 2727, 050027. [Google Scholar] [CrossRef]
- CHIRPS: Rainfall Estimates from Rain Gauge and Satellite Observations. Climate Hazards Center-UC Santa Barbara. Available online: https://www.chc.ucsb.edu/data/chirps (accessed on 30 August 2025).
- Jana, R.; Jana, N.C. Agricultural Vulnerability to Cyclones in Coastal West Bengal. DYSONA-Appl. Sci. 2026, 7, 61–72. [Google Scholar] [CrossRef]
- Naik, R.; Majhi, B. Explainable AI Reverse Verification Approach for Monthly Rainfall Prediction in Chhattisgarh, India. Theor. Appl. Climatol. 2025, 156, 412. [Google Scholar] [CrossRef]
- Kumar, V.; Kedam, N.; Kisi, O.; Alsulamy, S.; Khedher, K.M.; Salem, M.A. A Comparative Study of Machine Learning Models for Daily and Weekly Rainfall Forecasting. Water Resour. Manag. 2025, 39, 271–290. [Google Scholar] [CrossRef]
- Banik, R.; Biswas, A. Rainfall Prediction for Climate-Resilient Agriculture: A Robust Ensemble with SARIMA and LightGBM. Paddy Water Environ. 2025, 23, 263–275. [Google Scholar] [CrossRef]
- Zhuang, H.; Lehner, F.; DeGaetano, A.T. Improved Diagnosis of Precipitation Type with LightGBM Machine Learning. J. Appl. Meteorol. Climatol. 2024, 63, 437–453. [Google Scholar] [CrossRef]
- Pan, X.; Hou, J.; Gao, X.; Chen, G.; Li, D.; Imran, M.; Li, X.; Yang, N.; Ma, M.; Zhou, X. LSTM Model-Based Rapid Prediction Method of Urban Inundation with Rainfall Time Series. Water Resour. Manag. 2025, 39, 661–688. [Google Scholar] [CrossRef]
- Sivadasan, E.T.; Sundaram, N.M.; Santhosh, R. Deep Learning for Energy Forecasting Using Gated Recurrent Units and Long Short-Term Memory. J. Intell. Syst. Internet Things 2025, 14, 90. [Google Scholar] [CrossRef]
- Al-Samrraie, L.A.; Abdalla, A.M.; Alrawashdeh, K.A.-B.; Bsoul, A.A.; Awad, M.A.; Alzboon, K.; Al-Taani, A.A. Deep Learning Models Based on CNN, RNN, and LSTM for Rainfall Forecasting: Jordan as a Case Study. Math. Model. Eng. Probl. 2025, 12, 2456. [Google Scholar] [CrossRef]
- Yin, W.; Zhou, C.; Tian, Y.; Qiu, H.; Zhang, W.; Chen, H.; Liu, P.; Zhao, Q.; Kong, J.; Yao, Y. Accurate Rainfall Prediction Using GNSS PWV Based on Pre-Trained Transformer Model. Remote Sens. 2025, 17, 2023. [Google Scholar] [CrossRef]
- Zandi, O.; Zahraie, B.; Nasseri, M.; Behrangi, A. Stacking Machine Learning Models versus a Locally Weighted Linear Model to Generate High-Resolution Monthly Precipitation over a Topographically Complex Area. Atmos. Res. 2022, 272, 106159. [Google Scholar] [CrossRef]
- Zhou, Y.; Cui, Z.; Lin, K.; Sheng, S.; Chen, H.; Guo, S.; Xu, C.-Y. Short-Term Flood Probability Density Forecasting Using a Conceptual Hydrological Model with Machine Learning Techniques. J. Hydrol. 2022, 604, 127255. [Google Scholar] [CrossRef]
- Lu, H.; Li, F.; Gong, T.; Gao, Y.; Li, J.; Wang, G.; Qiu, J. Temporal Variability of Precipitation over the QINGHAI-TIBETAN Plateau and Its Surrounding Areas in the Last 40 Years. Int. J. Climatol. 2023, 43, 1912–1934. [Google Scholar] [CrossRef]
- Lu, H.-L.; Qiu, J.; Li, M.-J.; Zuo, H.-M.; Li, J.-L.; Hu, B.X.; Li, F.-F. Temporal and Spatial Variations in the Sub-Daily Precipitation Structure over the Qinghai–Tibet Plateau (QTP). Sci. Total Environ. 2024, 915, 170153. [Google Scholar] [CrossRef]
- Lu, H.; Qiu, J.; Hu, B.X.; Li, F. Potential Impact of Precipitation Temporal Structure on Meteorological Drought and Vegetation Condition: A Case Study on Qinghai-Tibet Plateau. J. Hydrol. Reg. Stud. 2024, 56, 102048. [Google Scholar] [CrossRef]
- Sun, P.; Qiu, J.; Zhang, W.; Gao, Y.; Li, J.; Li, F. Analysis of Concurrent Extreme Precipitation and Water Vapor Events on the Tibetan Plateau: Copula-Based Probability Modeling and Atmospheric Teleconnection. J. Hydrol. 2025, 661, 133695. [Google Scholar] [CrossRef]
- Amini, E.; Zolfaghari, A.; Kaboli, H.; Rahimi, M. Estimation of Rainfall Erosivity Map in Areas with Limited Number of Rainfall Station (Case Study: Semnan Province). Iran. J. Soil Water Res. 2022, 53, 2027–2044. [Google Scholar]
- He, J.; Li, S.; Wang, B.; Zhang, L.; Duan, K. Quantifying the Impacts of ENSO on Australian Summer Rainfall Extremes during 1960–2020. J. Hydrol. 2025, 654, 132834. [Google Scholar] [CrossRef]
- Mandal, T.; Das, J.; Rahman, A.T.M.S.; Saha, P.; Saha, S. Understanding the Teleconnections of ENSO and IOD with Rainfall Variation in India. Environ. Model. Assess. 2025, 1–31. [Google Scholar] [CrossRef]
- Tsai, W.Y.; Sakaeda, N.; Ruppert, J.H. Subseasonal-To-Seasonal (S2S) Prediction Skill of the Rainfall Diurnal Cycle Over the Maritime Continent and Its MJO Dependence. J. Geophys. Res. Atmos. 2025, 130, e2024JD043102. [Google Scholar] [CrossRef]
- Yang, Y.; Tan, G.; Shen, Z.; Zhang, Y.; Fei, Q.; Liu, X.; Dogar, M.A. Integrating Physical Dynamics into Ensemble ML for Improved Monthly Rainfall Forecasting. Earth Syst. Environ. 2025. [Google Scholar] [CrossRef]


| Model | Dropout | Loss | Optimizer | Batch | Epochs (max) | Early Stop |
|---|---|---|---|---|---|---|
| LSTM | 0.20 | Huber | Adam 1 × 10−3 | 64 | 80 | patience 10 |
| GRU | 0.20 | Huber | Adam 1 × 10−3, clipnorm = 1.0 | 64 | 80 | patience 10 |
| TCN | 0.20 | Huber | Adam 1 × 10−3, clipnorm = 1.0 | 64 | 80 | patience 10 |
| CNN (1D) | 0.15 | Huber (δ = 1.0) | Adam 1 × 10−3, clipnorm = 1.0 | 64 | 100 | patience 12 |
| Transformer | 0.10 | Huber (δ = 1.0) | Adam 1 × 10−3, clipnorm = 1.0 | 64 | 120 | patience 12 |
| Scenario | Base Models Used | Category |
|---|---|---|
| A | RF, XGB, MLP, LGBM | Best ML |
| B | RF, XGB, SVR, MLP, LGBM | All ML |
| C | LSTM, GRU, TCN, CNN, Transformer | All DL |
| D | RF, XGB, SVR, MLP, LGBM, LSTM, GRU | Light ML + DL |
| E | RF, LSTM | One ML + one DL |
| F | RF, XGB, LGBM, LSTM, GRU, TCN, CNN, Transformer | Small ML set + all DL |
| G | RF, XGB, LGBM | ML minimum (tree ensemble) |
| H | LSTM, GRU | Recurrent DL only |
| I | CNN, Transformer | DL spatial + |
| J | RF, XGB, MLP, LGBM, LSTM, GRU, TCN, CNN, Transformer | All models (exclude SVR) |
| K | RF, MLP | Simpler ML |
| L | SVR, LSTM | Non-tree ML + DL |
| M | RF, Transformer | Best ML + Best DL (hypothetical) |
| N | RF, XGB, SVR, LGBM | All tree + margin-based ML |
| O | GRU, CNN, Transformer | Non-LSTM DL |
| P | MLP, LSTM, GRU | Shallow NN + Recurrent NN |
| Q | RF, XGB, SVR, MLP, LGBM, LSTM, GRU, TCN, CNN, Transformer | Full stack |
| No | Model | MAE | RMSE | R2 | MAPE (%) |
|---|---|---|---|---|---|
| 1 | RF | 61.444188 | 84.423621 | 0.69648 | 45.056787 |
| 2 | XGB | 59.088476 | 80.30787 | 0.725353 | 45.903841 |
| 3 | SVR | 66.850178 | 90.365139 | 0.652255 | 50.787902 |
| 4 | MLP | 66.494233 | 89.419753 | 0.659493 | 54.942884 |
| 5 | LGBM | 60.390639 | 84.154525 | 0.698412 | 42.281571 |
| 6 | LSTM | 66.480116 | 89.583459 | 0.658245 | 48.597533 |
| 7 | GRU | 59.59246 | 80.753112 | 0.722299 | 51.325625 |
| 8 | TCN | 76.301859 | 107.763161 | 0.505462 | 62.699634 |
| 9 | CNN | 83.509829 | 118.2743 | 0.404284 | 75.991914 |
| 10 | TRANSFORMER | 85.433951 | 116.276754 | 0.424236 | 88.148625 |
| Scenario | Number of | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|
| Models | |||||
| A | 4 | 58.28445 | 74.89934 | 68.61568 | 0.761101 |
| B | 5 | 58.21054 | 74.75468 | 68.15332 | 0.762023 |
| C | 5 | 54.03069 | 69.93829 | 57.86597 | 0.7917 |
| D | 7 | 54.88516 | 70.2175 | 60.11231 | 0.790034 |
| E | 2 | 58.89576 | 77.21451 | 72.35184 | 0.746104 |
| F | 8 | 53.82676 | 69.33265 | 57.99148 | 0.795292 |
| G | 3 | 58.3688 | 74.97788 | 69.14402 | 0.7606 |
| H | 2 | 55.52901 | 71.48839 | 60.78105 | 0.782365 |
| I | 2 | 73.77387 | 98.26589 | 108.2156 | 0.588789 |
| J | 9 | 53.82123 | 69.32615 | 57.95161 | 0.795331 |
| K | 2 | 59.09539 | 77.08052 | 70.57744 | 0.746984 |
| L | 2 | 60.27887 | 79.57864 | 72.78444 | 0.730318 |
| M | 2 | 58.68729 | 76.96525 | 71.6339 | 0.74774 |
| N | 4 | 58.28895 | 74.8236 | 68.54438 | 0.761584 |
| O | 3 | 56.05623 | 73.97159 | 63.63283 | 0.766982 |
| P | 3 | 55.45571 | 71.40635 | 60.37016 | 0.782864 |
| Q | 10 | 53.73413 | 69.19845 | 57.61118 | 0.796084 |
| Metric | n | r (Pearson) | ρ (Pearson) | r (Spearman) | ρ (Spearman) |
|---|---|---|---|---|---|
| RMSE | 523 | 0.688864511 | 8.06 × 10−75 | 0.522441583 | 5.77 × 10−38 |
| MAE | 523 | 0.715706338 | 2.93 × 10−83 | 0.582148205 | 9.05 × 10−49 |
| MAPE | 523 | −0.273879234 | 1.88 × 10−10 | −0.4635174 | 3.23 × 10−29 |
| R2 | 523 | 0.171405655 | 8.16 × 10−5 | 0.229005504 | 1.19 × 10−7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jumadi, J.; Danardono, D.; Roziaty, E.; Ulinuha, A.; Supari, S.; Choy, L.K.; Sattar, F.; Nawaz, M. AI-Driven Ensemble Learning for Spatio-Temporal Rainfall Prediction in the Bengawan Solo River Watershed, Indonesia. Sustainability 2025, 17, 9281. https://doi.org/10.3390/su17209281
Jumadi J, Danardono D, Roziaty E, Ulinuha A, Supari S, Choy LK, Sattar F, Nawaz M. AI-Driven Ensemble Learning for Spatio-Temporal Rainfall Prediction in the Bengawan Solo River Watershed, Indonesia. Sustainability. 2025; 17(20):9281. https://doi.org/10.3390/su17209281
Chicago/Turabian StyleJumadi, Jumadi, Danardono Danardono, Efri Roziaty, Agus Ulinuha, Supari Supari, Lam Kuok Choy, Farha Sattar, and Muhammad Nawaz. 2025. "AI-Driven Ensemble Learning for Spatio-Temporal Rainfall Prediction in the Bengawan Solo River Watershed, Indonesia" Sustainability 17, no. 20: 9281. https://doi.org/10.3390/su17209281
APA StyleJumadi, J., Danardono, D., Roziaty, E., Ulinuha, A., Supari, S., Choy, L. K., Sattar, F., & Nawaz, M. (2025). AI-Driven Ensemble Learning for Spatio-Temporal Rainfall Prediction in the Bengawan Solo River Watershed, Indonesia. Sustainability, 17(20), 9281. https://doi.org/10.3390/su17209281








