Constructing a “Clustered–Boundary–Cellular” Model: Spatial Differentiation and Sustainable Governance of Traditional Villages in Multi-Ethnic China
Abstract
1. Introduction
2. Theoretical Framework
2.1. Theoretical Foundation and Evolution
2.2. The “Clustered–Boundary–Cellular” Model: A Contextual Framework
3. Materials and Methods
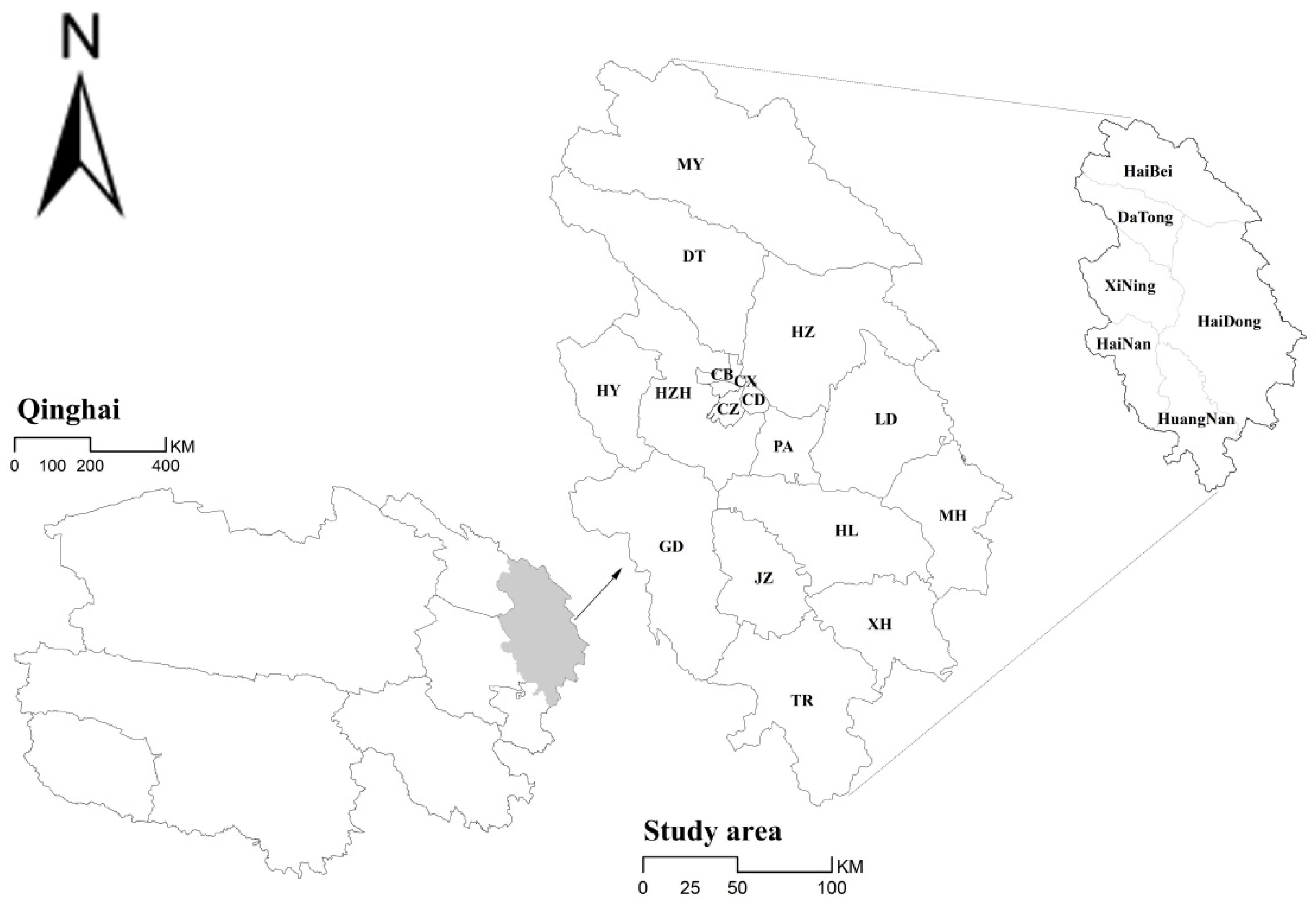
3.1. Study Area
3.2. Data Sources and Preprocessing
3.3. Research Methodology
3.3.1. Linking Methods to Hypotheses
3.3.2. Village Typology Classification: Operationalizing the Theoretical Framework
3.3.3. Spatial Pattern Analysis of Village Types
3.3.4. Statistical Testing of Driving Factors
3.3.5. Analysis of Driving Factors
4. Analysis and Results
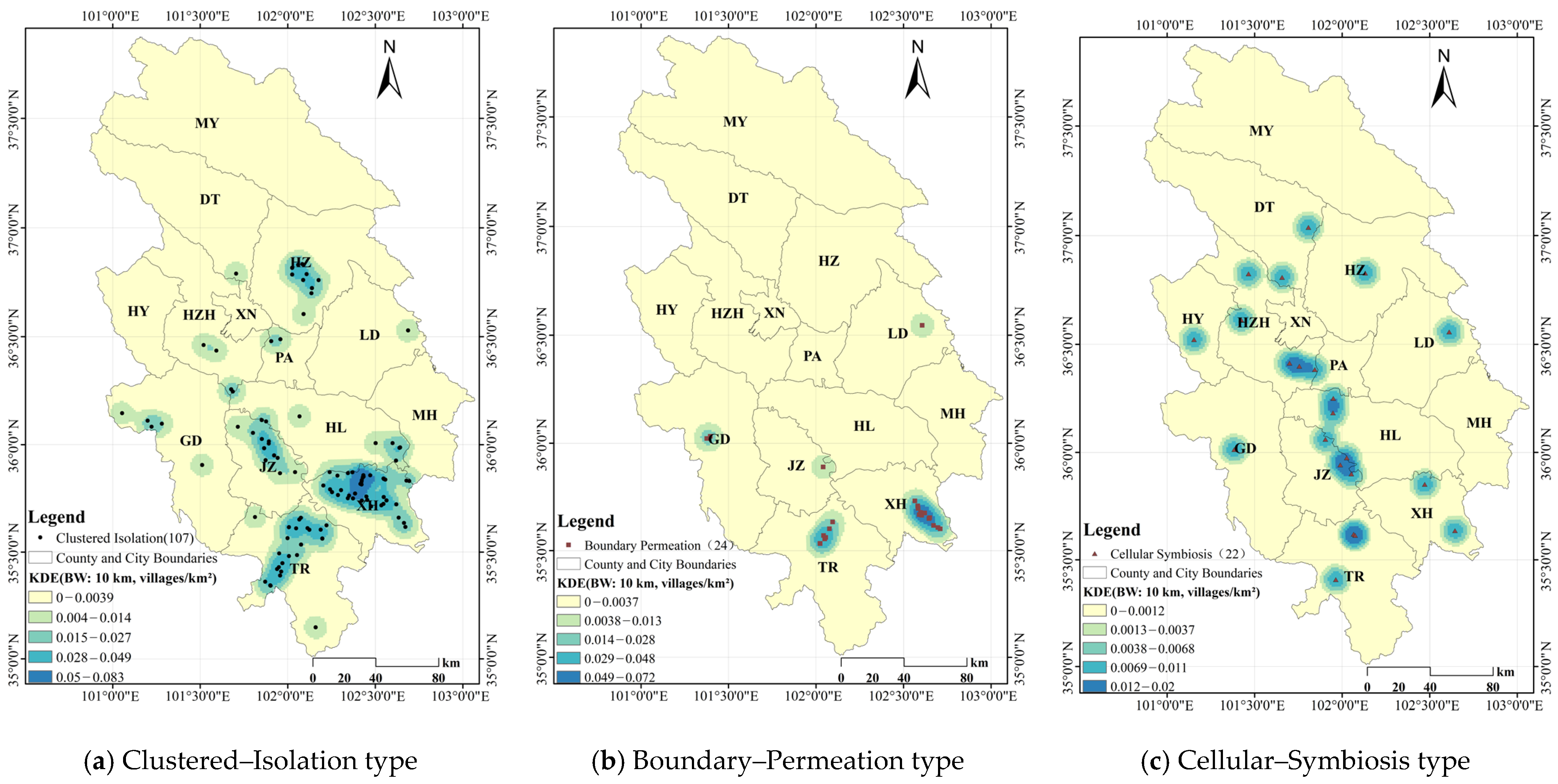
4.1. Typology and Spatial Distribution
4.2. Spatial Pattern Tests
4.2.1. Kernel Density Distribution Patterns
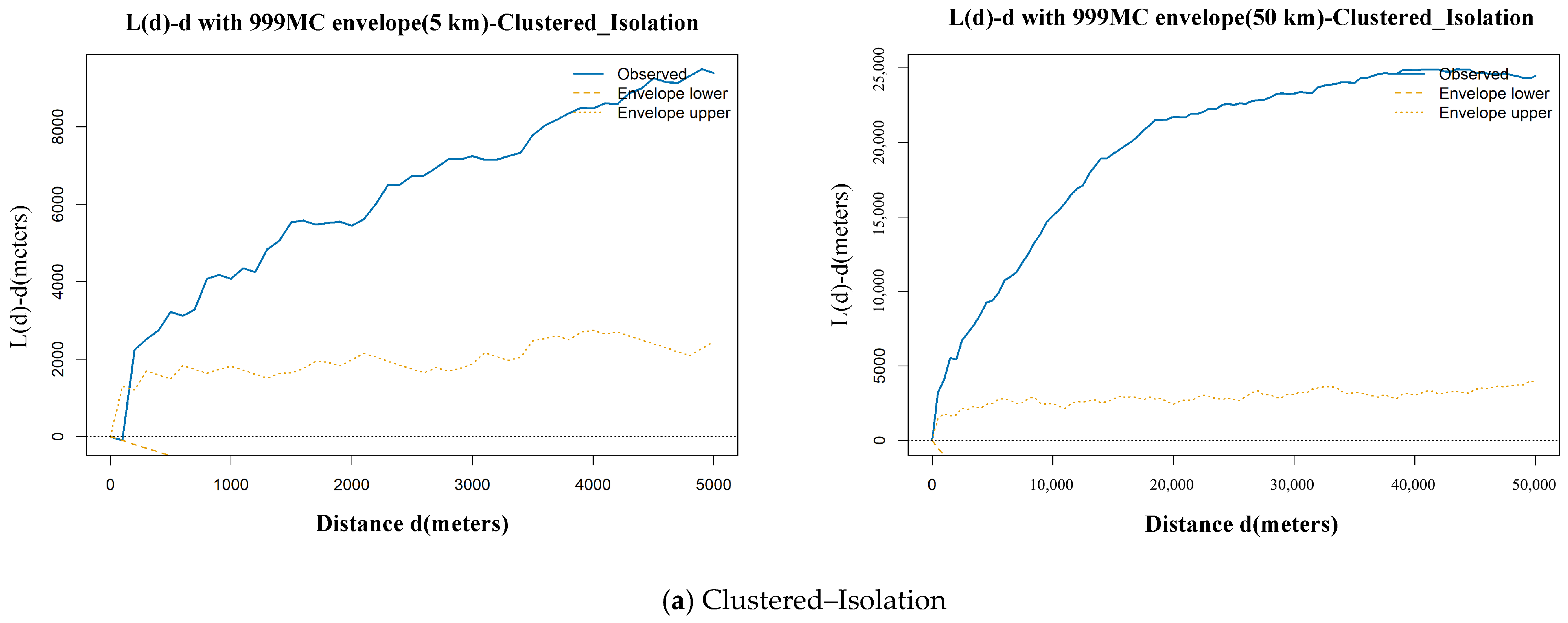
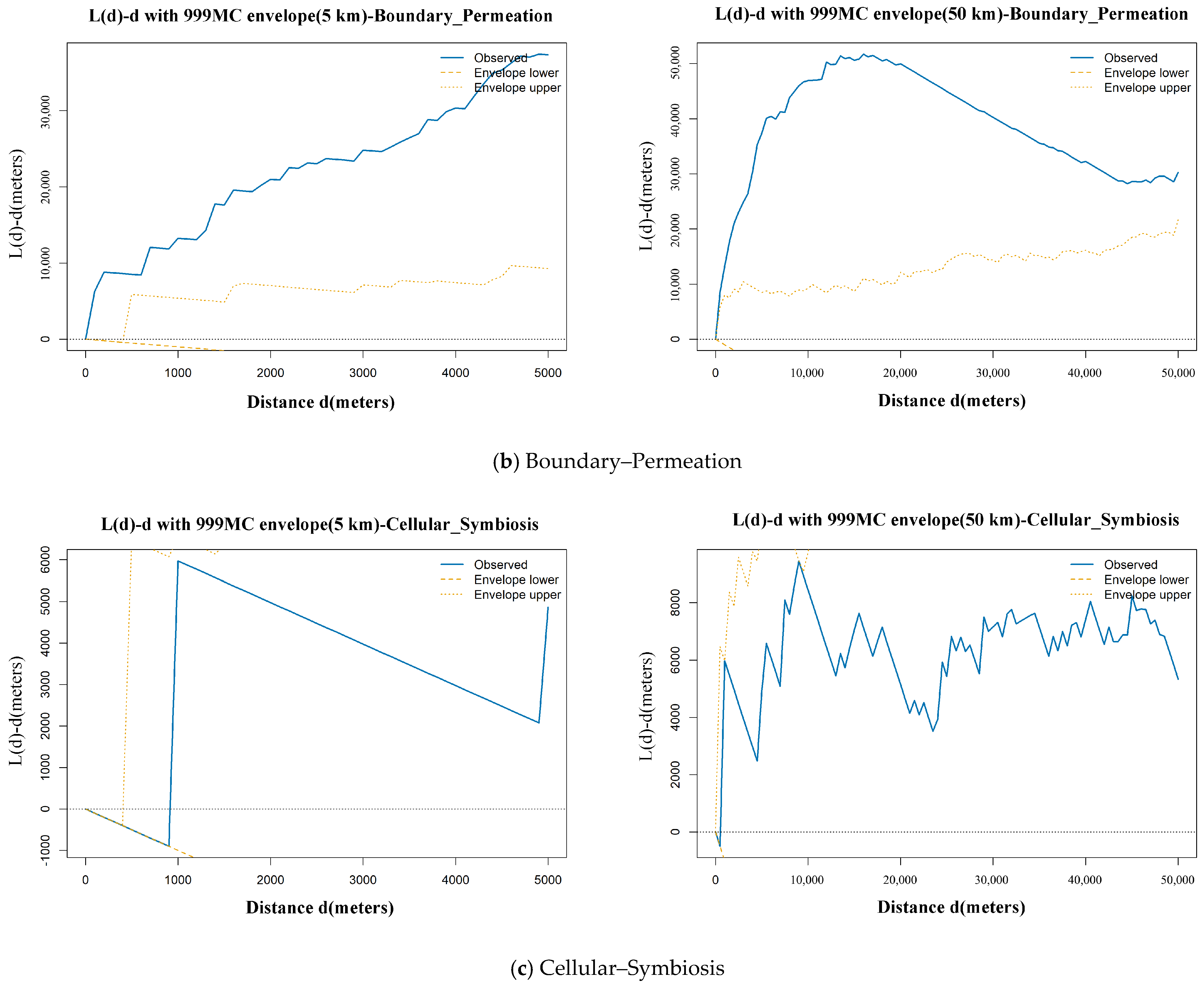
4.2.2. Ripley’s K/L Spatial Significance Test
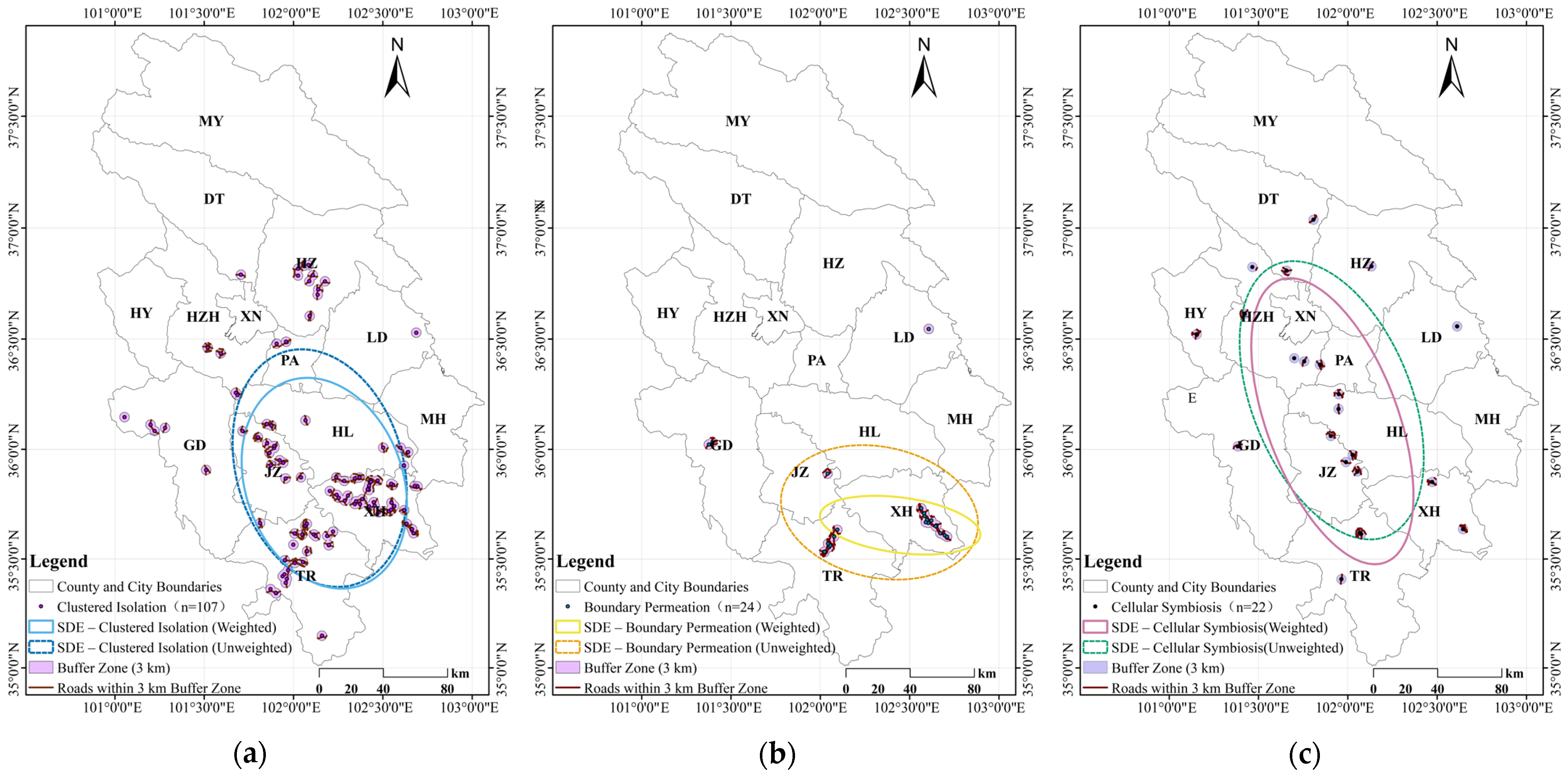
4.3. Directional and Anisotropy Analysis
4.4. Integrated Spatial Analysis of Influencing Factors
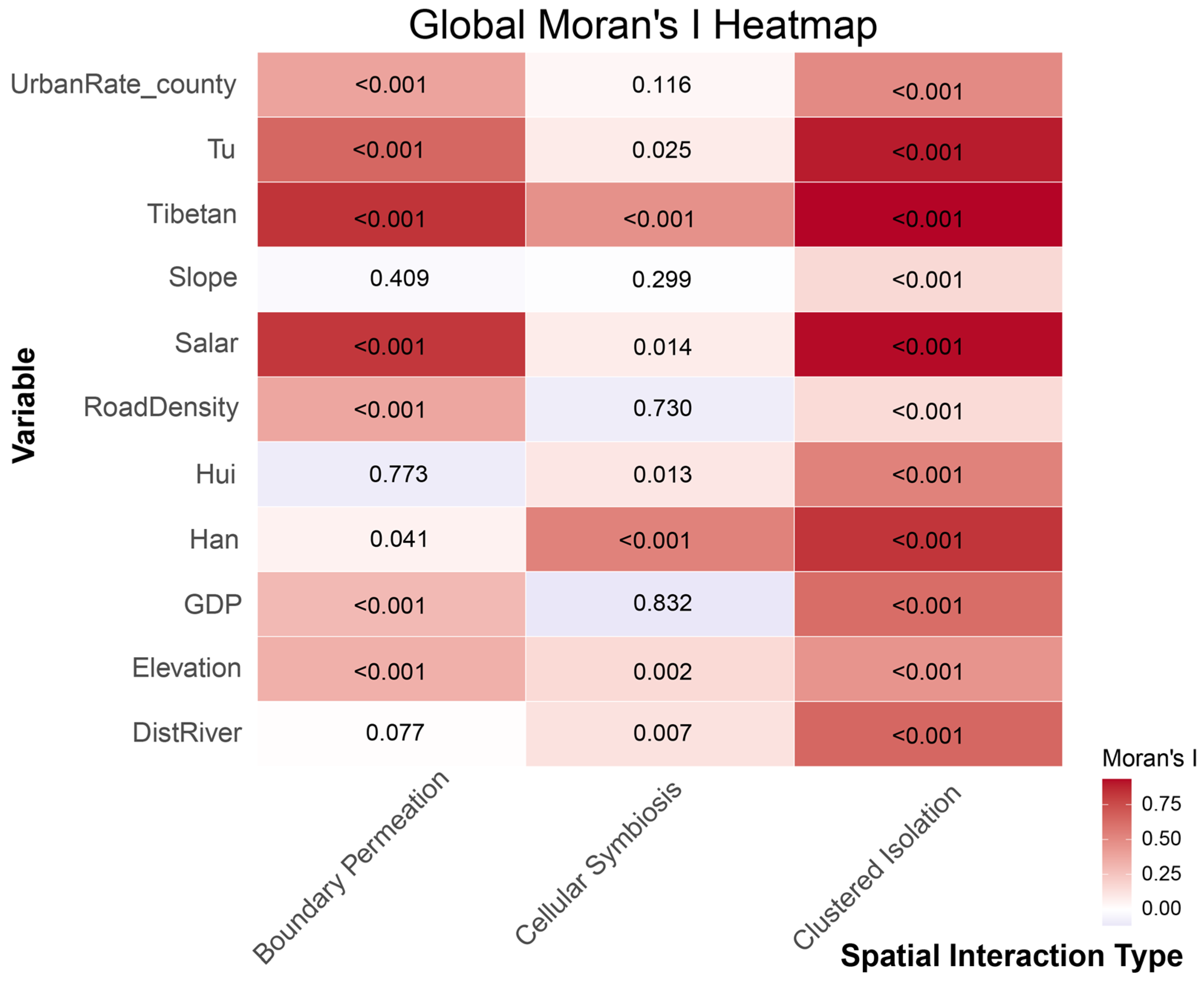
4.4.1. Global Spatial Autocorrelation
4.4.2. Spatial Differentiation of Influencing Factors Across Village Types
4.4.3. Analysis of Differentiated Influencing Factors of Village Types: Multinomial Logistic Regression Results
5. Discussion
5.1. Interpreting Spatial Patterns Through a Complementary Theoretical Lens
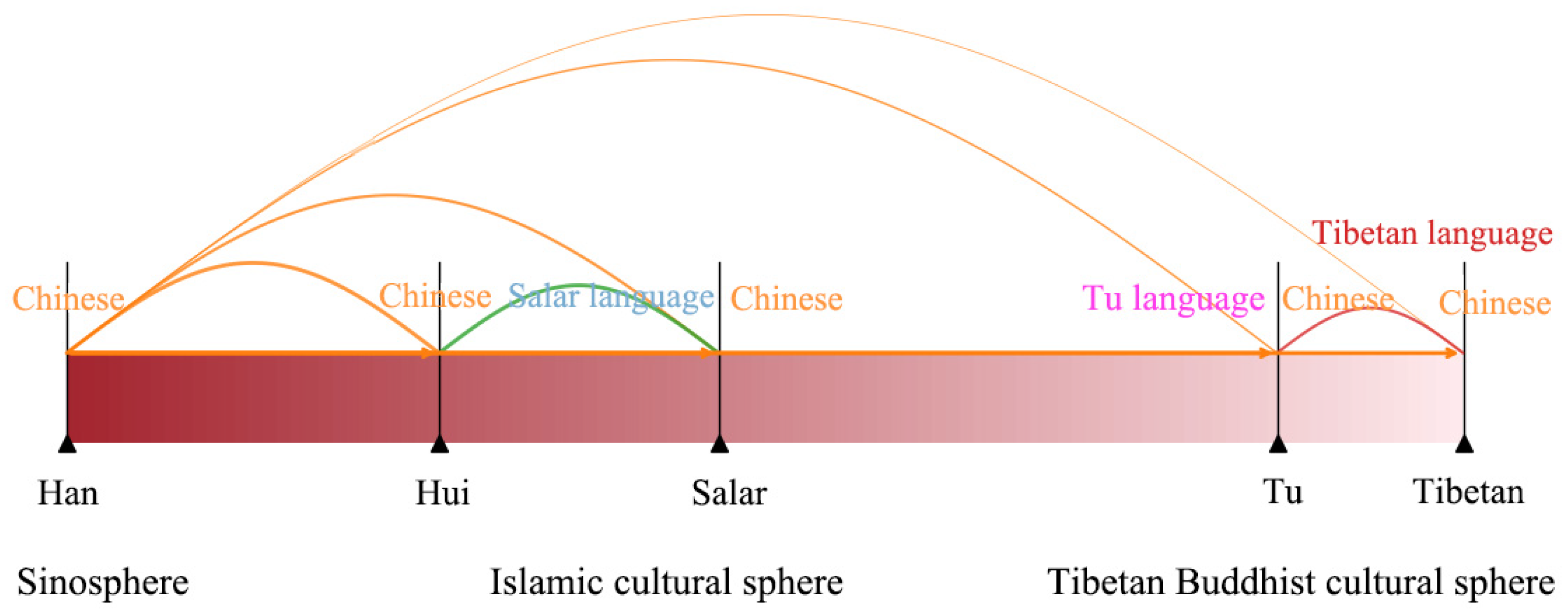
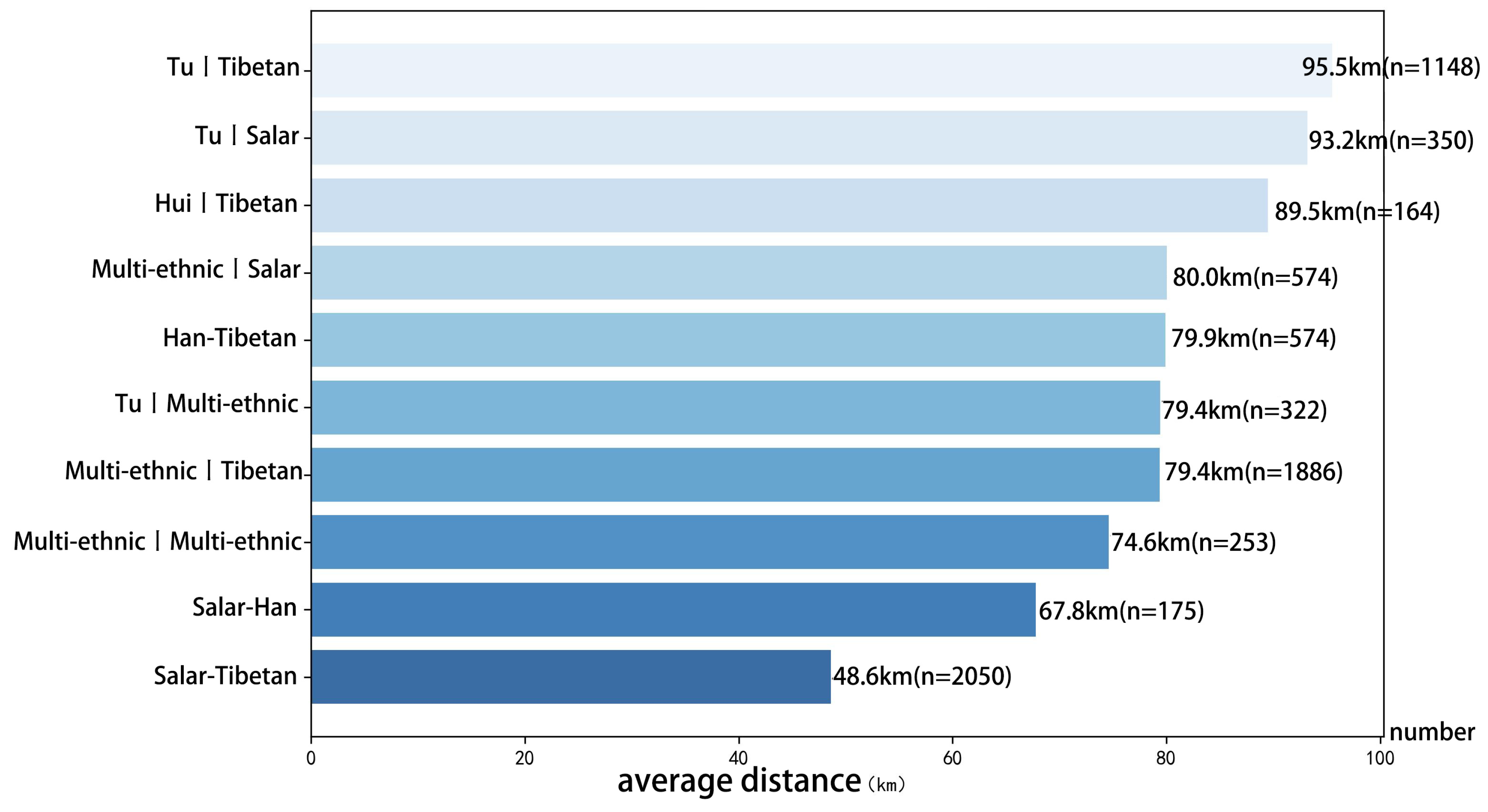
5.2. Synthesizing the Interplay of Natural Constraints and Socio-Cultural Adaptation
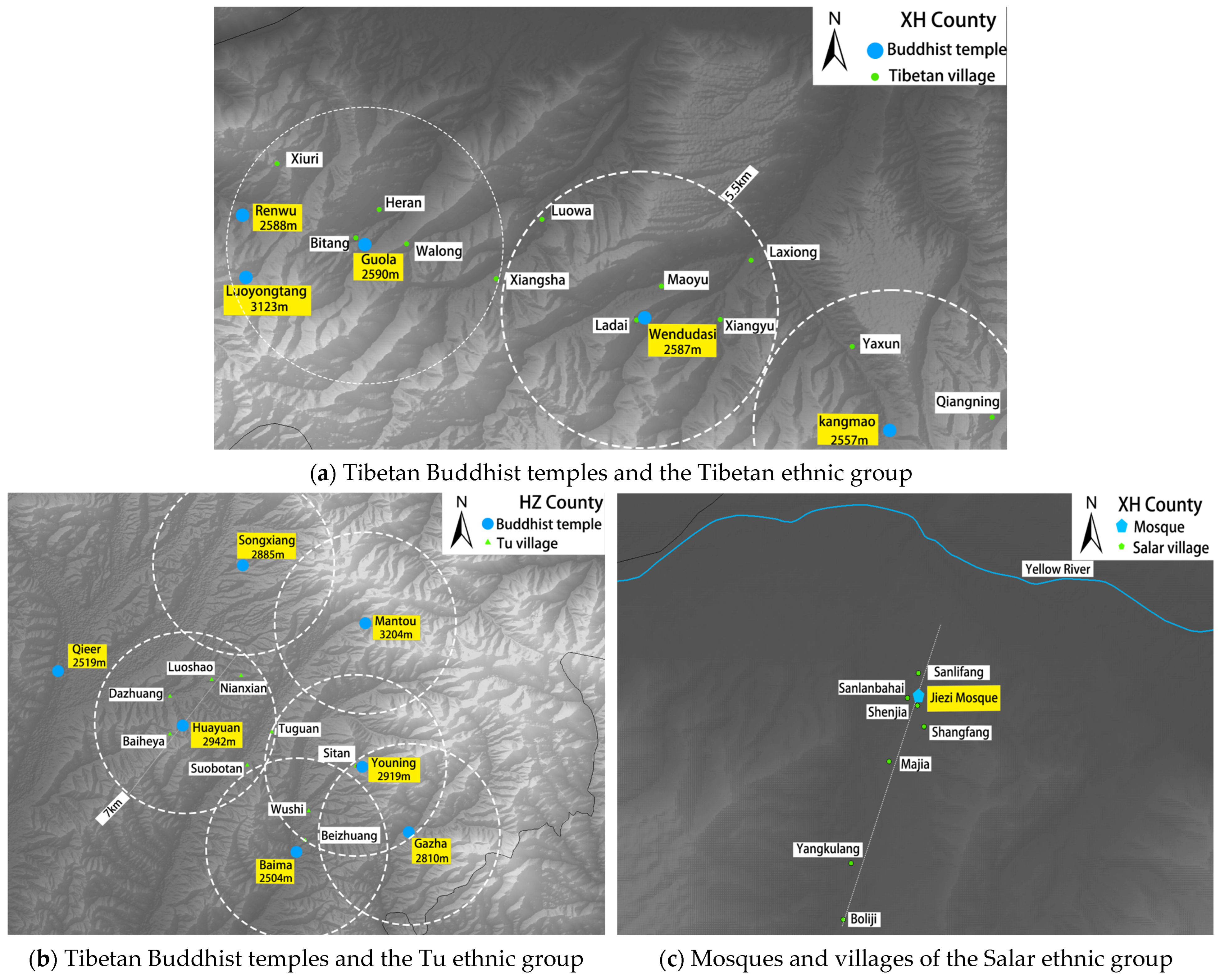
5.3. Religion as a Profound Organizing Logic in Socio-Spatial Formation
5.4. Infrastructure and Economic Change as Catalysts for Spatial Reorganization
5.5. Implications for Context-Sensitive Governance
5.6. Limitations and Avenues for Future Research
6. Conclusions
6.1. Principal Findings
6.2. Theoretical and Practical Contributions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Yu, M. Ethnic Inter-embeddedness: Current Situations and Prospects of the Research about the Path to the Construction of the Chinese National Community. J. Southwest Minzu Univ. 2024, 45, 28–37. [Google Scholar] [CrossRef]
- Yiftachel, O. Critical theory and ‘gray space’: Mobilization of the colonized. City 2009, 13, 240–256. [Google Scholar] [CrossRef]
- Han, Y.; He, M.-L.; Gao, J.-B.; Zheng, Q. Review on urban social exclusion in China and the Western countries from the perspective of space isolation. Hum. Geogr. 2020, 35, 26–34. [Google Scholar] [CrossRef]
- Sun, L.; Deng, A.; Zhang, H. On the Predicament and Solution of Ethnic Traditional Villages’ Tourism Activation: A Case Study of Leishan County, Qiandongnan. Guizhou Ethn. Stud. 2019, 40, 53–58. [Google Scholar] [CrossRef]
- Wei, X.; Hao, Y. Ethnic integration and inter-embeddedness: Formation mechanism of agro-pastoral interlace pattern in Hetao region. J. Hubei Minzu Univ. 2024, 42, 1–9. [Google Scholar]
- Getis, A. A history of the concept of spatial autocorrelation: A geographer’s perspective. Geogr. Anal. 2008, 40, 297–309. [Google Scholar] [CrossRef]
- Yuan, S.; Tang, G.; Zhang, H.; Gong, Q.; Yin, X.; Huang, G. Spatial distribution pattern of traditional villages and brief analysis of Han Chinese subgroup characteristics in Guangdong. Trop. Geogr. 2017, 37, 318–327. [Google Scholar] [CrossRef]
- Duan, C.; Bi, Z.; Huang, F. Spatial inter-embeddedness patterns of ethnic populations in China since the 21st century. Guangxi Ethn. Stud. 2021, 1–11. Available online: https://qikan.cqvip.com/Qikan/Article/Detail?id=7106083494 (accessed on 17 October 2025).
- Wang, H.-y.; Meng, Y.; Wu, W.; Zuo, Y.l. Study on Spatial Distribution Characteristics and Influencing Factors of Ethnic Villagesin Southwest Hubei Province. Resour. Environ. Yangtze Basin 2024, 33, 1273–1285. [Google Scholar]
- Fan, N.; Han, R.; Liang, K. Study on the spatial characteristics and influencing factors of rural tourism villages in Guizhou Province. World Reg. Stud. 2021, 30, 1308–1319. [Google Scholar] [CrossRef]
- Guo, S.; Yang, J.; Ma, C.; Gong, Y.; Gao, C.; Kang, X.; Li, R. Study on the Spatial Distribution Pattern of Traditional Villages and Its Influencing Factors in Yunnan Based on Geo-detector and GIS. J. Yunnan Norm. Univ. 2024, 44, 69–78. [Google Scholar] [CrossRef]
- Huang, L.; Xiong, K.; Jia, X.; Bao, G.; He, Y. The Spatial Distribution and Influencing Factors of Traditional Villages in Yunnan Province Based on GIS. J. Yunnan Agric. Univ. 2024, 18, 141–149. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, J.; Wang, J.; Xin, A. Spatial correlation between traditional villages and religious cultural heritage in the Hehuang region, Northwest China. J. Asian Archit. Build. Eng. 2024, 24, 3190–3202. [Google Scholar] [CrossRef]
- Zukin, S. Structures of Capital: The Social Organization of the Economy; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Lin, Y.; Lin, X. Karl Polanyi’s socio-economic thought and its contemporary relevance. Economist 2009, 47–52. [Google Scholar] [CrossRef]
- Wang, S. Embedded development of social work in China. Soc. Sci. Front. 2011, 206–222. [Google Scholar]
- Cao, F. The fourfold logic of promoting Chinese national community consciousness through cultural interconnectedness of all ethnic groups. Inn. Mong. Soc. Sci. 2025, 46, 21–28. [Google Scholar] [CrossRef]
- Wu, Y.; Li, H. Conceptualizing ethnic inter-embedding: A theoretical exploration. Natl. Forum 2015, 5–9. [Google Scholar] [CrossRef]
- Pei, S. Mutual embedding: A new direction in building an ethical community environment. Heilongjiang Natl. Ser. 2015, 111–115. [Google Scholar] [CrossRef]
- Silver, H. National conceptions of the new urban poverty: Social structural change in Britain, France, and the United States. Int. J. Urban Reg. Res. 1993, 17, 336–354. [Google Scholar] [CrossRef]
- Ma, W.; Li, X. Practical pathways for effective linkage between poverty alleviation and rural revitalization in ethnic regions: Investigation of Minning Town, Ningxia. Guizhou Ethn. Stud. 2022, 43, 49–55. [Google Scholar] [CrossRef]
- Li, Y.; Cao, J. Analysis of Ethnic Integration through Recent Changes in Ethnic Distribution of “Mountain and Flatland Structure” in Contemporary Yunnan: Three Cases from Xinping Yi and Dai Autonomous County. Ethn. Stud. 2021, 53–62. [Google Scholar]
- Gu, C.; Liu, J. Urban Sociology; Tsinghua University Press: Beijing, China, 2013; pp. 1196–1205. [Google Scholar]
- Church, A.; Frost, M.; Sullivan, K. Transport and social exclusion in London. Transp. Policy 2000, 7, 195–205. [Google Scholar] [CrossRef]
- Xiong, Y. Division and characteristics of river valley, low mountain, high mountain, and rocky forest areas in the Huangshui River Basin. Water Conserv. Sci. Technol. Econ. 2012, 18, 14–15. [Google Scholar] [CrossRef]
- Li, H.; Huang, Y.; Guo, W.; Hou, H.; Fan, M.; Qi, X.; Jia, P.; Guo, Q. Impacts of land use and spatial patterns on water quality at multi-spatiotemporal scales in Hehuang Valley. Environ. Sci. 2022, 43, 4042–4053. [Google Scholar] [CrossRef]
- Chang, Q. Structure and Prospective of Chinese Vernacular Architectural Pedigrees: An Objective Based on a Systematic Study of Sample Preservation and Holistic Regeneration. Archit. J. 2016, 1–9. [Google Scholar] [CrossRef]
- Li, D.; Li, J.; Jin, Y.; Zhang, C. Construction logic and spatial concepts of earth-walled dwellings in multi-ethnic Hehuang region. Built Herit. 2024, 1–12. [Google Scholar] [CrossRef]
- Tong, Y. GIS-based spatial differentiation of traditional villages in China. Hum. Geogr. 2014, 29, 44–51. [Google Scholar] [CrossRef]
- Enos, R.D.; Celaya, C. The Effect of Segregation on Intergroup Relations. J. Exp. Political Sci. 2018, 5, 26–38. [Google Scholar] [CrossRef]
- Florida, R.; Mellander, C. The Geography of Economic Segregation. Soc. Sci. 2018, 7, 123. [Google Scholar] [CrossRef]
- Uwayezu, E.; de Vries, W.T. Exploring the connection between spatial justice and land tenure security: Insights from inclusive urban (re)development schemes in Recife, Brazil. GeoJournal 2020, 87, 3365–3386. [Google Scholar] [CrossRef]
- Álvarez Velasco, S.; Liberona Concha, N. Irregularized Transits to the South: A Social Force in the Cross-Border Spatial Dispute in South America. J. Lat. Am. Caribb. Anthropol. 2025, 30, e70008. [Google Scholar] [CrossRef]
- Costa Bomfim, L. How Social Justice Planning Can Address Urban Inequities through Social Housing: From Theory to Practice. U. Porto J. Eng. 2024, 10, 85–100. [Google Scholar] [CrossRef]
- Wise, A.; Velayutham, S. (Eds.) Everyday Multiculturalism; Palgrave Macmillan: London, UK, 2009. [Google Scholar] [CrossRef]
- Li, T.; Li, C.; Zhang, R.; Cong, Z.; Mao, Y. Spatial Heterogeneity and Influence Factors of Traditional Villages in the Wuling Mountain Area, Hunan Province, China Based on Multiscale Geographically Weighted Regression. Buildings 2023, 13, 294. [Google Scholar] [CrossRef]
- Jia, X.; Li, F.; Cui, M.; Cheng, G.; Zhao, Y.; Ding, H.; Yu, B.; Lu, H. The geographical environmental characteristics of the distribution of Tibetans and other major ethnic groups in the Hehuang Valley and the differences in their production modes. China Sci. Earth Sci. 2019, 62, 706–716. [Google Scholar] [CrossRef][Green Version]
- Zhu, P. Formation and Integration of the Multi-National Culture in Qinghai. J. Tibet. Natl. Inst. 2006, 27, 75–80. [Google Scholar][Green Version]
- Xu, Y.; Dong, S.; Shen, H.; Xiao, J.; Li, S.; Gao, X.; Wu, S. Degradation significantly decreased the ecosystem multifunctionality of three alpine grasslands: Evidences from a large-scale survey on the Qinghai-Tibetan Plateau. J. Mt. Sci. 2021, 18, 357–366. [Google Scholar] [CrossRef]
- Chen, Y.; Shu, B.; Chen, Y.; Wei, D. Spatial distribution and potential poverty-returning factors of former poverty-stricken villages in the Liangshan Mountains, China. J. Mt. Sci. 2023, 20, 2692–2707. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, W.; Xiao, Y.; Shi, J.; Hu, X.; Yan, B. Temporal and spatial patterns of traditional village distribution evolution in Xiangxi, China: Identifying multidimensional influential factors and conservation significance. Herit. Sci. 2023, 11, 261. [Google Scholar] [CrossRef]
- Hao, Z.; Jiang, L.; Feng, Y.; Yu, Y. Morphology of earth-walled dwellings in Tongren under religious-cultural influences: Case study of Wutun Village. Huazhong Archit. 2025, 43, 153–157. [Google Scholar] [CrossRef]
- Banban, D. Harmony in diversity: An empirical study of harmonious co-existence in the multi-ethnic culture of Qinghai. Int. J. Anthropol. Ethnol. 2018, 2, 1. [Google Scholar] [CrossRef][Green Version]
- Jiang, B.; Jiang, T.; Si, J.; Huang, Y.; Du, Y.; Chen, Y. Mechanism of the connection between sacred and secular space: Settlement morphology characteristics in the multi-ethnic areas of the Gansu-Qinghai Plateau. Front. Earth Sci. 2025, 13, 1674493. [Google Scholar] [CrossRef]
- Puxuan, Z. The Spatial and Temporal Distribution of Tibetan Buddhism Temples of Ming in Qinghai. J. Tibet. Natl. Inst. 2010, 32–35. [Google Scholar] [CrossRef]
- Chen, Y.; Shu, B.; Amani-Beni, M.; Wei, D. Spatial distribution patterns of rural settlements in the multi-ethnic gathering areas, southwest China: Ethnic inter-embeddedness perspective. J. Asian Archit. Build. Eng. 2023, 23, 372–385. [Google Scholar] [CrossRef]
- Lei, Z.; Han, W.; Li, J. Spatial–Environmental Coupling and Sustainable Planning of Traditional Tibetan Villages: A Case Study of Four Villages in Suopo Township. Sustainability 2025, 17, 8766. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, X. Temporal-Spatial Distribution Characteristics and Impact Factors of Traditional Villages in Huizhou Area. Econ. Geogr. 2019, 39, 204–211. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, J.; Liu, D.; Jia, Y.; Jiang, L. Spatial structure identification and influencing mechanisms of Miao traditional villages in Guizhou Province. Econ. Geogr. 2021, 41, 232–240. [Google Scholar] [CrossRef]
- Tian, M.; Wei, J.; Liu, J. A comparative ethnic study on the urban integration of the migrant populations in the Qinghai-Tibet Plateau during the process of urbanization. J. Urban Aff. 2023, 47, 1063–1080. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, R.; Beni, M.A. Rural transformation development: Spatiotemporal evolution and mechanisms in the Garze-Ngawa-Liangshan region, Southwest China. J. Asian Archit. Build. Eng. 2024, 24, 4119–4135. [Google Scholar] [CrossRef]
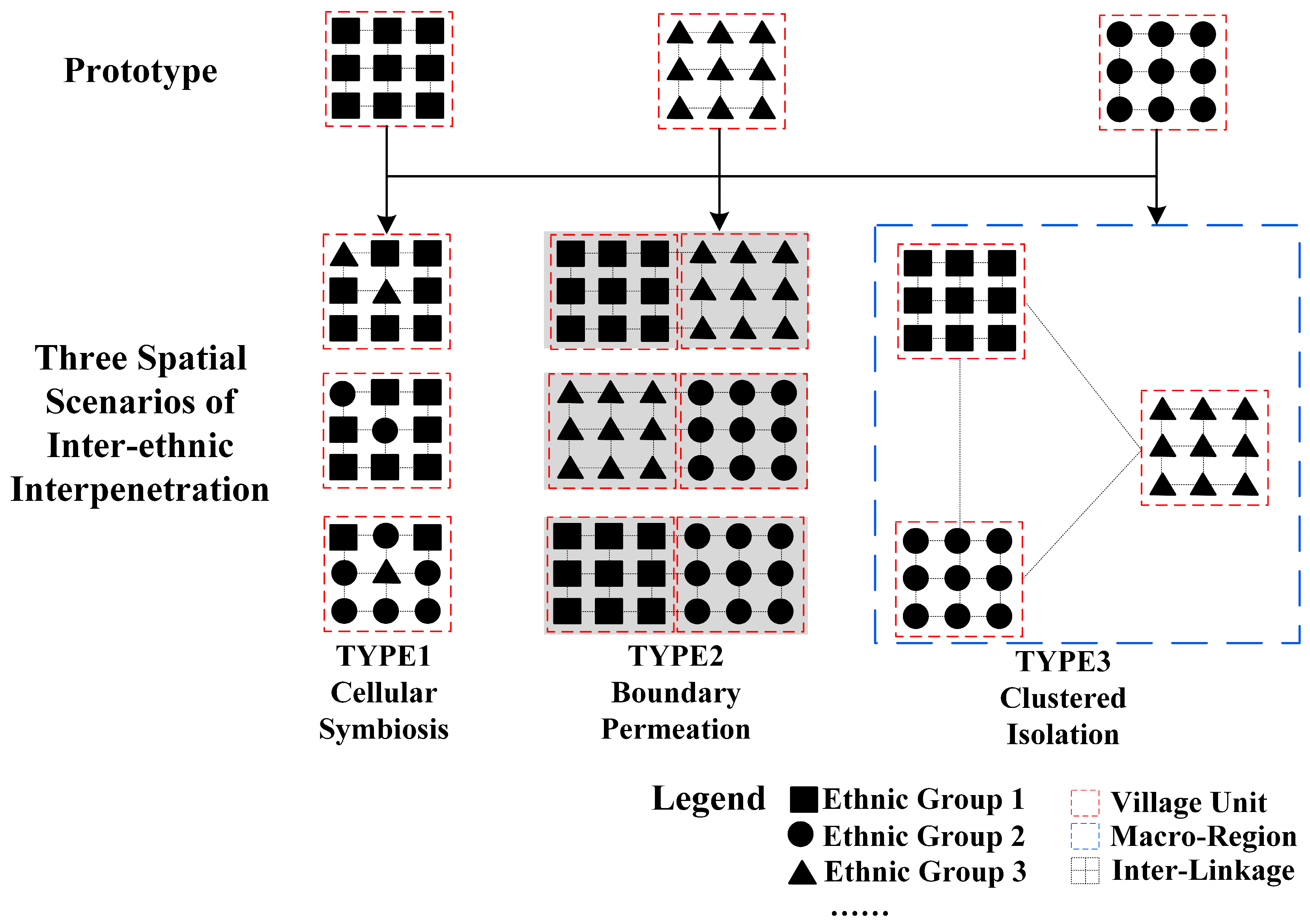

| Dimension | Clustered–Isolation Scenario | Boundary–Permeation Scenario | Cellular–Symbiosis Scenario |
|---|---|---|---|
| Defining Spatial Pattern | Spatially segregated, mono-ethnic clusters with definitive boundaries. | Settlements of distinct ethnic groups are adjacent, creating interfaces for interaction. | Multiple ethnic groups co-reside within a single village, creating a fine-grained, nested pattern. |
| Level of Inter-Embeddedness | Low | Medium (Functional) | High (Structural) |
| Hypothesized Primary Drivers | 1. Environmental determinism: Strong constraints from topography and hydrology. 2. Cultural Cohesion: Internal homogeneity reinforced by shared religion/culture, leading to spatial closure. | 1. Economic interdependence: Complementarity in production modes and trade. 2. Connectivity: Proximity to transport networks facilitates contact. | 1. Functional integration: Shared access to economic, administrative, or social services. 2. Cultural accommodation: Emergence of syncretic practices and shared identities over time. |
| Theoretical Spatial-Social Logic | Geographic segregation → cultural autonomy and preservation. | Geographic adjacency → socio-economic complementarity and limited exchange. | Spatial integration → functional interdependence and cultural symbiosis. |
| Method | Research Question/Hypothesis |
|---|---|
| Kernel Density Estimation (KDE) | To visualize and compare the spatial intensity and concentration of each village type. |
| Ripley’s K-function | To test deviations from Complete Spatial Randomness (CSR) and identify clustering/dispersion across scales. |
| Standard Deviational Ellipse (SDE) | To assess directional trends and examine the influence of transport infrastructure. |
| Kruskal–Wallis H test + Dunn/Wilcoxon | To compare environmental, infrastructural, and socio-economic attributes among village types. |
| Global Moran’s I | To evaluate the spatial autocorrelation of key driving factors. |
| Multinomial Logistic Regression | To identify key predictors influencing the probability of a village belonging to each typology. |
| Village Type | 1 km | 2 km | 3 km (Baseline) | 4 km | 5 km |
|---|---|---|---|---|---|
| Clustered–Isolation (Unadjusted) | 122 | 108 | 99 | 83 | 70 |
| Clustered–Isolation (Adjusted for Geographic Barriers) | 124 | 112 | 107 | 93 | 84 |
| Boundary–Permeation (Unadjusted) | 9 | 23 | 32 | 48 | 61 |
| Boundary–Permeation (Adjusted for Geographic Barriers) | 7 | 19 | 24 | 38 | 47 |
| Cellular–Symbiosis | 22 | 22 | 22 | 22 | 22 |
| Category | Number of Villages | Percentage (%) | Dominant Ethnic Groups | Elevation (m) | Slope (°) | Distance to Nearest River (m) | Local Road Network Density (km/km2) | |
|---|---|---|---|---|---|---|---|---|
| Mean ± SD | Pre-Merging | Post-Merging | ||||||
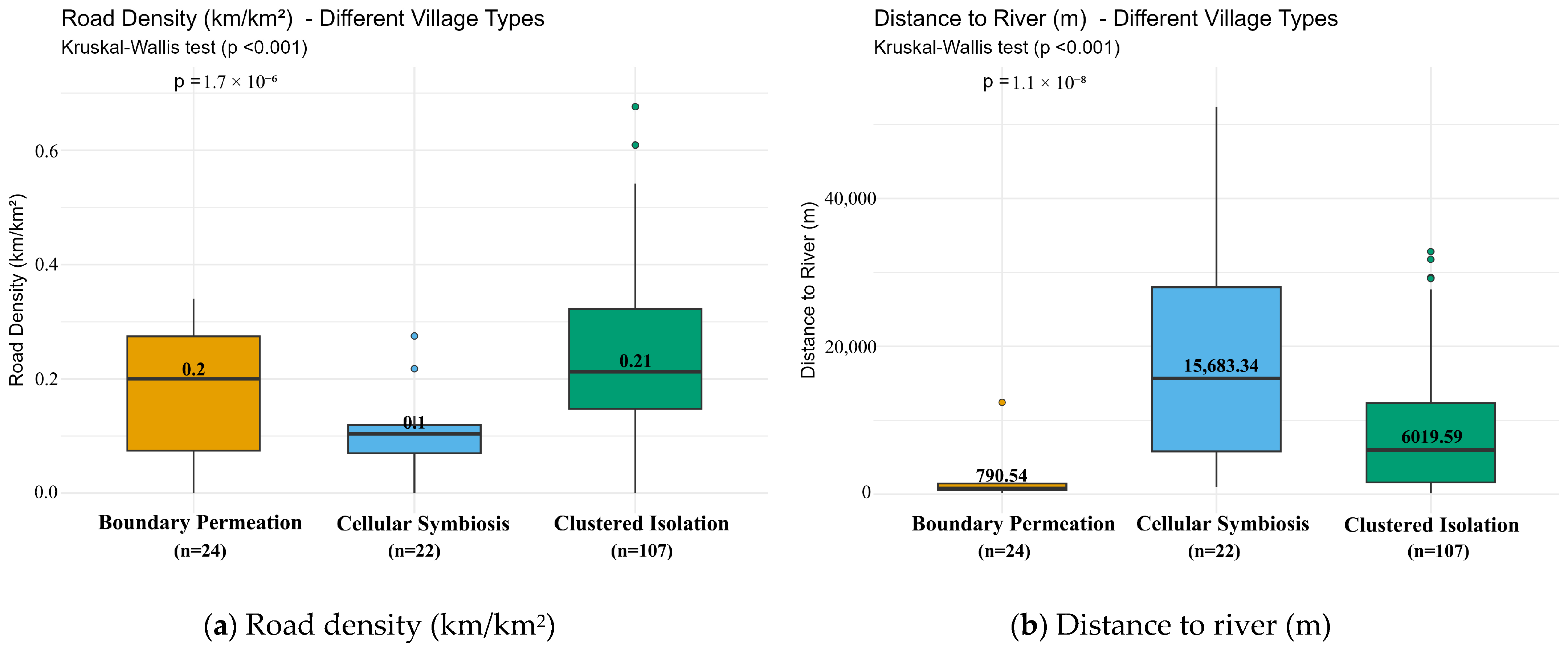
| Clustered–Isolation | 107 | 69.9% | Tibetan (68), Salar (23), Tu (11), Han (3), Hui (2) | 2493.36 ±362.22 | 6.71 ±5.27 | 8399.31 ±8239.21 | 0.25 ± 0.16 | 0.35 |
| Boundary–Permeation | 24 | 15.7% | Tibetan (15), Han (4), Salar (2), Tu (3) | 2476.25 ±225.19 | 8.87 ±4.76 | 1437.90 ±2396.73 | 0.18 ± 0.10 | 0.55 |
| Cellular–Symbiosis | 22 | 14.4% | Tibetan–Han (12), Tibetan–Han–Tu (3), Tibetan–Han–Hui–Tu (3), Tibetan–Han–Hui (3), Salar–Hui (1), Han–Hui (1) | 2485.09 ±316.45 | 8.91 ±4.96 | 18,139.72 ±14,438.50 | 0.10 ± 0.06 | 0.44 |
| Village Type | Scale | 0.5 km | 1.0 km | 2.0 km |
|---|---|---|---|---|
| Clustered–Isolation | Local scale | ** | ** | ** |
| Broad scale | ** | ** | ** | |
| Boundary–Permeation | Local scale | ** | ** | ** |
| Broad scale | ** | ** | ** | |
| Cellular–Symbiosis | Local scale | ns | ns | ns |
| Broad scale | ns | ns | ns |
| Village Type | Analysis | Major Axis Length (km) | 95% CI (km) | Minor Axis Length (km) | 95% CI (km) | Axis Ratio | Ellipse Area (km2) | 95% CI (km2) | Rotation Angle (°) | Main Direction |
|---|---|---|---|---|---|---|---|---|---|---|
| Clustered–Isolation | Unweighted | 122.81 | 111.17–134.45 | 84.25 | 76.27–92.23 | 1.46 | 8120.55 | 7598.55–8642.55 | 164.99 | NNW–SSE |
| Weighted | 109.73 | 99.33–120.13 | 79.50 | 71.95–87.05 | 1.38 | 6845.96 | 6415.39–7276.53 | 161.57 | NNW–SSE | |
| Boundary–Permeation | Unweighted | 101.17 | 91.16–111.18 | 66.25 | 59.74–72.76 | 1.53 | 5263.03 | 4590.48–5935.58 | 103.52 | ESE–WNW |
| Weighted | 81.92 | 73.87–89.97 | 28.04 | 25.93–30.15 | 2.92 | 1802.95 | 1572.53–2033.37 | 98.96 | ESE–WNW | |
| Cellular–Symbiosis | Unweighted | 147.82 | 134.00–161.64 | 79.94 | 72.39–87.49 | 1.85 | 9272.54 | 8301.43–10,243.65 | 159.60 | SSE–NNW |
| Weighted | 152.02 | 137.99–166.05 | 66.08 | 59.84–72.32 | 2.30 | 7883.72 | 7036.04–8731.40 | 161.23 | SSE–NNW |
| Village Type | Clustered–Isolation | Clustered–Isolation | Boundary–Permeation | Boundary–Permeation | Cellular–Symbiosis | Cellular–Symbiosis |
|---|---|---|---|---|---|---|
| I | p | I | p | I | p | |
| Elevation | 0.457 | <0.001 | 0.335 | <0.001 | 0.159 | 0.002 |
| Slope | 0.162 | <0.001 | −0.027 | 0.410 | −0.010 | 0.300 |
| Road Density | 0.154 | <0.001 | 0.380 | <0.001 | −0.088 | 0.730 |
| Dist River | 0.646 | <0.001 | 0.007 | 0.077 | 0.124 | 0.010 |
| Per capita GDP | 0.623 | <0.001 | 0.298 | <0.001 | −0.116 | 0.832 |
| Urban Rate_county | 0.498 | <0.001 | 0.391 | <0.001 | 0.036 | 0.116 |
| Han | 0.833 | <0.001 | 0.054 | 0.041 | 0.535 | <0.001 |
| Tibetan | 0.934 | <0.001 | 0.836 | <0.001 | 0.471 | <0.001 |
| Tu | 0.900 | <0.001 | 0.646 | <0.001 | 0.085 | 0.025 |
| Salar | 0.926 | <0.001 | 0.825 | <0.001 | 0.080 | 0.014 |
| Hui | 0.534 | <0.001 | −0.090 | 0.773 | 0.105 | 0.013 |
| Category | Variable | Coefficient | Std. Error | z-Value | p-Value | OR |
|---|---|---|---|---|---|---|
| Boundary–Permeation | Elevation | 3.6603 | 0.0001 | 40,420.193 | <0.001 | 38.8747 |
| Slope | 0.0022 | 0.0008 | 2.892 | 0.0038 | 1.0022 | |
| DistRiver | −0.0205 | 0.0016 | −12.703 | <0.001 | 0.9798 | |
| GDP | −0.0381 | 0.0035 | −11.013 | <0.001 | 0.9626 | |
| UrbanRate_county | −6.3051 | 0.0000 | −154,522.035 | <0.001 | 0.0018 | |
| Cellular–Symbiosis | Elevation | −0.0006 | 0.0002 | −3.765 | 0.0002 | 0.9994 |
| Slope | 0.0001 | 0.0000 | 2.243 | 0.0249 | 1.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, J. Constructing a “Clustered–Boundary–Cellular” Model: Spatial Differentiation and Sustainable Governance of Traditional Villages in Multi-Ethnic China. Sustainability 2025, 17, 9268. https://doi.org/10.3390/su17209268
Zhang Y, Li J. Constructing a “Clustered–Boundary–Cellular” Model: Spatial Differentiation and Sustainable Governance of Traditional Villages in Multi-Ethnic China. Sustainability. 2025; 17(20):9268. https://doi.org/10.3390/su17209268
Chicago/Turabian StyleZhang, Yaolong, and Junhuan Li. 2025. "Constructing a “Clustered–Boundary–Cellular” Model: Spatial Differentiation and Sustainable Governance of Traditional Villages in Multi-Ethnic China" Sustainability 17, no. 20: 9268. https://doi.org/10.3390/su17209268
APA StyleZhang, Y., & Li, J. (2025). Constructing a “Clustered–Boundary–Cellular” Model: Spatial Differentiation and Sustainable Governance of Traditional Villages in Multi-Ethnic China. Sustainability, 17(20), 9268. https://doi.org/10.3390/su17209268





