A Fully Coupled Sensitivity Analysis Framework for Offshore Wind Turbines Based on an XGBoost Surrogate Model and the Interpretation of SHAP
Abstract
1. Introduction
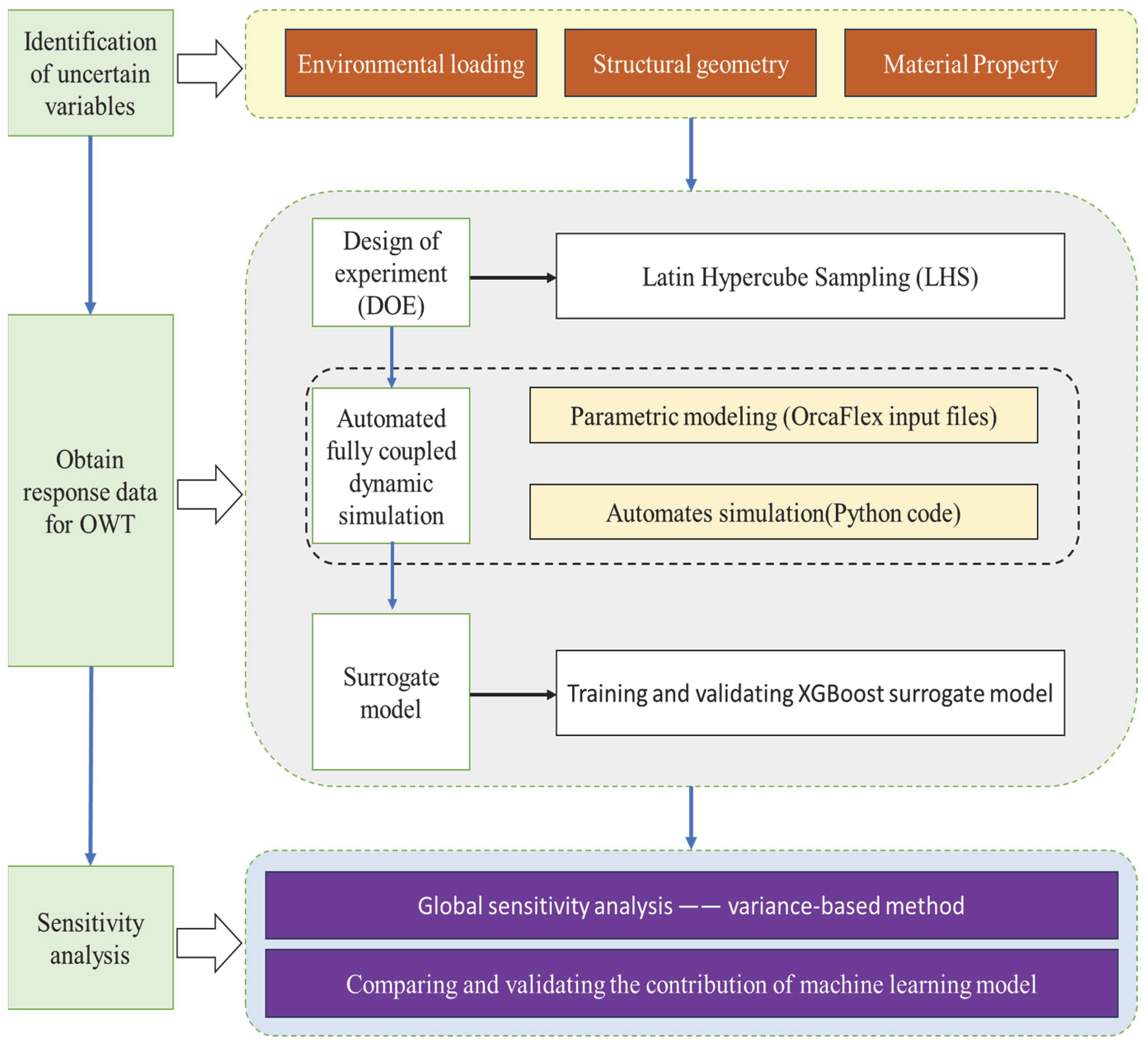
2. Framework for Conducting a Sensitivity Analysis on Offshore Wind Turbines
2.1. Brief Introduction to the Sensitivity Analysis Framework
- (1)
- The identification of uncertain variables for an OWT is the cornerstone and prerequisite for performing SA. As the primary sources of variability in the system’s response, their accurate definition directly determines the reliability and validity of the analysis results. These uncertainties include both external environmental variables at the OWT’s operational site and internal structural, geometric, and material parameters of the turbine itself [30,31,32]. Once identified, determining the distribution type and statistical characteristics for each key variable becomes the central task in quantifying uncertainty. This statistical data provides the essential input for the subsequent fully coupled dynamic simulations.
- (2)
- Based on the uncertainty variables identified in step 1 and their statistical characteristics, this step constructs an input parameter space that can represent all combinations of uncertainty through the development of an efficient sampling strategy. The primary objective of this process is to generate representative sample points for subsequent fully coupled dynamic simulations. This study employs the Latin Hypercube Sampling (LHS) [33] method. As an advanced stratified sampling technique, LHS is particularly suitable for multivariate analysis and offers considerable advantages over traditional Monte Carlo Sampling (MCS) [34,35] in terms of sampling efficiency. It should be noted that quasi-random sequences can achieve an even lower discrepancy and potentially higher convergence rate than LHS under the same sample size [36,37,38]. Nevertheless, LHS was retained here for its simple implementation and well-established performance in similar applications.
- (3)
- In theory, increasing the number of samples generated in step 2 enhances the accuracy of the uncertainty space representation. However, this also substantially increases computational costs, as each sample combination necessitates a complete, nonlinear, fully coupled dynamic simulation. An automated simulation execution module was developed to address this challenge and ensure analytical efficiency. The core function of this module is to seamlessly integrate the sampling and simulation stages. It automatically reads the sample matrix generated by LHS and produces corresponding simulation models by batch-modifying the base model files. It then invokes the numerical simulation software to conduct fully automated time-domain dynamic coupling analyses, eliminating the need for manual intervention.The dynamic analysis in this study is conducted using OrcaFlex (version 11.5b) software. OrcaFlex, developed by Orcina [39,40], is a leading commercial software package for dynamic analysis in marine engineering systems. It accurately simulates the coupled dynamic response of OWTs in complex marine environments. Numerical simulations are efficiently executed by integrating the automation module with OrcaFlex, providing a sufficient data foundation for the subsequent SA.
- (4)
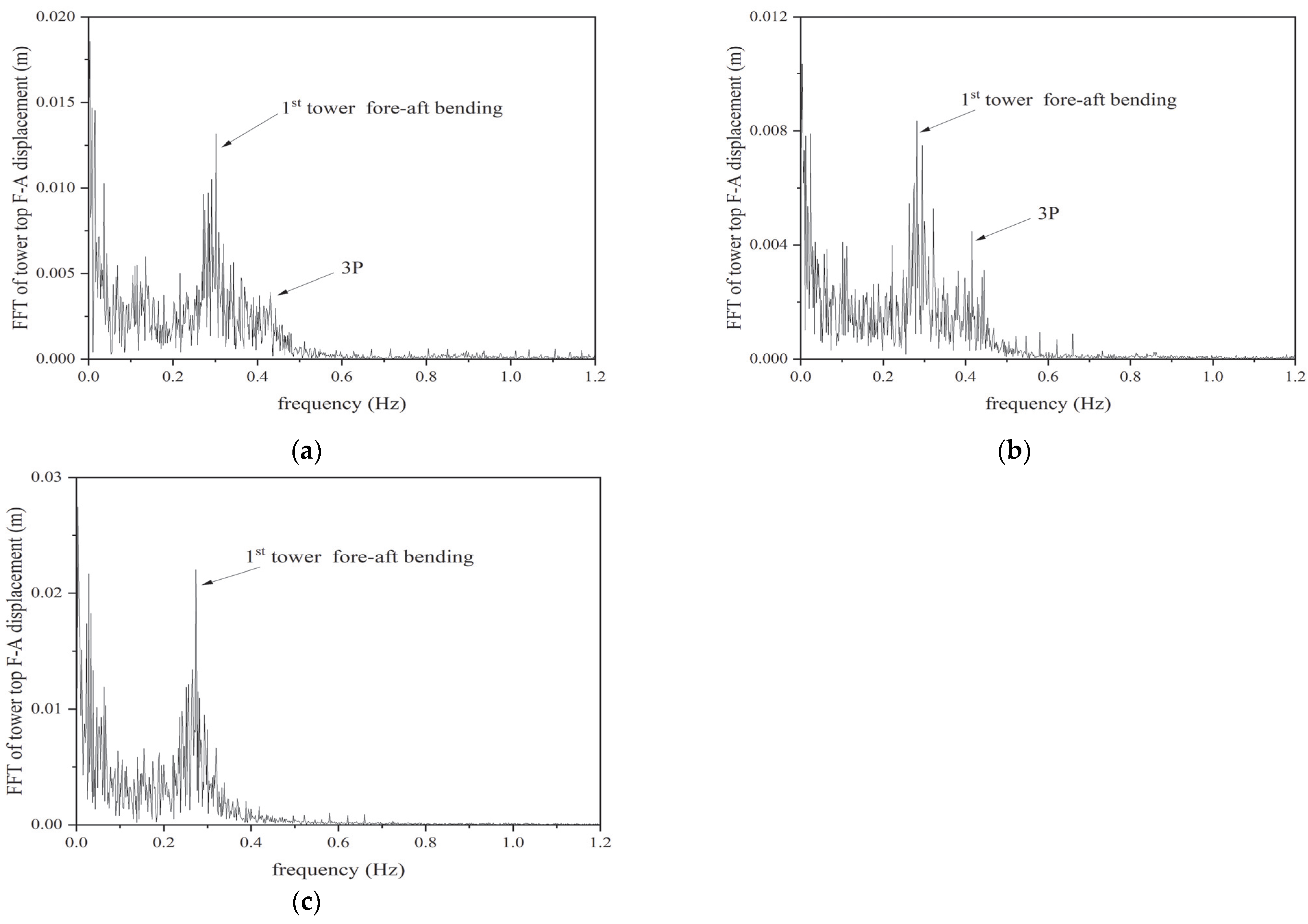
- After completing all time-domain dynamic coupling analyses, dynamic response indicators relevant to structural safety are collected for use in the subsequent SA. The structural dynamic response extracted in this study includes front-aft (F-A) displacement at the tower top, maximum von Mises stress at the tower base, F-A bending moment at the tower base, F-A displacement at the monopile top, and pitch angle at the monopile top.
- (5)
- Before performing SA, it is essential to construct a surrogate model that effectively captures the nonlinear relationship between the input uncertainty variables and the output structural response. Global SA methods, such as analysis of variance (ANOVA) or Sobol’s method, typically require tens of thousands of model evaluations to yield convergent results. Conducting the tens of thousands of model evaluations required for global SA using the high-fidelity OrcaFlex model directly would be computationally prohibitive. A surrogate model is a computationally efficient mathematical approximation of the original simulation. It replaces the original simulation model with minimal computational overhead, enabling structural response prediction of any input parameter combination within milliseconds [41,42,43,44]. This facilitates the application of global SA, which will otherwise be impractical due to excessive computational demands. This study employs the Extreme Gradient Boosting (XGBoost) machine learning model as the surrogate model [45]. Feature contribution analysis is then performed on its predictions and compared to the SA results for validation.
- (6)
- With a high-fidelity surrogate model established and validated, the final step of the framework involves executing the SA. This step quantitatively evaluates the contribution of each uncertain input variable to the variance of the OWT’s structural response. The variance-based Sobol method [46] is utilized in this study to complete this task. Tens of thousands, or more, model evaluations are conducted at negligible computational cost, utilizing the computational efficiency of the surrogate model to ensure.
2.2. Sampling of Random Variables
2.3. Fully Coupled Dynamic Time Domain Simulation of OWTs
2.4. Surrogate Model
2.5. Global Sensitivity Analysis Method
3. Benchmark OWT and Environmental Conditions
3.1. Benchmark OWT Description
3.2. Design Load Condition and Random Variables
4. Application Example
4.1. Validation of Surrogate Models
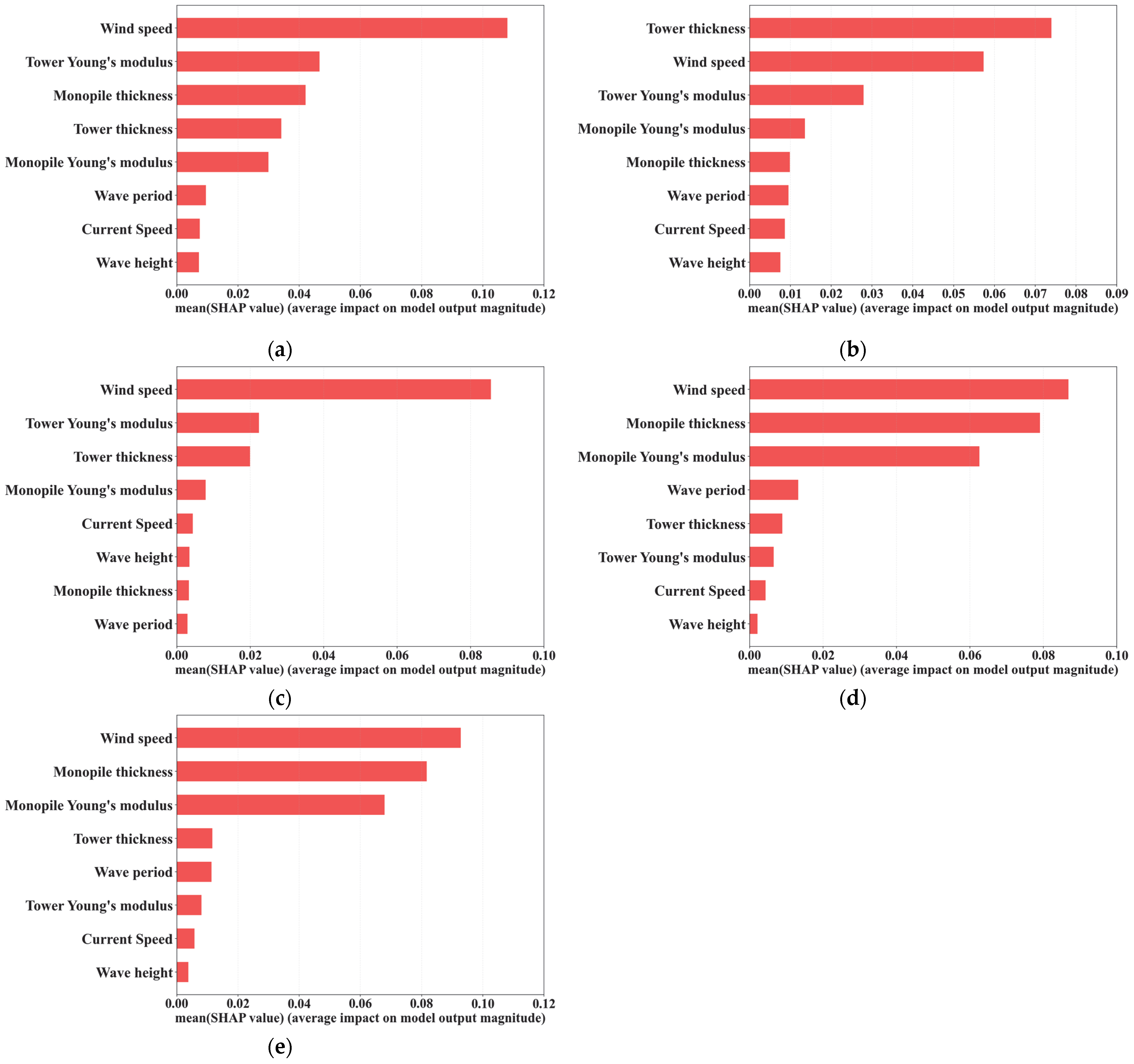
4.2. Sensitivity Analysis
5. Conclusions and Future Work
- 1.
- The sensitivity characteristics of the OWT strongly depend on the operational conditions. Under normal operating conditions (DLC 1.3 and DLC 1.6a), the system’s dynamic responses are primarily governed by external environmental variables, with wind speed identified as the most influential parameter. This indicates that an accurate characterization of the wind speed is paramount for structural performance assessment during power production.
- 2.
- A significant shift in the dominant sources of uncertainty is observed under shutdown survival conditions (DLC 6.2a). When the OWT is parked and feathered to endure extreme wind and wave events, its dynamic response is governed almost entirely by structural and material properties. The direct impact of environmental parameters becomes secondary. This result highlights the necessity of precise control over structural tolerances and material quality to ensure system survivability during ultimate limit states.
- 3.
- The cross-validation of methodologies confirms the high reliability of the research findings. Two analytical methods grounded in entirely different theoretical foundations, Sobol’s method and SHAP values, produce a consistent ranking of the importance of the uncertain variables. This strong agreement not only validates the accuracy of the constructed XGBoost surrogate model but also provides robust, dual-source confidence in the conclusions of the SA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANOVA | Analysis of Variance |
| CDF | Cumulative Distribution Function |
| COV | Coefficient of Variation |
| Dist | Distribution |
| DLC | Design Load Condition |
| ECM | Extreme Current Model |
| ESS | Extreme Sea State |
| ETM | Extreme Turbulence Model |
| EWM | Extreme Wind Model |
| F-A | Front-aft |
| LHS | Latin Hypercube Sampling |
| MCS | Monte Carlo Sampling |
| MSE | Mean Square Error |
| NCM | Normal Current Model |
| NRMSE | Normalized Root Mean Square Error |
| NSS | Normal Sea State |
| NTM | Normal Turbulence Model |
| OWT | Offshore Wind Turbine |
| RNA | Rotor–Nacelle Assembly |
| SA | Sensitivity Analysis |
| SHAP | SHapley Additive exPlanations |
| SSS | Severe Sea State |
| XGBoost | Extreme Gradient Boosting |
References
- Wang, Q.; Sun, X.; Wang, R.; Zhou, L.; Zhou, H.; Di, Y.; Li, Y.; Zhang, Q. Research on urban energy sustainable plan under the background of low-carbon development. Sustainability 2023, 15, 14206. [Google Scholar] [CrossRef]
- Li, Y.; Yin, W.; Leng, S.; Meng, Y.; Zhang, Y. Dynamic analysis of a spar-type floating offshore wind turbine under extreme operation gust. Sustainability 2025, 17, 5655. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Zhao, J.; Dong, K.; Dong, X.; Shahbaz, M. How renewable energy alleviate energy poverty? A global analysis. Renew. Energy 2022, 186, 299–311. [Google Scholar] [CrossRef]
- Hou, H.; Lu, W.; Liu, B.; Hassanein, Z.; Mahmood, H.; Khalid, S. Exploring the role of fossil fuels and renewable energy in determining environmental sustainability: Evidence from OECD countries. Sustainability 2023, 17, 2048. [Google Scholar] [CrossRef]
- Nispel, A.; Ekwaro-Osire, S.; Dias, J.P.; Cunha, A., Jr. Uncertainty quantification for fatigue life of offshore wind turbine structure. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part B Mech. Eng. 2021, 7, 040901. [Google Scholar] [CrossRef]
- Global Wind Report. 2025. Available online: https://www.gwec.net/reports/globalwindreport?mc_cid=ded24e409b&mc_eid=741e655e37#Download (accessed on 12 May 2025).
- Veers, P.; Dykes, K.; Lantz, E.; Barth, S.; Bottasso, C.L.; Carlson, O.; Clifton, A.; Green, J.; Green, P.; Holttinen, H.; et al. Grand challenges in the science of wind energy. Science 2019, 366, eaau2027. [Google Scholar] [CrossRef]
- Wang, J.; Ren, Y.; Shi, W.; Collu, M.; Venugopal, V.; Li, X. Multi-objective optimization design for a 15 MW semisubmersible floating offshore wind turbine using evolutionary algorithm. Appl. Energy 2025, 377, 124533. [Google Scholar] [CrossRef]
- Hu, L.; Shi, W.; Hu, W.; Chai, W.; Hu, Z.; Li, X. Short-term prediction of mooring tension for floating offshore wind turbines under typhoon conditions based on the VMD-MI-LSTM method. Renew. Sustain. Energy Rev. 2025, 216, 115606. [Google Scholar] [CrossRef]
- Cai, Y.; Zhao, H.; Li, X.; Shi, W.; Xiao, Q. Developing an OpenFOAM solver for coupled aero-hydrodynamic analysis of integrated structure with floating offshore wind turbine and aquaculture net cage. Coast. Eng. 2025, 198, 104720. [Google Scholar] [CrossRef]
- Guo, Z.; Hou, W.; Yao, H.; Liu, Y.; Zhang, Y. Dynamic responses of monopile offshore wind turbines under different wind-wave misalignment angles. Structures 2024, 69, 107454. [Google Scholar] [CrossRef]
- Li, J.; Cui, C.; Xiao, Z.; Wang, B.; Xu, C. Reliability and sensitivity analyses of monopile supported offshore wind turbines based on probability density evolution method with pre-screening of controlling parameters. Ocean Eng. 2024, 310, 118746. [Google Scholar] [CrossRef]
- Li, X.; Wu, Z.; Su, D.; Zhang, L. Reliability analysis of offshore monopile foundations considering multidirectional loading and soil spatial variability. Comput. Geotech. 2024, 166, 106045. [Google Scholar] [CrossRef]
- Han, F.; Wang, W.; Zheng, X.; Han, X.; Shi, W.; Li, X. Investigation of essential parameters for the design of offshore wind turbine based on structural reliability. Reliab. Eng. Syst. Saf. 2025, 245, 110601. [Google Scholar] [CrossRef]
- Thapa, M.; Missoum, S. Uncertainty quantification and global sensitivity analysis of composite wind turbine blades. Reliab. Eng. Syst. Saf. 2022, 222, 108345. [Google Scholar] [CrossRef]
- Shittu, A.A.; Mehmanparast, A.; Amirafshari, P.; Hart, P.; Kolios, A. Sensitivity analysis of design parameters for reliability assessment of offshore wind turbine jacket support structures. Int. J. Nav. Archit. Ocean Eng. 2022, 14, 100441. [Google Scholar] [CrossRef]
- Glišić, A.; Ferraz, G.; Schaumann, P. Sensitivity analysis of monopiles’ fatigue stresses to site conditions using Monte Carlo simulation. In Proceedings of the Twenty-Seventh International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; pp. 305–311. [Google Scholar]
- Velarde, J.; Kramhøft, C.; Sørensen, J.D. Global sensitivity analysis of offshore wind turbine foundation fatigue loads. Renew. Energy 2019, 140, 177–189. [Google Scholar] [CrossRef]
- Okpokparoro, S.; Sriramula, S. Uncertainty modeling in reliability analysis of floating wind turbine support structures. Renew. Energy 2021, 165, 88–108. [Google Scholar] [CrossRef]
- Huchet, Q.; Mattrand, C.; Beaurepaire, P.; Relun, N.; Gayton, N. AK-DA: An efficient method for the fatigue assessment of wind turbine structures. Wind Energy 2019, 22, 638–652. [Google Scholar] [CrossRef]
- Li, T.; Yang, Q.; Zhang, X.; Ma, Y. Efficient fatigue damage estimation of offshore wind turbine foundation under wind-wave actions. J. Constr. Steel Res. 2024, 221, 108903. [Google Scholar] [CrossRef]
- Bai, H.; Shi, L.; Aoues, Y.; Huang, C.; Lemosse, D. Estimation of probability distribution of long-term fatigue damage on wind turbine tower using residual neural network. Mech. Syst. Signal Process. 2023, 190, 110101. [Google Scholar] [CrossRef]
- Georgios, G.; Lio, W.H.; Meng, F. Surrogate models for wind turbine electrical power and fatigue loads in wind farm. Energies 2020, 13, 6360. [Google Scholar] [CrossRef]
- Wilkie, D.; Galasso, C. Gaussian process regression for fatigue reliability analysis of offshore wind turbines. Struct. Saf. 2021, 88, 102020. [Google Scholar] [CrossRef]
- Talaat, F.; Kabeel, A.E.; Shaban, W. The role of utilizing artificial intelligence and renewable energy in reaching sustainable development goals. Renew. Energy 2024, 235, 121311. [Google Scholar] [CrossRef]
- Liu, H.; Chang, L.; Tian, Y.; Chen, H.; Zhang, P.; Song, B.; Zheng, S.; Liu, T. Research on time-domain motion prediction of floating platforms based on XGBoost model. Ocean Eng. 2025, 332, 121393. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Demir, S.; Ozdemir, M.H.; Aylak, B.L.; Sariisik, G.; Abualigah, L. Data-driven interpretable ensemble learning methods for the prediction of wind turbine power incorporating SHAP analysis. Expert Syst. Appl. 2024, 237, 121464. [Google Scholar] [CrossRef]
- Sadiq, S.; Won, M.S.; Kim, H.J.; Hong, C. Hybrid finite element and machine learning approach for estimating lateral capacity of partially rock-socketed monopiles. Ocean Eng. 2025, 330, 121286. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Guo, Z.; Zhang, J.; Lü, Q. Robust design of monopiles for offshore wind turbines considering uncertainties in dynamic loads and soil parameters. Ocean Eng. 2022, 266, 112822. [Google Scholar] [CrossRef]
- Ramezani, M.; Choe, D.E.; Heydarpour, K.; Koo, B. Uncertainty models for the structural design of floating offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2023, 185, 113610. [Google Scholar] [CrossRef]
- Sheng, C.; Hong, H.P. Reliability and fragility assessment of offshore floating wind turbine subjected to tropical cyclone hazard. Struct. Saf. 2021, 93, 102138. [Google Scholar] [CrossRef]
- Liu, P.; Shang, D.; Liu, Q.; Yi, Z.; Wei, K. Kriging model for reliability analysis of the offshore steel trestle subjected to wave and current loads. J. Mar. Sci. Eng. 2022, 10, 25. [Google Scholar] [CrossRef]
- Huang, Y. A review of Monte Carlo and quasi-Monte Carlo sampling techniques. WIREs Comput. Stat. 2024, 16, e1637. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Yang, S.; He, Z.; Chai, J.; Meng, D.; Macek, W.; Branco, R.; Zhu, S. A novel hybrid adaptive framework for support vector machine-based reliability analysis: A comparative study. Structures 2023, 58, 105665. [Google Scholar] [CrossRef]
- Tsvetkova, O.; Ouarda, T.B.M.J. Quasi-Monte Carlo technique in global sensitivity analysis of wind resource assessment with a study on UAE. Renew. Sustain. Energy 2019, 11, 053303. [Google Scholar] [CrossRef]
- Tarantola, S.; Becker, W.; Zeitz, D. A comparison of two sampling methods for global sensitivity analysis. Comput. Phys. Commun. 2012, 183, 1061–1072. [Google Scholar] [CrossRef]
- OrcaFlex User Manual. Available online: https://www.orcina.com/webhelp/OrcaFlex/Default.htm (accessed on 4 June 2025).
- OrcaFlex API User Manual. Available online: https://www.orcina.com/webhelp/OrcFxAPI/Default.htm (accessed on 4 June 2025).
- Ren, C.; Xing, Y. AK-MDAmax: Maximum fatigue damage assessment of wind turbine towers considering multi-location with an active learning approach. Renew. Energy 2023, 215, 118977. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W. Long-term fatigue damage assessment for a floating offshore wind turbine under realistic environmental conditions. Renew. Energy 2020, 159, 570–584. [Google Scholar] [CrossRef]
- Liu, D.; Ferri, G.; Heo, T.; Marino, E.; Manuel, L. On long-term fatigue damage estimation for a floating offshore wind turbine using a surrogate model. Renew. Energy 2024, 225, 120238. [Google Scholar] [CrossRef]
- Quevedo-Reina, R.; Álamo, G.M.; Aznárez, J.J. ANN-based surrogate model for the structural evaluation of jacket support structures for offshore wind turbines. Ocean. Eng. 2025, 317, 119984. [Google Scholar] [CrossRef]
- Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A data-driven design for fault detection turbines using Random Forests and XGboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Donovan, D.; Burrage, K.; Burrage, P.; McCourt, T.A.; Thompson, B.; Yazici, E.S. Estimates of the coverage of parameter space by Latin Hypercube and Orthogonal Array-based sampling. Appl. Math. Model. 2018, 57, 553–564. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Sethuraman, L.; Venugopal, V. Hydrodynamic response of a stepped-spar floating wind turbine: Numerical modelling and tank testing. Renew. Energy 2013, 52, 160–174. [Google Scholar] [CrossRef]
- Yang, C.; Tzeng, Y.A.; Jhan, Y.T.; Cheng, C.; Yang, S. Typhoon eye-induced misalignment effects on the serviceability of floating offshore wind turbines: Insights Typhoon SOULIK. Energies 2025, 18, 490. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 305–311. [Google Scholar]
- Trizoglou, P.; Liu, X.; Lin, Z. Fault detection by an ensemble framework of Extreme Gradient Boosting (XGBoost) in the operation of offshore wind turbines. Renew. Energy 2021, 179, 945–962. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information, Long Beach, CA, USA, 4–9 December 2017; pp. 4768–4777. [Google Scholar]
- Hübler, C. Global sensitivity analysis for medium-dimensional structural engineering problems using stochastic collocation. Reliab. Eng. Syst. Saf. 2020, 195, 106749. [Google Scholar] [CrossRef]
- Mazetto, B.M.; Ritto, T.G. Uncertainty and global sensitivity analysis of wind turbines fatigue in non-ideal conditions. J. Vib. Eng. Technol. 2022, 10, 2391–2402. [Google Scholar] [CrossRef]
- Ballester-Ripoll, R.; Paredes, E.G.; Pajarola, R. Sobol tensor trains for global sensitivity analysis. Reliab. Eng. Syst. Saftey 2019, 183, 311–322. [Google Scholar] [CrossRef]
- Ganji, A.; Maier, H.R.; Dandy, G.C. A modified Sobol′ sensitivity analysis method for decision-making in environmental problems. Environ. Model. Softw. 2016, 75, 15–27. [Google Scholar] [CrossRef]
- Han, J.; Wang, L.; Ma, F.; Ge, Z.; Wang, D.; Li, X. Sensitivity analysis of geometric error for a novel slide grinder based on improved Sobol method and its application. Int. J. Adv. Manuf. Technol. 2022, 121, 6661–6684. [Google Scholar] [CrossRef]
- Bortolotti, P.; Tarres, H.C.; Dykes, K.; Merz, K.; Sethuraman, L.; Verelst, D.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy—WP2.1 Reference Wind Turbines; Technical Report No. NREL/TP-5000-73492; National Renewable Energy Laboratory: Golden, CO, USA, 2019. [Google Scholar]
- Morató, A.; Sriramula, S.; Krishnan, N.; Nichols, J. Ultimate loads and response analysis of a monopile supported offshore wind turbine using fully coupled simulation. Renew. Energy 2017, 101, 126–143. [Google Scholar] [CrossRef]
- IEC 61400-3; Wind Energy Generation Systems–Part 3-1: Design Requirements for Fixed Offshore Wind Turbines. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Morató, A.; Sriramula, S.; Krishnan, N. Kriging models for aero-elastic simulations and reliability analysis of offshore wind turbine support structures. Ships Offshore Struct. 2018, 14, 545–558. [Google Scholar] [CrossRef]
- Han, F.; Li, X.; Shi, W.; Wang, B.; Wang, W. Generic fully coupled framework for reliability assessment of offshore wind turbines under typical limit states. Eng. Struct. 2024, 304, 117692. [Google Scholar] [CrossRef]
- Vaziriazde, S.M.; Azizsoltani, H.; Halder, A. Reliability estimation of jacket type offshore platforms against seismic and wave loadings applied in time domain. Ship Offshore Struct. 2020, 17, 143–152. [Google Scholar] [CrossRef]
- Joint Committee on Structural Safety (JCSS). Probabilistic Model Code; Joint Committee on Structural Safety: Zurich, Switzerland, 2006. [Google Scholar]
- Yang, H.; Zhu, Y.; Lu, Q.; Zhang, J. Dynamic reliability based design optimization of the tripod sub-structure of offshore wind turbines. Renew. Energy 2015, 78, 16–25. [Google Scholar] [CrossRef]
- Han, F.; Wang, W.; Han, X.; Shi, W.; Li, X. Investigation of sensitivity analysis of crucial dynamic characteristics of offshore wind turbine utilizing polynomial chaos expansion. ASME J. Offshore Mech. Arct. Eng. 2025, 147, 052004. [Google Scholar] [CrossRef]
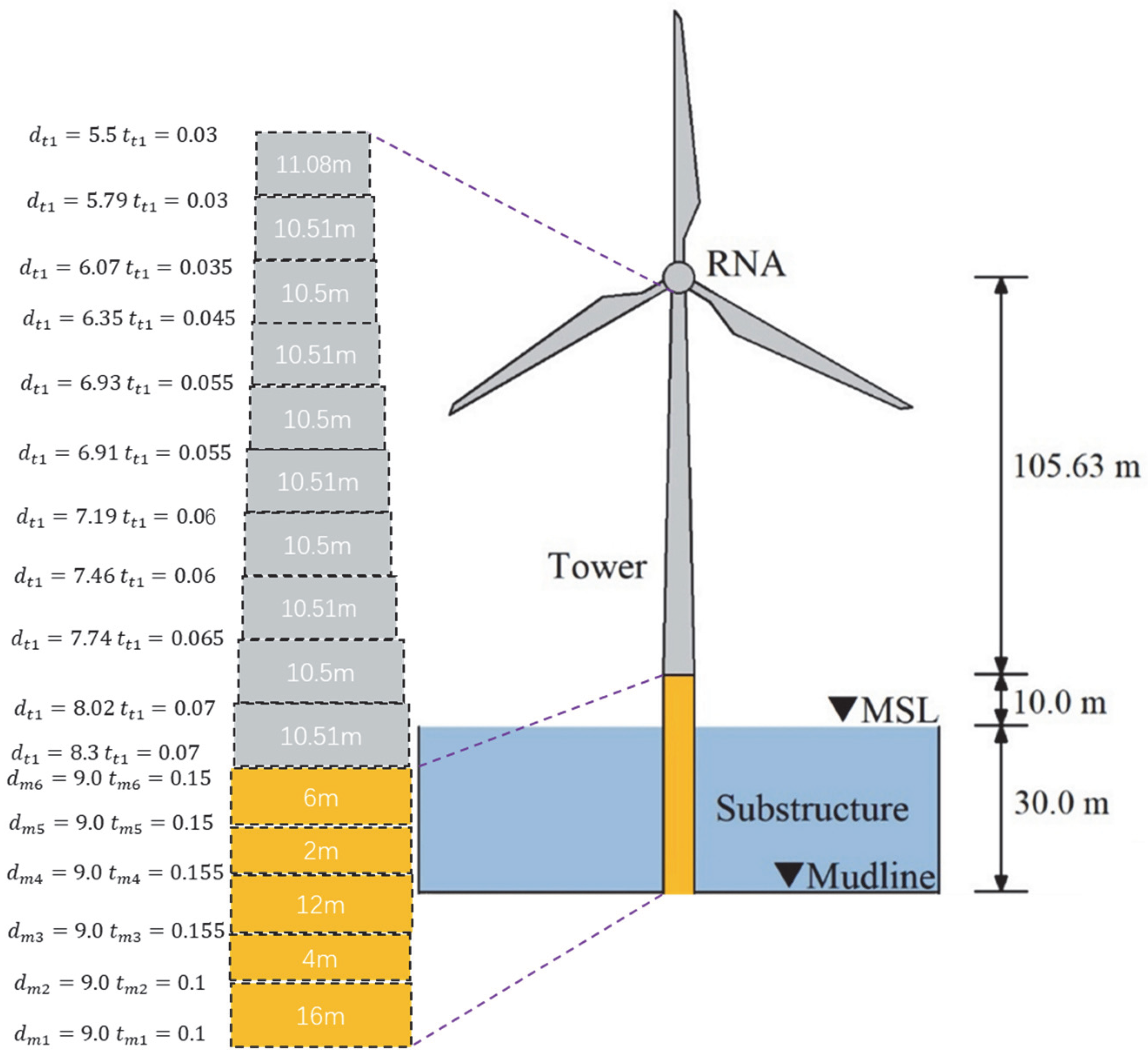


| Property | Description |
|---|---|
| Rated power | 10 MW |
| Key technical specifications of the OWT system | Upwind, 3 blades |
| Cut-in, rated, and cut-out wind speed | 4, 11, and 25 m/s |
| Cut-in and rated rotor speed | 6 and 8.68 rpm |
| Tower base elevation above mean sea level | 10 m |
| Tower height | 105.63 m |
| Tower top diameter, thickness | 5.5 m, 0.03 m |
| Tower base diameter, thickness | 8.3 m, 0.07 m |
| Monopile diameter, thickness | 9.0 m, 0.1 m |
| Element | DLC 1.3 | DLC 1.6a | DLC 6.2a |
|---|---|---|---|
| Operation state | Power production | Power production | Parked |
| Wind model | ETM | NTM | EWM |
| Wind speed | 14 m/s | 12 m/s | 40.375 m/s |
| Wave model | NSS | SSS | ESS |
| ) | 1.91 m|6.07 s | 8.07 m|11.3 s | 8.07 m|11.3 s |
| Current model | NCM | NCM | ECM |
| Current speed | 0.6 m/s | 0.6 m/s | 1.2 m/s |
| Wind/wave misalignment | 0° | 0° | 0° |
| Parameter | Dist. | Mean | Cov. | Ref. |
|---|---|---|---|---|
| (m/s) | Normal | Table 2 | 0.05 | [63] |
| (m) | Normal | Table 2 | 0.05 | [63] |
| (s) | Normal | Table 2 | 0.05 | [63] |
| (m/s) | Normal | Table 2 | 0.05 | [63] |
| (GPa) | Lognormal | 210 | 0.03 | [15,65,66] |
| (GPa) | Lognormal | 210 | 0.03 | [15,65,66] |
| (m) | Normal | Figure 2 | 0.03 | [63,67] |
| (m) | Normal | Figure 2 | 0.03 | [63,67] |
| Tower Top F-A Displacement | Tower Base Von Mises Stress | Tower Base F-A Bending Moment | Monopile Top F-A Displacement | Monopile Top Pitch Angle | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| CV 1 | TV 2 | CV | TV | CV | TV | CV | TV | CV | TV | |
| DLC 1.3 | 0.91 0.12% 3 | 0.87% | 0.87 0.1% | 0.85% | 1.3 0.15% | 1.12% | 1.49 0.18% | 1.55% | 1.29 0.11% | 1.27% |
| DLC 1.6a | 1.94 0.21% | 1.97% | 1.68 0.18% | 1.52% | 2.11 0.25% | 1.8% | 2.55 0.27% | 2.68% | 2.76 0.21% | 2.83% |
| DLC 6.2a | 1.3 0.16% | 1.27% | 0.78 0.13% | 0.69% | 0.71 0.11% | 0.79% | 2.12 0.27% | 2.17% | 1.81 0.25% | 1.95% |
| Tower top F-A displacement | 0.005 | 0.008 | 0.634 | 0.006 | 0.116 | 0.092 | 0.098 | 0.075 |
| Tower base von Mises stress | 0.005 | 0.010 | 0.265 | 0.013 | 0.053 | 0.658 | 0.016 | 0.017 |
| Tower base F-A bending moment | 0.002 | 0.003 | 0.889 | 0.003 | 0.064 | 0.049 | 0.005 | 0.010 |
| Monopile top F-A displacement | 0.001 | 0.007 | 0.419 | 0.001 | 0.004 | 0.005 | 0.315 | 0.267 |
| Monopile top pitch angle | 0.001 | 0.007 | 0.407 | 0.002 | 0.005 | 0.007 | 0.311 | 0.273 |
| Tower top F-A displacement | 0.006 | 0.014 | 0.625 | 0.003 | 0.088 | 0.101 | 0.076 | 0.122 |
| Tower base von Mises stress | 0.003 | 0.003 | 0.537 | 0.002 | 0.009 | 0.446 | 0.004 | 0.011 |
| Tower base F-A bending moment | 0.016 | 0.014 | 0.904 | 0.007 | 0.039 | 0.029 | 0.003 | 0.010 |
| Monopile top F-A displacement | 0.091 | 0.062 | 0.185 | 0.013 | 0.010 | 0.004 | 0.285 | 0.410 |
| Monopile top pitch angle | 0.022 | 0.029 | 0.249 | 0.001 | 0.003 | 0.002 | 0.315 | 0.393 |
| Tower top F-A displacement | 0.005 | 0.002 | 0.006 | 0.002 | 0.313 | 0.325 | 0.199 | 0.172 |
| Tower base von Mises stress | 0.002 | 0.002 | 0.001 | 0.001 | 0.002 | 0.985 | 0.001 | 0.002 |
| Tower base F-A bending moment | 0.007 | 0.108 | 0.074 | 0.005 | 0.612 | 0.047 | 0.124 | 0.068 |
| Monopile top F-A displacement | 0.005 | 0.001 | ~ | 0.001 | 0.001 | 0.003 | 0.538 | 0.460 |
| Monopile top pitch angle | 0.003 | 0.001 | 0.004 | 0.002 | 0.002 | 0.003 | 0.557 | 0.453 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Li, L.; Gao, X.; Xu, J.; Liu, X.; Gong, S.; Wang, W.; Shi, W.; Li, X. A Fully Coupled Sensitivity Analysis Framework for Offshore Wind Turbines Based on an XGBoost Surrogate Model and the Interpretation of SHAP. Sustainability 2025, 17, 9227. https://doi.org/10.3390/su17209227
Hu Z, Li L, Gao X, Xu J, Liu X, Gong S, Wang W, Shi W, Li X. A Fully Coupled Sensitivity Analysis Framework for Offshore Wind Turbines Based on an XGBoost Surrogate Model and the Interpretation of SHAP. Sustainability. 2025; 17(20):9227. https://doi.org/10.3390/su17209227
Chicago/Turabian StyleHu, Zhongbo, Liangxian Li, Xiang Gao, Jianfeng Xu, Xinyi Liu, Sen Gong, Wenhua Wang, Wei Shi, and Xin Li. 2025. "A Fully Coupled Sensitivity Analysis Framework for Offshore Wind Turbines Based on an XGBoost Surrogate Model and the Interpretation of SHAP" Sustainability 17, no. 20: 9227. https://doi.org/10.3390/su17209227
APA StyleHu, Z., Li, L., Gao, X., Xu, J., Liu, X., Gong, S., Wang, W., Shi, W., & Li, X. (2025). A Fully Coupled Sensitivity Analysis Framework for Offshore Wind Turbines Based on an XGBoost Surrogate Model and the Interpretation of SHAP. Sustainability, 17(20), 9227. https://doi.org/10.3390/su17209227







