The Economic–Cultural Dynamics of Urban Regeneration: Calibrating a Tripartite Evolutionary Game and Policy Thresholds for High-Quality Operational Renovation in China

Abstract

Cities worldwide are transitioning from demolition–redevelopment-driven expansion to high-quality regeneration centered on stock upgrading, cultural continuity, and long-term operations. Against the backdrop of China’s high-quality urban renewal phase guided by the “anti-massive demolition and construction” policy, this study constructs a calibrated tripartite evolutionary game among government, investors, and residents. By embedding culture–economy parameters—cultural renovation intensity (k), operational profit-sharing ratio between investors and residents (j), cultural identification coefficient (i), and cost-sharing coefficient (w)—we establish a behavioral interaction mechanism of “cultural value conversion–benefit-sharing–cultural identification–cost-sharing.” Simulations based on replicator dynamics demonstrate that sustained tripartite cooperation requires four conditions: cultural intensity surpasses the cost threshold (k ∈ [0.6, 0.7]); the profit-sharing ratio preserves market incentives (j ∈ [0.25, 0.35]); cultural identification reaches a minimum threshold (i ≥ 0.4); and residents’ cost-sharing does not exceed their benefit capacity (w ≤ 0.2). These findings reveal the core tension in China’s high-quality urban renewal stage—namely, the challenge of instituting sustainable operational mechanisms under cultural protection constraints—and globally provide a quantifiable policy toolbox for culture-led urban regeneration.

1. Introduction

Urban regeneration has transitioned from demolition–redevelopment-driven physical expansion to high-quality development centered on stock upgrading, cultural continuity, and long-term operations. Concurrently, governance models have shifted from single-actor dominance to government-market-community co-production, where enhanced public participation and state–society collaboration improve projects’ social legitimacy and operational sustainability [1,2,3].

China’s urban renewal has entered its third phase since 2021, guided by the anti-massive-demolition baseline that shapes a high-quality regeneration framework emphasizing stock improvement over large-scale demolition [4]. Building on this foundation, national policy in 2025 mandated transforming urban development modes, establishing a sustainable renewal regime and regulatory system, and comprehensively advancing urban regeneration initiatives to optimize urban structure, enhance functionalities, sustain cultural lineage, and elevate overall quality [5]. Policy emphasis has converged on integrated conservation and revitalization of historic districts coupled with operational excellence, providing institutional anchors and action boundaries for transitioning from short-term projects to long-term value operations. Empirical studies utilizing multi-source data and community-scale evaluations demonstrate that operations-led renewal in historic areas significantly enhances neighborhood vitality and regeneration efficiency, which strengthens the evidence base for culture-driven operational models in old city regeneration [6,7].

Despite accumulated practical experience, theoretical explanations lag behind in elucidating how governments, investors, and residents form stable strategies between high-quality operational regeneration and low-quality, fast-track redevelopment amidst stringent policy constraints and market incentives. EGT is particularly appropriate for modeling this complex, multi-stage interaction as it can capture the bounded rationality of stakeholders, their strategic learning over time, and identify the critical thresholds that lead to stable cooperative outcomes. While existing evolutionary game theory (EGT) studies have elucidated strategic evolution and policy thresholds among governments, developers, and the public in land redevelopment, industrial land conversion, and government-led renewal, they have not adequately incorporated the interdependent mechanisms linking cultural value conversion to economic returns, benefit redistribution, and endogenized participation costs [8,9,10].

Addressing China’s new urban renewal phase prioritizing historic district protection, activation, and operational quality, this study constructs a tripartite EGT framework among governments, investors, and residents centered on the strategic choice between high-quality operational regeneration and low-quality, fast-track redevelopment. We innovatively introduce four culture–economy parameters—cultural renovation intensity (k), operational profit-sharing ratio (j), cultural identification coefficient (i), and cost-sharing coefficient (w)—capturing the conversion efficiency from cultural capital to economic returns, the role of social identification in enhancing collaborative cohesion, benefit-sharing mechanisms, and the endogenization path of collaborative costs. Through replicator dynamics and stability analysis, we identify policy-market-community coordination conditions enabling evolutionary advantage for high-quality operational regeneration. The central hypothesis we test is that the stability of the high-quality outcome is not determined by any single factor, but by the conjunctive effect and compensatory relationships among the core culture–economy parameters (k, j, i, w). This provides a theoretically grounded and empirically calibrated basis for “combined rewards and penalties, co-construction, co-governance, and co-sharing” mechanisms in participatory, operations-led renewal.

This pursuit of high-quality, operational regeneration is fundamentally aligned with the goals of urban sustainability [1]. Moving beyond a narrow environmental definition, sustainable urban regeneration in this context entails a holistic approach that balances cultural sustainability (preserving historical continuity and fostering place identity), social sustainability (ensuring equitable benefit-sharing and inclusive community participation), and economic sustainability (establishing long-term operational viability rather than relying on short-term land capitalization). The tripartite evolutionary game constructed in this study, therefore, does not merely model strategic choices between development modes but simulates the pathways toward achieving this integrated sustainable development. The core parameters of k, j, i, and *w* are, in essence, policy variables that calibrate the trade-offs between these different dimensions of sustainability.

2. Literature Review

2.1. The Evolution of Urban Regeneration in the Chinese Context

Urban regeneration in China has undergone a profound paradigm shift, moving from extensive expansion and demolition-reconstruction towards connotative, high-quality development centered on stock enhancement, functional reconfiguration, and long-term sustainability [4,5,11]. This transition is deeply embedded in specific policy frameworks. The 2021 “anti-massive demolition and construction” policy fundamentally reshaped the action boundaries for urban renewal, explicitly prioritizing the integrated conservation and revitalization of historic districts [4]. This policy pivot was further reinforced by the 2025 Guiding Opinions, which mandated the establishment of a sustainable renewal regime and comprehensive advancement of urban regeneration initiatives [5].

Concurrently, practical approaches have evolved from large-scale redevelopment to block-scale micro-regeneration, heritage activation, and public space quality upgrading [11,12]. Empirical evaluations utilizing urban renewal pilot data demonstrate that this new model enhances functionality and vitality in existing urban areas [7]. However, this transition also presents challenges, such as the need to address potential risk redistribution to prevent new inequities and spatial exclusion [13]. Furthermore, research has begun to integrate urban renewal with broader public governance indicators like health-safety-environment (HSE), revealing that the effects on resident health and urban resilience are contingent upon the precision of policy instruments and spatial targeting [14]. Overall, China’s current high-quality development stage necessitates a parallel shift in governance, from developmentalism towards more managerial and operational modes of governance to achieve a balanced integration of historical continuity, industrial upgrading, and equitable accessibility [15].

2.2. Decision-Making and Multi-Stakeholder Governance in Urban Regeneration

The paradigm shift in urban regeneration has redefined its core challenge from a technical design issue to a complex socio-political process of multi-stakeholder governance and strategic decision-making, a transition analyzed through frameworks such as collaborative governance, institutional economics, and sustainable renewal theories [1,15]. The inherent complexity arises from significant information and power asymmetry among stakeholders [6], the fundamental tension between short-term financial returns and long-term social-cultural benefits, a central challenge documented in studies of gentrification and sustainable renewal [13,16], and the high transaction costs associated with negotiating and enforcing inclusive agreements [12].

Traditional top-down, government-led models often fail to incorporate local knowledge, leading to legitimacy deficits and implementation resistance [2,17]. Conversely, purely market-driven approaches risk prioritizing profitability over equity, frequently resulting in gentrification and cultural displacement [13,16]. In response, collaborative governance has emerged as a critical framework, emphasizing deliberative negotiation and co-production among public and private actors [18,19,20]. Its effectiveness hinges on institutional designs that foster trust, ensure transparency, and implement equitable benefit-sharing mechanisms [20]. Practices such as participatory planning, co-design workshops, and community benefit agreements have proven instrumental in aligning stakeholder incentives and enhancing project acceptability [2,21]. Evidence confirms that institutionalized participation not only mitigates conflict but also leverages local social capital to improve project resilience and outcomes [10].

Nevertheless, establishing robust collaboration is fraught with difficulties. Stakeholders frequently engage in strategic behaviors—such as opportunism, hold-out tactics, or free-riding—driven by divergent interests and risk perceptions [22]. Residents may distrust government and market intentions [6], investors remain cautious of community opposition and regulatory uncertainty [23], and governments must perpetually balance developmental goals with social welfare responsibilities [15]. These dynamics create a volatile environment where cooperation is often elusive without carefully calibrated incentives. Understanding these strategic interactions requires analytical frameworks capable of capturing their dynamic, iterative, and boundedly rational nature, paving the way for the application of computational models like evolutionary game theory.

2.3. The Application of Evolutionary Game Theory in Urban Renewal

As a dynamic modeling approach, Evolutionary Game Theory (EGT) simulates strategic learning and behavioral imitation among boundedly rational decision-makers through repeated interactions. It has been extensively applied to characterize the dynamic interplay among government, market, and society in urban regeneration, proving particularly effective for analyzing incentive-compatible conditions, policy–instrument thresholds, and strategy convergence pathways in complex governance settings [23,24,25].

In recent years, numerous studies have developed tripartite EGT models for characteristic Chinese contexts, such as urban-village regeneration [26,27] and inefficient industrial land redevelopment [8,9,28]. By integrating evolutionary games with system dynamics (SD) analysis, this literature identifies critical parameter ranges for regulatory intensity, penalty–subsidy schemes, and contractual incentive allocation mechanisms that lead to collaborative steady states or non-cooperative equilibria, findings often validated through numerical simulations and sensitivity analyses [26,27].

Studies grounded in institutional and contractual design demonstrate that combining bottom-up participation with formalized benefit-sharing mechanisms significantly improves collaboration quality and convergence speed [10,29]. Other contributions embed conflict formation and governance responses within evolutionary frameworks to explain phase-dependent strategy transitions and sources of strategic breakdown [27,28]. Furthermore, recent research has begun to incorporate more complex network structures and learning mechanisms, highlighting the potential for modeling deeper stakeholder interactions [30]. Compared with traditional static–equilibrium approaches, EGT provides stronger explanatory power for phase-wise equilibrium shifts, path dependence, and policy threshold effects, making it particularly suitable for China’s current policy and market context of high-quality, operations-oriented urban regeneration.

2.4. Research Gaps and Contributions of This Study

Despite substantial progress, most existing tripartite EGT models remain constrained by the traditional “cost–benefit–penalty–subsidy” framework, exhibiting three significant limitations relevant to China’s new urban renewal phase.

First, existing models fail to quantitatively model the linkage from cultural preservation intensity (k) to “intensity-tempo-cash flow” while incorporating governance constraints [31,32]. Second, few studies endogenize both the operational profit-distribution ratio (j) and cost-sharing coefficient (w) within a unified evolutionary framework, nor do they identify how their joint threshold configurations condition the emergence of evolutionarily stable strategies (ESS) [28,29]. Third, integrated modeling that couples institutionalized participation (which enhances residents’ cultural identification coefficient i), digitalization with phased delivery (which influences cost-sharing structures), performance-linked dividend mechanisms, and cross-scalar resource allocation remains underdeveloped, hindering the identification of a “minimum incentive package” for sustainable regeneration [1,33,34].

Addressing these gaps, this study constructs a tripartite EGT framework among governments, investors, and residents centered on the strategic choice in China’s cultural-conservation-led renewal context. We innovatively introduce four culture–economy parameters (k, j, i, w) to capture the conversion efficiency from cultural capital to economic returns, the role of social identification, benefit-sharing mechanisms, and the endogenization path of collaborative costs. This establishes a “cultural value conversion–social identification–benefit-sharing–cost co-bearing” interaction mechanism, aiming to identify critical thresholds and minimum incentive combinations that enable the high-quality strategy to become the ESS, thereby providing a calibrated testable basis for policy simulation.

3. Building and Analysis of Evolutionary Game Model

3.1. Assumptions and Key Variables

As an analytical framework for conflict and cooperation, game theory analyzes strategic decision-making interactions among multiple stakeholders. This study develops a tripartite evolutionary game model for urban regeneration among governments, investors, and residents. The definitions of all parameters are presented in Table 1. The basic assumptions are as follows:

Assumption 1. 

Each stakeholder can choose between two strategic options. The government’s strategy space comprises implementing active-guidance policies (x) or adopting laissez-faire approaches (1 − x); investors may pursue high-quality operational regeneration (y) or opt for rapid redevelopment (1 − y); residents can either actively participate in and cooperate with operational regeneration (z) or adopt passive responses (1 − z). The strategy probabilities satisfy (0 ≤ x, y, z ≤ 1), each representing the proportion of agents adopting the corresponding pure strategy. All stakeholders are risk-neutral and seek to maximize their respective utilities.

Assumption 2. 

Under the active guidance policy (x), the government bears a core policy implementation cost C_za and an additional policy cost C_zbt. It provides a subsidy R_zv to investors implementing high-quality operational regeneration, and a subsidy R_zc to residents demonstrating active cooperation. The government receives a base regeneration benefit B_za; obtains additional economic benefits B_zbt when investors act proactively; and acquires additional social benefits B_zct when residents participate actively. If investors engage in negative behavior, the government incurs an economic loss C_zc.

Under the laissez-faire policy (1 − x), the government only pays the core implementation cost C_za and receives B_za; when investors act proactively, it gains B_zbt but does not acquire B_zct; if investors behave negatively, it incurs a loss C_zd.

Assumption 3. 

If the investor pursues high-quality, operational regeneration (y), it bears a baseline cost C_va and an incremental infrastructure cost C_vbt, and pays rental compensation R_vc to residents. It receives baseline construction revenue B_va, incremental construction revenue B_vbt, and operating revenue (1 − j)·B_vct. If residents actively cooperate, the investor additionally obtains a collaborative benefit B_vdt.

If the investor adopts low-quality, rapid redevelopment (1 − y), it bears only the baseline cost C_va. Under the government’s active guidance policy, it must pay a governmental fine R_vz; if residents actively participate, it must pay compensation R_vd to residents.

Assumption 4. 

If residents actively participate (z) in high-quality, operational regeneration, they bear a baseline participation cost C_cb. When the investor pursues such regeneration, residents incur a temporary relocation and resettlement cost C_ca and agree to share the investor’s incremental infrastructure cost R_cv. They receive a baseline property income B_ca. Additionally, if the investor pursues high-quality regeneration, residents receive incremental property income B_cbt, incremental cultural identification benefits B_cct, and an operating dividend income (j·B_vct).

If residents respond negatively (1 − z), they do not bear C_cb. They still receive B_ca; however, even if the investor pursues high-quality regeneration, they receive B_cbt but neither B_cct nor the operating dividend (j·B_vct).

Table 1. Assumed Parameters in the Evolutionary Game Model.

Type	No.	Parameter	Meaning	Remarks
Core Parameters	1	k	Development intensity of high-quality cultural renovation and operation	0 ≤ k ≤ 1
	2	j	Operational profit-sharing ratio between investor and residents when the investor pursues high-quality regeneration and residents actively participate	0 ≤ j ≤ 1
	3	i	Residents’ cultural identification coefficient	0 ≤ i ≤ 1
	4	w	Proportion of incremental costs that residents are willing to share when actively cooperating	0 ≤ w ≤ 1
Government Parameters	5	Bza	Government’s basic economic benefit when the investor conducts baseline renovation
	6	Bzbt	Government’s incremental economic benefit when the investor pursues high-quality operational regeneration	Bzbt = k·Bzb
	7	Bzb	Base value of government’s incremental economic benefit from high-quality operational regeneration
	8	Bzct	Government’s incremental social benefit when the investor pursues high-quality regeneration and residents actively participate	Bzct = i·k·Bzc
	9	Bzc	Base value of government’s incremental social benefit from high-quality regeneration with resident participation
	10	Cza	Government’s basic policy implementation cost
	11	Czbt	Incremental policy cost under active government support	Czbt = (sk)·Czb
	12	Czb	Base value of incremental policy cost under active government support
	13	s	Coefficient of incremental policy cost under active government support
	14	Czc	Government’s loss due to negative social impact (e.g., resident complaints) when it actively guides but the investor adopts low-quality rapid redevelopment and residents respond negatively	Czc < Czd
	15	Czd	Government’s loss due to negative social impact (e.g., mass incidents) under laissez-faire policy, with low-quality investor behavior and negative resident response	Czc < Czd
	16	q	Coefficient of negative social impact loss for the government when residents cooperate but the investor adopts low-quality redevelopment	q ≥ 1, The government’s loss from negative social impact in the case of (1, 0, 1) is q·Czc.
	17	Rzv	Subsidy from government to investor under active support and high-quality regeneration by the investor
	18	Rzc	Subsidy from government to residents under active support and active resident cooperation
Investor Parameters	19	Bva	Investor’s basic construction revenue from low-quality rapid redevelopment
	20	Bvbt	Investor’s incremental construction revenue from high-quality operational regeneration	Bvbt = k·Bvb
	21	Bvb	Base value of investor’s incremental construction revenue from high-quality regeneration
	22	Bvct	Investor’s operational revenue from high-quality regeneration	Bvct = k·Bvc
	23	Bvc	Base value of investor’s operational revenue from high-quality regeneration
	24	Bvdt	Synergistic gain to investor (e.g., cost reduction, operational improvement) when residents actively support and investor pursues high-quality regeneration	Bvdt = i·k·Bvd
	25	Bvd	Base value of synergistic gain to investor from resident support and high-quality regeneration
	26	Cva	Investor’s basic cost for low-quality rapid redevelopment
	27	Cvbt	Investor’s incremental infrastructure cost for high-quality operational regeneration	Cvbt = mk·Cvb
	28	Cvb	Base value of incremental infrastructure cost for high-quality regeneration
	29	m	Impact coefficient of incremental infrastructure cost for high-quality regeneration
	30	Cvct	Investor’s operational cost for high-quality regeneration	Cvct = nk·Cvc
	31	Cvc	Base value of operational cost for high-quality regeneration
	32	n	Coefficient of operational cost for high-quality regeneration
	33	Rvc	Rental compensation paid by investor to residents for high-quality regeneration
	34	Rvz	Fine imposed by government on investor under active support but low-quality redevelopment by the investor
	35	Rvd	Compensation paid by investor to residents when residents actively cooperate but investor adopts low-quality redevelopment
Resident Parameters	36	Bca	Residents’ basic property income under low-quality rapid redevelopment
	37	Bcbt	Residents’ incremental property income under high-quality operational regeneration	Bcbt = k·Bcb
	38	Bcb	Base value of residents’ incremental property income from high-quality regeneration
	39	Bcct	Residents’ cultural identification gain when they actively cooperate and investor pursues high-quality regeneration	Bcct = i·k·Bcc
	40	Bcc	Base value of residents’ cultural identification gain from cooperation and high-quality regeneration
	41	Cca	Cost incurred by residents for temporary relocation and resettlement for high-quality regeneration by investor
	42	Ccb	Basic cost borne by residents for active cooperation
	43	Rcv	Amount residents are willing to share toward investor’s incremental infrastructure cost when actively cooperating	Rcv = w·(mk·Cvb)

Table 1. Assumed Parameters in the Evolutionary Game Model.

Type	No.	Parameter	Meaning	Remarks
Core Parameters	1	k	Development intensity of high-quality cultural renovation and operation	0 ≤ k ≤ 1
	2	j	Operational profit-sharing ratio between investor and residents when the investor pursues high-quality regeneration and residents actively participate	0 ≤ j ≤ 1
	3	i	Residents’ cultural identification coefficient	0 ≤ i ≤ 1
	4	w	Proportion of incremental costs that residents are willing to share when actively cooperating	0 ≤ w ≤ 1
Government Parameters	5	Bza	Government’s basic economic benefit when the investor conducts baseline renovation
	6	Bzbt	Government’s incremental economic benefit when the investor pursues high-quality operational regeneration	Bzbt = k·Bzb
	7	Bzb	Base value of government’s incremental economic benefit from high-quality operational regeneration
	8	Bzct	Government’s incremental social benefit when the investor pursues high-quality regeneration and residents actively participate	Bzct = i·k·Bzc
	9	Bzc	Base value of government’s incremental social benefit from high-quality regeneration with resident participation
	10	Cza	Government’s basic policy implementation cost
	11	Czbt	Incremental policy cost under active government support	Czbt = (sk)·Czb
	12	Czb	Base value of incremental policy cost under active government support
	13	s	Coefficient of incremental policy cost under active government support
	14	Czc	Government’s loss due to negative social impact (e.g., resident complaints) when it actively guides but the investor adopts low-quality rapid redevelopment and residents respond negatively	Czc < Czd
	15	Czd	Government’s loss due to negative social impact (e.g., mass incidents) under laissez-faire policy, with low-quality investor behavior and negative resident response	Czc < Czd
	16	q	Coefficient of negative social impact loss for the government when residents cooperate but the investor adopts low-quality redevelopment	q ≥ 1, The government’s loss from negative social impact in the case of (1, 0, 1) is q·Czc.
	17	Rzv	Subsidy from government to investor under active support and high-quality regeneration by the investor
	18	Rzc	Subsidy from government to residents under active support and active resident cooperation
Investor Parameters	19	Bva	Investor’s basic construction revenue from low-quality rapid redevelopment
	20	Bvbt	Investor’s incremental construction revenue from high-quality operational regeneration	Bvbt = k·Bvb
	21	Bvb	Base value of investor’s incremental construction revenue from high-quality regeneration
	22	Bvct	Investor’s operational revenue from high-quality regeneration	Bvct = k·Bvc
	23	Bvc	Base value of investor’s operational revenue from high-quality regeneration
	24	Bvdt	Synergistic gain to investor (e.g., cost reduction, operational improvement) when residents actively support and investor pursues high-quality regeneration	Bvdt = i·k·Bvd
	25	Bvd	Base value of synergistic gain to investor from resident support and high-quality regeneration
	26	Cva	Investor’s basic cost for low-quality rapid redevelopment
	27	Cvbt	Investor’s incremental infrastructure cost for high-quality operational regeneration	Cvbt = mk·Cvb
	28	Cvb	Base value of incremental infrastructure cost for high-quality regeneration
	29	m	Impact coefficient of incremental infrastructure cost for high-quality regeneration
	30	Cvct	Investor’s operational cost for high-quality regeneration	Cvct = nk·Cvc
	31	Cvc	Base value of operational cost for high-quality regeneration
	32	n	Coefficient of operational cost for high-quality regeneration
	33	Rvc	Rental compensation paid by investor to residents for high-quality regeneration
	34	Rvz	Fine imposed by government on investor under active support but low-quality redevelopment by the investor
	35	Rvd	Compensation paid by investor to residents when residents actively cooperate but investor adopts low-quality redevelopment
Resident Parameters	36	Bca	Residents’ basic property income under low-quality rapid redevelopment
	37	Bcbt	Residents’ incremental property income under high-quality operational regeneration	Bcbt = k·Bcb
	38	Bcb	Base value of residents’ incremental property income from high-quality regeneration
	39	Bcct	Residents’ cultural identification gain when they actively cooperate and investor pursues high-quality regeneration	Bcct = i·k·Bcc
	40	Bcc	Base value of residents’ cultural identification gain from cooperation and high-quality regeneration
	41	Cca	Cost incurred by residents for temporary relocation and resettlement for high-quality regeneration by investor
	42	Ccb	Basic cost borne by residents for active cooperation
	43	Rcv	Amount residents are willing to share toward investor’s incremental infrastructure cost when actively cooperating	Rcv = w·(mk·Cvb)

3.2. Establishing and Solving the Evolutionary Game Model

Based on the above assumptions and related variables, the pay-off matrix for the tripartite evolutionary game is obtained

Table 2. Tripartite Pay-off Matrix.

Investors		High-Quality Operational Regeneration(y)		Low-Quality Rapid Regeneration (1 − y)
Residents		Active Responses (z)	Passive Response (1 − z)	Active Responses (z)	Passive Response (1 − z)
Govern–ment	Active- Guidance Policies (x)	E1:(1, 1, 1)	E2:(1, 1, 0)	E3:(1, 0, 1)	E4:(1, 0, 0)
		Bza + Bzbt + Bzct − Cza − Czbt − Rzv − Rzc	Bza + Bzbt − Cza − Czbt − Rzv	Bza + Rvz − Cza − Czbt − q·Czc − Rzc	Bza + Rvz − Cza − Czbt − Czc
		Bva + Bvbt + (1 − j)·Bvct + Bvdt + Rzv + Rcv − Cva − Cvbt − Cvct − Rvc	Bva + Bvbt + Bvct + Rzv − Cva − Cvbt − Cvct − Rvc	Bva − Cva − Rvz − Rvd	Bva − Cva − Rvz
		Bca + Bcbt + Bcct + j·Bvct + Rvc + Rzc − Cca − Ccb − Rcv	Bca + Bcbt + Rvc − Cca	Bca + Rzc + Rvd − Ccb	Bca
	Laissez − Faire Policies (1 − x)	E5:(0, 1, 1)	E6:(0, 1, 0)	E7:(0, 0, 1)	E8:(0, 0, 0)
		Bza + Bzbt − Cza	Bza + Bzbt − Cza	Bza − Cza − q·Czd	Bza − Cza − Czd
		Bva + Bvbt + (1 − j)·Bvct + Bvdt + Rcv − Cva − Cvbt − Cvct − Rvc	Bva + Bvbt + Bvct + Bvdt − Cva − Cvbt − Cvct − Rvc	Bva − Cva − Rvd	Bva − Cva
		Bca + Bcbt + Bcct + j·Bvct + Rvc − Cca − Ccb − Rcv	Bca + Bcbt + Rvc − Cca	Bca + Rvd − Ccb	Bca

.

Expected earnings from government’s active-guidance policies, E_z1:

E_z1 = y · z · (B_za + B_zbt + B_zct − C_za − C_zbt − R_zv − R_zc) + y · (1 − z) · (B_za + B_zbt − C_za − C_zbt − R_zv)
+ (1 − y) · z · (B_za + R_vz − C_za − C_zbt − q·C_zc − R_zc) + (1 − y) · (1 − z) · (B_za + R_vz − C_za − C_zbt − C_zc)

(1)

Expected earnings from government’s laissez-faire approaches, E_z2:

E_z2 = y · z · (B_za + B_zbt − C_za) + y · (1 − z) · (B_za + B_zbt − C_za) + (1 − y) · z · (B_za − C_za − q·C_zd) + (1 − y) · (1 − z) · (B_za − C_za − C_zd)

(2)

Mean expected earnings for government, E_z3:

E_z3 = x · E_z1 + (1 − x) · E_z2

(3)

Iterative dynamic equation for local government’s policies, F(x) = x · (E_z1 − E_z3), where

F(x) = (C_zc − (i · k · B_zc) − C_zd − C_zc · q + C_zd · q) · x² · y · z + (C_zd − C_zc + R_vz + R_zv) · x² · y
+ (C_zd − C_zc + R_zc + C_zc · q − C_zd · q) · x² · z + ((s^k · C_zb) + C_zc − C_zd − R_vz) · x² + ((i · k · B_zc) − C_zc + C_zd + C_zc · q − C_zd · q) · x · y · z
+ (C_zc − C_zd − R_vz − R_zv) · x · y + (C_zc − C_zd − R_zc − C_zc · q + C_zd · q) · x · z + (C_zd − C_zc − (s^k · C_zb) + R_vz) · x

(4)

Expected earnings from investors’ high-quality operational regeneration, E_v1:

E_v1 = x · z · (B_va + B_vbt + (1 − j) · B_vct + B_vdt + R_zv + R_cv − C_va − C_vbt − C_vct − R_vc)
+ (1 − x) · z · (B_va + B_vbt + (1 − j) · B_vct + B_vdt + R_cv − C_va − C_vbt − C_vct − R_vc)
+ x · (1 − z) · (B_va + B_vbt + B_vct + R_zv − C_va − C_vbt − C_vct − R_vc)
+ (1 − x) · (1 − z) · (B_va + B_vbt + B_vct + B_vdt − C_va − C_vbt − C_vct − R_vc)

(5)

Expected earnings from investors’ low-quality rapid regeneration, E_v2:

E_v2 = x · z · (B_va − C_va − R_vz − R_vd) + (1 − x) · z · (B_va − C_va − R_vd) + x · (1 − z) · (B_va − C_va − R_vz) + (1 − x) · (1 − z) · (B_va − C_va)

(6)

Mean expected earnings for investors, E_v3:

E_v3 = y · E_v1 + (1 − y) · E_v2

(7)

Iterative dynamic equation for investors’ investments F(y) = y · (E_v1 − E_v3), where

F(y) = (i · k · B_vd − R_vz − R_zv) · x · y² + (i · k · B_vd) · x · y · z + (R_vz − (i · k · B_vd) + R_zv) · x · y + ((k · B_vc) − (w · (k^m · C_vb)) − R_vd
+ (k · B_vc) · (j − 1)) · y² · z + ((m^k · C_vb) − (k · B_vc) − (i · k · B_vd) − (k · B_vb) + (n^k · C_vc) + R_vc) · y² + ((w · (k^m · C_vb)) − (k · B_vc)
+ R_vd − (k · B_vc) · (j − 1)) · y · z + ((k · B_vb) + (k · B_vc) + (i · k · B_vd) − (m^k · C_vb) − ((n^k) · C_vc) − R_vc) · y − (i · k · B_vd) · x · y² · z

(8)

Expected earnings from residents’ active responses, E_c1:

EE_c1 = x · y · (B_ca + B_cbt + B_cct + j · B_vct + R_vc + R_zc − C_ca − C_cb − R_cv)
+ (1 − x) · y · (B_ca + B_cbt + B_cct + j · B_vct + R_vc − C_ca − C_cb − R_cv)
+ x · (1 − y) · (B_ca + R_zc + R_vd − C_cb) + (1 − x) · (1 − y) · (B_ca + R_vd − C_cb)

(9)

Expected earnings from residents’ passive responses, E_c2:

E_c2 = x · y · (B_ca + B_cbt + R_vc − C_ca) + (1 − x) · y · (B_ca + B_cbt + R_vc − C_ca) + x · (1 − y) · (B_ca) + (1 − x) · (1 − y) · B_ca

(10)

Mean expected earnings for residents, E_c3:

E_c3 = z · E_c1 + (1 − z) · E_c2

(11)

Iterative dynamic equation for residents’ responses F(z) = z · (E_c1 − E_c3), where

F(z) = R_zc · x · z + (w · m^k · C_vb − i · k · B_cc + R_vd − k · B_vc · j) · y · z²
+ ((i · k · B_cc) − (w · (m^k · C_vb)) − R_vd + (k · B_vc) · j) · y · z + (C_cb − R_vd) · z² + (R_vd − C_cb) · z − R_zc · x · z²

(12)

3.3. Analysis of Points of Equilibrium Under Evolutionarily Stable Strategy

Setting the replicator dynamic equations f(x), f(y), and f(z) of the tripartite evolutionary game to zero yields eight potential equilibrium points: E1(1, 1, 1), E2(1, 1, 0), E3(1, 0, 1), E4(1, 0, 0), E5(0, 1, 1), E6(0, 1, 0), E7(0, 0, 1), and E8(0, 0, 0).

The stability of each equilibrium point in this system of differential equations is determined by the eigenvalues of the corresponding Jacob matrix. For the tripartite game, the Jacob matrix is defined as

$$\mathrm{J}=\left\{\begin{array}{c}\begin{array}{ccc}{\displaystyle \frac{\partial \mathrm{F}\left(x\right)}{dx}}& {\displaystyle \frac{\partial F\left(x\right)}{dy}}& {\displaystyle \frac{\partial F\left(x\right)}{dz}}\\ {\displaystyle \frac{\partial F\left(y\right)}{dx}}& {\displaystyle \frac{\partial F\left(y\right)}{dy}}& {\displaystyle \frac{\partial F\left(y\right)}{dz}}\\ {\displaystyle \frac{\partial F\left(z\right)}{dx}}& {\displaystyle \frac{\partial F\left(z\right)}{dy}}& {\displaystyle \frac{\partial F\left(z\right)}{dz}}\end{array}\end{array}\right.=\left\{\begin{array}{c}\begin{array}{ccc}(2\mathrm{x}-1) · \mathrm{g}\left(1\right)& \mathrm{x} · (\mathrm{x}-1) · \mathrm{g}\left(2\right)& \mathrm{x}·(1-\mathrm{x}) · \mathrm{g}\left(3\right)\\ \mathrm{y} · (1-\mathrm{y}) · \mathrm{g}\left(4\right)& (1-2\mathrm{y}) · \mathrm{g}\left(5\right)& \mathrm{y}·(1-\mathrm{y}) · \mathrm{g}\left(6\right)\\ \mathrm{z} · (1-\mathrm{z}) · \mathrm{g}\left(7\right)& \mathrm{z}·(1-\mathrm{z}) · \mathrm{g}\left(8\right)& (1-2\mathrm{z}) · \mathrm{g}\left(9\right)\end{array}\end{array}\right.$$

(13)

where

• g(1) = C_zbt + C_zc − C_zd − R_vz − C_zc · y + C_zd · y − C_zc · z + C_zd · z + R_vz · y + R_zv · y + R_zc · z + C_zc · q · z − C_zd · q · z − B_zct · y · z + C_zc · y · z − C_zd · y · z − C_zc · q · y · z + C_zd · q · y · z
• g(2) = C_zd − C_zc + R_vz + R_zv − B_zct · z + C_zc · z − C_zd · z − C_zc · q · z + C_zd · q · z
• g(3) = C_zc − C_zd − R_zc − C_zc · q + C_zd · q + B_zct · y − C_zc · y + C_zd · y + C_zc · q · y − C_zd · q · y
• g(4) = R_vz − B_vdt + R_zv + B_vdt · z
• g(5) = B_vbt + B_vct + B_vdt − C_vbt − C_vct − R_vc − B_vdt · x + R_vz · x + R_zv · x + R_cv · z + R_vd · z − B_vct · j · z + B_vdt · x · z
• g(6) = R_cv + R_vd − B_vct · j + B_vdt · x
• g(7) = R_zc
• g(8) = B_cct − R_cv − R_vd + B_vct · j
• g(9) = R_vd − C_cb + B_cct · y + R_zc · x − R_cv · y − R_vd · y + B_vct · j · y

Following standard eigenvalue analysis of the Jacobian matrix, we assess the stability of the eight candidate equilibria in the replicator dynamic system of the tripartite evolutionary game. An equilibrium is classified as an evolutionarily stable strategy (ESS) if all three eigenvalues corresponding to it are negative, whereas it is unstable if at least one eigenvalue is positive. The eigenvalues λ for all eight candidate equilibria are summarized in

Table 3. Eigenvalue of points of equilibrium.

Point of Equilibrium	λ1	λ2	λ3
E1 (1, 1, 1)	(sk) · Czb − i · k · Bzc + Rzc + Rzv	mk · Cvb − i · k · Bvd − k · Bvb + nk · Cvc + Rvc − w · mk · Cvb − Rvd − Rvz − Rzv + k · Bvc · (j − 1)	Ccb − i · k · Bcc − k · Bvc · j + w · k · mk · Cvb − Rzc
E2 (1, 1, 0)	sk · Czb + Rzv	mk · Cvb − k · Bvc − k · Bvb + nk · Cvc + Rvc − Rvz − Rzv	i · k · Bcc − w · k · mk · Cvb + Rzc + k · Bvc · j − Ccb
E3 (1, 0, 1)	sk · Czb − Rvz + Rzc + Czc · q − Czd · q	k · Bvb + i · k · Bvd − mk · Cvb − Rvc + Rvd + Rvz + w · k · mk · Cvb − nk · Cvc + Rzv − k · Bvc · (j − 1)	Ccb − Rvd − Rzc
E4 (1, 0, 0)	sk · Czb + Czc − Czd − Rvz	k · Bvb + k · Bvc − mk · Cvb − nk · Cvc − Rvc + Rvz + Rzv	Rvd − Ccb + Rzc
E5 (0, 1, 1)	i · k · Bzc − sk · Czb − Rzc − Rzv	mk · Cvb − i · k · Bvd − k · Bvb + nk · Cvc − w · k · mk · Cvb + Rvc − Rvd + k · Bvc · (j − 1)	Ccb − i · k · Bcc + w · k · mk · Cvb − k · Bvc · j
E6 (0, 1, 0)	−sk · Czb − Rzv	mk · Cvb − k · Bvc − i · k · Bvd − k · Bvb + nk · Cvc + Rvc	i · k · Bcc − Ccb − w · k · mk · Cvb + k · Bvc · j
E7 (0, 0, 1)	Rvz − sk · Czb − Rzc − Czc · q + Czd · q	k · Bvb + i · k · Bvd − mk · Cvb − nk · Cvc − Rvc + w · k · mk · Cvb + Rvd − k · Bvc · (j − 1)	Ccb − Rvd
E8 (0, 0, 0)	Czd − Czc − sk · Czb + Rvz	k · Bvb + k · Bvc + i · k · Bvd − mk · Cvb − nk · Cvc − Rvc	Rvd − Ccb

.

The eigenvalues at the eight equilibria indicate that costs, subsidies, baseline returns, and incremental returns serve as fundamental determinants. The cultural renovation intensity (k), operational profit-sharing ratio (j), cultural identification coefficient (i), and cost-sharing coefficient (w) collectively and systematically govern the behavioral strategies of the government, investors, and residents in urban renewal. In alignment with typical developmental trajectories, high-quality, culture-led, operational regeneration in China can be categorized into three phases: initiation, growth, and maturation, across which the three parties exhibit distinct stable decisions.

• Initiation phase, as shown in Figure 1a: Rapid, construction-led redevelopment generates relatively high returns, low construction costs, and short payback periods, but yields low cultural-operational returns. Consequently, all three parties prefer low-quality rapid redevelopment—typically implemented through demolition and reconstruction—driving the system toward equilibrium E₈(0, 0, 0).
• Growth phase, as shown in Figure 1b: Although social problems induced by rapid construction become apparent, short-term returns remain high. The government and residents shift toward positive strategies; however, investors continue to prioritize low-quality rapid redevelopment due to substantial construction-phase returns. Thus, the tripartite dynamics evolve toward equilibrium E₃(1, 0, 1).
• Maturation phase, as shown in Figure 1c: Returns from rapid construction decline while its social costs intensify, whereas returns from high-quality, culture-led operations rise significantly. All three parties support high-quality, operational regeneration, leading the system to equilibrium E₁(1, 1, 1).

4. Simulation Results and Analysis

Advancing high-quality, operational regeneration in China’s historic urban areas and steering urban renewal toward a mature stage represent a crucial objective for urban investment in China, as it also enhances returns for all stakeholders. Accordingly, we select the stable equilibrium E₁(1, 1, 1) as the target state for simulation and evaluation. Within this framework, we conduct numerical simulations of the evolutionary trajectories for each player using Matlab 2024(b) to visualize how key factors within the replicator dynamic system influence the tripartite evolutionary process and its outcomes [29].

4.1. Parameter Calibration Methodology

This study calibrates the parameters based on three core principles: (1) The first is matching the magnitudes and structural relationships of returns and costs observed in mature, high-quality, culture-led, operational regeneration projects in China. Specifically, the investor’s operational incremental return (B_vc) must exceed the constructional incremental return (B_vb) and increase with the cultural intensity k, while operational and infrastructure costs rise with k as governed by the exponents m and n. (2) The second is ensuring a fiscally sustainable closed-loop system for benefit-sharing and risk allocation, guaranteeing that the fiscal constraints of subsidies (R_zv) and fines (R_vz) do not destabilize the government’s financial position. (3) The third is ensuring the sustainability of community participation by setting thresholds for the cultural identification coefficient (i) and cost-sharing coefficient (w) such that the resident participation rate (z) stabilizes within the positive domain, thereby avoiding free-rider problems and public backlash.

Furthermore, the calibration the four core culture–economy parameters (k, j, i, w) draw upon publicly available data and scholarly research from representative Chinese regeneration projects—including Enning Road (Guangzhou Yongqingfang), Nantou Ancient City (Shenzhen), Xintiandi (Shanghai), and 798 Art Zone (Beijing). This encompasses analysis of rental premium magnitudes, tenant mix compositions, phased investment and operational cost structures, community participation mechanisms, and benefit-sharing agreements [1,9,26,29,35,36,37,38,39].The translation of qualitative case observations and publicly available project data into quantitative values followed a two-step process: (1) identifying measurable proxy variables within each project that conceptually align with the model’s parameters, and (2) normalizing these proxy values or their derived indices to a [0, 1] scale to fit the model’s requirements. The specific calibration logic for each parameter is as follows:

(1)

Cultural Renovation Intensity (k): This was operationalized as the proportion of total initial investment allocated to cultural preservation, aesthetic enhancement, and public space quality upgrading (soft costs) versus pure structural redevelopment and infrastructure (hard costs). For instance, in cases like Yongqingfang, a significant portion of investment was directed towards restoring historical facades, creating public plazas, and cultural programming rather than mere rebuilding. Analysis of reported investment structures suggested a k value range of 0.5–0.7 for successful projects [36,37]. Our baseline value of k = 0.5 represents a moderate, feasible starting point within this range.

(2)

Operational Profit-Sharing Ratio (j): This was inferred from documented revenue-sharing agreements between property operators and residents/community cooperatives. For example, some projects feature agreements where a fixed percentage (e.g., 15–30%) of the operational profits from renovated properties are returned to the original community [10,40]. Our baseline value j = 0.3 falls squarely within this empirically observed range.

(3)

Cultural Identification Coefficient (i): This abstract concept was proxied using indicators of community engagement and place identity, such as the rate of resident/business retention post-renewal, participation rates in co-design workshops, the density and frequency of community-organized cultural activities, and positive media/social media sentiment analysis focusing on cultural continuity [6,40]. A higher retention rate and activity density correlated with a higher inferred i. Values were normalized to a 0–1 scale, with i = 0.4 set as a threshold for meaningful engagement based on case studies reporting successful community integration.

(4)

Cost-Sharing Coefficient (w): This was estimated based on documented examples of resident contributions, which are often non-monetary or structured to minimize burden. Examples include residents sharing a small fraction of maintenance costs for improved communal areas or contributing “sweat equity” during the renovation process, the monetary equivalent of which was estimated [29,39]. The baseline value w = 0.15 reflects a low, sustainable level of cost participation observed in practice.

The final baseline values (

Table 4. Assumptions of initial parameter values before simulation.

Parameter	k	j	i	w	Bzc	Czb	s	Czc	Czd	q	Rzv	Rzc
Assigned value	0.5	0.3	0.4	0.15	240	2	10	6	10	1.5	20	5
Parameter	Bvb	Bvc	Bvd	m	Cvb	Cvc	n	Rvc	Rvd	Rvz	Bcc	Ccb
Assigned value	10	90	20	9	17	18	3	3	2	2	15	10

) represent a synthesized scenario that captures the essential economic–cultural dynamics of these successful projects.

4.2. Analysis of the Cultural Transformation Intensity (k)

We assign the cultural renovation intensity k the values of 0.2, 0.35, 0.5, 0.65, and 0.8 sequentially and simulate the resulting evolutionary trajectories of the three players, as illustrated in Figure 2: government (panel a), investor (panel b), and residents (panel c). Variations in k have a decisive effect on strategic convergence. Only an appropriately calibrated k promotes convergence toward active strategies for all three parties, whereas an insufficiently low or excessively high k induces convergence to passive strategies. Specifically, at low levels of cultural renovation intensity (k = 0.2, 0.35), all parties tend to converge to passive behavior. As k increases, the system dynamics gradually shift toward active behavior. The speed of convergence to active behavior at k = 0.65 is higher than that observed at k = 0.5. However, an excessively high k value (e.g., k = 0.8) causes the system’s trajectory to revert toward passive behavior.

Furthermore, the three parties exhibit heterogeneous sensitivities to k. The investor is the most sensitive. This is because the costs associated with higher cultural renovation intensity escalate rapidly; once the cost increase surpasses the concomitant increase in returns, the investor’s strategy quickly evolves toward passive behavior. Residents are the most eager to raise the cultural renovation intensity. Their shift toward active behavior accelerates steadily with increasing k. Nevertheless, when k becomes excessively high, triggering the investor to revert to low-quality, rapid redevelopment (e.g., k = 0.8), residents are the slowest among the three parties to shift their strategy toward passive behavior. The government’s response to variations in k is relatively stable, generally maintaining a tendency toward active strategies. Notably, even at low k values (k = 0.2, 0.35), the government attempts to evolve toward an active strategy.

4.3. Analysis of the Profit-Sharing Ratio (j)

We assign the operational profit-sharing ratio (j) the values of 0.1, 0.2, 0.3, 0.4, and 0.5 sequentially and simulate its effect on the evolutionary strategies of the three players, as illustrated in Figure 3: government (panel a), investor (panel b), and residents (panel c).

Variations in j have a decisive effect on strategic convergence. Only an appropriately calibrated j promotes convergence toward active strategies for all three parties; both an insufficiently low or an excessively high j lead to convergence to passive strategies. Specifically, at low values (j = 0.1, 0.2), all three parties tend to converge to passive behavior. As j increases to 0.3, the tripartite dynamics gradually shift toward active behavior. However, a further increase in j beyond 0.4 causes the system’s trajectory to revert toward passive behavior.

Furthermore, the three parties exhibit heterogeneous sensitivities to j. The investor is the most sensitive. This is because the investor’s incremental operational returns decline as the share allocated to residents increases; once the associated cost increases outweigh the net gain in returns, the investor’s strategy rapidly evolves toward passive behavior. In contrast, residents are the most eager to raise j. Their transition toward active behavior accelerates steadily with increases in j. Nevertheless, when j becomes excessively high, prompting the investor to revert to low-quality, rapid redevelopment (e.g., j = 0.4, 0.5), residents are the slowest among the three parties to switch to passive behavior. The government’s response to variations in j is relatively stable, demonstrating a tendency to primarily follow the strategic adjustments made by the investor and residents.

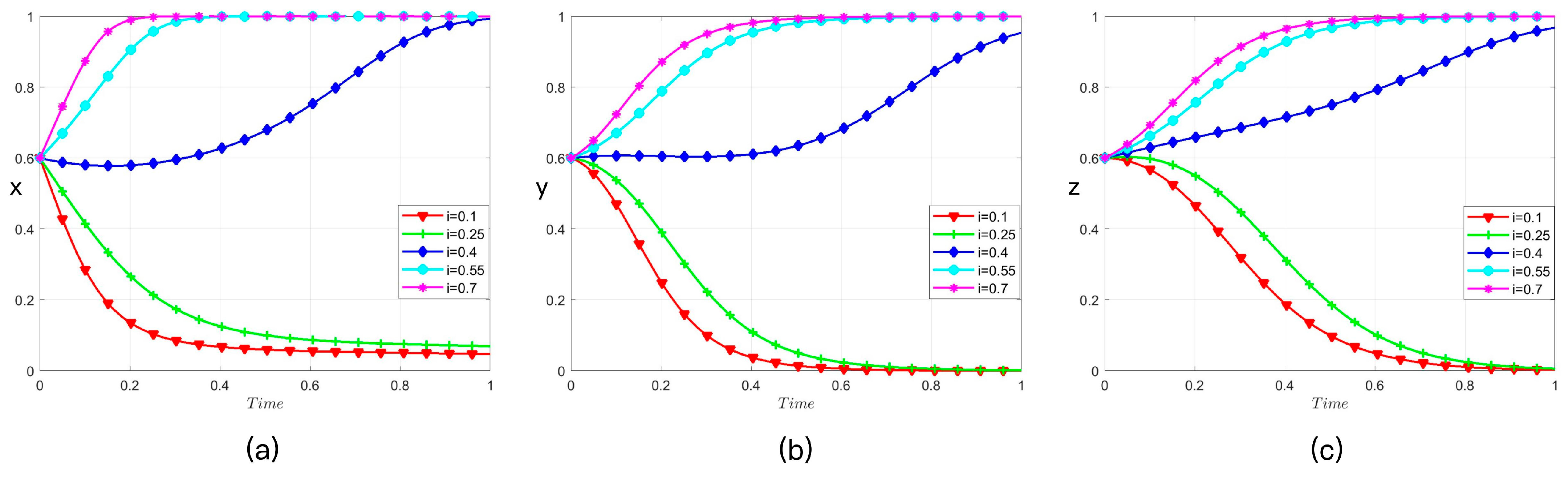
4.4. Analysis of the Cultural Identification Coefficient (i)

We assign the cultural identification coefficient (i) the values of 0.1, 0.25, 0.4, 0.55, and 0.7 sequentially and simulate its effect on the evolutionary strategies of the three parties, as illustrated in Figure 4: government (panel a), investor (panel b), and residents (panel c).

Increasing the cultural identification coefficient (i) promotes the evolution of all three parties toward active strategies. As i increases, all three parties demonstrate a faster transition to active behavior. Convergence toward active strategies is effectively promoted only when i exceeds a threshold value (i > 0.4); moreover, higher values of i further accelerate these convergent dynamics.

Furthermore, the three parties exhibit differing sensitivities to i. Although i is defined based on residents’ characteristics, they are the least sensitive to its variation. The government demonstrates the highest sensitivity, as it derives greater social incremental benefits (Bzct) from high-quality, culture-led regeneration when residents have a stronger cultural identification. The investor is more sensitive than residents; a higher i contributes to an expansion in the investor’s incremental operational returns (Bvct), enhancing its profitability.

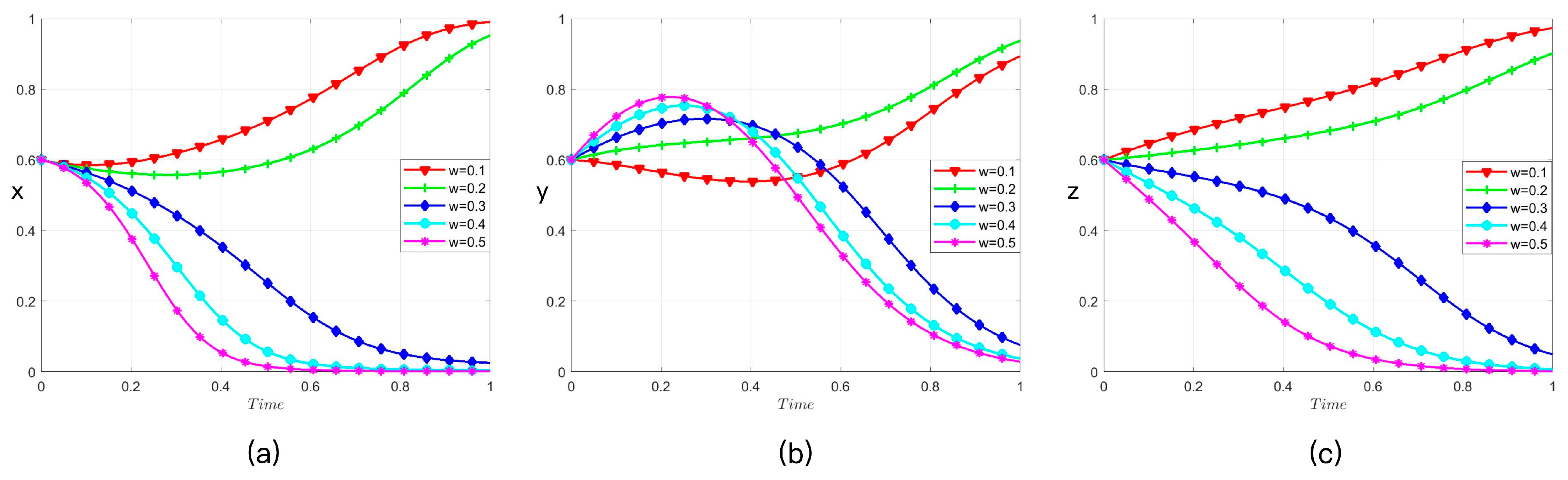
4.5. Analysis of the Cost-Sharing Coefficient (w)

We assign the cost-sharing coefficient (w) the values of 0.1, 0.2, 0.3, 0.4, and 0.5 sequentially and simulate its effect on the evolutionary strategies of the three parties, as illustrated in Figure 5: government (panel a), investor (panel b), and residents (panel c).

The cost-sharing coefficient (w) critically influences the convergence of strategies. Residents exhibit the highest sensitivity to w: as w increases, the initial financial burden they must bear rises substantially, which leads to a steady transition from active to passive behavior. The investor’s strategy initially becomes more active with increasing w, due to the reduced cost share. However, as residents evolve toward passive behavior, which diminishes collaborative synergy and potential returns, the investor’s strategy subsequently also transitions to passive behavior. The government does not derive direct benefits from variations in w; consequently, its strategic evolution is primarily influenced by (or: contingent upon) the behavioral changes in the residents.

5. Discussion

Based on the foregoing simulation results, the tripartite evolutionary game system achieves convergence most readily to the equilibrium E₁(1, 1, 1) within a specific parameter window characterized by moderate cultural renovation intensity (k), moderate operational profit-sharing (j), strong cultural identification (i), and low cost-sharing (w). Specifically, this window is defined by k ∈ [0.6, 0.7], j ∈ [0.25, 0.35], i ≥ 0.4, and w ≤ 0.2. Focusing on these four core parameters, the following coordination policies are proposed for the government, investors, and residents.

5.1. Regarding Cultural Renovation Intensity (k)

Implement phased investment coupled with gatekeeping assessments: Link the escalation of (k) to the achievement of Key Performance Indicators (KPIs) such as vacancy rates, public space vitality, and visitor return rates; allow only incremental increases in k upon meeting predefined thresholds to prevent one-time over-investment and nonlinear cost escalations.

Prioritize structural quality over physical scale: Emphasize micro-regeneration tactics, an operation-first sequence of interventions, and curated content programming; impose caps on the proportion of initial investment allocated to hard infrastructure construction and relocation; utilize phased contracts and reversible design approaches to mitigate sunk costs associated with project-community mismatch.

Strengthen risk management constraints: Establish clear investment ceilings and incorporate emergency exit clauses in contracts; conduct stress tests simulating adverse conditions (e.g., rental income downturns, visitation volatility) to empirically calibrate the upper bound for (k) and ensure financial sustainability.

5.2. Regarding the Operational Profit-Sharing Ratio (j)

Link dividend distribution to performance metrics: Initialize (j) within the range of 0.25–0.35 and couple its adjustments to service quality, social impact performance, and cash-flow coverage ratios. Utilize deferred payment structures, staged settlement, and performance-based clawback provisions to mitigate the short-term crowding out of investor incentives.

Introduce a dual-threshold regulatory mechanism: Establish a minimum guaranteed share (j_min) to secure residents’ participation expectations and a maximum cap (j_max) to safeguard capital for reinvestment and maintenance. Once project cash flows stabilize, gradually reduce (j) according to predefined rules in exchange for securing the investor’s commitment to long-term operation.

5.3. Regarding the Cultural Identification Coefficient (i)

Establish an end-to-end collaborative framework encompassing “co-deliberation, co-design, and co-operation” (e.g., through formal consultative procedures, participatory budgeting, and co-governance positions). Leverage formalized public participation mechanisms and strategic cultural brand-asset management to foster a sustained increase in i.

Promote content-driven revenue models: Implement continuous cultural programming, place-based intellectual property (IP) incubation, and partnerships with educational institutions to create a reinforcing feedback loop of “enhanced identification—increased visitation—improved cash flow”. Incorporate specific targets for i into urban renewal agreements and incentive clauses, making performance-linked payments contingent upon achieving a predetermined cultural identification threshold.

5.4. Regarding the Cost-Sharing Coefficient (w)

Adopt low-burden and alternative cost-sharing strategies: Maintain w at or below 0.20. Prioritize non-monetary contributions (e.g., volunteer hours, shared-space co-management), exemptions for vulnerable groups, and payment deferral options to prevent resident exit due to liquidity constraints.

Enhance service–cost reciprocity and transparency: Offset perceived resident burdens through staged service delivery and tangible service enhancements. Maintain a publicly accessible “cost–service ledger” subject to third-party audits to increase the acceptability and legitimacy of cost-sharing mechanisms.

5.5. Interdependencies and Policy Leverages for Sustainable Regeneration

Moving beyond isolated analysis, our model reveals critical parameter interdependencies, suggesting that policy interventions must be bundled for maximum efficacy. These insights are particularly vital for escaping the growth-phase trap of E₃(1, 0, 1), where government and residents support renewal but investors resist. A virtuous cycle links cultural intensity (k) and identification (i); investment in authentic culture boosts place attachment, which increases economic returns, justifying further investment. Conversely, a core trade-off exists between profit-sharing (j) and cost-sharing (w), as raising j to incentivize participation reduces investor net profit.

To break the E₃(1, 0, 1) deadlock, compensatory bundling is key. When cultural identification (i) is initially low, temporarily offering a higher profit-share (j) can attract investor participation. This cooperation fosters the conditions for i to grow organically, allowing j to later adjust to a sustainable level. Simultaneously, moderately increasing k enhances project profitability directly, making high-quality strategies intrinsically more attractive than relying solely on subsidies or fines. Thus, the most effective escape from the E₃(1, 0, 1) trap leverages synergistic parameter adjustments (k and j) rather than isolated fiscal tools, creating a self-reinforcing path toward the sustainable equilibrium E₁(1, 1, 1).

6. Conclusions

This study develops a tripartite evolutionary game model involving the government, investors, and residents to elucidate the core contradiction in China’s high-quality urban renewal phase—namely, the challenge of establishing a sustainable operational mechanism under cultural-protection constraints. Relative to prior studies, our primary contribution lies in the endogenous incorporation of the culture–economy parameters (k), (j), (i), and (w) within the game-theoretic framework, thereby revealing the micro-level driving mechanisms behind the ongoing transition toward high-quality, culture-led regeneration of historic districts. Simulation results indicate that effective tripartite coordination requires the simultaneous fulfillment of four conditions: the cultural renovation intensity (k) must exceed the cost threshold (k ∈ [0.6, 0.7]); the operational profit-sharing ratio (j) must preserve market incentives (j ∈ [0.25, 0.35]); the cultural identification coefficient (i) must reach its minimum threshold (i ≥ 0.4); and residents’ cost-sharing (w) must not surpass their benefit capacity (w ≤ 0.2). Crucially, moving from a discrete “policy toolbox” to an integrated strategic framework requires acknowledging these interactions. The recommended parameter ranges (k ∈ [0.6, 0.7], j ∈ [0.25, 0.35], i ≥ 0.4, w ≤ 0.2) should be treated as a coherent whole rather than isolated targets. The most successful regeneration projects will likely be those that manage these parameters not in silos, but as a dynamic, interconnected system, leveraging their synergies and carefully managing their trade-offs.

In conclusion, our findings offer concrete insights for achieving sustainable urbanism. Culturally, a sufficient intensity (k) ensures that renewal is not just a physical upgrade but a process of valorizing heritage, which is the cornerstone of cultural sustainability. Socially, a fair profit-sharing ratio (j) and enhanced cultural identification (i) foster community support and equity, underpinning social sustainability. Economically, the model demonstrates that viability is achieved not through demolition and quick sales, but through shared operational profits derived from a revitalized cultural economy, ensuring long-term economic sustainability. By identifying the thresholds that align the interests of government, market, and community, this study ultimately contributes to the foundational goal of sustainable development: meeting the needs of the present without compromising the ability of future generations to meet their own needs in our urban environments.

This study has several limitations. First, the measurement of the cultural identification coefficient (i) relies on retrospective case study analysis; future work could integrate large-scale survey data to construct more dynamic proxy variables. Second, the parameter calibration is derived from specific urban cases; therefore, its generalizability to resource-depleted cities (e.g., historically significant industrial regions in Northeast China) warrants further investigation. Future research could also explore a multi-level game framework incorporating considerations of intergovernmental fiscal decentralization, or adopt spatial econometric methods to capture the spatial spillover effects of urban renewal benefits.