Specialized vs. Diversified Agglomeration: Which More Effectively Enhances Urban Comprehensive Carrying Capacity? Evidence from Chinese Cities
Abstract
1. Introduction
2. Literature Review
2.1. Specialized Agglomeration and Urban CCP
2.2. Diversified Agglomeration and Urban CCP
3. Methodology
3.1. Variable Measurement
3.1.1. Explained Variable: Urban CCP
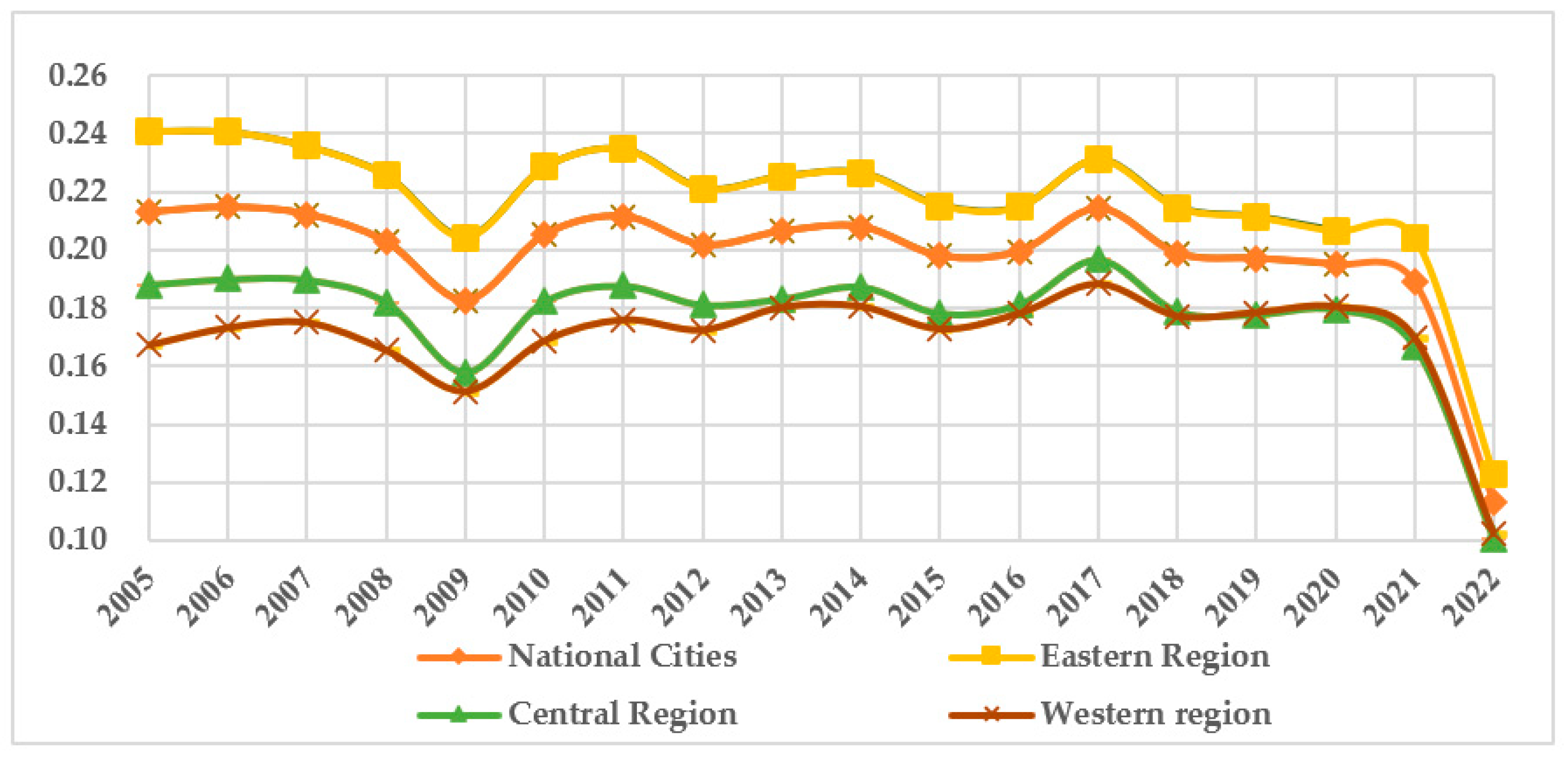
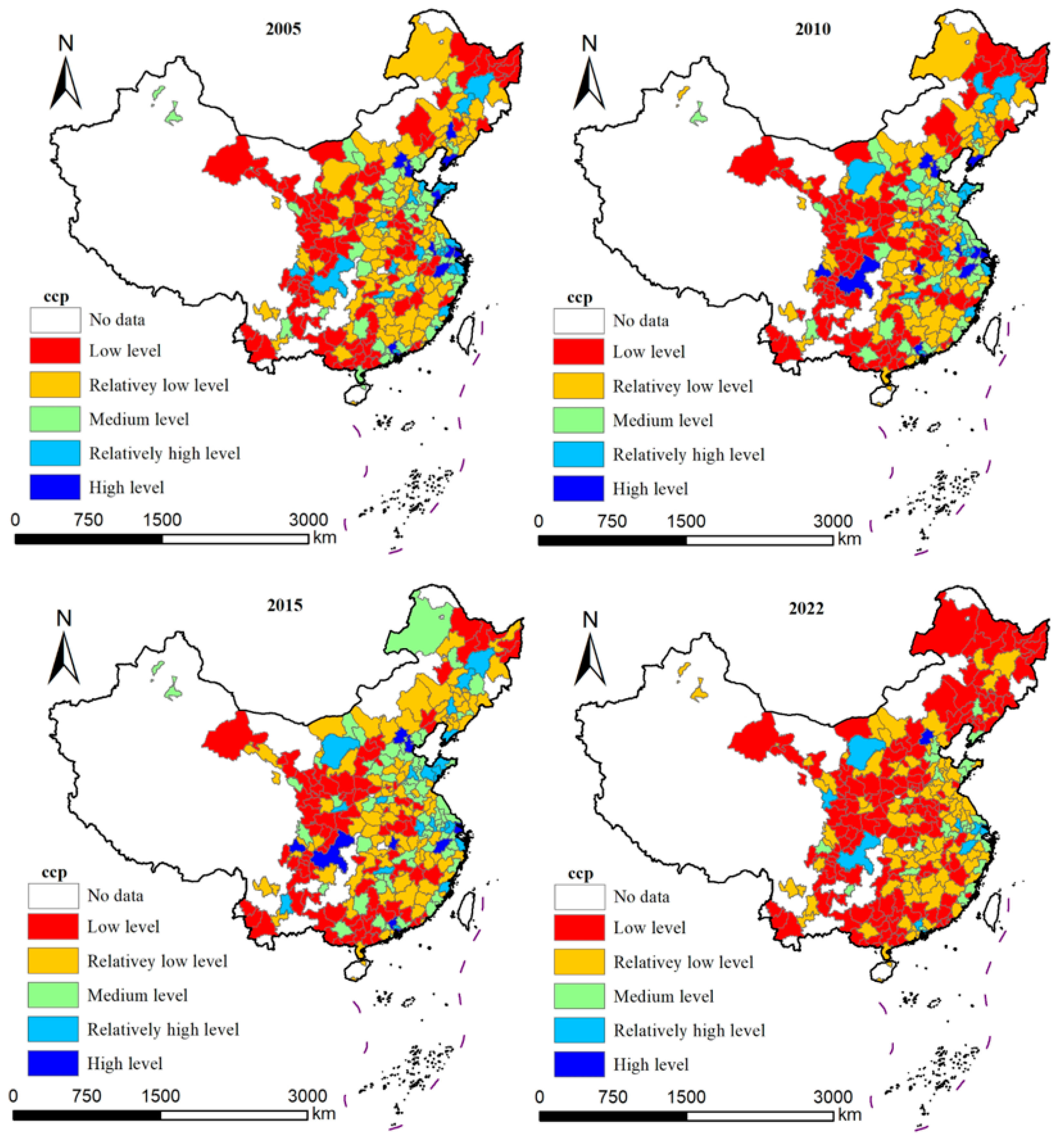
- Calculation of urban CCP
- 2.
- Temporal development characteristics of CCP
- 3.
- The spatial evolution pattern of CCP
3.1.2. Explanatory Variable: Industrial Agglomeration
3.1.3. Control Variables
3.2. Data Source
3.3. Model Building
3.3.1. Spatial Weight Matrix Setting
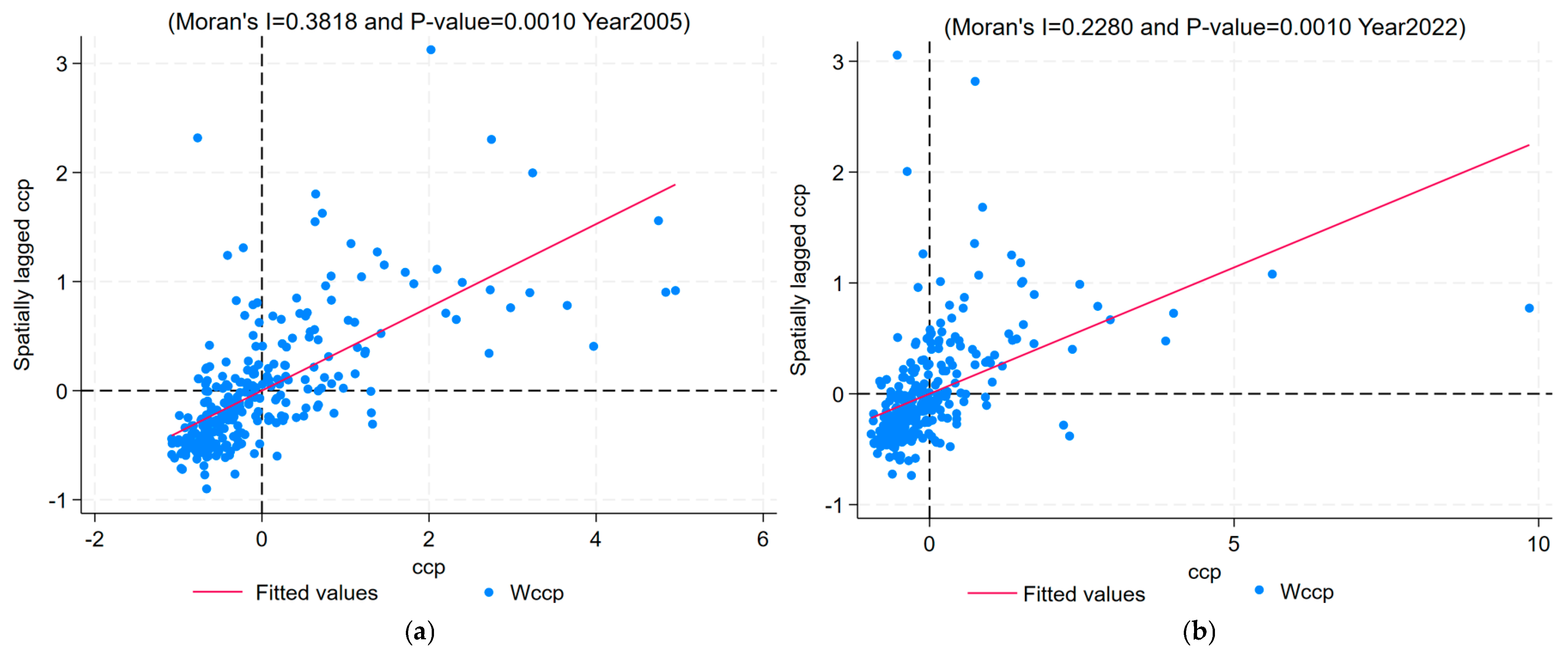
3.3.2. Spatial Correlation Test
- Global spatial correlation test
- 2.
- Local spatial correlation test
3.3.3. Construction of Spatial Econometric Model
3.3.4. Selection of Spatial Econometric Model
4. Results
4.1. Analysis of Baseline Regression Result
4.2. Analysis of Spatial Effect
4.3. Analysis of Heterogeneity
4.3.1. Regional Heterogeneity Analysis
4.3.2. Analysis of Economic Development Heterogeneity
4.4. Robustness Test
4.5. Further Analysis
5. Discussion
5.1. Regional Disparities in CCP
5.2. Specialized Agglomeration and CCP
5.3. Diversified Agglomeration and CCP
6. Conclusions and Implications
6.1. Main Conclusions
6.2. Policy Recommendations
6.3. Limitations and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, Y.; Wang, Y.; Wang, Y. Comprehensive evaluation and influencing factors of urban agglomeration water resources carrying capacity. J. Clean. Prod. 2021, 288, 125097. [Google Scholar] [CrossRef]
- Montgomery, M.R. The urban transformation of the developing world. Science 2008, 319, 761–764. [Google Scholar] [CrossRef]
- Chen, L.; Xu, L.; Yang, Z. Accounting carbon emission changes under regional industrial transfer in an urban agglomeration in China’s Pearl River Delta. J. Clean. Prod. 2017, 167, 110–119. [Google Scholar] [CrossRef]
- Savitch, H.V.; Gross, J.S.; Ye, L. Do Chinese cities break the global mold? Cities 2014, 41, 155–161. [Google Scholar] [CrossRef]
- Huang, X.; Guo, R.; Wang, W.; Li, X.; Fan, Y. Research on the Spatial Disparities and Convergence of Guangdong’s Urban Economy Based on Industrial Agglomeration and Industrial Proximity. Land 2024, 13, 73. [Google Scholar] [CrossRef]
- Xu, B.; Sun, Y. The impact of industrial agglomeration on urban land green use efficiency and its spatio-temporal pattern: Evidence from 283 cities in China. Land 2023, 12, 824. [Google Scholar] [CrossRef]
- Wang, T.; Yue, W.; Wu, T.; Zhang, X.; Xia, C. Human well-being related analysis on urban carrying capacity: An empirical study in Chinese mega-cities. J. Urban Aff. 2025, 47, 235–251. [Google Scholar] [CrossRef]
- Ren, W.; Xue, B.; Xie, X.; Zhao, B.; Li, J.; Han, B. Urban Comprehensive Carrying Capacity and Urbanization in Northeast China. Sustainability 2023, 15, 13649. [Google Scholar] [CrossRef]
- Lan, F.; Gong, X.; Da, H.; Wen, H. How do population inflow and social infrastructure affect urban vitality? Evidence from 35 large-and medium-sized cities in China. Cities 2020, 100, 102454. [Google Scholar] [CrossRef]
- Ciccone, A. Agglomeration effects in Europe. Eur. Econ. Rev. 2002, 46, 213–227. [Google Scholar] [CrossRef]
- Wei, Y.; Huang, C.; Li, J.; Xie, L. An evaluation model for urban carrying capacity: A case study of China’s mega-cities. Habitat Int. 2016, 53, 87–96. [Google Scholar] [CrossRef]
- Shen, N.; Peng, H. Can industrial agglomeration achieve the emission-reduction effect? Socio-Econ. Plan. Sci. 2021, 75, 100867. [Google Scholar] [CrossRef]
- Liu, J.; Cheng, Z.; Zhang, H. Does industrial agglomeration promote the increase of energy efficiency in China? J. Clean. Prod. 2017, 164, 30–37. [Google Scholar] [CrossRef]
- Zeng, D.Z.; Zhao, L. Pollution havens and industrial agglomeration. J. Environ. Econ. Manag. 2009, 58, 141–153. [Google Scholar] [CrossRef]
- Baldwin, R.E.; Martin, P. Agglomeration and regional growth. Handb. Reg. Urban Econ. 2004, 4, 2671–2711. [Google Scholar] [CrossRef]
- Zhang, Y.; Kong, J.; Zhang, Y.; Wang, H.; Deng, S. Case Study of Stratification, Spatial Agglomeration, and Unequal Logistics Industry Development on Western Cities in China. J. Urban Plann. Dev. 2022, 148, 05022009. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, B.; Wang, J.; Wu, Q.; Wei, Y.D. How does industrial agglomeration affect urban land use efficiency? A spatial analysis of Chinese cities. Land Use Policy 2022, 119, 106178. [Google Scholar] [CrossRef]
- Nakamura, R. Agglomeration economies in urban manufacturing industries: A case of Japanese cities. J. Urban Econ. 1985, 17, 108–124. [Google Scholar] [CrossRef]
- Han, F.; Xie, R.; Fang, J. Urban agglomeration economies and industrial energy efficiency. Energy 2018, 162, 45–59. [Google Scholar] [CrossRef]
- Marshall, A. Principles of Economics: An Introductory Volume; The MacMillan Press: London, UK, 1920. [Google Scholar]
- Jacobs, J. The Economics of Cities; Random House: New York, NY, USA, 1969. [Google Scholar]
- Duranton, G.; Puga, D. Diversity and specialisation in cities: Why, where and when does it matter? Urban Stud. 2000, 37, 533–555. [Google Scholar] [CrossRef]
- Han, F.; Xie, R.; Fang, J.; Liu, Y. The effects of urban agglomeration economies on carbon emissions: Evidence from Chinese cities. J. Clean. Prod. 2018, 172, 1096–1110. [Google Scholar] [CrossRef]
- Van der Panne, G. Agglomeration Externalities: Marshall versus Jacobs. J. Evol. Econ. 2004, 14, 593–604. [Google Scholar] [CrossRef]
- Rosenthal, S.S.; Strange, W.C. The determinants of agglomeration. J. Urban Econ. 2001, 50, 191–229. [Google Scholar] [CrossRef]
- Lan, F.; Sun, L.; Pu, W. Research on the influence of manufacturing agglomeration modes on regional carbon emission and spatial effect in China. Econ. Model. 2021, 96, 346–352. [Google Scholar] [CrossRef]
- Hardin, G. Carrying capacity and quality of life. Soc. Contract 1991, 12, 195–196. [Google Scholar]
- Kozlowski, J.M. Sustainable development in professional planning: A potential contribution of the EIA and UET concepts. Landsc. Urban Plan. 1990, 19, 307–332. [Google Scholar] [CrossRef]
- Cohen, J.E. Population growth and earth’s human carrying capacity. Science 1995, 269, 341–346. [Google Scholar] [CrossRef]
- Tehrani, N.A.; Makhdoum, M.F. Implementing a spatial model of Urban Carrying Capacity Load Number (UCCLN) to monitor the environmental loads of urban ecosystems. Case study: Tehran metropolis. Ecol. Indic. 2013, 32, 197–211. [Google Scholar] [CrossRef]
- Oh, K.; Jeong, Y.; Lee, D.; Lee, W.; Choi, J. Determining development density using the Urban Carrying Capacity Assessment System. Landsc. Urban Plan. 2005, 73, 1–15. [Google Scholar] [CrossRef]
- Hao, Y.; Song, J.; Zhang, S. Does industrial agglomeration affect the regional environment? Evidence from Chinese cities. Environ. Sci. Pollut. Res. 2022, 29, 7811–7826. [Google Scholar] [CrossRef]
- Duc, T.A.; Vachaud, G.; Bonnet, M.P.; Prieur, N.; Loi, V.D.; Anh, L.L. Experimental investigation and modelling approach of the impact of urban wastewater on a tropical river; a case study of the Nhue River, Hanoi, Viet Nam. J. Hydrol. 2007, 334, 347–358. [Google Scholar] [CrossRef]
- Santra, S. The effect of technological innovation on production-based energy and CO2 emission productivity: Evidence from BRICS countries. Afr. J. Sci. Technol. Innov. Dev. 2017, 9, 503–512. [Google Scholar] [CrossRef]
- Pei, Y.; Zhu, Y.; Liu, S.; Xie, M. Industrial agglomeration and environmental pollution: Based on the specialized and diversified agglomeration in the Yangtze River Delta. Environ. Dev. Sustain. 2021, 23, 4061–4085. [Google Scholar] [CrossRef]
- Shen, N.; Zhao, Y.; Wang, Q. Diversified agglomeration, specialized agglomeration, and emission reduction effect—A nonlinear test based on Chinese city data. Sustainability 2018, 10, 2002. [Google Scholar] [CrossRef]
- Peng, H.; Lu, Y.; Wang, Q. How does heterogeneous industrial agglomeration affect the total factor energy efficiency of China’s digital economy? Energy 2023, 268, 126654. [Google Scholar] [CrossRef]
- Boschma, R. Proximity and innovation: A critical assessment. Reg. Stud. 2005, 39, 61–74. [Google Scholar] [CrossRef]
- Abdel-Rahman, H.M. Agglomeration economies, types, and sizes of cities. J. Urban Econ. 1990, 27, 25–45. [Google Scholar] [CrossRef]
- Krugman, P. A model of innovation, technology transfer, and the world distribution of income. J. Polit. Econ. 1979, 87, 253–266. [Google Scholar] [CrossRef]
- Henderson, J.V. Marshall’s scale economies. J. Urban Econ. 2003, 53, 1–28. [Google Scholar] [CrossRef]
- Saito, H.; Gopinath, M. Plants’ self-selection, agglomeration economies and regional productivity in Chile. J. Econ. Geogr. 2009, 9, 539–558. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, X.; Li, J.; Ning, L. Does technological diversification matter for regional innovation capability? Evidence from China. Technol. Anal. Strateg. Manag. 2016, 28, 323–334. [Google Scholar] [CrossRef]
- Gao, T. Regional industrial growth: Evidence from Chinese industries. Reg. Sci. Urban Econ. 2004, 34, 101–124. [Google Scholar] [CrossRef]
- Wei, L.; Hou, Y. Effects of specialized and diversified industrial agglomeration on regional green development. Manag. Rev. 2021, 33, 22–33. [Google Scholar] [CrossRef]
- Murdoch III, J. Specialized vs. diversified: The role of neighborhood economies in shrinking cities. Cities 2018, 75, 30–37. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, X.; Pan, X.; Ma, X.; Tang, M. The spatial integration and coordinated industrial development of urban agglomerations in the Yangtze River Economic Belt, China. Cities 2020, 104, 102801. [Google Scholar] [CrossRef]
- Cheng, Z.; Jin, W. Agglomeration economy and the growth of green total-factor productivity in Chinese Industry. Socio-Econ. Plan. Sci. 2022, 83, 101003. [Google Scholar] [CrossRef]
- Hopton, M.E.; Cabezas, H.; Campbell, D.; Eason, T.; Garmestani, A.S.; Heberling, M.T.; Zanowick, M. Development of a multidisciplinary approach to assess regional sustainability. Int. J. Sustain. Dev. World Ecol. 2010, 17, 48–56. [Google Scholar] [CrossRef]
- Shao, Q.; Liu, X.; Zhao, W. An alternative method for analyzing dimensional interactions of urban carrying capacity: Case study of Guangdong-Hong Kong-Macao Greater Bay Area. J. Environ. Manag. 2020, 273, 111064. [Google Scholar] [CrossRef] [PubMed]
- Liao, S.; Du, X.; Shen, L.; Lv, M. Evaluation method for urban public service carrying capacity (UPSCC): A qualitative–quantitative bi-dimensional perspective. Int. J. Environ. Res. Public Health 2021, 18, 12539. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, F.; Tan, M.L.; Shi, J.; Johnson, V.C.; Kung, H.T. Remote sensing evaluation of Chinese mainland’s comprehensive natural resources carrying capacity and its spatial-temporal variation characteristics. Environ. Impact Assess. Rev. 2023, 101, 107104. [Google Scholar] [CrossRef]
- Benhabib, J.; Spiegel, M.M. The role of human capital in economic development evidence from aggregate cross-country data. J. Monet. Econ. 1994, 34, 143–173. [Google Scholar] [CrossRef]
- Eaton, J.; Eckstein, Z. Cities and growth: Theory and evidence from France and Japan. Reg. Sci. Urban Econ. 1997, 27, 443–474. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Z.; Cheng, S. Industrial agglomeration and haze pollution: Evidence from China. Sci. Total Environ. 2022, 845, 157392. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, B. How does new-type urbanization affect air pollution? Empirical evidence based on spatial spillover effect and spatial Durbin model. Environ. Int. 2022, 165, 107304. [Google Scholar] [CrossRef] [PubMed]
- Fu, Y.; Wang, Z. The Impact of Industrial Agglomeration on Urban Carbon Emissions: An Empirical Study Based on the Panel Data of China’s Prefecture-Level Cities. Sustainability 2024, 16, 10270. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- LeSage, J.; Pace, R.K. Introduction to Spatial Econometrics; Chapman and Hall/CRC: New York, NY, USA, 2009; pp. 42–88. [Google Scholar] [CrossRef]
- Anselin, L. Model validation in spatial econometrics: A review and evaluation of alternative approaches. Int. Reg. Sci. Rev. 1988, 11, 279–316. [Google Scholar] [CrossRef]
- Antonelli, C.; Crespi, F. Matthew effects and R&D subsidies: Knowledge cumulability in high-tech and low-tech industries. G. Econ. Ann. Econ. 2012, 71, 5–31. [Google Scholar]
- Elhorst, J.P. Dynamic spatial panels: Models, methods, and inferences. J. Geogr. Syst. 2012, 14, 5–28. [Google Scholar] [CrossRef]
- Lee, L.; Yu, J. A spatial dynamic panel data model with both time and individual fixed effects. Econom. Theory 2010, 26, 564–597. [Google Scholar] [CrossRef]
- Elhorst, J.P. Matlab software for spatial panels. Int. Reg. Sci. Rev. 2014, 37, 389–405. [Google Scholar] [CrossRef]
- Zheng, H.; He, Y. How does industrial co-agglomeration affect high-quality economic development? Evidence from Chengdu-Chongqing Economic Circle in China. J. Clean. Prod. 2022, 371, 133485. [Google Scholar] [CrossRef]
- Fan, W.; Wang, F.; Liu, S.; Chen, T.; Bai, X.; Zhang, Y. How does financial and manufacturing co-agglomeration affect environmental pollution? Evidence from China. J. Environ. Manag. 2023, 325, 116544. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Guan, M.; Zhan, L.; Liu, C.; Zhang, Z.; Jiang, H.; Zhang, Y.; Dong, G. Urban comprehensive carrying capacity and development order: A “Pressure-capacity-potential” Logical Framework. Front. Environ. Sci. 2022, 10, 935498. [Google Scholar] [CrossRef]
- Wu, X.; Peng, B. Urban comprehensive carrying capacity analysis in Zhejiang Province of China from the perspective of production, living, and ecological spaces. Geo-Spat. Inf. Sci. 2024, 27, 2179–2198. [Google Scholar] [CrossRef]
- Cui, Y. The influencing factors of carrying capacity of urban electricity infrastructure: Case study of six Chinese mega-cities. Energy 2023, 282, 128826. [Google Scholar] [CrossRef]
- Manshadi, Z.D.; Parivar, P.; Sotoudeh, A.; Sharifabadi, A.M. Modeling urban growth effects on carrying capacity in arid and semi-arid regions using system dynamics. Ecol. Modell. 2024, 487, 110565. [Google Scholar] [CrossRef]
- Shih, H.C.I.; Wijaya, K.C.; Hsueh, H.Y.; Hsu, Y.T. Away from over-populated development: Estimating urban carrying capacity with an integrated perspective of transportation and urban planning. Transp. Policy 2025, 162, 283–295. [Google Scholar] [CrossRef]
- Yan, L.; Ye, W.; Long, H.; Zhang, Q. The Influence of Innovative Resources on the Comprehensive Carrying Capacity of China’s Urban Agglomerations: A System Dynamics Perspective. Sustainability 2024, 16, 6191. [Google Scholar] [CrossRef]
- Yang, S.; Jahanger, A.; Hossain, M.R. How effective has the low-carbon city pilot policy been as an environmental intervention in curbing pollution? Evidence from Chinese industrial enterprises. Energy Econ. 2023, 118, 106523. [Google Scholar] [CrossRef]
- Innocenti, N.; Capone, F.; Lazzeretti, L. Knowledge networks and industrial structure for regional innovation: An analysis of patents collaborations in Italy. Papers Reg. Sci. 2020, 99, 55–73. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, Q.; Li, W.; Sun, D.; Huang, F. Intensifier of urban economic resilience: Specialized or diversified agglomeration? PLoS ONE 2021, 16, e0260214. [Google Scholar] [CrossRef] [PubMed]
| Secondary Indicator | Weight | Tertiary Indicator | Weight |
|---|---|---|---|
| Socio-economic carrying capacity (CCP1) | 0.3767 | Retail sales of consumer goods | 0.0981 |
| Actual utilized FDI | 0.1871 | ||
| Secondary industry share of GDP | 0.0140 | ||
| Natural population growth rate | 0.0113 | ||
| GDP per capita | 0.0410 | ||
| Average earnings of employed persons | 0.0252 | ||
| Natural resource carrying capacity (CCP2) | 0.0949 | Coverage rate of gas supply | 0.0042 |
| Urban construction land area | 0.0065 | ||
| Per capita green space | 0.0606 | ||
| Population density | 0.0131 | ||
| Per capita daily domestic water consumption | 0.0106 | ||
| Ecological environment carrying capacity (CCP3) | 0.1386 | Industrial sulfur dioxide emissions | 0.0054 |
| Industrial smoke and dust emissions | 0.0054 | ||
| Harmless treatment rate of domestic wastes | 0.0056 | ||
| Green coverage rate of built-up areas | 0.1117 | ||
| Centralized sewage treatment rate | 0.0105 | ||
| Public service carrying capacity (CCP4) | 0.2956 | Number of hospital beds | 0.0539 |
| Number of full-time primary and secondary school teachers per 10,000 students | 0.0288 | ||
| Number of college students per 10,000 population | 0.0627 | ||
| Library collection size | 0.1274 | ||
| Per capita daily domestic water consumption | 0.0228 | ||
| Infrastructure carrying capacity (CCP5) | 0.0942 | Number of public buses and trolleybuses per 10,000 population | 0.0386 |
| Paved road area per capita | 0.0244 | ||
| Road freight volume | 0.0052 | ||
| Drainage pipe density in built-up areas | 0.0260 |
| Symbol | Variable Name | Definition | Mean | SD | min | max |
|---|---|---|---|---|---|---|
| ccp | Urban CCP | The comprehensive evaluation method is used for calculation according to the indicators in Table 1 | 0.1980 | 0.1010 | 0.0509 | 0.7890 |
| ris | Specialized agglomeration | 4.432 | 5.460 | 1.272 | 106.7 | |
| rid | Diversified agglomeration | 2.161 | 0.868 | 0.713 | 6.455 | |
| pgdp | Economic development level (yuan) | Regional GDP per capita | 38,618 | 24,517 | 2662 | 321,557 |
| edu | Human capital (measured by the number of people) | Number of college students per 10,000 residents | 425 | 416 | 5 | 3189 |
| pop | Population density (person per km2) | Population per square kilometer | 3748 | 2706 | 27 | 20,093 |
| pbus | Level of infrastructure (measured by the number of vehicles) | Number of public buses per 10,000 residents | 8.202 | 7.049 | 0.320 | 225.50 |
| fdi | Level of foreign trade ($10,000) | FDI | 54,087 | 130,054 | 1.931 | 2,068,435.96 |
| Year | Wl | Wd | We | Wde |
|---|---|---|---|---|
| 2005 | 0.2445 *** | 0.1958 *** | 0.3818 *** | 0.2239 *** |
| 2006 | 0.2319 *** | 0.1886 *** | 0.3678 *** | 0.2163 *** |
| 2007 | 0.2478 *** | 0.2041 *** | 0.3711 *** | 0.2209 *** |
| 2008 | 0.2374 *** | 0.1988 *** | 0.3456 *** | 0.1903 *** |
| 2009 | 0.1641 *** | 0.1474 *** | 0.3331 *** | 0.2062 *** |
| 2010 | 0.1939 *** | 0.1739 *** | 0.3551 *** | 0.2023 *** |
| 2011 | 0.1770 *** | 0.1636 *** | 0.3509 *** | 0.2235 *** |
| 2012 | 0.1818 *** | 0.1649 *** | 0.3906 *** | 0.2036 *** |
| 2013 | 0.1857 *** | 0.1681 *** | 0.3531 *** | 0.1984 *** |
| 2014 | 0.1613 *** | 0.1482 *** | 0.3510 *** | 0.1768 *** |
| 2015 | 0.1633 *** | 0.1529 *** | 0.3085 *** | 0.1773 *** |
| 2016 | 0.1599 *** | 0.1439 *** | 0.3136 *** | 0.1773 *** |
| 2017 | 0.1509 *** | 0.1387 *** | 0.3141 *** | 0.1783 *** |
| 2018 | 0.1231 *** | 0.1213 *** | 0.3167 *** | 0.1746 *** |
| 2019 | 0.1295 *** | 0.1250 *** | 0.2815 *** | 0.1591 *** |
| 2020 | 0.1196 *** | 0.1172 *** | 0.2515 *** | 0.1428 *** |
| 2021 | 0.1454 *** | 0.1451 *** | 0.2881 *** | 0.1647 *** |
| 2022 | 0.1404 *** | 0.1218 *** | 0.2280 *** | 0.1336 *** |
| Test | Statistic | df | p-Value |
|---|---|---|---|
| LM-error | 823.542 *** | 1 | 0.000 |
| Robust LM-error | 131.448 *** | 1 | 0.000 |
| LM-lag | 735.167 *** | 1 | 0.000 |
| Robust LM-lag | 43.073 *** | 1 | 0.000 |
| Hausman test (χ2) | 257.22 *** | 13 | 0.000 |
| LR test for SAR (χ2) | 25.23 *** | 8 | 0.000 |
| Wald test for SAR (χ2) | 67.25 *** | 6 | 0.000 |
| LR test for SEM (χ2) | 42.31 *** | 8 | 0.000 |
| Wald test for SEM (χ2) | 71.60 *** | 6 | 0.000 |
| LR test both ind (χ2) | 901.22 *** | 14 | 0.000 |
| LR test both time (χ2) | 10,800.89 *** | 14 | 0.000 |
| Variables | Static SDM Model | Dynamic SDM Model | ||
|---|---|---|---|---|
| Model (16) | Model (17) | Model (18) | Model (19) | |
| Main | ||||
| L.CCP | 0.5310 *** (0.0411) | 0.5310 *** (0.0410) | ||
| ris | −0.00009 (0.0001) | −0.00007 (0.0001) | ||
| rid | 0.0005 (0.0006) | 0.0001 (0.0008) | ||
| lnpgdp | 0.0252 *** (0.0015) | 0.0251 *** (0.0015) | 0.0138 *** (0.0017) | 0.0137 *** (0.0018) |
| lnpop | −0.0037 *** (0.0007) | −0.0038 *** (0.0007) | −0.0042 *** (0.0009) | −0.0043 *** (0.0009) |
| lnfdi | 0.0049 *** (0.0003) | 0.0049 *** (0.0003) | 0.0032 *** (0.0006) | 0.0031 *** (0.0006) |
| lnpbus | 0.0136 *** (0.0009) | 0.0136 *** (0.0009) | 0.0105 *** (0.0009) | 0.0105 *** (0.0009) |
| lnedu | 0.0150 *** (0.0006) | 0.0150 *** (0.0006) | 0.0122 *** (0.0011) | 0.0122 *** (0.0010) |
| Wx | ||||
| ris | −0.0004 * (0.0002) | −0.0003 (0.0002) | ||
| rid | 0.0037 ** (0.0016) | 0.0030 (0.0019) | ||
| lnpgdp | 0.0024 (0.0037) | 0.0017 (0.0037) | 0.0079 (0.0056) | 0.0073 (0.0057) |
| lnpop | 0.0012 (0.0019) | 0.0010 (0.0019) | −0.0003 (0.0022) | −0.0004 (0.0022) |
| lnfdi | −0.0033 *** (0.0008) | −0.0034 *** (0.0008) | −0.0040 *** (0.0011) | −0.0041 *** (0.0011) |
| lnpbus | 0.0026 (0.0023) | 0.0020 (0.0023) | 0.0008 (0.0022) | 0.0005 (0.0021) |
| lnedu | 0.0024 (0.0015) | 0.0023 (0.0015) | 0.0007 (0.0015) | 0.0006 (0.0015) |
| rho | 0.1980 *** (0.0228) | 0.2000 *** (0.0228) | 0.1610 *** (0.0447) | 0.1630 *** (0.0444) |
| sigma2_e | 0.0005 *** (0.000009) | 0.0005 *** (0.000009) | 0.0004 *** (0.000042) | 0.0004 *** (0.000042) |
| N | 5112 | 5112 | 4828 | 4828 |
| R-sq | 0.394 | 0.394 | 0.826 | 0.825 |
| Direct Short-Term Effect | Indirect Short-Term Effect | Direct Long-Term Effect | Indirect Long-Term Effect |
|---|---|---|---|
| Variable | Model (18) | Model (19) |
|---|---|---|
| ris | rid | |
| Direct short-term effect | −0.0001 | 0.0002 |
| Indirect short-term effect | −0.0003 | 0.0036 |
| Total short-term effect | −0.0004 * | 0.0038 |
| Direct long-term effect | −0.0002 | 0.0006 |
| Indirect long-term effect | −0.0010 | 0.0100 |
| Total long-term effect | −0.0012 * | 0.0106 |
| Variables | Eastern Area | Central Area | Western Area | |||
|---|---|---|---|---|---|---|
| ris | rid | ris | rid | ris | rid | |
| Direct short-term effect | −0.00011 | 0.00008 | −0.00028 ** | 0.00281 ** | 0.00004 | −0.00263 * |
| Indirect short-term effect | −0.00002 | −0.00019 | 0.00003 *** | 0.00033 * | 0.00025 ** | 0.00003 |
| Total short-term effect | −0.00012 | −0.00011 | −0.00024 * | 0.00313 ** | 0.00029 | −0.00261 * |
| Direct long-term effect | −0.00023 | −0.00378 | −0.00045 ** | 0.00457 ** | 0.00019 | −0.00691 * |
| Indirect long-term effect | −0.00008 | −0.00543 | 0.00005 | 0.00056 * | 0.00076 | −0.00001 |
| Total long-term effect | −0.00031 | −0.00920 | −0.00039 * | 0.00513 ** | 0.00094 | −0.00692 * |
| Variable | High Income | Low Income | ||
|---|---|---|---|---|
| ris | rid | ris | rid | |
| Direct short-term effect | −0.00018 * | 0.00024 | 0.00007 | 0.00004 |
| Indirect short-term effect | −0.00057 | 0.00526 * | 0.00010 | −0.00067 |
| Total short-term effect | −0.00075 * | 0.00550 | 0.00017 * | −0.00062 |
| Direct long-term effect | −0.00040 * | 0.00074 | 0.00015 | 0.00008 |
| Indirect long-term effect | −0.00149 | 0.01340 | 0.00023 | −0.00153 |
| Total long-term effect | −0.00189 * | 0.01410 | 0.00038 | −0.00145 |
| Variable | Effect Decomposition | W1 | Wd | Wde | After Sample Replacement |
|---|---|---|---|---|---|
| ris | Direct short-term effect | −0.00011 | −0.00010 | −0.00008 | −0.00009 |
| Indirect short-term effect | −0.00011 | −0.00042 | −0.00079 | 0.000004 | |
| Total short-term effect | −0.00022 | −0.00052 | −0.00087 | −0.000086 | |
| Direct long-term effect | −0.00024 | −0.00025 | −0.00021 | −0.00017 | |
| Indirect long-term effect | −0.00030 | −0.00278 | −0.00637 | 0.00001 | |
| Total long-term effect | −0.00054 | −0.00303 | −0.00658 | −0.00016 | |
| rid | Direct short-term effect | 0.00014 | 0.00003 | −0.00011 | 0.00007 |
| Indirect short-term effect | −0.00075 | −0.00088 | 0.00491 | −0.00009 | |
| Total short-term effect | −0.00061 | −0.00085 | 0.00480 | −0.00002 | |
| Direct long-term effect | 0.00027 | 0.00004 | 0.00005 | 0.00010 | |
| Indirect long-term effect | −0.00173 | −0.00102 | 0.04380 | −0.00013 | |
| Total long-term effect | −0.00146 | −0.00098 | 0.04390 | −0.00003 |
| Variable | Effect Decomposition | CCP1 | CCP2 | CCP3 | CCP4 | CCP5 |
|---|---|---|---|---|---|---|
| ris | Direct short-term effect | −0.00004 | 0.00002 | −0.00003 | 0.00001 | −0.00006 *** |
| Indirect short-term effect | −0.00007 | 0.00004 | −0.00007 | −0.00026 *** | 0.00000 | |
| Total short-term effect | −0.00011 | 0.00005 * | −0.00010 * | −0.00025 *** | −0.00005 | |
| Direct long-term effect | −0.00012 | 0.00004 | −0.00005 | 0.00001 | −0.00010 *** | |
| Indirect long-term effect | −0.00030 | 0.00010 | −0.00011 | −0.00034 *** | −0.00000 | |
| Total long-term effect | −0.00042 | 0.00014 * | −0.00016 * | −0.00033 *** | −0.00010 | |
| rid | Direct short-term effect | −0.00037 | −0.00008 | 0.00003 | 0.00095 *** | −0.00017 |
| Indirect short-term effect | 0.00145 | −0.00023 | 0.00020 | 0.00108 | 0.00050 | |
| Total short-term effect | 0.00108 | −0.00031 | 0.00023 | 0.00203 ** | 0.00033 | |
| Direct long-term effect | −0.00098 | −0.00022 | 0.00005 | 0.00125 *** | −0.00030 | |
| Indirect long-term effect | 0.00518 | −0.00061 | 0.00035 | 0.00148 | 0.00095 | |
| Total long-term effect | 0.00420 | −0.00083 | 0.00040 | 0.00273 ** | 0.00065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Lan, F. Specialized vs. Diversified Agglomeration: Which More Effectively Enhances Urban Comprehensive Carrying Capacity? Evidence from Chinese Cities. Sustainability 2025, 17, 9064. https://doi.org/10.3390/su17209064
Gao M, Lan F. Specialized vs. Diversified Agglomeration: Which More Effectively Enhances Urban Comprehensive Carrying Capacity? Evidence from Chinese Cities. Sustainability. 2025; 17(20):9064. https://doi.org/10.3390/su17209064
Chicago/Turabian StyleGao, Man, and Feng Lan. 2025. "Specialized vs. Diversified Agglomeration: Which More Effectively Enhances Urban Comprehensive Carrying Capacity? Evidence from Chinese Cities" Sustainability 17, no. 20: 9064. https://doi.org/10.3390/su17209064
APA StyleGao, M., & Lan, F. (2025). Specialized vs. Diversified Agglomeration: Which More Effectively Enhances Urban Comprehensive Carrying Capacity? Evidence from Chinese Cities. Sustainability, 17(20), 9064. https://doi.org/10.3390/su17209064




