Sustainable Mining of Open-Pit Coal Mines: A Study on Intelligent Strip Division Technology Based on Multi-Source Data Fusion

Abstract

The rational delineation of open-pit mining areas constitutes the core foundation for achieving safe, efficient, economical, and sustainable mining operations. The quality of this decision-making directly impacts the economic benefits experienced throughout the mine’s entire lifecycle and the efficiency of resource recovery. Traditional open-pit mining area delineation relies on an experience-driven manual process that is inefficient and incapable of real-time dynamic data optimization. Thus, there is an urgent need to establish an intelligent decision-making model integrating multi-source data and multi-objective optimization. To this end, this study proposes an intelligent mining area division algorithm. First, a geological complexity quantification model is constructed, incorporating innovative adaptive discretisation resolution technology to achieve precise quantification of coal seam distribution. Second, based on the quantified stripping-to-mining ratio within grids, a block-growing algorithm generates block grids, ensuring uniformity of the stripping-to-mining ratio within each block. Subsequently, a matrix of primary directional variations in the stripping-to-mining ratio is constructed to determine the principal orientation for merging blocks into mining areas. Finally, intelligent open-pit mining area delineation is achieved by comprehensively considering factors such as the principal direction of mining areas, geological conditions, boundary shapes, and economic scale. Practical validation was conducted using the Shitoumei No. 1 Open-Pit Coal Mine in Xinjiang as a case study in engineering. Engineering practice demonstrates that adopting this methodology transforms mining area delineation from an experience-driven to a data-driven approach, significantly enhancing delineation efficiency. Manual simulation of a single scheme previously required approximately 15 days. Applying the methodology proposed herein reduces this to just 0.5 days per scheme, representing a 96% increase in efficiency. Design costs were reduced by approximately CNY 190,000 per iteration. Crucially, the intelligently recommended scheme matched the original design, validating the algorithm’s reliability. This research provides crucial support for theoretical and technological innovation in intelligent open-pit coal mining design, offering technical underpinnings for the sustainable development of open-pit coal mines.

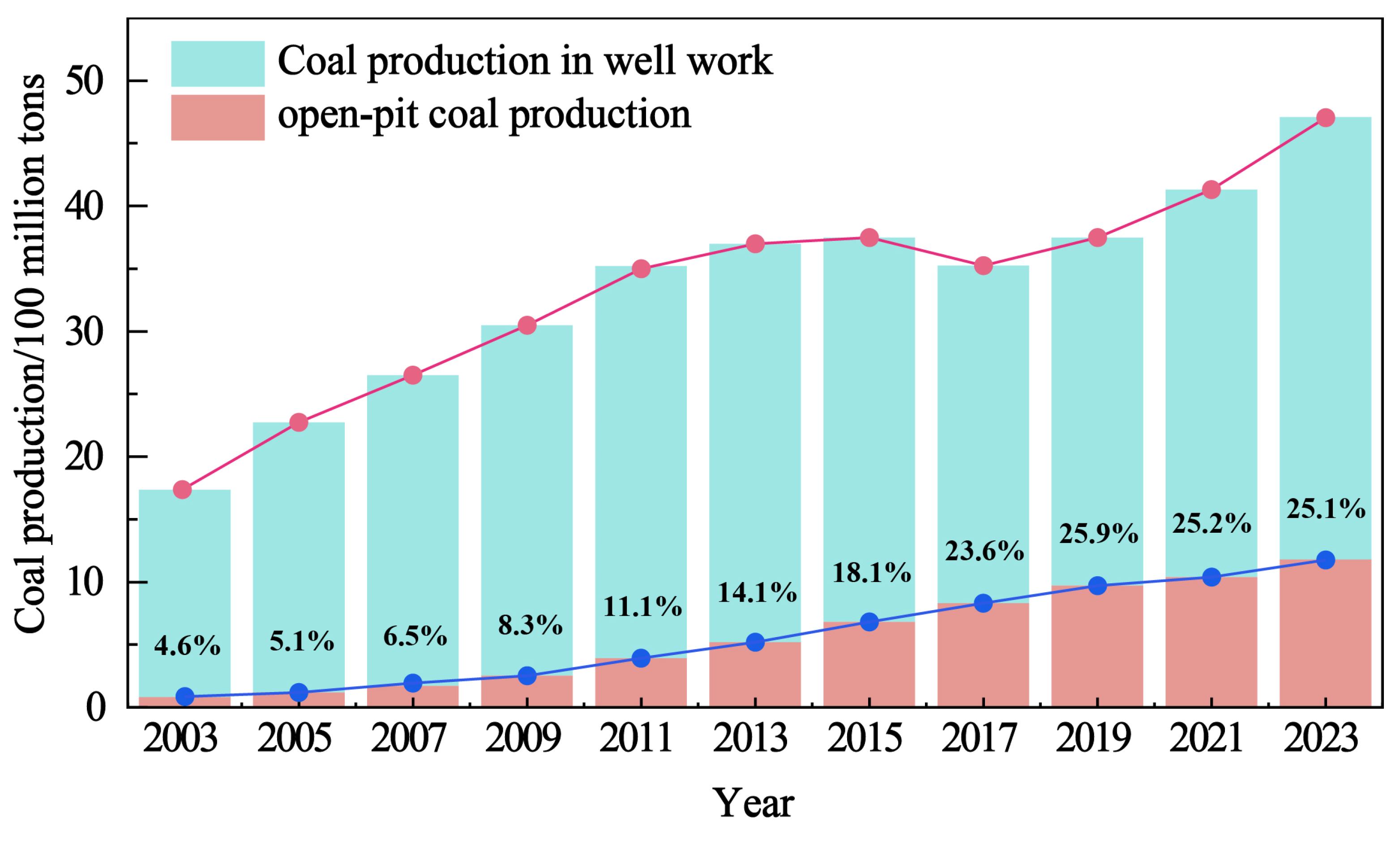
1. Introduction

In recent years, As shown in Figure 1, the development of open-pit coal mines in China has shown a trend of rapid growth. According to the latest data released by the National Energy Administration in 2024, the raw coal output of national open-pit coal mines reached 1.18 billion tons in 2023, accounting for 25.1% of the national total coal output. This represents a significant increase of 11 percentage points compared with 14.1% in 2013 [1]. This structural transformation signifies that China’s coal mining methods are undergoing a profound transformation, and the role of open-pit mining in safeguarding national energy security is becoming increasingly prominent.

In recent years, domestic research has predominantly focused on the intelligentization of mining equipment [2], while proposing low-carbon, high-efficiency, and safety-oriented intelligent construction models for open-pit mines [3,4]. Internationally, research has suggested that the future intelligent development of open-pit mines will be primarily centered on three core areas: production planning and scheduling, equipment management, and hierarchical control [5]. Specifically, within production planning, the focus has been on developing high-precision modeling techniques and highly efficient software for optimizing mine production design [6], alongside tackling key challenges in computational optimization and automation via intelligent algorithms [7].

An analysis of domestic and international research on open-pit mining sequence optimization demonstrates that recent international studies in this domain have been relatively limited. A notable exception is a study that proposed utilizing clustering methods to simplify the mining sequence problem for mining operations [8]. Domestic research on the optimization of open-pit mining processes has predominantly exhibited an evolutionary trajectory—shifting from idealized models toward complex real-world scenarios. Specifically, this evolution is evident across three key dimensions: in terms of spatial scope, studies have advanced from focusing on regular mining boundary conditions to addressing irregular ones; in terms of geological targets, the research focus has expanded from a single coal seam to composite coal seam systems; and in terms of temporal scale, planning paradigms have transitioned from static short-term planning to full life-cycle-oriented planning frameworks. Specific research developments are as follows: ① Before 2016, studies primarily focused on regular boundaries and single-seam models, assuming a horizontal seam distribution and linearly decreasing working line lengths, employing parallelogram approximation to simplify production capacity calculations. While mathematically concise, this model fails to represent composite seams, dynamic geological changes, or irregular boundary characteristics [9,10,11,12,13]. ② After 2016, research progressively addressed composite seam models within irregular boundaries. This involved constructing precise three-dimensional surface topography through adaptive dynamic working line methods, combined with a bench-segmented production representation, to quantify the impact of complex topography on mining and stripping volumes [14,15,16,17,18,19,20,21,22,23]. ③ Research into full-lifecycle stripping–dumping coupling models commenced in 2020. Based on the dynamic relationship between stripping volume and internal dumping space release, this approach proposes elastic strategies for controlling the internal dump height and morphology. By adopting a full-lifecycle perspective to achieve spatial matching between mining and dumping, this model systematically enhances resource utilization efficiency [24,25,26,27,28,29,30].

In summary, significant progress has been made in delineating open-pit mining areas. However, conventional methods predominantly rely on model-assisted calculations followed by manual division based on experience. This approach has yet to establish an intelligent decision-making model that integrates real-time data and multi-objective optimization algorithms to achieve automated mining area delineation. Traditional methods suffer from inefficiency and lack a dynamic adjustment mechanism that can respond in real-time to fluctuations in production capacity and geological conditions. To address the inefficiencies of conventional manual mining area delineation, this study proposes an intelligent mining area delineation technique based on the fusion of multiple data sources. By integrating historical drilling data, this technique automatically adapts to complex geological conditions, generating high-precision, grid-based discrete data. Driven by a block-growth algorithm, it automatically merges blocks to form a stripping ratio grid matrix, thereby determining the primary direction for consolidating the mining area. Subsequently, by integrating multi-source data including boundary shapes, coal seam occurrence conditions, and stripping ratio technical parameters, it enables the automated generation of mining area division schemes. The reliability of the algorithm was validated using the Shitoumei No. 1 open-cast coal mine in Xinjiang as an engineering case study. This approach enhances the efficiency of open-cast mine mining area division, provides theoretical support for intelligent open-cast mine design, and offers technical backing for the sustainable development of open-cast coal mines.

2. Project Background

The Shitoumei No. 1 Open-Pit Coal Mine has an annual production capacity of 35 million tons. The surface boundaries of the mining area extend approximately 6 km east–west and 5.6 km north–south; the subsurface boundaries measure approximately 4.8 km east–west and 4.7 km north–south. Geological reserves total 1649 Mt with a service life of 47 years. The primary exploitable coal seams across the area, from top to bottom, are Seams 9-3, 9-2, 9-1, 11, and 12, with an average total thickness of 50.52 m. Stripping employs a single-bucket-truck intermittent process, while coal extraction utilizes a semi-continuous mining method that comprises a single-bucket-truck and a semi-mobile crushing station with a belt conveyor. As illustrated in Figure 2, the mining area is subdivided into five sections: the initial mining zone in the south running east–west, followed by the second, third, and fourth mining zones in the north extending from west to east in a north–south orientation, with the southeastern section designated as a reserve area.

The primary coal seam at the Shitoumei No. 1 Open-Pit Mine is the 9-1 seam, with an average thickness of 27.4 m across the entire area. The overall trend of the coal seam is inclined from south to north and from west to east, with shallower burial on the western side and deeper burial on the eastern side. As the Shitoumei No. 1 Open-Pit Coal Mine features composite coal seams, with the primary 9-1 seam constituting the mineable layer across the entire area (accounting for 54% of total coal seam thickness), and given that all coal seams exhibit similar trends in dip and thickness variation (as illustrated in Figure 3), this study bases both the grid coal thickness variation and coal seam dip variation rate calculations on data from the 9-1 coal seam.

3. Method for Intelligent Mining Area Demarcation in Open-Pit Coal Mines

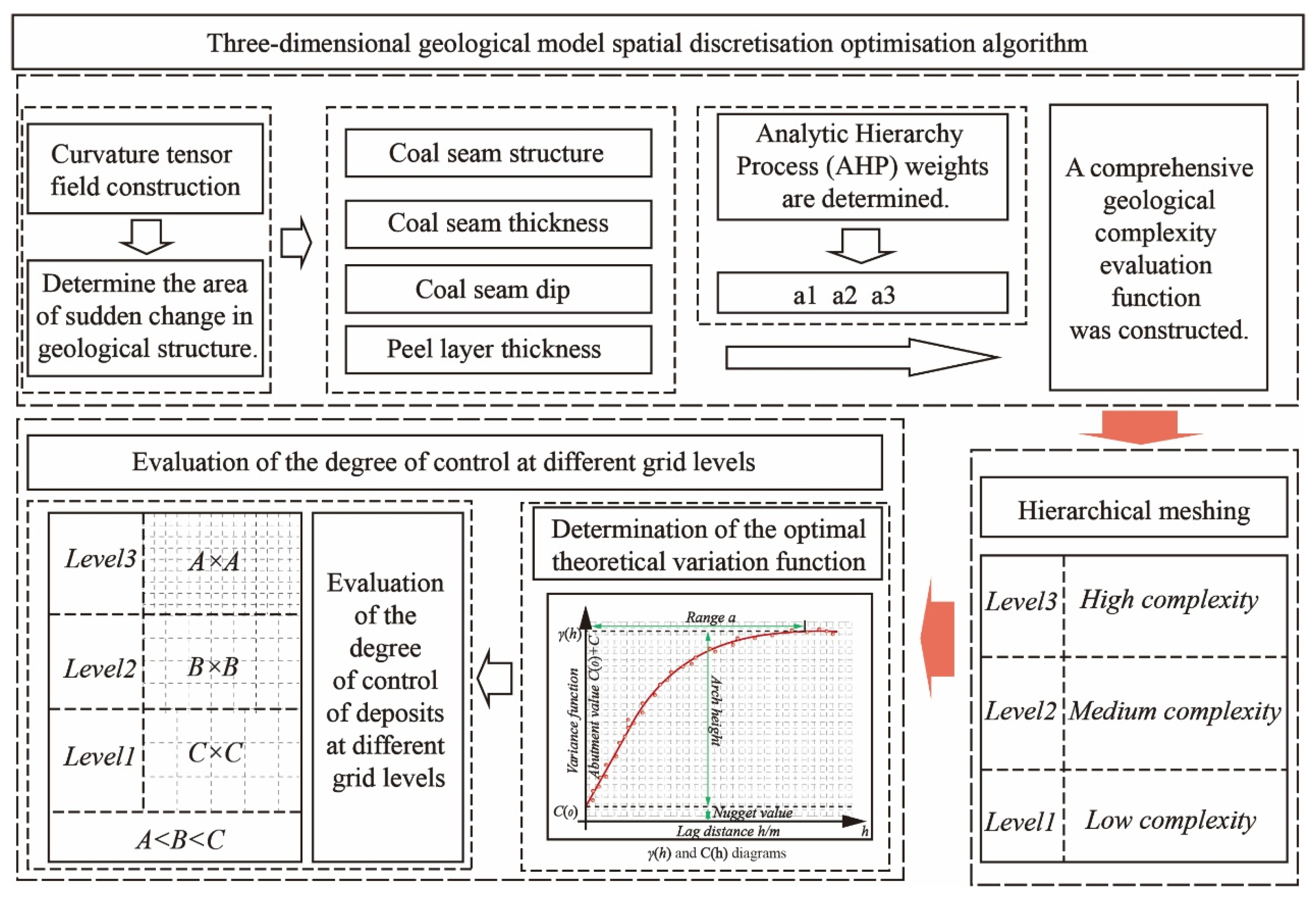
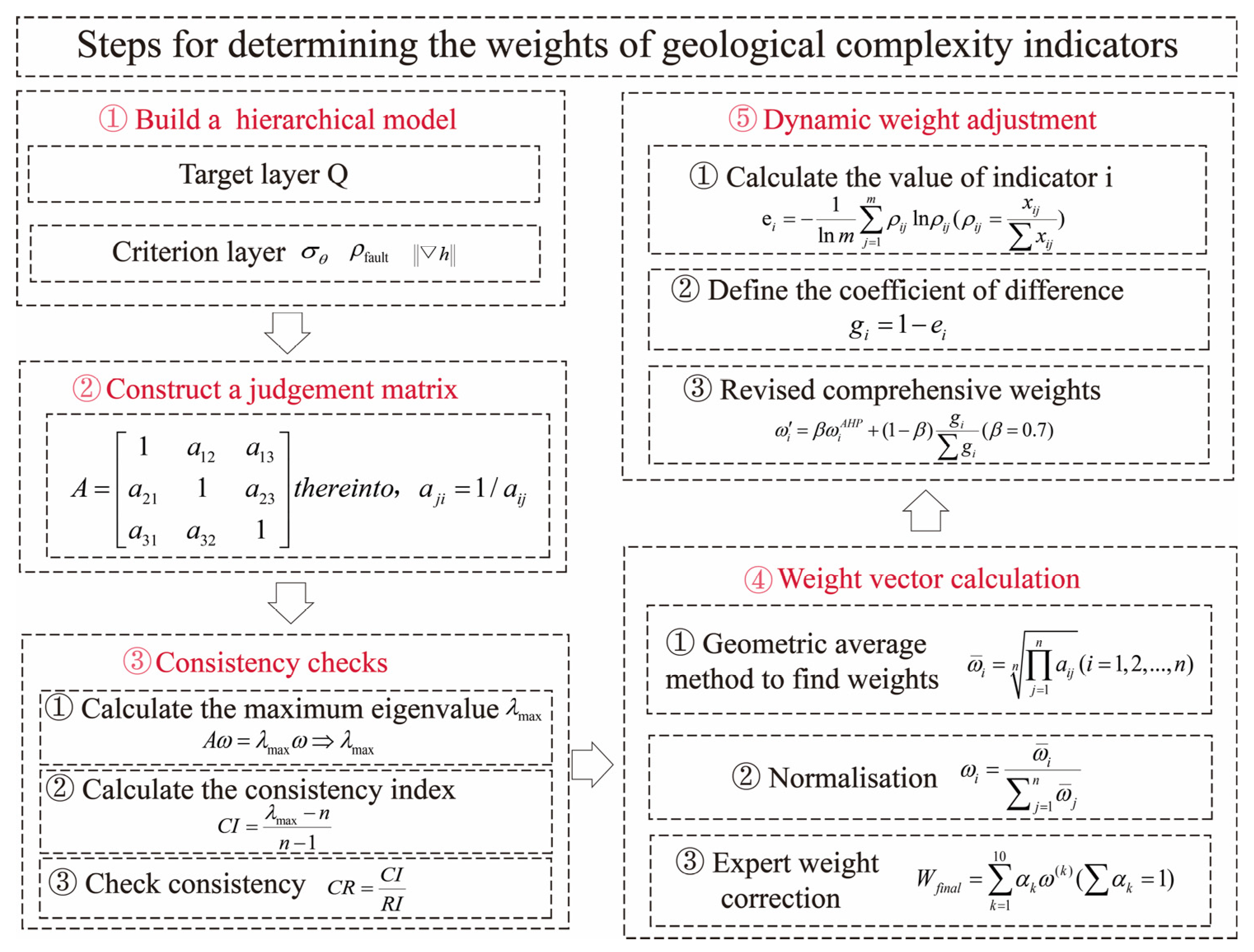
3.1. Construction of the Geological Complexity Quantification Model

To enhance the accuracy and computational efficiency of numerical modeling for coal seam geological structures, this study developed an adaptive discretization resolution methodology based on quantifying geological complexity. As illustrated in Figure 4, this technique first quantifies geological complexity through a dedicated quantification model. Subsequently, threshold segmentation is employed to classify mining areas according to complexity levels. Finally, Kriging is applied to perform intelligent grid partitioning for mining areas within each complexity zone. Taking the Shitoumei No. 1 open-cast coal mine as an engineering case study, a discretised grid for the mine’s stripping ratio was constructed.

In constructing the core method, a curvature tensor field was established to accurately quantify the thickness of the coal seam. By developing a model to calculate the curvature tensor of the coal seam interface, regions with abrupt changes in geological structure can be precisely identified, providing a key basis for recognizing structural boundaries in subsequent complexity analysis. Meanwhile, adhering to the concept of multi-indicator integration, a comprehensive geological complexity evaluation model is constructed (as shown in Figure 5). This model incorporates multi-dimensional geological parameters—including curvature characteristics (used to describe the degree of curvature of a surface at a specific point), the stratum dip angle, and the fault distribution density—into a unified evaluation system, forming a quantitative characterization method for geological complexity and providing a scientific benchmark for complexity classification in adaptive grid division.

(1) Construction of curvature tensor field: Establish a calculation model for the curvature tensor of the coal seam interface to identify regions with abrupt changes in geological structure.

$$C_{ij}={\displaystyle \frac{{\partial }^{2}h}{\partial x_i\partial x_j}}(i,j=1,2)$$

(1)

where h(x₁, x₂) denotes the thickness function, and the tensor eigenvalues can effectively characterize the characteristics of abrupt changes in the interface curvature.

(2) Based on the distribution of exploration boreholes, radial calculations are performed in three directions: horizontal (x), vertical (y), and diagonal (o). The curvature changes and dip angle changes in the coal seam and overburden layer interfaces are obtained for each direction, respectively. Using the average values of the three directions, the thickness increment and dip angle variation coefficient of the coal seam ${\sigma }_{\theta }$ and overburden layer in the basic region (the yellow area, as shown in Figure 5) are calculated; finally, based on the fault-affected area of the basic region, the fault density ${\rho }_{\mathrm{fault}}$ per unit area of the basic region is determined.

$$‖▽h‖={\displaystyle \frac{1}{n}}(\left|{\displaystyle \frac{{\partial }^2{h}_x}{\partial x_i\partial x_j}}\right|+\left|{\displaystyle \frac{{\partial }^2{h}_y}{\partial x_i\partial x_j}}\right|+\left|{\displaystyle \frac{{\partial }^2{h}_o}{\partial x_i\partial x_j}}\right|)$$

(2)

$${\sigma }_{\theta }={\displaystyle \frac{1}{n}}(\arctan ({\displaystyle \frac{\left|\Delta H_x\right|}{\Delta l_x}})+\arctan ({\displaystyle \frac{\left|\Delta H_y\right|}{\Delta l_y}})+\arctan ({\displaystyle \frac{\left|\Delta H_o\right|}{\Delta l_o}}))$$

(3)

$${\rho }_{fault}={\displaystyle \frac{S_D}{S_Z}}$$

(4)

where $‖▽h‖$ denotes the thickness increment, ${\sigma }_{\theta }$ denotes the dip angle variation coefficient, ${\rho }_{\mathrm{fault}}$ is defined as the fault density per unit area, n is the number of directions, h is the thickness in meters (m), H is the elevation in meters (m), $\Delta l$ is the variation distance in meters (m), $S_D$ is the fault-affected area in square meters (m²), $S_Z$ is the total area of the basic region in square meters (m²).

(3) Multi-indicator integrated complexity index: The first step of this index is to construct a comprehensive geological complexity evaluation function.

$$Q=a_1‖▽h‖+a_2{\sigma }_{\theta }+a_3{\rho }_{\mathrm{fault}}$$

(5)

where $‖▽h‖$ denotes the thickness increment, ${\sigma }_{\theta }$ denotes the dip angle variation coefficient, and ${\rho }_{\mathrm{fault}}$ is defined as the fault density per unit area. The weight coefficients a₁, a₂, and a₃ are determined through evaluation by geological experts using the Analytic Hierarchy Process (AHP).

(4) Determination of regional grid density for complex stratigraphic areas

The improved Otsu threshold segmentation algorithm is used to achieve adaptive division of grid subdivision thresholds: First, a regional feature histogram is constructed based on the complexity index Q; second, threshold segmentation is optimized through the inter-class variance maximization criterion; finally, morphological filtering is introduced to eliminate discrete noise interference. This algorithm can automatically generate optimal grid division thresholds according to the different data distribution characteristics.

$$G_{level}=\left\{\begin{array}{ll}Level3\hfill & Q>T_{crit}\hfill \\ Level2\hfill & 0.5T_{crit}\le Q\le T_{crit}\hfill \\ Level1\hfill & Q<0.5T_{crit}\hfill \end{array}\right.$$

(6)

Within the grid division system, a three-level resolution standard is adopted: Level 3 refers to high-density grids, suitable for complex geological regions; Level 2 refers to medium-density grids; and Level 1 serves as the basic grid level. To achieve a dynamic balance between structural detail capture accuracy and computational resource consumption, an exploration grid density evaluation model is introduced to conduct scientific quantitative analysis on the grid density of different levels, thereby forming an optimized configuration plan.

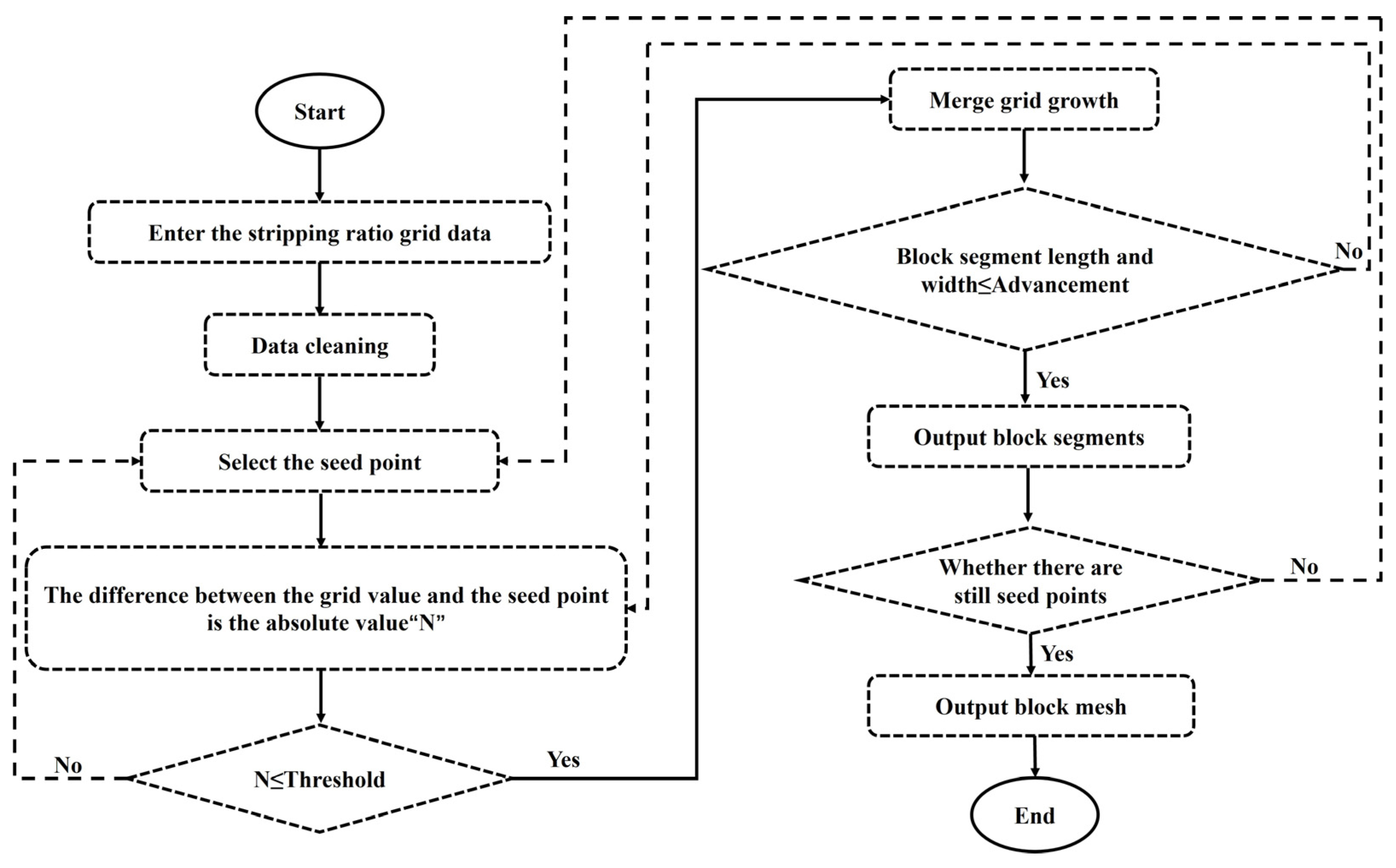
3.2. Block Growth Algorithm Based on Stripping Ratio Grids

The fundamental concept of the block–segment growth algorithm is to merge similar grid cells based on stripping ratio grid data by utilizing the stripping ratio indicator. The algorithm, illustrated in Figure 6, takes a stripping ratio data matrix as input and initiates growth from a seed point. During growth, a predefined absolute threshold for stripping ratio deviation is employed to control the uniformity of stripping ratios within blocks. To ensure block shapes meet mining requirements, the current block dimensions are calculated in real-time. Based on the mine’s advancement progress, a maximum growth range is established, and spatially adjacent grid cells with similar stripping ratios are aggregated to form a block. This method first requires identifying a seed stope ratio grid cell within the stope ratio gradient field as the origin of growth. It then progressively merges adjacent grid cells within the defined stope ratio tolerance threshold, continuing within the advance boundary until no further eligible stope ratio grid cells remain for merging, at which point growth ceases. Growth also ceases automatically when the advanced boundary is reached. A block segment is formed, after which a new seed growth point is determined. This process repeats until all stripping ratio grid cells within the mining boundary have been fully developed. The algorithm concludes, generating a block segment grid. This establishes the foundation for constructing the main direction matrix of stripping ratio variations in open-pit mines.

This algorithm adopts a dynamic seed growing strategy, as shown in Figure 7, and its core rules are as follows: First, it selects an initial seed point (with a stripping ratio of n₁) and calculates the absolute value of the difference between this seed point and its nearest grid n_θ in the spatial dimensions (x, y, o) and the feature dimension, where n_θ represents the adjacent grid in the θ-angle direction between n_x and n_y. If this absolute value is less than or equal to the preset threshold a, then n_θ is merged into the current growing area; if it is greater than a, it is necessary to verify the neighborhood features of n_θ in the x, y, and o directions: when there is a significant difference exceeding threshold a in at least one direction, the verification is determined to pass. At this point, n_ii (as shown in Figure 7, i.e., n₁, n₂, n₃, and n₄) is set as new seed points, the original seed point terminates extension in this growing direction, and instead, the new seed points continue expanding; if the verification fails to meet the significance condition in all directions, n_θ is still merged, and the original seed point maintains its growing state until it reaches the set boundary length of the growing range, then stops growing, and a new seed point is set. To simplify the algorithm’s growth rules, the seed point selection principle is set to commence from the southwest. Following the cessation of development at the first seed point, subsequent seed points are selected sequentially for growth in the order from south to north and from west to east.

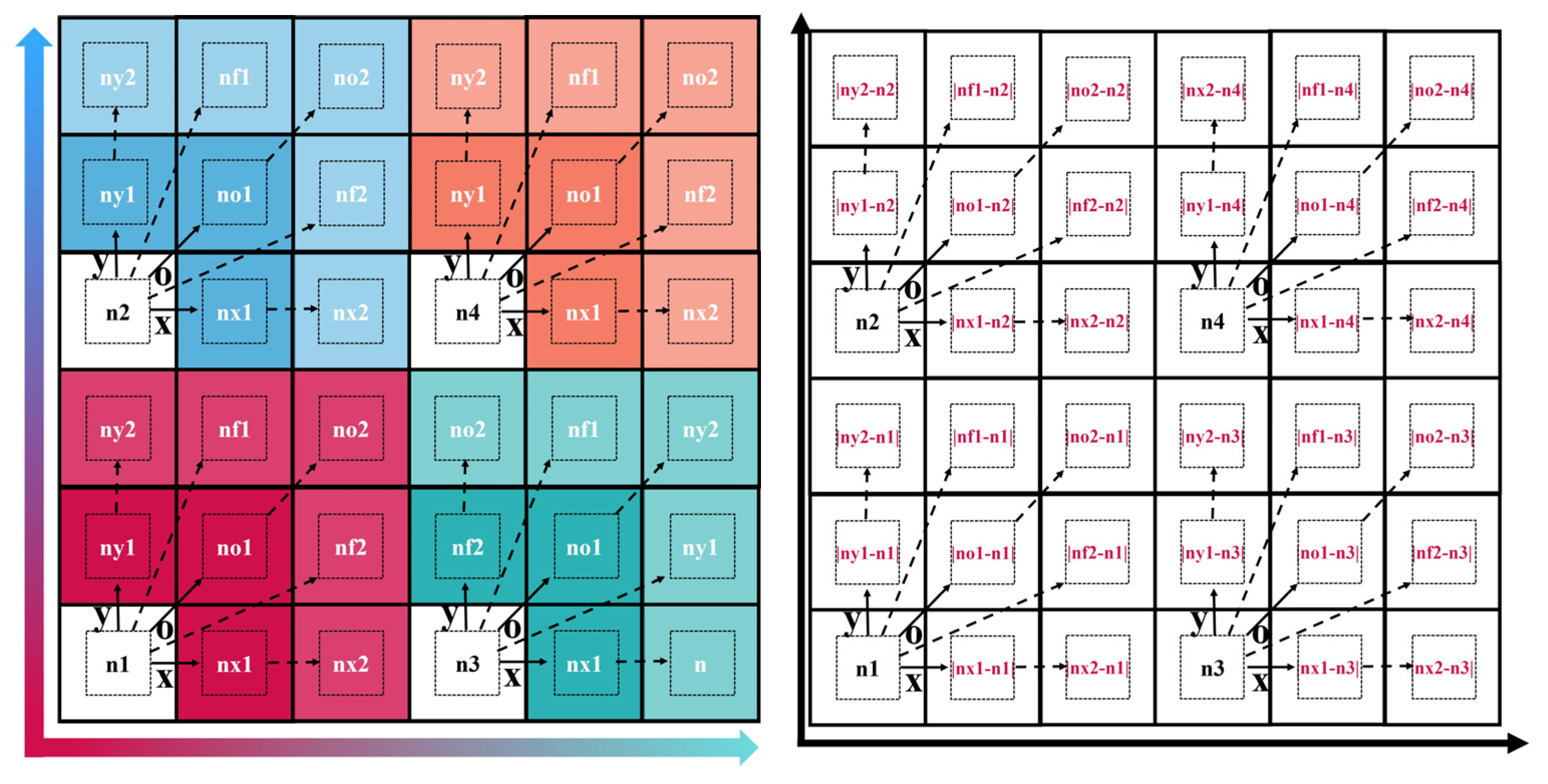
3.3. Construction of the Main Direction Matrix for Changes in the Stripping Ratio in Open-Pit Mines

When dividing panels in an open-pit mine, to ensure the smooth temporal and spatial continuity of the stripping ratio and improve mine production efficiency, one key principle is “small variation in stripping ratio”, that is, dividing panels as much as possible along the direction with small variation in the stripping ratio. The traditional method involves identifying areas with small variations in the stripping ratio by observing the density of stripping ratio contour lines. This method has the advantages of being simple, intuitive, and easy to operate; however, its disadvantages include low accuracy and high susceptibility to human subjectivity. To address this issue, based on the automatic generation of block grids for open-pit mines, a matrix of the main direction of stripping ratio variation has been constructed to determine the main direction for merging blocks into panels.

Taking the Shitoumei No. 1 Open-Pit Coal Mine as an example for illustration, as shown in Figure 8, using the extracted stripping ratio distribution matrix of the open-pit mine (as shown in Figure 8a), first, a 3 × 3 grid is extracted as the “unit matrix”—the numbers in the small grids represent the stripping ratio at the corresponding positions. Then, the main direction of the central grid (i.e., the main direction of the grid with a stripping ratio of 5.77 m³/t) is extracted, as shown in Figure 8b; the upper-left, upper, upper-right, left, right, lower-left, lower, and lower-right directions of the central grid are defined as eight analysis directions. As shown in Figure 8c, next, the differences between the stripping ratios of each adjacent grid and that of the central grid are calculated, respectively, and their absolute values are determined. The direction with the smallest absolute value is defined as the main direction of the central grid and marked with an arrow, as shown in Figure 8d. Using this method, calculations are performed for each unit matrix formed by every grid to determine its main direction; finally, all these directions constitute the stripping ratio main direction distribution matrix of the Shitoumei No. 1 Open-Pit Coal Mine.

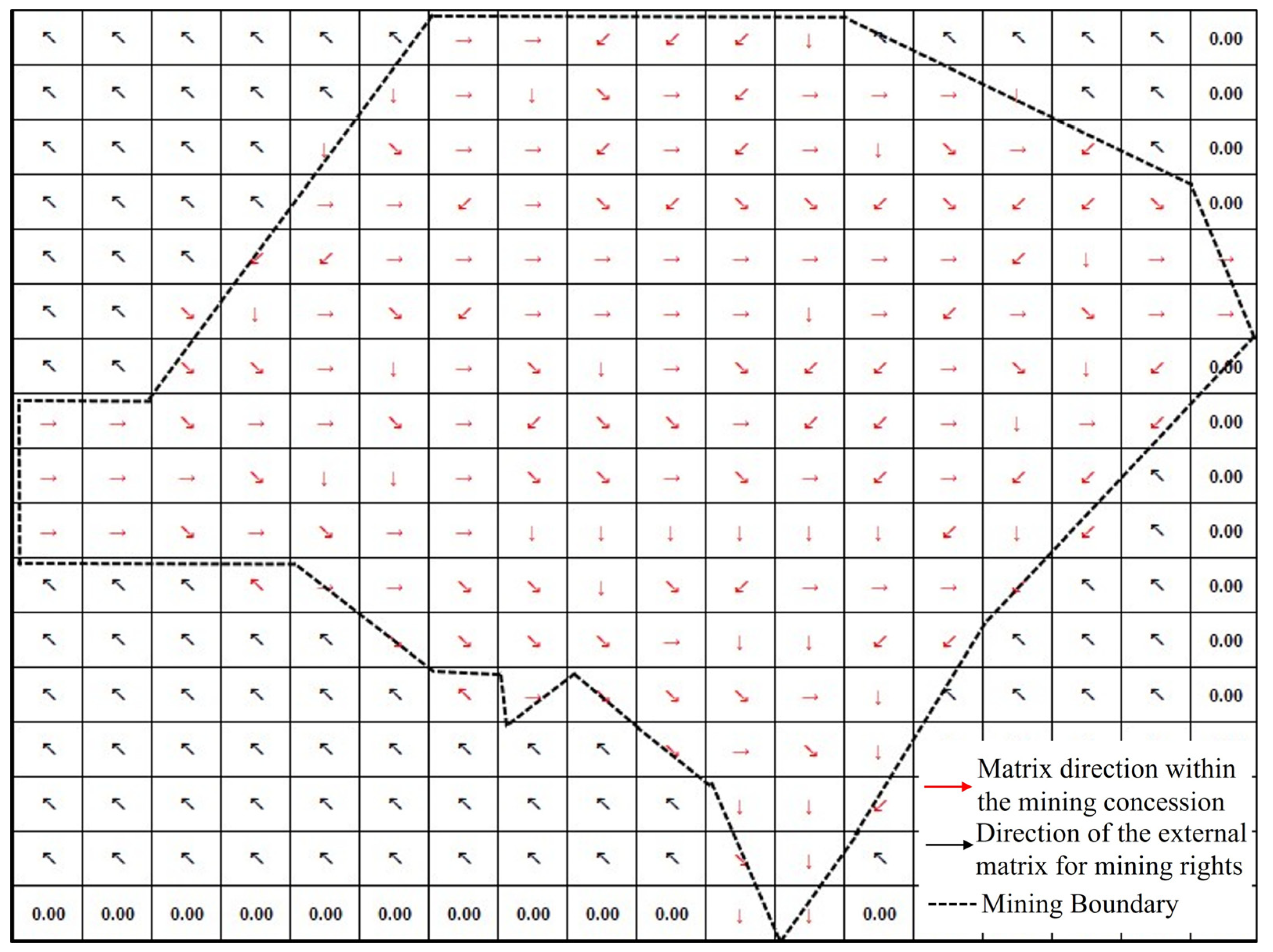
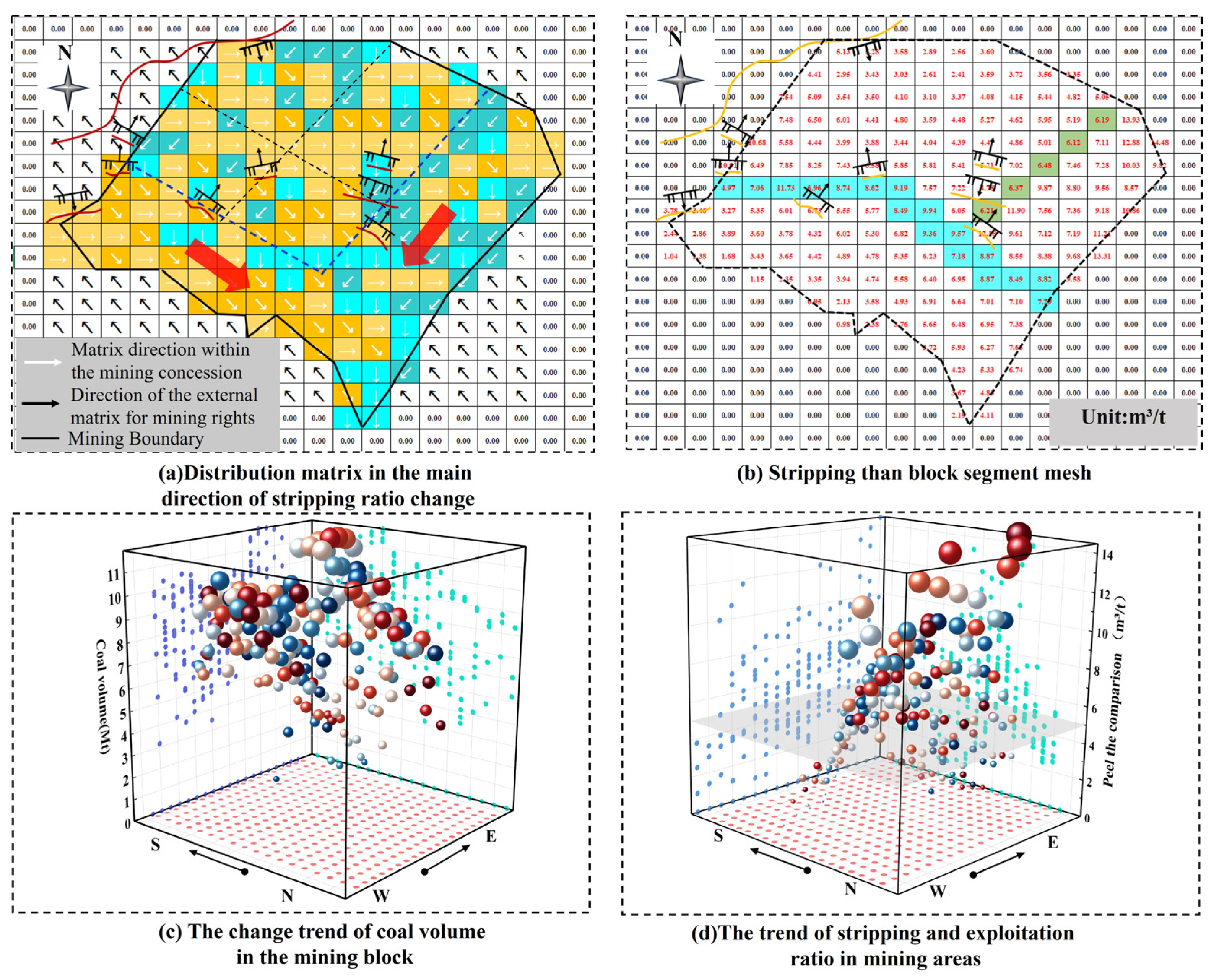
3.4. Mining Area Delineation Based on the Primary Direction of Stripping Ratio Variation

The delineation of mining areas necessitates consideration of multiple factors, including geological conditions, boundary configurations, and economic scale. Consequently, the core principles of intelligent mining area division algorithms, as illustrated in Figure 9, first determine the type of boundary shape. Based on this shape, the primary direction for mining area division is established: for narrow, elongated deposits, the major axis direction serves as the primary orientation; for regular deposits, the primary direction is determined by the distribution of the stripping ratio variation. Subsequently, fault parameters are analyzed to minimize their impact on mining operations, endeavoring to align boundaries with fault lines where feasible. Where this is unavoidable, the angle between the fault direction and the advance direction must be considered, as faults parallel to the advance direction exert a greater influence than those perpendicular to it.

As illustrated in Figure 10a, seed blocks are selected for serpentine merging perpendicular to the principal strike direction. Following each merger, as shown in Figure 10b,c, the average stripping ratio and total coal reserves of the merged blocks are dynamically updated. This ensures the minimum average stripping ratio for the mining area while satisfying the total coal reserves required for the service life. The delineation of areas with a pronounced principal direction is prioritized. For regions where the principal direction is unclear, they are delineated equally based on the coal volume and fault orientation. This algorithm optimizes the economic scale of mining units while ensuring geological homogeneity and spatial continuity within the mining area, providing theoretical support for intelligent open-pit mining.

The average stripping ratio refers to the ratio between the total amount of stripped rock and the total amount of mined ore in open-pit mining. It is the most important factor affecting the open-pit mining boundary and is directly related to key issues such as the mine’s construction speed, economic benefits, resource utilization, product quantity, and product quality. From an economic perspective, there is a reasonable limit for the open-pit mining boundary. The stripping ratio is the controlling index for determining this limit.

$${\overline{n}}_k={\displaystyle \frac{{\displaystyle {\sum }_1^k{V}_i}}{{\displaystyle {\sum }_1^k{M}_i}}}$$

(7)

where k represents the number of merged blocks, ${\overline{n}}_k$ represents the average extraction ratio of the merged k blocks (m³/t), $M_k$ is the total coal volume of the representative unit block segment i (Mt), and $V_k$ is the total amount of peeling found for form unit block segment i (Mm³).

The service life of a mine refers to the entire period from the mine’s commissioning to the completion of its mining operations. It is mainly determined by factors such as recoverable reserves, annual production capacity, and market demand.

$$T={\displaystyle \frac{{\displaystyle {\sum }_1^k{M}_i}}{A}}$$

(8)

where T represents the service life of the merged k block segments per year (a); A represents the annual production capacity of the mine (Mt/a).

4. Research Findings and Analysis

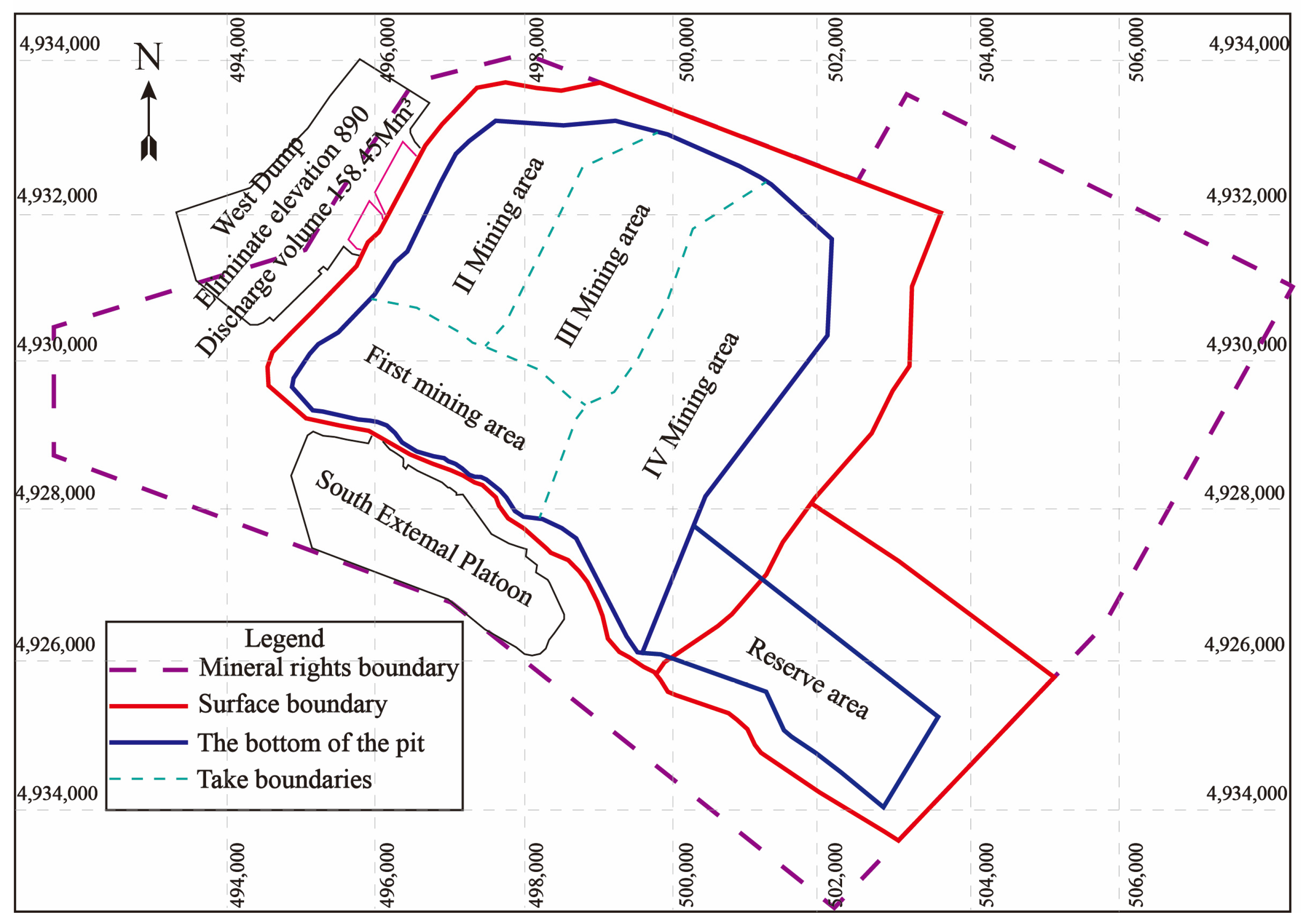
4.1. Case Study: Shitoumei No. 1 Open-Pit Coal Mine

Within the current mining boundaries of the Shitoumei Open-Pit Mine, a total of 19 exploration lines and 200 exploration drill holes have been established. As illustrated in Figure 11, a three-dimensional drill hole grid model was first constructed based on the mine’s exploration drilling data. Using this model, the thickness parameters of the 9-1 coal seam and the elevation data of the coal seam floor were determined, while the spatial distance characteristics of the drill holes at different spatial orientations were quantified. These parameters were substituted into Formulas (2)–(5) to quantify geological complexity. Subsequently, the Otsu thresholding algorithm was employed to adaptively determine grid subdivision thresholds, ultimately establishing a three-tier resolution standard: Level 3 denotes high-density grids (50 m × 50 m), which are suitable for areas with complex geological conditions; Level 2 represents medium-density grids (100 m × 100 m); Level 1 denotes the base grid tier (150 m × 150 m). Based on this multi-level grid system, the stripping ratio values for each grid cell are computationally derived.

Based on the statistical analysis of the stripping ratio dispersion at the Shitoumei No. 1 open-cast coal mine, the absolute threshold for the stripping ratio deviation during the growth process was set at 0.2 m³/t. Considering the equipment production capacity of the Shitoumei open-cast coal mine, a 400 m rate of advance was established, thereby defining a 400 m growth range. Sets of similar stripping ratios in all spatial directions within Figure 12a are aggregated to form a block segment. Using the block segment growth algorithm, as illustrated in Figure 12b, a block segment grid is generated.

Based on the generation of its block segment grid, the distribution matrix of the main direction of the stripping ratio variation was constructed, as shown in Figure 13, laying the foundation for the subsequent merging of block segments into mining areas.

The surface boundaries of the Shitoumei No. 1 open-cast coalfield extend approximately 6 km east–west and 5.6 km north–south; its deeper boundaries measure roughly 4.8 km east–west and 4.7 km north–south, forming a relatively regular quadrilateral shape. The distribution of the mining field based on the primary direction of stripping ratio variation is shown in Figure 14a. Within the field boundaries, 173 blocks were formed: 39 oriented northwest to southeast, 68 oriented due west to due east, 32 oriented due north to due south, and 34 oriented northeast to southwest. Faults divide the deposit into three distinct zones: southern, eastern, and northwestern. As depicted in Figure 14b, abrupt changes in the stripping ratio data delineate these three zones. As shown in Figure 14c, coal reserves within the blocks exhibit a trend of being larger in the southern and eastern zones and smaller in the northwestern zone. As illustrated in Figure 14d, the stripping ratio shows a trend of being lower in the southern and northwestern zones and higher in the eastern zone.

As shown in Figure 14a, the mining area is divided into three regions with faults as boundaries: in the southern region, blocks in the west–east direction account for 71%, which serves as the main direction; in the eastern region, blocks in the north–south direction account for 57%, which serves as the main direction; in the northwestern region, blocks in the west–east direction account for 61%, which serves as the main direction. Since the northwestern region is too large in scale, a new scheme was derived for this region by comprehensively considering faults, the main direction, and coal quantity.

Using the intelligent panel division algorithm, the panel division schemes for the Shitoumei No. 1 Open-Pit Coal Mine were generated, as shown in Figure 15 (the labels in the figure are for clarity only and do not represent the mining sequence). A total of four panel division schemes were generated.

As shown in Figure 15a, Scheme I consists of west–east panels in the southern part and three north–south panels in the northern part.

As shown in Figure 15b, Scheme II consists of west–east panels in the southern part (not reaching the boundary), north–south panels in the eastern part, and two north–south panels divided in the northwestern part.

As shown in Figure 15c, Scheme III consists of west–east panels in the southern part, north–south panels in the eastern part, and two west–east panels in the northwestern part.

As shown in Figure 15d, Scheme IV consists of north–south panels in the eastern part and three west–east panels in the western part.

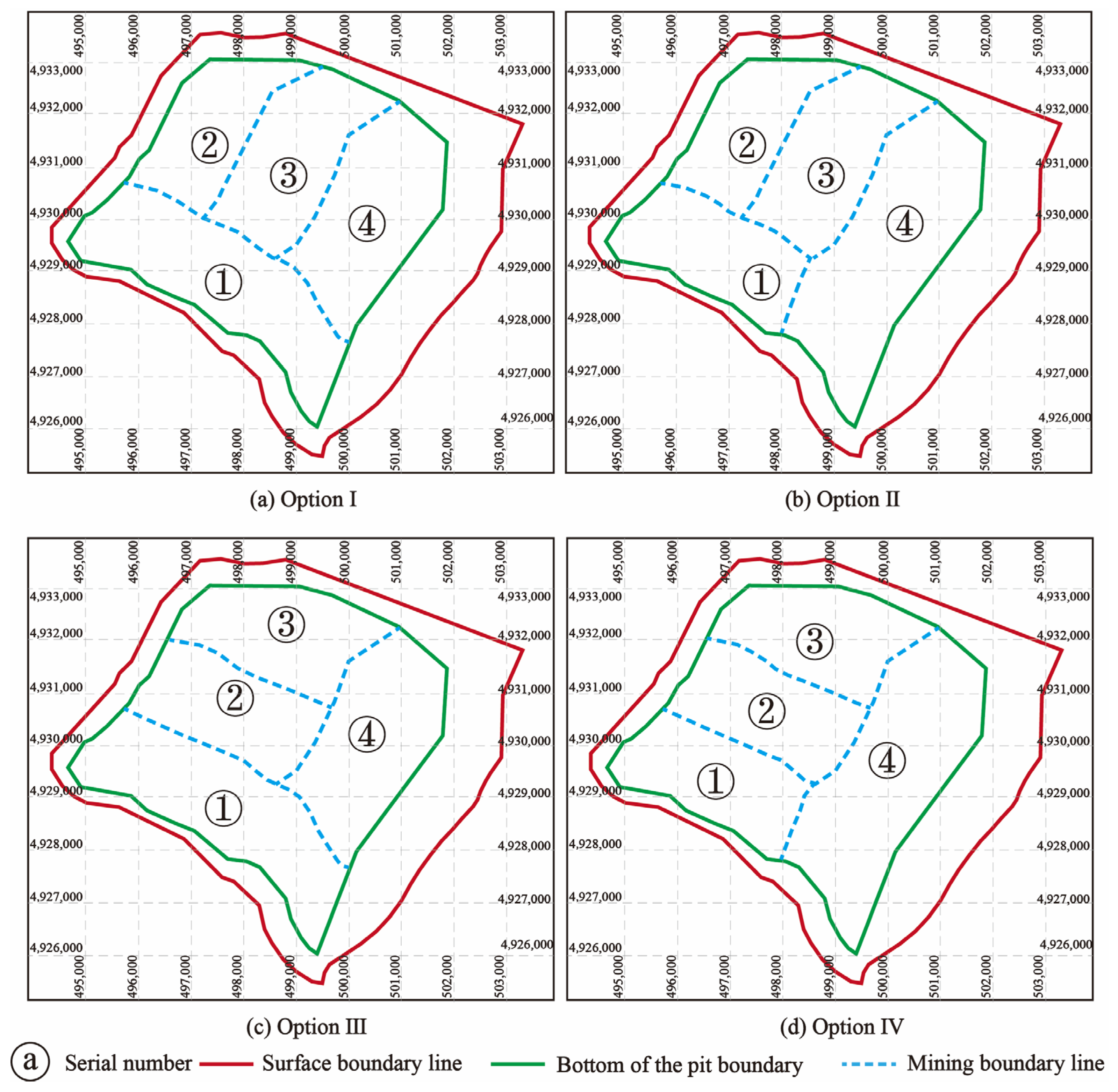
4.2. Comparative Analysis of Optimal Schemes for Shitoumei No. 1 Open-Pit Coal Mine

(1)

Analysis of Multi-source Data Indicators and Weighting for Mining Area Demarcation

The delineation of open-pit mining zones is primarily based on five key indicators: geological conditions, technical mining conditions, economic conditions, safety conditions, and environmental conditions, as illustrated in Figure 16. Each indicator is further subdivided into 15 secondary indicators. Subsequently, a grid-based method is employed to quantify the data for each indicator, followed by an analysis and evaluation of their respective weights.

Based on the factors influencing open-pit mining blocks, a multi-level evaluation system comprises five primary indicators and their detailed fifteen secondary indicators. This study employs the Analytic Hierarchy Process (AHP) to construct a hierarchical model that maps indicator relationships. A judgment matrix was developed through consultation with ten mining and geological experts, with composite weights determined using the eigenroot method. This approach achieves deep integration of expert judgment with mathematical modeling, as illustrated in the computational process depicted in Figure 17.

We next established a comprehensive evaluation model for open-pit mine block delineation, with the evaluation of delineation effectiveness designated as the objective layer (A). The criterion layers comprise geological suitability (B1), technical feasibility (B2), economic rationality (B3), safety and reliability (B4), and environmental compatibility (B5). Fifteen indicators were established as the indicator layer, denoted as C1, C2, C3, …, C15, to comprehensively evaluate the effectiveness of open-pit mine block delineation. The Analytic Hierarchy Process was employed to construct the A-B discrimination matrix, as shown in

Table 1. The discrimination matrix used for A-B classification of open-pit coal mining areas.

A	B1	B2	B3	B4	B5
B1	1	2	2	1.5	4
B2	0.5	1	1.2	0.8	2.5
B3	0.5	0.83	1	0.8	2.5
B4	0.67	1.25	1.25	1	3
B5	0.25	0.4	0.4	0.33	1

.

By calculating the consistency test, the maximum eigenvalue λmax = 5.032, the Consistency Index (CI) = 0.008, the Random Consistency Index (RI) = 1.12, and the Consistency Ratio (CR) = 0.007 < 0.1. These results verify that the test was passed.

As shown in Figure 18, the weights of each indicator were determined by using the model, and the following analysis was conducted for different levels. First, among the five criteria, geological adaptability has a weight of 0.352, making it the most significant factor in evaluating the strip division effect. Therefore, a technical method system of adaptive discretization resolution based on the quantification of geological complexity was constructed to accurately quantify the coal seam occurrence indicator data in mines.

(2)

Results of the Mining Area Division for Shitoumei No. 1 Open-Pit Coal Mine

In panel division, the main technical parameter referenced is the stripping ratio; the geological parameters include the resource recovery rate, orebodies continuity coefficient, and structural crossing density. To intelligently recommend the optimal scheme, evaluation was completed based on the principle of the degree of influence of each parameter on panel division, as specified with the priority order being resource recovery rate > stripping ratio > orebodies continuity coefficient > structural crossing density. The technical parameters of the intelligent panel division schemes for the Shitoumei No. 1 Open-Pit Coal Mine are shown in

Table 2. Technical parameters of the intelligent panel division schemes used for the Shitoumei No. 1 Open-Pit Coal Mine.

Scheme	Block	Coal Quantity (Mt)	Average Stripping Ratio (m3/t)	Stripping Ratio Variance	Mining Area Continuity Coefficient	Structural Density	Resource Recovery Rate
Scheme I	Panel I	579.98	4.9	2.6	100%	0.40%	94%
	Panel II	265.6	6.21	4.08	100%	0.20%
	Panel III	332.45	7.59	0.63	100%	0.70%
	Panel IV	379.64	17.08	5.37	100%	0.50%
Scheme II	Panel I	306.88	4.05	2.19	100%	0.45%	94%
	Panel II	265.6	6.21	4.08	100%	0.20%
	Panel III	332.45	7.59	0.63	100%	0.70%
	Panel IV	647.77	14.1	5.74	100%	0.37%
Scheme III	Panel I	579.98	4.9	2.62	100%	0.40%	88%
	Panel II	191.22	7.17	2.71	100%	0.57%
	Panel III	300.11	4.32	0.73	100%	0.00%
	Panel IV	379.64	17.08	5.37	100%	0.50%
Scheme IV	Panel I	306.88	4.05	2.19	100%	0.45%	87%
	Panel II	191.22	7.17	2.71	100%	0.57%
	Panel III	300.11	4.32	0.73	100%	0.00%
	Panel IV	647.77	14.1	5.74	100%	0.37%

.

Analysis of the proposed schemes indicates that Scheme I and Scheme II are prioritized for resource recovery rates. Scheme II demonstrates superior average stripping ratios across all mining areas compared with Scheme I, coupled with a relatively lower coefficient of variation in stripping ratios. Consequently, Scheme II is recommended for the division of the mining area at Shitoumei No.1 Open-Pit Coal Mine. The southwestern mining area extends beyond the boundary, while the eastern mining area follows a north–south orientation. The northwestern section is divided into two north–south mining areas, consistent with the original design in Figure 2, validating the algorithm’s feasibility. Compared with the original design, which required 15 days for zoning, the current approach only required 0.5 days, representing a 96% improvement in efficiency. Additionally, the cost reduction per zoning cycle amounted to approximately CNY 190,000.

4.3. Limitations of Previous Research

The essence of intelligent optimization in open-cast coal mining procedures lies in quantifying key indicators through digitalization, subsequently analyzing these digital metrics to extract critical information, and finally leveraging traditional optimization theories to achieve intelligent mining program optimization, thereby establishing a theoretical framework for intelligent mining program optimization. However, mining area delineation—a pivotal step in optimizing mining programs—has yet to be achieved through intelligent means. A review of existing literature reveals two significant limitations in current mining area delineation practices: First, theoretical research has yet to develop a framework compatible with intelligent delineation. Second, in practical application, traditional delineation relies on drilling data to construct models, generating a series of contour maps. Key information is extracted from these contour maps and three-dimensional block models, with manual, experience-based decisions made according to delineation criteria. Due to the considerable complexity of three-dimensional block models, computers currently cannot perform automated information extraction or logical deduction for delineating mining areas. This prevents real-time adjustments to accommodate shifts in mine production capacity and fluctuations in geological conditions, resulting in inefficient delineation processes and high labor costs.

4.4. Strengths of the Study

This study integrates data-driven paradigms with open-pit mining theory to develop a systematic methodology for open-pit mining area delineation, incorporating two core components: geological quantification and intelligent zoning. The research findings not only verify the algorithm’s efficacy and superiority over conventional methods but also carry significant implications for promoting the intelligent development of open-pit coal mines.

First, this study has realized a transition for mining area delineation from empirical-driven methods to data-driven approaches. Traditional mining area delineation relies predominantly on engineers’ empirical experience, leading to delineation outcomes characterized by high subjectivity and low efficiency. The intelligent partitioning algorithm proposed in this study, grounded in a geological complexity model, converts qualitative, fuzzy conventional geological understanding into precise, quantitatively computable grid-based data—thereby addressing the critical challenge of digital characterization of geological attributes. In the case of the Shitoumei No. 1 open-pit coal mine, the algorithm-generated recommendation scheme was consistent with the original experience-based design scheme, thus verifying the algorithm’s reliability. Furthermore, this study highlights that through scientific quantification and modeling, the expertise of mining specialists can be reproduced by data models. Additionally, the direct benefits—including a 96% increase in efficiency and a notable reduction in operational costs—offer economic corroboration of the inevitability of intelligent transition in the mining sector.

Second, innovations in methodologies offer a viable technical pathway for the digitalization of open-pit mining operations. This research is not limited to the application of a single algorithm, but rather the establishment of a series of integrated interlinked technological chains. Adaptive mesh generation enabled by a geological complexity model guarantees the scientific rigor of fundamental data; subsequently, a block growth algorithm generates initial blocks aligned with mining operation patterns. The final merger direction of mining areas is intelligently determined via the principal direction matrix for stripping ratio variation, thereby ensuring the engineering rationality of the zoning scheme. The establishment of a closed-loop system encompassing quantification and optimization addresses the dual constraints of static and isolated traditional approaches—thereby enabling dynamic, adaptive, and automated mining area delineation throughout the full process. Furthermore, the proposed system provides foundational models and core algorithmic underpinnings for the development of open-pit mine digital twin systems.

Finally, the case studies presented in this research provide valuable insights for the intelligent development of the open-pit mining sector. This study integrates intelligent algorithms including genetic algorithms with classical open-pit mining theory, effectively illustrating that intelligent methodologies serve as a technical extension of traditional open-pit mining theory. The constructed discrete stripping ratio grid and principal direction matrix serve as a sustainable digital platform for simulation and modeling, laying a robust data foundation for advanced applications in open-pit mining—such as subsequent open-pit mining plan optimization.

In summary, this research has made notable progress across three core dimensions: methodological innovation, technical implementation, and engineering application. Collectively, this research provides a viable solution for resolving key data bottlenecks and decision-making challenges in the intelligent development of open-pit coal mines.

5. Conclusions

(1) To address the key challenges of over-reliance on manual work, low efficiency, and static planning in traditional open-pit mining area delineation, this study develops and proposes a novel data-driven intelligent algorithm for open-pit mining area delineation. Taking the Shitoumei No. 1 open-pit coal mine as the research context, this study has achieved a paradigm shift from experience-driven to data-driven mining area delineation operations. The research results demonstrate that the zoning scheme recommended by the algorithm is consistent with the original design proposal, thereby validating the algorithm’s reliability. Meanwhile, the mining area delineation cycle has been reduced from 15 days to 0.5 days, resulting in an approximate 96% increase in efficiency. Additionally, the cost per delineation has decreased by around 190,000 Chinese Yuan (CNY), markedly improving both the economic viability and timeliness of mining area delineation.

(2) Through the construction of a geological complexity model, this study has realized the precise quantification of spatial grid density across different geological zones in the mining area. This method overcomes the inherent limitations of traditional contour line visualization methods in geological representation. Convert it into a high-density grid numerical representation. Application of this model in the Shitoumei No. 1 Open-Pit Coal Mine demonstrates that it effectively facilitates adaptive mesh refinement for mining geological modeling. This study constructed a discrete stripping ratio grid, thereby providing critical foundational data support for the intelligent development of the open-pit mine. This approach has effectively facilitated the transition of geological description from qualitative to quantitative analytical methodologies.

(3) This study integrates classical open-pit mining theory with block-based growth algorithms and further develops and proposes a novel block growth algorithm—enabling the efficient generation of block grids for open-pit mining operations. Through the construction of a principal direction matrix for stripping ratio variation, this study has realized the automated identification and generation of principal directions for mining area consolidation. This approach not only boosts the intelligence level of open-pit mining plan generation but also further facilitates the optimization of mining sequences and the improvement of resource recovery efficiency—bearing substantial practical significance for promoting the implementation of sustainable open-pit mining operations.