Influence of Stress on Gas Sorption Behavior and Induced Swelling in Coal: Implications for Sustainable CO₂ Geological Storage

Abstract

The influence of stress on gas sorption behavior and sorption-induced swelling in coal is critical for the success of CO₂-enhanced coalbed methane recovery (CO₂-ECBM) and geological carbon sequestration—a key strategy for mitigating climate change and promoting clean energy transitions. However, this influence remains insufficiently understood, largely due to experimental limitations (e.g., overreliance on powdered coal samples) and conflicting theoretical frameworks in existing studies. To address this gap, this study systematically investigates the effects of two distinct stress constraints—constant confining pressure and constant volume—on CO₂ adsorption capacity, adsorption kinetics, and associated swelling deformation of intact anthracite coal cores. An integrated experimental apparatus was custom-designed for this study, combining volumetric sorption measurement with high-resolution strain monitoring via the confining fluid displacement (CFD) method and the confining pressure response (CPR) method. This setup enables the quantification of CO₂–coal interactions under precisely controlled stress environments. Key findings reveal that stress conditions exert a regulatory role in shaping CO₂–coal behavior: constant confining pressure conditions enhance CO₂ adsorption capacity and sustain adsorption kinetics by accommodating matrix swelling, thereby preserving pore accessibility for continuous gas uptake. In contrast, constant volume constraints lead to rapid internal stress buildup, which inhibits further gas adsorption and accelerates the attainment of kinetic saturation. Sorption-induced swelling exhibits clear dependence on both pressure and constraint conditions. Elevated CO₂ pressure leads to increased strain, while constant confining pressure facilitates more gradual, sustained expansion. This is particularly evident at higher pressures, where adsorption-induced swelling prevails over mechanical constraints. These results help resolve key discrepancies in the existing literature by clarifying the dual role of stress in modulating both pore accessibility (for gas transport) and mechanical response (for matrix deformation). These insights provide essential guidance for optimizing CO₂ injection strategies and improving the long-term performance and sustainability of CO₂-ECBM and geological carbon storage projects, ultimately supporting global efforts in carbon emission reduction and sustainable energy resource utilization.

1. Introduction

Enhanced Coalbed Methane (ECBM) recovery through CO₂ injection has emerged as a promising dual-benefit technology, offering both enhanced methane (CH₄) production and secure geological CO₂ storage [1,2,3]. This approach directly addresses critical challenges in energy security and climate change mitigation [4,5,6]. However, field trials have consistently reported rapid declines in CO₂ injectivity, a phenomenon primarily attributed to adsorption-induced swelling of coal matrix [6]. This observation highlights the complex interplay between gas adsorption, mechanical deformation, and transport properties in coal reservoirs under in situ stress conditions [7,8,9]. Although extensive research has been conducted on coal–gas interactions [10,11,12], the influence of stress conditions on adsorption capacity, kinetic behavior, and associated deformation remains incompletely understood.

1.1. Stress Effects on Gas Adsorption Capacity

The adsorption capacity of coal for gases such as CO₂ and CH₄ is highly stress-dependent. Early investigations, however, primarily focused on unconfined conditions [13]. Conventional Langmuir-based adsorption models, while widely applied, often neglect stress effects, introducing significant uncertainties in predicting in situ reservoir behavior [14]. Subsequent experimental studies have confirmed that applied stress substantially reduces coal’s adsorption capacity for both CO₂ and CH₄. For instance, Hol et al. [15] observed that under 35 MPa uniaxial stress, bituminous coal exhibited a 5–50% reduction in CO₂ adsorption capacity compared to unstressed conditions. Similarly, Pone et al. [16] reported that confining stresses of 6.9 and 13.8 MPa reduced CO₂ sorption capacity by 39% and 64%, respectively, compared to powdered coal samples, while CH₄ uptake decreased by 85% and 91% under the same conditions. These reductions were attributed to stress-driven closure of nanopores and reduced accessibility to adsorption sites, highlighting the critical role of geomechanical constraints in coal–gas interactions.

The thermodynamic basis for stress-induced sorption reduction was systematically established by Hol et al. [17] and Liu et al. [18], who developed theoretical models incorporating the mechanical work required to overcome applied stress during adsorption-induced swelling. These models demonstrate that higher stress increases the chemical potential of adsorbed molecules, thereby decreasing their sorption affinity-a phenomenon consistently confirmed through experiments using both powdered and intact coal samples [19,20,21]. Significantly, Liu et al. [19] expanded this framework to water adsorption, revealing that stress-driven reduction in adsorption capacity is a universal phenomenon applicable to diverse adsorbates, including polar molecules such as H₂O.

1.2. Stress Effects on Adsorption Kinetics

Adsorption kinetics, which govern gas adsorption rate and equilibrium establishment, also exhibit pronounced stress dependence. Applied stress impedes gas diffusion within coal matrices through microfracture closure and transport pathway constriction. Siriwardane et al. [22] reported that confining pressures up to 50 MPa cause substantial permeability reduction, significantly extending CO₂ diffusion times.

Comparative studies reveal distinct kinetic behaviors between powdered and intact coal samples. Hol and Spiers [23] found powdered coal exhibits faster sorption kinetics due to greater surface area exposure, yet shows marked stress sensitivity-at 35 MPa, equilibrium attainment required 2–3 times longer than at 5 MPa. In contrast, intact samples displayed minimal kinetic variation due to their inherently limited pore connectivity [13].

Pone et al. [16] further quantified these effects, showing confined conditions cause significant decreases in CO₂ and CH₄ diffusion coefficients through macro- and mesopore compression. Their work revealed a dual-phase diffusion pattern: while CO₂ initially diffuses faster than CH₄, its steady-state diffusion rate becomes slower over extended periods, highlighting the competing influences of pore-filling dynamics and matrix swelling effects [16].

Anisotropic stress fields further complicate gas transport kinetics. Liu et al. [24] systematically characterized these directional effects through CH₄ diffusion experiments on cylindrical coal samples, revealing that diffusion perpendicular to bedding planes occurred 1.4 times faster than parallel diffusion under low-stress conditions. This anisotropy, however, progressively diminished at higher stress levels (>20 MPa) as stress-induced closure of transverse pores effectively homogenized the transport pathways.

1.3. Stress Effects on Adsorption-Induced Deformation

Gas-induced coal deformation exhibits stress-dependent behavior, where adsorption triggers swelling and desorption leads to shrinkage. Under unconfined conditions, CO₂ exposure typically produces volumetric expansions of 1–5% [25], or 1–3% as reported by van Bergen et al. [26]. However, applied stress substantially constrains these deformations. Harpalani and Mitra [27] demonstrated that lateral swelling could be completely suppressed when the effective stress reached approximately four times the CO₂ pressure.

The competition between adsorption-driven expansion and stress-induced compression was quantitatively characterized by Hol and Spiers [23]. Their results demonstrated that under hydrostatic CO₂ pressures up to 100 MPa, the net volumetric strain transitions from positive to negative at approximately 10–15 MPa CO₂ pressure. This stress-dependent behavior was further corroborated by Day et al. [28] who observed 30–40% reductions in swelling for Australian bituminous coal under 20 MPa confinement, attributed to stress-inhibited molecular rearrangement within the coal matrix.

Deformation anisotropy represents another critical aspect of coal’s mechanical response. Hol and Spiers [23] observed that swelling perpendicular to bedding planes exceeded parallel swelling by a factor of 1.4 in Brzeszcze coal, with this anisotropy being stress-amplified due to preferential closure of bedding-aligned cleats. Furthermore, permanent creep deformation observed in CO₂-saturated coal under cyclic loading [29] significantly impacts long-term reservoir integrity, as plastic strains progressively modify pore networks and sorption pathways [30].

1.4. Research Gaps and Objectives

Despite significant progress, fundamental discrepancies remain in the current understanding of how stress influences coal–gas interactions. Moreover, the combined effects of stress on gas adsorption capacity, adsorption kinetics, and coal deformation have not been systematically examined. This knowledge gap is further compounded by a critical methodological limitation: the prevalent use of powdered coal samples in sorption experiments fails to replicate in situ reservoirs’ heterogeneous pore structures and intact coal’s mechanical constraints [16]. This experimental gap highlights an urgent need for studies that employ confined, intact coal samples under reservoir-representative conditions, as such approaches are essential to resolving conflicting interpretations in existing literature.

This study aims to address these critical knowledge gaps by examining how stress affects three key areas: CO₂ adsorption capacity in confined coal, adsorption kinetics under variable stress, and the coupling mechanisms between gas adsorption and coal deformation. The findings are expected to improve reservoir models (which currently neglect stress-dependent adsorption effects and may thus overestimate storage capacities [15]), enhancing ECBM recovery predictability and the accuracy of reservoir performance/geological storage security assessments.

2. Experimental Methodology

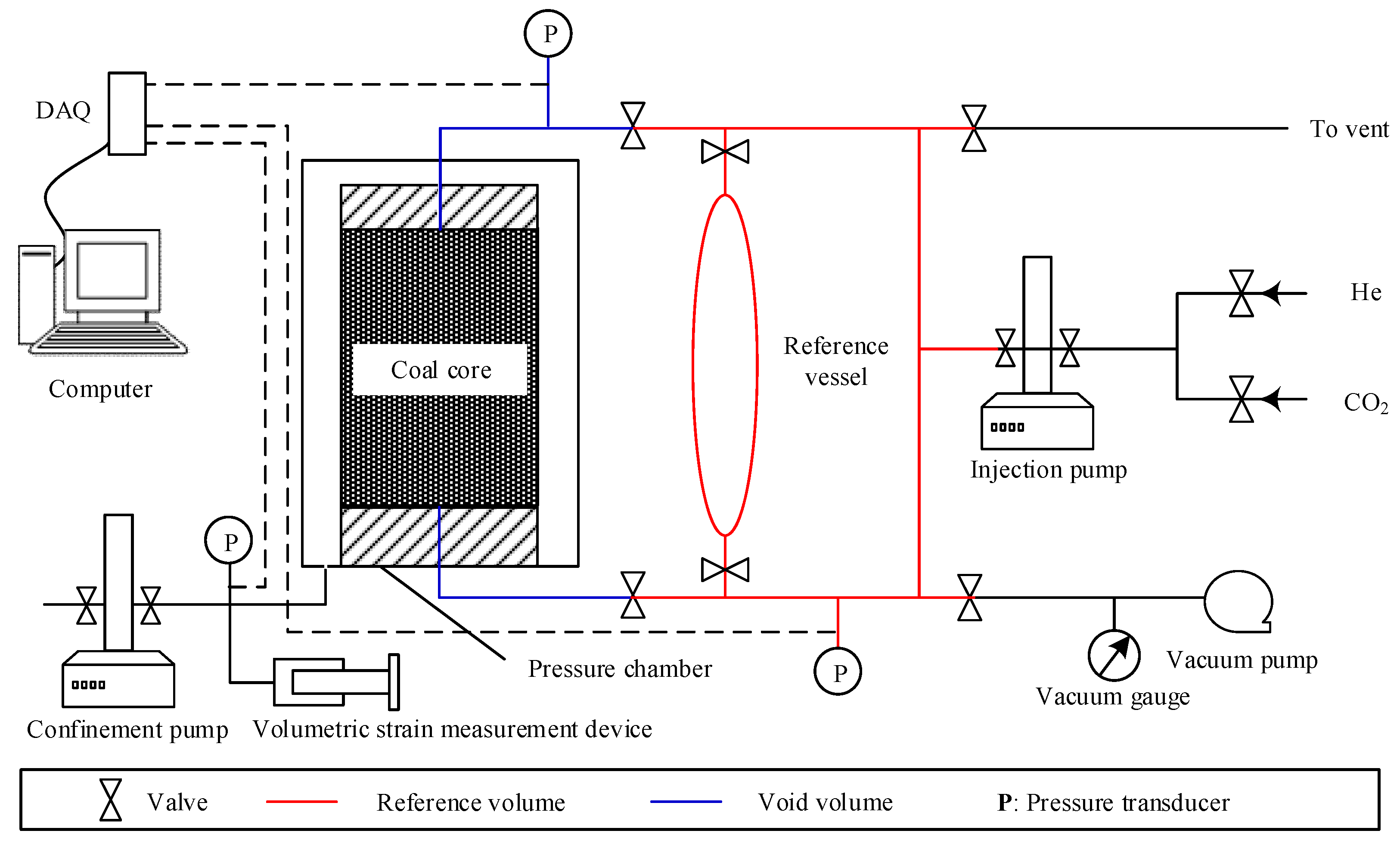
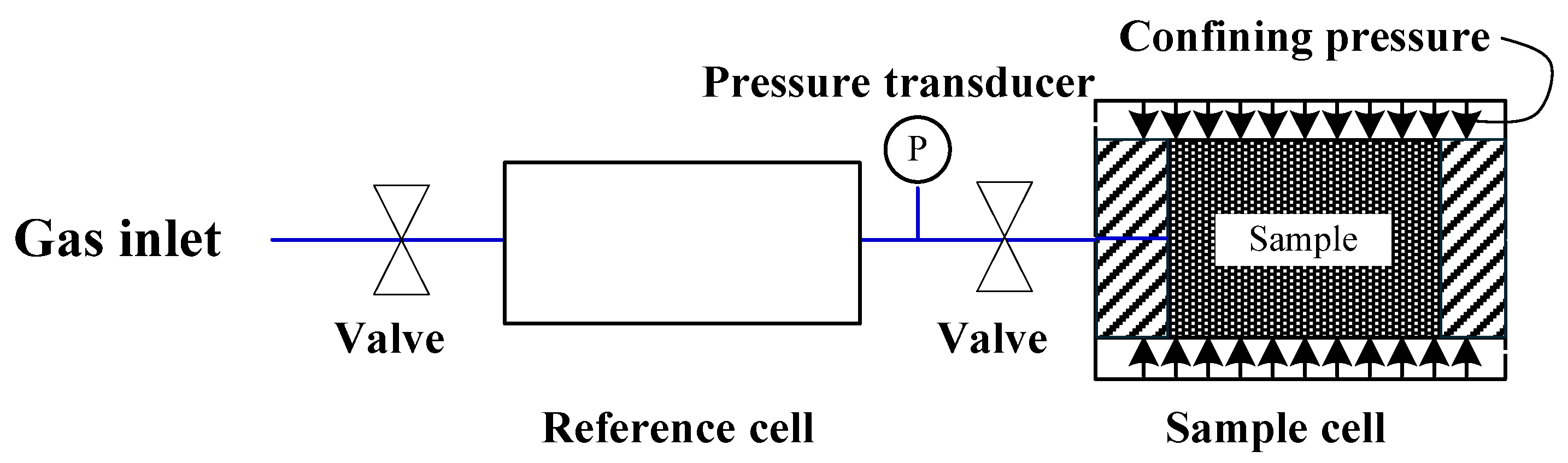
2.1. Experimental Apparatus

Figure 1 illustrates the schematic diagram of the experimental system developed for measuring coal adsorption, adsorption kinetics and sorption-induced swelling. This integrated system incorporates multiple functional components to achieve precise control and real-time monitoring of coal–gas interactions.

A pressure chamber serves as the core unit for measurements under diverse stress constraint conditions. It is connected to a reference vessel, which regulates the stable supply of gas to the coal sample. Additionally, a dedicated void volume section is integrated to compensate for dead volumes in the tubing and connecting joints, ensuring the accuracy of gas adsorption capacity measurements and enabling necessary post-measurement corrections. A confinement pump is employed to apply confining pressure to the coal core sample, which has nominal dimensions of approximately 25 mm in diameter and 50 mm in length. To prevent gas diffusion into the confining fluid under high-pressure conditions, the sample is first wrapped with a thin lead foil [31], then encased in a heat-shrinkable tube before installation into the pressure chamber. This lead foil barrier is critical: without it, CO₂ would permeate through the heat-shrinkable tube and dissolve into the confining fluid, leading to erroneous gas adsorption capacity calculations.

High-precision pressure transducers (marked as “P” in the diagram) are installed at multiple key locations to continuously monitor pressure variations in both the pressure chamber and reference volume throughout the experiment. A data acquisition (DAQ) system collects real-time readings from all sensors, and a computer processes these data to enable both real-time monitoring of experimental processes and subsequent offline analysis of the adsorption kinetics and adsorption capacity. Meanwhile, a volumetric strain measurement device is attached to the pressure chamber to quantify the sorption-induced swelling deformation of the coal core.

Prior to gas injection, a vacuum pump and a vacuum gauge are used to evacuate the entire system, ensuring a clean, gas-free initial environment that eliminates interference from residual gases. The system is supplied with He (for system volume calibration) and CO₂ (for adsorption experiments) through dedicated gas lines. An injection pump is used to deliver these gases into the system at a precise and controllable flow rate.

All components are connected using stainless steel tubing and manually operated valves to ensure hermetic sealing, thereby minimizing gas leakage and maintaining system integrity. To eliminate thermal fluctuations that could introduce errors into adsorption measurements, the pressure chamber, reference vessel, pressure transducers, valves, and connecting stainless steel tubing are fully submerged in a constant-temperature water bath (not illustrated in Figure 1). This ensures a stable temperature (±0.1 °C) is maintained throughout the experiment.

The experimental apparatus is designed to withstand a maximum pore pressure of 16.7 MPa and a maximum confining pressure of 25 MPa. The system operates within a temperature range from ambient to 100 °C, with a control accuracy of ±0.1 °C, and accommodates cylindrical coal samples measuring 25 mm in diameter and 50 mm in length. This configuration enables the measurement of adsorption isotherms, adsorption kinetic parameters, and corresponding swelling behavior of coal under a wide range of gas pressures, stress conditions, and precisely controlled temperatures, ultimately providing reliable, high-quality data for the systematic analysis of gas–coal interaction mechanisms.

2.2. Coal Sample Preparation

The coal blocks used in this study were sourced from coal seam #3 of the Shanxi Formation located in the southern Qinshui Basin, Shanxi Province, China. To prevent oxidization, the freshly collected coal samples were immediately wrapped in absorbent paper, vacuum-sealed in plastic bags, and stored at a constant temperature of 5 °C—this preservation protocol ensures the samples retain their in situ physicochemical properties prior to experimentation. These coal samples exhibit typical anthracite characteristics, with a key petrographic parameter: the mean maximum vitrinite reflectance (R_o,max) is 3.33%. Proximate analysis (on an air-dried basis) of the samples yields the following results: moisture content (M_ad) of 1.48%, ash yield (A_ad) of 13.12%, volatile matter (V_daf) of 6.32%, and fixed carbon (FC_ad) of 81.39%. Ultimate analysis (on a dry ash-free basis) reveals the elemental composition as follows: carbon content (C_daf) of 93.45%, hydrogen content (H_daf) of 2.15%, nitrogen content (N_daf) of 1.00%, and oxygen content (O_daf) of 2.98%.

The extraction and preparation of coal core samples presented considerable technical challenges due to the highly friable nature of the coal matrix. This friability often leads to sample fragmentation during machining processes, ultimately rendering the cores unusable. To address this issue, machining techniques were iteratively optimized to accommodate the coal’s inherent brittleness. Through this refinement process, a cylindrical coal core sample was successfully fabricated, with dimensions of 24.96 mm in diameter and 46.52 mm in length, and a mass of 34.14 g. This core sample was used as the experimental specimen for all subsequent tests in this study.

Moisture significantly influences the CO₂ sorption capacity of coal. To minimize its impact, the coal core was subjected to vacuum drying at 60 °C for 48 h before testing to remove residual moisture.

2.3. Experimental Conditions

High-purity CO₂ (purity > 99.99%) was used as the test gas in all experiments, and all measurements were performed at a constant temperature of 40 °C to eliminate thermal interference on adsorption and swelling behaviors.

To investigate the effect of pore gas pressure on the gas adsorption characteristics and sorption-induced swelling of coal, two discrete pore gas pressure levels were applied: 1 MPa and 2 MPa.

In terms of stress constraints, two distinct experimental conditions were designed to analyze the mechanical and sorptive responses of the coal sample, as detailed below:

(1)

Constraint 1 (Constant confining pressure): The confining pressure was maintained at a constant value throughout the experiment to simulate a stable external stress environment. This setup allowed the coal sample to undergo sorption-induced deformation without the need for external pressure adjustments. To achieve this condition, the target confining pressure was first applied to the sample using the confinement pump. Subsequently, the valve connecting the confinement pump and the pressure chamber was closed to isolate the system. During the entire adsorption test, the confining pressure was kept constant by fine-tuning the volumetric strain measurement device.

(2)

Constraint 2 (Constant volume): The total volume of the confining fluid (used to apply confining pressure) and the specimen was kept constant throughout the experiment. Under this condition, the volume of the confining fluid varies in response to gas sorption-induced deformation of the coal sample, which in turn alters the confining pressure. This setup ensures that variations in the experimental system are primarily driven by internal pressure fluctuations resulting from adsorption, rather than active regulation of the confining fluid volume. To establish this condition, the confining pressure was initially raised to the target value using the confinement pump. The valve between the confinement pump and the pressure chamber was then closed to disconnect the two systems. During the experiment, although adsorption-induced deformation of the coal sample resulted in fluctuations in confining pressure, the total volume of the confining fluid and the specimen was strictly maintained.

2.4. Experimental Procedure

All experiments were conducted using the apparatus described in Section 2.1, following the steps outlined below:

2.4.1. Sample Assembly

• Mount the prepared coal core sample into the pressure chamber. The internal structure of the pressure chamber is illustrated in Figure 2.

2.4.2. Confining Pressure Application

• Use the confinement pump to apply confining pressure to a present value—15 MPa was adopted in this study—to simulate the target external stress environment.

2.4.3. Vacuum Treatment

• Evacuate the entire experimental system (including the tubing network and the coal sample) using a vacuum pump for a period of 24 to 48 h. This step is critical to thoroughly remove residual moisture and air, eliminating their interference with subsequent gas sorption measurements.

2.4.4. Gas Injection

• Inject the high-purity test gas (CO₂) into the pre-calibrated reference vessel.
• Allow the gas to equilibrate thermally for a sufficient duration (several minutes). Thermal equilibrium is confirmed by the stabilization of pressure readings in the reference vessel.

2.4.5. Adsorption Initiation

• Open the valve connecting the reference vessel and the pressure chamber to establish gas communication between the two units, thereby initiating the gas adsorption process of the coal sample.

2.4.6. Pressure Monitoring & Equilibrium Determination

• Continuously monitor the pressures in both the reference vessel and the pressure chamber until they stabilize. A steady pressure in these components indicates that the coal sample has reached gas adsorption equilibrium.
• Analyze the gas adsorption capacity and adsorption kinetics of coal sample using the method detailed in Section 2.5 and Section 2.6.

2.4.7. Multi-Pressure Measurement

• Repeat Steps 2.4.4–2.4.6 with different preset pressures in the reference vessel. This iterative process enables the determination of coal adsorption capacities and adsorption kinetics under a series of distinct equilibrium pressures.

2.4.8. Sorption-Induced Swelling Measurement

• Under different stress conditions, the sorption-induced swelling deformation of the coal sample is measured using the method described in Section 2.7.

2.5. Adsorption Measurement Method

The gas adsorption capacity of coal samples was determined using a volumetric method based on Boyle’s law. As illustrated in Figure 3, the experimental setup for this method comprises two interconnected chambers—a reference cell and a sample cell—separated by a control valve.

The reference cell volume (V_r) was calibrated with high precision prior to experiments. The coal sample was placed in the sample cell (integrated with the pressure chamber described in Section 2.1). Meanwhile, the void volume (V_s)-which includes both the internal dead volume of the system (e.g., tubing and joints) and the pore volume of the coal sample-was determined through a series of helium (He) expansion tests, leveraging He’s inert nature (i.e., non-sorption on coal) to avoid interference with volume calibration. This void volume calibration procedure involves three key steps: (1) pressurizing the reference cell with high-purity helium to a preset pressure, (2) performing controlled helium expansion from the reference cell into the sample cell (with the coal sample installed), and (3) calculating the amount of helium molecules at each stage (pre- and post-expansion) using fundamental gas laws. The core calculation principle is expressed as follows:

$$n_{total}={\displaystyle \frac{P_1{V}_r}{Z_{1}R{T}_1}}$$

(1)

where V_r denotes the calibrated volume of the reference cell, P₁ represents the initial pressure of helium in the reference cell, Z₁ is the compressibility factor the initial pressure of helium in the reference cell, R is the universal gas constant (8.314 J·mol⁻¹·K⁻¹) and T₁ is the experimental temperature, which is maintained at 40 °C (313.15 K) by a thermostatically controlled water bath.

Once the pressure in the reference cell stabilizes, the valve separating the reference and sample cells is opened, allowing the gas to expand into the void volume (V_s) of the sample cell. Since helium is a non-adsorbing gas under these conditions, the observed pressure drop after expansion is solely attributed to the increase in available volume rather than gas adsorption. As a result, the total number of free gas molecules in the system remains unchanged, allowing the void volume of the sample cell to be calculated using the following equation:

$$V_s={\displaystyle \frac{n_{total}{Z}_{2}R{T}_2}{P_1}}-V_r$$

(2)

where P₂, Z₂ and T₂ represent the equilibrium pressure, compressibility factor, and temperature of the gas, respectively. All compressibility factors (Z₂) were calculated using NIST’s REFPROP software (NIST, version 2007), which implements highly accurate equations of state for the studied gases (helium and CO₂ in this study). This enables precise determination of Z₂ values at any given experimental pressure-temperature condition through thermodynamic property interpolation.

When an adsorbing gas is introduced from the reference cell into the sample chamber, the observed pressure reduction results from two concurrent mechanisms: (1) volumetric expansion of the gas into the void space of the sample cell, and (2) adsorption of the gas onto the solid surface of the coal sample. Since adsorbed gas molecules become bound to the substrate and no longer contribute to gas-phase pressure, the gas adsorption capacity of the coal sample can be quantified through the following relationship:

$$n_{ads}^{excess}=n_{total}-n_{free}$$

(3)

where n_total represents the theoretical total moles of gas initially contained in the reference cell (under the assumption of zero adsorption), and n_free denotes the experimentally determined moles of gas remaining in the free phase at equilibrium. The latter is calculated as follows:

$$n_{free}={\displaystyle \frac{P_2\left(V_r+V_s\right)}{R{T}_2{Z}_2}}$$

(4)

where V_r and V_s denote the calibrated volumes of the reference cell and sample cell, respectively. After completing the measurement at each equilibrium pressure, the experiment follows an iterative protocol: (1) closing the interconnecting valve, (2) repressurizing the reference cell to a higher target pressure, and (3) repeating the expansion-adsorption measurement. This cyclic process is repeated until a complete adsorption isotherm is obtained over the desired pressure range.

2.6. Sorption Kinetics Measurement Method

The measurement of sorption kinetics in coal is critical for understanding gas transport mechanisms, especially in key applications such as coalbed methane (CBM) recovery and CO₂ geological storage. For gases (e.g., CH₄ and CO₂) in coal, sorption kinetics are typically determined via a volumetric method. This method involves monitoring the pressure decay over time as gas adsorbs onto or desorbs from coal particles under carefully controlled experimental conditions [32].

In previous studies, numerous modeling approaches have been used to describe gas sorption kinetics in coal; among these, two primary models are most prominent: the unipore diffusion model and the bidisperse diffusion model. Despite the simplicity of its underlying assumptions, the unipore diffusion model often yields a reasonably accurate approximation of experimental sorption data. Thus, this study adopted the unipore approach to model the observed sorption kinetics.

The unipore diffusion model typically employs Fick’s second law of diffusion to describe sorption kinetics. For a spherical coal particle with constant surface concentration, the fractional gas uptake or release can be mathematically expressed as

$${\displaystyle \frac{M_t}{M_{\mathrm{\infty }}}}=1-{\displaystyle \frac{6}{{\pi }^2}}{\sum }_{n=1}^{\mathrm{\infty }}{\displaystyle \frac{1}{n^2}}exp\left(-{\displaystyle \frac{D{n}^2{\pi }^{2}t}{r_p^2}}\right)$$

(5)

where

• M_t: mass of gas sorbed at time t,
• M_∞: equilibrium sorbed mass,
• D: diffusion coefficient (units: cm²/s),
• r_p: particle radius (units: cm).

2.7. Swelling Measurement Method

Under constant confining pressure conditions, swelling measurements were performed using a confining fluid displacement (CFD) method, whose principle is illustrated in Figure 4. During the swelling process, the volumetric strain measurement device was continuously adjusted to maintain a constant confining pressure. The resulting displacement of confining fluid (ΔV_{confining fluid}), measured with high precision by the device, provides direct quantification of sample swelling through the following relationship:

ε_v = ΔV_{confining fluid}/V_sample

(6)

The measurement system provides a resolution of 0.1 μL. For standard core samples with dimensions of Φ25 mm × 50 mm (nominal volume = 24.5 mL), this resolution corresponds to a volumetric strain measurement accuracy of ±4 με (microstrain).

Under constant volume conditions, swelling measurements were carried out using the confining pressure response (CPR) method, which relies on the principle of internal “volume compensation” within the closed system. During the adsorption process, the confining pressure was allowed to vary freely in response to sample deformation, while the total volume of the confining fluid and the specimen remained strictly constant. The resulting change in confining pressure (∆σ_c), measured with high accuracy by a pressure transducer, was used to indirectly quantify the volumetric strain of the sample through the following pre-calibrated relationship:

$${ϵ}_v=-{\beta }_{sys}·{\displaystyle \frac{V_{system}}{V_{sample}}}·∆{\sigma }_c$$

(7)

where β_sys is the system compressibility, V_system is the initial total volume of the confining fluid and specimen, and V_sample is the initial volume of the sample.

The system compressibility (β_sys) represents the most critical parameter in this experimental setup. Prior to conducting tests, the entire closed pressure chamber system-either without a sample or containing a rigid metal block-must be calibrated. This is achieved by finely adjusting the confinement pump to inject or withdraw a micro-volume of fluid (∆V_pump) while simultaneously recording the corresponding change in confining pressure (∆σ_c). The system compressibility is then calculated using the following equation:

$${\beta }_{sys}=∆V_{pump}/\left(V_0·∆{\sigma }_c\right)$$

(8)

Here, V₀ represents the initial total volume of the system, defined as the sum of the confining fluid volume and the sample volume. The coefficient β_sys quantifies the volume of fluid that must be injected or withdrawn to change the system pressure by one unit and is expressed in units of Pa⁻¹ (or 1/Pa).

3. Results and Discussion

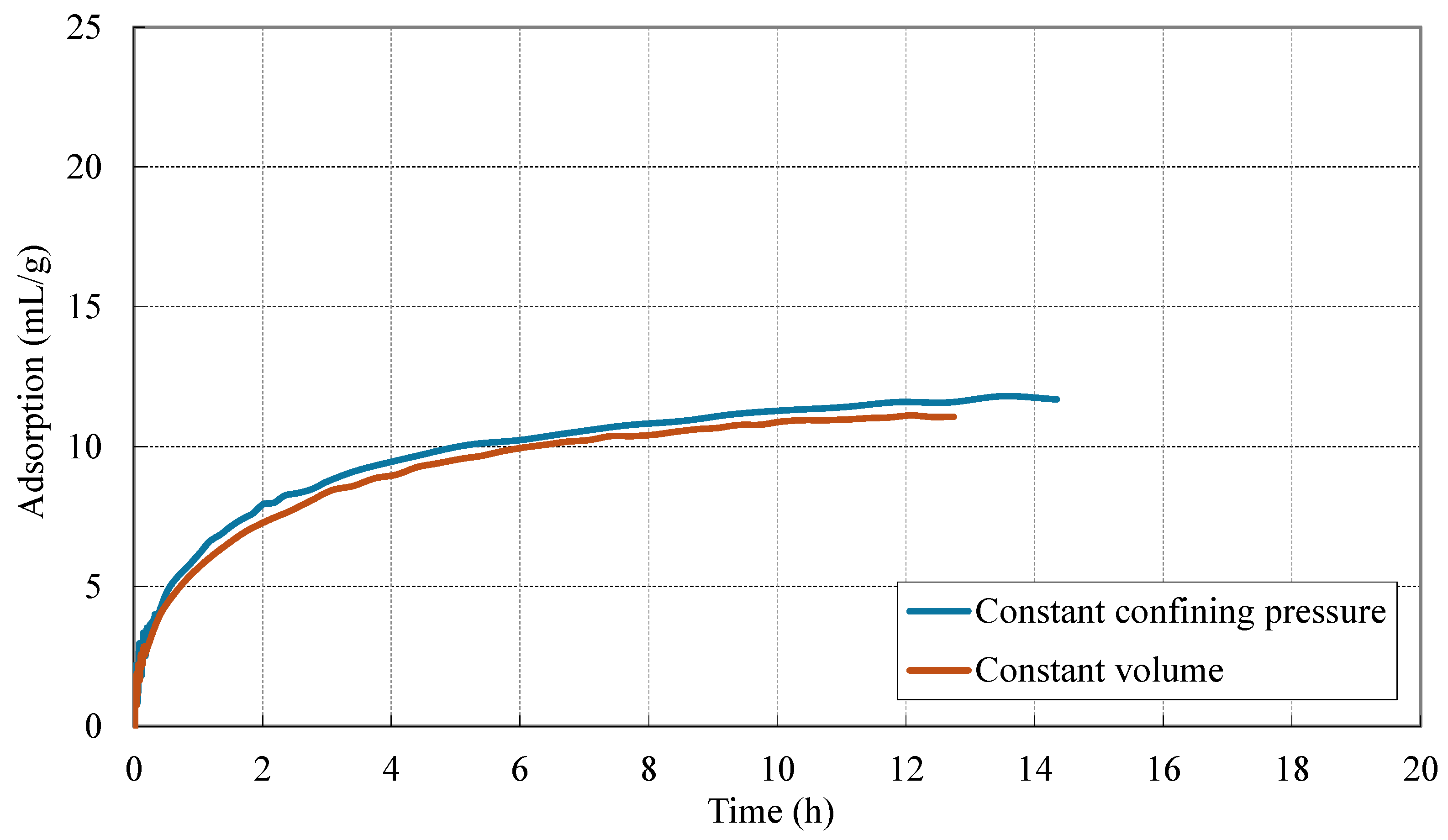
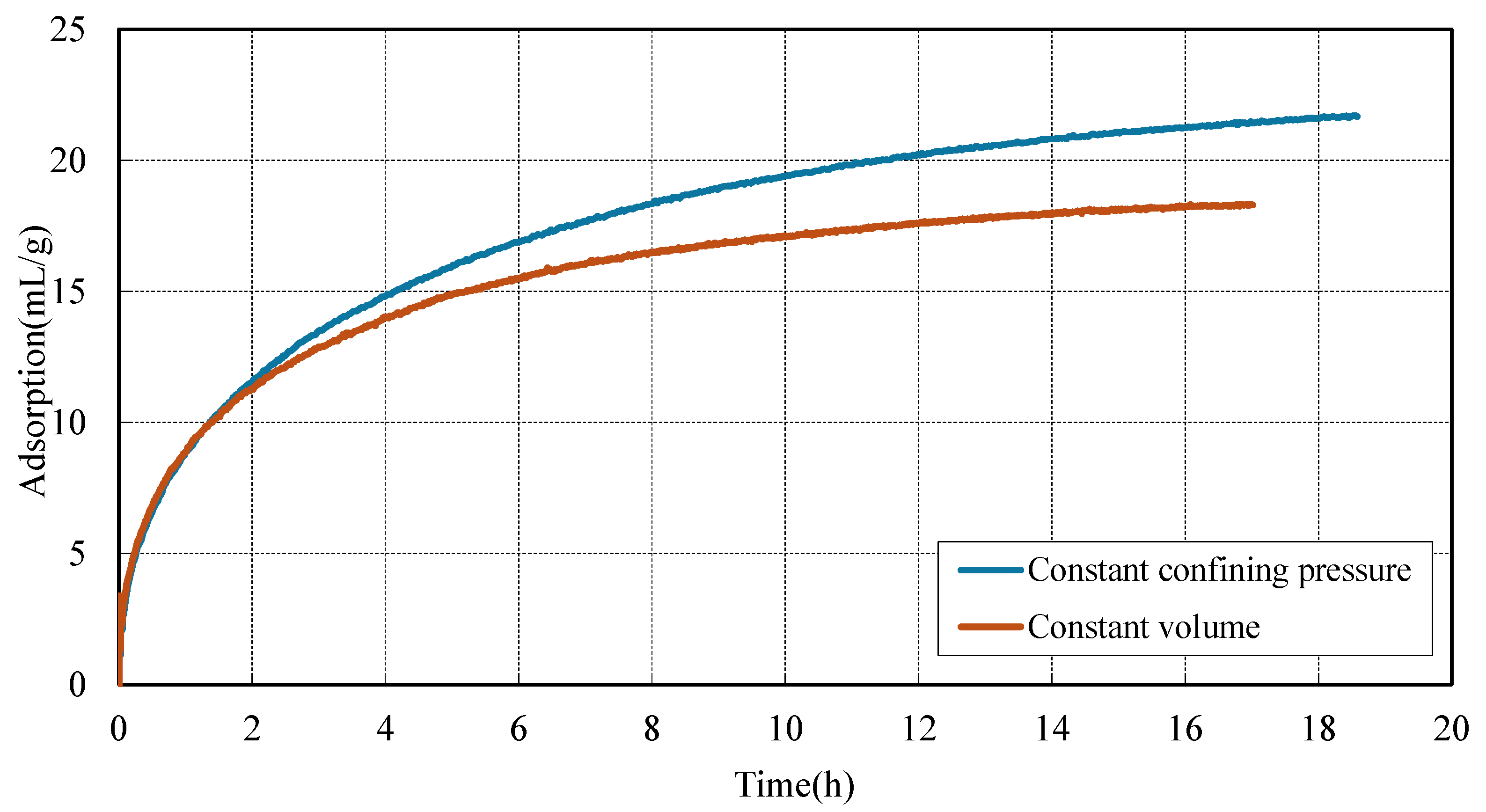
3.1. Adsorption Behavior of CO₂ in Coal Under Different Stress Constraint Conditions

To investigate how stress constraints affect CO₂ adsorption in coal, experiments were conducted under two distinct boundary conditions-constant confining pressure and constant volume-at CO₂ pressures of 1 MPa and 2 MPa, respectively. The adsorption process curves derived from these tests are presented in Figure 5 and Figure 6. Across both constraint scenarios, a consistent trend emerges: coal’s CO₂ adsorption capacity increases with time, eventually plateauing at a quasi-steady state. Regardless of the stress conditions applied, the adsorption process follows a similar trend: an initial rapid uptake, followed by a slower increase until stabilization. A notable distinction between the two constraint modes is that, at any equivalent time point, coal under constant confining pressure consistently exhibits higher adsorption capacity than when subjected to constant volume conditions.

As illustrated in Figure 6, for both constraint types, the total amount of CO₂ adsorbed at 2 MPa is substantially higher than that at 1 MPa (Figure 5). This difference can be attributed to the stronger mass transfer driving force generated by higher CO₂ pressure, which promotes the penetration and retention of CO₂ molecules within the coal matrix. This observation aligns with classical adsorption isotherm theory, which states that within a specific pressure range, gas adsorption on porous solids increases as pressure rises. Additionally, the initial adsorption rate at 2 MPa is significantly faster-likely a result of the steeper pressure gradient, which accelerates the early-stage diffusion of CO₂ molecules and the filling of pores in the coal.

The results further reveal that mechanical boundary conditions exert a profound influence on the adsorption process. Under constant confining pressure, coal is allowed to undergo volumetric swelling as it adsorbs CO₂. This controlled expansion not only accommodates the deformation of the coal matrix but also maintains the accessibility of pores, creating favorable conditions for continued CO₂ adsorption. In contrast, constant volume conditions physically restrict coal expansion. When CO₂ adsorption induces swelling, this restriction leads to a rapid buildup of internal stress within the coal. This accumulated stress inhibits further gas uptake, reducing both the ultimate adsorption capacity and the time required to reach quasi-equilibrium. As a result, compared to systems under constant confining pressure, constant volume systems exhibit lower CO₂ adsorption and enter the saturation phase at an earlier stage.

Table 1. Equilibrium CO₂ adsorption capacities under different stress constraints.

CO2 Pressure (MPa)	Constraint Type	Equilibrium Adsorption Capacity (mL/g)
1	Constant Confining Pressure	11.83
1	Constant Volume	11.13
2	Constant Confining Pressure	21.66
2	Constant Volume	18.29

summarizes the equilibrium adsorption capacities under different stress constraints and CO₂ pressures. Overall, both CO₂ pressure and mechanical constraint regimes play critical roles in shaping the CO₂ adsorption behavior of coal. Higher gas pressure enhances adsorption capacity and kinetics, while constant confining pressure conditions support greater gas uptake than constant volume scenarios by alleviating swelling-induced restrictions. These insights highlight the importance of integrating coal’s mechanical response with its adsorption performance when designing and optimizing carbon capture, utilization, and storage (CCUS) operations in confined coal reservoirs. To maximize storage efficiency, operational strategies must strike a balance injection pressure and the inherent geomechanical constraints of the coal formation.

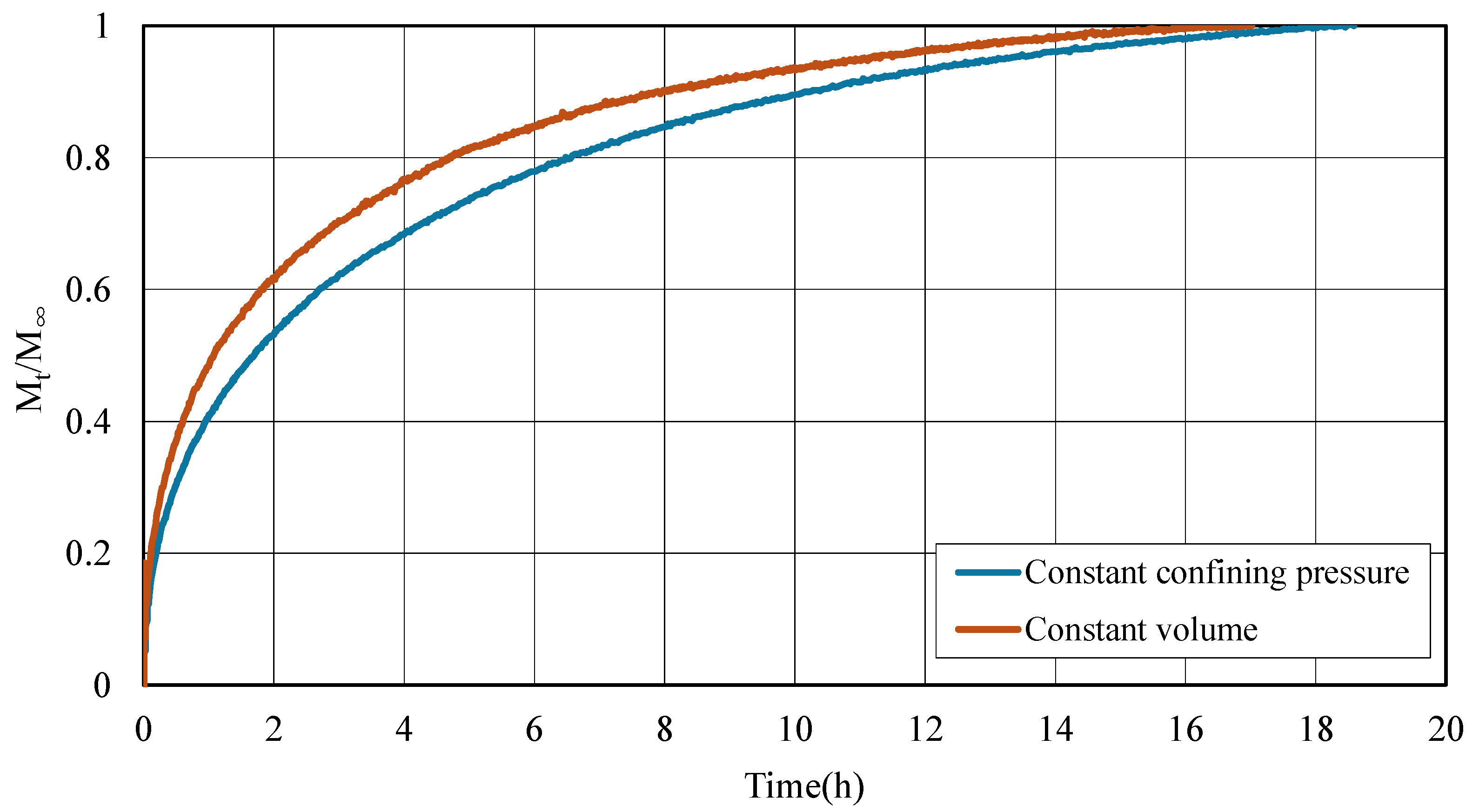
3.2. Adsorption Kinetics of CO₂ in Coal Under Different Stress Constraint Conditions

Figure 7 and Figure 8 showcase the CO₂ adsorption kinetic curves of coal under constant confining pressure and constant volume conditions, measured at CO₂ pressures of 1 MPa and 2 MPa, respectively. In both figures, the normalized adsorption quantity (denoted as M_t/M_∞) increases over time. Here, M_t represents the adsorption capacity at time t and M_∞ is the equilibrium adsorption capacity. The ratio gradually approaches 1, indicating that the coal is reaching adsorption equilibrium. The kinetic profiles under both constraints share a characteristic two-phase behavior: an initial stage of rapid adsorption, followed by a slower transition to quasi-equilibrium.

As illustrated in Figure 7, under both constraint conditions, 80% of the equilibrium CO₂ adsorption capacity at 1 MPa was attained within the first 4 h. When the CO₂ pressure was increased to 2 MPa (Figure 8), however, the time required to reach 80% of the equilibrium adsorption capacity differed significantly between the two constraint modes: it took approximately 5 h under constant volume conditions, in contrast to around 7 h under constant confining pressure. These results indicate a coupled influence of pressure and mechanical constraints on CO₂ adsorption kinetics. Under constant confining pressure, coal is permitted to swell as it adsorbs CO₂. This swelling can alter the coal’s pore structure, which may slow the initial adsorption rate. However, this volume adjustment supports a more sustained adsorption process in later stages by creating additional space available to accommodate further CO₂ uptake. In contrast, constant volume conditions limit the space available for adsorption-induced expansion. The initial rapid increase in M_t/M_∞ under constant volume is due to the quick occupation of the most accessible adsorption sites. As adsorption proceeds, coal swelling leads to a buildup of internal stress: while this stress may initially enhance the adsorption rate, it also causes the readily available sites to saturate more quickly. Consequently, compared to the initial rapid stage, the system approaches equilibrium at a slower pace in the later phase.

In summary, both CO₂ pressure and mechanical constraints significantly influence the adsorption kinetics of coal, albeit through distinct mechanisms. Higher pressure accelerates the overall adsorption process and improves the utilization of coal’s adsorption capacity. In contrast, stress constraints primarily affect the initial adsorption rate and the kinetics of equilibrium attainment, an effect that is more pronounced at higher pressures. These findings provide critical guidance for optimizing injection pressure and geomechanical management in CCUS projects, where a balance must be struck between achieving high initial sequestration rates and ensuring long-term storage integrity through appropriate constraint control.

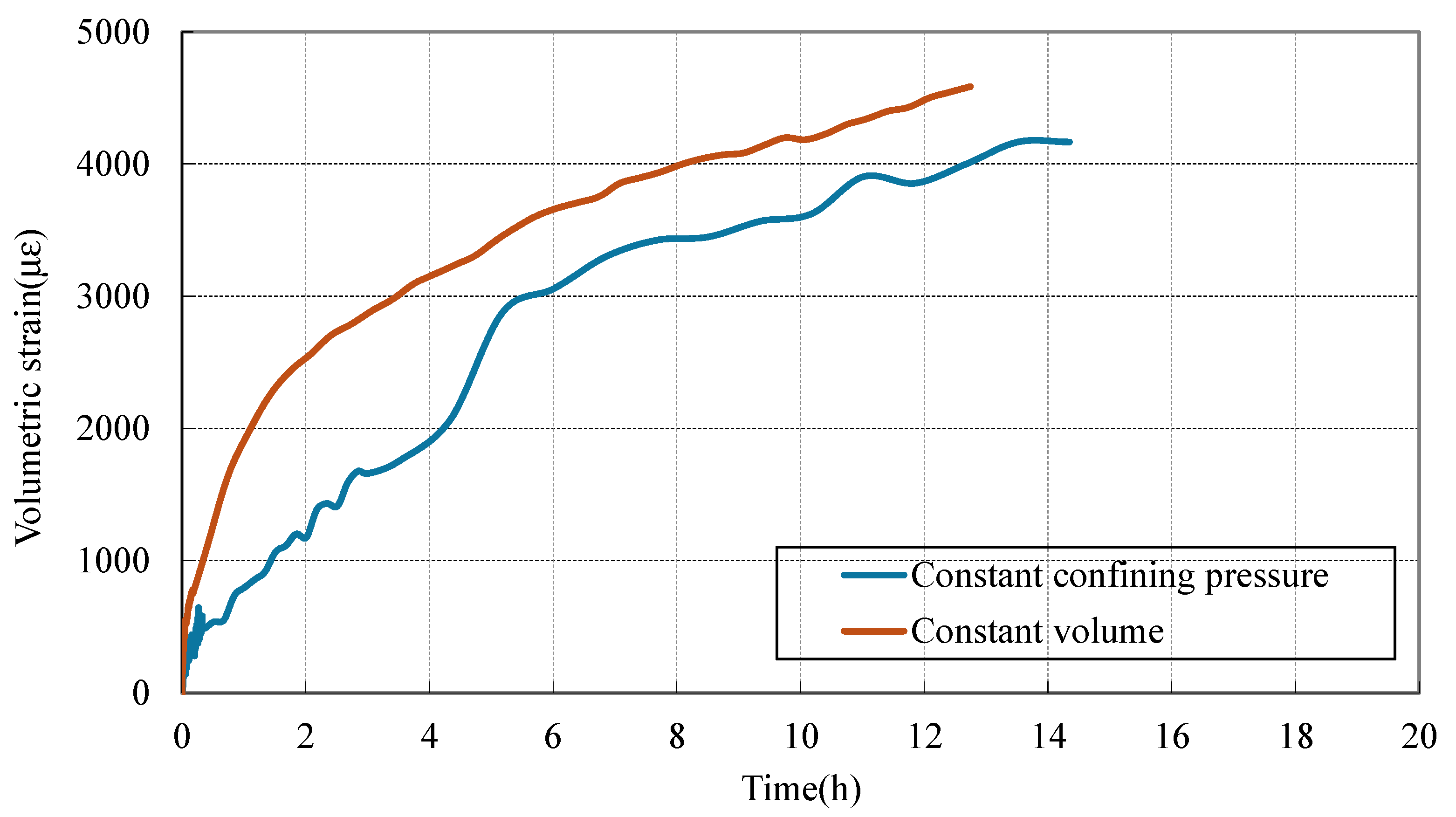
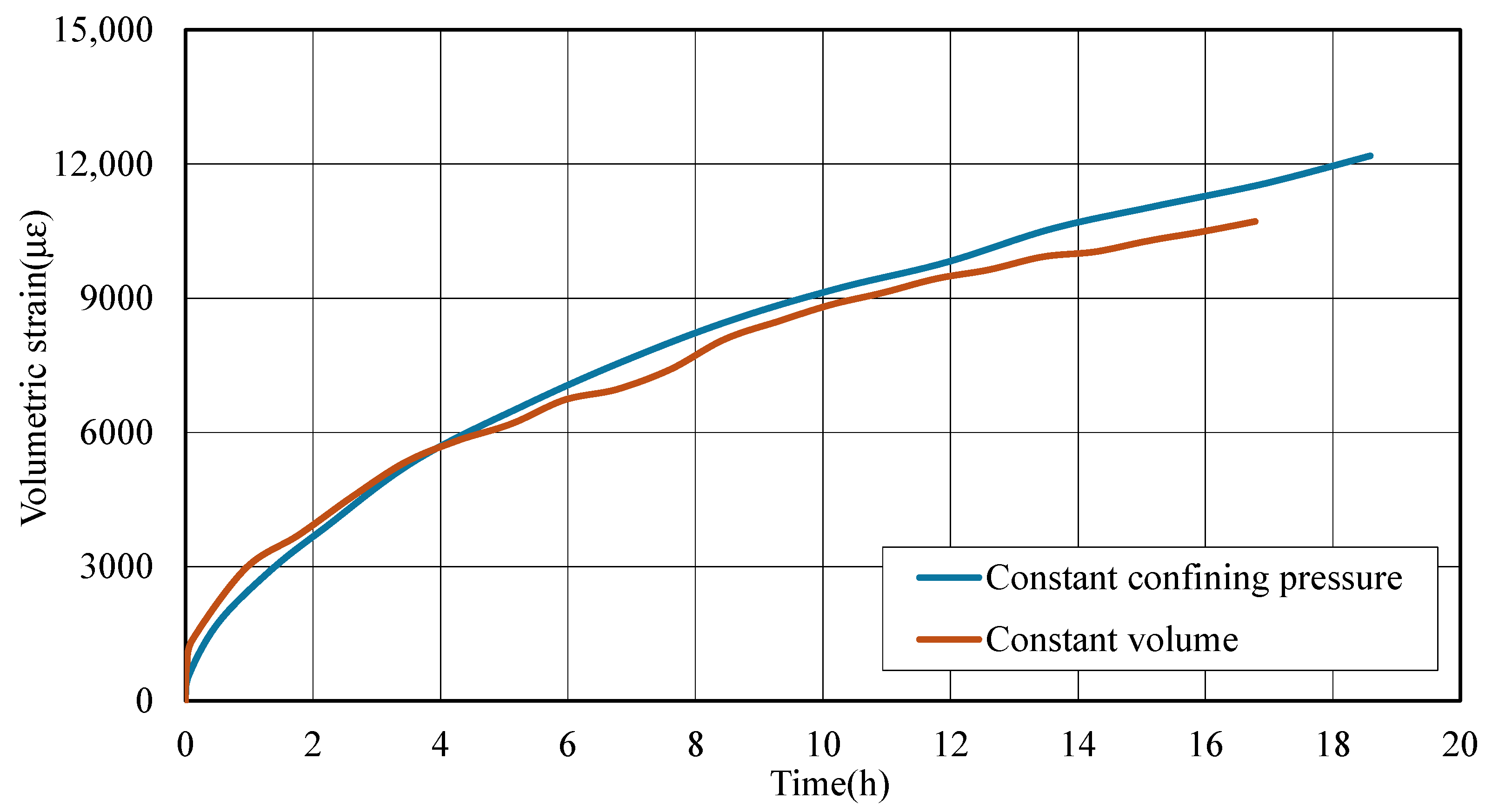
3.3. Deformation Behavior of Coal During CO₂ Adsorption Under Different Stress Constraint Conditions

Figure 9 and Figure 10 depict how coal strain evolves over time during CO₂ adsorption, measured under constant confining pressure and constant volume conditions at gas pressures of 1 MPa and 2 MPa, respectively. In both figures, strain accumulates progressively throughout the adsorption process, but the pattern of accumulation differs notably between the two constraint modes. Under constant volume conditions, strain rises sharply in the initial stage, after which it increases at a relatively steady rate. Under constant confining pressure, strain also builds over time, but its kinetic characteristics and final magnitude are distinctly different from those observed under constant volume. Specifically, at 1 MPa (Figure 9), the early-stage strain under constant volume is higher than that under constant confining pressure. At 2 MPa (Figure 10), however, the strain under constant confining pressure surpasses that under constant volume after a certain period of adsorption.

The impact of CO₂ pressure on strain development is clear: under both constraint conditions, the total strain generated at 2 MPa is substantially greater than that at 1 MPa. This observation aligns with fundamental adsorption principles. Specifically, higher CO₂ pressure enhances the amount of CO₂ adsorbed by the coal. This increased adsorption subsequently induces more significant swelling of the coal matrix. Based on poroelasticity theory, the increased internal pressure resulting from greater CO₂ adsorption further contributes to the development of larger strain. Additionally, the strain-time curve at 2 MPa exhibits a more continuous and stable growth pattern. This is due to the sustained driving force under higher pressure. This force facilitates continuous CO₂ penetration into the coal matrix. As a result, it promotes more uniform and progressive swelling deformation over time.

Mechanical boundary conditions play a pivotal role in moderating the coal’s deformation response. Under constant volume confinement, coal is prevented from expanding freely. As CO₂ adsorption triggers swelling, internal stress rises rapidly, leading to an immediate, sharp initial strain response. Although the fixed volume limits further expansion in later stages, continuous CO₂ adsorption still drives a gradual increase in strain. In contrast, under constant confining pressure, coal exhibits greater freedom for early-stage expansion compared to the constant volume scenarios. However, this expansion is still continuously restrained by the confining pressure. As adsorption progresses, strain evolution is governed by the balance between the swelling drive force from CO₂ adsorption and the mechanical constraint imposed by the confining pressure. At higher pressures (e.g., 2 MPa), the driving force for adsorption-induced swelling becomes more dominant than the confining restraint. This leads to greater overall strain, especially during the later stages of adsorption.

In summary, both CO₂ pressure and mechanical constraints significantly influence the evolution and ultimate magnitude of coal strain induced by CO₂ adsorption. Higher pressure enhances the overall strain, while the stress constraint conditions influence both the rate and extent of strain development in a complex, pressure-dependent manner. Under constant volume conditions, initial strain increases rapidly due to the swift buildup of internal stress. Under constant confining pressure, by contrast, strain develops more continuously. This is especially evident at higher CO₂ pressures, where adsorption-induced swelling dominates over mechanical constraint. These findings offer valuable insights for predicting deformation and ensuring stability in coal reservoirs targeted for CO₂ storage, as the interaction between gas pressure and in situ stress ultimately determines the formation’s geomechanical response.

4. Implications for CO₂ Geological Storage

The experimental findings from this study provide several important implications for the design and implementation of CO₂ geological storage in coal seams, as outlined below:

(1)

Injection Strategy Optimization: The observed improvements in CO₂ adsorption capacity under higher gas pressures suggest that moderate injection pressures can improve storage efficiency. However, the trade-off between increased adsorption and potential risk of fracture activation must be carefully evaluated to avoid compromising the integrity of the caprock.

(2)

Stress Constraint Management: The contrasting behaviors of coal under constant confining pressure (typical of stable, laterally unconfined reservoir regions) and constant volume (representative of rigid, low-permeability surrounding rock) highlight the critical influence of in situ stress states on CO₂ injectivity and storage stability. Conditions of constant confining pressure (e.g., in coal seams overlain by deformable shale) facilitate controlled coal swelling, promote sustained gas uptake, and are more favorable for maintaining long-term injectivity. In contrast, constant volume scenarios (e.g., coal seams confined by rigid sandstone or carbonate rock) lead to rapid internal stress buildup, which may cause premature saturation and a reduction in effective storage capacity. However, due to the inherent complexity and heterogeneity of real geological conditions, actual reservoirs often exhibit more complex and variable constraint behaviors than the simplified binary scenarios of constant confining pressure and constant volume. This complexity represents a critical aspect that requires greater consideration in future practical geological storage engineering.

(3)

Deformation and Stability Prediction: The strong positive correlation between CO₂ adsorption and coal strain, particularly under elevated pressure, highlights the necessity of incorporating poroelastic effects into reservoir models. Accurate prediction of adsorption-induced swelling and its consequences for permeability and fracture networks is crucial for evaluating reservoir stability and storage security. However, it is important to note that extrapolating lab-scale strain measurements to reservoir-scale predictions involves significant challenges and limitations. These include the effects of geological heterogeneity, differences in scale, and long-term creep behavior, which are difficult to fully capture in laboratory experiments. Heterogeneity at the field scale, such as variations in coal composition and the presence of natural fractures, may lead to non-uniform deformation and complex mechanical responses that differ from idealized laboratory conditions. Additionally, time-dependent effects such as creep and fatigue under sustained load and adsorption cycles could further alter deformation behavior over extended periods. To enhance predictive accuracy, it is essential to employ upscaled models that integrate geomechanical constraints with realistic reservoir architectures and temporal evolution.

(4)

Anisotropy and Heterogeneity Considerations: Although not explicitly addressed in this study, previous reports on stress-dependent anisotropy in coal swelling [23] and diffusion [24] indicate that site-specific structural features, such as bedding orientation and cleat geometry, should be integrated into large-scale storage simulations to improve predictive accuracy.

(5)

Long-Term Performance Monitoring: The persistence of strain and internal stress under constrained conditions emphasizes the need for continuous monitoring of geomechanical responses throughout both injection and post-injection phases. Techniques such as passive seismic monitoring and periodic strain mapping can aid in early detection of containment loss or structural deformation.

These implications confirm that successful CO₂ storage in coal reservoirs requires a coupled understanding of gas transport, adsorption thermodynamics, and geomechanical responses. Future efforts should focus on scaling up these experimental insights to field-level models and validating their performance under real reservoir conditions.

5. Conclusions

This study experimentally investigates the influence of stress constraints on CO₂ adsorption behaviors and sorption-induced swelling in intact anthracite coal cores. The key conclusions are as follows:

(1)

CO₂ pressure enhances sorption capacity. Under identical stress conditions, CO₂ adsorption capacity at 2 MPa is significantly higher than that at 1 MPa. This enhancement is attributed to the stronger mass transfer driving force provided by elevated pressure, which accelerates CO₂ diffusion into the coal matrix and promotes more efficient pore filling.

(2)

Stress constraints modulate adsorption behavior and kinetics. Under constant confining pressure, coal exhibits consistently higher adsorption capacities compared to constant volume conditions. This enhanced adsorption is attributed to the ability of the coal matrix to swell volumetrically, which helps preserve pore accessibility and promotes continuous gas uptake. In contrast, under constant volume constraints, the restriction on expansion leads to a rapid buildup of internal stress. This stress accumulation not only hinders further adsorption but also accelerates the approach to saturation. Consequently, although initial gas uptake occurs more rapidly under constant volume conditions, early saturation is reached due to the limited capacity for matrix expansion.

(3)

Sorption-induced swelling is pressure- and constraint-dependent. Driven by increased CO₂ adsorption, higher CO₂ pressure (2 MPa) results in greater total strain compared to 1 MPa. Under constant volume, initial strain rises sharply due to rapid stress accumulation, while constant confining pressure enables more continuous, progressive swelling—especially at higher pressures, where adsorption-driven expansion dominates over mechanical restraint.

These findings highlight the critical interplay between geomechanics and gas sorption in coal reservoirs. For practical applications, they emphasize the necessity of integrating stress-dependent sorption and deformation behaviors into reservoir models for CO₂-ECBM and geological storage. Such considerations will improve the accuracy of predictions for storage capacity, gas injectivity, and long-term reservoir integrity, ultimately supporting the safe and efficient deployment of carbon storage technologies in coal formations.

While this study provides valuable insights into the stress-dependent behavior of CO₂ adsorption and induced swelling in coal, several limitations should be acknowledged: (1) The experiments were conducted using a single intact anthracite core sample, which may limit the generalizability of the results to other coal ranks or formations with different petrophysical properties. Furthermore, the CO₂ pressure range applied (up to 2 MPa) was relatively low compared to actual reservoir conditions; experiments at higher pressures would better simulate in situ scenarios and help validate the observed trends. Future research should incorporate multiple coal samples of varying ranks and structural characteristics, extend experimental conditions to higher pressures and stresses, and investigate the effects of cyclic injection to evaluate long-term mechanical and sorption behavior. Integrating these findings into field-scale models will also be critical for predicting practical CO₂ storage performance. (2) Although the current study provides qualitative mechanistic interpretations based on poroelastic theory, a comprehensive quantitative theoretical framework that integrates adsorption thermodynamics, diffusion kinetics, and mechanical response under different boundary conditions is essential for predictive modeling. The development of such a model is the focus of our subsequent work.