Abstract
The reliability of public transport connectivity is influenced by factors such as route design, frequency, availability and infrastructure. Using a shortest path algorithm, we identify up to “k” space–time paths for each origin–destination pair (OD), considering schedules and maximum tolerable waiting times. We propose four reliability indicators and an approachability indicator to assess transport supply. These indicators are calculated at path, OD and network levels using two sets of equations. This framework enables fleet managers to evaluate and compare strategies to improve connectivity reliability and equity, such as increasing route frequency, optimizing lengths or expanding the network. Enhancing connectivity reliability encourages modal shifts to public transport, while improving approachability minimizes resource usage, contributing to sustainability. An application to the bus network of a city in Brittany, France, demonstrates the practical use of these indicators in evaluating and optimizing transport strategies.
1. Introduction
This work applies to all forms of public transport (bus, metro, trains, trams, etc.) as long as fixed timetables and lines are provided. It is also applicable in cases of interchanges between different modes, where connectivity reliability is particularly important for sustainable development [1]. For users, the reliability of public transport and the level of transport supply are essential. The condition of a fleet affects passenger comfort and various dimensions of reliability. This includes the age of the vehicles as well as the logistics of their maintenance.
Fleet managers evaluate various reliability factors and the level of transport supply. Numerous studies (Section 2, State of the Art) have analyzed many dimensions of reliability; generally, only the shortest path linking an origin to a destination is considered, even though all paths connecting origins to destinations contribute to overall reliability.
Our contribution (summarized in Section 3) involves characterizing the contribution to reliability of “k” paths for each origin–destination (OD) pair. These paths are identified, for every departure time, using a “k” shortest paths algorithm [2], which is implemented in space–time, taking into account timetables and a limit on the maximum tolerable waiting time (Appendix A). We provide fleet managers with a set of indicators (Section 4) that are useful for identifying the most disadvantaged origin–destination pairs and for comparing service improvement projects. The validation method is also provided. Appendix B and Appendix C include refinements and the calibration of the indicators.
In Section 5, equations detail the contribution of various paths to reliability and unreliability (defined here as one minus reliability). An application (Section 6) to the bus network of a city in Brittany demonstrates how to interpret and use these indicators. It also shows the impact of delays on connectivity indicators, while the impact of node closures is illustrated in Appendix D.
2. State of the Art
Wakabayashi and Iida defined reliability as ‘‘the probability of a device performing its purpose adequately for the period intended under the operating conditions encountered’’ [3]; applied to transport networks, it is, according to Nicholson, “the probability that a trip can be successfully finished within a specified time interval” [4]. Reliability is generally used to describe the stability, certainty and predictability of travel conditions [5,6].
Understanding the causes and consequences of unreliability, assessing reliability, possibly modeling it and proposing its enhancement are useful for developing networks and allocating capacity for the appraisal of transportation projects and for passenger route choice, as well as for diagnosing critical locations in transportation infrastructure.
In a public transportation network, the main causes of unreliability are, according to Mahdavi et al., failure in physical infrastructure or fleet service [7] and uncertainty in travel demand and travel time.
2.1. Failure in the Connection Between Origins and Destinations
Bell and Iida defined connectivity reliability as the probability of having a connection between a pair of nodes when one or more links are removed [8]. Similar definitions are proposed in [9,10,11]. Kim gave flow reliability and topological reliability indicators based on the supply at the OD level and the bus route level [12].
Wang et al. [13] studied the reliability of connectivity in the face of attacks on certain nodes or links in a network; they built a random attack model, simulating different scenarios in which network nodes are randomly attacked with a certain probability. This produces a score and rank for each network node. By assessing network connectivity and reliability, their model contributes to a better understanding of network vulnerabilities and helps formulate effective strategies to mitigate risk and improve network efficiency.
Vulnerability is perhaps more important than reliability outside major urban centers, where a network is sparse and accessibility should be the main consideration. This is why D’Este and Taylor [14] developed algorithmic and visualization tools to identify specific “weak points” of networks. Jenelius et al. [15] developed several link importance indices and site exposure indices, based on the increase in the generalized cost of travel when links are closed. These indices should guide road authorities in setting maintenance and repair priorities. Szymula et al. assessed vulnerability by finding the critical combination of links in a railway network; to remedy this vulnerability, they developed two heuristics (based on mixed-integer programming) for rerouting and rescheduling trains [16].
There is vulnerability in the level of service (LOS) when transport demand increases, leading to additional delays. It is not possible to recalculate the network equilibrium for all possible demand configurations [17]. However, Connors et al. [18], by introducing explicit functional relationships between demands and service levels, were able to run a stochastic user equilibrium (SUE) model to assess the influence of travel demand on the LOS.
Using real trip distribution, Rodriguez et al. [19] analyzed the consequences of disruptions of riding times or the number of missed trips for each network link in the event of an incident. Critical links appeared where line density was low and ridership was high. The result was a measure of the vulnerability of lines and stations.
Yap et al. [20] considered an integrated, total, multi-level public transport network. They incorporated, when identifying and quantifying link vulnerability, both exposure to non-recurrent disturbances and the impacts of these disturbances. The method quantifies the benefits of measures in terms of robustness, which is a support to the decision-making process of public transport operators and authorities regarding the implementation of robustness measures.
Ye and Taylor [21], for measuring and ranking the vulnerability of stations, developed a model that assesses the influence of nodes’ disruption on network flow patterns; an input of this model is an extended version of a single shortest path problem while considering passenger flows. The result should help decision-makers to decide which stations are the most important to protect during special events.
Cats and Jenelius established a vulnerability curve showing the relationship between network performance and the degradation of route or link capacities [22]. For a rail network, Liu [23,24] determined the economic value of reserve capacity and determined its impact for enhancing reliability and robustness; disturbances cause train delays as well as cancelations. Taylor and D’Este developed a method for diagnosing critical points in transportation infrastructure [25].
In road networks, if some edges or vertices of a graph representing a network are broken, dynamic graphs [26] are often used to update the shortest path from the initial shortest path, which takes less time than finding a new shortest path.
2.2. Uncertainty on Travel Time or Travel Demand
A trip may not be completed on time due to an increase in travel time. Travel time reliability is assessed by indicators based on travel time variability [27]; these indicators intervene in the overall reliability at (at least) three levels:
- As a component in project appraisal [28,29]. For an economic appraisal, it is necessary, according to Taylor, to estimate the value of travel time reliability [30]; Benezech and Coulombel estimated the value of the service interval and the value of service reliability [31].
- To suggest ways of enhancing overall reliability. Muñoz, after analyzing the sources of irregularity, proposed to regularize headways, thereby improving reliability [32]. Artan and Sahin developed a stochastic model, to be used in the timetable design phase, to prevent the impact of cumulative delays on reliability [33].
- To offer passengers the most reliable routes. Waiting-time reliability has an impact on the passenger route choice; this was evaluated by Shelat [34]. Khani developed a stochastic algorithm capable of proposing the most reliable route (in terms of time) [35]; in addition, backup itineraries were proposed by Redmond [36].
Excessive passenger demand may also prevent a trip from being completed on time. To reduce this negative effect, Liu optimized reserve capacity [23]. Many works, initially carried out for road networks, could be adapted to public transportation networks; Clark and Walting modeled network travel time reliability based on daily demand variability [37]. Chen [38] and Yang [39] defined capacity reliability as the probability that a network can meet a certain traffic demand at a required level of service, while taking into account drivers’ route choice behavior.
2.3. Reliability and Accessibility
According to Kim and Song, accessibility refers to the ease with which passengers can make their journeys between a network’s origin and destination stations [40].
Travel time reliability and accessibility are closely related concepts [25]; Bimpou and Ferguson integrated day-to-day travel time reliability into the measurement of accessibility [41].
Connectivity reliability and accessibility are also closely related. Kim and Song combined accessibility and topological reliability in a single indicator [42]. Taylor proposed an approachability index, equal to the ratio between the Euclidean distance between an origin and a destination and the actual length of the path connecting the origin and destination [43].
2.4. Reliability and Modal Choice
Another advantage of reliability indicators, such as those proposed here, is that they reflect the levels of the main factors describing the quality of the public transport offer. These factors are service frequency, proximity to the trip origin/destination, network coverage and the number of bus changes required, travel time and connectivity reliabilities. According to various socio-economic studies [1,44,45], the high quality of these factors improves modal choice for public transport, hence achieving sustainability.
2.5. Innovative Enhancements to Established Connectivity Approaches
The analysis in Section 2.1, “Failure in the Connection Between Origins and Destinations”, can be categorized into two primary areas: links and paths. The former focuses on identifying critical links, those whose failure causes the most significant disruptions and who thus require reinforcement. The latter adopts a dual perspective, identifying origin–destination (OD) pairs where service is critical due to either prohibitive user conditions or unreliable access.
We propose enhancing this dual approach, particularly for public transit networks, where the number of feasible paths connecting an origin to a destination is typically lower than in road networks. This allows us to examine all reasonable paths, those characterized by tolerable waiting times or distances from the origin to the nearest transit stop. Using a change the reference format s algorithm, without relying on a dynamic graph model, we can generate these paths. To the best of our knowledge, this methodology has not been explored extensively and offers several advantages, provided that the algorithm is implemented with proper time–space constraints and includes actual timetables for a given day.
- Providing useful paths for users and quantifying network flexibility: While the total number of paths per OD pair may not be inherently significant due to overlaps, any OD pair with zero paths directly signals a disconnection. The extent of overlaps is also quantified; in particular, we determine how many distinct paths the paths found correspond to, which is a measure of the network’s flexibility.
- Managing link failures and path quality: Disconnected paths or OD pairs become apparent when links fail. Additionally, paths that include excessive transfers or detours—quantified as the ratio of public transport mileage to the direct Euclidean distance—can be identified and eliminated.
Despite these strengths, our method does not fully address all aspects of connectivity reliability. Integrating it with established work on critical links and paths could significantly enhance its effectiveness.
2.5.1. Accounting for User Behavior
Socio-economic studies, such as those discussed in Section 2.4, indicate that users exhibit varied behaviors and tolerance thresholds regarding the distance to the nearest transit stop, expected waiting times and delays. For an OD pair to be considered connected for a particular user type, thresholds for these factors must not be exceeded. Therefore, our algorithm must be re-executed to accommodate different user profiles and their respective tolerance levels.
Furthermore, as delays are a significant concern, to take account of the user’s behavior, it is necessary to repeat the running of the algorithm for the different types of users, according to their thresholds.
As users are sensitive to unexpected delays, the delays measured by the work on travel time variability and reliability described in Section 2.2, “Uncertainty on Travel Time or Travel Demand”, should be input data for our algorithm. Delays reduce connectivity reliability because a path must be removed if its waiting time, combined with delays, exceeds a threshold or if connections are missed. Depending on the severity of delays, paths are either retained with no change to reliability or eliminated entirely, reducing the overall connectivity reliability. To capture the impact of delays, the algorithm must account for multiple delay scenarios.
2.5.2. Incorporating Demand and Capacity
An allocation method, such as those highlighted in Section 2.2, is essential for assessing whether the identified paths can accommodate passenger demand. When transit fleet capacity is insufficient, passengers face delays that may lead to path cancelations if waiting times exceed user tolerance levels. This can reduce both the number of connected OD pairs and overall connectivity reliability. Given the inherent uncertainty in travel demand, stochastic demand allocation methods should be prioritized.
2.5.3. Approachability Indicator
The approachability indicator, outlined in Section 2.3, serves as both an input and output in our model:
- Input: It helps exclude paths deemed unreasonable due to excessive lengths relative to Euclidean distances.
- Output: It is extended from path-level analysis to encompass OD pairs, nodes and the entire network.
In summary, our enhancements to established approaches integrate user behavior, delay scenarios and capacity constraints while maintaining a focus on generating realistic and effective paths. This comprehensive methodology advances the understanding and management of connectivity reliability in transit networks.
3. Research Contribution
Users recognize that the number of reasonable paths between an origin and a destination is very limited in a public transport network, unlike in road networks. We take this fact into account by developing, in line with Jaber et al. [46], a path algorithm capable of finding all reasonable paths and then deriving some theoretical and practical consequences to assist fleet managers in improving a service and passengers in using the service:
- Equivalence degree. When a path overlaps with the previous paths linking the same origin to the same destination, only part of the path, which we call the “equivalence degree” (between 0 and 1), needs to be taken into account in the reliability equation. Calculating this degree derives from the point-wise mutual information used in information theory. A factorization equation involving these degrees gives the contribution of each path to network reliability. The sum of these degrees for all paths connecting an origin–destination pair (or for the entire network) characterizes the flexibility of the public transport service concerning broken lines. Projects aimed at improving flexibility promote the use of public transport and support sustainable development.
- The reliability logarithm and uncertainty of a path. The absolute value of the reliability logarithm of a path is equal to the Shannon information of the event that “the path is functioning,” which measures its uncertainty [47]. This value is equal to the product of the failure rate and the path length, meaning that the path length represents risk exposure; the longer the path, the higher the uncertainty. This facilitates an intuitive understanding of path reliability.
- The reliability logarithm and reduced risk exposure of an origin–destination pair. The absolute value of the reliability logarithm of an origin–destination pair is equal to the Shannon information of the event that “the origin–destination pair is connected”. It is also equal to the product of the failure rate and the risk exposure. As the existence of alternative paths reduces uncertainty, risk exposure decreases and is therefore less than the length of the shortest path. We call this reduced exposure the “reduced length” of the origin–destination pair. This highlights the gain provided by alternative paths as a reduction in length.
- Approachability indicator. The “approachability indicator,” whose inverse was developed for a path by Taylor [43], is based on the ratio of distance traveled to distance as the crow flies. Here, it is generalized for all paths connecting the same origin–destination pair. This indicator identifies which origin–destination pairs should be prioritized for improvement.
4. Power Indicators of Reliability and Approachability
A path, φ(ω), effectively connects an OD, ω, when all its elements operate. Let us consider the case where all elements have the same operating probability, p. The elements of a path being disjoint, the events corresponding to the fact that an element operates, are independent. The reliability of the path φ, denoted by , is then the product of the probabilities of these events:
where N(φ(ω)) is the number of elements of the path φ(ω).
4.1. Explanation of the Power Model
The parameter p represents the probability that no unforeseen event will lead to trip cancelation. Different indicators are defined in Equations (6)–(12), with different values of p depending on whether the event concerns the availability of buses/drivers, stops or network links. Different event types may concern the same indicator; in this case, assuming independence between event types, p is modeled as the product of the probabilities of the event types. The parameter p must be carefully calibrated. For example, the types of events affecting bus/driver availability are breakdowns, damage, illness, strikes, etc. The parameter p also depends on the fleet structure and the existence of a vehicle reserve; the refining of the power model is presented in Appendix B.
4.2. Calibration of the Power Model
Appendix B provides information on how to estimate p, its variance and its confidence interval.
4.3. Validation of the Power Model
Validation of the power model should be threefold:
- Independence Assumption: The assumption of independence between the elements of the path (more precisely, between events affecting these elements) is not a given. Is the value of p calibrated with paths including a single element (where p1 is used) consistent with that for subsets of paths with two elements (where p2 is used) … or m elements (where pm is used)? In other words, when successively calibrating p with these subsets, are the different estimates of p inside the confidence interval?
- Randomness of Events: The model can be expected to be validated if the occurrence of events (breakdowns, etc.) is truly random and independent. However, we know that the frequency of certain events varies according to weather conditions and the time of year (road works are often scheduled during summer vacations), etc. Thus, the study period should be divided into classes combining the day type and weather conditions, and the model should be calibrated and validated for each class.
- Spatial Stability: The stability of p in space should be validated. When successively calibrating p across different parts of the same network, how do the estimates of p compare with the confidence interval?
- Temporal Stability: The stability of p through time should be validated. When successively calibrating p in different periods with the network, how do the different estimates of p compare with the confidence interval? (See Appendix B for the confidence intervals.)
4.4. Logarithm of the Power Model
Let us assume that the number of failures of an element is distributed according to a Poisson distribution with a parameter, λ (the failure rate); the probability of the event “zero failure” is e−λ, i.e., p = e−λ, or λ = −Log(p).
The reciprocal function of Equation (1) relates the number of elements to reliability:
The absolute value of the logarithm of the probability of an event, which measures its uncertainty, is known as its Shannon information [43]. According to Equation (2), the path φ(ω) has Shannon information equal to the product of its number of elements and the failure rate.
Let us consider the set (ai) of elements in the network. When the elements ai have different operating probabilities, p(ai), all strictly less than 1, let us consider the most reliable element, called a0, and define p such that p = p(a0). We can say that the reliability of any element, ai, is the same as that of ri independent elements (with ri ≥ 1) similar to a0, provided that
p(ai) = p ri—i.e.,: ri = Log(p(ai))/Log(p)
Thus, the element ai “counts” for ri elements. Equations (1) and (2) remain valid if we replace N(φ(ω)) by the following new count of elements:
In the following, for the sake of simplicity, we will continue to refer to N(φ(ω)) instead of the new count.
Let φ1(ω) be, among all paths linking ω, the shortest one (i.e., with the smallest number of elements); it is also the most reliable.
Let NCOD be the number of connected ODs in the network. We apply Equation (2) to the shortest path, φ1(ω), of each connected OD, ω. Taking the arithmetic average, we obtain as the first member of the new equation, , the arithmetic average of the numbers of elements, N(φ1(ω)), and in the second member, we obtain the arithmetic average of the logarithms of R(φ1(ω)). That is to say that the logarithm of the geometric average (denoted by ) of R(φ1(ω)) is as follows:
, in the first member, does not depend on p. Note that, in addition to , we need to count the unconnected ODs.
When an estimation of the traffic demand per OD is available, we replace in Equation (5) the coefficient 1/NCOD with the proportion of the demand of OD, ω; the result becomes the arithmetic mean (over travelers) of the numbers of elements of the shortest paths.
Different indicators are built according to whether we consider a path a set of buses, stops, links or kilometers. Let us note pbus, pstop, plink and plength, the probabilities that a bus, a stop, a link or “a kilometer” are operating. These probabilities replace the probability “p” used in Equations (1)–(5).
Five indicators are proposed for any path, φ:
- Bus Availability Reliability
This indicator is linked to the number of bus changes between the origin and destination. This indicator, combined with the shortest path algorithm, indicates origin–destinations that are disadvantaged or even prohibitive for users. This provides arguments for targeting certain priority origin–destinations in order to reduce the number of connections (by creating direct lines), a condition for reinforcing the modal shift towards public transport, a more sustainable mode of transport than the car.
- 2.
- Bus Stop Reliability
- 3.
- Link Reliability
- 4.
- Travel Length Reliability
For some types of failure, the average failure rate is constant by length unit, which implies an exponential distribution of failures. Then, the operating probability of the link ai of the length Li is linked to the failure rate of this link, denoted by λi, in the following equation:
As above, for sake of simplicity, we consider that the failure rate by unit length is the same for all links, i.e., λi = λ for whatever “i”. The corresponding operating probability per length unit is plength, such that
plength = e–λ i.e., Log(plength) = −λ
Let L(φ) be the length of the path φ. The travel length reliability for the path φ is as follows:
- 5.
- Standard-length Indicator of transport supply
The reliability of an OD pair obviously decreases as the Euclidean distance between an origin and destination increases. To focus on the quality of transport supply and compare ODs independently of their Euclidean distance, we propose an indicator for a path, φ(ω), equal to the ratio between the actual length of the path and the Euclidean distance of ω, exactly the inverse of the approachability index proposed by Michael Taylor [43]. The Euclidean distance is denoted by Dmin(ω); let us define Lstandard(ai, ω) as the standard length of the element ai for the OD ω, equal to the ratio Lstandard(ai)/Dmin(ω). Let us define the sinuosity of the path φ(ω) (denoted by Lstandard (φ(ω))) by the ratio L(φ(ω))/Dmin(ω). The sinuosity of the path would be minimal and equal to 1 for a perfectly straight path. An indicator, called the “standard-length indicator”, is defined by replacing, in Equation (11), the length with the standard length and the probability p with the value pstandard, to be specified later:
Let be the average, over all connected ODs, of the sinuosity L(φ1(ω))/Dmin(ω) of the first paths (the less sinuous and also the shortest) connecting the ODs. For improving the equity of transport supply, the bus fleet manager should improve the service for ODs (or nodes) where the standard-length indicator is low. This improves the service for the user and also saves resources (energy, pollution), which increases sustainability Note that our approach is only descriptive; it would be interesting to link it to works addressing optimal lines’ planning [48], where a « bus line overlap coefficient » is defined and computed.
Selecting the Value of pstandard
We propose two adjustments for pstandard (described in Appendix C) for two different purposes:
- -
- A low standard-length indicator may be due to topological constraints on the road network (sinuosity, one-way roads), poor bus line design (long, winding bus lines) or poor bus line supply (insufficient number of lines and line-to-line connections, insufficient service frequency). Comparing the value of this indicator to that of the bus reliability indicator (which is only sensitive to the third cause) can help discriminate the cause. To facilitate comparison between the two indicators, pstandard is adjusted so as to obtain, on average over the shortest paths, the same value for both indicators.
- -
- To enable comparisons between two service improvement projects, we can increase frequency and create a more direct route.
5. Contribution to the Reliability and Unreliability of a Path
An algorithm described in Appendix A provides, for a given departure time, up to k paths per OD pair, taking into account the timetables and a constraint on the maximum admissible waiting time.
5.1. Summary
- Using the inclusion/exclusion principle (Equation (13)), the reliability of an OD is computed from the reliability of the various paths linking it.
- The absolute logarithm of an OD’s reliability, divided by the failure rate, defines the “OD number of elements” as smaller than or equal to the number of elements of the shortest path linking the OD (Equation (14)).
- The absolute logarithm of the geometric mean of the ODs’ reliability (overall connected OD pairs) divided by the failure rate is the arithmetic mean of the “OD numbers of elements” (Equation (15)); it is smaller than or equal to the mean of the number of elements of the shortest paths, with the reduction in the number of elements giving the contribution of alternative paths to reliability.
- The contribution of alternative paths is also equivalent to a decrease in the failure rate.
- OD’s unreliability, defined here as “One minus reliability”, is expressed, using the chain rule in probability, as the product of the contributions of the paths linking the OD (Equations (19) and (26)); this reveals two characteristics of each path: its degrees of independence (Equation (21)) and of equivalence (Equation (23)). The sum of the equivalence degrees, over all paths linking an OD, quantifies the contribution of alternative paths to unreliability (Equation (27)); these sums per OD are used in Equation (28), which gives the unreliability logarithm for all connected ODs.
5.2. Equations of Reliability
Let M be the number of elements in a network and ai be an element. Let xi be such that xi = 1, with the probability p, when the element ai operates; otherwise, xi = 0, with the probability 1 − p. The state of the network is described by the vector {x1… xi …xM}. The number of such states is 2M; the set of such states is denoted as S. The event “path φj is operating” (or “is off”) corresponds to the subset Sj of S (or to its complement, ). The probability of Sj is the path reliability R(φj(ω)).
When k paths {φj(ω), j = 1, k} link an OD, ω, the reliability R(ω) is the probability that at least one path is operating; it is equal to the probability of the union of the subset Sj. Such a probability (without double counting) is given by an equation from de Moivre known as the inclusion–exclusion principle [49]:
Let us apply, like in Equation (2), the reciprocal function of reliability, i.e., the function Log(.)/Log(p), to R(ω); the result, denoted as N′(ω,p), defines the “OD number of elements” for the OD ω, which generalizes at the OD level the number of elements in a path:
N′(ω,p) = Log(R(ω))/Log(p) i.e.,: (−Log(R(ω)))= −Log(p). N′(ω,p) = λ.N′(ω,p)
From Equations (2) and (14), it follows that the reliability provided by the k paths is equal to that which would result from a single path with a number of elements, N′(ω,p). As R(ω) is greater than the reliability of the shortest path, R(φ1), and as the function (−Log(.) is decreasing, then N′(ω,p) is less than N(φ1).
With the length reliability indicator, N′(ω,plength) is called the “OD number of elements” of ω. According to Equation (14), the Shannon information of ω is the product of N′(ω,p) and failure rate (which is the information of an element).
Let Rgeometric(p) be the geometric mean (over all connected ODs) of the R(ω). Rgeometric(p) is necessary greater than .
In line with Equation (5), by applying Equation (14) for all connected ODs and then taking the arithmetic mean, we obtain the following:
where is the arithmetic mean of the N′(ω,p) and is the geometric mean of R(ω).
is smaller than because is greater than .
The contribution of alternative paths is equivalent to reducing the mean of the number of elements from to .
Equation (15) applies to all five indicators, replacing p with pbus, pstop, plink, plength and pstandard. Note that for the standard-length indicator, is the “average sinuosity” of the network; it indicates the level of the transport supply in the network and is used to compare different networks or different improvement levels in the same network.
In the case where only two paths connect ω, the equation giving N′(ω, p) is simple; we demonstrated (but the demonstration is not included here) that N′(ω, p) is a decreasing function of p.
In the case where all paths share a common part, the contribution of this part to N′(ω, p) remains equal to its number of elements; there is no reduction in these common elements. In the case of two paths, we demonstrated (the demonstration is not included here) that when p tends to 1, N′(ω, p) decreases to the number of elements of the common part, thus decreasing to zero when paths are disjoint.
These properties spread over to the arithmetic mean . Plotting on the same figure and ) embodies the contribution of alternative paths. Figure 1 displays the evolution of and according to p in the case of the travel length reliability (defined in Equation (11)). The “OD number of elements” is then the “OD length”; it was computed for the bus network of Rennes in Britanny (see Section 6).
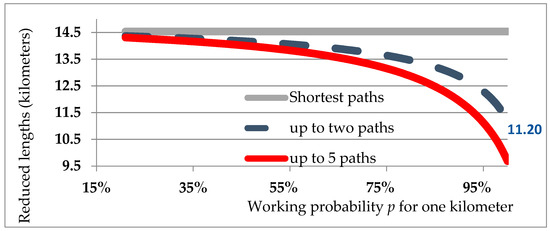
Figure 1.
Average “OD lengths” in the Rennes bus network according to the operating probability.
The arithmetic average of the shortest path lengths ( = 14.5 km) is displayed by the green horizontal straight line. , the average of the “lengths” of the OD pairs, is displayed by the blue dashed curve (up to two paths) or the red curve (up to five paths). In the case of “up to two paths”, when p tends to 1, ) tends to 11.2 km, which is the average length of overlaps; note that for ODs connected by a single path, the entire length of the path is counted as an overlap.
When p tends to zero, tends to (no reduction).
Remark 1.
It is also interesting to analyze reliability at the level of an individual node (or set of nodes). For a given node, let us define “node reliability” as the average (either geometric or arithmetic) of R(ω) for all ODs whose origin or destination is that node. Equations (5) and (15) generalize easily to the node level.
5.3. Interpretation of the Increase in Reliability Due to Alternative Paths
For a single OD, ω, the contribution of alternative paths is equivalent to an increase in the operating probability p up to the greater probability p′ or, equivalently, to a reduction in the failure rate from -Log(p) to –Log(p’). The equivalent operating probability p′ with which the reliability of the only shortest path φ1 would become R(ω) is such (after rewriting of Equation (2)) that
N(φ1) = Log’(R(ω))/Log(p′)
For the whole set of connected ODs, in line with Equation (5), the value p′ which convenes is such that
5.4. Equations of Unreliability
In this subsection, unreliability, i.e., the quantity “1-reliability”, is decomposed into a product of factors, each of which is related to the unreliability of a path. This decomposition shows the impact of any path.
The event “path j is off” corresponds to the set . An OD is disconnected when the first, second, … kth paths are simultaneously off; this corresponds to the set . The probability of this set is referred to as “unreliability”, denoted as V(ω), and is equal to 1 − R(ω).
Using the chain rule of probability that combines conditional probabilities [50], the unreliability of an OD is factored as follows:
The jth factor of the product is equal to = V(φj (ω)) only when the path φj(ω) is disjoint from all previous paths, since in this case the condition ”the previous paths do not operate” is independent of whether φj (ω) operates or not. Otherwise, . The full demonstration is not given here. Intuitively, the condition means that, whatever z (1 ≤ z ≤ j − 1), the path z does not operate; now, the more overlaps there are between the paths z and j, the more likely it is that the element of z that does not operate belongs to the path j, so there is an increase in the probability that the path j does not operate.
Let us write this jth factor as follows:
β(p,φj(ω)) is equal to 1 when the path φj(ω) is disjoint from all previous paths (independence) and is less than 1 otherwise. Recall that ).
In order to compare the contribution φj(ω) with that of φ1(ω), let us write the following:
The denominator of the equation of γ is related to (instead of for β). As the most reliable (and thus the least vulnerable) path has been put first,
γ(p, φj(ω)) ≤ β(p, φj(ω))
As the conditional probability is itself a probability distribution, the complement (with respect to the value 1) of this jth factor is . This last term corresponds to the increase in reliability for ω when moving from j-1 to j paths; it combines terms already calculated when applying the inclusion–exclusion principle (Equation (13))
Let us note α(p,(ω)) as the following ratio:
We can also write
In information theory, the logarithm in basis 2 of α(p, φ j(ω)) is known as the “pointwise mutual information” between the events: and Sj [51].
Let α(p, φ1(ω)) = β(p, φ1(ω)) = γ(p, φ1(ω)) = 1 (whatever p is). The new factorization of V(ω) is as follows:
α(p, φ j(ω)), β(p, φ j(ω)) and γ(p, φ j(ω)) are called the “independence coefficient”, “independence degree” and “equivalent degree”.
The inequality β(p,φ j(ω)) ≤ α(p,φ j(ω)) is obtained by studying Equation (26); β is an increasing function of α.
When the path φj is disjoint from the previous paths, the event Sj is independent of ; then, the condition “|Sj” of Equation (25) has no impact on , and then α(p, φ j(ω)) = 1.
Otherwise, the path φj(ω) has a common part with a previous path. α(p, φ j(ω)) and β(p, φ j(ω)) are smaller than 1; we demonstrated, in the case that j = 2 (but the demonstration is not included here), that they decrease when the overlap between φ j and the previous path increases. When the path φ j includes a previous path, φ j’, φ j does not contribute to unreliability (nor reliability). Indeed, in this case, and thus .
, implying that the jth factor of Equation (19) or Equation (26) equals 1; then, α(p, φ j(ω)) = β(p, φj(ω)) = 0.
In the case that j = 2, we demonstrated (the demonstration is not included here) that when p increases from 0 to 1, α and β decrease from 1 to the proportion in the path φ1 of the number of elements which do not belong to the path φ2.
By applying the logarithm function to both members of Equation (26) and replacing 1-R(φ1(ω)) with V(φ 1(ω)) and 1-R(φ j(ω)) with V(φ j(ω)), it follows that
The numbering of the paths 2…k has an impact on the factorization in Equations (24) and (25) and thus on the coefficients α, β and γ, which are therefore not unique; however, when the purpose is to evaluate the gain due to an additional path, this new path is in all cases the last one, so the coefficients α, β and γ for this last path are not disputable. Fortunately, the sum (from 1 to k) of the equivalence degrees, γ, does not depend on the numbering of the paths 2…k; indeed, according to Equation (27), this sum is the ratio Log(V(ω))/Log(V(φ1(ω))). This sum is necessarily less than (or equal to) k. It is as if there were, for ω, only Ʃj = 1…k γ(p, φ j(ω)) paths independent and equivalent to φ1.
The geometric mean of unreliability is obtained by multiplying the products of factors of Equation (26) for whatever ω (ω between 1 and NCOD) and then taking the NCOD root; its logarithm is obtained by the following equation:
The average (over connected ODs) of the sums (from 1 to k) of the equivalence degrees is the average of the ratio Log(V(ω))/Log(V(φ1(ω))). This average, always between 1 and k, characterizes the impact of alternative paths; it is close to 1 when there are few alternative paths or when these paths largely overlap or are much longer than the shortest path.
When the traffic demand per OD is known, unreliability is calculated per user; Equation (28) gives the arithmetic mean of the logarithms of unreliability per user, provided that the coefficient 1/NCOD is replaced by the proportion of the OD demand ω.
6. Results: Application for a City in Brittany
The Greater Rennes area in Brittany, France, includes 43 communes, served by 148 bus lines; there are 707 bus stops, 680 of which are taken into account here. Each bus stop is considered here both an origin and a destination, giving 680 × 679 ODs; the network is represented in Figure 2.
Figure 2.
Map of Greater Rennes area bus network (extracted from https://www.star.fr, accessed on 30 March 2022).
The algorithm searched for a maximum of k = 5 paths per OD. The criterion to be minimized was the number of connections between buses; the maximum waiting time allowed was one hour, and for a user departure time of 8:00, 90.6% of ODs were connected. This might seem low, but it is not unusual for some nodes not to be connected at certain times of day. Each connected OD pair was linked by an average of 2.48 paths; here, paths that were identical in space and simply shifted in time are eliminated (see Appendix A). Another run, made with k = 10, showed that, in general (for 97.2% of connected ODs), there were nine paths or fewer per connected OD.
6.1. Reliability Due to the Shortest Path and to Alternative Paths for Four Indicators
When several paths connected the same OD, the path ranked first (the shortest) depended on the indicator; for the link, bus, length or standard-length indicators, it was, respectively, the path with the fewest links, the fewest buses taken in succession, the shortest path in length or the least sinuous path.
Table 1 provides numerical values for reliability for 4 indicators. The parameter plength was arbitrarily set to 96%, which corresponded to the failure rate λ per kilometer equal to 0.383 (i.e., Log(0.96) = −0.383= −λ). With the length reliability indicator, the arithmetic mean of the reliability of the shortest paths was 0.581; to facilitate comparisons between indicators (see Appendix C, Equation (A17)), plink, pbus and pstandard were chosen to obtain the same average reliability. This occurred for plink = 97.1%; pbus = 80.3%; and pstandard = 70.8%. This does not imply that, after the inclusion of alternative paths, average reliabilities remained equal, because the gain in reliability due to alternative paths depended on the indicator chosen.

Table 1.
Reliability and standard indicators for four indicators (shortest paths and all paths) (no initial/final walks).
The average length of the shortest paths was 14.54 km; the average sinuosity for the less sinuous (shortest) paths per OD was 1.65 (see the heading “” above).
The average, over all connected ODs, of the average number of path elements for an OD was higher than the average for the shortest paths alone (heading ), with alternative paths having a higher number of elements than the shortest paths.
The improvement provided by the alternative paths was equivalent to a reduction in length from = 14.54 km (the average length of the shortest paths) to 10.91 km (, the average of “OD length”) and a reduction in sinuosity from = 1.65 (shortest paths) to = 1.22.
The overlaps between the 2.48 paths per connected OD led to an average sum of independence degrees between 1.43 and 1.53 (according to the indicator), as if there were between 1.43 and 1.53 independent (i.e., disjoint) paths per connected OD. The average sum of equivalence degrees was between 1.37 and 1.42, as if there were, on average per OD, between 1.37 and 1.42 paths independent and equivalent to the first (shortest) one.
6.2. Gain When Initial and/or Final Walks Were Allowed
Allowing initial or final walks (here, up to 400 m) increased the percentage of connected ODs (from 90.6% to 90.6% to 96.9%) and increased the number of paths per connected OD (from 2.48 to 3.92).The average, over all connected ODs, of the average number of path elements per OD was necessarily higher than the average of the “OD number of elements”; see Table 2.

Table 2.
The average of the average number of path elements per OD and average of the “OD numbers of elements” for 4 indicators (initial/final walks allowed).
6.3. Reliability Along Bus Line #9
The network is structured around nodes where many bus lines connect. Users entering the network at these nodes are favored in terms of the bus reliability indicator. Conversely, the closure of such a node has a major negative impact on both the number of connected ODs and the reliability of those still connected (this point is developed in Appendix D). A study of the evolution of reliability along a bus line (the 8.3 km-long line #9) shows how to understand and use the various indicators. The map of line #9 is provided in blue on Figure 3.
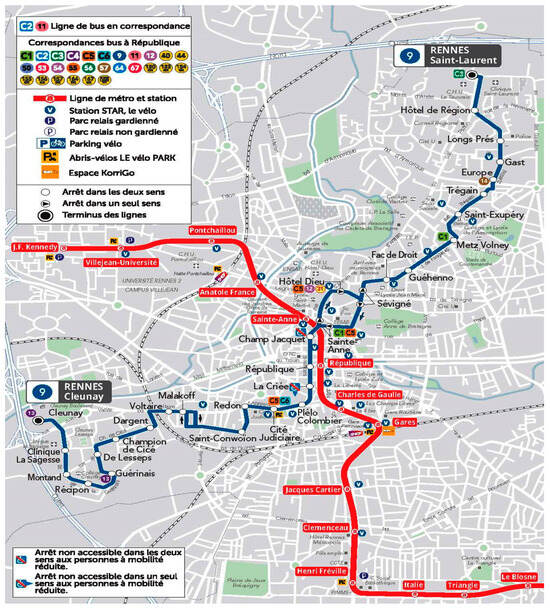
Figure 3.
Line #9 (in blue) in Rennes, from Cleunay to Saint-Laurent (extracted from https://www.star.fr, accessed on 30 March 2022).
The node reliability is the arithmetic average of the reliability of ODs that have this node as the origin or destination. The reliability of successive bus stops along bus line #9 is shown in Figure 4 for four reliability indicators.
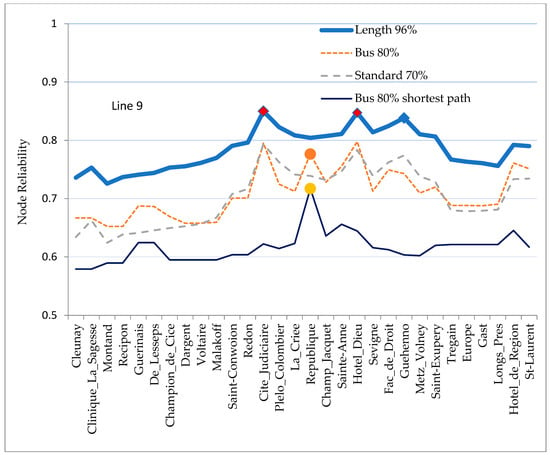
Figure 4.
Bus reliability, length reliability and standard-length indicator for nodes of line #9 (no initial/final walks; probability value p is adjusted for comparisons).
Some interesting dots, highlighted by colored circles or diamonds, are commented on below.
When a node (a bus stop) is served by a large number of lines, the shortest paths from this node to many destinations often consist of a single bus. These shortest paths have a single element for bus reliability, resulting in a high bus reliability indicator (shortest paths only). This is particularly evident at “République,” which is served by 19 bus lines. In contrast, the other bus stops on line #9 generally have a bus reliability indicator (shortest paths only) of just over 0.6, (at pbus = 80%), slightly higher than the average bus reliability (shortest paths only) for the whole network (0.581); this is due to the fact that the density of bus lines is higher in the city (where line #9 is located) than in the rest of Greater Rennes.
The increase in bus reliability between the curves for bus 80% shortest path and bus 80% all paths is due to alternative paths. The existence of alternative paths is favored when several lines serve a bus stop, implying several ways to reach it. For such nodes, the bus reliability indicator (all paths) is high. This is the case at “Cité Judiciaire” and “Hôtel Dieu”, served by five lines, as shown in Figure 3.
The standard-length indicator is close to the bus reliability indicator firstly because it has been calibrated to be equal to it, on average, over the network and secondly because, for an OD, a good (or bad) offer generally allows more direct (or less direct) paths, which results in a high (or low) standard-length indicator, as is the case for the bus reliability indicator. We note that at République the standard-length indicator is not as high as bus reliability, perhaps because the paths are not as direct, due to the presence of the river “La Vilaine” which imposes topological constraints on the road network
Length reliability is greater than 0.736, higher than that of the Rennes network (0.674). Indeed, as line #9 is more central than average, the paths to or from a node on this line are shorter than average. This is particularly true for nodes that are central to line #9.
6.4. Impact of Travel Delays on Connectivity Reliability
Delays reduce connectivity reliability, as seen in Section 2.5. Our approach was to characterize traffic conditions by a number of scenarios; for example, we divided traffic conditions into 100 scenarios. In one scenario, corresponding to a percentile, the travel time for each link was the corresponding percentile of the travel time; running the algorithm for this scenario would not provide the same percentile of connectivity reliability indicators but would give a good idea of what is happening to connectivity reliability for that traffic condition. Collecting the results for all scenarios gives an idea of the distribution of connectivity reliability in relation to the distribution of traffic conditions.
We illustrated this approach using a very simple example, with six scenarios. In one scenario, for each bus line, the traffic delay was either 0, 5, 25, 45, 55 or 57 min (for whatever the line and whatever the number of links traveled for this line in the path were). We considered a single origin (Cleunay, terminus of line 9) and all destinations (679). We used the “k” shortest paths algorithm with k = 10. The waiting time threshold (plus delay) was 60 min. Table 3 provides, for each scenario, the delay (in minutes), the number of ODs connected to Cleunay, the number of paths from Cleunay, the number of paths per OD connected and the bus connectivity reliability (with pbus = 80.3%).

Table 3.
Impact of delays on bus connectivity reliability at bus stop “Cleunay”.
7. Limitations and Future Work
This work has some limitations that can be addressed in future research.
- Regarding the shortest path algorithm: Certain paths should be eliminated when they include irrelevant detours, whose sole purpose is to circumvent the maximum waiting time constraint by replacing part of the waiting time with unnecessary travel time in these detours. This issue could be avoided by first calculating the shortest paths in space (without time constraints), as these paths have no detours, and then proposing the elimination of space–time paths that are significantly longer than the shortest paths.
- Incorporating travel delay scenarios: When travel delays make certain connections impossible or when delays exceed a certain threshold, connectivity reliability is discontinuously reduced, and certain OD pairs may become disconnected. Including delay scenarios (based on an analysis of travel time variability and reliability) as input data would make the approach more realistic.
- Integration with stochastic models: The approach would better address reliability issues if it were combined, after obtaining the paths between origin–destination pairs, with a stochastic assignment model that accounts for travel demand and its random nature. Under-capacity situations, for instance, can lead to delays that reduce connectivity reliability or even disconnect certain OD pairs.
- Network reliability metrics: The geometric average of OD reliability overemphasizes ODs with very low reliability, while the geometric average of OD unreliability overemphasizes ODs with very high reliability. This suggests that replacing geometric averages with arithmetic averages might be more appropriate.
- Addressing poorly connected ODs: The current approach does not explain why certain ODs are not connected at a given time. Additional tools, such as optimization tools mentioned in the state of the art, are required to propose potential solutions, such as increasing frequencies, creating a new line or extending an existing line.
8. Conclusions
In this paper, we investigated connectivity reliability in public transportation networks by analyzing the space–time paths connecting origins and destinations, based on real schedules and routes. With an algorithm that searches for reasonable paths, we identified up to ’k’ paths for each origin–destination pair (OD) in the space–time domain, that is to say virtually all reasonable paths. As there are different types of elements (buses, stops, links, …), there are different indicators. One of the indicators relates to the number of bus changes between an origin and destination. The number of bus changes highlights disadvantageous ODs, helping to prioritize improvements that reduce connections and promote a modal shift to public transport, thereby enhancing sustainability.
The reliability of a path is a power function of the reliability of its elements. When different types of events affect the reliability of a given type of element, the power function is extended to a product of power functions. The length of a path (i.e., its number of elements) appears equal to the opposite of the logarithm of the path reliability, divided by the failure rate (which is the opposite of the logarithm of the reliability of a path element).
The “OD number of elements” or “OD length”, a new concept, is defined as the opposite of the OD reliability logarithm divided by the failure rate. When several paths connect an OD, this is the length of the fictitious single path which, for the same reliability, would replace all the paths; the OD length is less than the length of the shortest path, the reduction in length characterizing the contribution of alternative paths. This extends to the average length over all connected ODs, provided that the geometric average is taken into account.
Additionally, we introduced the “degree of independence” and “degree of equivalence” to quantify path overlap. These provide deeper insights into network redundancy and robustness. For an OD, the sum of the degrees of equivalence, rather than the raw number of paths connecting it, reveals the flexibility of the service.
By iterating the calculations for each characteristic point of the travel time distribution, we can estimate the impact of this distribution on connectivity reliability.
The “standard length indicator” is based on the ratio {actual number of kilometers/Euclidean distance} of a path, i.e., its sinuosity (which is the inverse of approachability). For an OD, the more alternative paths there are in time or space, the higher the standard length indicator is and the less “OD sinuosity” there is. This new concept makes it possible to compare the equity of transport supply for different ODs, whatever their Euclidean length, or even to compare different networks. Service improvement projects can be compared based on their performance against this indicator. Fleet managers could define an expected quality of service per OD by a threshold for “OD sinuosity” and select the project that leads to the largest number of ODs below this threshold (or to the largest number of users concerned when the demand per OD is known). Within the standard length indicator, the bus fleet manager may improve the design of lines and the connections of origin–destinations (or nodes) where the indicator is low. This improves service for the user and saves resources (energy, pollution), thereby increasing sustainability.
Our approach offers actionable tools for optimizing transport networks, enhancing user experience and advancing sustainability. Future research could explore the impacts of dynamic travel conditions or extend the analysis to multimodal networks.
Our findings in the Greater Rennes area illustrate the potential of alternative paths to improve reliability: While the shortest paths had an average length of 14.54 km, the average OD length was reduced to 10.91 km, with sinuosity dropping from 1.65 to 1.22. This demonstrates the gains in connectivity reliability. On average, connected ODs had 2.48 paths, but the degree of equivalence reduced this to 1.42, highlighting areas for improvement.
Author Contributions
Conceptualization, N.B.; reliability indicators, T.C.; methodology, S.M.H.M. and N.B.; software, M.A.; link with probability and information theory, N.B. and S.M.H.M.; writing, N.B.; data collection, N.B.; data processing, M.A.; supervision, T.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are unavailable due to privacy.
Acknowledgments
The authors thank KEOLIS-Rennes for the data of the STAR network.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| α(p, φj(ω)) | The independence coefficient of the jth path φj of the OD ω for the probability p. |
| β(p, φ j(ω)) | The independence degree of the jth path φj of the OD pair ω for the probability p. |
| γ(p, φ j(ω)) | The equivalence degree of path φj relative to the shortest path φ1(ω). |
| λ | The failure rate per unit length (=−logarithm of the operating probability). |
| λi | The failure rate per unit length for the link ai. |
| φ j(ω) | The jth path connecting the origin–destination (OD) pair ω. |
| ω | An origin–destination pair. |
| The average number of links (over all ODs) of the shortest paths. | |
| ai | One element of the path φ. |
| The average number of successive buses (over all ODs) of the shortest paths. | |
| Dmin(ω) | Euclidean distance between the origin and destination of ω. |
| L(ai), L(φ) | The length of the element ai and length of the path φ. |
| Lstandard(ai, ω) | The length of element ai divided by the Euclidean distance Dmin(ω). |
| Lstandard (φ(ω)) | The length of the path φ(ω) divided by the Euclidean distance Dmin(ω). |
| L’(ω, φ) | The “length” of OD pair ω at the probability level p. |
| The average number of kilometers (over all ODs) for the shortest paths. | |
| M | The number of elements of the network. |
| N(φ) | The number of elements of the path φ. |
| N′(ω,p) | The “OD number” of elements for the OD ω. |
| The average number of elements (over all ODs) for the shortest paths. | |
| The average of “OD numbers” of elements (over all ODs) for the probability p. | |
| NCOD | The number of connected origin–destination pairs. |
| The average number of bus stops (over all ODs) for the shortest paths. | |
| p, p (ai) | The operating probability; the operating probability for the element ai. |
| pbus, pstop, plink | The operating probability for a bus, a bus stop or a link. |
| plength | The operating probability per unit of length. |
| pstandard | The chosen parameter for the standard indicator. |
| ri | The count for the element ai when its operating probability differs from p. |
| R(φ), R(ω) | Reliability for the path φ for an origin–destination pair, ω. |
| Rarithmetic (p) | The arithmetic mean of ODs’ reliability (over all connected ODs) for the probability p. |
| Rgeometric (p) | The geometric mean of ODs’ reliability (over all connected ODs) for the probability p. |
| The geometric mean (over all connected ODs) of the shortest path’s reliability. | |
| The arithmetic mean (over all connected ODs) of the shortest path’s reliability. | |
| Rbus, Rlink Rstop | Reliability indicators based on buses’, links’ or stops’ availability per path. |
| Rlength | A reliability indicator based on the length of a link. |
| Rstandard | An approachability indicator based on the path’s sinuosity. |
| Sets of network states such that the path φj is operating (or not). | |
| The average sinuosity (over all ODs) of the shortest paths. | |
| V(φ), V(ω) | The unreliability (i.e., one minus reliability) of the path φ or of the OD pair ω. |
| Vgeometric(p) | The geometric mean of unreliability (over all connected ODs) for the probability p. |
Appendix A. k Shortest Paths Algorithm in a Public Transportation Network
This algorithm is based on the Dijkstra algorithm [52] and provides the shortest paths from an origin to all destinations for a given departure time
Appendix A.1. Modelization of the Network
Origins and destinations are modeled by nodes in space; their coordinates (latitude, longitude) are given; and the departure time is required for the origin. Links are created between two bus stops or train stations when a bus (or a train) serves these stops in succession; their length is required. Other links (initial or final walks) are created between the origin of the pedestrian and each nearby bus stop or train station (whose Euclidean distance is less than a certain threshold) and between each bus stop or train station near the destination of the pedestrian and that destination; their cost is based on their length and duration (derived from their length).
In this document, the origins and destinations of pedestrians are placed at bus stops (or train stations).
Different nodes are created for each bus stop (or train station): First, there is the “entrance” (reached by an initial walk); its time is equal to the starting time plus the duration of the initial walk. Second, there is the “exit” (from which a final walk goes to the final destination); its time is computed by the algorithm. Two other types of node are created in {space × time}: “Departure platforms” are created, throughout the day, for each bus (or train) departing from this stop at the departure time. “Arrival platforms” are created for each bus (or train) arriving at this stop at the arrival time; however, if two (or more) buses (or trains) arrive at this stop at the same time, only one “arrival platform” is created.
From the entrance node, “get on bus” links are created to travel towards all «departure platforms» of the same bus stop (or train station); their cost is the cost of the time between the times of the two nodes.
From each departure platform, two links are created, depending on whether the passenger gets off at the next stop or continues on the line: The first one, named « travel and get off », arrives at an arrival platform at the next stop, where the user get off this bus (or train); its cost is based on its length and duration (including delay). The second link, named “travel” link, is created unless the next bus stop (or train station) is the terminus. It arrives at the «departure platform» at the next stop; the cost of the “travel” links is based on its length and scheduled duration.
All «arrival platforms» at a bus stop (or train station) are sorted by increasing time and are linked all throughout the day by «waiting links»; the cost of a waiting link is derived from the time difference between the two arrival times.
For each departure platform, the last previous arrival platform at the same stop which is compatible with getting on a bus (or train) is selected and «”change and get on bus”» links this arrival platform to the departure platform, with its cost being the cost of the connection plus the cost of the time difference between these two nodes.
An « exit » link is also created (with a cost equal to 0) between each arrival platform and the exit.
Also, a user starts from his origin; walks (eventually 0 m) to an entrance node; selects a «get on bus» link towards a departure platform; successively selects different travel links toward successive «departure platforms» of the same bus (or train); and selects a «travel and get off» link toward an arrival platform where they will then either exit (go to the exit node and take a final walk to their destination) or change bus (or train), possibly using one or several waiting links, before selecting a «change and get on bus» link towards a departure platform, etc.
Figure A1 provides the model of the network.
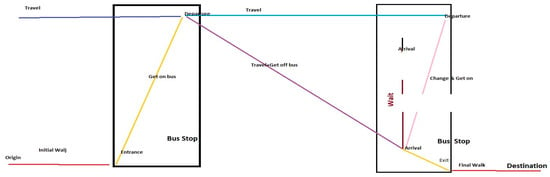
Figure A1.
Model of network.
Appendix A.2. The Steps of the Algorithm
To obtain the k shortest paths, we created k occurrences (i.e., duplicated k times) for most nodes and links. The label-setting used in the Dijsktra algorithm was modified accordingly, and a loop prevention module was added: “travel” links and ”travel and get off” links were discarded when their destination in space had already been reached earlier in the same path. When a bus reached an arrival platform, the “get on bus” link corresponding to the same bus line (opposite direction) was deleted.
Appendix A.3. Discarding Certain Paths
During the step-by-step creation by the algorithm of a path from an origin to a destination, at a certain time, the possibility of continuing the path by connecting to another bus line is subject to the following conditions:
- Only the first available bus (or train) on each line is considered. There is no point in waiting for taking the second bus (or train). This is obtained by discarding certain “get on bus” links.
- When two lines share a common trunk, a user does not alternate between the two lines. Alternation is avoided by rejecting the further creation of a path when a previously created path has the same stops and, globally, the same lines. This is obtained by discarding certain “get on bus” links. Note that this rejection implies rejecting paths that are identical in space but offset in time; these rejected paths can be easily reintroduced afterwards.
- The sum of waiting time and delays should be below a predefined threshold. This threshold applies either to the total waiting time (plus delays) since the origin of the path or to the local waiting time (plus local delays) at every bus stop. This second option was taken here in the numerical application. This constraint is satisfied by discarding appropriate “waiting” links.
- Note that a path including all lines of a previously created path with, in addition, other lines should be analyzed. The path can be useful in the event of the closure of one or more stops on one of the lines. Otherwise, it is either of the following:
- -
- A shortcut, if the “other line” taken allows a user to overtake and arrive earlier than the first path; this is especially the case when the first path created is a circular line. An unrealistic detour which is avoided by discarding, when arriving at an arrival platform, a “get on bus” link towards a departure platform corresponding to a bus line which has been taken in a previously created path with an earlier bus.
Appendix B. The Power Model: Refinement and Calibration
This appendix provides insights on the power model. It gives methods for estimating the parameter p and its variance. To be concrete, we deal here with the power model associated with the bus/driver reliability indicator; the method developed can be generalized to other indicators.
The problems addressed here are as follows:
- The fact that several types of events affect the indicator (unpredicted maintenance, …);
- The lack of homogeneity in the vehicle fleet;
- The existence of “reserves” for both buses and drivers.
The parameter p is the operating probability resulting from several types of events:
- Typically, the availability of a bus driven by its driver results from the availabilities of the vehicle (breakdowns, damage, degradations) and drivers (illnesses, strikes, assaults). These types of events are assumed to be independent. We address here the uncertain part of the availabilities; the operating probability p is not decreased, nor is the bus reliability, when events (and their consequences) are planned. Normal vehicle maintenance, if correctly planned, does not alter reliability; appropriate maintenance models were developed by Panic [53].
Let k be the number of unpredicted event types; pj (1 ≤ j ≤ k) is the probability that no type j event occurs. Let N be the number of scheduled trips (in a calibration set) and nj be the number of type j events leading to cancelation. Then, pj is estimated by
The variance of the estimation is (A2).
The distribution of the number of events is a binomial distribution, B(N,pj). A confidence interval around pj is estimated using the Gaussian approximation of the binomial distribution B(N,pj). This approximation is considered valid as soon as both nj and N − nj are greater than 5 (or, better, more than 10).
pj = nj/N
Assuming that the different types of event occur independently, the probability p that no event (whatever the type) occurs is estimated by the product of the probability pj:
The variance of this estimation is estimated by
The proof of this is in [54].
Appendix B.1. A Lack of Homogeneity in the Vehicle Fleet
Let r be the number of categories of vehicle types, Fi (1 ≤ i ≤ r) be the number of vehicles of type I and F be their sum (i.e., the size of the fleet). Let pi (1 ≤ i ≤ r) be the operating probability of vehicles of type i.
The probability that the first bus considered in a path is of type i is Fi/F. The operating probability, denoted by p(1), of the first bus considered in a path is the weighted average of probabilities
The variance of the estimate of p(1) is
pi and are estimated from Equations (A1) and (A2), where the number of events leading to cancelation and the number of scheduled trips are restricted to vehicles of type i.
Let us consider that, successively, m buses are taken in a path. Let us consider, for instance, that the first bus is of type i; the probability that the second bus is of type “i” is (Fi − 1)/(F − 1), whereas for j ≠ I, the probability that the second bus is of type j is Fj/(F − 1), etc. The probability that, in m choices, m1…mi…mr vehicles of the categories 1, …i …r are chosen (with = m) is
Such a configuration has an operating probability of
Thus, considering all configurations, m1…mi…mr with = m, the operating probability of the path is p(m) such that, for m choices,
The operating probability depends on the number of elements of the path, which makes the calculation more cumbersome.
Appendix B.2. Existence of “Reserves” for Buses (or for Drivers)
Let us consider that only F′ buses are necessary (F′ < F) which correspond to a reserve of F-F′ vehicles. We propose two methods for modifying p in order to take into account this reserve.
- (a)
- The reserve is open as soon as a vehicle is unavailable.
The probability that f vehicles are operating uses the binomial distribution B(F,p):
The probability that there are at least F′ operating vehicles is
When no reserve fleet is considered, the power model implies that the probability that all necessary vehicles (F′) are operating is pF′.
Using a power model with a reserve fleet should introduce a change from p, in p′ such that
As this sum is difficult to calculate, it is worthwhile to use the Gaussian approximation of the binomial distribution B(F,p), i.e.,
Let Г(.) be the cumulative distribution of the Gaussian distribution N(0,1). Then,
- (b)
- A reserve by vehicle.
The second possibility for the use of the reserve consists of considering that each “necessary” vehicle disposes of a part of the reserve equal to (F − F′)/F′; the probability that neither the vehicle nor the vehicles of its reserve operate is
Thus, the operating probability (including the recourse to the reserve) is
The lower and upper bounds of the confidence for p′ are estimated by replacing, in Equation (A14) or Equation (A16), the estimate of p, sometimes with the lower bound and sometimes with the upper bound of the confidence interval for p.
Appendix C. Adjustments of pstandard
Appendix C.1. Adjustment of pstandard for Easier Comparison Between Standard Indicator and Bus Reliability Indicator
pstandard is adjusted so as to equalize the geometric means (over all connected ODs, considering only one path, the most reliable per OD) of the two indicators. By applying Equation (1) to both indicators, it follows that pstandard must be the solution of
where and are the arithmetic means (calculated by considering only the shortest paths) of the number of buses to be taken per path and the sinuosity of the paths.
Appendix C.2. Adjustment of pstandard According to Payoff Between Sinuosity and Number of Independent Paths
Improving the service to an OD pair, ω, can be conducted by creating a new route, which is less sinuous, by increasing the frequency or the number of paths connecting ω. The first decision reduces users’ travel time; the last two reduce their waiting time. Equaling the impacts of these decisions on the standard indicator makes it possible to determine which increase in frequency or in the number of alternative paths is equivalent to reducing sinuosity.
The bus fleet manager might select pstandard such that the standard indicator of an OD-pair ω (connected by k independent paths, each of the sinuosity s) is equivalent to the one of the OD pair ω’ (connected by a single path of the sinuosity 1). Since independence allows the use of a multiplicative scheme for unreliability, pstandard must be such that
For a given number of (independent) paths, k, the function s(pstandard|k), which gives s with respect to pstandard, is obtained from Equation (A18) as
Figure A2 gives pstandard (on the X-axis) according to the sinuosity (on the Y-axis) for different values of k. For a higher sinuosity, a higher pstandard should be taken.
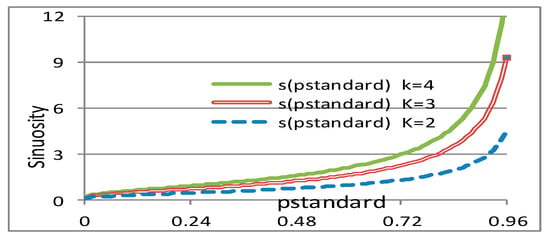
Figure A2.
Sinuosity according to the value of pstandard and of the number of independent paths.
Appendix D. Impact of Closing One Bus Stop on Network Reliability
“Closing” means here that each bus line passing by the closed bus stop is divided into two: one ends at the stop just before the closed bus stop; and the second begins at the first bus stop after the closed bus stop. Necessarily, some OD pairs are subtracted (those whose origin or destination is the closed bus stop). When there are C bus stops (and thus C origins and C destinations) in the network, the number of OD pairs is C ∗ (C − 1); when closing a bus stop, it decreases to (C − 1) ∗ (C − 2). The decrease is equal to 2 ∗ (C − 1), and the relative decrease is 2/C. The factor 2 is used because the closed bus stop is both the origin and the destination of (C − 1) OD pairs. The relative decrease is higher than 2/C when connecting possibilities decrease. For instance, let us consider the closing of the third bus stop of the line with no connecting possibility at the two first bus stops; these two first bus stops would be heavily impacted by the closing of the third one. In addition, other OD pairs are disconnected when the waiting time to use a complicated path that travels around the closed stop exceeds the maximum allowed. Let us define the “normalized” decrease as the relative decrease in the number of connected ODs divided by 2/C. This normalized decrease no longer depends on the network size; its absolute value is greater than 1.
We calculated the network reliability and the normalized decrease in connected ODs in eleven cases (each time closing a node on line #9) and plotted both curves on Figure A3. The decreases in reliability and in the normalized number of connected OD seem to be roughly proportional, sometimes drastically so when a very important node is closed.
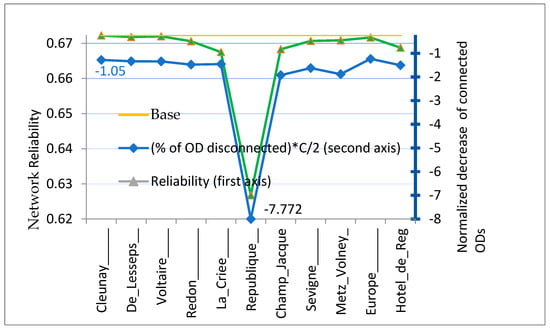
Figure A3.
Network reliability (length indicator at p = 96%) and normalized decrease in connected ODs for the closing of eleven bus stops on Line #9.
Here, no initial/final walk is considered. The normalized decrease varies (in absolute value) between 1.05 (when the terminus “Cleunay”, or many other stops, are closed) and 7.77 (when République is closed); this normalized decrease corresponds to a decrease in the percentage of connected ODs from 90.6% (République open) to 88.5% (République closed).
The network reliability is, here, the arithmetic average of the length reliability for still-connected ODs; with this calculation method, the closure of a secondary stop has practically no impact on the average reliability of the network. When République is closed, it decreases from 0.674 to 0.628; in addition, the average number of buses taken increases from 2.95 to 3.98.
Allowing initial or final walks (up to 400 m) makes it possible to bypass the closure of “République”; then, the percentage of connected ODs increases up to 96%.
References
- Yang, H.; Liang, Y. Examining the Connectivity between Urban Rail Transport and Regular Bus Transport. Sustainability 2023, 15, 7644. [Google Scholar] [CrossRef]
- Sakarovitch, M. The k shortest chains in a graph. Transp. Res. 1968, 2, 1–11. [Google Scholar] [CrossRef]
- Wakabayashi, H.; Iida, Y. Upper and lower bounds of terminal reliability of road networks: An efficient method with Boolean algebra. J. Nat. Disaster Sci. 1992, 14, 29–44. [Google Scholar]
- Nicholson, A. Assessing Transport Reliability: Malevolence and User Knowledge. In Proceedings of the 1st International Symposium on Transportation Network Reliability (INSTR); Emerald Group Publishing Limited: Bingley, UK, 2003. [Google Scholar] [CrossRef]
- Mattsson, L.-G.; Jenelius, E. Vulnerability and resilience of transport systems: A discussion of recent research. Transp. Res. Part A Policy Pract. 2015, 81, 16–34. [Google Scholar] [CrossRef]
- Mahdavi-Moghaddam, S.M.H.; Bhouri, N. A synthetic indicator for structuring resilient public transport operation. In Sustainable and Resilient Infrastructure; Taylor and Francis Ltd.: Abingdon, UK, 2024; pp. 1–27. [Google Scholar] [CrossRef]
- Mahdavi-Moghaddam, S.M.H.; Bhouri, N.; Scemama, G. Dynamic Resilience of Public Transport Network: A Case Study for Fleet-Failure in Bus Transport Operation of New Delhi. Transp. Res. Procedia 2020, 47, 672–679. [Google Scholar] [CrossRef]
- Bell, M.G.H.; Iida, Y. Transportation Network Analysis; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1997. [Google Scholar] [CrossRef]
- Liu, J.; Peng, Q.; Chen, J.; Yin, Y. Connectivity reliability on an urban rail transit network from the perspective of passenger travel. Urban. Rail Transit. 2020, 6, 1–14. [Google Scholar] [CrossRef]
- Soltani-Sobh, A.; Heaslip, K.; Stevanovi, A.; Khoury, J.E.; Song, Z. Evaluation of transportation network reliability during unexpected events with multiple uncertainties. Int. J. Disaster Risk Reduct. 2016, 17, 128–136. [Google Scholar] [CrossRef]
- Oliveira, E.L.; Portugal, L.-D.-S.; Porto, W., Jr. Indicators of reliability and vulnerability: Similarities and differences in ranking links of a complex road system. Transp. Res. Part A Policy Pract. 2016, 88, 195–208. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C.; Chun, Y. Network Reliability and Resilience of Rapid Transit Systems. Prof. Geogr. 2016, 68, 53–65. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Feng, Y.; Cao, Y.; Guo, Z.; Liu, Z. Assessing the Connectivity Reliability of a Maritime Transport Network: A Case of Imported Crude Oil in China. J. Mar. Sci. Eng. 2023, 11, 1597. [Google Scholar] [CrossRef]
- D’Este, G.M.; Taylor, M.A.P. Network vulnerability: An approach to reliability analysis at the level of national strategic transport networks. In The Network Reliability of Transport; Bell, M.G.H., Iida, Y., Eds.; Emerald: Bingley, UK, 2003; pp. 23–44. [Google Scholar]
- Jenelius, E.; Petersen, T.; Mattsson, L.-G. Importance and exposure in road network vulnerability analysis. Transp. Res. Part A 2006, 40, 537–560. [Google Scholar] [CrossRef]
- Szymula, C.; Bešinović, N. Passenger-centered vulnerability assessment of railway networks. Transp. Res. Part B Methodol. 2020, 136, 30–61. [Google Scholar] [CrossRef]
- Orlando, V.M.; Baquela, E.G.; Bhouri, N.; Lotito, P.A. Analytical and simulation-based estimation of public transport demand. Transp. Res. Procedia 2022, 62, 727–734. [Google Scholar] [CrossRef]
- Connors, R.D.; Watling, D.P. Assessing the demand vulnerability of equilibrium traffic networks via network aggregation. Netw. Spat. Econ. 2014, 15, 365–395. [Google Scholar] [CrossRef]
- Rodriguez-Nunez, E.; Garcia-Palomares, J.C. Measuring the vulnerability of public transport networks. J. Transp. Geogr. 2014, 35, 50–63. [Google Scholar] [CrossRef]
- Yap, M.D.; van Oort, N.; van Nes, R.; van Arem, B. Identification and quantification of link vulnerability in multi-level public transport networks: A passenger perspective. Transportation 2018, 45, 1161–1180. [Google Scholar] [CrossRef]
- Ye, Q.; Kim, H. Assessing network vulnerability using shortest path network problems. J. Transp. Saf. Secur. 2019, 13, 1–25. [Google Scholar] [CrossRef]
- Cats, O.; Erik Jenelius, E. Beyond a complete failure: The impact of partial capacity degradation on public transport network vulnerability. Transp. B: Transp. Dyn. 2018, 6, 77–96. [Google Scholar] [CrossRef]
- Liu, J.; Schonfeld, P.M.; Yin, Y.; Peng, Q.; Ranjitkar, P. Effects of Link Capacity. Reductions on the Reliability of an Urban Rail Transit Network. J. Adv. Transp. 2020, 1, 1–15. [Google Scholar] [CrossRef]
- Liu, J.J.; Schonfeld, P.M.; Zhan, S.; Du, B.; He, M.; Wang, K.C.P.; Yin, Y. The Economic Value of Reserve Capacity Considering the Reliability and Robustness of a Rail Transit Network. J. Transp. Eng. Part A Syst. 2023, 149, 04023046. [Google Scholar] [CrossRef]
- Taylor, M.A.P.; D’Este, G.M. Transport network vulnerability: A method for diagnosis of critical locations in transport infrastructure systems. In Critical Infrastructure; Murray, A.T., Grubesic, T.H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 9–30. [Google Scholar]
- Tan, Y. A New Shortest Path Algorithm Generalized on Dynamic Graph for Commercial Intelligent Navigation for Transportation Management. arXiv 2019, arXiv:1905.04469. [Google Scholar]
- Bhouri, N.; Kauppila, J. Managing Highways for Better Reliability—Assessing Reliability Benefits of Ramp Metering. Transp. Res. Rec. 2011, 2229, 1–7. [Google Scholar] [CrossRef]
- Zang, Z.; Xu, X.; Qu, K.; Chen, R.; Chen, A. Travel Time reliability in transportation networks: A review of methodological Developments. Transp. Res. Part C. Emerg. Technol. 2022, 143, 103866. [Google Scholar] [CrossRef]
- Bhouri, N.; Aron, M.; Scemama, G. Travel Time Reliability with and Without the Dynamic Use of the Hard Shoulder: Field Test From a French Motorway. J. Traffic Transp. Eng. (Engl. Ed.) 2016, 3, 520–530. [Google Scholar] [CrossRef][Green Version]
- Taylor, M.A.P. Travel through time: The story of research on travel time reliability. Transp. B Transp. Dyn. 2013, 1, 174–194. [Google Scholar] [CrossRef]
- Benezech, V.; Coulombel, N. The value of service reliability. Transp. Res. Part B 2013, 58, 1–15. [Google Scholar] [CrossRef]
- Muñoz, J.C.; Soza-Parra, J.; Raveau, S. A comprehensive perspective of unreliable public transport services costs. Transp. A Transp. Sci. 2020, 16, 734–748. [Google Scholar] [CrossRef]
- Artan, M.S.; Şahin, I. A stochastic model for reliability analysis of periodic train timetables. Transp. B Transp. Dyn. 2023, 11, 572–589. [Google Scholar] [CrossRef]
- Shelat, S.; Cats, O.; van Oort, N.; van Lint, J.W.C. Evaluating the impact of waiting time reliability on route choice using smart card data. Transp. A: Transp. Sci. 2023, 19, 2028929. [Google Scholar] [CrossRef]
- Khani, A. An onroute shortest path algorithm for reliable routing in schedule-based transit networks considering transfer failure probability. Transp. Res. Part B 2019, 126, 549–564. [Google Scholar] [CrossRef]
- Redmond, M.; Campbell, A.M.; Ehmke, J.F. Reliability in public transit networks considering backup itineraries. Eur. J. Oper. Res. 2022, 300, 852–864. [Google Scholar] [CrossRef]
- Clark, S.; Watling, D. Modelling network reliability under stochastic demand. Transp. Res. Part B 2005, 39, 119–140. [Google Scholar] [CrossRef]
- Chen, A.; Yang, H.; Lo, H.K.; Tang, W.H. Capacity reliability of a road network: An assessment methodology and numerical results. Transp. Res. B 2002, 36, 225–252. [Google Scholar] [CrossRef]
- Yang, H.; Lo, K.K.; Tang, W.H. Travel time versus capacity reliability of a road network. In Reliability of Transport Networks; Bell, M.G.H., Cassir, C., Eds.; Research Studies Press Ltd.: Baldock, UK, 2000; pp. 119–138. [Google Scholar]
- Kim, H.; Song, Y. Examining accessibility and reliability in the evolution of subway systems. J. Public Transp. 2015, 18, 89–106. [Google Scholar] [CrossRef]
- Bimpou, K.; Ferguson, N.S. Dynamic accessibility: Incorporating day-to-day travel time reliability into accessibility measurement. J. Transp. Geogr. 2020, 89, 102892. [Google Scholar] [CrossRef]
- Kim, H.; Song, Y. An integrated measure of accessibility and reliability of mass transit systems. Transportation 2018, 45, 1075–1100. [Google Scholar] [CrossRef]
- Taylor, M.A.P. Dense network traffic models, travel time reliability and traffic management. Ii: Application to Network reliability. J. Adv. Transp. 2010, 33, 235–251. [Google Scholar]
- Hasan, A.; Hasan, U.; AlJassmi, H.; Whyte, A. Transit Behaviour and Sociodemographic Interrelation: Enhancing Urban Public-Transport Solutions. Eng 2023, 4, 1144–1155. [Google Scholar] [CrossRef]
- Gaschi-Uciecha, A. The Problem of Reliability in Public Transport for the Metropolis GMZ Area-Pilots Studies. Sustainability 2023, 15, 3199. [Google Scholar] [CrossRef]
- Jaber, S.; Bhouri, N.; Aron, M.; Mahdavi-Moghaddam, S.M.H. Connectivity reliability for assessing public transport networks. In Proceedings of the EWGT23, 25th Euro Working Group on Transportation Networks, University of Cantabria, Santander, Spain, 6–8 September 2023; Volume 3, p. hal-04273985. [Google Scholar]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois: Urban, IL, USA, 1949. [Google Scholar]
- Wei, Y.; Jiang, N.; Li, Z.; Zheng, D.; Chen, M.; Zhang, M. An Improved Ant Colony Algorithm for Urban Bus Network Optimization Based on Existing Bus Routes. ISPRS Int. J. Geo-Inf. 2022, 11, 317. [Google Scholar] [CrossRef]
- Van Lint, J.H.; Wilson, R.M. A Course in Combinatorics; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications, 3rd ed.; Wiley: New York, NY, USA; London, UK; Sydney, Australia, 1958; Volume 1, ISBN 978-0-471-25708-0. [Google Scholar]
- Fano, R.M. Transmission of Information: A Statistical Theory of Communication; MIT Press: Cambridge, MA, USA, 1961; Chapter 2. [Google Scholar]
- Dijkstra, E.W. A note on two problems with connection to graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Panic, S.; Petrović, V.; Drašković, S.; Kontrec, N.; Milojević, S. Performance Analysis of Hybrid FSO//RF Communication System with Receive Diversity in the Presence of Chi-Square/Gamma Turbulence and Rician Fading. Available online: https://scidar.kg.ac.rs/handle/123456789/19785 (accessed on 2 December 2024).
- Distribution of the Product of Two Random Variables. Available online: https://en.wikipedia.org/wiki/Distribution_of_the_product_of_two_random_variables (accessed on 3 December 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).