Green Investment and Emission Reduction in Supply Chains Under Dual-Carbon Regulation: A Dynamic Game Perspective on Coordination Mechanisms and Policy Insights

Abstract

This study examines green investment and emission reduction strategies in a two-tier supply chain under dual-carbon regulation that combines a carbon tax with a cap-and-trade mechanism. A multi-stage dynamic game model is developed, in which the manufacturer reduces emissions through recycling efforts and investments in green technology. We compare optimal decisions under centralized, decentralized, and coordinated structures, and propose an enhanced bilateral cost-sharing contract to improve collaboration. Numerical experiments validate the theoretical results, and sensitivity analyses provide further insights. The results show that while both carbon tax and permit trading increase emission reduction, the carbon tax may lower manufacturer profit, underscoring the need for coordinated policy design. Benchmarking proves more effective than grandfathering in stimulating green investment, particularly under high carbon prices and strong consumer environmental preferences. The proposed contract alleviates free riding, enhances overall supply chain profitability, and improves emission reduction performance. Policy implications highlight the importance of prioritizing benchmark allocation, promoting consumer environmental awareness, and encouraging firms to integrate carbon asset management with technological innovation. This research provides both theoretical and practical insights for designing effective carbon policies and collaborative mechanisms in green supply chains.

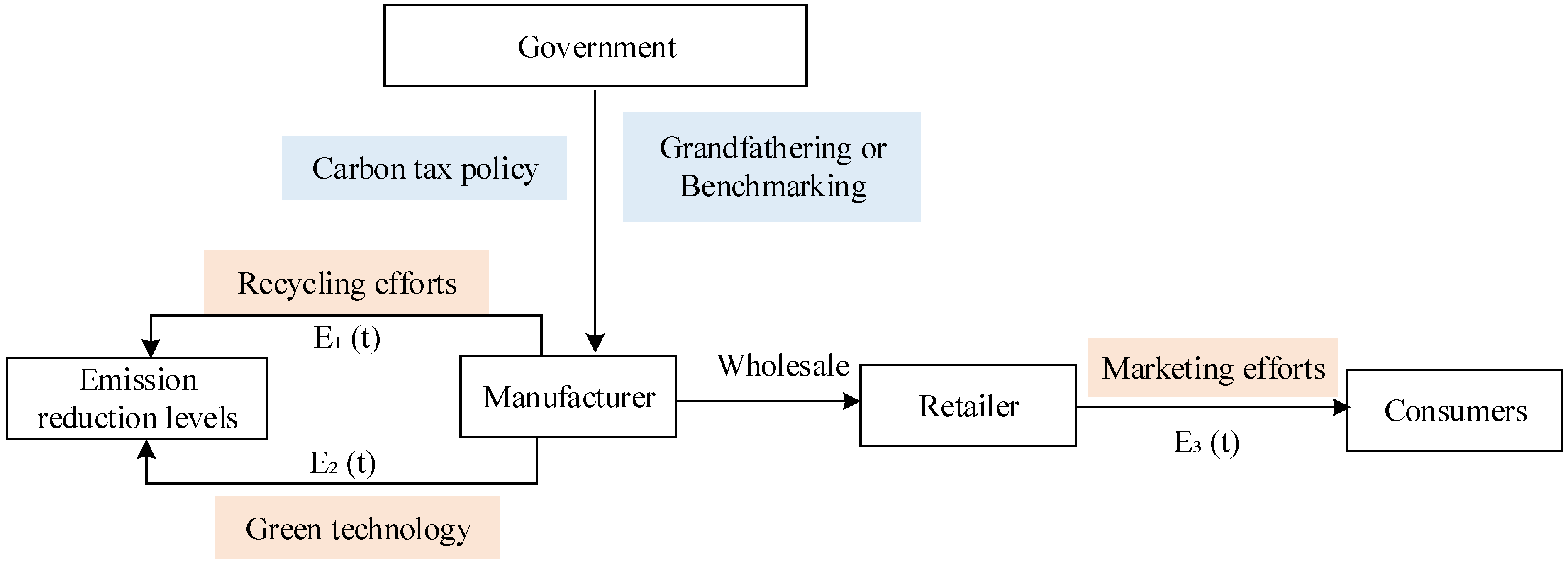
1. Introduction

Global climate change is accelerating due to the rapid accumulation of carbon dioxide and other greenhouse gases (GHGs) from human activities [1]. Over the past two decades, fossil fuel-related CO₂ emissions have risen at an average annual rate exceeding 1.5%, threatening human security and economic stability [2]. To mitigate these risks, the UNFCCC, through instruments such as the Kyoto Protocol and the Paris Agreement, aims to limit global warming to 1.5–2 °C above pre-industrial levels. In this context, China has committed to peak carbon emissions before 2030 and achieve carbon neutrality by 2060, reflecting a strategic shift in national priorities and contributing to global net-zero efforts.

Manufacturing remains one of the most carbon-intensive sectors, contributing over 40 percent of China’s total CO₂ emissions. Industries such as steel, chemicals, and cement remain reliant on energy-intensive processes and legacy technologies, making emission reductions in these domains particularly challenging [3]. Even more challenging is the carbon footprint embedded throughout global supply chains. Indirect emissions arising from upstream and downstream activities, classified as Scope 3 emissions, can exceed 70% of a manufacturing firm’s total emissions. This often-overlooked source of pollution represents a significant hidden burden that cannot be resolved through production-site interventions alone [4]. In recent years, global supply chains have witnessed increasing investment in low-carbon technologies and circular economy practices. For instance, renewable energy integration, electrification of logistics, and recycling-based remanufacturing have become mainstream strategies in developed economies, while emerging markets such as China are scaling up pilot projects in green factories and digitalized recycling networks. These trends reflect a structural shift from isolated corporate initiatives toward system-wide supply chain decarbonization.

Among the policy tools currently in widespread use, carbon taxes and emissions trading systems (ETS) have emerged as the most validated and market-efficient instruments [5]. Each offers distinct advantages: ETS promotes dynamic efficiency and innovation, while carbon taxes offer cost predictability and ease of enforcement. Recent studies underscore the difficulty of achieving both quantity and price stability with a single instrument [6]. Consequently, combining carbon taxes with ETS is increasingly recognized as a strategy to harness complementary benefits and policy synergies [7,8].

Beyond regulation, consumer demand for low-carbon products is rising sharply. Recent surveys show that over 60% of Chinese consumers are willing to pay a premium for goods with carbon labels, prompting global brands such as Starbucks and IKEA to launch carbon footprint labeling in China with notable commercial success. Upstream manufacturers have integrated carbon reduction into core operations through green technologies and remanufacturing [5,9]. For example, Gree reduced product-level emissions by 18% between 2017 and 2020, while Lenovo procured over 280 million kWh of renewable electricity in 2020, thereby avoiding approximately 220,000 tonnes of greenhouse gas emissions. Firms such as BYD, Dell, and Tesla combine green technology adoption with circular economy practices, including electrification, modular design, and automated recycling, to achieve comprehensive end-to-end carbon reductions. Downstream retailers, including Gome, actively promote environmentally sustainable products, enhancing consumer engagement and demand while reinforcing firm profitability [10]. Although upstream and downstream actors often prioritize independent interests, coordinated strategies across production, marketing, and brand-building can enable joint emission reductions. This demonstrates the benefits of supply chain-wide mitigation when incentives are aligned [11]. However, these market-driven initiatives remain highly sensitive to external factors such as carbon trading prices, tax regimes, and consumer preferences, which can substantially influence equilibrium outcomes and economic performance, posing challenges for firms and policymakers. While studies, such as [12,13], address the impact of carbon regulatory policies on supply chain equilibrium decisions, few have systematically compared the effects of dual carbon policies, highlighting a critical gap addressed by the present analysis.

To address these gaps, this study aims to investigate how hybrid carbon policies, combined with market forces, shape supply chain behavior and outcomes. Specifically, it examines the strategic allocation of resources across green technology investment, recycling, and marketing under varying regulatory and market conditions. The core research questions are:

1.

Under dual carbon regulation composed of different quota allocation mechanisms and carbon tax, how should supply chain members determine their long-term recycling efforts, green technology investments, and marketing initiatives?

2.

Can an improved bilateral cost-sharing contract effectively incentivize equilibrium investment decisions across upstream and downstream supply chain members?

3.

How do variations in critical parameters, such as carbon trading prices, carbon tax levels, and the strength of consumer green preferences, shape the equilibrium strategies and economic performance of supply chain participants?

Unlike much of the existing literature, which often focuses on single-policy instruments or neglects consumer preferences, this study evaluates the strategic responses of manufacturers and retailers under hybrid regulatory regimes combining carbon taxation with either grandfathering or benchmarking allocation mechanisms. The study constructs a dynamic differential game model to capture the evolving interactions among regulatory policy, consumer awareness, and firm-level strategic investments. This approach provides empirically grounded insights for carbon pricing, environmental disclosure, and cross-sectoral decarbonization strategies. Furthermore, the proposed modeling framework and simulation results offer actionable guidance for carbon-intensive industries seeking to align decarbonization with economic viability, yielding broad relevance across sectors and national contexts.

The main contributions of this study can be concluded in three aspects. First, it develops a dynamic differential game model to capture the evolving interplay of green technology investment, emission reduction, and strategic interactions between manufacturers and retailers under combined carbon taxation and quota allocation mechanisms. Second, it integrates behavioral and market factors, including shifts in consumer environmental awareness and resource allocation across technology, recycling, and marketing initiatives, to evaluate how policy architecture shapes long-term environmental and economic outcomes. Third, it introduces an improved bilateral cost-sharing contract to promote coordinated emission reductions, providing both theoretical insights and actionable guidance for policy design and industry strategies, thereby offering broad relevance across sectors and national contexts.

The paper is organized as follows: Section 2 reviews the relevant literature. Section 3 introduces the modeling assumptions. Section 4 develops three decision models and analyzes the equilibrium results. Section 5 provides a comparison of the different equilibrium results. Section 6 investigates the effect of key factors on the equilibrium decisions using numerical analysis. Section 7 summarizes the findings, implications for management, and suggestions for future research.

2. Literature Review

2.1. Carbon Quota Allocation Mechanisms

Most studies on carbon allowance allocation adopt a macroeconomic perspective, emphasizing regional optimization and aggregate emissions outcomes. However, such perspectives often overlook the strategic interactions occurring within supply chains, where manufacturers, retailers, and regulators operate under heterogeneous objectives. Game theory offers a robust framework for capturing these decentralized dynamics, revealing how firms adapt investment, pricing, and production strategies under carbon constraints.

Recent research has applied this perspective to investigate how allocation mechanisms influence firm behavior. Grandfathering has been shown to benefit firms with low carbon efficiency or those in heavily polluted regions, while benchmarking tends to drive stronger environmental outcomes in cleaner settings or among high-efficiency actors [14,15]. Financial considerations further shape these responses. For example, carbon rights repurchase schemes enable capital-constrained firms to obtain financing and improve abatement performance [16]. Studies have also highlighted that profits peak at specific allocation thresholds under grandfathering, whereas benchmarking enhances both consumer surplus and environmental benefits when benchmark levels exceed critical values [17].

Despite the growing use of carbon markets, the interaction between allocation rules and other regulatory tools, particularly carbon taxes, remains insufficiently studied. Prior research largely relies on static models and single-sector analysis. By incorporating dynamic settings and multiple regulatory levers, the present study examines how combined mechanisms affect emission strategies and supply chain coordination. We model decentralized, centralized, and collaborative decision structures to clarify the conditions under which different allocation schemes are most effective. This analysis also provides insight into the behavioral logic underlying firm-level carbon abatement.

2.2. Investing in Emission Reductions Under Carbon Constraints

Extensive research has explored how carbon regulations incentivize firm-level investment in emission-reduction technologies [18]. Among the most influential policy instruments are cap-and-trade systems and carbon taxes [19], both of which substantially affect corporate strategy and operational choices. Higher carbon prices under trading mechanisms are found to promote greener production [20], while cap-and-trade frameworks often favor agency-based models and remanufacturing strategies by offsetting regulatory costs through investment efficiency gains. In contrast, carbon taxes stimulate innovation and technology adoption, though their effectiveness depends on marginal abatement costs and emissions asymmetries. Moderate tax rates may fail to spur investment, while excessive taxation can hinder innovation and reduce output. Comparative studies present mixed findings. Some suggest that carbon taxes and trading systems yield similar welfare outcomes in multiproduct manufacturing. Others indicate that cap-and-trade schemes more effectively reduce emissions, enhance competitiveness, and support environmental objectives.

Despite these insights, most prior work remains confined to static or single-policy frameworks, offering limited exploration of hybrid regulatory environments. The interplay between tax instruments and quota allocation mechanisms, particularly in dynamic supply chain contexts, remains underexplored. To address this gap, the present study develops dynamic models encompassing decentralized, centralized, and coordinated decision structures, integrating both carbon taxes and differentiated cap allocation rules. This approach clarifies how regulatory interactions shape firm investment behavior and system-wide emission strategies. It also lays a foundation for developing more adaptive and effective climate policies.

2.3. Joint Supply Chain Emission Reduction

The intensifying challenge of carbon emissions has highlighted the necessity of adopting a supply chain-wide perspective on emission reduction. Effective coordination between upstream and downstream partners is essential for achieving substantial and sustained carbon abatement. While early studies primarily focused on static models of joint emission reduction [20,21,22,23], the inherently multi-period nature of emission efforts necessitates dynamic modeling to capture evolving strategic interactions over time.

Recent research has introduced dynamic frameworks, exploring how cost-sharing contracts and dual abatement technologies influence emission strategies and performance outcomes. For example, Wang et al. [24] examined the influence of cap-and-trade regulations on JER decisions and found that while such mechanisms encourage higher emission reduction efforts by both manufacturers and retailers, they do not necessarily improve profits. Xia et al. [25] incorporated carbon emission allowances and firms’ social preferences, showing that social preferences can increase the revenues of other supply chain participants. Similarly, Dou et al. [12] investigated low-carbon cooperation under partially paid allowance policies and highlighted the long-term effects of dynamic coordination, while Zhang et al. [13] studied hybrid carbon policies and emphasized the importance of sustained partnerships between upstream and downstream members. These studies show that integrating retailer promotional efforts and sharing abatement costs can lead to Pareto improvements, enhancing both environmental and economic outcomes across the supply chain. Moreover, under formal carbon regulations, coordinated contracts, such as bilateral cooperation agreements, quota-sharing schemes, and hybrid mechanisms combining revenue-sharing and transfer payments, have been shown to outperform non-cooperative strategies in both emission reduction and profit generation.

This study builds upon and extends existing work by jointly considering carbon taxes and multiple carbon quota allocation methods, including grandfathering and benchmarking. It further advances the literature by incorporating refined bilateral cost-sharing mechanisms within a dynamic setting, offering new insights into how supply chain partners can align incentives and coordinate more effectively under hybrid carbon regulations.

2.4. Research Gaps

Table 1. Differences between this paper and existing studies.

Papers	Carbon Tax	Allocation Methods		Dynamic/Static	Emission Reduction Investment	Independent Decision	Simultaneous Decision	JER
		G	B
[26]		√	√	static	GT	√		√
[27]		√	√	static	RE	√	√
	√	√		static	CA	√	√
		√		dynamic	CA	√	√
[28]		√	√	dynamic	CA + AE	√	√
[12]			√	dynamic	CA + AE	√		√
	√	√		static	CA	√	√	√
[29]		√	√	static	GT	√	√
[30]		√	√	dynamic	CA
[17]		√	√	static	CA	√	√
This paper	√	√	√	dynamic	GT + CE + AE	√	√	√

Not: G: grandfathering; B: benchmarking; JER: Joint emission reduction; GT: green technology investment; RE: renewable energy investment; CA: carbon abatement investment; CE: recycling efforts; AE: advertising efforts.

situates this study within the existing literature on supply chain coordination for emission reduction, highlighting critical gaps. Recent years have seen growing interest in how carbon taxation and cap-and-trade policies influence strategic decisions within supply chains. However, most studies adopt static models, neglecting the dynamic evolution of green technology investment and emission reduction behaviors, which limits insight into firms’ optimal long-term responses. Although prior research has begun to explore the effects of carbon taxation and quota trading mechanisms on corporate strategies, the literature remains largely fragmented, with limited attention to hybrid regulatory environments. In particular, the interplay between different quota allocation rules and carbon tax policies has yet to be thoroughly examined. Moreover, current studies seldom capture how supply chain actors co-evolve under multiple, and sometimes conflicting, policy stimuli. Addressing these gaps, this study analyzes low-carbon investment strategies across centralized and decentralized decision-making structures, and introduces an enhanced bi-directional cost-sharing mechanism to promote coordinated emission reductions.

3. Problem Definition and Model Formulation

This study examines a low-carbon supply chain consisting of a manufacturer and a retailer operating under dual carbon regulation. The system combines an emissions trading scheme (ETS) with a carbon tax. The government, as the regulatory authority, sets emission caps, imposes carbon taxes on manufacturers, and allows allowance trading in the carbon market. In this setting, the manufacturer engages in green technology R&D and recycling efforts to reduce emissions, while the retailer undertakes marketing efforts to stimulate consumer demand for low-carbon products. A continuous-time dynamic system captures how these strategies jointly influence emission trajectories and market demand over time. The manufacturer operates in both product and carbon markets, whereas the retailer participates only in the product market. Product transactions follow a wholesale–retail pricing structure, with the manufacturer selling to the retailer, who then sets retail prices for consumers. As production activities account for the majority of carbon emissions in the supply chain [31], regulatory measures primarily target the manufacturer. Emission allowances are allocated at no cost based on either grandfathering or benchmarking schemes, consistent with established ETS practices [32]. This modeling framework enables a nuanced analysis of strategic interactions under hybrid carbon pricing and offers insights into the alignment of profit-maximizing behavior with environmental policy goals.

The following assumptions are given in this paper:

Assumption 1.

Investment in recycling efforts, green technology R&D, and low-carbon marketing is modeled as one-time strategic decisions, each exhibiting diminishing marginal returns. Accordingly, the associated cost functions are specified as quadratic in their respective decision variables, consistent with prior studies [33,34,35,36]. Specifically, the manufacturer’s cost of recycling effort is given by $C_1(t)={\displaystyle \frac{1}{2}}{\eta }_1{E}_1^2(t)$, the cost of green technology investment by $C_2(t)={\displaystyle \frac{1}{2}}{\eta }_2{E}_2^2(t)$, and the retailer’s marketing cost by $C_3(t)={\displaystyle \frac{1}{2}}{\eta }_3{E}_3^2(t)$, where $E_1(t)$, $E_2(t)$ and $E_3(t)$ denote the levels of recycling, green R&D, and marketing efforts, respectively, and ${\eta }_1$, ${\eta }_2$ and ${\eta }_3$ are positive cost coefficients reflecting inverse efficiency. A higher coefficient indicates lower investment efficiency. Figure 1 depicts the overall structure of the model. Consistent with established conventions [7,31,37], production costs are omitted for tractability, as green technology investment typically dwarfs marginal production costs. For instance, in new energy vehicle battery manufacturing, multi-billion-RMB R&D in solid-state batteries and automated recycling systems far outweighs unit-level production costs. This simplification, widely adopted in prior studies, preserves the validity of our key insights. The unit-level carbon reduction evolves dynamically with manufacturers’ recycling and green technology investment, governed by Equation (1):

$$\left\{\begin{array}{c}\dot{\tau }(t)=\vartheta \alpha \epsilon E_1(t)+\beta E_2(t)-k\tau (t)\\ \tau (0)={\tau }_0\end{array}\right.$$

(1)

Here, parameter  $\alpha$  captures the marginal effect of recycling efforts on emission reduction, while  $\epsilon$  denotes the sensitivity of recycling activities, and  $\vartheta$  represents the carbon-saving efficiency of remanufacturing. The coefficient  $\beta$  reflects the effectiveness of green technology in reducing emissions, and  $k$  indicates the natural decay rate of the achieved emission reduction. The manufacturer’s environmental performance is defined as the difference between its emission cap and actual carbon emissions. Under the grandfathering-plus-tax scheme, performance is measured as  $T^G=E_G-\left(e_{0}Q\left(t\right)-\tau (t)\right)$, while under the benchmarking-plus-tax scheme, it is  $T^B=E_{B}Q\left(t\right)-\left(e_{0}Q\left(t\right)-\tau (t)\right)$, where  $E_G$  and  $E_B$  denote the carbon allowances allocated under the respective mechanisms,  $e_0$  is the baseline unit emission, and  $Q\left(t\right)$  is the product demand at time t. The term  $e_{0}Q\left(t\right)-\tau (t)$  represents total emissions after accounting for recycling and green R&D efforts. A lower emission level under a given cap signals better environmental performance and enhances the manufacturer’s reputation. Both recycling and green technology investments contribute to emission reduction.

Assumption 2.

Manufacturers participate in the carbon trading market by purchasing additional allowances or selling surplus quotas [38]. Thus, under both grandfathering and benchmarking allocation schemes, the manufacturer’s carbon cost or revenue at time t is expressed as Equation (2):

$$\mathrm{\Gamma }\left(t\right)=\left\{\begin{array}{cc}{p}_c\left(E_G-\left(e_{0}Q\left(t\right)-\tau (t)\right)\right)& \mathrm{Grandfathering}\\ p_c\left(E_{B}Q\left(t\right)-\left(e_{0}Q\left(t\right)-\tau (t)\right)\right)& \mathrm{Benchmarking}\end{array}\right.$$

(2)

where $p_c$ denotes the carbon price, modeled as an exogenous constant shaped by aggregate market forces and independent of individual firm actions. Given that regulatory mechanisms, such as compliance periods in national carbon markets, set price floors and ceilings to dampen volatility, we assume a stable carbon price over the analysis horizon. A long-term perspective is incorporated through a dynamic model with an infinite time horizon [10].

Assumption 3.

The government levies a fixed carbon tax $p_t$ on manufacturers, with $p_t<p_c$, defined by  Equation (3):

$$p_t\left(e_{0}D\left(t\right)-\tau (t)\right)$$

(3)

This tax targets manufacturers exclusively [39,40].

Assumption 4.

As environmental awareness rises, consumers are increasingly willing to pay premiums for eco-friendly products. Consequently, demand depends not only on baseline levels but also positively on manufacturers’ emission reductions and other non-price factors. Assuming these effects independently influence demand, the demand function can be expressed as Equation (4):

$$Q(t)=Q_0+h\tau (t)+x(t)$$

(4)

where $Q_0$ is baseline demand, $h$ ($0<h<1$) measures sensitivity to emission reductions, higher $h$ signals stronger consumer environmental consciousness, and $x(t)$ reflects the retailer’s marketing effort, normalized with unit sensitivity for model tractability without altering equilibrium outcomes. Adopting the Vidale-Wolfe (V-W) framework [41], the dynamic relationship between retailer marketing effort and demand growth is given by Equation (5):

$$\left\{\begin{array}{c}{\displaystyle \frac{dx(t)}{dt}}=\gamma E_3(t)\sqrt{1-x(t)}-\zeta x(t)\\ \tau (0)={\tau }_0\end{array}\right.$$

(5)

where  $\gamma$  captures marketing effectiveness, and  $\zeta$  is the decay constant. Demand changes reflect the net effect of market share gained through marketing offset by attrition factors such as product substitution.

Assumption 5.

Both manufacturer and retailer are risk-neutral rational agents, sharing a common discount rate  $\rho$ ($0<\rho <1$), aiming to maximize long-term expected profits.

4. Different Green Technology Investment Scenarios

4.1. Model DG: Decentralized Decision-Making Under Grandfathering and Carbon Tax

In Model DG, the government allocates carbon emission allowances to manufacturers based on their historical emissions, following a grandfathering scheme. As a result, each firm receives a fixed quota of free allowances, denoted by $E_G$. The manufacturer’s actual emissions may deviate from this quota, leading to a tradable surplus or deficit defined as $E_G-e_{0}Q\left(t\right)$. A positive value implies a surplus of allowances, which can be sold on the carbon market at price $p_c$, generating revenue; a negative value indicates a shortage, requiring the purchase of additional permits, thereby incurring costs. The profit functions for the manufacturer and the retailer are defined by Equations (6) and (7), respectively:

$$\underset{E_1,E_2}{\max } J_M^{DG}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\begin{array}{l}\underset{\mathrm{Wholesale} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_m\left(Q_0+x(t)+h\tau (t)\right)+{\mathrm{\Pi }}_n\vartheta E_1(t)}}+\underset{\mathrm{Carbon} \mathrm{trading} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_c\left[E_G-e_0\left(Q_0+h\tau (t)+x(t)\right)+\tau (t)\right]}}\\ -\underset{\mathrm{Carbon} \mathrm{tax} \mathrm{to} \mathrm{be} \mathrm{paid} \mathrm{by} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_t\left(\left(e_0\left(Q_0+h\tau (t)+x(t)\right)\right)-\tau (t)\right)}}-\underset{\mathrm{Different} \mathrm{investment} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{\left[{\displaystyle \frac{1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{1}{2}}{\eta }_2{E}_2^2(t)\right]}}\end{array}\right\}dt$$

(6)

$$\underset{E_3}{\max } J_R^{DG}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\underset{\mathrm{Retail} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_r\left(Q_0+h\tau (t)+x(t)\right)}}-\underset{\mathrm{Cost} \mathrm{of} \mathrm{marketing} \mathrm{efforts} \mathrm{for} \mathrm{the} \mathrm{retailer}}{\underbrace{{\displaystyle \frac{1}{2}}{\eta }_3{E}_3^2(t)}}\right\}dt$$

(7)

By applying optimal control theory to the model DG, we derive the equilibrium strategies for both manufacturer and retailer, the optimal trajectories of the state variables, and the maximum expected long-term profit, as summarized in Proposition 1.

Proposition 1.

In model DG:

(1) 

The optimal investment decision-making decisions for manufacturers and retailers are: $E_1^{DG\ast }={\displaystyle \frac{\vartheta \left({\mathrm{\Pi }}_n+\alpha \epsilon m_1\right)}{{\eta }_1}}$, $E_2^{DG\ast }={\displaystyle \frac{\beta m_1}{{\eta }_2}}$, $E_3^{DG\ast }={\displaystyle \frac{\sqrt{1-x^{DG\ast }}\left(-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}\right)}{\gamma {\eta }_3}}$.

(2) 

The trajectories of the product abatement level and the incremental demand induced by the marketing effort are, respectively: ${\tau }^{DG\ast }(t)={\tau }_{\infty }^{DG\ast }+({\tau }_0-{\tau }_{\infty }^{DG\ast })e^{-kt}$, $x^{DG\ast }(t)=x_{\infty }^{DG\ast }+(x_0-x_{\infty }^{DG\ast })e^{-\left({\displaystyle \frac{\sqrt{{\eta }_3\left({\eta }_3{\left(\zeta +\rho \right)}^2+2{\gamma }^2{\mathrm{\Pi }}_r\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}+\zeta \right)t}$.

$$\begin{gathered} \mathit{and} {\tau }_{\infty }^{DG\ast }={\displaystyle \frac{\frac{{\beta }^2\left(\left(\left(1-e_{0}h\right)\left(p_c+p_t\right)\beta \right)+h{\beta }^2{\mathrm{\Pi }}_m\right)}{{\eta }_2\left(k+\rho \right)}+\frac{\alpha \epsilon {\vartheta }^2\left({\mathrm{\Pi }}_n+\alpha \epsilon m_1\right)}{{\eta }_1}}{k}}, \\ {x}_{\infty }^{DG\ast }={\displaystyle \frac{\frac{\sqrt{{\eta }_3\left({\eta }_3{\left(\zeta +\rho \right)}^2+2{\gamma }^2{\mathrm{\Pi }}_r\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}{\frac{\sqrt{{\eta }_3\left({\eta }_3{\left(\zeta +\rho \right)}^2+2{\gamma }^2{\mathrm{\Pi }}_r\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}+\zeta }} \end{gathered}$$

${\tau }_{\infty }^{DG\ast }$ and $x_{\infty }^{DG\ast }$ are the steady-state values of the two state variables at $t\to \infty$.

(3) 

The long-term benefits of a low-carbon supply chain system are:

$$J_M^{DG\ast }=e^{-\rho t}\left(m_1{\tau }^{DG\ast }(t)+m_2{x}^{DG\ast }(t)+m_3\right)$$

$$J_R^{DG\ast }=e^{-\rho t}\left(n_1{\tau }^{DG\ast }(t)+n_2{x}^{DG\ast }(t)+n_3\right)$$

And

$$\left\{\begin{array}{l}{m}_1={\displaystyle \frac{p_c-e_{0}h{p}_c+p_t-e_{0}h{p}_t+h{\mathrm{\Pi }}_m}{k+\rho }}\\ m_2={\displaystyle \frac{{\eta }_3\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m\right)}{\sqrt{{\eta }_3\left(2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}}}\\ m_3=E_G{p}_c-e_0\left(p_c+p_t\right)Q_0+{\displaystyle \frac{m_2{n}_2{\gamma }^2}{{\eta }_3}}+Q_0{\mathrm{\Pi }}_m+{\displaystyle \frac{{m_1}^2\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)+2m_1\alpha \epsilon {\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n+{\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n^2}{2{\eta }_1{\eta }_2}}\\ n_1={\displaystyle \frac{h{\mathrm{\Pi }}_r}{k+\rho }}\\ n_2={\displaystyle \frac{-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}}{{\gamma }^2}}\\ n_3={\displaystyle \frac{n_2^2{\gamma }^2}{2{\eta }_3}}+{\displaystyle \frac{n_1\left(m_1{\beta }^2{\eta }_1+m_1{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2+\alpha \epsilon {\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n\right)}{{\eta }_1{\eta }_2}}+Q_0{\mathrm{\Pi }}_r\end{array}\right.$$

Proposition 1 reveals that under the decentralized decision model DG, the manufacturer’s equilibrium strategy remains time-invariant, while the retailer’s optimal marketing effort exhibits explicit time dependence, as further elaborated in Corollary 1.

Corollary 1.

Assume $e_0<{\displaystyle \frac{1}{h}}+{\displaystyle \frac{{\mathrm{\Pi }}_m}{p_c+p_t}}$, and  $e_0^{\prime }={\displaystyle \frac{1}{h}}$. Then, the following regularities emerge:

(1) 

The initial carbon quota  $E_G$  does not affect the manufacturer’s equilibrium strategy. However, when  $e_0<e_0^{\prime }$  , both recycling effort  $E_1^{DG\ast }$  and green technology investment  $E_2^{DG\ast }$  increase with rising carbon price  $p_c$  and carbon tax  $p_t$; conversely, when  $e_0>e_0^{\prime }$, these efforts decline.

(2) 

The retailer’s optimal marketing effort  $E_3^{DG\ast }$  remains invariant to changes in  $p_c$,  $p_t$  and  $E_G$, reflecting its insulation from direct carbon cost exposure.

(3) 

The product’s carbon reduction level  ${\tau }_{\infty }^{DG\ast }$  and the demand increment  $x_{\infty }^{DG\ast }$  induced by marketing are not influenced by  $E_G$; however, when  $e_0<e_0^{\prime }$,  ${\tau }_{\infty }^{DG\ast }$  rises with  $p_c$  and  $p_t$, and declines otherwise.

Corollary 1 reveals the tripartite effects of mixed regulation combining grandfathered quotas with a carbon tax. First, the manufacturer’s equilibrium decisions are decoupled from initial quota size but remain highly sensitive to carbon price signals. This finding is consistent with evidence from the EU Emissions Trading Scheme, where empirical studies show that rising allowance prices significantly stimulated low-emission firms to adopt energy-efficient technologies, while high-emitting firms tended to adopt conservative compliance strategies [42]. Second, the retailer’s marketing decisions are driven by market demand and remain stable under policy fluctuations, echoing findings from China’s regional ETS pilots where downstream firms largely responded to consumer demand rather than quota allocations [43]. Third, greater recycling and green R&D elevate carbon efficiency and brand equity, whereas reduced efforts suppress both, consistent with firm-level evidence that recycling programs in South Korea’s ETS enhanced both carbon efficiency and corporate image [44].

4.2. Model DB: Decentralized Decision-Making Under Benchmarking and Carbon Tax

In Model DB, carbon allowances are allocated using a benchmarking mechanism, whereby the government sets emission quotas based on the average carbon intensity across comparable firms within the industry. Under this dual regulatory framework, manufacturers receive emission permits proportional to industry benchmarks rather than historical emissions. Consequently, the profit functions of both the manufacturer and retailer are defined by Equations (8) and (9), respectively:

$$\underset{E_1,E_2}{\max } J_M^{DB}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\begin{array}{l}\underset{\mathrm{Wholesale} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_m\left(Q_0+x(t)+h\tau (t)\right)+{\mathrm{\Pi }}_n\vartheta E_1(t)}}+\underset{\mathrm{Carbon} \mathrm{trading} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_c\left[\left(E_B-e_0\right)\left(Q_0+h\tau (t)+x(t)\right)+\tau (t)\right]}}\\ -\underset{\mathrm{Carbon} \mathrm{tax} \mathrm{to} \mathrm{be} \mathrm{paid} \mathrm{by} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_t\left(\left(e_0\left(Q_0+h\tau (t)+x(t)\right)\right)-\tau (t)\right)}}-\underset{\mathrm{Different} \mathrm{investment} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{\left[{\displaystyle \frac{1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{1}{2}}{\eta }_2{E}_2^2(t)\right]}}\end{array}\right\}dt$$

(8)

$$\underset{E_3}{\max } J_R^{DB}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\underset{\mathrm{Retail} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_r\left(Q_0+h\tau (t)+x(t)\right)}}-\underset{\mathrm{Cost} \mathrm{of} \mathrm{marketing} \mathrm{efforts} \mathrm{for} \mathrm{the} \mathrm{retailer}}{\underbrace{{\displaystyle \frac{1}{2}}{\eta }_3{E}_3^2(t)}}\right\}dt$$

(9)

Assuming an interior solution (see Appendix A), the feedback Stackelberg equilibrium strategies in the benchmarked and carbon tax are given by:

Proposition 2.

In model DB:

(1) 

The optimal investment decision-making decisions for manufacturers and retailers are: $E_1^{DB\ast }={\displaystyle \frac{\vartheta \left({\mathrm{\Pi }}_n+\alpha \epsilon s_1\right)}{{\eta }_1}}$, $E_2^{DB\ast }={\displaystyle \frac{\beta s_1}{{\eta }_2}}$, $E_3^{DB\ast }={\displaystyle \frac{\sqrt{1-x^{DB\ast }}\left(-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}\right)}{\gamma {\eta }_3}}$.

(2) 

The trajectories of the product abatement level and the incremental demand induced by the marketing effort are, respectively:

$${\tau }^{DB\ast }(t)={\tau }_{\infty }^{DB\ast }+({\tau }_0-{\tau }_{\infty }^{DB\ast })e^{-kt}$$

$$x^{DB\ast }(t)=x_{\infty }^{DB\ast }+(x_0-x_{\infty }^{DB\ast })e^{-\left({\displaystyle \frac{\sqrt{{\eta }_3\left({\eta }_3{\left(\zeta +\rho \right)}^2+2{\gamma }^2{\mathrm{\Pi }}_r\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}+\zeta \right)t}$$

where

$$\begin{gathered} {\tau }_{\infty }^{DB\ast }={\displaystyle \frac{\alpha \epsilon {\vartheta }^2{\mathrm{\Pi }}_n+\frac{\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)\left(\left(1-e_{0}h\right)\left(p_c+p_t\right)+E_{B}h{p}_c+h{\mathrm{\Pi }}_m\right)}{{\eta }_2\left(k+\rho \right)}}{k{\eta }_1}}, \\ {x}_{\infty }^{DB\ast }={\displaystyle \frac{\frac{\sqrt{{\eta }_3\left({\eta }_3{\left(\zeta +\rho \right)}^2+2{\gamma }^2{\mathrm{\Pi }}_r\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}{\frac{\sqrt{{\eta }_3\left({\eta }_3{\left(\zeta +\rho \right)}^2+2{\gamma }^2{\mathrm{\Pi }}_r\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}+\zeta .}} \end{gathered}$$

${\tau }_{\infty }^{DB\ast }$ and $x_{\infty }^{DB\ast }$ are the steady-state values of the two state variables at $t\to \infty$.

(3) 

The long-term benefits of a low-carbon supply chain system are:

$$J_M^{DB\ast }=e^{-\rho t}\left(s_1{\tau }^{DB\ast }(t)+s_2{x}^{DB\ast }(t)+s_3\right)$$

$$J_R^{DB\ast }=e^{-\rho t}\left(z_1{\tau }^{DB\ast }(t)+z_2{x}^{DB\ast }(t)+z_3\right)$$

$$\mathit{and} \left\{\begin{array}{l}{s}_1={\displaystyle \frac{\left(1-e_{0}h\right)\left(pc+pt\right)+h{\mathrm{\Pi }}_m}{k+\rho }}+{\displaystyle \frac{E_{B}h{p}_c}{k+\rho }}\\ s_2={\displaystyle \frac{{\eta }_3\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m\right)}{\sqrt{{\eta }_3\left(2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}}}\\ s_3={\displaystyle \frac{s_2{z}_2{\gamma }^2}{{\eta }_3}}+Q_0\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m\right)+{\displaystyle \frac{{s_1}^2\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)+2s_1\alpha \epsilon {\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n+{\eta }_2{\vartheta }^2{{\mathrm{\Pi }}_n}^2}{2{\eta }_1{\eta }_2}}\\ z_1={\displaystyle \frac{h\mathrm{\Pi }r}{k+\rho }}\\ z_2={\displaystyle \frac{-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}}{{\gamma }^2}}\\ z_3={\displaystyle \frac{{z_2}^2{\gamma }^2}{2{\eta }_3}}+{\displaystyle \frac{z_1\left(s_1{\beta }^2{\eta }_1+s_1{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2+\alpha \epsilon {\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n\right)}{{\eta }_1{\eta }_2}}+Q_0{\mathrm{\Pi }}_r\end{array}\right.$$

Building on the above analysis, Corollary 2 is formally established.

Corollary 2.

Let $e_0^{\prime }={\displaystyle \frac{1}{h}}$, $e_0^{″}=E_B+{\displaystyle \frac{1}{h}}$. The sensitivity of equilibrium strategies to key policy parameters in the DB model follows these patterns:

(1) 

For manufacturers, equilibrium investment levels respond asymmetrically to the carbon allowance benchmark ($E_B$). Specifically, when  $e_0<e_0^{\prime }$, both recycling effort ($E_1^{DB\ast }$) and green technology investment ($E_2^{DB\ast }$) increase with rising carbon trading price ($p_c$) and carbon tax ($p_t$). When  $e_0>e_0^{″}$, the opposite holds. In the intermediate range  $e_0^{″}<e_0<e_0^{″}$,  $E_1^{DB\ast }$  rises with  $p_c$  but falls with  $p_t$, while  $E_2^{DB\ast }$  shows the reverse trend.

(2) 

For retailers,  $p_c$,  $p_t$  and  $E_B$  have no significant effect on their optimal marketing strategy (E₃), consistent with Corollary 1.

(3) 

Changes in  $p_c$,  $p_t$, and  $E_B$  affect the steady-state carbon abatement level (${\tau }_{\infty }^{DG\ast }$) in a manner aligned with shifts in manufacturer strategies, as  ${\tau }_{\infty }^{DG\ast }$  is determined directly by recycling and green technology efforts.

This corollary highlights three critical implications of the benchmark-based allocation under a carbon tax regime. First, manufacturers’ investment behavior is co-determined by carbon price signals and allocation benchmarks. While firms with low baseline emissions leverage higher $p_c$ and $p_t$ to reinforce their carbon advantage, high-emitting firms may reduce investment to mitigate excessive costs. Such heterogeneity is reflected in China’s national carbon market, where performance-based benchmarking in the power sector allows efficient plants to benefit from surplus allowances, whereas less efficient plants face compliance costs that reduce incentives for additional investment [45]. In intermediate cases, the dual pressure leads to strategic substitution between short-term recycling and long-term innovation. Second, retailers remain unaffected by regulatory levers, as their strategies are primarily market-driven. Finally, abatement outcomes closely track manufacturers’ behavioral responses, consistent with observations from California’s carbon market, where firm-level abatement correlated strongly with upstream producers’ technology adoption and investment strategies [46]. These findings offer policy insight for calibrating dynamic carbon pricing paths and allocation thresholds across heterogeneous firms.

4.3. Model CG: Centralized Decision-Making Under Grandfathering and Carbon Tax

Under centralized decision-making, the manufacturer and retailer cooperate to maximize the total profit of the entire supply chain. In Model CG, the government allocates a fixed quantity of carbon allowances to the manufacturer. Consequently, the joint profit function of the integrated supply chain can be expressed as Equation (10):

$$\underset{E_1,E_2,E_3}{\max } J_{SC}^{CG}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\begin{array}{l}\underset{\mathrm{sales} \mathrm{proceeds}}{\underbrace{\left({\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\left(Q_0+x(t)+h\tau (t)\right)+\vartheta E_1(t)\mathrm{\Pi }n}}+\underset{\mathrm{Carbon} \mathrm{trading} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_c\left[\left(E_G-e_0\left(Q_0+h\tau (t)+x(t)\right)\right)+\tau (t)\right]}}-\\ \underset{\mathrm{Different} \mathrm{investment} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{\left[{\displaystyle \frac{1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{1}{2}}{\eta }_2{E}_2^2(t)+{\displaystyle \frac{1}{2}}{\eta }_3{E}_3^2(t)\right]}}-\underset{\mathrm{Carbon} \mathrm{tax} \mathrm{to} \mathrm{be} \mathrm{paid} \mathrm{by} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_t\left(\left(e_0\left(Q_0+h\tau (t)+x(t)\right)\right)-\tau (t)\right)}}\end{array}\right\}dt$$

(10)

Assuming an interior solution (see Appendix A), the feedback Stackelberg equilibrium strategies in the benchmarked and carbon tax are given by:

Proposition 3.

In model CG:

(1) 

The optimal investment decision-making decisions for manufacturers and retailers are: $E_1^{CG\ast }={\displaystyle \frac{\vartheta \left({\mathrm{\Pi }}_n+\alpha \epsilon a_1\right)}{{\eta }_1}}$, $E_2^{CG\ast }={\displaystyle \frac{\beta \left(\left(1-e_{0}h\right)\left(p_c+p_t\right)+h\left({\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\right)}{{\eta }_2\left(k+\rho \right)}}$, $E_3^{CG\ast }={\displaystyle \frac{\sqrt{1-x^{CG\ast }}\left(-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}\right)}{\gamma {\eta }_3}}$.

(2) 

The trajectories of the product abatement level and the incremental demand induced by the marketing effort are, respectively:

$${\tau }^{CG\ast }(t)={\tau }_{\infty }^{CG\ast }+({\tau }_0-{\tau }_{\infty }^{CG\ast })e^{-kt}$$

$$x^{CG\ast }(t)=x_{\infty }^{CG\ast }+(x_0-x_{\infty }^{CG\ast })e^{-\left({\displaystyle \frac{\sqrt{{\eta }_3\left(2{\gamma }^2\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}+\zeta \right)t}$$

and

$$\begin{gathered} {\tau }_{\infty }^{CG\ast }={\displaystyle \frac{\alpha \epsilon {\vartheta }^2{\mathrm{\Pi }}_n+\frac{\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)\left(\left(1-e_{0}h\right)\left(p_c+p_t\right)+h\left({\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\right)}{{\eta }_2\left(k+\rho \right)}}{k{\eta }_1}}, \\ {x}_{\infty }^{CG\ast }={\displaystyle \frac{\frac{\sqrt{{\eta }_3\left(2{\gamma }^2\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}{\frac{\sqrt{{\eta }_3\left(2{\gamma }^2\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}+\zeta }} \end{gathered}$$

${\tau }_{\infty }^{CG\ast }$ and $x_{\infty }^{CG\ast }$ are the steady-state values of the two state variables at $t\to \infty$.

(3) 

The long-term benefits of a low-carbon supply chain system are:

$$J_{SC}^{CG\ast }=e^{-\rho t}\left(a_1{\tau }^{CG\ast }(t)+a_2{x}^{CG\ast }(t)+a_3\right)$$

and

$$\left\{\begin{array}{l}{a}_1={\displaystyle \frac{\left(1-e_{0}h\right)p_c+\left(1-e_{0}h\right)p_t+h{\mathrm{\Pi }}_m+h{\mathrm{\Pi }}_r}{k+\rho }}\\ a_2={\displaystyle \frac{-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}}{{\gamma }^2}}\\ a_3={\displaystyle \frac{1}{2}}\left(2E_G{p}_c+{\displaystyle \frac{a_2^2{\gamma }^2}{{\eta }_3}}+{\displaystyle \frac{a_2^2\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)+2a_1\alpha \epsilon {\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n+{\eta }_2{\vartheta }^2{{\mathrm{\Pi }}_n}^2}{{\eta }_1{\eta }_2}}+2Q_0\left(-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\right)\end{array}\right.$$

4.4. Model CB: Centralized Decision-Making Under Benchmarking and Carbon Tax

In Model CB, carbon allowances are allocated according to a benchmarking mechanism, where the government sets quotas based on the industry’s average carbon intensity. Under this centralized framework, the manufacturer and retailer cooperate to maximize the total profit of the integrated supply chain. Accordingly, the joint profit function can be expressed as Equation (11):

$$\underset{E_1,E_2,E_3}{\max } J_{SC}^{CB}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\begin{array}{l}\underset{\mathrm{sales} \mathrm{proceeds}}{\underbrace{\left({\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\left(Q_0+x(t)+h\tau (t)\right)+\vartheta E_1(t)\mathrm{\Pi }n}}-\underset{\mathrm{Different} \mathrm{investment} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{\left[{\displaystyle \frac{1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{1}{2}}{\eta }_2{E}_2^2(t)+{\displaystyle \frac{1}{2}}{\eta }_3{E}_3^2(t)\right]}}+\\ \underset{\mathrm{Carbon} \mathrm{trading} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_c\left[\left(E_B-e_0\right)\left(Q_0+h\tau (t)+x(t)\right)+\tau (t)\right]}}-\underset{\mathrm{Carbon} \mathrm{tax} \mathrm{to} \mathrm{be} \mathrm{paid} \mathrm{by} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_t\left(\left(e_0\left(Q_0+h\tau (t)+x(t)\right)\right)-\tau (t)\right)}}\end{array}\right\}dt$$

(11)

Assuming an interior solution (see Appendix A), the feedback Stackelberg equilibrium strategies in the benchmarked and carbon tax are given by:

Proposition 4.

In model CB:

(1) 

The optimal investment decision-making decisions for manufacturers and retailers are: $E_1^{CB\ast }={\displaystyle \frac{\vartheta \left({\mathrm{\Pi }}_n+\alpha \epsilon b_1\right)}{{\eta }_1}}$, $E_2^{CB\ast }={\displaystyle \frac{\beta b_2}{{\eta }_2}}$, $E_3^{CB\ast }={\displaystyle \frac{\sqrt{1-x^{CB\ast }}\left(-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}\right)}{\gamma {\eta }_3}}$.

(2) 

The trajectories of the product abatement level and the incremental demand induced by the marketing effort are, respectively:

$${\tau }^{CB\ast }(t)={\tau }_{\infty }^{CB\ast }+({\tau }_0-{\tau }_{\infty }^{CB\ast })e^{-kt}$$

$$\begin{gathered} x^{CB\ast }(t)=x_{\infty }^{CB\ast }+(x_0-x_{\infty }^{CB\ast })e^{-\left({\displaystyle \frac{\sqrt{{\eta }_3\left(2{\gamma }^2\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}+\zeta \right)t} \\ \mathit{and} {\tau }_{\infty }^{CB\ast }={\displaystyle \frac{\alpha \epsilon {\vartheta }^2{\mathrm{\Pi }}_n+\frac{\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)\left(\left(1-e_{0}h+E_{B}h\right)p_c+p_t+h\left(-e_{0}pt+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\right)}{{\eta }_2\left(k+\rho \right)}}{k{\eta }_1}}, \\ {x}_{\infty }^{CB\ast }={\displaystyle \frac{\frac{\sqrt{{\eta }_3\left(2{\gamma }^2\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}}{\frac{\sqrt{{\eta }_3\left(2{\gamma }^2\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}-{\eta }_3\left(\zeta +\rho \right)}{{\eta }_3}+\zeta }} \end{gathered}$$

${\tau }_{\infty }^{CB\ast }$ and $x_{\infty }^{CB\ast }$ are the steady-state values of the two state variables at $t\to \infty$.

(3) 

The long-term benefits of a low-carbon supply chain system are:

$$J_{SC}^{CB\ast }=e^{-\rho t}\left(b_1{\tau }^{CB\ast }(t)+b_2{x}^{CB\ast }(t)+b_3\right)$$

and

$$\left\{\begin{array}{l}{b}_1={\displaystyle \frac{\left(1-e_{0}h+E_{B}h\right)p_c+\left(1-e_{0}h\right)p_t+h\left({\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)}{k+\rho }}\\ b_2={\displaystyle \frac{-{\eta }_3\left(\zeta +\rho \right)+\sqrt{{\eta }_3\left(2{\gamma }^2\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)+{\eta }_3{\left(\zeta +\rho \right)}^2\right)}}{{\gamma }^2}}\\ b_3={\displaystyle \frac{1}{2}}\left(\begin{array}{l}{\displaystyle \frac{a_2^2{\gamma }^2}{{\eta }_3}}+{\displaystyle \frac{a_1^2\left({\beta }^2{\eta }_1+{\alpha }^2{\epsilon }^2{\eta }_2{\vartheta }^2\right)+2a_1\alpha \epsilon {\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n+{\eta }_2{\vartheta }^2{\mathrm{\Pi }}_n^2}{{\eta }_1{\eta }_2}}+\\ 2Q_0\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)\end{array}\right).\end{array}\right.$$

4.5. Model FG: Coordinated Decision-Making Under Grandfathering and Carbon Tax

This section introduces an improved bilateral cost-sharing contract strategy to enhance low-carbon supply chain performance under mixed regulation policies. Recognizing that the retailer’s marketing efforts contribute significantly to enhancing the product’s low-carbon reputation, the manufacturer agrees to subsidize a portion (${\sigma }_3$, where $0<{\sigma }_3<1$) of the retailer’s marketing costs. Simultaneously, under the manufacturer-initiated contract, the retailer shares a portion of sales revenue with the manufacturer to jointly cover the latter’s investment in recycling (${\sigma }_1$) and green technology (${\sigma }_2$), where both ${\sigma }_1$ and ${\sigma }_2$ lie in the interval (0, 1). Within this framework, each party independently determines their optimal levels of recycling effort, green technology investment, and marketing intensity, while internalizing mutual benefits under the designed contractual structure. The mechanism aims to achieve a Pareto improvement, aligning individual incentives with system-wide sustainability goals and promoting synergistic low-carbon development. Accordingly, the objective functions of the manufacturer and retailer in Model FG are defined by Equations (12) and (13), respectively:

$$\underset{E_1,E_2}{\max } J_M^{FG}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\begin{array}{l}\underset{\mathrm{Wholesale} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_m\left(Q_0+x(t)+h\tau (t)\right)+\vartheta E_1(t){\mathrm{\Pi }}_n}}-\underset{\mathrm{Manufacturer}\text{'}\mathrm{s} \mathrm{abatement} \mathrm{investment} \mathrm{costs} \mathrm{after} \mathrm{cost} \mathrm{sharing}}{\underbrace{[{\displaystyle \frac{1-{\sigma }_1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{1-{\sigma }_2}{2}}{\eta }_2{E}_2^2(t)]}}-\underset{\mathrm{Shared} \mathrm{marketing} \mathrm{costs}}{\underbrace{{\displaystyle \frac{{\sigma }_3}{2}}{\eta }_3{E}_3^2(t)}}+\\ \underset{\mathrm{Carbon} \mathrm{trading} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_c\left[\left(E_G-e_0\left(Q_0+h\tau (t)+x(t)\right)\right)+\tau (t)\right]}}-\underset{\mathrm{Carbon} \mathrm{tax} \mathrm{to} \mathrm{be} \mathrm{paid} \mathrm{by} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_t\left(\left(e_0\left(Q_0+h\tau (t)+x(t)\right)\right)-\tau (t)\right)}}\end{array}\right\}dt$$

(12)

$$\underset{E_3}{\max } J_R^{FG}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\underset{\mathrm{Retail} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_r\left(Q_0+h\tau (t)+x(t)\right)}}-\underset{\mathrm{Cost} \mathrm{of} \mathrm{marketing} \mathrm{efforts} \mathrm{for} \mathrm{the} \mathrm{retaile}}{\underbrace{{\displaystyle \frac{1-{\sigma }_3}{2}}{\eta }_3{E}_3^2(t)}}-\underset{\mathrm{Shared} \mathrm{investment} \cos \mathrm{ts} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{\left({\displaystyle \frac{{\sigma }_1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{{\sigma }_2}{2}}{\eta }_2{E}_2^2(t)\right)}}\right\}dt$$

(13)

Assuming an interior solution (see Appendix A), the feedback Stackelberg equilibrium strategies in the benchmarked and carbon tax are given by:

Proposition 5.

Let $e_0<{\displaystyle \frac{p_c+p_t+h\left({\mathrm{\Pi }}_m+{\mathrm{\Pi }}_r\right)}{h\left(p_c+p_t\right)}}$, then in model FG:

(1) 

The optimal investment decision-making decisions for manufacturers and retailers are $E_1^{FG\ast }={\displaystyle \frac{\vartheta \left({\mathrm{\Pi }}_n+\alpha \epsilon u_1\right)}{{\eta }_1\left(1-{\sigma }_1\right)}}$, $E_2^{FG\ast }={\displaystyle \frac{\beta u_1}{{\eta }_2\left(1-{\sigma }_2\right)}}$, $E_3^{FG\ast }={\displaystyle \frac{\sqrt{1-x^{FG\ast }}\left({\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{\sigma }_3\right)\right)\left(-1+{\sigma }_3\right)}\right)}{\gamma {\eta }_3\left(1-{\sigma }_3\right)}}$.

(2) 

The trajectories of the product abatement level and the incremental demand induced by the marketing effort are, respectively:

$${\tau }^{FG\ast }(t)={\tau }_{\infty }^{FG\ast }+({\tau }_0-{\tau }_{\infty }^{FG\ast })e^{-kt}$$

$$\begin{gathered} x^{FG\ast }(t)=x_{\infty }^{FG\ast }+(x_0-x_{\infty }^{FG\ast })e^{-\left({\displaystyle \frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{\sigma }_3\right)\right)\left(-1+{\sigma }_3\right)}}{{\eta }_3\left(1-{\sigma }_3\right)}}+\zeta \right)t} \\ \mathit{and} {\tau }_{\infty }^{FG\ast }={\displaystyle \frac{\frac{\alpha {\vartheta }^2\left({\mathrm{\Pi }}_n+\frac{\alpha \epsilon \left(-\left(\left(-1+e_{0}h\right)\left(p_c+p_t\right)\right)+h{\mathrm{\Pi }}_m\right)}{k+\rho }\right)}{{\eta }_1\left(1-{\sigma }_1\right)}+\frac{\beta \left(\left(-1+e_{0}h\right)\left(p_c+p_t\right)\beta -h\beta {\mathrm{\Pi }}_m\right)}{{\eta }_2\left(k+\rho \right)\left(1-{\sigma }_2\right)}}{k}}, \\ {x}_{\infty }^{FG\ast }={\displaystyle \frac{\frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Gamma }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{\sigma }_3\right)\right)\left(-1+{\sigma }_3\right)}}{{\eta }_3\left(1-{\sigma }_3\right)}}{\frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Gamma }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{\sigma }_3\right)\right)\left(-1+{\sigma }_3\right)}}{{\eta }_3\left(1-{\sigma }_3\right)}+\zeta }} \end{gathered}$$

${\tau }_{\infty }^{FG\ast }$ and $x_{\infty }^{FG\ast }$ are the steady-state values of the two state variables at $t\to \infty$.

(3) 

The long-term benefits of a low-carbon supply chain system are:

$$J_M^{FG\ast }=e^{-\rho t}\left(u_1{\tau }^{FG\ast }(t)+u_2{x}^{FG\ast }(t)+u_3\right)$$

$$J_R^{FG\ast }=e^{-\rho t}\left(y_1{\tau }^{FG\ast }(t)+y_2{x}^{FG\ast }(t)+y_3\right)$$

$$\mathit{and} \left\{\begin{array}{l}{u}_1={\displaystyle \frac{\left(1-e_{0}h\right)\left(p_c+p_t\right)+h{\mathrm{\Pi }}_m}{k+\rho }}\\ u_2={\displaystyle \frac{{\eta }_3\left(A+C\sqrt{B}\right)\left(1-{\sigma }_3\right){\sigma }_3+{\gamma }^2\sqrt{2{\eta }_3{\mathrm{\Pi }}_r\rho \left(1-{\sigma }_3\right){\sigma }_3+\sqrt{B}}\left({\mathrm{\Pi }}_m+e_0\left(p_c+p_t\right)\left(1-{\sigma }_3\right)-\left({\mathrm{\Pi }}_m-{\mathrm{\Pi }}_r\right){\sigma }_3\right)}{{\gamma }^2\left(2{\gamma }^2{\mathrm{\Pi ;}}_r-{\eta }_{3}C\left(1-{\sigma }_3\right)\right)\left(1-{\sigma }_3\right)}}\\ u_3=E_G{p}_c-e_0\left(p_c+p_t\right)Q_0+Q_0{\mathrm{\Pi }}_m-{\displaystyle \frac{{\vartheta }^2{\left(m_1\alpha \epsilon +{\mathrm{\Pi }}_n\right)}^2}{2{\eta }_1\left(-1+{\sigma }_1\right)}}+{\displaystyle \frac{{m_1}^2{\beta }^2}{2{\eta }_2-2{\eta }_2{\sigma }_2}}-{\displaystyle \frac{n_2{\gamma }^2\left(2m_2\left(-1+{\sigma }_3\right)+n_2{\sigma }_3\right)}{2{\eta }_3{\left(-1+{\sigma }_3\right)}^2}}\\ y_1={\displaystyle \frac{h{\mathrm{\Pi }}_r}{k+\rho }}\\ y_2={\displaystyle \frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{\sigma }_3\right)\right)\left(-1+{\sigma }_3\right)}}{{\gamma }^2}}\\ y_3={\displaystyle \frac{1}{2}}\left(\begin{array}{l}2Q_0{\mathrm{\Pi }}_r-{\displaystyle \frac{{\vartheta }^2\left(m_1\alpha \epsilon +{\mathrm{\Pi }}_n\right)\left(2n_1\alpha \epsilon \left(-1+{\sigma }_1\right)+\left(m_1\alpha \epsilon +{\mathrm{\Pi }}_n\right){\sigma }_1\right)}{{\eta }_1{\left(-1+{\sigma }_1\right)}^2}}-\\ {\displaystyle \frac{m_1^2{\beta }^2}{{\eta }_2{\left(-1+{\sigma }_2\right)}^2}}-{\displaystyle \frac{m_1\left(m_1+2n_1\right){\beta }^2}{{\eta }_2\left(-1+{\sigma }_2\right)}}+{\displaystyle \frac{{n_2}^2{\gamma }^2}{{\eta }_3-{\eta }_3{\sigma }_3}}\end{array}\right)\end{array}\right.$$

where $A=-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(1-{\sigma }_3\right)$, $B={\eta }_{3}A\left(1-{\sigma }_3\right)$, $C={\left(\zeta +\rho \right)}^2$.

Introducing a bilateral cost-sharing coordination contract significantly enhances overall supply chain profit compared to decentralized scenarios and even achieves the optimal level attainable under centralized decision-making. However, this system-wide improvement does not necessarily translate into higher profits for individual stakeholders relative to their decentralized benchmarks. For the mechanism to be practically viable, it must satisfy incentive compatibility constraints, specifically $V_M^{FG\ast }\ge V_M^{DG\ast }$, $V_R^{FG\ast }\ge V_R^{DG\ast }$. When these conditions are met, rational actors have the motivation to adopt the proposed mechanism. Otherwise, the absence of individual rationality would render the contract unsustainable. To address cases where the original contract fails to satisfy these constraints, we propose an enhanced coordination mechanism: a profit-sharing extension to the bilateral cost-sharing agreement. This refined contract redistributes the total coordinated profit $V_M^{FG\ast }\ge V_M^{DG\ast }$, $V_R^{FG\ast }\ge V_R^{DG\ast }$ between the manufacturer and the retailer. Let $\phi \in \left(0,1\right)$ denote the manufacturer’s share of the joint profit, while the retailer receives $1-\phi$. The valid range of $\phi$ that ensures both parties’ participation incentives is formally defined in Proposition 5.

Corollary 3.

If the total profit under the coordinated mechanism exceeds that of the decentralized case, there exists a feasible range of profit-sharing ratios, denoted by $\phi \in \left[{\displaystyle \frac{V_M^{DG\ast }}{V^{FG\ast }}},1-{\displaystyle \frac{V_R^{DG\ast }}{V^{FG\ast }}}\right]$, that guarantees individual rationality for both supply chain members.

This implies that when the manufacturer’s profit share $\phi$ falls within this interval, the improved coordination contract not only enhances overall supply chain performance but also ensures Pareto improvements for both parties. The exact value of $\phi$ depends on the relative bargaining power and negotiation dynamics between the manufacturer and the retailer.

4.6. Model FB: Coordinated Decision-Making Under Benchmarking and Carbon Tax

Building on the improved bilateral cost-sharing contract, the profit functions of the manufacturer and the retailer based on the hybrid regulation of the benchmarking and the carbon tax are defined by Equations (14) and (15), respectively:

$$\underset{E_1,E_2}{\max } J_M^{FB}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\begin{array}{l}\underset{\mathrm{Wholesale} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_m\left(Q_0+h\tau (t)+x(t)\right)+\vartheta E_1{\mathrm{\Pi }}_n}}+\underset{\mathrm{Carbon} \mathrm{trading} \mathrm{costs} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_c\left[\left(E_B-e_0\right)\left(Q_0+h\tau (t)+x(t)\right)+\tau \right]}}-\\ \underset{\mathrm{Carbon} \mathrm{tax} \mathrm{to} \mathrm{be} \mathrm{paid} \mathrm{by} \mathrm{the} \mathrm{manufacturer}}{\underbrace{p_t\left(\left(e_0\left(Q_0+h\tau (t)+x(t)\right)\right)-\tau \right)}}-\underset{\mathrm{Manufacturer}\text{'}\mathrm{s} \mathrm{abatement} \mathrm{investment} \mathrm{costs} \mathrm{after} \mathrm{cost} \mathrm{sharing}}{\underbrace{[{\displaystyle \frac{1-{\sigma }_1^{\prime }}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{1-{{\sigma }^{\prime }}_2}{2}}{\eta }_2{E}_2^2(t)]}}-\underset{\mathrm{Shared} \mathrm{marketing} \mathrm{costs}}{\underbrace{{\displaystyle \frac{{{\sigma }^{\prime }}_3}{2}}{\eta }_3{E}_3^2(t)}}\end{array}\right\}dt$$

(14)

$$\underset{E_3}{\max } J_R^{FB}={\displaystyle {\int }_0^{\infty }{e}^{-\rho t}}\left\{\underset{\mathrm{Retail} \mathrm{revenue}}{\underbrace{{\mathrm{\Pi }}_r\left(Q_0+h\tau (t)+x(t)\right)}}-\underset{\mathrm{Cos}\mathrm{t} \mathrm{of} \mathrm{marketing} \mathrm{efforts} \mathrm{for} \mathrm{the} \mathrm{retaile}}{\underbrace{{\displaystyle \frac{1-{\sigma }_3^{\prime }}{2}}{\eta }_3{E}_3^2(t)}}-\underset{\mathrm{Shared} \mathrm{investment} \cos \mathrm{ts} \mathrm{for} \mathrm{the} \mathrm{manufacturer}}{\underbrace{\left({\displaystyle \frac{{{\sigma }^{\prime }}_1}{2}}{\eta }_1{E}_1^2(t)+{\displaystyle \frac{{{\sigma }^{\prime }}_2}{2}}{\eta }_2{E}_2^2(t)\right)}}\right\}dt$$

(15)

Assuming an interior solution (see Appendix A), the feedback Stackelberg equilibrium strategies in the benchmarked and carbon tax are given by:

Proposition 6.

In model FB:

(1) 

The optimal investment decision-making decisions for manufacturers and retailers are $E_1^{FB\ast }={\displaystyle \frac{\vartheta \left({\mathrm{\Pi }}_n+\alpha \epsilon s_1\right)}{{\eta }_1\left(1-{{\sigma }^{\prime }}_1\right)}}$, $E_2^{FB\ast }={\displaystyle \frac{\beta s_1}{{\eta }_2\left(1-{{\sigma }^{\prime }}_2\right)}}$, $E_3^{FB\ast }=-{\displaystyle \frac{\sqrt{1-x^{FB\ast }}\left({\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3^{\prime }\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2\mathrm{\Pi }r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{{\sigma }^{\prime }}_3\right)\right)\left(-1+{{\sigma }^{\prime }}_3\right)}\right)}{\gamma {\eta }_3\left(1-{{\sigma }^{\prime }}_3\right)}}$.

(2) 

The trajectories of the product abatement level and the incremental demand induced by the marketing effort are, respectively:

$${\tau }^{FB\ast }(t)={\tau }_{\infty }^{FB\ast }+({\tau }_0-{\tau }_{\infty }^{FB\ast })e^{-kt}$$

$$\begin{gathered} x^{FB\ast }(t)=x_{\infty }^{FB\ast }+(x_0-x_{\infty }^{FB\ast })e^{-\left({\displaystyle \frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{{\sigma }^{\prime }}_3\right)\right)\left(-1+{{\sigma }^{\prime }}_3\right)}}{{\eta }_3\left(1-{{\sigma }^{\prime }}_3\right)}}+\zeta \right)t} \\ \mathit{and} {\tau }_{\infty }^{FB\ast }={\displaystyle \frac{\frac{\alpha \epsilon {\vartheta }^2\left({\mathrm{\Pi }}_n+\frac{\alpha \epsilon \left(\left(1-e_{0}h\right)\left(p_c+p_t\right)+E_{B}h{p}_c+h{\mathrm{\Pi }}_m\right)}{k+\rho }\right)}{{\eta }_1\left(1-{\sigma }_1^{\prime }\right)}+\frac{{\beta }^2\left(\left(1-e_{0}h\right)\left(p_c+p_t\right)+E_{B}h{p}_c+h{\mathrm{\Pi }}_m\right)}{{\eta }_2\left(k+\rho \right)\left(1-{\sigma }_2^{\prime }\right)}}{k}}, \\ {x}_{\infty }^{FB\ast }={\displaystyle \frac{\frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3^{\prime }\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{{\sigma }^{\prime }}_3\right)\right)\left(-1+{{\sigma }^{\prime }}_3\right)}}{\gamma {\eta }_3\left(1-{\sigma }_3^{\prime }\right)}}{\frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3^{\prime }\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{\sigma }_3^{\prime }\right)\right)\left(-1+{\sigma }_3^{\prime }\right)}}{\gamma {\eta }_3\left(1-{\sigma }_3^{\prime }\right)}+\zeta }} \end{gathered}$$

${\tau }_{\infty }^{FB\ast }$ and $x_{\infty }^{FB\ast }$ are the steady-state values of the two state variables at $t\to \infty$.

(3) 

The long-term benefits of a low-carbon supply chain system are:

$$J_M^{FB\ast }=e^{-\rho t}\left(s_1{\tau }^{FB\ast }(t)+s_2{x}^{FB\ast }(t)+s_3\right)$$

$$J_R^{FB\ast }=e^{-\rho t}\left(z_1{\tau }^{DB\ast }(t)+z_2{x}^{DB\ast }(t)+z_3\right)$$

$$\mathit{and} \left\{\begin{array}{l}{s}_1={\displaystyle \frac{\left(1-e_{0}h\right)\left(p_c+p_t\right)+E_{B}h{p}_c+h{\mathrm{\Pi }}_m}{k+\rho }}\\ s_2={\displaystyle \frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3^{\prime }\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{{\sigma }^{\prime }}_3\right)\right)\left(-1+{{\sigma }^{\prime }}_3\right)}}{{\gamma }^2}}\\ s_3=Q_0\left(E_B{p}_c-e_0\left(p_c+p_t\right)+{\mathrm{\Pi }}_m\right)-{\displaystyle \frac{{\vartheta }^2{\left(s_1\alpha \epsilon +{\mathrm{\Pi }}_n\right)}^2}{2{\eta }_1\left(-1+{\sigma }_1^{\prime }\right)}}+{\displaystyle \frac{s_1^2{\beta }^2}{2{\eta }_2-2{\eta }_2{{\sigma }^{\prime }}_2}}-{\displaystyle \frac{z_2{\gamma }^2\left(2s_2\left(-1+{{\sigma }^{\prime }}_3\right)+z_2{\sigma }_3^{\prime }\right)}{2{\eta }_3{\left(-1+{{\sigma }^{\prime }}_3\right)}^2}}\\ z_1={\displaystyle \frac{h{\mathrm{\Pi }}_r}{k+\rho }}\\ z_2={\displaystyle \frac{{\eta }_3\left(\zeta +\rho \right)\left(-1+{\sigma }_3^{\prime }\right)+\sqrt{{\eta }_3\left(-2{\gamma }^2{\mathrm{\Pi }}_r+{\eta }_3{\left(\zeta +\rho \right)}^2\left(-1+{{\sigma }^{\prime }}_3\right)\right)\left(-1+{{\sigma }^{\prime }}_3\right)}}{{\gamma }^2}}\\ z_3={\displaystyle \frac{1}{2}}\left(\begin{array}{l}2Q_0{\mathrm{\Pi }}_r-{\displaystyle \frac{{\vartheta }^2\left(s_1\alpha \epsilon +{\mathrm{\Pi }}_n\right)\left(2z_1\alpha \epsilon \left(-1+{{\sigma }^{\prime }}_1\right)+\left(s_1\alpha \epsilon +{\mathrm{\Pi }}_n\right){{\sigma }^{\prime }}_1\right)}{{\eta }_1{\left(-1+{{\sigma }^{\prime }}_1\right)}^2}}-\\ {\displaystyle \frac{s_1^2{\beta }^2}{{\eta }_2{\left(-1+{{\sigma }^{\prime }}_2\right)}^2}}-{\displaystyle \frac{s_1\left(s_1+2z_1\right){\beta }^2}{{\eta }_2\left(-1+{{\sigma }^{\prime }}_2\right)}}+{\displaystyle \frac{z_2^2{\gamma }^2}{{\eta }_3-{\eta }_3{{\sigma }^{\prime }}_3}}\end{array}\right)\end{array}\right.$$

Corollary 4.

If the coordinated mechanism yields a higher total system profit than that under decentralized decision-making, then there exists a valid profit-sharing interval  ${\phi }^{\prime }\in \left[{\displaystyle \frac{V_M^{DB\ast }}{V^{FB\ast }}},1-{\displaystyle \frac{V_R^{DB\ast }}{V^{FB\ast }}}\right]$  such that individual rationality constraints are strictly satisfied for both parties.

5. Comparison Analysis

Building on the equilibrium results derived under decentralized, centralized, and coordinated decision-making frameworks, this section systematically compares the equilibrium strategies across key dimensions: recycling effort, green technology investment, marketing effort, emission reduction level, and product demand.

5.1. Comparison of Equilibrium Investment Strategies

Corollary 5.

Under decentralized decision-making, manufacturers allocate greater investment toward both recycling efforts and green technology under the benchmarking–carbon tax policy (DB) compared to the grandfathering–carbon tax policy (DG), i.e., $E_1^{DB\ast }>E_1^{DG\ast }$, $E_2^{DB\ast }>E_2^{DG\ast }$, while retailer marketing efforts remain unchanged, $E_3^{DB\ast }=E_3^{DG\ast }$. Similarly, under centralized decision-making, investment levels satisfy $E_1^{CB\ast }>E_1^{CG\ast }$, $E_2^{CB\ast }>E_2^{CG\ast }$ and $E_3^{CB\ast }=E_3^{CG\ast }$.

Benchmarking-based allocation proves more effective than grandfathering in stimulating upstream low-carbon investment. Grandfathering, which links allowances to historical emissions, often motivates firms to comply by reducing production rather than upgrading technologies. This reliance on historical baselines creates path dependence, weakens the green transition, and disadvantages efficient firms. In contrast, benchmarking establishes uniform carbon-intensity standards, directly connecting allocations to technological performance. This mechanism encourages efficiency gains, clean technology adoption, and enhanced recycling, while promoting green R&D as a source of competitive advantage. Importantly, the two mechanisms signal distinct behavioral responses across the supply chain: grandfathering risks locking firms into compliance through output reduction, whereas benchmarking actively rewards innovation and low-emission production. Overall, benchmarking enhances both fairness and effectiveness in emission reduction, highlighting its critical role in aligning regulatory design with sustainable industrial transformation.

Corollary 6.

Comparing centralized and coordinated decision-making with their decentralized counterparts under identical regulatory settings reveals further distinctions:

(1) 

For manufacturers:

• Under grandfathering + carbon tax:  $E_1^{CG\ast }=E_1^{FG\ast }>E_1^{DG\ast }$  and  $E_2^{CG\ast }=E_2^{FG\ast }>E_2^{DG\ast }$
• Under benchmarking + carbon tax:  $E_1^{CB\ast }=E_1^{FB\ast }>E_1^{DB\ast }$  and  $E_2^{CB\ast }=E_2^{FB\ast }>E_2^{DB\ast }$

(2) 

For retailers:

• Under grandfathering + carbon tax: $E_3^{CG\ast }=E_3^{FG\ast }>E_3^{DG\ast }$
• Under benchmarking + carbon tax: $E_3^{FB\ast }=E_3^{CB\ast }>E_3^{DB\ast }$

These findings underscore the crucial role of coordination in internalizing supply chain externalities. Centralized and coordinated regimes mitigate inefficiencies of decentralized decisions by aligning firm-level actions with system-wide optimization. Specifically, manufacturers achieve more consistent investments in clean technologies through shared returns and joint management of carbon-related costs, while retailers enhance marketing efforts under profit-sharing arrangements that mitigate operational uncertainty. Collectively, these results emphasize the importance of governance architecture: effective carbon allocation must be coupled with integrated decision frameworks to unlock system-wide sustainability gains and guide the direction of low-carbon transitions.

5.2. Comparison of Product Emission Reduction and Market Demand

Corollary 7.

(1) By comparing the steady-state values of emission reduction levels in different mixed regulatory policies under decentralized decision-making, we can obtain  ${\tau }_{\infty }^{DB\ast }>{\tau }_{\infty }^{DG\ast }$; (2) there exists ${\tau }_{\infty }^{DG\ast }<{\tau }_{\infty }^{CG\ast }={\tau }_{\infty }^{FG\ast }$ under mixed regulation of grandfathering and carbon tax policies; (3) there exists ${\tau }_{\infty }^{DB\ast }<{\tau }_{\infty }^{FB\ast }={\tau }_{\infty }^{CB\ast }$ under mixed regulation of benchmarking and carbon tax policies.

These findings demonstrate that greater investment in recycling and green innovation significantly enhances firms’ capacity for emission reduction and strengthens their competitive position. Benchmarking-based allocation again proves more effective than grandfathering, as it rewards lower carbon intensity rather than historical emissions, thereby incentivizing technological upgrades and recycling initiatives. Furthermore, centralized decision-making consistently achieves higher emission reductions by harmonizing manufacturers’ and retailers’ strategies toward system-wide optimization, whereas decentralized structures often fragment incentives. Finally, coordination mechanisms play a decisive role in shaping steady-state outcomes. Their effectiveness ultimately depends on whether incentive structures are perceived as equitable, transparent, and scientifically grounded, which is essential for sustaining long-term low-carbon collaboration.

Corollary 8.

(1) By comparing the corresponding steady-state levels of market demand in different mixed regulatory policies under decentralized decision-making, we can obtain  $Q_{\infty }^{CB\ast }>Q_{\infty }^{CG\ast }$; (2) there exists $Q_{\infty }^{DG\ast }<Q_{\infty }^{CG\ast }=Q_{\infty }^{FG\ast }$ under mixed regulation of grandfathering and carbon tax policies; (3) there exists $Q_{\infty }^{DB\ast }<Q_{\infty }^{CB\ast }=Q_{\infty }^{FB\ast }$ under mixed regulation of benchmarking and carbon tax policies.

The results reveal that emission reduction significantly shapes consumer demand, as higher abatement levels enhance trust in firms’ environmental responsibility and stimulate purchasing intent. Demand closely follows variations in τ, with benchmark-based allocation consistently outperforming grandfathering by better incentivizing green innovation. Moreover, both coordinated and centralized governance generate higher demand than decentralized structures, emphasizing the value of alignment across supply chain actors. Overall, integrating benchmark mechanisms with collective decision-making offers the most effective pathway to strengthen both emission performance and market competitiveness.

6. Numerical Analysis

To ensure scientific rigor and comparability, this study adopts a parameter-setting approach that balances theoretical consistency with practical relevance. Key baseline parameters are held constant to isolate the dynamic effects of core variables. Company A integrates green technologies, including hydrogen-based equipment, adaptive energy management, and vacuum insulation, and implements recycling initiatives, while downstream retailers conduct green marketing to highlight product environmental attributes. Parameter values are drawn from three complementary sources: established studies on carbon regulation (e.g., [47,48,49]), firm-level practices in emission-intensive sectors, and prior research on mixed carbon policies [38,50]. All variables are normalized for computational stability, with representative settings such as $e_0=1$, ${\pi }_n=2$, ${\pi }_m=16$, ${\pi }_r=9$, $\beta =0.8$, $\alpha =0.7$, $Q_0=20$, $k=0.7$, $h=0.6$, $\epsilon =0.8$, $\zeta =0.5$, $\vartheta =4$, $\rho =0.9$, ${\eta }_1=20$, ${\eta }_2=30$, ${\eta }_3=15$, $\gamma =0.7$. Parameters related to mixed carbon policies are set as $p_c=5$, $p_t=1$, $E_B=0.9$ and $E_G=20$, aligning with empirical ranges reported in earlier studies. When analyzing the effect of a specific parameter, all other variables were kept fixed to highlight marginal influences. For instance, when examining the role of h in shaping equilibrium investment strategies, parameters such as $p_c$ and $p_t$ were maintained at their baseline values. While the parameter settings are not unique, they are chosen to illuminate the qualitative interrelationships among regulatory mechanisms and firm strategies, rather than to provide absolute quantitative predictions [35,51].

6.1. Optimal Trajectories of Supply Chain State Variables

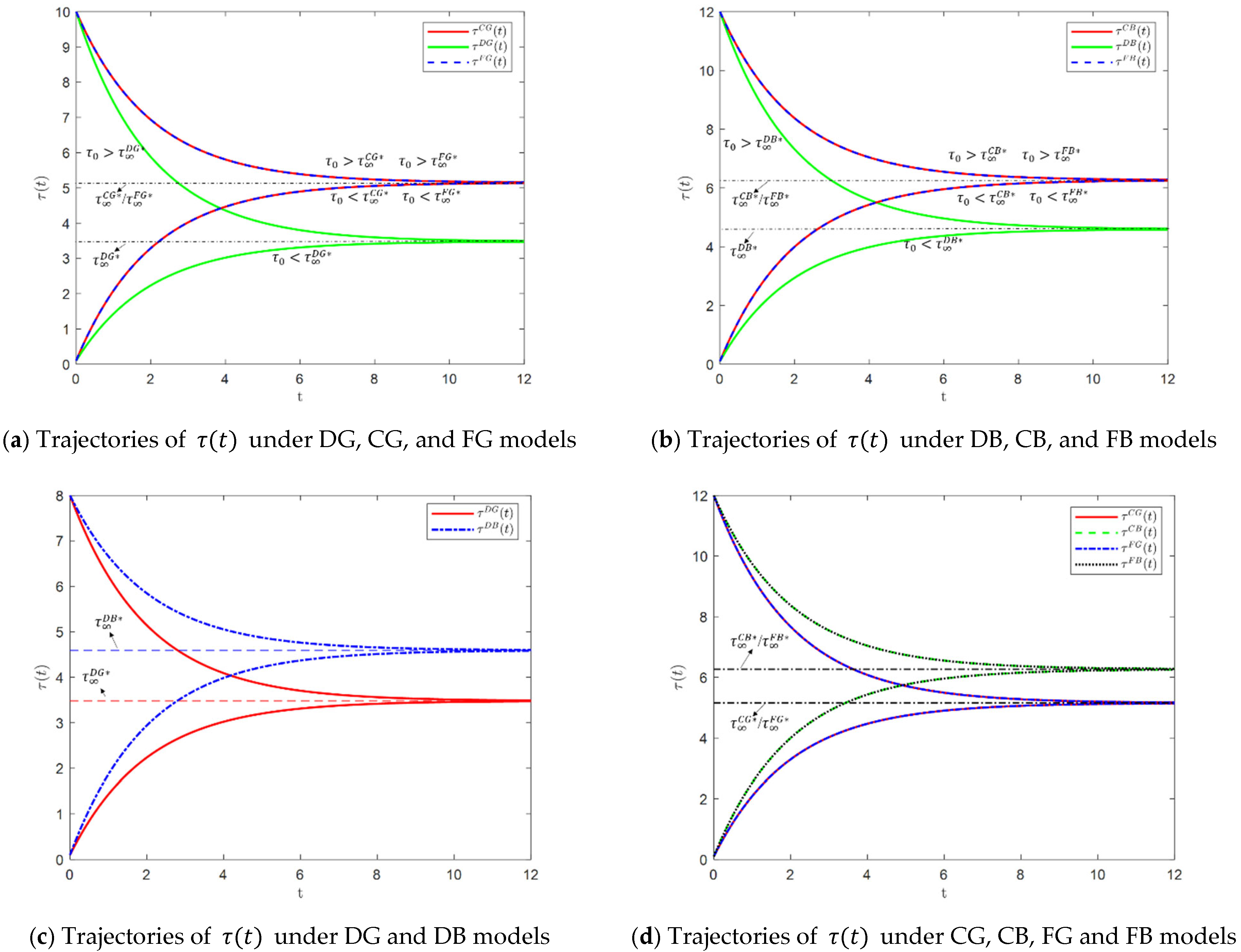
Figure 2 and Figure 3 illustrate the optimal time-evolution trajectories of supply chain emission reduction levels.

Figure 2a,b illustrate the dynamic trajectories of product emission reductions under two dual-policy scenarios across different decision structures. The results indicate that introducing coordination into decentralized systems substantially enhances emission reduction performance, demonstrating the effectiveness of coordinated strategies in motivating corporate green initiatives. Moreover, the evolution of reduction levels exhibits a convergence property: initially high levels gradually decline, while initially low levels rise until stabilization. This suggests the system’s intrinsic dynamic stability. Crucially, the steady-state outcome is not determined by initial conditions but by the interaction between decision-making structures and regulatory policy design.

Figure 2c,d further demonstrate that, across all governance modes, benchmarking-based regimes consistently yield higher emission reductions than grandfathering-based ones. This finding supports Corollary 7 and highlights the pivotal role of carbon allowance allocation mechanisms. Benchmarking policies, by setting uniform performance baselines, act as implicit incentives that stimulate technological upgrading and carbon-efficiency improvements. When combined with carbon taxes, benchmarking schemes also enhance consumer recognition of firms’ environmental commitment, thereby strengthening market competitiveness. These insights offer robust theoretical and practical guidance for the design of integrated carbon regulation frameworks.

Figure 3 illustrates the dynamic evolution of demand increments driven by marketing efforts under two dual-policy regimes: “grandfathering + carbon tax” and “benchmarking + carbon tax.” Under the grandfathering scheme, coordinated and centralized decision structures yield identical marketing effort levels, both lower than those in decentralized governance. In contrast, under the benchmarking scheme, coordinated and centralized strategies result in consistently higher demand increments than decentralized systems. The system’s trajectory is also influenced by initial marketing effort levels: low initial values lead to rising and stabilizing demand, while high initial values result in an early decline before convergence. These patterns highlight that while initial conditions shape short-term dynamics, long-run outcomes are determined by governance structures and policy instruments. Importantly, carbon regulation exerts indirect effects on retailers by altering upstream cost structures, ultimately shaping the effectiveness of downstream marketing efforts and the resulting market demand.

6.2. Impact Analysis of Product Emission Reduction

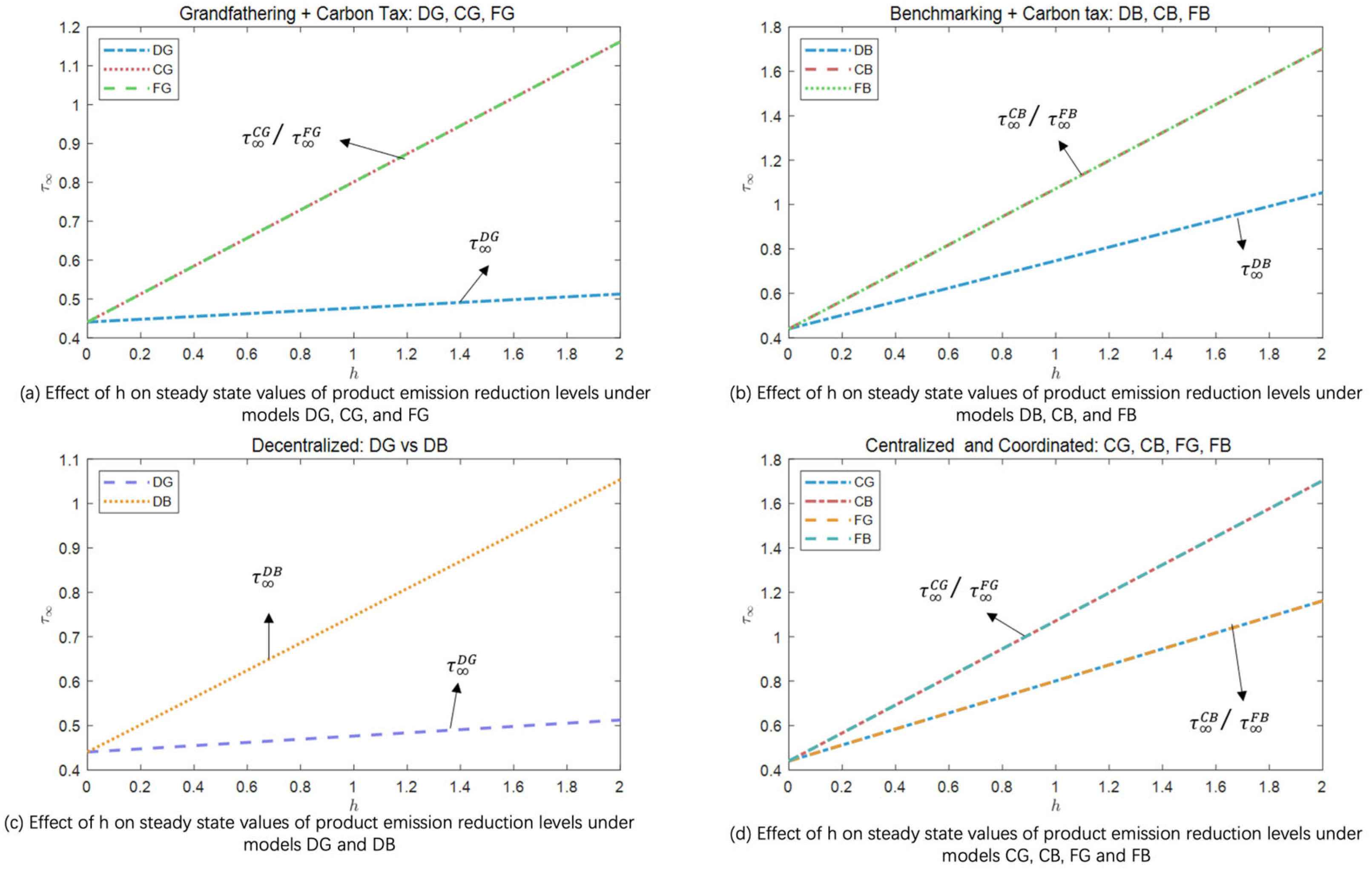
Figure 4 and Figure 5 examine how carbon trading prices, carbon tax levels, and consumer green preferences influence product emission reduction under two dual-policy regimes.

Figure 4 presents the simulation results corresponding to Corollary 7, illustrating how product emission reduction levels respond dynamically to carbon trading prices and carbon tax rates under various policy combinations and decision-making strategies. Across all scenarios: decentralized, centralized, and coordinated, an increase in carbon price leads to a corresponding rise in emission reduction efforts, confirming the effectiveness of both carbon trading and taxation in incentivizing low-carbon transitions. However, the response to carbon trading prices is consistently more pronounced than to carbon tax rates. This difference highlights the greater market flexibility of trading schemes, which enable firms to adjust emissions dynamically through allowance transactions and cost-optimized investments. In contrast, carbon taxes impose a fixed burden, resulting in slower and less responsive behavior.

Figure 4a,b further demonstrate that centralized and coordinated governance structures yield higher emission reductions than decentralized systems under both grandfathering and benchmarking regimes. This suggests that integrated strategies more efficiently allocate abatement resources and share information across supply chains. Moreover, Figure 4c,d show that, under identical decision-making structures, benchmarking-based policies consistently outperform grandfathering in enhancing emission reductions. Benchmarking ties allowances to historical performance or industry best practices, thereby avoiding the inertia and weakened incentives often associated with historical allocation schemes.

As the parameter h captures consumers’ preference for green products, a higher value of h reflects stronger environmental awareness and heightened sensitivity to product carbon footprints. Under such conditions, manufacturers are more inclined to intensify investment in green technologies to improve emission reduction performance, thereby strengthening market competitiveness and brand reputation. Furthermore, stronger green preferences may also drive practices such as remanufacturing and eco-design, accelerating the green transition of the entire supply chain. This dynamic reveals a positive feedback loop between consumer preference and corporate abatement behavior: stronger green preferences increase demand for low-carbon products, which in turn raise the marginal returns on green investments, incentivizing manufacturers to further reduce emissions. This mechanism offers micro-level behavioral support for the policy proposition that “consumption drives green production”. Therefore, in addition to supply side instruments such as taxes and carbon allowances, governments should place greater emphasis on demand-side strategies by promoting green awareness, enhancing eco-labeling systems, and fostering low-carbon values. These efforts are essential to catalyze a broader societal transition in which sustainable consumption drives sustainable production.

6.3. Impact Analysis of Supply Chain Profit

This section investigates how dual carbon policies and consumer environmental preferences affect both individual supply chain profits and overall system profitability. Building on the results in Section 5, the analysis centers on the steady-state outcomes as time approaches infinity. This approach provides insights into the ways carbon regulatory mechanisms and consumer green preferences jointly shape emission reduction levels and the economic performance of the supply chain. Figure 6 and Figure 7 present the effects of carbon trading prices, carbon tax rates, and consumer environmental awareness on firm-level profits and total system profit, respectively.

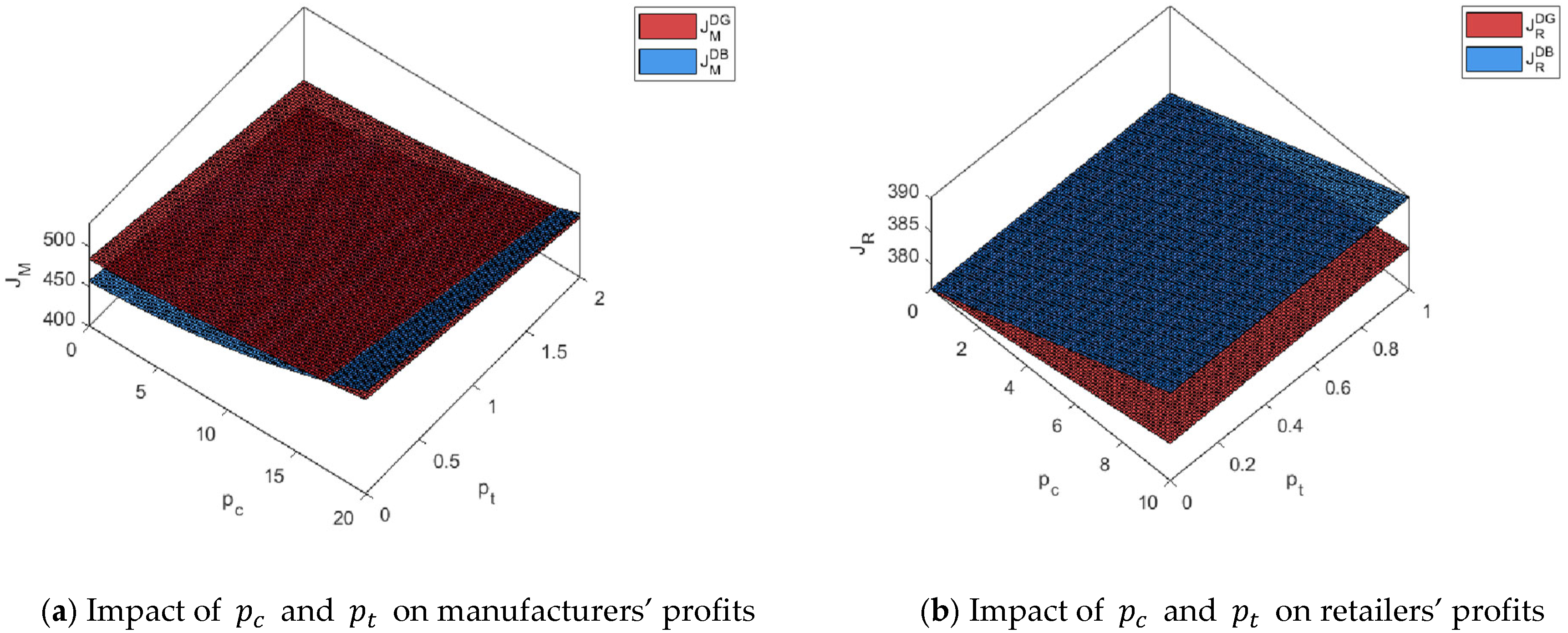
Figure 6a shows that under decentralized decision-making, manufacturer profits decline as carbon tax rates increase but rise with higher carbon trading prices. This occurs because carbon taxes directly raise unit production costs, reducing profitability, while carbon trading provides positive incentives by allowing firms to profit from emission allowances. These dynamics reveal the complementary nature of the two policy instruments in shaping profit outcomes. Additionally, when carbon trading prices are low, manufacturers earn higher profits under grandfathering; however, beyond a certain threshold, benchmarking’s stronger incentives lead to superior profits, highlighting its efficiency and profitability advantage in high carbon price environments. Figure 6b shows that retailer profits, though not directly affected by carbon taxes, increase indirectly through enhanced emission reductions. In the DG and DB scenarios, rising carbon taxes boost emission reduction levels, enhancing product green attributes and market acceptance, thereby increasing retailer profits. Notably, retailer profits consistently exceed those under grandfathering in the “benchmarking + carbon tax” scenario, underscoring the role of well-designed allowance mechanisms in fostering upstream-downstream collaboration and shared gains. Overall, these results emphasize that effective carbon pricing requires a careful balance between incentives and costs to maximize emission reductions and enhance supply chain profitability.

Figure 7 presents the effects of the consumer green preference coefficient (h) on manufacturer and retailer profits under decentralized decision-making. The results reveal a distinct nonlinear increase in profitability for both upstream and downstream firms as h rises. Stronger consumer preferences for low-carbon products enhance market attractiveness, stimulate demand, and thereby boost overall supply chain profitability. In particular, Figure 7a shows that for any given level of h, manufacturers operating under the “benchmarking + carbon tax” scheme (DG model) consistently outperform those under the “grandfathering + carbon tax” regime (DB model). This pattern is consistent with the trend observed in Figure 6a: although grandfathering initially offers cost advantages under low carbon prices due to its reliance on historical emissions, rising green demand strengthens the performance incentives embedded in benchmarking, enabling proactive firms to capture higher carbon revenues and surpass the profitability of their grandfathered counterparts. Figure 7b further demonstrates that retailer profits are systematically higher under benchmarking, with the gap between the two allocation schemes widening as h increases. This suggests that growing consumer green preferences not only enhance acceptance of low-carbon products but also amplify the positive spillover effects of upstream emission-reduction investments on downstream sales. Benchmarking thus reinforces incentive alignment across the supply chain, generating system-level synergies. They also suggest that combining performance-based carbon allocation with policies promoting green consumption provides a robust pathway toward supply chains that are both economically viable and environmentally sustainable.

Figure 8a,b illustrate the evolution of total supply chain profits under dual carbon regulation across different decision-making structures. In both “grandfathering + carbon tax” and “benchmarking + carbon tax” regimes, system profits decline as carbon tax rates rise but increase with higher carbon trading prices. This dual effect reflects the nature of policy instruments: while carbon taxes directly raise production costs and compress margins, higher trading prices strengthen incentives for emission reduction, thereby enhancing overall profitability. Moreover, centralized and coordinated structures consistently outperform decentralized ones in terms of system profits, underscoring the value of inter-firm collaboration in improving resource allocation and emission efficiency. Figure 8c,d further show that, under decentralized governance, both policy regimes follow similar trajectories: profits increase with trading prices but fall with higher carbon taxes. Notably, at low carbon prices, grandfathering performs better due to its leniency toward historical emissions. However, once trading prices surpass a threshold, benchmarking yields greater incentives and higher profits. This advantage becomes more pronounced under centralized and coordinated settings. These findings suggest that profit performance is shaped by the interaction between pricing mechanisms and decision structures. Policymakers should therefore prioritize benchmarking-based trading systems, complemented by moderate carbon taxes, to guide firms toward green investment while securing long-term economic sustainability in low-carbon supply chains.

Figure 9 illustrates how consumer green preference (h) influences total supply chain profit. As shown in Figure 9a,b, profits increase nonlinearly with higher values of h across all decision-making structures. This indicates that stronger consumer preference for low-carbon products substantially boosts demand, thereby improving the profitability of green supply chains. Moreover, profits under centralized and coordinated decision-making consistently exceed those under decentralized governance, underscoring the effectiveness of strategic alignment in maximizing system efficiency and economic performance. Figure 9c further compares the “grandfathering + carbon tax” and “benchmarking + carbon tax” regimes under decentralized decisions. The grandfathering policy consistently yields higher profits, echoing the trend observed in Figure 7a. This can be attributed to the leniency of grandfathering toward historical emissions, which grants firms more generous initial allowances, reducing carbon cost burdens in the absence of coordination. However, under centralized and coordinated regimes, Figure 9d shows that the benchmarking policy generates higher total profits, with this advantage becoming more pronounced as h increases. This outcome highlights the performance-based nature of benchmarking, which provides stronger incentives for firms to invest in green technologies and drives greater emission-reduction synergy across the supply chain. Therefore, consumer green preference not only directly expands the green product market but also indirectly enhances the efficacy of carbon policies under different governance structures. These results suggest that policymakers should prioritize benchmarking-based allocation schemes and adopt coordination mechanisms to align environmental objectives with long-term economic sustainability.

7. Discussions

7.1. Research Findings

This study develops a dynamic decision-making model based on differential game theory to analyze green investment and emission reduction strategies under dual carbon regulatory frameworks. It focuses on two widely adopted hybrid policy schemes: grandfathering combined with a carbon tax, and benchmarking combined with a carbon tax. The analysis considers decentralized, centralized, and coordinated decision structures to uncover how policy instruments, behavioral governance, and consumer preferences jointly influence the formation of low-carbon supply chains.

The results suggest that both policy regimes contribute to enhanced emission reduction performance, but carbon trading prices appear to provide a stronger marginal incentive for firms to invest in green technologies than carbon taxes. This indicates the effectiveness of market-based carbon allocation in stimulating dynamic emission reduction efforts. Benchmarking performs better than grandfathering in high carbon price environments and when green consumption demand is strong, offering higher profits and greater emission reductions. These findings indicate that performance-linked allocation schemes may be particularly suitable for supporting long-term climate goals.

In addition, increased consumer preference for green products is likely to raise manufacturers’ marginal returns on green investment. This creates a positive feedback loop in which consumer demand stimulates technological upgrading, resulting in enhanced profitability and deeper emission cuts. The alignment of consumer preferences with regulatory incentives may strengthen the linkage between production and consumption in low-carbon transitions.

Finally, coordinated and centralized strategies tend to outperform decentralized decision-making in terms of system efficiency and profit outcomes. Under dual carbon policies and rising consumer awareness, introducing cost-sharing coordination mechanisms may further improve resource allocation across the supply chain. This enables joint optimization of emission targets and economic benefits, supporting sustainable supply chain development.

7.2. Managerial Implications

From a regulatory perspective, the complementary effects of dual carbon policies could be strategically utilized. While carbon taxes provide a steady marginal pressure for emissions reduction, they may constrain firm profitability. In contrast, allowance prices within carbon trading systems offer greater flexibility and market responsiveness, enabling a more balanced trade-off between incentive strength and operational feasibility. Therefore, it is advisable for governments to consider benchmarking-based allocation schemes and complement them with moderate carbon taxes, which may enhance both regulatory effectiveness and firm-level acceptance. During the early stages of policy implementation, benchmarking may serve as a transitional mechanism, with gradual incorporation of grandfathering adjustments to accommodate sectoral heterogeneity as institutional capacity develops.

On the demand side, reinforcing incentives through environmental education and promoting green consumption may help amplify the transmission of carbon policy signals via market demand. Strengthening the supporting infrastructure of carbon markets, including pricing mechanisms, transparency, and trading rules, may foster sustained enterprise participation and more stable carbon revenues.

At the firm level, manufacturers are encouraged to monitor carbon price trends, improve green technologies, and treat carbon assets as strategic resources. High-performing firms under benchmarking may obtain surplus allowances, enabling the conversion of emissions efficiency into economic advantage. Retailers, responding to increasing consumer preference for green products, could consider brand greening, certification, and low-carbon marketing collaborations to strengthen market share and supply chain responsiveness.

Finally, implementing cost-sharing and benefit-distribution mechanisms across the supply chain may facilitate collaborative emissions reduction. Aligning incentives between upstream and downstream partners helps prevent free-riding and promotes synchronized green transformation.

7.3. Limitations and Future Research Directions

This study has several limitations that suggest avenues for future research. First, incorporating retailers’ roles in emission reduction or joint strategies would improve practical relevance. Second, expanding the policy framework to include carbon offsetting and accounting for carbon price volatility and uncertainty could enhance robustness; future work should also explore parameter sensitivity by varying key factors across plausible ranges to assess equilibrium stability. Third, beyond the simplified two-tier supply chain, future work may examine competitive or multi-tier networks, incorporate production costs into the model, or endogenize government as a welfare-maximizing decision maker. Finally, empirical calibration using market or firm-level data would strengthen parameter validity and align the benchmark model with real-world practice.