Application of Traffic Load-Balancing Algorithm—Case of Vigo

Abstract

Urban traffic congestion is a significant challenge faced by cities globally, resulting in delays, increased emissions, and diminished quality of life. This study introduces an innovative traffic load-balancing algorithm developed as part of the IN2CCAM Horizon 2020 project, which was specifically tested in the city of Vigo, Spain. The proposed method incorporates short-term traffic forecasting through machine learning models—primarily Long Short-Term Memory (LSTM) networks—alongside a dynamic routing algorithm designed to equalize travel times across alternative routes. Historical speed and volume data collected from Bluetooth sensors were analyzed and modeled to predict traffic conditions 15 min ahead. The algorithm was implemented within the PTV Vissim microsimulation environment to assess its effectiveness. Results from 20 distinct traffic scenarios demonstrated significant improvements: an increase in average speed of up to 3%, an 8% reduction in delays, and a 10% decrease in total standstill time during peak weekday hours. Furthermore, average emissions of CO₂, NO_x, HC, and CO were reduced by 4% to 11% across the scenarios. These findings highlight the potential of integrating predictive analytics with real-time load balancing to enhance traffic efficiency and promote environmental sustainability in urban areas. The proposed approach can further support policymakers and traffic operators in designing more sustainable mobility strategies and optimizing future urban traffic management systems.

1. Introduction

Traffic congestion is a significant social issue faced by nearly all major cities today. It arises when the demand for road usage exceeds the network’s capacity, but it can be alleviated through effective traffic management strategies. Various techniques, including demand management, optimization of traffic signal timings, and traffic balancing, have been developed and implemented to address this challenge. Travelers typically opt for the least congested routes, selecting paths that minimize travel time to lessen the effects of traffic congestion, often relying on mobile applications to identify the quickest options. Both traffic management methods and route planning software fundamentally depend on accurately predicting near-future traffic conditions. In addition to these general causes, it is essential to note that road traffic volumes exhibit specific temporal distribution patterns. On weekdays, the traffic volume across particular road types follows regular hourly trends; however, during public holidays, these patterns are notably disrupted, resulting in significant variations in daily traffic distribution. Such temporal characteristics of traffic flow play a crucial role in analyzing and understanding congestion dynamics. Previous research has examined this issue in detail, highlighting the differences between public holidays and workday traffic distributions across selected road network elements [1]. Incorporating these temporal variations into congestion analysis enhances the accuracy of traffic prediction and provides a more comprehensive perspective for developing effective management strategies.

The IN2CCAM project (Enhancing Integration and Interoperability of the CCAM Eco-System) is conducted within the framework of the Horizon 2020 program. Istanbul Okan University participates in the project as one of the partner institutions. The primary objective is to design, implement, and validate innovative technologies and services that support both infrastructure and end-users. This includes the integration of connected and autonomous vehicles (Cooperative, Connected, and Automated Mobility—CCAM) for both passenger and freight transportation. The overarching goal of IN2CCAM is to benefit all citizens by fully embedding CCAM services into the transportation system. With driverless cars, buses, and trucks operated by Artificial Intelligence (AI)-based vehicle control systems, the project aims to significantly reduce road accidents caused by human error, thereby enhancing road safety. Additionally, this initiative is expected to have positive environmental impacts, such as reducing emissions and optimizing traffic flow to prevent unnecessary travel. It also promotes inclusiveness by ensuring that the elderly and individuals with disabilities can access and benefit from transportation services. This comprehensive approach is centered on the implementation and integration of advanced physical, digital, and operational infrastructures to enhance CCAM services and improve both safety and traffic efficiency.

IN2CCAM comprises 21 partners from nine European countries. The project aims to implement digital and operational CCAM solutions across six living labs. The pioneering living labs where the proposed driverless vehicles will be tested in real traffic conditions are located in Tampere (Finland), Trikala (Greece), Turin (Italy), and Vigo (Spain). Additionally, Bari (Italy) and Quadrilatero (Portugal) will serve as follower living labs, evaluating CCAM services in large simulation environments and conducting impact assessments. The IN2CCAM consortium will share the results and findings from the CCAM integration process in both urban and peri-urban traffic with the public.

Vigo, one of the pioneering living labs within IN2CCAM, is located in northwest Spain and has a population of 292,817. It is a significant urban center renowned for its intense industrial activity, particularly in the automotive and shipbuilding sectors. The city features a bustling fresh fish port -one of the leading ports in Europe- along with a container terminal and various commercial enterprises. However, the city’s dense activity, challenging geography, and irregular growth give rise to a range of transportation challenges.

This study developed a load-balancing algorithm to address traffic demand in the city center of Vigo. The algorithm redistributes traffic across multiple route alternatives to optimize network performance, with the primary goal of equalizing travel times on all alternative routes between designated points. The effectiveness of this algorithm was assessed using the PTV Vissim 2023 microsimulation software.

In the grand scheme of sustainable transportation, reducing traffic and improving the efficient use of existing infrastructure are crucial for cutting energy demand and emissions. As urban regions expand, methodologies that enhance traffic flow with a lean reliance on large-scale new construction promote sustainability by reducing the environmental burden of mobility systems. Dynamic traffic regulation strategies, such as the load-balancing algorithm, are beneficial for enhancing mobility and optimizing resources in the context of sustainable urban development. This makes them efficient tools in building a robust and environmentally friendly transport system.

A longstanding theoretical tension in traffic assignment arises between user equilibrium (UE) and system optimum (SO), as articulated in Wardrop’s principles [2]. Under UE, each driver minimizes their individual travel time, leading to a stable yet often suboptimal outcome for the entire system. By contrast, SO seeks to minimize total travel time across the network, which may require deviations from individually optimal routes. Most existing studies on dynamic routing and load balancing implicitly align with the UE framework, since drivers are modeled as rational agents optimizing their own trips. However, this emphasis on individual rationality overlooks the gap between user-based and system-wide efficiency. In this study, while the simulation framework reproduces driver behavior consistent with UE, the proposed load-balancing algorithm functions as a corrective mechanism that guides routing decisions toward more balanced traffic distributions. In this sense, the method can be regarded as a step toward reconciling UE with SO. It demonstrates potential both as a practical congestion management tool and as a contribution to the theoretical discussion on the trade-off between individual choice and collective efficiency.

The main contributions and innovative aspects of this study can be summarized as follows:

• This paper presents the first combination of 15-min Bluetooth-based short-term traffic forecasts and a real-time load-balancing algorithm. This link effectively connects predictive modeling to dynamic routing decisions.
• It introduces a solid data processing framework that combines Monte Carlo-based methods for filling in missing data with a decade’s worth of high-resolution Bluetooth data. This ensures the reliability and completeness of the input.
• The proposed approach has been thoroughly tested under 20 realistic peak-hour scenarios in PTV Vissim, showing its practical use and strength beyond theoretical development. Additionally, the simulation workflow is designed to be replicable and focused on supporting decision making.
• It provides valuable insights for both local and central governments, as well as mobility service providers working on data-driven congestion reduction.

All the codes used in this study are provided in the GitHub link: https://github.com/OnurPSR/IN2CCAM/ which exists since 1 August 2025.

2. Literature Review

As urban populations grow and vehicle ownership rises, transportation-related challenges have emerged as significant issues in medium- and large-sized cities. These challenges lead to traffic congestion, economic losses, accidents, wasted time during commutes, and environmental impacts associated with transportation [3,4,5]. Public transportation services often face platform failures and deteriorating service quality in high-demand situations, such as natural disasters, pandemics, and holiday periods [6]. In these circumstances, effective traffic management becomes crucial. Without a sound strategy, rising user demand can result in bottlenecks, interruptions, and delays [7].

Congestion management strategies generally fall into two categories: congestion prevention and congestion control. Congestion prevention takes a proactive approach to safeguard the network from overload, while congestion control reacts to congestion that has already occurred within the network [8,9]. Given the current limitations in modifying transportation infrastructure and the insufficient information available to drivers, traditional shortest path algorithms are widely employed. Algorithms such as Dijkstra and A* are commonly used to identify optimal routes and minimize travel times. Alongside these, dynamic path planning algorithms address unique situations [5,10,11,12]. Dynamic path planning algorithms often utilize big data predictive analysis technologies to assess traffic conditions and forecast future scenarios, thereby enabling the estimation of the most suitable routes [13].

One alternative method, multi-agent simulation, emphasizes the individual active components within a system. This approach allows for flexibility in designing heterogeneous actors that interact with one another and their environment [14]. Conversely, reinforcement learning is a modeling technique inspired by behavioral psychology, where the system is conceptualized as agents interacting with their surroundings [15].

Another approach is optimization. In the realm of traffic engineering, optimization focuses on routing traffic across the network to enhance overall performance and efficiently utilize resources. Effective traffic management can improve service accessibility while optimizing resource use and minimizing operational costs [16]. Classical optimization methods typically involve offline routing based on a pre-estimated or predefined traffic matrix [17,18,19]. These methods function effectively as long as actual traffic patterns closely align with the predefined matrix. However, they often struggle to accommodate traffic fluctuations in unexpected scenarios, which has led to the implementation of online dynamic load-balancing techniques [17]. Load balancing enhances efficiency and mitigates the risk of overload by distributing traffic across multiple units, ensuring optimal resource utilization [20]. A notable drawback of this method is the potential for interruptions that may arise during the rebalancing of the routing protocol amidst congestion [17]. Another strategy involves robust static routing, which considers multiple potential traffic matrices to identify a routing configuration that ensures optimal performance across all scenarios [17,21,22].

In unusual road situations, traffic management centers redirect drivers to alternative routes. This approach not only enhances the efficiency and capacity of the network but also mitigates the risk of secondary accidents that can occur due to congestion [23]. In recent years, intelligent navigation systems—similar to active traffic management functions—have been developed. These systems calculate routes that minimize travel times by leveraging congestion predictions derived from the speed and location data of all devices using the application [23].

In earlier studies, Zhang et al. introduced a Dynamic Hybrid Routing framework aimed at optimizing traffic flow [17]. This approach focuses on rebalancing traffic by choosing and implementing the most suitable pre-configured routing scenario in response to fluctuations in traffic conditions. Conversely, Li et al. addressed the challenge of load balancing by formulating it as a non-linear programming problem. They then applied deep learning techniques, combined with traffic predictions, to address this optimization problem [20].

The primary objective of active traffic management is to enhance system performance by utilizing traffic assignment algorithms. In this regard, dynamic routing algorithms and traffic simulations, which help predict traffic patterns, are becoming increasingly vital for designers of active traffic systems. Active traffic management is a crucial concern, not only due to its impact on productivity loss but also because it influences fuel consumption [23].

Modern routing techniques can gather traffic congestion data using both real-time and historical information. Real-time data can be sourced from loop detectors, cameras, toll port data, or mobile phone signals. While today’s prevalent navigation systems typically direct users to the route with the shortest travel time, a significant strategic challenge persists [24]. These systems generally guide drivers based on periodically updated data, which can lead to an excessive concentration of vehicles on the “optimal” route. Consequently, this can lead to increased travel times due to congestion. Additionally, subsequent drivers often make their routing decisions before the impacts of earlier traffic flows are reflected in the system. As a result, directing the majority of vehicles to the “best route” can paradoxically create traffic bottlenecks and lead to longer overall travel times [24].

To address the routing challenge, various algorithms have been developed that employ a cooperative routing approach, taking into account both the predicted traffic volume and estimated travel times [24]. Liu et al. introduced a participatory navigation system that utilizes data from collaborative location and route selections made by vehicles to forecast traffic speed and future traffic flow [24]. Roughgarden’s research suggests that routing without coordination yields suboptimal outcomes [25]. In this context, Wilkie et al. introduced a self-aware re-routing algorithm that integrates historical traffic data with planner-predicted routes. The algorithm explicitly considers the potential for each vehicle’s planned trajectory to exacerbate congestion on the roads; marginally, it utilizes [26].

The use of traffic simulations to assess the potential impacts of policies and strategies has become increasingly essential, particularly as transportation systems become more complex with the incorporation of new active traffic management techniques. The models applied in these analyses are typically categorized as equilibrium models (traffic assignment models) and non-equilibrium models (simulation models) [23]. While equilibrium models fall short in addressing unexpected events, non-equilibrium models are necessary to fill that gap. However, in densely populated and congested urban areas, information is often lacking, especially in situations where various stakeholders, such as smartphone applications and traffic management centers, employ different management strategies [23].

Liang and Wakahara conducted a SUMO microsimulation in a medium-sized area of London, demonstrating that proactive dynamic re-routing can significantly reduce average travel times [27]. In their study, Wang et al. tested an algorithm within SUMO that aimed to address congestion. The process began with calculating the immediate turn for a vehicle approaching a congested road segment, followed by a recalibration of the remaining route [7]. This algorithm achieved an impressive reduction of up to 51.50% in average travel time.

Urban traffic management has been an active research area, encompassing traffic prediction, routing, and load balancing. Traditional parametric models, such as the Kalman filter (KF) [28], exponential smoothing (ES) [29], and the autoregressive integrated moving average (ARIMA) family [30], have been widely applied for traffic prediction. However, these models assume stationary time series, which is often not the case, especially for non-linear traffic data [31]. Non-parametric approaches, including K-nearest neighbor (KNN) [32] and support vector regression (SVR) [33], provide greater flexibility but require careful parameter tuning. Deep learning models, such as stacked autoencoders (SAEs), deep belief networks (DBNs), and artificial neural networks (ANNs), have been explored for their superior predictive capabilities [34]. Standard ANNs, however, cannot explicitly capture temporal dependencies; they often function primarily as output aggregators in deeper network architectures [34]. Recurrent neural networks (RNNs) address this limitation by learning sequential dependencies, making them suitable for time-series prediction. Vanilla RNNs suffer from vanishing gradient issues [35], which are mitigated by long short-term memory (LSTM) networks and gated recurrent units (GRUs) [36]. RNNs are often implemented in stacked layers or encoder–decoder frameworks [37], compressing input sequences into context vectors. While effective, static context vectors may create bottlenecks, limiting the model’s ability to capture complex temporal patterns.

In addition to accurate traffic prediction, effective routing and load balancing are essential for minimizing congestion and improving network efficiency. Traditional shortest-path routing and uniform load distribution approaches are limited in their responsiveness to dynamic traffic conditions. Popularity-based routing methods, such as Polaris, distribute traffic according to road usage patterns, mitigating congestion and lowering CO₂ emissions [38]. Quantum-inspired optimization algorithms provide scalable solutions to complex routing problems, outperforming classical optimization methods in specific urban networks [39]. Strength-optimized weight balancing dynamically adjusts traffic flow to prevent network congestion [40], while adaptive load balancing using Road Side Units (RSUs) redistributes traffic based on network conditions [41]. Smart Route Determining with Load Balancing (SRD-LB) integrates real-time traffic data and environmental factors to optimize routing and reduce travel time [42].

While these schemes represent tremendous advancements over the conventional approach, the most serious problems remain in properly integrating prediction into routing and load balancing. Most dynamic routing algorithms, particularly those based on Reinforcement Learning (RL), respond quickly to real-time data. This quick response can lead to delays or loss of information, resulting in poor clustering. Cars may end up following a limited number of routes, making traffic worse instead of better. Additionally, merging predictive models with load balancing brings up issues with timing and accuracy. If re-routing is too aggressive, it can disrupt traffic; if it is too cautious, it might fail to prevent congestion under changing conditions. These challenges require a broader strategy that utilizes effective traffic predictions and adjusts vehicle schedules across the network to avoid bottlenecks and enhance overall performance.

These constraints drive this current work, which suggests an integrated urban traffic control model. The model combines traffic prediction optimization and load balancing, routing based on not only near-future forecasts but also more abstract network states and long-term traffic patterns. The proposed approach enhances efficiency and reliability in urban road networks by directly addressing issues such as poor clustering, prediction uncertainty, and dynamic load balancing. This is especially important in complex areas, such as Vigo. The combined approach is far superior to conventional approaches, as it provides practical guidance for traffic operators and policymakers who aim to optimize congestion control, minimize travel time, and mitigate environmental impacts.

Technologies such as autonomy and connectivity can significantly enhance system performance [43]. Through vehicle-to-vehicle (V2V) and vehicle-to-infrastructure (V2I) communications, vehicles can exchange information without requiring extensive sensor deployment across the network, thereby improving the overall travel experience [43,44]. V2V communication enables vehicles to access local traffic data, thereby alleviating the computational burden on centralized systems, while automation facilitates real-time responses [44].

A study analyzing 2900 rows of vehicle data, recorded hourly from January to May 2021 at the Başakşehir Mahmutbey Junction in Istanbul, aimed to predict both traffic volume and speed values [45]. To achieve this, an LSTM–based prediction method was employed. Its results were compared with those obtained from linear regression, Random Forest (RF), Support Vector Machines (SVMs), Multi-Layer Perceptron (MLP), Convolutional Neural Networks (CNNs), and RNNs. The LSTM method yielded significantly superior results across all evaluation metrics, including mean squared error, root mean squared error, mean absolute error, and R² values. Specifically, it achieved an R² score of 0.897 for volume prediction and 0.883 for speed prediction.

In another study, researchers sought to predict average speed using data from 15 traffic density measurement stations and 10 weather stations in Istanbul, covering the period from 1 January 2020 to 1 January 2021 [46]. Utilizing four different ANNs along with two SVM models, the General Regression Neural Network (GRNN) model demonstrated the highest performance, attaining an R² value of 0.899.

Additionally, another investigation focused on predicting average flow speed under various conditions along the D100 Highway at the entrance to Tuzla District in Istanbul [47]. This study systematically examined the meteorological factors that affect traffic flow speed, including temperature, humidity, wind speed, prevailing weather conditions, weekdays, and working hours. It further sought to predict average flow speed by analyzing different combinations of these influencing factors. The performance of the developed model was rigorously evaluated by examining the discrepancies between observed and predicted speeds. The analysis indicated that the differences ranged from a minimum of 0.09 km/h to a maximum of 5.98 km/h, demonstrating the model’s predictive accuracy.

A groundbreaking study utilizing the LSTM method to predict near-future traffic speeds was conducted in Beijing, China [48]. This research utilized data from two microwave sensors positioned on a highway to forecast both traffic volume and speed. The performance of the model was evaluated against three RNN architectures, SVM, ARIMA, and Kalman Filters. The LSTM model outperformed all other methods in terms of mean absolute percentage error and mean squared error.

Another significant study focused on traffic speed prediction in Chicago, USA [49]. This study employed various pre-processing techniques to support seven distinct deep learning models aimed at predicting average flow speeds along a 13-mile segment of Interstate 55 (I-55) Highway. The top-performing model achieved an R² value of 0.85, effectively forecasting traffic speeds during both a sports event and rainy conditions.

Additionally, research utilizing data from two publicly available datasets—METR-LA and TaxiBJ—alongside data from the Chengdu Highway in Chengdu, China, aimed to predict traffic [50]. This study employed a graph-based CNN and compared its performance with that of five different methodologies, including LSTM. The evaluation used mean absolute error, root mean squared error, and mean absolute percentage error as performance measures, revealing that the graph-based CNN delivered superior results across all metrics.

A recent review extensively analyzed modern deep learning-based traffic prediction methods, with a particular focus on CNN, RNN, and LSTM, while highlighting the strengths and weaknesses inherent to these deep learning approaches [51].

Traffic prediction has evolved in recent years from traditional time series and deep learning methods to graph-based methods. These new methods explicitly model spatial dependencies in road networks. GNNs have been utilized with open-government data to achieve better performance than traditional methods, such as ARIMA and historical averages. This is because they can effectively manage spatial and temporal interactions within urban traffic systems [52].

Subsequently, more advanced architectures, such as the Dynamic Graph Spatial-Temporal Neural Network (DGSTN), have been proposed to overcome the limitations of static graph models. Equipped with adaptive spatial self-attention and dynamic graph generation, these models can better describe changing traffic conditions. As a result, they outperform traditional LSTM-based models in terms of prediction performance [53]. This shift from static to dynamic graph models shows the advantage of flexibility in modeling changing traffic networks.

Another issue is how to retain prediction capability with new traffic data over time. In 2025, a continual learning framework based on Spatial-Temporal Graph Convolutional Recurrent Networks and regularization techniques, including the Elastic Weight Consolidation and Memory Aware Synapses, is presented. This method enables the learning of new traffic patterns without forgetting the old ones, resulting in more robust real-time prediction [54].

Alongside progress in traffic prediction methods, the development of Vehicle-to-Everything (V2X) communication has enabled cooperative traffic prediction. Among the deep learning models, Bidirectional Long Short-Term Memory (BiLSTM), GRU, and LSTM, we can see that including V2X communication data significantly enhances the prediction performance. These results indicate the usefulness of cooperative vehicle systems in traffic management [55]. Moreover, hybrid models that combine GNNs and Deep Reinforcement Learning (DRL) have been used in optimizing resource allocation for V2X communication networks, demonstrating the broader applications of graph-based learning outside the realm of traffic flow prediction [56].

Additionally, contrastive learning has been recently introduced into GNN-based traffic forecasting models. The Contrastive Learning Multi-Graph Convolution Network (CLMGCN) utilizes temporal data augmentation and contrastive representation learning to enhance feature learning. The model, supported by multiple graph structures, has been shown to outperform traditional graph convolutional models. It confirms that representation learning is effective for traffic forecasting [57].

These developments collectively indicate an interesting direction for research in graph-based, adaptive, and communication-aware prediction models. GNN-based models naturally capture network-level dependencies in a more straightforward manner than LSTM-based ones. V2X models enhance predictions by leveraging information from the cooperation of traffic states. With the addition of continuous learning and contrastive learning, adaptiveness and robustness are enhanced further. This work contributes by placing an LSTM-based prediction model within the context of a real-world decision support system, taking into account these emerging trends for future applications.

3. Materials and Methods

Initially, the traffic data collected for the city of Vigo was assessed, revealing sensor-related gaps within the time series data. These gaps were addressed through a Monte Carlo simulation, followed by short-term traffic forecasting conducted using Machine Learning techniques. Rather than relying solely on current traffic conditions, load balancing was implemented based on anticipated traffic conditions projected for the next 15 min. Ultimately, the traffic load-balancing process aimed to distribute demand in a manner that would achieve equilibrium in travel times on roads within the city center. The effectiveness of the developed load-balancing algorithm was evaluated within the PTV Vissim microsimulation environment. This section provides a comprehensive overview of the studies conducted.

3.1. Traffic Prediction

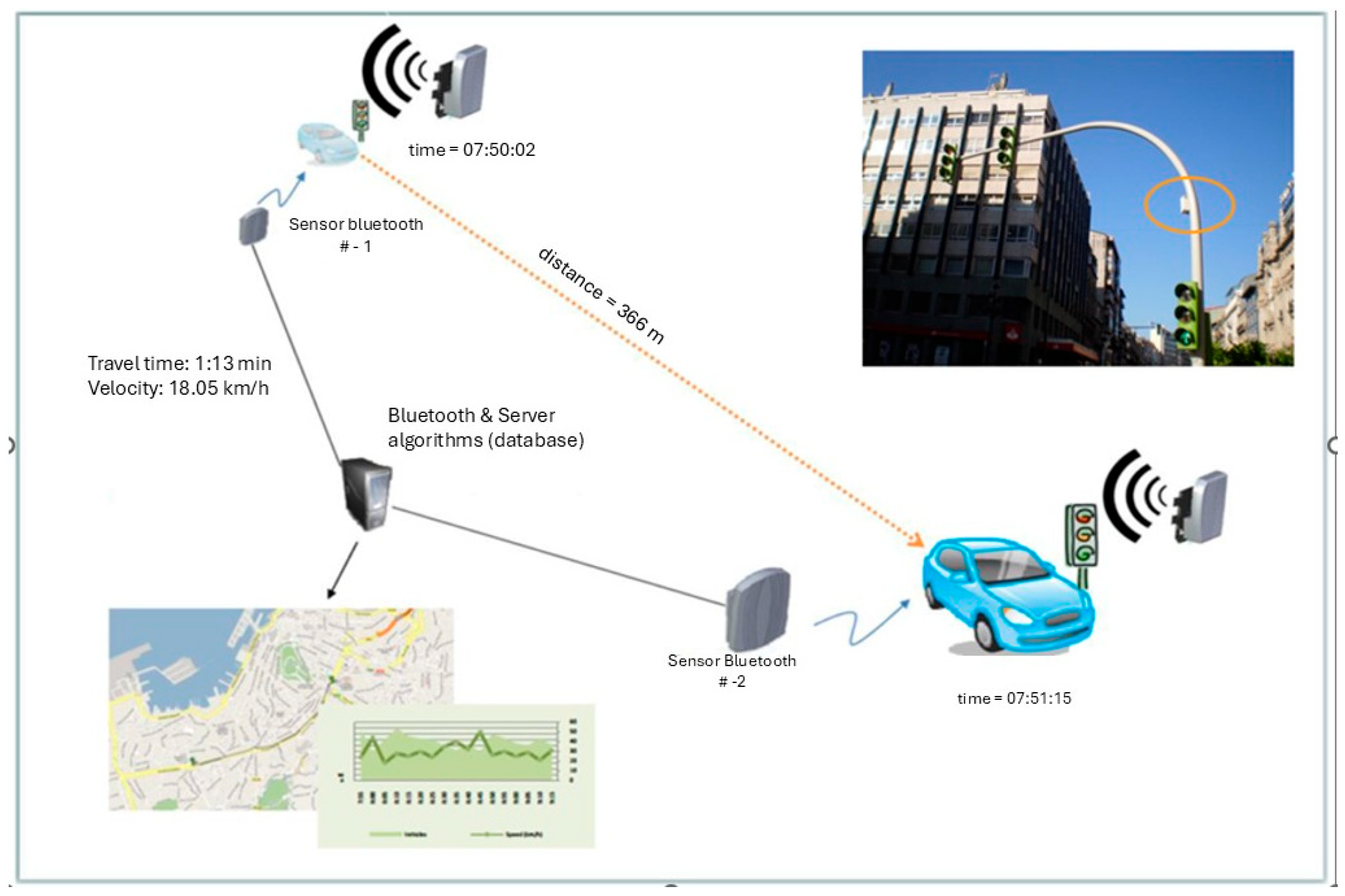
In 2013, the city of Vigo launched a network of 80 Bluetooth sensors. These sensors anonymously capture the Bluetooth MAC (Medium Access Control) addresses of devices, including smartphones and vehicle systems, at various locations throughout the city. The timestamps of these detections are recorded, and an algorithm refines and filters the data to calculate the travel time between two Bluetooth sensor locations. Figure 1 illustrates the Bluetooth sensor detection architecture in Vigo.

The journey between each pair of sensors is referred to as a Vector, with its length and trajectory determined by a set of geographic coordinates. The city publishes all data about these vectors through an API REST (Application Programming Interface, Representational State Transfer) service.

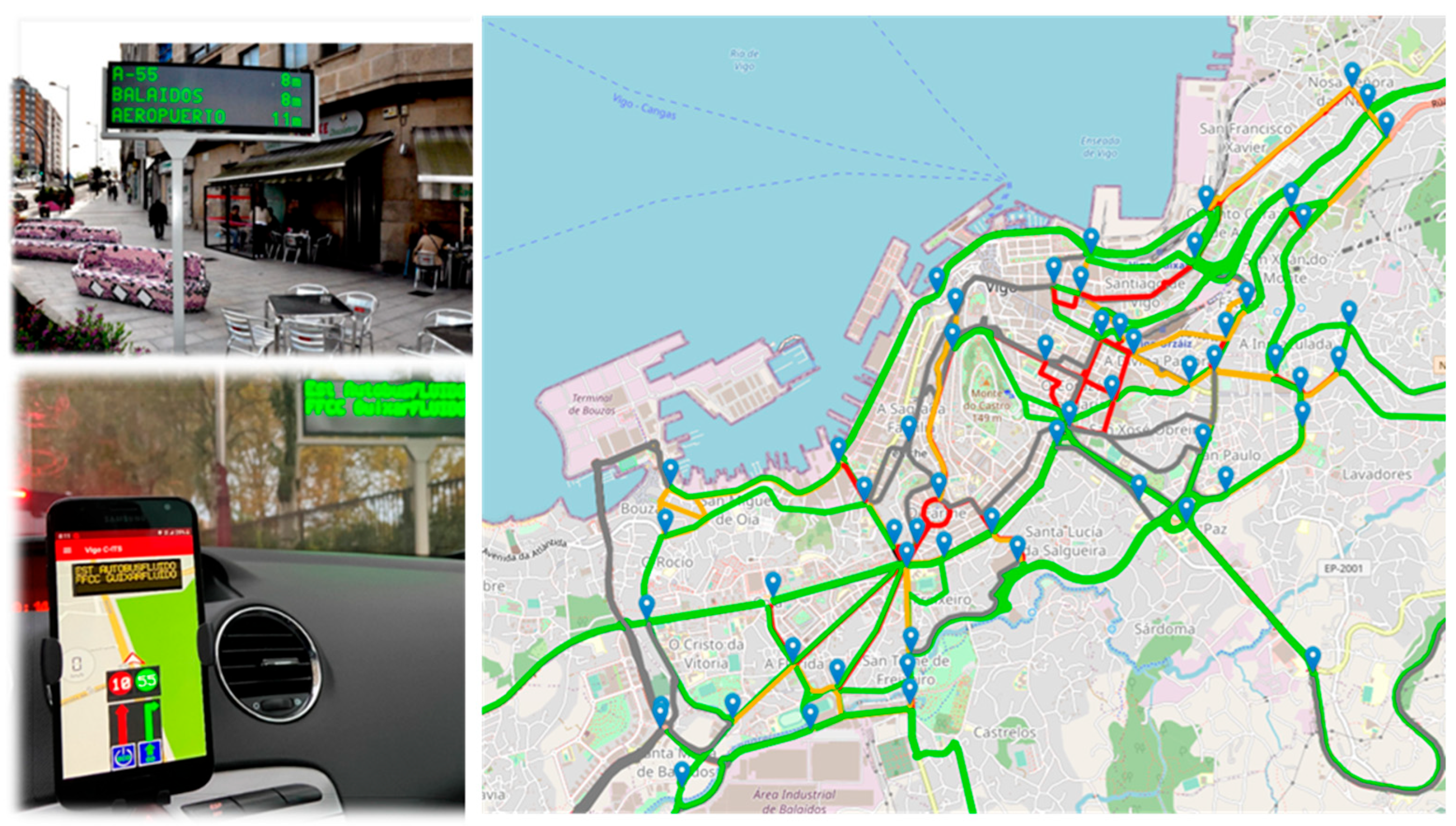
The system’s algorithm computes travel times for all vectors every three minutes. The resulting data are made available through the Vigo website, the Vigo Driving Application (APP) V1.4, and in a JSON (JavaScript Object Notation) file formatted for open data. Travel times for points of interest are displayed on physical Variable Message Panels (VMPs) and Virtual VMPs (IVI—In Vehicle Information messages) within the Vigo Driving APP (see Figure 2).

The thresholds that determine each vector color are as follows:

• Medium Speed > 30 km/h—green.
• 20 km/h < Medium Speed < 30 km/h—green.
• 15 km/h < Medium Speed < 20 km/h—yellow.
• 10 km/h < Medium Speed < 15 km/h—orange.
• Medium Speed < 10 km/h—red.

The data collected by the Bluetooth sensor network is utilized to deliver real-time information to drivers and the traffic management system. Furthermore, all records are stored in a database with a resolution of 3 min. This database contains approximately 10 years of data for each vector, detailing trip times and average speeds. Given the substantial size of the full database, the resolution has been adjusted to 15 min. The final dataset now comprises 112 months of recorded data for 281 vectors, with a compressed size of 2.7 GB.

To assess traffic load and vehicle counts, an experimental study was conducted at the onset of the system’s deployment and is regularly updated. This is essential since not all vehicles and drivers are equipped with Bluetooth-enabled devices. In 2014, the Municipality of Vigo installed Bluetooth sensors in the city and subsequently conducted a study to measure their effectiveness in detecting vehicles. This study utilized inductive loops and video camera recordings to assess the proportion of total vehicles that were detected by the Bluetooth sensors. The study contrasts the actual number of vehicles measured (using inductive loops or video recordings) with the number of detected Bluetooth devices. Findings indicate that the Bluetooth system captures 30% of the total vehicle count in the city, allowing for extrapolation of vehicle numbers for each vector based on this measurement. This rate is also consistent with those reported in some studies in the literature [58,59,60,61]. For this study, information obtained from the Municipality of Vigo served as the basis, and no additional field studies were conducted to verify this rate.

Taking all of this into account, the historical data provided for traffic model training spans the period from 2014 to 2024 and is structured as seen in

Table 1. Structure of historical traffic data in Vigo.

Vector ID	Vector Description	Vector Length (m)	Time Stamp	Detected Devices (ud)	Matches (ud)	Probes (ud)	Clusters (ud)	Scans per Device	Avgspeed15 (km/h)	Traveltime15 (s)	Losstime15	Quality15
97	Av. Madrid—Seminario a Av. Madrid—Estacion	1378	2023-11-02T07: 15:00Z	440	99	86	0	9.11	38.4	130	5.88	0.94
247	Av. Clara Campoamor desde Parque Tecnologico a Estrada do Foxo	792	2023-11-02T08: 00:00Z	278	99	86	0	8.02	48.7	58.7	0	0.93
114	Gran Via—Carmen A Gran Via—Tarragona	381	2023-11-02T10: 15:00Z	276	99	89	0	10.1	36	38.2	3.92	0.94
97	Av. Madrid—Seminario a Av. Madrid—Estacion	1389	2023-11-02T17: 15:00Z	467	99	88	2	8.96	34.9	144	20.1	0.94
114	Gran Via—Carmen a Gran Via—Tarragona	381	2023-11-03T12: 45:00Z	337	99	91	0	10.1	33.9	41	6.69	0.94

.

Table 2. Explanation of the historical data fields.

Parameter	Explanation
Detected Devices	Number of unique wireless devices detected at the destination sensor.
Matches	Number of matches between origin and destination sensor (including outliers).
Probes	Number of quality matches between the origin and destination sensor (excluding outliers).
Clusters	Number of clusters detected between origin and destination (including outliers). Clusters consist of a group of devices (two or more) that are detected simultaneously and are already known to the system as devices traveling together in the exact vehicle.
Scans per device	The average number of times each device has been scanned (detected) at the destination sensor.
Speed (km/h)	The calculated real-time vector speed. The calculated average speed of the vehicles over the full distance of the vector from the origin sensor to the destination sensor.
Travel time	The calculated real-time vector travel time. The calculated average time it took the vehicles to travel the full distance from the origin sensor to the destination sensor.
Loss time	The calculated real-time vector loss time is based on the typical speed settings of the vector. The calculated average time the vehicles lost due to delays when travelling the full distance of the vector from the origin sensor to the destination sensor. If the speed is faster, the loss of time is zero. The loss of time of traffic moving at a slower speed is the time lost in reference to the time it would take at the typical speed.
Quality	The statistical quality of the gathered data. The quality is, above all, based on dispersion, recentness, and quantity. 0.01 is 1% (poor quality). 0.99 is 99% (excellent quality).

offers explanations of the historical data fields. The obtained dataset does not contain any Bluetooth MAC address data for the detected devices. Therefore, there are no issues concerning General Data Protection Regulation (GDPR) compliance or the ethical handling of mobility data.

The number of vehicles recorded in each database (DB) registry is calculated through the extrapolation of the ’Probes’ parameter, grounded in experimental data as previously discussed. For example, in the first line of the illustration, there are 86 quality matches (Probes). This allows us to estimate the total number of vehicles that passed during the 15 min. By dividing 86 by 0.33, the estimated total is approximately 260 vehicles. In the conducted study, a ±5% margin of error was added to this value to ensure data randomness.

Hourly flow rates and average flow speed data were collected from 80 Bluetooth sensors in Vigo, Spain, recording information every 15 min from September 2014 to November 2023 across 281 origin–destination pairs. The methodology employed involved detecting devices at both the starting and exit sensors; if a device was detected at both locations, it was classified as moving within a vehicle. This approach effectively prevents the misidentification of pedestrians or lower-speed vehicles, such as bicycles, as motor vehicles. Furthermore, when multiple Bluetooth devices were detected at the duplicate entry and exit times, they were considered as separate devices within a single motor vehicle, with all being evaluated as a single unit.

In the study, five of these origin–destination pairs were selected for sampling, and a separate simulation was conducted for each pair. Traffic speed predictions were then conducted specifically for these pairs. Despite continuous data collection from the sensors, some data were missing due to disruptions in collection and transmission to the traffic control center. Consequently, specific time intervals contain incomplete data. After that, data pre-processing was performed, and any missing data were synthesized using a Monte Carlo simulation technique. The equations used for these purposes are presented in Equations (1) and (2).

x_min = max(x_hourmin, x_daymin, x_monthmin)

(1)

x_max = min(x_hourmax, x_daymax, x_monthmax)

(2)

In the equations, x_min denotes the minimum value that can be assigned to the missing data, while x_max signifies the maximum value. The terms x_hourmin and x_hourmax represent the smallest and largest values, respectively, recorded at the same hour across different days within the dataset. x_daymin and x_daymax represent the lowest and highest values recorded on the same day of the week, respectively. Similarly, x_monthmin and x_monthmax denote the smallest and largest values observed within the same month of the year. To better understand the method, consider the Aerop. Hasta Ap–9 Túnel Da Madroa origin–destination pair, where the average speed data for 17 May 2020 (Sunday), between 19:00–19:15, is assumed to be missing. First, all speed values for the 19:00–19:15 interval in the data obtained for this origin–destination (O-D) pair were collected. The smallest of these values is defined as x_hourmin and the largest as x_hourmax. Similarly, for the same sensor pair, the smallest speed value obtained across all Sundays is defined as x_daymin and the largest as x_daymax. The smallest speed value obtained within May 2020 is defined as x_monthmin and the largest as x_monthmax. The largest of the minimum values is defined as the lower bound (x_min), and the smallest of the maximum values is defined as the upper bound (x_max). After establishing the lower and upper limits for the potential values of the missing data, a random value is generated, conforming to a normal distribution within these boundaries, to fill in the gaps. The pseudo code of the Monte Carlo technique is given as Algorithm 1.

Algorithm 1. Pseudo Code of the Monte Carlo Technique
1:	Proc GENERATE_NULL_VALUE(data, O, D, missingtimestamp):
2:	Input:
3:	data ← dataset of speed values
4:	O, D ← origin-destination pair
5:	missingtimestamp ← time of missing data (date + time interval)
6:	Output:
7:	xmissing ← imputed value for the missing data
8:	// Step 1: Extract contextual information
9:	hour     ← hour(missingtimestamp)
10:	day       ← day_of_week(missingtimestamp)
11:	month    ← month(missingtimestamp)
12:	// Step 2: Collect candidate values from dataset
13:	hourvalues ← all values from data[O,D] at same hour across different days
14:	dayvalues ← all values from data[O,D] on same day_of_week across dates
15:	monthvalues ← all values from data[O,D] in same month across years
16:	// Step 3: Compute bounds
17:	xhourmin ← min(hourvalues)
18:	xhourmax← max(hourvalues)
19:	xdaymin ← min(dayvalues)
20:	xdaymax ← max(dayvalues)
21:	xmonthmin ← min(monthvalues)
22:	xmonthmax ← max(monthvalues)
23:	xmin ← max(xhourmin, xdaymin, xmonthmin)   // lower bound
24:	xmax ← min(xhourmax, xdaymax, xmonthmax)   // upper bound
25:	// Step 4: Generate random value within bounds
26:	meanval ← (xmin + xmax)/2
27:	stdval ← (xmax − xmin)/6    // 99.7% normal distribution rule
28:	Repeat
29:	xmissing ← random_normal(meanval, stdval)
30:	Until xmin ≤ xmissing ≤ xmax
31:	Return xmissing

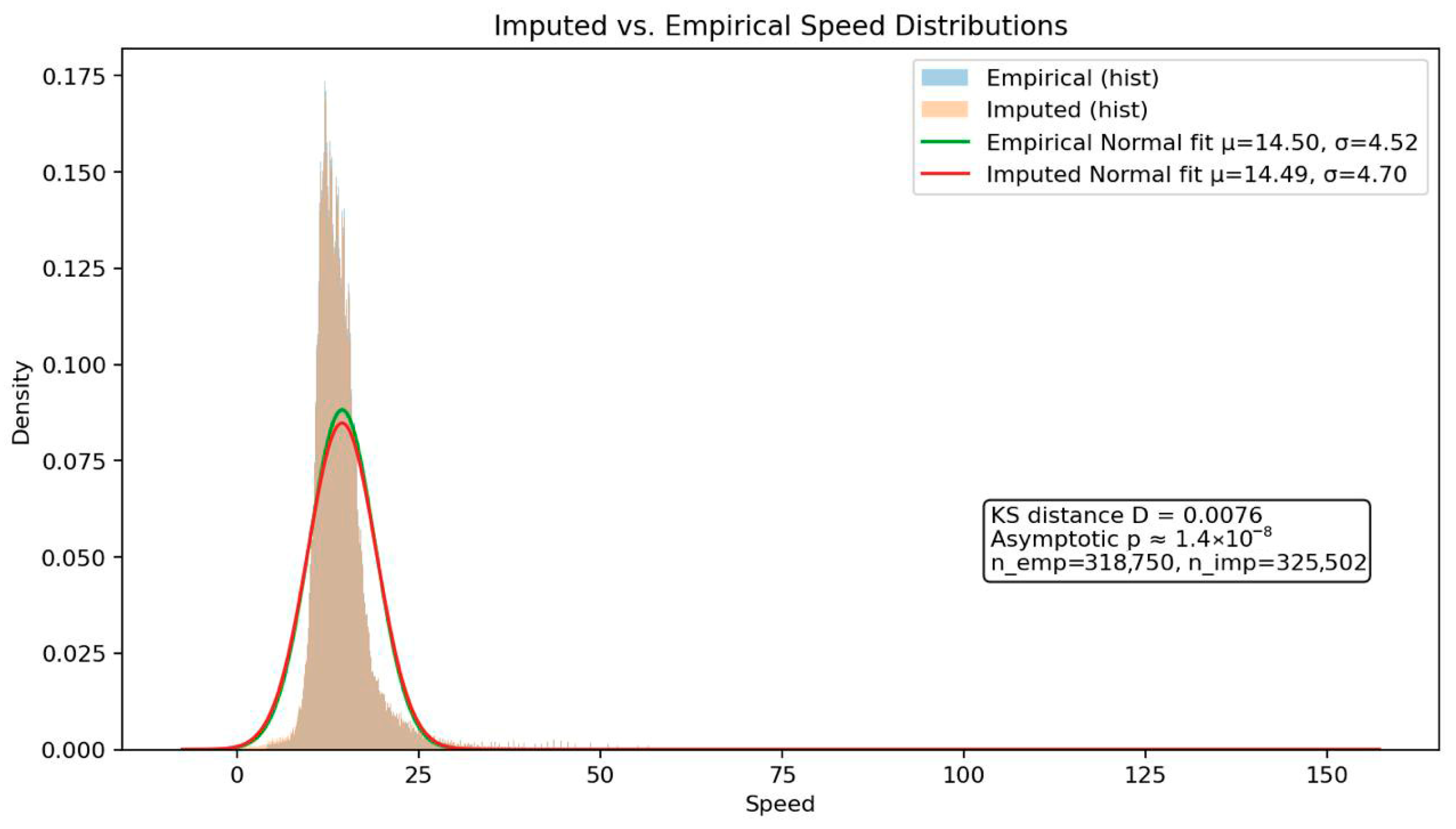
The imputed versus empirical speed distributions are shown in Figure 3.

3.2. Machine Learning Models

The machine learning methods outlined below were employed to predict traffic volume for five start–end pairs along the 281. A separate model was developed for each start–end pair of data. Each method utilized the last eight traffic speed values, reflecting the average traffic speed over the previous 2 h, as input features. The single output value represents the anticipated traffic speed 15 min in advance. Although the Bluetooth sensors in the city of Vigo began to be installed in 2014, not all of the sensors from which data were obtained in this study were installed that year. Instead, the network reached its current state through the gradual addition of sensors at locations where they were needed. Therefore, data from 2014 to 2021 were used for training the models, data from 2022 for validation, and data from 2023 for the test set. Considering the entire dataset, approximately 80% of the total data was allocated for training, 10% for validation, and 10% for testing. Evaluation of performance was conducted exclusively on the test set. All models were developed using the Python programming language (3.10.12).

3.2.1. Multiple Linear Regression

Multiple Linear Regression (MLR) is a fundamental statistical technique that models the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data. The primary goal of this method is to identify the best-fitting line that minimizes the sum of squared residuals (SSR), which quantifies the discrepancy between observed and predicted values. One of the key advantages of linear regression is its ability to provide clear interpretations of the relationships among variables. The coefficients in the model signify how much the dependent variable changes in response to a one-unit change in the independent variable while keeping all other variables constant.

3.2.2. Support Vector Regression

SVR is an extension of the SVM algorithm designed for regression tasks. It functions by identifying a function that approximates the data within a defined margin of error, which makes it effective in high-dimensional spaces and resilient to overfitting, particularly with smaller datasets. SVR employs the kernel trick to transform input data into a higher-dimensional space, enabling it to address non-linear relationships. The algorithm aims to find a hyperplane that fits the data with the least possible deviation within a specified threshold, known as epsilon.

One of the key advantages of SVR is its flexibility in managing non-linear data through various kernel functions, including linear, polynomial, and radial basis functions. This adaptability enables SVR to conform to various data structures, making it suitable for a wide range of applications. Furthermore, SVR is memory-efficient, as it relies on a subset of the training points (support vectors) in its decision function.

3.2.3. Random Forest Regressor

The Random Forest Regressor (RFR) is an ensemble learning technique that constructs multiple decision trees and produces predictions by averaging the outputs of these individual trees. This method, referred to as bootstrap aggregating or bagging, enhances both accuracy and robustness. Each tree is created from a random subset of the training data, which helps mitigate overfitting and improve the model’s generalization capabilities. The diversity among the trees enables the Random Forest to effectively capture complex interactions between features, making it a powerful tool for regression tasks.

The key advantages of Random Forest include its efficiency in handling high-dimensional data and large datasets. It accommodates both numerical and categorical variables, demonstrating robustness against outliers and noise. Additionally, the algorithm offers measures of feature importance, providing valuable insights into the underlying data structure. However, it can be computationally demanding and memory-intensive, especially when a large number of trees are utilized. While the ensemble nature of the model may reduce interpretability compared to single decision trees, this trade-off is often justified by the substantial gains in predictive accuracy.

3.2.4. Multi-Layer Perceptron Regressor

An MLP is a type of artificial neural network designed to model complex relationships through multiple layers of interconnected neurons. An MLP comprises an input layer, one or more hidden layers, and an output layer. Each neuron in a layer is connected to every neuron in the subsequent layer, forming a dense network capable of learning intricate patterns within the data. The network employs an activation function in each layer to introduce non-linearity, enabling it to capture complex, non-linear relationships. Training the model involves backpropagation, during which the weights are adjusted iteratively to minimize prediction error.

The advantages of MLPs lie in their ability to approximate any continuous function, provided that a sufficient number of neurons and training data are available. This flexibility makes them suitable for a diverse range of applications, including image and speech recognition, financial forecasting, and medical diagnosis. One of the model’s key strengths is its capacity to handle large datasets and capture complex dependencies among features. However, MLPs require significant computational resources, particularly when dealing with deep networks comprising numerous layers and neurons. The training process can also be slow and may necessitate a substantial amount of data to avoid overfitting. Additionally, MLP models can be challenging to interpret, as their complex network structure does not readily provide insights into the relationships between variables.

3.2.5. AdaBoost Regressor

AdaBoost Regressor (ABR), which stands for Adaptive Boosting, is an ensemble learning technique that combines multiple weak learners to create a robust predictive model. The algorithm operates by sequentially adding weak learners, typically in the form of decision stumps, to the model. Each learner is trained to correct the errors made by its predecessors, with increased emphasis placed on instances that were misclassified. This iterative process continues until either a specified number of weak learners is reached or no further improvements can be achieved. AdaBoost is particularly effective in enhancing the performance of weak models, although it can be sensitive to noisy data and outliers.

The strength of AdaBoost lies in its ability to enhance the accuracy of weak models by focusing on challenging instances. The algorithm dynamically adjusts the weights of the training data, placing greater importance on those that are more difficult to predict. This targeted approach enables the model to learn from its errors and gradually improve. However, AdaBoost is also at risk of overfitting, especially when dealing with noisy data, as it may pay excessive attention to outliers. Furthermore, the performance of AdaBoost is influenced by the selection of weak learners and the number of iterations, necessitating careful tuning and validation.

3.2.6. Gradient Boosting Regressor

Gradient Boosting Regressor (GBR) is an ensemble learning technique that constructs models sequentially, with each new model aiming to rectify the errors made by its predecessors. This approach leverages the strengths of multiple simple models to generate a robust predictive model. Each model in the sequence is trained on the residuals of the previous model, progressively minimizing the overall prediction error. The iterative nature of Gradient Boosting enhances its performance, making it an effective method for capturing complex patterns within data. This technique excels with structured data and can achieve impressive predictive accuracy.

One of the primary advantages of Gradient Boosting is its flexibility in accommodating various loss functions, which can be customized to address specific problems. This versatility enables Gradient Boosting to be applied across a wide range of applications, including regression, classification, ranking, and other complex tasks. Furthermore, the algorithm demonstrates commendable resilience to overfitting, particularly when parameters are adjusted with meticulous care. Its capability to manage both numerical and categorical data, along with its efficiency in processing large datasets, positions Gradient Boosting as a favored choice in numerous machine learning endeavors.

3.2.7. k-Nearest Neighbor Regressor

KNN is a non-parametric algorithm utilized for both classification and regression tasks. It predicts the value of a new data point by considering the ’k’ nearest neighbors from the training set. This method operates on the premise that similar data points tend to be clustered together, making KNN both intuitive and straightforward to implement. In regression tasks, KNN determines predictions by calculating the average value of the ’k’ nearest neighbors. Its simplicity and intuitive design contribute to the popularity of KNN across various applications, including pattern recognition and data mining.

The primary advantages of KNN include its straightforwardness and flexibility, as it does not impose any assumptions regarding the underlying data distribution. It effectively handles both classification and regression tasks, demonstrating resilience against noisy data. However, KNN can be computationally demanding, particularly with large datasets, due to the need to calculate distances for all data points in the training set for each prediction. This can result in high memory usage and slower prediction times. Additionally, the algorithm’s performance is heavily influenced by the choice of ’k’ and the distance metric, requiring extensive cross-validation to optimize these parameters. KNN is also sensitive to the scale of the data, necessitating the use of appropriate normalization or standardization to ensure accurate results.

3.2.8. Extra Tree Regressor

The Extra Tree Regressor (ETR), also known as Extremely Randomized Trees, is an ensemble learning technique that enhances prediction accuracy and robustness by averaging the outputs of multiple decision trees. This approach involves constructing numerous trees using the entire dataset while selecting split points at random, thereby increasing diversity among the trees. This inherent randomness helps to mitigate overfitting, rendering Extra Trees more resilient than standard decision trees or even Random Forests in certain situations. The algorithm effectively manages both numerical and categorical variables, demonstrating robustness in the presence of outliers and noise within the data.

One of the key advantages of the Extra Trees Regressor is its capability to accommodate diverse data types and provide estimates of feature importance, which are crucial for gaining insights into the underlying data structure. The random selection of split points yields a diverse set of trees, which enhances the model’s ability to generalize to new data. Furthermore, Extra Trees is computationally efficient and lends itself to parallelization, thus making it scalable for large datasets. However, the model may be less interpretable compared to simpler models such as linear regression, as it consists of an ensemble of multiple trees. It can also be memory-intensive, necessitating considerable storage for the ensemble. While randomness typically helps reduce overfitting, it may occasionally lead to increased bias if the model is not correctly tuned. Therefore, careful parameter tuning and validation are essential to achieve optimal performance.

3.2.9. Long Short-Term Memory

LSTM networks are a specialized form of RNNs that effectively capture long-term dependencies in sequential data, making them particularly suited for time series prediction. LSTMs address the shortcomings of traditional RNNs by incorporating mechanisms such as input, output, and forget gates, which regulate the flow of information. This enables the network to retain relevant information over extended periods while discarding irrelevant data. As a result, LSTMs excel in various tasks, including time series forecasting, speech recognition, and natural language processing.

The primary advantage of LSTMs lies in their robustness when handling sequential data, where the relationships between data points over time are critical. This characteristic makes them highly effective for applications demanding precise time series predictions, such as financial market forecasting, weather prediction, and energy load forecasting. By effectively managing the vanishing gradient problem—a common challenge in standard RNNs—LSTMs maintain performance across long sequences.

Despite their strengths, LSTMs do have limitations. They are computationally intensive and require considerable training time and resources, particularly when working with large datasets. The complexity of the model can complicate the interpretation of its internal workings and the relationships it captures. Additionally, hyperparameter tuning for LSTMs can be intricate, often necessitating extensive experimentation to achieve optimal performance. Nevertheless, the advantages of LSTMs in managing complex sequential data establish them as invaluable tools within the machine learning toolkit.

In summary, LSTM networks are potent methods for modeling and predicting sequential data due to their capacity to capture long-term dependencies while alleviating common issues faced by traditional RNNs. Although they are resource-intensive and require careful tuning, their applications across various fields highlight their significance and effectiveness in time series analysis.

3.2.10. Comparison of Model Performances

The performance metrics (R² and Mean Squared Error, MSE) obtained from the Deep Learning models for each start–end pair are presented in

Table 3. R² Value of the Models.

Performance	Aerop. Hasta Ap-9 Túnel Da Madroa	Florida-Padre Seixas A Ricardo Mella	Martinez Garrido-Burgos A Aragon-Jenaro	Praza Da Estacion A Garcia Barbon	Pso Alfonso XII—G Portela—Berbes
MLR	0.844	0.697	0.747	0.792	0.971
SVR	0.848	0.681	0.733	0.796	0.972
RFR	0.840	0.678	0.728	0.783	0.973
MLP	0.853	0.708	0.753	0.804	0.976
ABR	0.750	0.701	0.742	0.831	0.955
GBR	0.853	0.707	0.754	0.802	0.974
KNN	0.826	0.655	0.707	0.768	0.971
ETR	0.833	0.662	0.720	0.774	0.972
LSTM	0.953	0.918	0.907	0.952	0.993

and

Table 4. MSE Value of the Models.

Performance	Aerop. Hasta Ap-9 Túnel Da Madroa	Florida-Padre Seixas A Ricardo Mella	Martinez Garrido-Burgos A Aragon-Jenaro	Praza Da Estacion A Garcia Barbon	Pso Alfonso XII—G Portela—Berbes
MLR	15.282	29.082	11.341	8.483	71.137
SVR	14.861	30.558	11.958	8.314	69.796
RFR	15.677	30.922	12.186	8.837	67.333
MLP	14.377	27.982	11.039	7.985	63.403
ABR	24.526	28.803	11.438	25.235	113.920
GBR	14.369	28.122	11.026	8.071	63.936
KNN	17.039	33.126	13.091	9.477	72.928
ETR	16.325	32.394	12.547	9.207	69.935
LSTM	14.765	29.238	9.186	8.366	78.988

. As indicated by the tables, the LSTM model has exhibited significantly superior performance in terms of R² across all origin–destination pairs when compared to the other models. However, with respect to mean squared error (MSE), it outperformed the other models only in the Martinez Garrido–Burgos and Aragon–Jenaro pairs. In the cases of Aeropuerto Hasta Ap-9 Tunnel Da Madroa, GBR, Florida–Padre Seixas A Ricardo Mella, and Praza Da Estacion A Garcia Barbon Ve Pso Alfonso XII–G Portela–Berbes, the MLP model demonstrated the best performance. Nevertheless, the performance of the LSTM model closely approached that of these models. In both tables, the best values are highlighted in bold. The hyperparameters of the LSTM model are presented in

Table 5. Hyperparameters of the LSTM Model.

Component	Hyperparameter	Search Space	Final Value
Model Input	Input Sequence Length	[3, 4, 5, 6, 7, 8, 9, 10]	8
Model Input	Prediction Horizon	[15 min]	15 min
Model Input	Hidden Layer Size	[5, 10, 15, 20, 25, 30, 35, 40, 45, 50]	15
Model Input	Number of Layers	[1, 2, 3, 4]	2
Model Input	Batch Size	[32, 64, 128]	64
Regularization	Early Stopping Patience	[8]	8
Optimizer	Loss Function	[Adam Optimizer]	Adam Optimizer
Optimizer	Learning Rate	[1 × 10−3, 5 × 10−4]	1 × 10−3
Normalizer	-	-	-
Window Length	-	-	-
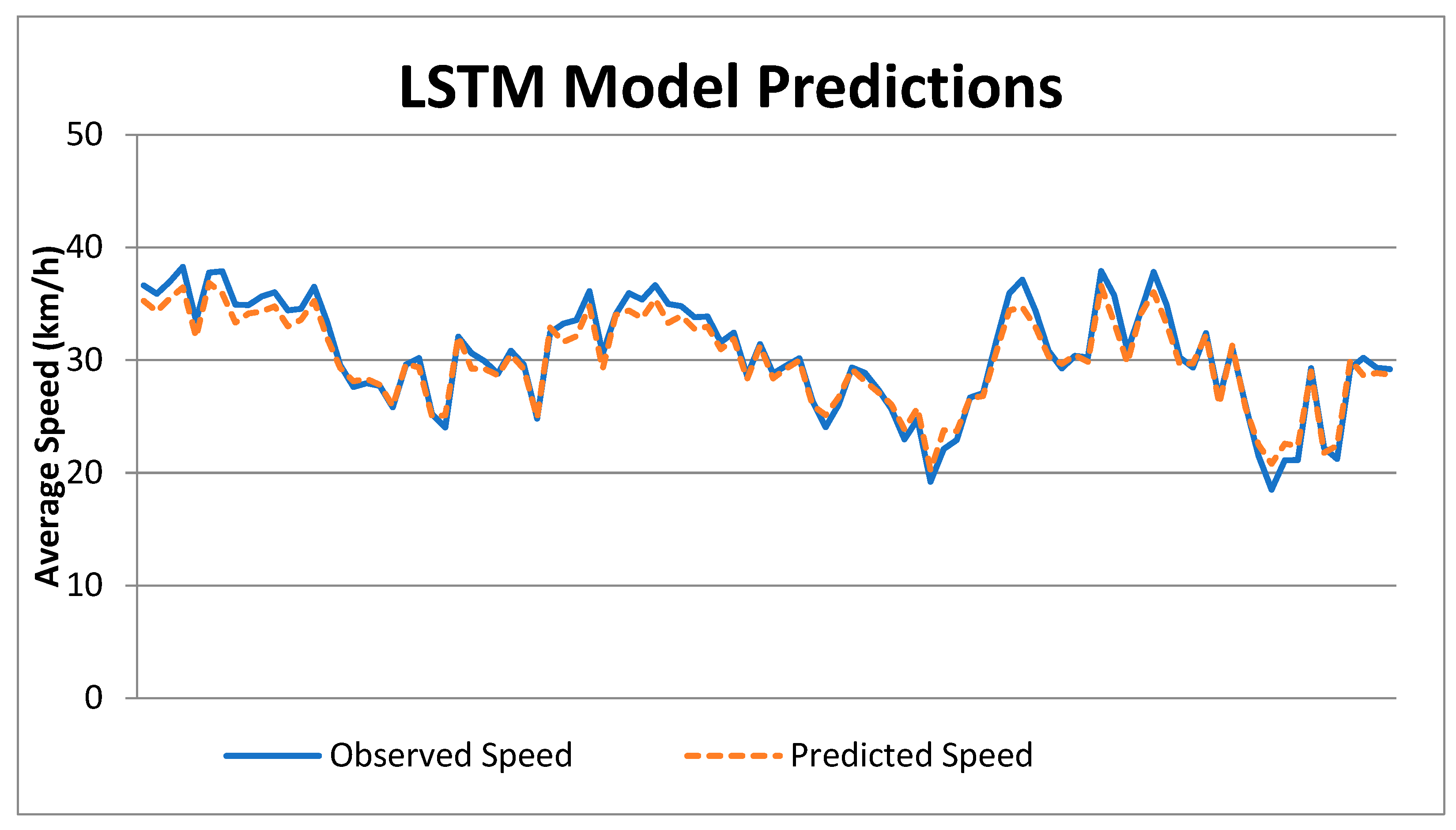
Stride	-	-	-

. To visualize the prediction performance of the LSTM model, the predicted speed values derived from the speed data obtained at Martinez Garrido-Burgos A Aragon-Jenaro for a single day are illustrated in Figure 4.

The results indicate that the models perform well in estimating traffic volume through time-series analysis using machine learning methods, with the LSTM model demonstrating the highest levels of performance among those tested. Accurate traffic predictions are crucial for various applications, including demand management, optimizing traffic signal timings, and balancing traffic flow. Nonetheless, models trained solely on historical traffic speed data, despite achieving high accuracy, exhibit limitations in anticipating changes in traffic conditions. Additionally, they tend to provide average values during peak and trough periods of demand, including speed estimates.

3.3. Load-Balancing Algorithm

Load balancing has its roots in computer technology. It refers to the process of distributing resources—such as servers, processors, and storage units—across a network or system in an equitable manner to optimize performance. This approach not only enhances the efficiency of network or system operations but also bolsters resilience against potential overloads.

The primary objective of load balancing is to effectively distribute traffic or queues directed towards resources experiencing high demand. By ensuring that traffic is evenly distributed among available resources, load balancing helps prevent resource overload. It mitigates the risks associated with single points of failure, which can lead to performance degradation.

This technique is particularly prevalent in large-scale networks and server clusters, where it plays a crucial role in ensuring high availability and performance. By reducing the likelihood of system crashes, load balancing improves user experiences and supports business continuity. A variety of load-balancing algorithms and technologies are employed to cater to differing requirements.

In the realm of transportation engineering, load balancing can be likened to the role of a traffic police officer, who alleviates congestion by directing vehicles to optimal positions. This systematic approach not only prevents accidents but also ensures that vehicles reach their destinations as efficiently and swiftly as possible. Traffic load balancing, therefore, refers to the balanced distribution of traffic across various resources in a network, resulting in more effective resource utilization and improved network performance.

Implementing traffic load balancing is crucial for increasing operational efficiency, saving time and resources, and minimizing environmental impacts in road transportation. Consequently, transportation companies and logistics operations can strategically adopt these practices to reap significant benefits, particularly in large distribution centers, logistics hubs, and warehouses, where effective traffic management is essential. This not only helps to lower costs but also improves delivery timelines.

Achieving effective transportation efficiency can be accomplished through several methods:

Route Optimization: This process ensures that the chosen route is the most accurate, based on time and distance parameters. To optimize routes, various factors must be taken into account, including the number and locations of necessary visit points along the route, as well as the timing of these visits. By optimizing transportation routes, vehicles can take shorter and more efficient paths, resulting in reduced fuel consumption and time savings. Effective route optimization not only enhances distribution and transportation processes but also supports business growth through cost-effectiveness.

Vehicle Tracking Systems: Global Positioning System (GPS)-based vehicle tracking systems facilitate real-time monitoring of vehicles, allowing for route adjustments based on current traffic conditions and helping to balance traffic load.

Capacity Planning: Efficient transportation capacity planning organizes vehicles and shipments according to demand, thereby preventing unnecessary trips made by empty vehicles.

Multiple Distribution Centers: For larger companies, utilizing multiple distribution centers to distribute loads yields positive outcomes by balancing traffic and minimizing delivery times.

Transportation Diversification: Employing a diverse range of interoperable transportation modes—such as trucks, trains, and ships—helps to balance traffic loads and reduce costs.

Traffic Routing: Traffic routing algorithms can effectively be employed to steer clear of congested areas.

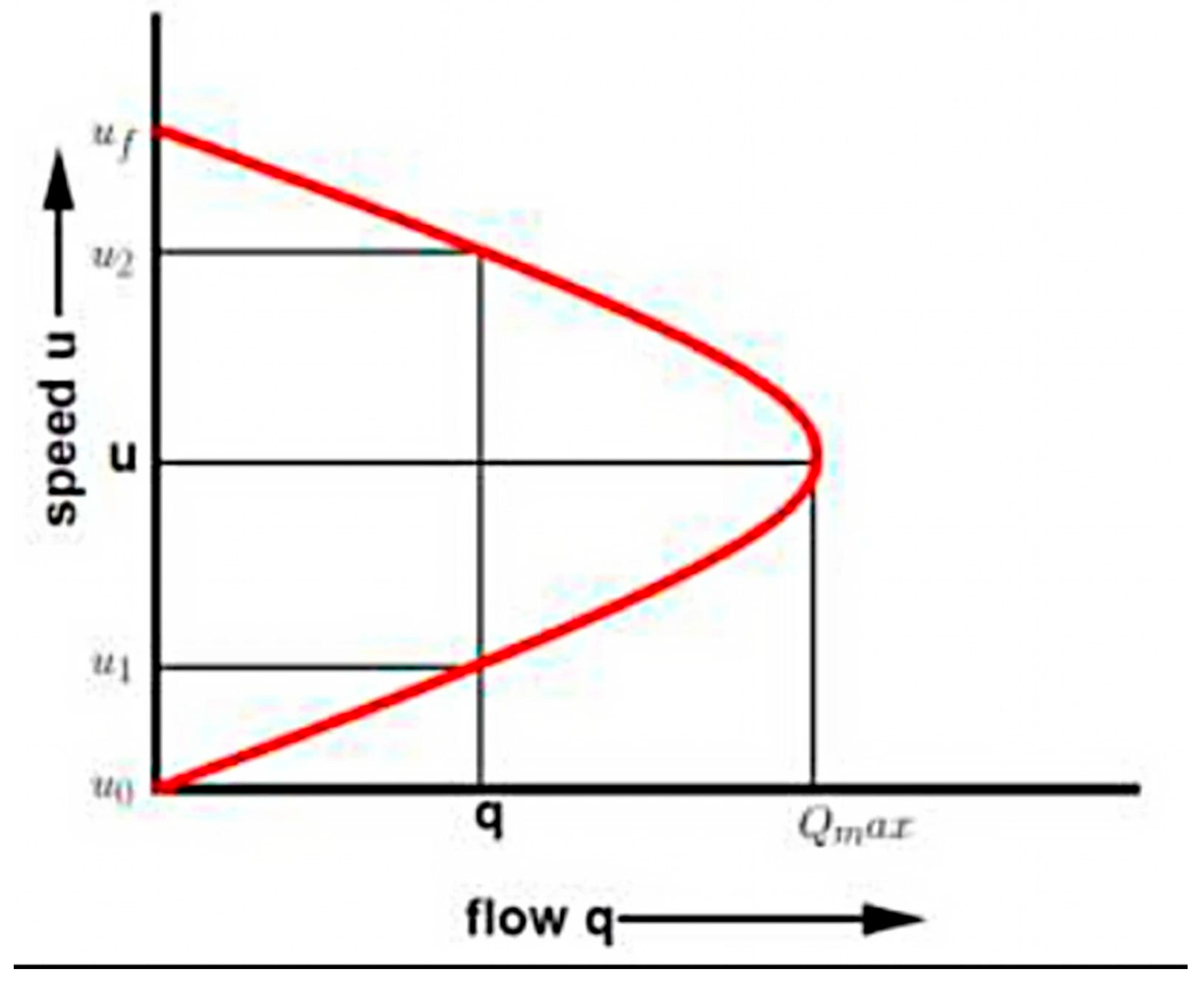
In the IN2CCAM project, the development of a load-balancing algorithm began with classifying roads in the city center of Vigo into four categories based on their respective legal speed limits. For each category, the boundary conditions of traffic flow were determined. These conditions included free flow speed (u_s), jam density (k_jam), and maximum flow (Q_max), which were calculated based on the number of lanes in one direction, ranging from one to four. Utilizing these values, the fundamental relationship between speed and flow was derived individually for each road, as illustrated in Figure 5.

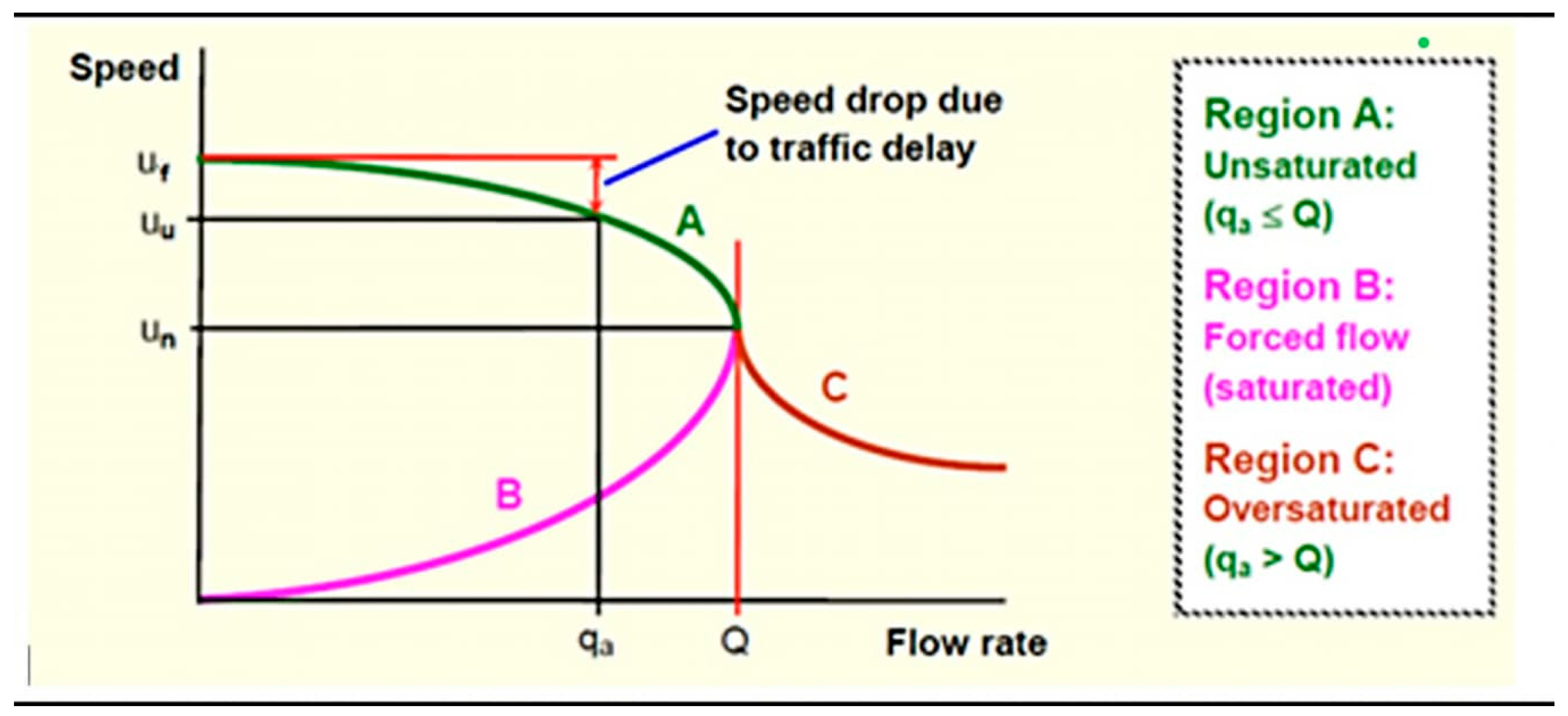
The speed–flow relationship predicts a decline in flow when demand surpasses Q_max; however, it fails to address how speed is affected when demand exceeds capacity. Consequently, for the saturated flow conditions depicted in Figure 6, the shift in speed resulting from demand exceeding capacity was determined by symmetrically reflecting the forced flow section of the graph around the capacity point. This approach enabled the derivation of individual curves that illustrate how vehicle demand affects flow speed on each road in the city center of Vigo.

The developed load-balancing algorithm determines the optimal route between any two points by taking into account current road congestion. It subsequently guides vehicles along these routes to distribute traffic evenly and prevent bottlenecks. As each new vehicle contributes to the load on its selected path, the algorithm recalibrates the conditions and may suggest an alternative route for subsequent vehicles.

Initially, a weighted and directed graph is constructed to represent all possible transactions between roads. The algorithm incorporates two distinct weights: the distances between roads and the travel durations between them (Equations (3)–(5)).

G = (V, E, d, τ)

(3)

d:E ⟶ R_(>0)

(4)

τ:E ⟶ R_(>0)

(5)

In this context, V represents the set of roads, E signifies the set of directed connections, d denotes the length of edge E in kilometers, and τ indicates the expected travel time in minutes.

Once the graph is created, an adjacency matrix is generated to facilitate recursive calculations and enable traversal of all nodes. Based on the structured data, all potential paths between the source and destination are determined using a depth-first algorithm with an exhaustive search method.

The 15-min prediction results are used to determine how many seconds it will take for a driver to use a route, considering the car congestion on that route. With the prediction results using discrete time blocks of 1–20 s, a car congestion threshold dataset is constructed. Each column represents a car congestion threshold, which is needed at maximum to travel at that time in seconds. The weights of the duration and distance parameters are tested in different proportions.

The path with the shortest distance is identified with depth-first approach, and, subsequently, all paths whose distance is less than λ times the shortest distance are filtered for evaluation, where λ is a tuned threshold set by the Sobol test.

The duration of the filtered paths is then calculated in relation to the road’s load. To evaluate the optimal path, durations and distances of roads are normalized with respect to their minimum and maximum values, and a weighted average approach is employed. The weight α balances time and distance and is tuned via the Sobol sensitivity test. The procedure is given as Equations (6) and (7).

$$\tilde{\mathrm{d}}={\displaystyle \frac{\mathrm{d}-{\mathrm{d}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathrm{d}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{d}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}, \tilde{\mathrm{t}}={\displaystyle \frac{\mathrm{t}-{\mathrm{t}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\mathrm{t}}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{t}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}$$

(6)

Weighted average = α(duration) + (1 − α/100)(distance)

(7)

The weighted average is calculated based on the priority assigned to the variables of duration and distance. After computing the weighted average for each candidate path, the one with the lowest value is selected. Subsequently, the travel times for the roads along that route are updated. Each time a new vehicle is routed from the source to the destination, these same steps are repeated. As traffic increases, travel times may change, which can alter the recommended path compared to the initial suggestion. Evaluations of the results are analyzed using the First-order Sobol Sensitivity Test. Based on the parameters within the specified range, 512 tests have been conducted.

Table 6. Parameters of the Load-Balancing Algorithm.

Parameter	Search Space
Depth Range	[10, 40]
α Range	[0, 1.0]
γ Range	[2.0, 4.0]

and

Table 7. Sobol Sensitivity Scores of the Load-Balancing Algorithm.

Parameter	S1 Index	S1 Confidence Score
Depth	0.000000	0.000000
α	0.592330	0.093727
γ	0.225597	0.081464

present the parameters of the load balancing algorithm and the Sobol sensitivity scores of the algorithm, respectively. The change in the depth range had zero variance in the Sobol Sensitivity Test, as it was observed that the algorithm’s convergence determination depends on 10 or fewer recursions.

The pseudo-code of the load-balancing algorithm is given as Algorithm 2.

Algorithm 2. Pseudo Code of the Load-Balancing Algorithm
1:	Proc ENUMERATE_PATHS(G, s, t, Dmax):
2:	Input: G = (V, E, d, τ)
3:	s ← source vertex
4:	t ← destination vertex
5:	Dmax ← recursion depth limit
6:	Output: P ← list of tuples (π, dist(π))
7:	Procedure DFS(cur, depthleft, path, distacc):
8:	If depth_left = 0:
9:	Return
10:	For each (cur, nxt) ∈ E:
11:	de ← d(cur, nxt)
12:	If nxt = t:
13:	π ← path ▹ [cur, nxt]
14:	Append (π, distacc + de) TO P
15:	Continue
16:	If nxt ∈ path:
17:	Continue
18:	DFS(nxt,
19:	depthleft − 1,
20:	path ▹ [cur, nxt],
21:	distacc + de)
22:	Initialise empty list P
23:	DFS(s, Dmax, [], 0)
24:	Return P

The description of the pseudo-code is provided in Appendix A.

4. Traffic Simulations

The PTV Vissim 2023 software was employed to simulate traffic conditions. The analysis was constrained by the software’s 1000 km road drawing limit and the complexity of mapping Bluetooth data to individual road segments. Consequently, the study concentrated on a designated sample area rather than the entire city of Vigo. During the simulation phase, the geographic boundaries of this sample area were established to ensure an accurate representation of the region, as shown in Figure 7.

The road network of the selected sample area was represented in the simulation model. The representation incorporated key parameters, including the number of lanes, lane width, geometric characteristics, road classification, intersections, and turning movement data for both right and left turns. Figure 8 displays the roads included in the simulation model.

In the next phase, traffic control devices were integrated into the simulation model for the designated area in Vigo. This involved defining the locations and phases (red, yellow, and green lights) of each traffic signal, as depicted in Figure 9. In the simulations, the same signal plans were implemented during weekend peak hours as well. Subsequently, the routes of public transportation lines within the sample area were incorporated, along with the placement of stops and the frequency of service. In the following steps, these transportation routes, stop locations, and service frequencies were systematically added to the simulation. In the final stage, the hourly traffic flow for each road segment was established in the simulation, with average speeds reflecting the vehicle composition.

Scenario preparation is essential for evaluating traffic performance under varying traffic conditions. In this context, multiple scenarios are developed using a calibrated and validated simulation model. By employing a load-balancing algorithm designed to distribute traffic load more evenly, simulations of load-balancing applications are conducted for historical dates and times within the modeled area. Each scenario aims to compare the algorithm’s effectiveness in balancing traffic and its responsiveness to different traffic situations. These scenarios incorporate various traffic conditions from different times, including both peak and off-peak hours. The analyses will yield insights into the algorithm’s efficacy in managing traffic flow and assessing potential changes in traffic performance.

For the analysis, traffic conditions during peak hours over a ten-day period in 2023 were examined. A dataset was prepared to select these days, taking into account factors such as weekdays versus weekends, seasonal variations (summer versus winter), whether schools were in session, and differing weather conditions. The identified peak hour periods for the city are as follows: on weekdays, the morning peak spans from 07:30 to 08:30, while the evening peak occurs from 17:15 to 18:15. On weekends, the morning peak is from 11:00 to 12:00, and the evening peak is from 18:00 to 19:00. A detailed overview of the included days and their corresponding conditions can be found in

Table 8. The dates used to create the simulations.

Date	Day	Season	Special Condition	School	Weather Conditions
1 January 2023	Sunday	Winter	New Year (Holiday)	Closed	13.5 °C, Rain
22 January 2023	Sunday	Winter	None	Closed	12.0 °C, Sunny
16 January 2023	Monday	Winter	None	Open	12.0 °C, Rain
10 June 2023	Saturday	Summer	None	Closed	20.0 °C, Cloudy
16 June 2023	Friday	Summer	None	Open	25.0 °C, Sunny
9 July 2023	Sunday	Summer	None	Closed	21.0 °C, Partially Cloudy
25 July 2023	Tuesday	Summer	None	Open	23.0 °C, Sunny
15 August 2023	Tuesday	Summer	Assumption of Mary (Holiday)	Open	25.0 °C, Sunny
11 November 2023	Saturday	Winter	None	Closed	18.0 °C, Rain
22 November 2023	Wednesday	Winter	None	Open	15.0 °C, Sunny

.

In the Vigo study, vehicle volume and speed data were collected using Bluetooth sensors deployed at multiple locations across the network. This approach correlated detected vehicles rather than relying solely on counts at individual road sections or on origin–destination matrices derived from start and end zones. The Bluetooth sensors were assumed to operate with an accuracy of 30%, a value periodically updated by the Traffic Management Centre of Vigo through comparisons with inductive loop measurements on main roads. Accordingly, the measured volume data were scaled by a factor of 3.33 to estimate total traffic. In addition, a ±5% normally distributed error term was added to ensure randomness. These route-based data were subsequently allocated to individual road segments, allowing for the determination of total hourly traffic volume for each segment. The O-D demand matrix used in the simulation conducted for 16 January 2023, at 17:15, is presented in

Table 9. The O-D matrix used in the simulation conducted for 16 January 2023—17:15.

Zone	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	R	S	T
A	-	303	303	181			209	209			73		209	73	309	309	309	309
B	163	-	829	503			14	14			112	112	126	112		112	112
C	163	600	-	619		56	56	14			112	112	126	112		112	112
D	163	600	600	-	559	256	256	303	303	303	418	174	335	174		194	194
E	97	359	359	359	-	256	256	303	303	303	363	128	256	120		194	194
F	58	150	150	89		-	312				67	46	312	65		67	67
G	600	260	260	155		285	-	493			117	100	530	169		117	117
H	97	359	239	239	239	285	426	-	303	303	363	128	218	120		139	139
I	68	239	239	239	239		218	239	-	529	443	221	216	207		241	241
J	83	239	239	239	239		270	239	635	-	547	270	270	253		294	294
K	83	329	239	239	239		170	239	635	635	-	170	170	253		1056	1056
L							270	270			229	-	270	229		229	229
M							493	493			229	229	-	229		229	229
N	83						170	170			762	170	170	-		762	762
O	186										460			460	-	859	859	492	306
P	186	239	239	239	239			239	635	635	635			460	952	-	1956	492	306
R	186	239	239	239	239			239	635	635	635			460	952	1587	-	492	306
S	186														859	859	859	-	306
T															550	550	550	550	-

, while the O-D demand matrix used in the simulation conducted for 10 June 2023, at 18:00, is presented in

Table 10. The OD matrix used in the simulation conducted for 10 June 2023—18:00.

Zone	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	R	S	T
A	-	87									126	203	116	30	163	163	163	163
B	117	-	576	539	257	37	37	135	145	145	40	87	87	36		120	120
C	117	319	-	539	257	37	37	135	145	145		12	37	25		120	120
D	117	319	396	-	296	116	116	180	180	180	170	45	116	30		159	159
E	64	172	221	283	-	116	116	180	180	180	170	45	116	30		159	159
F	69	83	83	90	90	-	153	15	21	21	19	2	153
G	106	124	124	124	69	160	-	263	30	30	27	3	230
H	101	160	153	134	193	160	236	-	180	180	170	45	77	30		159	159
I	37	98	126	160	160		74	160	-	372	365	94	38	56		309	309
J	37	98	126	160	216		132	160	492	-	515	54	54	79		436	436
K	37	98	126	160	160		156	160	492	492	-	156	156	156		755	755
L	46						209	209			96	-	209	96		96	96
M	106	124	124	124	69		209	209	30	30	96	203	-	96		96	96
N	46						156	156			319	156	156	-		319	319
O	106										193			193	-	722	722	742	636
P	145	98	126	160	160			160	492	492	550	59	59	59	193	-	1477	742	636
R	145	98	126	160	160			160	492	492	550	59	59	193	193	1485	-	742	636
S	106														722	722	722	-	636
T															566	566	566	566	-

. In both tables, the rows represent origins and the columns represent destinations. In both tables, the diagonal cells in the OD matrix were marked with ‘–’ to indicate that trips with the exact origin and destination are not considered, since no travel demand is defined in such cases.

Table 11. Name of the zone represented by each letter.

Letter	Zone
A	Praza de América
B	Monumento Á Xente do Mar
C	Av. de Castelao
D	VG-20
E	Coia
F	Av. da Florida, 197–191
G	Rúa Padre Seixas
H	A Florida
I	Rúa de Citroën
J	Rúa dos Olimpícos
K	Av. do Alcalde Portanet
L	Av. do Fragoso
M	Rúa Martín Echegaray, 1
N	Av. do Fragoso
O	Av. de Balaídos, 2
P	Av. do Alcalde Portanet, 1
R	Av. de Castrelos, 236
S	Av. de Antonio Palacios, 54
T	Camiño Freixeiro

lists the segment represented by each letter.

For traffic simulations to yield reliable and accurate results, it is essential to conduct the processes of calibration and validation meticulously. Calibration involves fine-tuning the model to ensure it aligns with real-world data. During this phase, model parameters, such as vehicle speeds and signal timings, are adjusted based on observed traffic conditions. Real traffic data is collected and utilized to construct the model. Validation, on the other hand, evaluates the accuracy of the calibrated model by testing it against various datasets. Both calibration and validation are critical for ensuring the model’s realism and dependability, thus enabling decision-makers to formulate strategies based on credible and trustworthy results.

During the calibration process, distinct scenarios were established for morning and evening peak hours over 10 days, with vehicle volumes and speeds allocated to various scenarios for each day. The simulation runtime was set to 3600 s, accompanied by a 900-s warm-up period. Each scenario was executed with 48 random seeds and run 10 times to minimize variability, using the average results for analysis. The model calibration was conducted with consideration for driver behaviors. Since the considered road network consists of urban roads, the calibration was performed based on the parameters of the Wiedemann 74 car-following model [63]. The Wiedemann 74 model has three parameters: the average standstill distance, the additive part of the safety distance, and the multiplicative part of the safety distance. During the calibration process, the values of these three parameters were adjusted to ensure that the traffic volumes and average speed values on each link matched the observed values. As a result of the calibration, the parameters were set as follows: average standstill distance = 2 m, additive part of safety distance = 2, and multiplicative part of safety distance = 3.

Over the course of the ten days analyzed, a total of 20 primary scenarios—comprising one-hour intervals during both morning and evening peak times—were executed in the simulations for the validation process. The average traffic flow speeds for each road segment were validated using the GEH (Geoffrey E. Havers) statistic. The GEH statistic is a widely recognized non-linear metric in traffic engineering that compares volume values derived from model data with those observed in real-world data. A GEH value of less than 5 indicates a well-calibrated model, which is interpreted as a discrepancy of 0.5 vehicles per hour. Feldman provides the formula used to calculate the GEH value as Equation (8) [64].

$$GEH=\sqrt{{\displaystyle \frac{2{\left(Q_{model}-Q_{observation}\right)}^2}{\left(Q_{model}+Q_{observation}\right)}}}$$

(8)

The acceptance criteria for the GEH value are set as follows: values from 0 to 5 indicate a well-established model, values between 5 and 10 require further investigation, and values exceeding 10 are considered unacceptable [64]. The field data (Q_observation) and model outputs (Q_model) were divided into 15-min intervals and evaluated using the GEH statistic. Notably, all GEH values resulting from the comparison between the model and real-world data are below 5, demonstrating the model’s alignment with observed data and reinforcing its reliability. The GEH values for each road segment across the 20 scenarios were calculated using both model and observed data (see

Table 12. GEH values for each road segment across the 20 scenarios.

Section Number	1 January 2023		16 January 2023		22 January 2023		10 June 2023		16 June 2023		9 July 2023		25 July 2003		15 August 2023		11 November 2023		22 November 2023
	11:00	18:00	07:30	17:15	11:00	18:00	11:00	18:00	07:30	17:15	11:00	18:00	07:30	17:15	07:30	17:15	11:00	18:00	07:30	17:15
1	0.77	0.91	0.69	0.98	0.79	0.70	0.12	0.82	0.87	0.86	0.88	0.85	0.93	0.77	0.80	0.80	3.37	0.81	0.84	0.92
2	0.70	0.29	0.55	0.18	0.66	0.43	0.85	0.09	0.08	0.84	0.43	0.19	1.12	1.64	0.15	0.37	0.70	0.05	0.35	2.20
3	0.32	0.63	0.47	0.02	0.83	0.04	0.36	0.65	0.56	0.88	0.63	0.43	0.50	0.76	1.33	0.24	2.27	0.08	0.79	0.70
4	0.02	0.17	0.74	0.63	0.40	0.26	0.11	0.17	0.06	0.49	0.24	0.36	0.62	0.10	0.37	0.82	0.43	0.21	0.49	0.96
5	0.17	1.19	0.21	0.69	0.95	0.31	0.72	0.04	0.17	0.66	0.06	1.00	0.07	1.07	0.06	0.16	0.44	0.08	0.24	0.73
6	1.09	1.65	0.30	1.14	0.42	1.17	0.59	0.14	0.38	1.14	0.68	0.46	1.24	1.49	3.16	0.30	0.87	0.13	0.22	1.97
7	0.17	0.50	0.67	3.56	0.42	0.17	0.19	0.67	0.11	0.25	0.15	0.25	0.77	0.44	0.38	0.18	0.11	0.48	0.69	0.29
8	0.62	2.82	0.03	1.48	0.34	0.72	0.60	0.30	0.51	0.32	0.01	0.09	0.73	0.95	0.33	0.26	1.04	0.11	0.21	2.14
9	1.02	0.85	0.84	0.90	0.97	0.74	0.27	0.70	0.50	0.96	0.19	1.06	0.46	1.66	0.69	0.33	3.40	0.91	0.63	0.72
10	0.74	1.95	3.54	4.55	0.46	0.27	1.21	0.77	1.37	0.68	1.21	0.93	1.97	2.15	1.06	0.96	1.59	0.82	2.28	0.81
11	0.61	2.27	0.44	0.86	0.47	0.03	0.34	0.31	2.13	0.25	0.18	0.63	0.07	0.37	0.12	0.09	0.67	0.76	0.35	1.14
12	0.02	0.31	0.32	0.08	0.12	0.33	0.46	0.60	0.10	0.04	1.07	0.37	0.63	0.70	0.24	0.52	0.58	0.38	0.48	0.43
13	0.01	3.77	0.17	2.43	0.01	0.21	0.27	0.30	2.32	0.06	0.06	0.41	0.36	0.42	0.00	0.21	0.70	0.04	0.11	1.58
14	0.53	0.37	0.23	3.02	0.04	0.44	0.42	0.06	3.97	0.22	0.08	0.35	0.53	0.28	0.07	0.08	0.49	0.10	0.10	2.72
15	0.15	0.43	0.22	2.15	1.09	0.02	0.24	0.51	0.17	0.16	0.58	0.25	0.43	0.80	0.56	0.24	0.06	0.63	1.60	0.48
16	0.33	0.07	0.26	1.73	3.61	0.26	0.22	0.25	0.18	0.22	0.08	0.03	0.23	0.31	0.17	0.02	0.33	0.02	2.76	0.60
17	0.47	0.35	1.20	1.30	1.00	1.46	0.48	0.27	0.53	0.80	1.39	0.12	0.15	0.52	1.05	2.34	0.94	0.05	4.04	8.94
18	0.37	0.46	0.44	3.17	0.40	0.18	0.54	0.55	0.38	0.39	0.37	0.36	0.20	0.15	0.05	0.35	0.54	0.40	0.42	0.35
19	1.10	1.04	0.66	0.89	0.56	0.80	2.93	0.78	0.89	0.57	0.69	1.16	1.02	2.27	1.04	1.01	0.91	0.04	0.63	0.21
20	0.48	0.66	0.68	0.66	0.65	0.50	0.84	0.71	0.02	0.70	0.46	0.63	0.44	2.91	0.71	0.48	0.44	0.62	0.73	0.72
21	0.40	0.44	0.33	0.25	0.23	0.26	0.07	0.32	0.27	0.44	0.44	0.46	0.39	0.02	0.45	0.40	0.32	0.40	0.50	0.38
22	0.39	0.10	0.19	0.12	0.24	0.51	2.46	0.06	0.39	0.07	0.46	0.14	0.39	0.06	0.48	0.19	0.02	0.01	1.28	1.10
23	1.03	0.86	0.56	0.64	0.69	0.80	0.63	0.69	0.88	0.26	0.75	0.74	0.91	1.43	0.92	0.62	0.55	0.01	1.43	0.62
24	0.19	0.53	0.56	0.51	0.40	0.38	0.43	0.45	0.17	0.58	0.46	0.62	0.61	1.36	1.38	0.51	0.50	0.60	0.66	0.55
25	0.97	0.84	0.60	0.61	0.77	0.85	0.62	0.67	0.82	0.20	0.77	0.78	0.88	1.41	0.85	0.62	0.54	0.30	0.88	0.70
26	0.16	2.84	0.27	1.32	0.23	0.58	0.11	0.26	1.80	1.34	0.43	0.71	0.61	1.07	1.10	0.46	0.96	0.26	3.42	1.36
27	0.35	0.33	0.31	0.15	0.52	0.18	0.02	0.25	0.43	0.23	0.08	2.48	0.12	0.17	0.25	0.29	1.75	0.16	0.30	0.80
28	0.49	0.00	0.25	2.93	0.15	0.12	0.20	0.07	0.56	0.06	0.58	0.57	0.39	0.85	0.69	0.59	0.37	0.33	0.01	0.81
29	0.29	6.05	0.11	2.73	0.39	0.10	0.08	1.84	0.01	0.26	0.38	0.26	0.08	0.23	0.35	0.15	1.17	0.30	0.70	0.54
30	0.58	0.34	0.14	0.18	1.02	1.83	0.06	0.05	0.45	0.47	0.27	0.06	0.66	0.18	1.19	2.55	0.97	0.12	0.55	3.34
31	0.02	0.20	0.03	0.44	0.16	1.02	0.27	4.53	0.02	0.72	0.03	0.69	0.76	0.24	0.09	0.19	0.86	1.41	0.16	0.65
32	0.35	0.09	0.70	0.05	0.63	0.82	1.49	0.31	0.15	1.10	0.70	0.21	1.36	0.10	0.49	1.07	0.08	0.06	0.45	1.22
33	0.16	0.30	0.18	0.04	0.21	0.60	0.37	0.42	0.03	0.31	0.24	1.08	0.58	0.06	0.79	0.42	0.05	0.17	0.38	0.93
34	0.00	0.04	0.33	0.36	0.07	0.04	0.80	0.04	0.12	0.25	0.55	0.37	0.60	0.15	0.34	0.10	0.58	0.90	0.14	0.26
35	0.08	0.35	0.11	0.01	0.34	0.13	0.21	0.37	0.38	0.02	0.33	1.84	0.19	0.03	0.04	0.05	0.22	0.07	0.12	0.30
36	0.27	0.36	0.14	1.55	0.16	0.14	0.01	0.17	0.04	0.19	0.18	0.29	0.06	0.50	0.22	0.06	0.00	0.03	0.25	0.17
37	0.17	0.24	0.01	1.85	0.09	0.32	0.35	1.44	0.23	0.72	0.21	2.66	2.06	0.26	0.15	0.18	0.42	0.33	0.30	0.48
38	0.45	0.71	0.74	0.19	2.17	0.84	0.10	2.40	0.13	1.05	0.63	0.05	1.35	0.05	1.30	0.30	2.14	0.13	0.73	0.76
39	0.11	0.03	0.74	0.13	0.16	0.08	0.13	0.01	1.99	0.15	0.47	1.41	0.26	0.34	0.08	0.47	0.19	0.50	1.21	0.11
40	0.39	0.01	0.10	8.80	0.05	0.06	0.36	0.11	0.46	0.03	0.46	0.53	0.39	0.90	0.71	0.52	0.18	0.22	0.14	0.58
41	0.12	0.17	0.01	0.00	0.47	0.32	0.14	0.37	0.03	0.32	0.18	2.22	0.18	0.03	0.33	0.13	0.13	0.07	0.11	0.81
42	0.31	0.29	0.11	4.32	0.20	0.10	0.58	0.16	1.25	0.17	0.71	0.44	0.44	0.06	0.06	0.00	0.16	0.74	2.78	0.25
43	0.04	0.65	0.48	0.02	1.66	0.10	0.20	0.22	0.72	0.68	0.35	0.21	0.43	0.85	1.40	0.30	2.21	0.18	0.88	0.62
44	0.06	0.48	0.58	0.52	0.28	0.39	0.28	0.38	0.48	0.44	0.31	0.07	0.26	0.05	0.26	0.61	1.58	2.80	0.59	0.88

). The GEH values obtained from each seed for each road segment on 10 June 2023 are presented in

Table 13. GEH values obtained from each seed for each road segment for 10 June 2023—18:00.

Section Number	Seed
	1	2	3	4	5	6	7	8	9	10
1	0.46	0.09	1.60	0.47	0.94	2.69	0.18	0.46	1.52	2.28
2	1.33	0.00	1.44	0.11	1.44	0.21	0.77	1.24	0.65	0.88
3	1.00	0.22	1.86	0.06	0.89	1.70	0.34	0.80	1.11	0.83
4	0.17	1.80	1.72	0.42	2.09	0.00	2.00	0.17	0.46	1.35
5	1.22	0.09	0.53	1.01	0.92	0.27	0.55	1.22	0.55	0.00
6	1.33	0.11	1.34	0.42	1.54	0.22	0.32	1.14	0.54	0.99
7	0.91	0.49	0.07	1.49	0.21	1.20	0.77	1.56	0.62	0.70
8	1.96	0.14	0.64	0.42	1.37	0.21	1.29	0.49	0.64	0.42
9	0.57	0.29	0.67	2.03	0.29	1.00	2.47	0.29	0.48	1.23
10	0.28	1.17	0.37	0.37	1.35	1.70	0.00	1.09	0.91	1.61
11	1.53	0.18	0.37	0.18	1.37	0.36	0.36	0.37	0.18	0.18
12	1.40	0.60	1.73	0.30	0.00	1.07	0.91	1.40	0.60	1.07
13	0.92	1.25	0.50	1.40	0.66	0.14	2.21	2.80	0.07	0.88
14	0.88	1.25	0.22	1.84	1.21	0.99	1.69	2.37	0.17	0.56
15	0.65	0.24	0.16	0.49	0.40	0.65	1.06	1.32	0.40	0.57
16	0.14	0.27	0.00	2.20	0.14	1.73	0.53	0.14	1.30	0.55
17	0.39	0.42	0.38	1.84	1.88	1.39	2.63	0.73	0.26	0.64
18	0.97	0.77	0.18	0.22	1.83	1.44	1.61	0.55	0.51	0.00
19	0.00	1.30	0.85	1.81	1.30	1.22	0.92	0.39	1.22	1.37
20	0.76	0.76	1.59	0.10	1.04	0.48	0.79	1.23	0.86	1.13
21	0.12	0.72	0.63	0.96	0.24	0.24	1.56	1.45	1.56	0.00
22	0.51	0.08	1.54	0.72	0.04	1.12	1.00	1.41	1.06	0.79
23	0.30	0.85	0.41	0.26	0.70	1.72	1.54	1.83	0.00	0.63
24	0.33	0.41	1.02	1.15	0.07	0.07	1.09	1.81	1.56	0.18
25	0.30	0.89	0.41	0.19	0.63	1.69	1.65	1.79	0.04	0.52
26	0.52	0.69	1.01	1.39	0.33	0.03	2.22	0.46	1.29	0.56
27	0.46	0.47	0.20	0.13	1.49	1.35	0.59	0.13	0.33	0.26
28	0.28	0.14	0.89	0.21	0.34	0.42	0.49	1.56	0.95	0.14
29	1.07	1.33	1.12	2.46	2.41	1.17	2.31	2.36	1.62	2.46
30	0.49	0.54	0.27	2.24	0.80	0.76	2.46	1.00	0.96	0.22
31	5.15	5.67	3.46	3.30	6.02	6.43	2.76	4.02	4.41	4.30
32	1.74	0.71	0.00	1.27	0.53	1.79	2.21	0.00	1.23	0.41
33	0.16	1.03	0.33	0.68	0.68	0.50	0.50	0.32	0.50	0.50
34	1.60	0.24	0.12	0.86	0.59	0.24	1.27	0.36	0.98	0.98
35	0.85	1.44	0.64	0.73	1.34	2.25	1.09	0.18	0.47	0.28
36	1.71	1.88	0.21	2.12	0.64	1.62	0.43	0.53	2.19	1.42
37	1.17	1.02	1.59	2.29	0.22	0.74	2.35	1.52	1.73	1.66
38	2.29	0.72	2.14	3.15	1.53	1.91	4.70	2.99	1.76	2.99
39	2.14	0.86	0.46	2.51	0.53	1.02	0.77	0.99	0.71	0.52
40	0.63	0.91	0.89	0.42	0.14	0.35	0.21	1.06	0.95	0.41
41	0.33	1.41	0.00	0.56	1.41	2.02	0.95	0.48	0.33	0.33
42	2.27	1.63	0.24	2.23	0.00	0.93	0.86	0.64	1.16	0.78
43	1.29	0.20	0.75	0.97	0.35	1.43	1.07	0.71	0.65	0.20
44	0.73	2.31	2.06	0.39	1.71	0.30	2.76	0.13	0.78	1.62

. In both tables, the best values are highlighted in bold, and the values exceeding 5 are shown in red.

After calibrating and validating the primary scenarios, the impacts of load balancing on traffic conditions and performance were systematically analyzed. This analysis was conducted in collaboration with the Traffic Control Centre (TCC) to examine vehicle participation levels of 25%, 50%, 75%, and 100%. To facilitate this, four sub-scenarios were created for each primary scenario, resulting in a total of 80 scenarios (20 main scenarios multiplied by four increments). In these scenarios, dynamic assignment was employed to redistribute vehicles across different routes based on road segment delay rates, effectively balancing the traffic load. This approach aimed to alleviate congestion and decrease emissions by optimizing vehicle distribution throughout the network.

The performance of the traffic network and emissions were analyzed using load balancing. For scenarios demonstrating an improvement of more than 5% in traffic network performance, load balancing was examined at levels of 25%, 50%, 75%, and 100%. Conversely, in situations yielding lower performance improvements, only the outcome of 100% load balancing was considered. Moreover, for the scenarios simulating 25 July 2023, load balancing was not applicable due to the exceedingly low traffic volume recorded on that day.

5. Results

The evaluation of 20 distinct scenarios involving load balancing focused on several key metrics: average speeds, total travel time, total delays, total number of stops, and total standstill time. Additionally, the study examined the effects of re-routing vehicles by 25%, 50%, and 75% in scenarios where the impact of these re-routed vehicles was significant. The results indicate that weekday scenarios with 100% load balancing exhibited significant improvements. Average speeds increased by 3%, and total travel time was reduced by 3%. Furthermore, total delays decreased by 8%, the total number of stops fell by 6%, and total standstill time declined by 10%. Conversely, weekend scenarios exhibited more modest improvements. Average speeds rose by 1%, and total travel time decreased by 1%. Total delays decreased by 4%, the number of stops fell by 4%, and total standstill time declined by 5%.

Emission calculations were established for each vehicle type utilizing an external emission model in PTV Vissim 2023 software. This emission model was developed based on the research conducted by Nouri and Morency [65]. Through this model, the values for CO (Carbon monoxide), CO₂ (Carbon dioxide), NO_X (Nitrogen oxides), and HC (Hydrocarbons) were determined for each scenario. In the City of Vigo, the Euro-class mix of vehicles in traffic in 2023 is presented in Figure 10. In the simulation environment, the vehicle distributions were also aligned with these proportions. The definitions of the classes in the figure are as follows:

• Without label: All gasoline prior to 2001 or that does not comply with Euro III—all diesels before 2006 or that do not comply with Euro IV.
• Label B: All gasoline vehicles registered on or after 1 January 2001 or that comply with Euro III. All diesels registered on or after 1 January 2006 or complying with Euro IV and Euro V.
• Label C: All gasoline vehicles registered on or after 1 January 2006 or that comply with Euro IV, Euro V, or Euro VI. All diesels registered on or after 1 September 2015 or Euro VI compliant.
• ECO Label: All hybrid or plug-in hybrid vehicles with an electric range of less than 40 km. All vehicles powered by natural gas, compressed natural gas (CNG), or liquefied petroleum gas (LPG), and that also meet the requirements of label C.
• Zero Emissions Label: All electrified vehicles with an electric range of more than 40 km, whether pure electric, plug-in hybrids, or extended range electric. All vehicles are powered by hydrogen or fuel cells.

Table 14. Simulation scenario results.

Date	Hours	Total Number of Vehicles	Compliance Rates	Number of Re-Routed Vehicles	Percentages of Re-Routed Vehicles	Metric	Average Speed (km/h)	Total Travel Time (s)	Total Delay (s)	Total Number of Stops	Total Standstill Time (s)
January 2023	11:00	1714	0%	0	0.00%	Mean	23.07	503,936	126,151	4292	95,803
						Standard Error (SE)	0.06	4401	1692	47	1341
						Standard Deviation (SD)	0.20	13,916	5350	149	4239
			100%	22	1.30%	Mean	23.07	503,566	126,111	4290	95,848
						SE	0.06	4337	1689	47	1344
						SD	0.20	13,715	5340	149	4249
	18:00	3266	0%	0	0.00%	Mean	21.39	1,003,433	311,034	8832	242,589
						SE	0.22	11,803	10,291	169	9390
						SD	0.70	37,325	32,543	535	29,693
			25%	7	0.21%	Mean	21.60	993,783	301,152	8715	23,3209
						SE	0.22	9611	9579	156	8835
						SD	0.70	30,394	30,291	493	27,940
			50%	13	0.40%	Mean	22.17	971,354	276,393	8323	210,186
						SE	0.13	7495	5800	91	5368
						SD	0.42	23,701	18,340	288	16,976
			75%	20	0.61%	Mean	22.33	955,391	267,677	8122	202,987
						SE	0.18	7686	7212	113	6626
						SD	0.58	24,305	22,805	358	20,955
			100%	26	0.80%	Mean	22.69	951,607	258,554	8064	193,451
						SE	0.15	8154	5827	101	5298
						SD	0.46	25,785	18,426	320	16,754
16 January 2023	07:30	6280	0%	0	0.00%	Mean	17.25	2,336,233	901,756	25,288	708,572
						SE	0.13	19,262	18,438	493	16,352
						SD	0.42	60,911	58,305	1561	51,708
			25%	23	0.37%	Mean	17.58	2,294,527	861,612	24,114	673,821
						SE	0.23	32,260	30,497	789	26,076
						SD	0.73	102,017	96,440	2494	82,459
			50%	45	0.72%	Mean	17.85	2,254,945	825,209	23,668	638,707
						SE	0.21	28,499	27,045	672	23,361
						SD	0.66	90,121	85,524	2125	73,874
			75%	68	1.08%	Mean	18.28	2,176,157	763,051	22,002	588,171
						SE	0.19	24,217	22,823	608	19,595
						SD	0.59	76,580	72,172	1923	61,964
			100%	90	1.43%	Mean	17.94	2,266,038	824,290	23,907	636,073
						SE	0.20	24,076	24,624	663	21,718
						SD	0.63	76,135	77,867	2098	68,678
	17:15	5651	0%	0	0.00%	Mean	13.52	2,749,739	1,361,450	50,257	996,171
						SE	0.19	31,363	33,335	1472	24,750
						SD	0.60	99,178	105,413	4656	78,267
			25%	33	0.58%	Mean	13.02	2,780,350	1,431,411	54,207	1,047,835
						SE	0.17	31,642	33,168	1668	24,456
						SD	0.55	100,061	104,885	5276	77,337
			50%	66	1.17%	Mean	14.59	2,534,783	1,155,643	43,507	830,769
						SE	0.13	22,910	22,357	1085	16,669
						SD	0.42	72,448	70,700	3432	52,713
			75%	99	1.75%	Mean	15.21	2,434,978	1,059,101	40,459	750,733
						SE	0.16	25,024	24,907	1152	18,750
						SD	0.51	79,132	78,764	3642	59,292
			100%	132	2.34%	Mean	15.31	2,437,517	1,054,394	41,122	740,273
						SE	0.10	15,625	15,172	845	10,124
						SD	0.30	49,412	47,977	2671	32,014
22 January 2023	11:00	3752	0%	0	0.00%	Mean	20.89	1,220,339	317,487	10,310	235,439
						SE	0.09	7473	5272	79	4757
						SD	0.28	23,633	16,670	250	15,042
			100%	25	0.67%	Mean	20.95	1,216,423	314,650	10,265	232,851
						SE	0.08	6919	4908	78	4445
						SD	0.26	21,878	15,520	248	14,058
	18:00	4266	0%	0	0.00%	Mean	23.91	1,117,878	283,160	9290	208,501
						SE	0.08	6755	4228	164	2903
						SD	0.25	21,361	13,370	518	9180
			100%	20	0.47%	Mean	24.01	1,115,526	281,352	9193	207,384
						SE	0.08	6418	4137	149	2928
						SD	0.26	20,296	13,082	471	9260
10 June 2023	11:00	5557	0%	0	0.00%	Mean	19.22	1,643,711	540,860	17,844	347,020
						SE	0.21	20,199	18,485	835	12,744
						SD	0.65	63,875	58,454	2639	40,301
			25%	9	0.16%	Mean	19.22	1,645,431	540,127	17,762	346,541
						SE	0.18	19,544	17,205	737	11,816
						SD	0.55	61,802	54,407	2332	37,364
			50%	18	0.32%	Mean	18.53	1,955,242	653,072	19,318	454,041
						SE	0.10	11,397	10,408	445	8070
						SD	0.32	36,041	32,914	1406	25,518
			75%	27	0.49%	Mean	19.29	1,639,913	531,501	17,553	338,714
						SE	0.17	15,915	14,191	632	9934
						SD	0.55	50,329	44,875	2000	31,413
			100%	36	0.65%	Mean	19.31	1,638,716	535,911	17,775	343,343
						SE	0.21	20,102	18,732	897	12,838
						SD	0.66	63,567	59,236	2837	40,596
	18:00	4463	0%	0	0.00%	Mean	20.57	1,312,556	399,401	12,338	252,407
						SE	0.12	7772	7285	302	5038
						SD	0.38	24,578	23,037	955	15,931
			100%	25	0.56%	Mean	20.67	1,306,238	393,963	12,152	249,146
						SE	0.10	7131	6010	241	4115
						SD	0.31	22,550	19,004	763	13,012
16 June 2023	07:30	5416	0%	0	0.00%	Mean	18.16	2,019,782	704,366	20,957	495,634
						SE	0.21	24,180	24,224	773	20,134
						SD	0.68	76,462	76,604	2443	63,669
			25%	16	0.30%	Mean	18.40	1,987,682	673,218	20,132	469,969
						SE	0.12	11,584	12,557	401	10,809
						SD	0.37	36,631	39,709	1268	34,181
			50%	36	0.66%	Mean	18.53	1,955,242	653,072	19,318	454,041
						SE	0.10	11,397	10,408	445	8070
						SD	0.32	36,041	32,914	1406	25,518
			75%	48	0.89%	Mean	18.54	1,960,590	655,086	19,428	455,639
						SE	0.10	11,196	10,295	438	8192
						SD	0.30	35,406	32,554	1385	25,906
			100%	63	1.16%	Mean	17.94	2,266,038	824,290	23,907	636,073
						SE	0.20	24,076	24,624	663	21,718
						SD	0.63	76,135	77,867	2098	68,678
	17:15	4735	0%	0	0.00%	Mean	20.09	1,611,435	508,416	13,495	340,938
						SE	0.09	10,551	7997	161	6590
						SD	0.28	33,367	25,290	508	20,839
			100%	28	0.59%	Mean	20.49	1,585,600	481,233	13,043	317,666
						SE	0.08	8946	6681	152	5411
						SD	0.25	28,289	21,127	482	17,110
9 July 2023	11:00	3771	0%	0	0.00%	Mean	17.16	1,397,382	500,138	20,146	290,550
						SE	0.24	19,159	19,168	1498	11,712
						SD	0.75	60,587	60,616	4736	37,037
			25%	18	0.48%	Mean	17.12	1,399,422	503,642	20,514	296,185
						SE	0.22	16,346	16,837	1237	10,557
						SD	0.68	51,691	53,244	3913	33,384
			50%	36	0.95%	Mean	17.25	1,388,914	490,556	19,839	282,966
						SE	0.28	23,085	20,511	1475	10,895
						SD	0.87	73,002	64,862	4665	34,452
			75%	54	1.43%	Mean	17.36	1,364,835	471,289	17,798	269,563
						SE	0.16	11,156	10,686	717	5629
						SD	0.51	35,278	33,792	2268	17,801
			100%	72	1.91%	Mean	17.94	1,335,044	436,039	15,527	253,098
						SE	0.27	19,389	17,887	1127	10,471
						SD	0.84	61,312	56,565	3564	33,113
	18:00	4316	0%	0	0.00%	Mean	21.50	1,247,485	383,579	11,560	256,969
						SE	0.14	10,201	9174	418	5959
						SD	0.43	32,260	29,012	1321	18,844
			100%	27	0.63%	Mean	21.69	1,234,614	374,096	11,265	250,984
						SE	0.11	9524	7693	323	5046
						SD	0.35	30,118	24,326	1020	15,958
25 July 2023	07:30	1765	0%	0	0.00%	Mean	26.03	444,972	101,658	3395	77,910
						SE	0.08	2902	1023	26	895
						SD	0.26	9176	3234	81	2831
	17:15	459	0%	0	0.00%	Mean	23.53	130,296	28,728	958	21,s883
						SE	0.11	1464	302	10	249
						SD	0.33	4631	955	32	787
15 August 2023	07:30	1772	0%	0	0.00%	Mean	20.78	541,290	125,442	3788	87,780
						SE	0.05	4305	1318	32	910
						SD	0.17	13,613	4168	102	2876
			100%	15	0.85%	Mean	20.84	538,250	124,458	3761	86,995
						SE	0.06	4020	1415	33	925
						SD	0.19	12,712	4476	104	2924
	17:15	3964	0%	0	0.00%	Mean	19.84	117,7651	334,049	10,342	227,660
						SE	0.15	12,284	9913	434	6555
						SD	0.47	38,846	31,349	1374	20,729
			100%	17	0.43%	Mean	19.91	1,169,459	330,160	10,176	222,767
						SE	0.15	10,780	9310	414	5952
						SD	0.46	34,088	29,441	1308	18,821
11 November 2023	11:00	4350	0%	0	0.00%	Mean	21.76	1,317,746	397,785	11,445	248,679
						SE	0.07	5864	4365	131	2658
						SD	0.21	18,545	13,804	414	8405
			100%	22	0.51%	Mean	21.85	1,314,453	395,567	11,523	247,457
						SE	0.08	6777	5463	192	3498
						SD	0.25	21,431	17,276	608	11,060
	18:00	4582	0%	0	0.00%	Mean	15.80	1,816,194	558,036	16,167	392,465
						SE	0.13	17,757	13,806	341	12,108
						SD	0.40	56,152	43,658	1078	38,289
			100%	28	0.61%	Mean	16.12	1,782,191	524,976	15,550	363,198
						SE	0.10	15,279	11,384	292	9921
						SD	0.32	48,317	36,000	925	31,372
22 November 2023	07:30	6356	0%	0	0.00%	Mean	14.51	2,775,045	14,23,219	47,222	1,036,773
						SE	0.18	31,631	32,057	1478	22,893
						SD	0.57	100,027	101,374	4675	72,394
			25%	18	0.28%	Mean	14.65	2,748,529	1,394,999	46,673	1,011,053
						SE	0.15	32,090	29,856	1227	22,617
						SD	0.48	101,478	94,414	3880	71,521
			50%	36	0.57%	Mean	14.75	2,724,019	1,372,566	46,365	990,563
						SE	0.20	37,908	37,077	1689	27,169
						SD	0.63	119,875	117,248	5342	85,917
			75%	54	0.85%	Mean	14.86	2,715,552	1,359,277	46,116	978,052
						SE	0.20	36,787	36,922	1644	27,598
						SD	0.64	116,330	116,759	5200	87,271
			100%	71	1.12%	Mean	14.80	2,722,753	1,367,256	46,717	982,040
						SE	0.14	24,642	24,463	1197	17,447
						SD	0.44	77,923	77,358	3784	55,173
	17:15	5684	0%	0	0.00%	Mean	12.92	2,703,575	1,400,838	57,059	957,045
						SE	0.11	25,927	23,695	1485	15,233
						SD	0.35	81,989	74,931	4696	48,172
			100%	43	0.76%	Mean	13.27	2,638,698	1,331,439	54,870	903,383
						SE	0.10	23,005	20,496	1048	14,781
						SD	0.32	72,747	64,814	3313	46,740

and

Table 15. Emission results obtained from the simulations.

Date	Hours	Compliance Rates	Total CO2 (t)	Total HC (kg)	Total NOX (kg)	Total CO (kg)
1 January 2023	11:00	0%	0.63	0.18	0.16	9.84
		100%	0.63	0.18	0.16	9.83
	18:00	0%	1.27	0.36	0.32	19.78
		25%	1.26	0.35	0.31	19.59
		50%	1.23	0.34	0.31	19.15
		75%	1.21	0.34	0.30	18.84
		100%	1.21	0.34	0.30	18.77
16 January 2023	07:30	0%	2.98	0.83	0.74	46.35
		25%	2.93	0.82	0.73	45.53
		50%	2.88	0.81	0.72	44.74
		75%	2.87	0.80	0.71	44.63
		100%	2.86	0.80	0.71	44.47
	17:15	0%	3.51	0.98	0.87	54.59
		25%	3.35	0.95	0.84	52.02
		50%	3.23	0.91	0.81	50.33
		75%	3.11	0.87	0.77	48.36
		100%	3.11	0.87	0.77	48.43
22 January 2023	11:00	0%	1.55	0.43	0.39	24.14
		100%	1.55	0.43	0.39	24.06
	18:00	0%	1.42	0.40	0.35	22.09
		100%	1.42	0.40	0.35	22.04
10 June 2023	11:00	0%	2.09	0.59	0.52	32.58
		25%	2.10	0.59	0.52	32.62
		50%	2.09	0.59	0.52	32.55
		75%	2.09	0.59	0.52	32.51
		100%	2.09	0.58	0.52	32.49
	18:00	0%	1.67	0.47	0.42	25.98
		100%	1.66	0.47	0.41	25.85
16 June 2023	07:30	0%	2.54	0.71	0.63	39.49
		25%	2.50	0.70	0.62	38.83
		50%	2.46	0.69	0.61	38.20
		75%	2.46	0.69	0.61	38.31
		100%	2.47	0.69	0.61	38.40
	17:15	0%	2.05	0.58	0.51	31.94
		100%	2.02	0.57	0.50	31.44
9 July 2023	11:00	0%	1.78	0.50	0.44	27.64
		25%	1.78	0.50	0.44	27.68
		50%	1.77	0.49	0.44	27.47
		75%	1.73	0.49	0.43	26.99
		100%	1.70	0.48	0.42	26.40
	18:00	0%	1.59	0.44	0.39	24.68
		100%	1.57	0.44	0.39	24.43
25 July 2023	07:30	0%	0.56	0.16	0.14	8.66
	17:15	0%	0.15	0.04	0.04	2.37
15 August 2023	07:30	0%	0.68	0.19	0.17	10.57
		100%	0.68	0.19	0.17	10.51
	17:15	0%	1.50	0.42	0.37	23.28
		100%	1.49	0.42	0.37	23.12
11 November 2023	11:00	0%	1.68	0.47	0.42	26.08
		100%	1.67	0.47	0.42	26.02
	18:00	0%	2.31	0.65	0.58	35.98
		100%	2.27	0.64	0.57	35.32
22 November 2023	07:30	0%	3.54	0.99	0.88	55.09
		25%	3.51	0.98	0.87	54.56
		50%	3.48	0.97	0.87	54.07
		75%	3.47	0.97	0.86	53.91
		100%	3.46	0.97	0.86	53.89
	17:15	0%	3.45	0.97	0.86	53.72
		100%	3.37	0.94	0.84	52.43

present the scenarios and their corresponding emission results, respectively. The implementation of load-balancing measures has led to reductions in traffic congestion and delays, which in turn have diminished stop-and-go movements and lowered emissions. On average days, this has resulted in approximately a 4% decrease in levels of CO₂, NO_x, HC, and CO. On days with heavier traffic, this reduction can reach as high as 11%.

6. Discussion

The implementation of the traffic load-balancing algorithm revealed significant advantages in enhancing overall network performance and reducing environmental impacts. By identifying congested road segments and redistributing traffic flows in real-time, the proposed system achieved measurable improvements in average speed, travel time, and emissions across various simulation scenarios. These outcomes demonstrate the algorithm’s ability to optimize route choices based on anticipated traffic conditions dynamically.

A notable strength of this study is its integration of machine learning-based short-term traffic forecasting with microsimulation modeling. Unlike traditional methods that rely solely on current traffic data, this approach facilitates proactive traffic management by predicting near-future conditions. This capability is especially relevant in urban settings that experience frequent demand fluctuations due to temporal, meteorological, or event-related factors.

One limitation of the conducted study is that vehicle volume and speed data were obtained from Bluetooth sensors. The information that Bluetooth sensors can detect approximately 30% of the actual traffic volume was obtained from previous studies carried out by the Municipality of Vigo. In the current study, vehicle volumes were scaled based on this value by multiplying by 3.33, and a randomly varying error term of ±5% was added. It was considered that a 30% sampling rate would represent the actual average speed with high accuracy (±10.6% for a population of 200 vehicles and ±8.7% for a population of 300 vehicles), and the values obtained from the sensors were used in the modeling. Using alternative detection methods to obtain vehicle volumes and average speeds with higher accuracy (considering the vehicle types as well) would increase the reliability of the study.

Another limitation of this study is that the LSTM models were developed considering traffic conditions within a two-hour historical time window. Extending the time horizon and incorporating exogenous/spatial features such as weather, holidays, events, or neighboring link conditions could further improve the performance of the LSTM models. However, each additional parameter increases model complexity and the computational load required. In particular, under a 100% compliance rate scenario, all vehicles in the city would communicate with the TCC, and repeated calculations would be required for each route. Therefore, the number of parameters included in the model has been kept as low as possible. Consequently, a model reflecting the trade-off between accuracy and simplicity was established, with simplicity dominating. Nevertheless, the LSTM models achieve R² values above 0.9, demonstrating that accuracy is well beyond merely acceptable. Adding more parameters to the LSTM models could further enhance performance. In future studies, additional parameters could be incorporated into LSTM models to improve prediction performance. However, the practical applicability of the model should also be considered in such cases.

A further limitation of this study is that pedestrian movements and trips made with non-motorized modes, such as micromobility systems, were not considered in the microsimulation. The traffic data obtained from Vigo Municipality does not include pedestrian activity or vehicles operating at low speeds, such as micromobility modes. Pedestrian interactions with motorized traffic primarily occur when crossing the street, typically during the red signal phase for motor vehicles. Given that the actual signal phases and timings used in the city were incorporated into the simulation, one may argue that pedestrian traffic was, to some extent, implicitly taken into account. However, including pedestrian and non-motorized vehicle traffic in the simulation would enable a much more realistic representation of traffic conditions. This, however, would proportionally increase the computational burden. Therefore, the objectives of the simulation should be carefully defined, and an appropriate balance should be struck between simplicity and accuracy.

The findings are particularly encouraging for cities like Vigo, which feature irregular urban layouts and varied traffic patterns. The scalability of this approach indicates its potential applicability in a broader range of contexts. Similar frameworks could be modified to suit other urban centers with distinct traffic dynamics, infrastructure configurations, and varying levels of data availability. Future research may focus on adapting the algorithm for larger and more complex metropolitan networks, or on integrating multimodal transportation systems, including public transit, bicycles, and micromobility options.

Additionally, while this study predominantly examined passenger vehicles, broadening the model to include freight vehicles, ride-sharing systems, and connected autonomous vehicles (CAVs) would yield a more thorough assessment of network-wide performance in mixed traffic scenarios. By incorporating V2V and V2I communications into the load-balancing framework, the responsiveness and efficiency of highly interconnected urban environments could be significantly enhanced.

The results of this paper underscore the dual importance in real-life settings of the algorithm presented here: that it improves traffic network operation, as well as its sustainability. Through the redistribution of demand and the reduction in congestion, the approach avoids unnecessary fuel consumption and CO₂ emissions, thus contributing to a push for sustainable traffic systems. The approach can also synchronize with other innovative mobility modes, such as electrification and shared mobility, to create a more sustainable urban mobility ecosystem. From a policy perspective, such decision support can serve as a foundation for various planning processes.

The results clearly demonstrate that traffic load balancing, when integrated with predictive analytics and simulation-based validation, presents a feasible solution for optimizing urban traffic. This approach not only helps alleviate congestion and mitigate environmental effects but also aligns with the broader goals of sustainable urban mobility and intelligent transportation systems.

In conclusion, the identification of congested road segments and the application of load-balancing strategies have yielded positive outcomes regarding both traffic network performance and emission reduction. This methodology could be effectively implemented not just in the city of Vigo but also in various other cities and countries across different scales. Furthermore, the study could be expanded to encompass not only passenger vehicles but also other modes of transportation and their integration. The findings suggest that merging load balancing with intelligent transportation systems can significantly enhance urban quality of life while lessening the environmental impact associated with transportation.

7. Conclusions

This study proposed and evaluated a traffic load-balancing algorithm designed for the city of Vigo, Spain, as part of the IN2CCAM Horizon 2020 project. The algorithm incorporated short-term traffic predictions, primarily generated using LSTM models, alongside a dynamic routing mechanism intended to redistribute traffic demand and optimize network performance. Results from various simulation scenarios indicated improvements in average travel speed, reductions in delays and periods of standstill, and measurable decreases in pollutant emissions.

The findings confirm that integrating predictive analytics with dynamic load balancing can yield significant advantages for urban traffic management. This approach not only facilitates a more efficient utilization of existing infrastructure but also enhances environmental sustainability by reducing fuel consumption and emissions. Additionally, the methodology offers practical value for policymakers and local authorities, serving as a decision-support tool to inform the development of more adaptive and inclusive mobility strategies.

Future research should concentrate on extending the application of the proposed algorithm to various cities with differing traffic and infrastructure characteristics, as well as incorporating more advanced prediction models such as GNNs. These advancements will enhance the approach’s adaptability and robustness, contributing to the establishment of smarter and more sustainable urban transportation systems.