Research on Multi-Timescale Optimization Scheduling of Integrated Energy Systems Considering Sustainability and Low-Carbon Characteristics
Abstract
1. Introduction
2. Comprehensive Energy System Optimization Dispatch Model Incorporating Demand Response and Green Certificate–Carbon Joint Trading
2.1. Integrated Demand Response Model
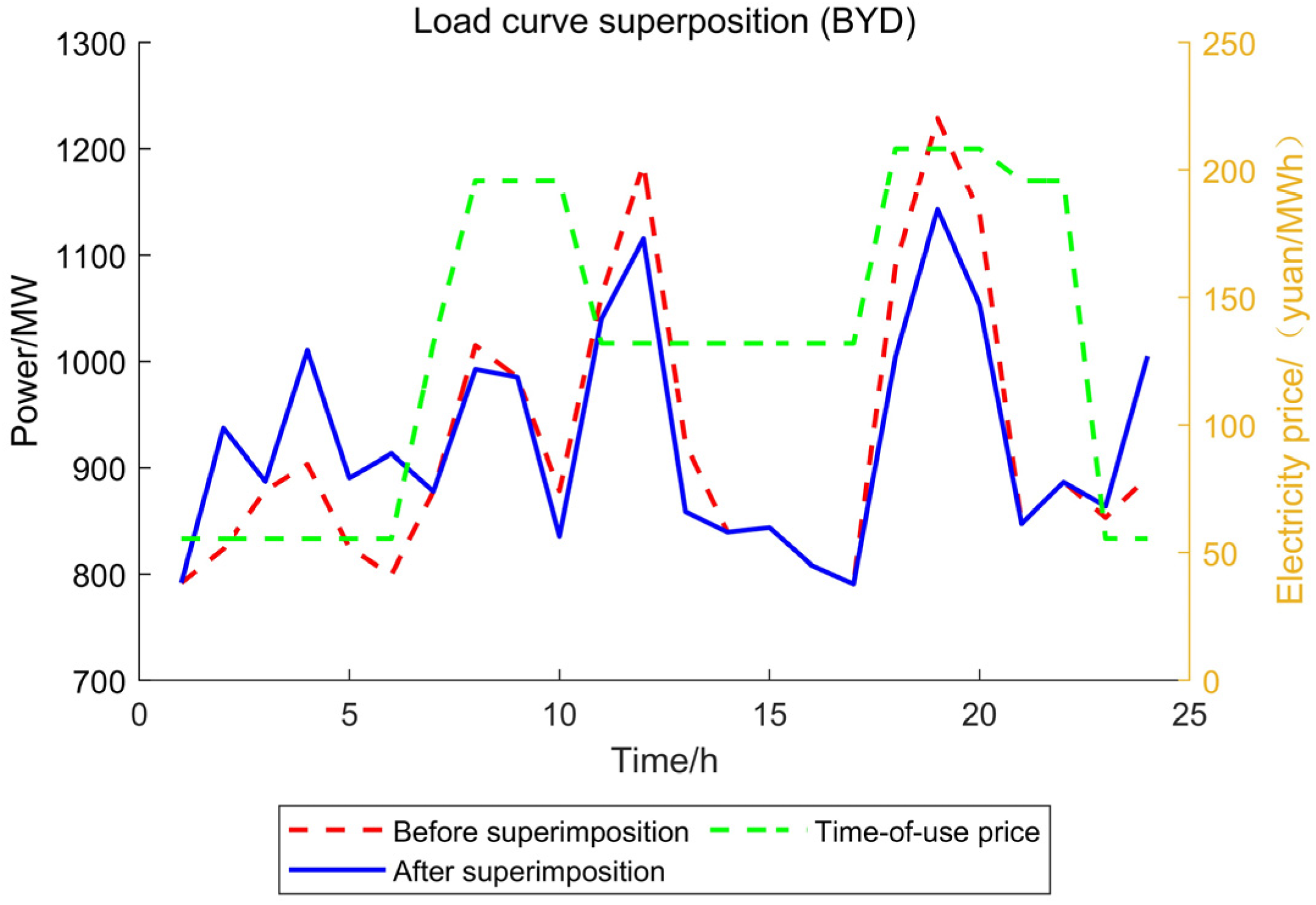
2.1.1. Price-Based Electricity Demand Response Model
2.1.2. Incentive-Based Electric Load Demand Response Model
2.1.3. Incentive-Based Thermal Load Demand Response Model
2.1.4. Demand Response Concept for Cold Load Based on Ambiguous Feeling
2.1.5. Price-Based Load Demand Response Model
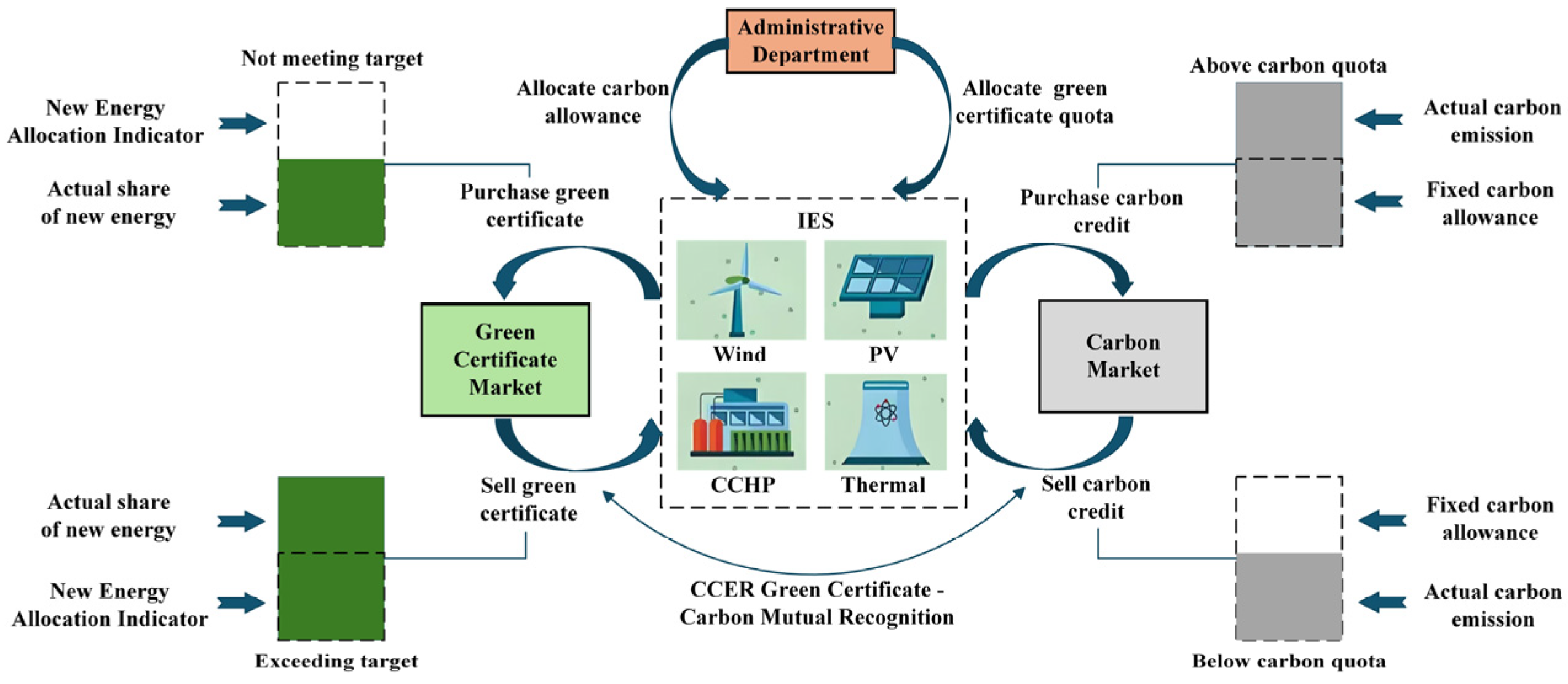
2.2. Green Certificate–Carbon Joint Trading Mechanism
2.3. Virtual Energy Storage Modeling Including Electric Vehicles
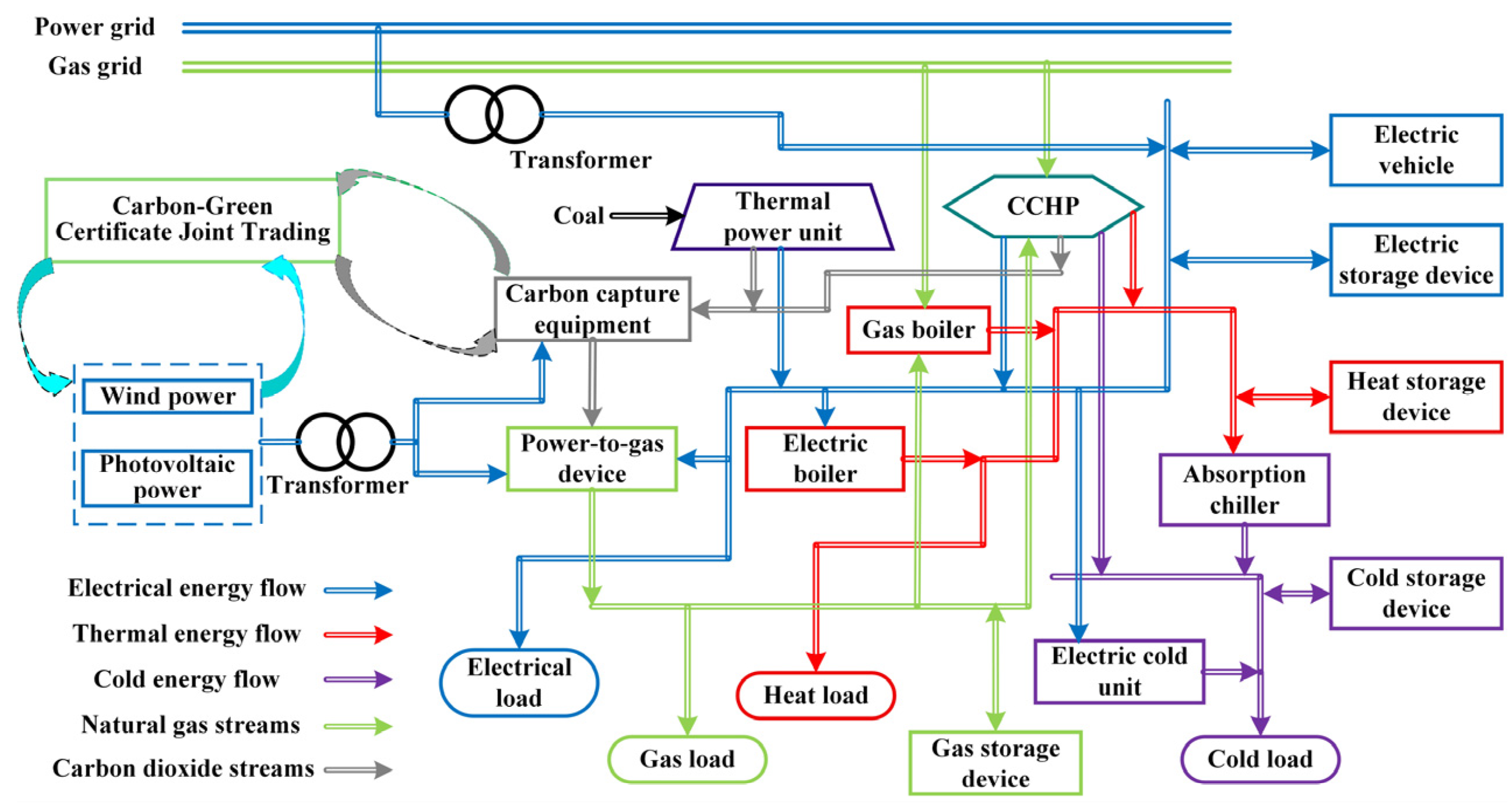
3. Modeling of Multi-Timescale Integrated Energy Systems
3.1. Combined Cooling, Heat, and Power (CCHP) Model
3.2. Gas Boiler (GB) Model
3.3. Absorption Chiller (AC) Model
3.4. Electrical Energy Conversion Model
3.5. Energy Storage Device Model
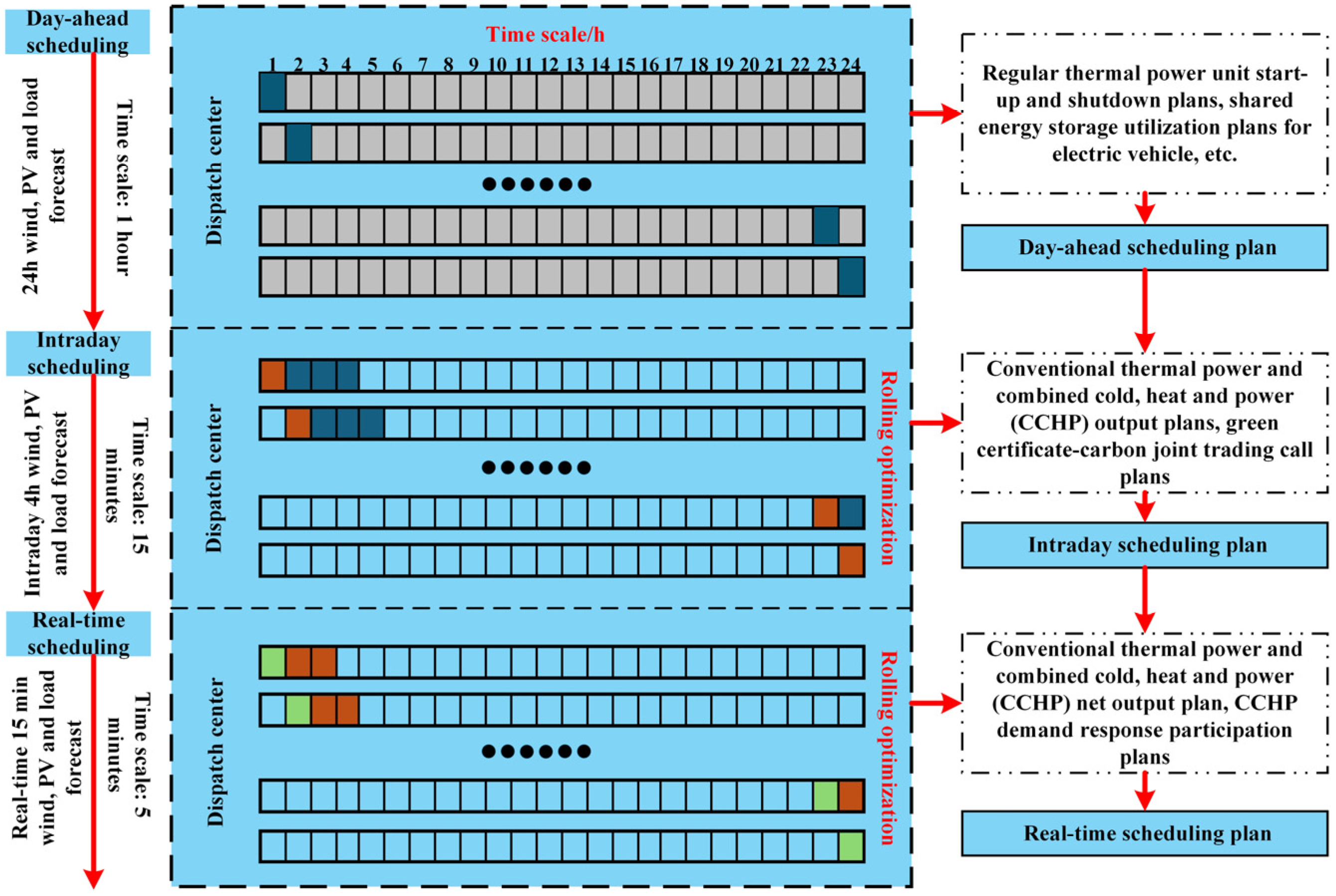
3.6. Multi-Timescale Scheduling Strategy
4. Multi-Timescale Optimization Scheduling of Integrated Energy Systems
4.1. Day-Ahead Scheduling Phase
4.1.1. Objective Function
4.1.2. Constraints
4.2. Intraday Dispatch Phase
4.2.1. Objective Function
4.2.2. Constraints
4.3. Real-Time Scheduling Phase
4.3.1. Objective Function
4.3.2. Constraints
5. Case Study Analysis
5.1. Day-Ahead Analysis
5.2. Intraday Analysis
5.3. Real-Time Analysis
6. Conclusions
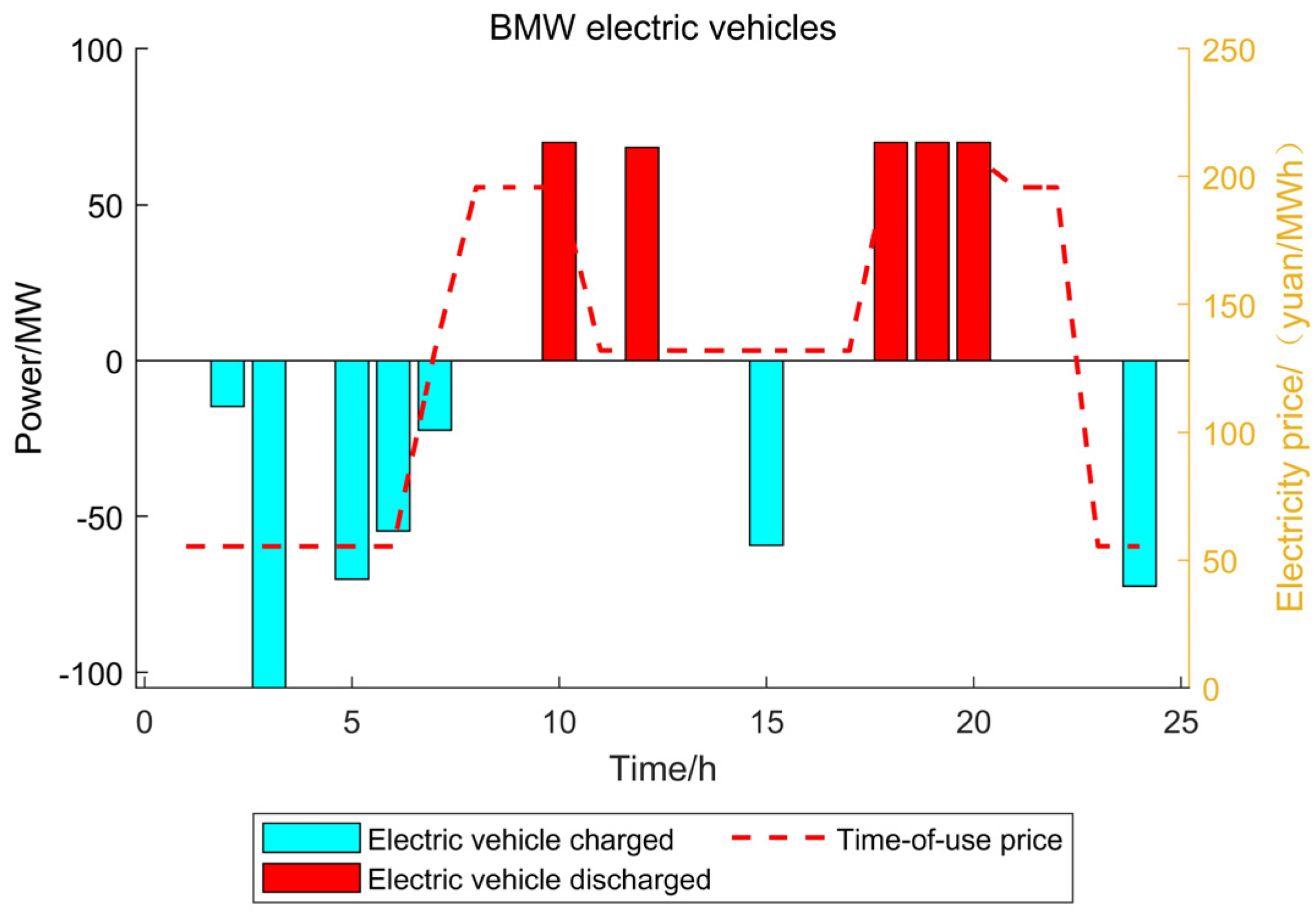
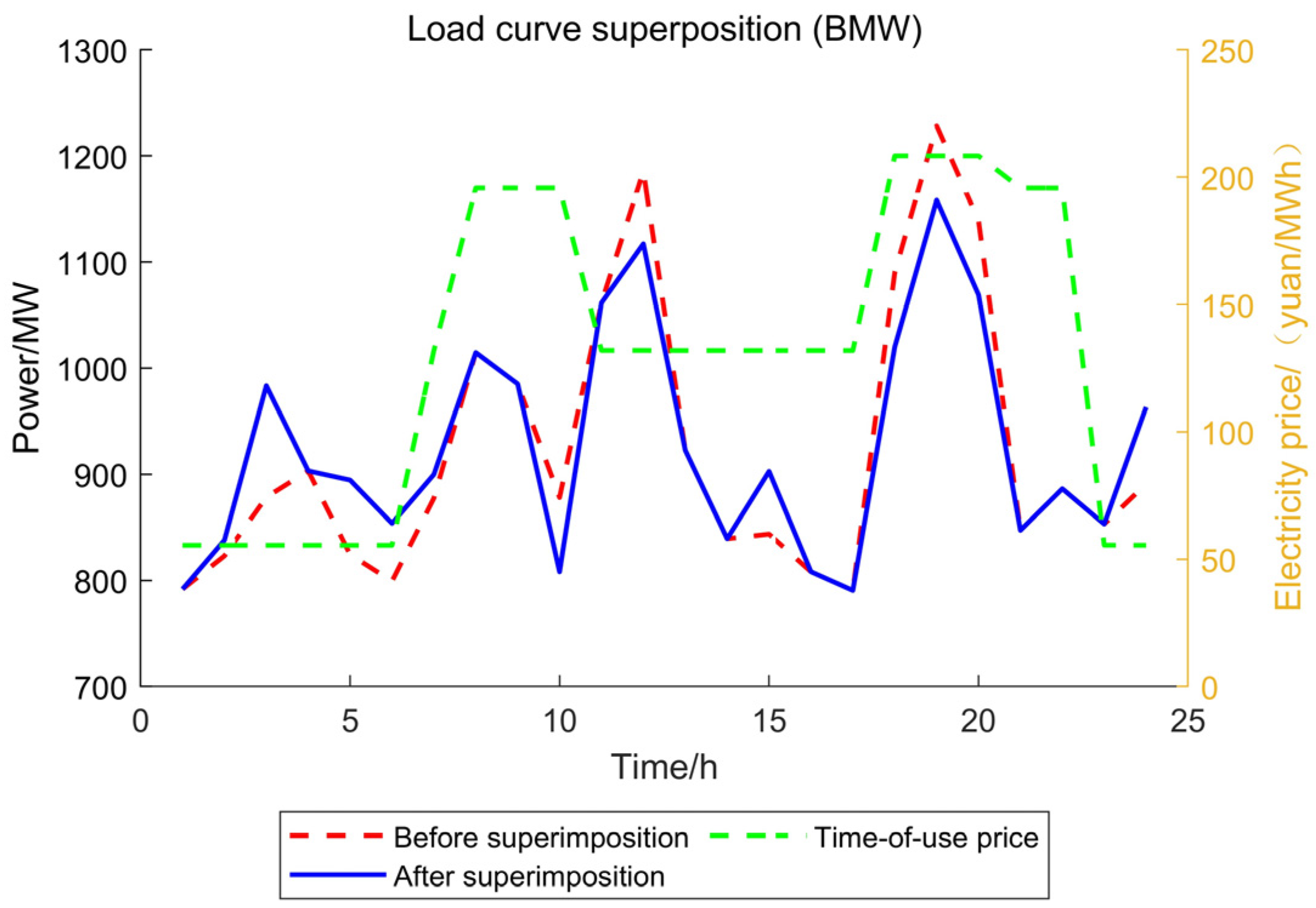
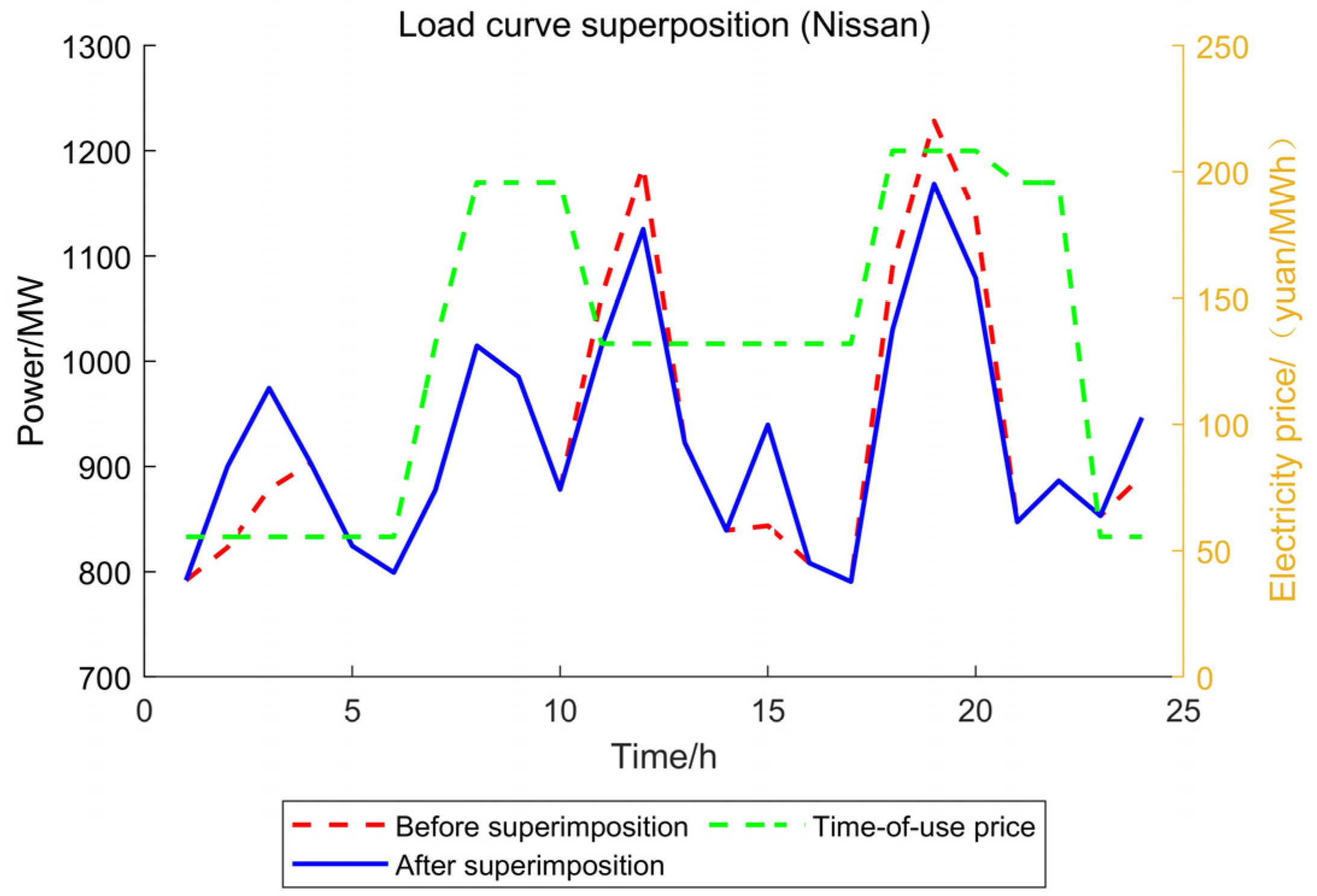
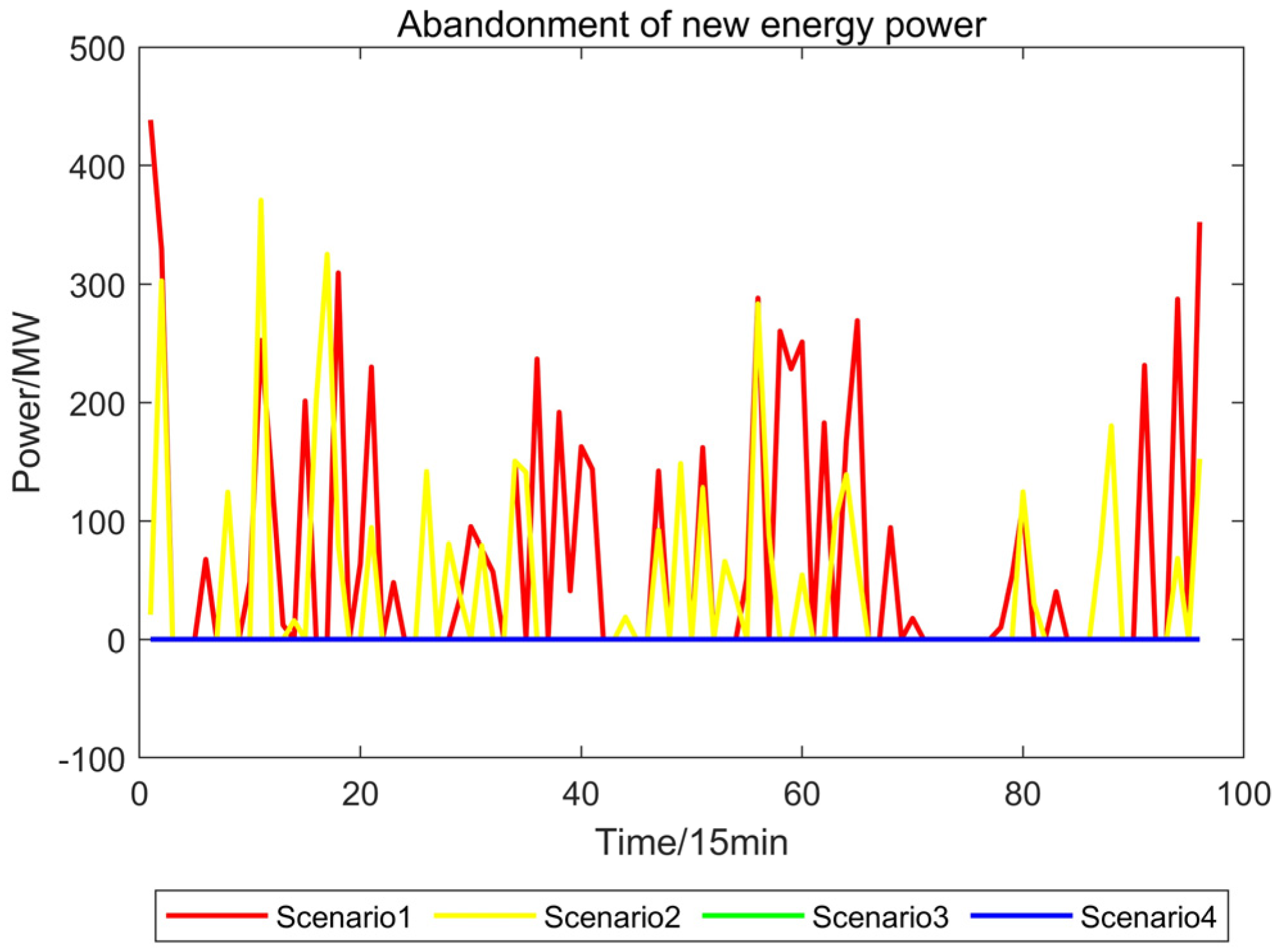
- Shared energy storage systems, such as electric vehicles, with their flexible spatial and temporal characteristics and rapid response capabilities, can charge during off-peak periods and discharge during peak periods. This alleviates peak-period load pressure, prevents energy waste during off-peak periods, enhances the integration of renewable energy sources like wind and PV power, and reduces curtailment of wind and PV energy.
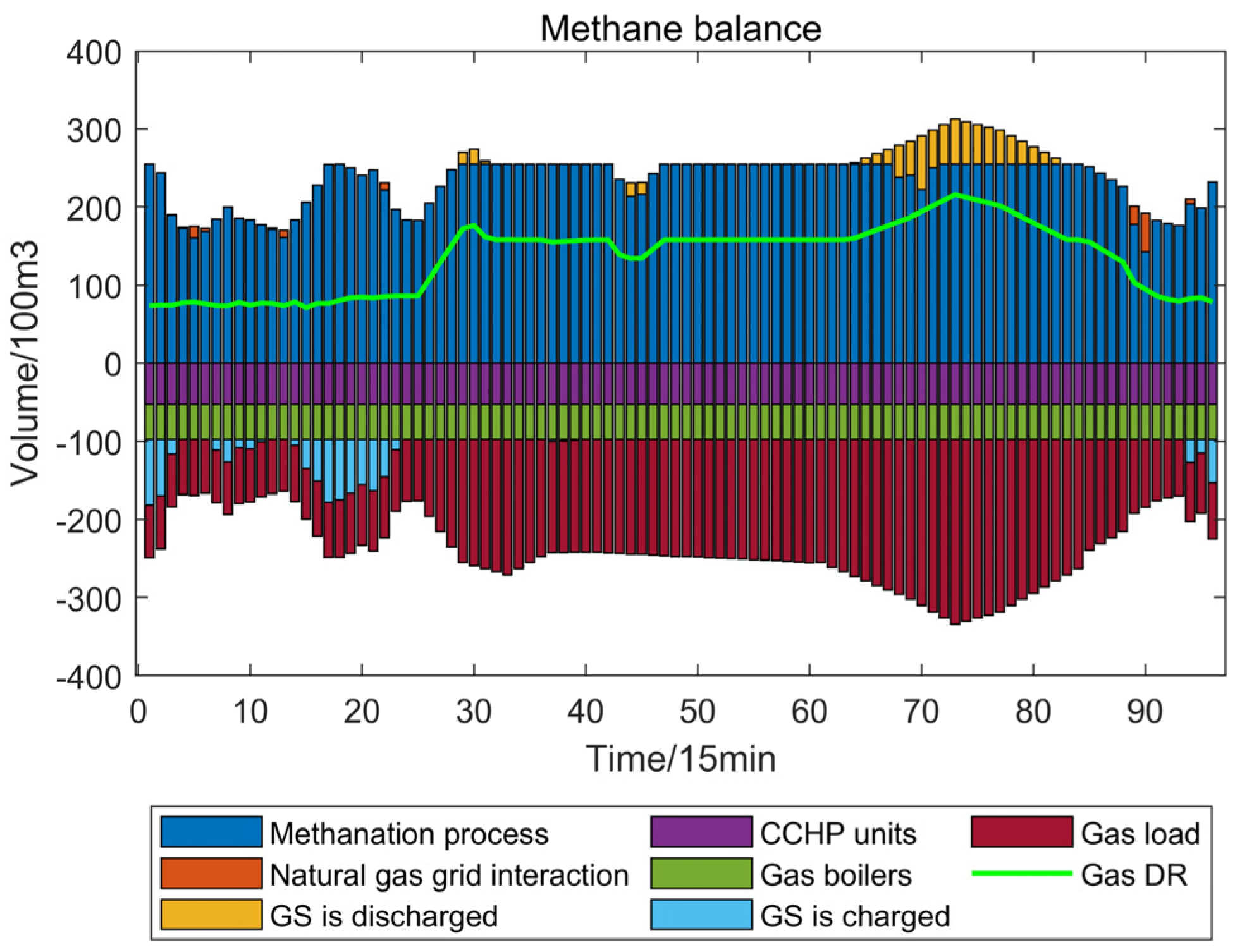
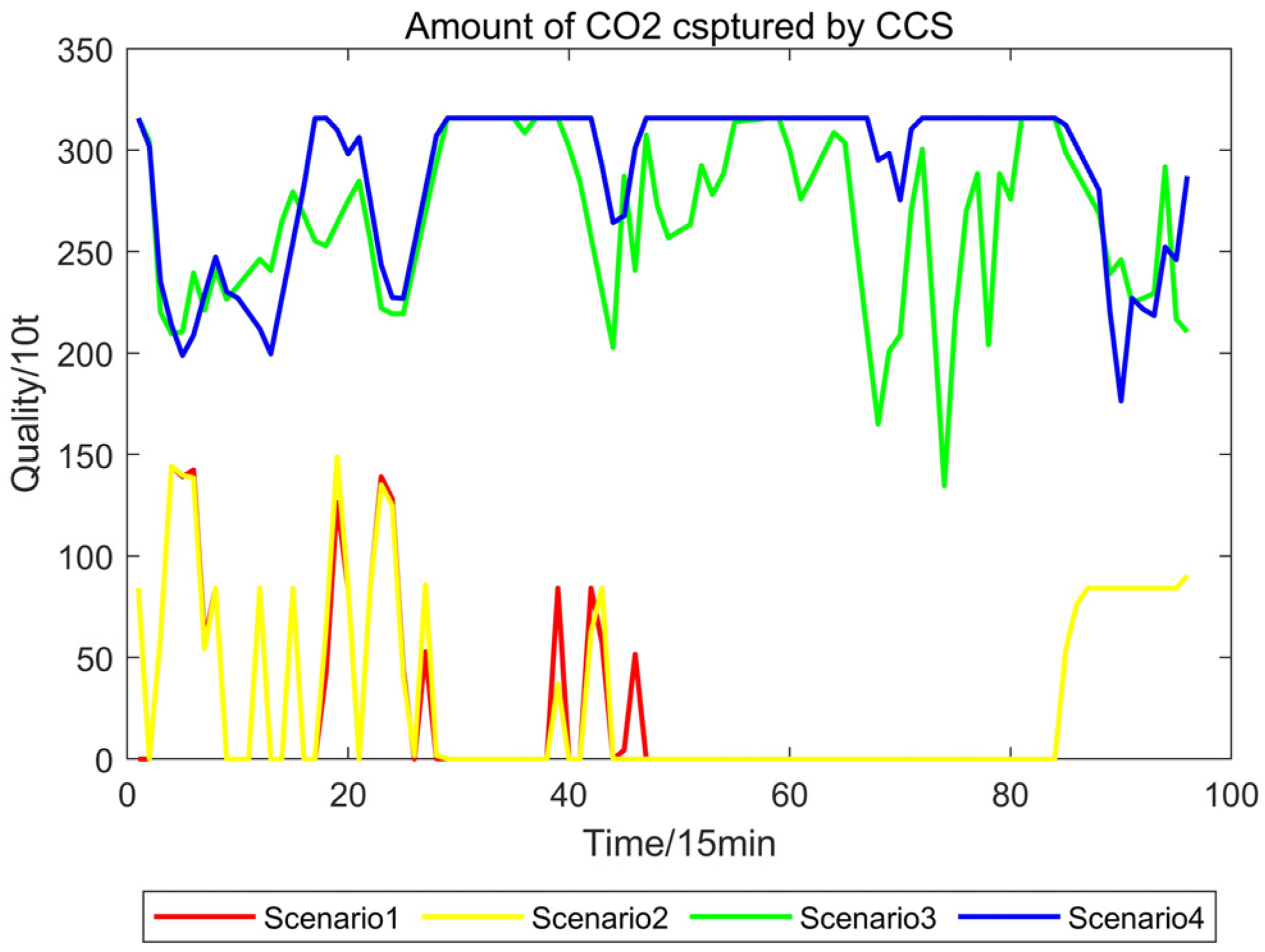
- Mechanisms for incentives and penalties are used in the green certificate–carbon joint trading market. On the one hand, by trading excess green certificates, the green certificate trading market encourages the system’s continued incorporation of renewable energy sources like PV and wind. On the other hand, it lowers the system’s CO2 emissions and improves CCS’s capacity to collect carbon through the carbon trading market. The system’s overall economic efficiency can be increased by converting extra green certificates into carbon emission rights.
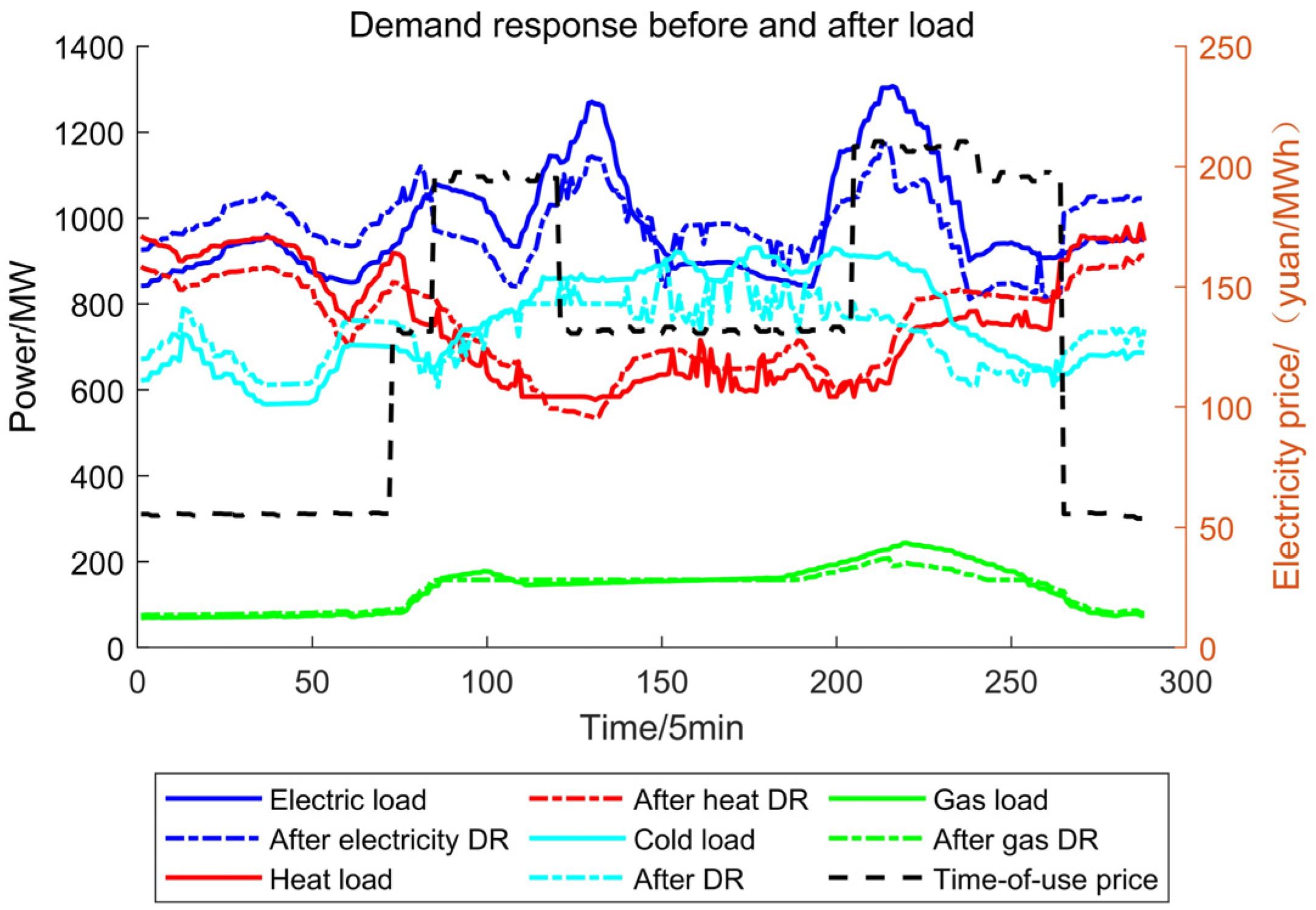
- Cold, heat, gas, and electricity demand response can be achieved through price-based and incentive-based mechanisms to transfer and reduce various loads, thereby smoothing load fluctuations, reducing output fluctuations of power generation units, making output more reasonable, lowering energy costs, improving energy utilization efficiency, enhancing energy supply flexibility, and promoting interaction between users and the energy system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IES | Integrated energy systems |
| EVs | Electric vehicles |
| V2G | Vehicle-to-grid |
| TGCs | Tradable green certificates |
| ETS | Emission trading schemes |
| ISOs | Independent System Operators |
| P2G | Power-to-gas |
| IDR | Integrated demand response |
| CET | Carbon trading |
| GCT | Green certificate trading |
| CCER | Chinese Certified Emission Reductions |
| CCHP | Combined cooling, heat, and power |
| GB | Gas boiler |
| AC | Absorption chiller |
| EB | Electric boiler |
| EC | Electric chiller |
| CCS | Carbon capture and storage |
References
- Yuan, Y.; Miao, A.K.; Wu, H.; Zhu, J.P.; Wang, Z.M.; Qian, K. Research framework and key issues in low-carbon integrated energy systems. High Volt. Eng. 2024, 50, 4019–4036. [Google Scholar] [CrossRef]
- Mei, S.; Li, B.; Wang, H.; Wang, J.; Wang, Y.; Liu, Z.; Chen, Y.; Zhang, L.; Wu, W.; Guo, X. Multi-objective optimal scheduling of microgrid with electric vehicles. Energy Rep. 2022, 8, 4512–4524. [Google Scholar] [CrossRef]
- Yue, Y.; Zhang, Q.; Zhang, J.; Yu, F.; Chen, X.; Mao, L.; Liu, Y.; Zhao, H. Orderly charging and discharging group scheduling strategy for electric vehicles. Appl. Sci. 2023, 13, 13156. [Google Scholar] [CrossRef]
- Kapoor, A.; Patel, V.S.; Sharma, A.; Kumar, R.; Singh, S.N.; Reddy, M.J.B.; Thomas, T.; Wei, L. Centralized and decentralized pricing strategies for optimal scheduling of electric vehicles. IEEE Trans. Smart Grid 2022, 13, 2234–2244. [Google Scholar] [CrossRef]
- Mahato, D.; Aharwal, V.K.; Sinha, A. Multi-objective optimization model and hybrid optimization algorithm for electric vehicle charge scheduling. J. Exp. Theor. Artif. Intell. 2024, 36, 1645–1667. [Google Scholar] [CrossRef]
- Li, M.; Aksoy, M.; Samad, S.; Wong, K.P.; Lie, T.T.; Tang, Y.; Wang, C.; Liu, F. Optimal energy management and scheduling of a microgrid with integrated electric vehicles and cost minimization. Soft Comput. 2024, 28, 2015–2034. [Google Scholar] [CrossRef]
- Chen, J.; Mao, L.; Liu, Y.; Wang, X.; Li, Z.; Wei, F.; Zhang, H.; Sun, L. Multi-objective optimization scheduling of active distribution network considering large-scale electric vehicles based on NSGAII-NDAX algorithm. IEEE Access 2023, 11, 97259–97273. [Google Scholar] [CrossRef]
- Yang, F.; Yu, S.; Meng, C.; Zhang, H.; Wu, L.; Zhou, Q.; Li, X. A three-stage optimization of charging scheduling of electric vehicles considering electricity price and user selection. Electr. Eng. 2024, 106, 4737–4746. [Google Scholar] [CrossRef]
- Yang, J.; Yu, F.; Ma, K.; Jiang, T.; Sun, W.; Li, Y.; Wang, Z.; Liu, L. Optimal scheduling of electric-hydrogen integrated charging station for new energy vehicles. Renew. Energy 2024, 224, 120224. [Google Scholar] [CrossRef]
- Xie, T.; Ma, K.; Zhang, G.; Zhao, Y.; Wang, H.; Chen, L.; Liu, X. Optimal scheduling of multi-regional energy system considering demand response union and shared energy storage. Energy Strategy Rev. 2024, 53, 101413. [Google Scholar] [CrossRef]
- Qiao, J.; Mi, Y.; Shen, J.; Wang, C.; Li, X.; Zhang, Z. Optimization schedule strategy of active distribution network based on microgrid group and shared energy storage. Appl. Energy 2025, 377, 124681. [Google Scholar] [CrossRef]
- Sun, X.; Chen, J.; Yang, S.; Liu, H.; Wang, Y.; Li, R.; Zhang, W.; Xu, F. Optimal scheduling of multi-regional integrated energy systems with shared energy storage under dynamic rental prices mechanism. J. Energy Storage 2025, 106, 114902. [Google Scholar] [CrossRef]
- Chai, Z.; Liu, J.; Zhang, Y.; Wang, H.; Chen, L.; Zhou, Q.; Yang, X. Optimal scheduling strategy of regional power system dominated by renewable energy considering physical and virtual shared energy storage. Energies 2023, 16, 2506. [Google Scholar] [CrossRef]
- Li, X.; Deng, J.; Liu, J. Energy-carbon-green certificates management strategy for integrated energy system using carbon-green certificates double-direction interaction. Renew. Energy 2025, 238, 121937. [Google Scholar] [CrossRef]
- Tan, J.; Pan, W.; Li, Y.; Zhang, C.; Yang, F.; Liu, S.; Wu, H. Energy-sharing operation strategy of multi-district integrated energy systems considering carbon and renewable energy certificate trading. Appl. Energy 2023, 339, 120835. [Google Scholar] [CrossRef]
- Li, J.; Xu, L.; Wang, L.; Zhao, Y.; Zhang, H.; Chen, T.; Liu, X. Operation optimization of regional integrated energy systems with hydrogen by considering demand response and green certificate-carbon emission trading mechanisms. Energies 2024, 17, 3190. [Google Scholar] [CrossRef]
- Chen, H.; Wu, H.; Li, H.; Wang, X.; Zhang, Y.; Liu, Z.; Yang, F. Bi-level optimal scheduling of integrated energy systems considering incentive-based demand response and green certificate-carbon trading mechanisms. Energy Rep. 2025, 13, 330–344. [Google Scholar] [CrossRef]
- Ma, T.; Peng, L.; Wu, G.; Zhou, Y.; Li, X.; Wang, C.; Zhang, Z. Research on multi-scale electricity-carbon-green certificate market coupling trading based on system dynamics. Processes 2025, 13, 109. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, Z.; Chen, J.; Wang, L.; Liu, Y.; Zhang, H.; Zhao, F. Optimization of low-carbon operation in a combined electrical, thermal, and cooling integrated energy system with liquid carbon dioxide energy storage and green certificate and carbon trading mechanisms. Processes 2025, 13, 372. [Google Scholar] [CrossRef]
- Zheng, B.; Bao, Z.; Yang, L. Design and equilibrium analysis of integrated market of ISO-led carbon emissions, green certificates and electricity considering their interplay. Energy Econ. 2023, 126, 107022. [Google Scholar] [CrossRef]
- Li, L.; Song, K.; Xu, W.; Zhang, Y.; Wang, H.; Liu, J.; Yang, C. System dynamics simulation of policy synergy effects: How tradable green certificates and carbon emission trading shape electricity market sustainability. Appl. Sci. 2025, 15, 4086. [Google Scholar] [CrossRef]
- Hou, H.; Ge, X.; Yan, Y.; Chen, L.; Wang, Z. An integrated energy system ‘green-carbon’ offset mechanism and optimization method with Stackelberg game. Energy 2024, 294, 130617. [Google Scholar] [CrossRef]
- Gong, X.; Li, X.; Zhong, Z. Strategic bidding of virtual power plants in integrated electricity-carbon-green certificate market with renewable energy uncertainties. Sustain. Cities Soc. 2025, 121, 106176. [Google Scholar] [CrossRef]
- Tang, Z.; Yin, Y.; Chen, C.; Zhang, L.; Wu, H.; Zhou, F.; Liu, X. A synergistic planning framework for low-carbon power systems: Integrating coal-fired power plant retrofitting with a carbon and green certificate market coupling mechanism. Energies 2025, 18, 2403. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhang, D.; Wang, Y.; Li, H.; Chen, X.; Liu, L. Optimal operation of integrated energy systems considering energy trading and integrated demand response. Energy Rep. 2024, 11, 3307–3316. [Google Scholar] [CrossRef]
- Hua, H.; Du, C.; Chen, X.; Wang, Y.; Zhang, Z.; Li, T.; Liu, W. Optimal dispatch of multiple interconnected-integrated energy systems considering multi-energy interaction and aggregated demand response for multiple stakeholders. Appl. Energy 2024, 376, 124256. [Google Scholar] [CrossRef]
- Lyu, X.; Liu, T.; Liu, X.; Zhang, Y.; Wu, H.; Wang, S. Low-carbon robust economic dispatch of park-level integrated energy system considering price-based demand response and vehicle-to-grid. Energy 2023, 263, 125739. [Google Scholar] [CrossRef]
- Guo, W.; Wang, Q.; Liu, H.; Chen, L.; Zhao, Y.; Yang, F.; Li, X. Multi-energy collaborative optimization of park integrated energy system considering carbon emission and demand response. Energy Rep. 2023, 9, 3683–3694. [Google Scholar] [CrossRef]
- Li, W.; He, M.; Cai, T. Low-carbon economic dispatch of hydrogen-containing integrated energy system considering stepped demand response. Energy Rep. 2024, 11, 4222–4232. [Google Scholar] [CrossRef]
- Zheng, B.; Hou, X.; Xu, S.; Zhang, Y.; Wang, L.; Liu, C.; Zhao, H. Strategic optimization operations in the integrated energy system through multitime scale comprehensive demand response. Energy Sci. Eng. 2024, 12, 2236–2257. [Google Scholar] [CrossRef]
- Meng, Z.; Dong, F.; Chi, L. Optimal dispatch of integrated energy system with P2G considering carbon trading and demand response. Environ. Sci. Pollut. Res. 2023, 30, 104284–104303. [Google Scholar] [CrossRef]
- Tang, J.; Liu, J.; Sun, T.; Zhang, H.; Wang, Y.; Chen, L.; Yang, X. Multi-time-scale optimal scheduling of integrated energy system considering demand response. IEEE Access 2023, 11, 135891–135904. [Google Scholar] [CrossRef]
- Luo, Y.; Hao, H.; Yang, D.; Li, X.; Wu, Z.; Zhang, F.; Wang, L. Multi-objective optimization of integrated energy systems considering ladder-type carbon emission trading and refined load demand response. J. Mod. Power Syst. Clean Energy 2023, 12, 828–839. [Google Scholar] [CrossRef]
- Li, Y.; Li, R.; Shi, L.; Wang, C.; Zhang, X. Adjustable capability evaluation of integrated energy systems considering demand response and economic constraints. Energies 2023, 16, 8048. [Google Scholar] [CrossRef]
- Ma, C.; Hu, Z. Low-carbon economic scheduling of integrated energy system considering flexible supply-demand response and diversified utilization of hydrogen. Sustainability 2025, 17, 1749. [Google Scholar] [CrossRef]


| Formula | Numerical Value | Formula | Numerical Value | Formula | Numerical Value | Formula | Numerical Value |
|---|---|---|---|---|---|---|---|
| 0.00033 | 0 | 10 | 0.92 | ||||
| 16.7 | 400 | 800 | 0.92 | ||||
| 890 | 0 | 10 | 0.95 | ||||
| 200 | 300 | 600 | 0.95 | ||||
| 500 | 0 | 10 | 0.96 | ||||
| 50 | 100 | 550 | 0.96 | ||||
| 400 | 0 | 10 | 0.94 | ||||
| 0 | 200 | 750 | 0.94 | ||||
| 300 |
| Day-Ahead Costs/Yuan | Scenarios | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Total | 3,308,602.1902 | 3,178,548.8247 | 2,869,491.0196 | 2,845,294.0451 |
| Coal consumption | 1,782,701.2533 | 1,665,088.6132 | 1,769,101.6459 | 1,689,070.8571 |
| Start-stop | 89,674.6464 | 90,870.3084 | 87,881.1535 | 88,837.683 |
| Wind power curtailment | 4430.313 | 2405.3686 | 0 | 0 |
| Abandoned photovoltaic | 2512.8956 | 1209.375 | 0 | 0 |
| Green certificate–carbon joint | 0 | 0 | −528,682.7552 | −542,965.7424 |
| Purchase | 1,395,970.1759 | 1,327,779.1668 | 1,438,416.6162 | 1,344,359.9088 |
| DR call | 0 | 0 | 0 | 163,840.5373 |
| Daily depreciation | 33,312.906 | 32,535.9286 | 37,974.7704 | 34,963.9829 |
| Charging and discharging compensation | 0 | 58,660.0642 | 64,799.5789 | 56,657.4737 |
| Intraday Costs/Yuan | Scenarios | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Total | 3,253,261.1386 | 3,112,109.508 | 2,778,761.6073 | 2,741,305.2372 |
| Coal consumption | 1,798,454.2268 | 1,684,731.4151 | 1,788,427.9664 | 1,691,084.0524 |
| Deadweight | 22,388.7701 | 5578.5103 | 530.8451 | 53.2271 |
| Wind power curtailment | 4434.8498 | 2530.517 | 0 | 0 |
| Abandoned photovoltaic | 2521.8122 | 1215.2064 | 0 | 0 |
| Green certificate–carbon joint | 0 | 0 | −535,402.3241 | −543,638.8248 |
| Purchase | 1,392,051.4516 | 1,324,739.6795 | 1,422,971.2538 | 1,339,330.5876 |
| DR call cost | 0 | 0 | 0 | 162,839.8771 |
| Daily depreciation | 33,410.0281 | 33,376.0354 | 37,294.9151 | 34,876.573 |
| Charging and discharging compensation | 0 | 59,938.1443 | 64,938.951 | 56,759.7448 |
| Real-Time Costs/Yuan | Scenarios | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Total | 3,208,027.402 | 3,112,262.6016 | 2,751,033.7028 | 2,722,225.8371 |
| Coal consumption | 1,763,133.1128 | 1,679,983.174 | 1,758,867.1736 | 1,678,414.2587 |
| Deadweight | 22,645.1127 | 5674.5475 | 574.6165 | 63.7128 |
| Wind power curtailment | 4513.8112 | 2573.4773 | 0 | 0 |
| Abandoned photovoltaic | 2486.1665 | 1200.7199 | 0 | 0 |
| Green certificate–carbon joint | 0 | 0 | −538,757.3568 | −544,455.1625 |
| Purchase | 1,381,839.1706 | 1,329,145.474 | 1,427,959.3328 | 1,334,742.1386 |
| DR call | 0 | 0 | 0 | 162,171.4956 |
| Daily depreciation | 33,410.0281 | 33,701.3947 | 37,362.9007 | 35,070.8173 |
| Charging and discharging compensation | 0 | 59,983.8144 | 65,027.0361 | 56,218.5765 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Liu, X. Research on Multi-Timescale Optimization Scheduling of Integrated Energy Systems Considering Sustainability and Low-Carbon Characteristics. Sustainability 2025, 17, 8899. https://doi.org/10.3390/su17198899
Jiang H, Liu X. Research on Multi-Timescale Optimization Scheduling of Integrated Energy Systems Considering Sustainability and Low-Carbon Characteristics. Sustainability. 2025; 17(19):8899. https://doi.org/10.3390/su17198899
Chicago/Turabian StyleJiang, He, and Xingyu Liu. 2025. "Research on Multi-Timescale Optimization Scheduling of Integrated Energy Systems Considering Sustainability and Low-Carbon Characteristics" Sustainability 17, no. 19: 8899. https://doi.org/10.3390/su17198899
APA StyleJiang, H., & Liu, X. (2025). Research on Multi-Timescale Optimization Scheduling of Integrated Energy Systems Considering Sustainability and Low-Carbon Characteristics. Sustainability, 17(19), 8899. https://doi.org/10.3390/su17198899






