1. Introduction
Integration of renewable energy sources (RESs) into distribution networks (DNs) are usually associated with several operational challenges, including increased power losses, voltage fluctuations, grid congestion, and reduced flexibility in meeting variable demand [
1,
2,
3,
4,
5]. These challenges are made more complex by the inherent variability of renewable generation, since changes in wind speed and solar irradiance can cause voltage instability and further losses. To maintain reliable and efficient operation, it is crucial to determine the optimal size and placement of distributed generation (DG) units, as their allocation strongly influences power losses, voltage stability, and overall system performance. Two factors are vital for meeting technical goals that address grid conditions while causing the least power loss: strong planning strategies plus full consideration of the effects of uncertainty and increased loads. These factors translate into elevated grid stress due to additional forms of energy consumption, larger populations and urban areas, and burgeoning electric vehicle uptake.
Prior studies related to distribution network (DN) allocation/sizing of RESs and/or electric vehicle charging stations (EVCSs) have introduced various techniques for establishing the most effective solutions [
1]. Objective functions employed in most technically focused efforts have targeted decreased voltage instability and network losses by emphasizing enhanced VSIs and diminished TVD [
2]. Some researchers have employed evolutionary algorithms: genetic algorithms (GAs) in conjunction with a novel holomorphic embedding load-flow method (HELM) [
3]; a new algorithm called chaotic student psychology based optimization (CSPBO) [
4]; and particle swarm optimization (PSO) applied for DG and EVCS location and sizing [
5]. In attempts to mitigate detrimental effects on peak loads, power losses, voltage deviations, and thermal limit violations arising from EVCS incorporation into a DN, others have targeted the enhancement of EVCS planning by developing coordinated charging schemes and techniques for optimizing EVCS positioning [
6]. The following subsections present details about and published reports related to DGs and optimization methods.
Small-scale sources of electrical power with direct consumer-side DN linkage close to load centers are known collectively as “distributed generation.” DGs can be either renewable (wind and solar) or non-renewable, with their labeling reflecting how they are connected and the level of their voltage. DN-side interfaces can be low voltage (LV) or medium voltage (MV), but consumer-side links are usually just low voltage (LV). Bidirectional power flow resulting from substantial DG integration transforms passive distribution networks (DNs) into active distribution networks (ADNs). DGs provide numerous advantages: voltage reinforcement, decreased system losses, enhanced power quality, elevated maximum capacity, balanced load distribution across DN sections, stronger grids, and improved system stability. However, the stochastic nature of renewable energy generation (REG) and nonlinear EV fleets necessitates additional study with respect to voltage support, loss reduction, costly reinforcement postponements, and curtailment of greenhouse gas (GHG) emissions [
7,
8]. Enhanced ADN planning and sizing must address the role of EV loads and energy storage systems in grid stability factors such as changeable demand and load shaving. Complicated choices related to decision variables for siting and sizing time-shifting EV loads involve multiple divergent objectives. Operators who assess objectives/criteria across planning horizons need to be mindful of updated distribution parameters and future needs [
9].
Metaheuristics are an often-used category of optimization techniques based on adaptable, smart algorithms that mirror nature to discover near-optimal solutions for complex problems whose solutions are unobtainable using conventional computation. Taking less processing time [
10], these algorithms excel at unraveling optimization problems characterized by nonlinearity, multimodality, and combinatoric constituents: in short, ideal for optimal DG [
11] and EVCS [
12] placement. Metaheuristic methods engender superior solutions due to their double focus on exploration and exploitation of the solution space. The literature reports on a broad spectrum of metaheuristics [
13]. Most notably efficient and flexible are GAs, derived from natural selection, with crossover and mutation operators to produce evolved solutions in later generations [
14]; PSO, which mimics birds’ swarming and information-sharing activities [
15]; and grey wolf optimization (GWO) [
16].
GWO copies gray wolves’ leadership ranking and collaborative hunting tactics [
17]. This strong metaheuristic optimizer, with its simpler, more flexible approach involving fewer control parameters also has the most rapidly expanding acceptance rate. The design derives from a wolf pack’s social hierarchy: alpha (α) wolves lead hunting operations, beta (β) and delta (δ) wolves help with decisions, and omega (ω) wolves follow along. This organization creates a dynamic equilibrium between the two GWO processes: exploration (encircling prey), and exploitation (hunting or attacking prey). During exploration, the wolves surround possible prey by trying out different search configurations. The ranking of the alpha, beta, and delta wolves provides a crucial governing structure, with the alpha wolf denoting the best solution. In the exploitation phase, the wolves converge on the prey by modifying their locations with respect to alpha, beta, and delta wolves. An analysis of GWO versus common heuristics, such as PSO, a gravitational search algorithm (GSA), differential evolution (DE), expectation propagation (EP), and an envelope strategy (ES), revealed that GWO generated comparable outcomes [
17]. Relative to other methods, GWO needs fewer parameters, is suitable for both continuous and discrete scenarios, and is a top metaheuristic for exploring complicated multi-objective search spaces. GWO’s scalability makes it a superb choice for dealing with the diverse sizes and dimensions of complex power system problems [
18], particularly the optimization of DG [
19] and EVCS [
20] positioning since the scale or complexity can vary according to grid dimensions, number of DGs, and multi-dimensionality frequently renders the solution space hard to navigate. The study reported in [
21] was the first to suggest GWO for locating and sizing multiple DGs in a distributed system, based on multiple objectives: reactive power loss (
) minimization and voltage profile enhancement, all without violation of system limits. On the IEEE 69-bus test system, GWO outclassed a GSA and a bat algorithm (BA). Another researcher [
22] evaluated GWO against four metaheuristics in regard to determining ideal DG placement: PSO, GWO, a whale optimization algorithm (WOA), and a backtracking search algorithm (BSA). Six IEEE 33-bus distribution system scenarios were tested, with GWO most often surpassing other techniques. For the work presented here, we chose GWO as the starting optimal allocation approach due to its formidable balancing of exploration and exploitation search phases.
Although highly effective, GWO is also subject to deficiencies: sluggish or early convergence plus sensitivity to the starting population. For multi-modal functions, standard GWO is susceptible to becoming stuck in local optima, considerably slowing the convergence rate in subsequent evolution stages [
23]. GWO searches favor exploitation because every wolf (candidate solution) is attracted to the α, β, and δ wolves, thus accelerating convergence toward these wolves and impairing the range and variety of the search so that it might not cover the complete solution space. These drawbacks have led to the creation of a number of GWO variants: an evolutionary population dynamics (EPD) operator [
24]; a Lévy flight operator for enhancing exploration [
25]; a PSO-derived nonlinear control parameter with an improved position-updating equation for optimizing balanced exploration/exploitation [
23]; a fuzzy hierarchical operator for mimicking hunting [
26]; refraction learning for dealing with global optimization issues [
27]; astrophysics principles for directing GWO handling of numerical and engineering optimization [
28]; a chaotic logistic map, OBL, DE, and a disruption operator (DO) for maximizing global optimization [
29]; exploration-enhanced GWO (EEGWO), with an adjusted position-updating equation [
30]; and a random walk strategy for elevating global searches [
31].
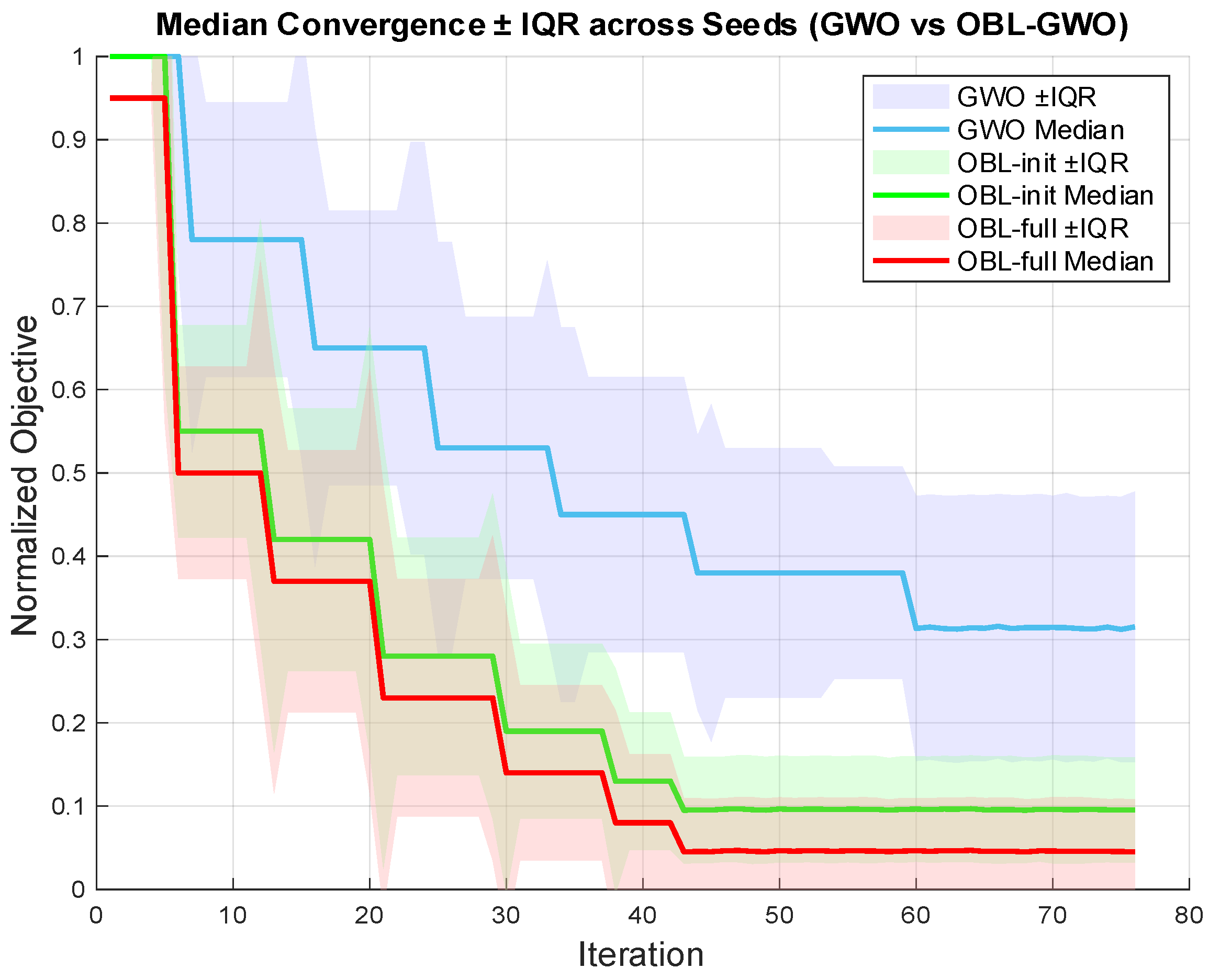
Opposition-based learning (OBL) is an inventive machine learning methodology inspired by diametrically opposed interrelationships among elements. The basic idea is for each possibility (guess) under consideration to be assessed at the same time as its corresponding opposite in order to expedite the discovery of the best solution. OBL accelerates the convergence of a metaheuristic algorithm because the opposite location for each entity in the population is computed both as a starting determinant during the first algorithm stage and also for every iteration. Opposite possibilities are estimated for each population solution and are then merged with the initial suggested solutions. From the entire population, the top solutions whose size equals that of the population are chosen.
Since OBL can elevate the GWO search process, it appears in newly developed techniques, such as opposition-based GWO (OGWO) [
32], which combines OBL and a jumping rate to facilitate the algorithm’s exit from a local optimum with no added computation intricacy. A nonlinear function also progressively modifies parameter
for exploration/exploitation congruence relative to varied restrictions and objectives. In [
33], the researchers employed an explorative equation, which established capacity of OBL for improving the convergence precision and global search efficacy of GWO. The authors of [
34] tackled feature choice and global optimization by introducing a hybrid method based on merging a harmony search (HS) algorithm with GWO coupled with OBL. A further concept was to adjust parameter vector “C’’ in the exploration phase to harmonize GWO exploration and exploitation while integrating an innovative random OPL methodology in order to assist the population in escaping from local optima [
35]. Studies were conducted using 23 popular disparate benchmark test functions and 30 benchmark problems: results indicated that the proposed technique enhanced global optimization outcomes. OBL has thus demonstrated potential for alleviating the stagnation in local optima that undermines GWO efficacy. For this DG positioning study, we selected OBL to enhance GWO due to its verified power to boost algorithm execution [
33,
36].
Recent research continues to point out the difficulties in building models that stay reliable when operating conditions change. For instance, the limitations of conventional methods have been emphasized by the reliability studies when confronted with uncertain environments and system complexity [
37,
38]. Similarly, work on intelligent fault diagnosis demonstrates how domain shifts caused by changing operating states can undermine the generalization of data-driven approaches, necessitating adaptive transfer learning strategies [
39,
40]. While these studies originate from fields such as machinery diagnostics, acoustics, and reliability engineering, the underlying research gaps of uncertainty, robustness, and adaptability to real-world variability are directly relevant to ADN. These gaps form the motivation for the present work, which tackles them by applying OBL-GWO to achieve optimal DG allocation under seasonal and stochastic conditions.
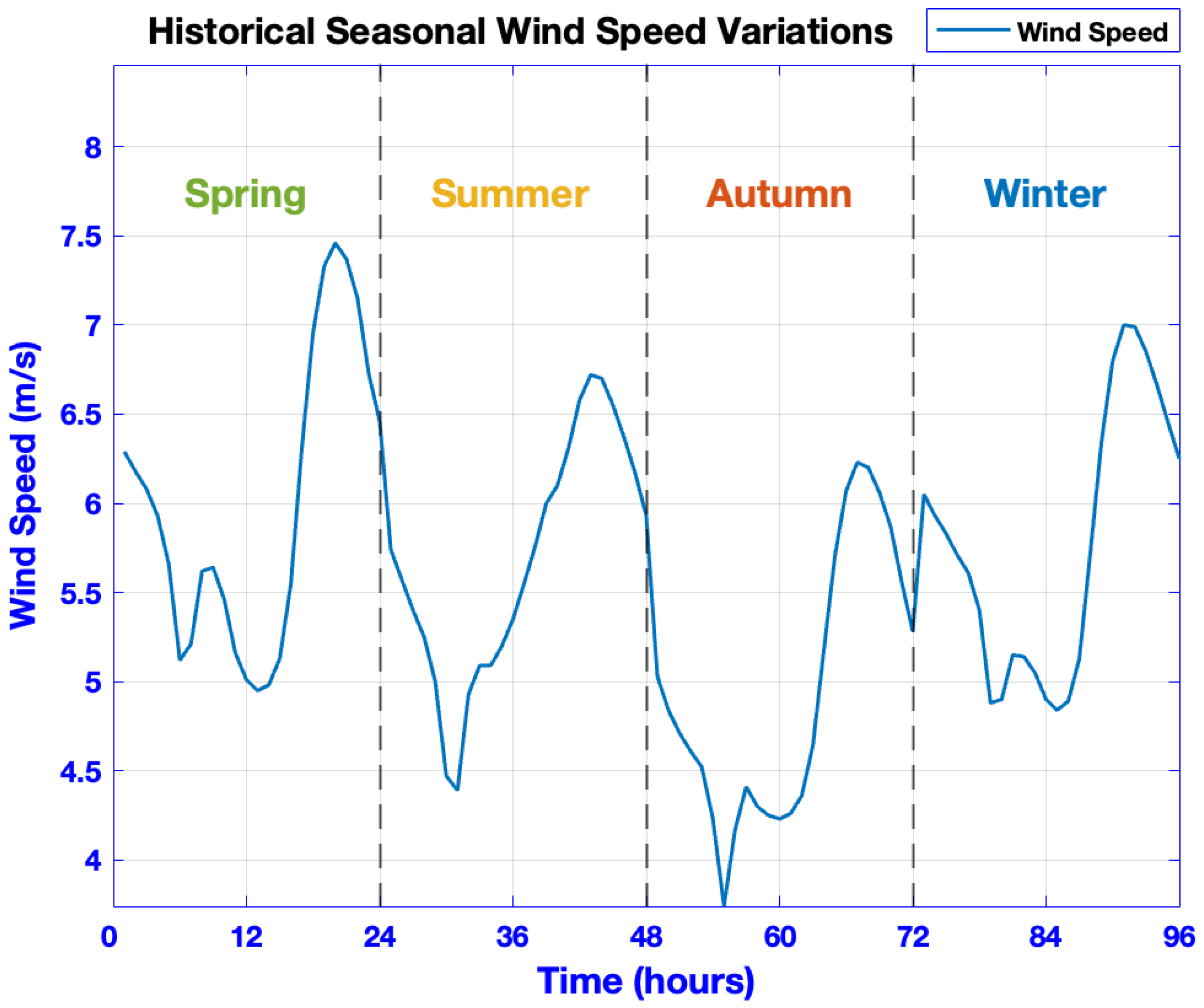
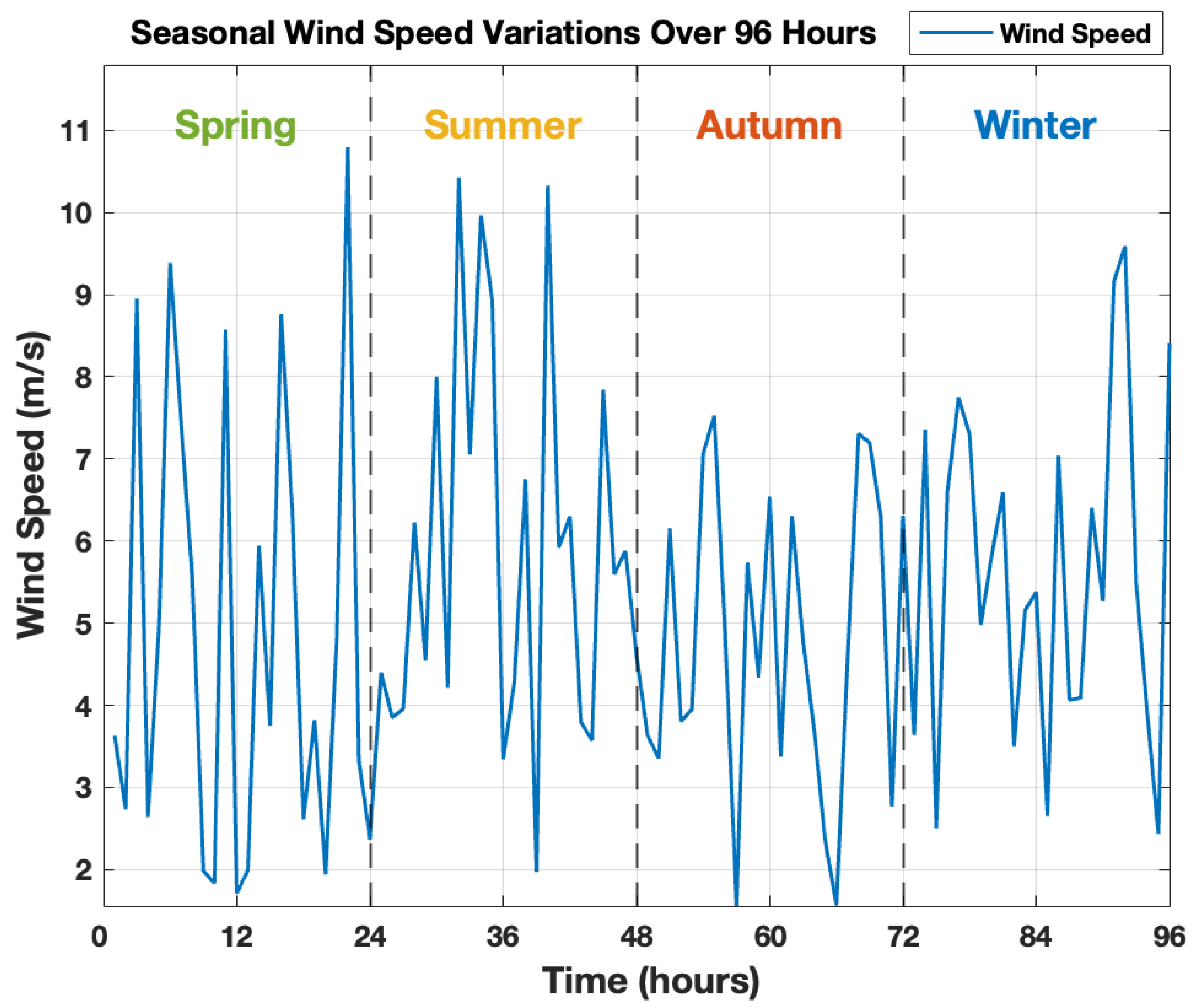
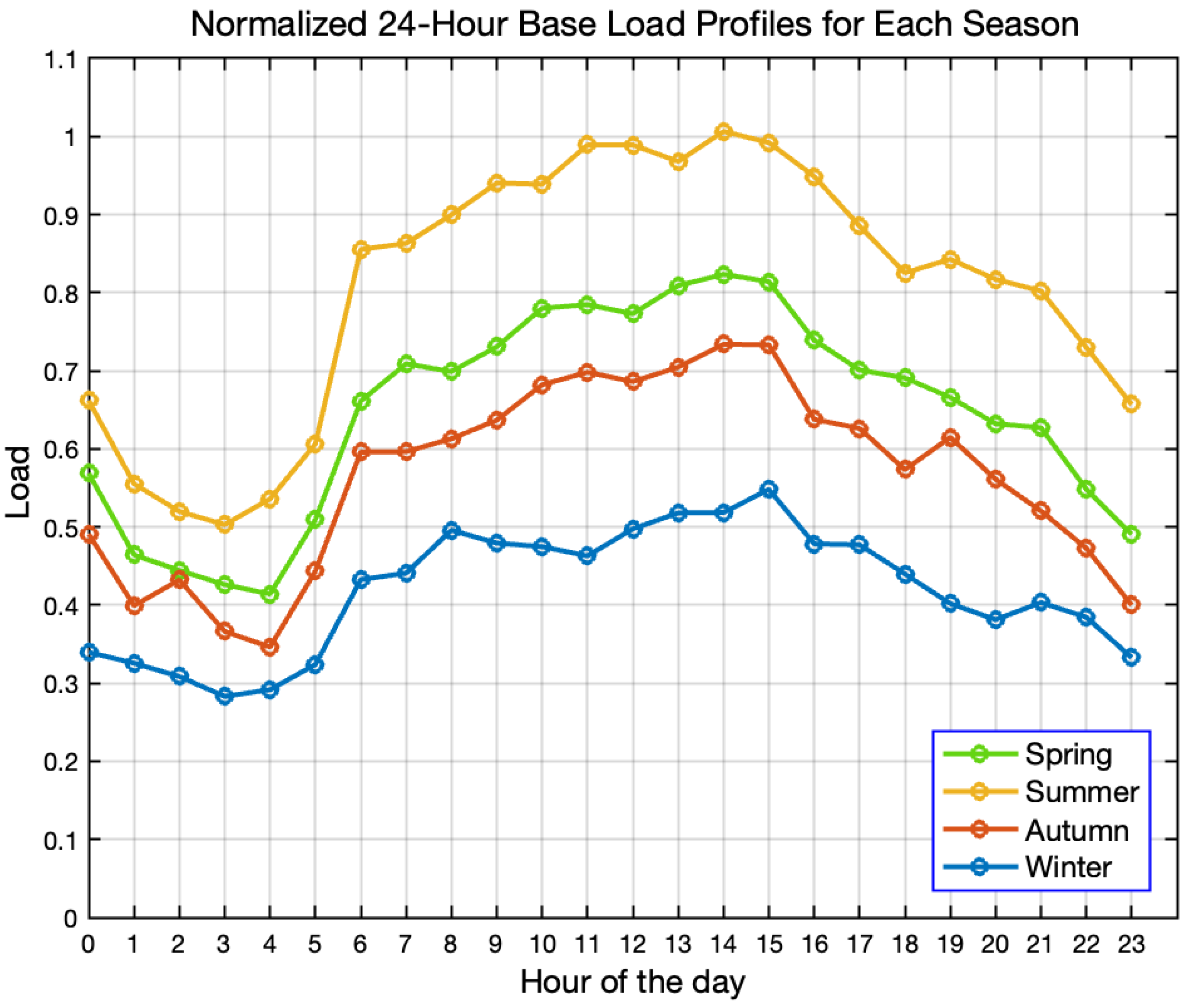
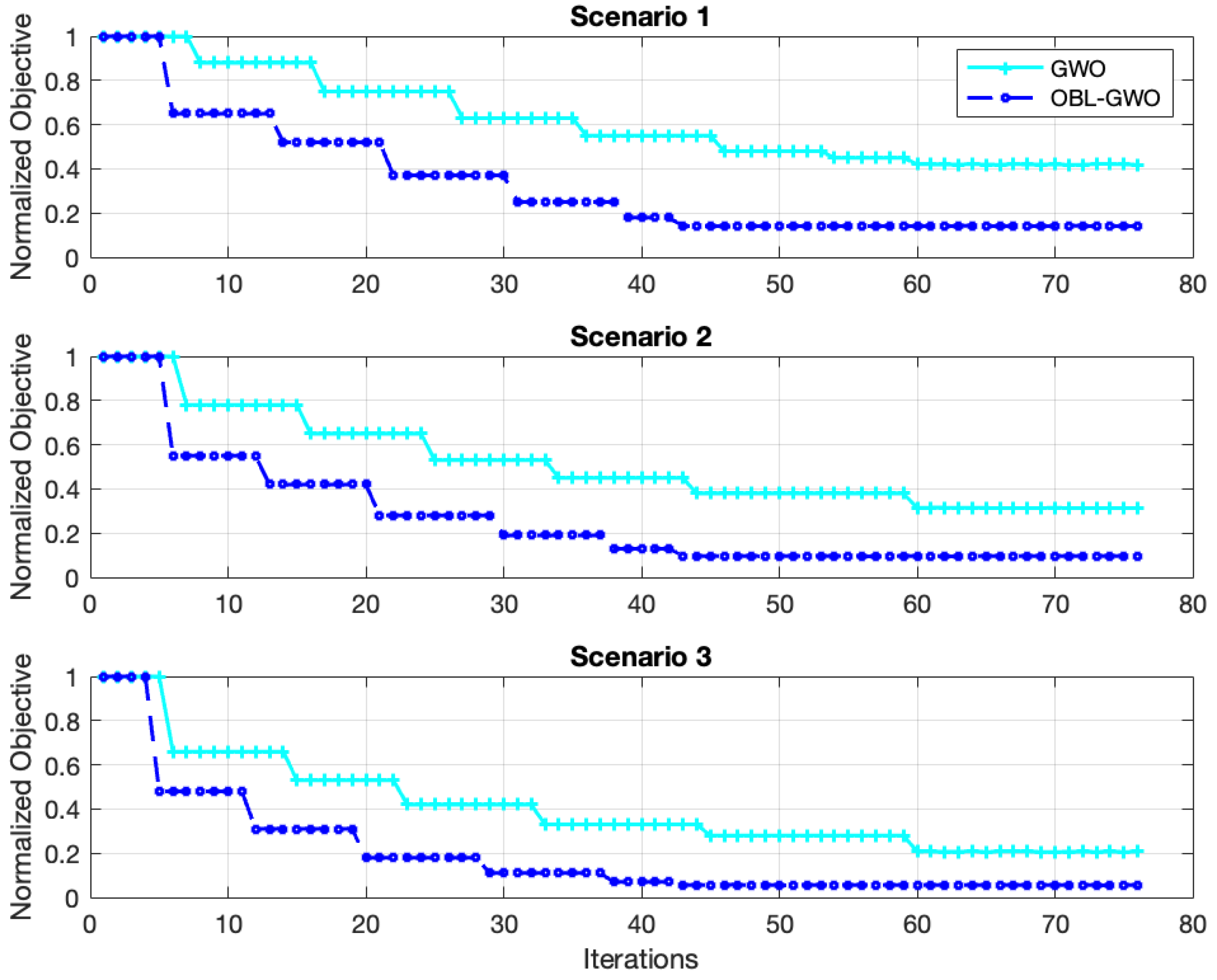
The above scrutiny of published work identifies gaps in previously reported research for tackling the distribution of DG sizes and locations in DNs. The metaheuristic techniques that predominate in most explorations of DG placement issues exhibit the deficiencies described for GWO. While OBL-GWO has proven effective in allocating PV-DGs, wind-based DGs involve distinct technical and stochastic characteristics. This study evaluates the adaptability and performance of OBL-GWO for optimal wind DG allocation under probabilistic and seasonal conditions. The proposed augmentation of GWO with OBL for wind turbine generation (WTG) positioning addressed the main research gap. While not ensuring a global optimum solution, the developed methodology generates outcomes superior to reported results obtained from recognized optimization methods. An additional notable gap was uncovered: lack of real-world weather or demand data included in prior modeling, which failed to encapsulate important dimensions related to seasonal variability, a factor that should be examined in analyzing the stochasticity and uncertainty associated with both generation and demand. The aim was to fill these gaps by optimizing multiple technical objectives: minimized power losses (
) and TVD, improved VSI, and voltage profiles kept within ±5% of allowable limits.
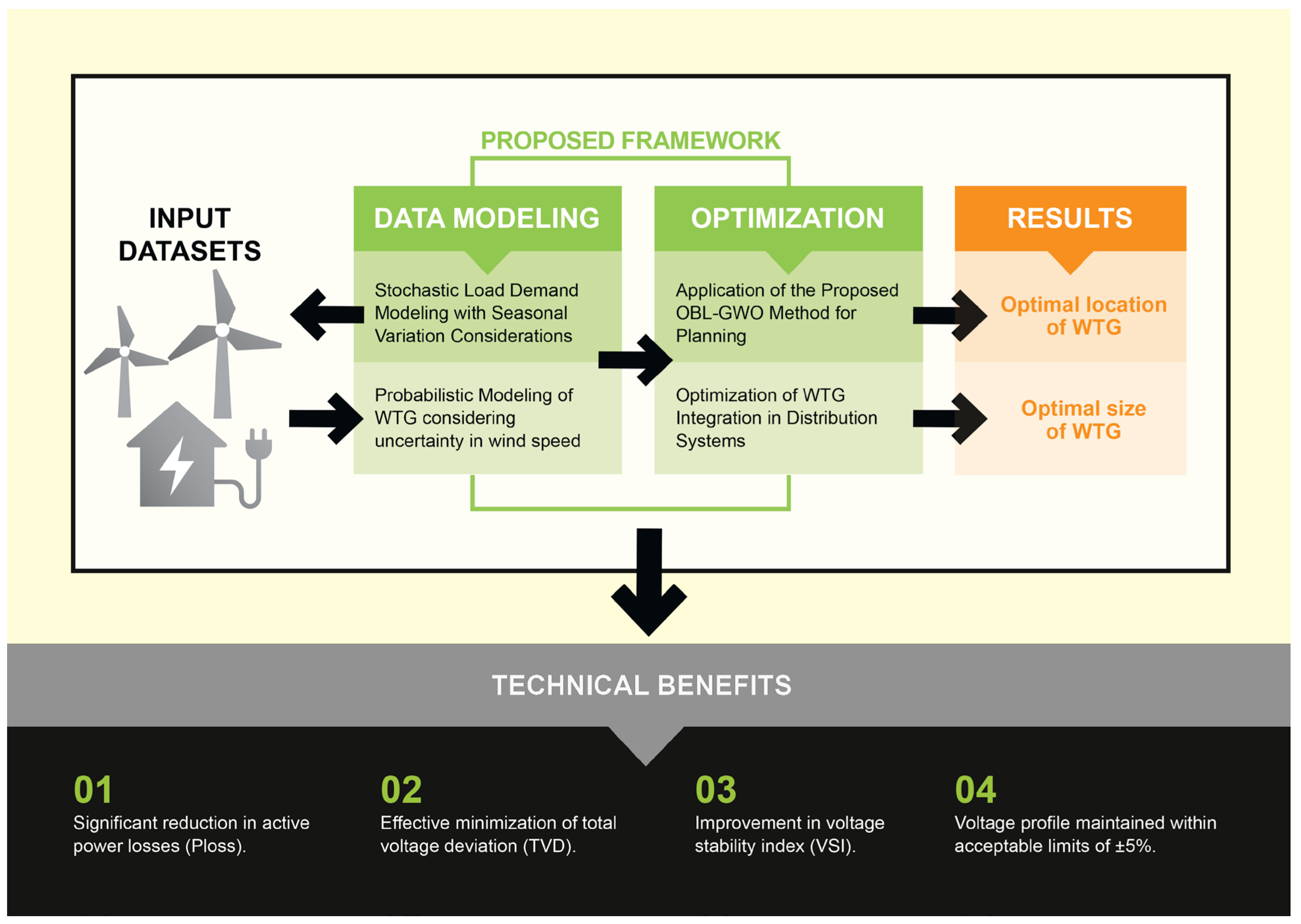
Figure 1 outlines the primary stages of the developed framework and optimization methodology. Real-world operational variations often cause domain shifts that reduce the performance of data-driven diagnostic or optimization models, highlighting the need for adaptive techniques under uncertain conditions [
40].
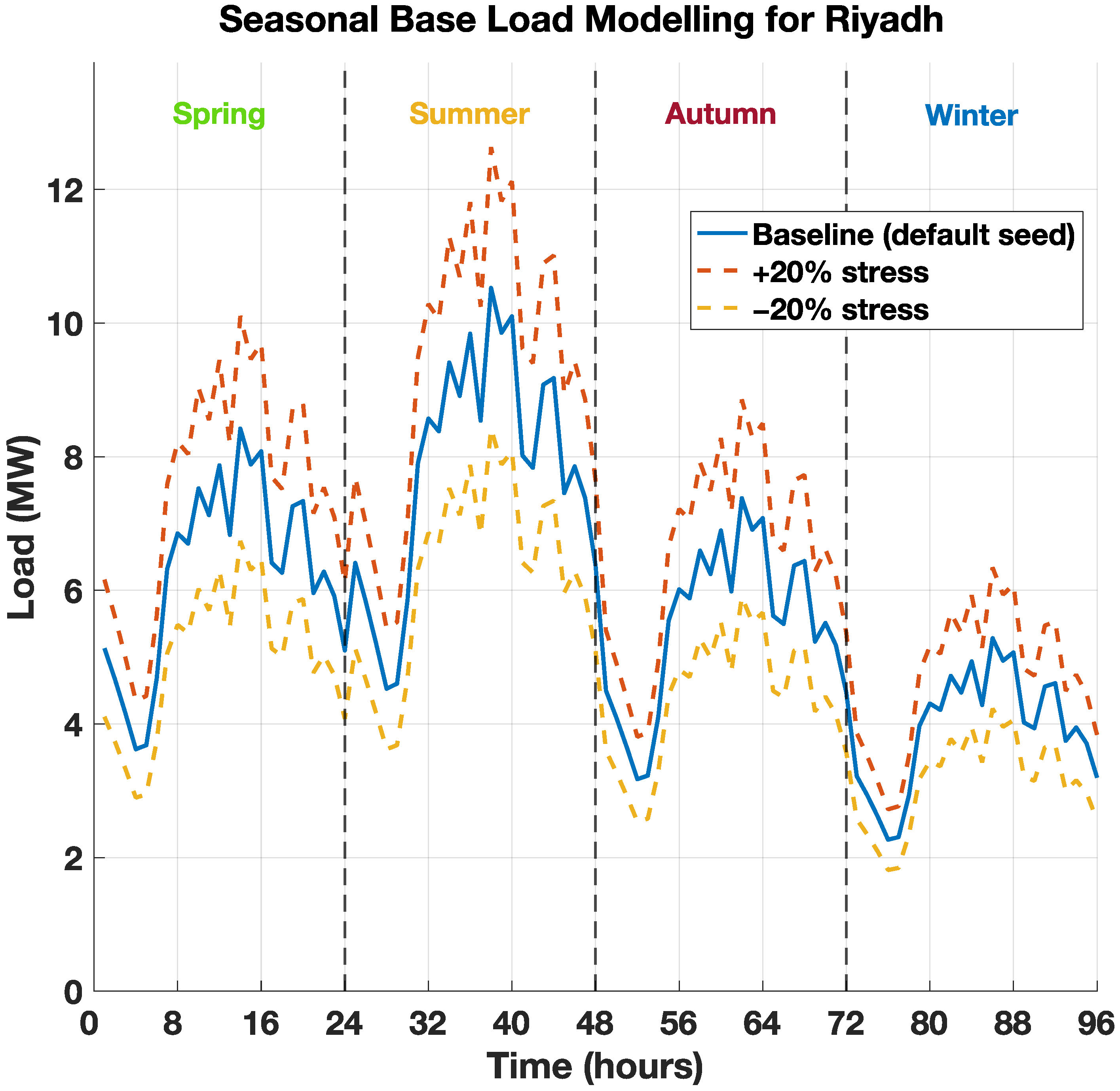
Unlike prior OBL-GWO variants that evaluate on deterministic benchmark functions or generic engineering tests, this work is the first to deploy OBL-GWO for WT siting/sizing in a radial ADN under seasonal stochasticity and multi-year growth. As summarized in
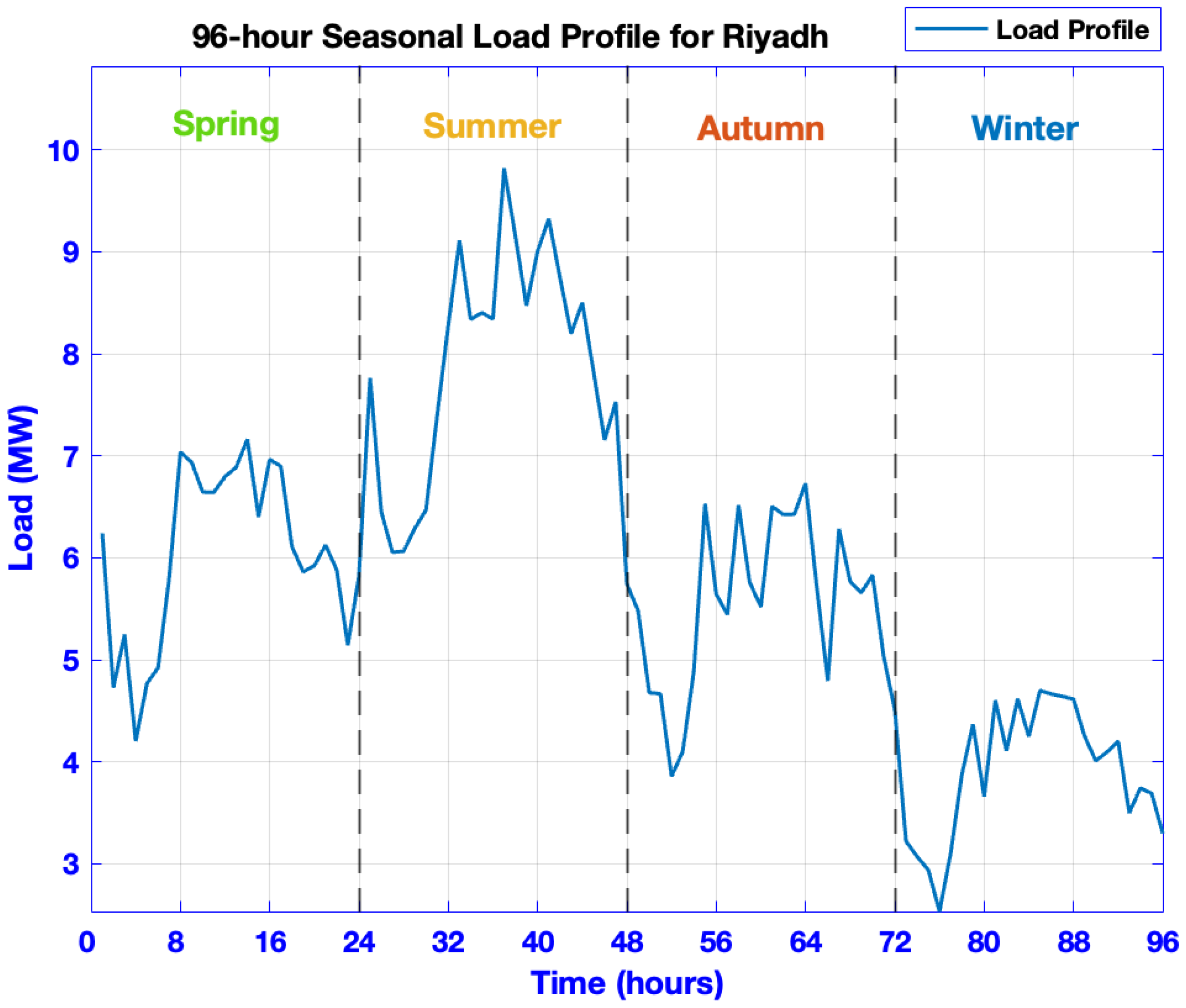
Table 1, we build a 5-year Riyadh wind-and-load database, model seasonal wind via Weibull and stochastic load noise, incorporate demand growth (5.48%/yr over 20 years) into the planning baseline, and validate it on IEEE-33 with multi-objective technical metrics (P
loss, TVD, VSI, and
). Furthermore, the proposed approach has been benchmarked against the standard GWO as well as several widely recognized metaheuristic techniques reported in the literature. The combination of OBL-GWO using real seasonal data and considering load growth in the planning of ADN is, to our knowledge, absent from prior OBL-GWO literature.
The work presented in this paper offers several key contributions, including:
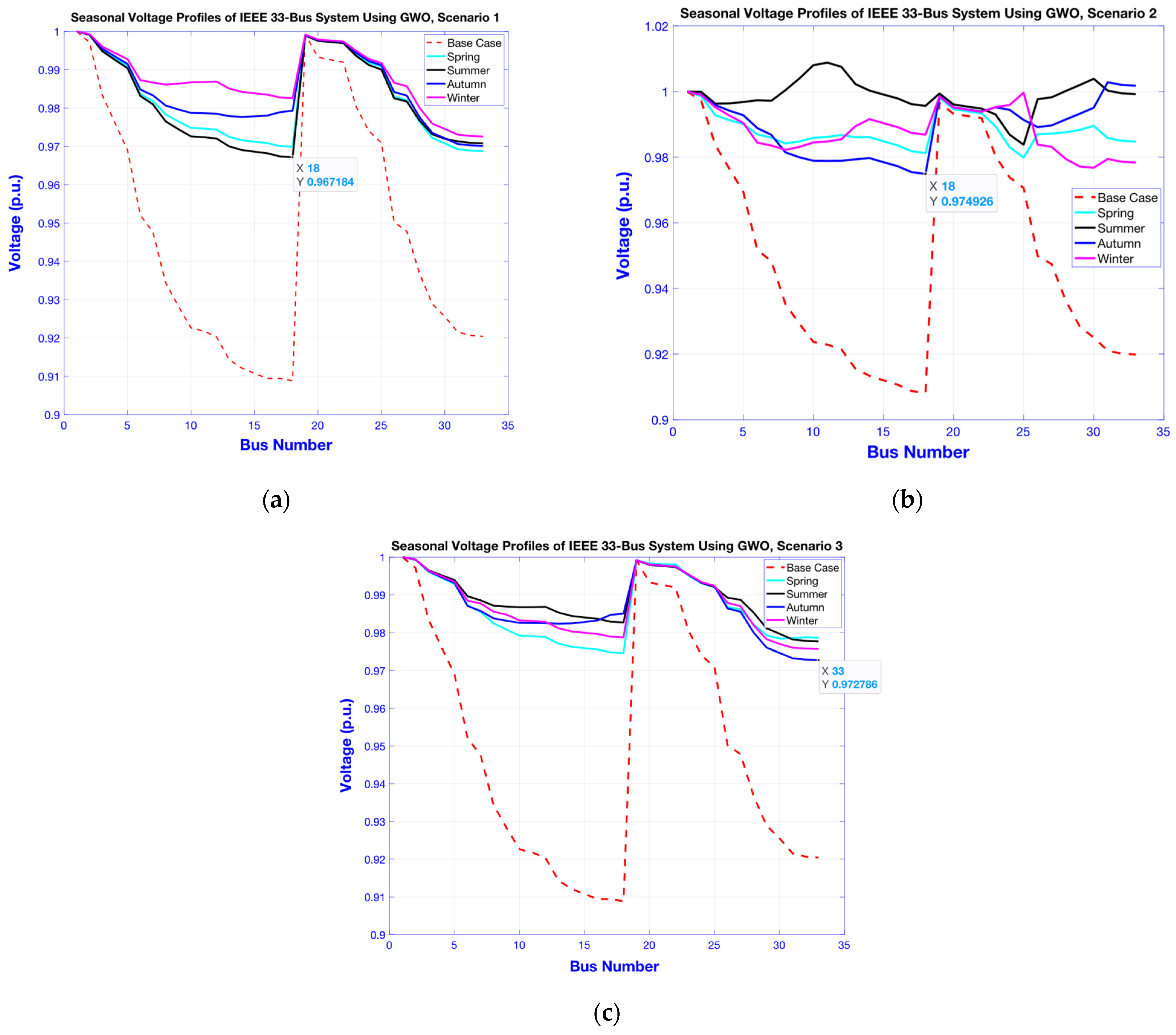
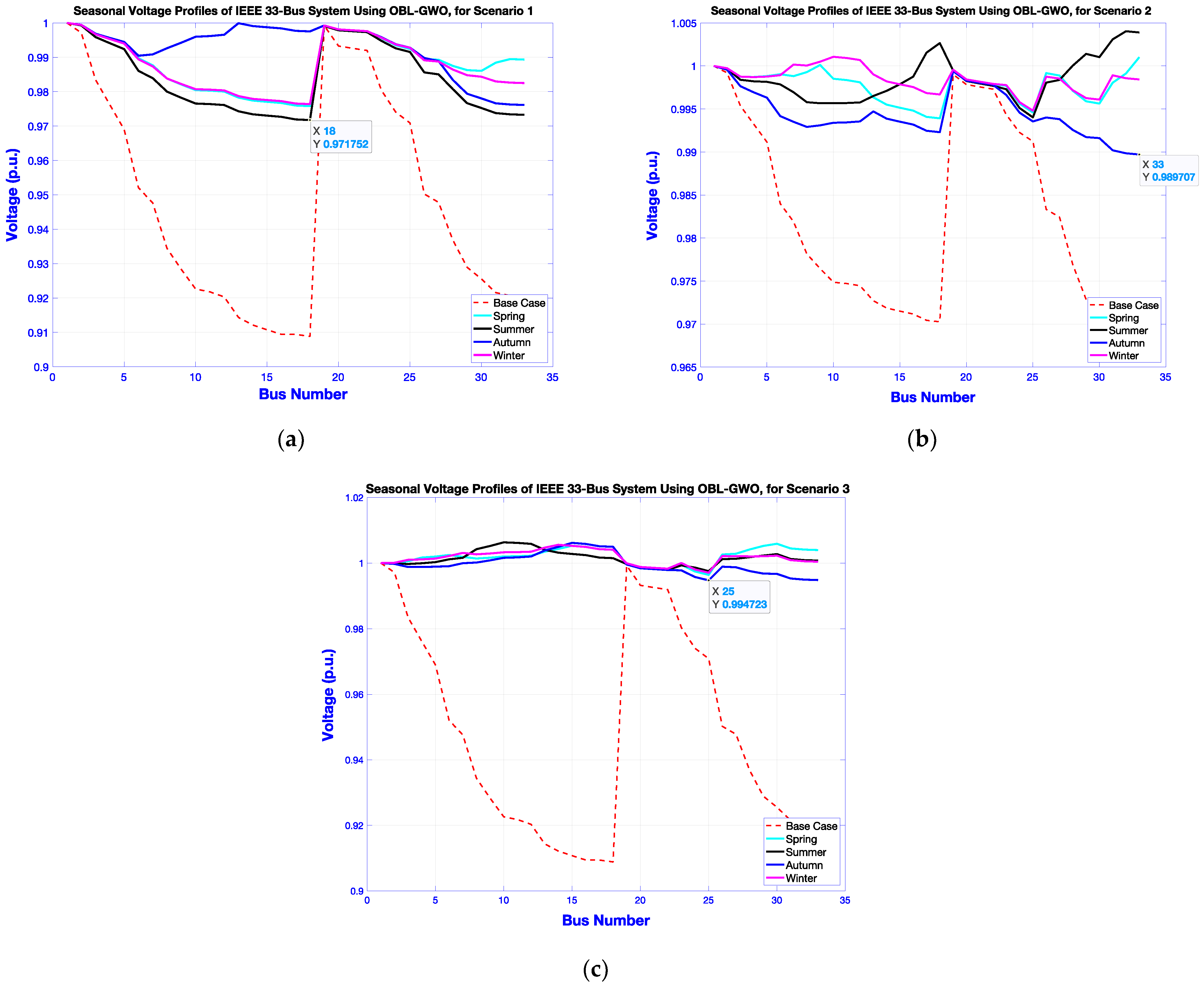
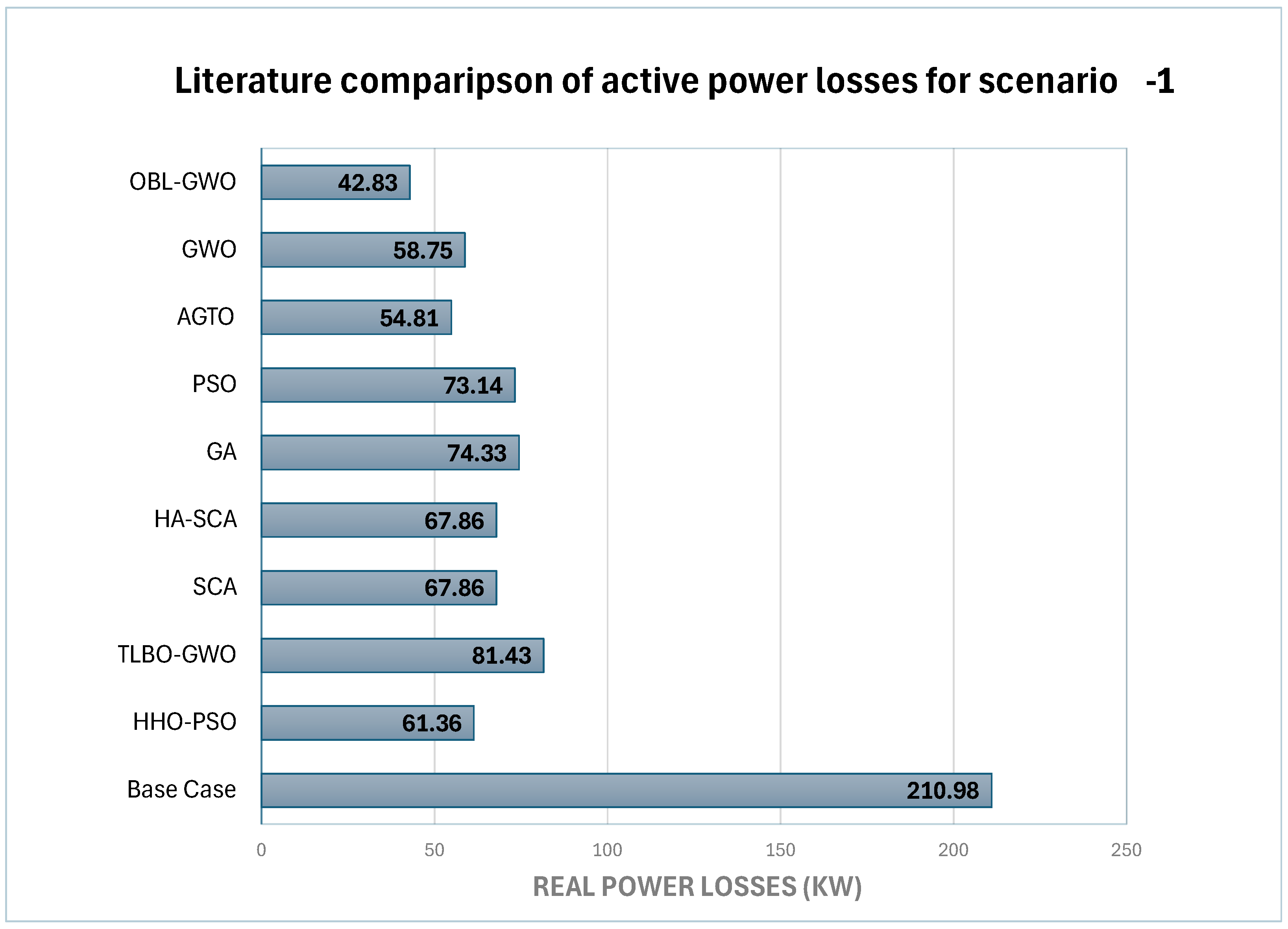
Execution of the OBL-GWO method for optimal allocation of WTG-based DGs in a radial distribution network, achieving up to 95.16% reduction in active power losses compared with the base case and 79.7–95.16% reduction compared with standard GWO across different scenarios.
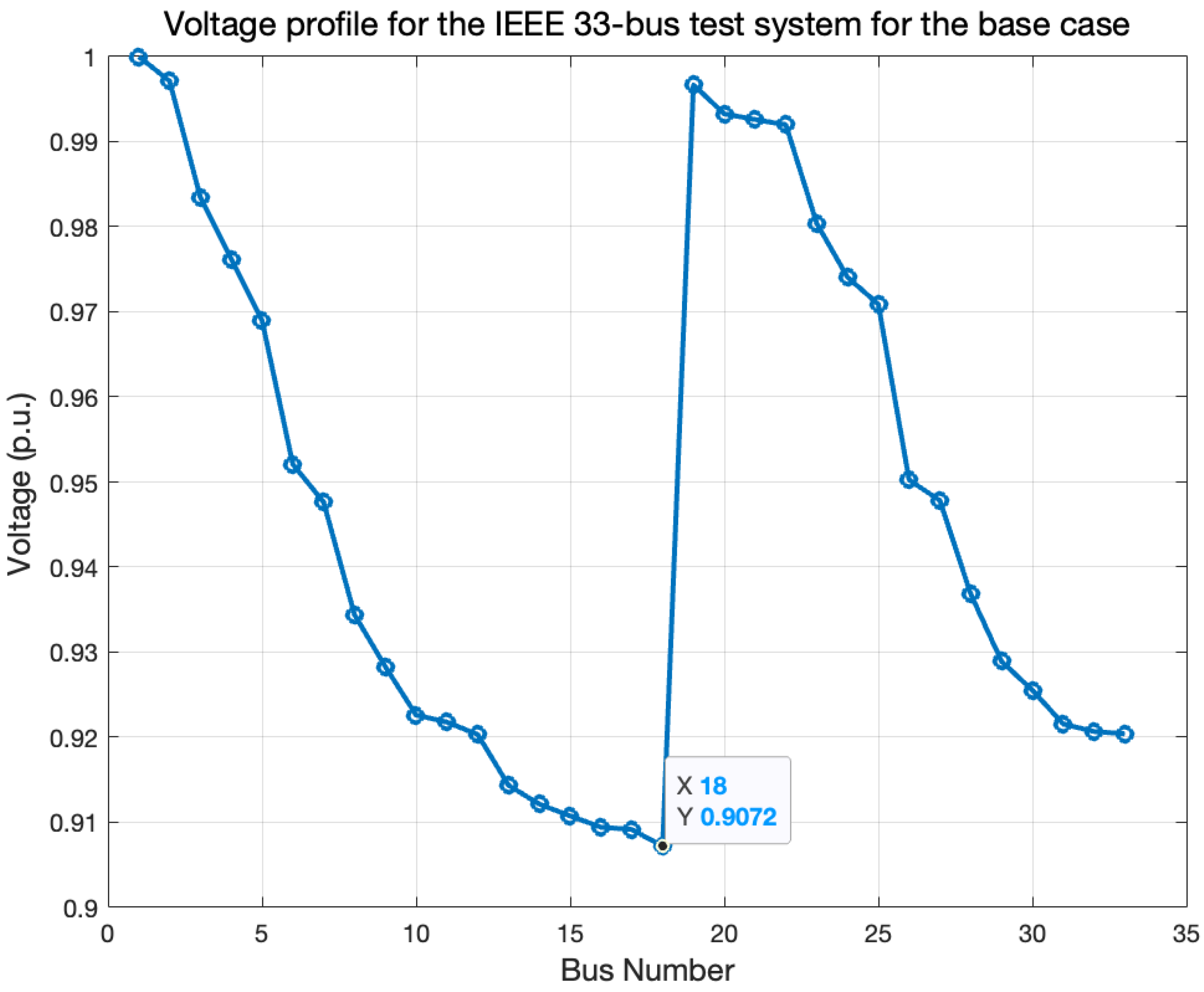
Improvement in TVD by 96–99.7% and enhancement of the VSI by nearly 30%, with the minimum bus voltage raised from 0.907 p.u. (base case) to 0.994 p.u. under the proposed method.
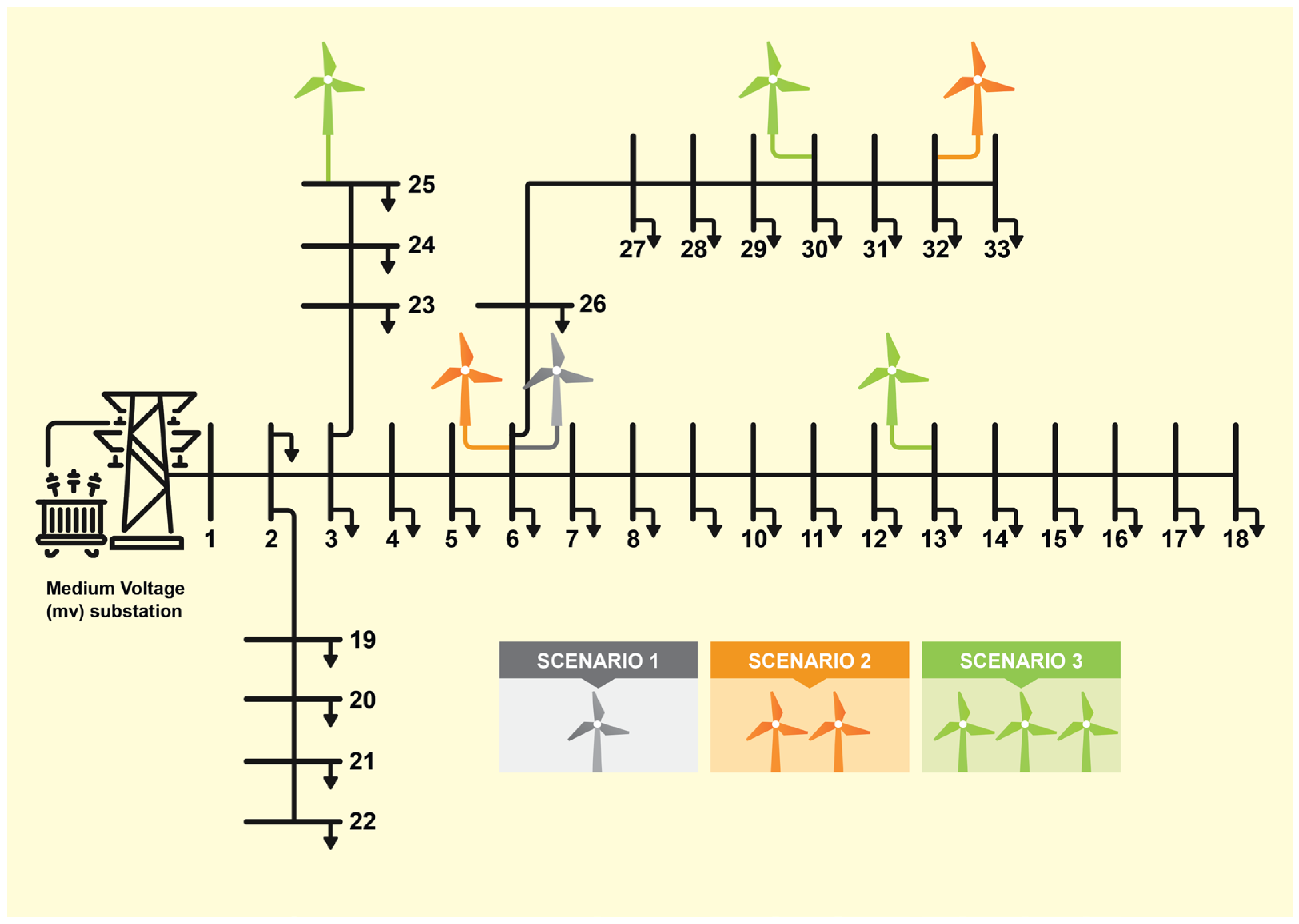
Development and use of a five-year database of actual measurements of wind speed and load profile for Riyadh, Saudi Arabia to capture seasonal variability and stochasticity of both demand and generation for more realistic modeling.
Performance benchmarking and validation of the proposed methodology against benchmark techniques published in the literature using the IEEE 33-bus system across multiple WTG-DG penetration scenarios, confirming superior performance in terms of loss reduction and voltage profile improvement.
4. Multi-Objective Function Formulation
Optimizing the technical benefits of WTG placement in ADNs involved four technical parameters:
,
, TVD, and the VSI. These factors are evaluated simultaneously, alongside compliance with relevant operational constraints, as outlined in the following subsection. The mathematical formulation of the multi-objective function (MOF) is defined in Equation (18) with each factor normalized using the Weighted Sum Method (WSM). Each parameter is divided by its base value for harmonious and viable optimization that enables technical factors to be compared at identical scales, with equal weights assigned, and with balanced compromises among objective functions. This process also keeps the algorithm from being dominated by objectives with higher absolute values.
where
stands for the MOF, and
,
,
, and
are weighting coefficients for each optimization factor such that the sum of the absolute coefficient values equals 1. Most verification and standardization research has involved WSM in which the weighting coefficients are divided equally. The four weights were thus fixed at 0.25 each, to be later modified according to decision-maker or planner preferences. To verify robustness, we have tested additional weight samples, such as (0.40, 0.40, 0.10, 0.10) and (0.10, 0.10, 0.40, 0.40) to emphasize loss reduction and voltage stability, respectively. As shown in
Table 4, varying the weights did not change the scenario ranking or optimal locations. It only shows marginal shifts in objective values, confirming robustness of the default equal weighting.
The set values , , , and designate the system performance metrics of the IEEE 33-bus base case. , , , and respectively denote the objective functions for , TVD, and VSI, which are detailed below.
Results showed that only marginal shifts in optimal locations and sizes, with all cases preserving the same ranking of scenarios and significant improvements over the base case. This indicates that the chosen equal weighting does not bias the conclusions. It should be noted that weighted-sum formulations automatically turn multiple objectives into a single scalar value. This can make it difficult to see the whole Pareto front and miss out on trade-off solutions. However, in this study the objectives were found to be largely aligned, making the equal-weight WSM formulation adequate for practical ADN planning.
4.1. System Constraints
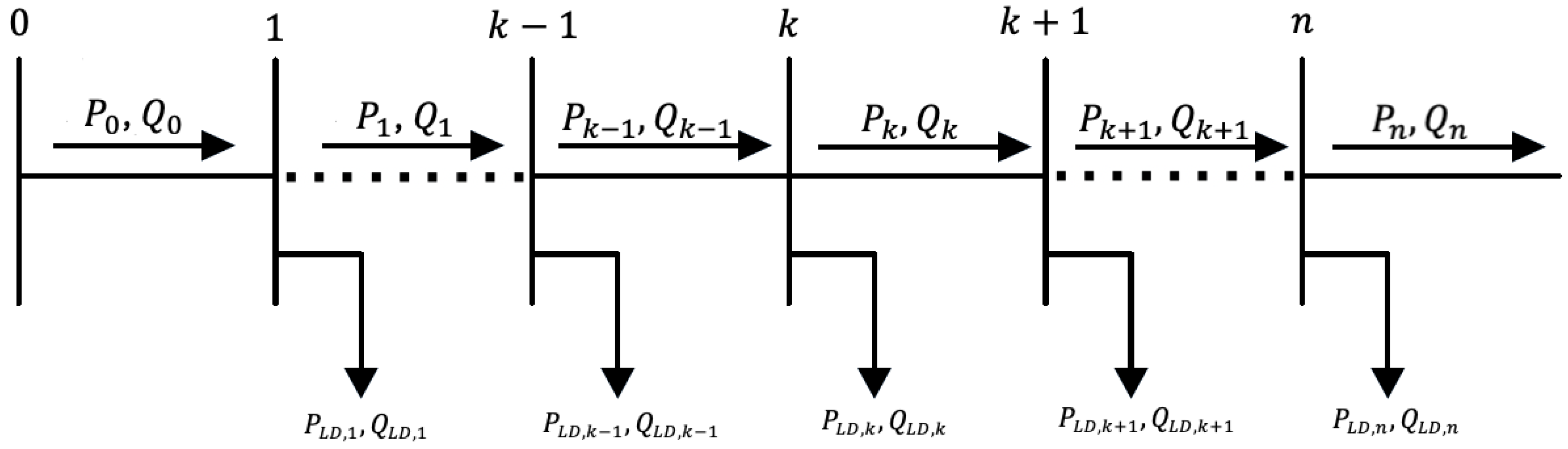
For the best DN operation and planning, several constraints must be in force to guarantee that the system provides reliability and stability within physical and operational limits. These restrictions are essential for specifying the feasible solution space for optimization problems, especially for DG positioning and sizing. The main system constraints examined in this study are detailed below: power balance, voltage, current, DG capacity, DG location, and DG power factor. The methodology for confirming the system’s operational viability through power flow calculations is also described.
4.1.1. Power Balance Constraint
Power flow analysis requires that a mandatory equality constraint termed power balance be fulfilled as a means of ascertaining that demand power plus power losses equate to total generation. This balance must be satisfied for both active and reactive power elements, as detailed in Equation (19) and Equation (20), respectively, [
51]:
where
k denotes the number of DGs;
and
represent bus and branch numbers;
and
indicate the respective reactive and active power injected by the main substation; and
and
stand for the reactive and active power, respectively, produced by the
DG.
4.1.2. Voltage Constraints
The purpose of voltage constraints is to verify that voltage magnitude
at any bus
i is within
of the RDN rated voltage. As set out in Equation (21), in per unit calculations, this figure falls between a
value of 0.95 p.u. and a
value of 1.05 p.u.; Voltage deviations outside 0.95–1.05 p.u. are penalized using a quadratic penalty function. A soft violation within 0.90–0.95 or 1.05–1.10 p.u. incurs a moderate penalty (10
2), while violations beyond 0.90–1.10 p.u. incur a large penalty (10
4), effectively restoring feasibility.
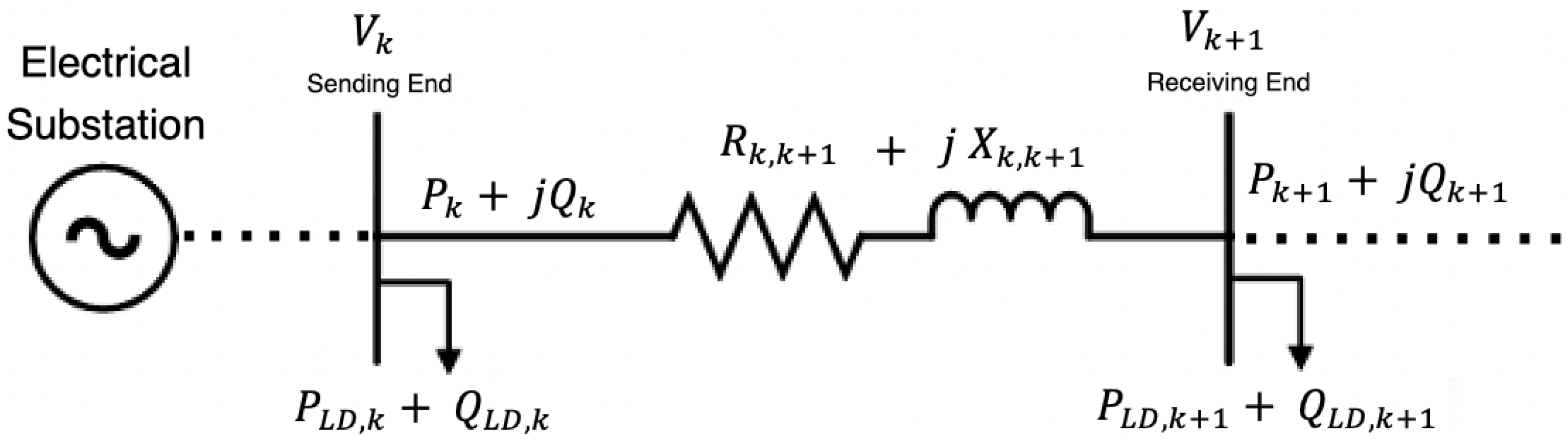
4.1.3. Branch Current Constraints
Line overloads were penalized proportionally to the overload percentage. Exceeding the thermal limit by 1% incurred a linear penalty scaled by 10
3, which grows with the severity of the violation. To fulfill current or thermal limits, the branch current
between nodes
and
cannot be greater than that branch’s maximum capacity
as stipulated in Equation (22):
4.1.4. DG Capacity Constraints
Starting DG capacity is specified according to explicit minimum and maximum active and reactive power output capacities, respectively, as detailed in Equations (23) and (24) [
38]. The minimum–maximum generation bounds for each DG were defined such that the total installed DG capacity does not exceed 100% of the IEEE 33-bus system base capacity, corresponding to an upper limit of 3.715 MVA. Solutions proposing DG capacities outside the specified min–max bounds were discarded by assigning a fixed penalty (10
5), ensuring only feasible DG sizes remained. The achieved total DG capacities per scenario are reported in the results tables and show that the optimal solutions did not reach this upper bound. This ensures penetration remains realistic without artificially limiting the feasible search space.
4.1.5. DG Location Constraints
The limit expressed in Equation (25) prevents a DG unit from being installed at the slack bus (bus #1) since it serves as the slack bus. Equation (26) allows no more than a single DG to be placed at any individual bus, all while still adhering to the restriction on the maximum number of buses:
where
and
indicate the position of the
th and
th DG,
is the number of buses.
4.1.6. DG Power Factor Constraints
When the optimal DG power factor must be established, to make certain that DG units are operating productively, the power factor is restricted to an upper limit of 1 and a lower limit of 0.9, as defined in Equation (27). Further, we have assumed that DGs are constrained to operate within 0.9 ≤ PF ≤ 1.0, indicating unity to lagging operation. This assumption ensures that DGs are primarily expected to inject active power while providing limited reactive power support (Q > 0). Leading PF operation (absorbing reactive power) was not included. The PF was assumed to be fixed during optimization rather than dynamically scheduled on an hourly basis. Moreover, power factor violations below 0.9 were penalized linearly with a weight of 10
3, ensuring that the optimizer always converged to feasible PF values within the 0.9–1.0 range.
To enforce these operational limits during optimization, a penalty-based constraint handling mechanism was adopted. For any candidate solution, violations of voltage, branch current, DG capacity, DG location, or DG power factor constraints were translated into additive penalty terms. Equation (28) represents the overall penalized objective function:
where
is our main multi-objective function, ΔV, ΔI, and ΔPF denote the respective violations,
is the number of location violations, and α values (
) are empirically tuned penalty coefficients (with α = 10
2 for voltage, α = 10
3 for current, and α = 10
5 for DG penetration in the reported runs). This formulation used to ensure that infeasible solutions are assigned sufficiently large penalties to restore feasibility while preserving search efficiency.